Forecasting Multi-Wave Epidemics Through Bayesian Inference

Abstract

We present a simple, near-real-time Bayesian method to infer and forecast a multiwave outbreak, and demonstrate it on the COVID-19 pandemic. The approach uses timely epidemiological data that has been widely available for COVID-19. It provides short-term forecasts of the outbreak’s evolution, which can then be used for medical resource planning. The method postulates one- and multiwave infection models, which are convolved with the incubation-period distribution to yield competing disease models. The disease models’ parameters are estimated via Markov chain Monte Carlo sampling and information-theoretic criteria are used to select between them for use in forecasting. The method is demonstrated on two- and three-wave COVID-19 outbreaks in California, New Mexico and Florida, as observed during Summer-Winter 2020. We find that the method is robust to noise, provides useful forecasts (along with uncertainty bounds) and that it reliably detected when the initial single-wave COVID-19 outbreaks transformed into successive surges as containment efforts in these states failed by the end of Spring 2020.

1 Introduction

At the time of writing this paper, in December 2020, the US is deep in the throes of the Fall wave of the COVID-19 pandemic. Over the last 8 months, many COVID-19 models e.g., Ref. [14], have been used to forecast the spread of the disease and the consequent demand for medical resources (Ref. [3]). In fact, models and the data that they are built on, have played a central role in forecasting the spread, and consequently preparing for it (see Ref. [4]), and have become the topic of news reporting (e.g., Ref. [5]). It would be safe to say that the abundance of COVID-19 data (newly detected cases, as well as deaths; see Ref. [2]), coupled with models, have been widely used to understand the COVID-19 pandemic and its multiple waves.

In this paper, we develop a methodology by which we can provide short-term forecasts (about 10 days ahead) of COVID-19 evolution, which can then be used for medical planning e.g., hospital demand and logistics. In the current context, this implies an outbreak with multiple waves, each with a potentially different cause. Our focus is on providing accurate, actionable predictions in a timely manner, using the latest available data and without using specialized computational resources, so that such forecasts may be computed daily, and for a multitude of regions. Such modeling efforts do exist (as in Ref. [9, 10]), and some are quite well-known (see Ref. [3, 14]). Such a forecasting and planning methodology requires some quantification of the trustworthiness of the forecasts so that appropriate hedges and margins may be included in resource planning and logistics. Finally, it is also helpful for such a methodology to herald the arrival of a new, if incipient, surge/wave of infections, as it indicates the failure of containment efforts. Our methodology provides both these capabilities.

The construction of a near-real-time forecasting technique, predicated on timely COVID-19 data, poses a few challenges, especially if multiple waves are expected. Multiple waves in the current epidemic have been driven by increased social mixing caused by lockdown-exhaustion (see Ref. [10]) or the premature opening of the economic activity, followed by flouting of social-distancing rules and super-spreading (e.g., Ref. [16]). However, there are no direct ways of measuring social mixing in near-real-time. Mobility of a population can be measured quite promptly using mobile phone data, but that is an indirect measure of social mixing - coupled with proper social distancing and other precautions, a mobile population need not spread a disease. The frequenting of restaurants, bars and indulgence in other social activities is a reliable proxy of social mixing, but collecting real-time quantitative data is difficult. Thus a disease model that relies on information on social mixing (or enhanced disease transmission because of it) often has difficulties in predicting the start of a new wave of infections.

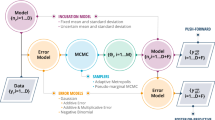
One way of circumventing these difficulties is to postulate an unseen, parameterized infection rate curve (i.e., number of people infected every data), with multiple waves if need be, and infer the infection rate from observed data (a time-series of detected cases, as available in repositories such as Ref. [2]). Such a model, for a single wave, was developed by the authors in Ref. [21]. It used Bayesian inference to estimate the parameters of the infection rate curve as a probability density function, to capture the shortcomings of the estimation process. This infection rate curve, in conjunction with a disease model (specifically, just the incubation period distribution of COVID-19) could be used to provide short-term probabilistic forecasts of the evolution of COVID-19 i.e., provide bounds on the trustworthiness of the forecasts. The inference and forecasting process is computationally fast, taking less than one hour to process regional data. The model, extended to a multiwave outbreak, would satisfy all the prerequisites of a near-real-time forecasting and planning system for COVID-19 and is the topic of this investigation. It is conceptually simple, as it only requires us to postulate a parameterized, multi-wave infection-rate curve, but poses a few practical challenges:

• The observed data is noisy and could, erroneously, indicate the arrival of a new surge, which could then disappear as more data became available. Not being able to reliably decide such a fundamental aspect of an outbreak could seriously erode trust in any modeling effort. Thus there needs to be a rigorous method to select the number of waves to include in the infection rate curve, with is then used for forecasting purposes.

• A multiwave infection rate curve will be complex i.e., have many parameters, and may be difficult to infer from noisy observable data. However, if the parameters admit a natural partitioning e.g., if a subset of parameter control the first wave, it may be possible to infer the multiwave infection rate curve piecemeal, using subsets of the observed data.

In this paper, we develop solutions to these practical difficulties, and extend our original one-wave model to three waves. We address the question of the number of waves to include in the infection rate curve by model selection i.e., we fit one- and multi-wave models to data and select between them using information-theoretic criteria. Finally, we exploit the “partition-able” nature of the infection rate curve’s parameters to infer them piecemeal, with the novelty lying in the method by which we use previous inferences to formulate empirical priors for a high-dimensional estimation problem. These priors stabilize the inverse problem and accelerate the computations, thus making the inferences feasible, practical and scalable to a multi-wave epidemic.

The paper is structured as follows. In Sect. 2, we review our previous model, and in Sect. 3, we introduce the data. The new model and numerical algorithm are described in Sect. 4, which are them proven on two- and three-wave COVID-19 outbreaks, using data from New Mexico, California and Florida. Discussions and conclusions, which follow thereafter, complete the paper.

2 Modeling Approach

We present here an epidemiological model to characterize and forecast the rate at which people turn symptomatic from disease over time. The model is an extension of previous work by Safta et al [21] for a single infection wave to epidemics exhibiting multiple infection waves. For the purpose of this work, we assume that once people develop symptoms, they have ready access to medical services and can be diagnosed readily. From this perspective, these forecasts represent a lower bound on the actual number of people that are infected with COVID-19 as the people currently infected, but still incubating, are not accounted for. A fraction of the population infected might also exhibit minor or no symptoms at all and might not seek medical advice. Therefore, these cases will not be part of patient counts released by health officials. The epidemiological model consists of two canonical elements: an infection rate model and an incubation rate model. One or more infection rate models are then combined through a convolution with the incubation rate model to yield the number of cases that turn symptomatic daily. We briefly describe below the mathematical formulation for the single wave model, followed by a description of the multiple wave approach. For more details on the single wave model the reader is refered to Ref. [21]. Finally, some considerations for the data used to fit the models are discussed in this section

2.1 Single Wave Model

The single wave model consists of an infection rate component convolved with information about the incubation rate once a person is infected. The infection rate model is given by [21]

$$\begin{aligned} f_\Gamma (t;k,\theta ,t_0)=\theta ^{-k}(t-t_0)^{k-1}\exp (-(t-t_0)/\theta )\big /\Gamma (k) \end{aligned}$$

(1)

where $f_\Gamma (\cdot )$ it the probability density function (PDF) of the gamma distribution, with shape k and scale $\theta$ parameters strictly positive. The time parameter $t_0$ represents the start of the epidemic. The choice of values for the pair $(k,\theta )$ can accomodate both sharp increases in the number of infections, which would correspond to strained medical resources, as well as weaker gradients corresponding to a smaller pressure on the available medical resources.

The results presented in this paper employ a lognormal incubation distribution for COVID-19 [17]. The PDF, $f_{LN}$, and cumulative distribution function (CDF), $F_{LN}$, of the lognormal distribution are given by

$$\begin{aligned} f_{LN}(t;\mu ,\sigma )=\frac{1}{t\sigma \sqrt{2}}\exp \left( -\frac{(\log t-\mu )^2}{2\sigma ^2}\right) \end{aligned}$$

(2)

$$\begin{aligned} F_{LN}(t;\mu ,\sigma )=\frac{1}{2}\mathrm {erfc} \left( -\frac{\log t-\mu }{\sigma \sqrt{2}}\right) \end{aligned}$$

(3)

In this work we model the mean $\mu$ as Student’s t distribution with $n=36$ degrees of freedom which provided the closest agreement for the 95% CI with the data in Ref. [17]. Similarly, the standard deviation $\sigma$ is assumed to have a chi-square distribution. The resulting 95% CIs are [1.48, 1.76] and [0.320, 0.515] for $\mu$ and $\sigma$, respectively.

With these assumptions the number of people infected and with completed incubation period at time $t_i$ can be written as a convolution between the infection rate and the cumulative distribution function for the incubation distribution [8, 20, 22]

$$\begin{aligned} N_i =N\int _{t_0}^{t_i} f_\Gamma (\tau -t_0;k,\theta ) F_{LN}(t_i-\tau ;\mu ,\sigma )d\,\tau \end{aligned}$$

(4)

where N is the total number of people that will be infected throughout the epidemic. This formulation assumes independence between the calendar date of the infection and the incubation distribution. Using Eq (4), the number of people developing symptoms in the time interval $t_{i-1},t_i$ is computed as

$$\begin{aligned} n_i\approx N(t_i-t_{i-1})\int _{t_0}^{t_i} f_\Gamma (\tau -t_0;k,\theta ) f_{LN}(t_i-\tau ;\mu ,\sigma )d\,\tau \end{aligned}$$

(5)

Here, we approximate the difference $F_{LN}(t_i-\tau ;\mu ,\sigma )-F_{LN}(t_{i-1}-\tau ;\mu ,\sigma )$ as

$$\begin{aligned}&F_{LN}(t_i-\tau ;\mu ,\sigma )-F_{LN}(t_{i-1}-\tau ;\mu ,\sigma ) \approx \nonumber \\&\quad (t_i-t_{i-1})f_{LN}(t_i-\tau ;\mu ,\sigma ) \end{aligned}$$

(6)

Numerical tests (results not shown) indicate that this approximation has a negligible impact on the model inference results presented in this paper. Ref [21] provides more details for the single wave model.

2.2 Multiple Wave Model

The multiple wave model is an extension of the single wave model presented in the previous section. In this paper, a set of infection curves are superimposed to model the evolution of the epidemic that exhibits multiple peaks in several countries and regions in US. The resulting model has can be written as

$$\begin{aligned} n_i=&\int _{t_0}^{t_i} \left( \sum _{j=1}^K N_j f_\Gamma (\tau -t_0-\varDelta t_j;k_j,\theta _j) \right) \nonumber \\&\times \left( F_{LN}(t_i-\tau ;\mu ,\sigma )-F_{LN}(t_{i-1}-\tau ;\mu ,\sigma )\right) d\,\tau \end{aligned}$$

(7)

where $N_j$ is the number of people infected by wave j, while $k_j$ and $\theta _j$ are the shape parameters for wave j. The multiwave model has an additional parameter, $\varDelta t_j$, which represents the time in days between $t_0$ and the start of wave j. By definition, $\varDelta t_1=0$. The one wave model can be recovered from Eq. (7) by setting $K=1$.

As for the one wave model, we can approximate the CDF difference term using the PDF, leading to an expression for the multiple wave model analogous to Eq (5)

$$\begin{aligned}&n_i\approx (t_i-t_{i-1}) \int _{t_0}^{t_i} \left( \sum _{j=1}^K N_j f_\Gamma (\tau -t_0-\varDelta t_j;k_j,\theta _j) \right) \nonumber \\&\quad \times f_{LN}(t_i-\tau ;\mu ,\sigma )d\,\tau \end{aligned}$$

(8)

3 Data

The number of people developing symptoms daily $n_i$, computed through Eqs. (7), or  (8) are compared to data obtained from several sources at the national, state, or regional levels. We found that, for some states or regions, the reported daily counts exhibited a significant amount of noise. This is caused by variation in testing capabilities and sometimes by how data is aggregated from region to region. To filter the noise observed in daily case count data, we make use of 7-day rolling averages. We chose this rolling average because it is often used by governments and media outlets to present data on Covid-19 cases, hospitalizations, and deaths. Time series of daily counts ${\varvec{y}}$ (unfiltered) and $\hat{{\varvec{y}}}$ (filtered) for two states are presented in Fig. 1. For the remainder of this paper we will only use filtered data to infer epidemiological parameters. For notational convenience, we will drop the hat and refer to the filtered data as ${{\varvec{y}}}$.

Fig. 1

Daily confirmed cases of COVID-19 aggregated at state level, shown in black symbols, and the corresponding 7-day averaged data shown with red lines and symbols

4 Statistical Methodology

Given data, ${\varvec{y}}$, in the form of time-series of daily counts and the model predictions $n_i$ for the number of new symptomatic counts daily, we will employ a Bayesian framework to calibrate the epidemiological model parameters. The discrepancy between the data and the model is written as

$$\begin{aligned} {{\varvec{y}}} = {{\varvec{n}}}(\varTheta )+\epsilon \end{aligned}$$

(9)

where ${{\varvec{y}}}$ and ${{\varvec{n}}}$ are arrays containing the data and model predictions

$$\begin{aligned} {{\varvec{y}}}=\{y(t_1),y(t_2),\ldots ,y(t_d)\},\,\, {{\varvec{n}}}=\{n_1(\varTheta ),n_2(\varTheta ),\ldots ,n_d(\varTheta )\}. \end{aligned}$$

Here, d is the number of data points, $\varTheta$ is a vector of model parameters, and $\epsilon$ represents the statistical discrepancy between the model and the data. The discrepancy $\epsilon$ is discussed in more detail in Sect. 4.1.

The elements of $\varTheta$ depend on the number of waves being modeled.

$$\begin{aligned} \varTheta =\varTheta ^{(1)}\cup \varTheta ^{(2)}\cup \ldots \cup \varTheta ^{(K)}\cup \varTheta ^{(\epsilon )} \end{aligned}$$

(10)

where $\varTheta ^{(i)}$ are the parameter for the i-th wave of infections, K is the number of waves and $\varTheta ^{(\epsilon )}$ are parameters for the error model, to be discussed in Sect. 4.1. For the first wave, the parameters are the same as for the single wave model

$$\begin{aligned} \varTheta ^{(1)}=\{t_0,N_1,k_1,\theta _1\} \end{aligned}$$

(11)

The parameters for subsequent waves are similar to the first wave set, except the start of the epidemic $t_0$ is replaced by the time shift with respect to $t_0$, i.e.

$$\begin{aligned} \varTheta ^{(i)}=\{\varDelta t_i,N_i,k_i,\theta _i\}\,\,\,i=2,\ldots ,K \end{aligned}$$

(12)

The error model encapsulates, in this context, both errors in the observations as well as errors due to imperfect modeling choices. The observation errors include variations due to testing capabilities as well as errors when tests are interpreted. Values for the vector of parameters $\varTheta$ can be estimated in the form of a multivariate PDF via Bayes theorem

$$\begin{aligned} p(\varTheta \vert {{\varvec{y}}})\propto p({{\varvec{y}}}\vert \varTheta ) p(\varTheta ) \end{aligned}$$

(13)

where $p(\varTheta \vert {{\varvec{y}}})$ is the posterior distribution we are seeking after observing the data ${{\varvec{y}}}$, $p({{\varvec{y}}}\vert \varTheta )$ is the likelihood of observing the data ${{\varvec{y}}}$ for a particular set of values for the model parameters $\varTheta$, and $p(\varTheta )$ encapsulates any prior information available for the model parameters. Bayesian methods are well-suited for dealing with heterogeneous sources of uncertainty, in this case from our modeling assumptions, i.e. model and parametric uncertainties, as well as the communicated daily counts of COVID-19 new cases, i.e. experimental or observational errors.

4.1 Likelihood Construction

In this work we use a stochastic formulation for the incubation model. The incubation model is stochastic with mean and standard deviation of its natural logarithm treated as Student’s t and $\chi ^2$ random variables, respectively, as discussed in Sect. 2.1. Let us denote the underlying independent random variables by ${{\varvec{\xi }}}=\{\xi _\mu ,\xi _\sigma ,\}$. The model prediction $n_i({{\varvec{\xi }}})$ is now a random variable induced by ${{\varvec{\xi }}}$ plugged in Eq (4), and ${{\varvec{n}}}({{\varvec{\xi }}})$ is a random vector.

A deterministic formulation for the incubation model could also be used. In this case the mean and standard deviation of the incubation model are fixed at their nominal values and the model prediction $n_i$ for day $t_i$ is a scalar value that depends on $\varTheta$ only. Although in this paper we only present results with the stochastic formulation, the deterministic formulation is useful for understanding the likelihood function. For a deterministic incubation model the statistical discrepancy $\epsilon$ between ${{\varvec{n}}}$ and ${{\varvec{y}}}$ is modeled a zero-mean Multivariate Normal (MVN) distribution. Under this assumption the likelihood $p({{\varvec{y}}}\vert \varTheta )$ for a deterministic incubation model can be written as

$$\begin{aligned}&p({{\varvec{y}}}\vert \varTheta )=\pi _{{{\varvec{n}}}(\varTheta )}({{\varvec{y}}}) \nonumber \\&\quad =(2\pi )^{-D/2}\vert C_{{\varvec{n}}}\vert ^{-1/2}\exp \left( -\frac{1}{2}({{\varvec{y}}}-{{\varvec{n}}}(\varTheta ))^T C_{{\varvec{n}}}^{-1}({{\varvec{y}}}-{{\varvec{n}}}(\varTheta ))\right) \end{aligned}$$

(14)

The covariance matrix $C_{{\varvec{n}}}$ can in principle be parameterized, e.g. square exponential or Matern models, and the corresponding parameters inferred jointly with $\varTheta$. However, given the sparsity of data, we neglect correlations across time and presume a diagonal covariance matrix with diagonal entries computed as

$$\begin{aligned} C_{{{\varvec{n}}},ii}=\sigma _i^2=(\sigma _a+\sigma _m\, n_i(\varTheta ))^2 \end{aligned}$$

(15)

The additive, $\sigma _a$, and multiplicative, $\sigma _m$, components will be inferred jointly with the model parameters $\varTheta$,

$$\begin{aligned} \varTheta =\varTheta ^{(1)}\cup \varTheta ^{(2)}\cup \ldots \cup \varTheta ^{(K)}\cup \varTheta ^{(\epsilon )}, \, \varTheta ^{(\epsilon )} = \{\log \sigma _a,\log \sigma _m\}. \end{aligned}$$

Here, we infer the logarithm of these parameters to ensure they remain positive. Under these assumptions, the MVN likelihood in Eq. (14) is written as a product of independent Gaussian densities

$$\begin{aligned} p({{\varvec{y}}}\vert \varTheta )=&\prod _{i=1}^D\pi _{n_i(\varTheta )}(y_i) \nonumber \\ =&(2\pi )^{-D/2}\prod _{i=1}^D \sigma _i^{-1} \exp \left( -\frac{(y_i-n_i)^2}{2\sigma _i^2}\right) \end{aligned}$$

(16)

where $\sigma _i$ is given by Eq (15).

For the stochastic incubation model the likelihood reads as

$$\begin{aligned} p({{\varvec{y}}}\vert \varTheta )=\pi _{{{\varvec{n}}}(\varTheta ),{{\varvec{\xi }}}}({{\varvec{y}}}), \end{aligned}$$

(17)

which we simplify by assuming independence of the discrepancies between different days, arriving at

$$\begin{aligned} \pi _{{{\varvec{n}}}(\varTheta ),{{\varvec{\xi }}}}({{\varvec{y}}}) =\prod _{i=1}^D\pi _{n_i(\varTheta ),{{\varvec{\xi }}}}(y_i). \end{aligned}$$

(18)

In the stochastic construction, the likelihood elements for each day $\pi _{n_i(\varTheta ),{{\varvec{\xi }}}}(y_i)$ are not analytically tractable anymore due to the variability in the incubation model parameters and the non-linear epidemiological model. One can resort to likelihood evaluations via kernel density estimates by sampling ${{\varvec{\xi }}}$ for each sample of $\varTheta$, and combining these samples with samples of the assumed discrepancy $\epsilon$, in order to arrive at an estimate of $\pi _{n_i(\varTheta ),{{\varvec{\xi }}}}(y_i)$. Alternatively, by sampling a single value of ${{\varvec{\xi }}}$ for each sample of $\varTheta$, one can achieve an unbiased estimate of the likelihood $\pi _{n_i(\varTheta ),{{\varvec{\xi }}}}(y_i)$, and given the independent-component assumption, this also leads to an unbiased estimate of the full likelihood $\pi _{{{\varvec{n}}}(\varTheta ),{{\varvec{\xi }}}}({{\varvec{y}}})$. This serves as the basis of the pseudo-marginal sampling algorithm discussed below.

4.2 Posterior Sampling

A Markov chain Monte Carlo (MCMC) algorithm is used to sample from the posterior density $p(\varTheta \vert {\varvec{y}})$. MCMC is a class of techniques that allows sampling from a posterior distribution by constructing a Markov Chain that has the posterior as its stationary distribution. In particular, we use an adaptive Metropolis algorithm [12]. A key step in this approach is the accept-reject mechanism. Each sample of $\varTheta$, drawn from a proposal $q(\cdot \vert \varTheta _i)$ is accepted with probability

$$\begin{aligned} \alpha (\varTheta _{i+1},\varTheta _i)=\min \left( 1,\frac{p(\varTheta _{i+1}\vert {\varvec{y}}) q(\varTheta _i\vert \varTheta _{i+1})}{p(\varTheta _{i}\vert {\varvec{y}})q(\varTheta _{i+1}\vert \varTheta _{i})}\right) \end{aligned}$$

where $p(\varTheta _{i}\vert {\varvec{y}})$ and $p(\varTheta _{i+1}\vert {\varvec{y}})$ are the values of the posterior PDFs evaluated at samples $\varTheta _{i}$ and $\varTheta _{i+1}$, respectively. In this work we employ symmetric proposals, $q(\varTheta _i\vert \varTheta _{i+1})=q(\varTheta _{i+1}\vert \varTheta _{i})$. In the stochastic incubation model, we employ the unbiased estimate of the approximate likelihood as described in the previous section. In other words, at each MCMC step we draw a random sample ${{\varvec{\xi }}}$ from its distribution, and then we estimate the likelihood in a way similar to the deterministic incubation model, in Eqs. (16). This is the essence of the pseudo-marginal MCMC algorithm [7] guaranteeing that the accepted MCMC samples correspond to the posterior distribution.

Figure 2 displays 1D and 2D joint marginal distributions based on two-wave model results. We used the Raftery-Lewis diagnostic [19] to determine the number of MCMC samples required for converged statistics corresponding to stationary posterior distributions for $\varTheta$. The required number of samples is of the order $o(10^5-10^6)$ depending on the geographical region employed in the inference. The resulting Effective Sample Size [15] varies between 8, 000 and 15, 000 samples depending on each parameter which is sufficient to estimate joint distributions for the model parameters.

Fig. 2

1D and 2D joint marginal distributions the components of $\varTheta =\{t_0,N_1,k_1,\theta _1,\varDelta t_2,N_2,k_2,\theta _2,\log \sigma _a, \log \sigma _m\}$ for data from California up to 2020-08-19. Distance correlations [24] for each pair of parameters is displayed about each joint marginal distribution

We use the distance correlation measure, ${{\mathscr {R}}}(X,Y)$, to ascertain the degree of dependence in the posterior distributions for pairs of parameters. This measure estimates the dependence between two random variables. Given random variables X and Y with finite first moments, the ${{\mathscr {R}}}(X,Y)\in [0,1]$ is defined as

$$\begin{aligned} {{\mathscr {R}}}(X,Y)=\frac{\vartheta ^2(X,Y)}{\sqrt{\vartheta ^2(X)\vartheta ^2(Y)}} \end{aligned}$$

(19)

where $\vartheta ^2(X,Y)$ is the “distance covariance” between X and Y and $\vartheta ^2(X)$ is the “distance variance”, $\vartheta ^2(X)=\vartheta ^2(X,X)$. The distance covariance $\vartheta ^2(X,Y)$ is defined as

$$\begin{aligned} \vartheta ^2(X,Y)=&E(||X-X'||||Y-Y'||) )\nonumber \\&\quad +E(||X-X'||)E(||Y-Y'||)\nonumber \\&\quad -2E(||X-X'||||Y-Y''||) ) \end{aligned}$$

(20)

where $(X',Y')$, $(X'',Y'')$ are independent and identically distributed random variables, with the same joint density as (X, Y). The distance correlation values for each pair of parameters are estimated using the MCMC samples drawn from their posterior distribution using the algorithm presented in [24].

Distance correlation values, shown on top of 2D marginal density subplots in Fig. 2, reveal the relationships between a number of model parameters inside each wave and between waves. For instance, the scale $\theta _1$ of the first wave exhibits strong dependencies on both the total number of symptomatic counts $N_1$ and the shape $k_1$ of the first wave. A similar dynamic is observed for the second wave. Across these two waves, $N_2$ and $\delta t_2$ show stronger connections with the first wave while the infection rate parameters $k_2$ and $\theta _2$ are only showing relevant connections inside the second wave. The correlations can be explained by how the infection rate curve varies with each parameter. For instance, $\theta _i$ corresponds to the time scale of the infection curve; increasing it makes the curve shorter and will stretch it over a longer time interval. Therefore, to maintain an approximate fit to a set of case data, the symptomatic count $N_i$ will need to be increased if $\theta _i$ is increased. A similar explanation can be made for the negative correlation between $k_i$ and $\theta _i$. These correlations show the importance of estimating joint PDFs, and the potential shortcomings for assuming independent PDFs for each model parameter.

This information can be used to aid in model construction and gauge the connection between model components. For this application space, and this will be discussed later in the paper, the depedencies between model parameters can be used to assess whether the epidemic waves can be considered separately, i.e. the model inference and forecast can be independently applied to each epidemic wave.

4.3 Prior Construction

The multi-wave results presented in this paper use priors constructed sequentially based on parameters’ statistics obtained with symptomatic counts for earlier epidemic waves. This allows us to insert temporal dependency information corresponding to early waves to enhance the robustness of the multi-wave model. To illustrate our prior construction techniques we first consider the case where we use statistics from one-wave model results to form a prior for the two-wave model. It is important that the one-wave model results should correspond to a time horizon over which there is still only one wave, such as a horizon that ends sometime in the range of dates indicated by the red box in Fig. 3.

Fig. 3

Schematic showing new case data with three infection waves. The red box indicates a range of final dates for which one-wave model chain statistics have been used to generate priors for a two-wave model. The blue box indicates a range of final dates for which two-wave model chain statistics have been used to generate priors for a three-wave model

Several approaches can be considered to construct the prior information for the first wave parameters $t_0,N_1,k_1,\theta _1$. For example the posterior samples extracted from the one-wave MCMC chain can be used with either parametric, e.g. multi-variate Gaussian, or non-parametric, e.g. kernel density estimates, approaches to provide priors for the two-wave inference. This information can be used directly in the model inference or further simplified in the form of uniform priors with bounds informed by the means and standard deviations of the one-wave results. This gives us an informed guess for part of the parameters, limiting the region of parameter space that an MCMC approach needs to explore. A smaller parameter range increases the chance that MCMC is able to find regions of high likelihood $p\left( {{\varvec{y}}} | \varTheta \right)$, making the model more robust. The prior distributions for the parameters corresponding to the second wave should be chosen to include values that approximate the case data well; these distributions may need to be selected by trial and error, although $\varDelta t_j$ can be estimated by visually inspecting raw daily new case data.

This prior construction technique can be extended to the multi-wave case by sequentially computing one-, two-, and then up to N-wave models using new case data that only shows the corresponding amount of infection waves. For example, we can construct a prior for a three-wave model by fitting a two-wave model to data taken up to the dates in the blue box in Fig. 3. This could be extended to as many waves as desired by sequentially finding a time horizon containing $N-1$ waves, running the model with $N-1$ waves, then using statistics from the model results to generate prior distributions for the first $N-1$ waves in an N-wave model over a longer time horizon.

In this paper, we use Gaussian prior distributions for $t_0$ and $\varDelta t_j$, uniform prior distributions for all other model parameters, and uniform prior distributions for $\log \sigma _a$ and $\log \sigma _m$. For Gaussian prior distributions the mean and variance are estimated from the one-wave chain. For uniform prior distributions the upper and lower bounds are set equal to $\mu _{chain} \pm 3 \sigma _{chain}$, where $\mu _{chain}$ and $\sigma _{chain}$ are the mean and standard deviation computed from the one-wave chain. Note that positive parameters $N_j,k_j,\theta _j$ are restricted to positive values; that is, the lower bound is set to zero if $\mu _{chain} - 3 \sigma _{chain}<0$.

Finally, we note that the prior construction should not be overly constraining for the parameters of the early epidemic waves. Depending on the regional spread dynamics, the epidemic waves can be clustered together or well separated in time. For example in the scehamtic shown in Fig. 3 the third wave is already underway during the downslope of the second wave. In this case the two-wave model parameters already contain some impact of the symptomatic counts from the third wave and the corresponding priors generated from the two-wave model results should allow the parameters for the first two waves  to adjust as more information becomes available.

4.4 Predictive Assessment

We will employ Bayesian posterior-predictive distributions [18] to assess the predictive skill of the proposed statistical model of the COVID-19 disease spread. The Bayesian posterior-predictive distribution, defined in Eq. (21) is computed by marginalization of the likelihood over the posterior distribution of model parameters $\varTheta$:

$$\begin{aligned} p_{\mathrm {pp}}\left( {\varvec{y}}^{\mathrm {(pp)}}\vert {\varvec{y}}\right) =\int _{{\varvec{\varTheta }}} p({\varvec{y}}^{\mathrm {(pp)}}\vert \varTheta ) p(\varTheta \vert {\varvec{y}}) d\varTheta . \end{aligned}$$

(21)

In practice, we estimate the marginal $p_{\mathrm {pp}}\left( y_i^{\mathrm {(pp)}}\vert {\varvec{y}}\right)$ for each day i through sampling. Using MCMC samples of $\varTheta$ from the posterior distribution, we evaluate the model ${\varvec{n}}(\varTheta )$ and add random noise consistent with the likelihood model settings presented in Sect. 4.1. The resulting samples are used to compute marginal statistics in hindcast mode to check consistency between the model ${\varvec{n}}$, the data ${\varvec{y}}$, and the choice for the statistical discrepancy ${\varvec{\epsilon }}$ between them. The same approach is also used to generate $p_{\mathrm {pp}}\left( y_i^{\mathrm {(pp)}}\vert {\varvec{y}}\right)$ in a forecast mode, where day i refers to a date beyond the set of dates with data available for training. These forecasts are limited, however, to 7–10 ahead since the model proposed here does not account for evolutions that modify the infection rate dynamics, e.g. changes in social behavior over the region of interest.

4.5 Model Comparison

Quantitative comparisons between one-, two-, and three-wave models are made with the Akaike Information Criteria (AIC), Bayesian Information Criteria (BIC), and the Continuous Ranked Probability Score (CRPS). Each of these is defined below, starting with AIC [6],

$$\begin{aligned} AIC = 2 m_{\varTheta } - 2 \ln L_{max}, \end{aligned}$$

(22)

where $m_{\varTheta }$ is the number of parameters in $\varTheta$ and $L_{max}$ is the maximum value of the likelihood $p({{\varvec{y}}}\vert \varTheta )$. In this context, $L_{max}$ is estimated from MCMC results, picking the sample with the maximum likelihood value in the chain. Given a choice of models with one or more waves, the model with the smallest AIC value is considered to be the highest quality by providing the best trade-off between complexity and goodness of fit.

BIC is defined as [23]

$$\begin{aligned} BIC = m_{\varTheta } \ln d - 2 \ln L_{max}, \end{aligned}$$

(23)

where d is the number of observations, equal to the length of the array ${\varvec{n}}$ from Eq (9), and $m_{\varTheta }$ and $L_{max}$ are defined above. Given a choice of models, the model with the smallest BIC value is preferable to those with larger values. In the context of this paper, the data count d is the same for all models. Given that $d>\exp (2)$ for all results presented in this paper, it is expected that BIC will add a stronger penalty to multi-wave models compared to AIC since $m_{\varTheta }$ increases by 4 for each additional wave.

CRPS [11] measures the difference between the CDF of the provided data and that of the forecast/predicted data, i.e., data generated based on the posterior predictive distribution. It is computed by summing up marginal distributions for each day that data is available

$$\begin{aligned} CRPS = \frac{1}{d} \sum _{j=1}^{d} \int _{-\infty }^{\infty } \left( \mathscr {F}_{pp,j}\left( y^{(pp)}_j| {{\varvec{y}}} \right) - \mathscr {H}_{y_j}\left( y^{(pp)}_j \right) \right) ^2 dy^{(pp)}_j, \end{aligned}$$

(24)

where $y^{(pp)}_j \equiv y^{(pp)}(t_j)$ is new daily case predictions on day j obtained via the posterior-predictive distribution Eq. (21), $y_j \equiv y(t_j)$ is new daily case data on day j and $\mathscr {F}_{pp,j}$ is the 1-D marginal posterior predictive CDF for day j computed using 1-D marginal posterior predictive distributions

$$\begin{aligned} \mathscr {F}_{pp,j}( y^{(pp)}_j | {{\varvec{n}}} ) = \int _{-\infty }^{y^{(pp)}_j} p_{pp,j} \left( y^{(pp)'}_j | {{\varvec{n}}} \right) dy^{(pp)'}_j \end{aligned}$$

(25)

where

$$\begin{aligned} p_{pp,j} \left( y^{(pp)}_j | {{\varvec{n}}} \right) = \int p_{pp}({{\varvec{y}}}^{(pp)} | {{\varvec{y}}}) d{{\varvec{y}}}^{(pp)}_{\sim j} \end{aligned}$$

(26)

is the marginal 1-D posterior predictive density corresponding to day j, based on $p_{pp}\left( {{\varvec{y}}}^{(pp)} | {{\varvec{y}}} \right)$ computed in Eq. 21. Here, $d{{\varvec{y}}}^{(pp)}_{\sim j} \equiv dy^{(pp)}_1 \cdots dy^{(pp)}_{j-1} dy^{(pp)}_{j+1} \cdots dy^{(pp)}_d$. The CDF of the provided case data ${\varvec{y}}$ is approximated as a Heaviside function [13] centered at $y_j$, $\mathscr {H}_{y_j}(y^{(pp)}_j) = 1_{y^{(pp)}_j \ge y_j}$. Similar to AIC and BIC, the model with the smallest value of CRPS is selected.

5 Results

The statistical models described above are applied to data available from public repositories [1, 2]. We will present results corresponding to the states of New Mexico, California, and Florida to gauge the agreement between the model and the data. We will also provide short-term forecasts, typically 7–10 days ahead.

The posterior-predictive figures presented in this section and the remainder of the manuscript show posterior-predictive distributions with darker shades near the median and lighter shades towards the 2.5 and 97.5 quantile levels marked with dashed lines. The 25–75 interquartile range is marked with green lines. These quantile levels are estimated by sampling the posterior-predictive distributions using (21).

The blue shades correspond to hindcast dates along with black symbols marking the data used for model calibration. The red shades correspond to forecast and the white circles mark the data collected after the forecasts were made. These can be used to visually assess the quality of forecasts.

5.1 New Mexico, Spring/Summer 2020

We first demonstrate the two-wave model for New Mexico using the reported daily new case data from May to August 2020. Two-wave model forecasts are compared with one-wave forecasts qualitatively for New Mexico and quantitatively using AIC, BIC, and CRPS for all three states.

Fig. 4

One-wave model calibration and forecast for New Mexico on 2020-05-13

The prior for the two-wave model is constructed using the workflow described in the Sect. 4.3 using one-wave model data. Specifically, a one-wave model forecast from 2020-05-13 is used for all three states. This date was chosen because only one wave is clearly visible in the new case data, as seen in Fig. 4.

Fig. 5

Comparison of one-wave and two-wave model calibration and forecasts for New Mexico

Using our data-informed prior distribution, a two-wave model run was performed every week from 2020-05-20 until 2020-08-26. One-wave model runs are also available for the same dates. Figure 5 shows one-wave and two-wave forecasts side by side for three dates, 2020-06-24, 2020-07-15, and 2020-08-19. These three dates correspond to a short time before the increase in cases at the start of the second wave, near the peak of the second wave, and when the second wave in cases had noticeably declined, respectively.

On 2020-06-24 , shown in Fig. 5a and  b, the one-wave model predicts a continuing decline in cases, since it is designed to capture one wave, so  the early stages of a second wave are treated as noise. The two-wave model is capable of fitting a second wave, but there is no clear uptick in cases as of 2020-06-24. Because of this, the forecast is highly uncertain, and the distribution includes the impact of a second wave as well as a continued slow decline in cases.

On 2020-07-15 and 2020-08-19, the two-wave model provides a more accurate forecast with far less uncertainty compared to the one-wave model. Since the one-wave model lacks the fidelity needed to capture the second wave, the model infers much large values of the error model parameters, $\sigma _a$ and $\sigma _m$, resulting in higher uncertainty in the 2020-07-15 and 2020-08-19 forecasts in Fig. 5c and e. The ability of the two-wave model to capture a second increase in infections allows it to infer a smaller error with respect to past case data, resulting in less uncertainty in its forecasts, in Fig. 5d and f.

The information criteria and CRPS scores confirm the conclusions drawn from the visual comparison of the one- and two-wave model results for the range of dates presented above. Figure 6 shows the AIC, BIC and CRPS are all smaller for the two-wave model after 2020-06-24, which is around the time when the number of daily symptomatic counts point to the onset of the second wave. Before 2020-06-24, the one- and two-wave model forecasts have similar values of AIC, BIC, and CRPS. Up until that date, only one wave of new cases is discernible from the data, so the one-wave model is sufficient to fit the data.

Fig. 6

Comparison of information criteria (AIC, BIC) and CRPS for the single and two-wave model results for New Mexico

5.2 California and Florida, Spring/Summer 2020

The interplay between one- and two-wave model can vary from region to region depending on the evolution of the daily symptomatic counts. Figure 7 shows results for California and Florida, respectively. For California, the second wave starts while the first wave is still near its peak, while for Florida the first wave has a prolonged downslope before the second wave takes hold.

Fig. 7

Two-wave model results for California and Florida

Figures 8 and 9 show AIC, BIC, and CRPS values corresponding to California and Florida, respectively. Like New Mexico, both these states had a smaller initial rise in new cases followed by a second, larger increase in new cases. The results corresponding to the end of May and beginning of June indicate only a slight advantage for the two-wave model. At later times the two-wave model is better able to capture the evolution of daily symptomatic counts compared to the one-wave model, as shown by AIC, BIC, and CRPS in Figs. 8 and 9.

Fig. 8

Comparison of information criteria (AIC, BIC) and CRPS for the single and two-wave model results for California

Fig. 9

Comparison of information criteria (AIC, BIC) and CRPS for the single and two-wave model results for Florida

Although New Mexico and Florida have two fairly distinct peaks in new cases in April and July, this is not the case for California. Instead, new cases were observed to rise during March, then leveled off during April and May before rising dramatically in late May. Despite the absence of two clear peaks in the daily symptomatic counts for California, the two-wave model offers an improvement in accuracy over the one-wave model. This improvement in accuracy shows that the superposition of infection waves can approximate an epidemic with dynamics that increase monotonically but do so at a rate which changes significantly over time.

5.3 New Mexico, Fall/Winter 2020

We now discuss results obtained with an increasing number of waves. We demonstrate a three-wave model for New Mexico using the reported daily new case data from the beginning of the pandemic to December 2020. The prior distributions for the first two infection waves are generated using two-wave model results from 2020-08-26. Figure 10 shows the three-wave forecast, which captures all three infection waves and predicts new cases to keep increasing rapidly. These results demonstrate that the proposed prior construction technique enables our approach to be used for multiple waves if needed.

Fig. 10

Three-wave model results for New Mexico on 2020-10-21 and 2020-12-21

6 Discussion

The previous section demonstrates the increase in model quality that can be obtained by adding additional infection waves for an epidemic model to infer. However, care must be taken when more than one wave is considered. The larger parameter spaces required to infer more infection waves provide more model fidelity, but also pose a more difficult estimation problem. In higher dimensional parameter spaces, it can be difficult for MCMC to find a sample with a sufficiently large posterior density value to proceed to a new sample. This is observed for the two-wave model when the prior distribution density $p\left( \varTheta \right)$ spans a relatively large parameter range. This is overcome by constructing a prior distribution with tighter distributions for the first wave parameters $t_0, N_1, k_1, \theta _1$, inferred from a one-wave model using data only containing the first wave as explained in Sect. 4.3. This empirical prior construction technique is also demonstrated for the three-wave model, where tighter distributions for the first two waves were obtained from two-wave model results. Note that the statistics-based prior estimates used in this paper are one possible prior distribution choice; future work with Bayesian epidemiological models will explore other choices, e.g. constructing correlations between adjacent regions and running the model inferences simultaneously over these regions.

Finally, it should be noted that the multi-wave epidemic model is not always necessary to capture multiple waves. For example, consider the case that a country, state, or region recovers from a first wave, then has very low new daily cases for some amount of time before the onset of a second wave, as was seen in Spain and several other European countries in September 2020. In such a case, it is far simpler and less computationally expensive to fit a one-wave model separately for each wave.

7 Conclusion

This paper demonstrates a method for producing short-term forecasts based only on observing daily symptomatic counts for an infectious disease outbreak with multiple infection waves. The method presented in this paper is an extension of our prior work on infering single waves for partially-observed epidemics. We apply our algorithms to the COVID-19 pandemic of 2020, using data spanning from March through December 2020. The model calibration and subsequent forecast is formulated in a Bayesian framework, predicated on a model for the incubation distribution. The posterior distributions for latent parameters that describe the infection rate curves are sampled via Markov chain Monte Carlo. The forecast consists of a posterior-predictive distribution for the convolution between the one or more infection waves and the incubation model, for a range of dates immediately following the daily symptomatic counts used for calibration.

The method is applied to data aggregated at the state level. The approach is sufficiently generic and can also be applied to county-level or country-level data. We present results for California, Florida, and New Mexico. In all three cases the two-wave models are shown to outperform the one-wave model. The two-wave model provides a better fit to past data and an improved forecast with far less uncertainty than the one-wave model. This improved performance is demonstrated qualitatively by model forecasts for various dates in June, July, and August, and quantitatively via information criteria and Continuous Rank Predictive Score results. These performance indicators can be used to determine the appropriate model parsimony for the data available.

We also present a three-wave model results for New Mexico in October/December 2020. These results indicate the flexibility of the underlying model to capture the initial wave in cases starting in March 2020 along with the subsequent waves starting in June and September 2020. We provide guidance on how to apply the multi-wave model to cases with three or more waves, in particular how to construct informative priors. We also point out that the multi-wave model is unnecessary for cases in which the waves are clearly separated by long periods of low case counts; in these cases it is better to fit separate one-wave models.

Like the original one-wave model, the main shortcoming of the multi-wave model is the reliance on the times series of new case data for calibration. The lack of testing during the early stages of an epidemic suggests the daily symptomatic counts are likely an under-count. However, our approach, with its emphasis on simplicity and reliance on easily observed data is meant to used for medical resource forecasting in situations with limited available data where more complicated epidemiological models are likely to encounter difficulties. While our approach could be modified to account for factors such as increased testing, this would increase the number of parameters, possibly leading to identifiability challenges during the early stages of the epidemic when data is sparse.