1 Introduction

Many types of nonlinear Schrödinger equations are used in several areas like plasma physics, nonlinear optics, systems of fiber communications, Bose–Einstein condensates of atoms, and fluid dynamics [1–8]. In the field of optical fibers, this type of equations describes confident types of optical soliton propagation in the fibers and pulse spread over two-mode optical fibers [2]. Also, the beam propagation in crystals is modeled using this type of equations. In [6] the behavior of soliton interactions has been real-time imaged and explored using Bose–Einstein condensates of atoms with awesome collisions limited to a quasi-one-dimensional waveguide. The propagation of rogue waves in oceans is characterized by nonlinear Schrödinger-type equations as well [9]. Solitary waves generated by this type of equations are frequently named vector solitons as they typically have two components. For all previous models, the study of the soliton interactions (collisions) is an important issue and imposes the investigation of the soliton reflections from walls. It is known that vector solitons are passing-through collisions and can be trapped or bounced off each other.

In this study, we emphasize two important equations:

  • \((2 + 1)\)-dimensional nonlinear Schrödinger equation (NLS),

    $$\begin{aligned} \textstyle\begin{cases} \mathrm{i}u_{t} + u_{xx} + u_{yy} + \alpha \vert u \vert ^{2}u = 0& \text{in } \Omega \times [ 0, T ], \\ u ( x,y,0 ) = u_{0} &\text{in } \Omega, \end{cases}\displaystyle \end{aligned}$$
    (1)

    with the conservative invariants

    $$\begin{aligned} \begin{aligned}&C_{1} ( t ) = \int _{ - \infty }^{\infty } \int _{ - \infty }^{\infty } \bigl\vert u ( t ) \bigr\vert ^{2}\,\mathrm{d}x \,\mathrm{d}y, \\ &C_{2} ( t ) = \int _{ - \infty }^{\infty } \int _{ - \infty }^{\infty } \frac{1}{2} \bigl( \bigl\vert u_{x} ( t ) \bigr\vert ^{2} + \bigl\vert u_{y} ( t ) \bigr\vert ^{2} \bigr) - \frac{\alpha }{4} \bigl\vert u ( t ) \bigr\vert ^{4}\,\mathrm{d}x \,\mathrm{d}y, \end{aligned} \end{aligned}$$
    (2)

    satisfying the conditions \(\frac{\mathrm{d}}{\mathrm{d}t}C_{1} ( t ) = \frac{\mathrm{d}}{\mathrm{d}t}C_{2} ( t ) = 0\).

  • \((2 + 1)\)-dimensional system of coupled nonlinear Schrödinger equation (CNLS),

    $$\begin{aligned} \textstyle\begin{cases} \mathrm{i}u_{t} + \frac{1}{2} ( u_{xx} + u_{yy} ) + \alpha ( \vert u \vert ^{2} + \beta \vert v \vert ^{2} )u = 0, \\ \mathrm{i}v_{t} + \frac{1}{2} ( v_{xx} + v_{yy} ) + \alpha ( \beta \vert u \vert ^{2} + \vert v \vert ^{2} )v = 0& \text{in } \Omega \times [ 0, T ], \\ u ( x,y,0 ) = u_{0},\qquad v ( x,y,0 ) = v_{0} &\text{in } \Omega, \end{cases}\displaystyle \end{aligned}$$
    (3)

    with the conservative invariants

    $$\begin{aligned} \begin{aligned}&I_{1} ( t ) = \int _{ - \infty }^{\infty } \int _{ - \infty }^{\infty } \bigl\vert u ( t ) \bigr\vert ^{2}\,\mathrm{d}x \,\mathrm{d}y, I_{2} ( t ) = \int _{ - \infty }^{\infty } \int _{ - \infty }^{\infty } \bigl\vert v ( t ) \bigr\vert ^{2}\,\mathrm{d}x \,\mathrm{d}y, \\ &I_{3} ( t ) = \int _{ - \infty }^{\infty } \int _{ - \infty }^{\infty } \frac{1}{2} \bigl( \bigl\vert u_{x} ( t ) \bigr\vert ^{2} + \bigl\vert u_{y} ( t ) \bigr\vert ^{2} + \bigl\vert v_{x} ( t ) \bigr\vert ^{2} + \bigl\vert v_{y} ( t ) \bigr\vert ^{2} \bigr)\\ &\phantom{I_{3} ( t ) =}{} - \frac{\alpha }{2} \bigl( \bigl\vert u ( t ) \bigr\vert ^{4} + \bigl\vert v ( t ) \bigr\vert ^{4} \bigr) - \beta \bigl\vert u ( t ) \bigr\vert ^{2} \bigl\vert v ( t ) \bigr\vert ^{2}\,\mathrm{d}x \, \mathrm{d}y, \end{aligned} \end{aligned}$$
    (4)

    satisfying the conditions \(\frac{\mathrm{d}}{\mathrm{d}t}I_{1} ( t ) = \frac{\mathrm{d}}{\mathrm{d}t}I_{2} ( t ) = \frac{\mathrm{d}}{\mathrm{d}t}I_{3} ( t ) = 0\).

Here \(\Omega \subset \mathbb{R}^{2}\) is a bounded domain, \(T< \infty \), α, β are real parameters, \(\mathrm{i} = \sqrt{ - 1}\), and the functions u, v are complex-valued in x, y, and t, and represent wave amplitudes. When \(\beta =0\), the CNLS system (3) turns into two decoupled NLS equations, whereas for \(\beta =1\), it is named the Manakov system. Both of decoupled NLS equation and Manakov system are integrable, and the collision of solitons is considered elastic, whereas for other β values, the systems are not integrable, where the soliton collision is considered inelastic. It is known that for both \((1+ 1)\)-dimensional integrable systems of CNLS and NLS, we can analytically calculate exact solutions describing solitons reflections. However, in \((2+ 1)\)-dimensions, these systems lose their integrability and hence one depends on numerical techniques for exploring the phenomena of solitons reflections and collisions. In literature, there are few researches that analytically investigate the reflection and collisions of solitons for \((1+ 1)\)-dimensional systems because of the integrability properties [10–14]. Various numerical approaches have been presented for solving nonlinear Schrödinger-type equations [15–20]. Recently, the reflection of solitons due to walls of the \((2+ 1)\)-dimensional cubic NLS is studied numerically using an explicit–implicit scheme by Crank–Nicolson finite element technique [21]. The authors studied the reflection of a single soliton to wall for the NLS subjected to three boundary condition types, whereas they did not consider soliton collisions in their study. In this paper, we extend the investigation of [21] to capture both collisions and reflections of solitons for NLS and CNLS by a robust explicit numerical scheme using the method of lines (MOL) [22–28]. The developed scheme will be examined for accuracy and stability. We have deduced that the scheme is conditionally stable in the linearized form. The behavior of soliton collisions and reflections to walls needs the considered systems to be subjected to appropriate boundary conditions. In our study, we consider Dirichlet and Neumann boundary conditions. One of the applications of this research is examined in [29].

This paper is arranged as follows. In Sect. 2, we briefly explain the MOL and construct a finite difference scheme for the \((2+ 1)\)-dimensional CNLS. Section 3 contains a stability analysis of the developed scheme. Numerical experiments with several initial conditions describing solitons interactions of \((2+ 1)\)-dimensional NLS and CNLS are given in Sect. 4. Illustration of many soliton collisions and reflection scenarios and validation of numerical results are discussed in Sect. 4 as well. Conclusions are collected in Sect. 5.

2 Method of lines for CNLS

To utilize the method of lines for solving \((2+ 1)\)-dimensional nonlinear Schrödinger type equations, we consider the CNLS system (3) as an illustration. Firstly, we must decompose the complex-valued functions u, v in their real and imaginary portions by considering

$$\begin{aligned} \textstyle\begin{cases} u = \psi _{1} + \mathrm{i}\psi _{2}, \\ v = \psi _{3} + \mathrm{i}\psi _{4}, \end{cases}\displaystyle \end{aligned}$$
(5)

where \(\{ \psi _{j} \} _{j = 1}^{4}\) are real-valued functions. By substituting Eq. (5) into system (3) we get the following system in a matrix form:

$$\begin{aligned} \boldsymbol{\psi }_{t} + \frac{1}{2}\mathbf{{B}} ( \boldsymbol{\psi }_{xx} + \boldsymbol{\psi }_{yy} ) + \alpha \mathbf{F} ( \boldsymbol{\psi } )\boldsymbol{\psi } = \mathbf{0}, \end{aligned}$$
(6)

where

$$\begin{aligned} &\boldsymbol{\psi } = \begin{bmatrix} \psi _{1} \\ \psi _{2} \\ \psi _{3} \\ \psi _{4} \end{bmatrix}, \qquad\mathbf{B} = \begin{bmatrix} 0 & 1 & 0 & 0 \\ - 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & - 1 & 0 \end{bmatrix},\qquad \mathbf{F} ( \boldsymbol{\psi } ) = \begin{bmatrix} 0 & r_{1} & 0 & 0 \\ - r_{1} & 0 & 0 & 0 \\ 0 & 0 & 0 & r_{2} \\ 0 & 0 & - r_{2} & 0 \end{bmatrix}, \\ &r_{1} = \bigl( \psi _{1}^{2} + \psi _{2}^{2} \bigr) + \beta \bigl( \psi _{3}^{2} + \psi _{4}^{2} \bigr)\quad\text{and}\quad r_{2} = \beta \bigl( \psi _{1}^{2} + \psi _{2}^{2} \bigr) + \bigl( \psi _{3}^{2} + \psi _{4}^{2} \bigr). \end{aligned}$$

Based on to the MOL, the spatial coordinates x and y in system (6) are discretized with uniformly two-dimensional rectangular mesh of \(M\times N\) points, where \(x_{\mathrm{m}}=a + m \Delta x\), \(y_{\mathrm{n}}=b + n \Delta y\), \(m= 1, 2,\ldots, M\), \(n= 1, 2,\ldots, N\), \(\Omega = [a, b] \times [c, d]\), and \(\Delta x = (b-a)/M\), \(\Delta y = (d-c)/N\) are the spatial grid step sizes. The 2nd-order central finite difference formula is applied to approximate the spatial 2nd-order derivatives at each mesh point. Then the well-known 4th-order Runge–Kutta method (RK4) is used as a time integrator for solving the resulting system of 1st-order ordinary differential equations (ODEs) corresponding to the predefined initial data using an appropriate time step Δt for \(0\leq t \leq T\). Applying the 2nd-order central finite difference operator to system (6) leads to the following 1st-order system of ODEs:

$$\begin{aligned} \frac{\mathrm{d}\boldsymbol{\psi }_{m,n}}{\mathrm{d}t} = \mathbf{R} ( \boldsymbol{\psi }_{m,n} ), \end{aligned}$$
(7)

where

$$\begin{aligned} \begin{aligned} \mathbf{R} ( \boldsymbol{\psi }_{m,n} ) ={}&{ -} \frac{1}{2}\mathbf{ {B}} \biggl( \frac{\boldsymbol{\psi }_{m + 1,n} - 2\boldsymbol{\psi }_{m,n} + \boldsymbol{\psi }_{m - 1,n}}{\Delta x^{2}} + \frac{\boldsymbol{\psi }_{m,n + 1} - 2\boldsymbol{\psi }_{m,n} + \boldsymbol{\psi }_{m,n - 1}}{\Delta y^{2}} \biggr) \\ &{}- \alpha \mathbf{F} ( \boldsymbol{\psi }_{m,n} )\boldsymbol{\psi }_{m,n}. \end{aligned} \end{aligned}$$
(8)

We obtain the solution of system (7) by utilizing RK4 as follows:

$$\begin{aligned} \boldsymbol{\Psi }_{m,n}^{k + 1} = \boldsymbol{\Psi }_{m,n}^{k} + \frac{1}{6} \bigl[ \mathbf{K}_{\mathbf{1}} + 2 ( \mathbf{K}_{\mathbf{2}} + \mathbf{K}_{\mathbf{3}} ) + \mathbf{K}_{\mathbf{4}} \bigr], \end{aligned}$$
(9)

where k is the index of time t, and

$$\begin{aligned} \begin{aligned}&\mathbf{K}_{\mathbf{1}} = \Delta t \mathbf{R} \bigl( \boldsymbol{\Psi }_{m,n}^{k} \bigr),\qquad \mathbf{K}_{\mathbf{2}} = \Delta t \mathbf{R} \biggl( \boldsymbol{\Psi }_{m,n}^{k} + \frac{1}{2}\mathbf{K}_{\mathbf{1}} \biggr), \\ &\mathbf{K}_{\mathbf{3}} = \Delta t \mathbf{R} \biggl( \boldsymbol{\Psi }_{m,n}^{k} + \frac{1}{2}\mathbf{K}_{\mathbf{2}} \biggr),\qquad \mathbf{K}_{\mathbf{4}} = \Delta t \mathbf{R} \bigl( \boldsymbol{\Psi }_{m,n}^{k} + \mathbf{K}_{\mathbf{3}} \bigr). \end{aligned} \end{aligned}$$
(10)

Scheme (9) is of 2nd order in space and of 4th order in time with an explicit nature. It is quite easy to be implemented and gives accurate results as we will discuss later. There is only one disadvantage, the stability restriction, which will be investigated in the next section.

3 Scheme stability

To deduce the stability restriction condition for Scheme (9), we apply a linearized von Neumann stability analysis. The linear form of system (6) can be written in the following version:

$$\begin{aligned} \boldsymbol{\psi }_{t} = - \frac{1}{2}\mathbf{{B}} ( \boldsymbol{\psi }_{xx} + \boldsymbol{\psi }_{yy} ) - \alpha r \mathbf{{B}} \boldsymbol{\psi }, \end{aligned}$$
(11)

where \(r = \max \{ r_{1}, r_{2} \} \).

Based on the von Neumann stability, we represent the solution of the linear system (11) in a single Fourier mode as

$$\begin{aligned} \boldsymbol{\Psi }_{m,n}^{k} = \boldsymbol{\xi }^{k}e^{\mathrm{i}\lambda m\Delta x}e^{\mathrm{i}\gamma n\Delta y},\quad m = 1, 2, \ldots, M \text{ and } n = 1, 2, \ldots, N, \end{aligned}$$
(12)

where \(\lambda, \gamma \) are real constants, and ξ is the amplification vector. Substituting of (12) into system (11) leads to the equation

$$\begin{aligned} \widetilde{\mathbf{R}} \bigl( \boldsymbol{\Psi }_{m,n}^{k} \bigr) = \varepsilon \mathbf{B} \boldsymbol{\Psi }_{m,n}^{k}, \end{aligned}$$
(13)

where \(\widetilde{\mathbf{R}}\) is the RHS of (11) after the discretization of spatial derivatives, and ε is defined as

$$\begin{aligned} \varepsilon = - \biggl( \frac{\cos ( \lambda \Delta x ) - 1}{\Delta x^{2}} + \frac{\cos ( \gamma \Delta y ) - 1}{\Delta y^{2}} + \alpha r \biggr). \end{aligned}$$
(14)

Substituting of (13) into (9) leads to the following equation in a matrix form:

$$\begin{aligned} \mathbf{L} = \mathbf{I} + \sum_{j = 1}^{4} \frac{1}{j!} ( \Delta t\varepsilon \mathbf{B} )^{j}, \end{aligned}$$
(15)

where I denotes the identity matrix. The eigenvalues of L denoted by the symbol Λ. The eigenvalues of the matrix εB are \(\pm \mathrm{i} \varepsilon \). According to the von Neumann analysis, a required condition for the scheme to be stable is that \(\max_{j} \vert \Lambda _{j} \vert \le 1, j = 1, 2, \ldots, 4\). Calculating the eigenvalues of the matrix L, we get

$$\begin{aligned} \vert \Lambda _{j} \vert ^{2} = 1 + \frac{ ( \Delta t\varepsilon )^{8}}{576} - \frac{ ( \Delta t\varepsilon )^{6}}{72},\quad \forall j = 1, 2, \ldots, 4. \end{aligned}$$
(16)

From Eqs. (14) and (16) we get that \(\vert \Lambda _{j} \vert \le 1\) if the following restriction is achieved:

$$\begin{aligned} \Delta t \le \frac{\sqrt{2}}{2 ( ( \Delta x^{2} )^{ - 1} + ( \Delta y^{2} )^{ - 1} ) - \alpha r}. \end{aligned}$$
(17)

With the same procedure of linearized von Neumann stability analysis, we can deduce the following condition of stability in case of NLS Eq. (1):

$$\begin{aligned} \Delta t \le \frac{\sqrt{2}}{4 ( ( \Delta x^{2} )^{ - 1} + ( \Delta y^{2} )^{ - 1} ) - \alpha \max \{ \vert u \vert ^{2} \} }. \end{aligned}$$
(18)

4 Numerical experiments

To examine the robustness of the considered scheme in capturing soliton interactions and reflections from solid walls for 2D nonlinear Schrödinger-type equations, we consider various numerical experiments related to NLS in Sects. 4.1 and 4.2 and CNLS in the followed subsections. We examine the conservation of the developed scheme by calculating the conserved invariants at various selected times. We utilize composite-trapezoidal rule to compute the integrals in the conserved invariant formulas. Throughout all the considered numerical experiments, we apply the zero Neumann conditions (\(\partial u / \partial n = \partial v / \partial n = 0\) on ∂Ω) to all domain boundaries. Only for the first experiment, we apply also the zero Dirichlet conditions (\(u = v = 0\) on ∂Ω) in addition to Neumann conditions to illustrate how the soliton interacts to the wall for both types of boundary conditions as a generalization to the other numerical experiments. For all the considered experiments, we computed the numerical solutions using the step sizes \(\Delta x = 0.05\), \(\Delta y = 0.02\), and \(\Delta t = 10^{-4}\) over the computational domain \(\Omega =[-20, 20] \times [-5, 5]\) up to \(T= 60\), except for the first experiment, in which the domain is taken as \(\Omega = [-5, 5] \times [-1, 1]\) up to \(T= 10\) for comparison. The numerical results of the problems related to CNSL system are calculated for \(\alpha =1\).

4.1 Elastic reflection of a single soliton for NLS

In this experiment, we study the NLS Eq. (1) subjected to the following initial condition of a single soliton solution [20, 21]:

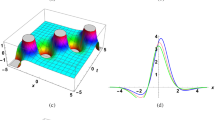
$$\begin{aligned} u_{0} = \eta \sqrt{\frac{2}{\alpha }} \operatorname{sech} \bigl( \eta ( x - x_{1} ) \bigr) \mathrm{e}^{\mathrm{i} ( s ( x - x_{1} ) )}, \end{aligned}$$
(19)

where \(x_{1}\), η, and s are arbitrary parameters standing for the initial location of soliton wave, wave speed, and wave amplitude/width, respectively. For comparison with earlier work [21], we selected the parameters in (19) as \(\alpha =\eta =s=2\) and \(x_{1}=0\). The modulus value of the solution is plotted vs different values of time in 1D, 2D, and 3D surface visualizations. This problem is solved subjected to both Dirichlet and Neumann conditions to show how the soliton behaves at the wall for both cases. All the results discussed here are related to the solution subjected to the zero Neumann boundary conditions. Figures 1–3 and Table 1 display the results in case of considering the Neumann conditions, whereas Fig. 4 displays the results when considering the Dirichlet conditions. A comparison of the single soliton reflection between results of our study and the results obtained in [21] is presented in Fig. 1. It is acknowledged that the soliton waves of the nonlinear Schrödinger equation can suffer by instability particularly for the focusing type when the value of α is positive. From Fig. 1 we can note that the spread of the soliton wave remains stable throughout the investigation, and the reflection is elastic (perfect). The soliton reflection can be also realized in Fig. 2, where the amplitude of the soliton wave is plotted along the horizontal cross section line (\(y= 0\)).

Figure 1
figure 1

A comparison of a one soliton elastic reflection trajectory between (a) the present results and (b) the results obtained in [21] up to \(t= 2\)

Full size image
Figure 2
figure 2

A comparison of soliton wave amplitudes between (a) the present results and (b) the results obtained in [21] at \(y= 0\) (cross sections) up to \(t= 2\)

Full size image
Figure 3
figure 3

(a) 3D surface plot and (b) contours plots of \(|u |\) along the horizontal cross section line for Experiment 4.1 (zero Neumann conditions)

Full size image
Figure 4
figure 4

(a) 3D surface plot and (b) contours plots of \(|u |\) along the horizontal cross section line for Experiment 4.1 (zero Dirichlet conditions)

Full size image
Table 1 Conservative invariants of the experiment 4.1 at various times
Full size table

The values of the invariants \(C_{1} (t)\) and \(C_{2} (t)\) for this example are shown in Table 1. Setting \(u(t)= u_{0}\) and integrating (2) analytically over the considered domain yield, \(C_{1} (0) = 7.999999964\) and \(C_{2} (0) = 10.66666653\). The authors of [21] concluded that the invariants \(C_{1}\) and \(C_{2}\) are conserved at the values of 7.9999999 and 10.5, respectively, up to \(t= 3\). In our study, we have extended the simulation time up to \(t= 10\) for capturing more soliton reflections to left and right walls. Table 1 clearly illustrates that \(C_{1}\) is exactly conserved at 7.99999996 and agrees precisely with the analytic value at \(t= 0\), whereas \(C_{2}\) is closely conserved at 10.62 and differs a little from the analytic value. At the moments in which the soliton wave is reflected from the wall (e.g., \(t \approx 1.25\) and \(t\approx 8.4\)), \(C_{1}\) is also precisely conserved, whereas \(C_{2}\) is almost conserved due to the reflection to the wall.

For more explanation of the behavior of soliton reflections to walls, a 3D surface and contour plots describing the solution modulus along the horizontal cross section line of the domain are displayed in Fig. 3 (using the zero Neumann conditions) and Figs. 4 (using the zero Dirichlet conditions) up to \(t= 10\). During the simulation time interval, it can be shown that the wave is perfectly reflected two times from the left wall and two times from the right wall as well. From Figs. 3 and 4 we can conclude that the soliton reflections are elastic (perfect) for the two types of boundary conditions; however, the soliton interactions at the boundaries are dissimilar. The soliton wave can undergo an unlimited number of interactions at each boundary of a finite domain. The soliton during the reflection to the wall experiences several variations in its profile and finally reverse its direction and recover its primary profile. We refer to [10] for more detailed information about the differences between soliton reflections in both types of boundary conditions. From the results discussed previously we can note that our results are very consistent with the results obtained in [21].

4.2 Elastic reflections and collisions of two solitons for NLS

In this experiment, we selected the initial condition subjected to Eq. (1) as a superposition of two opposite solitons with same speed and different initial locations and amplitudes. Here we consider

$$\begin{aligned} u_{0} = \sum_{j = 1}^{2} \eta _{j} \sqrt{\frac{2}{\alpha }} \operatorname{sech} \bigl( \eta _{j} ( x - x_{j} ) \bigr) \mathrm{e}^{\mathrm{i} ( s_{j} ( x - x_{j} ) )}, \end{aligned}$$
(20)

where the parameters are chosen as \(\alpha =2\), \(\eta _{1}=1\), \(\eta _{2}=1.5\), \(s_{2}=-s_{1}= 0.5\), and \(x_{1}=-x_{2}=10\). The value of \(|u|\) is displayed in 2D and 3D surface plots. The trajectories of two solitons interactions and reflections are displayed in Fig. 5. Figure 6 displays the 3D surface plot and contours of soliton wave modulus along the horizontal line. The scenario of soliton collisions and reflections during the simulation can be realized from Figs. 5 and 6. As expected, the two waves hold their features after the collisions and reflections and remain stable during the traveling period. Here the soliton reflections and collisions are elastic because there are no small wavelets appeared between the two solitons after the collisions and reflections and the system of this problem is indeed integrable. During the simulation period \(0\leq t \leq 60\), there are two collisions at \(t\approx 9.0\) and \(t\approx 46.0\), and one reflection for each soliton wave at \(t\approx 27.5\). The solitons throughout the boundary reflections experience some changes in their shapes and then recover their original shapes and reverse their directions after collision to wall. As was previously noted, the solitons can experience an infinite number of elastic interactions (collisions or reflections) throughout any finite domain because such solitons would not possess any decaying through the propagation.

Figure 5
figure 5

Trajectory of two solitons elastic collisions and reflections for Experiment 4.2

Full size image
Figure 6
figure 6

(a) 3D surface plot and (b) contours plots of \(|u |\) along the horizontal cross section line for Experiment 4.2

Full size image

In Table 2 the conserved invariants \(C_{1}\) and \(C_{2}\) at different selected times are calculated. The conservative values \(C_{1} (0)\) and \(C_{2} (0)\) are computed by integrating (2) numerically when \(u(t)= u_{0}\) over the domain Ω. Table 2 obviously shows that \(C_{1}\) is precisely conserved at 49.999999, whereas \(C_{2}\) is almost conserved at −8.3 up to \(t= 60\). At the moments at which the soliton waves interacted to the boundaries (\(t\approx 27.5\)), \(C_{1}\) is again conserved, whereas \(C_{2}\) is nearly conserved due to the deformations caused by the interactions with the walls.

Table 2 Conservative quantities of Experiment 4.2 at various times
Full size table

4.3 Elastic reflections and collisions of two solitons for CNLS

In this experiment, we consider the CNLS system (2) subjected to initial conditions described by a superposition of two solitons that move in same direction with different speeds, initial locations, and amplitudes. Here we use the following initial conditions considered in [15]:

$$\begin{aligned} u_{0} = v_{0} = \sum_{j = 1}^{2} \sqrt{\frac{2 \eta _{j}}{1 + \beta }} \operatorname{sech} \bigl( \sqrt{2 \eta _{j}} ( x - x_{j} ) \bigr) \mathrm{e}^{\mathrm{i} ( s_{j} ( x - x_{j} ) )}. \end{aligned}$$
(21)

The parameters in Eq. (21) are chosen as follows: \(\eta _{1}=0.5\), \(\eta _{2}=1.0\), \(s_{1}=0.1\), \(s_{2}=1.0\), \(x_{1}=0\), \(x_{2}= -10\), and \(\beta =2/3\). Here the solutions u and v are identical. The simulation of the soliton collisions and reflections of this experiment are displayed in Fig. 7. A 3D surface and contour plot of soliton waves along the horizontal cross section line are shown in Fig. 8. The scenario of different interactions of the considered solitons during the simulation can be realized from these figures. Observe that the two solitons, which move in the same direction but with unalike speeds, interact each other two times (near \(t\approx 9.0\) and \(t\approx 44.5\)) and then separate after the collisions without any change in shapes or speeds. During the period of simulation, there is one reflection of the fast soliton initially located at \(x= -10\) near t ≈28.5. The fast soliton experiences a little deformation in its profile after the interaction with the right wall and then recovers its original shape when reversing its way. Here the soliton–soliton and soliton–wall interactions are elastic. As a cause of the elastic interactions, the solitons can experience an infinite number of collisions or reflections without any decaying during the propagation.

Figure 7
figure 7

Trajectory of two solitons elastic collisions and reflections for Experiment 4.3

Full size image
Figure 8
figure 8

(a) 3D surface plot and (b) contours plots of \(|u |\) along the horizontal cross section line for Experiment 4.3

Full size image

From Table 3 we can state that the invariants \(I_{1}\) and \(I_{2}\) are conserved at 28.9694486, whereas the invariant \(I_{3}\) is practically conserved at 1.673267 excluding the values calculated during the moments of the soliton reflection at right boundary. We can see that all the invariants are conserved during and after the interactions.

Table 3 Conservative quantities of Experiment 4.3 at various times
Full size table

4.4 Inelastic interactions of two solitons for CNLS

In the next investigation, we consider two interactions scenarios reported in [30], which describe the inelastic soliton collisions. The inelastic interactions can be occurred when the CNLS system is not exactly/analytically solvable. Moreover, the value of β has a significant effect in determining the behavior of solitons interaction in a long-time simulation. In this numerical experiment the CNLS system (2) is solved subjected to the following initial conditions:

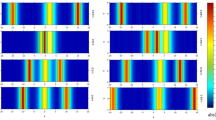
$$\begin{aligned} \begin{aligned}&u_{0} = \sqrt{2 \eta _{1}} \operatorname{sech} ( \sqrt{2 \eta _{1}} x - x_{1} ) \mathrm{e}^{\mathrm{i} ( s_{1} x )}, \\ &v_{0} = \sqrt{2 \eta _{2}} \operatorname{sech} ( \sqrt{2 \eta _{2}} x - x_{2} ) \mathrm{e}^{\mathrm{i} ( s_{2} x )}. \end{aligned} \end{aligned}$$
(22)

Here we have chosen the two initial solitons in such way that they move in an opposite direction with equal velocity, dissimilar initial locations, and different amplitudes. Firstly, we take \(\eta _{1}=1.2\), \(\eta _{2}=1.0\), s\(_{1}= -s_{2}= 0.6\), \(x_{2}= -x_{1}=10\), and \(\beta =2/3\). The scenarios of soliton collisions and reflections are displayed in Figs. 9–12. In these figures the trajectories of soliton interactions are presented in 1D, 2D, 3D surface and contour plots.

Figure 9
figure 9

Trajectory of inelastic collisions and reflections of (a) \(|u |\) and (b) \(|v |\) for Experiment 4.4

Full size image
Figure 10
figure 10

3D surface plots of (a) \(|u |\) and (b) \(|v |\) along the horizontal cross section line for Experiment 4.4

Full size image
Figure 11
figure 11

Contour plots of (a) \(|u |\) and (b) \(|v |\) along the horizontal cross section line for Experiment 4.4

Full size image
Figure 12
figure 12

Soliton waves amplitudes for (a) \(|u |\) and (b) \(|v |\) along the horizontal cross section line at selected values of t for Experiment 4.4

Full size image

Note that the two soliton waves collided at \(t\approx 11.5\). After the collision, the waves break up, and their polarizations are shifted because of the collision. Due to soliton energy, they are somewhat transferred from the polarization axis of one soliton to the other. Moreover, the two solitons pass over one another with a slight change in their profiles, and daughter waves are generated accompanied with small wavelets. As shown in Figs. 9–12, the generated daughter waves are small ones and split off from the original wave and spread alongside it, however, in a reversed direction.

Both original solitons and daughter waves are collided and reflected to the walls at \(t\approx 46.5\). They experience some deformation in their profiles during the moments of reflection and then recover their past profiles in a reverse direction but with small decaying because of the appearance of small wavelets. Here the soliton collections are inelastic, whereas the wave interactions to the walls remain perfect. Up to \(t= 60\), the invariants \(I_{1}\) and \(I_{2}\) are conserved at 30.983866 and 28.284271, respectively, whereas the invariant \(I_{3}\) is almost conserved at −11.2523 excluding the values calculated during the moments of reflections. It is worth noting that the value of \(I_{1}\), \(I_{2}\), and \(I_{3}\) at \(t= 46.5\) (the moment at which the waves hit the walls) equal 30.983866, 28.284271, and −11.6352, respectively.

Generating new inelastic interactions can be achieved when considering a relatively large value of the parameter β and moderate values of waves velocities. As an example, we present another interesting scenario of the solitons interactions when \(\beta =3\) and \(s_{1}=-s_{2}= 0.4\). In Fig. 13 the trajectory and the 3D surface plots of this interaction are displayed for the soliton wave solution |u|, just for clarification. Recently, such interactions were examined in [31].

Figure 13
figure 13

(a) Interaction trajectory and (b) 3D surface plot along \(y= 0\) of the soliton \(|u |\) for Experiment 4.4 when \(\beta = 3\) and \(s_{1} = -s_{2}= 0.4\)

Full size image

5 Conclusion

In this investigation, we developed a robust numerical scheme based on the MOL for solving 2D nonlinear Schrödinger-type equations such as NLS and CNLS. We have examined many scenarios of elastic and inelastic soliton collisions. We investigated the soliton reflections from the boundaries as well for various numerical experiments. The change in the type of boundary conditions affects the wave characteristic only during a wall collision. The numerical results demonstrate that, in the case of elastic interactions, the vector solitons experience an unlimited number of collisions and reflections from the walls without any change in their shapes except at the walls. However, for inelastic interactions, the solitons suffer from some deformation and energy decaying, where the daughter wave and small wavelets start to appear. We verified the accuracy of the numerical results through calculating the conserved invariants of the considered systems and comparing current results with some existing ones. This accuracy reflects the efficiency of the developed scheme in capturing soliton collisions and reflections of nonlinear Schrödinger-type equations or any other systems that can generate solitons. In this paper, we offer new results related to soliton reflections of 2D nonlinear Schrödinger-type equations.