Introduction

Graph theory has been considered to play an important role when it comes to its application in dealing with real-life situations. The fuzzy graph theory has its own significance as application of fuzzy set theory has no limits. In 1975, Rosenfeld [9] introduced the concept of fuzzy graphs. Yeh and Bang [22] also introduced fuzzy graphs independently. Fuzzy graphs are useful to represent relationships which deal with uncertainty and it differs greatly from classical graphs. It has numerous applications to problems in computer science, electrical engineering, system analysis, operations research, economics, networking routing, transportation, etc. After Rosenfeld [9], the fuzzy graph theory increases with its various types of branches, such as fuzzy tolerance graph [13], fuzzy threshold graph [12], bipolar fuzzy graphs [7, 8], balanced interval-valued fuzzy graphs [4, 6], fuzzy planar graphs [11], etc. Also, several works have been done on fuzzy graphs by Samanta and Pal [14].

Atanassov [1, 2] developed the concept of intuitionistic fuzzy set (IFS) as an extension of fuzzy set that [23] deals with uncertain situations in a better way as its structure is not limited to membership grades only. The concept of intuitionistic fuzzy sets is a better tool to use due to its diverse structure describing membership as well as non-membership grades of an element. The theory of intuitionistic fuzzy sets has been remarkably used in some areas so far. Shannon and Atanassov [15] introduced the concept of intuitionistic fuzzy graphs in 1994. Parvathi and Karunambigai [5] gave a definition for intuitionistic fuzzy graph as a special case of intuitionistic fuzzy graphs defined by Shannon and Atanassov [16]. Sankar Sahoo and Madhumangal Pal [10] defined three types of products, namely direct product, semi-strong product, and strong product. Yaqoob et al. [21] discussed the four basic operations, namely Cartesian product, composition, union, and join of complex intuitionistic fuzzy graphs. Yahya Mohamed and Mohamed Ali [19, 20] defined modular and max product on intuitionistic fuzzy graph. In this paper, the complement of max product of two intuitionistic fuzzy graphs and the degree of a vertex in the complement of this product are studied under regularity conditions. The max product of intuitionistic fuzzy graphs is applied to solve the decision-making problem in school determination. The research paper is organized as follows: “Introduction” presents the literature review of fuzzy graphs and intuitionistic fuzzy graphs. In “Preliminaries”, we have provided some basic concepts of intuitionistic fuzzy graphs. The definition of complement of max product on two intuitionistic fuzzy graphs and its degree are given in “Complement of max product of intuitionistic fuzzy graphs”. In “Applications of max product of intuitionistic fuzzy graphs in school determination”, we studied an application of intuitionistic fuzzy graphs in school determination using normalized hamming distance. This distance function was used to measure the distance between each student and each school. The schools in which each of the students has been enrolled were determined using normalized hamming distance function based on examination that is performed for transition to high school education. The result is determined by calculating the smallest distance between each student and each school. In “Conclusion”, we conclude present studies and recommendations for future studies.

Preliminaries

Throughout this paper, assume that \(G^{*} = \left( {V,E} \right)\) is a crisp graph and \(G\) is an intuitionistic fuzzy graph, where \(V\) is a non-empty vertex set and \(E\) is an edge set.

Definition 2.1

[5] An intuitionistic fuzzy graph is of the form \(G = \left( {\left( {\sigma _{1} ,\sigma _{2} } \right),\left( {\mu _{1} ,\mu _{2} } \right)} \right)\) on \(G^{*} = \left( {V,E} \right)\) and

  1. 1.

    \(V\, = \,\left\{ {x_{1} ,x_{2} ,\,...,\,x_{n} } \right\}\), such that \(\sigma _{1} :V \to \left[ {0,1} \right]\) and \(\sigma _{2} ~:V~ \to ~\left[ {0,1} \right]\) denote the degree of membership and non-membership of the element \(x_{i} \, \in \,~V\) respectively, such that \(0\, \le ~\,\sigma _{1} \left( {x_{i} } \right)\, + \,\sigma _{2} \left( {x_{i} } \right)\, \le ~\,1\) for all \(~x_{i} \in ~V\) \(\left( {i\, = \,1,2,3,\, \ldots ,\,n} \right)\).

  2. 2.

    \(\mu _{1} :~V \times V \to ~\left[ {0,1} \right]\) and \(~\mu _{2} ~:V \times V \to \left[ {0,1} \right]\), where \(\mu _{1} \left( {x_{i} ,x_{j} } \right)\) and \(\mu _{2} \left( {x_{i} ,x_{j} } \right)\) denote the degree of membership and degree of non-membership values of the edge \(\left( {x_{i} ,x_{j} } \right)\), respectively, such that \(\mu _{1} \left( {x_{i} ,x_{j} } \right) \le \sigma _{1} \left( {x_{i} } \right) \wedge \sigma _{1} \left( {x_{j} } \right)\) and \(\mu _{2} \left( {x_{i} ,x_{j} } \right) \le \sigma _{2} \left( {x_{i} } \right) \vee \sigma _{2} \left( {x_{j} } \right)\); \(0\, \le \,\mu _{1} \left( {x_{i} x_{j} } \right)\, + \,\mu _{2} \left( {x_{i} x_{j} } \right)\, \le ~\,1\), for every edge \(\left( {x_{i} ,x_{j} } \right)\).

For notational convenience, instead of representing an edge as \(\left( {x,y} \right)\), we denote this simply by \(xy\).

Definition 2.2

[5] An intuitionistic fuzzy graph \(G~ = ~\left( {\left( {\sigma _{1} ,\sigma _{2} } \right),\left( {\mu _{1} ,\mu _{2} } \right)} \right)\) is called strong intuitionistic fuzzy graph if \(\mu _{1} \left( {x_{i} x_{j} } \right) = \sigma _{1} \left( {x_{i} } \right) \wedge \sigma _{1} \left( {x_{j} } \right)\) and \(\mu _{2} \left( {x_{i} x_{j} } \right) = \sigma _{2} \left( {x_{i} } \right) \vee \sigma _{2} \left( {x_{j} } \right),~\forall ~x_{i} x_{j} \in E,~~i \ne j\).

Definition 2.3

[5] An intuitionistic fuzzy graph \(G~ = ~\left( {\left( {\sigma _{1} ,\sigma _{2} } \right),\left( {\mu _{1} ,\mu _{2} } \right)} \right)\) is called complete intuitionistic fuzzy graph if \(\mu _{1} \left( {x_{i} x_{j} } \right)\, = \,\sigma _{1} \left( {x_{i} } \right) \wedge \sigma _{1} \left( {x_{j} } \right)\) and \(\mu _{2} \left( {x_{i} x_{j} } \right)\, = \,\sigma _{2} \left( {x_{i} } \right) \vee \sigma _{2} \left( {x_{j} } \right),~\,\forall ~x_{i} ,~x_{j} \, \in \,~V\), \(i \ne j\).

Definition 2.4

[3] Let \(G = \left( {\left( {\sigma _{1} ,\sigma _{2} } \right),\left( {\mu _{1} ,\mu _{2} } \right)} \right)\) be an intuitionistic fuzzy graph, and then, the order of \(G\) is defined to be \(O\left( G \right) = \left( {O_{{\sigma _{1} }} \left( G \right),O_{{\sigma _{2} }} \left( G \right)} \right)\) where \(O_{{\sigma _{1} }} \left( G \right) = \mathop \sum \nolimits_{{x \in V}} \sigma _{1} \left( x \right)\) and \(O_{{\sigma _{2} }} \left( G \right) = \mathop \sum \nolimits_{{x \in V}} \sigma _{2} \left( x \right)\).

Definition 2.5

[3] Let \(G = \left( {\left( {\sigma _{1} ,\sigma _{2} } \right),\left( {\mu _{1} ,\mu _{2} } \right)} \right)\) be an intuitionistic fuzzy graph, then the size of G is defined to be \(S\left( G \right)\, = \,\left( {S_{{\mu _{1} }} \left( G \right),S_{{\mu _{2} }} \left( G \right)} \right)\) where \(S_{{\mu _{1} }} \left( G \right) = \mathop \sum \nolimits_{{xy \in E}} \mu _{1} \left( {xy} \right)\) and \(S_{{\mu _{2} }} \left( G \right) = \mathop \sum \nolimits_{{xy \in E}} \mu _{2} \left( {xy} \right)\).

Definition 2.6

[5] The complement of an intuitionistic fuzzy graph \(G = \left( {V,E} \right)\) is an intuitionistic fuzzy graph \(\bar{G} = \left( {\overline{{\left( {\sigma _{1} ,\sigma _{2} } \right)}} ,\overline{{\left( {\mu _{1} ,\mu _{2} } \right)}} } \right)\), where \(\overline{{\left( {\sigma _{1} ,\sigma _{2} } \right)}} = \left( {\sigma _{1} ,\sigma _{2} } \right)\) and \(\overline{{\left( {\mu _{1} ,\mu _{2} } \right)}} = \left( {\bar{\mu }_{1} ,\bar{\mu }_{2} } \right)\), where \(\bar{\mu }_{1} \left( {xy} \right) = \sigma _{1} \left( x \right) \wedge \sigma _{1} \left( y \right) - \mu _{1} \left( {xy} \right)\) and \(\bar{\mu }_{2} \left( {xy} \right) = \sigma _{2} \left( x \right) \vee \sigma _{2} \left( y \right) - \mu _{2} \left( {xy} \right)\), \(\forall xy \in E\).

Definition 2.7

[5] Let \(G = \left( {\left( {\sigma _{1} ,\sigma _{2} } \right),\left( {\mu _{1} ,\mu _{2} } \right)} \right)\) be an intuitionistic fuzzy graph. The degree of a vertex \(x\) in \(G\) is denoted by \(d_{G} \left( x \right)\, = \,\left( {d_{1}^{G} \left( x \right),d_{2}^{G} \left( x \right)} \right)\) and defined by \(d_{1}^{G} \left( x \right)\, = \,\mathop \sum \nolimits_{{x \ne y}} \mu _{1}^{G} (xy)\, = \,\sum \nolimits_{{\left( {x,y} \right) \in E}} \mu _{1}^{G} \left( {xy} \right)\) and \(d_{2}^{G} \left( x \right)\, = \,\mathop \sum \nolimits_{{x \ne y}} \mu _{2}^{G} \left( {xy} \right)\, = \,\mathop \sum \nolimits_{{\left( {x,y} \right) \in E}} \mu _{2}^{G} \left( {xy} \right)\), where \(d_{1}^{G} \left( x \right)\) is the sum of membership grades of the edges incident to the vertex \(x\) and \(d_{2}^{G} \left( x \right)\) is the sum of non-membership grades of the edges incident to the vertex \(x\).

Definition 2.8

[19] An intuitionistic fuzzy graph \(G~ = ~\left( {\left( {\sigma _{1} ,\sigma _{2} } \right),\left( {\mu _{1} ,\mu _{2} } \right)} \right)\) is called regular intuitionistic fuzzy graph if \(d_{G} \left( x \right)\, = \,\left( {d_{1}^{G} \left( x \right),d_{2}^{G} \left( x \right)} \right)\, = \,\left( {k_{1} ,k_{2} } \right)\) for all \(x\, \in \,V\), where \(k_{1}\) and \(k_{2}\) are constants.

Definition 2.9

[20] Let \(G_{1} :\left( {\left( {\sigma _{1}^{{G_{1} }} ,\sigma _{2}^{{G_{1} }} } \right),\left( {\mu _{1}^{{G_{1} }} ,\mu _{2}^{{G_{1} }} } \right)} \right)\) and \(G_{2} :\left( {\left( {\sigma _{1}^{{G_{2} }} ,\sigma _{2}^{{G_{2} }} } \right),\left( {\mu _{1}^{{G_{2} }} ,\mu _{2}^{{G_{2} }} } \right)} \right)\) be two intuitionistic fuzzy graphs. The max product of two intuitionistic fuzzy graph \(G_{1}\) and \(G_{2}\) is denoted by \(G_{1} \times _{m} G_{2} = \left( {V_{1} \times _{m} V_{2} ,E_{1} \times _{m} E_{2} } \right)\), \(E_{1} \times _{m} E_{2} \, = \,\{ \left( {x_{1} ,~y_{1} } \right)\left( {x_{1} ,~y_{2} } \right)~/~x_{1} \, = \,x_{2} ,~y_{1} y_{2} \, \in \,E_{2} ~\;{\text{or}}\;~y_{1} \, = \,y_{2} ,~\;x_{1} x_{2} \, \in \,E_{1}\)} by \(\sigma _{1}^{{G_{1} \times _{m} G_{2} }} \left( {x_{1} ,~y_{1} } \right)\, = ~\,\sigma _{1}^{{G_{1} }} \left( {x_{1} } \right) \vee \sigma _{1}^{{G_{2} }} \left( {y_{1} } \right),~\;~\sigma _{2}^{{G_{1} \times _{m} G_{2} }} \left( {x_{1} ,~y_{1} } \right)\, = \,~\sigma _{2}^{{G_{1} }} \left( {x_{1} } \right) \wedge \sigma _{2}^{{G_{2} }} \left( {y_{1} } \right)\), for all \(\left( {u_{1} ,~v_{1} } \right) \in V_{1} \times ~V_{2}\) and

$$ \mu _{1}^{{G_{1} \times _{m} G_{2} }} \left( {\left( {x_{1} ,y_{1} } \right)\left( {x_{2} ,y_{2} } \right)} \right) = \left\{ {\begin{array}{*{20}l} {\sigma _{1}^{{G_{1} }} \left( {x_{1} } \right) \vee \mu _{1}^{{G_{2} }} \left( {y_{1} y_{2} } \right)} & {{\text{if}}\,x_{1} \, = \,x_{2} ,~\,y_{1} y_{2} \, \in \,E_{2} } \\ {\mu _{1}^{{G_{1} }} \left( {x_{1} x_{2} } \right) \vee \sigma _{1}^{{G_{2} }} \left( {y_{1} } \right)} & {{\text{if}}\,y_{1} \, = \,y_{2} ,~\,x_{1} x_{2} \, \in \,E_{1} \,} \\ \end{array} } \right\} $$
(1)
$$ \mu _{2}^{{G_{1} \times _{m} G_{2} }} \left( {\left( {x_{1} ,y_{1} } \right)\left( {x_{2} ,y_{2} } \right)} \right) = \left\{ {\begin{array}{*{20}l} {\sigma _{2}^{{G_{1} }} \left( {x_{1} } \right) \wedge \mu _{2}^{{G_{2} }} \left( {y_{1} y_{2} } \right)} & {{\text{if}}\,x_{1} = x_{2} ,\,y_{1} y_{2} \, \in \,E} \\ {\mu _{2}^{{G_{1} }} \left( {x_{1} x_{2} } \right) \wedge \sigma _{2}^{{G_{2} }} \left( {y_{1} } \right)} & {{\text{if}}\,y_{1} = y_{2} ,\,x_{1} x_{2} \, \in \,E_{1} } \\ \end{array} } \right\} $$
(2)

Example 2.1

Let \(G_{1}^{*} = \left( {V_{1} ,E_{1} } \right)\) and \(G_{2}^{*} = \left( {V_{2} ,E_{2} } \right)\) be two crisp graphs, such that \(V_{1} \, = \,\left\{ {u_{1} ,u_{2} ,u_{3} } \right\},\;~V_{2} \, = \,\left\{ {v_{1} ,v_{2} } \right\},\;E_{1} \, = \,\left\{ {u_{1} u_{3} ,u_{2} u_{3} } \right\},\;E_{2} \, = \,\left\{ {v_{1} v_{2} } \right\}\). Consider two intuitionistic fuzzy graphs \(G_{1} = \left( {\left( {\sigma _{1}^{{G_{1} }} ,\sigma _{2}^{{G_{1} }} } \right),\left( {\mu _{1}^{{G_{1} }} ,\mu _{2}^{{G_{1} ~}} } \right)} \right)\) and \(G_{2} = \left( {\left( {\sigma _{1}^{{G_{2} }} ,\sigma _{2}^{{G_{2} }} } \right),\left( {\mu _{1}^{{G_{2} }} ,\mu _{2}^{{G_{2} ~}} } \right)} \right)\) and \(G_{1} \times _{m} G_{2}\) as follows (Tables 1, 2):

Table 1 Vertex set of \(G_{1} \times _{m} G_{2}\)
Full size table
Table 2 Edge set of \(G_{1} \times _{m} G_{2}\)
Full size table

Theorem 2.1

[20] If \(G_{1} :\left( {\left( {\sigma _{1}^{{G_{1} }} ,\sigma _{2}^{{G_{1} }} } \right),\left( {\mu _{1}^{{G_{1} }} ,\mu _{2}^{{G_{1} }} } \right)} \right)\) and \(G_{2} :\left( {\left( {\sigma _{1}^{{G_{2} }} ,\sigma _{2}^{{G_{2} }} } \right),\left( {\mu _{1}^{{G_{2} }} ,\mu _{2}^{{G_{2} }} } \right)} \right)\) are two intuitionistic fuzzy graphs. Then, \(G_{1} \times _{m} G_{2}\) is also an intuitionistic fuzzy graph.

Theorem 2.2

[20] If \(G_{1} :\left( {\left( {\sigma _{1}^{{G_{1} }} ,\sigma _{2}^{{G_{1} }} } \right),\left( {\mu _{1}^{{G_{1} }} ,\mu _{2}^{{G_{1} }} } \right)} \right)\) and \(G_{2} :\left( {\left( {\sigma _{1}^{{G_{2} }} ,\sigma _{2}^{{G_{2} }} } \right),\left( {\mu _{1}^{{G_{2} }} ,\mu _{2}^{{G_{2} }} } \right)} \right)\) are two strong intuitionistic fuzzy graphs. Then, \(G_{1} \times _{m} G_{2}\) is also a strong intuitionistic fuzzy graph.

Theorem 2.3

[20] If \(G_{1}\) and \(G_{2}\) are two complete intuitionistic fuzzy graphs, then \(G_{1} \times _{m} G_{2}\) is not a complete intuitionistic fuzzy graph.

Theorem 2.4

[20] If \(G_{1}\) and \(G_{2}\) are two connected intuitionistic fuzzy graph, then \(G_{1} \times _{m} G_{2}\) is also a connected intuitionistic fuzzy graph.

Complement of max product of intuitionistic fuzzy graphs

Definition 3.1

The complement of max product of two intuitionistic fuzzy graphs \(G_{1} ~ = \left( {\left( {\sigma _{1}^{{G_{1} }} ~,\sigma _{2}^{{G_{1} }} } \right),\left( {\mu _{1}^{{G_{1} }} ,\mu _{2}^{{G_{1} }} } \right)} \right)\) and \(G_{2} = \left( {\left( {\sigma _{1}^{{G_{2} }} ,\sigma _{2}^{{G_{2} }} } \right),\left( {\mu _{1}^{{G_{2} }} ,\mu _{2}^{{G_{2} }} } \right)} \right)\) is an intuitionistic fuzzy graphs \(\overline{{G_{1} \, \times _{m} \,G_{2} }} \, = \,\left( {\left( {\overline{{\sigma _{1}^{{G_{1} }} \, \times _{m} \,\sigma _{1}^{{G_{2} }} }} } \right)\left( {\overline{{\sigma _{2}^{{G_{1} }} \times _{m} \sigma _{2}^{{G_{2} }} }} } \right),\left( {\overline{{\mu _{1}^{{G_{1} }} \times _{m} \mu _{1}^{{G_{2} }} }} } \right)\left( {\overline{{\mu _{2}^{{G_{1} }} \times _{m} \mu _{2}^{{G_{2} }} }} } \right)} \right)\) on \(G^{*} = \left( {V,E} \right)\) and \(\overline{{V_{1} \times _{m} V_{2} }} = V_{1} \times _{m} V_{2}\) and \(\overline{{E_{1} \times _{m} E_{2} }} = \left\{ {\left( {x_{1} ,y_{1} } \right)\left( {x_{2} ,y_{2} } \right){\text{|}}\begin{array}{*{20}c} {x_{1} = x_{2} ,~y_{1} y_{2} \in E_{2} ~\left( {or} \right)y_{1} = y_{2} ,~x_{1} x_{2} \in E_{1} ~\left( {or} \right)~~} \\ {x_{1} x_{2} \in E_{1} ,~y_{1} y_{2} \notin E_{2} ~\left( {or} \right)~x_{1} x_{2} \notin E_{1} ,~y_{1} y_{2} \in E_{2} ~\left( {or} \right)} \\ {x_{1} x_{2} \in E_{1} ,~y_{1} y_{2} \in E_{2} ~\left( {or} \right)~x_{1} x_{2} \notin E_{1} ,~y_{1} y_{2} \notin E_{2} ~} \\ \end{array} } \right\}\)\(\left( {\overline{{\sigma _{1}^{{G_{1} }} \times _{m} \sigma _{1}^{{G_{2} }} }} } \right)\left( {x_{1} ,y_{1} } \right)\, = \,\left( {\sigma _{1}^{{G_{1} }} \times _{m} \sigma _{1}^{{G_{2} }} } \right)\left( {x_{1} ,y_{1} } \right)\, = \,\sigma _{1}^{{G_{1} }} \left( {x_{1} } \right) \vee \sigma _{1}^{{G_{2} }} \left( {y_{1} } \right)\), \(\left( {\overline{{\sigma _{2}^{{G_{1} }} \times _{m} \sigma _{2}^{{G_{2} }} }} } \right)\left( {x_{1} ,y_{1} } \right)\, = \,\left( {\sigma _{2}^{{G_{1} }} \times _{m} \sigma _{2}^{{G_{2} }} } \right)\left( {x_{1} ,y_{1} } \right)\, = \,\sigma _{2}^{{G_{1} }} \left( {x_{1} } \right) \wedge \sigma _{2}^{{G_{2} }} \left( {y_{1} } \right)\), where \(x_{1} \in V_{1}\) and \(y_{1} \in V_{2}\).

$$ \begin{aligned} \left( {\overline{{\mu _{1}^{{G_{1} }} \times _{m} \mu _{1}^{{G_{2} }} }} } \right)\left( {\left( {x_{1} ,y_{1} } \right),\left( {x_{2} ,y_{2} } \right)} \right) \\ & \quad = \left\{ {\begin{array}{*{20}c} {\left( {\sigma _{1}^{{G_{1} }} \times _{m} \sigma _{1}^{{G_{2} }} } \right)\left( {x_{1} ,y_{1} } \right) \wedge \left( {\sigma _{1}^{{G_{1} }} \times _{m} \sigma _{1}^{{G_{2} }} } \right)\left( {x_{2} ,y_{2} } \right) - \left( {\mu _{1}^{{G_{1} }} \times _{m} \mu _{1}^{{G_{2} }} } \right)\left( {\left( {x_{1} ,y_{1} } \right),\left( {x_{2} ,y_{2} } \right)} \right)\quad } & {~{\text{if}}~x_{1} = x_{2} ,~y_{1} y_{2} \in E_{2} } \\ \begin{gathered} \left( {\sigma _{1}^{{G_{1} }} \times _{m} \sigma _{1}^{{G_{2} }} } \right)\left( {x_{1} ,y_{1} } \right) \wedge \left( {\sigma _{1}^{{G_{1} }} \times _{m} \sigma _{1}^{{G_{2} }} } \right)\left( {x_{2} ,y_{2} } \right) - \left( {\mu _{1}^{{G_{1} }} \times _{m} \mu _{1}^{{G_{2} }} } \right)\left( {\left( {x_{1} ,y_{1} } \right),\left( {x_{2} ,y_{2} } \right)} \right)\quad \hfill \\ \left( {\sigma _{1}^{{G_{1} }} \times _{m} \sigma _{1}^{{G_{2} }} } \right)\left( {x_{1} ,y_{1} } \right) \wedge \left( {\sigma _{1}^{{G_{1} }} \times _{m} \sigma _{1}^{{G_{2} }} } \right)\left( {x_{2} ,y_{2} } \right)~~ \hfill \\ \end{gathered} & \begin{gathered} ~~{\text{if}}~y_{1} = y_{2} ,~x_{1} x_{2} \in E_{1} \hfill \\ {\text{otherwise}} \hfill \\ \end{gathered} \\ {\text{~}} & {} \\ \end{array} } \right. \\ \end{aligned} $$
(3)
$$ \begin{aligned} & \left( {\overline{{\mu _{2}^{{G_{1} }} \times _{m} \mu _{2}^{{G_{2} }} }} } \right)\left( {\left( {x_{1} ,y_{1} } \right),\left( {x_{2} ,y_{2} } \right)} \right) \\ & \quad = \left\{ {\begin{array}{*{20}l} {\left( {\sigma _{2}^{{G_{1} }} \times _{m} \sigma _{2}^{{G_{2} }} } \right)\left( {x_{1} ,y_{1} } \right) \vee \left( {\sigma _{2}^{{G_{1} }} \times _{m} \sigma _{2}^{{G_{2} }} } \right)\left( {x_{2} ,y_{2} } \right) - \left( {\mu _{2}^{{G_{1} }} \times _{m} \mu _{2}^{{G_{2} }} } \right)\left( {\left( {x_{1} ,y_{1} } \right),\left( {x_{2} ,y_{2} } \right)} \right)~~~~} \hfill & {~~~{\text{if}}~x_{1} = x_{2} ,~y_{1} y_{2} \in E_{2} } \hfill \\ {\left( {\sigma _{2}^{{G_{1} }} \times _{m} \sigma _{2}^{{G_{2} }} } \right)\left( {x_{1} ,y_{1} } \right) \vee \left( {\sigma _{2}^{{G_{1} }} \times _{m} \sigma _{2}^{{G_{2} }} } \right)\left( {x_{2} ,y_{2} } \right) - \left( {\mu _{2}^{{G_{1} }} \times _{m} \mu _{2}^{{G_{2} }} } \right)\left( {\left( {x_{1} ,y_{1} } \right),\left( {x_{2} ,y_{2} } \right)} \right)} \hfill & {~~{\text{if}}~y_{1} = y_{2} ,~x_{1} x_{2} \in E_{1} } \hfill \\ {\left( {\sigma _{1}^{{G_{1} }} \times _{m} \sigma _{1}^{{G_{2} }} } \right)\left( {x_{1} ,y_{1} } \right) \vee \left( {\sigma _{1}^{{G_{1} }} \times _{m} \sigma _{1}^{{G_{2} }} } \right)\left( {x_{2} ,y_{2} } \right)} \hfill & {{\text{otherwise}}} \hfill \\ \end{array} .} \right. \\ \end{aligned} $$
(4)

Example 3.2

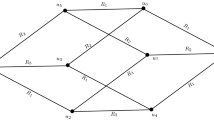
Consider the two intuitionistic fuzzy graphs as shown in Figs. 1 and 2 and their corresponding max product \(G_{1} \times _{m} G_{2}\) shown in Fig. 3.

Fig. 1
figure 1

Intuitionistic fuzzy graph \(G_{1}\)

Full size image
Fig. 2
figure 2

Intuitionistic fuzzy graph \(G_{2}\)

Full size image

Then, the complement of max product of \(G_{1}\) and \(G_{2}\) is shown in Fig. 4.

Theorem 3.1

Let \(G_{1}\) and \(G_{2}\) be two regular intuitionistic fuzzy graphs. If underlying crisp graphs \(G_{1}^{*}\) and \(G_{2}^{*}\) are complete graphs and \(\sigma _{1}^{{G_{1} }} ,\sigma _{2}^{{G_{1} }} ,\sigma _{1}^{{G_{2} }} ,\sigma _{2}^{{G_{2} }}\) are constants which satisfy \(~\sigma _{1}^{{G_{1} }} \ge \mu _{1}^{{G_{2} }} ,\) \(\sigma _{2}^{{G_{1} }} \le \mu _{2}^{{G_{2} }}\); \(\sigma _{1}^{{G_{2} }} \ge \mu _{1}^{{G_{1} }}\), \(\sigma _{2}^{{G_{2} }} \le \mu _{2}^{{G_{1} }}\); \(\sigma _{1}^{{G_{1} }} > \mu _{1}^{{G_{1} }}\), \(\sigma _{2}^{{G_{1} }} < \mu _{2}^{{G_{1} }}\) and \(\sigma _{1}^{{G_{2} }} > \mu _{1}^{{G_{2} }}\), \(\sigma _{2}^{{G_{2} }} < \mu _{2}^{{G_{2} }}\). Then, complement of max product of two intuitionistic fuzzy graphs \(G_{1}\) and \(G_{2}\) is regular intuitionistic fuzzy graph.

Proof:

Let \(G_{1}\) and \(G_{2}\) be two regular intuitionistic fuzzy graphs. The underlying crisp graphs \(G_{1}^{*}\) and \(G_{2}^{*}\) are complete graphs of degrees \(d_{1}\) and \(d_{2}\) for every vertices of \(V_{1}\) and \(~V_{2}\).

Given that \(\sigma _{1}^{{G_{1} }} ,\sigma _{2}^{{G_{1} }} ,\sigma _{1}^{{G_{2} }}\) and \(\sigma _{2}^{{G_{2} }}\) are constants, say \(\sigma _{1}^{{G_{1} }} \left( x \right) = c_{1} ,~\) \(\sigma _{2}^{{G_{1} }} \left( x \right) = c_{2} ,~~\forall ~x \in V_{1}\) \(\sigma _{1}^{{G_{2} }} \left( y \right) = c_{3} ,\) \(~\sigma _{2}^{{G_{2} }} \left( y \right) = c_{4}\) \(\forall ~y \in V_{2}\) and \(~\sigma _{1}^{{G_{1} }} \ge \mu _{1}^{{G_{2} }} ,\) \(\sigma _{2}^{{G_{1} }} \le \mu _{2}^{{G_{2} }}\); \(\sigma _{1}^{{G_{2} }} \ge \mu _{1}^{{G_{1} }}\), \(\sigma _{2}^{{G_{2} }} \le \mu _{2}^{{G_{1} }}\).

By theorem, max product of two regular intuitionistic fuzzy graphs is regular intuitionistic fuzzy graph.

Consider \(\left( {x_{1} ,y_{1} } \right) \in \left( {\overline{{\sigma _{1}^{{G_{1} }} \times _{m} \sigma _{1}^{{G_{2} }} }} } \right)\)

$$ \begin{aligned} d_{1}^{{\overline{{G_{1} \times _{m} G_{2} }} }} \left( {x_{1} ,y_{1} } \right) & = \mathop \sum \limits_{{\left( {x_{1} ,y_{1} } \right)\left( {x_{2} ,y_{2} } \right) \in E}} \left( {\overline{{\mu _{1}^{{G_{1} }} \times _{m} \mu _{1}^{{G_{2} }} }} } \right)\left( {\left( {x_{1} ,y_{1} } \right)\left( {x_{2} ,y_{2} } \right)} \right)~ \\ & = \mathop \sum \limits_{{x_{1} = x_{2} ,~~y_{1} y_{2} \in E_{1} }} \left( {\sigma _{1}^{{G_{1} }} \times _{m} \sigma _{1}^{{G_{2} }} } \right)\left( {x_{1} ,y_{1} } \right) \wedge \left( {\sigma _{1}^{{G_{1} }} \times _{m} \sigma _{1}^{{G_{2} }} } \right)\left( {x_{2} ,y_{2} } \right)~ - \left( {\mu _{1}^{{G_{1} }} \times _{m} \mu _{1}^{{G_{2} }} } \right)\left( {\left( {x_{1} ,y_{1} } \right)\left( {x_{2} ,y_{2} } \right)} \right) \\ & \quad + \mathop \sum \limits_{{y_{1} = y_{2} ,~~x_{1} x_{2} \in E_{1} }} \left( {\sigma _{1}^{{G_{1} }} \times _{m} \sigma _{1}^{{G_{2} }} } \right)\left( {x_{1} ,y_{1} } \right) \wedge \left( {\sigma _{1}^{{G_{1} }} \times _{m} \sigma _{1}^{{G_{2} }} } \right)\left( {x_{2} ,y_{2} } \right)~ - \left( {\mu _{1}^{{G_{1} }} \times _{m} \mu _{1}^{{G_{2} }} } \right)\left( {\left( {x_{1} ,y_{1} } \right)\left( {x_{2} ,y_{2} } \right)} \right) \\ & \quad + \mathop \sum \limits_{{x_{1} x_{2} \in E_{1} ,y_{1} y_{2} \notin E_{2} }} \left( {\sigma _{1}^{{G_{1} }} \times _{m} \sigma _{1}^{{G_{2} }} } \right)\left( {x_{1} ,y_{1} } \right) \wedge \left( {\sigma _{1}^{{G_{1} }} \times _{m} \sigma _{1}^{{G_{2} }} } \right)\left( {x_{2} ,y_{2} } \right)~ \\ & \quad + \mathop \sum \limits_{{x_{1} x_{2} \notin E_{1} ,y_{1} y_{2} \in E_{2} }} \left( {\sigma _{1}^{{G_{1} }} \times _{m} \sigma _{1}^{{G_{2} }} } \right)\left( {x_{1} ,y_{1} } \right) \wedge \left( {\sigma _{1}^{{G_{1} }} \times _{m} \sigma _{1}^{{G_{2} }} } \right)\left( {x_{2} ,y_{2} } \right) \\ & \quad + \mathop \sum \limits_{{x_{1} x_{2} \in E_{1} ,y_{1} y_{2} \in E_{2} }} \left( {\sigma _{1}^{{G_{1} }} \times _{m} \sigma _{1}^{{G_{2} }} } \right)\left( {x_{1} ,y_{1} } \right) \wedge \left( {\sigma _{1}^{{G_{1} }} \times _{m} \sigma _{1}^{{G_{2} }} } \right)\left( {x_{2} ,y_{2} } \right) \\ & \quad + \mathop \sum \limits_{{x_{1} x_{2} \notin E_{1} ,y_{1} y_{2} \notin E_{2} }} \left( {\sigma _{1}^{{G_{1} }} \times _{m} \sigma _{1}^{{G_{2} }} } \right)\left( {x_{1} ,y_{1} } \right) \wedge \left( {\sigma _{1}^{{G_{1} }} \times _{m} \sigma _{1}^{{G_{2} }} } \right)\left( {x_{2} ,y_{2} } \right). \\ \end{aligned} $$

Since \(G_{1}^{*}\) and \(G_{2}^{*}\) are complete graphs, then

$$ \begin{aligned} d_{1}^{{\overline{{G_{1} \times _{m} G_{2} }} }} \left( {x_{1} ,y_{1} } \right) & = \mathop \sum \limits_{{x_{1} = x_{2} ,~~y_{1} y_{2} \in E_{2} }} \left( {\sigma _{1}^{{G_{1} }} \times _{m} \sigma _{1}^{{G_{2} }} } \right)\left( {x_{1} ,y_{1} } \right) \wedge \left( {\sigma _{1}^{{G_{1} }} \times _{m} \sigma _{1}^{{G_{2} }} } \right)\left( {x_{2} ,y_{2} } \right)~ \\ & \quad - \left( {\mu _{1}^{{G_{1} }} \times _{m} \mu _{1}^{{G_{2} }} } \right)\left( {\left( {x_{1} ,y_{1} } \right)\left( {x_{2} ,y_{2} } \right)} \right) \\ ~ & \quad + ~~\mathop \sum \limits_{{y_{1} = y_{2} ,~~x_{1} x_{2} \in E_{1} }} \left( {\sigma _{1}^{{G_{1} }} \times _{m} \sigma _{1}^{{G_{2} }} } \right)\left( {x_{1} ,y_{1} } \right) \wedge \left( {\sigma _{1}^{{G_{1} }} \times _{m} \sigma _{1}^{{G_{2} }} } \right)\left( {x_{2} ,y_{2} } \right)~ \\ & \quad - \left( {\mu _{1}^{{G_{1} }} \times _{m} \mu _{1}^{{G_{2} }} } \right)\left( {\left( {x_{1} ,y_{1} } \right)\left( {x_{2} ,y_{2} } \right)} \right) \\ ~ & \quad + ~\mathop \sum \limits_{{x_{1} x_{2} \in E_{1} ,y_{1} y_{2} \in E_{2} }} \left( {\sigma _{1}^{{G_{1} }} \times _{m} \sigma _{1}^{{G_{2} }} } \right)\left( {x_{1} ,y_{1} } \right) \wedge \left( {\sigma _{1}^{{G_{1} }} \times _{m} \sigma _{1}^{{G_{2} }} } \right)\left( {x_{2} ,y_{2} } \right) \\ & \quad - \left( {\mu _{1}^{{G_{1} }} \times _{m} \mu _{1}^{{G_{2} }} } \right)\left( {\left( {x_{1} ,y_{1} } \right)\left( {x_{2} ,y_{2} } \right)} \right) \\ ~\quad + \mathop \sum \limits_{{x_{1} x_{2} \in E_{1} ,y_{1} y_{2} \in E_{2} }} \left( {\sigma _{1}^{{G_{1} }} \times _{m} \sigma _{1}^{{G_{2} }} } \right)\left( {x_{1} ,y_{1} } \right) \wedge \left( {\sigma _{1}^{{G_{1} }} \times _{m} \sigma _{1}^{{G_{2} }} } \right)\left( {x_{2} ,y_{2} } \right)~. \\ \end{aligned} $$
(5)

Similarly

$$ \begin{aligned} d_{2}^{{\overline{{G_{1} \times _{m} G_{2} }} }} \left( {x_{1} ,y_{1} } \right) & = \mathop \sum \limits_{{x_{1} = x_{2} ,~~y_{1} y_{2} \in E_{2} }} \left( {\sigma _{2}^{{G_{1} }} \times _{m} \sigma _{2}^{{G_{2} }} } \right)\left( {x_{1} ,y_{1} } \right) \vee \left( {\sigma _{2}^{{G_{1} }} \times _{m} \sigma _{2}^{{G_{2} }} } \right)\left( {x_{2} ,y_{2} } \right)~ \\ & \quad - \left( {\mu _{2}^{{G_{1} }} \times _{m} \mu _{2}^{{G_{2} }} } \right)\left( {\left( {x_{1} ,y_{1} } \right)\left( {x_{2} ,y_{2} } \right)} \right) \\ ~ & \quad + \mathop \sum \limits_{{y_{1} = y_{2} ,~~x_{1} x_{2} \in E_{1} }} \left( {\sigma _{2}^{{G_{1} }} \times _{m} \sigma _{2}^{{G_{2} }} } \right)\left( {x_{1} ,y_{1} } \right) \vee \left( {\sigma _{2}^{{G_{1} }} \times _{m} \sigma _{2}^{{G_{2} }} } \right)\left( {x_{2} ,y_{2} } \right)~ \\ & \quad - \left( {\mu _{2}^{{G_{1} }} \times _{m} \mu _{2}^{{G_{2} }} } \right)\left( {\left( {x_{1} ,y_{1} } \right)\left( {x_{2} ,y_{2} } \right)} \right) \\ ~ & \quad + \mathop \sum \limits_{{x_{1} x_{2} \in E_{1} ,y_{1} y_{2} \in E_{2} }} \left( {\sigma _{2}^{{G_{1} }} \times _{m} \sigma _{2}^{{G_{2} }} } \right)\left( {x_{1} ,y_{1} } \right) \vee \left( {\sigma _{2}^{{G_{1} }} \times _{m} \sigma _{2}^{{G_{2} }} } \right)\left( {x_{2} ,y_{2} } \right). \\ \end{aligned} $$
(6)

Case (i) : If \(\sigma _{1}^{{G_{1} }} \left( x \right)\, \le \,\sigma _{1}^{{G_{2} }} \left( y \right)\) and \(\sigma _{2}^{{G_{1} }} \left( x \right)\, \ge \,\sigma _{2}^{{G_{2} }} \left( y \right)\) for all \(x\, \in \,V_{1}\) and \(y\, \in \,V_{2}\).

By Eq. (5)

$$ \begin{aligned} d_{2}^{{\overline{{G_{1} \times _{m} G_{2} }} }} \left( {x_{1} ,y_{1} } \right) & = \mathop \sum \limits_{{x_{1} = x_{2} ,~~y_{1} y_{2} \in E_{2} }} \left( {\sigma _{2}^{{G_{1} }} \left( {x_{1} } \right) \wedge \sigma _{2}^{{G_{2} }} \left( {y_{1} } \right)} \right) \vee \left( {\sigma _{2}^{{G_{1} }} \left( {x_{2} } \right) \wedge \sigma _{2}^{{G_{2} }} \left( {y_{2} } \right)} \right)~ \\ & \quad - \left( {\mu _{1}^{{G_{1} }} \times _{m} \mu _{1}^{{G_{2} }} } \right)\left( {\left( {x_{1} ,y_{1} } \right)\left( {x_{2} ,y_{2} } \right)} \right) \\ ~ & \quad + ~\mathop \sum \limits_{{y_{1} = y_{2} ,~~x_{1} x_{2} \in E_{1} }} \left( {\sigma _{1}^{{G_{1} }} \left( {x_{1} } \right) \vee \sigma _{1}^{{G_{2} }} \left( {y_{1} } \right)} \right) \wedge \left( {\sigma _{1}^{{G_{1} }} \left( {x_{2} } \right) \vee \sigma _{1}^{{G_{2} }} \left( {y_{2} } \right)} \right)~~ \\ & \quad - \left( {\mu _{1}^{{G_{1} }} \times _{m} \mu _{1}^{{G_{2} }} } \right)\left( {\left( {x_{1} ,y_{1} } \right)\left( {x_{2} ,y_{2} } \right)} \right) \\ & \quad + \mathop \sum \limits_{{x_{1} x_{2} \in E_{1} ,y_{1} y_{2} \in E_{2} }} \left( {\sigma _{1}^{{G_{1} }} \left( {x_{1} } \right) \vee \sigma _{1}^{{G_{2} }} \left( {y_{1} } \right)} \right) \wedge \left( {\sigma _{1}^{{G_{1} }} \left( {x_{2} } \right) \vee \sigma _{1}^{{G_{2} }} \left( {y_{2} } \right)} \right) \\ & = \mathop \sum \limits_{{x_{1} = x_{2} ,~~y_{1} y_{2} \in E_{2} }} \left( {\sigma _{1}^{{G_{1} }} \left( {x_{1} } \right) \vee \sigma _{1}^{{G_{2} }} \left( {y_{1} } \right)} \right) \wedge \left( {\sigma _{1}^{{G_{1} }} \left( {x_{2} } \right) \vee \sigma _{1}^{{G_{2} }} \left( {y_{2} } \right)} \right)~. \\ \end{aligned} $$

By Eq. (6)

$$ \begin{aligned} d_{2}^{{\overline{{G_{1} \times _{m} G_{2} }} }} \left( {x_{1} ,y_{1} } \right) & = \mathop \sum \limits_{{x_{1} = x_{2} ,~~y_{1} y_{2} \in E_{2} }} \left( {\sigma _{2}^{{G_{1} }} \left( {x_{1} } \right) \wedge \sigma _{2}^{{G_{2} }} \left( {y_{1} } \right)} \right) \vee \left( {\sigma _{2}^{{G_{1} }} \left( {x_{2} } \right) \wedge \sigma _{2}^{{G_{2} }} \left( {y_{2} } \right)} \right)~ \\ & \quad - \left( {\overline{{\mu _{2}^{{G_{1} }} \times _{m} \mu _{2}^{{G_{2} }} }} } \right)\left( {\left( {x_{1} ,y_{1} } \right)\left( {x_{2} ,y_{2} } \right)} \right) \\ ~ & \quad + \mathop \sum \limits_{{y_{1} = y_{2} ,~~x_{1} x_{2} \in E_{1} }} \left( {\sigma _{2}^{{G_{1} }} \left( {x_{1} } \right) \wedge \sigma _{2}^{{G_{2} }} \left( {y_{1} } \right)} \right) \vee \left( {\sigma _{2}^{{G_{1} }} \left( {x_{2} } \right) \wedge \sigma _{2}^{{G_{2} }} \left( {y_{2} } \right)} \right)~ \\ & \quad - \left( {\overline{{\mu _{2}^{{G_{1} }} \times _{m} \mu _{2}^{{G_{2} }} }} } \right)\left( {\left( {x_{1} ,y_{1} } \right)\left( {x_{2} ,y_{2} } \right)} \right) \\ & \quad + \mathop \sum \limits_{{x_{1} x_{2} \in E_{1} ,y_{1} y_{2} \in E_{2} }} \left( {\sigma _{2}^{{G_{1} }} \left( {x_{1} } \right) \wedge \sigma _{2}^{{G_{2} }} \left( {y_{1} } \right)} \right) \vee \left( {\sigma _{2}^{{G_{1} }} \left( {x_{2} } \right) \wedge \sigma _{2}^{{G_{2} }} \left( {y_{2} } \right)} \right). \\ \\ \end{aligned} $$

Since by the definition of max product of two intuitionistic fuzzy graphs

$$ \begin{aligned} d_{1}^{{\overline{{G_{1} \times _{m} G_{2} }} }} \left( {x_{1} ,y_{1} } \right) & = \mathop \sum \limits_{{x_{1} = x_{2} ,~~y_{1} y_{2} \in E_{2} }} \sigma _{1}^{{G_{2} }} \left( {y_{1} } \right) - \left( {\mu _{1}^{{G_{1} }} \times _{m} \mu _{1}^{{G_{2} }} } \right)\left( {\left( {x_{1} ,y_{1} } \right)\left( {x_{2} ,y_{2} } \right)} \right) \\ & \quad + \mathop \sum \limits_{{y_{1} = y_{2} ,~~x_{1} x_{2} \in E_{1} }} \sigma _{1}^{{G_{2} }} \left( {y_{1} } \right) - \left( {\overline{{\mu _{1}^{{G_{1} }} \times _{m} \mu _{1}^{{G_{2} }} }} } \right)\left( {\left( {x_{1} ,y_{1} } \right)\left( {x_{2} ,y_{2} } \right)} \right) \\ & \quad + \mathop \sum \limits_{{x_{1} x_{2} \in E_{1} ,y_{1} y_{2} \in E_{2} }} c_{3} \\ & = \mathop \sum \limits_{{x_{1} = x_{2} ,~~y_{1} y_{2} \in E_{2} }} \sigma _{1}^{{G_{2} }} \left( {y_{1} } \right) - \sigma _{1}^{{G_{1} }} \left( {x_{1} } \right) \vee \mu _{1}^{{G_{2} }} \left( {y_{1} y_{2} } \right) \\ & \quad + \mathop \sum \limits_{{y_{1} = y_{2} ,~~x_{1} x_{2} \in E_{1} }} \sigma _{1}^{{G_{2} }} \left( {y_{1} } \right) - \mu _{1}^{{G_{1} }} \left( {x_{1} x_{2} } \right) \vee \sigma _{1}^{{G_{2} }} \left( {y_{1} } \right) + \mathop \sum \limits_{{x_{1} x_{2} \in E_{1} ,y_{1} y_{2} \in E_{2} }} c_{3} \\ & = \mathop \sum \limits_{{x_{1} = x_{2} ,~~y_{1} y_{2} \in E_{2} }} c_{3} - \sigma _{1}^{{G_{1} }} \left( {x_{1} } \right) + \mathop \sum \limits_{{y_{1} = y_{2} ,~~x_{1} x_{2} \in E_{1} }} c_{3} - \sigma _{1}^{{G_{2} }} \left( {y_{1} } \right) + c_{3} d_{{G_{2} }}^{*} \left( {y_{1} } \right)d_{{G_{1} }}^{*} \left( {x_{1} } \right) \\ \\ \end{aligned} $$

Similarly

$$ d_{2}^{{\overline{{G_{1} \times _{m} G_{2} }} }} \left( {x_{1} ,y_{1} } \right)\, = \,\left( {c_{4} - c_{2} } \right)d_{{G_{2} }}^{*} \left( {y_{1} } \right)\, + \,c_{4} d_{{G_{2} }}^{*} \left( {y_{1} } \right)d_{{G_{1} }}^{*} \left( {x_{1} } \right). $$

Since \(G_{1}\) and \(G_{2}\) are two regular intuitionistic fuzzy graphs & \(G_{1}^{*}\) and \(G_{2}^{*}\) are complete graphs, then \(\mu _{1}^{{G_{1} }}\) and \(\mu _{1}^{{G_{2} }}\) are constants say \(\left( {e_{1} ~,e_{2} } \right)\) and \(\left( {e_{3} ,e_{4} } \right)\).

\(d_{1}^{{\overline{{G_{1} \times _{m} G_{2} }} }} \left( {x_{1} ,y_{1} } \right)\, = \,\left( {c_{3} - c_{1} } \right)d_{2} \, + \,c_{3} d_{1} d_{2}\),

\(d_{2}^{{\overline{{G_{1} \times _{m} G_{2} }} }} \left( {x_{1} ,y_{1} } \right)\, = \,\left( {c_{4} - c_{2} } \right)d_{2} \, + \,c_{4} d_{1} d_{2}\).

Case (ii) : If \(\sigma _{1}^{{G_{1} }} \left( x \right) \ge \sigma _{1}^{{G_{2} }} \left( y \right)\) and \(\sigma _{2}^{{G_{1} }} \left( x \right) \le \sigma _{2}^{{G_{2} }} \left( y \right)\) for all \(x \in V_{1}\) and \(y \in V_{2}\)

$$ \begin{aligned} d_{1}^{{\overline{{G_{1} \times _{m} G_{2} }} }} \left( {x_{1} ,y_{1} } \right) = & \mathop \sum \limits_{{x_{1} = x_{2} ,~~y_{1} y_{2} \in E_{2} }} \sigma _{1}^{{G_{1} }} \left( {x_{1} } \right) - \left\{ {\sigma _{1}^{{G_{1} }} \left( {x_{1} } \right) \vee \mu _{1}^{{G_{2} }} \left( {y_{1} ,y_{2} } \right)} \right\}~ \\ & \quad + \mathop \sum \limits_{{y_{1} = y_{2} ,~~x_{1} x_{2} \in E_{1} }} \sigma _{1}^{{G_{1} }} \left( {y_{1} } \right) - \left\{ {\sigma _{1}^{{G_{2} }} \left( {y_{1} } \right) \vee \mu _{1}^{{G_{1} }} \left( {x_{1} ,x_{2} } \right)} \right\} \\ & \quad + \mathop \sum \limits_{{x_{1} x_{2} \in E_{1} ,y_{1} y_{2} \in E_{2} }} \sigma _{1}^{{G_{1} }} \left( {x_{1} } \right) \\ = & \mathop \sum \limits_{{x_{1} = x_{2} ,~~y_{1} y_{2} \in E_{1} }} c_{1} - \sigma _{1}^{{G_{1} }} \left( {x_{1} } \right) + \mathop \sum \limits_{{y_{1} = y_{2} ,~~x_{1} x_{2} \in E_{2} }} c_{1} - \sigma _{1}^{{G_{2} }} \left( {y_{1} } \right) + c_{1} d_{{G_{2} }}^{*} \left( {y_{1} } \right)d_{{G_{1} }}^{*} \left( {x_{1} } \right) \\ = & \left( {c_{1} - c_{1} } \right)d_{2} + \left( {c_{1} - c_{3} } \right)d_{1} + c_{1} d_{1} d_{2} = \left( {c_{1} - c_{3} } \right)d_{1} + c_{1} d_{1} d_{2} \\ = & \mathop \sum \limits_{{x_{1} = x_{2} ,~~y_{1} y_{2} \in E_{1} }} c_{1} - \sigma _{1}^{{G_{1} }} \left( {x_{1} } \right) + \mathop \sum \limits_{{y_{1} = y_{2} ,~~x_{1} x_{2} \in E_{2} }} c_{1} - \sigma _{1}^{{G_{2} }} \left( {y_{1} } \right) + c_{1} d_{{G_{2} }}^{*} \left( {y_{1} } \right)d_{{G_{1} }}^{*} \left( {x_{1} } \right). \\ \end{aligned} $$

Similarly

$$ d_{2}^{{\overline{{G_{1} \times _{m} G_{2} }} }} \left( {x_{1} ,y_{1} } \right)\, = \,\left( {c_{4} - c_{2} } \right)d_{1} \, + \,c_{4} d_{1} d_{2} . $$

Hence, complement of max product of two regular intuitionistic fuzzy graphs is regular.

Theorem 3.2

Let \(G_{1}\) and \(G_{2}\) be two regular intuitionistic fuzzy graphs of the underlying crisp graphs; \(G_{1}^{*}\) and \(G_{2}^{*}\) are regular graphs with the vertex sets; and edge sets of \(G_{1}\) and \(G_{2}\) are different constants which satisfies \(~\sigma _{1}^{{G_{1} }} > \mu _{1}^{{G_{2} }} ,\) \(\sigma _{2}^{{G_{1} }} < \mu _{2}^{{G_{2} }}\); \(\sigma _{1}^{{G_{2} }} > \mu _{1}^{{G_{1} }}\), \(\sigma _{2}^{{G_{2} }} < \mu _{2}^{{G_{1} }}\); \(\sigma _{1}^{{G_{1} }} > \mu _{1}^{{G_{1} }}\), \(\sigma _{2}^{{G_{1} }} < \mu _{2}^{{G_{1} }}\) and \(\sigma _{1}^{{G_{2} }} > \mu _{1}^{{G_{2} }}\), \(\sigma _{2}^{{G_{2} }} < \mu _{2}^{{G_{2} }}\). Then, complement of the max product of two regular intuitionistic fuzzy graphs \(G_{1}\) and \(G_{2}\) is regular intuitionistic fuzzy graph.

Proof:

Let \(G_{1}\) and \(G_{2}\) be two regular intuitionistic fuzzy graphs. The underlying crisp graphs \(G_{1}^{*}\) and \(G_{2}^{*}\) are regular graphs of degrees \(g_{1}\) and \(g_{2}\) for every vertices in \(V_{1}\) and \(~V_{2}\).

Given that \(\sigma ^{{G_{1} }} ,\sigma ^{{G_{2} }} ,~~\mu ^{{G_{1} }}\) and \(\mu ^{{G_{2} }}\) are constants, say \(\sigma _{1}^{{G_{1} }} \left( x \right) = c_{1} ,~\) \(\sigma _{2}^{{G_{1} }} \left( x \right) = c_{2} ,~~\forall ~x \in V_{1}\) \(\sigma _{1}^{{G_{2} }} \left( y \right) = c_{3} ,\) \(~\sigma _{2}^{{G_{2} }} \left( y \right) = c_{4}\) \(\forall ~y \in V_{2}\),\(~\mu _{1}^{{G_{1} }} \left( {x_{1} y_{1} } \right) = e_{1} ,\mu _{2}^{{G_{1} }} \left( {x_{1} y_{1} } \right) = e_{2} ,~~\mu _{1}^{{G_{2} }} \left( {x_{1} y_{1} } \right) = e_{3} ,\mu _{2}^{{G_{2} }} \left( {x_{1} y_{1} } \right) = e_{4}\) and \(~\sigma _{1}^{{G_{1} }} > \mu _{1}^{{G_{2} }} ,\) \(\sigma _{2}^{{G_{1} }} < \mu _{2}^{{G_{2} }}\); \(\sigma _{1}^{{G_{2} }} > \mu _{1}^{{G_{1} }}\), \(\sigma _{2}^{{G_{2} }} < \mu _{2}^{{G_{1} }}\).

Consider \(\left( {x_{1} ,y_{1} } \right) \in \left( {\overline{{\sigma _{1}^{{G_{1} }} \times _{m} \sigma _{1}^{{G_{2} }} }} } \right)\).

Case (i) : If \(\sigma _{1}^{{G_{1} }} \left( x \right) \le \sigma _{1}^{{G_{2} }} \left( y \right)\) and \(\sigma _{2}^{{G_{1} }} \left( x \right) \ge \sigma _{2}^{{G_{2} }} \left( y \right)\) for all \(x \in V_{1}\) and \(y \in V_{2}\)

$$ \begin{aligned} d_{1}^{{\overline{{G_{1} \times _{m} G_{2} }} }} \left( {x_{1} ,y_{1} } \right) & = \mathop \sum \limits_{{x_{1} = x_{2} ,~~y_{1} y_{2} \in E_{2} }} \left( {\sigma _{1}^{{G_{1} }} \left( {x_{1} } \right) \vee \sigma _{1}^{{G_{2} }} \left( {y_{1} } \right)} \right) \wedge \left( {\sigma _{1}^{{G_{1} }} \left( {x_{2} } \right) \vee \sigma _{1}^{{G_{2} }} \left( {y_{2} } \right)} \right)~ \\ & \quad - \left( {\mu _{1}^{{G_{1} }} \times _{m} \mu _{1}^{{G_{2} }} } \right)\left( {\left( {x_{1} ,y_{1} } \right)\left( {x_{2} ,y_{2} } \right)} \right) \\ & \quad + \mathop \sum \limits_{{y_{1} = y_{2} ,~~x_{1} x_{2} \in E_{1} }} \left( {\sigma _{1}^{{G_{1} }} \left( {x_{1} } \right) \vee \sigma _{1}^{{G_{2} }} \left( {y_{1} } \right)} \right) \wedge \left( {\sigma _{1}^{{G_{1} }} \left( {x_{2} } \right) \vee \sigma _{1}^{{G_{2} }} \left( {y_{2} } \right)} \right)~ \\ & \quad - \left( {\mu _{1}^{{G_{1} }} \times _{m} \mu _{1}^{{G_{2} }} } \right)\left( {\left( {x_{1} ,y_{1} } \right)\left( {x_{2} ,y_{2} } \right)} \right) \\ & \quad + \mathop \sum \limits_{{~x_{1} x_{2} \in E_{1} ,y_{1} y_{2} \notin E_{2} }} \left( {\sigma _{1}^{{G_{1} }} \left( {x_{1} } \right) \vee \sigma _{1}^{{G_{2} }} \left( {y_{1} } \right)} \right) \wedge \left( {\sigma _{1}^{{G_{1} }} \left( {x_{2} } \right) \vee \sigma _{1}^{{G_{2} }} \left( {y_{2} } \right)} \right)~ \\ & \quad + \mathop \sum \limits_{{~x_{1} x_{2} \notin E_{1} ,y_{1} y_{2} \in E_{2} }} \left( {\sigma _{1}^{{G_{1} }} \left( {x_{1} } \right) \vee \sigma _{1}^{{G_{2} }} \left( {y_{1} } \right)} \right) \wedge \left( {\sigma _{1}^{{G_{1} }} \left( {x_{2} } \right) \vee \sigma _{1}^{{G_{2} }} \left( {y_{2} } \right)} \right)~ \\ & \quad + \mathop \sum \limits_{{x_{1} x_{2} \notin E_{1} ,y_{1} y_{2} \notin E_{2} }} \left( {\sigma _{1}^{{G_{1} }} \left( {x_{1} } \right) \vee \sigma _{1}^{{G_{2} }} \left( {y_{1} } \right)} \right) \wedge \left( {\sigma _{1}^{{G_{1} }} \left( {x_{2} } \right) \vee \sigma _{1}^{{G_{2} }} \left( {y_{2} } \right)} \right) \\ & \quad + \mathop \sum \limits_{{x_{1} x_{2} \in E_{1} ,y_{1} y_{2} \in E_{2} }} \left( {\sigma _{1}^{{G_{1} }} \left( {x_{1} } \right) \vee \sigma _{1}^{{G_{2} }} \left( {y_{1} } \right)} \right) \wedge \left( {\sigma _{1}^{{G_{1} }} \left( {x_{2} } \right) \vee \sigma _{1}^{{G_{2} }} \left( {y_{2} } \right)} \right) \\ & = \mathop \sum \limits_{{x_{1} = x_{2} ,~~y_{1} y_{2} \in E_{2} }} \sigma _{1}^{{G_{2} }} \left( {y_{1} } \right) - \left\{ {\sigma _{1}^{{G_{1} }} \left( {x_{1} } \right) \vee \mu _{1}^{{G_{2} }} \left( {y_{1} ,y_{2} } \right)} \right\} \\ & \quad + \mathop \sum \limits_{{y_{1} = y_{2} ,~~x_{1} x_{2} \in E_{1} }} \sigma _{1}^{{G_{2} }} \left( {y_{1} } \right) - \left\{ {\sigma _{1}^{{G_{2} }} \left( {x_{2} } \right) \vee \mu _{1}^{{G_{1} }} \left( {x_{1} ,x_{2} } \right)} \right\} \\ & \quad + \mathop \sum \limits_{{x_{1} x_{2} \in E_{1} ,~~y_{1} y_{2} \notin E_{2} }} c_{3} + \mathop \sum \limits_{{x_{1} x_{2} \notin E_{1} ,~~y_{1} y_{2} \in E_{2} }} c_{3} + \mathop \sum \limits_{{x_{1} x_{2} \notin E_{1} ,y_{1} y_{2} \notin E_{2} }} c_{3} + \mathop \sum \limits_{{x_{1} x_{2} \in E_{1} ,y_{1} y_{2} \in E_{2} }} c_{3} \\ & = \left( {c_{3} - c_{1} } \right)g_{2} + \left( {c_{1} - c_{1} } \right)g_{1} + c_{3} d_{{G_{1}^{*} }} \left( {x_{1} } \right)\left| {\overline{{E_{2} }} } \right| + c_{3} \left| {\overline{{E_{1} }} } \right|d_{{G_{2}^{*} }} \left( {y_{1} } \right) + c_{3} \left| {\overline{{E_{1} }} } \right|\left| {\overline{{E_{2} }} } \right| \\ & \quad + c_{3} d_{{G_{2}^{*} }} \left( {x_{2} } \right)~d_{{G_{1}^{*} }} \left( {x_{1} } \right), \\ \end{aligned} $$

where \(\left| {\overline{{E_{1} }} } \right|\) and \(\left| {\overline{{E_{2} }} } \right|\) are the degree of vertex of complement graphs \(G_{1}^{*}\) and \(G_{2}^{*}\).

\(d_{1}^{{\overline{{G_{1} \times _{m} G_{2} }} }} \left( {x_{1} ,y_{1} } \right)\, = \,\left( {c_{3} - c_{1} } \right)g_{2} \, + \,c_{3} g_{1} \left| {\overline{{E_{2} }} } \right|\, + \,c_{3} g_{2} \left| {\overline{{E_{1} }} } \right|\, + \,c_{3} \left| {\overline{{E_{1} }} } \right|\left| {\overline{{E_{2} }} } \right|\, + \,c_{1} g_{1} g_{2}\).

Similarly

\(d_{2}^{{\overline{{G_{1} \times _{m} G_{2} }} }} \left( {x_{1} ,y_{1} } \right) = \left( {c_{4} - c_{2} } \right)g_{2} + c_{4} g_{1} \left| {\overline{{E_{2} }} } \right| + c_{4} g_{2} \left| {\overline{{E_{1} }} } \right| + c_{4} \left| {\overline{{E_{1} }} } \right|\left| {\overline{{E_{2} }} } \right| + c_{2} g_{1} g_{2}\).

This is true for all vertices of \(\overline{{V_{1} \times _{m} V_{2} }}\).

Case (ii) : If \(\sigma _{1}^{{G_{2} }} \left( x \right) \le \sigma _{1}^{{G_{1} }} \left( y \right)\) and \(\sigma _{2}^{{G_{2} }} \left( x \right) \ge \sigma _{2}^{{G_{1} }} \left( y \right)\) for all \(x \in V_{1}\) and \(y \in V_{2}\).

$$ \begin{aligned} d_{1}^{{\overline{{G_{1} \times _{m} G_{2} }} }} \left( {x_{1} ,y_{1} } \right) & = \mathop \sum \limits_{{x_{1} = x_{2} ,~~y_{1} y_{2} \in E_{2} }} \left( {\sigma _{1}^{{G_{1} }} \left( {x_{1} } \right) \vee \sigma _{1}^{{G_{2} }} \left( {y_{1} } \right)} \right) \wedge \left( {\sigma _{1}^{{G_{1} }} \left( {x_{2} } \right) \vee \sigma _{1}^{{G_{2} }} \left( {y_{2} } \right)} \right)~ \\ & \quad - \left( {\mu _{1}^{{G_{1} }} \times _{m} \mu _{1}^{{G_{2} }} } \right)\left( {\left( {x_{1} ,y_{1} } \right)\left( {x_{2} ,y_{2} } \right)} \right) \\ & \quad + \mathop \sum \limits_{{y_{1} = y_{2} ,~~x_{1} x_{2} \in E_{1} }} \left( {\sigma _{1}^{{G_{1} }} \left( {x_{1} } \right) \vee \sigma _{1}^{{G_{2} }} \left( {y_{1} } \right)} \right) \wedge \left( {\sigma _{1}^{{G_{1} }} \left( {x_{2} } \right) \vee \sigma _{1}^{{G_{2} }} \left( {y_{2} } \right)} \right)~ \\ & \quad - \left( {\mu _{1}^{{G_{1} }} \times _{m} \mu _{1}^{{G_{2} }} } \right)\left( {\left( {x_{1} ,y_{1} } \right)\left( {x_{2} ,y_{2} } \right)} \right) \\ & \quad + \mathop \sum \limits_{{~x_{1} x_{2} \in E_{1} ,y_{1} y_{2} \notin E_{2} }} \left( {\sigma _{1}^{{G_{1} }} \left( {x_{1} } \right) \vee \sigma _{1}^{{G_{2} }} \left( {y_{1} } \right)} \right) \wedge \left( {\sigma _{1}^{{G_{1} }} \left( {x_{2} } \right) \vee \sigma _{1}^{{G_{2} }} \left( {y_{2} } \right)} \right)~ \\ & \quad + \mathop \sum \limits_{{~x_{1} x_{2} \notin E_{1} ,y_{1} y_{2} \in E_{2} }} \left( {\sigma _{1}^{{G_{1} }} \left( {x_{1} } \right) \vee \sigma _{1}^{{G_{2} }} \left( {y_{1} } \right)} \right) \wedge \left( {\sigma _{1}^{{G_{1} }} \left( {x_{2} } \right) \vee \sigma _{1}^{{G_{2} }} \left( {y_{2} } \right)} \right)~ \\ & \quad - \left( {\mu _{1}^{{G_{1} }} \times _{m} \mu _{1}^{{G_{2} }} } \right)\left( {\left( {x_{1} ,y_{1} } \right)\left( {x_{2} ,y_{2} } \right)} \right) \\ & \quad + \mathop \sum \limits_{{x_{1} x_{2} \notin E_{1} ,y_{1} y_{2} \notin E_{2} }} \left( {\sigma _{1}^{{G_{1} }} \left( {x_{1} } \right) \vee \sigma _{1}^{{G_{2} }} \left( {y_{1} } \right)} \right) \wedge \left( {\sigma _{1}^{{G_{1} }} \left( {x_{2} } \right) \vee \sigma _{1}^{{G_{2} }} \left( {y_{2} } \right)} \right) \\ & \quad + \mathop \sum \limits_{{x_{1} x_{2} \in E_{1} ,y_{1} y_{2} \in E_{2} }} \left( {\sigma _{1}^{{G_{1} }} \left( {x_{1} } \right) \vee \sigma _{1}^{{G_{2} }} \left( {y_{1} } \right)} \right) \wedge \left( {\sigma _{1}^{{G_{1} }} \left( {x_{2} } \right) \vee \sigma _{1}^{{G_{2} }} \left( {y_{2} } \right)} \right) \\ \end{aligned} $$
$$ \begin{aligned} d_{1}^{{\overline{{G_{1} \times _{m} G_{2} }} }} \left( {x_{1} ,y_{1} } \right) & = \mathop \sum \limits_{{x_{1} = x_{2} ,~~y_{1} y_{2} \in E_{2} }} \sigma _{1}^{{G_{1} }} \left( {x_{2} } \right) - \sigma _{1}^{{G_{1} }} \left( {x_{1} } \right) \\ & \quad + \mathop \sum \limits_{{y_{1} = y_{2} ,~~x_{1} x_{2} \in E_{1} }} \sigma _{1}^{{G_{1} }} \left( {x_{2} } \right) - \sigma _{1}^{{G_{2} }} \left( {y_{1} } \right) \\ & \quad + \mathop \sum \limits_{{x_{1} x_{2} \in E_{1} ,~~y_{1} y_{2} \notin E_{2} }} \sigma _{1}^{{G_{2} }} \left( {x_{1} } \right) \\ & \quad + \mathop \sum \limits_{{x_{1} x_{2} \notin E_{1} ,~~y_{1} y_{2} \in E_{2} }} \sigma _{1}^{{G_{1} }} \left( {x_{1} } \right) \\ & \quad + \mathop \sum \limits_{{x_{1} x_{2} \notin E_{1} ,~~y_{1} y_{2} \notin E_{2} }} \sigma _{1}^{{G_{1} }} \left( {x_{1} } \right) \\ & \quad + \mathop \sum \limits_{{x_{1} x_{2} \in E_{1} ,~~y_{1} y_{2} \in E_{2} }} \sigma _{1}^{{G_{1} }} \left( {x_{1} } \right), \\ \end{aligned} $$

where \(E_{1}\) and \(E_{2}\) are the degree of the vertex of complement graphs of complement graphs \(G_{1}^{*}\) and \(G_{2}^{*}\)

$$ \begin{aligned} d_{1}^{{\overline{{G_{1} \times _{m} G_{2} }} }} \left( {x_{1} ,y_{1} } \right)\, & = \left( {c_{1} - c_{1} } \right)g_{1} \\ & \quad + \left( {c_{1} - c_{3} } \right)g_{2} + c_{1} g_{1} \left| {\overline{{E_{2} }} } \right| + c_{1} g_{2} \left| {\overline{{E_{1} }} } \right| + c_{1} \left| {\overline{{E_{1} }} } \right|\left| {\overline{{E_{2} }} } \right| + c_{1} g_{1} g_{2} \\ & = \left( {c_{1} - c_{3} } \right)g_{2} + c_{1} g_{1} \left| {\overline{{E_{2} }} } \right| + c_{1} g_{2} \left| {\overline{{E_{1} }} } \right| + c_{1} \left| {\overline{{E_{1} }} } \right|\left| {\overline{{E_{2} }} } \right| + c_{1} g_{1} g_{2} . \\ \end{aligned} $$

Similarly

$$ d_{2}^{{\overline{{G_{1} \times _{m} G_{2} }} }} \left( {x_{1} ,y_{1} } \right) = \left( {c_{2} - c_{4} } \right)g_{2} + c_{2} g_{1} \left| {\overline{{E_{2} }} } \right| + c_{2} g_{2} \left| {\overline{{E_{1} }} } \right| + c_{2} \left| {\overline{{E_{1} }} } \right|\left| {\overline{{E_{2} }} } \right| + c_{2} g_{1} g_{2} . $$

This is true for all vertices in \(\overline{{V_{1} \times _{m} V_{2} }}\).

Hence, complement of modular product of two regular intuitionistic fuzzy graphs is regular.

Applications of max product of intuitionistic fuzzy graphs in school determination

Let \(X\, = \,\left\{ {x_{1} ,x_{2} ,\, \ldots ,\,x_{n} } \right\}\) be the universe of discourse. Let \(A\, = \,\left\{ {\left\langle {x,~\mu _{1}^{A} \left( x \right),\mu _{2}^{A} \left( x \right)} \right\rangle :x \in X} \right\}\) and \(B\, = \,\left\{ {\left\langle {x,~\mu _{1}^{B} \left( x \right),\mu _{2}^{B} \left( x \right)} \right\rangle :x \in X} \right\}\) be two intuitionistic fuzzy sets in X. Szmidt and Kacprzyk [17, 18] proposed the following distance measure between \(A\) and B:

The Normalized Hamming Distance

$$ d\left( {A,B} \right) = \frac{1}{{2n}}\mathop \sum \limits_{{i = 1}}^{n} \left( {\left| {\mu _{1}^{A} \left( {x_{i} } \right) - \mu _{1}^{B} \left( x \right)} \right| + \left| {\mu _{2}^{A} \left( {x_{i} } \right) - \mu _{2}^{B} \left( x \right)} \right|} \right). $$

Suppose that \(S\, = \,\left\{ {S_{1} ,S_{2} ,\,~ \ldots ,\,S_{n} } \right\}\) be a set of schools, \(P\, = \,\left\{ {p_{1} ,p_{2} ,\, \ldots ,\,p_{m} } \right\}\) be a set of papers, and \(Q\, = \,\left\{ {q_{1} ,q_{2} ,\, \ldots ,\,q_{t} } \right\}\) be a set of students.

Let \(R_{1}\) be a relation between school points and each subject paper, and relation \(R_{2}\) be a relation between students and their corresponding subject entrance score.

We can describe the distance between the students and the schools using the following matrix:Equation as Image

Applying the fact that shortest distance between two intuitionistic fuzzy sets shows more similarity between them, therefore, it can be described that for the student \(q_{i}\) is to be enroll in the school corresponding to \(\mathop {\min }\limits_{{\text{i}}} \left\{ {d\left( {q_{i} ,S_{j} } \right)} \right\}\).

Here, we have considered a set of schools \(~S = \left\{ {S_{1} ,S_{2} ,S_{3} ,S_{4} ,S_{5} } \right\}\), \(P =\){Tamil (Ta), English (Eng), Mathematics (Mat), Science (Sci), Social Science (Sos)} be a set of papers and \(Q = \{\)Ali, Mathew, Sunil, Yusuf, Joseph}.

In Figs. 5 and 6, we assume that \(G_{1} = \left( {Q,~\left\{ {N_{1} ,N_{2} ,N_{3} ,N_{4} ,N_{5} } \right\}} \right)\) is an intuitionistic fuzzy graph of the set of students and \(G_{2} = \left( {S,\left\{ {N_{1}^{'} ,N_{2}^{'} ,N_{3}^{'} ,N_{4}^{'} ,N_{5}^{'} } \right\}} \right)\) is an intuitionistic fuzzy graph of the set of schools, where \(Q = \{\) Ali, Mathew, Sunil, Yusuf, Joseph and \(S = \left\{ {S_{1} ,S_{2} ,S_{3} ,S_{4} ,S_{5} } \right\}\)

Fig. 3
figure 3

Max Product \(G_{1} \times _{m} G_{2}\)

Full size image
Fig. 4
figure 4

Complement of max product of \(G_{1}\) and \(G_{2}\)

Full size image

.

Fig. 5
figure 5

Intuitionistic fuzzy graph \(G_{1}\)

Full size image
Fig. 6
figure 6

Intuitionistic fuzzy graph \(G_{2}\)

Full size image

The relation between school points and subject papers and the relation between students and their corresponding average entrance marks are given in Tables 3 and 4, respectively.

Table 3 Relation between school points and subject papers
Full size table
Table 4 Relation between students and their corresponding average entrance marks
Full size table

In the following table, we have used intuitionistic fuzzy sets as a tool, since it incorporates the membership grades (the average marks of the questions that have been correctly answered by the student) and the non-membership grades (the average marks of the questions that have been incorrectly answered by the student).

The max product of \(G_{1}\) and \(G_{2} ~\) is shown in Fig. 7.

Fig. 7
figure 7

Max product \(G_{1} \times _{m} G_{2}\)

Full size image

The following decision matrix has been obtained by finding distance between each student (Table 3) and each school (Table 4) using normalized hamming distance function depending upon the their entrance marks.

 

\(S_{1}\)

\(S_{2}\)

\(S_{3}\)

\(S_{4}\)

\(S_{5}\)

Ali

0.079167

0.084167

0.09

0.108333

0.125

Mathew

0.104167

0.1175

0.106667

0.058333

0.075

Sunil

0.0875

0.1675

0.14

0.091667

0.108333

Yusuf

0.1625

0.12583

0.08167

0.15

0.11667

Joseph

0.07083

0.1175

0.12333

0.09167

0.09167

From the above decision matrix, less distance between the student and school implies more possibility to get enrollment in the corresponding school. Therefore, the student Ali is to enroll in the school \(S_{1}\), the student Mathew is to enroll in the school \(S_{4}\), the student Sunil is to enroll in the school \(S_{1}\), the student Yusuf is to enroll in the school \(S_{3}\), and the student Joseph is to enroll in the school \(S_{1}\).

Conclusion

Graph theory has numerous applications in solving various networking problems encountered in different fields such as signal processing, transportation, and error codes. In particularly, the shortest path problem is a well-known combinatorial optimization problem in graph theory. Intuitionistic fuzzy graph models are more practical and useful than fuzzy graph models as it provides membership and non-membership grades for representing imprecise information which occur in real-life situations. This paper has introduced the complement of max product of two intuitionistic fuzzy graphs. Using the max product, the different types of structural models can be combined to produce a better one. The special attention on the regularity in the complement of two intuitionistic fuzzy graphs has been given as it can be applied widely in designing reliable communication and network systems. Finally, an application of intuitionistic fuzzy graphs in decision-making concern the school determination for the students based on their entrance score has been presented. In future, we are going to extend our work to: (1) Pythagorean fuzzy graphs; (2) Interval-valued Pythagorean fuzzy graphs, and (3) Spherical fuzzy graphs.