Introduction

In December 2019, a typical pneumonia occurred in Wuhan City, the capital of Hubei Province, China. On December 31st, the Health Commission of Wuhan reported 27 cases, and the disease quickly spread to other provinces in a short time with the Spring Festival Travel Rush. Initially, this virus was called the SARS-COV-2. On January 30th, 2020, WHO classified the Novel Coronavirus Pneumonia epidemic (NCP) as a public health emergency of international concern, and the NCP outbreak began to attract the attention of countries around the world. On February 11th, 2020, the disease was named as the Corona Virus Disease 2019 (COVID-19) by World Health Organization.

Mathematical modelling can be employed to better understand the dynamics of contagious diseases and simulate different scenarios, providing additional tools for health authorities to better propose adequate policies. Nowadays, a multitude of mathematical models have been employed to describe the dynamics of infectious diseases. The compartmental models especially the SIR and SIRD models have been widely used, due to their mathematical simplicity. First of all, the research works concerning SIR model are analyzed. Dhanwant and Ramanathan (2020) analyzed the COVID-19 spread in different countries, and identified the main feature of COVID-19 growth by using the SIR model. To forecast the outcome of the COVID-19, some scholars used the SIR model and estimated the epidemic model parameters (Vattay 2020; Bagal et al. 2020). Some research works have improved the SIR model. Martnez-Guerra and Flores-Flores (2021) proposed the Asymptomatic-Susceptible-Infective-Removed (A-SIR) model. Yang et al. (2021) proposed a SIR model with time fused coefficients but no time delay. Alenezi et al. (2021) used the sensible SIR model to analyze and predict the outbreak of COVID-19 in Kuwait. Turkyilmazoglu (2021) examined the SIR model to propose an analytical approach for providing an explicit formula associated with a straightforward computation of peak time of the outbreak. Furthermore, in some papers, the effect of prevention and control strategies was taken into account in SIR model. Bittihn and Golestanian (2020) proposed a strategy of containment based on fluctuations in the SIR model. Kumar (2020) used an age-structured SIR model with social distance and Bayesian imputation to study the progress of the COVID-19 epidemic in India. Geng et al. (2021) used the SIR model exploring the ramifications of targeted intervention on spatial patterns of new infections in the population agglomeration template. Deng et al. (2021) proposed a non-smooth SIR Filippov system to investigate the impacts of three control strategies (media coverage, vaccination and treatment) on the spread of an infectious disease. Lazebnik et al. (2021) developed an extended mathematical SIR model, allowing a multidimensional analysis of the impact of non-pharmaceutical intervention on the pandemic. Fu et al. (2021) extended the classic SIR model to find optimal decision making to balance economy and public health in the process of vaccination rollout. Depending on the proportions of variants and the public health strategies adopted, including anti-COVID-19 vaccination, Dimeglio et al. (2021) raised a modified SIR epidemiological model to predict how the spread of the virus in regions of France will vary.

Next, the research works involving SIRD model are analyzed. Many scholars have estimated the parameters of the SIRD model and analyzed the spread of the COVID-19. Fernndez et al. (2020) used data on death to estimate a standard SIRD model of COVID-19. Sen and Sen (2021) provided a modified SIRD model to analyze data of the pandemic and estimated and compared the key parameters. Gatta et al. (2021) modeled mobility data through a graph series in order to infer the parameters of SIR and SIRD models. Lobato et al. (2021) applied a methodology based on a double loop iteration process to estimate the parameters of SIRD model. Pacheco and Lacerda (2021) proved with the SIRD model that the approach of quantifying the different rates by means of function estimation was very robust and consistent. Gupth et al. (2021) used the SIRD compartment model for parameter estimation and prediction of COVID-19. Ananthi et al. (2021) predicted the infection spread and recovery rate of the epidemic by simulating model and checked the vulnerability. Additionally, a fractional-order SIRD model (Jahanshahi et al. 2021; Nisar et al. 2021) was introduced to predict the development of the COVID-19. Some scholars used SIRD model to estimate the basic reproduction number of the COVID-19 (Lounis and Raeei 2021; Al-Raeei 2021). The impact of prevention and control measures have been taken into account in SIRD models to analyze this epidemic (Zheng et al. 2021; Jason and Gunawan 2021).

In addition to SIR and SIRD, there were also some research works using other models. Susceptible-Exposed-Infective-Recovered (SEIR) (Yang et al. 2020; Peng et al. 2020) was used to analyze this epidemic. Chen et al. (2020) proposed a novel dynamical system with time delay to describe the outbreak of 2019-nCoV in China. Hellewell et al. (2020) used the stochastic transmission model to quantify the potential effectiveness of contact tracing and isolation of cases at controlling an acute respiratory syndrome coronavirus 2 (SARS-CoV-2)-like pathogen. Liu et al. (2020) developed a Susceptible-Infective-Reported-Unreported (SIRU) model to describe this epidemic. Their research focused on the effect of the Chinese imposed public policies designed to contain this epidemic, and the number of reported and unreported cases that have occurred. Lin et al. (2019) proposed conceptual models for the outbreak in Wuhan with the consideration of individual behavioural reaction and governmental actions. Prediction of NACP and the plateau phases of COVID-19 in China were investigated (Pei 2020; Zeng et al. 2020). Transmission potential and severity of COVID-19 (Remuzzi and Remuzzi 2020; Shim et al. 2020; Fanelli and Piazza 2020) were investigated. Model comparison works (Vytla et al. 2021; Chen et al. 2021) have also been done.

Of course, these researches about the COVID-19 were of great significance, but in the process of modeling, these scholars did not consider time delay and time-varying coefficients at the same time. For the adopted SIRD and SIR model, the incubation delay is non-negligible and should be included. Besides, their coefficients are usually not constant but time-dependent. In this paper, we study the development of the COVID-19 through a non-autonomous SIRD (S-Susceptible, I-Infected, R-Recovered, D-Dead) or SIR (S-Susceptible, I-Infected, R-Removed) epidemic models with time delay. They are two different models, mainly because R represents different meanings. In the SIRD model, R represents the cumulative or total number of the recovered groups, while in the SIR model, R represents the cumulative total of the recovered and dead groups. Since in some cities where the scale of the epidemic is small and there is almost no death, it is not appropriate to use the SIRD model, so we have proposed the SIR model. Using finite difference method, we find that the cure rates in Wuhan City, Hubei Province, China Mainland are approximately the linear increasing functions and their death rates are the piecewisely decreasing functions, and the cure rate in Hubei Province outside Wuhan (abbreviated as Hubei-Non-Wuhan or HNW) is the approximately linear increasing function and its death rate is nearly a constant. The SIRD model is suitable for these regions. However, the cure rates in Beijing, Shanghai, Zhejiang and Anhui Provinces are the approximately linear increasing functions and their death rates are nearly the very small constants. Therefore SIR model are suitable for them. According to the data released by the National Health Commission, the parameters of the model are accurately estimated, so as to effectively simulate the long-term development of the epidemic. We make a long-term prediction of numbers of current confirmed and accumulative dead cases of COVID-19 in some regions of China. We can estimate the turning points and the end time of COVID-19 and the maximum numbers of dead cases.

The structure of this paper is as the following. In Sect. 2, the SIRD and SIR models are introduced. The models’ parameter estimation and numerical solutions are presented in Sect. 3. The long-term predictions of some regions are presented in Sect. 4. The conclusion and discussion are given in Sect. 5.

Model building

This section introduces two non-autonomous time-delayed epidemic models of COVID-19 in China.

SIRD model

The subjects of SIRD model are susceptible, infected, recovered, and dead. The population under study is presumed to be invariant. Obviously, \(S(t)+I(t)+R(t)+D(t)=N\). In the model, natural and birth and death rates are not considered. We use the following symbols to mark the numbers of people in each category:

S(t):

Susceptible, representing the number of people who do not have infectious diseases at time t, but are likely to have infectious diseases;

I(t):

Infected, representing the number of people who get infectious diseases at time t;

R(t):

Recovered, representing the cumulative or total number of the recovered groups at time t;

D(t):

Dead, representing the cumulative or total number of the dead groups at time t.

In the paper, the highlights of the model lie in the following:

Firstly, time delay is introduced to describe the virus incubation period. Infected cases go through an incubation period of \(\tau\) days before showing significant symptoms. Once symptoms appear, the infected person will seek treatment and be transformed to the confirmed case. Many works did not consider the effect of the incubation delay. But actually this delay is long, even up to more than 20 days, and its effect on the dynamic is crucial. So we have to introduce it into the model and consider its effect on the dynamics and stability. In this paper, we take the mean value, 4 days, as the incubation delay.

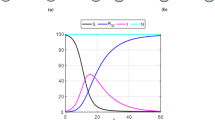
Secondly, according to the data of the early 16 days issued by the National Health Commission, we find that perhaps the cure rates in Wuhan City, Hubei Province, and China Mainland are the approximately linear increasing functions and their death rates are a piecewisely decreasing functions. We verify this argument by the data of longer periods of 25, 40, or 45 days. The reason is that the medical resources and treatment measures have been increased and improved rapidly from January 24th. The results of cure rates and death rates are displayed in Fig. 1a–f. The cure rate in Hubei-Non-Wuhan is approximately a linear increasing function and its death rate is nearly a constant. The results of cure and death rates are shown in Fig. 1g, h. Therefore, in our model the cure rate is approximated to be a linear increasing function. By the finite difference method, we accurately obtain the death rate functions. It is very crucial for the modeling and long-term prediction of the COVID-19 in China.

Through analysis, we can get the non-autonomous time-delayed dynamic model of COVID-19 in China in these regions as the following:

$$\begin{aligned} \begin{array}{ccl} \frac{dS}{dt}&{}=&{}-\frac{\beta S(t-\tau ) I(t-\tau )}{N}, \\ \frac{dI}{dt}&{}=&{}-(\gamma (t)+\mu (t)) I+\frac{\beta S(t-\tau ) I(t-\tau )}{N}, \\ \frac{dR}{dt}&{}=&{}\gamma (t) I, \\ \frac{dD}{dt}&{}=&{}\mu (t) I. \end{array} \end{aligned}$$
(1)

In the above model, \(\beta\) represents the rate of transmission for the susceptible to the infected. In model (1), we take the values of the incubation delay \(\tau\) as the mean value, 4 days. Let’s take \(\gamma (t)=\kappa t\), where \(\kappa\) is a constant and \(\gamma (t)\) represents the cure rate of the infected people. \(\mu (t)\) represents the death rate of infected cases. According to the model, \(\gamma (t)\) is approximately equal to the number of newly cured cases per day divided by the current number of infected cases on the present day. \(\mu (t)\) nearly equals the number of newly deaths per day divided by the current number of infected cases on the present day. From Eq.(1), we obtained the following expressions,

$$\begin{aligned} \begin{array}{ccl} \gamma (t)&{}\approx &{}\frac{R(t+1)-R(t)}{I(t)},\\ \mu (t)&{}\approx &{}\frac{D(t+1)-D(t)}{I(t)}. \end{array} \end{aligned}$$
(2)
Fig. 1
figure 1

Curves of cure and mortality rates of different regions in China

Full size image

SIR model

The subjects of SIR model are the susceptible, infected and removed groups. The removed group includes the dead and cured cases. Since in some regions, COVID-19 is not so serious and the number of infected, recovered and dead cases are very small; sometimes the number of dead cases is even 0, so the SIRD model will not work due to the big relative errors of R and D. We combine R (Recovered) and D (Dead) into one category as R (Removed). We use the following symbols to mark the numbers of people in each category:

S(t):

Susceptible, representing the number of people who do not have infectious diseases at time t, but are likely to have infectious diseases;

I(t):

Infected, representing the number of people who develop infectious diseases at time t;

R(t):

Removed, representing the cumulative total of the recovered and dead groups at time t.

Since Beijing, Shanghai and Zhejiang Province are not the outbreak sites, their numbers of deaths will be relatively small. Therefore we use the SIR model rather than the SIRD model for these regions. By the finite difference method, we find that the removed rates are approximately a linear increasing function. The results of removed rates in Beijing and Zhejiang Province are shown in Fig. 2a, b. So, in the model the removed rates are assumed to be linear functions of time t. Through analysis, we can get the non-autonomous time-delayed SIR epidemic model for these regions as the following:

$$\begin{aligned} \begin{array}{ccl} \frac{dS}{dt}&{}=&{}-\frac{\beta S(t-\tau ) I(t-\tau )}{N}, \\ \frac{dI}{dt}&{}=&{}-\eta (t) I+\frac{\beta S(t-\tau ) I(t-\tau )}{N}, \\ \frac{dR}{dt}&{}=&{}\eta (t) I. \\ \end{array} \end{aligned}$$
(3)

In the above model, \(\beta\) represents the rate of transmission from the susceptible to the infected, \(\eta (t)\) represents the removed rate of infected people. Let’s set \(\eta (t)=\kappa t\), where \(\kappa\) is a constant. According to the model, \(\eta (t)\) is equal to the number of newly removed cases on that day divided by the current number of infected patients on that day. From Eq.(3), we obtained the following expression,

$$\begin{aligned} \begin{array}{ccl} \eta (t)\approx & {} \frac{R(t+1)-R(t)}{I(t)}. \end{array} \end{aligned}$$
(4)
Fig. 2
figure 2

Curves of removed rates in Beijing and Zhejiang Province

Full size image

Estimation of parameters in the delayed SIRD and SIR models

Due to the adjustment of the standard of diagnosis of COVID-19 in China on February 12th, 2020 and the revision of data of COVID-19 on April 17th, 2020, we use the data of February 14th as the initial functions of S(t), I(t), R(t), D(t) for the DDEs (1) and use the data from February 15th, 2020 to February 29th, 2020 to estimate the parameters of the delayed SIRD epidemic model in Wuhan City, Hubei Province, China Mainland, Hubei-Non-Wuhan, then make their long-term predictions and compare them with real data from March 1st, 2020 to April 16th, 2020. We use the data of February 7th as the initial functions of S(t), I(t), R(t) for the DDEs (3) and use the data from February 8th, 2020 to February 22nd, 2020 to estimate parameters of the delayed SIR epidemic model in Beijing and Anhui Province. We use the data of February 5th as the initial functions of S(t), I(t), R(t) for the DDEs (3) and use the data from February 6th, 2020 to February 20th, 2020 to estimate parameters of the delayed SIR epidemic model in Shanghai and Zhejiang Province, then make the long-term predictions and compare them with real data until the end of the epidemic. Since we do not know exactly the real initial functions, here we have to take the constants functions as the initial functions of the non-autonomous DDEs, which will potentially induce errors.

SIRD model parameters inversion

In the SIRD model, the parameters to be estimated are \(\beta\) and \(\kappa\). From Fig. 1b, d, f, we see that \(\mu (t)\) is a piecewise function. \(\mu (t)\) is divided into \(t<10\) and \(10\le t\le 15\), and we get \(\mu (t)\) by calculating the average value separately. From Fig. 1h, we see that the death rate of Hubei-Non-Wuhan is nearly a constant, and \(\mu (t)\) is obtained by calculating the 15-day average. The value of \(\mu (t)\) is shown in Table 1.

Table 1 Death rates in different regions in China
Full size table

Based on the least square method, we use the Isqnonlin function built in Matlab to carry out parameter inversion and get the optimal parameter solutions. We choose the data of the February 14th as the initial functions of S(t), I(t), R(t), D(t). Here, we use R-squared to evaluate the results of the parameter estimations of the developed models. Results of model evaluation are shown in Table 2. Based on the official data, we get the results of parameter inversion as shown in Table 3.

Table 2 Model evaluation
Full size table
Table 3 SIRD model parameter inversion
Full size table

SIR model parameter inversion

In the SIR model, the parameters to be estimated are \(\beta\) and \(\kappa\), too. As in "SIRD model parameters inversion" section, we choose the corresponding initial functions of Beijing, Shanghai, Zhejiang Province and Anhui Province. We present the results of model evaluation in Table 4 and the results of parameter inversion in Table 5.

Table 4 Model evaluation
Full size table
Table 5 SIR model parameter inversion
Full size table

Long-term prediction

The parameters \(\beta\) and \(\kappa\) obtained in Sect. 3 are substituted into Eqs. (1) and (3) respectively, and the numerical method is carried out to simulate the evolutions of S(t), I(t), R(t), D(t) or S(t), I(t), R(t).

Long-term predictions of Wuhan City, Hubei Province, China Minland and Hubei-Non-Wuhan

In Fig. 3, the predicted data for current infected is compared with its real data. In Fig. 4, the predicted data for cumulative death is compared with its real data. Since the parameter estimation of the data of China Mainland is over fitting, the long-term prediction error is larger. Here, we take a minor disturbance to the estimated parameters of China Mainland, and then use the disturbed parameters to make its long-term prediction. In Fig. 3, we take \(\beta =0.019097\), \(\kappa =0.006246\). In these figures, solid curves describe the evolution curves of model (1) with the estimated parameters and points represent the officially published data. The blue dots stand for data used to estimate the parameters, and the red dots are the real data for the long-term prediction. Figure 3 indicates that the numbers of current infected will decrease after a peak. The peak is the turning point of the epidemic and the arrival of the turning point shows that the epidemic is under control. Wuhan City, Hubei Province and China Mainland are expected to end the epidemic at the end of April. Hubei-Non-Wuhan is expected to end the epidemic at the end of March. Figure 4 shows that the predicted numbers of final death are very close to their actual data. And both the total tendencies of the current infected and dead cases agree very well with each other.

Fig. 3
figure 3

The predictions of numbers of the current infected cases in Wuhan City, Hubei Province, China Mainland and Hubei-Non-Wuhan. Solid curve is the evolution curve of the current infected in model (1), dots represent the true data of the current infected issued by the government. The blue dots stand for data used to estimate the parameters, and the red dots are the real data for the long-term prediction

Full size image
Fig. 4
figure 4

The predictions of numbers of the cumulative death in Wuhan City, Hubei Province, China Mainland and Hubei-Non-Wuhan. Solid curve is the evolution curve of the cumulative death in model (1), and dots are the true data of the death issued by goverment. The blue dots stand for data used to estimate the parameters, and the red dots are the real data for the long-term prediction

Full size image

Long-term predictions of Beijing, Shanghai, Zhejiang and Anhui Provinces

In Fig. 5, we compare the predicted data for the current infected with their real data. Since the parameter estimation of the data of Beijing also appear over fitting, the long-term prediction error is larger. Here, we take a minor disturbance to the estimated parameters of Beijing, and then use the disturbed parameters to make predictions. In Fig. 5, we take \(\beta =0.025581\), \(\kappa =0.005905\). And the total tendencies agree very well with each other. In these figures, solid curves describe the evolution of model (3) with the estimated parameters and points represent officially published data. The blue dots stand for real data used to estimate the parameters, and the red dots are the real data for the long-term prediction. Figure 5 suggests that the numbers of the current infected decrease after the turning point and the epidemic is gradually under control. Beijing are expected to finish the epidemic at the middle of April. Shanghai, Zhejiang and Anhui Provinces are expected to finish the epidemic at the end of March.

Fig. 5
figure 5

The prediction numbers of the current infected cases in Beijing, Shanghai, Zhejiang Province and Anhui Province. Solid curve is the evolution curve of the current infected in model (3), dots represent the true data of the current infected issued by the government. The blue dots stand for data used to estimate the parameters, and the red dots are the real data for the long-term prediction

Full size image

Conclusion

SIRD and SIR epidemic models are classical and effective mathematical models of infectious disease. The SIRD model is suitable for epidemics with a large scale and a large number of death. If the scale of the epidemic is small and the death rate is low, the prediction error with the SIRD model may increase, and it is better to use the SIR model. During the modeling phase, we researched many complex models, such as the SEIR(D) model, where E represents the number of the exposed persons. Since the data of exposed persons has been not accurate statistics, there is no way to predict it precisely. Finally, we find that the simpler the model is the better the prediction effect. It is advisable to employ the SIRD and SIR to predict the COVID-19.

In this paper, SIRD model is used to describe the development of COVID-19 in Wuhan City and other regions and SIR model is used to establish the development of COVID-19 in Beijing and other regions. The simulation results indicate that the long-term predictions are in good agreement with the actual data published by the government. Our dynamic SIRD and SIR models are very effective in predicting the tendencies, especially the turning points, the end time and sizes of the current infected of COVID-19 epidemic and the highest numbers of death.

The recovery rate significantly increases and the death rate gradually decreases. From these figures, we can also estimate the duration and end of the COVID-19. Because the government has imposed the very strict, scientific and effective containment measures, we get a lower and lower rate of transmission and a relatively quick control of the epidemic. As China concentrated all its efforts on curing the infected and researching treatment options, the cure rate increases and death rate decreases quickly. Our paper may provide us an easy and effective method to predict the long-term evolution of COVID-19.