Characterizing slope regions

Abstract

This paper provides a theoretical characterization of monotonically connected image surface regions, called slope regions. The characterization is given by several topological properties described in terms of critical points relative to the region. We formally prove the necessary and sufficient conditions that a region needs to satisfy to be a slope region. We also provide a prototype of slope regions which is general and contains, as particular cases, the prototypes studied and published in previous conference papers.

1 Introduction

A digital image can be visualized as a 2.5D continuous surface by defining a continuous height (intensity) map $h:\mathbb {R}^2 \rightarrow \mathbb {R}$. The set of points in the surface with same height are called level sets (Osher and Fedkiw 2003). The critical sets (local minima, local maxima and saddles) of the surface can be just points but, in general, they are connected level sets. Intuitively, preserving critical sets and their connectivity will preserve the structure of the space because, extrema (i.e., local minima and local maxima) are surrounded by closed level curves if not artificially interrupted by the boundary of the data. Level curves intersect exclusively at saddles. In terms of earth topography, the configuration of critical points connected by monotonic curves in the surface were discussed a long time ago in Cayley (1859), Maxwell (1870).

The monotonic curves delineate surface patches, called slope regions, with the property that every pair of points inside such a patch can be connected by a monotonic curve. This way, slope regions may be seen as filling the space between the critical sets of the surface (see Kropatsch 2019b). A planar triangle is a simple example of a slope region and any triangular mesh partitions the surface into a set of slope regions. The space between critical sets of the surface can always be partitioned into slope regions. The corresponding decomposition of the surface with minimal number of slope regions preserving critical sets is called a minimal slope complex. In general, this partition is not unique and allows certain task and data-specific adaptations but every element of such a partition satisfies the requirements of the general prototype of slope regions given in this paper. First, such general prototype allows to check if a region-based partition (e.g. an image segmentation) is a valid slope complex (i.e., a cell decomposition of the surface where each 2-cell is a slope region) as we will see later. Second, it opens the door to set the grounds to construct a “slope grammar” describing all possible combinations of valid slope regions.

Regarding related works, the concepts of integral lines and Morse-Smale (MS) complexes were previously defined in Edelsbrunner et al. (2003b), Edelsbrunner et al. (2003a) and Edelsbrunner and Harer (2009), with the intention to build a hierarchy of increasingly coarse MS complexes. In that case, the decomposition is made into regions of uniform flow using integral lines. Specifically, MS complexes are built using a real-valued smooth map over the surface, with non-degenerated critical points. We will see later that the concept of integral line has great similarity to the monotonic curves of our approach although monotonic curves are geometrically less constrained.

Many efficient algorithms can be found in the literature to compute consistent MS complexes. For example, in Gyulassy et al. (2014), the authors presented an efficient algorithm to compute consistent MS complexes using a divide-and-conquer strategy for dealing with large data. In Sorgente et al. (2018), the authors introduced a novel algorithm using discrete gradient flow paths to decompose a 3D object into an atlas of disk-like charts. In Comic et al. (2010), the authors computed maximal cells of the ascending and descending Morse complexes through a watershed approach. Nevertheless, since the computation of slope complexes is not the goal of the paper, we only introduce here a first step to it and the comparison of slope complexes and MS-like complexes is left as future work.

With respect to other closely related technique such as Reeb graphs and complexes, in Marzantowicz et al. (2015), the authors characterized the Reeb graphs for functions f on manifolds ${{\mathcal {M}}}$ with concrete properties. For example, if ${{\mathcal {M}}}$ has finite fundamental group, then the Reeb graph of f is a tree.

Critical sets can appear in many different configurations. A catalogue of different configurations of the critical points and slope districts was discussed in Lee (1984). The author also provided visualizations of the “slope districts” (a simpler version of slope regions) using Critical Point Configuration Graphs constructed using peaks (local maxima), dales (local minima) and passes (saddle points). In Rosin (1995), the authors described a technique for extracting the slope districts from smooth discrete images and produce a hierarchical description in terms of linked slope districts.

Related conference publications published: In Kropatsch (2019a), given a 2D continuous surface, not necessarily being piecewise linear or smooth, we defined slope regions as simply connected components such that any two points in them are connected by a monotonic path, where the intersection between them are allowed. We introduced the concept of slope complexes which are particular cases of 2-dimensional (2D) CW-complexes in which each 2-cell is a slope region. From this start point, we proposed a prototype of slope regions with the constraint that their outer boundary is composed by exactly two monotonic curves. We explored how to create and reduce slope complexes, by describing a basic process to reduce the number of slope regions without affecting the bounding critical points, obtaining a simplified slope complex. The computation of slope complexes was made in Kropatsch (2019a) only in the case in which the height map is piecewise linear and slope regions are planar triangles obtained from a triangulation of a 2D continuous surface. In Cerman et al. (2016), we produced superpixel hierarchies (combinatorial graph pyramids) that are multiresolution segmentations of the given picture and where critical points are preserved along the pyramid. In Kropatsch (2019b), we approached the study of slope complexes from the point of view of the neighborhood graph of a digital picture. Its vertices can be interpolated to form a 2-manifold with critical points, where slopes and plateaus being the ones recognized by local binary patterns (LBPs). Neighborhood graph produces a cell decomposition of the manifold, where each 2-cell is a slope region. In Kropatsch (2019b), we showed that each level of the pyramid produces a slope complex. Slope complexes in different levels of the pyramid are always homeomorphic to disks. We also addressed the question whether there is a minimal number of slope regions that completely cover the 2.5D surface between a given set of critical points. We also provided a formula to count the minimum number of slope regions required to represent the surface, given the number of critical points. In Batavia et al. (2019b), we used the representation of a surface by a neighborhood (primal) graph and its dual, where the modifications in the primal graph are reflected in the dual. The vertices of such graphs are categorized into maximum, minimum, slope or saddle depending on the orientation of their incident edges. We introduced the orientation of the edges in the dual graph and showed that the LBP category of the dual vertex is consistent with the corresponding face in the primal graph, by providing an interpretation in the image context. Besides, we introduced a technique to orient monotonic paths with level curves in the primal graph and provided necessary and sufficient conditions for both primal and dual graph to merge two slope regions. In Batavia et al. (2019a), we introduced a second prototype with the aim of characterizing slope regions with the constraint that the outer boundary is a level curve. We provided necessary conditions for their existence and we showed that a well-composed 2D digital image can be partitioned into slope regions categorized into one of the two previously described prototypes. Finally, in Batavia et al. (2021), we proposed a Topology-preserving Irregular Image Pyramid (TIIP) algorithm including a hierarchical method to build an irregular image pyramid that preserves slopes regions. The algorithm operates on combinatorial maps which implicitly encode the structure of the image on the higher level of the pyramid with a compact representation. The use of combinatorial maps supports parallel processing with time complexity of $O(\log (d))$, where d is the diameter (in pixels) of the largest region after the simplification is made. With the TIIP algorithm, we were able to reconstruct images using as few as 30% of the color values and the information stored on top of the pyramid, although preserving fine details including the texture of the image. An example of an original and reconstructed image is showed in Fig. 1.

Fig. 1

Example of an image A and its reconstruction F using the TIIP algorithm introduced in Batavia et al. (2021). Observe that the reconstruction D of the original background B lost information while the original fine details C are preserved in E after the reconstruction

In this paper, necessary and sufficient conditions for a region to be slope are formally provided for the first time, obtaining a simple and complete characterization of slope regions and, as a consequence, a prototype for slope regions, which is general and complete. We also prove that prototypes described in previous papers are particular cases of our general prototype described here. Each result (Theorem, Lemma, Corollary) presented in this paper without a previous reference is original and new.

From the application point of view, Cerman et al. (2016) provided an algorithm where the neighborhood graphs were used to represent a digital image. By a sequence of edge contraction and edge removal operations, we reduced the graph and stack them to form an irregular graph pyramid. Later, irregular graph pyramids were used for multi-resolution image segmentation. Similar approaches were used in Wei et al. (2018) for multi-resolution image segmentation using a super pixel hierarchy. The characterization of slope regions presented in this paper opens a door to design robust algorithms to compute slope regions that could be used for image processing tasks such as geometric modeling, or filtering on segments with particular topological properties.

The paper is organized as follows. Section 2 is devoted to present the main definitions and basic tools that will be used throughout this paper. We also introduce the concept of monotonic curves, which will be the key point and reference of our work. Section 3 contains the theoretical results of the paper. We introduce the notion of slope regions, for which we use the concept of monotonic curves, and prove preliminary results which will lead us to obtain a complete characterization of the slope regions at the end of the section.

In Sect. 4, we approach the study of cell decomposition through the use of slope regions and prove that there is a natural way to move from a slope region to a 2-cell. Section 5 focuses on the general prototype of slope regions presented here for the first time, containing the prototypes published in previous conference papers as particular cases, with the aim of giving a combinatorial representation for such regions. Finally, Sect. 6 concludes the paper.

2 Preliminaries

Let us introduce several definitions based on a map $h:\mathbb {R}^2 \mapsto \mathbb {R}$ with the only requirement of h being continuous but not necessarily smooth.

A curve $\pi : [0,1]\rightarrow \mathbb {R}^2$ is a continuous map. It is simple if $\pi |_{(0,1)}$ is one-to-one. Otherwise, it is folded. It is monotonic if there is no interval $[a,b]\subset (0,1)$ being a 1-extremum. Let im$\,\pi$ be the set $\{p\in \mathbb {R}^2: p=\pi (t)$ for some $t\in [0,1]$}.

Definition 1

(1-extrema) Let $\pi : [0,1] \rightarrow \mathbb {R}^2$ be a curve and let $[a,b]\subset [0,1]$. Suppose that $h(\pi (t))=c$ for some $c\in \mathbb {R}$ and for all $t\in [a,b]$. Then, [a, b] is a 1-minimum (1-min) if there exists $\epsilon > 0$ such that $c< h(\pi (s))$ for all s in a neighborhood $((a-\epsilon , b+\epsilon )\setminus [a,b])\cap [0,1]$. Similarly, [a, b] is a 1-maximum (1-max) if $c> h(\pi (s))$ for all $s \in ((a-\epsilon ,b+\epsilon )\setminus [a,b])\cap [0,1]$. Finally, [a, b] is a 1-extremum if it is a 1-max or a 1-min. If $a=b$, then [a, a] is a 1-extremum point.

Definition 2

(level curve) A level curve $\gamma : [0,1] \rightarrow \mathbb {R}^2$ is a curve satisfying that there exists a constant $c \in \mathbb {R}$ such that $h(\gamma (t))=c$, for all $t \in [0,1]$.

Observe that a level curve is a particular case of monotonic curve. A level curve can also be part of a monotonic curve. Observe that all curves considered in this paper (including level curves) are connected.

Remark 1

A strictly monotonic curve, excluding level curves, is either increasing or decreasing. It is always bounded by a 1-max and a 1-min. This allows us to consider monotonic curves with a natural orientation. In our illustrations: an arrow from point a to point b represents a monotonic curve with endpoints a and b such that $h(a)> h(b)$. When the curve is exactly a level curve, no arrow is pictured. See Fig. 2.

Fig. 2

Level curves as part of a monotonic curve

An example of monotonic curve is shown in Fig. 2. The intervals [0, x] and [y, 1] are level-curve 1-extrema (1-max and 1-min respectively). Observe that no closed sub-interval of (0, 1) can be a 1-extremum.

A disk D of radius $r>0$ centered at a point $p\in \mathbb {R}^2$ is the set $D=\{q\in \mathbb {R}^2$ such that $d(p,q)\le r\}.$ The interior of D is $\mathrm {int}(D)=\{q\in \mathbb {R}^2$ such that $d(p,q)< r\}$ and the boundary of D is $\partial D=\{q\in \mathbb {R}^2$ such that $d(p,q)= r\}$.

A set $X\subseteq \mathbb {R}^2$ is disconnected if there exist two open sets $U_1\subseteq \mathbb {R}^2$ and $U_2\subseteq \mathbb {R}^2$ such that $X_1\subseteq U_1$, $X_2\subseteq U_2$, $X=X_1\cup X_2$ and $U_1\cap U_2=\emptyset$. Otherwise, X is connected. The set X is bounded if it is contained in a disk.

A hole of X is a bounded connected component of $\mathbb {R}^2\setminus X$. The set X is monotonically connected if it is connected and for any two different points p and q of X there exists a monotonic curve $\pi : [0,1] \rightarrow X$, with $\pi (0)=p$ and $\pi (1)=q$. The topological interior of X, denoted as $\mathrm {topint}(X)$, is defined as the largest open subset of X. The frontier of X, denoted as $\mathrm {fr}( X)$, is defined as $X\setminus \mathrm {topint}(X)$.

Definition 3

(plateau) A plateau $P_c$ is a bounded closed connected subset of $\mathbb {R}^2$ satisfying that $h(p)=c$ for all $p \in P_c$.

Observe that a plateau $P_c$ can be, for example, just a point in ${\mathbb {R}}^2$, a level curve or even the union of a set of level curves. A plateau may also contain holes.

Definition 4

(categories of plateaus) Let $P_c$ be a plateau.

• $P_c$ is a 2-minimum (2-min) if there exists a monotonically connected open set $U\subseteq \mathbb {R}^2$ satisfying that $P_c\subset U$ and $h(q)>c$ for every $q \in U\setminus P_c$.

• $P_c$ is a 2-maximum (2-max) if there exists a monotonically connected open set $U\subseteq \mathbb {R}^2$ satisfying that $P_c\subset U$ and $h(q)<c$ for every $q \in U\setminus P_c$.

• $P_c$ is a 2-saddle if for all open set $U\subseteq \mathbb {R}^2$ satisfying that $P_c\subset U$ then U is not monotonically connected.

A 2-extremum is either a 2-min or a 2-max. A 2-critical plateau is either a 2-extremum or a 2-saddle.

Let us recall that a homeomorphism is a bicontinuous bijective map. Now, let us introduce the concept of region.

Definition 5

(region) Let R be a subset of $\mathbb {R}^2$ and let D be a disk. The subset R is a region if it can be obtained as the image of a continuous surjective map $f: D\rightarrow R$ (that is, $R=\,$im$\,f$) satisfying that $f|_{\partial D}$ is a continuous curve and $f|_{\mathrm {int}(D)}$ is a homeomorphism.

Observe that the same region R could be obtained using different continuous surjective maps $f:D\rightarrow R$.

Definition 6

(boundary, outer boundary and interior of a region) Let R be a region obtained as the image of a continuous surjective map $f: D\rightarrow R$. The set of points in im$\,f|_{\mathrm {int}( D)}$, denoted as $int_f(R)$, is called the interior of R. Similarly, the set of points in im$\,f|_{\partial D}$, denoted by $\partial _f R$, is called the boundary of R. See Fig. 3.

The outer boundary of R is the image of a simple curve $\pi :[0,1]\rightarrow \partial _f R$, which divides the plane $\mathbb {R}^2$ in two connected components, one, containing R, bounded by im$\,\pi$ and one unbounded.

For the sake of simplicity, the interior and boundary of R will be denoted, respectively, as $\mathrm {int}(R)$ and $\partial R$, when it is not considered relevant to explicitly mention the function f. Besides, as we will see later, folded curves are needed for connecting the holes to the outer boundary.

Definition 7

(plateau region) A region being a plateau is called a plateau region.

Fig. 3

A pictorial example of a continuous surjective map f from a disk D to a region R. a The map f restricted to the boundary of D. b The map f restricted to the interior of D

Remark 2

Let R be a region. Then, $\mathrm {int}(R)$ lies in $\mathrm {topint}(R)$ and $\mathrm {fr}(R)$ lies in $\partial R$. Besides, $\mathrm {int}(R)$ is homeomorphic to a disk whereas $\mathrm {topint}(R)$ does not need to be. Finally, $\partial R$ is necessarily connected, whereas $\mathrm {fr}(R)$ is not. See Fig. 4.

Fig. 4

The boundary, the interior, the frontier, and the topological interior of a region R

Definition 8

(categories of plateaus relative to a region) Let R be a region and $P_c\subset R$ a plateau then:

• $P_c$ is an R-minimum (R-min) if there exists an open set $U\subseteq \mathbb {R}^2$ satisfying that $U\cap R$ is monotonically connected, $P_c\subset U\cap R$ and $h(q)>c$ for every $q \in U\cap R\setminus P_c$.

• $P_c$ is an R-maximum (R-max) if there exists an open set $U\subseteq \mathbb {R}^2$ satisfying that $U\cap R$ is monotonically connected, $P_c\subset U\cap R$ and $h(q)<c$ for every $q \in U\cap R\setminus P_c$. An R-extremum is either an R-min or an R-max.

Observe that an R-extremum that lies in the topological interior of R is, in fact, a 2-extremum. Conversely, a 2-extremum lying in the frontier of R is an R-extremum.

3 Slope regions

In this section we formally introduce the concept of slope region and study several preliminary results required to prove the necessary and sufficient conditions that any slope region needs to satisfy. As a main result, we provide and prove a complete and general characterization of slope regions.

Definition 9

(slope region) A slope region S is a monotonically connected region.

Notice that a plateau region is a trivial and particular case of slope regions, due to all points in the plateau region are connected by level curves, which are monotonic curves.

3.1 Necessary conditions of slope regions

Let us study properties that any slope region must satisfy.

Theorem 1

If S is a slope region then S does not contain any 2-saddle in its topological interior and it is either a plateau region or it is a region with maximally one R-max and one R-min.

Proof

By definition of slope regions there exists a monotonic curve between any two points in S, which directly implies that S cannot contain 2-saddles in its topological interior. Since S is not a plateau and it is closed and bounded, then S contains, at least, one R-max and one R-min. Neither two R-maxima nor two R-minima can be connected by a monotonic curve in S, then S cannot contain neither two or more R-maxima, nor two or more R-minima. $\square$

Lemma 1

The boundary of a slope region S is always either a level curve or it contains exactly one 1-max and one 1-min.

Proof

If for all $p\in \partial S$ we have that $h(p)=c$, for some $c\in \mathbb {R}$, then the proof is complete. Otherwise, $\partial S$ is a continuous non-level curve. Then, it has at least one 1-max I and one 1-min J (recall that I and J could be closed intervals or just points). Let us prove that $\partial S$ has exactly one 1-max and one 1-min. By contradiction, suppose that $\partial S$ has, for instance, another 1-max, denoted by $I'$. Consider two points $p\in I$ and $p'\in I'$. Assume that $h(p)\le h(p')$.

Since S is a slope region then there exists a monotonic curve $\pi :[0,1]\rightarrow S$ joining p and $p'$.

Now, since I is a 1-max, $p\in I$ with $h(p)\le h(p')$ and $\pi$ is monotonic then, necessarily, there exist $s,s'\in [0,1]$ such that $\pi (s), \pi (s')\in \partial S$, $h(p)\le h(\pi (s))\le h(\pi (s'))\le h(p')$ and $\pi ((s,s'))$ lies in $\mathrm {int}(S)$. Therefore, $\pi |_{[s,s']}$ divides S in, at least, two disjoint sets $S_1$ and $S_2$, and hence, $\partial S$ can be divided in two different continuous curves $\pi _1:[0,1]\rightarrow \partial S$ and $\pi _2:[0,1]\rightarrow \partial S$, one lying in $S_1$ and the other lying in $S_2$. Suppose that the 1-min J lies in $\pi _1$. Then, there exists another one 1-min $J'$ lying in $\pi _2$ since $\pi _2$ is a continuous curve. Consider $q\in J$ and $q'\in J'$. Assume that $h(q)\le h(q')$. Then, there exists a monotonic curve ${\hat{\pi }}:[0,1]\rightarrow S$ between q and $q'$. By similar reasoning as before, ${\hat{\pi }}$ crosses the interior of S and, then, there exists a point $r \in \mathrm {int}(S)$ such that $r\in \,$im$\,\pi \cap \,$im$\,{\hat{\pi }}$. For such point r, we have $h(q)\le h(r)\le h(q')<h(p)\le h(r)\le h(p')$ which is a contradiction. $\square$

3.2 Sufficient conditions of slope regions

Let us prove that sufficient conditions for a region R to be a slope region are: (a) R does not contain any 2-saddle in its topological interior, (b) R is either a plateau region or it contains one R-max and one R-min, and (c) $\partial R$ is either a level curve or it contains one 1-max and one 1-min.

From now on, let c be a value between the lowest and the highest h-values for the given continuous map h. Let $L_c=\{p\in R$ such that $h(p)=c\}$, being R a given region. The level set¹$L_c$ could be non-connected, so it might not be a plateau.

Lemma 2

Let R be a region with no 2-saddle in its topological interior, and with, exactly, one R-max and one R-min. Let $X=R\setminus L_c$. Then $X\ne \emptyset$ is composed by at most two connected components.

Proof

First, R is not a plateau then $X\ne \emptyset$. Let ${\bar{X}}$ be the closure² of X. Then, ${\bar{X}}$ is a subset of R, since R is closed. Moreover, since $R=X\cup L_c$ then ${\bar{X}}\setminus X$ is a subset of $L_c$. By contradiction, suppose that X is composed by more than two connected components, for instance, three connected components $X_1$, $X_2$ and $X_3$. Let ${\bar{X}}_i$ be the closure of $X_i$ for $i=1,2,3$. Since $\bar{X_i}\setminus X_i$ is a subset of $L_c$ and ${\bar{X}}_i\not \subseteq L_c$, for $i=1,2,3$, then ${\bar{X}}_i$ cannot be a plateau. An R-max (resp. R-min) relative to region ${\bar{X}}_i$ will be denoted by ${\bar{X}}_i$-max (resp. ${\bar{X}}_i$-min), for $i=1,2,3$. Now, since each ${\bar{X}}_i$ is closed and bounded, then there is at least one ${\bar{X}}_i$-min and one ${\bar{X}}_i$-max, for $i=1,2,3$. Without loss of generality, suppose that an ${\bar{X}}_1$-max coincides with the R-max. Then the rest of the ${\bar{X}}_i$-maxima cannot lie in $X_i$, for any $i=1,2,3$, since R only contains one R-max. Consequently, the rest of the ${\bar{X}}_i$-maxima lie in ${\bar{X}}_i\setminus X_i\subseteq L_c$, for $i=1,2,3$. Similarly, the R-min can coincide with an ${\bar{X}}_1$-min, an ${\bar{X}}_2$-min or an ${\bar{X}}_3$-min. Without loss of generality, suppose that the R-min coincides with an ${\bar{X}}_2$-min. Then, by the same reason as above, the rest of the ${\bar{X}}_i$-minima lie in $L_c$, for $i=1,2,3$. We conclude that one ${\bar{X}}_3$-max and one ${\bar{X}}_3$-min lie in $L_c$ and no ${\bar{X}}_3$-extremum lies in $X_3$. Then, necessarily, ${\bar{X}}_3\subseteq L_c$, which is a contradiction. $\square$

The previous lemma is used to prove that a level set contained in a region with specific constraints is always connected.

Lemma 3

Let R be a region with exactly one R-max, one R-min and without any 2-saddle in its topological interior. Assume that the boundary of R, $\partial R$, is either a level curve or it contains exactly one 1-max and one 1-min. Then $L_c$ is connected, where $L_c=\{p\in R$ such that $h(p)=c\}$.

Proof

Let $X=R\setminus L_c$. By Lemma 2, we know that X is composed by at most two connected components. First, observe that both, the R-max and the R-min, cannot belong to a same connected component of X, named Y, otherwise, there would exist a curve in Y between the R-max and the R-min and a point p in the curve satisfying that $h(p)=c$ which is not possible since $X\cap L_c=\emptyset$. Now, the next two cases can be distinguished:

• X is connected. Since both the R-max and the R-min cannot belong to X, then $L_c$ must be the R-max or the R-min. Therefore, by definition of R-extremum, $L_c$ is connected.

• X is composed by two connected components $X_1$ and $X_2$. By contradiction, suppose that $L_c$ is disconnected. Similar to what was done in the proof of Lemma 2, we can assume that the R-max lies in $X_1$ and the R-min lies in $X_2$. Then, $h(x_1)>c$ for all $x_1\in X_1$ and $h(x_2)<c$ for all $x_2\in X_2$.

Now, suppose that for some connected component L of $L_c$, we have that $L\cap {{{\bar{X}}}}_1=\emptyset$. In that case, we could find an open set $U\subset \mathbb {R}^2$ such that: $L\subset U\cap R\subset R\setminus {\bar{X}}_1$; $U\cap ( L_c \setminus L)=\emptyset$ (since L is a connected component of $L_c$); and $U\cap R$ is monotonically connected (since R has no 2-saddles in its topological interior). Then $U\cap R\subset L\cup X_2$ and, in that case, we conclude that L is an R-max (since $h(x_2)<c$ for all $x_2\in X_2$), which is a contradiction. A similar case occurs when $L\cap {{{\bar{X}}}}_2=\emptyset$.

Let us prove then that if $L_c$ is disconnected then there always exists a connected component L of $L_c$ such that $L\cap {{{\bar{X}}}}_1=\emptyset$ or $L\cap {{{\bar{X}}}}_2=\emptyset$, leading to the previous contradiction.

The different possibilities that can occur are the following:

• $\partial R\subseteq L_c$ (in such case, $\partial R$ is a level curve). Since $\partial R$ is connected, then $\partial R\subseteq L$ for some connected component L of $L_c$. Now, if $L\cap {{{\bar{X}}}}_1=\emptyset$ or $L\cap {{{\bar{X}}}}_2=\emptyset$, the proof has finished. Otherwise, assume that $L\cap {{{\bar{X}}}}_1\ne \emptyset$ and $L\cap {{{\bar{X}}}}_2\ne \emptyset$ and suppose that ${{{\bar{X}}}}_1\cap \partial R\ne \emptyset$. Let $L'$ be another connected component of $L_c$. Then, in particular, $L\cap L'=\emptyset$. Since $\partial R\subseteq L$ then $L'\subset \mathrm {int}(R)$ and necessarily $L'\cap {\bar{X}}_1=\emptyset$.

• $\partial R\subseteq X$. Since $\partial R$ is connected, assume, without loss of generality, that $\partial R\subseteq X_1$. Then $L_c$ and ${{{\bar{X}}}}_2$ lie in $\mathrm {int}(R)$. Therefore, ${\bar{X}}_2\setminus X_2\subseteq L_c$. Let L and $L'$ be two different connected components of $L_c$. Since $\partial R\subseteq X_1$, $X_1$ is connected and $X=X_1\cup X_2$ then $X_2$ has no holes (otherwise, either $X_1$ is not connected or ${{{\bar{X}}}}_2\cap \partial R\ne \emptyset$), then ${{{\bar{X}}}}_2\setminus X_2$ is connected and lies in one connected component of $L_c$, for example, L. Therefore, $L'\cap {{{\bar{X}}}}_2=\emptyset$.

• If $\partial R\not \subseteq L_c$ and $\partial R\not \subseteq X$ then, necessarily, $\partial R$ is not a level-curve. Then, $\partial R$ has exactly one 1-max and one 1-min. Two cases may arise: (1) One 1-extremum of $\partial R$ lies in $L_c$ and the other lies in X. Suppose, without loss of generality that the 1-min lies in $L_c$ and the 1-max lies in $X_1$. Then, $\partial R\subseteq L\cup X_1$ for some connected component L of $L_c$. Now, if $L\cap {{{\bar{X}}}}_2=\emptyset$, the proof has finished. Otherwise, ${{{\bar{X}}}}_2$ lies in $\mathrm {int}(R)$ and following a reasoning similar than above, ${{{\bar{X}}}}_2\setminus X_2\subseteq L$, concluding that $L'\cap {{{\bar{X}}}}_2=\emptyset$. (2) The two 1-extrema of $\partial R$ lie in X. Then, necessarily, the 1-max lies in $X_1$ and the 1-min lies in $X_2$. Then $\partial R\subseteq X\cup L_c$. Now, if there is a connected component L of $L_c$ such that $\partial R\cap L\ne \emptyset$ and either $L\cap {{{\bar{X}}}}_1=\emptyset$ or $L\cap {{{\bar{X}}}}_2=\emptyset$, the proof has finished. Otherwise, as before, there would exist another connected component $L'$ inside $\mathrm {int}(R)$ satisfying that $L'\cap {{{\bar{X}}}}_1= \emptyset$ or $L'\cap {{{\bar{X}}}}_2= \emptyset$, concluding the proof.

$\square$

The next result establishes sufficient conditions for a region R to be a slope region. Briefly, the next result shows that if R satisfies some constraints, it is always possible to construct a monotonic curve between any two points in R concatenating certain monotonic curves and level curves contained in R.

Theorem 2

If R is a region with no 2-saddles in its topological interior, with exactly one R-max and one R-min, and such that the boundary of R is either a level curve or it contains exactly one 1-max and one 1-min, then R is a slope region.

Proof

Let us prove that any two different points $p,q\in R$ can be joined by a monotonic curve in R.

First, suppose that $h(p)=h(q)=c$. In this case, $p,q \in L_c$ and, since $L_c$ is connected by Lemma 3, then there is a level curve (which is a particular case of monotonic curve) between p and q in R. Now, assume, without loss of generality, that $h(p)<h(q)$. Since R is connected, there is a curve $\pi : [0,1]\rightarrow R$ from p to q. If $\pi$ is monotonic then the proof is complete. Otherwise, since $\pi$ is continuous and [0, 1] is a bounded and closed set and due to $h(p)<h(q)$, there exists $n \ge 1$ (n can be infinite) such that there are subsets $[t_{i},s_i]$, for $1\le i\le n$, with $0\le t_1<s_1\le t_2<s_2\le \cdots \le t_{n}<s_n\le 1$ for which, every $\pi |_{[t_{i},s_i]}$, for $1\le i\le n$, is a monotonic increasing curve, that is, $h(\pi (t_{i})) < h(\pi (s_{i}))$ for $1\le i\le n$ and satisfying that $h(\pi (t_{i}))\le h(\pi (t_{i+1}))$ and $h(\pi (s_{i}))\le h(\pi (s_{i+1}))$ for $1\le i<n$; $h(\pi (s_{i})) = h(\pi (t_{i+1}))$ for $1\le i<n$; and related to p and q, it must verify that $h(p)=h(\pi (t_{1}))$ and $h(\pi (s_{n}))=h(q)$.

Besides, since $h(\pi (s_{i})) =h(\pi (t_{i+1}))$, for $1\le i<n$, by Lemma 3, there exists a level curve between $s_{i}$ and $t_{i+1}$, for $1\le i<n$, named $\gamma _{i}$. Moreover, since $h(p)=h(\pi (t_{1}))$ and $h(\pi (s_{n}))=h(q)$, there are also two level curves, one between p and $t_1$, denoted by $\gamma _{p}$, and other between $s_{n}$ and q, named $\gamma _{q}$. Then, a monotonic curve $\pi _{pq}$ can be constructed from p to q by the union of the monotonic curves $\pi |_{[t_{i},s_i]}$, for $1\le i\le n$, the level curves $\gamma _{i}$, for $1\le i< n$, $\gamma _{p}$, and $\gamma _{q}$, as follows:

$$\begin{aligned} \pi _{pq}=\gamma _{p} \cup \, \pi |_{[p,s_1]} \cup \, \gamma _1 \cup \, \pi |_{[t_2,s_2]} \cup \, \gamma _2 \cup \, \ldots \, \cup \, \gamma _{n-1} \cup \, \pi |_{[t_n,s_n]} \cup \, \gamma _{q}. \end{aligned}$$

Hence, there always exists a monotonic curve between any two different points in R, and therefore, R is a slope region. $\square$

As an immediate consequence of Theorems 1 and 2, we conclude this section with the characterization of slope regions.

Corollary 1

A region S is a slope region if and only if S satisfies the following conditions:

• S does not contain 2-saddles in its topological interior.

• S is either a plateau region (possibly with holes) or it contains exactly one R-max and one R-min.

• The boundary of S is either a level curve or it contains exactly one 1-max and one 1-min.

As a consequence, a slope region contains at most one 2-max and one 2-min.

4 Slope complexes

In this section we define a slope complex as a cell decomposition of the plane $\mathbb {R}^2$ such that the 2-cells are slope regions and the 1-cells are monotonic curves.

Using our approach, critical points can be degenerated, and monotonic curves do not necessarily follow the steepest slope, as used in Edelsbrunner et al. (2003b). Table 1 summarizes the different constraints to build MS complexes and slope complexes.

Table 1 The input of MS decomposition and slope decomposition

A detailed definition of cell complexes can be found, for example, in Chapter 1 of Hatcher (2000).

Briefly, to construct a cell decomposition of the plane $\mathbb {R}^2$ begin with a discrete space ${{\mathcal {T}}}_0\subset \mathbb {R}^2$ whose elements are called 0-cells or vertices. The space ${{\mathcal {T}}}_1\subset \mathbb {R}^2$ is obtained by attaching simple curves with endpoints in ${{\mathcal {T}}}_0$. Such curves are also called 1-cells or edges. To obtain ${{\mathcal {T}}}_2$, attach regions (also called 2-cells or faces) in a way such that the boundary of each region is the union of a finite number of edges of ${{\mathcal {T}}}_1$. If ${{\mathcal {T}}}_2=\mathbb {R}^2$, then ${{\mathcal {T}}}_0\subset {{\mathcal {T}}}_1\subset {{\mathcal {T}}}_2$ is a cell decomposition of $\mathbb {R}^2$.

In order to capture, in a cell decomposition of the plane, the behaviour of the continuous map $h:\mathbb {R}^2\rightarrow \mathbb {R}$, the cell decomposition and the map h need to satisfy several constraints.

First, we need the extra-condition for the continuous map h of not having accumulation points of 2-critical plateaus.

Remark 3

Let $p\in \mathbb {R}^2$. Let $D_{\epsilon }$ be the disk centered at a point $p\in \mathbb {R}^2$ with radius $\epsilon$. If, for any $\epsilon >0$, $D_{\epsilon }$ contains an infinite number of 2-critical plateaus then p cannot be contained in any slope region.

The next definition provides the structure of a cell decomposition formed by slope regions.

Definition 10

(slope complex) A slope complex K is a cell decomposition of $\mathbb {R}^2$ satisfying the following conditions:

• 1. Each region of K is a slope region.

• 2. For each 2-critical plateau P, there is a vertex of K which is a point of P.

• 3. For each slope region S and each R-extremum P, there is a vertex of K which is a point of P.

Fig. 5

General prototype of slope regions. The possibility of the existence of more holes is illustrated by dashed lines: Extra holes can be connected by paths to the three holes represented in the picture or to the outer boundary with the only constraint that all the paths can be joined together connecting $\oplus$ and $\ominus$ by exactly two different monotonic paths

To end this section, the following result guarantees that we can always compute a slope complex from a decomposition in slope regions.

Proposition 1

The boundary $\partial S$ of a slope region S can always be decomposed into a finite set of vertices and edges. If $\partial S$ is a continuous curve with exactly one 1-max and one 1-min, then $\partial S$ can be decomposed in two different sets of edges and vertices satisfying that each of these sets corresponds to a monotonic curve from a vertex being a point of the R-max to a vertex being a point of the R-min.

Proof

By Lemma 1, $\partial S$ can only be a level curve or a continuous curve with exactly one 1-max and one 1-min. Firstly, if $\partial S$ is a level curve then it can be decomposed in a finite set of simple level curves, and each of these curves can be decomposed in one or two vertices and one edge. Secondly, if $\partial S$ is a continuous curve with exactly one 1-max and one 1-min, then it can be decomposed in two different monotonic curves between the 1-max and the 1-min. Each monotonic curve can be decomposed in simple monotonic curves being edges with endpoints being vertices. If the 1-max (resp. the 1-min) is a vertex of the R-max (resp. the R-min), then the proof is complete. Otherwise, there exists a monotonic curve $\pi _{max}$ (resp. $\pi _{min}$) between any point of the R-max and the 1-max (resp. the R-min and the 1-min). Besides, such curves do not intersect $\partial S$, since the h-values of the points of $\partial S$ are lower (resp. higher) than the h-values of the points in $\pi _{max}$ (resp. $\pi _{min}$). For a similar reason, they do not intersect each other. Finally, decomposing such monotonic curves $\pi _{max}$ and $\pi _{min}$ in simple curves being edges, with endpoints being vertices, and joining them to the previous sets of vertices and edges, we obtain two finite sets of edges $\partial S$ that correspond to exactly two monotonic curves between one vertex of the R-max and one vertex of the R-min. $\square$

Fig. 6

A 2.5D mesh plot illustrating an “inclined slope region” and its prototype representation

5 Prototype of slope regions

As we have shown in Sect. 3, the slope regions have been univocally characterized, but they may have different arrangements, and then, different appearances. Hence it becomes necessary to sum up the common properties of all slope regions in a simple representation called “prototype”. A prototype is the combinatorial structure of a slope region. Therefore, prototypes show all the features that a corresponding slope region will exhibit. The prototypes are flexible and it is possible to remove certain elements (e.g., holes) which will result in different configurations of slope regions, but always keeping the same properties provided in Corollary 1. In this section, we first recall two already known prototypes of slope regions. Later, we sum up the two prototypes into a complete and general one, in terms of the elements provided by the characterization of slope regions: the two extrema relative to the region together with the boundary of the region, with the assurance that it represents any slope region. We end up the section with some examples of slope-region decomposition of a given gray-level image.

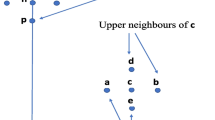
Figure 5 is the graphical representation through graphs of the general prototype representing all the possible configurations of slope regions. Paths represent the corresponding curves on the surface. Similarly, closed paths represent curves with same endpoint. An arrow on a path indicates that the corresponding curve is monotonic. An arrow from point a to point b indicates that $h(a)\ge h(b)$. The absence of arrows on a path indicates that the path represents a level curve. Observe that due to the characterization of slope regions given in this paper, all the possible configurations of slope regions have similar elements: there is the region R bounded by the outer boundary connecting the 1-max $m_1$ and the 1-min $m_2$.

In the topological interior of the region we could have an R-max $\oplus$ and the R-min $\ominus$. Each R-extremum is a vertex of the prototype, with possibly closed paths (representing level curves) attached (see Fig. 7). The R-max $\oplus$ and the R-min $\ominus$ are connected to $m_1$ and $m_2$ respectively by a monotonic path. The orientation of the path is from $\oplus$ to $m_1$ and from $m_2$ to $\ominus$ since $h(\oplus )$ $\ge$ $h(m_1)$ and $h(m_2)$ $\ge$ $h(\ominus )$. Intuitively, each hole represents a bounded connected set of points in $\mathbb {R}^2$ that cannot be connected to the points in R by a monotonic curve. Therefore, a hole cannot be a part of the slope region because it contradicts Definition 9. Intuitively, all the holes are connected to the boundary such that the interior of the region is homeomorphic to a disk. Holes can be further classified depending on their occurrence. Namely, (a) “inclined” holes surrounded by the monotonic paths $(\oplus , m_1)$ and $(m_2,\ominus )$ (example: $Hole_1$ and $Hole_2$ in Fig. 5); and (b) “horizontal” holes attached to such monotonic paths (example: $Hole_3$ in Fig. 5). More holes can be connected by paths to the holes represented in Fig. 5 or to the outer boundary with the constraint that all the paths can be joined together connecting $\oplus$ and $\ominus$ by exactly two different monotonic paths. The possibility of the existence of more holes is illustrated in Fig. 5) by dashed lines. Observe that horizontal holes can appear attached to other holes or to the outer boundary by level paths (see, for example, Fig. 6).

Observe that the two monotonic paths ${\hat{a}}$ and ${\check{a}}$ connecting $\oplus$ and $p_1$ in Fig. 5 are the same: they represent that there is a monotonic curve in the region which is obtained as the identification of both of them, ${\hat{a}}$ and ${\check{a}}$. Similar observation can be made for paths ${\hat{b}}$, ${\check{b}}$, ${\hat{c}}$, ${\check{c}}$, ${\hat{d}}$, ${\check{d}}$, or even for $h_5$ and $h_6$, which represent the same curve and, in that case, it must be a level curve. Otherwise, the resulting curve from the R-min to the R-max is not monotonic which is a necessary condition for the boundary of a slope region, as we proved in Sect. 3. The complete traversal along the boundary of the general prototype can be described as follows: $(\oplus , {\hat{a}}, h_1, {\hat{b}}, m_1, e, m_2, {\hat{d}}, h_4, {\hat{c}}, \ominus , {\check{c}}, h_3, {\check{d}}, m_2, {\hat{g}}, p_5, h_5, p,h,p$, $h_6$, $p_5$, ${\hat{f}}, m_1, {\check{b}}, h_2, {\check{a}}, \oplus )$. The paths responsible for connecting the elements $\oplus$, $\ominus$ and holes to the outer boundary are a subset of the complete boundary of the slope region, and they are intuitively called as “the folding of the boundary”. “Folding” and“unfolding” has also been used in Edelsbrunner et al. (2003b) for treating degenerated saddle points.

The general prototype presented in Fig. 5 is a generalized version of Prototype 1 (“inclined slope region”) mentioned in Kropatsch (2019a). An example of a 2.5D mesh plot and its graphical representation corresponding to Prototype 1 is given in Fig. 6. Observe that there can be many holes (as mentioned above) inside the slope region and that the outer boundary of the region is surrounded by exactly two monotonic paths connecting the 1-max $m_1$ and the 1-min $m_2$. Prototype 2 (“horizontal slope region”) mentioned in Batavia et al. (2019a) can also be obtained from the general prototype presented in Fig. 5, by replacing the monotonic paths in the outer boundary by paths representing level curves.

In the general prototype, if the R-max $\oplus$ (resp. R-min $\ominus$) is absent, vertex $m_1$ (resp. $m_2$) will become the R-max (resp. R-min). Besides, the absence of the R-max and the R-min together with the outer boundary of R being a level curve, will result in a plateau region.

To end up this part of the section, observe that the “crater” in Fig. 7 is an example of a slope region that is not a MS manifold. The R-max and the R-min in Fig. 7 are represented by one vertex and a closed level path attached. Intuitively, the R-max surrounds the crater and the R-min surrounds the foothill and coincides with the outer boundary of the region. Besides, the R-max and the R-min are connected by two monotonic paths in its prototype representation, being the complete boundary of the region described by the closed path $(\ominus ,b,{\hat{a}},\oplus ,h,{\check{a}},\ominus )$.

Fig. 7

A 2.5D mesh plot illustrating a “crater” and its prototype representation

5.1 Slopes in an image landscape

Let us now consider the digital image pictured in Fig. 8 and a 2.5D surface obtained by defining a continuous “height” (intensity) map $h:\mathbb {R}^2 \rightarrow \mathbb {R}$ by interpolating the gray level of the pixels. In the picture, the local minima, local maxima and saddle plateaus are surrounded, respectively, by a blue, red and green closed curve.

Fig. 8

a A digital image and, with the local minima, local maxima and saddle plateaus surrounded, respectively, by blue, red and green closed curves. b–d Different slope-region decomposition of the same image

The following examples of slope-region decomposition show both plateau regions and non-plateau slope regions S connecting R-max to R-min with folded boundaries forming monotonic paths. As per Corollary 1, a non-plateau slope region S contains exactly one R-max and one R-min. Therefore, the minimum number of slope regions required to decompose the image is three (see, for example, Fig. 8b). Also for any slope-region decomposition, either the saddle plateau is one region of the decomposition, or the saddle plateau is divided into respective slope regions (as shown by dashed lines in Fig. 8d).

The main advantage of slope decomposition over watershed or MS decomposition is the flexibility to choose the size of the slope region and the receptive field of the local extrema. Also, unlike MS decomposition algorithms, we allow holes inside the slope region. Depending on the constraints for optimization, following are a few examples of slope-region decompositions:

• Figure 8b. No holes.

• Figure 8c. A slope region as large as possible (the yellow slope region surrounding the whole image with holes which indeed are slope regions).

• Figure 8d. The local maximum has larger receptive field.

6 Conclusions and future work

In this paper, we have provided a complete characterization of monotonically connected regions, so-called slope regions, in terms of their main topological elements, namely, their critical points and the critical points on their boundary.

Moreover, a decomposition of a 2.5D surface in slope regions preserves the arrangements between critical points of the surface. We have also provided a general prototype of slope regions, in terms of graphs, that fulfills the characterization presented here.

For future work, we plan to extend the theory of slope regions to slope volumes and slope manifolds embedded in ${{\mathbb {R}}}^3$ to exploit the topological properties of 3D spaces.

The work can very well be compared with the concept of dyads and dendrites mentioned in Bertrand (2013) and Bertrand (2014).

We also plan to work on persistence measures which will be useful to eliminate the insignificant critical points. Besides, we plan to prove that MS complexes can be seen as particular cases of slopes complexes. Finally, Cerman et al. (2016) can be considered as a first step in the computation of slope complexes and we plan to continue this work in the very near future.

Regarding future applications, with the complete characterization of slope regions at hand, we could compute minimal slope complexes (slope complexes with minimal number of slope regions preserving critical points) and these minimal slope complexes could be used for robust image classification tasks, for example. Besides, notice that any hill-climbing optimization (such as back-propagation in neural networks) inside a slope region reaches the 2-max (if contained in the interior of the slope region). Consequently, iterative optimization on a given surface converges whenever the starting point is inside the slope region having the global maximum, even if there are other local maxima in the surface.

Besides, since a decomposition of a 2.5D surface into slope regions endows topological and structural properties, such decomposition could be used for applications such as segmentation, object recognition or geometric modeling.