1 Introduction

Recent progress in Additive Manufacturing (AM) and micro-fabrication technologies has opened up a whole new set of possibilities for the realization of metamaterials, i.e., artificial microstructures that exhibit properties and behaviors extending beyond the capabilities of ordinary materials [1]. In the context of mechanical metamaterials [2, 3], besides characteristics such as low mass density and high stiffness or strength [4, 5], in recent years also elastic flexibility and tailored buckling [6, 7], pentamode, auxetic and chiral effects [8,9,10], negative thermal expansion [11], or programmable behavior such as deployability and self-assembly [12,13,14] have been explored. Such mechanical metamaterials are realized by cellular microstructures, often beam lattices, which can be fabricated not only from stiff metals, but also from flexible, elastically deformable and multi-functional materials such as polymers, elastomers, or hydrogels. These metamaterials pave a pathway for a wide variety of multifunctional applications, such as energy harvesting and storage [15], bio-medics and medical devices [16], soft robotics [17], and many more [3].

The mechanical modeling of such flexible beam lattices is particularly challenging, since their microstructure and soft material constituents allow for geometrically large elastic deformations that are accompanied by instabilities due to strut buckling [7, 18], resulting in a highly nonlinear and anisotropic effective behavior. Full-scale simulation using 3D continuum finite elements (FE) is generally not feasible and also (geometrically) nonlinear 3D beam element discretizations can become computationally expensive and only feasible for lattices with a moderate amount of cells [19]. Furthermore, to resolve instabilities and ensure convergence of iterative solution schemes, nonlinear post-buckling analysis methods, such as buckling-mode perturbations [18, 20], are required, which incur further computational effort and complication.

Multiscale simulation approaches are generally preferred for microstructured objects and metamaterials, which have already been widely applied to lattice structures in the linear, infinitesimal strain regime, also for multiscale design and topology optimization [21,22,23,24]. Such approaches require that the microstructure is periodic and sufficiently small compared to the macroscale, i.e., that scales are separated. Then, the effective behavior for the microstructure can be homogenized from a representative unit cell (RUC) to relate the stress-strain response from microscale to macroscale, where the structure can then be regarded as a continuum [25].

In the context of nonlinear problems, the micro-to-macro transition can either be performed concurrently, using FE2 methods, or sequentially, using homogenized effective constitutive models [26, 27]. The concurrent approach has already been successfully applied to beam lattice structures in [20, 28], even including higher-gradient and curvature effects. However, it is computationally expensive, since solving a macroscale problem requires the solution of many microscale problems—one for each FE quadrature point in each iteration. Furthermore, in [20] only relatively small compressive strain ranges were investigated for buckling-dominated 3D lattices (\(-0.6\)% for a BCC structure and \(-5\)% for an Octet structure), which indicates that the concurrent multiscale approach also suffers from stability issues. For sequential nonlinear multiscale simulation, the main challenge is to formulate and identify an effective constitutive model, which—in the case of elastic beam lattices—should be hyperelastic for finite elastic deformations, reflect the anisotropy/material symmetry of the microstructure, and closely represent the actual microstructural behavior, which is highly nonlinear due to differences in stretch, bending, or buckling-dominated deformations. For simpler 2D and moderately nonlinear 3D lattices, analytical constitutive models were developed in [29,30,31,32]. However, for buckling-driven 3D lattices, analytically formulated models do not provide the necessary flexibility [33], which suggests the use of data-driven methods. In recent years, many such data-driven constitutive modeling approaches have been presented for anisotropic, hyperelastic, and inelastic material behavior, e.g., using reduced basis models [34, 35], clustering techniques such as self-consistent clustering analysis [36,37,38], polynomial or spline interpolation [39,40,41], or machine mearning (ML) with artificial neural networks (ANN) [42,43,44,45,46,47,48,49,50]. To the best of our knowledge, only in [51] ANN-based constitutive models have been applied to the multiscale simulation of highly geometrically nonlinear, buckling-prone microstructures. However, the work is restricted to 2D applications, material symmetry is not considered in the material model formulation, and the accuracy of the effective constitutive model itself is not assessed.

Generally, to ensure both accuracy and efficiency, data-driven constitutive models should:

  1. (1)

    Be flexible in terms of their formulation so that highly nonlinear behavior can be represented;

  2. (2)

    Incorporate as much structure of the problem as possible to ensure generalization capabilities (i.e., they should be physics-informed, e.g., by being formulated as hyperelastic, objective and respecting material symmetry);

  3. (3)

    Require only sparse calibration data or involve smart data acquisition strategies to save computational or experimental resources; and

  4. (4)

    Allow efficient evaluation to save computation time and effort when employed in (multiscale) finite element simulations.

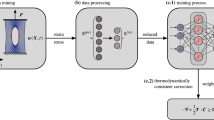
Thus, the goal of this work is to develop a nonlinear sequential multiscale method for the simulation of the highly nonlinear finite deformation behavior of elastic 3D beam lattices using accurate and efficient, yet flexible ML-based constitutive models based on ANNs, inspired by our previous work [33]. On the microscale, the RUC of a body-centered cubic (BCC) lattice is modelled as geometrically exact 3D beam structure with a linear elastic constitutive model, which results in a nonlinear, hyperelastic effective behavior. However, as mentioned above, these microstructures are prone to instabilities due to beam buckling, which—in practice—occur due to imperfections during manufacturing. For nonlinear post-buckling analysis, here only geometrical perturbations of the beam centerline are considered, while material and cross-section shape are assumed as ideal, in contrast to, e.g. [52, 53]. While usually eigenforms of the structure are prescribed as perturbations, see [18, 20, 53,54,55], here a purely stochastic approach is pursued. As we will demonstrate, this not only reduces the manual effort of bucking eigenvalue analysis, but also significantly reduces parasitic stresses in the homogenized responses, cf. [18]. The homogenized effective energy potentials and stresses obtained for various applied deformation gradients are then used as training and validation data for ANN-based constitutive models. To assesses their accuracy, generalization capabilities and efficiency in terms of required training data and evaluation times, three types of material models are compared: a hyperelastic model fulfilling exactly the cubic anisotropy, a hyperelastic model approximating the cubic anisotropy through data augmentation, cf. [44], and an elastic, stress-based model also approximating the cubic anisotropy through data augmentation. Hereby, it is shortly remarked that [44] considers data augmentation only in terms of the values of the elastic energy density, whereas the present work extends this approach also to stress values. In terms of material symmetry, the approaches of this work rely on the group symmetrization of [33] and the approximation through data augmentation. These approaches are applicable to arbitrary symmetry groups without any of the restrictions of invariant-based approaches relying on structural tensors and human-driven decisions on which invariants to consider. Finally, the hyperelastic ANN-based constitutive models are implemented into a nonlinear FEM so that the sequential multiscale simulation can be executed and verified in terms of convergence behavior and comparison with full-scale simulation of BCC lattice structures. Altogether, we summarize the main contributions of this work as:

  • Development, ANN-based implementation and validation of a sequential multiscale method for highly nonlinear, buckling-driven 3D beam lattices.

  • Evaluation of different anisotropic, ANN-based effective constitutive models for finite deformations in terms of accuracy and computation times. For learning the material symmetry, data augmentation approaches for strain energy densities and stresses are shown to increase the network training times, but significantly reduce their inference times.

  • Evaluation of efficient data generation strategies for the homogenization of microstructural instabilities using a stochastic perturbation approach, avoiding further computational expenses of eigenform-based approaches.

The manuscript is organized as follows. The description of the framework for the simulation and homogenization of the microscale RUCs is presented in Sect. 2, including the stochastic perturbation approach and its verification. Then, the constitutive modeling framework using ANNs is established in Sect. 3, the models are trained with the microscale data and compared against each other in terms of accuracy and computational performance. In Sect. 4, the nonlinear FE multiscale simulations are performed with the calibrated models and compared to full-scale simulations of lattice structures. Finally, the manuscript concludes with a summary and outlook in Sect. 5.

2 Microstructure modeling and simulation

2.1 Beam modeling of lattice unit cells

In this work, beam lattices are mechanically modeled as geometrically exact, shear-deformable 3D beam structures [56, 57]. This beam model captures large deformations and rotations of the beam centerline \(\varvec{r}:[0,L]\rightarrow \mathbb {R}^3\) and its cross-section, which is described by an orthonormal field \(\varvec{R}:[0,L]\rightarrow SO(3)\). However, due to the use of a linear elastic constitutive model that is characterized by the Young’s modulus E and Poisson’s ration \(\nu \) of an isotropic material, it is only applicable to moderate strains. The balance equations of linear and angular momentum read as:

$$\begin{aligned} \begin{array}{rl} \varvec{f}'(s) + \bar{\varvec{f}}(s) =&{} \varvec{0},\\ \varvec{m}'(s)+\varvec{r}'(s)\times \varvec{f}(s)+ \bar{\varvec{m}}(s) =&{} \varvec{0}, \end{array} \quad \forall s\in (0,L), \end{aligned}$$
(1)

where \(\varvec{f}\) and \(\varvec{m}\) are the internal forces and moments, which are computed in terms of the kinematic unknowns \(\varvec{r}\) and \(\varvec{R}\), \(\bar{\varvec{f}}\) and \(\bar{\varvec{m}}\) are externally applied distributed forces and moments, which are always zero here for homogenization purposes, and \('=d/ds\) denotes the arc-length derivative. As boundary conditions (BCs) at \(s=0\) and \(s=L\), either centerline positions and rotations (essential / Dirichlet BC) or forces and moments (natural / Neumann BC) must be prescribed.

For solving the boundary value problems (BVPs), here the beam model is numerically discretized by the isogeometric collocation method from [58]. First, the centerline curve is parameterized as a B-spline or non-uniform rational B-spline (NURBS) curve:

$$\begin{aligned} \varvec{r}_h(s) = \sum _{i=1}^n N_i(s) \varvec{r}_i, \end{aligned}$$
(2)

where \(N_i:[0,L]\rightarrow \mathbb {R}\) are \(C^{p-1}\)-continuous NURBS basis functions of a certain degree \(p>0\) with \(\ell =n-p\) internal elements and \(\varvec{r}_i\in \mathbb {R}^3\) are the n corresponding control points—similar to shape functions and nodal displacements in classical FEM. For more details on NURBS and isogeometric methods, see [59] and [60], respectively. Here the cross-section rotations \(\varvec{R}_h\) are parameterized in terms of unit quaternions and then also discretized as NURBS curves. Substituting these discretizations of the kinematic unknowns into the balance equations (1) and evaluating them at n suitable collocation points then yields a nonlinear system of equations, which can be solved using Newton’s method in order to determine the deformed configuration of the beam, see [58] for details.

Beam structures consisting of several beams can be modeled by aggregating the discertizations and nonlinear systems of the individual beams into one. Joints, where two or more beam end-points meet at a node and are coupled together, are here assumed to be rigid, i.e., the centerline displacements (and thus the positions in the current configuration) and the changes of the cross-section orientations have to be equal for all k coupled end-points:

$$\begin{aligned} \begin{aligned} \varDelta \varvec{r}^1&=\cdots = \varDelta \varvec{r}^k \qquad (\Leftrightarrow \; \varvec{r}_h^1=\cdots =\varvec{r}_h^k), \\ \varDelta \varvec{R}^1&=\cdots = \varDelta \varvec{R}^k \ . \end{aligned} \end{aligned}$$
(3)

Here, we use superscript indices to indicate quantities that relate to the end-points (nodes) of different beams, i.e., \(r^j_h\) is the centerline position of the j-th beam of the joint, which is given by either the first or last control point of the discretization of that beam. Furthermore, forces and moments have to be transferred at the joints, i.e., the balances of forces and moments have to be fulfilled:

$$\begin{aligned} \sum _{i=1}^k I^j \varvec{f}^j = \varvec{0}, \qquad \sum _{i=1}^k I^j \varvec{m}^j = \varvec{0}\ , \end{aligned}$$
(4)

where \(I^j=-1\) if \(s=0\) for the beam end-point, i.e., \(\varvec{r}^j=\varvec{r}^j_h(0)=\varvec{r}^j_1\), or \(I^j=1\) if \(s=L\), i.e., \(\varvec{r}^j=\varvec{r}^j_h(L)=\varvec{r}^j_n\). These constraints must also be implemented into the resulting nonlinear system, see [58] for details.

2.2 Stochastic perturbation approach for nonlinear post-buckling analysis

Since beams and beam structures are prone to structural instabilities such as buckling, nonlinear solution schemes such as Newton-Raphson and arc-length methods, in which converged solutions are computed iteratively for incrementally increasing applied loads or displacements, often suffer from convergence problems at the onset of buckling. Nonlinear post-buckling methods try to overcome this issue typically by applying some perturbation to the BVP, such that the instability and ambiguity of the solution are overcome. These perturbations, which are typically applied to the undeformed geometric configuration in the context of numerical methods, can also be associated with uncertainties in geometric parameters, e.g., stemming from manufacturing inaccuracies and tolerances.

Here, a stochastic, geometric perturbation approach is employed, in which the centerline curves of the initially perfectly straight struts of a beam lattice structure are perturbed. Since the struts are initially straight, they are simply defined by their two end-points and parameterized as linear line segments, i.e., “NURBS” with \(p=1,\ell =1,n=2\). Now, order elevation to increase the degree of the NURBS to \(p>1\) (p-refinement) and subdivison into \(\ell >1\) equidistant elements (h-refinement) are performed, yielding a \(C^{p-1}\)-continuous NURBS curve with \(n=p+\ell \) control points, which still exactly represent a straight line, compare (2) and see [59] for details.

Now, the struts are perturbed normal to the tangential direction \(\varvec{r}'\) of the beam, i.e., within the cross-section plane. Therefore only two parameters are needed to perturb each individual control point \(\varvec{r}_i\): the magnitude \(a_i\in \mathbb {R}\) and the angle \(\psi _i\in [-\frac{\pi }{2},+\frac{\pi }{2})\) of the perturbation (around the axis defined by \(\varvec{d}^3=\varvec{r}'\) and starting from the \(\varvec{d}^1\)-axis, as defined by the orthonormal frame \(\varvec{R}=(\varvec{d}^1,\varvec{d}^2,\varvec{d}^3)\)). From a practical point of view, the magnitude is assumed to be normally distributed around a mean of 0 with a variance of \(\sigma ^2\), i.e., \(a_i\in \mathcal {N}(0,\sigma ^2)\), and the angle uniformly distributed, i.e., \(\psi _i\in \mathcal {U}(-\frac{\pi }{2},+\frac{\pi }{2})\), where \(+\frac{\pi }{2}\) is excluded from the distribution as opposed to a uniform distribution as in literature [61]. These uncorrelated random perturbations are applied to the inner (non-end) points of each beam, yielding the perturbed control points as:

$$\begin{aligned} \varvec{r}_i^*=\varvec{r}_i + a_i \left( \sin \psi _i\,\varvec{d}_i^1 + \cos \psi _i\,\varvec{d}_i^2 \right) , \quad i=2,\ldots ,n-1. \end{aligned}$$
(5)

However, for boundary points that are connected to other beams, as it is always the case for the nodes of a periodic lattice structure, the tangential direction of the beam is ambiguous and it must be ensured that \(\varvec{r}^1=\cdots =\varvec{r}^k\) holds, similar to (3). Thus, the perturbation:

$$\begin{aligned} {\varvec{r}^j}^* = \varvec{r}^j + \begin{pmatrix} a_x \\ a_y \\ a_z \end{pmatrix}, \end{aligned}$$
(6)

with three separate perturbations \(a_{x,y,z}\in \mathcal {N}(0,\sigma ^2)\), is applied to the node, i.e., for each beam end-point of the joint, \(j=1,\ldots ,k\). For the RUC of a lattice microstructure, this applies not only to nodes inside the cell, but also to periodically connected nodes on opposing boundary faces and edges, which have to be identified for that purpose.

The stochastic perturbation procedure is illustrated in Fig. 1, which shows the centerlines at a joint with 4 beams in the unperturbed configuration and in 3 random perturbations. In summary, the perturbations are controlled by three parameters: the NURBS refinement given by p and \(\ell \), as well as the magnitude given in terms of the variance \(\sigma ^2\).

Fig. 1
figure 1

Illustration of stochastic perturbations of beam centerlines at a joint with 4 beams

Full size image

2.3 Microstructural homogenization framework

The present work aims at the multiscale simulation of the mechanical behavior of elastic beam lattices subject to finite deformations. For this purpose, a separation of scales between the macroscopic lattice structure and its periodic microstructure are assumed. Furthermore, the effective constitutive behavior of the microstructure is characterized by a representative unit cell (RUC), which is given by a domain \(\varOmega _0\subset \mathbb {R}^3\), and assumed to be hyperelastic, i.e., an effective elastic energy density W exists. For any quantity defined on the microscopic continuum \(\phi :\varOmega _0\rightarrow \mathbb {R}\), or in the same way also for tensor-valued quantities, averages over the reference configuration of the RUC are denoted as:

$$\begin{aligned} \langle \phi \rangle = \frac{1}{V_0} \int _{\varOmega _0} \phi (\varvec{X}) \mathrm {d}\varOmega _0, \end{aligned}$$
(7)

where \(V_0=|\varOmega _0|\) is the volume of the RUC. Hereby, a local elastic energy density \(W^\mu \) depending on the local deformation gradient \(\varvec{F}^\mu \) within the RUC is assumed as known. The local first Piola-Kirchhoff stress tensor is defined as \(\varvec{P}^\mu = {\partial W^\mu }/{\partial \varvec{F}^\mu }\). The effective deformation gradient \(\varvec{F}\) is defined as:

$$\begin{aligned} \varvec{F}= \langle \varvec{F}^\mu \rangle \ . \end{aligned}$$
(8)

The effective elastic energy density W, also referred to as the effective potential, is defined as:

$$\begin{aligned} W = \langle W^\mu \rangle \ . \end{aligned}$$
(9)

The effective potential W depends implicitly on the effective deformation gradient \(\varvec{F}\) through the solution of the microscopic boundary value problem of the RUC, i.e., \(W = W(\varvec{F})\). Further, the effective potential W fully describes the effective constitutive behavior of the hyperelastic RUC. Hereby, the effective stress is defined as:

$$\begin{aligned} \varvec{P}= \frac{\partial W}{\partial \varvec{F}}. \end{aligned}$$
(10)

To fulfill the Hill-Mandel condition [26]:

$$\begin{aligned} \langle \varvec{P}^\mu : \delta \varvec{F}^\mu \rangle = \varvec{P}: \delta \varvec{F}\ , \end{aligned}$$
(11)

within this work affine and periodic displacement boundary conditions are used to impose an effective \(\varvec{F}\) on the RUC, which implies:

$$\begin{aligned} \varvec{P}= \langle \varvec{P}^\mu \rangle \ . \end{aligned}$$
(12)
Fig. 2
figure 2

Illustration of the RUC of a BCC lattice with random centerline perturbations

Full size image
Table 1 Boundary condition types and applied displacement gradients for the different deformation modes (BC “p”: periodic, BC “d”: affine displacement)
Full size table

For the homogenization of the effective behavior of a beam lattice microstructure, each beam of the RUC is first perturbed as described in Sect. 2.2. For instance, Fig. 2 shows a body-centered cubic beam lattice with perturbed struts. Then, the RUC is subjected to several effective deformation modes, which are specified in terms of a displacement gradient \(\varvec{H}=\varvec{F}-\varvec{I}\), which is applied to the boundary nodes of the RUC either as an affine displacement (Dirichlet, “d”) or periodic displacement (“p”) BC:

$$\begin{aligned} \begin{aligned} {``{\hbox {d}}\text {''}}&:&\varvec{u}^j&= \varvec{H}\varvec{r}^j, \\ {``{\hbox {p}}\text {''}}&:&\varvec{u}^{j_+}-\varvec{u}^{j_{-}}&= \varvec{H}(\varvec{r}^{j_{+}}-\varvec{r}^{j_{-}}) \quad \wedge \\&\varvec{f}^{j_{-}} + \varvec{f}^{j_{+}}&=\mathbf {0}, \quad \varvec{m}^{j_{-}} + \varvec{m}^{j_+}=\mathbf {0}. \end{aligned} \end{aligned}$$
(13)

Here, \(\varvec{r}^j\in \mathbb {R}^3,\, j\in \mathcal {B}\) are the reference centerline positions of each node on the boundary of the RUC, where \(\mathcal {B}\) is the set of all boundary nodes, or \(\varvec{r}^{j_+},\varvec{r}^{j_-}\in \mathbb {R}^3\), \( \{{j_-},{j_+}\}\in \mathcal {B}^\pm \) are the pairs of nodes on opposite boundaries, respectively, and \(\varvec{u}^j,\varvec{u}^{j_+},\varvec{u}^{j_-}\in \mathbb {R}^3\) their corresponding displacements. To realize scenarios that can correspond to practical, experimentally conductable mechanical tests, e.g., uniaxial tension with prescribed deformation in the \(x_1\)-direction, unconstrained displacements in \(x_2,x_3\)-direction and only \(P_{11}\ne 0\), “d” and “p” BC may vary component-wise, see Table 1. The displacement gradients are applied in a step-wise manner, i.e., \(\varvec{H}=\varvec{H}(\lambda )\), where the factor \(\lambda \) is increased in steps of 0.003 until the desired end values of \(\lambda _{stop}=\pm 0.3\) (for tension and compression) are reached, resulting in 201 data points for each mode and perturbation. It should be noted also that the rotational BC for the nodes are always periodic boundary condition (PBC), i.e., all connecting corners need to rotate in the same way independent of the applied displacement gradient.

For discrete microstructures such as beam lattices, the resulting effective strain energy densities \(W(\varvec{F})\) and stresses \(\varvec{P}(\varvec{F})\) resulting from these simulations can in fact not be computed as volume averages via (9) and (12), since there is not microscopic continuum. However, the effective strain energy density \(W(\varvec{F})\) can be computed as the sum of all strain energies of the beams of the RUC, divided by the volume \(V_0\) of the RUC. Furthermore, by converting the volume averages to boundary integrals, the averaged first Piola-Kirchhoff stress tensor is computed as:

$$\begin{aligned} \varvec{P}(\varvec{F}) = \frac{1}{V_0} \sum _{j \in \mathcal {B}} \varvec{f}^j \otimes \varvec{r}^j, \end{aligned}$$
(14)

where \(\varvec{f}^j\) are the internal forces at the node \(\varvec{r}^j\), cf. (1) and (4).

2.4 Numerical results and verification

Fig. 3
figure 3

Depicting \(p:=\text{ tr }(\varvec{P})/3\) over \(\lambda \) for volumetric compression both with all runs (top) and with the runs remaining after discarding the unstable buckling band (bottom)

Full size image
Fig. 4
figure 4

Uniaxial deformation mode. All 9 components of \(\varvec{P}\) are shown over \(\lambda \) for the reference data, as well as all 206 stochastic perturbations and their mean values

Full size image

The numerical framework for the finite strain homogenization of the effective behavior of beam lattice microstructures based on nonlinear post-buckling analysis using a stochastic perturbation approach is now being applied to a BCC lattice RUC. Here, and for the reminder of the manuscript, the size of the microstructure is taken as \(L=10\) mm, i.e., \(V_0=10^3 \hbox { mm}^{3}\), the aspect ratio is \(a=d/L=0.1\), i.e., the beam diameters are \(d=2r=1\) mm, and the material parameters are \(E=0.53\) MPa and \(\nu =0.45\). Furthermore, the stochastic perturbations are applied with a spline refinement of \(p=2,\ell =8\) and a variance \(\sigma ^2=0.1r\). These parameters were heuristically determined such that impact of perturbations on the results at small strains is minimized, while reliable convergence is achieved in the (post-) buckling regimes. Furthermore, the following verifications were performed to ensure the validity of the approach:

2.4.1 Consistency checks.

To assess the impact of instabilities and perturbations on the numerical results, first a simple consistency check between the numerically computed \(W(\varvec{F})\) and \(\varvec{P}(\varvec{F})\) is performed. Consider the implicit dependency with respect to the process parameter \(\lambda \) and expand \(W(\lambda )=W(\varvec{F}(\lambda ))\) around some \(\hat{\lambda }\) as follows:

$$\begin{aligned} W(\lambda ) = W(\hat{\lambda }) + \frac{\partial W}{\partial \lambda }(\hat{\lambda }) \cdot (\lambda - \hat{\lambda }) + \mathcal {O}(\lambda ^2) \ . \end{aligned}$$
(15)

We now focus our attention on the tangent \(t(\hat{\lambda }) = {\partial W}/{\partial \lambda }(\hat{\lambda })\) and apply the chain rule:

$$\begin{aligned} \begin{aligned} t(\hat{\lambda })&= \frac{\partial W}{\partial \lambda }(\hat{\lambda }) = \frac{\partial W}{\partial \varvec{F}}(\varvec{F}(\hat{\lambda })):\frac{\partial \varvec{F}}{\partial \lambda }(\hat{\lambda }) \\&= \varvec{P}(\varvec{F}(\hat{\lambda })) : \frac{\partial \varvec{F}}{\partial \lambda }(\hat{\lambda }) \ . \end{aligned} \end{aligned}$$
(16)

In view of the discrete simulation results, the identities in (16) motivate the introduction of the following quantities for the second-order finite difference approximation of \(t(\lambda _n) = t_n\) at an incremental simulation step n:

$$\begin{aligned} t_n^{W}= & {} \frac{W_{n+1} - W_{n-1}}{\lambda _{n+1} - \lambda _{n-1}} \ , \end{aligned}$$
(17)
$$\begin{aligned} t_n^{P}= & {} \varvec{P}_n : \frac{\varvec{F}_{n+1} - \varvec{F}_{n-1}}{\lambda _{n+1} - \lambda _{n-1}} \ , \end{aligned}$$
(18)

where \(W_n=W(\lambda _n)\), etc. The tangent approximations \(t_n^{W}\) and \(t_n^{P}\) can be computed independently based on the results for \(W, \varvec{F}\) and \(\varvec{P}\) at steps \(\lambda _n\). The consistency of the simulation results can then be evaluated based on the relative error:

$$\begin{aligned} e_n = \left| \frac{t_n^{W} - t_n^{P}}{t_n^{W}} \right| \ . \end{aligned}$$
(19)

The present work considers the results of a simulation campaign for \(\varvec{H}(\lambda )\) as sufficiently consistent and acceptable if in a maximum of 6 out of the 201 simulation steps \(e_n\) surpasses \(10\%\), 3 for \(\lambda < 0\) and 3 for \(\lambda > 0\). Otherwise, a new random perturbation is applied an the simulation is re-run. All numerical results shown in the following passed this consistency check.

Fig. 5
figure 5

Biaxial deformation mode. All 9 components of \(\varvec{P}\) are shown over \(\lambda \) for the reference data, as well as all stochastic 206 perturbations and their mean values

Full size image
Fig. 6
figure 6

Shear-combined deformation mode. All 9 components of \(\varvec{P}\) are shown over \(\lambda \) for the reference data, as well as all 206 stochastic perturbations and their mean values

Full size image

2.4.2 Buckling bands and outliers

During compression on multiple axis, e.g., during the volumetric mode, it occurs that simulation results for some “outlier” perturbations are stiffer compared to the majority of other perturbations and buckle at higher stresses, see Fig. 3 (top). It can be seen that while the majority of runs follows roughly the same path, i.e., is on the same “band”, there are some simulations following a somewhat stiffer path and buckling only later, i.e., at a higher magnitude of applied strain. From this second band, some simulations jump back onto the first band, while the rest remains on this stiffer band. Overall, it seems that this stiffer band represents an unstable equilibrium path and thus at higher compression many solutions fall back to the softer, stable band. In order to eliminate these outliers, all simulation runs, where the trace of \(\varvec{P}\) is greater than 1.25 times the average of all runs at \(\lambda =-0.018\), were discarded, see Fig. 3 (bottom). From the 250 simulations with random perturbations executed, we obtained 206 perturbations on the lower band, i.e., with a stable equilibrium path according to the aforementioned criterion. This results in a rejection of 44 perturbations and a rejection rate of \(17.6\%\).

2.4.3 Comparison with reference data

The data obtained by the stochastic perturbation approach is now compared to reference data from [18], where deterministic perturbations were applied from a preceding computation of buckling eigenmodes of the RUC. Figures 4, 5, and 6 show the reference data, all stochastic perturbations (206 for each mode after discarding outliers), and their mean values for the components of \(\varvec{P}\) over \(\lambda \) for uniaxial, biaxial, and shear-combined deformation modes, respectively. Due to the applied boundary conditions and symmetries of the structure that result in a cubic anisotropy of the effective behavior, only some stress components should be non-zero and some of those should be equal, e.g., \(P_{11}=P_{22}\ne 0\) for biaxial deformation. As can be seen in the figures, the perturbation approach with a fixed, deterministic magnitude and shape introduces “parasitic” non-zero stress components, such as \(P_{12}\) and \(P_{21}\) in uniaxial compression in Fig. 4, which are fairly substantial compared to \(P_{11}\). With the stochastic approach used here, these parasitic stresses vanish (almost) in the mean values, while the paths and values of the main, non-zero stress components agree well for both approaches. This shows that the stochastic perturbation approach delivers reliable results and is able to diminish parasitic stress effects, which are undesirable for fitting effective constitutive models using the homogenized microstructural simulation data.

3 Effective constitutive modeling with ANNs

3.1 Basic material theory considerations

In the present work, some material-theoretic aspects are considered for the constitutive behavior and following model formulation, namely material symmetry and objectivity.

For the lattice structures considered here, anisotropic behavior is expected corresponding to the symmetry group of the hyperelastic RUC. We, therefore, consider the standard anisotropy conditions for hyperelastic materials for the effective potential, see, e.g., [62]:

$$\begin{aligned} W(\varvec{F}) = W(\varvec{F}\varvec{Q}) \quad \forall \varvec{F}\in Inv^+, \varvec{Q}\in \mathrm {G}\ , \end{aligned}$$
(20)

where \(Inv^+\) denotes the set of all invertible second-order tensor with positive determinant and \(\mathrm {G}\) refers to the material symmetry group. The present work considers only finite material symmetry groups and denotes the number of elements in \(\mathrm {G}\) as \(\#(\mathrm {G})\). The material symmetry conditions for the effective potential (20) imply the following conditions on the effective first Piola-Kirchhoff stress tensor:

$$\begin{aligned} \varvec{P}(\varvec{F}) = \varvec{P}(\varvec{F}\varvec{Q})\varvec{Q}^T \quad \forall \varvec{F}\in Inv^+, \varvec{Q}\in \mathrm {G} \ . \end{aligned}$$
(21)

For the present work \(\mathrm {G}\) correspond to the symmetry group of cubic materials, which for hyperelastic materials is sufficiently described by the cubic group of \(\#(\mathrm {G}) = 24\) rotation operations.

Additionally, material objectivity, see, e.g., [63],

$$\begin{aligned} W(\varvec{F}) = W(\varvec{Q}\varvec{F}) \quad \forall \varvec{F}\in Inv^+, \varvec{Q}\in \mathrm {SO(3)} \ , \end{aligned}$$
(22)

is to be considered in the model formulation. Material objectivity can be achieved through an intermediate variable dependency on the right Cauchy-Green tensor \(\varvec{C}= \varvec{F}^T\varvec{F}\) or Green’s strain tensor \(\varvec{E}= (\varvec{C}- \varvec{I})/2\), i.e.:

$$\begin{aligned} W(\varvec{F}) = \hat{W}(\varvec{E}) \ . \end{aligned}$$
(23)

Hereby it should be noted that the corresponding second Piola-Kirchhoff stress tensor \(\varvec{S}= \varvec{F}^{-1}\varvec{P}\) fulfills then:

$$\begin{aligned} \varvec{S}(\varvec{E}) = \frac{\partial \hat{W}}{\partial \varvec{E}}(\varvec{E}) \ . \end{aligned}$$
(24)

Further material-theoretic properties are not taken into account in this work. Thereby, it should be noted that, for instance, material stability, polyconvexity and further properties are appealing, but they lie outside of the scope of the present investigation. It should also be noted that the symmetries of the unperturbed RUC are broken by any perturbation approach used for nonlinear post-buckling analysis, see Sect. 2.2. However, since the perturbations are small and random, we still assume that the effective behavior complies to the prescribed material anisotropy.

3.2 Constitutive models based on ANNs

3.2.1 Formulation of constitutive models

On the one hand, the present work approaches the formulation of constitutive models based on the ideas of [33] and, on the other hand, focusing on the approximation of some material-theoretic properties through partial data augmentation, cf. [44].

The work of [33] proposes to use machine learning and artificial neural networks at the core of the model formulation. More specifically, feed-forward neural networks (FFNNs) are used for the formulation of hyperelastic and elastic models. The hyperelastic model of [33] uses a core FFNN potential \(\hat{W}^\mathrm {FFNN}(\varvec{E})\) and a group symmetrization with respect to \(\mathrm {G}\), yielding the model:

$$\begin{aligned} \begin{aligned} W^\mathsf {Wsym}(\varvec{F})&= \hat{W}^\mathsf {Wsym}(\varvec{E})\ , \\ \hat{W}^\mathsf {Wsym}(\varvec{E})&= \frac{1}{\#(\mathrm {G})} \sum _{\varvec{Q}\in \mathrm {G}} \hat{W}^\mathrm {FFNN}(\varvec{Q}^T\varvec{E}\varvec{Q}) \ . \end{aligned} \end{aligned}$$
(25)

The approach (25) fulfills per definition all material symmetry conditions (20), (21) and the material objectivity condition (22). The corresponding stress derived of (25) will be denoted as:

$$\begin{aligned} \varvec{P}^\mathsf {Wsym}(\varvec{F}) = \frac{\partial W^\mathsf {Wsym}}{\partial \varvec{F}}(\varvec{F}) = \varvec{F}\frac{\partial \hat{W}^\mathsf {Wsym}}{\partial \varvec{E}}(\varvec{E}) \ . \end{aligned}$$
(26)

The present work further consider two additional models in view of the approximation of properties, which may be expensive in terms of model complexity. The hyperelastic model of [33] uses a group symmetrization for the exact fulfillment of the known material symmetry. The present work investigates how well this property can be approximated by 1.) a hyperelastic model directly using a FFNN:

$$\begin{aligned} \begin{aligned} W^\mathsf {Wdir}(\varvec{F})&= \hat{W}^\mathrm {FFNN}(\varvec{E})\ , \\ \varvec{P}^\mathsf {Wdir}(\varvec{F})&= \frac{\partial W^\mathsf {Wdir}}{\partial \varvec{F}}(\varvec{F}) = \varvec{F}\frac{\partial W^\mathrm {FFNN}}{\partial \varvec{E}}(\varvec{E}) \ , \end{aligned} \end{aligned}$$
(27)

and 2.) an elastic model also directly using a FFNN for the second Piola-Kirchhoff tensor:

$$\begin{aligned} \varvec{P}^\mathsf {Pdir}(\varvec{F}) = \varvec{F}\varvec{S}^\mathrm {FFNN}(\varvec{E}) \ . \end{aligned}$$
(28)

The models (27) and (28), of course, do not fulfill, in general, the corresponding material symmetry conditions. But since the transformation rules are known, a simple data-augmentation can be considered such that the direct models (27) and (28) may be able to intrinsically approximate the material symmetry.

The symmetrized model (25) is, from a computational point of view, far more expensive than the direct ones (27) and (28) due to calling \(\#(\mathrm {G})\) times the core FFNNs in the group symmetrization for every given input \(\varvec{F}\). It is therefore expected that the direct models (27) and (28) have an advantage in terms of evaluation speed.

3.2.2 Implementation and technical details

Implementation framework All three material models \(W^\mathsf {Wsym}(\varvec{F})\) as in (25), \(W^\mathsf {Wdir}(\varvec{F})\) as in (27) and \(\varvec{P}^\mathsf {Pdir}(\varvec{F})\) as in (28) have been implemented in Python, version 3.7.8, with the TensorFlow library, version 2.3.1 [64]. All subsequent timings correspond to a system with a Nvidia GTX 970 GPU with 4GB of GDDR5 RAM, an Intel Xeon E3-1231 v3 CPU and 24GB of DDR3 RAM, on which the operating system is Microsoft Windows 10 Pro N, version 20H2.

Networks From an implementation point of view, it should be noted that both potential FFNNs \(\hat{W}^\mathrm {FFNN}(\varvec{E})\) of (25) and (27) can be easily implemented with a six-dimensional input (corresponding to the six degrees of freedom of \(\varvec{E}\)) and a one-dimensional output. Analogously, the stress FFNN \(\varvec{S}^\mathrm {FFNN}(\varvec{E})\) of (28) can be implemented with a six-dimensional input and output (corresponding to the six degrees of freedom of \(\varvec{E}\) and \(\varvec{S}\)). All FFNNs have been implemented using the swish activation function in all hidden layers and the identity activation function in the output layer. All resulting networks are then infinitely differentiable. The architecture of the implemented FFNNs for the three considered models is tabulated in Table 2.

Table 2 FFNN architectures used within the hyperelastic models \(W^\mathsf {Wsym}\), \(W^\mathsf {Wdir}\) and the elastic model \(\varvec{P}^\mathsf {Pdir}\) (HL: hidden layers)
Full size table

Taking [33] as a reference, 3 hidden layers seem to be sufficient for the approximation of the effective constitutive behavior of the cubic beam lattice materials investigated therein, such that the present work follows this result. Hereby, the symmetrized hyperelastic model \(W^\mathsf {Wsym}\) uses in the present work 12 neurons per hidden layer. The direct hyperelastic model \(W^\mathsf {Wdir}\) considers 18 neurons per hidden layer since it needs higher internal complexity in order to approximate the material symmetry from the given data. The elastic model \(\varvec{P}^\mathsf {Pdir}\) considers 22 neurons per hidden layer due to additional complexity needed due to the loss of the hyperelasticity structure.

Vector matrix operations Further, the matrix operation \(\varvec{Q}^T\varvec{E}\varvec{Q}\) is linear in \(\varvec{E}\), such that a matrix-vector-operation on the chosen six degrees of freedom of \(\varvec{E}\) can be constructed. For instance, the vector:

$$\begin{aligned} \underline{E}= (E_{11}, E_{12}, E_{13}, E_{22}, E_{23}, E_{33})^T, \end{aligned}$$
(29)

can be used to carry the six degrees of freedom of \(\varvec{E}\) and the operation \(\varvec{Q}^T\varvec{E}\varvec{Q}\) can be performed as \(\underline{\underline{Q}}\underline{E}\) with the \(6 \times 6\) matrix:

$$\begin{aligned} \begin{aligned} \underline{\underline{Q}}=&\left( \!\!\! \begin{array}{ccc} Q_{11}^2 &{} 2Q_{11}Q_{21} &{} 2Q_{11}Q_{31} \\ Q_{11}Q_{12} &{} Q_{12}Q_{21}+Q_{11}Q_{22} &{} Q_{12}Q_{31}+Q_{11}Q_{32} \\ Q_{11}Q_{13} &{} Q_{13}Q_{21}+Q_{11}Q_{23} &{} Q_{13}Q_{31}+Q_{11}Q_{33} \\ Q_{12}^2 &{} 2Q_{12}Q_{22} &{} 2Q_{12}Q_{32} \\ Q_{12}Q_{13} &{} Q_{13}Q_{22}+Q_{12}Q_{23} &{} Q_{13}Q_{32}+Q_{12}Q_{33} \\ Q_{13}^2 &{} 2Q_{13}Q_{23} &{} 2Q_{13}Q_{33} \end{array} \right. \\&\cdots \left. \begin{matrix} Q_{21}^2 &{} 2Q_{21}Q_{31} &{} Q_{31}^2 \\ Q_{21}Q_{22} &{} Q_{22}Q_{31}+Q_{21}Q_{32} &{} Q_{31}Q_{32} \\ Q_{21}Q_{23} &{} Q_{23}Q_{31}+Q_{21}Q_{33} &{} Q_{31}Q_{33} \\ Q_{22}^2 &{} 2Q_{22}Q_{32} &{} Q_{32}^2 \\ Q_{22}Q_{23} &{} Q_{23}Q_{32}+Q_{22}Q_{33} &{} Q_{32}Q_{33} \\ Q_{23}^2 &{} 2Q_{23}Q_{33} &{} Q_{33}^2 \end{matrix} \right) . \end{aligned} \end{aligned}$$
(30)

Stress computation through automatic differentiation. The gradient \(\varvec{S}(\varvec{E}) = {\partial \hat{W}}/{\partial \varvec{E}}\) is relevant for the hyperelastic models \(W^\mathsf {Wsym}\) and \(W^\mathsf {Wdir}\) for the computation of stresses. Here, the automatic differentiation routines of TensorFlow have been used. The differentiation is carried out with respect to the vector \(\underline{E}\) such that a corresponding six-dimensional stress vector \(\underline{S}= {\partial \hat{W}}/{\partial \underline{E}}\) is obtained, which is then recasted as the full symmetric tensor \(\varvec{S}\) with basic tensor operations. The final stress output for the first Piola-Kirchhoff stress is then computed as \(\varvec{P}= \varvec{F}\varvec{S}\).

3.2.3 Data augmentation and considered datasets

For any hyperelastic simulation yielding a hyperelastic dataset:

$$\begin{aligned} D = \{(\varvec{F}_1, W_1, \varvec{P}_1), \dots \} \ , \end{aligned}$$
(31)

here, the group augmentation is defined as:

$$\begin{aligned} \mathrm {G}\star D = \bigcup _{(\varvec{F}, W, \varvec{P}) \in D} \big \{(\varvec{F}\varvec{Q}, W, \varvec{P}\varvec{Q}): \varvec{Q}\in \mathrm {G}\big \} \ . \end{aligned}$$
(32)

More explicitly, for a dataset D containing \(\#(D)\) data points \((\varvec{F}, W, \varvec{P})\), the dataset \(\mathrm {G}\star D\) contains \(\#(\mathrm {G}) \cdot \#(D)\) corresponding data points. For the investigation of cubic unit cells at hand, a dataset D is augmented 24-fold. Consideration of augmented datasests for the training of the direct models (27) and (28) offers the option of approximating the known material symmetry intrinsically.

It should be shortly noted that the group-based data augmentation \(\mathrm {G}\star D\) goes beyond the approach of [44]. In [44] only \(\varvec{F}\) and W were considered for Nickel and no illustration of the stress behavior is displayed. Therefore, in [44] it remains unclear how well a data augmentation only on \(\varvec{F}\) and W works for the approximation of the group symmetry in terms of the stress evaluation. The present investigation is concerned directly with the resulting stresses \(\varvec{P}\) of the unit cells, since in engineering the stresses are of major importance. Calibration of hyperelastic models based only on \(\varvec{F}\) and W could potentially yield models with fairly similar \(W(\varvec{F}) = W(\varvec{F}\varvec{Q})\) for some \(\varvec{Q}\in G\), but with vastly different gradients/stresses. In order to avoid this scenarios from the beginning, the data augmentation is immediately extended to \(\mathrm {G}\star D\) in order to optimize models based (1) on readily available data for \(\varvec{F}\), W and \(\varvec{P}\), and (2) all corresponding implications of the material symmetry.

Table 3 \(\mathrm {MSE}^P\) for all training and evaluation deformation modes, showing averaged values ± standard deviation with respect to the symmetry group \(\mathrm {G}\)
Full size table

In the following, the calibration dataset \(D^c\) without any group augmentation corresponds to the simulation results collected from the first five modes of Table 1, namely uniaxial, biaxial, volumetric, planar and shear, averaged over all 206 considered runs. This means that in \((\varvec{F}, W, \varvec{P})\), \(\varvec{F}\) is the average of the deformation gradient over all 206 runs for the corresponding fixed simulation step and corresponding simulation mode. For W and \(\varvec{P}\) the analogous averages are computed, which—based on the small absolute deviations visible in Figs. 4, 5 and 6—are considered as sensible. Each simulation mode has 201 simulation steps, i.e., \(D^c\) contains \(\#(D^c) = 5 \cdot 201 = 1005\) data points. The testing modes of Table 1, namely biaxial-0.5, biaxial-0.33 and shear-combined, denoted by the dataset \(D^t\), are excluded from the calibration dataset \(D^c\), but monitored during calibration in order to avoid overfitting. The group augmented calibration dataset \(\mathrm {G}\star D^c\) will be used only for the direct approaches with corresponding objective functions, as to be presented in the following section.

3.2.4 Training approach

The standard mean squared error (\(\mathrm {MSE}\)) of a model \(\mathsf {M}\in \{\mathsf {Wsym},\mathsf {Wdir},\mathsf {Pdir}\}\) with respect to a hyperelastic dataset D is considered here as a suitable objective or loss function:

$$\begin{aligned} {\displaystyle \mathrm {MSE}^W\!(D)}= & {} \frac{1}{\#(D)}\! \sum _{(\varvec{F}, W, \varvec{P}) \in D} (W - W^{\mathsf {M}}(\varvec{F}))^2, \end{aligned}$$
(33)
$$\begin{aligned} {\displaystyle \mathrm {MSE}^P\!(D)}= & {} \frac{1}{9\#(D)}\! \sum _{\scriptscriptstyle (\varvec{F}, W, \varvec{P}) \in D} \sum _{i,j=1}^3 (P_{ij} - P^{\mathsf {M}}_{ij}(\varvec{F}))^2\!,\end{aligned}$$
(34)
$$\begin{aligned} \mathrm {MSE}(D)= & {} \mathrm {MSE}^W(D) + \mathrm {MSE}^P(D). \end{aligned}$$
(35)

The symmetrized hyperelastic model \(\mathsf {Wsym}\) is trained with \(\mathrm {MSE}(D^c)\), while the direct alternative \(\mathsf {Wdir}\) is trained with \(\mathrm {MSE}(\mathrm {G}\star D^c)\) based on the augmented calibration dataset. The elastic direct model \(\mathsf {Pdir}\) is trained with \(\mathrm {MSE}^P(\mathrm {G}\star D^c)\), i.e., only based on the stress data.

The implemented models are trained with their respective loss functions using the Adam optimizer, cf. [65], at what \(D^t\) is used as validation dataset. The training of a model is stopped if the loss function with respect to \(D^t\) does not improve over 50 epochs. Model instances were created and trained until for every model an instance was found yielding an \(\mathrm {MSE}^P(\mathrm {G}\star D^t)\) value below 1000 for the stresses.

3.3 Results

The calibrated models \(W^\mathsf {Wsym}\), \(W^\mathsf {Wdir}\) and \(\varvec{P}^\mathsf {Pdir}\) are now compared based on the stress error \(\mathrm {MSE}^P\). Hereby, for every single simulation mode the \(\mathrm {MSE}^P\) is computed, and its average and standard deviation with respect to \(\mathrm {G}\) are calculated. As shown in Table 3, the hyperelastic model \(W^\mathsf {Wsym}\) yields, of course, the same value for \(\mathrm {MSE}^P\) for every \(\varvec{Q}\in \mathrm {G}\) and zero standard deviation with respect to \(\mathrm {G}\), since it fulfills the material symmetry by construction. Based on the chosen training settings, \(W^\mathsf {Wsym}\) yields, however, approximately twice the \(\mathrm {MSE}^P\) compared to its direct alternative \(W^\mathsf {Wdir}\) for the deformation modes of the calibration dataset \(D^c\). The elastic direct model \(\varvec{P}^\mathsf {Pdir}\) yields the best quantitative results in terms of \(\mathrm {MSE}^P\) with respect to the modes in \(D^c\), but has the highest standard deviations for \(\varvec{Q}\in \mathrm {G}\).

Fig. 7
figure 7

Comparison of unit cell simulations (continuous lines) and ANN models (dashed lines) for uniaxial deformation

Full size image
Fig. 8
figure 8

Comparison of unit cell simulations (continuous lines) and ANN models with data augmentation (dashed lines) for uniaxial deformation with a rotation \(\varvec{Q}\in G\) of \(120^{\circ }\) around the \([1,1,1]^T\)-axis applied to \(\varvec{F}\)

Full size image
Fig. 9
figure 9

Comparison of unit cell simulations (continuous lines) and ANN models without data augmentation (dashed lines) for uniaxial deformation with a rotation \(\varvec{Q}\in G\) of \(120^{\circ }\) around the \(\left[ 1,1,1\right] ^T\)-axis applied to \(\varvec{F}\)

Full size image

After comparing the errors w.r.t. the calibration modes in \(D^c\), the generalization qualities of the different models, i.e., the ability of a model to predict data it has not seen yet in training, is assessed using the three test modes. The first two test modes are essentially (non-equi-) biaxial deformations, where both axes are experiencing different strains. Both modes lead to similar results, as can be seen in the biaxial-0.5 and biaxial-0.33 rows in Table 3. It should be noted that the first model tends to maintain the same \(\mathrm {MSE}^P\) as in the training modes, whereas the other two models are giving higher \(\mathrm {MSE}^P\). Lastly, not only different tension/compression strains are applied to the models, but also a scenario, where tension/compression is combined with shear strains as depicted by shear-combined. Here, the generalization abilities of the models can be seen even more clearly. Row shear-combined in Table 3 shows that \(\mathsf {Wsym}\) and \(\mathsf {Wdir}\) maintain somewhat accurate predictions, but \(\mathsf {Pdir}\) shows a much higher \(\mathrm {MSE}^P\). These observations suggest that the generalization abilities of the hyperelastic model including the symmetrization \(\mathsf {Wsym}\) are slightly better than without in \(\mathsf {Wdir}\), while the elastic, stress-based model \(\mathsf {Pdir}\) generalizes much worse, though providing far more accurate results on the training data.

Fig. 10
figure 10

Comparison of unit cell simulations (continuous lines) and ANN models (dashed lines) for shear-combined deformation

Full size image
Fig. 11
figure 11

Comparison of unit cell simulations (continuous lines) and ANN models (dashed lines) for shear-combined deformation with a rotation \(\varvec{Q}\in G\) of \(270^{\circ }\) around the \(\left[ 0,0,1\right] ^T\)-axis applied to \(\varvec{F}\)

Full size image

These findings can be confirmed in Fig. 7, which shows that the \(\mathsf {Pdir}\) model performs better on the data used for training. In this context, it should be highlighted that the data augmentation is actually crucial for the success of the sleeker models, as can be seen in comparison between Fig. 8, where the fully calibrated models are shown, and Fig. 9, where the models trained with the non-augmented data used for calibration of \(\mathsf {Wsym}\) are shown. The comparison demonstrates the deterioration of the prediction quality w.r.t. rotations for the \(\mathsf {Wdir}\) and \(\mathsf {Pdir}\) models when the material symmetry is not part of the calibration data, i.e., when the calibration only uses \(D^c\) instead of \(G\star D^c\).

When looking at the generalization abilities of the models, the stress model \(\mathsf {Pdir}\) (trained again with data augmentation) still delivers accurate predictions of the test data for the shear-combined deformation mode shown in Fig. 10 (though not as accurate as for the training data), its much worse accuracy w.r.t. symmetry rotations can be seen in Fig. 11. This explains the large standard deviation for \(\mathsf {Pdir}\) in Table 3 when considering the shear-combined scenario. Furthermore, the visualizations indicate the good generalization properties of the \(\mathsf {Wsym}\) and \(\mathsf {Wdir}\) models and also show that the direct hyperelastic model maintains reasonable accuracy w.r.t. material symmetry.

3.3.1 Performance aspects

Besides the quality of their fit of the microstructure simulations, also the performance of the ANN-based constitutive models should be considered when choosing a network for later use in a macroscale FE computation. Therefore, a comparison of the execution times of the three models \(\mathsf {Wsym}, \mathsf {Wdir}\), and \(\mathsf {Pdir}\) is conducted. For this purpose, all three models are build in TensorFlow and a number of random deformation gradients \(\varvec{F}\) is used as input for the network. In Table 4, the number of deformation gradients \(\varvec{F}\) samples the model has to evaluate is shown in the first column. In the other columns, the corresponding evaluation time each model needed is shown as the average of 100 executions. The sample sizes are doubled as long as the system is able to run the computation. Generally, the times for each model remain roughly constant until a certain number of samples is reached, since evaluations can be performed in parallel by the GPU. Furthermore, it can be seen that the \(\mathsf {Wsym}\) model is about one order of magnitude slower compared to the \(\mathsf {Wdir}\) model, though the architecture is slightly smaller, see Table 2, which is due to the symmetry group transformations involved, compare (25). Modelling the stresses directly through the \(\mathsf {Pdir}\) model results in a minor speed-up, as it reduced the time needed by the hyperelastic potential model \(\mathsf {Wdir}\) by about a third, which probably stems from the additional automatic differentiation required for obtaining \(\varvec{P}=\partial W/\partial \varvec{F}\) for the potential-based, hyperelastic models. Considering that the stress model has the worst generalization abilities compared to \(\mathsf {Wdir}\) and that \(\mathsf {Wsym}\) is an order of magnitude slower compared to the direct model, the \(\mathsf {Wdir}\) model seems the most reasonable choice to use in production.

For comparison, the time needed to compute the response of one randomly perturbed RUC is—depending on the prescribed deformation \(\varvec{F}\)—around 45 s. So even in the case that one singular perturbation is sufficient, the constitutive model evaluations are faster by a factor of about 250 (for \(\mathsf {Wsym}\)) up to 4600 (for \(\mathsf {Wdir}\)). Since multiple runs with different perturbations are necessary in order to minimize the parasitic stresses, as well as due to the fact that parallelization is possible for the models, these factors merely form the lower bound for the speedup. Thus, a sequential multiscale simulation using an ANN-based constitutive model, which will be demonstrated in the following Section, can be expected to show a similar speed-up compared to a concurrent FE2 multiscale approach.

Table 4 Evaluation timings for different models (average time of 100 evaluations of the given number of \(\varvec{F}\) samples)
Full size table

4 Macroscale simulation and verification

4.1 Nonlinear FEM with ANN-based material models

For the sequential multiscale simulation of elastic beam lattices, the structures are now macroscopically modelled as hyperelastic continua, which are governed by the weak form:

$$\begin{aligned} \begin{aligned} \int _\varOmega \delta \hat{W}(\varvec{E}(\varvec{u}))\, dV = \int _\varOmega \delta \varvec{u}\cdot \varvec{f}\, dV + \int _{\varGamma _n} \delta \varvec{u}\cdot \varvec{g}\, dS , \end{aligned} \end{aligned}$$
(36)

where \(\varOmega \subset \mathbb {R}^3\) is the domain occupied by the microstructured continuum, \(\varvec{u}:\varOmega \rightarrow \mathbb {R}^3\) the sought displacement conforming to the Dirichlet boundary condition \(\varvec{u}=\bar{\varvec{u}}\) on \(\varGamma _d\subset \partial \varOmega \), \(\varvec{f}:\varOmega \rightarrow \mathbb {R}^3\) the internal body forces, and \(\varvec{g}:\varGamma _n\subset \partial \varOmega \rightarrow \mathbb {R}^3\) the traction forces applied as Neumann boundary conditions. The variation of the strain energy can be further expressed as:

$$\begin{aligned} \begin{aligned} \delta \hat{W}&= \delta \varvec{E}: \frac{\partial \hat{W}}{\partial \varvec{E}} = \delta \varvec{E}: \varvec{S}(\varvec{E}) = \nabla \delta \varvec{u}: \varvec{P}(\varvec{F}) \\&= \delta \varvec{F}: \varvec{P}(\varvec{F}) = \delta \varvec{F}: \frac{\partial W}{\partial \varvec{F}} = \delta W, \end{aligned} \end{aligned}$$
(37)

compare (23) and (24). Here, the effective behavior of lattice unit cells is incorporated in the formulation through the homogenized constitutive models, i.e., the ANN-based potentials \(W^\mathsf {Wsym}\) and \(W^\mathsf {Wdir}\), as introduced and trained above.

The finite element discretization of this nonlinear mechanical problem is then implemented in the open-source high performance multiphysics finite element software NGsolve, version 6.2.2102 [66]. NGsolve provides a convenient implementation of variational models, which is here used with the ANN-based potentials \(W^\mathsf {Wsym}\) and \(W^\mathsf {Wdir}\). For this purpose, the weights and biases of the trained networks are exported from TensorFlow and all operations for their evaluation, as well as further derivations for linearization, are taken care of by NGsolve.

4.2 Numerical results and verification

For the application and verification of the multiscale implementations, a cube of size \(0.1\times 0.1\times 0.1\) m3 with BCC lattice microstructure (with aspect ratio \(a=0.1\)) is investigated. The lattice cube is subject to a clamped stretch, i.e., the left and right surface are completely fixed and both surfaces are forced to part from each other using Dirichlet-BCs. In this scenario, no external forces are present, i.e., \(\varvec{f}=0,\,\varvec{g}=0\). The deformation is characterized by the parameter \(\lambda \), which describes the incrementally applied strain on the right surface as a fraction of the position of the right side, whilst all other displacements on the sides are set to be zero:

$$\begin{aligned} \varvec{u}|_{\varGamma _{left}}=\varvec{0}, \quad \varvec{u}|_{\varGamma _{right}}=\left( \lambda X_1, 0, 0\right) ^T, \end{aligned}$$
(38)

with \(\varGamma _{left} = \{X_1=0\}\) and \(\varGamma _{right} = \{X_1=0.1\ \text {m}\}\).

4.2.1 Convergence study

To verify the implementation with the ANN-based potentials, first a finite element convergence study is carried out. For this purpose, tetrahedron meshes of degree 1, 2, and 3 are constructed and subsequently refined. The simulations were then executed up to \(\lambda =0.1\) using the \(\mathsf {Wdir}\) model. Figure 12 shows the resulting total strain energies \(\Pi (\varvec{u})=\tfrac{1}{2}\int _\varOmega \hat{W}(\varvec{E}(\varvec{u}))\, dV\) at \(\lambda =0.1\) plotted against the number of elements in the refined meshes. The lines represent the different element degrees, i.e., the degree 1 represents linear tetrahedrons, 2 quadratic, and 3 cubic. It can be observed that all element formulations converge with higher element count and that the accuracy and speed of convergence increases with degree. This behavior is, of course, to be expected and simply confirms that the constitutive models and their linearizations must be correctly implemented in the FE context. When considering the performance apart from the pure stability, the solutions that seem most promising are the quadratic tet with 596 elements, resulting in an energy of \(30.4\ \text {mJ}\) and the cubic tet with 122 elements, resulting in an energy of \(30.4\ \text {mJ}\) as well. Compared to the minimal energy the computations showed of \(30.1\ \text {mJ}\), this is an error of about \(1\%\), which seems acceptable for the following further evaluations.

Fig. 12
figure 12

Convergence study for order elevation and mesh refinement for the clamped stretch test at \(\lambda =0.1\)

Full size image

4.2.2 Comparison with fully simulated beam lattices

Fig. 13
figure 13

Comparison of internal energy (top) and response force (bottom) over applied strain \(\lambda \) for different scenarios both homogenized (FE \(\mathsf {Wdir}\), FE \(\mathsf {Wsym}\)) and full-scale (\(5\times 5\times 5\), \(7\times 7\times 7\))

Full size image

After having verified that the homogenized constitutive models are suitable for FE calculations, it is to be verified whether the effective models and sequential multiscale simulation accurately describe the behavior of beam lattices. For this purpose, the same setup as described above with a lattice cube subject to clamped tension was implemented using lattices of \(5\times 5\times 5\) and \(7\times 7\times 7\) BCC RUCs.

Fig. 14
figure 14

Visualization of the clamped stretch of the lattice cube at \(\lambda =0.25\) with the \(\mathsf {Wdir}\) multiscale continuum model as greyed-out body, the \(5\times 5\times 5\) lattice in blue and the \(7\times 7\times 7\) lattice in red. (Color figure online)

Full size image
Fig. 15
figure 15

Visualization of the clamped compression of the lattice cube at \(\lambda =-0.05\) with the \(\mathsf {Wdir}\) multiscale continuum model as greyed-out body, the \(5\times 5\times 5\) lattice in blue and the \(7\times 7\times 7\) lattice in red. (Color figure online)

Full size image

In order to assess the reasonable agreement of the homogenized model and the fully resolved, direct lattice simulation with beam elements, the simulation just as described above is conducted for tension with \(\lambda \) up to \(+0.25\) and for compression with \(\lambda \) up to \(-0.15\), where possible. Not all models show good convergence in compressive scenarios as is discussed in the next paragraph. The resulting strain energies, as well as the resulting reaction forces on \(\varGamma _{right}\), are plotted over the applied strain \(\lambda \) in Fig. 13. For the fully-resolved lattices, we executed a maximum of 5 simulations with random perturbations for both compression and tension. Up until loss of convergence, these simulations are indistinguishable in terms of their energy and force values and thus only the ones with the highest attained strains are plotted. Even though only relatively few unit cells are used in order to reduce the computational effort of the fully resolved simulations, i.e., no proper separation of scales applies, the homogenized models result in strain energies and forces close to those of the full-scale simulations. Especially the strain energy plot shows good agreement of the homogenized models with the full scale simulation. The forces of the different simulations also agree reasonably well; especially on the compression side the buckling effect in the homogenized models is clearly visible in the flattening of the curve. Whilst being not as sharp as on the full-scale simulation, which also applies to the data fit itself as shown in Fig. 7, this nevertheless shows the capability of the generated models and the multiscale method to predict the buckling-dominated behavior of metamaterials fairly well. Furthermore, the results from the tension simulations (at \(\lambda =0.25\)) are visualized in Fig. 14, while the results form the compression simulations (at \(\lambda =-0.05\)) are shown in Fig. 15. Also here, a good visual agreement of the deformed shapes can be observed.

It should also be noted that the homogenized models are numerically more stable compared to the full-scale simulations, which also require perturbations in order to resolve the onset of buckling, resulting in the ability to compute higher compressive strains. However, in compression, at some point convergence issues also occur for the continuum FEM with \(\mathsf {Wdir}\) (at \(\lambda \approx {-0.09}\)) and \(\mathsf {Wsym}\) (at \(\lambda \approx {-0.14}\)), which can be seen from the prematurely terminated compression curves in Fig. 13. This might probably be related to loss of ellipticity and a lack of uniqueness of the solutions obtainable from the ANN-based models, which could potentially be resolved by incorporating polyconvexity conditions [67] into the models in future work. Despite that, the results demonstrate the ability of the obtained models to predict the behaviour of the metamaterials under large compressive strains, where the effect of the buckling is clearly visible in the flattening of the curves. Even though the ANN-based models also exhibit convergence issues, they are still much faster and more stable than direct numerical simulations.

5 Conclusions

A sequential nonlinear multiscale method for the simulation of elastic beam lattices was developed in this work, showing that metamaterials subject to large deformations and instabilities can be efficiently and accurately described using highly flexible, data-driven effective constitutive models formulated upon artificial neural networks.

For the generation of calibration data for effective constitutive models, a stochastic perturbation approach for nonlinear post-buckling analysis of RUCs has been introduced, which does not require preceding eigenmode analysis and mode selection. By considering multiple instances and averaging, parasitic stress components of the effective stress-strain responses could be significantly reduced compared to an eigenmode-based reference approach with a single perturbation. Using this method, homogenized energy densities and stress tensors of the BCC unit cell were obtained for various prescribed deformation modes (uniaxial tension, volumetric tension, shear, etc.).

The generated data was then used to train and evaluate three different ANN-based constitutive models: (1) \(\mathsf {Wsym}\), a hyperelastic model incorporating the finite symmetry group of the RUC, (2) \(\mathsf {Wdir}\), a hyperelastic model trained to show anisotropic behavior through data augmentation, and (3) \(\mathsf {Pdir}\), an elastic, stress-based model also trained through data augmentation. By comparing the resulting MSE of the Piola-Kirchhoff stress tensor, it could be observed that the stress model \(\mathsf {Pdir}\), whilst possessing superior qualities on the training dataset, showed inferior generalization abilities when evaluated on the validation dataset. In contrast, the hyperelastic models \(\mathsf {Wsym}\) and \(\mathsf {Wdir}\) showed good generalization abilities with only slightly increased errors with respect to the validation dataset. In terms of computational performance, the direct hyperelastic model \(\mathsf {Wdir}\) evaluates much faster than the model \(\mathsf {Wsym}\) due the computational expenses of the \(\mathsf {Wsym}\) model through the group symmetrization. This performance advantage of the \(\mathsf {Wdir}\) model puts up with a comparably small loss in prediction quality when reproducing the anisotropy of the cell, as well as in a neglectable loss in the generalization ability on the test data. This suggests that hyperelastic models should be preferred and that approximation of the material symmetry through data augmentation is favorable if computational performance is prioritized over accuracy and physical exactness of the material model.

The homogenized, anisotropic, hyperelastic material models were then implemented into a nonlinear FE code for sequential multiscale simulation and delivered good results when compared to full-scale simulations of BCC lattice structures. Besides the advantages of computational effort and therefore time-savings, the homogenized continuum models also prevail in the aspect of complexity. The convergence behavior of the continuum models is not dependent on perturbations for post-buckling analysis. Further, it is less intrusive and much easier to implement a model based on the hyperelastic energy density compared to implementing a model based on the internal structure of a lattice and add corresponding lattice perturbations throughout the macroscopic structure. Therefore, the multiscale approach speeds up the development process in two ways: the generation of the system to be simulated and the computation of the simulation itself.

The presented sequential multiscale framework based on anisotropic (hyper)elastic ANN-models could be readily applied to the multiscale modeling of other beam lattice RUCs, as well as other types of elastic microstructures, such as (minimal) surface-based foams or composites. In this context, other symmetry groups and parametric microstructures could be investigated, cf. [68], even with potentially varying symmetries. Further, future work should be directed towards including further desirable properties into the constitutive formulations, such as material stability, and extend the framework towards thermodynamically consistent time-dependent and inelastic modeling, which is particularly important for applications of additively manufactured, polymeric lattices.