Skip to main content
SpringerLink
Log in

A solution method for free vibrration analysis of the elastically joined functionally graded shells

  • Regular Article
  • Published:
The European Physical Journal Plus Aims and scope Submit manuscript

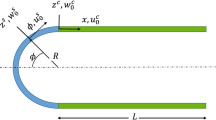
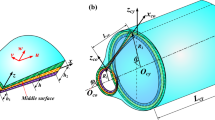
Abstract

In this paper, for the first time, the free vibration characteristics of a joined shell structure in which three shells of revolution made of functionally graded material are elastically bonded are reported. The structure of the joined shell is formed by elastically bonding double-curved shells to both sides of the cylindrical shell in the middle, and the hyperbolic shells have elliptic, parabolic, and hyperbolic shapes. The Haar wavelet discretization method (HWDM), one of the effective, convenient and accurate numerical solution methods, is applied to investigate the free vibration behavior of various elastically joined functionally graded shells (EJFGSs). The theoretical model of the EJFGSs is formulated based on first-order shear deformation theory (FSDT). The displacement and rotation of arbitrary point of the EJFGS are expended as Haar wavelet series in the meridian direction and as a Fourier series in the circumferential direction. The boundary condition at both ends of the EJFGS and the continuous condition between its shells are modeled by the spring stiffness technique. By solving the governing equation of the whole system, the vibration characteristics of the EJFGS such as the natural frequency and the corresponding mode shape can be obtained. Through the comparisons with the previous literature and finite element method (FEM) results, the accuracy and reliability of our method are verified. Finally, new free vibration analysis results of various EJFGSs, which can be used as benchmark data for researchers in this field, are reported with parameter study.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

Data Availability

The data that supports the findings of this study are available within the article.

References

  1. M.S. Qatu, Vibration of Laminated Shells and Plates (San Diego, CA, Elsevier Ltd, 2004)

    MATH  Google Scholar 

  2. A.W. Leissa, Vibration of shells, NASA SP-288, Washington, D.C., 1973.

  3. J.N. Reddy, Mechanics of Laminated Composite Plates and Shells: Theory and Analysis, 2nd edn. (CRC Press, LLC, Boca Raton, Florida, 2003)

    Book  Google Scholar 

  4. J.N. Reddy, Theory and Analysis of Elastic Plates and Shells, 2nd edn. (CRC Press, LLC, Boca Raton, Florida, 2007)

    Google Scholar 

  5. Y. Qu, X. Long, S. Wu, G. Meng, A unified formulation for vibration analysis of composite laminated shells of revolution including shear deformation and rotary inertia. Compos. Struct. 98, 169–191 (2013)

    Article  Google Scholar 

  6. Q.S. Wang et al., Free vibrations of composite laminated doubly-curved shells and panels of revolution with general elastic restraints. Appl. Math. Model. 46, 227–262 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  7. Q.S. Wang et al., Vibrations of Composite Laminated Circular Panels and Shells of Revolution with General Elastic Boundary Conditions via Fourier-Ritz Method. Curved and Layer. Struct. 3(1), 105–136 (2016)

    Google Scholar 

  8. Y. Chen et al., Free vibration analysis of circular cylindrical shell with non-uniform elastic boundary constraints. Int. J. Mech. Sci. 74, 120–132 (2013)

    Article  Google Scholar 

  9. G. Jin et al., An exact solution for the free vibration analysis of laminated composite cylindrical shells with general elastic boundary conditions. Compos. Struct. 106, 114–127 (2013)

    Article  Google Scholar 

  10. Z. Su et al., A unified solution for vibration analysis of functionally graded cylindrical, conical shells and annular plates with general boundary conditions. Int. J. Mech. Sci. 80, 62–80 (2014)

    Article  Google Scholar 

  11. T. Ye et al., A unified Chebyshev-Ritz formulation for vibration analysis of composite laminated deep open shells with arbitrary boundary conditions. Arch. Appl. Mech. 84, 441–471 (2014)

    Article  ADS  MATH  Google Scholar 

  12. F. Tornabene, A. Liverani, G. Caligiana, FGM and laminated doubly curved shells and panels of revolution with a free-form meridian: a 2-D GDQ solution for free vibrations. Int. J. Mech. Sci. 53, 446–470 (2011)

    Article  Google Scholar 

  13. F. Tornabene, E. Viola, Free vibrations of four-parameter functionally graded parabolic panels and shells of revolution. Eur. J. Mech. A/Solids 28, 991–1013 (2009)

    Article  ADS  MATH  Google Scholar 

  14. F. Tornabene et al., Free vibrations of composite oval and elliptic cylinders by the generalized differential quadrature method. Thin-Walled Struct. 97, 114–129 (2015)

    Article  Google Scholar 

  15. F. Tornabene, Free vibration analysis of functionally graded conical, cylindrical shell and annular plate structures with a four-parameter power-law distribution. Comput. Methods Appl. Mech. Engrg. 198, 2911–2935 (2009)

    Article  ADS  MATH  Google Scholar 

  16. X. Chen, K. Ye, Free vibration analysis for shells of revolution using an exact dynamic stiffness method. Math. Probl. Eng. 2016, 1–28 (2016)

    MathSciNet  MATH  Google Scholar 

  17. J.G. Kim, J.K. Lee, H.J. Yoon, Free vibration analysis for shells of revolution based on p-version mixed finite element formulation. Finite Elem. Anal. Des. 95, 12–19 (2015)

    Article  Google Scholar 

  18. O.J. Al-Khatib, G.R. Buchanan, Free vibration of a paraboloidal shell of revolution including shear deformation and rotary inertia. Thin-Walled Struct. 48, 223–232 (2010)

    Article  Google Scholar 

  19. T. Irie, G. Yamada, Y. Muramoto, Free vibration of joined conical-cylindrical shells. J. Sound Vib. 95(1), 31–39 (1984)

    Article  ADS  Google Scholar 

  20. Y.S. Lee, M.S. Yang, H.S. Kim et al., A study on the free vibration of the joined cylindrical-spherical shell structures. Comput. Struct. 80(27–30), 2405–2414 (2002)

    Article  Google Scholar 

  21. E. Efraim, M. Eisenberger, Exact vibration frequencies of segmented axisymmetric shells. Thin-Walled Struct. 44(3), 281–289 (2006)

    Article  Google Scholar 

  22. M. Caresta, N.J. Kessissoglou, Free vibrational characteristics of isotropic coupled cylindrical–conical shells. J. Sound Vib. 329(329), 733–751 (2010)

    Article  ADS  Google Scholar 

  23. W.C.L. Hu, J.P. Raney, Experimental and analytical study of vibrations of joined shells. Aiaa J. 5(5), 976–980 (2012)

    Article  ADS  Google Scholar 

  24. J.H. Kang, Three-dimensional vibration analysis of joined thick conical-cylindrical shells of revolution with variable thickness. J. Sound Vib. 331(18), 4187–4198 (2012)

    Article  ADS  Google Scholar 

  25. X. Ma et al., An analytical method for vibration analysis of cylindrical shells coupled with annular plate under general elastic boundary and coupling conditions. J. Vib. Control 2(6), 691–693 (2015)

    Google Scholar 

  26. X. Ma et al., Free and forced vibration analysis of coupled conical–cylindrical shells with arbitrary boundary conditions. Int. J. Mech. Sci. 88, 122–137 (2014)

    Article  Google Scholar 

  27. Y. Qu et al., A new method for vibration analysis of joined cylindrical-conical shells. J. Vib. Control 19(16), 2319–2334 (2012)

    Article  MATH  Google Scholar 

  28. Y. Qu et al., Vibration analysis of ring-stiffened conical–cylindrical–spherical shells based on a modified variational approach. Int. J. Mech. Sci. 69(4), 72–84 (2013)

    Article  Google Scholar 

  29. Y. Qu et al., A modified variational approach for vibration analysis of ring-stiffened conical-cylindrical shell combinations. Euro. J. Mech. A 37(3), 200–215 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  30. S. Wu, Y. Qu, H. Hua, Vibration characteristics of a spherical–cylindrical–spherical shell by a domain decomposition method. Mech. Res. Commun. 49(3), 17–26 (2013)

    Article  ADS  Google Scholar 

  31. S. Wu, Y. Qu, H. Hua, Vibrations characteristics of joined cylindrical-spherical shell with elastic-support boundary conditions. J. Mech. Sci. Technol. 27(5), 1265–1272 (2013)

    Article  Google Scholar 

  32. X. Xie, H. Zheng, G. Jin, Integrated orthogonal polynomials based spectral collocation method for vibration analysis of coupled laminated shell structures. Int. J. Mech. Sci. 98, 132–143 (2015)

    Article  Google Scholar 

  33. M. Chen et al., Free and forced vibration of ring-stiffened conical-cylindrical shells with arbitrary boundary conditions. Ocean Eng. 108, 241–256 (2015)

    Article  Google Scholar 

  34. Z. Su, G. Jin, Vibration analysis of coupled conical-cylindrical-spherical shells using a Fourier spectral element method. Acoust. Soc. Am. J. 140(5), 3925–3940 (2016)

    Article  ADS  Google Scholar 

  35. Q. Wang, K. Choe, D. Shi, K. Sin, Vibration analysis of the coupled doubly-curved revolution shell structures by using Jacobi-Ritz method. Int. J. Mech. Sci. 135, 517–531 (2018)

    Article  Google Scholar 

  36. Q. Bin et al., A unified Jacobi-Ritz formulation for vibration analysis of the stepped coupled structures of doubly-curved shell. Compos. Struct. (2019). https://doi.org/10.1016/j.compstruct.2019.04.027

    Article  Google Scholar 

  37. J. Lee, Free vibration analysis of joined spherical-cylindrical shells by matched Fourier-Chebyshev expansions. Int. J. Mech. Sci. 122, 53–62 (2017)

    Article  Google Scholar 

  38. F. Pang, H. Li, K. Choe et al., Free and forced vibration analysis of airtight cylindrical vessels with doubly curved shells of revolution by using Jacobi-ritz method. Shock. Vib. (2017). https://doi.org/10.1155/2017/4538540

    Article  Google Scholar 

  39. H. Li et al., A semi analytical solution for free vibration analysis of combined spherical and cylindrical shells with non-uniform thickness based on Ritz method. Thin-Walled Struct. 145, 106443 (2019). https://doi.org/10.1016/j.tws.2019.106443

    Article  Google Scholar 

  40. H. Li et al., Free vibration analysis of uniform and stepped combined paraboloidal, cylindrical and spherical shells with arbitrary boundary conditions. Int. J. Mech. Sci. (2018). https://doi.org/10.1016/j.ijmecsci.2018.06.021

    Article  Google Scholar 

  41. Q. Gong et al., Application of Ritz method for vibration analysis of stepped functionally graded spherical torus shell with general boundary conditions. Compos. Struct. 243, 112215 (2020). https://doi.org/10.1016/j.compstruct.2020.112215

    Article  Google Scholar 

  42. F. Pang et al., Application of flügge thin shell theory to the solution of free vibration behaviors for spherical-cylindrical-spherical shell: A unified formulation. Eur. J. Mech./A Solids 74, 381–393 (2019)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  43. K. Choe, Q. Wang, J. Tang, C. Shui, Vibration analysis for coupled composite laminated axis-symmetric doubly-curved revolution shell structures by unified Jacobi-Ritz method. Compos. Struct. 194, 136–157 (2018). https://doi.org/10.1016/j.compstruct.2018.04.035

    Article  Google Scholar 

  44. K. Choe et al., Free vibration analysis of coupled functionally graded (FG) doubly-curved revolution shell structures with general boundary conditions. Compos. Struct. 194, 136–157 (2018)

    Article  Google Scholar 

  45. H. Bagheri, Y. Kiani, M.R. Eslami, Free vibration of FGM conical-spherical shells. Thin-Walled Struct. 160, 107387 (2021). https://doi.org/10.1016/j.tws.2020.107387

    Article  Google Scholar 

  46. C. Zhang et al., Analytical study on longitudinal vibration characteristics of the coupled shaft and conical-cylindrical shell. Ocean Eng. 223(1), 108691 (2021). https://doi.org/10.1016/j.oceaneng.2021.108691

    Article  Google Scholar 

  47. M. Zarei et al., On the free vibration of joined grid-stiffened composite conical-cylindrical shells. Thin-Walled Struct. 161, 107565 (2021)

    Article  Google Scholar 

  48. L. Tian, T. Ye, G. Jin, Vibration analysis of combined conical-cylindrical shells based on the dynamic stiffness method. Thin-Walled Struct. (2020). https://doi.org/10.1016/j.tws.2020.107260

    Article  Google Scholar 

  49. Qi. He et al., Analysis of vibration characteristics of joined cylindrical-spherical shells. Eng. Struct. 218, 110767 (2020). https://doi.org/10.1016/j.engstruct.2020.110767

    Article  Google Scholar 

  50. M.A. Kouchakzadeh, M. Shakouri, Free vibration analysis of joined cross-ply laminated conical shells. Int. J. Mech. Sci. 78, 118–125 (2014)

    Article  Google Scholar 

  51. H. Bagheri, Y. Kiani, M.R. Eslami, Free vibration of joined conical-conical shells. Thin-Walled Struct. 120, 446–457 (2017)

    Article  MATH  Google Scholar 

  52. Q. Tang et al., Nonlinear response analysis of bolted joined cylindrical-cylindrical shell with general boundary condition. J. Sound Vib. 443, 788–803 (2019)

    Article  ADS  Google Scholar 

  53. S. Sarkheil, Mahmoud Saadat Foumani, Free vibrational characteristics of rotating joined cylindrical-conical shells. Thin-Walled Struct. 107, 657–670 (2016)

    Article  Google Scholar 

  54. M. Shakouri, M.A. Kouchakzadeh, Free vibration analysis of joined conical shells: Analytical and experimental study. Thin-Walled Struct. 85, 350–358 (2014)

    Article  Google Scholar 

  55. C.F. Chen, C.H. Hsiao, Haar wavelet method for solving lumped and distributed parameter systems. IEEE Proc. Contr. Theor. Appl. 114(1), 87–94 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  56. C.H. Hsiao, State analysis of linear time-delayed systems via Haar wavelets. Math. Comput. Simulat. 44(5), 457–470 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  57. C.H. Hsiao, W.J. Wang, Haar wavelet approach to nonlinear stiff systems. Math. Comput. Simulat. 57, 347–353 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  58. Ü. Lepik, Numerical solution of differential equations using Haar wavelets. Math. Comput. Simulat. 68, 127–143 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  59. Ü. Lepik, Solving PDEs with the aid of two-dimensional Haar wavelets. Comput. Math. Appl. 61, 1873–1879 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  60. Z. Shi, Y.Y. Cao, A spectral collocation method based on Haar wavelets for Poisson equations and biharmonic equations. Math. Comput. Model. 54, 2858–2868 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  61. Z. Shi, Y.Y. Cao, Application of Haar wavelet method to eigenvalue problems of high order differential equations. Appl. Math. Model. 36, 4020–4026 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  62. N.M. Bujurke, C.S. Salimath, S.C. Shiralashetti, Computation of eigenvalues and solutions of regular Sturm-Liouville problems using Haar wavelets. J. Comput. Appl. Math. 219, 90–101 (2008)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  63. J. Majak, M. Pohlak, M. Eerme, T. Lepikult, Weak formulation based Haar wavelet method for solving differential equations. Appl. Math. Comput. 211(2), 488–494 (2009)

    MathSciNet  MATH  Google Scholar 

  64. M. Kirs et al., Haar wavelet method for vibration analysis of nanobeams. Waves Wavelets Fractals Adv. Anal. 2, 20–28 (2016)

    Article  Google Scholar 

  65. H. Hein, L. Feklistova, Free vibrations of non-uniform and axially functionally graded beams using Haar wavelet. Eng. Struct. 33, 3696–3701 (2011)

    Article  Google Scholar 

  66. H. Hein, L. Feklistova, Computationally efficient delamination detection in composite beams using Haar wavelets. Mech. Syst. Signal. Pr. 25, 2257–2270 (2011)

    Article  Google Scholar 

  67. C. Zhang, Z. Zhong, Three-dimensional analysis of functionally graded plate based on the Haar wavelet method. Acta Mech. Solida Sin. 20(2), 95–102 (2007)

    Article  Google Scholar 

  68. B.H. Kim, H. Kim, T. Park, Nondestructive damage evaluation of plates using the multi-resolution analysis of two-dimensional Haar wavelet. J. Sound Vib. 292, 82–104 (2006)

    Article  ADS  Google Scholar 

  69. X. Xie et al., A numerical solution for vibration analysis of composite laminated conical, cylindrical shell and annular plate structures. Compos. Struct. 111, 20–30 (2014)

    Article  Google Scholar 

  70. X. Xie et al., Free vibration analysis of composite laminated cylindrical shells using the Haar wavelet method. Compos. Struct. 109, 169–177 (2014)

    Article  Google Scholar 

  71. X. Xie et al., Free vibration analysis of cylindrical shells using the Haar wavelet method. Int. J. Mech. Sci. 77, 47–56 (2013)

    Article  Google Scholar 

  72. X. Xie et al., Free vibration analysis of functionally graded conical shells and annular plates using the Haar wavelet method. Appl. Acoust. 85, 130–142 (2014)

    Article  Google Scholar 

  73. X. Xie, H. Zheng, G. Jin, Free vibration of four-parameter functionally graded spherical and parabolic shells of revolution with arbitrary boundary conditions. Compos. Part B Eng. 77, 59–73 (2015). https://doi.org/10.1016/j.compositesb.2015.03.016

    Article  Google Scholar 

  74. G. Jin, X. Xie, Z. Liu, The Haar wavelet method for free vibration analysis of functionally graded cylindrical shells based on the shear deformation theory. Compos. Struct. 108, 435–448 (2014)

    Article  Google Scholar 

  75. R. Talebitooti, V.S. Anbardan, Haar wavelet discretization approach for frequency analysis of the functionally graded generally doubly-curved shells of revolution. Appl. Math. Model. 67, 645–675 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  76. K. Kim et al., Application of Haar wavelet method for free vibration of laminated composite conical–cylindrical coupled shells with elastic boundary condition. Phys. Scr. 96, 035223 (2021). https://doi.org/10.1088/1402-4896/abd9f7

    Article  ADS  Google Scholar 

Download references

Acknowledgements

The authors would like to thank the anonymous reviewers for carefully reading the paper and their very valuable comments. The authors gratefully acknowledge the supports from Pyongyang University of Mechanical Engineering of DPRK. In addition, the authors would like to take the opportunity to express my hearted gratitude to Dr. Paeksan Jang who made contribution to the completion of my article.

Author information

Authors and Affiliations

  1. Information Center, Kim Chaek University of Technology, Pyongyang, 950003, Democratic People’s Republic of Korea

    Kwangil An & Yongsu Jon

  2. Department of Engineering Machine, Pyongyang University of Mechanical Engineering, Pyongyang, 999093, Democratic People’s Republic of Korea

    Kwanghun Kim & Cholsik Kim

  3. Department of Information Engineering, Chongjin Mine & Metal University, Chongjin, 999091, Democratic People’s Republic of Korea

    Sok Kim

Authors
  1. Kwangil An
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yongsu Jon
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Kwanghun Kim
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Sok Kim
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Cholsik Kim
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Kwanghun Kim.

Ethics declarations

Conflict of interest

No potential conflict of interest was reported by the authors.

Appendices

Appendix 1: Detailed expressions of the constant coefficients \(L_{ij}^{\psi } ,C_{ij}^{\psi } ,R_{ij}^{\psi }\)

  • For left double-curved shell

    $$ \begin{gathered} L_{11}^{0} = - A_{11} R_{{\varphi_{l} }}^{2} \cos^{2} \varphi_{l} - A_{12} R_{{\varphi_{l} }} R_{{0_{l} }} \sin \varphi_{l} - A_{66} n^{2} R_{{\varphi_{l} }}^{2} - \kappa A_{66} R_{{0_{l} }}^{2} \hfill \\ L_{11}^{1} = A_{11} \cos \varphi_{l} R_{{\varphi_{l} }} R_{{0_{l} }} - A_{11} R_{{0_{l} }}^{2} \frac{1}{{R_{{\varphi_{l} }} }}\frac{{dR_{{\varphi_{l} }} }}{{d\varphi_{l} }},\,\,\,\,\,\,L_{11}^{2} = A_{11} R_{{0_{l} }}^{2} ,\,\,\,\,\,L_{12}^{0} = - \left( {A_{11} + A_{66} } \right)n\cos \varphi_{l} R_{{\varphi_{l} }}^{2} , \hfill \\ L_{12}^{1} = \left( {A_{12} + A_{66} } \right)nR_{{\varphi_{l} }} R_{{0_{l} }} ,\,\,\,\,\,L_{13}^{0} = - A_{11} \sin \varphi_{l} \cos \varphi_{l} R_{{\varphi_{l} }}^{2} + A_{11} \cos \varphi_{l} R_{{\varphi_{l} }} R_{{0_{l} }} - A_{11} R_{{0_{l} }}^{2} \frac{1}{{R_{{\varphi_{l} }} }}\frac{{dR_{{\varphi_{l} }} }}{{d\varphi_{l} }} \hfill \\ L_{13}^{1} = A_{11} R_{{0_{l} }}^{2} + A_{12} \sin \varphi_{l} R_{{\varphi_{l} }} R_{{0_{l} }} + \kappa A_{66} R_{{0_{l} }}^{2} \hfill \\ L_{14}^{0} = - B_{11} R_{{\varphi_{l} }}^{2} \cos^{2} \varphi_{l} - B_{12} R_{{\varphi_{l} }} R_{{0_{l} }} \sin^{2} \varphi_{l} - B_{66} n^{2} R_{{\varphi_{l} }}^{2} + \kappa A_{66} R_{{0_{l} }}^{2} R_{{\varphi_{l} }} \hfill \\ L_{14}^{1} = B_{11} \cos \varphi_{l} R_{{\varphi_{l} }} R_{{0_{l} }} - B_{11} R_{{0_{l} }}^{2} \frac{1}{{R_{{\varphi_{l} }} }}\frac{{dR_{{\varphi_{l} }} }}{{d\varphi_{l} }},\,\,\,\,\,\,L_{14}^{2} = B_{11} R_{{0_{l} }}^{2} \hfill \\ L_{15}^{0} = - \left( {B_{11} + B_{66} } \right)n\cos \varphi_{l} R_{{\varphi_{l} }}^{2} ,\,\,\,\,\,L_{15}^{1} = \left( {B_{12} + B_{66} } \right)nR_{{\varphi_{l} }} R_{{0_{l} }} \hfill \\ \end{gathered} $$
    $$ \begin{gathered} L_{21}^{0} = - \left( {A_{11} + A_{66} } \right)n\cos \varphi_{l} R_{{\varphi_{l} }}^{2} ,\,\,\,\,\,\,L_{21}^{1} = - \left( {A_{12} + A_{66} } \right)nR_{{0_{l} }} R_{{\varphi_{l} }} \hfill \\ L_{22}^{0} = - A_{66} \cos^{2} \varphi_{l} R_{{\varphi_{l} }}^{2} + A_{66} \sin \varphi_{l} R_{{0_{l} }} R_{{\varphi_{l} }} - A_{11} n^{2} R_{{\varphi_{l} }}^{2} - \kappa A_{66} \sin^{2} \varphi_{l} R_{{\varphi_{l} }}^{2} \hfill \\ L_{22}^{1} = A_{66} \cos \varphi_{l} R_{{0_{l} }} R_{{\varphi_{l} }} - A_{66} R_{{0_{l} }}^{2} \frac{1}{{R_{{\varphi_{l} }} }}\frac{{dR_{{\varphi_{l} }} }}{{d\varphi_{l} }},\,\,\,\,\,\,L_{22}^{2} = A_{66} R_{{0_{l} }}^{2} , \hfill \\ L_{23}^{0} = - A_{11} n\sin \varphi_{l} R_{{\varphi_{l} }}^{2} - \kappa A_{66} n\sin \varphi_{l} R_{{\varphi_{l} }}^{2} - A_{12} nR_{{0_{l} }} R_{{\varphi_{l} }} ,\,\,\,\,\,L_{24}^{0} = - \left( {B_{11} + B_{66} } \right)n\cos \varphi_{l} R_{{\varphi_{l} }}^{2} , \hfill \\ L_{24}^{1} = - \left( {B_{12} + B_{66} } \right)nR_{{0_{l} }} R_{{\varphi_{l} }} ,\,\,\,\,\,L_{25}^{0} = - B_{66} \cos^{2} \varphi_{l} R_{{\varphi_{l} }}^{2} + B_{66} \sin \varphi_{l} R_{{0_{l} }} R_{{\varphi_{l} }} - B_{11} n^{2} R_{{\varphi_{l} }}^{2} + \kappa A_{66} \sin \varphi_{l} R_{{0_{l} }} R_{{\varphi_{l} }}^{2} \hfill \\ L_{25}^{1} = B_{66} \cos \varphi_{l} R_{{0_{l} }} R_{{\varphi_{l} }} - B_{66} R_{{0_{l} }}^{2} \frac{1}{{R_{{\varphi_{l} }} }}\frac{{dR_{{\varphi_{l} }} }}{{d\varphi_{l} }},\,\,\,\,\,\,L_{25}^{2} = B_{66} R_{{0_{l} }}^{2} \hfill \\ \end{gathered} $$
    $$ \begin{gathered} L_{31}^{0} = - A_{12} \cos \varphi_{l} R_{{0_{l} }} R_{{\varphi_{l} }} - A_{11} \sin \varphi_{l} \cos \varphi_{l} R_{{\varphi_{l} }}^{2} + \kappa A_{66} \cos \varphi_{l} R_{{0_{l} }} R_{{\varphi_{l} }} + \kappa A_{66} R_{{0_{l} }}^{2} \frac{1}{{R_{{\varphi_{l} }} }}\frac{{dR_{{\varphi_{l} }} }}{{d\varphi_{l} }} \hfill \\ L_{31}^{1} = - A_{11} R_{{0_{l} }}^{2} - A_{12} \sin \varphi_{l} R_{{0_{l} }} R_{{\varphi_{l} }} - \kappa A_{66} R_{{0_{l} }}^{2} ,\,\,\,\,\,L_{32}^{0} = - \left( {A_{11} + \kappa A_{66} } \right)n\sin \varphi_{l} R_{{\varphi_{l} }}^{2} - A_{12} nR_{{0_{l} }} R_{{\varphi_{l} }} \hfill \\ L_{33}^{0} = - A_{11} R_{{0_{l} }}^{2} - A_{12} \sin \varphi_{l} R_{{0_{l} }} R_{{\varphi_{l} }} - A_{11} \sin \varphi_{l} R_{{\varphi_{l} }}^{2} - \kappa A_{66} n^{2} R_{{\varphi_{l} }}^{2} \hfill \\ L_{33}^{1} = \kappa A_{66} \cos \varphi_{l} R_{{0_{l} }} R_{{\varphi_{l} }} - \kappa A_{66} R_{{0_{l} }}^{2} \frac{1}{{R_{{\varphi_{l} }} }}\frac{{dR_{{\varphi_{l} }} }}{{d\varphi_{l} }},\,\,\,\,\,L_{33}^{2} = \kappa A_{66} R_{{0_{l} }}^{2} \hfill \\ L_{34}^{0} = \kappa A_{66} \cos \varphi_{l} R_{{0_{l} }} R_{{\varphi_{l} }}^{2} - B_{12} \cos \varphi_{l} R_{{0_{l} }} R_{{\varphi_{l} }} - B_{11} \sin \varphi_{l} \cos \varphi_{l} R_{{\varphi_{l} }}^{2} \hfill \\ L_{34}^{1} = \kappa A_{66} \cos \varphi_{l} R_{{0_{l} }} R_{{\varphi_{l} }}^{2} - B_{11} R_{{0_{l} }}^{2} - B_{12} \sin \varphi_{l} R_{{0_{l} }} R_{{\varphi_{l} }} \hfill \\ L_{35}^{0} = \kappa A_{66} \cos \varphi_{l} R_{{0_{l} }} R_{{\varphi_{l} }}^{2} - B_{12} nR_{{0_{l} }} R_{{\varphi_{l} }} - B_{11} n\sin \varphi_{l} R_{{\varphi_{l} }}^{2} \hfill \\ \end{gathered} $$
    $$ \begin{gathered} L_{41}^{0} = - B_{12} \sin \varphi_{l} R_{{0_{l} }} R_{{\varphi_{l} }} - B_{11} \cos^{2} \varphi_{l} R_{{\varphi_{l} }}^{2} - B_{66} n^{2} R_{{\varphi_{l} }}^{2} + \kappa A_{66} R_{{\varphi_{l} }} R_{{0_{l} }}^{2} \hfill \\ L_{41}^{1} = B_{11} \cos \varphi_{l} R_{{0_{l} }} R_{{\varphi_{l} }} - B_{11} R_{{0_{l} }}^{2} \frac{1}{{R_{{\varphi_{l} }} }}\frac{{dR_{{\varphi_{l} }} }}{{d\varphi_{l} }},\,\,\,\,\,L_{41}^{2} = B_{11} R_{{0_{l} }}^{2} ,\,\,\,\,\,L_{42}^{0} = - \left( {B_{11} + B_{66} } \right)n\cos \varphi_{l} R_{{\varphi_{l} }}^{2} , \hfill \\ L_{42}^{1} = \left( {B_{12} + B_{66} } \right)nR_{{0_{l} }} R_{{\varphi_{l} }} ,\,\,\,\,\,L_{43}^{0} = B_{11} \sin \varphi_{l} \cos \varphi_{l} R_{{\varphi_{l} }}^{2} + B_{11} \cos \varphi_{l} R_{{0_{l} }} R_{{\varphi_{l} }} - B_{11} R_{{0_{l} }}^{2} \frac{1}{{R_{{\varphi_{l} }} }}\frac{{dR_{{\varphi_{l} }} }}{{d\varphi_{l} }} \hfill \\ L_{43}^{1} = B_{11} R_{{0_{l} }}^{2} + B_{12} \sin \varphi_{l} R_{{0_{l} }} R_{{\varphi_{l} }} + \kappa A_{66} R_{{\varphi_{l} }} R_{{0_{l} }}^{2} \hfill \\ L_{44}^{0} = - D_{12} \sin \varphi_{l} R_{{0_{l} }} R_{{\varphi_{l} }} - D_{11} \cos^{2} \varphi_{l} R_{{\varphi_{l} }}^{2} - D_{66} n^{2} R_{{\varphi_{l} }}^{2} - \kappa A_{66} R_{{\varphi_{l} }}^{2} R_{{0_{l} }}^{2} \hfill \\ L_{44}^{1} = D_{11} \cos \varphi_{l} R_{{0_{l} }} R_{{\varphi_{l} }} - D_{11} R_{{0_{l} }}^{2} \frac{1}{{R_{{\varphi_{l} }} }}\frac{{dR_{{\varphi_{l} }} }}{{d\varphi_{l} }},\,\,\,\,\,L_{44}^{2} = D_{11} R_{{0_{l} }}^{2} \hfill \\ L_{45}^{0} = - \left( {D_{11} + D_{66} } \right)n\cos \varphi_{l} R_{{\varphi_{l} }}^{2} ,\,\,\,\,\,L_{45}^{1} = \left( {D_{12} + D_{66} } \right)nR_{{0_{l} }} R_{{\varphi_{l} }} \hfill \\ \end{gathered} $$
    $$ \begin{gathered} L_{51}^{0}\, { = } - \left( {B_{11} + B_{66} } \right)n\cos \varphi_{l} R_{{\varphi_{l} }}^{2} ,\,\,\,\,\,L_{51}^{1} = - \left( {B_{12} + B_{66} } \right)nR_{{0_{l} }} R_{{\varphi_{l} }} \hfill \\ L_{52}^{0} = \kappa A_{66} \sin \varphi_{l} R_{{0_{l} }} R_{{\varphi_{l} }}^{2} - B_{11} n^{2} R_{{\varphi_{l} }}^{2} - B_{66} \cos^{2} \varphi_{l} R_{{\varphi_{l} }}^{2} + B_{66} \sin \varphi_{l} R_{{0_{l} }} R_{{\varphi_{l} }} \hfill \\ L_{52}^{1} = B_{66} \cos \varphi_{l} R_{{0_{l} }} R_{{\varphi_{l} }} - B_{66} R_{{0_{l} }}^{2} \frac{1}{{R_{{\varphi_{l} }} }}\frac{{dR_{{\varphi_{l} }} }}{{d\varphi_{l} }},\,\,\,\,\,\,L_{52}^{2} = B_{66} R_{{0_{l} }}^{2} \hfill \\ L_{53}^{0} = - B_{11} n\sin \varphi_{l} R_{{\varphi_{l} }}^{2} - B_{12} nR_{{0_{l} }} R_{{\varphi_{l} }} + \kappa A_{66} nR_{{0_{l} }} R_{{\varphi_{l} }}^{2} ,\,\,\,\,\,L_{54}^{0} = - \left( {D_{11} + D_{66} } \right)n\cos \varphi_{l} R_{{\varphi_{l} }}^{2} , \hfill \\ L_{54}^{1} = - \left( {D_{12} + D_{66} } \right)nR_{{0_{l} }} R_{{\varphi_{l} }} ,\,\,\,\,\,L_{55}^{0} = - D_{11} n^{2} R_{{\varphi_{l} }}^{2} - D_{66} \cos^{2} \varphi_{l} R_{{\varphi_{l} }}^{2} + D_{66} \sin \varphi_{l} R_{{0_{l} }} R_{{\varphi_{l} }} - \kappa A_{66} \sin \varphi_{l} R_{{0_{l} }}^{2} R_{{\varphi_{l} }}^{2} \hfill \\ L_{55}^{1} = D_{66} \cos \varphi_{l} R_{{0_{l} }} R_{{\varphi_{l} }} - D_{66} R_{{0_{l} }}^{2} \frac{1}{{R_{{\varphi_{l} }} }}\frac{{dR_{{\varphi_{l} }} }}{{d\varphi_{l} }},\,\,\,\,\,\,L_{52}^{2} = D_{66} R_{{0_{l} }}^{2} \hfill \\ \end{gathered} $$

  • For cylindrical shell

    $$ \begin{gathered} C_{{11}}^{1} = - A_{{66}} n^{2} ,\;\;\;C_{{11}}^{3} = A_{{11}} R^{2} ,\;\;\;C_{{12}}^{2} = A_{{12}} Rn{\text{ + }}A_{{66}} Rn,\;\;\;\;C_{{13}}^{2} = A_{{12}} R,\; \hfill \\ C_{{14}}^{1} = - B_{{66}} n^{2} ,\;\;C_{{14}}^{3} = B_{{11}} R^{2} ,\;\;\;\;C_{{15}}^{2} = B_{{12}} Rn{\text{ + }}B_{{66}} Rn \hfill \\ C_{{21}}^{2} = - A_{{12}} Rn - A_{{66}} Rn,\;\;C_{{22}}^{1} = - A_{{22}} n^{2} - \kappa A_{{44}} ,\;\;C_{{22}}^{3} = A_{{66}} R^{2} ,\;C_{{23}}^{1} = - A_{{22}} n - \kappa A_{{44}} n, \hfill \\ C_{{24}}^{2} = - B_{{12}} Rn - B_{{66}} Rn,\,\,\,C_{{25}}^{1} = - B_{{22}} n^{2} + \kappa A_{{44}} R,\;\;\;C_{{25}}^{3} = B_{{66}} R^{2} \hfill \\ C_{{31}}^{2} = A_{{12}} R,\;\;\;C_{{32}}^{1} = A_{{22}} n{\text{ + }}\kappa A_{{44}} n,\;\;C_{{33}}^{1} = \kappa A_{{44}} n^{2} + A_{{22}} ,\;\;\;C_{{33}}^{3} = - \kappa A_{{55}} R^{2} ,\;\;\; \hfill \\ C_{{34}}^{2} = B_{{12}} R - \kappa A_{{55}} R^{2} ,\;C_{{35}}^{1} = B_{{22}} n{\text{ - }}\kappa A_{{44}} Rn,\; \hfill \\ C_{{41}}^{1} = - B_{{66}} n^{2} ,\;\;\;C_{{41}}^{3} = B_{{11}} R^{2} ,\;\;C_{{42}}^{2} = B_{{12}} Rn{\text{ + }}B_{{66}} Rn,\;\;\;\;C_{{43}}^{2} = B_{{12}} R - \kappa A_{{55}} R^{2} ,\;\; \hfill \\ C_{{44}}^{1} = - D_{{66}} n^{2} - \kappa A_{{55}} R^{2} ,\;\;C_{{44}}^{3} = D_{{11}} R^{2} ,\;\;\;\;\;C_{{45}}^{2} = D_{{12}} Rn{\text{ + }}D_{{66}} Rn,\; \hfill \\ C_{{51}}^{2} = - B_{{12}} Rn - B_{{66}} Rn,\;\;C_{{52}}^{1} = \kappa A_{{44}} R - B_{{22}} n^{2} ,\;\;\;C_{{52}}^{3} = B_{{66}} R^{2} ,\;C_{{53}}^{1} = \kappa A_{{44}} Rn - B_{{22}} n,\; \hfill \\ C_{{54}}^{2} = - D_{{12}} Rn - D_{{66}} Rn,\;\;C_{{55}}^{1} = - D_{{22}} n^{2} - \kappa A_{{44}} R^{2} ,\;\;\;\;\;C_{{55}}^{3} = D_{{66}} R^{2} \hfill \\ \end{gathered} $$

  • For right double-curved shell

    $$ \begin{gathered} R_{11}^{0} = - A_{11} R_{{\varphi_{r} }}^{2} \cos^{2} \varphi_{r} - A_{12} R_{{\varphi_{r} }} R_{{0_{r} }} \sin \varphi_{r} - A_{66} n^{2} R_{{\varphi_{r} }}^{2} - \kappa A_{66} R_{{0_{r} }}^{2} \hfill \\ R_{11}^{1} = A_{11} \cos \varphi_{r} R_{{\varphi_{r} }} R_{{0_{r} }} - A_{11} R_{{0_{r} }}^{2} \frac{1}{{R_{{\varphi_{r} }} }}\frac{{dR_{{\varphi_{r} }} }}{{d\varphi_{r} }},\,\,\,\,\,\,R_{11}^{2} = A_{11} R_{{0_{r} }}^{2} ,\,\,\,\,\,R_{12}^{0} = - \left( {A_{11} + A_{66} } \right)n\cos \varphi_{r} R_{{\varphi_{r} }}^{2} , \hfill \\ R_{12}^{1} = \left( {A_{12} + A_{66} } \right)nR_{{\varphi_{r} }} R_{{0_{r} }} ,\,\,\,\,\,R_{13}^{0} = - A_{11} \sin \varphi_{r} \cos \varphi_{r} R_{{\varphi_{r} }}^{2} + A_{11} \cos \varphi_{r} R_{{\varphi_{r} }} R_{{0_{r} }} - A_{11} R_{{0_{r} }}^{2} \frac{1}{{R_{{\varphi_{r} }} }}\frac{{dR_{{\varphi_{r} }} }}{{d\varphi_{r} }} \hfill \\ R_{13}^{1} = A_{11} R_{{0_{r} }}^{2} + A_{12} \sin \varphi_{r} R_{{\varphi_{r} }} R_{{0_{r} }} + \kappa A_{66} R_{{0_{r} }}^{2} \hfill \\ R_{14}^{0} = - B_{11} R_{{\varphi_{r} }}^{2} \cos^{2} \varphi_{r} - B_{12} R_{{\varphi_{r} }} R_{{0_{r} }} \sin^{2} \varphi_{r} - B_{66} n^{2} R_{{\varphi_{r} }}^{2} + \kappa A_{66} R_{{0_{r} }}^{2} R_{{\varphi_{r} }} \hfill \\ R_{14}^{1} = B_{11} \cos \varphi_{l} R_{{\varphi_{r} }} R_{{0_{r} }} - B_{11} R_{{0_{r} }}^{2} \frac{1}{{R_{{\varphi_{r} }} }}\frac{{dR_{{\varphi_{r} }} }}{{d\varphi_{r} }},\,\,\,\,\,\,R_{14}^{2} = B_{11} R_{{0_{r} }}^{2} \hfill \\ R_{15}^{0} = - \left( {B_{11} + B_{66} } \right)n\cos \varphi_{r} R_{{\varphi_{r} }}^{2} ,\,\,\,\,\,R_{15}^{1} = \left( {B_{12} + B_{66} } \right)nR_{{\varphi_{r} }} R_{{0_{r} }} \hfill \\ \end{gathered} $$
    $$ \begin{gathered} R_{21}^{0} = - \left( {A_{11} + A_{66} } \right)n\cos \varphi_{r} R_{{\varphi_{r} }}^{2} ,\,\,\,\,\,\,R_{21}^{1} = - \left( {A_{12} + A_{66} } \right)nR_{{0_{r} }} R_{{\varphi_{r} }} \hfill \\ R_{22}^{0} = - A_{66} \cos^{2} \varphi_{r} R_{{\varphi_{r} }}^{2} + A_{66} \sin \varphi_{r} R_{{0_{r} }} R_{{\varphi_{r} }} - A_{11} n^{2} R_{{\varphi_{r} }}^{2} - \kappa A_{66} \sin^{2} \varphi_{r} R_{{\varphi_{r} }}^{2} \hfill \\ R_{22}^{1} = A_{66} \cos \varphi_{r} R_{{0_{r} }} R_{{\varphi_{r} }} - A_{66} R_{{0_{r} }}^{2} \frac{1}{{R_{{\varphi_{r} }} }}\frac{{dR_{{\varphi_{r} }} }}{{d\varphi_{r} }},\,\,\,\,\,\,R_{22}^{2} = A_{66} R_{{0_{r} }}^{2} , \hfill \\ R_{23}^{0} = - A_{11} n\sin \varphi_{r} R_{{\varphi_{r} }}^{2} - \kappa A_{66} n\sin \varphi_{r} R_{{\varphi_{r} }}^{2} - A_{12} nR_{{0_{r} }} R_{{\varphi_{r} }} ,\,\,\,\,\,R_{24}^{0} = - \left( {B_{11} + B_{66} } \right)n\cos \varphi_{r} R_{{\varphi_{r} }}^{2} , \hfill \\ R_{24}^{1} = - \left( {B_{12} + B_{66} } \right)nR_{{0_{r} }} R_{{\varphi_{r} }} ,\,\,\,\,\,R_{25}^{0} = - B_{66} \cos^{2} \varphi_{r} R_{{\varphi_{r} }}^{2} + B_{66} \sin \varphi_{r} R_{{0_{r} }} R_{{\varphi_{r} }} - B_{11} n^{2} R_{{\varphi_{r} }}^{2} + \kappa A_{66} \sin \varphi_{r} R_{{0_{r} }} R_{{\varphi_{r} }}^{2} \hfill \\ R_{25}^{1} = B_{66} \cos \varphi_{r} R_{{0_{r} }} R_{{\varphi_{r} }} - B_{66} R_{{0_{r} }}^{2} \frac{1}{{R_{{\varphi_{r} }} }}\frac{{dR_{{\varphi_{r} }} }}{{d\varphi_{r} }},\,\,\,\,\,\,R_{25}^{2} = B_{66} R_{{0_{r} }}^{2} \hfill \\ \end{gathered} $$
    $$ \begin{gathered} R_{31}^{0} = - A_{12} \cos \varphi_{r} R_{{0_{r} }} R_{{\varphi_{r} }} - A_{11} \sin \varphi_{r} \cos \varphi_{r} R_{{\varphi_{r} }}^{2} + \kappa A_{66} \cos \varphi_{r} R_{{0_{r} }} R_{{\varphi_{r} }} + \kappa A_{66} R_{{0_{r} }}^{2} \frac{1}{{R_{{\varphi_{r} }} }}\frac{{dR_{{\varphi_{r} }} }}{{d\varphi_{r} }} \hfill \\ R_{31}^{1} = - A_{11} R_{{0_{l} }}^{2} - A_{12} \sin \varphi_{r} R_{{0_{r} }} R_{{\varphi_{r} }} - \kappa A_{66} R_{{0_{r} }}^{2} ,\,\,\,\,\,R_{32}^{0} = - \left( {A_{11} + \kappa A_{66} } \right)n\sin \varphi_{r} R_{{\varphi_{r} }}^{2} - A_{12} nR_{{0_{r} }} R_{{\varphi_{r} }} \hfill \\ R_{33}^{0} = - A_{11} R_{{0_{r} }}^{2} - A_{12} \sin \varphi_{r} R_{{0_{r} }} R_{{\varphi_{r} }} - A_{11} \sin \varphi_{r} R_{{\varphi_{r} }}^{2} - \kappa A_{66} n^{2} R_{{\varphi_{r} }}^{2} \hfill \\ R_{33}^{1} = \kappa A_{66} \cos \varphi_{r} R_{{0_{r} }} R_{{\varphi_{r} }} - \kappa A_{66} R_{{0_{r} }}^{2} \frac{1}{{R_{{\varphi_{r} }} }}\frac{{dR_{{\varphi_{l} }} }}{{d\varphi_{r} }},\,\,\,\,\,R_{33}^{2} = \kappa A_{66} R_{{0_{r} }}^{2} \hfill \\ R_{34}^{0} = \kappa A_{66} \cos \varphi_{r} R_{{0_{r} }} R_{{\varphi_{r} }}^{2} - B_{12} \cos \varphi_{r} R_{{0_{r} }} R_{{\varphi_{r} }} - B_{11} \sin \varphi_{r} \cos \varphi_{r} R_{{\varphi_{r} }}^{2} \hfill \\ R_{34}^{1} = \kappa A_{66} \cos \varphi_{r} R_{{0_{r} }} R_{{\varphi_{r} }}^{2} - B_{11} R_{{0_{r} }}^{2} - B_{12} \sin \varphi_{r} R_{{0_{r} }} R_{{\varphi_{r} }} \hfill \\ R_{35}^{0} = \kappa A_{66} \cos \varphi_{r} R_{{0_{r} }} R_{{\varphi_{r} }}^{2} - B_{12} nR_{{0_{r} }} R_{{\varphi_{r} }} - B_{11} n\sin \varphi_{r} R_{{\varphi_{r} }}^{2} \hfill \\ \end{gathered} $$
    $$ \begin{gathered} R_{41}^{0} = - B_{12} \sin \varphi_{r} R_{{0_{r} }} R_{{\varphi_{r} }} - B_{11} \cos^{2} \varphi_{r} R_{{\varphi_{r} }}^{2} - B_{66} n^{2} R_{{\varphi_{r} }}^{2} + \kappa A_{66} R_{{\varphi_{r} }} R_{{0_{r} }}^{2} \hfill \\ R_{41}^{1} = B_{11} \cos \varphi_{r} R_{{0_{r} }} R_{{\varphi_{r} }} - B_{11} R_{{0_{r} }}^{2} \frac{1}{{R_{{\varphi_{r} }} }}\frac{{dR_{{\varphi_{r} }} }}{{d\varphi_{r} }},\,\,\,\,\,R_{41}^{2} = B_{11} R_{{0_{r} }}^{2} ,\,\,\,\,\,R_{42}^{0} = - \left( {B_{11} + B_{66} } \right)n\cos \varphi_{r} R_{{\varphi_{r} }}^{2} , \hfill \\ R_{42}^{1} = \left( {B_{12} + B_{66} } \right)nR_{{0_{r} }} R_{{\varphi_{r} }} ,\,\,\,\,\,R_{43}^{0} = B_{11} \sin \varphi_{r} \cos \varphi_{r} R_{{\varphi_{r} }}^{2} + B_{11} \cos \varphi_{r} R_{{0_{r} }} R_{{\varphi_{r} }} - B_{11} R_{{0_{r} }}^{2} \frac{1}{{R_{{\varphi_{r} }} }}\frac{{dR_{{\varphi_{r} }} }}{{d\varphi_{r} }} \hfill \\ R_{43}^{1} = B_{11} R_{{0_{r} }}^{2} + B_{12} \sin \varphi_{r} R_{{0_{r} }} R_{{\varphi_{r} }} + \kappa A_{66} R_{{\varphi_{r} }} R_{{0_{r} }}^{2} \hfill \\ R_{44}^{0} = - D_{12} \sin \varphi_{r} R_{{0_{r} }} R_{{\varphi_{r} }} - D_{11} \cos^{2} \varphi_{r} R_{{\varphi_{r} }}^{2} - D_{66} n^{2} R_{{\varphi_{r} }}^{2} - \kappa A_{66} R_{{\varphi_{r} }}^{2} R_{{0_{r} }}^{2} \hfill \\ R_{44}^{1} = D_{11} \cos \varphi_{r} R_{{0_{r} }} R_{{\varphi_{r} }} - D_{11} R_{{0_{r} }}^{2} \frac{1}{{R_{{\varphi_{r} }} }}\frac{{dR_{{\varphi_{r} }} }}{{d\varphi_{r} }},\,\,\,\,\,R_{44}^{2} = D_{11} R_{{0_{r} }}^{2} \hfill \\ R_{45}^{0} = - \left( {D_{11} + D_{66} } \right)n\cos \varphi_{l} R_{{\varphi_{l} }}^{2} ,\,\,\,\,\,R_{45}^{1} = \left( {D_{12} + D_{66} } \right)nR_{{0_{l} }} R_{{\varphi_{l} }} \hfill \\ \end{gathered} $$
    $$ \begin{gathered} R_{51}^{0} { = } - \left( {B_{11} + B_{66} } \right)n\cos \varphi_{r} R_{{\varphi_{r} }}^{2} ,\,\,\,\,\,R_{51}^{1} = - \left( {B_{12} + B_{66} } \right)nR_{{0_{r} }} R_{{\varphi_{r} }} \hfill \\ R_{52}^{0} = \kappa A_{66} \sin \varphi_{r} R_{{0_{r} }} R_{{\varphi_{r} }}^{2} - B_{11} n^{2} R_{{\varphi_{r} }}^{2} - B_{66} \cos^{2} \varphi_{r} R_{{\varphi_{r} }}^{2} + B_{66} \sin \varphi_{r} R_{{0_{r} }} R_{{\varphi_{r} }} \hfill \\ R_{52}^{1} = B_{66} \cos \varphi_{r} R_{{0_{r} }} R_{{\varphi_{r} }} - B_{66} R_{{0_{r} }}^{2} \frac{1}{{R_{{\varphi_{r} }} }}\frac{{dR_{{\varphi_{r} }} }}{{d\varphi_{r} }},\,\,\,\,\,\,R_{52}^{2} = B_{66} R_{{0_{r} }}^{2} \hfill \\ R_{53}^{0} = - B_{11} n\sin \varphi_{r} R_{{\varphi_{r} }}^{2} - B_{12} nR_{{0_{r} }} R_{{\varphi_{r} }} + \kappa A_{66} nR_{{0_{r} }} R_{{\varphi_{r} }}^{2} ,\,\,\,\,\,R_{54}^{0} = - \left( {D_{11} + D_{66} } \right)n\cos \varphi_{r} R_{{\varphi_{r} }}^{2} , \hfill \\ R_{54}^{1} = - \left( {D_{12} + D_{66} } \right)nR_{{0_{r} }} R_{{\varphi_{r} }} ,\,\,\,\,\,R_{55}^{0} = - D_{11} n^{2} R_{{\varphi_{r} }}^{2} - D_{66} \cos^{2} \varphi_{r} R_{{\varphi_{r} }}^{2} + D_{66} \sin \varphi_{r} R_{{0_{r} }} R_{{\varphi_{r} }} - \kappa A_{66} \sin \varphi_{r} R_{{0_{r} }}^{2} R_{{\varphi_{r} }}^{2} \hfill \\ R_{55}^{1} = D_{66} \cos \varphi_{r} R_{{0_{r} }} R_{{\varphi_{r} }} - D_{66} R_{{0_{r} }}^{2} \frac{1}{{R_{{\varphi_{r} }} }}\frac{{dR_{{\varphi_{r} }} }}{{d\varphi_{r} }},\,\,\,\,\,\,R_{52}^{2} = D_{66} R_{{0_{r} }}^{2} \hfill \\ \end{gathered} $$

Appendix 2. Detailed expressions of the mass and stiffness matrix

$$ \begin{gathered} {\mathbf{K}}_{{dd}} = \left[ {\begin{array}{*{20}c} {{\mathbf{K}}_{{dd,l}} } & {\mathbf{0}} & {\mathbf{0}} \\ {\mathbf{0}} & {{\mathbf{K}}_{{dd,c}} } & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{0}} & {{\mathbf{K}}_{{dd,r}} } \\ \end{array} } \right],\quad {\mathbf{K}}_{{bd}} = \left[ {\begin{array}{*{20}c} {{\mathbf{K}}_{{bd,l}} } & {\mathbf{0}} & {\mathbf{0}} \\ {\mathbf{0}} & {{\mathbf{K}}_{{bd,c}} } & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{0}} & {{\mathbf{K}}_{{bd,r}} } \\ \end{array} } \right] \hfill \\ {\mathbf{K}}_{{bb}} = \left[ {\begin{array}{*{20}c} {{\mathbf{K}}_{{bb,l}} } & {\mathbf{0}} & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{0}} & {{\mathbf{K}}_{{bb,r}} } \\ {{\mathbf{K}}_{{bb,l1}} } & {{\mathbf{K}}_{{bb,lc}} } & {\mathbf{0}} \\ {{\mathbf{K}}_{{bb,cl}} } & {{\mathbf{K}}_{{bb,c0}} } & {\mathbf{0}} \\ {\mathbf{0}} & {{\mathbf{K}}_{{bb,c1}} } & {{\mathbf{K}}_{{bb,cr}} } \\ {\mathbf{0}} & {{\mathbf{K}}_{{bb,rc}} } & {{\mathbf{K}}_{{bb,r1}} } \\ \end{array} } \right],\quad {\mathbf{K}}_{{bd}} = \left[ {\begin{array}{*{20}c} {{\mathbf{K}}_{{bd,l}} } & {\mathbf{0}} & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{0}} & {{\mathbf{K}}_{{bd,r}} } \\ {{\mathbf{K}}_{{bd,l1}} } & {{\mathbf{K}}_{{bd,lc}} } & {\mathbf{0}} \\ {{\mathbf{K}}_{{bd,cl}} } & {{\mathbf{K}}_{{bd,c0}} } & {\mathbf{0}} \\ {\mathbf{0}} & {{\mathbf{K}}_{{bd,c1}} } & {{\mathbf{K}}_{{bd,cr}} } \\ {\mathbf{0}} & {{\mathbf{K}}_{{bd,rc}} } & {{\mathbf{K}}_{{bd,r1}} } \\ \end{array} } \right] \hfill \\ {\mathbf{A}}_{d} \;= \left[ {{\mathbf{A}}_{{dl}} ,{\mathbf{A}}_{{dc}} ,{\mathbf{A}}_{{dr}} } \right]^{T} ,{\mathbf{A}}_{b} = \left[ {{\mathbf{A}}_{{bl}} ,{\mathbf{A}}_{{bc}} ,{\mathbf{A}}_{{br}} } \right]^{T} \hfill \\ {\mathbf{A}}_{{d\varsigma }} = \left[ {\varvec{a}_{\varsigma } ,\;\varvec{b}_{\varsigma } ,\;\varvec{c}_{\varsigma } ,\;\varvec{d}_{\varsigma } ,\;\varvec{e}_{\varsigma } } \right]^{T} ,{\mathbf{A}}_{{b\varsigma }} = \left[ {\varvec{f}_{\varsigma } ,\;\varvec{g}_{\varsigma } ,\;\varvec{h}_{\varsigma } ,\;\varvec{k}_{\varsigma } ,\;\varvec{l}_{\varsigma } } \right]^{T} \hfill \\ \end{gathered} $$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

An, K., Jon, Y., Kim, K. et al. A solution method for free vibrration analysis of the elastically joined functionally graded shells. Eur. Phys. J. Plus 136, 767 (2021). https://doi.org/10.1140/epjp/s13360-021-01748-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1140/epjp/s13360-021-01748-7

Search

Navigation