1 Introduction

For a graph G, by \(L(G)^2\) we denote the square of the line graph of G – that is, vertices of \(L(G)^2\) are edges of G and two edges \(e,f\in E(G)\) are adjacent in \(L(G)^2\) if at least one vertex of e is adjacent to a vertex of f and \(e\ne f\). The strong chromatic index of G, denoted by \(s'(G)\), is the chromatic number of \(L(G)^2\). This notion was introduced in 1983 by Fouquet and Jolivet [18].

We are motivated by a line of research that asks for maximum possible value of the strong chromatic index of a graph with given maximum degree \(\varDelta \). In 1985, Erdős and Nešetřil formulated the following conjecture [13]; see also [2].

Conjecture 1

If G is a graph with maximum degree \(\varDelta \), then

$$\begin{aligned} s'(G)\le \left\{ \begin{array}{ll} \frac{5}{4}\varDelta ^2,&{}\hbox {for even}\, \varDelta ,\\ \frac{5}{4}\varDelta ^2-\frac{2\varDelta -1}{4},&{}\hbox {for odd}\, \varDelta . \end{array}\right. \end{aligned}$$

Conjecture 1 would be sharp, as wittnessed by the graph obtained from 5-cycle by blowing each vertex up to an independent set of size roughly \(\frac{\varDelta }{2}\) – note that the square of the line graph of such graphs is always a clique. Conversely, if \(L(G)^2\) is a clique for some graph G of maximum degree \(\varDelta \), then the number of edges of G is at most the bound from Conjecture 1, and equality holds only for aforementioned blowups of \(C_5\) [8].

A simple greedy argument shows that \(s'(G)\le 2\varDelta ^2\), and even a small improvement over the constant 2 is nontrivial. Molloy and Reed in 1997 gave an upper bound of \(\left( 2-\epsilon \right) \varDelta ^2\) for \(\epsilon \approx 0.002\) [26], which was subsequently improved by Bruhn and Joos [6] to \(1.93\varDelta ^2\), by Bonamy, Perrett and Postle [5] to \(1.835\varDelta ^2\), and recently by Hurley, de Joannis de Verclos and Kang [23] to \(1.772\varDelta ^2\); those results apply only for sufficiently large \(\varDelta \).

This problem has also been studied for restricted classes of graphs, including: bipartite graphs [15, 16], \(C_4\)-free graphs [25], random graphs [17], graphs of bounded degeneracy [4, 7, 11], planar graphs [16, 22, 24], unit distance graphs [10] and graphs of maximum degree 3 and 4 [1, 9, 19,20,21]. In particular, the strong chromatic index of a claw-free graph with maximum degree \(\varDelta \) is at most \(1.125\varDelta ^2+\varDelta \) [12].

We study a related problem of bounding the clique number of the square of the line graph. For a graph G, a strong clique in G is a clique in \(L^2(G)\); the maximum size of a strong clique is \(\omega \left( L^2(G)\right) \). Proving an upper bound on the size of strong cliques should be easier than giving an upper bound on the strong chromatic index, because \(\omega \left( L^2(G)\right) \le s'(G)\), and it would provide supporting evidence for the conjecture of Erdős and Nešetřil; it is also a challenging problem on its own. Consider the following relaxation of Conjecture 1, posed by Faudree, Gyárfás, Schelp and Tuza [16]; see also [2].

Conjecture 2

If G is a graph with maximum degree \(\varDelta \), then

$$\begin{aligned} \omega \left( L^2(G)\right) \le \left\{ \begin{array}{ll} \frac{5}{4}\varDelta ^2,&{}\hbox {for even}\,\varDelta ,\\ \frac{5}{4}\varDelta ^2-\frac{2\varDelta -1}{4},&{}\hbox {for odd}\,\varDelta . \end{array}\right. \end{aligned}$$

Conjecture 2 remains open, but is closer to being proved than Conjecture 1. The second author proved that \(\omega \left( L^2(G)\right) \le \frac{3}{2}\varDelta ^2\) [28], which was improved to \(\frac{4}{3}\varDelta ^2\) by Faron and Postle [14]. There are also sharp results for specific classes of graphs: for bipartite graphs the upper bound is \(\varDelta ^2\) [16] (sharp for complete bipartite graphs), and for triangle-free graphs it is \(\frac{5}{4}\varDelta ^2\) [3, Theorem 4.1.5] (sharp for blowups of \(C_5\)).

Since the strong chromatic index of claw-free graphs is at most \(1.125\varDelta ^2+\varDelta \) [12], Conjecture 2 is obviously true for this class of graphs (for \(\varDelta \ge 12\) and \(\varDelta =8,10\)). However, the constant 1.125 is probably far from optimal; we would like to know the sharp bound. Our contribution is that we reduce the upper bound to around \(\varDelta ^2\).

Theorem 1

If G is a claw-free graph with maximum degree \(\varDelta \), then

$$\begin{aligned} \omega \left( L^2(G)\right) \le \varDelta ^2 + \frac{1}{2}\varDelta . \end{aligned}$$

2 Proof of Theorem 1

Let us define some basic notions. We say that two edges e, f (\(e\ne f\)) of a graph G are joined in G if they are adjacent in G or there is some other edge which is adjacent to both of them in G. Note that in a strong edge-coloring of G any two edges which are joined must have distinct colors.

Let G be a graph and S be a subset of the vertex set of G. G[S] denotes the subgraph of G induced by S. We say that a graph G is H-free if G does not contain H as an induced subgraph. A claw is a complete bipartite graph \(K_{1,3}\). \(K_{1,3}\)-free graphs are called claw-free.

We start by proving auxiliary lemmas that are variations of Turan’s Theorem, adapted to our setting. Proofs are inspired by the classic proofs of Turan’s Theorem (the first one uses induction and the second one uses equivalence classes).

Lemma 1

Let A, B be disjoint sets such that \(\left| A \right| \ge \left| B \right| \). Let G be a graph with the vertex set \(V(G)=A\cup B\). Denote by \(E_A\), \(E_B\) and \(E_{AB}\) respectively the set of edges with both endpoints in A, the set of edges with both endpoints in B and the set of edges with one endpoint in A and one endpoint in B; let \(e_A\), \(e_B\) and \(e_{AB}\) be the size of the respective set.

If every two edges \(e\in E_A\), \(f\in E_B\) are joined, then \(e_A+e_B-e_{AB}\le { \left| A\right| \atopwithdelims ()2 }\).

Proof

We will proceed by induction on \(\left| B \right| \). Note that the lemma is true for \(\left| B \right| <2\), because in this case \(e_B=0\) and \(e_A\le { \left| A\right| \atopwithdelims ()2 }\). Now suppose that the lemma is true if the two sets have size \(\left| A \right| - 2\) and \(\left| B \right| -2\) respectively.

Let G be a graph that maximizes the sum \(e_A+e_B-e_{AB}\). Consider two cases.

Case 1: \(e_A=0\) or \(e_B=0\). Note that \(e_A+e_B\le { \left| A\right| \atopwithdelims ()2 }\), because \(\left| B\right| \le \left| A\right| \), and \(e_{AB}\ge 0\), so \(e_A+e_B-e_{AB}\le { \left| A\right| \atopwithdelims ()2 }\) as desired.

Case 2: \(e_A>0\) and \(e_B>0\). We claim that there are vertices \(u,v\in A\) and \(w,x\in B\) such that \(uv,vx,wx\in E(G)\) and \(uw,ux,vw\notin E(G)\). Indeed, if this was not the case, then every edge inside A would be joined to every edge inside B by at least two edges, so removing from G an edge contributing to \(e_{AB}\) would not violate the required condition – contradicting the maximality of G.

Let \(A'=A\setminus \lbrace u,v\rbrace \) and \(B'=B\setminus \lbrace w,x\rbrace \). By \(e_{A'}\), \(e_{B'}\) and \(e_{A'B'}\) we denote the number of edges with both endpoints in \(A'\), the number of edges with both endpoints in \(B'\) and the number of edges with one endpoint in \(A'\) and one endpoint in \(B'\), respectively. Also, for a vertex \(y\in A'\cup B'\), by s(y) we denote the contribution of edges incident with y and a vertex from \(\lbrace u,v,w,x\rbrace \) towards the sum \(e_A +e_B-e_{AB}\) – that is, for \(y\in A'\), s(y) is the number of neighbors of y in \(\lbrace u,v\rbrace \) minus the number of neighbors of y in \(\lbrace w,x\rbrace \) and for \(y\in B'\), s(y) is the number of neighbors of y in \(\lbrace w,x\rbrace \) minus the number of neighbors of y in \(\lbrace u,v\rbrace \). Using this notation, we can write

$$\begin{aligned} e_A+e_B-e_{AB}\le e_{A'}+e_{B'}-e_{A'B'} + \sum _{y\in A'\cup B'}s(y) + 1. \end{aligned}$$
(1)

Now we claim that \(s(y)\le 1\) for all \(y\in A'\cup B'\). Suppose for the contrary that \(s(y)\ge 2\) for some \(y\in A'\). It implies that y is adjacent to both u and v and not adjacent to w and x – it follows that the edge uy is not joined to the edge wx, which contradicts the assumption on G. The same argument hold for \(y\in B'\) when (u, v) and (w, x) are exchanged. Therefore, from inequality 1 we obtain

$$\begin{aligned} e_A+e_B-e_{AB}\le e_{A'}+e_{B'}-e_{A'B'} + \left| A\right| +\left| B\right| - 3. \end{aligned}$$
(2)

By the induction assumption \(e_{A'}+e_{B'}-e_{A'B'}\le {\left| A\right| -2 \atopwithdelims ()2}\), therefore

$$\begin{aligned} e_A+e_B-e_{AB}\le \frac{\left( \left| A\right| -2\right) \left( \left| A\right| -3\right) }{2}+ \left| A\right| +\left| B\right| - 3 = { \left| A\right| \atopwithdelims ()2 } +\left| B\right| -\left| A\right| , \end{aligned}$$
(3)

which completes the proof by \(\left| A \right| \ge \left| B \right| \). \(\square \)

Lemma 2

Let A, B be disjoint sets. If G is a graph with \(V(G)=A\cup B\) such that

  1. (i)

    A does not contain an independent set of size 3,

  2. (ii)

    for every three vertices x, y, z, such that \(x, y\in A\) and \(z\in B\), if \(xy\notin E(G)\), then \(xz\in E(G)\) or \(yz\in E(G)\),

then the number of edges incident to a vertex from A in G is at least \( {\left\{ \begin{array}{ll} {a\atopwithdelims ()2}&{}\text { if } a<b, \\ {a\atopwithdelims ()2}-\frac{\left( a-b\right) ^2}{4} &{}\text { if } a \ge b. \end{array}\right. }\)

Proof

Let A and B be fixed. Let G be a graph on \(A\cup B\) that satisfies (i) and (ii) and has the minimum possible number of edges.

Claim

There are no three vertices \(u,v,w\in A\) such that \(uv\notin E(G)\) and \(uw,vw \in E(G)\).

Suppose for the contrary that there are three such vertices u, v, w. We will construct a graph \(G'\) with fewer edges, contradicting the minimality of G.

Case 1: Either u or v has smaller degree than w. Without loss of generality we assume that it is u. We obtain \(G'\) by removing all edges incident to w and adding an edge from w to each neighbor of u except w and to u. Note that \(\left| E(G') \right| =\left| E(G) \right| - \deg _G(w)+\deg _G(u)<\left| E(G) \right| \).

Note that \(G'\) satisfies (i) – if there existed an independent set S of size 3 in \(G'\), then S would contain w, because only edges incident to w were changed, and would not contain u, because \(uw\in E(G')\). But \(S\setminus \lbrace w \rbrace \cup \lbrace u\rbrace \) would be an independent set in G of the same cardinality, which is a contradiction.

\(G'\) also satisfies (ii). To see this, consider a vertex \(z\in B\) and \(x\in A\) such that \(xw\notin E(G')\). We have \(xu\notin E(G)\), so either \(xz\in E(G)\) or \(uz\in E(G)\) – then we have \(xz\in E(G')\) or \(wz\in E(G')\) respectively.

Case 2: Both u and v have at least as large degree as w. In this case we obtain \(G'\) by removing all edges incident to u and v, adding edges from u and v to every neighbor of w and adding edges uv, uw and vw. Note that the degrees of u, v and w in \(G'\) are equal to \(\deg _G(w)\), but an edge uv counts towards both \(\deg _{G'}(u)\) and \(\deg _{G'}(v)\). Therefore, we have \(\left| E(G') \right| =\left| E(G) \right| -\deg _G(u)-\deg _G(v) + 2\deg _G(w) - 1 < \left| E(G) \right| \).

Note that \(G'\) satisfies (i) because – as in the previous case – for every independent set S in \(G'\) either \(S\setminus \lbrace u, v\rbrace \cup \lbrace w\rbrace \) is an independent set in G of the same cardinality or S is disjoint from \(\lbrace u, v, w\rbrace \).

\(G'\) satisfies (ii) because for every \(z\in B\) and \(x\in A\) such that \(xu \notin E(G')\) or \(xv\notin E(G')\) we have \(xw\notin E(G)\), so either \(xz\in E(G')\) or \(uz, vz, wz\in E(G')\). This completes the proof of the claim.

Consider a relation \(\sim \subseteq A^2\) such that \(x\sim y\) iff \(xy\in E(G)\) or \(x=y\). From Claim 2 it follows that \(\sim \) is an equivalence relation on A. Since there are no independent sets of size 3 in A, \(\sim \) has at most two equivalence classes.

Let X be the second largest equivalence class of \(\sim \) – note that X may be an empty set. Set \(x:=\left| X\right| \), \(a:=\left| A\right| \) and \(b:=\left| B\right| \).

Claim

Each vertex from B has at least x neighbors in A.

Let \(z\in B\). Note that either z is adjacent to all vertices from \(A\setminus X\) – which gives at least \(a-x\ge x\) neighbors of z in A – or z is not adjacent to some \(v\in A\setminus X\). In the latter case z must be adjacent to all vertices from X by (ii), which again gives at least x neighbors in A – therefore, the proof of the claim is complete.

Now we can count the number of edges of G incident to a vertex from A. By the definition of X, there are exactly \({x \atopwithdelims ()2}+{a-x \atopwithdelims ()2}\) edges with both endpoints in A and, by Claim 2, there are at least bx edges from A to B, which totals to at least

$$f(x):={a \atopwithdelims ()2} + x^2 + \left( b-a\right) x$$

edges. Note that f is a quadratic function in x that has minimum in point \(x_{\min }=\frac{a-b}{2}\) and in increasing for \(x>x_{\min }\). Therefore, we have

$$\begin{aligned} f(x)\ge \left\{ \begin{array}{lr} f(x_{\min }), &{} \text {for } x_{\min } \ge 0,\\ f(0), &{} \text {for } x_{\min } < 0. \end{array} \right. \end{aligned}$$

Therefore, we get

$$\begin{aligned} f(x)\ge \left\{ \begin{array}{lr} {a\atopwithdelims ()2}-\frac{\left( a-b\right) ^2}{4}, &{} \text {for } a \ge b,\\ {a\atopwithdelims ()2}, &{} \text {for } a < b, \end{array} \right. \end{aligned}$$

which completes the proof. \(\square \)

Now we are ready to prove Theorem 1.

Proof of Theorem 1

Let \(v_1, v_2\) \(\in V(G)\) be vertices of G such that \(e = v_1v_2 \in E(G)\) and e is an edge from a strong clique H with maximum size in G; we will think of H as a subgraph of G induced by the edges of the maximum strong clique.

Let \(D_1\) be a set of vertices of G which are adjacent to \(v_1\) in G and are not adjacent to \(v_2\) in G, \(D_2\) be a set of vertices of G which are adjacent to \(v_2\) in G and are not adjacent to \(v_1\) in G and \(D_3\) be a set of vertices of G which are adjacent to both \(v_1\) and \(v_2\) in G (see Fig. 1). Let \(|D_1| = d_1\), \(|D_2| = d_2\), and \(|D_3| = d_3\). We have:

$$\begin{aligned}&d_1, d_2, d_3 \ge 0, \end{aligned}$$
(4)
$$\begin{aligned}&d_1, d_2, d_3 \le \varDelta - 1, \end{aligned}$$
(5)
$$\begin{aligned}&d_1 + d_3 \le \varDelta - 1, \end{aligned}$$
(6)
$$\begin{aligned}&d_2 + d_3 \le \varDelta - 1. \end{aligned}$$
(7)

Without loss of generality, we can assume that \(d_1 \ge d_2\).

Fig. 1
figure 1

Sets \(D_1, D_2, D_3\)

Full size image

Note that \(G[D_1]\) is a clique – if there where two vertices \(x, y \in D_1\), such that \(xy \notin E(G)\), then edges \(xv_1, yv_1, v_1v_2\) would form an induced claw in G. Similarly \(G[D_2]\) is a clique. Moreover, \(G[D_3]\) contains no independent set of size 3, as it would form an induced claw in G together with v1.

Note that every edge of H except e is joined to e, so it is incident to at least one vertex from \(D_1\cup D_2 \cup D_3\). Now we will count the number of edges in H. We claim that this number is at most

$$\begin{aligned} \varDelta \left( d_1 + d_2 + d_3\right) - {d_1\atopwithdelims ()2} - 2{d_2\atopwithdelims ()2} - {d_3 \atopwithdelims ()2} + 1 + I_{d_3 > d_1 + d_2}\frac{(d_3 - d_1 - d_2)^2}{4}, \end{aligned}$$
(8)

where \(I_{d_3>d_1+d_2}\) is 1 when \(d_3>d_1+d_2\) and 0 otherwise. We obtain (8) as follows.

First we count the number of edges with exactly one endpoint in \(D_1\cup D_2\). All vertices from \(D_1\) are incident to at most \(\varDelta d_1\) edges. We know that \(G[D_1]\) is a clique, so all its edges have two endpoints in \(D_1\) – we should not count them here, but we did it twice. Similarly for \(D_2\). In H there are also some edges with one endpoint in \(D_1\) and one in \(D_2\). We counted them twice as well. Let \(e_{D_1D_2}\) mean the number of such edges. Therefore the number of edges with exactly one endpoint in \(D_1\cup D_2\) is at most

$$\begin{aligned} \varDelta (d_1 + d_2) - 2{d_1\atopwithdelims ()2} - 2{d_2\atopwithdelims ()2} - 2e_{D_1D_2}. \end{aligned}$$
(9)

Now we add edges with both endpoints in \(D_1\cup D_2\). Let \(e_{D_1}\) mean the number of edges of H from \(G[D_1]\), and \(e_{D_2}\) mean the number of edges of H from \(G[D_2]\). The number of edges in H with both endpoints in \(D_1\cup D_2\) is

$$\begin{aligned} e_{D_1} + e_{D_2} + e_{D_1D_2}. \end{aligned}$$
(10)

The sum of (9) and (10) is

$$\begin{aligned} \varDelta (d_1 + d_2) - 2{d_1\atopwithdelims ()2} - 2{d_2\atopwithdelims ()2} + e_{D_1} + e_{D_2} - e_{D_1D_2}. \end{aligned}$$
(11)

Let S be a graph with the vertex set \(D_1\cup D_2\) such that \(xy\in E(S)\) if \(x\in D_1, y\in D_2\) and \(xy\in E(G)\) or \(x,y\in D_i\) and \(xy\in E(H)\). The graph S fulfills the assumptions of Lemma 1 with \(A=D_1\) and \(B=D_2\). So \(e_{D_1} + e_{D_2} - e_{D_1D_2} \le {d_1\atopwithdelims ()2}\). Therefore (11) is at most

$$\begin{aligned} \varDelta (d_1 + d_2) - {d_1\atopwithdelims ()2} - 2{d_2\atopwithdelims ()2}. \end{aligned}$$
(12)

Next we add to (12) edges from H that are incident to at least one vertex from \(D_3\); there are at most \(\varDelta d_3\) of them. We obtain

$$\begin{aligned} \varDelta (d_1 + d_2 + d_3) - {d_1\atopwithdelims ()2} - 2{d_2\atopwithdelims ()2}. \end{aligned}$$
(13)

Edges with one endpoint in \(D_1\cup D_2\) and one endpoint in \(D_3\) and edges with both endpoints in \(D_3\) are counted twice in (13) and will be subtracted. We can calculate their number by Lemma 2. Let S be a subgraph of G induced by \(V(S)=D_1\cup D_2 \cup D_3\). Note that for every three vertices \(x,y\in D_3\) and \(z\in D_1\cup D_2\) if \(xy\notin E(S)\), then \(xz\in E(S)\) or \(yz\in E(S)\), as it would form an induced claw together with z. Moreover, we have that \(D_3\) contains no independent set of size 3. Thus the graph S fulfills the assumptions of Lemma 2 with \(A=D_3\) and \(B=D_1\cup D_2\). Therefore, the number of edges in question is at least \({d_3 \atopwithdelims ()2} - I_{d_3>d_1+d_2} \frac{\left( d_3-d_1-d_2\right) ^2}{4}\). After subtracting it from (13) we obtain

$$\begin{aligned} \varDelta (d_1 + d_2 + d_3) - {d_1\atopwithdelims ()2} - 2{d_2\atopwithdelims ()2} - {d_3 \atopwithdelims ()2} + I_{d_3>d_1+d_2} \frac{\left( d_3-d_1-d_2\right) ^2}{4}. \end{aligned}$$
(14)

To obtain (8) we add 1 to (14) – because e has not been counted.

Claim

The expression (8), subject to constraints (4, 5, 6, 7), is at most \(\varDelta ^2 + \frac{1}{2}\varDelta \).

We prove Claim 2 in the appendix.

By Claim 2 the proof is complete. \(\square \)

3 Further Research

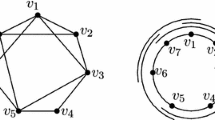
We proved that the size of a strong clique in a claw-free graph with maximum degree \(\varDelta \) is at most \(\varDelta ^2 + \frac{1}{2}\varDelta \). The constant next to delta is less than \(\frac{5}{4}\) from Conjecture 2 but we believe that the optimal constant is much smaller than that. A size of the biggest strong clique which we were able to construct is around \(\frac{9}{16}\varDelta ^2\). The example for any \(\varDelta \) can be obtained from the graph \(G_1\), presented in Fig. 2, by blowing up each vertex to a clique of size \(\frac{\varDelta }{4}\). In the constructed graph every two edges with endpoints in different cliques are joined, so all them create a strong clique. We want to construct a claw-free graph with a bigger strong clique or improve our upper bound.

Fig. 2
figure 2

The graph \(G_1\)

Full size image

We do not have any results for the maximum size of a strong clique in \(K_{1, t}\)-free graphs with maximum degree \(\varDelta \) for \(t>3\). The only known result is \(\left( 2-\frac{1}{t-2} \right) \varDelta ^2\), which is an upper bound for the strong chromatic index of \(K_{1, t}\)-free graphs. Is it possible to tell something more about strong cliques in such graphs? Maybe for unit disks graphs? For them we know that the strong chromatic index is at most \(1.625\varDelta ^2\).