1 Introduction

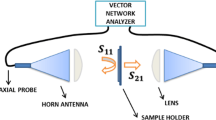
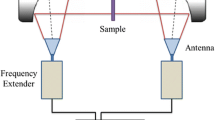
Measurements of relative complex permittivity (\(\varepsilon _{r}\)) in the terahertz (THz) band are required for engineering designs of THz devices (e.g., lenses, waveguide, filters, etc.) (Hammler et al. 2016; Sahin et al. 2018a; Kazemipour et al. 2015; Yang et al. 2019; Güneşer 2019; Ali et al. 2017; Moradiani et al. 2020; Farmani et al. 2020). Free-space techniques have been widely used for dielectric characterization at THz frequencies, particularly since recent advances in THz components and instrumentation have made them more convenient and accurate (Zhang et al. 2017; Sahin et al. 2018b; Tosaka et al. 2015; Ghalichechian and Sertel 2015). The advances in the THz measurement can be summarized as two parts: (1) the gate-reflect-line (GRL) calibration technique and lens are used for the measurement system to improve the accuracy of the measurements (Zhang et al. 2017); (2) the environment of the calibration and the measurement is set to be clear to remove the impact of water vapor and O2 absorption lines (Sahin et al. 2018b), that also improve the accuracy of the measurements. However, the reflection coefficient (S\(_{11}\)) of the material under test (MUT) is still hard to be measured above 300 GHz (Kazemipour et al. 2015; Lamb 1996). Since only the transmission coefficient (S\(_{21}\)) can be used for the characterization above 300 GHz, the \(\varepsilon\) \(_{r}\) of the MUT needs be extracted by the iterative algorithms.

But the iterative extraction techniques (e.g., Newtons method) restrict the application of the free-space transmission techniques, because the convergent values of the extracted \(\varepsilon _{r}\) vary with the initial guesses for the iterative extraction techniques (see Fig. 5 in Zhang et al. 2017). Some publications simply ignored the problem on multiple convergent values (see Hammler et al. 2016; Sahin et al. 2018b; Tosaka et al. 2015), some experimentally reported the phenomena of getting multiple results and proposed method to obtain a right initial value by using \(S_{11}\) and \(S_{21}\) (Yang et al. 2019; Zhang et al. 2017), though \(S_{11}\) is hard to be measured. While in Ghalichechian and Sertel (2015) technique without detailed analysis was proposed to estimate permittivity from \(S_{21}\) in Zhang et al. (2017). But the technique fails to work when the electrical length of the MUT is large. In addition, the empirical value at low frequency of the MUT was adopted as the initial value for the iterative techniques to extract the \(\varepsilon _{r}\) in the THz band (Ghalichechian and Sertel 2015). If there is a new material or the value of the \(\varepsilon\) \(_{r}\) of the MUT in the THz band is much different from the value at low frequencies (see Fig. 10 in Seiler and Plettemeier (2019)). The extracted value of the permittivity is incorrect if the estimated value is far away from the true value (Yang et al. 2019). How to get a right initial-guess for the iterative extraction techniques is still an open-question.

In this paper, the proper initial-value for the iterative extraction techniques is estimated by using the properties of the measured \(S_{21}\) in the THz band. The availability of the proposed technique is verified by various known materials (e.g. PMMA, PVC, Teflon, Glass, Crosslinked SUEX, etc.) in the THz-band.

2 Theory and technique

A schematic of a MUT with thickness of t is shown in Fig.1. The MUT is measured in free-space. According to the analytical multilayer transmission model, transmission through a dielectric slab with thickness t can be expressed as Farmani et al. (2020)

$$\begin{aligned} S_{21}=\frac{4\sqrt{\varepsilon _r}e^{-j\omega \sqrt{\mu _0\varepsilon _0}\sqrt{\varepsilon _r}t}}{(1+\sqrt{\varepsilon _r})^2-(1-\sqrt{\varepsilon _r})^2e^{-j2\omega \sqrt{\mu _0\varepsilon _0}\sqrt{\varepsilon _r}t}} \end{aligned}$$
(1)

where \(\varepsilon _{r}=\varepsilon _{r}'-j\varepsilon _{r}''\) is the relative complex permittivity of the MUT, \(\omega\) is the angular frequency, and t is outside of the square.

Fig. 1
figure 1

A schematic of a MUT measured in free-space

Full size image

If the thickness of the MUT is larger than one or more wavelengths, the \(S_{21}\) changes periodically with the frequency (Hammler et al. 2016). In the THz band, the wavelengths of the electromagnetic waves are short that the thickness of the MUT can be longer than one or more wavelengths. In this work, we estimate the permittivity of the MUT from the \(S_{21}\) by using the special properties.

2.1 Method 1: using properties of \(|S_{21}|\)

For low-loss materials, when the thickness of the MUT is an integer multiple of half-wavelength (\(\lambda /2\)) inside the MUT, there is a sharp peak in the measured \(|S_{21}|\) due to Fabry CPerot effects (Ghalichechian and Sertel 2015). When there are two peaks in the measured \(|S_{21}|\) and the MUT is non-dispersive or weakly dispersive between the two peak frequencies, the phase constants at the two frequencies can be derived as

$$\begin{aligned} \beta _1= & {} n\pi /t \end{aligned}$$
(2)
$$\begin{aligned} \beta _2= & {} (n+1)\pi /t \end{aligned}$$
(3)

where n is a positive integer.

As \((\alpha +j\beta )^2=-\omega ^2\mu _0\varepsilon _0(\varepsilon _{r}'-j\varepsilon _{r}'')\) and loss constant \(\alpha\) is approximately equal to zero for low-loss materials, we can derive

$$\begin{aligned} \beta ^2\approx \omega ^2\mu _0\varepsilon _0\varepsilon _{r}' \end{aligned}$$
(4)

Combining Eqs. (2)–(4), the permittivity between the two peak frequencies of the MUT can be estimated as

$$\begin{aligned} \varepsilon _{r}'\approx \left(\frac{1}{2t\sqrt{\varepsilon _0\mu _0}\Delta {f_1}}\right)^2 \end{aligned}$$
(5)

where \(\Delta {f_1}\) is the difference between the two peak frequencies.

2.2 Method 2: using properties of \(S_{21}\)

The method 1 is efficient when there are two or more peaks in the \(|S_{21}|\). However, the peaks are not obvious when the MUT is thick as shown in Sahin et al. (2019). Because, the loss increases with the thickness, the resonance decreases with the loss. The difference between the peak and regular values is small. Therefore, we cannot use Eq. (5) for \(\varepsilon _r'\) estimation when the MUT is thick.

For the thick MUT, there are more frequencies where t is an integer multiple of wavelength inside the MUT. For the MUT with low loss tangent, the Eq. (1) can be approximately expressed as

$$\begin{aligned} S_{21}\approx \frac{4\sqrt{\varepsilon _r'}e^{-j\omega \sqrt{\mu _0\varepsilon _0}\sqrt{\varepsilon _r'}t}}{(1+\sqrt{\varepsilon _r'})^2-(1-\sqrt{\varepsilon _r'})^2e^{-j2\omega \sqrt{\mu _0\varepsilon _0}\sqrt{\varepsilon _r'}t}} \end{aligned}$$
(6)

As seen in Eq. (6), the \(\angle {S_{21}}\) is approximately \(180^\circ\) when the thickness of the MUT is an integer multiple of wavelength inside the MUT. We processed the two \(|S_{21}|\) at two frequencies where \(\angle S_{21}\) are equal \(180^\circ\) , the permittivity of the MUT can be estimated as

$$\begin{aligned} \varepsilon _{r}'\approx (\frac{1}{t\sqrt{\varepsilon _0\mu _0}\Delta {f_2}})^2 \end{aligned}$$
(7)

where \(\Delta {f_2}\) is the difference between the two frequencies.

2.3 Application procedures of the two methods

The application procedures of the proposed methods are shown as follows:

  • Step 1: choose the method according to the characteristics of the \(S_{21}\). If the number of the peaks in the \(|S_{21}|\) is more than the number of the frequencies where the values of \(\angle {S_{21}}\) are equal to \(180^\circ\) , the method 1 is chosen. Otherwise, the method 2 is chosen.

  • Step 2: determine the dispersion characteristics of the MUT. If all \(\Delta {f_1}\) (or \(\Delta {f_2}\)) are approximate for the MUT, the MUT is non-dispersive over the entire measured frequency range. Otherwise, the MUT is dispersive over the entire measured frequency range.

  • Step 3.1: for the MUT which is non-dispersive over the entire measured frequency range, the average value of the \(\Delta {f_1}\) (or \(\Delta {f_2}\)) is used for the permittivity estimation.

  • Step 3.2: for the MUT which is dispersive over the entire measured frequency range, the value of the \(\Delta {f_1}\) (or \(\Delta {f_2}\)) is used for the permittivity estimation between the two adjacent frequencies. We can see that \(\Delta {f}\) would be used for different frequency band. If the materials whose permittivity change dramatically with frequency are measured, we should make them thick enough, that the permittivity between the \(\Delta {f}\) changes a little. Then the proposed can be efficient.

  • Step 4: Newtons method with the estimated initial value (permittivity) is performed.

3 Examples and discussion

3.1 The non- or weak dispersive samples in the literature

To validate the proposed technique, the \(|S_{21}|\) in the figures of Hammler et al. (2016), Kazemipour et al. (2015), Sahin et al. (2018b) and Bourreau et al. (2006) are used for determining the \(\Delta {f}\). We obtained the peak frequencies of the \(|S_{21}|\) and processed the frequencies by Eq. (4). In theoretical, the values of the \(|S_{21}|\) and the \(|S_{21}|\) are equal to each other. The permittivity calculated by Eq. (5) agrees well with the extracted values in the literature as show in Table 1. The error between the calculated values and the values in the literature ranges from 0.36 to 5.20%. However, the phase angles of the \(S_{21}\) are not presented in Kazemipour et al. (2015), Sahin et al. (2018b) and Bourreau et al. (2006). We cannot determine the \(\varepsilon _{r}\) over the entire measured frequency range by using the Newtons method.

Table 1 Comparison of extracted values with literature values
Full size table

In this work, we used the extracted in Kazemipour et al. (2015) and Sahin et al. (2018b) to simulate the \(S_{21}\) in the THz band. The \(\varepsilon _{r}\) of the materials are put into Eq. (1). The simulation method is shown in Seiler and Plettemeier (2019). The simulated S-parameters are calculated using the values of \(\varepsilon _{r}\) (Bourreau et al. 2006). That is reasonable, because the measured and simulated S21 in free-space at THz frequencies are almost the same (see Fig. 6 in Bourreau et al. (2006)). In our previous work, S-parameters simulated in the THz band have been further proved for validating extraction techniques (Yang et al. 2019).

Since the measurable frequency range is different when using a vector network analyzer (VNA) and by TDS (time-domain spectroscopy) (Tosaka et al. 2015), PMMA, PVC, Teflon, Plexiglas (a kind of Glass) with various thicknesses were simulated between 260 and 400 GHz (VNA measurement THz band) and the Crosslinked SUEX with various thicknesses were simulated between 100 and 2000 GHz (TDS measurement THz band). As shown in Fig. 2, the \(S_{21}\) of the PMMA is presented as an example to show that the S21 can be analyzed by the methods in Sect. 2.

Fig. 2
figure 2

\(S_{21}\) of three PMMA samples with different thickness

Full size image

As shown in Table 2, we estimated the \(\varepsilon _r'\) of these materials by using Eqs. (5) and (7). The estimated values approximate to the true values. It is found that the equations may not be applicable simultaneously in some cases. For example, the \(\varepsilon _r'\) of the 8 mm PMMA needs to be estimated by Eq. (5) as the peaks are not obvious for the \(|S_{21}|\) of the PMMA, and the \(\varepsilon _r'\) of the 2 mm PVC needs to be estimated by Eq. (5) as the thickness of the PVC is less than a wavelength. Thus, the two proposed methods for \(\varepsilon _r'\) estimation should be used simultaneously. After estimation, the estimated \(\varepsilon _r'\) is adopted as the initial-value for the Newtons method. The tolerance of the algorithm is set to be 10e−7 according to Zhang et al. (2017). For each frequency, it takes about 0.14 second to converge using the initial value estimated by the proposed.

The extracted values of the Teflon, PVC, glass and crosslinked SUEX agree well with the true values as shown in Figs. 3 and 4. That further validates the proposed methods.

Table 2 Estimated initial values (\(\varepsilon _r'\)) for the iterative algorithm
Full size table
Fig. 3
figure 3

Extracted complex permittivity of 16 mm Teflon, 8 mm PVC and 6 mm glass samples

Full size image
Fig. 4
figure 4

Extracted complex permittivity of 1 mm crosslinked SUEX

Full size image

3.2 The dispersive sample in the literature

Those samples in the Part A have minimal variation in \(\varepsilon _r\) from low to high frequencies. To further show the excellent performance of the proposed, a dispersive sample Benzocyclobutene (BCB) with thickness of 2 mm is used for validation. The \(\varepsilon _r'\) is obtained from Seiler and Plettemeier (2019). The permittivity of the BCB is about 5.5 at 0.5 GHz, and is about 2.6 in the THz band as shown in Fig. 5. The permittivity of the BCB at low frequency is twice than that at the terahertz frequency.

As shown in Fig. 6, the extracted \(\varepsilon _r'\) of the BCB is wrong when using the permittivity at 4, 4.5 and 5 GHz as the initial values which are far away from the true values. And the values of the \(\varepsilon _r'\) extracted by the proposed method agree well with the true values.

Fig. 5
figure 5

Permittivity of BCB [obtained from Fig. 10 in Seiler and Plettemeier (2019)]

Full size image
Fig. 6
figure 6

Extracted complex permittivity of 2 mm BCB with different initial values from 220 to 330 GHz

Full size image

4 Conclusions

In this work, a technique is proposed to estimate the permittivity of the MUT from the measured \(S_{21}\). The estimated permittivity is a correct initial-value for the iterative technique which extracts the \(\varepsilon _r\) from the \(S_{21}\). Since only the \(S_{21}\) can be efficiently measured in the THz band, the proposed is important for material characterization at THz frequencies. The proposed technique is efficient when the measured \(|S_{21}|\) have peak values at multiple frequencies or the measured values of the \(\angle {S_{21}}\) are equal to \(180^\circ\) at multiple frequencies.