Introduction

Quantum computers have developed rapidly in recent years, with remarkable improvements in control, quality and scale. While the presently available quantum computers have been used for realising many protocols and algorithms in quantum theory, it is interesting and important to consider the ability of such devices to realise predictions of quantum theory that cannot be explained by any conceivable classical model. A hallmark example of genuine quantum predictions is the violation of Bell inequalities, which has been demonstrated amongst others in a five-qubit transmon quantum computer1 and a 14-qubit ion-trap quantum computer2.

The last decade has seen much attention directed at more sophisticated correlation experiments performed in quantum networks. These networks feature several parties that are connected through a given topology which may feature entangled states or quantum communication channels. Quantum networks are increasingly becoming practically viable3,4, they have impactful potential applications5,6 and they raise new conceptual questions. The crucial conceptual feature, which sets quantum networks apart from classical networks, is that initially independent entangled states distributed within the network can become globally entangled via the procedure of entanglement-swapping. Therefore, in contrast to e.g. traditional Bell experiments, entangled measurements (i.e. projections of several distinct qubits onto an entangled basis) are indispensable to understanding and realising quantum correlations in networks. In particular, the paradigmatic Bell-State Measurement (BSM), known from quantum teleportation7 and entanglement-swapping8, is at the heart of many schemes for quantum correlations in networks (see e.g.9,10,11,12) For the simplest network, quantum nonlocality has recently been experimentally demonstrated on optical platforms13,14,15.

Here, we explore the ability of IBM quantum computers to realise quantum correlations that both defy classical models and certify entangled operations. These experiments can be seen as simulations of quantum networks as they realise the quantum correlations required for a quantum network on a single device. While previous experiments with optical setups have demonstrated e.g. nonlocality in the simplest network based on entangled measurements, superconducting circuits provide a platform where advanced quantum networks based on multi-qubit entangled measurement can be implemented. Due to free access to their superconducting quantum computers, IBM offers a convenient platform for such exploration16. Currently there are in total 19 quantum devices consisting of up to 65 superconducting qubits on the IBM cloud, with around half of them being publicly available. Sophisticated quantum circuits can be built through the IBM Quantum Lab with Qiskit17, which is an open-source software development kit for working with quantum computers at the level of pulses, circuits and application modules.

In this work, we focus on two qualitatively different networks. Firstly, we consider a task in which entangled measurements are used to enhance quantum correlations beyond the limitations of classical protocols18. In this task, N nodes share an N-qubit state and perform qubit transformations of their shares which they then relay to a final node that performs an N-qubit BSM (see Fig. 1). The magnitude of the quantum-over-classical advantage serves to certify the degree of entanglement present in the measurement under the sole assumption that the quantum computer operates on qubits. We report quantum advantages for N = 2, …, 9 but fail to observe an advantage for N = 10. Importantly, for N = 9, we can certify large-scale entanglement: our initially uncharacterised 512-outcome measurement has at least 82 entangled basis elements. Secondly, we consider the so-called star network in which a central node separately shares entanglement with N initially independent nodes (see Fig. 2). By implementing an N-qubit BSM in the central node, global entanglement can be established and quantum nonlocality can be demonstrated by violating a network Bell inequality11. We report quantum violations for N = 2, 3, 4, 5 while for N = 6 we are unable to find a violation. Finally, we go beyond BSMs and consider correlation experiments based on the recently proposed quantum Elegant Joint Measurement19. We realise this two-qubit entangled measurement and violate the bilocal Bell inequalities of ref. 20. We also present a realisation of a quantum protocol in triangle-shaped configuration.

Fig. 1: Communication network.
figure 1

Independent nodes share an N-qubit entangled state on which they perform qubit transformations. The shares are communicated to a central node which deterministically accesses information about the collective inputs of the N other nodes by performing an N-qubit BSM. This gives rise to a quantum-over-classical advantage which enables certification of the degree of entanglement present in the measurement of the central node.

Full size image
Fig. 2: Star network.
figure 2

A central node independently shares five pairs of entangled qubits with separate nodes. By performing a BSM on five qubits, the central node renders the five initially independent nodes in a globally entangled state. With suitable local measurements, the correlations in the network become nonlocal.

Full size image

Results

Certification of entangled measurements in communication network

Consider the communication network illustrated in Fig. 1. An N-qubit state is distributed between N separate nodes. Each node receives an independent input corresponding to two bits xk, yk ∈ {0, 1}2, for k = 1, …, N, and implements a transformation of the incoming qubit. The transformed qubits are then communicated to a central node where they are collectively measured. The N-qubit measurement has 2N possible outputs labelled by the bit-string b ≡ b1…bN ∈ {0, 1}N. In this network, the state, transformations and measurement are uncharacterised up to an assumption of a qubit Hilbert space. The task is for the central node to recover knowledge about the input set \({\{{x}_{k},{y}_{k}\}}_{k}\). Specifically, a successful information retrieval corresponds to

$${b}_{1} = \mathop{\bigoplus}\limits_{k = 1}^{N}{x}_{k}\quad \,\text{and}\,\quad {b}_{k}={y}_{k}\oplus {y}_{1},$$
(1)

for k = 2, …, N. Thus, only one of the 2N possible outcomes of the measurement is considered successful.

Quantum theory offers a solution to the task18. Let the nodes share the N-qubit Greenberger-Horne-Zeilinger (GHZ) state \(\left|\,\text{GHZ}\,\right\rangle =\frac{1}{\sqrt{2}}({\left|0\right\rangle }^{\otimes N}+{\left|1\right\rangle }^{\otimes N})\) and each perform local unitary operations corresponding to either \({\mathbb{1}}\), σX, σZ or σY (denoting the Pauli observables). The central node then performs an N-qubit BSM, i.e. a projection onto a basis of GHZ-like states

$$\left|{M}_{b}\right\rangle ={\sigma }_{Z}^{{b}_{1}}\otimes {\sigma }_{X}^{{b}_{2}}\otimes \ldots \otimes {\sigma }_{X}^{{b}_{N}}\left|\,\text{GHZ}\,\right\rangle ,$$
(2)

whose outcome is guaranteed to satisfy the winning condition (1). However, classical models that rely on the communication of binary messages can still partially perform the task. Denoting the average probability of satisfying all winning conditions (1) by \({p}_{N}^{\,\text{win}\,}\), the following limitations apply to classical and restricted quantum models18:

$${p}_{N}^{\text{win}}\mathop{\le }\limits^{\text{Classical}}\frac{1}{2}\mathop{\le }\limits^{\begin{array}{l}\,{\text{At}}\, {\text{most}}\, {\text{m}}\, {\text{entangled}}\,\\ \,{\text{measurement}}\, {\text{operators}}\,\end{array}}\frac{1}{2}\left(1+\frac{m}{{2}^{N}}\right)\mathop{\le }\limits^{\text{Quantum}}1.$$
(3)

Theoretically one can reach \({p}_{N}^{\,\text{win}\,}=1\,\forall N\) with the aforementioned quantum protocol. However, every \({p}_{N}^{\,\text{win}\,}>1/2\) already constitutes a proof of stronger-than-classical correlations. This quantum correlation advantage is an advantage in communication complexity, where using a restricted amount of communication leads to a superior performance in terms of communication efficiency when using quantum instead of classical resources.

Furthermore, the second inequality in (3) constitutes a bound respected by every possible quantum protocol in which the measurement in the central node has at most m entangled basis elements. Therefore, the magnitude of the quantum advantage also determines a lower bound on the number of operators in the measurement that are certified as entangled, which is given by

$$m=\lceil (2{p}_{N}^{\,\text{win}\,}-1){2}^{N}\rceil .$$
(4)

We have implemented the quantum protocol for N = 2, …, 10 with Qiskit17 on the ibmq_montreal 27-qubit quantum computer16. The results of the experiments are presented in Table 1. The standard deviation in \({p}_{N}^{\,\text{win}\,}\) is no larger than 10−3 for N < 10. We find a quantum-over-classical advantage for N = 2, …, 9 but not for N = 10. For the simplest case (N = 2), we obtain a large quantum advantage and certify all four basis elements as entangled. As expected, the quantum advantage decreases as N increases. Interestingly, however, the reduction is nearly linear (around five percentage points for each subsequent N) which attests to the scalability of the operations. Due to the slow decrease in the quantum advantage, we can report increasingly large entanglement certification: the most sizable entanglement is certified for N = 9. In this case, our initially uncharacterised nine-qubit measurement has 512 possible outcomes. Via Eq. (3), we can certify that at least 82 measurement operators must be entangled. For N = 10 we were not able to find any quantum advantage. The main reason is that a larger N means a larger number of qubits in the protocol, which then requires larger number of CNOT gates and an increased circuit depth. This leads to an increased noise accumulation in the protocol. An additional reason is that on a 27-qubit quantum computer some qubits and some connections perform better than others. While the provided average errors allow for a good estimate, it is still not straightforward which qubits to use in the experiment to optimise \({p}_{N}^{\,\text{win}\,}\). For N < 10, we considered several different qubit architectures and repeated the experiments many times. However, the experiment for N = 10 has over a million circuits and took approximately three days to perform. Therefore, we could not repeat it as many times in search of a large \({p}_{N}^{\,\text{win}\,}\). As also noted in previous works,1 we remark that the quantum computers typically are not stable as the results of our experiments vary significantly in time on otherwise identical implementations.

Table 1 Results for N-qubit communication network experiments on the ibmq_montreal quantum computer.
Full size table

Furthermore, in the Supplementary Information we re-examine our results after applying measurement error-mitigation, which allows us to amplify the measured value of \({p}_{N}^{\,\text{win}\,}\).

Star network nonlocality

We proceed to consider a network of the type illustrated in Fig. 2. A central node, B, is connected to N other nodes, A1, …, AN, through independent sources emitting pairs of particles. The branch-nodes each have independent binary inputs \(\bar{x}\equiv {x}_{1},\ldots ,{x}_{N}\in \{0,1\}\) and produce binary outputs \(\bar{a}\equiv {a}_{1},\ldots ,{a}_{N}\in \{0,1\}\) while the central node has a fixed setting and produces an output b ≡ b1…bN ∈ {0, 1}N that can take 2N different values. The probability distribution in the network is written \(p(\bar{a},b| \bar{x})\). It is said to admit a local model, that respects the independence of the N sources, if it can be written in the form

$$p(\bar{a},b| \bar{x})=\int d\bar{\lambda }\left(\mathop{\prod }\limits_{i=1}^{N}{q}_{i}({\lambda }_{i})p({a}_{i}| {x}_{i},{\lambda }_{i})\right)p(b| \bar{\lambda }),$$
(5)

where λi is the local variable associated to the i’th source, qi is its probability density and \(\bar{\lambda }=({\lambda }_{1},\ldots ,{\lambda }_{N})\). Reference 11 introduced Bell inequalities respected by all source-independent local models:

$${{\mathcal{S}}}_{N}\equiv \frac{1}{{2}^{N-2}}\mathop{\sum }\limits_{j=1}^{{2}^{N-1}}| {I}_{j}{| }^{1/N}\le 1,$$
(6)

where \({I}_{1},\ldots ,{I}_{{2}^{N-1}}\) are suitable linear combinations of \(p(\bar{a},b| \bar{x})\). See Supplementary Information for further details on the inequalities. A quantum violation of (6) is possible if each source distributes a maximally entangled two-qubit state \(\left|\psi \right\rangle =\frac{\left|00\right\rangle +\left|11\right\rangle }{\sqrt{2}}\), the branch-nodes A1, …, AN measure the observables \(\frac{{\sigma }_{X}+{\sigma }_{Y}}{\sqrt{2}}\) and \(\frac{{\sigma }_{X}-{\sigma }_{Y}}{\sqrt{2}}\) and the central node performs the N-qubit BSM (2). This leads to the quantum violation \({{\mathcal{S}}}_{N}=\sqrt{2}\) for every N. Note, that N corresponds to the number of branches, and it implies that the quantum setup is implemented on 2N qubits.

We have implemented this quantum protocol with Qiskit17 on the ibmq_almaden 20-qubit quantum computer16 for star networks with N = 2, 3, 4, 5, 6. The results of the experiments are presented in Table 2. The standard deviations associated to the statistical fluctuations for \({{\mathcal{S}}}_{N}\) for N = 2, …, 6 are in all cases smaller than 2 × 10−3. We find a quantum violation of the source-independent local bound for N = 2, 3, 4, 5 but fail to observe a violation for N = 6. With an increasing number of qubits, the size of the joint measurement increases and therefore also the noise. When considering the nearly linear decrease of the measured \({{\mathcal{S}}}_{N}\) values for N = 2, 3, 4, 5, it is not unexpected that for N = 6 the value falls below threshold \({{\mathcal{S}}}_{N}=1\). For the simplest case (N = 2), the quantum violation is already far from the theoretical maximum of \(\sqrt{2}\), which attests to the demanding nature of falsifying source-independent local models. However, the relatively small decrease in the violation magnitude for each subsequent N attests to the scalability of the experiment.

Table 2 Results for N-branch star network nonlocality experiments on the ibmq_almaden quantum computer.
Full size table

Moreover, in our proof-of-principle demonstration, the sources are not perfectly independent, e.g. due to cross talk21,22,23. We have estimated the degree of source-independence in our experiments by evaluating the worst-case Kullback-Leibler (KL) divergence (i.e. the relative entropy, maximised over all settings \(\bar{x}\)) between the marginal distribution \(p(\bar{a}| \bar{x})\) and would-be marginal distribution had the sources been perfectly independent; \(\mathop{\prod }\nolimits_{i = 1}^{N}p({a}_{i}| \bar{x})\). In Table 2, we see that the worst-case KL-divergence is nearly vanishing for N = 2 and remains low also for larger N.

Finally, in the Supplementary Information, we re-examine the results of our experiments after applying error-mitigating post-processing to the measured probabilities.

Experiments based on the Elegant Joint Measurement

While our main focus has been on Bell-State Measurements, there has recently been a proposal of another natural, yet qualitatively different, entanglement-swapping measurement that has a high degree of symmetry. This so-called Elegant Joint Measurement (EJM)19, which projects two qubits onto a basis of partially (but equally) entangled states with a tetrahedral symmetry, has been placed at the heart of several protocols for quantum networks. For instance, ref. 20 considered the simplest star network (N = 2) and proposed a source-independent Bell inequality tailored to be violated with the EJM performed in the central node. This test of quantum correlations is conceptually different and practically more challenging than the previously considered scenario based on the BSM: the quantum correlations are significantly more fragile to imperfections and the circuit implementation of the EJM requires more entangling gates. In ref. 20 it was shown that the EJM can be implemented by using Hadamard gates \(H=\frac{1}{\sqrt{2}}{\sum }_{i,j = 0,1}{(-1)}^{ij}\left|i\right\rangle \left\langle j\right|\), phase gates \(S:= {R}_{z}(\pi /2)=\left|0\right\rangle \left\langle 0\right|+i\left|1\right\rangle \left\langle 1\right|\), controlled phase gates \(C{R}_{z}(\pi /2)=\left|0\right\rangle \left\langle 0\right|\otimes {\mathbb{1}}+\left|1\right\rangle \left\langle 1\right|\otimes S\) and controlled not gates \(CNOT=\left|0\right\rangle \left\langle 0\right|\otimes {\mathbb{1}}+\left|1\right\rangle \left\langle 1\right|\otimes {\sigma }_{X}\) in the following configuration:

$$\left|{\text{EJM}}_{k}\right\rangle =CNOT(H\otimes {\mathbb{1}})C{R}_{z}(\pi /2)(S\otimes S)(H\otimes H)\left|{k}_{1}{k}_{2}\right\rangle ,$$
(7)

for k ≡ k1k2 ∈ {0, 1}2. We implemented the EJM in the context of two experiments: a test of the bilocal Bell inequalities of ref 20. and a test of the quantum triangle network discussed in ref. 19

The bilocal scenario is the simplest star network (corresponding to N = 2), i.e., it features three nodes in a line configuration where the first and second as well as the second and third are connected. The two branch-nodes each receive inputs x, z ∈ {1, 2, 3}, respectively, which determine the bases in which they perform their measurements, while the central node performs always the same measurement. They obtain outputs a, c ∈ {1, − 1} and b ∈ {1, 2, 3, 4}, respectively. From the resulting conditional probability distribution p(a, b, c∣x, z), one can then determine the conditional single-party correlators \({E}_{b}^{A}(x):= \frac{1}{3}{\sum }_{a,c,z}a\,p(a,c| b,x,z)\) and \({E}_{b}^{C}(z):= \frac{1}{3}{\sum }_{a,c,x}c\,p(a,c| b,x,z)\) as well as the conditional two-party correlator \({E}_{b}^{AC}(x,z):= {\sum }_{a,c}ac\,p(a,c| b,x,z)\). Denote the four vertices of a tetrahedron by the coordinates \({\overrightarrow{m}}_{1}=(+1,+1,+1)\), \({\overrightarrow{m}}_{2}=(+1,-1,-1)\), \({\overrightarrow{m}}_{3}=(-1,+1,-1)\), \({\overrightarrow{m}}_{4}=(-1,-1,+1)\) and define \({m}_{b}^{k}\) as the kth element of \({\overrightarrow{m}}_{b}\). Reference20 introduced the bilocal Bell inequality

$$\begin{array}{lll}{\mathcal{B}}\,:= \,\mathop{\sum}\limits_{x,b}\sqrt{p(b)(1-{m}_{b}^{x}{E}_{b}^{A}(x))}+\mathop{\sum}\limits_{z,b}\sqrt{p(b)(1+{m}_{b}^{z}{E}_{b}^{C}(z))}\\ \quad\quad\,+\mathop{\sum}\limits_{x\ne z,b}\sqrt{p(b)(1-{m}_{b}^{x}{m}_{b}^{z}{E}_{b}^{AC}(x,z))}\\ \quad\quad\,\le 12\sqrt{3}+2\sqrt{15}\approx 28.531.\end{array}$$
(8)

In the quantum setup the two sources each distribute singlet states \(\left|{\psi }^{-}\right\rangle =\frac{\left|01\right\rangle -\left|10\right\rangle }{\sqrt{2}}\), the central node performs the EJM and the two branch-nodes perform the measurements σX, σY, σZ. Theoretically this gives the violation \({\mathcal{B}}=12\sqrt{6}\approx 29.39\). Running the experiment on the ibmq_manhattan 65-qubit quantum computer, the resulting probability distribution yielded the value \({\mathcal{B}}=28.648\pm 0.008\). This constitutes a small but statistically significant violation of the source-independent local bound.

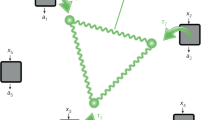
Furthermore, it is conjectured that the EJM can reveal quantum correlations also in a triangle-shaped network19, i.e. a network featuring three nodes that are pairwise connected (see Fig. 3). Each node performs a single measurement and obtains an output a, b, c ∈ {1, 2, 3, 4} respectively. The resulting probability distribution has a local model that respects the independence of the three sources if it can be written as

$$p(a,b,c)=\int d\alpha d\beta d\gamma {p}_{A}(a| \beta ,\gamma ){p}_{B}(b| \alpha ,\gamma ){p}_{C}(c| \alpha ,\beta ),$$
(9)

where (α, β, γ) are local variables. While it is known that there exist quantum correlations that do not admit the above form24, no noise-robust examples are presently known. It is, however, conjectured that noise-robust quantum correlations are obtained if all three sources emit a singlet state \(\left|{\psi }^{-}\right\rangle =\frac{\left|01\right\rangle -\left|10\right\rangle }{\sqrt{2}}\) and all three nodes perform the EJM on the two independent qubits at their disposal. The corresponding probability distribution in the network is fully described by three cases:

  1. (i)

    when all outcomes are equal we have \(p(r,r,r)=\frac{25}{256}\) for r = 1, 2, 3, 4,

  2. (ii)

    when precisely two outcomes are equal we have \(p(r,r,s)=\frac{1}{256}\) for all r ≠ s (including permutations of the labels),

  3. (iii)

    when all outcomes are different we have \(p(r,s,t)=\frac{5}{256}\) for all r ≠ s ≠ t ≠ r.

We have realised this quantum protocol on the ibmq_montreal 27-qubit quantum computer and the ibmq_johannesburg 20-qubit quantum computer. The two experimentally obtained probability distributions, as well as the theoretical one, are shown in Fig. 4. While the four peaks for a = b = c are quite distinguishable, the noise prevents us from always clearly identifying the cases of two and three different outcomes. The coupling map of the ibmq_johannesburg device was better suited as we could perform the experiment on a ring of six qubits, while on the ibmq_montreal device we had to choose six qubits on a ring of twelve qubits (see SM). Nevertheless, as the error rates on the ibmq_montreal device are smaller, the KL-divergences between the experimental and theoretical distributions are very similar with 0.272 for the resulting distribution of the ibmq_johannesburg device and 0.277 for the one of the ibmq_montreal device.

Fig. 3: Triangle network.
figure 3

Three nodes pairwise share pairs of entangled qubits and each perform the Elegant Joint Measurement on their respective qubit pair.

Full size image
Fig. 4: Triangle network results.
figure 4

Histogram of the probability distribution of the quantum triangle network. The green distribution corresponds to the theoretical prediction, while the purple and orange correspond to the outcomes of experiments conducted on the ibmq_montreal device and the ibmq_johannesburg device, respectively.

Full size image

However, there presently exists no criterion for determining whether our measured correlations can be simulated in a source-independent local model. Determining whether our measured correlations elude all source-independent local models remains an open problem.

Discussion

We have reported demonstrations of quantum predictions that defy general classical models in scalable experiments featuring up to ten qubits in which the central component is the implementation of sophisticated entangled measurements of many qubits. Our experiments mirror the conditions encountered in quantum networks, but are rightfully viewed as simulations of networks since all physical qubits are confined to a single IBM quantum processor. Our results demonstrate the power and scalability of these state-of-the-art devices, most notably allowing for the certification of a nine-qubit measurement with 82 entangled basis elements. They also offer an avenue for asserting the quality of a quantum computer based on whether (and to what extent) it can generate quantum correlations that elude classical models. Finally, our results also indicate the prospects for real-life local area quantum networks based on transmon quantum computers in which physical distances can be mediated by microwave photons. While this quantum transduction might still be a few years ahead, there have already been significant steps towards developing such a quantum-coherent, bidirectional transducer between microwave and optical frequencies25,26,27,28,29,30,31. This would be an interesting endeavour for future research.

Methods

Experimental optimisation

All of the devices we used operate on superconducting transmon qubits located in a fridge with a temperature of roughly 15 mK. In order to find the most suitable devices, including the choice of which qubits to use, we have considered the connectivity maps to minimise the number of overhead CNOT gates, together with the performance of the individual qubits and connecting gates, such as the T1 and T2 times, the measurement errors and the CNOT gate fidelities. The quantum volume32 is also a good indicator for the overall performance of the different devices. However, when only a small subset of qubits of a device is used, the fact that there is quite some variation between different qubits on the same device, makes the optimal choice not straightforward. The final optimisation was in our case performed empirically, i.e. by testing the most promising configurations and comparing them. We do not know of any rigorous and general method to find the best device, and suspect that this would be challenging since we observe that the performance of different devices varies substantially depending on the choice of circuits to be implemented.

Communication network

For the communication network, we considered several devices before choosing the ibmq_montreal 27-qubit quantum computer due to its comparatively high performance. The relatively small two-qubit gate errors, large coherence times and small readout errors on up to ten connected qubits resulted in a larger success probability and therefore allowed us to certify more entangled operators. Each experiment features 4N circuits which are realised using a different set of local unitaries (exemplified in SM). The GHZ-state and the BSM are realised using a Hadamard gate followed by several CNOT gates acting pairwise between the N qubits. Since different qubits on the device are subject to different gate errors, relaxation times and dephasing times, we have strived to choose our N working qubits favourably. In order to enable the practical implementation of the exponentially growing number of circuits, we have exploited that the measured winning probability is constant in N. This allows us to exponentially reduce the number of shots per circuit while maintaining a low standard deviation for \({p}_{N}^{\,\text{win}\,}\) (see SM). Therefore, each circuit was implemented in 24576 shots (N = 2), 8192 shots (N = 3, 4), 1024 shots (N = 5), 128 shots (N = 6), 32 shots (N = 7, 8), 16 shots (N = 9) and 8 shots (N = 10), leading to a standard deviation (statistical error) no larger than 10−3 in the estimate of \({p}_{N}^{\,\text{win}\,}\) for N < 10 (see Supplementary Information for details).

Star network

Similarly, for the star network, we also considered several IBM devices but focused on the ibmq_almaden 20-qubit quantum computer due to its favourable qubit architecture, the good results and the fact that it supports the experiment for N = 2, 3, 4, 5, 6. Specifically, the connectivity allows for the six qubits that form the central node to be each connected to another branch node, such that no swap gates are needed to address the corresponding two-qubit gates. The experiments require 2N different circuits, each corresponding to a set of local measurements (exemplified in SM). In order to keep the standard deviation low, we performed an increasing number of shots per circuit as we increased N. For each circuit we have implemented approximately 1.2 × 105 shots (N = 2, 3), 2 × 105 shots (N = 4, 5) and 4.9 × 106 shots (N = 6), leading to a standard deviation no larger than 2 × 10−3 in the estimate of \({{\mathcal{S}}}_{N}\) for N = 2, …, 6 (see Supplementary Information for details).

Bilocal scenario

For the bilocal scenario, we needed four qubits connected in a line that were notably robust. We run the experiment on all promising devices, but were only able to demonstrate a violation of the inequality of ref. 20 using the ibmq_manhattan 65-qubit quantum computer. We ran 3.3 × 105 shots per setup.

Triangle scenario

Since there presently does not exist a noise-robust Bell-type inequality for the quantum correlations targeted in our experiment in the triangle scenario, it is not straightforward to determine how faithfully our result matches the theoretical quantum predictions. We considered the KL-divergence between the experimental and theoretical distribution and obtained the best results using the ibmq_montreal 27-qubit quantum computer and the ibmq_johannesburg 20-qubit quantum computer, which can be explained by their small readout and two-qubit gate errors and their suitable connectivity map, respectively.