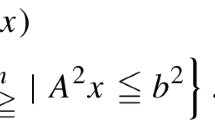On generalized surrogate duality in mixed-integer nonlinear programming

Abstract

The most important ingredient for solving mixed-integer nonlinear programs (MINLPs) to global $\epsilon$-optimality with spatial branch and bound is a tight, computationally tractable relaxation. Due to both theoretical and practical considerations, relaxations of MINLPs are usually required to be convex. Nonetheless, current optimization solvers can often successfully handle a moderate presence of nonconvexities, which opens the door for the use of potentially tighter nonconvex relaxations. In this work, we exploit this fact and make use of a nonconvex relaxation obtained via aggregation of constraints: a surrogate relaxation. These relaxations were actively studied for linear integer programs in the 70s and 80s, but they have been scarcely considered since. We revisit these relaxations in an MINLP setting and show the computational benefits and challenges they can have. Additionally, we study a generalization of such relaxation that allows for multiple aggregations simultaneously and present the first algorithm that is capable of computing the best set of aggregations. We propose a multitude of computational enhancements for improving its practical performance and evaluate the algorithm’s ability to generate strong dual bounds through extensive computational experiments.

1 Introduction

We consider a mixed-integer nonlinear program (MINLP) of the form

$$\begin{aligned} \min _{x \in X} \; \left\{ c^{\mathsf {T}}x \mid g_i(x) \le 0 \text { for all }i \in {\mathscr {M}}\right\} , \end{aligned}$$

(1)

where $X:= \{x \in {\mathbb {R}}^{n-p} \times {\mathbb {Z}}^{p} \mid Ax \le b\}$ is a compact mixed-integer linear set, each $g_i :{\mathbb {R}}^n\rightarrow {\mathbb {R}}$ is a factorable continuous function [41], and ${\mathscr {M}}:= \{1,\ldots ,m\}$ denotes the index set of nonlinear constraints. Such a problem is called nonconvex if at least one $g_i$ is nonconvex, and convex otherwise. Many real-world applications are inherently nonlinear, and can be formulated as a MINLP. See, e.g., [28] for an overview.

The state-of-the-art algorithm for solving nonconvex MINLPs to global $\epsilon$-optimality is spatial branch and bound, see, e.g., [30, 51, 52], whose performance highly depends on the tightness of the relaxations used. Those relaxations are typically convex, and are iteratively refined by branching, cutting planes, and variable bound tightening, e.g., feasibility- and optimality-based bound tightening [8, 50].

As a result of the rapid progress during the last decades, current solvers can often handle a moderate presence of nonconvex constraints efficiently. This progress opens the door for practical use of potentially tighter nonconvex relaxations in MINLP solvers. One example are MILP relaxations, see [11, 43, 68]. In this paper, we go one step further and explore a nonconvex relaxation referred to as surrogate relaxation [21].

Definition 1

(Surrogate relaxation) For a given $\lambda \in {\mathbb {R}}^m_+$, we call the following optimization problem a surrogate relaxation of (1)

$$\begin{aligned} S(\lambda ) := \min _{x \in X} \; \left\{ c^{\mathsf {T}}x \mid \sum _{i \in {\mathscr {M}}} \lambda _i g_i(x) \le 0 \right\} . \end{aligned}$$

(2)

Let ${\mathscr {F}}\subseteq {\mathbb {R}}^n$ be the feasible region of the original problem (1), and let $S_\lambda \subseteq {\mathbb {R}}^n$ be the feasible region of a surrogate relaxation given in (2). Throughout the whole paper we assume that ${\mathscr {F}}$ is not empty. Clearly, ${\mathscr {F}}\subseteq S_\lambda$ holds for every $\lambda \in {\mathbb {R}}^m_+$, and as such (2) provides a valid lower bound of (1). Moreover, solving (2) might be computationally more convenient than solving the original problem (1), since there is only one nonconvex constraint in $S(\lambda )$. Note that one may turn $S_\lambda$ into a continuous relaxation of (1) by removing the integrality restrictions. However, in this work we purposely choose to retain integrality in the relaxation and compare directly to the optimal value of (1) as opposed to its continuous relaxation.

The quality of the bound provided by $S(\lambda )$ may be highly dependent on the value of $\lambda$, and therefore it is natural to consider the surrogate dual problem in order to obtain the tightest surrogate relaxation.

Definition 2

(Surrogate dual). The following optimization problem is the surrogate dual of (1):

$$\begin{aligned} \sup _{\lambda \in {\mathbb {R}}^m_+} \; S(\lambda ). \end{aligned}$$

(3)

The function $S$ is only lower semi-continuous [27], thus, there might be no $\lambda$ such that $S(\lambda )$ is equal to (3). The surrogate dual is closely related to the well-known Lagrangian dual ${\max _{\lambda \in {\mathbb {R}}^m_+}} L(\lambda )$, where

$$\begin{aligned} L(\lambda ) := \min _{x \in X} \left\{ c^{\mathsf {T}}x + \sum _{i \in {\mathscr {M}}} \lambda _i g_i(x) \right\} \text {,} \end{aligned}$$

(4)

but always results in a bound that is at least as good [27, 35], i.e.,

$$\begin{aligned} S(\lambda ) \ge L(\lambda )&\quad \text { for all }\lambda \in {\mathbb {R}}^m_+. \end{aligned}$$

(5)

Figure 1 shows the difference between $S(\lambda )$ and $L(\lambda )$ on the two-dimensional instance of Example 1 below. In contrast to $L : {\mathbb {R}}^m_+ \rightarrow {\mathbb {R}}$, which is a continuous and concave function, $S: {\mathbb {R}}^m_+ \rightarrow {\mathbb {R}}$ is only quasi-concave [27] and is, in general, discontinuous. As shown in Fig. 1, the main difficulty in optimizing $S(\lambda )$ is that the function is most of the time “flat”, and leads to nontrivial dual bounds for only a small subset of the $\lambda$-space.

Example 1

Consider the following nonconvex problem

$$\begin{aligned} \begin{aligned} \min \quad&-y \\ \text {s.t.}\quad&g_1(x,y):=2xy + x^2 - y^2 - x \le 0 , \\&g_2(x,y):=-xy - 0.3x^2 - 0.2y^2 - 0.5x + 1.5y \le 0 , \\&(x,y)\in [0, 1]^2 , \end{aligned} \end{aligned}$$

which attains its optimal value $-0.37$ at $(x^*,y^*) \approx (0.52,0.37)$. The surrogate dual is

$$\begin{aligned} \sup _{(\lambda _1,\lambda _2) \in {\mathbb {R}}_+^2} \left\{ \begin{aligned} \min \quad&-y \\ \text {s.t.}\quad&\lambda _1 g_1(x,y) + \lambda _2 g_2(x,y) \le 0 \\&(x,y)\in [0, 1]^2 \end{aligned} \right\} , \end{aligned}$$

and the Lagrangian dual is

$$\begin{aligned} \max _{(\lambda _1,\lambda _2) \in {\mathbb {R}}_+^2} \left\{ \begin{aligned} \min \quad&-y + \lambda _1 g_1(x,y) + \lambda _2 g_2(x,y) \\ \text {s.t.}\quad&(x,y)\in [0, 1]^2 \end{aligned} \right\} . \end{aligned}$$

The value of the surrogate dual is $S(0.56,0.44) \approx -0.38$, and the value of the Lagrangian dual is $L(0.67,0.82) \approx -0.78$. Neither dual proves optimality of $(x^*,y^*)$.

Fig. 1

Plot of the surrogate and Lagrangian relaxations values for the MINLP detailed in Example 1. For display purposes, we plot both relaxations with respect to $\lambda _1$ only. Note that since the surrogate relaxation is invariant to scaling, we can add a normalization constraint which makes $\lambda _1$ the only free parameter

Contribution In this paper, we revisit surrogate duality in the context of mixed-integer nonlinear programming. To the best of our knowledge, surrogate relaxations have never been considered for solving general MINLPs. The first contribution of the paper is an algorithm capable of solving a generalized surrogate dual that allows for multiple aggregations of the nonlinear constraints simultaneously. We also prove its convergence guarantees. Secondly, we present computational enhancements to make the algorithm practical. Our developed algorithm allows us to compare the performance of the classical surrogate relaxation with the generalized one. Finally, we provide an exhaustive computational analysis using publicly available benchmark instances, and we show the practical utility of our proposed approach.

Structure The rest of the paper is organized as follows. In Sect. 2, we present a literature review of surrogate duality. Sect. 3 discusses an algorithm from the literature for solving the classic surrogate dual problem and our new computational enhancements. In Sect. 4, we review a generalization of surrogate relaxations from the literature. Afterward, in Sect. 5, we adapt an algorithm for the classic surrogate dual problem to the general case and prove its convergence. An exhaustive computational study on publicly available benchmark instances is given in Sect. 6. Afterward, Sect. 7 presents ideas for future work on how to include surrogate relaxations in the tree search of spatial branch and bound. Section 8 presents concluding remarks.

2 Background

Surrogate constraints were first introduced by Glover [21] in the context of zero-one linear integer programming problems. He defined the strength of a surrogate constraint according to the dual bound achieved by it—the same notion we use. Extensions were provided by Balas [5] and Geoffrion [20], although under an alternative notion of strength. Glover [22] provided a unified view on these approaches and proposed a generalization where only a subset of constraints are used in an aggregation, leaving the rest explicitly enforced.

A theoretical analysis of surrogate duality in a nonlinear setting was first presented by Greenberg and Pierskalla [27]. This includes results such as quasi-concavity of the surrogate relaxation and a comparison with the Lagrangian dual. They also proposed a generalization using multiple disjoint aggregation constraints. A similar generalization allowing multiple aggregations was later proposed by Glover [23]. These were proposed without computational evaluation. Regarding the link with Lagrangian duality, Karwan and Rardin [35] presented necessary conditions for having no gap between the Lagrangian and surrogate duals. Constraint qualification conditions for the surrogate dual have been exhaustively studied, see [23, 49, 58] and references therein.

The first algorithmic method for solving (3) is attributed to Banerjee [7]. In the context of integer linear programming, he proposed a Benders’ approach similar to the one considered by us in order to find the best multipliers. Karwan [34] expanded on this approach, including a refinement of that of Banerjee and subgradient-based methods. Independently, Dyer [17] proposed similar methods to those of Karwan. Karwan and Rardin [35, 38] further developed both Benders- and subgradient-based approaches. Other search procedures for solving (3) involve consecutive Lagrangian dual searches [39, 53] and heuristics [19].

From a different perspective, Karwan and Rardin [37] described the interplay between the branch-and-bound trees of an integer programming problem and its surrogate relaxations. Later on, Sarin et al. [54] showed how to integrate their Lagrangian-based multiplier search proposed in [53] into branch and bound.

Surrogate constraints have been used in various applications: in primal heuristics for IPs [24], knapsack problems with a quadratic objective function [15], the job shop problem [18], generalized assignment problems [46], among others. We refer the reader to [3, 25] for reviews on surrogate duality methods including other applications and alternative methods for generating surrogate constraints not based on aggregations.

To the best of our knowledge, the efforts for practical implementations of multiplier search methods have mainly focused on linear integer programs. This focus can be explained by the maturity of computational optimization tools available during the time where most of these implementations have been developed. We are only aware of two exceptions: the entropy approach to nonlinear programming (see [59, 67]) which uses an entropy-based surrogate reformulation instead of a weighted sum of the constraints; and the work by Nakagawa [45], who considered separable nonlinear integer programming and presented a novel, albeit expensive, algorithm for solving the surrogate dual.

Regarding the generalization of the surrogate dual that considers multiple aggregated constraints, we are not aware of any work considering a multiplier search method with provable guarantees or a computational implementation of a heuristic approach. We are only aware of the discussion by Karwan and Rardin [36] where they argue that the lack of desirable structures (such as quasi-concavity) may impair some multiplier searches for the surrogate dual generalizations proposed by Greenberg and Pierskalla [27] and Glover [23].

3 Surrogate duality in MINLPs

While surrogate duality in its broader definition can be applied to any MINLP, to the best of our knowledge, only mixed-integer linear programming problems have been considered for practical applications. Much less attention has been given to the general MINLP case, due to the potential nonconvexity of the resulting problems. Figure 2 illustrates the possible drawbacks and benefits of a nonconvex surrogate relaxation, namely, potentially tight convex relaxations (Fig. 2c), nonconvex (Fig. 2a and 2d), and even disconnected (Fig. 2b) feasible regions.

Fig. 2

Surrogate relaxations for the nonconvex optimization problem in Example 1. The feasible region defined by each nonlinear constraint is blue and the set $S_{\lambda }$ is orange (line shaded). $S_{\lambda }$ can be nonconvex, disconnected, convex, or reverse convex (color figure online)

In this section, we investigate the trade-off between the computational effort required to solve surrogate relaxations and the quality of the resulting bounds. We review how to solve the surrogate dual (3) via a Benders’ algorithm (see [7, 17, 34]) and how to overcome some of the computational difficulties that arise. As we mentioned in Sect. 2, alternative algorithms for solving the surrogate dual exist. However, we use a Benders’ approach because its extension to the generalized surrogate dual problem (Sect. 4) is more direct. It is unclear if, e.g., subgradient-based algorithms can be extended to work for the generalization.

3.1 Solving the surrogate dual via Benders

The Benders’ algorithm is an iterative approach that alternates between solving a master and a sub-problem. The master problem searches for an aggregation vector $\lambda \in {\mathbb {R}}_+^m$ and the sub-problem solves (2) to evaluate $S(\lambda )$. Note that the value of an optimal solution $\bar{x}$ of $S(\lambda )$, i.e., $c^{\mathsf {T}}{{\bar{x}}}$, is a valid dual bound for (1). To ensure that the point ${{\bar{x}}}$ is not considered in later iterations, i.e., ${{\bar{x}}} \not \in S_{\lambda '}$, the Benders’ algorithm uses the master problem to compute a new vector $\lambda ' \in {\mathbb {R}}_+^m$ that ensures $\sum _{i \in {\mathscr {M}}} \lambda '_i g_i({{\bar{x}}}) > 0$. This can be done by maximizing constraint violation. More precisely, given ${\mathscr {X}}$ the set of previously generated points of the sub-problems, the master problem is the following linear program:

$$\begin{aligned} {\max _{\varPsi ,\lambda }} \;&\varPsi \nonumber \\ \text {s.t.}&\sum _{i \in {\mathscr {M}}} \lambda _i g_i({{\bar{x}}}) \ge \varPsi \qquad \text { for all }{{\bar{x}}} \in {\mathscr {X}}, \nonumber \\&\left\| \lambda \right\| _1 \le 1, \nonumber \\&\lambda \in {\mathbb {R}}^m_+. \end{aligned}$$

(6)

The normalization constraint $\left\| \lambda \right\| _1 \le 1$ can be added without loss of generality, and it is used to avoid unboundedness of (6). The resulting scheme, formalized in Algorithm 1, terminates once the solution value of (6) is smaller than a fixed value $\epsilon \ge 0$. Note that, with this stopping criterion, the best bound D found by the algorithm is “subject to $\epsilon$-feasibility”. This means that when the algorithm stops, it holds that

$$\begin{aligned} \forall \lambda \in {\mathbb {R}}^{m}_+, \Vert \lambda \Vert _1 \le 1 ,\,\exists {\bar{x}}\in {\mathscr {X}},\, c^{\mathsf {T}}{\bar{x}} \le D \wedge \sum _{i \in {\mathscr {M}}} \lambda _i g_i({{\bar{x}}}) < \epsilon . \end{aligned}$$

If a numerical feasibility tolerance of $\epsilon$ is used in a solver (which is usually the case), then for every surrogate relaxation, some ${\bar{x}}\in {\mathscr {X}}$ would be considered feasible and thus prevent the dual bound from improving. The consideration of $\epsilon$ here is meant mostly for accommodating these numerical tolerances.

An illustration of the algorithm for Example 1 is given in Fig. 3.

Remark 1

Instead of finding an aggregation vector that maximizes the violation of all points in ${\mathscr {X}}$, Dyer [17] uses an interior point for the polytope in (6). This can be achieved by scaling $\varPsi$ in each constraint of (6) depending on the values $g_i({{\bar{x}}})$ for each $i \in {\mathscr {M}}$. In our experiments, however, we have observed that maximizing the violation significantly improves the quality of the computed dual bounds.

Using the analysis in [7], Karwan [34] proved the following in the linear case.

Theorem 1

Denote by $((\lambda ^t, \varPsi ^t))_{t \in {\mathbb {N}}}$ the sequence of values obtained in Step 6 of Algorithm 1 for $\epsilon = 0$. Let OPT be the value of the surrogate dual (3). If all $g_i$ are linear for all $i \in {\mathscr {M}}$, then Algorithm 1 either

• terminates in T steps, in which case $\max _{1 \le t \le T} S(\lambda ^t) = OPT$, or

• the sequence $(S(\lambda ^t))_{t \in {\mathbb {N}}}$ has a sub-sequence converging to OPT.

We prove a stronger version of this theorem in Sect. 5 that also works for nonlinear constraints. This stronger result, in particular, shows finite convergence of the algorithm for $\epsilon >0$. Note that the convergence of the algorithm only relies on the solution of an LP and a nonconvex problem $S(\lambda )$, and does not make any assumption on the nature of $S(\lambda )$ besides the fact that it can be solved.

Fig. 3

Algorithm 1 applied to Example 1. The black point is the optimal solution to the original problem, the dashed lines correspond to the variable bounds, the light blue regions are the feasible sets of each nonlinear constraint, and the orange (line shaded) region is $S_{\lambda }$ for the different values of $\lambda \in {\mathbb {R}}_+^2$ that are computed by the algorithm. The red points are the optimal solutions at each iteration and any red point becomes blue in the next iteration as part of the set ${\mathscr {X}}$. The algorithm converges after seven iterations, and the best multiplier $\lambda ^* \approx (0.56, 0.44)$ was found after five iterations (color figure online)

3.2 Algorithmic enhancements

In this section, we present computational enhancements that speed up Algorithm 1 and improve the quality of the dual bound that can be achieved from (3). For the sake of completeness, we also discuss techniques that have been tested but did not improve the quality of the computed dual bounds significantly.

3.2.1 Refined MILP relaxation

Instead of only using the initial linear constraints $Ax\le b$ to define $X$ in (1), we exploit a linear programming (LP) relaxation of (1) that is available in LP-based spatial branch and bound. This relaxation contains $Ax \le b$ but also linear constraints that have been derived from, e.g., integrality restrictions of variables (e.g., MIR cuts [48] and Gomory cuts [26]), gradient cuts [32], RLT cuts [56], SDP cuts [57], or other valid underestimators for each $g_i$ with $i \in {\mathscr {M}}$. Using a linear relaxation $A'x \le b'$ with

$$\begin{aligned} X' := \{ x \in X\mid A'x \le b' \} \end{aligned}$$

(7)

in the definition of $S_{\lambda }$ improves the value of (3) because a relaxed version of the nonlinear constraint $g_i(x) \le 0$ is captured in $S_\lambda$ even if $\lambda _i$ is zero.

Another way to strengthen the linear relaxation is to make use of objective cutoff information. If there is a feasible, but not necessarily optimal, solution $x^*$ to (1), the linear relaxation can be strengthened with the inequality $c^{\mathsf {T}}x \le c^{\mathsf {T}}x^*$. This inequality preserves all optimal solutions of (1) and can improve the performance when solving (3) (for example, an objective cutoff can lead to dual reductions found by reduced-cost strengthening).

3.2.2 Dual objective cutoff in the sub-problem

An undesired phenomenon in Algorithm 1 is that the sequence of dual bounds provided by $c^{\mathsf {T}}{{\bar{x}}}$ in Step 3 might not be monotone. One way to overcome this problem is to add a dual objective cutoff $c^{\mathsf {T}}x \ge D$ to the sub-problem $S(\lambda )$, thus enforcing monotonicity in the sequence of dual bounds. This does not change the convergence/correctness guarantees of Algorithm 1 and it can improve the progress of the subsequent dual bounds. Moreover, such cutoff can be used to filter the set ${\mathscr {X}}$ and thus reduce the size of the LP  (6). For example, in Fig. 3 the two last iterations could be avoided.

However, this cutoff has an unfortunate drawback: it increases degeneracy, which affects essential components of a branch-and-bound solver, e.g., pseudocost branching [9]. In the case of Algorithm 1, adding this cutoff significantly increases the time for solving the sub-problem, resulting in an overall negative effect on the algorithm. We confirmed this with extensive computational experiments and decided not to include this feature in our final implementation.

Fortunately, we can still carry dual information through different iterations and improve the performance of the algorithm.

3.2.3 Early stopping in the sub-problem

One important ingredient to speed up Algorithm 1, proposed by Karwan [34] and Dyer [17] independently, is an early stopping criterion while solving $S(\lambda )$. In our setting, problem $S(\lambda )$ is the bottleneck of Algorithm 1.

Assume that Algorithm 1 proved a dual bound D in some previous iteration. It is possible to stop the solving process of $S(\lambda )$ if a point ${{\bar{x}}} \in S_{\lambda }$ with $c^{\mathsf {T}}{{\bar{x}}} \le D$ has been found. The point ${{\bar{x}}}$ both provides a new inequality for (6) violated by $\lambda$ (as ${{\bar{x}}} \in S_{\lambda }$) and shows $S(\lambda ) \le D$, i.e., $\lambda$ will not lead to a better dual bound. All convergence and correctness statements regarding Theorem 1 remain valid after this modification.

Furthermore, we can apply the same idea for any choice of D. In this scenario, D would act as a target dual bound that we want to prove. Since the Benders’ algorithm is computationally expensive, one might require a minimum improvement in the dual bound. Empirically, we observed that solving $S(\lambda )$ to global optimality for difficult MINLPs requires a lot of time. However, finding a good quality solution for $S(\lambda )$ is usually fast. This allows us to early stop most of the sub-problems and only spend time on those sub-problems that will likely result in a dual bound that is at least as good as the target value D.

3.3 Initial empirical observations

For the implementation of Algorithm 1, we use the MINLP solver SCIP

• 1. to construct a linear relaxation $A'x \le b'$ for (1),

• 2. to find a feasible solution $x^*$ to (1) to be used as an objective cutoff $c^{\mathsf {T}}x \le c^{\mathsf {T}}x^*$ when solving $S(\lambda )$, and

• 3. to use it as a black box to solve each $S(\lambda )$ sub-problem.

We provide extensive details of our implementation and the results in Sect. 6, but we would like to summarize some important observations to the reader.

Our proposed algorithmic enhancements proved to be key for obtaining a practical algorithm for the surrogate dual, especially the use of a refined MILP relaxation. The achieved dual bounds by only using the initial linear relaxation in Algorithm 1 were almost always dominated by the dual bounds obtained by the refined MILP relaxation. Thus, utilizing the refined MILP relaxation seems mandatory for obtaining strong surrogate relaxations. Our computational study in Sect. 6 shows that our algorithmic enhancements of Algorithm 1 allows us to compute dual bounds that close on average 35.0% more gap (w.r.t. the best known primal bound) than the dual bounds obtained by the refined MILP relaxations, i.e., S(0), on 469 affected instances.

While the overall impact of this “classic” surrogate duality is positive, we observed that the dual bound deteriorates with increasing number of nonlinear constraints; aggregating a large number of nonconvex constraints into a single constraint may not capture the structure of the underlying MINLP. For this reason, in the next Section we propose the use of a generalized surrogate relaxation for solving MINLPs, which includes multiple aggregation constraints.

4 Generalized surrogate duality

In the following, we discuss a generalization of surrogate relaxations that has been introduced by [23]. Instead of a single aggregation, it allows for $K \in {\mathbb {N}}$ aggregations of the nonlinear constraints of (1). The nonnegative vector $\lambda = (\lambda ^1, \lambda ^2, \ldots , \lambda ^K) \in {\mathbb {R}}^{K m}_+$ encodes these K aggregations

$$\begin{aligned} \sum _{i \in {\mathscr {M}}} \lambda ^k_i g_i(x) \le 0, \quad k \in \{1,\ldots ,K\} \end{aligned}$$

of the nonlinear constraints. Note that, for convenience, we are denoting as $\lambda _i^k$ the component $\lambda _{(k-1)m+i}$ of the $\lambda$ vector, as it can also be seen as the i-th component of the $\lambda ^k$ sub-vector. For a vector $\lambda \in {\mathbb {R}}^{K m}_+$, the feasible region of the K-surrogate relaxation is given by the intersection

$$\begin{aligned} S^{K}_\lambda := \bigcap _{k=1}^{K} S_{\lambda ^k} , \end{aligned}$$

where $S_{\lambda ^k}$ is the feasible region of the surrogate relaxation $S(\lambda ^k)$ for $\lambda ^k \in {\mathbb {R}}^m_+$. It clearly follows that $S^{K}_\lambda$ is a relaxation for (1). The best dual bound for (1) generated by a K-surrogate relaxation is given by

$$\begin{aligned} \sup _{\lambda \in {\mathbb {R}}^{K m}_+} S^{K}(\lambda ) , \end{aligned}$$

(8)

which we call the K-surrogate dual. Note that scaling each $\lambda ^k \in {\mathbb {R}}^m_+$ individually by a positive scalar does not affect the value of $S^{K}(\lambda )$, i.e.,

$$\begin{aligned} S^{K}(\ldots , \lambda ^k, \ldots ) = S^{K}(\ldots , \alpha \lambda ^k, \ldots ) \end{aligned}$$

for any $\alpha > 0$. Therefore, it is possible to impose additional normalization constraints $\left\| \lambda ^k\right\| _1 \le 1$ for each $k \in \{1, \ldots , K\}$.

In [27], a related generalization was proposed, although not computationally tested. The paper considers a partition of constraints which are aggregated; equivalently, the support of sub-vectors $\lambda ^k$ are assumed to be fixed and disjoint. Glover’s generalization [23] does not make any assumption on the structure of the $\lambda ^k$ sub-vectors. As we argue below, this makes a significant difference for two reasons: (a) selecting the “best” partition of constraints a-priori is a challenging task and (b) restricting the support of sub-vectors $\lambda ^k$ to be disjoint can weaken the bound given by (8).

The function $S^{K}$ remains lower semi-continuous for any choice of K. The proof idea is similar to the one given by Glover [23] for the case of $K=1$.

Proposition 1

If $g_i$ is continuous for every $i \in {\mathscr {M}}$ and $X$ is compact, then $S^{K}: {\mathbb {R}}^{K m}_+ \rightarrow {\mathbb {R}}$ is lower semi-continuous for any choice of K.

Proof

Let $(\lambda ^t)_{t \in {\mathbb {N}}} \subseteq {\mathbb {R}}^{K m}_+$ a sequence that converges to $\lambda ^*$. We denote the k-th sub-vector of $\lambda ^t$ as $\lambda ^{t,k}$. Denote with $x^t \in X$ an optimal solution of $S^{K}(\lambda ^t)$.

We need to show that $S^{K}(\lambda ^*) \le \liminf _{t \rightarrow \infty } S^{K}(\lambda ^t)$.

By definition, there exists a subsequence $(\lambda ^\tau )_{\tau \in {\mathbb {N}}}$ of $(\lambda ^t)_{t \in {\mathbb {N}}}$ such that $S^{K}(\lambda ^\tau ) \rightarrow \liminf _{t \rightarrow \infty } S^{K}(\lambda ^t)$.

Since $X$ is compact, there exists a subsequence $(x^l)_{l \in {\mathbb {N}}}$ of $(x^\tau )_{\tau \in {\mathbb {N}}}$ such that $\lim _{l \rightarrow \infty } x^l = x^*$. As $(\lambda ^l)_{l \in {\mathbb {N}}}$ is a subsequence of $(\lambda ^\tau )_{\tau \in {\mathbb {N}}}$, we have that $\lim _{l \rightarrow \infty } S^{K}(\lambda ^l) = \liminf _{t \rightarrow \infty } S^{K}(\lambda ^t)$. From $x^l \in S^{K}_{\lambda ^l}$ it follows that

$$\begin{aligned} \sum _{i \in {\mathscr {M}}} {\lambda _{i}^{l,k}} \, g_i(x^l) \le 0 \end{aligned}$$

for every $k \in \{1, \ldots , K\}$, which is equivalent to

$$\begin{aligned} \max _{1 \le k \le K} \sum _{i \in {\mathscr {M}}} {\lambda _{i}^{l,k}} \, g_i(x^l) \le 0 \, . \end{aligned}$$

Because the $g_i$ are continuous and the maximum of continuous functions is still continuous, it follows that

$$\begin{aligned} \max _{1 \le k \le K} \sum _{i \in {\mathscr {M}}} {(\lambda ^*)^{k}_i} \, g_i(x^*) = \lim _{l \rightarrow \infty } \max _{1 \le k \le K} \sum _{i \in {\mathscr {M}}} {\lambda _{i}^{l,k}} \, g_i(x^l) \le 0. \end{aligned}$$

Hence, $x^*$ is feasible but not necessarily optimal for $S^{K}(\lambda ^*)$. Therefore,

$$\begin{aligned} S^{K}(\lambda ^*) \le c^{\mathsf {T}}x^* = \lim _{l \rightarrow \infty } c^{\mathsf {T}}x^l = \lim _{l \rightarrow \infty } S^{K}(\lambda ^l) = \liminf _{t \rightarrow \infty } S^{K}(\lambda ^t) \, . \end{aligned}$$

$\square$

One important difference to the classic surrogate dual is that $S^{K}(\lambda )$ is no longer quasi-concave, even for the case of $K=2$ and two linear constraints, as the following example shows.

Example 2

Let $K=2$ and consider the linear program

$$\begin{aligned} \begin{aligned} \min \quad&y \\ \text {s.t.}\quad&4x - 8y + 3.2 \le 0 , \\&5x - y - 1.5 \le 0 , \\&(x,y) \in [0,1]^2 . \end{aligned} \end{aligned}$$

Due to the symmetry of the generalized surrogate dual, $S^{2}(\lambda ) = S^{2}(\mu ) \approx 0.30$ holds for the aggregation vectors $\lambda := ((0.7,0.3),(0.3,0.7))$ and $\mu := ((0.3,0.7),(0.7,0.3))$. However, using the convex combination $\lambda / 2 + \mu / 2$ we have that $S^{2}(\lambda / 2 + \mu / 2) \approx 0.19$, which is smaller than $S^{2}(\lambda )$ and $S^{2}(\mu )$ and thereby shows that $S^{2}$ is not quasi-concave.

See Fig. 4 for an illustration of the counterexample.

Fig. 4

A visualization of Example 2 that shows that $S^{K}$ is in general not quasi-concave for $K > 1$. The blue line shaded region (left) is the feasible set defined by two original inequalities. The orange region (center) depicts both $S^{2}_\lambda$ and $S^{2}_\mu$, while the green region (right) is their convex combination $S^{2}_{(\lambda +\mu ) / 2}$. The example shows $S^{2}(\lambda ) = S^{2}(\mu ) > S^{2}((\lambda + \mu )/2)$, which proves that $S^{2}$ is not quasi-concave (color figure online)

Since $S^{K}$ may not be quasi-concave, gradient descent-based algorithms for optimizing (3), as in [34], become inadequate for solving (8). Even though (8) is substantially more difficult to solve than (3), it might be beneficial to consider larger K to obtain tight relaxations for (1). The following proposition formalizes this. We omit its proof as it is elementary.

Proposition 2

The inequality

$$\begin{aligned} \sup _{\lambda \in {\mathbb {R}}^{K m}_+} S^{K}(\lambda ) \le \sup _{\lambda \in {\mathbb {R}}^{(K+1) m}_+} S^{K+1}(\lambda ) \end{aligned}$$

(9)

holds for any $K \in {\mathbb {N}}$. Furthermore, $\sup _{\lambda \in {\mathbb {R}}^{m^2}_+} S^{m}(\lambda )$ is equal to the value of (1).

The following example shows that going from $K=1$ to $K=2$ can have a tremendous impact on the quality of the surrogate relaxation:

Example 3

Consider the following NLP with four nonlinear constraints and four unbounded variables:

$$\begin{aligned} \min \quad&-x - y \\ \text {s.t.}\quad&x^3 - z \le 0 \\&x^3 + z \le 0 \\&y^2 + w \le 0 \\&y^2 - w \le 0 \end{aligned}$$

It is easy to see that (0, 0, 0, 0) is the optimal solution.

First, we show that the classic surrogate dual is unbounded. For an aggregation $\lambda \in {\mathbb {R}}^4$, the sole constraint in the corresponding surrogate relaxation is

$$\begin{aligned} (\lambda _1 + \lambda _2)x^3 + (-\lambda _1 + \lambda _2)z + (\lambda _3 + \lambda _4)y^2 + (\lambda _3 - \lambda _4)w \le 0. \end{aligned}$$

If either $\lambda _1 \ne \lambda _2$ or $\lambda _3 \ne \lambda _4$, then the relaxation is clearly unbounded, as z and w are free variables with coefficient 0 in the objective. If $\lambda _1 = \lambda _2$ and $\lambda _3 = \lambda _4$, the aggregation reads $2\lambda _1 x^3 + 2\lambda _3 y^2 \le 0$. We split this case in two: (1) if $\lambda _1 = 0$, then $(x,y,w,z) = (M,0,0,0)$ is feasible for any M. (2) Otherwise, we can set $(x,y,w,z) = (-M,2M,0,0)$ and $2\lambda _1 x^3 + 2\lambda _3 y^2 = -2\lambda _1 M^3 + 8\lambda _3 M^2.$ The last expression is negative for large enough M.

In both cases the objective evaluates to $-M$. Letting $M\rightarrow \infty$ shows unboundedness.

Now consider the two aggregations $\lambda = (\lambda ^1,\lambda ^2)$ with $\lambda ^1 = (1/2,1/2,0,0)$ and $\lambda ^2 = (0,0,1/2,1/2)$. Using the 2-surrogate relaxation obtained from $\lambda$ immediately implies $x \le 0$ and $y = 0$, which proves optimality of (0, 0, 0, 0).

5 An algorithm for the K-surrogate dual

Even though (8) yields a strong relaxation for large K, it is computationally more challenging to solve than (3). To the best of our knowledge, there is no algorithm in the literature known that can solve (8). Due to the missing quasi-concavity property of $S^{K}$, it is not possible to adjust each aggregation vector independently; an alternating-type method based on the $K=1$ case could provide weak bounds.

In this section, we present the first algorithm for solving (8). The idea of the algorithm is the same as before: a master problem will generate an aggregation vector $(\lambda ^1, \ldots , \lambda ^K)$ and the sub-problem will solve the K-surrogate relaxation corresponding to $(\lambda ^1, \ldots , \lambda ^K)$. The only differences to Algorithm 1 are that we replace the LP master problem by a MILP master problem and solve $S^{K}(\lambda ^1,\ldots ,\lambda ^K)$ instead of $S(\lambda )$.

Generalizing Algorithm 1 Assume that we have a solution ${{\bar{x}}}$ of problem $S^{K}(\lambda ^1, \ldots , \lambda ^K)$. In the next iteration, we need to make sure that ${{\bar{x}}}$ is infeasible for at least one of the aggregated constraints. This can be written as a disjunctive constraint

$$\begin{aligned} \bigvee _{k=1}^K \left( \sum _{i \in {\mathscr {M}}} \lambda ^k_i g_i({{\bar{x}}}) > 0 \right) . \end{aligned}$$

(10)

As in (6), we replace the strict inequality by maximizing the activity of $\sum _{i \in {\mathscr {M}}} \lambda ^k_i g_i({{\bar{x}}})$ for all $k \in \{1,\ldots ,K\}$. The master problem then reads as

$$\begin{aligned} {\max _{\varPsi ,\lambda }} \quad&\varPsi \nonumber \\ \text {s.t.}\quad&\bigvee _{k=1}^K \left( \sum _{i \in {\mathscr {M}}} \lambda ^k_i g_i({{\bar{x}}}) \ge \varPsi \right)&\text { for all }{{\bar{x}}} \in {\mathscr {X}}, \nonumber \\&\left\| \lambda ^k\right\| _1 \le 1,\, \lambda ^k \in {\mathbb {R}}_+^m&\text { for all }k \in \{1,\ldots ,K\} , \end{aligned}$$

(11)

where ${\mathscr {X}}$ is the set of generated points of the sub-problems.

Solving the master problem The disjunction in the master problem (11) is encoding $K^{|{\mathscr {X}}|}$ many LPs, thus an enumeration approach for tackling the disjunction is impractical. Instead, we use a, so-called, big-M formulation. This enables us to solve (11) with moderate running times. Such MILP formulation of (11) reads

$$\begin{aligned} {\max _{\varPsi ,\lambda } }\quad&\varPsi \nonumber \\ \text {s.t.}\quad&\sum _{i \in {\mathscr {M}}} \lambda ^k_i g_i({{\bar{x}}}) \ge \varPsi - M (1 - z_k^{{{\bar{x}}}})&\text { for all }k \in \{1,\ldots ,K\},\, {{\bar{x}}} \in {\mathscr {X}}, \nonumber \\&\sum _{k = 1}^{K} z_k^{{{\bar{x}}}} = 1&\text { for all }{{\bar{x}}} \in {\mathscr {X}}, \nonumber \\&z_k^{{{\bar{x}}}} \in \{0,1\}&\text { for all }k \in \{1,\ldots ,K\}, \, {{\bar{x}}} \in {\mathscr {X}}, \nonumber \\&\left\| \lambda ^k\right\| _1 \le 1,\, \lambda ^k \in {\mathbb {R}}_+^m&\text { for all }k \in \{1,\ldots ,K\} , \end{aligned}$$

(12)

where M is a large constant. A binary variable $z_k^{{{\bar{x}}}}$ indicates if the k-th disjunction of (11) is used to cut off the point ${{\bar{x}}} \in {\mathscr {X}}$. Due to the normalization $\left\| \lambda ^k\right\| _1 \le 1$, it is possible to bound M by $\max _{i \in {\mathscr {M}}} |g_i({{\bar{x}}})|$. Even more, since the optimal $\varPsi$ values of (12) are non-increasing, we could use the optimal $\varPsi _{prev}$ of the previous iteration as a bound on M. Thus, it is possible to bound M by $\min \{\max _{i \in {\mathscr {M}}} |g_i({{\bar{x}}})|, \varPsi _{prev}\}$.

Remark 2

Big-M formulations are typically not considered strong in MILPs, given their usual weak LP relaxations. Other formulations in extended spaces can yield better theoretical guarantees (see, e.g., [6, 10, 62]). The drawback of these extended formulations is that they require to add copies of the $\lambda$ variables depending on the number of disjunctions, which in our case is rapidly increasing.

In [61], the author proposes an alternative that does not create variable copies, but that can be costly to construct unless special structure is present.

In our case, as we discuss in Sect. 5.2.2, we do not require a tight LP relaxation of (11) and thus we opted to use (12).

The algorithm for the K-surrogate dual problem is stated in Algorithm 2. For details on the exact meaning of “subject to $\epsilon$-feasibility”, please see the discussion following Algorithm 1. The following example shows that Algorithm 2 can compute significantly better dual bounds than Algorithm 1.

Example 4

We briefly discuss the results of Algorithm 2 for the genpooling_lee1 instance from MINLPLib. The instance consists of 20 nonlinear, 59 linear constraints, 9 binary, and 40 continuous variables after preprocessing. The classic surrogate dual, i.e., $K=1$, could be solved to optimality, whereas for $K=2$ and $K=3$ the algorithm hit the iteration limit. Nevertheless, the dual bound $-4829.6$ achieved for $K=2$ and the dual bound $-4864.87$ for $K=3$ are significantly better than the dual bound of $-5246.0$ for $K=1$, see Fig. 5.

Fig. 5

Results of Algorithm 2 for the instance genpooling_lee1 for different choices of K. The first plot shows the progress of the proved dual bound and the second plot the value of $\varPsi$ for the first 600 iterations. The blue line is the optimal solution value of the MINLP and the yellow line that of the MILP relaxation (color figure online)

5.1 Convergence

In the following, we show that the dual bounds obtained by Algorithm 2 converge to the optimal value of the K-surrogate dual. The idea of the proof is similar to the one presented by [38] for the case of $K=1$ and linear constraints.

Theorem 2

Denote by $((\lambda ^t, \varPsi ^t))_{t \in {\mathbb {N}}}$ the sequence of values obtained after solving (11) in Algorithm 2 for $\epsilon = 0$. Let OPT be the optimal value of the K-surrogate dual (8). The algorithm either

• (a) terminates in T steps, in which case $\max _{1 \le t \le T} S^{K}(\lambda ^t) = OPT$, or

• (b) $\sup _{t \ge 1} S^{K}(\lambda ^t) = OPT$.

Proof

As in Proposition 1, we denote the k-th sub-vector of $\lambda ^t$ as $\lambda ^{t,k}$. Let $x^t \in X$ be an optimal solution obtained from solving $S^{K}(\lambda ^t)$ at iteration t.

(a) If the algorithm terminates after T iterations, i.e., $\varPsi ^T = 0$, then for any choice $\lambda \in {\mathbb {R}}^{K m}$, there is at least one point $x^1,\ldots ,x^T$ that is feasible for $S^{K}(\lambda )$. This implies $OPT=\max _{1 \le t \le T} \{ c^{\mathsf {T}}x^t \}$.

(b) Now assume that the algorithm does not converge in a finite number of steps, i.e., $\varPsi ^t > 0$ for all $t \ge 1$. Since $(\varPsi ^t)_{t\in {\mathbb {N}}}$ defines a decreasing sequence which is bounded below by 0, it must converge to a value $\varPsi ^* \ge 0$. The same holds for any subsequence of $(\varPsi ^t)_{t\in {\mathbb {N}}}$. Furthermore, the sequence $(\lambda ^t,x^t)_{t\in {\mathbb {N}}}$ belongs to a compact set: indeed, $\left\| \lambda ^t\right\| _1 \le 1$ for all $t\in {\mathbb {N}}$ and $X$ is assumed to be compact. Therefore, there exists a subsequence of $(\varPsi ^t, \lambda ^t, x^t)_{t\in {\mathbb {N}}}$ that converges. With slight abuse of notation, we denote this subsequence by $(\varPsi ^l, \lambda ^l, x^l)_{l\in {\mathbb {N}}}$. To summarize, we have that

• $\lim _{l \rightarrow \infty } \varPsi ^l = \varPsi ^* \ge 0$,

• $\lim _{l \rightarrow \infty } \lambda ^l = \lambda ^*$, and

• $\lim _{l \rightarrow \infty } x^l = x^*$.

for some $(\varPsi ^*, \lambda ^*, x^*)$.

First, we show $\varPsi ^* = 0$. Note that $x^l$ is an optimal solution to $S^{K}(\lambda ^l)$. This means that $x^l$ satisfies all aggregation constraints, i.e., $\sum _{i \in {\mathscr {M}}} {\lambda _{i}^{l,k}} \, g_i(x^l) \le 0$ for all $k = 1, \ldots , K$, which is equivalent to the inequality $\max _{1 \le k \le K} \sum _{i \in {\mathscr {M}}} {\lambda _{i}^{l,k}} \, g_i(x^l) \le 0$. After solving (11), we know that $\varPsi ^l$ is equal to the minimum violation of the disjunction constraints for the points $x^1,\ldots ,x^{l-1}$. This implies the inequality

$$\begin{aligned} \varPsi ^l = \min _{1 \le t \le l-1} \max _{1 \le k \le K} \sum _{i \in {\mathscr {M}}} {\lambda _{i}^{l,k}} \, g_i(x^t) \le \max _{1 \le k \le K} \sum _{i \in {\mathscr {M}}} {\lambda _{i}^{l,k}} \, g_i(x^{l-1}) , \end{aligned}$$

which uses the fact that the minimum over all points $x^1,\ldots ,x^{l-1}$ is bounded by the value for $x^{l-1}$. Both inequalities combined show that

$$\begin{aligned} \max _{1 \le k \le K} \sum _{i \in {\mathscr {M}}} {\lambda _{i}^{l,k}} \, g_i(x^l) \le 0 < {\varPsi ^l} \le \max _{1 \le k \le K} \sum _{i \in {\mathscr {M}}} {\lambda _{i}^{l,k}}\, g_i(x^{l-1}) \end{aligned}$$

for all $l \ge 0$. Using the continuity of $g_i$ and the fact that the maximum of finitely many continuous functions is continuous, we obtain

$$\begin{aligned} \max _{1 \le k \le K} \sum _{i \in {\mathscr {M}}} {(\lambda ^*)_{i}^{k}} \, g_i(x^*) \le 0 \le {\varPsi ^*} \le \max _{1 \le k \le K} \sum _{i \in {\mathscr {M}}} {(\lambda ^*)_{i}^{k}} \, g_i(x^*) , \end{aligned}$$

which shows $\varPsi ^* = 0$.

Next, we show that $\sup _{t \ge 1} S^{K}(\lambda ^t) = OPT$.

Clearly, $\sup _{t \ge 1} S^{K}(\lambda ^t) \le OPT$.

Let us now prove that $\sup _{t \ge 1} S^{K}(\lambda ^t) \ge OPT$.

Take any $\epsilon > 0$ and let ${{\bar{\lambda }}}$ be such that $S^{K}(\bar{\lambda }) \ge OPT - \epsilon$. Such ${{\bar{\lambda }}}$ always exists by definition of OPT. Furthermore, via a re-scaling we may assume $\Vert {{\bar{\lambda }}}^k\Vert \le 1$ for all $k \in \{1, \ldots , K\}$.

By definition,

$$\begin{aligned} \varPsi ^l \ge \min _{1 \le t \le l-1} \max _{1 \le k \le K} \sum _{i \in {\mathscr {M}}} {{{\bar{\lambda }}}_{i}^k} \, g_i(x^t). \end{aligned}$$

Computing the limit when l goes to infinity, we obtain

$$\begin{aligned} 0 \ge \inf _{1 \le t} \max _{1 \le k \le K} \sum _{i \in {\mathscr {M}}} {{{\bar{\lambda }}}_{i}^k} \, g_i(x^t). \end{aligned}$$

Let ${{\bar{x}}}$ be $x^{t_0}$ if the infimum is achieved at $t_0$ or $x^*$ if the infimum is not achieved.

Then,

$$\begin{aligned} \max _{1 \le k \le K} \sum _{i \in {\mathscr {M}}} {{{\bar{\lambda }}}_{i}^k} \, g_i({{\bar{x}}}) \le 0. \end{aligned}$$

This last inequality implies that ${{\bar{x}}}$ is feasible for $S^{K}({{\bar{\lambda }}})$.

Hence,

$$\begin{aligned} OPT - \epsilon \le S^{K}({{\bar{\lambda }}}) \le c^{\mathsf {T}}{{\bar{x}}} \le \sup _{t \ge 1} S^{K}(\lambda ^t). \end{aligned}$$

Since $\epsilon > 0$ is arbitrary, we conclude that $\sup _{t \ge 1} S^{K}(\lambda ^t) \ge OPT$. $\square$

The proof of Theorem 2 shows that $(\varPsi ^t)_{t \in {\mathbb {N}}}$ always converges to zero. Therefore, the proof also establishes that Algorithm 2 terminates after a finite number of steps for any $\epsilon > 0$.

5.2 Computational enhancements

We now discuss computational enhancements additional to those discussed in Sect. 3.2 for improving the performance of Algorithm 2. Due to the increasing complexity of the master problem with each iteration, solving the MILP  (11) is for most instances the bottleneck of Algorithm 2. For this reason, most of our computational enhancements are devoted to reduce the computational effort spent in the master problem.

As in the case $K=1$, we also report techniques that we did not include in our final implementation.

5.2.1 Multiplier symmetry breaking

One difficulty of the K-surrogate dual is that (11) and (12) might contain many equivalent solutions. For example, any permutation $\pi$ of the set $\{1,\ldots ,K\}$ implies that the sub-problem $S^{K}(\lambda )$ with $\lambda = (\lambda ^1,\ldots ,\lambda ^K)$ is equivalent to $S^{K}(\lambda ^{\pi })$ with $\lambda ^\pi = (\lambda ^{\pi _1},\ldots ,\lambda ^{\pi _K})$. This can heavily impact the solution time of the master problem. We refer to [40] for an overview of symmetry in integer programming. Ideally, in order to break symmetry, we would like to impose $\lambda ^1 \succeq _{\text {lex}} \lambda ^2 \succeq _{\text {lex}} \ldots \succeq _{\text {lex}} \lambda ^K$ where $\succeq _{\text {lex}}$ indicates a lexicographical order. Such order can be imposed using linear constraints with additional binary variables and big-M constraints. However, this yields prohibitive running times. Two more efficient alternatives that only partially break symmetries, are as follows. First, the constraints

$$\begin{aligned} \lambda ^1_1 \ge \lambda ^2_1 \ge \ldots \ge \lambda ^K_1 \end{aligned}$$

(13)

enforce that $\lambda ^1,\ldots ,\lambda ^K$ are sorted with respect to the first component. The drawback of this sorting is that if $\lambda ^k_1 = 0$ for all $k \in \{1,\ldots ,K\}$, then (13) does not break any of the symmetry of (12). Our second idea for breaking symmetry is to use

$$\begin{aligned} \begin{aligned} \lambda ^{j}_j&\ge \lambda _{j}^k&\text { for all }j \in \{1,\ldots ,K-1\} \text { for all }k \in \{j+1,\ldots ,K\}. \end{aligned} \end{aligned}$$

(14)

In our experiments, we observed that slightly better dual bounds could be computed when using (13) instead of (14). However, the overall impact was not significant, and we decided to not include this in our final implementation.

5.2.2 Early stopping of the master problem

Solving (12) to optimality in every iteration of Algorithm 2 is computationally expensive for $K\ge 2$. On one hand, the true optimal value of $\varPsi$ is needed to decide whether the algorithm terminated. On the other hand, to ensure progress of the algorithm it is enough to only compute a feasible point $(\varPsi ,\lambda ^1,\ldots ,\lambda ^K)$ of (12) with $\varPsi > 0$. We balance these two opposing forces with the following early stopping method.

While solving (12), we have access to both a valid dual bound $\varPsi _{d}$ and primal bound $\varPsi _{p}$ such that the optimal $\varPsi$ is contained in $[\varPsi _p,\varPsi _d]$. Note that the primal bound can be assumed to be nonnegative as the vector of zeros is always feasible for (12). Let $\varPsi ^t_d$ and $\varPsi ^t_p$ be the primal and dual bounds obtained from the master problem in iteration t of Algorithm 2. We stop the master problem in iteration $t+1$ as soon as $\varPsi ^{t+1}_p \ge \alpha \varPsi ^t_d$ holds for a fixed $\alpha \in (0,1]$. The parameter $\alpha$ controls the trade-off between proving a good dual bound $\varPsi ^{t+1}_d$ and saving time for solving the master problem. On the one hand, $\alpha = 1$ implies

$$\begin{aligned} \varPsi ^{t+1}_p \ge \alpha \varPsi ^{t}_d \ge \alpha \varPsi ^{t+1}_d = \varPsi ^{t+1}_d , \end{aligned}$$

which can only be true if $\varPsi ^{t+1}_p = \varPsi ^{t+1}_d$ holds. This equality proves optimality of the master problem in iteration $t+1$. On the other hand, setting $\alpha$ close to zero means that we would stop as soon as a non-trivial feasible solution to the master problem has been found. In our experiments, we observed that setting $\alpha$ to 0.2 performs well.

5.2.3 Constraint filtering

Another potential way of alleviating the computational burden of solving the master problem, is to reduce the set of nonlinear constraints to only those that are needed for a good quality solution of (8). Of course, this set of constraints is unknown in advance and challenging to compute because of the nonconvexity of the MINLP.

We tested different heuristics to preselect nonlinear constraints. We used the violation of the constraints with respect to the LP, MILP, and convex NLP relaxation of the MINLP, as measures of “importance” of nonlinear constraints. We also used the connectivity of nonlinear constraints in the variable-constraint graph¹ for discarding some constraints. Unfortunately, we could not identify a good filtering rule that results in strong bounds for (8).

However, we were able to find a way of reducing the number of constraints considered in the master problem without imposing a strong a-priori filter: an adaptive filtering, which we call support stabilization. We specify this next.

5.2.4 Support stabilization

Direct implementations of Benders-based algorithms, much like column generation approaches, are known to suffer from convergence issues. Deriving “stabilization” techniques that can avoid oscillations of the $\lambda$ variables and tailing-off effects, among others, are a common goal for improving performance, see, e.g., [4, 16, 60].

We developed a support stabilization technique to address the exponential increase in complexity of the master problem (12) and to prevent the oscillations of the $\lambda$ variables. Once Algorithm 2 finds a multiplier vector that improves the overall dual bound, we restrict the support to that of the improving dual multiplier. This restricts the search space and drastically improves solution times. Once stalling is detected (which corresponds to finding a local optimum of (8)), we remove the support restriction until another multiplier vector that improves the dual bound is found. This technique not only improves solution times, but also leads to better bounds on (8) in fewer iterations.

5.2.5 Trust-region stabilization

While the previous stabilization alleviates some of the computational burden in the master problem, the non-zero entries of the $\lambda$ vectors can (and do, in practice) vary significantly from iteration to iteration. To remedy this, we incorporated a classic stabilization technique: a box trust-region stabilization, see [14]. Given a reference solution $({\hat{\lambda }}^1, \ldots , {\hat{\lambda }}^k)$, we impose the following constraint in (12)

$$\begin{aligned} \Vert (\lambda ^1, \ldots , \lambda ^k) - ({\hat{\lambda }}^1, \ldots , {\hat{\lambda }}^k) \Vert _\infty \le \delta \end{aligned}$$

for some parameter $\delta$. This prevents the $\lambda$ variables from oscillating excessively. In addition, by removing the trust-region when stalling is detected, we are able to preserve the convergence guarantees of Theorem 2. In our implementation, we maintain a fixed $({\hat{\lambda }}^1, \ldots , {\hat{\lambda }}^k)$ until we obtain a bound improvement or the algorithm stalls. When any of this happens, we remove the box and compute a new $({\hat{\lambda }}^1, \ldots , {\hat{\lambda }}^k)$ with (12) without any stabilization added.

Remark 3

We also tested another stabilization technique inspired by column generation’s smoothing by [65] and [47]. Let $\lambda ^{best}$ be the best found primal solution so far and let $\lambda ^{new}$ be the solution of the current master problem. Instead of using $\lambda ^{new}$ as a new multiplier vector, we choose a convex combination between $\lambda ^{best}$ and $\lambda ^{new}$.

While this stabilization technique improved the performance of Algorithm 2 with respect to the algorithm with no stabilization, it performed significantly worse than the trust-region stabilization. Therefore, we did not include it in our final implementation.

6 Computational experiments

In this section, we present a computational study of the classic and generalized surrogate duality on publicly available instances of the MINLPLib [42]. We conduct three main experiments to answer the following questions:

• 1. ROOTGAP: How much of the root gap with respect to the MILP relaxation can be closed by using the K-surrogate dual?

• 2. BENDERS: How much do the ideas of Sect. 5 improve the performance of Algorithm 2?

• 3. DUALBOUND: Can Algorithm 2 improve on the dual bounds obtained by the MINLP solver SCIP?

Our ideas are embedded in the MINLP solver SCIP [55]. We refer to [1, 63, 64] for an overview of the general solving algorithm and MINLP features of SCIP.

6.1 Experimental setup

In all experiments, Algorithm 2 is called after the root node has been completely processed by SCIP. All generated and initial linear inequalities are added to $S_\lambda$.

For the ROOTGAP experiment, we run Algorithm 2 for one hour for each choice of $K \in \{1,2,3\}$. To measure the improvement in using $K+1$ instead of K, we use the best found aggregation vector of K as an initial point for $K+1$.

In the BENDERS experiment we focus on $K=3$ and do not start with an initial point for the aggregation vector. This allows us to better analyze the impact of each proposed enhancement. We compare the following settings:

• DEFAULT: Algorithm 2 with all enhancements described in Sects. 3.2 and 5.2.

• PLAIN: Plain version of Algorithm 2 with no enhancement.

• NOSTAB: Same as DEFAULT but without using the trust-region of Sect. 5.2.5 and support stabilization of Sect. 5.2.4.

• NOSUPP: Same as DEFAULT but without using the support stabilization.

• NOEARLY: Same as DEFAULT but without using early termination for the master problem, described in Sect. 5.2.2.

Each of the five settings uses a time limit of one hour.

Finally, in the DUALBOUND experiment we evaluate how much the dual bounds obtained by SCIP can be improved by Algorithm 2. First, we collect the dual bounds for all instances that could not be solved by SCIP within three hours. Afterward, we apply Algorithm 2 for $K=3$, a time limit of three hours, and set a target dual bound (see Sect. 3.2.3) of

$$\begin{aligned} D + (P-D) \cdot 0.2, \end{aligned}$$

where D is the dual bound obtained by default SCIP and P be the best known primal bound reported in the MINLPLib. This means that we aim for a gap closed reduction of at least 20% and early stop each sub-problem in Algorithm 2 that will provably lead to a smaller reduction.

During all three experiments, we use a gap limit of $10^{-4}$ for each sub-problem of Algorithm 2. Additionally, we chose a dual feasibility tolerance of $10^{-8}$ (SCIP ’s default is $10^{-7}$) and a primal feasibility tolerance of $10^{-7}$ (SCIP ’s default is $10^{-6}$).

Stabilization details The trust-region and support stabilization have been implemented as follows. Both stabilization methods are applied once an improving aggregation $\lambda ^*$ could be found. Each entry $\lambda _i$ with $\lambda _i^* = 0$ is fixed to zero. Otherwise, the domain of $\lambda _i$ is restricted to the interval

$$\begin{aligned} \left[ \max \{0,\lambda _i^* - 0.1\},\min \{1,\lambda _i^* + 0.1\}\right] . \end{aligned}$$

Once a new improving solution has been found, we update the trust region accordingly. We remove the trust region and support stabilization in case no improving solution could be found for 20 iterations.

Test set We used the publicly available instances of the MINLPLib [42], which at time of the experiments contained 1683 instances. We selected the instances that were available in OSiL format and consisted of nonlinear expressions that could be handled by SCIP, in total 1671 instances.

Gap closed We use the gap closed in order to compare dual bounds. Let $d_1 \in {\mathbb {R}}$ and $d_2 \in {\mathbb {R}}$ be two dual bounds for (1) and $p \in {\mathbb {R}}$ a reference primal bound. The gap closed improvement is measured by the function $GC: {\mathbb {R}}^3 \rightarrow [-1,1]$ defined as

$$\begin{aligned} GC(p,d_1,d_2) := {\left\{ \begin{array}{ll} 0, &{} \text { if } d_1 = d_2 \\ +1 - \frac{p - d_1}{p - d_2}, &{} \text { if } d_1 > d_2 \\ -1 + \frac{p - d_2}{p - d_1}, &{} \text { if } d_1 < d_2 \end{array}\right. }. \end{aligned}$$

Performance evaluation To evaluate algorithmic performance we use the shifted geometric means, which provide a measure for relative differences. The shifted geometric mean of values $v_1, \ldots , v_N \ge 0$ with shift $s \ge 0$ is defined as

$$\begin{aligned} \left( \prod _{i=1}^N (v_i + s) \right) ^{1/N} - s. \end{aligned}$$

This measure avoids results being dominated by outliers with large absolute values, and also avoids an over-representation of differences among very small values. See also the discussion in [1, 2, 29]. As shift values we use 10 seconds for averaging over running time and $5\%$ for averaging over gap closed values.

Hardware and software The experiments were performed on a cluster of 64bit Intel Xeon X5672 CPUs at 3.2 GHz with 12 MB cache and 48 GB main memory. In order to safeguard against a potential mutual slowdown of parallel processes, we ran only one job per node at a time. We used a development version of SCIP with CPLEX  12.8.0.0 as LP  solver [31], the graph automorphism package bliss  0.73 [33] for detecting MILP symmetry, the algorithmic differentiation code CppAD  20180000.0 [12] and Ipopt  3.12.11 with Mumps  4.10.0 [44] as NLP solver [13, 66].

6.2 Computational results

ROOTGAP Experiment From all instances of MINLPLib, we filter those for which SCIP ’s MILP relaxation proves optimality in the root node, no primal solution is known, or SCIP aborted due to numerical issues in the LP solver. This leaves $633$ instances for the ROOTGAP experiment.

Figure 6 visualizes the achieved gap closed values via scatter plots. The plots show that for the majority of the instances we can close significantly more gap than the MILP relaxation. There are $173$ instances for which $K=2$ closes at least $1\%$ more gap than $K=1$, and even more gap can be closed using $K=3$. There are $21$ instances for which $K=1$ could not close any gap, but $K=2$ could close some. On $11$ additional instances $K=3$ could close gap, which was not possible with $K=2$. Finally, comparing $K=2$ and $K=3$ shows that on $105$ instances $K=3$ could close at least $1\%$ more gap than $K=2$. Interestingly, for most of these instances $K=2$ could already close at least $50\%$ of the root gap.

Aggregated results are reported in Table 1 and we refer to the supplementary material for detailed instance-wise results. First, we observe an average gap reduction of $18.4\%$ for $K=1$, $21.4\%$ for $K=2$, and $23.4\%$ for $K=3$, respectively. The same tendency is true when considering groups of instances that are defined by a bound on the minimum number of nonlinear constraints. For example, for the $391$ instances with at least 20 nonlinear constraints after preprocessing, $K=2$ and $K=3$ close $1.6\%$ and $2.8\%$ more gap than $K=1$, respectively. Table 1 also reports results when filtering out the $164$ instances for which less than $1\%$ gap was closed by Algorithm 2. We consider these instances unaffected. On the $469$ affected instances we close on average up to $46.9\%$ of the gap, and we see that $K=3$ closes $4.7\%$ more gap than $K=2$ and $11.9\%$ more than $K=1$.

These results show that using surrogate relaxations has a significant impact on reducing the root gap. Additionally, using the generalized surrogate dual for $K=2$ and $K=3$ reduces significantly more gap than the classic surrogate dual.

Fig. 6

Scatter plot comparing the root gap closed values of the ROOTGAP experiment comparing $(K=1,K=2)$, $(K=1,K=3)$, and $(K=2,K=3)$. For example, each point $(x,y) \in [0,1]^2$ in the top left plot corresponds to an instance for which $100x\%$ of the gap is closed by $K=1$ and $100y\%$ closed by $K=2$

Table 1 Aggregated results for the ROOTGAP experiment

BENDERS Experiment Table 2 reports aggregated results for the BENDERS experiment. We refer to the supplementary material for detailed instance-wise results.

First, we observe that the DEFAULT performs significantly better than PLAIN. Table 2 shows that on $100$ of the $457{}$ affected instances DEFAULT closes at least 1% more gap than PLAIN. Only on $36$ instances PLAIN closes more gap, but over all instances it closes on average $13.1\%$ less gap than DEFAULT. On instances with a larger number of nonlinear constraints, DEFAULT performs even better: on the $107$ instances with at least 50 nonlinear constraints, DEFAULT computes $35$ times a better and only $1$ time a worse dual bound than PLAIN. For these $107$ instances, PLAIN closes $25.8$% less gap than DEFAULT. Interestingly, there are instances for which PLAIN could not close any gap but DEFAULT could. There is no instance for which the opposite is true.

Next, we analyze which components of Algorithm 2 are responsible for the significantly better performance of DEFAULT compared to PLAIN. Table 2 shows that DEFAULT dominates NOSTAB, NOSUPP, and NOEARLY with respect to the average gap closed and the difference between the number of wins and the number of losses on each subset of the instances. The most important component is the early termination of the master problem. By disabling this feature, Algorithm 2 closes $11.8$% less gap on all instances and even $23.7$% on those which have at least 50 nonlinear constraints.

Regarding both stabilization techniques, Table 2 seems to suggest that they are not crucial. However, both techniques are important to exploit the $\lambda$ space in a more structured way, which help us to find better aggregation vectors faster. To visualize this, we use the instance genpooling_lee1 from Example 4. Figure 7 shows the achieved dual bounds in each iteration of Algorithm 2 for DEFAULT and NOSTAB. Both settings run with an iteration limit of 600. First, we observe that the achieved dual bound of $-4775.26$ with DEFAULT is significantly better than the dual bound of $-5006.95$ when using NOSTAB. The best dual bound is found after 97 iterations by DEFAULT and after 494 iterations with NOSTAB. The steepest improvement in the dual bounds for DEFAULT is seen between iterations 62 and 112, where the support was fixed and the trust region was enforced. After iteration 112 the algorithm removed both stabilizers and no further dual bound improvement could be found. In the iterations where no stabilization is used by DEFAULT, we do not observe any pattern indicating which of the two settings finds a better dual bound—the behavior seems rather random. This randomness, and the large time limit used, might explain the similar results for DEFAULT and NOSTAB of Table 2.

Table 2 Aggregated results for the BENDERS experiment

Fig. 7

Comparison of the achieved dual bounds and the obtained aggregation vectors during Algorithm 2 for DEFAULT (left) and NOSTAB (right) on genpooling_lee1 using $K=3$. The red dashed curve shows the best found dual bound so far, whereas the blue curve shows the computed dual bound in every iteration (color figure online)

DUALBOUND Experiment For this experiment, we include all instances which could not be solved by SCIP with default settings within three hours, have a final gap of at least ten percent, terminate without an error, and contain at least four nonlinear constraints. This leaves in total $209$ instances for the DUALBOUND experiment. The supplementary material reports detailed results on the subset of instances for which the Algorithm 2 was able to improve on the bound obtained by SCIP with default settings, which was the case for $53$ of the $209$ instances. On these, the average gap of $284.3$% for SCIP with default settings could be reduced to an average gap of $142.8$%.

Two notable subsets of instances are the challenging polygon* instances and four of the facloc* instances. In these, Algorithm 2 finds better bounds than the reported best known dual bounds from the MINLPLib, as shown in Table 3.

Table 3 Dual bounds computed by SCIP, Algorithm 2, and the best known dual bounds reported in the MINLPLib for all polygon* and four facloc* instances

7 Surrogate duality during the tree search

While we obtain strong dual bounds with Algorithm 2, complex instances still require branching in order to solve them to provable optimality. In this section, we show a promising technique to incorporate Algorithm 2 into spatial branch and bound. We discuss this technique in two instances of MINLPLib, while a full implementation is subject of future work.

Since Algorithm 2 is too costly to be used in every node of a branch-and-bound tree, our technique focuses on extracting information of a single execution of Algorithm 2 in the root node, and reuses this information throughout the tree.

Let $\varLambda := \{\lambda _1, \ldots , \lambda _L\} \subseteq {\mathbb {R}}^{K m}$ be the set of aggregation vectors that have been computed during Algorithm 2 in the root node, and that imply a tighter dual bound than the MILP relaxation. Instead of using Algorithm 2 in a node v, we select an aggregation vector $\lambda$ from $\varLambda$ and solve $S^{K}_v(\lambda )$, which is equal to $S^{K}(\lambda )$ except that the global linear relaxation is replaced with a locally valid linear relaxation for v. If $S^{K}_v(\lambda )$ results in a better dual bound than the local MILP relaxation, i.e., $S^{K}_v(0)$, then we skip the remaining aggregation vectors in $\varLambda$ and continue with the tree search. If the dual bound does not improve, then we discard $\lambda$ in the sub-tree with root v.

The intuition behind discarding aggregations as we search down the tree is twofold. First, since the aggregations are computed in the root node, their ability to provide good dual bounds is expected to deteriorate with the increasing depth of an explored node. Second, we would like to alleviate the computational load of checking for too many aggregations as the branch-and-bound tree-size increases. The idea is stated in Algorithm 3; the algorithm assumes $C_r = \varLambda$ for the root node r. In Fig. 8 we illustrate Algorithm 3 for the instance himmel16.

Fig. 8

Visualization of Algorithm 3 for the instance himmel16 of the MINLPLib. The size of the aggregation pool has been limited to three and we used bread-first-search as the node selection strategy. The colors determine $|C_v|$ at each node v: green for three, blue for two, orange for one, white for zero aggregations. Red square nodes could be pruned by Algorithm 3, i.e., the proven dual bound exceeds the value of an incumbent solution (color figure online)

In principle, Algorithm 3 can lead to stronger dual bounds in local nodes of the branch-and-bound tree, which could result in a smaller tree. However, for the challenging instances of the DUALBOUND experiment we observed that solving $S^{K}_v(\lambda )$ is too costly and almost always runs into the time limit. In these cases, Algorithm 3 was not able to improve the dual bound. An exception to this behavior is instance multiplants_mtg1c², which contains 28 nonlinear constraints, 193 continuous variables, and 104 integer variables. SCIP with default settings proves a dual bound of $-4096.04$. This bound is improved by Algorithm 2 to $-3161.13$, and Algorithm 3 can further improve it to $-2935.58$. This last bound improvement happens in the early stages of the tree search; there were only seven nodes for which a better local dual bound was found, and the aggregation candidates were quickly filtered out. After this, SCIP was not able to improve the dual bound any further. In total, SCIP processed 491860 nodes.

8 Summary and future work

In this article, we studied theoretical and computational aspects of surrogate relaxations for MINLPs. We developed the first algorithm to solve a generalization of the surrogate dual problem that allows multiple aggregations of nonlinear constraints. We also proposed computational enhancements and discussed a first idea on how to exploit surrogate duality in a spatial branch-and-bound solver.

Our extensive computational study on the heterogeneous set of publicly available instances of the MINLPLib shows that surrogate duality can lead to significantly better dual bounds than using SCIP with default settings. Additionally, our experiments show that the presented computational enhancements are important to obtain good dual bounds for problems with a large number of nonlinear constraints. Finally, our tree experiments show that using the result of Algorithm 2 during the tree search can lead to significantly better dual bounds than solving MINLPs with standard spatial branch and bound, although in this latter direction the research is still preliminary.

There are two open questions related to generalized surrogate duality we would like to highlight. First, consider the case that each constraint of (1) is quadratic, i.e., $g_i(x) = x^{\mathsf {T}}Q_i x + q_i^{\mathsf {T}}x + b_i$ for each $i \in {\mathscr {M}}$. Adding the constraints $\sum _{i \in {\mathscr {M}}} \lambda ^k_i Q_i \succeq 0$ for all $k \in \{1,\ldots ,K\}$ to the master problem (12) enforces that each sub-problem is a convex mixed-integer quadratically-constrained program. This increases the complexity of the master problem but, at the same time, reduces the complexity of the sub-problems. It would be interesting to understand this trade-off computationally. Second, it remains an open question how a pure surrogate-based spatial branch-and-bound approach could perform in practice. Warm-start strategies based on the generated points ${\mathscr {X}}$ of a parent node and branching rules based on surrogates relaxations are some examples of tools that could be developed in order to successfully incorporate surrogate duality into branch and bound.