Learning (k,l)-context-sensitive probabilistic grammars with nonparametric Bayesian approach

Abstract

Inferring formal grammars with nonparametric Bayesian approach is one of the most powerful approach for achieving high accuracy from unsupervised data. In this paper, mildly-context-sensitive probabilities, called (k, l)-context-sensitive probabilities, are defined on context-free grammars (CFGs). Inferring CFGs where the probabilities of rules are identified from contexts can be seen as a kind of dual approaches for distributional learning, in which the contexts characterize the substrings. We can handle the data sparsity for the context-sensitive probabilities by the smoothing effect of the hierarchical nonparametric Bayesian models such as Pitman–Yor processes (PYPs). We define the hierarchy of PYPs naturally by augmenting the infinite PCFGs. The blocked Gibbs sampling is known to be effective for inferring PCFGs. We show that, by modifying the inside probabilities, the blocked Gibbs sampling is able to be applied to the (k, l)-context-sensitive probabilistic grammars. At the same time, we show that the time complexity for (k, l)-context-sensitive probabilities of a CFG is $O(|V|^{l+3}|w|^3)$ for each sentence w, where V is a set of nonterminals. Since it is computationally too expensive to iterate sufficient times especially when |V| is not small, some alternative sampling algorithms are required. Therefore, we propose a new sampling method called composite sampling, with which the sampling procedure is separated into sub-procedures for nonterminals and for derivation trees. Finally, we demonstrate that the inferred (k, 0)-context-sensitive probabilistic grammars can achieve lower perplexities than other probabilistic language models such as PCFGs, n-grams, and HMMs.

1 Introduction

In recent years, while machine learning methods such as neural networks have made remarkable progress, methods for learning and acquiring grammars as well as the grammatical structure of the sentences from only plaintext data have not been greatly developed.

In the theoretical framework of grammar acquisition, methods that divide sentences into contexts and substrings, and then construct grammars by grouping or aligning their common parts are generally called distributional learning. The idea of distributional learning has been studied and implemented in deterministic systems (van Zaanen, 2000) and generative models (Klein and Manning, 2002).

In recent studies, theoretical aspects of distributional learning have been developed in deterministic learning frameworks such as learning in the limit and the Minimally Adequate Teacher (MAT) model (Angluin, 1987). A series of subclasses of context-free grammars (CFGs) have been shown to be learnable using distributional approaches. Methods of distributional learning are mainly divided into primal and dual approaches (Yoshinaka, 2011, 2012). Roughly speaking, the difference between the primal and dual approaches is that the nonterminal symbols in the inferred CFGs are represented by substrings or contexts, respectively. A subclass of CFGs is said to have the q-FKP (Finite Kernel Property) if their nonterminals are characterized by q contexts. CFGs that have the q-FKP can be learned by primal approaches, in which nonterminals are obtained by grouping contexts that have similar substrings. On the other hand, a subclass of CFGs is said to have the q-FCP (Finite Context Property) if their nonterminals are characterized by q substrings. CFGs that have the q-FCP can be learned by dual approaches, in which nonterminals are obtained by grouping substrings that have similar contexts. Both approaches and properties are quite symmetric and define parallel hierarchies of language classes.

In the context of probabilistic learning, several positive theoretical results have been obtained for distributional approaches. Clark (2006) showed that non-terminally separated (NTS) languages are PAC (probably approximately correct)-learnable from positive samples if the target distributions satisfy properties represented by several parameters, such as $\mu$-distinguishability. All NTS languages are able to be generated from CFGs that have the 1-FKP.

Other fundamental classes that can be learned by primal and dual approaches have also been shown to be learnable in a PAC sense (Shibata and Yoshinaka, 2013). These results are useful steps from the viewpoint of understanding the learnable subclasses of CFGs, but their algorithms are not efficient in terms of required amount of data if the goal is to learn grammars with high accuracy from real-world data. In this paper, we apply nonparametric Bayesian methods to learning CFGs following an idea of dual approaches for distributional learning.

Particularly, inspired by the characteristic idea of distributional learning, which is to build up CFGs from the bottom by grouping similar patterns of contexts and/or substrings, we are interested in defining stochastic models on CFGs which has more flexible probabilities than probabilistic context-free grammars (PCFGs) have. PCFGs have drawbacks in capturing natural mutual dependencies between contexts and substrings; it is impossible for PCFGs to capture dependency between a context and a substring when a nonterminal that generates the substring is given. PCFGs assume that each rule is stochastically independent. However, mutual dependencies beyond the nonterminal symbol usually exist and are not ignorable in actual natural languages. Our aim is to separate subtle mutual dependencies between contexts and substrings from definition of nonterminal symbols. In this paper, (k,l)-Context-Sensitive Probabilistic Grammars, which allow contexts and substrings to have mutual dependencies beyond nonterminal symbols, is proposed (see Sect. 8.1 for details). From the viewpoint of language classes, the class of (k, l)-context-sensitive grammars is equivalent to the class of CFGs because the length of contexts ($k+l$) is finite; using the local context can yield sparser grammars which are a better fit to the data than generic CFGs.”

While various definitions for (k,l)-context-sensitive probabilities over substrings are possible, we adopt a nonparametric Bayesian model called Pitman–Yor Process (PYP) to define (k,l)-context-sensitive probabilities. Nonparametric Bayesian inferences have been applied to various probabilistic models such as n-gram models where n can be infinite (Teh, 2006b) and PCFGs where the nonterminals can be infinite (Liang et al., 2007). The Details of the definition of the generative model with PYPs are described in Sect. 4.3.

In Sect. 2, we define a derivation as a sequence of elements in $(\Sigma \cup V)^*$, where $\Sigma$ and V respectively denote the set of terminal symbols and the set of nonterminal symbols of a CFG. We also define derivation trees and (k, l)-context-sensitive probabilities and show several lemmas which are used in the later sections. In Sects.  3 and 4, a nested structure of prior distributions for (k, l)-context-sensitive probabilities is introduced using hierarchical PYPs. The intuitive reason why the definition of the hierarchical structure of prior distributions is important is that it implies the way of smoothing and thus has a large influence on posterior probabilities or nonparametric estimates especially when the number of occurrences is zero. In Sect. 5, we describe how CFGs with (k, l)-context-sensitive probabilities are sampled from the posterior distribution. The blocked sampling algorithm for CFGs with (k, l)-context-sensitive probabilities and its computational cost are shown. In Sect. 6, to reduce the computational cost of the blocked sampling, composite sampling algorithms are proposed. Two concrete algorithms for composite sampling and their computational cost are shown. In Sect. 7, through experiments with real-wold data, we show that CFGs with (k, 0)-context-sensitive probabilities learned by a composite sampling algorithm can achieve higher accuracy than the smoothing n-gram model called modified kneser–Ney (MKN), which is known to give high accuracy. The experiments are performed only for $l=0$ because of the exponential increase of the computational cost regarding l (as shown in Theorem 1).

2 Preliminaries: operations and trees for derivations

2.1 Operations for derivations

A CFG is a tuple $G=\left\langle \Sigma ,V,R,S \right\rangle$, where $\Sigma$ is the set of terminal symbols, V is the set of nonterminal symbols, R is the set of production rules, and S is the initial symbol. We let $A,B,\ldots$ denote nonterminals, $a,b,\ldots$ denote terminals, $x,y,\ldots$ denote elements in $\Sigma ^*$, $\alpha ,\beta ,\ldots$ denote elements in $(\Sigma \cup V)^*$, and $\lambda$ denote the empty string in this paper.

We assume CFGs to be Chomsky normal form (CNF) in this study; every rule has a form in either $A\rightarrow a$ or $A\rightarrow BC$. We call the form in $A\rightarrow a$ type-0 and the form in $A\rightarrow BC$ type-2.

We call a binary relation $\Rightarrow _G$ one step derivation when $\alpha \Rightarrow _G \beta$ iff $\alpha = \alpha ' A \alpha ''$, $\beta = \alpha ' \gamma \alpha ''$ for some rule $A \rightarrow \gamma \in R$ . If a grammar G is clearly identified from the context, we omit G from $\Rightarrow _G$. If we have $\alpha \Rightarrow \beta$ with a rule $r \in R$, we write $\alpha \Rightarrow ^r \beta$. In this paper, we define a derivation as a sequence of elements in $(\Sigma \cup V)^*$ as follows.

Definition 1

(derivation) A sequence $(\alpha _1, \ldots , \alpha _k)$ is called a derivation iff $\alpha _i \Rightarrow \alpha _{i+1}$ for all $i \in [1, k-1]$ and referred as $\alpha _1\Rightarrow \cdots \Rightarrow \alpha _k$.

A derivation $\alpha _1 \Rightarrow \cdots \Rightarrow \alpha _k$ is called a left-most derivation iff $\alpha _i = x A \alpha '_i$, $\alpha _{i+1} = x \gamma \alpha '_i$ for some $A\rightarrow \gamma \in R$ and $x \in \Sigma ^*$. If $S \Rightarrow ^* \alpha$, $\alpha$ is called a sentential form. A sentential form $\alpha$ is called a sentence if $\alpha \in \Sigma ^*$.

Definition 2

(set of possible derivations) We call $[\alpha {\mathop {\Rightarrow }\limits ^{*}}\beta ]$ the set of the possible left-most derivations from $\alpha$ to $\beta$:

$$\begin{aligned}{}[\alpha {\mathop {\Rightarrow }\limits ^{*}}\beta ] = \{ (\gamma _1,\ldots , \gamma _m)\ |&\forall m \in \mathbb {N}, \gamma _1=\alpha , \gamma _m = \beta \text {, and } \gamma _1 \Rightarrow \cdots \Rightarrow \gamma _{m} \text { is a }\\&\text {left-most derivation} \} \end{aligned}$$

For example, suppose that G is in CNF whose rules are $R=\{S \rightarrow AA, A \rightarrow BC, A|B|C \rightarrow a \}$. Then,

$$\begin{aligned}{}[ S {\mathop {\Rightarrow }\limits ^{*}}aaa ] = \{(S, AA, BCA, aCA, aaA, aaa), (S, AA, aA, aBC, aaC, aaa) \}. \end{aligned}$$

In the following, we show a disjoint decomposition property (Lemma 1) with respect to the sets of the possible derivations. This lemma serves as a tool to ensure the correctness of the sampling algorithms (e.g., Algorithm 2) of derivation trees, which need to be distributed according to the (k, l)-context-sensitive probability. As we will see in Sect. 3, (k, l)-context-sensitive probabilities depend on the order of the steps of the derivation for each sentence. At each step of the derivation, the generation probability is determined up to the context around the head nonterminal. However, if the order of derivation changes, its context can also change. Thus, in this study, we restrict the order of derivations to the left-most one. Hereafter, we call ‘left-most derivation’ simply as ‘derivation’.

Definition 3

(concatenation of derivations) Let $d_1$ and $d_2$ be left-most derivations where $d_1 = (\alpha _1,\ldots , \alpha _m)$ and $d_2 = (B, \beta _2,\ldots , \beta _n)$ for some $m,n \in \mathbb {N}$. Suppose that $\alpha _m = xB\gamma$ for some x and $\gamma$. The concatenation of $d_1$ and $d_2$ is defined as :

$$\begin{aligned} d_1 \oplus d_2 {\mathop {=}\limits ^{\mathrm {def}}}(\alpha _1,\ldots , \alpha _m,\ x\beta _2 \gamma , \ldots , x\beta _n \gamma ). \end{aligned}$$

Note that $d_1 \oplus d_2$ is defined only if $\alpha _m$ includes B as the first nonterminal in itself.

Definition 4

(concatenation of sets of possible derivations) For $[\alpha {\mathop {\Rightarrow }\limits ^{*}}\alpha ']$ and $[B {\mathop {\Rightarrow }\limits ^{*}}\beta ]$, where $\alpha ' = xB\gamma$, the concatenation of them is defined as :

$$\begin{aligned}{}[\alpha {\mathop {\Rightarrow }\limits ^{*}}\alpha '] \otimes [B {\mathop {\Rightarrow }\limits ^{*}}\beta ] {\mathop {=}\limits ^{\mathrm {def}}}\{d_1 \oplus d_2\ |\ d_1 \in [\alpha {\mathop {\Rightarrow }\limits ^{*}}\alpha '], d_2 \in [B {\mathop {\Rightarrow }\limits ^{*}}\beta ] \}. \end{aligned}$$

For the case that $\alpha ' \ne xB\gamma$ for any x and $\gamma$, we define $[\alpha {\mathop {\Rightarrow }\limits ^{*}}\alpha '] \otimes [B {\mathop {\Rightarrow }\limits ^{*}}\beta ]$ as the empty set.

From the definition of the concatenation of derivations, we have the following fact:

Fact 1

$[\alpha {\mathop {\Rightarrow }\limits ^{*}}xB\gamma ] \otimes [B {\mathop {\Rightarrow }\limits ^{*}}\beta ] \subset [\alpha {\mathop {\Rightarrow }\limits ^{*}}x\beta \gamma ]$.

The equality does not necessarily hold for the Fact 1, because there can be another path from $\alpha$ to $x\beta \gamma$ except for being routed through $xB\gamma$. For example, suppose that the rules of G are $R=\{S \rightarrow AA, A \rightarrow AA, A \rightarrow a \}$ and think of a derivation $h = (S, AA, AAA, aAA, aaA, aaa)$. Then, we have $h \in [ S {\mathop {\Rightarrow }\limits ^{*}}aaa ]$. However, $[ S {\mathop {\Rightarrow }\limits ^{*}}aA ] = \{ (S, AA, aA) \}$ and aA does not appear in h. Thus $[ S {\mathop {\Rightarrow }\limits ^{*}}aA ] \otimes [ A {\mathop {\Rightarrow }\limits ^{*}}aa] \not = [ S {\mathop {\Rightarrow }\limits ^{*}}aaa]$.

Lemma 1

(decomposition of sets of possible derivations) Let G be a CFG in CNF. For every $A \in V$ and $w \in \Sigma ^{\ge 2}$, we have

$$\begin{aligned}{}[A{\mathop {\Rightarrow }\limits ^{*}}w] = \bigsqcup _{\begin{array}{c} B,C \in V \\ u,v \in \Sigma ^+ s.t. w=uv \end{array}} [A{\mathop {\Rightarrow }\limits ^{*}}BC] \otimes [B{\mathop {\Rightarrow }\limits ^{*}}u] \otimes [C{\mathop {\Rightarrow }\limits ^{*}}v], \end{aligned}$$

where $\bigsqcup$ represents the disjoint union.

Proof

From Fact 1, we have $[A{\mathop {\Rightarrow }\limits ^{*}}BC] \otimes [B{\mathop {\Rightarrow }\limits ^{*}}u] \otimes [C{\mathop {\Rightarrow }\limits ^{*}}v] \subset [A{\mathop {\Rightarrow }\limits ^{*}}uv]$. In addition, all $[A\Rightarrow BC] \otimes [B{\mathop {\Rightarrow }\limits ^{*}}u] \otimes [C{\mathop {\Rightarrow }\limits ^{*}}v]$ have clearly no intersection since if B or C is different, the first rule of the derivation is different and if u is different, some rule in the derivation from B to u is different. Thus what remains is to show that (1) for every $d\in [A{\mathop {\Rightarrow }\limits ^{*}}w]$, we have $d\in [A\Rightarrow BC] \otimes [B{\mathop {\Rightarrow }\limits ^{*}}u] \otimes [C{\mathop {\Rightarrow }\limits ^{*}}v]$ for some B, C, u, v.

Suppose that $d = (A, \alpha _1,\ldots , \alpha _m) \in [A{\mathop {\Rightarrow }\limits ^{*}}w]$ where $\alpha _m = w$. To yield a substring with length of more than 1, the first rule of a derivation has to be a type-2 rule, that is $\alpha _1 = BC$ for some B, C. Since B yields some u which is a prefix of w, we have $\alpha _{i} = \beta _{i} C$ for each $i \in [2,k]$ for some $k < m$, where $B \Rightarrow \beta _2 \Rightarrow \cdots \Rightarrow \beta _{k-1} \Rightarrow u$. Then, since C yields $v = u^{-1} w$, we have $\alpha _{i} = u \gamma _i$ for each $i \in [k,m]$, where $C \Rightarrow \gamma _{k+1} \Rightarrow \cdots \Rightarrow \gamma _{m-1} \Rightarrow v$. Here, for $w = uv \in \Sigma ^*$, we define $u^{-1}w = v$, i.e., $u^{-1}w$ denotes removing the prefix u from w.

Let $d_1 = (A, BC)$, $d_2 = (B, \beta _2, \ldots , \beta _{k-1}, u)$ and $d_3 = (C, \gamma _{k+1}, \ldots , \gamma _{m-1}, v)$. We have $d_1 \in [A {\mathop {\Rightarrow }\limits ^{*}}BC]$, $d_2 \in [B {\mathop {\Rightarrow }\limits ^{*}}u]$, $d_3 \in [C {\mathop {\Rightarrow }\limits ^{*}}v]$ and $d = d_1 \oplus d_2 \oplus d_3$, that is $d \in [A{\mathop {\Rightarrow }\limits ^{*}}BC] \otimes [B{\mathop {\Rightarrow }\limits ^{*}}u] \otimes [C{\mathop {\Rightarrow }\limits ^{*}}v]$. $\square$

As we will discuss in Sect. 5, in order to sample derivation trees faster, we propose a method to separate the calculation for tree shapes from the calculation for nonterminals. To do so, we have to consider the case that the nonterminals that occur in the derivations are restricted. Suppose that some condition $\mathcal {C}$ is given for derivations. we let $[\gamma \Rightarrow ^{*|\mathcal {C}} \beta ]$ denote $\{ d \in [\gamma {\mathop {\Rightarrow }\limits ^{*}}\beta ] \ |\ d \text { satisfies } \mathcal {C} \}$. we call $[\gamma \Rightarrow ^{*|\mathcal {C}} \beta ]$ as the set of derivations restricted by $\mathcal {C}$ from $\gamma$ to $\beta$.

2.2 Derivation trees

We define derivation trees as follows.

Definition 5

(Derivation Tree) Let G be a CFG in CNF. An A-derivation tree of G for a substring u is defined as an ordered and labeled tree which satisfies:

• Labels of leaves are in $\Sigma$, those of internal nodes are in V and that of the root node is A.

• Each internal node o has either one leaf node or several internal nodes as its child nodes.

• If an internal node o has some ordered child nodes whose labels are $B_1,\ldots , B_m \in V$ in order, there is a production $C \rightarrow B_1 \ldots B_m \in R$ for some $C \in V$ ($m=1$ or 2 as G is in CNF). We call this as the corresponding rule of o.

• u equals the sequence obtained by concatenating all labels in the leaves in order.

We simply call u the yield of the A-derivation tree. We call an S-derivation tree a derivation tree simply. For a sentence w, we let $\mathcal {T}(w)$ denotes the set of derivation trees whose yield is w.

Let w(i, j) denote the substring of a sentence $w=a_1 \ldots a_m$ from the i-th letter to the j-th, i.e., $w(i,j) = a_i \ldots a_j$. Suppose that a derivation tree T for the sentence w is given. For each internal node o whose label is A, the sequence obtained by concatenating its children’s leaves is a substring of w. We call such substring as the yield of o. If $j < i$, we define $w(i,j) = \lambda$.

Let $I_{|w|}$ denote the set of intervals: $I_{|w|} = \{(i,j) \in \mathbb {N}^2 | 1\le i\le j \le |w|\}$. For each $(i,j) \in I_{|w|}$, a substring w(i, j) is called a constituent if w(i, j) is derived from one nonterminal and a distituent (Klein and Manning 2002) otherwise. If w(i, j) is a constituent, the internal node whose yield is w(i, j) is identified uniquely. We write $X(i,j)$ as the corresponding nonterminal of such node. Note that $X(1,|w|) = S$.

Fact 2

Let T be a derivation tree of G for w and G be in CNF. Suppose that w(i, j) is a constituent. If $i\ne j$, its corresponding rule equals $X(i,j) \rightarrow X(i,k)X(k+1, j)$ for some $k\in \mathbb {N}$ and $i \le k < j$ . If $i=j$, its corresponding rule equals $X(i,i) \rightarrow w(i,i)$.

A derivation tree T of w identifies the left-most derivation of w, which is represented by a sequence of rules $r_1, \ldots , r_m$.

Fact 3

Let T be a derivation tree of G for w and G is in CNF. Every sentential form in a left-most derivation of w corresponding to T has the form

$$\begin{aligned} w(1,j_0) X(i_1, j_1)\ldots X(i_k, j_k), \end{aligned}$$

where $0\le j_0 \le |w|$, $j_{a + 1} = i_{a+1}$ for all $a \in \{0,\ldots , k-1\}$ and $j_k = |w|$ for some $k \ge 0$.

There is a bijection between $[A{\mathop {\Rightarrow }\limits ^{*}}w]$ and the set of A-derivation trees whose yield is w.

2.3 Probabilistic CFGs and inside probabilities

Let G be a CFG $\left\langle \Sigma , V, R, S \right\rangle$, and $R_A$ be the set of all rules with A on the left-hand side. A Probabilistic CFG (PCFG) is a tuple $\left\langle G, P \right\rangle$, where P is a map $R \rightarrow [0,1]$ and satisfies for all $A \in V$, $\sum _{r \in R_A} P(r) = 1$.

Let $\left\langle G, P \right\rangle$ be a PCFG, and $d = \alpha _1 \Rightarrow ^{r_1} \cdots \Rightarrow ^{r_{k-1}} \alpha _k$ be a derivation for G. P(d) is defined by $P(r_1)\ldots P(r_{k-1})$. For the set of possible derivations $[\alpha {\mathop {\Rightarrow }\limits ^{*}}\beta ]$, we define $P([\alpha {\mathop {\Rightarrow }\limits ^{*}}\beta ])$ as $\sum _{d \in [\alpha {\mathop {\Rightarrow }\limits ^{*}}\beta ]} P(d)$.

The inside probability (Lari and Young, 1990) $P^{\mathrm {IN}}(A|i,j)$ for $w \in \Sigma ^*$ and $1\le i\le j \le |w|$ is defined as $P([A{\mathop {\Rightarrow }\limits ^{*}}w(i,j)])$. If G is in CNF, it follows from the row of total probability that for every $A \in V$ and $1\le i\le j \le |w|$,

• if $i\ne j$,

  $$\begin{aligned} P^{\mathrm {IN}}(A|i,j) = \sum _{A\rightarrow BC \in R_A} \sum _{k=i}^{j-1} P(A\rightarrow BC) P^{\mathrm {IN}}(B|i,k) P^{\mathrm {IN}}(C|k+1,j), \end{aligned}$$

• and if $i=j$, $P^{\mathrm {IN}}(A|i,i) = P(A\rightarrow w_i).$

3 (k,l)-context-sensitive probabilistic grammars

Suppose that a sentence w is yielded with the rules $r_1,\ldots , r_m$ in a CFG G.

$$\begin{aligned} S \Rightarrow ^{r_1} \alpha _1 \Rightarrow ^{r_2} \cdots \Rightarrow ^{r_m} \alpha _m = w \end{aligned}$$

In probabilistic CFGs, the probability of w with the above derivation is given by the product of the probabilities for all rules, $P(r_1)\cdots P(r_m)$. In order to make the probability assigned to a rule $A \rightarrow \alpha$ depend on contexts, naively, it appears to be appropriate if we define $P(A \rightarrow \alpha | (x,y) )$ for each context $(x,y) \in \Sigma ^* \times \Sigma ^*$ where $S{\mathop {\Rightarrow }\limits ^{*}}xAy$. However, since x and y are also yielded from some nonterminals, it is hard to define the probability for a derivation tree only by multiplying probabilities of rules defined above unless all rules are linear. Thus we have to consider probabilities where each rule is applied in each step in a derivation. With context-sensitive probabilities, different orders of derivation give different probabilities for a single derivation tree. For example, the two derivations $d_1: S \Rightarrow AB \Rightarrow aB \Rightarrow ab$ and $d_2: S \Rightarrow AB \Rightarrow Ab \Rightarrow ab$ have the same probability $P(S\rightarrow AB)P(A\rightarrow a)P(B\rightarrow b)$ in PCFG, but not in a CFG with context-sensitive probabilities:

$$\begin{aligned} \Pr (d_1)&= P(S\rightarrow AB| (\varepsilon , \varepsilon ))P(A\rightarrow a | (\varepsilon , B))P(B\rightarrow b | (a, \varepsilon )),\\ \Pr (d_2)&= P(S\rightarrow AB| (\varepsilon , \varepsilon ))P(A\rightarrow a | (\varepsilon , b))P(B\rightarrow b | (A, \varepsilon )). \end{aligned}$$

To make left contexts be always in $\Sigma ^*$, we assume that all the derivations are leftmost derivations in the following.

Definition 6

((k, l)-context-sensitive probabilities on rules) Let G be a CFG $\left\langle \Sigma , V, R, S \right\rangle$. Let $R_A$ be the set of all production rules with A on the left-hand side. For each $A \in V$, and each $(x, \alpha ) \in \Sigma ^{\le k} \times V^{\le l}$, we call a discrete probability distribution over $R_A$ given $(x, \alpha )$ as (k, l)-context-sensitive probabilities on rules. The (k, l)-context-sensitive probability of $A\rightarrow \beta \in R_A$ is denoted by:

$$\begin{aligned} P( A \rightarrow \beta \mid A, \left\langle x,\alpha \right\rangle ). \end{aligned}$$

Since the nonterminal on the left-hand side is always the same as the first nonterminal in the conditional part, we abbreviate the above notation to $P( A \rightarrow \beta \mid \left\langle x,\alpha \right\rangle )$.

We call a CFG with context-sensitive probabilities on rules as (k, l)-context-sensitive probabilistic grammar ((k, l)-CSPG).

Since the length of the context is finite, the probabilistic language that any (k, l)-CSPG defines theoretically can be represented by some PCFG with a huge number of nonterminal symbols¹ (and vice versa). Of course, there are significant differences as probabilistic models; they have different posteriors for the same data and thus different algorithms for learning. This is similar to the fact that the (k, l)-local substitutable languages (Coste et al., 2012) theoretically forms a subclass of the regular languages because of the finite length of $k+l$.

For any context with an arbitrary length $\left\langle x, \alpha \right\rangle \in \Sigma ^* \times V^*$ and any rule $A \rightarrow \beta \in R$, we can expand the definition of context-sensitive probabilities as follows:

$$\begin{aligned} P(A \rightarrow \beta | \left\langle x, \alpha \right\rangle ) {\mathop {=}\limits ^{\mathrm {def}}}P(A \rightarrow \beta | \langle \text {suffix}^{ k}(x), \text {prefix}^{ l}(\alpha ) \rangle ), \end{aligned}$$

where $\text {suffix}^{k}(\gamma )$ represents the suffix of $\gamma$ with a length of k if $|\gamma |>k$, otherwise $\gamma$. $\text {prefix}^{l}(\gamma )$ is defined in the similar way.

Let $r_1,\ldots , r_m$ ($m^\ge 1$) be the sequence of rules identified by some left-most derivation $d \in [\gamma {\mathop {\Rightarrow }\limits ^{*}}\beta ]$. For any context $(x,\alpha ) \in \Sigma ^* \times V^*$, we have

$$\begin{aligned} x \gamma \alpha = x y_1 A_1 \beta _1 \alpha \Rightarrow ^{r_1} \cdots \Rightarrow ^{r_{m-1}} x y_{m} A_{m}\beta _{m} \alpha \Rightarrow ^{r_m} x \beta \alpha , \end{aligned}$$

(1)

where $d = ( y_1 A_1 \beta _1, \ldots , y_{m} A_{m}\beta _{m}, \beta )$ and $\gamma = y_1 A_1 \beta _1$.

Definition 7

(probability for a derivation) Let $\text {Emit}(d\ | \left\langle x,\alpha \right\rangle )$ denote the sequence of the triplets of the rules and the left and right contexts, which are identified from the derivation represented in Eq. 1:

$$\begin{aligned} \text {Emit}( d\ | \left\langle x,\alpha \right\rangle ) {\mathop {=}\limits ^{\mathrm {def}}}( (r_1, xy_1, \beta _1\alpha ), \ldots , (r_m, xy_{m}, \beta _{m}\alpha ) ). \end{aligned}$$

The probability of d given $(x,\alpha )$ is defined as:

$$\begin{aligned} P( d\ | \left\langle x,\alpha \right\rangle ) {\mathop {=}\limits ^{\mathrm {def}}}\prod _{i=1}^{M}P( r_i\ | \left\langle xy_i, \beta _i\alpha \right\rangle ), \end{aligned}$$

where $(r_i, xy_i, \beta _i\alpha )$ is the i-th element of $\text {Emit}(d\ | \left\langle x, \alpha \right\rangle )$ and $M = |\text {Emit}(d | \left\langle x, \alpha \right\rangle )|$.

For a A-derivation tree $T_A$, we let $\text {Emit}(T_A | \left\langle x,\alpha \right\rangle ) = \text {Emit}(d_{T_A} | \left\langle x,\alpha \right\rangle )$ and $P( T_A | \left\langle x,\alpha \right\rangle ) = P( d_{T_A} | \left\langle x,\alpha \right\rangle )$, where $d_{T_A}$ is a left-most derivation which is naturally identified from $T_A$. For a S-derivation tree T, we let P(T) denote $P(T | \left\langle \lambda ,\lambda \right\rangle )$ and $\text {Emit}(T)$ denote $\text {Emit}(T | \left\langle \lambda ,\lambda \right\rangle )$.

Definition 8

(probability for a set of possible derivations) The probability for a set of possible derivations $[\gamma \Rightarrow ^{*|\mathcal {C}} \beta ]$ given a context $\left\langle x,\alpha \right\rangle$ is defined as:

$$\begin{aligned} P( [ \gamma \Rightarrow ^{*|\mathcal {C}} \beta ] \ | \left\langle x,\alpha \right\rangle ) {\mathop {=}\limits ^{\mathrm {def}}}\sum _{d \in [ \gamma \Rightarrow ^{*|\mathcal {C}} \beta ] } P( d\ | \left\langle x,\alpha \right\rangle ). \end{aligned}$$

If $\left\langle x,\alpha \right\rangle = \left\langle \lambda , \lambda \right\rangle$, we abbreviated the above to $P( [ \gamma \Rightarrow ^{*|\mathcal {C}} \beta ] )$. For example, the probability where a derivation tree has a yield w is given by $P( [ S \Rightarrow ^{*} w ] )$. Note that the left context x is explicitly determined from the sample sentence whereas the right context $\alpha$ is not. This implies that, from the viewpoint of computational cost, the length of $\alpha$ is problematic whereas the length of x is not, as we will discuss in Sect. 5.2.

The following lemma describes the relationship between the concatenation of derivations and the probabilities of them, which is useful together with Lemma 1 for proving the correctness of the sampling algorithms for derivation trees.

Lemma 2

(probability for concatenation of sets of derivations) For each $[\alpha {\mathop {\Rightarrow }\limits ^{*}}xB\gamma ]$, $[B {\mathop {\Rightarrow }\limits ^{*}}\beta ]$ and context $\left\langle y,\delta \right\rangle$, we have

$$\begin{aligned} P ( [\alpha {\mathop {\Rightarrow }\limits ^{*}}xB\gamma ] \otimes [B {\mathop {\Rightarrow }\limits ^{*}}\beta ] \ | \left\langle y,\delta \right\rangle ) = P( [\alpha {\mathop {\Rightarrow }\limits ^{*}}xB\gamma ] \ | \left\langle y,\delta \right\rangle )\ P( [B {\mathop {\Rightarrow }\limits ^{*}}\beta ] \ | \left\langle yx,\gamma \delta \right\rangle ). \end{aligned}$$

Proof

From Definition 4,

$$\begin{aligned} P ( [\alpha {\mathop {\Rightarrow }\limits ^{*}}xB\gamma ] \otimes [B {\mathop {\Rightarrow }\limits ^{*}}\beta ] \ | \left\langle y,\delta \right\rangle ) = \sum _{\begin{array}{c} \ d_1 \in [\alpha {\mathop {\Rightarrow }\limits ^{*}}xB\gamma ] \text {, } d_2 \in [B {\mathop {\Rightarrow }\limits ^{*}}\beta ] \end{array} } P( d_1\oplus d_2\ | \left\langle y,\gamma \right\rangle ). \end{aligned}$$

(2)

Let $d_1 = (\alpha _1,\ldots , \alpha _m)$ and $d_2 = (B, \beta _2,\ldots , \beta _n)$, where $\alpha _1=\alpha$, $\alpha _m = xB\gamma$ and $\beta _n = \beta$. Since $d_1\oplus d_2 = (\alpha _1,\ldots , \alpha _m,\ x\beta _2 \gamma , \ldots , x\beta _n \gamma )$ from Definition 3 and the definition of $\text {Emit}(\cdot )$,

$$\begin{aligned} \text {Emit}( d_1\oplus d_2\ | \left\langle y,\delta \right\rangle ) = \text {Emit}( d_1 | \left\langle y,\delta \right\rangle ) + \text {Emit}( d_2 | \left\langle yx,\gamma \delta \right\rangle ), \end{aligned}$$

where $+$ above denotes the usual concatenation of two sequences. Thus, from Definition 7, we have $P( d_1\oplus d_2\ | \left\langle y,\gamma \right\rangle )= P(d_1 | \left\langle y,\delta \right\rangle ) P(d_2 | \left\langle yx,\gamma \delta \right\rangle )$. Consequently,

$$\begin{aligned} \text {Eq.}~2&= \sum _{ d_1 \in [\alpha {\mathop {\Rightarrow }\limits ^{*}}xB\gamma ] } \sum _{ d_2 \in [B {\mathop {\Rightarrow }\limits ^{*}}\beta ] } P(d_1 | \left\langle y,\delta \right\rangle ) P(d_2 | \left\langle yx,\gamma \delta \right\rangle )\\&= P( [\alpha {\mathop {\Rightarrow }\limits ^{*}}xB\gamma ] \ | \left\langle y,\delta \right\rangle )\ P( [B {\mathop {\Rightarrow }\limits ^{*}}\beta ] \ | \left\langle yx,\gamma \delta \right\rangle ). \end{aligned}$$

$\square$

4 Generative models for (k,l)-context-sensitive PCFGs using hierarchical Pitman–Yor processes

4.1 Pitman–Yor processes

Let X be a countable set. A Pitman–Yor Process (PYP) over X, denoted by $\text{ PYP }(\theta ,d,H)$, is a distribution over distributions over X described as follows (Pitman and Yor, 1997; Ishwaran and James, 2003; Teh, 2006a, b). PYP consists of two components: (1) the two-parameter GEM (abbreviation for Griffiths, Engen and McCloskey) distribution (Feng, 2010), whose parameters are concentration $\theta > 0$ and $0\le d < 1$, and (2) the base measure H, which is an arbitrary distribution over X. $\theta$ and d are called discount and concentration parameters, respectively.

The GEM is a distribution over distributions over natural numbers ${\mathbb {N}}$ defined as follows. Let $(Y_1, Y_2, \ldots )$ be a sequence of random variables where $Y_k$ are independently taken from the $Beta(1-d, \theta +kd)$ distribution. Beta(a, b) is a probability distribution over [0, 1], whose shape can be adjusted by the parameters $a > 0$ and $b > 0$. For instance, from $Beta(1-d, \theta )$, the larger $d < 1$ and $\theta$, the more likely it is to sample values close to 0. The sequence of random variables $(V_1, V_2, \ldots )$ obtained from Y by the following way is called the two-parameter GEM process: $V_1 = {Y_1}$ and $V_k = {(1-Y_1)\ldots (1-Y_{k-1})Y_k}$ for $k>1$. This is also called stick-breaking process because if a stick with a length of 1 is randomly cut according to the ratio of $Beta (1-d, \theta +kd)$ recursively, the length of k-th peace corresponds to $V_k$. Since $\sum _{k=1}^{\infty } V_k = 1$, we regard a sampled sequence of V as a distribution over ${\mathbb {N}}$.

Intuitively, thanks to the discount factor d, while assigning probabilities to observed samples according to their frequencies, a PYP gives more probabilities to unseen samples even if the number of the kinds of the observed samples increases. This nature helps PYPs to be suitable for the power-law distribution that symbols in natural text corpus, such as the frequencies of words, commonly have.

Each natural number $k\in {\mathbb {N}}$, is also assigned to some $x \in X$ with a probability H(x). Let $(\delta _1, \delta _2, \ldots , )$ is a sequence of i.i.d. random variables of X whose distributions are H. Since the sequence $\delta$ can assign natural numbers to some $x \in X$ multiple times, in order to obtain the probability for x, we need to sum up $V_{\delta _k}$ for all k:

$$\begin{aligned} G = \sum _{k=1}^{\infty } V_{\delta _k}, \end{aligned}$$

which is the definition of $\text{ PYP }(\theta ,d,H)$ over X. As a PYP is equivalent to a Dirichlet process (DP) if $d=0$, PYPs can be seen as a natural argumentation of DPs.

$\delta$ can be thought of a stochastic map from ${\mathbb {N}}$ to X, which is called table assignment. Tables, or the arguments of $\delta$, are not observable and thus treated as hidden variables.

The posterior probability that an element $x\in X$ is drawn via a table k for c(x, k) times, where c(x, k) is an integer greater than or equal to 0, is simply written as $H(x){V_k}^{c(x,k)}$. Suppose that m is the number of samples and $x_1,\ldots ,x_m$ is are the samples taken from $\text{ PYP }(\theta ,d,H)$. Let $k_1,\ldots ,k_m$ are hidden variables that represent tables corresponding to those samples and c(x, k) is the number of occurrences of (x, k) in $(x_1,k_1),\ldots ,(x_m,k_m)$. The posterior probability of a new sample $(x_{m+1}, k_{m+1})$ given $(x_1,k_1),\ldots ,(x_m,k_m)$ is calculated as follows by marginalizing all $V_k$ (Pitman and Yor, 1997; Feng, 2010):

$$\begin{aligned} \Pr \left( (x_{m+1},k_{m+1}) \mid (x_1,k_1),\ldots ,(x_m,k_m) \right) = {\left\{ \begin{array}{ll} \frac{\theta + |U_m|d}{m+\theta } H(x_{m+1}) &{}\text {if } k_{m+1} \not \in U_m,\\ \frac{c(x_{m+1},k_{m+1})-d}{m+\theta } &{}\text {otherwise,} \end{array}\right. } \end{aligned}$$

(3)

where $U_m$ is the set of unique numbers of $(k_1,\ldots ,k_m)$, and $|U_m|$ is the cardinality of $U_m$. We can obtain the joint probability $\Pr ((x_1,k_1),\ldots$ $,(x_m,k_m) )$ by recursively multiplying Eq. 3m times. The above marginal posterior distribution is called the Chinese restaurant process (CRP) representation for the PYP (Teh, 2006a). The experiments in this paper are performed by utilizing the CRP representation; we do not calculate the stick-breaking distributions $(V_1,V_2,\ldots )$ but directly sample tables $(k_1,\ldots ,k_m)$ according to Eq. 3.

The intuitive meaning of relationship between PYP (and DP) and its base measure is that the prediction probability of $x \in X$ is smoothed by the base measure H(x) when x is rarely observed. In fact, if x does not appear at all, the upper term in the right side of Eq. 3 is the prediction probability that $x_{m+1} = x$, which is proportional to H(x).

When the base measure H is also a random variable whose distribution is another PYP, i.e., H is a distribution that is drawn from another PYP $\text{ PYP }(\theta ,d,H)$ over X recursively, $\text{ PYP }(\theta ,d,H)$ is called a hierarchical PYP(HPYP). Hierarchy of PYPs represents the hierarchy of smoothing intuitively. In this paper, we write $P \sim \text{ PYP }(\theta ,d,H)$ if a distribution P over X is distributed according to $\text{ PYP }(\theta ,d,H)$.

4.2 General forms for hierarchies of base measures

Suppose that we want to estimate the posterior distribution of $x \in X^m$ given $y \in Y^n$, where X and Y are some countable sets, e.g., $V\cup \Sigma$. Generally speaking, sequences are usually sparse because $|X^m|$ grows exponentially in real-world datasets like most text corpora are so; each sequence is rarely exactly same as another sequence. When inferring the posterior distribution, the base measure plays an important role to get around such sparsity. If a sentence w is drawn for the first time, the posterior probability for that sentence is approximately equal to its base measure H(w) as mentioned in the previous section.

Let $P_{X^m}( \cdot \mid y )$ be a conditional distribution over $X^m$ given $y\in Y^n$, and sampled from a PYP where the base measure is $H_{y}$:

$$\begin{aligned} P_{X^m}( \cdot \mid y ) \sim \text{ PYP }(\theta _y,d_y,H_{y}). \end{aligned}$$

If $|X^m \times Y^n|$ is small enough and the size of data is large enough, the posterior distribution equals approximately the ratio of the occurrences of $x \in X^m$ given y. In that case, the effect of the base measure is ignorable since the number of occurrences of each pattern can be much larger than the parameters $\theta$ and d. On the other hand, if $|X^m \times Y^n|$ is large and data is limited, some sort of smoothing method needs to be applied to obtain an appropriate estimate. Defining appropriate recursive hierarchies of base measures is one of the promising solutions.

There are two approaches for constructing hierarchical PYPs: (1) decreasing the length of y (Definition 9-1) and (2) decreasing the length of x (Definition 9-2).

Definition 9

(types of base measures) Suppose that $y \in Y^n$ and $\text{ PYP }(\theta _y, d_y, H_{y})$ over $X^m$ are given. Let z be a prefix (or suffix) of y.

• 1. We call a base measure $H_{y}$ the aggregation of y with respect to z if

  $$\begin{aligned} H_{y} \sim \text{ PYP }(\theta _z,d_z,H_{z}). \end{aligned}$$

• 2. We call a base measure $H_{y}$ the decomposition of $X^m$ if, for each $a_1\cdots a_m \in X^m$,

  $$\begin{aligned} H_{y} (a_1\cdots a_m) = \text{ PYP }\left( \theta _y, d_y, \prod _{i=1}^{m} H_{y,i}(a_i) \right) , \end{aligned}$$

  where $H_{y,i}$ for each i is some distribution over X given y.

For example, suppose that the set of samples from $Y^n$ are $\{ abcc, abee \}$. Both $H_{abcc} (\cdot )$ and $H_{abee} (\cdot )$ have the same base measure $H_{ab} (\cdot )$ if they are aggregated with respect to the prefix ab (Definition 9-1). When both abcc and abee appear only once, $H_{abcc} (x)$ and $H_{abee} (x)$ are equal to $H_{ab} (x)$ thanks to Eq. 3. They are not needed to be estimated independently.

As another example, suppose that the set of samples from $X^m$ are $\{ ab, cd \}$ given $y \in Y^n$. Then, for an unseen sample $ad \in X^m$, $H_{y}(ad)$ has the same base measure $H_{y}(a)H_{y}(d)$ if it is decomposed with respect to $X^m$ (Definition 9-2). Since $H_{y}(a)$, $H_{y}(b)$, $H_{y}(c)$, and $H_{y}(d)$ are the factors of the base measures for $H_{y}(ab)$ and $H_{y}(cd)$, $H_{y}(a)H_{y}(d)$ can be estimated to some extent without observing ad.

The construction of hierarchies of PYPs, intuitively speaking, is equivalent to constructing a sort of a priori knowledge through the nested prior distribution of HPYPs. Owing to the effect of this nested prior, the posterior over $X^m$ given $Y^n$ is smoothed appropriately.

4.3 Hierarchical PYPs for CFGs

Let $G=\left\langle \Sigma , V, R, S \right\rangle$ be a CFG and P be a probability for R. We define hierarchical PYPs over rules of G as the prior distribution of P in different ways below. Let A be a nonterminal, the rules of which have two nonterminals on the left. $R_A$ denotes the set of rules with A as left hand side and any combination of two non-terminals as right hand side, i.e., $R_A = \{A \rightarrow BC \mid B,C \in V \}$. Then we draw a distribution over $R_A$ from a PYP as:

$$\begin{aligned} P(A\rightarrow \cdot \ \cdot ) \sim \text{ PYP }(\theta _A, d_A , H_{A}), \end{aligned}$$

where $H_{A}$ is a distribution over $V\times V$. We can define $H_{A}$ in two different manners by selecting whether the decomposition of $V\times V$ or the aggregation of A occurs first.

In the former case, the base measure $H_{A}$ is defined as follows. B and C are assumed to be drawn independently from $H_{A,1}$ and $H_{A,2}$, i.e., $H_A(BC) = H_{A,1}(B) H_{A,2}(C)$. Then, $H_{A,i}$ is recursively defined for each i as

$$\begin{aligned} H_{A,i} \sim \text{ PYP }(\theta _{\lambda ,i}, d_{\lambda ,i}, H_{\lambda ,i}). \end{aligned}$$

$H_{\lambda ,i}$ is again drawn recursively from a PYP, the base measure of which is the uniform distribution:

$$\begin{aligned} H_{\lambda ,i} \sim \text{ PYP }( \theta _{\text {Uni}}, d_{\text {Uni}}, \text {Uniform}). \end{aligned}$$

Liang et al. (2007) defined infinite PCFGs using the hierarchy described above.

In the latter case, $H_{A}$ is given by the aggregation of A with respect to $\lambda$ first. $H_{A}$ is assumed to be taken from a PYP, where the base measure $H_{\lambda }$ is shared for all $A \in V$:

$$\begin{aligned} H_{A} \sim \text{ PYP }( \theta _{\lambda }, d_{\lambda }, H_{\lambda }). \end{aligned}$$

Then, $H_{\lambda }$ is defined as a decomposition of $V\times V$, which is the domain of $H_{\lambda }$: $H_{\lambda }(BC) = H_{\lambda ,1}(B) H_{\lambda ,2}(C)$. $H_{\lambda ,i}$ are again sampled recursively from a PYP:

$$\begin{aligned} H_{\lambda ,i} \sim \text{ PYP }( \theta _{\text {Uni}}, d_{\text {Uni}}, \text {Uniform}). \end{aligned}$$

In the case where a nonterminal A has rules with a terminal $a \in \Sigma$ on the right, $|\Sigma |$ is often too large to assume that $P(A \rightarrow \cdot )$ has a uniform prior distribution. The distribution from which a is generated is assumed to be sampled from a PYP whose base measure is the uniform distribution over $\Sigma$:²

$$\begin{aligned} P(A \rightarrow \cdot ) \sim \text{ PYP }(\theta _{\text {Uni}}, d_{\text {Uni}}, \text {Uniform}). \end{aligned}$$

4.4 Hierarchical PYPs for (k, l)-context-sensitive probabilistic grammars

The definition of $P(A \rightarrow \beta \mid \left\langle x,\alpha \right\rangle )$ requires different parameters for each $\left\langle x,\alpha \right\rangle$. Recent studies show that nonparametric Bayesian models such as hierarchical PYPs have excellent smoothing capacities in this situation. As described in Sect. 4.2, the definitions of hierarchies of PYPs have many variations, which depend on the order of the aggregation of contexts $\left\langle x,\alpha \right\rangle$ and the decomposition of the right-hand side of the rule $\beta$. In the following, we first aggregate each of x and $\alpha$ in $\left\langle x,\alpha \right\rangle$ recursively and then decompose $\beta$. We sometimes write $P(A \rightarrow \beta \mid \left\langle x,\alpha \right\rangle )$ as $P(\beta \mid A, \left\langle x,\alpha \right\rangle )$ below. When a grammar is in CNF, $P(\cdot \mid A, \left\langle x, \alpha \right\rangle )$ is a distribution over the union of $V\times V$ and $\Sigma$.

$$\begin{aligned} P( \cdot \mid A, \left\langle x, \alpha \right\rangle ) \sim \text{ PYP }( \theta _{A,\pi \left\langle x,\alpha \right\rangle }, d_{A,\pi \left\langle x,\alpha \right\rangle }, H_{A,\pi \left\langle x,\alpha \right\rangle } ). \end{aligned}$$

$\pi \left\langle x,\alpha \right\rangle$ is defined as follows:

$$\begin{aligned} \pi \left\langle x,\alpha \right\rangle = {\left\{ \begin{array}{ll} (\pi _\mathtt {L}(x),\alpha ) &{}\text {if } |x| > |\alpha |,\\ (x, \pi _\mathtt {R}(\alpha )) &{}\text {otherwise,}\\ \end{array}\right. } \end{aligned}$$

where $\pi _\mathtt {L}(a \beta ) = \beta$ and $\pi _\mathtt {R}(\beta a) = \beta$ for $\beta \in (V\cup \Sigma )^*$ and $a \in V\cup \Sigma$. The distribution $H_{A,\left\langle x,\alpha \right\rangle }$ over $V\times V$ given A and $(x,\alpha )$ is defined recursively using $\pi$ as:

$$\begin{aligned} H_{A,\pi ^{i}\left\langle x,\alpha \right\rangle } \sim \text{ PYP }( \theta _{A,\pi ^{i+1}\left\langle x,\alpha \right\rangle }, d_{A,\pi ^{i+1}\left\langle x,\alpha \right\rangle }, H_{A,\pi ^{i+1}\left\langle x,\alpha \right\rangle } ), \end{aligned}$$

for $i = 0,\ldots ,|x\alpha |$. After these recursive definitions of base measures are complete, we define the distribution $H_{A,(\lambda , \lambda ) }$ over $V\times V$ given A in the same manner as Liang’s hierarchy described the previous section. That is, first, it is defined by decomposition of $V\times V$,

$$\begin{aligned} H_{A,(\lambda , \lambda ) } \sim \text{ PYP }(\theta ,d, J_{A,1} J_{A,2} ). \end{aligned}$$

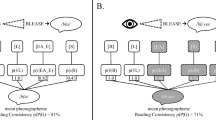
Then, $J_{A,i}$ for each i is defined as:

$$\begin{aligned} J_{A,i} \sim \text{ PYP }(\theta , d, J_i). \end{aligned}$$

Finally, $J_{i} \sim \text{ PYP }(\theta _{\text {Uni}}, d_{\text {Uni}}, \text {Uniform})$ (Fig. 1).

Fig. 1

The hierarchy of PYPs for (k, l)-context-sensitive probabilistic grammars

5 Inference method

In Bayesian approaches, generally, the goal of grammatical inference is to obtain the posterior distribution over all grammars in a target class: P(G|W) for all $G \in \mathcal {C}$, where $\mathcal {C}$ is a target class and W is the set of given i.i.d. sentences. If P(G|W) is obtained, the posterior or predictive probability for a new sentence w is obtained by $P(w|W) = \sum _{G \in C} P(w|G) P(G|W)$. However, calculating neither P(G|W) for each G nor P(w|W) is feasible in many cases especially if the class allows grammars in it to have ambiguities with respect to derivations of sentences, such as NFAs and CFGs. Even so, by using appropriate sampling algorithms, the learner can output multiple likely grammars $G_1 \cdots G_m$ according to approximated P(G|W). When the grammars are sampled, probabilities assigned to rules of grammars $\pi _1,\ldots ,\pi _m$ are also sampled at the same time. After the likely grammars and probabilities of their rules are sampled, the predictive probability is approximately calculated by $\sum _{i=1}^{m} P(w|G_i, \pi _i)/m$. In practice, we usually set $m=1$ since we need a single grammar as a simple and explainable solution.

5.1 Blocked Gibbs sampling

Gibbs sampling is a representative Markov chain Monte Carlo (MCMC) algorithm, which is known to give relatively high accuracy approximations as a method for the Bayesian inference of probabilistic models where the marginalization of all unknown parameters is unfeasible, such as HMMs and PFAs. Gibbs sampling can be roughly divided into two types: pointwise sampling and blockwise sampling, based on how many variables are changed each time. Generally speaking, blockwise sampling is known to be less trapped in a local optimum while its computational cost is relatively high.

It is not straightforward to apply pointwise sampling for inferring the derivation trees of PCFGs in CNF because we have to consider many possible derivation trees. To apply pointwise Gibbs sampling, a single rule that is used to generate some sentence is replaced whereas the other rules remain fixed. However, if the length of the right-hand side of the rule is changed by the replacement, this replacement forces the subsequent rules to change because the sequence of nonterminals is shifted. Thus, to ensure that pointwise Gibbs sampling is achieved successfully, rule replacements have to be limited so the shape of derivation tree is not changed. However, these limited replacements fail to sample the derivation trees of the given sentences. Even if it is possible to keep the shape of the derivation trees (for instance, that is possible when the target class is the class of regular grammars), the pointwise sampling does not work efficiently because some parameters are highly correlated in the posterior.

The blocked Gibbs sampling proposed by Johnson et al. (2007b) is blockwise Gibbs sampling while fixing the probability for the production rules. Since fixing them is an approximation, another procedure called Metropolis-Hastings (MH) correction, which decides whether the sampled tree is accepted or not, is applied to ensure the correctness of the sampling, after each derivation tree is sampled for each sentence. The new derivation tree is sampled in the following steps as described in Algorithm 1: (1) The expected production probabilities are calculated according to the counts of their occurrences (Line 4). (2) The inside probabilities are calculated (Line 5,6). (3) The proposed derivation tree is generated randomly from S using the inside probabilities (Line 5,6) and rejected with some probability in order to compensate for the difference from the true probability (Line 7,8).

We let R in the initial grammar G be the set of all the possible production rules, i.e., $R = \{ A\rightarrow a | A\in V\} \cup \{ A\rightarrow a | A\in V, a\in \Sigma \} \cup \{ A\rightarrow BC | A,B,C \in V \}$. The first derivation trees are sampled so that all of them consist of a single nonterminal. Because of the nature of PYPs, even though all derivation trees consist of one nonterminal, the rules containing other nonterminals also have slightly non-zero posterior probabilities.

In Algorithm 1, $T_{i}$ denotes the derivation tree and the tables of PYP for the sentence $w_i$. $T_{\lnot i}$ denotes $T_1,\ldots , T_{i-1}, T_{i+1}, \ldots , T_N$, and $\Pr (T | T_{\lnot i})$ represents the posterior probability of T given $T_{\lnot i}$. $\Pr (T | T_{\lnot i})$ is calculated recursively by Eq. 3 through the hierarchy of base measures described in Sect. 4.3. By replacing $x_i$ in Eq. 3 with the i-th element of the sequence $\text {Emit}(T)$ (Definition 7), we have

$$\begin{aligned} \Pr (T | T_{\lnot i} ) = \prod _{k=1}^{m} \Pr \left( (r_k,x_k,\alpha _k)\ |\ (r_{[1:k-1]},x_{[1:k-1]},\alpha _{[1:k-1]}), \ T_{\lnot i} \right) , \end{aligned}$$

(4)

where $r_{[1:k-1]}$ denotes a sequence $r_k,\ldots , r_{k-1}$ (an empty sequence if $k=1$). Tables in Eq. 3, which are hidden parameters for derivation trees, are sampled together with derivation trees. Although hyper parameters such as $\theta _A$ and $d_A$ in PYPs also should be sampled, we omit describing a procedure for them here (refer to Teh, 2006b).

Line 8 is a MH sampling from $T_i$ to $T_{\text {nw}}$, where the proposal distribution from $T \in \mathcal {T}(w_i)$ to $T' \in \mathcal {T}(w_i)$ is $P_0( T' |w_i)$. We have the following proposition from general theorems about MH and MCMC algorithms for discrete state spaces; e.g., refer to Theorems 19.4-6 in DasGupta (2011).

Proposition 1

Let ($T_1^{(i)}, \ldots , T_M^{(i)}$) be the i-th outputs of Algorithm 1. For each $(r,x,\alpha ) \in R \times \Sigma ^{\le k} \times V^{\le l}$, as $N \rightarrow \infty$, $\frac{1}{N}\sum _{i=1}^{N}\Pr ((r,x,\alpha )| T_1^{(i)}, \ldots , T_M^{(i)}) {\mathop {\longrightarrow }\limits ^{a.s.}} \Pr ( (r,x,\alpha ) | w_1,\ldots ,w_M)$.

If $P_0(T )$ is close to $\Pr (T | T_{\lnot i} )$ for each T, replacements of trees are almost always accepted by the MH sampling since the probability in Line 8 is approximately 1.

In fact, $P_0$ at Line 4, which the blocked sampling uses to sample T (Line 6), is defined as: $P_0(r | \left\langle x,\alpha \right\rangle ) = \Pr ((r,x,\alpha ) | T_{\lnot i} )$ for each $(r, x, \alpha ) \in R \times \Sigma ^{\le k} \times V^{\le l}$. From the definitions of $P_0(T )$, we have

$$\begin{aligned} P_0(T ) = \prod _{k=1}^{m} \Pr ( (r_k, x_k,\alpha _k) | T_{\lnot i}). \end{aligned}$$

(5)

Comparing Eqs. 5 to 4, we can seen that $P_0(T)$ is a good approximation for $\Pr (T | T_{\lnot i})$, especially when M is sufficiently large. Practically, the acceptance rate of the MH correction (Line 8) is very close to 1. The only reason for inserting the MH correction is to guarantee theoretical correctness.

In the following section and Sect. 6, we state how we can efficiently sample a derivation tree T according to $P_0(T|w_i)$. Note that all algorithms in those sections are focused on sampling a derivation tree for a sentence w from a given (k, l)-context-sensitive distribution $P_0$.

5.2 Blocked sampling for each derivation tree

In this section, we assume that (k, l)-context-sensitive probabilities $P: R \times \Sigma ^{\le k} \times V^{\le l} \rightarrow (0,1]$ are already given for a CFG in CNF G. Under such assumption, we pursue methods to correctly sample derivation trees for CFGs with (k, l)-context-sensitive probabilities. We show that it is possible to sample them efficiently by modifying the inside probabilities for PCFGs.

First, for the case of the usual PCFGs, we confirm that the nature of the inside probabilities described in Preliminaries hold and a derivation tree can be sampled by using that. From Lemma 1, for $i\ne j$, we have

$$\begin{aligned}{}[A{\mathop {\Rightarrow }\limits ^{*}}w(i,j)] = \bigsqcup _{A\rightarrow BC \in R,\ k\in [1,j)} [A{\mathop {\Rightarrow }\limits ^{*}}BC] \otimes [B {\mathop {\Rightarrow }\limits ^{*}}w(i,k)] \otimes [C {\mathop {\Rightarrow }\limits ^{*}}w(k+1,j)]. \end{aligned}$$

Thus, from Lemma 2 and the fact that all context can be ignored, we have the following equation:

$$\begin{aligned} P([A{\mathop {\Rightarrow }\limits ^{*}}w(i,j)]) = \sum _{A\rightarrow BC \in R} \sum _{k=i}^{j-1} P([A{\mathop {\Rightarrow }\limits ^{*}}BC]) P([B {\mathop {\Rightarrow }\limits ^{*}}w(i,k)] ) P([C {\mathop {\Rightarrow }\limits ^{*}}w(k+1,j)]). \end{aligned}$$

For a CFG G with a (0,0)-context-sensitive probability P, that is a PCFG $\left\langle G,P \right\rangle$, recall that the inside probability $P^{\mathrm {IN}}(A|i,j)$ for a sentence w is defined as $P([A{\mathop {\Rightarrow }\limits ^{*}}w(i,j)])$. From the fact that $P([A{\mathop {\Rightarrow }\limits ^{*}}BC]) = P(A\rightarrow BC)$, the above equation is represented as

$$\begin{aligned} P^{\mathrm {IN}}(A|i,j) = \sum _{A\rightarrow BC \in R} \sum _{k=i}^{j-1} P(A\rightarrow BC) P^{\mathrm {IN}}(B|i,k) P^{\mathrm {IN}}(C|k+1,j). \end{aligned}$$

(6)

In addition, we have $P^{\mathrm {IN}}(A|i,i) = P(A\rightarrow w_i)$ in the similar way.

$P^{\mathrm {IN}}(A|1,|w|)$ can be calculated in time $O(|w|^3 |V|^3)$ because (1) for each i,j, and A, we need to calculate the sum of the left sides of Eq. 6, which needs $O(|V|^2|w|)$ multiplications, and (2) we need to repeat the calculation of Eq. 6$O(|V||w|^2)$ times from the bottom to the top in the derivation tree. To sample a derivation tree, we may just choose both $A\rightarrow BC$ and k in the above equation according to $P(A\rightarrow BC) P^{\mathrm {IN}}(B|i,k) P^{\mathrm {IN}}(C|k+1,j)$ from the top to the bottom.

If the probabilities assigned to the derivation is context sensitive, the probability that a nonterminal yields a substring depends on its context. By expanding the definition of the inside probabilities for PCFGs above, those for (k,l)-context-sensitive PCFGs are defined as follows.

Definition 10

(inside probabilities for (k, l)-CSPG) Let G be a CFG and P be (k,l)-context-sensitive probabilities of G. $P([A {\mathop {\Rightarrow }\limits ^{*}}w]\ | \left\langle x,\alpha \right\rangle )$ is called the inside probability for $A \in V$ and $w \in L(A)$ given a context $\left\langle x, \alpha \right\rangle \in \Sigma ^* \times V^*$.

Since the left context of substring w(i, j) is $w(1,i-1)$, for $w \in L(G)$, $A \in V$, $\alpha \in V^*$, and $i,j \in \mathbb {N}$ such that $i \le j \le |w|$, the inside probability can be written as:

$$\begin{aligned} P^{\mathrm {IN}}(A | i,j, \alpha ) {\mathop {=}\limits ^{\mathrm {def}}}P( [A {\mathop {\Rightarrow }\limits ^{*}}w(i,j)]\ | \left\langle w(1,i-1), \alpha \right\rangle ). \end{aligned}$$

Note that the left context of A, that is $w(1,i-1)$, is uniquely identified from the given sentence w. Thus, from the definition of (k, l)-context-sensitive CFGs, $P^{\mathrm {IN}}_s(A | i,j, \alpha ))$ is uniquely identified by w, A and the prefix of $\alpha$ with a length of no more than l.

Fact 4

For $\alpha \in V^{> l}$, $P^{\mathrm {IN}}(A | i,j, \alpha ) =P^{\mathrm {IN}}(A | i,j, \alpha ')$ , where $\alpha '$ is a prefix of $\alpha$ such that $|\alpha '| = l$.

Lemma 3

(property of inside probabilities for (k, l)-CSPG) Let $w\in L(G), A \in V ,\alpha \in V^*, (i, j) \in I_{|w|}$. If $i \ne j$,

$$\begin{aligned} P^{\mathrm {IN}}(A|i,j,\alpha ) = \sum _{ BC \in V^2 s.t. A\rightarrow BC \in R_A }\sum _{k=i}^{j-1} f_{(x,\alpha )}( B,C, k), \end{aligned}$$

(7)

where $x = w(1,i-1)$ and

$$\begin{aligned} f_{(x,\alpha )}( B,C, k) = P(A\rightarrow BC | \left\langle x,\alpha \right\rangle )P^{\mathrm {IN}}(B|i,k, C\alpha ) P^{\mathrm {IN}}(C|k+1,j, \alpha ). \end{aligned}$$

In addition,

$$\begin{aligned} P^{\mathrm {IN}}(A|i,i,\alpha ) = P(A\rightarrow w_i\ | \left\langle w(1,i-1),\alpha \right\rangle ). \end{aligned}$$

(8)

Proof

If $i \ne j$, from Lemmas 1 and 2, we have

$$\begin{aligned} P([A{\mathop {\Rightarrow }\limits ^{*}}w(i,j)]\ |\left\langle x,\alpha \right\rangle ) = \sum _{A\rightarrow BC \in R} \sum _{k=i}^{j-1}&P([A{\mathop {\Rightarrow }\limits ^{*}}BC]\ |\left\langle x,\alpha \right\rangle ) \\&\cdot P([B {\mathop {\Rightarrow }\limits ^{*}}w(i,k)] \ |\left\langle x,C\alpha \right\rangle ) \\&\cdot P([C {\mathop {\Rightarrow }\limits ^{*}}w(k+1,j)] \ |\left\langle xw(i,k),C\alpha \right\rangle ). \end{aligned}$$

Substituting $x = w(i,j)$ and recalling the definition of $P^{\mathrm {IN}}$, we have Eq. 7.

If $i=j$, since $P([A{\mathop {\Rightarrow }\limits ^{*}}a\ | \left\langle x,\alpha \right\rangle ]) = P(A\rightarrow a\ |\left\langle x,\alpha \right\rangle )$, we have Eq. 8. $\square$

Note that the left context x is identified uniquely by i and a given sentence w. Thus, we do not need to calculate the inside probabilities for all the combinations of the left contexts. This means that the length of the left context, or k, is irrelevant to the time complexity when the inside probabilities are calculated. In contrast, the length of the right context affects both space and time complexities. From Fact 4, at least, $P^{\mathrm {IN}}$ require variables with a size of $|V|^{l+1}|w|^2$. Since $|V|^2|w|$ additions are required for calculating each $P^{\mathrm {IN}}(A|i,j,\alpha )$ from Lemma 3, we have the following fact.

Fact 5

Let G be a CFG in CNF and P be a (k,l)-context-sensitive probability for G. For a sentence w, the time complexity required to calculate all the inside probabilities $P^{\mathrm {IN}}$ is $O(|V|^{l+3}|w|^3)$.

It is easy to sample a derivation tree T according to $P(T|w) = P(T ) /\sum _{T' \in \mathcal {T}(w)} P(T')$ if $P^{\mathrm {IN}}$ is given.

Algorithm 2 describes how to sample a derived tree according to P(T|w). First, it calculates all inside probabilities at line 1, and then samples the derivation tree based on the pre-calculated inside probabilities. In the while loop, a sentence is generated by applying the rule one by one in the same procedure as the leftmost derivation, where the inside probability is used to determine which rule is applied.

Theorem 1

Algorithm 2 outputs a derivation tree $T \in \mathcal {T}(w)$ with probability P(T|w) in time $O(|V|^{l+3}|w|^3)$.

Proof

Let $d_T$ be the left-most derivation naturally identified from T. Let $P(d_T|w) = P(d_T ) / P([S {\mathop {\Rightarrow }\limits ^{*}}w])$. Then we have $P(T|w) = P(d_T |w )$ from the definition. Let $d_T = (\alpha _1,\ldots , \alpha _{M})$ where $\alpha _1 = S$ and $\alpha _{M}=w$. For each $\alpha _m$ where $m < M$, we have $\alpha _m = w(1, i_0-1)A_1\ldots A_n$ for some $i_0\ge 1$ and $n \ge 1$. From Fact 2, the sequence $i_0< i_1< \cdots < i_n = |w|+1$ such that

$$\begin{aligned} d_T \in [S{\mathop {\Rightarrow }\limits ^{*}}xA_1\cdots A_n]\otimes [A_1{\mathop {\Rightarrow }\limits ^{*}}w(i_0, i_1-1)] \otimes \cdots \otimes [A_n{\mathop {\Rightarrow }\limits ^{*}}w(i_{n-1}, i_n-1)] \end{aligned}$$

is identified uniquely from $d_T$. Let $J_{m}$ denote the sequence $(i_0,\ldots , i_n)$. We show that in Algorithm 2, $J_1,\ldots , J_{M}$ as well as $\alpha _1, \ldots , \alpha _{M}$ are sampled sequentially so that $d_T \sim P(d_T | w)$. As the base step, $\alpha _1 = (S)$ and $J_1 = (0,w)$ with probability one. Suppose that $\alpha _1,\ldots ,\alpha _m$ and $J_1,\ldots , J_m$ be sampled according to the following probability:

$$\begin{aligned}&P(\alpha _1,\ldots ,\alpha _m,J_1,\ldots , J_m|w)\\&\quad = \frac{ P( \{(\alpha _1,\ldots ,\alpha _m)\} \otimes [A_1{\mathop {\Rightarrow }\limits ^{*}}w(i_0, i_1-1)] \cdots \otimes [A_n{\mathop {\Rightarrow }\limits ^{*}}w(i_{n-1}, i_n-1)] ) }{ P([S{\mathop {\Rightarrow }\limits ^{*}}w] ) }, \end{aligned}$$

where $\alpha _m = w(1, i_0)A_1\ldots A_n$ and $J_{m} = (i_0,\ldots , i_n)$. If $i_0 \ne i_1-1$, from Lemma 2, we have for each $A_1\rightarrow BC$ and k such that $i_0\le k< i_1$,

$$\begin{aligned}&P(\alpha _1,\ldots ,\alpha _{m+1},J_1,\ldots , J_{m+1}|w) \\&\quad = c \cdot P( [A_1{\mathop {\Rightarrow }\limits ^{*}}BC] \otimes [B {\mathop {\Rightarrow }\limits ^{*}}w(i_0, k)] \otimes [C {\mathop {\Rightarrow }\limits ^{*}}w(k,i_1-1)] \ | \left\langle w(1, i_0-1), A_2 \cdots A_n \right\rangle )\\&\quad = c \cdot f_{(w(1, i_0-1), A_2 \cdots A_n)}( B,C, k), \end{aligned}$$

where $\alpha _{m+1} = BCA_2 \cdots A_n$, $J_{m+1} = (i_0,k,i_1,\ldots , i_n)$ , and c is the invariant term with respect to B, C, k. In fact, the algorithm samples B, C, k according to the above probability in Line 10. If $i_0 = i_1-1$, we have $\alpha _{m+1}=w(1,i_0)w_{i_1}A_2\cdots A_n$ and $J_{m+1} = (i_1,\ldots ,i_n)$ with probability one. $\square$

6 Composite samplings for (k, l)-context-sensitive probabilistic grammars

In this section, we propose an approach which reduces the time complexity of the blocked sampling shown in the previous section. The most computationally expensive part of the blocked sampling is calculating the inside probabilities. In calculating the inside probabilities, the main reason of the expensive cost is that we need to calculate the probabilities of rules for all possible combinations of nonterminals in rules and right contexts. In order to avoid this circumstance, we divide derivation trees to into the shapes of derivation trees and the assignment of nonterminals for substrings. We call such sampling approach composite sampling. In the following subsection, we propose a composite sampling algorithm where nonterminals are assigned for all substrings involving distituent ones. We implement this algorithm in the experiments. We suppose that (k,l)-context-sensitive probabilities $P: R \times \Sigma ^{\le k} \times V^{\le l} \rightarrow (0,1]$ are given for a CFG in CNF G.

6.1 Composite sampling via sampling both constituent and distituent nodes

For a sentence w and the set of intervals $I_{|w|}$, we call a map $\mathcal {H}: I_{|w|} \rightarrow V$ such that $H(1,|w|) = S$ an assignment of nonterminals for $I_{|w|}$ . We write $\mathcal {H}(i,j) \Rightarrow ^{*|\mathcal {H}} w(i,j)$ iff $\mathcal {H}(i,j) {\mathop {\Rightarrow }\limits ^{*}}w(i,j)$ and the appeared nonterminals can be restricted by $\mathcal {H}$, i.e., for every constituent substring $w(i',j')$ of w(i, j), the corresponding nonterminal is $\mathcal {H}(i',j')$. In the following, we propose a composite sampling algorithm that separates sampling $\mathcal {H}$ and sampling shapes of derivation trees. First $\mathcal {H}(i,j)$ is sampled for each (i, j) with the probability described later, then a derivation tree is sampled from the set of derivation trees where all nonterminals of nodes are restricted by $\mathcal {H}$. A derivation tree is sampled efficiently through the modified inside probabilities as shown in the following.

Definition 11

(set of restricted possible derivation trees) Let $\mathcal {T}(A, w, i, j, \mathcal {H})$ denote the set of derivation trees such that

• the head node is A,

• their yields equal w(i, j),

• and for each constituent substring $w(i', j')$ where $i\le i' \le j' \le j$, the corresponding nonterminal satisfies that $X(i',j') = \mathcal {H}(i',j')$.

We call $\mathcal {T}(A, w, i, j, \mathcal {H})$ the set of the possible derivation trees restricted by $\mathcal {H}$ with respect to A, w, i, and j. In particular, we write $\mathcal {T}(S, w, 1, |w|, \mathcal {H})$ as $\mathcal {T}(w , \mathcal {H})$.

To separate sampling $T \in \mathcal {T}(w , \mathcal {H})$ and sampling $\mathcal {H}$, we define a joint distribution over $\Sigma ^*$, the set of all derivation trees and maps $I_{|w|} \rightarrow V$ as follows:

$$\begin{aligned} P(w, T, \mathcal {H}) {\mathop {=}\limits ^{\mathrm {def}}}{\left\{ \begin{array}{ll} P(T) \prod \nolimits _{ w(i,j) \text { is distituent for } T } Q_{ij}(\mathcal {H}(i,j)| w) &{}\text { if } T \in \mathcal {T}(w , \mathcal {H}) , \\ 0 &{}\text { otherwise }, \end{array}\right. } \end{aligned}$$

(9)

where $Q_{ij}(\cdot |w)$ is a distribution over V given w and (i, j), such that $Q_{ij}( A|w) \ne 0$ for all $A\in V$ (Fig. 2).

In Eq. 9, we find that $\mathcal {H}$ are auxiliary variables that are independent of other variables such as T and w. By marginalizing $\mathcal {H}(i,j)$ for all distituent (i, j), we have

$$\begin{aligned} P(w, T) = \sum _{\mathcal {H}} P(w, T, \mathcal {H}) = {\left\{ \begin{array}{ll} P(T ) &{}\text { if } T \in \mathcal {T}(w), \\ 0 &{}\text { otherwise}, \end{array}\right. } \end{aligned}$$

(10)

since $\sum _{A\in V} Q_{i,j}(A|w) = 1$ for all i, j.

The above equation means that $Q_{ij}$ does not affect the target distribution P(T|w), and thus, can be chosen arbitrary. In addition, we can allow $Q_{ij}(\cdot |w)$ to depend on $T_{\lnot i}$ and thus depends on $P_0$ of Algorithm 1 since its transition probabilities of the Markov chain are invariant even if the proposal distribution is depending on $T_{\lnot i}$. Intuitively, although it may be weird that distituent nonterminals are sampled from Q and thus have arbitrary biases, those biases are canceled during sampling the tree shape as Lemma 4 will show.

We sample both $\mathcal {H}$ and T through Gibbs sampling. First, we fix T and sample $\mathcal {H}(i,j)=A$ for each (i, j) so that

$$\begin{aligned} A \sim {\left\{ \begin{array}{ll} Q_{ij}(A|w) &{} \text {if } w(i,j) \text { is distituent for } T,\\ P( X(i,j) = A| T_{\lnot (i,j)} ) &{} \text {if } w(i,j) \text { is constituent for } T, \end{array}\right. } \end{aligned}$$

where $P( X(i,j) = A | T_{\lnot (i,j)} )$ is the probability that the nonterminal X(i, j) of the node (i, j) is replaced with A in the derivation tree T. This is easy to calculate since only 2 rules around node (i, j) are replaced and thus what we have to do is calculate their difference. Then a derivation tree $T_\text {nw}$ is sampled with the probability $P([S {\mathop {\Rightarrow }\limits ^{*|\mathcal {H}}} w])$.

Note that, although $T_\text {nw}$ obtained the above procedure does not directly drawn from $P(T_\text {nw}|w)$ , the transition from the old derivation tree T to $T_\text {nw}$ forms an appropriate MCMC.

Fig. 2

Sampling constituent and distituent nodes

The inside probabilities restricted by H defined in Definition 12 satisfy Lemma 4.

Definition 12

(inside probabilities for restricted set of derivation trees) Let G be a CFG and P be a (k,l)-context-sensitive probability of G. For $A \in V$, $w \in L(G)$, $(i,j) \in I_{|w|}$, and $(x, \alpha ) \in \Sigma ^* \times V^*$, the inside probability restricted by $\mathcal {H}$ is defined as follows:

$$\begin{aligned} P([A{\mathop {\Rightarrow }\limits ^{*|\mathcal {H}}} w(i,j)], \mathcal {H}\mid \left\langle x,\alpha \right\rangle ) {\mathop {=}\limits ^{\mathrm {def}}}&\left( \prod _{w(i,j) \text { is constituent for } T} \frac{ 1 }{Q_{ij}(\mathcal {H}(i,j)| w)} \right) \cdot q \\&\cdot P( [A{\mathop {\Rightarrow }\limits ^{*|\mathcal {H}}} w(i,j)] \mid \left\langle x,\alpha \right\rangle ) , \end{aligned}$$

where $q = \prod _{(i,j) \in I_{|w|}} Q_{ij}(\mathcal {H}(i,j)| w)$. Note that the last term of the above equation can be written as:

$$\begin{aligned} P( [A{\mathop {\Rightarrow }\limits ^{*|\mathcal {H}}} w(i,j)] \mid \left\langle x,\alpha \right\rangle ) = \sum _{T_A \in \mathcal {T}(A,w,i,j,\mathcal {H})}P(T_A | \left\langle x,\alpha \right\rangle ). \end{aligned}$$

The denominator of the second term in the above equation exists in order to cancel $Q_{ij}(\mathcal {H}(i,j)| w)$ of constituent (i, j), as seen from Eq. 9. The following lemma is shown in the similar way to Lemma 3:

Lemma 4

(property of inside probabilities for restricted set of derivation trees) Let $w\in L(G)$, $A \in V$, $\alpha \in V^*$, $(i, j) \in I_{|w|}$ and

$$\begin{aligned} P^{\mathrm {IN}}( i,j,\alpha ) {\mathop {=}\limits ^{\mathrm {def}}}\ q^{-1}\ P([A{\mathop {\Rightarrow }\limits ^{*|\mathcal {H}}} w(i,j)], \mathcal {H}\ | \left\langle x,\alpha \right\rangle ) . \end{aligned}$$

If $i \ne j$,

$$\begin{aligned} P^{\mathrm {IN}}( i,j,\alpha ) = \frac{1}{Q_{ij}(\mathcal {H}(i,j)| w)} \sum _{k=i}^{j} f(i,k,j,\alpha ), \end{aligned}$$

where

$$\begin{aligned} f(i,k,j,\alpha ) =&P(\mathcal {H}(i,j) \rightarrow \mathcal {H}(i,k)\mathcal {H}(k+1,j)\ | \left\langle w(1,i-1),\alpha \right\rangle )\\&\cdot P^{\mathrm {IN}}(i,k, \mathcal {H}(k+1,j) \alpha )\ P^{\mathrm {IN}}(k+1, j, \alpha ). \end{aligned}$$

In addition,

$$\begin{aligned} P^{\mathrm {IN}}(i,i,\alpha ) = \frac{P(\mathcal {H}(i,i)\rightarrow w_i\ | \left\langle w(1,i-1),\alpha \right\rangle ) }{ Q_{ii}(\mathcal {H}(i,i)| w)}. \end{aligned}$$

From Lemma 4, the inside probabilities restricted by $\mathcal {H}$ are calculated in time $O(|w|^3|V|^{l})$. The algorithm to sample T restricted by $\mathcal {H}$ is obtained by replacing the Line 10 of Algorithm 2 as:

• 1. Sample k with a probability proportional to $f(i,k,j,\alpha )$ in Lemma 4, where $\alpha$ is the sequence of nonterminals in Z.

• 2. Substitute $\mathcal {H}(i,k)$ and $\mathcal {H}(k+1,j)$ into B and C, respectively.

With the above modified algorithm, we have the following theorem. The proof is done in the similar way to that of Theorem 1.

Theorem 2

Let G be a (k, l)-CSPG. Let $P_G(T, w, \mathcal {H})$ be the joint probability given by G (Eq. 9), where w is in $\Sigma ^*$ and $\mathcal {H}$ is an assignment of nonterminals for the interval set $I_{|w|}$. For any (k, l)-CSPG G, any string w, and any assignment $\mathcal {H}$, there is an algorithm which outputs $T \in \mathcal {T}(w, \mathcal {H})$ such that $T \sim P_G( T | w,\mathcal {H})$ and runs in time $O(|w|^3|V|^{l})$.

7 Experiments

7.1 Main experiments

In the experiments, we assess the following two points: a) the effect of (k, l)-CS probabilities in terms of the prediction accuracy, and b) the mixing speed and the practical computational costs of the proposed sampling algorithms. For (a), we compare (k, l)-CSPGs with changing k and their sampling algorithms, as well as other probabilistic language models. In the implementation, we set l to 0 because the existence of the left contexts increases the oder of the time complexity and thus the sampling procedure is not able to be iterated sufficient times. In addition, for (b), the running time for each iteration and the learning curves of the composite sampling algorithms are compared to those of the block sampling.

We extracted sentences from the Brown corpus (Francis and Kucera, 1982) with lengths of less than 16, and use them as the dataset for the experiments. Part-of-speech tags in Brown corpus annotated in the corpus were assumed to be terminals. The size of the dataset is 23,988, and the size of $\Sigma$, in which a symbol representing the end of the sentence is included, is 302. 10% of the dataset is used for testing, and the remaining is used for training.

We performed experiments for the cases that $(k,l)=(0,0)$, (1, 0) and (2, 0). Learning (0, 0)-CSPG with the blocked sampling is equivalent to learning infinite PCFGs (Liang et al., 2007).

Two sampling algorithms are implemented: one is the blocked sampling and the other is a composite sampling introduced in Sect. 6.1. In this implement of the composite sampling, we let

$$\begin{aligned} Q_{ij}(A|w) = P(S \Rightarrow ^{*|\mathcal {H'}} w(1,i-1) A) P (A \Rightarrow ^{*|\mathcal {H'}} w(i, j)\ |\ \left\langle w(1,i-1), \varepsilon \right\rangle , i, j), \end{aligned}$$

where $H'$ is the previous assignment of nonterminals for $I_{|w|}$. The time complexity for computing above equations is $O(|w|^2|V|^l)$.

Despite the above sampling procedure of the distituent nodes, $\mathcal {H}$ can offer likely nonterminals for each (i, j) as constituent nodes, and thus make it easy to change the shape of derivation trees. This allows samples of derivation trees to be mixed well and makes learning efficient.

As shown in Fig. 3a, compared to the blocked sampler, the proposed sampler obtains a better final score than the blocked sampler, though it slowly mixes in the early stage. The slow mixing is considered to be the effect of the pointwise sampling for nonterminals in the proposed sampling method.

Fig. 3

Comparing the proposed sampling with the blocked sampling for (0,0)-CSPG. The number of sentences is 23,988(train:21,589 test:2399) and the number of terminals $|\Sigma |$ is 302. The CPU of the machine where the experiments are done is Core i7-3930K

Figure 3b shows the practical computational cost of both methods as a function of the number of nonterminals. The cost of the blocked sampling is extremely high for the large number of nonterminals, while that of the proposed algorithm is small and the slope is relatively flat. Since the number of nonterminals increases as the time is elapsed, the blocked sampler becomes inefficient except for the early stage and thus does not give better results than the proposed sampler finally.

Figure 4a shows the result of the proposed sampler for learning CFGs with (1, 0)-context-sensitive probabilities. The mixing speed appears to be faster and the final score is better than it of PCFGs. The numbers of nonterminals are around 50 though they still appear to grow in the last stage (Fig. 4b).

Fig. 4

Experimental results for learning CFGs with (1, 0)-context-sensitive probabilities with the proposed sampler

In the following, we compare our models to other language models; Modified Kneser–Ney (Kneser and Ney, 1995) (MKN) and Hidden Markov models (HMMs). MKN is known to be a smoothed n-gram language model that gives low perplexities. HMMs are also compared. For learning HMMs, we used a python library called hmmlearn,³ which implements the EM algorithm for HMMs. First, as Table 1 shows, (1, 0)-CSPG learned by the proposed sampler has the highest score, which is better than the best one of both MKNs and HMMs. Each score in Table 1 represents the prediction accuracy, which is the average of $- \log P(s)$ for a sentence s in test data. The score of (1, 0)-CSPG is slightly better than those of (0, 0)-CSPG and (2, 0)-CSPG with composite sampling.⁴ In addition, the numbers of nonterminals for CFGs with (1, 0)-context-sensitive probabilities are smaller than those for PCFGs. This is a natural result because the existence of contexts allows multiple probabilities to be assigned to a nonterminal in (1, 0)-context-sensitive PCFGs. Since the smaller number of nonterminals gives the smaller computational cost for sampling, learning CFGs with (1, 0)-context-sensitive probabilities has the effect of reducing the actual computational cost compared to learning PCFGs.

Table 1 Comparing proposed algorithms to a baseline algorithm (modified Kneser–Ney;MKN)

7.2 Supplemental experiments

In this subsection, we have several experiments to explore the following three aspects of the model (k,0)-CSPGs:

• effects of exclusiveness of type-0 and type-2 rules,

• effects of suitable choice of distituent distribution Q,

• effects of length of left context k.

In the following experiments, we evaluate the algorithms using perplexities after a given number of iterations or a given time. Convergence to the proper posterior distributions is unlikely using Gibbs samplers for (k, 0)-PCFGs because the models do not have simple structures.⁵ Thus, it is not easy to separate the effect of mixing speed and the capability of the model. Increasing mixing speed is often crucial in practice, even if it is difficult to make the Markov chain converge.

7.2.1 Effects of exclusiveness of type-0 and type-2 rules

In the previous section, it is assumed that nonterminals can be divided into two classes exclusively, depending on whether they have type-0 rules or type-2 rules. While that assumption does not lose generality in practice by adding a terminal like EOS to the end of the sentence, in CNF, it is common for every nonterminal to be assumed to belong to both classes. We can define CSPGs in which every nonterminal possibly has both types. The probability of a rule with A on the left-hand side is given by multiplying the probability of the type of A by the probability of the rule given the type; i.e., $P(BC\mid A,\left\langle x,\alpha \right\rangle ) = P(\text{ type-2 } \mid A) P_{\text {type-2}}(BC\mid A,\left\langle x,\alpha \right\rangle )$ and $P(a\mid A,\left\langle x,\alpha \right\rangle ) = P(\text{ type-0 } \mid A) P_{\text {type-0}}(a\mid A,\left\langle x,\alpha \right\rangle )$. In the following, the former is referred to as Exclusive model, and the latter is referred to as Two-in-one model.

The experiments were carried out using a part of Brown corpus as in the experiments in the previous section. The total number of data is 2,000 for training data and 200 for test data. Block sampling was used for training. Generally, in MCMC sampling, the longer the number of iterations of training, the closer to the true posterior distribution. Therefore, training was carried out until 1,000 epochs were reached or 15 h had passed.

Fig. 5

Comparison of learning results between Exclusive model and Two-in-one model. 16 cores on Xeon(R) Gold 6140 were used in parallel

Figure 5 shows the training results for both models. First, in conclusion, Exclusive model scored higher than the Two-in-one model. In Exclusive model, the score (the average of log P(sentence) ) increases rapidly at the very early stage of learning, and even if the learning progresses, the difference from Two-in-one model does not close (Fig. 5a). This result can be explained in terms of the calculation time of sampling per sentence. Even if the theoretical posterior probabilities do not change much, the sampling speed is important for obtaining better prediction accuracy in a finite time. Taking the number of iteration on the horizontal axis as shown in Fig. 5b and d, it can be seen that the scores of both models are getting closer as the learning progresses, while the total number of nonterminals does not change much between the two models. This is because the nonterminals are divided into the two classes in Exclusive model. Since the computational time of block sampling is $O(|w|^3|V|^3)$ per sentence, the calculation time can be reduced to theoretically 1/8 in Exclusive model compared to Two-in-one model if the total numbers of nonterminals are the same. Figure 5c shows the relationship between the number of valid nonterminals, which are nonterminals that appear at least once in the sampled trees, and the calculation time per iteration. Exclusive model can process approximately twice as many nonterminals as Two-in-one model in the same calculation time.

7.2.2 Effects of distituent distributions (Q)

Theoretically, Q, which is a distribution for sampling distituent nodes used in the composite sampling, can be any distribution. However, practically, if $Q_{ij}$ does not assign a suitable nonterminal to the distituent node of position (i, j), that node is less likely to be sampled, resulting in poor mixing speed and slow learning. To investigate how Q effects learning speed, we implemented the following five distributions as $Q_{ij}$:

• (Rand) Uniform distribution over the valid nonterminals: $Q_{ij}(A) = 1/|V_{>0}|$, where $V_{>0}$ denotes the set of the valid nonterminals.

• (Freq) A distribution according to the frequency of occurrences of each nonterminal among the valid nonterminals: $Q_{ij}(A) = \#(A)/|\sum _{B\in V_{>0}} \#(B)|$, where $\#(A)$ denotes the number of occurrences of the nonterminal A in all sampled derivation trees.

• (Left) A distribution according to the frequency of occurrences of each nonterminal such that $w_i$ is derived from it as the first terminal:

  $$\begin{aligned} Q_{ij}(A|w) = \frac{ \#(A{\mathop {\Rightarrow }\limits ^{*}}w_i*)+ \alpha }{\sum _{B\in V_{>0}}\#(B{\mathop {\Rightarrow }\limits ^{*}}w_i *)+1} \end{aligned}$$

  where $\alpha = 1/|V_{>0}|$ (a smoothing parameter).

• (Right) Symmetrical to the above:

  $$\begin{aligned} Q_{ij}(A|w) = \frac{\#(A{\mathop {\Rightarrow }\limits ^{*}}*w_j)+ \alpha }{\sum _{B\in V_{>0}}\#(B{\mathop {\Rightarrow }\limits ^{*}}*w_j)+1} \end{aligned}$$

• (Pair) A distribution according to the frequency of occurrences of each nonterminal such that the terminals $w_i$ and $w_j$ are derived from it as the first terminal and the last terminal respectively:

  $$\begin{aligned} Q_{ij}(A|w) = \frac{\#(A{\mathop {\Rightarrow }\limits ^{*}}w_i * w_j)+\alpha }{\sum _{B\in V_{>0}}\#(B{\mathop {\Rightarrow }\limits ^{*}}w_i*w_j)+1} \end{aligned}$$

In the above, $\#(A{\mathop {\Rightarrow }\limits ^{*}}a*)$, $\#(A{\mathop {\Rightarrow }\limits ^{*}}*a)$, and $\#(A{\mathop {\Rightarrow }\limits ^{*}}a*b)$ denote the numbers of occurrences of A such that A is used for deriving ay, ya, and ayb for some $y \in \Sigma ^*$ in all the sampled trees, respectively.

Since sampling from above Qs can be done very fast, their computational costs are almost negligible compared to the computational cost for HPYPs.

The same dataset as in the previous experiments (a part of Brown corpus) was used. The target model for training is (1,0)-CSPG, and learning was performed by the composite sampling using the above five Q distributions. Training was carried out for 3,000 epochs.

Fig. 6

Comparison of learning results among 5 different distributions of Q with the composite sampling. A single core on Xeon(R) Gold 6140 was used for each experiment

Table 2 Comparison of learning results when changing types of distituent distribution on a small subset of Brown

As shown in Fig. 6a, Pair clearly outperforms other Q distributions with respect to prediction accuracy. In terms of both the calculation time and the number of iterations (Fig. 6b), the mixing speed of Pair distribution for Q is the fastest from the very beginning compared to other Q distributions. If the number of valid nonterminals is the same, the calculation time per sentence does not change for any distribution of Q because the calculation time for every Q is negligible. Therefore, the differences of time among Qs for completion of 3000 epochs are due to the differences in the numbers of valid nonterminals.

The distribution Pair predicts the probability that the nonterminal yields the substring using the terminals at both ends of it. Among the above distributions, Pair has the highest accuracy in predicting a nonterminal that yield the substring. Compared to other Qs, the shape of the derivation tree changes most smoothly using Pair because Pair can pick up the most suitable nonterminals to the distituent nodes.

Table 2 shows the final learning results for Qs. As mentioned above, Pair has the highest score and outperforms the best score of MKN. Freq was finally the second most accurate, and as expected, Rand was the least accurate.

7.2.3 Effects of length of left context

In these final experiments, we verify how changing the size k in the (k, 0)-SGPS model affects the learning results. The experiment was carried out using Penn Treebank (PTB) corpus. We used the part of speech tag as terminals and excluded sentences longer than 20. The size of training data is 18,565 and that of test data is 2,063. The number of terminals is 41. Composite sampling with the distribution Pair is used as the learning method. Learning was carried out until 1000 epochs were reached or 15 h had passed.

Fig. 7

Comparison of learning results among (0,0)-CSPGs to (5,0)-CSPGs for PTB datasets. 16 cores on Xeon(R) Gold 6140 was used for each experiment

Figure 7a and b show the scores as the functions of the elapsed time and the iterations. The score is highest when k is 2. The training completed 1000 epochs within 15 h only when $k=$ 2 or 3. From the graphs of the numbers of the valid nonterminals (Fig. 7d), we can see why the computational cost changes greatly depending on k. In particular, when $k=$ 0,1,or 5, the number of the nonterminals grows quickly from the early stage of learning. Such increase in the number of the nonterminals is the cause of increase in the computational cost.

Figure 7c shows the relationship between the numbers of the nonterminals and the scores. The slopes of the scores with respect to the numbers of the nonterminals are steep when $k =$ 0,1, or 2, while the slopes are flat when $k = 4,5$. Since the calculation time becomes longer as the number of the nonterminals becomes larger, the flatness of those slopes hinders the progress of learning.

Table 3 summarizes the final learning results of (k, 0)-CSPGs. As mentioned above, the score is highest when $k = 2$, which outperforms the best score of MKNs. The best score of MKNs is obtained at 9-gram for PTB, which is more than twice as long as for Brown corpus. A similar phenomenon is observed for learning (k, 0)-CSPGs; the model with $k = 2$ was the most accurate for PTB, while the model with $k = 1$ was the most accurate for Brown. In PTB corpus, it is more effective to build models that can take longer contexts into account.

From the Bayesian perspective, removing burn-in and taking an ergodic average (i.e., sampling scores multiple times and averaging them) are recommended. In fact, they make the scores lower: the score of the ergodic average with $k=2$ is 28.83 on PTB data, which is the best score among the listed scores in Table 3. On the other hand, when our aim is to learn an explicit grammar, taking a mixture of multiple grammars makes it difficult to interpret the learning results.

Table 3 Comparison of learning results when changing the length of left contexts on PTB

8 Related work

We have described largely two subjects in this paper. One is about the definition of mildly context-sensitive probabilities for CFGs using hierarchical PYPs, and the other is about new approaches proposed for efficient sampling which we call composite samplings.

In terms of context-sensitiveness, History-based Grammars, proposed by Black et al. (1993), is a very closely related approach to the (k,l)-CSPGs. They categorize all contexts emerged in left-most derivations, and use those categories as conditions when production rules are applied. Regarding nonparametric Bayseian models on CFGs, several recent studies have proposed various models which can relax the property of independence for the respective rules of PCFGs. For example, it is shown that learning tree substitution grammars (TSGs) from parse tree-annotated data yields high accuracy when parsing sentences. The rules of TSGs are elementary trees or tree fragments, instead of the production rules used in CFGs (Cohn et al., 2010; Shindo et al., 2012). TSGs can capture the dependencies between contexts and substrings. TSGs are learned from given trees in treebanks such as PTB in their methods. The adaptor grammars proposed by Johnson et al. (2007a) comprise a general framework that can weaken the independence between contexts and substrings in PCFGs. Pitman–Yor adaptor grammars were defined as a subclass of adaptor grammars, where the production probabilities depend on the number of subtrees in the derivation trees.

For efficient sampling, slice sampling called beam sampling (Gael et al., 2008) is can be applied to infer PCFGs (Takei et al., 2009). Blunsom and Cohn (2010) applied the slice sampling to infer synchronous grammars. Slice sampling is a method to cut off the rules when they are resampled by ignoring rules with enough small probabilities which is less than a given threshold. It is known to be effective real in terms of computational cost in many cases while it is not proven so far that it reduces the order of computational cost theoretically. Slice sampling can be combined with our method of composite sampling. When we sample nonterminals given derivation trees, while we used pointwise sampling or blocked sampling, applying slice sampling should reduce the practical computational cost significantly.

In Sect. 4.3, we assumed the base measure of the emissions ($H_{A}(a)$ for $a \in \Sigma$, or the base measure of $P(A\rightarrow \cdot )$ ) is uniform. Generally speaking, when $\Sigma$ is a set of words, a character-level language models are often introduced to represent morphological information (Clark, 2003) in various probabilistic language models. For example, Blunsom and Cohn (2011) incorporate a bigram model for word emissions into hidden Markov models. Mochihashi et al. (2009) also utilize a hierarchical Pitman–Yor language model (Teh, 2006b) for word segmentation tasks.

8.1 Connection to distributional learning

We begin with considering making the dual approach to be probabilistic by defining a distribution over substrings for each context: Let $P_{\text{ substr }}( \cdot | (l,r) )$ be a distribution over the substrings that a context (l, r) accepts. As the distribution of substrings should be nonparametric naively, PYPs are a suitable probabilistic model to describe such distributions:

$$\begin{aligned} P_{\text{ substr }}( \cdot | (l,r) ) \sim \text{ PYP }(\theta ,d,H_A), \end{aligned}$$

where A is a nonterminal and the base measure $H_A$ depends only on A and not on (l, r).⁶$H_A$ is analogous to L(A) in the deterministic dual approach, i.e., after a set of substrings are drawn from $H_A$, the probabilities over the set depend on (l, r). Intuitively, the advantage of the definition given above is that the distribution over L(A) can depend on (l, r), unlike probabilistic context-free grammars (PCFGs). In PCFGs, the probabilities of contexts and of substrings are independent for every nonterminal A: $P( S {\mathop {\Rightarrow }\limits ^{*}}lAr {\mathop {\Rightarrow }\limits ^{*}}lur) = P( S {\mathop {\Rightarrow }\limits ^{*}}lAr ) P(A {\mathop {\Rightarrow }\limits ^{*}}u)$.

However, there are two problems with the generative model described above. One problem is the sparsity of the substrings that each context accepts. The contexts are often sparse since the number of the patterns of the contexts exponentially increases as their length increases. Consequently, the number of substrings per context is almost zero in many cases. To avoid this, we can take advantage of the hierarchies of the base measures of PYPs by assuming that each context generates rules instead of substrings with probability $P_{\text{ rule }}(\cdot | lAr )$ and:

$$\begin{aligned} P_{\text{ rule }}(\cdot | lAr ) \sim \text{ PYP }(\theta ,d,H_{\pi (lAr)}), \end{aligned}$$

(11)

where $\pi$ is an arbitrary function that decreases the length of l or r from the outside, e.g., $\pi (lAra) = lAr$ or $\pi (alAr) = lAr$ for any letter a. $H_{\pi (lAr)}$ is obtained recursively.

Another problem is that the generative model defined in Eq. 11 fails to define the probabilities for generated sentences, unless all the rules are linear. Equation 11 assumes that the context (l, r) of A is known before a rule $A \rightarrow \alpha$ is generated. The contexts for rules should be pairs of sequences that include nonterminals around the nonterminal, to which the objective rule is applied. In order to avoid that, we use the leftmost derivation to define the contexts of the rules. Finally, we obtain almost the same model with (k,l)-Context-Sensitive Probabilistic Grammars with PYPs, of which details are described in Sect. 4.4.

9 Conclusion

We show that taking a value of k that is not zero gives good results in terms of both prediction accuracy and computational cost in the experiments. On the other hand, as shown in Sect. 5.1, the time complexity of the blocked sampler and the proposed sampler are proportional to $|V|^{l+3}$ and $|V|^{l+1}$, respectively. Taking a value of l that is not zero increases the time complexity significantly. Since the computational cost become critical, the proposed sampler may be of advantage when $l \ne 0$.

In all the experimental results shown here, the prediction probabilities for the test data monotonically increase and basically do not decrease no matter how much the learning progresses. That is one of the advantages of the Bayesian methods, which is the effect of the parameters (the probabilities of the rules and the derived trees) being sampled according to the posterior distribution.

In this study, the way of constructing the hierarchies of base measures is straightforward, and it may be appropriate in general cases. It is likely that these hierarchies will fail to capture the appropriate patterns of contexts in many cases. Pickhardt et al. (2014) proposed the use of combinations of skipped n-grams for smoothing and showed that those combinations actually yielded better result. For (k, l)-context-sensitive PCFGs, we should examine whether it might be possible to mix the orders of constructing the hierarchies of base measures.

As for the relation to the recent development of neural models, standard neural language models such as LSTMs (Hochreiter and Schmidhuber, 1997) and Transformers (Vaswani et al. 2017) do not learn grammatical structures without supervision. In the context of applying neural networks to unsupervised learning of grammatical structures, several recent studies incorporate neural models to calculate the probabilities of production rules in PCFGs (Kim et al., 2019; Zhu et al., 2020). Those methods are fundamentally on traditional PCFG models, in which a probability is assigned to each production rule. Incorporating neural models into the probabilities of the production rules of (k,l)-CSPCGs with the nonparametric Bayesian model remains as future work.