Imprimitive groups synchronizing a transformation of non-uniform kernel

Abstract

In this paper, we provide a method to determine when transitive imprimitive groups synchronize a transformation of non-uniform kernel, that is, we give the condition of $\langle G,\alpha \rangle$ being a synchronizing semigroup where G is transitive imprimitive and $\alpha$ is transformation of non-uniform kernel.

1 Introduction

Suppose that a deterministic finite automata $A=(Q,\Sigma )$ is such that all but one letters from the alphabet $\Sigma$ act as permutations of the state set Q and the exceptional letter acts as a transformation with non-uniform kernel. In other words, the automata A can be regarded as a transformation semigroup $\langle G,\alpha \rangle$ where G is a permutation group and $\alpha$ is a non-invertible transformation. Which properties of the permutation group G ensure that $\langle G,\alpha \rangle$ becomes a synchronizing semigroup?

This question has attracted the attention of many experts, and they have obtained a lot of innovative results about primitive groups. In 1995, Rystov in [1] proved that a transitive permutation group of degree of n is primitive if and only if it synchronizes every map of rank $n-1$. In 2009, Neumann in [2] proved that any non-synchronizing primitive group fails to synchronize some uniform transformation.that the primitive group G synchronizes some special maps. In 2013, Araújo, Bentz and Cameron in [3] provided two methods to find non-synchronizing but almost synchronizing groups, that is, G is a primitive group and it synchronizes every non-uniform transformation.

In this paper, we are interested in the case that the groups G are transitive imprimitive. Let $\Delta$ be a non-trivial block of G and $\Sigma =\{\Delta g ~|~ g\in G\}$ be the system of blocks containing $\Delta$. For transitive imprimitive groups, it is easy to see that every imprimitive group fails to synchronize a non-uniform transformation which its kernel classes are contained in a system of blocks of G (see Theorem 2.7 in [4]). Meanwhile, observe that there are many primitive groups G which are contained in a union of imprimitive groups, that is, $G=\bigcup _{i=1}^t H_i$ where $H_i$ is a imprimitive group. Araújo et al in [5] prove that there are infinite families of primitive groups entirely composed of imprimitive permutations (A permutation $g\in S_n$ is said to be imprimitive if there exists an imprimitive group containing g.). Further, if H is an imprimitive subgroup of the primitive group G and $\langle H,\alpha \rangle$ is a synchronizing semigroup for $\alpha$ being a non-invertible transformation, then $\langle G,\alpha \rangle$ must be a synchronizing semigroup. Hence it is natural to consider that when $\langle G,\alpha \rangle$ is synchronizing where G is imprimitive. In section 3, we provide a method to determine when imprimitive groups synchronize a transformation of non-uniform kernel, that is, we give the condition of $\langle G,\alpha \rangle$ being a synchronizing semigroup where G is transitive imprimitive and $\alpha$ is transformation of non-uniform kernel.

2 Notation and preliminary results

Let $T_n$ and $S_n$ be the full transformation semigroup and the symmetric group on $X_n=\{1,2,\cdots ,n\}$, respectively. A partition $\rho$ of $X_n$ is a non-synchronizing partition for $G\le S_n$ if there is a subset T of $X_n$ such that $|P\cap T^g|=1$ for all parts P of $\rho$ and all g in G. The set T is called a G-regular section for $\rho$. A partition $\rho$ of $X_n$ is said to be uniform if all its parts have the same size. Given an equivalence relation $\rho$ on $X_n$ define

$$\begin{aligned} E_\rho =\{\{xg,yg\}\in X_n^{\{2\}}: x\equiv y(mod\rho ),x\ne y,g\in G\} \end{aligned}$$

and given $T\subseteq X_n$ define

$$\begin{aligned} E_T=\{\{xg,yg\}\in X_n^{\{2\}}: x, y\in T,x\ne y,g\in G\}. \end{aligned}$$

Here $X^{\{2\}}$ is the set of unordered pairs, that is 2-subsets, from $X_n$. Then define $\Gamma _\rho$ and $\Gamma _T$ to be the graphs with vertex set $X_n$ and edge sets $E_\rho$ and $E_T$, respectively. We will denote adjacency in $\Gamma _\rho$ by $\thicksim$. The neighborhood of an element x in $\Gamma _\rho$ will be denoted by $\Gamma _\rho (x)=\{y : x\thicksim y \}$ and the closed neighborhood of x in $\Gamma _\rho$ will be denoted by $\Gamma _\rho [x]=\{x\}\cup \{y : x\thicksim y \}$.

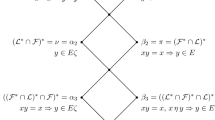
Suppose that $\rho$ is a G-non-synchronizing partition of $X_n$ as witnessed by a section T. If G is a primitive group, then $\Gamma _\rho$ is vertex-transitive and $\Gamma _\rho$ is the complement of $\Gamma _T$. If G is an imprimitive group, the result is not necessarily true. For example, let $G=\langle (1,2,3,4,5,6)\rangle$ be a cyclic group on $X_6$. Suppose that $\rho _1=\{[1,4],[2,3]$ $,[5,6]\}$ and $T_1=\{1,3,5\}$. Then $\Gamma _{\rho _1}$ is vertex-transitive and $\Gamma _{\rho _1}$ is the complement of $\Gamma _{T_1}$ (see Picture (1,2)). Suppose that $\rho _2=\{[1,4],[2,5],[3,6]\}$ and $T_2=\{1,2,3\}$. Then $\Gamma _{\rho _2}$ is not vertex-transitive and $\Gamma _{\rho _2}$ is the complement of $\Gamma _{T_2}$ (see Picture (3,4)). Suppose that $\rho _3=\{[1,2],[3,4],[5,6]\}$ and $T_3=\{1,3,5\}$. Then $\Gamma _{\rho _3}$ is vertex-transitive and $\Gamma _{\rho _3}$ is not the complement of $\Gamma _{T_3}$ (see Picture (5,6)). Suppose that $\rho _4=\{[1,4],$ $[2,5],[3,6]\}$ and $T_4=\{1,3,5\}$. Then $\Gamma _{\rho _4}$ is not vertex-transitive and $\Gamma _{\rho _4}$ is not the complement of $\Gamma _{T_4}$ (see Picture (7,8)).

Lemma 2.1

Suppose that $G\le S_n$ is a transitive and imprimitive group and $\rho$ is a G-non-synchronizing partition of $X_n$ as witnessed by a section T. Then

• (1) T is a largest clique in $\Gamma _T$;

• (2) P is a maximal clique in $\Gamma _\rho$.

Proof

The result is implicit in the proof of Lemma 2.6 (see [2]). Then the proof is omitted. $\square$

Lemma 2.2

Suppose that $\rho$ is a G-non-synchronizng partition and P is a part of $\rho$. Then

$$\begin{aligned} \bigcap _{x\in P}\Gamma _\rho [x]=P. \end{aligned}$$

Proof

By Lemma 2.1, P is a maximal clique in $\Gamma _\rho$. Clearly P is contained in the intersection on the left; if the intersection contained an additional point z, then $P\cup \{z\}$ would be a clique, a contradiction. $\square$

The next lemma is the Lemma 2.4 (see [4]).

Lemma 2.3

Let G be a transitive and imprimitive group on $X_n$ with non-trivial blocks $\Delta$ and let $\alpha \in T_n\setminus S_n$ with $rank(\alpha ^2)=rank(\alpha )$. Then $\langle G,\alpha \rangle$ is a completely regular semigroup if and only if $ker(\alpha )=\{\Delta g ~|~ g\in G\}$ or $im(\alpha )=\Delta$ and $|A_i\cap \Delta g|=1$ for all $A_i\in ker(\alpha )$ and all $g\in G$.

At last, in order to formulate our main theorem, we recall some definitions. Let $\rho$ be a G-non-synchronizing partition of $X_n$ as witnessed by a section T and P be a part of $\rho$. We define the parameter m(P, T) to be the smallest number m such that the intersection of the closed neighborhoods of any m points of P in $\Gamma _\rho$ is equal to P, that is,

$$\begin{aligned} m(P,T)= min\{ |A|: A\subseteq P, \bigcap _{x\in A}\Gamma _\rho [x]=P\}. \end{aligned}$$

We define a parameter m(G) as follows: m(G) is the maximum of m(P, T). We also need an additional condition. For two distinct G-non-synchronizing partitions $\rho$ and $\sigma$ of the same rank k, let $M(\rho ,\sigma )=\frac{|\rho \cap \sigma |}{k}$; and set M(G) to be the maximum over all such pairs.

3 The main results

We will show that imprimitive groups G synchronize a kind of special transformations with $m(G)=2$ and $M(G)\le 1/2$ (see Theorem 3.8).

Lemma 3.1

Let G be a transitive group on $X_n$ and $\alpha \in T_n$ be a transformation whose kernel is a non-uniform partition. If the semigroup $S=\langle G,\alpha \rangle$ is non-synchronizing, then there exists a map $q\in S$ such that $rank(q)>k_S$, $rank(qgq)\in \{rank(q),k_S\}$ for all $g\in G$, and that there exists an $h\in G$ with $rank(qhq)=k_S$ where $k_S$ is the smallest rank of the transformations in S.

Proof

The proof of this lemma follows in a same way of Lemma 3 in [3]. Let

$$\begin{aligned} Q=\{a\in \langle G,\alpha \rangle : rank(a)>k_S~and~(\exists h\in G)~rank(aha)=k_S\}. \end{aligned}$$

As $rank(\alpha )>k_S$, there exist elements $g_1,\cdots ,g_m\in G$ such that $rank(\alpha g_1\alpha \cdots \alpha g_{m-1}\alpha )>k_S$ and $rank(\alpha g_1\alpha \cdots \alpha g_{m}\alpha )=k_S$. This implies that

$$\begin{aligned} rank((\alpha g_1\alpha \cdots \alpha g_{m-1}\alpha )g_m(\alpha g_1\alpha \cdots \alpha g_{m-1}\alpha ))\le rank(\alpha g_1\alpha \cdots \alpha g_{m}\alpha )=k_S \end{aligned}$$

and in fact $rank((\alpha g_1\alpha \cdots \alpha g_{m-1}\alpha )g_m(\alpha g_1\alpha \cdots \alpha g_{m-1}\alpha ))=k_S$, as $k_S$ is the smallest rank possible. Hence Q is non-empty. Let $q\in Q$ be of minimal rank. We claim that q satisfies the desired property.

By definition of Q, $rank(q)>k_S$ and there exists $h\in G$, with $rank(qhq)=k_S$. Let $g\in G$. If $rank(qgq)>k_S$, then $rank((qgq)h(qgq))=rank(qg(qhq)gq)\le rank(qhq)=k_S$. As above, it follows that $rank((qgq)h(qgq))=k_S$. Thus $qgq\in Q$ and as q has minimal rank in Q, $rank(qgq)=rank(q)$. The result follows. $\square$

Corollary 3.2

If q, h satisfy the condition of lemma 3.1, then $\langle G,qhq\rangle$ is a completely regular semigroup.

Proof

Since $rank(qhq)=k_S$, then $rank((qhq) g (qhq))=rank(qhq)$ for all $g\in G$. Thus $\langle G,qhq\rangle$ is a completely regular semigroup.

Theorem 3.3

Let G be a transitive imprimitive group on $X_n$ and $\alpha \in T_n$ be a transformation whose kernel is a non-uniform partition. Let $\Omega$ be the set of all systems of blocks of G.

• (1) If there exists $\Sigma \in \Omega$ such that $A_i\subseteq \Delta g$ for all $A_i\in ker(\alpha )$ and $\Delta g\in \Sigma$, then $\langle G,\alpha \rangle$ is a non-synchronizing semigroup and $ker(qhq)=\Sigma$ for $\Sigma \in \Omega$.

• (2) Suppose that there is $A\in ker(\alpha )$ such that $A\nsubseteq \Delta$ for all blocks $\Delta$ of G. If $\langle G,\alpha \rangle$ is a non-synchronizing semigroup, then $|A_i\cap \Delta g|=1$ for all $A_i\in ker(qhq)$ and all $g\in G$.

Proof

• (1) By the result of Theorem 2.7 in [4], $\langle G,\alpha \rangle$ is a non-synchronizing semigroup. By Lemma 2.3 and Corollary 3.2, we can find that $ker(qhq)=\Sigma$ for $\Sigma \in \Omega$.

• (2) Since there is $A\nsubseteq \Delta$ for all blocks $\Delta$ of G and ker(qhq) is uniform, then a block of ker(qhq) is either a block of $ker(\alpha )$ or a union of blocks from $ker(\alpha )$. By Lemma 2.3 and Corollary 3.2, since $\langle G,\alpha \rangle$ is a non-synchronizing semigroup, then $|A_i\cap \Delta g|=1$ for all $A_i\in ker(qhq)$ and all $g\in G$.

$\square$

Note that, from Corollary 3.2, we find that ker(qhq) is a G-non-synchronizing partition as witnessed by the section im(qhq). Meanwhile, by Theorem 3.3, there are two kinds of G-non-synchronizing partitions for a transitive imprimitive group G, but ker(qhq) is the only G-non-synchronizing partition for the semigroup $\langle G,\alpha \rangle$.

Now we make an assumption that G is a transitive imprimitive group with $m(G)=2$ and $M(G)\le 1/2$ and $\rho$ is a G-regular partition of $X_n$ as witnessed by a section T. Further, suppose that $\Gamma _\rho$ is vertex-transitive and $\Gamma _\rho$ is the complement of $\Gamma _T$.

The following lemma is a direct consequence of $m(G)=2$.

Lemma 3.4

Suppose that $T\subseteq X_n$ is a G-regular section for two non-synchronizing partitions $\rho$ and $\sigma$. If $x\not =y$ and $y\in [x]_\rho \cap [x]_\sigma$, then $[x]_\rho =[x]_\sigma$

Proof

Since $\Gamma _\rho$ ($\Gamma _\sigma$) is the complement of $\Gamma _T$, $\Gamma _\rho$ ($\Gamma _\sigma$) is vertex-transitive and $m(G)=2$, then $[x]_\rho =\Gamma _\rho [x]\cap \Gamma _\rho [y]=[x]_\sigma$. $\square$

Remark 3.5

The result of Lemma 3.4 need not be true when $\Gamma _\rho$ ($\Gamma _\sigma$) is not vertex-transitive. Let $G=\langle (1,9)(2,10)(3,11)(4,12)(5,14)(6,13)(7,16)(8,15),$ (1, 5)(2, 6)(3, 16)(4, 15)(7, 11)(8, 12)(9, 14) (10, 13),  $(1,8,6,11)(2,7,5,12)(3,9,15,13)(4,10,16,14) \rangle$ (TransitiveGroup(16, 2) in GAP [6]). Suppose that $\rho =\{[1,2,5,6], [3,4,15,16],$ [7, 8,  $11,12],[9,10,13,14]\}$ and $\sigma =\{[1,5,9,14],[2,6,$ 10, 13], [3, 7, 11, 16], [4,  $8,12,15]\}$ are two non-synchronizing partitions for G as witnessed by the same section $T=\{1,4,7,13\}$. But, as $m(G)=2$, the result in Lemma 3.4 is false.

The next two results will show that if the semigroup $\langle G,\alpha \rangle$ is non-synchronizing, then the transformation q will take a special form.

Lemma 3.6

If $k_S>1$, then for any $g\in G$, a block of ker(qgq) is either a block of ker(q) or a union of singleton blocks from ker(q).

Proof

For q satisfying the condition of Lemma 3.1, if $rank(qgq)=k_S$ for $g\in G$, then the result being trivially true otherwise. Let $A_1$ and $A_2$ be distinct blocks of ker(q) such that $A_1\cup A_2$ is contained in a block B of ker(qgq), say $A_1q=\{a_1\}$ and $A_2q=\{a_2\}$ with $a_1\not =a_2$.

As $k_S>1$, $\{B,X_n-B\}$ is a partition of $X_n$. Since B is not a block of G, then there exists an $h\in G$ such that $a_1h\in B$ and $a_2h\notin B$. Note that for any $a\in G$, im(qgq)a is a section for both ker(qgq) and ker(qhqgq) (otherwise, qgqaqhqgq would have rank smaller that qgq). So, by the previous lemma, we know that any two blocks of ker(qgq) and ker(qhqgq) that have two elements in common must agree.

However, the $A_1$-block of ker(qgq) contains $A_2$ while the $A_1$-block of ker(qhqgq) dose not. Hence $A_1$ cannot contain two elements and must be a singleton. The general result follows by symmetry. $\square$

Lemma 3.7

Let $k_S>1$. Then the partition ker(q) consists of r sets of order 1, and s sets of order $p>1$, such that r is a multiple of p, $r<sp$, $r\ge 1$, $s\ge 1$.

Proof

For qgq as above, $rank(qgq)=k_S$. In order for qgq to have smaller rank then q, only singleton classes of ker(q) can form larger blocks of ker(qgq) by the previous lemma. As ker(qgq) is uniform (see Theorem 2.1 in [2]), the non-singleton classes must have the same size, say p. Moreover, the singletons must combine in multiples of p. As q is non-uniform we also get that $s,r\ge 1$.

Since $ker(qgq)(=\rho )$ is a G-non-synchronizing partition as witnessed by the section $im(qgq)(=T)$ and we have assumed that $\Gamma _\rho$ is the complement of $\Gamma _T$, then the singleton classes of ker(q) which are not in a same block of G can form larger blocks of ker(qgq). Now pick an element $d\notin im(q)$ and an image f of a non-singleton block of ker(q). It is easy to find that d and f are not in a same block of G. Then there is $h\in G$ be such that dh is in the union of the singleton classes of ker(q) and fh is in its complement. Note that $rank(qhq)< rank(q)$ as $dhq\notin im(qhq)$, and hence $rank(qhq)=k_S$. However this require that h maps all images of singleton classes into non-singleton classes (of ker(q)). As h also maps f into this set, if follows that r is strictly less than sp. $\square$

Now we are ready to prove our theorem.

Theorem 3.8

Let G be a transitive imprimitive group on $X_n$ with $m(G)=2$ and $M(G)\le 1/2$. If $\alpha \in T_n$ is a transformation where $ker(\alpha )$ is non-uniform and there is a non-singleton class $A\in ker(\alpha )$ such that $A\nsubseteq \Delta$ for all blocks $\Delta$ of G, then $\langle G,\alpha \rangle$ is a synchronizing semigroup.

Proof

Assume otherwise, that is, let $k_S>1$ and q be a transformation satisfying the conditions of Lemma 3.4 and Lemma 3.7. Suppose that $rank(qgq)=k_S$ for $g\in G$. Since $ker(\alpha )$ is non-uniform and there is a non-singleton class $A\in ker(\alpha )$ such that $A\nsubseteq \Delta$ for all blocks $\Delta$ of G, then $|A_i\cap \Delta g|=1$ for all $A_i\in ker(qgq)$ and all $g\in G$. Let $(a,b)\in ker(qgq)$ such that $(a,b)\notin ker(q)$. Let $h\in G$ satisfy $aqh\in B$, $bqh\notin B$ for some block B of ker(qgq).

Consider the functions qhqgq and qgq, both of rank $k_S$. Note that im(qgq) must ba a G-regular section for both ker(qhqgq) and ker(qgq). All non-singleton blocks of ker(q) are in ker(qgq) by Lemma 3.6. The same holds for ker(qhqgq), as it needs to be uniform and contained in ker(q).

By Lemma 3.7 we have that the number of these blocks is larger than $k_S/2$. Our assumption $M(G)\le 1/2$ now shows that $ker(qgq)=ker(qhqhq)$. However, it is easy to check that $(a,b)\notin ker(qhqqq)$.

Hence $k_S=1$ and $\langle G,\alpha \rangle$ is a synchronizing semigroup. $\square$

The parameter m(G) induces an hierarchy on transitive imprimitive groups. We hope that this hierarchy helps classifying the pair $(G,\alpha )$ such that the semigroup $\langle G,\alpha \rangle$ is synchronizing where G is transitive imprimitive and $\alpha$ is a non-invertible transformation. In [7], we have proved that $m(G)=2$ implies $M(G)=0$ for G being primitive. This need not be true when G is transitive imprimitive (Since a G-non-synchronizing partition might be contained in a system of blocks of G.). At last, we give some examples of imprimitive groups with $m(G)=2$.

Example 3.9

Suppose that G are imprimitive groups on $X_n$ ($n<16$). Then G is $m(G)=2$.

• (1) $n=4$, $G\cong C(4), D(4)$;

• (2) $n=6$, $G\cong F_{18}(6), F_{18}(6):2, F_{36}(6), F_{36}(6):2$;

• (3) $n=8$, $G\cong E(8):A_4, 1/2[E(4)^2:S_3]2, E(8):S_4, [A(4)^2]2, [1/2.S(4)^2]2,$ $1/2[S(4)^2]2$,$[S(4)^2]2;$

• (4) $n=10$, $G\cong [5^2]2, [1/2.D(5)^2]2, 1/2[D(5)^2]2, [5^2:4]2,[5^2:4]2_2, [5^2:4_2]2,$ $[5^2:4_2]2_2$,$[D(5)^2]2, [1/2.F(5)^2]2, 1/2[F(5)^2]2, [F(5)^2]2, [A(5)^2]2, [1/2.S(5)^2]2,$ $1/2[S(5)^2]2, [S(5)^2]2$;

• (5) $n=12$, $G\cong M_{10}(12), PGL(2,9)(12), M_{10.2}(12), [L(6)^2]2, 1/2[(L(6):2)^2]2,$ $[1/2.(L(6):2)^2]2$,$[(L(6):2)^2]2, [A(6)^2]2, [1/2.S(6)^2]2, 1/2[S(6)^2]2, [S(6)^2]2;$

• (6) $n=14$, $G\cong [7^2]2, 1/2[D(7)^2]2, [1/2.D(7)^2]2, [7^2:3]2, [7^2:3_3]2, L_7:2(14),$ $[D(7)^2]2,[1/6_-.F_{42}(7)^2]2_2, [1/6_+.F_{42}(7)^2]2_2, [7^2:6]2, [7^2:6_3]2,$ $1/2[1/2.F_{42}(7)^2]2, [D(7)^2:3_3]2, [D(7)^2:3]2, [D(7)^2:3]2, 1/2[F_{42}(7)^2]2,$ $[1/2.F_{42}(7)^2]2, [F_{42}(7)^2]2, [L(7)^2]2, [A(7)^2]2, 1/2[S(7)^2]2,[1/2.S(7)^2]2, [S(7)^2]2.$