Abstract
Recent progress in the understanding of the behavior of the interference channel has led to valuable insights: first, discrete signaling has been discovered to have tangible benefits in the presence of interference, especially when one does not wish to decode the interfering signal, i.e., the interference is treated as noise, and second, the capacity of the interference channel as a function of the interference link gains is now understood to be highly irregular, i.e., non-monotonic and discontinuous. This work addresses these two issues in an integrated and interdisciplinary manner: it utilizes discrete signaling to approach the capacity of the interference channel by developing lower bounds on the mutual information under discrete modulation and treating interference as noise, subject to an outage set, and addresses the issue of sensitivity to link gains with a liquid metal reconfigurable antenna to avoid the aforementioned outage sets. Simulations illustrate the effectiveness of our approach.
Similar content being viewed by others
1 Introduction
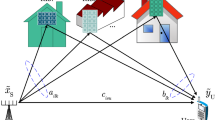
One of the main difficulties in communication over wireless networks is interference, many of whose characteristics can be modeled and understood via the Gaussian interference channel [1] (see Fig. 1). This model, which can be used as a building block for other interference networks, has a capacity that is not known in the most general case, but in recent years much progress has been made in understanding its complicated behavior, e.g., [2].
It is known that capacity of this channel model is non-monotonic in the strength of interference links. In particular, if the interference is strong enough, the capacity of each link is equivalent to interference-free capacity [3]. More recent developments have shown that the capacity of the interference channel is very sensitive to channel coefficients; the operational significance of this fact is in the proliferation of sets or “pockets” in the vector space of channel gains, called “outage sets,” that are unable to support a desired set of transmission rates.
Furthermore, evidence has been accumulating [4] that discrete signaling imparts tangible benefits in managing interference, because if applied at the right scale, it can push interference to locations in the signal space that are less damaging to the desired signal. This is especially important when the decoder does not know the structure of the interference, or for complexity reasons does not wish to decode the interference.
Motivated by the observations made above, this paper makes contributions to interference mitigation that are of an interdisciplinary nature, via advances in signaling and coding as well as antenna design. The two key components of this paper mirror the issues highlighted above: (1) to get as close to the capacity of the interference channel as possible via discrete signaling and to efficiently and accurately characterize these achievable rates and (2) to address the issue of the sensitivity of the interference channel capacity with respect to link gains. The former is addressed by developing new bounds on the mutual information of the two-user Gaussian Interference channel under discrete modulations, subject to an outage set. The latter is addressed by a reconfigurable antenna technology to avoid as much as possible the aforementioned outage sets.
For a discrete modulation transmission strategy at the transmitter, and a receiver that does not decode or peel off the interference (also known as treating interference as noise, specifically TINnoTS—Treating interference as noise with no time sharing [4]), we calculate a bound on mutual information with a constant gap \(O\left( \log \gamma \right)\) to capacity (excepting an outage set) in the strong interference channel (where capacity is known). Our technique builds on Ozarow and Wyner [5], and the gap is an improvement over the \(O\left( \log \left( \gamma ^{-1}\ln {\mathrm{min}} \left\{ h_1^2P,h_2^2P\right\} \right) \right)\) gap reported in [4] with mixed inputs.
For avoiding the channel gains leading to outage, we propose to use liquid metal reconfigurable antennas. Liquid metal devices and circuits have been implemented using various reported techniques [6,7,8,9,10,11]. Liquid metal antennas have the capability of changing the radiation [12, 13], polarization [14, 15], and resonant frequency of individual antennas [16, 17], thereby modifying the gains between different nodes in a manner beyond what is possible with signal processing alone. The feasibility of avoiding problematic or singular channel gains with liquid metal antennas is demonstrated via experimental extraction of the operating parameters of the proposed liquid metal antennas and then using these parameters in extensive simulations of the channel states produced by the liquid metal antennas and matching it with the low minimum-distance channel gains suggested by analysis.
An early version of this work appeared in [18]; the present paper goes beyond [18] in the following aspects: (a) Theorem 2 is reformulated and its expression is distinct from the results of [18], (b) Sect. 5 on successive interference cancellation is novel, (c) Sect. 6.1 involving analytical and simulation modeling based on a dipole model is new, (d) several insightful simulations, including those represented in Figs. 9, 11, 12, are novel with respect to [18].
1.1 Definitions and notation
Throughout the paper, we use pulse amplitude modulation (PAM) for transmitted signals. Specifically, by n-PAM modulation we mean a uniform distribution over the points
which results in zero mean and unit variance.
The support of a real-valued random variable, denoted with \({{\text{supp}}}[\cdot ]\), is the set of points \(x\in {\mathbb{R}}\) that have nonzero probability under that random variable. The cardinality of a set (including that of a support) is denoted with \(|\cdot |\). The symbol \(\sim\) is used as an operator which means a random variable being drawn according to a probability law, e.g., \({\mathcal{N}}\left( \beta \right)\) denotes a Gaussian probability law with zero mean and variance \(\beta \in {\mathbb{R}}^{+}\). With a constant on the right hand side, e.g., \(a\sim b\), this notation indicates that a, b are of the same order.
2 Methods
The aim of the paper is to show that a combination of discrete modulation and liquid metal antennas can be used to achieve close to capacity in interference channels while treating interference as noise.
The methodology used is fairly unique. The paper combines information theory calculations, specifically novel bounds on discrete modulation, with realistic simulations of liquid metal antennas. The simulations were conducted with ANSYS High-Frequency Structure Simulator (HFSS) software. The simulated antenna patterns are fed into the information theory bounds, while transmit powers are set at realistic values, as shown in results section.
3 Channel model and discrete modulation
As argued in Introduction, to investigate the effect of interference, we consider the interferencer channel in Fig. 1.
The received signals are
where the random variables \(X_{i},X_{j},Z_{i},Z_{j}\) are mutually independent, \(Z_{i},Z_{j}\sim {\mathcal{N}}(N)\) are independent Gaussian random variable with variance N, and \({\mathbb{E}}\left[ X_{1}^{2}\right] ,{\mathbb{E}}\left[ X_{2}^{2}\right] \le 1\), and P is the power constraint on the transmitters. The coefficients \(h_{1}\) and \(h_{2}\) are the channel gains.
As shown in Fig. 1 and Eq. (2), we only consider the symmetric interference channel. In principle, results can be generalized to non-symmetric channels, but results become quite messy; in many expositions on the interference channel [1, 2], the authors start with the symmetric channel, which we will follow. In line with the symmetry of the channel, we will consider symmetric capacity, i.e., where the users share the capacity equally.
There are a few cases where the capacity of the interference channel is known. If the interference is (very) weak, \(|h_{2}|\ll |h_{1}|\), specifically \(\frac{|h_{2}|}{|h_{1}|}\left( 1+h_{2}^{2}\frac{P}{N}\right) \le \frac{1}{2}\), the sum capacity is achieved by using Gaussian signaling and treating interference as noise (TIN) [19, 20],
i.e., a symmetric capacity of \(C=\frac{1}{2} \log \left( \frac{h_{1}^{2}{P/N}}{1+h_{2}^{2}{P/N}}\right)\) On the other hand, if the interference is strong \(|h_{2}|>|h_{1}|\), capacity can be achieved with Gaussian signaling and joint decoding at the receivers [21, 22], achieving the following symmetric capacity
While treating interference as noise might be optimal for weak interference, the rate (3) is far from capacity (4) for strong interference. However, [4] showed that when discrete modulation is used, it is often possible to get close to the capacity (4) with TIN (specifically TINnoTS—treating interference as noise with no time sharing). This is explained in Fig. 2. To decode the desired signal, we can simply take the modulus with respect to the interfering signal [4, Sect. VIII] and then decode as though there was no interference. Specifically, we “fold” the signal into the interval \(\left[ -|h_2|\sqrt{\frac{3}{n^2-1}},|h_2|\sqrt{\frac{3}{n^2-1}}\right]\) for n odd (see (1)). This only requires knowledge of the modulation of the interfering signal, not the encoding. Thus, discrete modulation is advantageous for treating interference as noise.
In this paper, we extend the results in [4] to show that TINnoTS can always get close to capacity, except in a few outage regions. We will then show that these outage regions can be avoided through liquid metal antennas.
A major issue with discrete modulation is that it is difficult to calculate mutual information and therefore achievable rate. An elegant lower bound was derived by Ozarow and Wyner in [5] and improved in [4]. Let \(X_d\) be any discrete random variable; then
where \(c_{0}=\frac{1}{2}\log \left( \frac{2\pi e}{12}\right)\), \(H(\cdot )\) is discrete entropy; the key parameter in this bound is \(d_{{\mathrm{min}} }(h_{1}X_{d})\), which is the smallest distance between constellation points in the received signal. This bound, for the point-to-point channel, can also be used to bind the achievable rate in the interference channel. Let
be the received signal at receiver 1 before noise is added. Notice that except on a set of probability zero of \(h_1, h_2\) there is a one-to-one map \((X_1,X_2)\leftrightarrows {\widetilde{X}}_d\) as \(X_1\) and \(X_2\) are discrete. We can then bound the achievable rate by
Here (a) is from the chain rule of entropy [23]: \(I({{\widetilde{X}}}_d;Y_1)=I(X_1,X_2;Y_1)=I(X_1;Y_1)+I(X_2;Y_1|X_1)\), where in the first step we have used the one-to-one map \((X_1,X_2)\leftrightarrows {\widetilde{X}}_d\). The inequality (b) is because mutual information is upper bounded by entropy, and (c) is from (5).
Minimum distance. Minimum distance of sum of two PAM signals with \(n=10\) as a function of \(h_2\) with \(h_{1}=1\). \(d_{{\mathrm{min}} }\left( {\widetilde{X}}_{d}\right)\) is plotted by calculating the smallest distance in the sum constellation \(\sqrt{h_{1}^{2}P}X_{1}+\sqrt{h_{2}^{2}P}X_{2}\) with \(X_{1},X_{2}\) generated as n-PAM inputs
The bound depends critically on \(d_{{\mathrm{min}} }\left( {\widetilde{X}}_{d}\right)\). The minimum distance of a sum of discrete distributions is a complicated function. Even if each distribution has a large minimum distance, the sum can have a small minimum distance, and the minimum distance is very sensitive to the values of \(h_{1}\) and \(h_{2}\) (Fig. 3). Small changes can lead to large changes in \(d_{{\mathrm{min}} }\). For some values of \(h_{1}\) and \(h_{2}\) the rate can be very small. This leads to the second thrust in this paper: the only way to overcome this problem is to change \(h_{1}\) and \(h_{2}\), perhaps by small amounts. For this purpose, we analyze liquid metal antennas.
We first present an improved lower bound.
Proposition 1
Let \(p_{{\mathrm{max}} }={\mathrm{max}} \{P(X_{d})\}\) be the maximum probability assumed by the discrete random variable \(X_{d}\) and \(c_{2}=\frac{1}{2}\log \left( \frac{2}{e}\right)\). Then,
The proof is in “Proof of Proposition 1” Appendix.
The bound (8) does not utilize special functions (e.g., error function) and offers analytical convenience similar to the Ozarow–Wyner bound. The benefit of (7) in Proposition 1 is that it is both analytical while close to the numerical bound of [4, Eq. (18a)].
4 Treating interference as noise (TIN)
As discussed above, we consider the strong interference regime with capacity given by (4). For large P, the second term in (4) dominates, which expresses that the the receiver has to jointly be able to decode the two messages. We will show that by instead treating interference as noise, we can achieve essentially the same rate, specificallyFootnote 1
where c is a constant independent of P, but potentially dependent on \(h_{1},h_{2}\). This is called a constant gap approximation [2]. When P is large, this is close to capacity as the first term increases while the second stays constant.
The following Theorem formalizes this:
Theorem 2
In the strong interference regime \(\left| h_{2}\right| >\left| h_{1}\right|\), discrete modulation achieves a constant gap to capacity,
as follows
-
1.
\(h_{2}^{2}\ge h_{1}^{4}\frac{P}{N}\): (10) is true for all values of \(h_{1},h_{2}\) and c is independent of \(h_{1},h_{2}\).
-
2.
\(h_{1}^{2}<h_{2}^{2}<h_{1}^{4}\frac{P}{N}\): Let
$$\begin{aligned} {\tilde{h}}_{i}\triangleq 2^{\mathrm{frac}(\frac{1}{2}\log (h_{i}^{2}{P/N}))}\in [1,2), \end{aligned}$$where \(\mathrm{frac}(x)\triangleq x-\lfloor x\rfloor\). Then for every \(0<\gamma <1\) there exists a set \(B\in [1,2)^{2}\) with area less than \(\gamma <1\) so for \({\tilde{h}}_{1},{\tilde{h}}_{2}\notin B\), (10) is true and where now \(c=O(\log \gamma )\).
The proof is in “Proof of Theorem 2” Appendix.
For Case (1) of Theorem 2, from the proof it can be seen that the rate can be achieved with symmetrical PAM modulation with
On the other hand, in Case (2), the rate is achieved with
In Fig. 4, we use the bound developed in Sect. 3 and the input specified in (11) to illustrate the constant gap to capacity. The constant gap in Case (2) was obtained by a probabilistic argument, where the channel coefficients \(\left( h_{1},h_{2}\right)\) were varied while keeping other parameters fixed. This is because the minimum distance of the received signals varies (see Fig. 5), thus affecting the achievable rate using PAM inputs.
Gap to capacity using PAM input specified in (11). Here \(h_{2}=\sqrt{h_{1}^{4}\frac{P}{N}+\frac{h_{1}^{2}}{2}}\). The top curve ‘blue dashed line’ is the analytic lower bound of Eq. (5). The curve in the middle plotted with ‘green line’ is the analytic lower bound of Prop. 1, and the marker ‘red square’ is the numerical lower bound using Eq. (26). Analytical bounds only need the value of \(d_{{\mathrm{min}} }\left( Y_{i}-Z_{i}\right)\), whereas the numerical bound (26) requires the entire \({\text{supp}}\left[ \sqrt{h_1^2P}X_{i}+\sqrt{h_2^2P}X_{j}\right]\)
Minimum distance. Minimum distance at the receiver \(Y_{1}\) for the discrete constellation \({\widetilde{X}}_d\) as the channel coefficients vary. Here \(P/N=27.3\) dB, and we use n from (12)
Theorem 2 is significant as it achieves constant gap to capacity for the complete strong interference channel. It contradicts the claim in [4, Sect. IV B, Remark 6] that an improvement from the log–log gap might be impossible. Case 2), as opposed to Case 1), relies on certain good channel coefficients \(\left( h_{1},h_{2}\right)\) to achieve a constant gap independent of P, from capacity using discrete inputs. The set of channel coefficients where this is not possible are termed as bad channel coefficients as they lead to outages whose probability can be controlled.
Outages is of course a problem in a fixed channel. The outages are permanent, i.e., little information can be transmitted. They are an unfortunate downside to use of discrete modulation and can only be avoided by changing \(h_{1}\) or \(h_{2}\). In Sect. 6, we therefore consider liquid metal antennas to deal with the outages.
5 Successive interference cancellation (SIC)
In successive interference cancellation, the receiver decodes the interfering signal first, subtracts it from the received signal, and then decodes the desired signal. We show that using discrete modulation can also increase the rate of SIC.
In [24], the authors showed that by dividing each user’s transmission into multiple streams and alternatingly decoding the streams, higher rates can be achieved. Specifically, User i transmits \(X_{i}=\sum _{k=1}^{L}X_{i}^{\left\{ k\right\} }\), and the decoding order is
It turns out that using discrete modulation for the streams can further increase rate. Now, instead of treating interference as Gaussian noise when decoding higher layers, it is treated as discrete noise, and the techniques for treating interference as noise from Sect. 4 can be used.
Unfortunately, it is difficult to calculate exact rate expressions, so we instead show this with an example. When using discrete modulation, one has to optimize over the number of streams L, the power allocation for each stream \(\mathtt{P}_{k}\) and the number of levels \(n_{k}\). For the former two, we heuristically use the same parameters as for the Gaussian case, and we then numerically optimize over \(n_{k}\).
Figure 6 shows the performance in one case. In this case \(L=2\) (which is optimum for the Gaussian case). We calculate rate two ways: using [4, Eq. (18a)] (the lower bound) and using numerical integration for calculating entropies of mixture Gaussians. We plot the performance of two schemes SIC and TIN: 2 Layers in Fig. 6. The sum rate for both users in the SIC case is found to be
whereas for the TIN: 2 Layers case is
We briefly discuss rate expressions for the SIC scheme. Consider the receiver at \(Y_{2}\) interested in layers \(X_{2}^{\left\{ 1\right\} }\) and \(X_{2}^{\left\{ 2\right\} }\) (of User 2). The rate for Layer 1 is the minimum of two terms. The first term \(I\left( X_{2}^{\left\{ 1\right\} };Y_{1}\right)\) exists as \(X_{2}^{\left\{ 1\right\} }\) is interference to User 1 and needs to be decoded and peeled off. The second term \(I\left( X_{2}^{\left\{ 1\right\} };Y_{2}\mid X_{1}^{\left\{ 1\right\} }\right)\) ensures User 2 can successfully decode Layer 1 after subtracting the interference of Layer 1 from User 1. Similar is the case for Layer 2 which is decoded first at User 1 (after decoding \(X_{2}^{\left\{ 1\right\} },X_{1}^{\left\{ 1\right\} }\)) and then at User 2. The lower bounds for each scheme are also plotted. For the SIC scheme, we use the following lower bound.
In the TIN: 2 Layers case, we lower bound the expression in (14) with
Here, the mutual information terms with a subscript ‘DTD,’ e.g., \(I_{\mathrm{DTD}}\) \(\left( Y_{1};Y_{1}-Z_{1}\right)\), are lower bounds to the usual mutual information expression \(I\left( Y_{1};Y_{1}-Z_{1}\right)\). These are calculated via the numerical lower bound provided in [4, Eq. (18a)], or (26).
Performance of successive interference cancellation. Here \(P/N=37\) dB and \(h_{1}=1\). The top curve ‘red line’ is the upper bound by evaluating \(0.5\log \left( 1+h_2^2\frac{P}{N}+h_1^2\frac{P}{N}\right)\). The markers ‘green asterisk’ and ‘blue plus’ are lower bounds for Discrete Modulated inputs with SIC. Similarly, The markers ‘green square box’ and ‘violet circle’ are lower bounds for Discrete Modulated inputs with 2 layers and TIN. In each scheme, the first marker is evaluated using a numerical bound and the latter is plotted with the analytical lower bound. The ‘black triangle’ marker is the rate with Gaussian Modulation as proposed in [24]
The important conclusions for this figure are
-
Discrete modulation outperforms Gaussian modulation. This is proved by Proposition 1 and further by numerical integration.
-
The discrete modulation uses PAM and therefore has a shaping loss. Using binomial modulation or quantized Gaussian would give a further gain.
-
Treating interference as noise with discrete modulation is mostly better than successive interference cancellation with Gaussian modulation.
-
Successive interference cancellation with discrete modulation gives a modest gain over treating interference as noise with discrete modulation.
-
The fluctuations in the curves are not due to inaccurate numerical calculation. They are due to the outage behavior explained in Sect. 3, which also affects successive interference cancellation.
6 Minimizing outages with liquid metal antennas
Reconfigurable antennas with adjustable directive gain have the potential to minimize network outages by varying the channel coefficients. One approach to realizing reconfigurable antennas is using liquid metal as the radiating element [6, 7, 9,10,11,12,13,14,15,16,17]. To quantify the effects of liquid metal reconfigurable antennas, an interference channel is simulated assuming standard microstrip patch antennas as the transmitters (\({\mathrm{Tx}}_1\) and \({\mathrm{Tx}}_2\)) and two reconfigurable liquid metal dipole antennas as the receivers (\({\mathrm{Rx}}_1\) and \({\mathrm{Rx}}_2\)) in a square configuration (Fig. 7). The microstrip patch antenna is designed to radiate at 1.58 GHz, with a maximum gain of 7.1 dBi at 0° with respect to receiver \({\mathrm{Rx}}_1\) and a gain of 2.9 dBi at 45° with respect to \({\mathrm{Rx}}_2\). The distance between each transmitter–receiver pair is varied between 100 and 500 m. Figure 8a shows the architecture of a liquid metal dipole antenna which is capable of reconfigurable lengths and orientations, resulting in variable radiation patterns with lobes and nulls in varying direction.

Adapted from [14]
Liquid metal antennas. The reconfigurable liquid metal dipole antenna (a) device structure (b) simulated radiation patterns. This structure allows the flexibility to vary independently both the length and orientation in each arm.
6.1 Analytical and simulation modeling for finite-length dipoles
To obtain the channel performance discussed in Sect. 4, the channel coefficients \(h_1\) and \(h_2\) are calculated from the ratio of the transmitted power and received power using the Friis equation [25]
where \(d_1\) and \(d_2\) are the distances in [m] between \(Tx_1-Rx_1\) and \(Tx_1-Rx_2\), respectively; \(r_1\) and \(r_2\) are the angle rotations for receiving antennas as illustrated in Fig. 8; \(\theta _1=0^\circ\) and \(\theta _2=45^\circ\) are the angles between \(Tx_1-Rx_1\) and \(Tx_1-Rx_2\), respectively; \(G_{T_x} (0)=7.1\) dBi and \(G_{T_x} (\pi /4 )= 2.9\) dBi are the gains of \(T_x\) at angle \(\theta _1\) and \(\theta _2\), respectively. The gain of an antenna can be calculated from [25]:
where \(D_m\) is the maximum directivity and \(F_n(\theta )\) is the normalized power density function. The receiving antennas in Fig. 7 are assumed to be dipole antennas, with \(F_n(\theta )\) and \(D_m\) for a finite-length dipole antenna calculated from [25]:
where \(\Omega _A\) is defined as the beam solid angle and L is the dipole length \([n\times \lambda ]\)
Although a dipole antenna is typically operated at the frequency where its physical length corresponds to 0.5\(\lambda\), Fig. 9 shows the change in radiation pattern when the physical length is increased to 2\(\lambda\) and 3\(\lambda\). The simulations were conducted with ANSYS High-Frequency Structure Simulator (HFSS) software, with the dipoles modeled as 500-μm-diameter wires separated by a 1-mm gap. Changing the length of the dipole while keeping the operating frequency constant results in a variety of radiation patterns, with lobes and nulls in varying directions. Figure 10 illustrates the contrast in directive gain at − 90° and − 45°, corresponding to the directions of the two transmitters in Fig. 7. The contrast in gain results in a corresponding contrast in the channel coefficients. A dipole antenna with a variable length can be realized by using liquid metal as the radiating elements, enabling adaptive reconfiguration of the radiation pattern.
6.2 Liquid metal antennas
Gallium-based liquid metal alloys have been used to implement reconfigurable antennas that change operating frequency [17], polarization [15], and radiation pattern [12, 13]. Galinstan is a non-toxic eutectic liquid metal that is made of gallium, indium, and tin, with an electrical conductivity of \(3.5\times 10^{5}\) S/m and a surface tension of 0.535 N/m [26]. Actuating Galinstan to realize a pattern-reconfigurable liquid metal antenna can alter the receivers’ gain, providing a wide range of antenna states. Here, liquid metal is used to realize a pattern-reconfigurable antenna that can alter its gain and radiation pattern to increase achievable capacity.
In [14], we reported the experimental results of a liquid metal polarization-pattern-reconfigurable dipole antenna. The liquid metal was electrically actuated using a low-voltage (5-VDC) electrocapillary actuation [27] signal to create five discrete states. Each state was active at a time when the liquid metal is actuated to fill the arms of the desired state, corresponding to the angle of the dipole antenna arms (0°, ± 45°, and ± 90° configurations). These states varied the polarizations and the radiation patterns. The device architecture (Fig. 8a) can be modified to enable more states by adjusting the length of each arm, thus enhancing the tunability of the channel coefficients (\(h_{1}\) and \(h_{2}\)). To implement dipole elements of any length, a gallium-based liquid metal such as Galinstan is used in the dipole arms. The lengths of the arms can be continuously changed using hybrid electrocapillary actuation [27]. Figure 8b shows that this gives flexibility in changing the channel coefficients, which is of crucial importance in the interference channel because of the sensitivity to channel coefficients. This would be difficult to achieve with other technologies. The total number of simulated states for this architecture is 87, obtained by varying both the dipole arm lengths (from 0.1\(\lambda\) to 3\(\lambda\) with a step of 0.1\(\lambda\)), the angle between the arms (Fig. 11), and creating superpositions of the previously mentioned states (Fig. 12).
7 Results and discussion
We now show the results of using discrete modulation together with liquid metal antennas in the setup in Fig. 7.
As mentioned above, for each distance d we simulate 87 channel states which we denote \({\mathcal{S}}_{d}=\left\{ \left( h_{1,1},h_{2,1}\right) ,\left( h_{1,2},h_{2,2}\right) ,\ldots \left( h_{1,87},h_{2,87}\right) \right\}\). Our goal is specifically to demonstrate how liquid metal antennas can be used to avoid outages; outages happen for channel coefficients in states that satisfy the condition of Case 2) in Theorem 2, and we therefore only consider channel coefficients in the following set
The transmit power is \(4\times 10^{-10}\) W/Hz, which corresponds to a received SNR of around 25 dB at a distance of 250 m.
Capacity for antenna states. For different liquid metal states that satisfy \(h_{1}^{2}<h_{2}^{2}<h_{1}^{4}\frac{P}{N}\), we plot the capacity with Gaussian inputs ‘\(-\square -\) and the achievable sum rate (via the lower bound in Proposition 1) using discrete PAM inputs ‘\(-\circ\)’
To visualize the variability in the performance across different antenna states, in Fig. 13 we plot both the achievable rate with discrete modulated n-PAM signals and the capacity. The achievable rate for PAM inputs is plotted using the lower bound developed in Proposition 1. The number of levels n is based on Theorem 2, specifically (12). For reference, at 25 dB the interference-free capacity per user is 4 bits, i.e., a sum capacity of 8 bits. We notice from the figure that the capacity varies only moderately with the state: most states give a good rate. On the other hand, the achievable rate varies widely and many states give poor performance, which is exactly the outage behavior. The figure illustrates how liquid metal antennas can avoid the outages: The capacity is maximized in state 9, but the rate with discrete modulation is poor; moving to state 12 gives a rate close to maximum capacity.
Gap to capacity. The plot shows the ratio of achievable rate to capacity for different channel coefficients (i.e., due to a change in the geometry of the setup in Fig. 7). From top to bottom, the curves represent the maximum, average, and minimum performance for all states in \({\mathcal{S}}_d^{\prime}\) of the liquid metal antenna of Fig. 8
In Fig. 14, we illustrate the variability of rate with discrete modulation for different distances, d. The y-axis is the ratio of the sum rate achieved using discrete modulation to the capacity.
We further investigate the behavior in Fig. 13 by plotting the metrics
Here \(R_{\mathrm{discrete}}(s^*)\) denotes the rate with discrete modulation in the state \(s^*\) that maximizes capacity. For example, in Fig. 13\(s^*\) is state 9, so (24) is the ratio of discrete rate to capacity in state 9. On the other hand, (23) is the ratio of the maximum discrete rate, achieved in state 12, to the maximum capacity achieved in state 9. The metrics are plotted in Fig. 15. The result can be seen as evidence that the liquid metal antennas are not only maximizing capacity, but also fine-tuning the channel to avoid outages. Namely, \(\rho _1(d)>\rho _2(d)\) means that the capacity-maximizing state is in outage. The liquid metal antenna can then move to a similar state which gives a much higher rate. In the figures, this happens when the receivers are close to the transmitters.
8 Conclusion
This paper investigated interference reduction via discrete modulation and liquid metal antennas. Discrete modulation can be used to reduce the effect of interference when treated as noise. The tradeoff is that there are certain configurations where the rate is very bad, leading to outage regions. A key insight of this paper is to utilize discrete modulation for good performance excepting some few weak spots and using liquid metal antennas to mitigate any weaknesses of discrete modulation.
Availability of data and materials
The datasets used and/or analyzed during the current study are available from the corresponding author on reasonable request.
Notes
We use C for capacity and R for achievable rate.
Abbreviations
- TIN:
-
Treating interference as noise
- TINnoTS:
-
Treating interference as noise with no time sharing
- PAM:
-
Pulse amplitude modulation
- SIC:
-
Successive interference cancellation
- GHz:
-
Giga hertz
- Tx:
-
Transmitter
- Rx:
-
Receiver
- dB:
-
Decibel
- dBi:
-
Decibel for isotropic antenna
- HFSS:
-
High-Frequency Structure Simulator
- VDC:
-
Voltage direct current
References
A.E. Gamal, Y.H. Kim, Network Information Theory (Cambridge University Press, Boston, 2011)
R.H. Etkin, D.N.C. Tse, H. Wang, Gaussian interference channel capacity to within one bit. IEEE Trans. Inf. Theory 54(12), 5534–5562 (2008). https://doi.org/10.1109/tit.2008.2006447
A. Carleial, A case where interference does not reduce capacity. IEEE Trans. Inf. Theory (Corresp.) 21(5), 569–570 (1975)
A. Dytso, D. Tuninetti, N. Devroye, Interference as noise: friend or foe? IEEE Trans. Inf. Theory 62(6), 3561–3596 (2016). https://doi.org/10.1109/tit.2016.2553098
L.H. Ozarow, A.D. Wyner, On the capacity of the Gaussian channel with a finite number of input levels. IEEE Trans. Inf. Theory 36(6), 1426–1428 (1990). https://doi.org/10.1109/18.59937
D.J. Hartl, G.J. Frank, G.H. Huff, J.W. Baur, A liquid metal-based structurally embedded vascular antenna: I. Concept and multiphysical modeling. Smart Mater. Struct. 26(2), 025001 (2016). https://doi.org/10.1088/1361-665X/aa5142
K.S. Elassy, T.K. Akau, W.A. Shiroma, S. Seo, A.T. Ohta, Low-cost rapid fabrication of conformal liquid–metal patterns. Appl. Sci. 9(8), 1565–1578 (2019). https://doi.org/10.3390/app9081565
A.M. Watson, K. Elassy, T. Leary, M.A. Rahman, A. Ohta, W. Shiroma, C.E. Tabor, Enabling reconfigurable all-liquid microcircuits via Laplace barriers to control liquid metal. In: IEEE MTT-S International Microwave Symposium, pp. 188–191. IEEE, Boston, MA, USA (2019). 978-1-7281-1310-4
M. Wang, C. Trlica, M.R. Khan, M.D. Dickey, J.J. Adams, A reconfigurable liquid metal antenna driven by electrochemically controlled capillarity. J. Appl. Phys. 117(19), 194901 (2015). https://doi.org/10.1063/1.4919605
V. Bharambe, D.P. Parekh, C. Ladd, K. Moussa, M.D. Dickey, J.J. Adams, Liquid–metal-filled 3-D antenna array structure with an integrated feeding network. IEEE Antennas Wirel. Propag. Lett. 17(5), 739–742 (2018). https://doi.org/10.1109/LAWP.2018.2813309
M.U. Memon, K. Ling, Y. Seo, S. Lim, Frequency-switchable half-mode substrate-integrated waveguide antenna injecting eutectic gallium indium (EGaIn) liquid metal alloy. J. Electromagn. Waves Appl. 16, 2207–2215 (2015). https://doi.org/10.1080/09205071.2015.1087347
G.B. Zhang, R.C. Gough, M.R. Moorefield, K.S. Elassy, A.T. Ohta, W.A. Shiroma, An electrically actuated liquid–metal gain-reconfigurable antenna. Int. J. Antennas Propag. 2018, 1–7 (2018). https://doi.org/10.1155/2018/7595363
A.M. Morishita, C.K.Y. Kitamura, A.T. Ohta, W.A. Shiroma, A liquid–metal monopole array with tunable frequency, gain, and beam steering. IEEE Antennas Wirel. Propag. Lett. 12, 1388–1391 (2013). https://doi.org/10.1109/LAWP.2013.2286544
G.B. Zhang, R.C. Gough, M.R. Moorefield, K.J. Cho, A.T. Ohta, W.A. Shiroma, A liquid–metal polarization-pattern-reconfigurable dipole antenna. IEEE Antennas Wirel. Propag. Lett. 17(1), 50–53 (2018)
M. Wang, M.R. Khan, M.D. Dickey, J.J. Adams, A compound frequency-and polarization-reconfigurable crossed dipole using multidirectional spreading of liquid metal. IEEE Antennas Wirel. Propag. Lett. 16, 79–82 (2017)
M.R. Khan, G.J. Hayes, J.-H. So, G. Lazzi, M.D. Dickey, A frequency shifting liquid metal antenna with pressure responsiveness. Appl. Phys. Lett. 99(117), 013501 (2011). https://doi.org/10.1063/1.4919605
J.H. Dang, R.C. Gough, A.M. Morishita, A.T. Ohta, W.A. Shiroma, Liquid–metal frequency-reconfigurable slot antenna using air-bubble actuation. Electron. Lett. 51(21), 1630–1632 (2015). https://doi.org/10.1049/el.2015.2782
M.U. Baig, K.S. Elassy, A. Høst-Madsen, A. Ohta, W. Shiroma, A. Nosratinia, Managing interference through discrete modulation and liquid metal antennas. In: IEEE 88th Vehicular Technology Conference (VTC-Fall), pp. 1–5 (2018)
V.S. Annapureddy, V.V. Veeravalli, Gaussian interference networks: sum capacity in the low-interference regime and new outer bounds on the capacity region. IEEE Trans. Inf. Theory 55(7), 3032–3050 (2009). https://doi.org/10.1109/TIT.2009.2021380
X. Shang, G. Kramer, B. Chen, Throughput optimization for multi-user interference channels. In: MILCOM 2008—IEEE Military Communications Conference, pp. 1–7 (2008). https://doi.org/10.1109/MILCOM.2008.4753283
H. Sato, The capacity of the Gaussian interference channel under strong interference. IEEE Trans. Inf. Theory IT 27(6), 786–788 (1981)
M.H.M. Costa, On the Gaussian interference channel. IEEE Trans. Inf. Theory 31(5), 607–615 (1985)
T.M. Cover, J.A. Thomas, Elements of Information Theory, 2nd edn. (Wiley, New York, 2006)
Y. Zhao, C.W. Tan, A.S. Avestimehr, S.N. Diggavi, G.J. Pottie, On the maximum achievable sum-rate with successive decoding in interference channels. IEEE Trans. Inf. Theory 58(6), 3798–3820 (2012). https://doi.org/10.1109/tit.2012.2190040
C.A. Balanis, Antenna Theory: Analysis and Design, 4th edn. (Wiley, Hoboken, NJ, 2016), p. 1104
T. Liu, P. Sen, C.-J. Kim, Characterization of nontoxic liquid–metal alloy Galinstan for applications in microdevices. J. Microelectromech. Syst. 21(2), 443–450 (2012)
R.C. Gough, A.M. Morishita, J.H. Dang, M.R. Moorefield, W.A. Shiroma, A.T. Ohta, Rapid electrocapillary deformation of liquid metal with reversible shape retention. Micro Nano Syst. Lett. 3(4), 1–9 (2015)
T.M. Apostol, Mathematical Analysis (Addison-Wesley, Boston, 1974)
M.U. Baig, A. Høst-Madsen, A. Nosratinia, Discrete modulation for interference mitigation. IEEE Trans. Inf. Theory 66(5), 3026–3039 (2020)
M.V. Berry, Z.V. Lewis, On the Weierstrass–Mandelbrot fractal function. Proc. R. Soc. Lond. A 370(1743), 459–484 (1980)
E. Guariglia, Entropy and fractal antennas. Entropy 18, 3 (2016). https://doi.org/10.3390/e18030084
E. Guariglia, S. Silvestrov, Fractional-wavelet analysis of positive definite distributions and wavelets on \(\mathscr{D}^{\prime }({\mathbb{C}})\), in Engineering Mathematics II. ed. by S. Silvestrov, M. Rančić (Springer, Cham, 2016), pp. 337–353
E. Guariglia, Harmonic Sierpinski gasket and applications. Entropy 20, 9 (2018). https://doi.org/10.3390/e20090714
E. Guariglia, Primality, fractality, and image analysis. Entropy 21(3), 304 (2019). https://doi.org/10.3390/e21030304
L. Yang, H. Su, C. Zhong, Z. Meng, H. Luo, X. Li, Y.Y. Tang, Y. Lu, Hyperspectral image classification using wavelet transform-based smooth ordering. Int. J. Wavelets Multiresolut. Inf. Process. 17(06), 1950050 (2019). https://doi.org/10.1142/S0219691319500504
X. Zheng, Y.Y. Tang, J. Zhou, A framework of adaptive multiscale wavelet decomposition for signals on undirected graphs. IEEE Trans. Signal Process. 67(7), 1696–1711 (2019). https://doi.org/10.1109/TSP.2019.2896246
Funding
This work was supported in part by the NSF Grants EECS-1546980, EECS-1546969, CCSS-1711689, and EECS-1923751.
Author information
Authors and Affiliations
Contributions
M.U.B. developed the information theory in the article and generated numerical results; K.S.E. developed the electromagnetic theory and provided channel simulations; A.H.M. and A.N. supervised the information theory development; A.T.O. and W.A.S. supervised the development of the electromagnetic theory. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
1.1 Proof of Proposition 1
We first need the following lemma
Lemma 3
Let \(\alpha \ge 0\), \(s_{j},s_{i}\in {\text{supp}}\left\{ X_{d}\right\}\) and \(g\left( n,\alpha \right) =\sum _{j=1,j\ne i}^{n}e^{-\alpha \left( s_{i}-s_{j}\right) ^{2}}\). For \(\alpha \ge 0\) , we have
Proof
Note that we can always re-label the \(\left\{ s_{j}\right\} _{j=1,j\ne i}^{n}\) such that \(s_{1}\) is the closest point (in distance) to \(s_{i}\), \(s_{2}\) is the next closest, and so on. Clearly, \(\left| s_{i}-s_{j}\right| \ge d_{{\mathrm{min}} }\left( X_{d}\right)\) by definition. Now for any j we have
and this allows us to upper bound \(g\left( n,\alpha \right)\) with \(2\sum _{j=1}^{\frac{n-1}{2}}e^{-\alpha j^{2}d_{{\mathrm{min}} }^{2}\left( X_{d}\right) }\). Making use of [28, Sect. 8.12], we get (25). Proving the last inequality in the lemma is simple and omitted. \(\square\)
We start with a numerical bound reported in [4, Eq. (18a)] as follows
where \(s_{i}\in {\text{supp}}\left\{ X_{d}\right\}\), \(\tilde{p_{i}}=\Pr \left\{ X_{d}=s_{i}\right\}\), and \(c_{1}=\frac{1}{2}\log \left( 2\pi e\right)\). This result is leveraged below to produce an analytical bound that improves the Ozarow–Wyner bound in Eq. (5).
We can now prove the proposition. The main idea is to bound the summation in (26) using a staircase approximation.
where in (a) we use Lemma 3 with \(\alpha =\frac{1}{4}\frac{P}{N}\).
1.2 Proof of Theorem 2
A constant gap approximation to capacity is relevant for large P, so throughout this section we assume that P is sufficiently large. The transmissions \(X_{i}\) are symmetrical n-PAM modulations where n is the number of discrete levels \(X_{i}\) may take, i.e., \(n=\left| {\text{supp}}\left[ X_{i}\right] \right|\). Furthermore, for a PAM input it should be easy to verify (see (1)) that \(d_{{\mathrm{min}} }\left( X_{i}\right) =\sqrt{\frac{12}{n_{i}^{2}-1}}.\)
The two cases require distinct proofs and are treated individually.
1.2.1 Case 1: \(h_{2}^{2}\ge h_{1}^{4}\frac{P}{N}\)
For the very strong interference regime, \(h_{2}^{2}\ge h_{1}^{2}\left( 1+h_{1}^{2}\frac{P}{N}\right)\), the result was proved in [4, Th. 7]. We therefore only have to prove it for \(h_{2}^{2}<h_{1}^{2}\left( 1+h_{1}^{2}\frac{P}{N}\right)\). Choose \(n=\left\lceil \sqrt{\frac{3}{4}}\frac{|h_{2}|}{|h_{1}|}\right\rceil\), and we may bound
Using the result in [4, Prop. 2], we know the minimum distance of the discrete constellation \(\sqrt{P}\left( h_{1}X_{1}+h_{2}X_{2}\right)\) as
For a fixed constant \(c>0\) and Proposition 1 or Eq. (5), we get
We now lower bound the
where the last inequality follows since the P is large. The above estimate allows us to state that \(R\ge \frac{1}{2}\log \left( \frac{3}{4}\frac{h_{2}^{2}}{h_{1}^{2}|}\right) -c_{1}\), for some constant \(c_{1}>0\). Finally, it is easy to verify that
for some constant \(c_{3}>0\).
1.3 Case 2: \(h_{1}^{2}<h_{2}^{2}<h_{1}^{4}\frac{P}{N}\)
For large P, we can write the signal at receiver \(i,j\in \left\{ 1,2\right\}\) as
Recall \({\tilde{h}}_{i}\in [1,2)\) was defined as the fractional part of \(h_i\) in the log domain, and \(\ell _i \triangleq \log _2 \frac{h_i}{{\tilde{h}}_i}\); therefore, \(\ell _i\in {\mathbb{Z}}^{+}.\) Now set \(n=\left\lfloor \left( 1+h_{1}^{2}\frac{P}{N}+h_{2}^{2}\frac{P}{N}\right) ^{\frac{1}{4}}\right\rfloor -1\) and \(m=\frac{n-1}{2}\). It is easy to show
In this case, we have the following bound for \(d_{{\mathrm{min}} }\left( Y_{i}-Z_{i}\right)\), using [29, Prop. 2] for certain channel gains \(h_{1},h_{2}\).
To arrive at (a), we first lower bound the term \(d_{{\mathrm{min}} }\left( X_{i}\right)\) with \(\frac{\sqrt{12}}{n}\) and then use the upper bound on n using Eq. (27). At \(\left( b\right)\), we make use of the following relation
and lower bound the constants \(\tilde{h_{i}}\) to arrive at a constant that depends on \(\gamma ,h_{1}\) and \(h_{2}.\) Finally, note that for the channel realizations \(h_{1},h_{2}\) where the above bound on \(d_{{\mathrm{min}} }\left( Y_{i}-Z_{i}\right)\) holds we have
which allows us to use Eq. (6) and Proposition 1 to bound \(R\ge \log \left( n\right) -O\left( \log \gamma \right) .\)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Baig, M.U., Elassy, K.S., Høst-Madsen, A. et al. Leveraging discrete modulation and liquid metal antennas for interference reduction. J Wireless Com Network 2021, 158 (2021). https://doi.org/10.1186/s13638-021-02019-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13638-021-02019-w