Remarks on Stationary and Uniformly-rotating Vortex Sheets: Rigidity Results

Abstract

In this paper, we show that the only solution of the vortex sheet equation, either stationary or uniformly rotating with negative angular velocity $\Omega$, such that it has positive vorticity and is concentrated in a finite disjoint union of smooth curves with finite length is the trivial one: constant vorticity amplitude supported on a union of nested, concentric circles. The proof follows a desingularization argument and a calculus of variations flavor.

1 Introduction

A vortex sheet is a weak solution of the 2D Euler equations:

$$\begin{aligned} v_t + v \cdot \nabla v = -\nabla p, \quad \nabla \cdot v = 0, \end{aligned}$$

(1.1)

whose vorticity $\omega = \text {curl}(v)$ is a delta function supported on a curve or a finite number of curves $\Gamma _i = z_i(\alpha ,t)$, i.e.

$$\begin{aligned} \omega (x,t) = \sum _{i} \varpi _i(\alpha ,t) \delta (x - z_i(\alpha ,t)). \end{aligned}$$

(1.2)

Here $\varpi _i(\alpha ,t)$ is the vorticity strength on $\Gamma _i$ with respect to the parametrization $z_i$, and the above equation is understood in the sense that

$$\begin{aligned} \int _{{\mathbb {R}}^2} \varphi (x) d\omega (x,t) = \sum _{i} \int \varphi (z_i(\alpha ,t))\varpi _i(\alpha ,t) d\alpha \end{aligned}$$

for all test functions $\varphi (x)\in C_0^\infty ({\mathbb {R}}^2)$.

The motivation of the study of the equation (1.1) with vortex sheet initial data comes from the fact that in fluids with small viscosity, flows separate from rigid walls and corners [24, 32]. To model it, one may think of a solution to (1.1) with one incompressible fluid where the velocity changes sign in a discontinuous (tangential) way across a streamline z. This discontinuity induces vorticity in z.

The equations of motion of $\varpi _i$ and $z_i$ can be derived by means of the Birkhoff–Rott operator [7, 21, 24, 35], namely:

$$\begin{aligned} BR(z,\varpi )(x,t) =\frac{1}{2\pi } PV\int \frac{(x-z(\beta ,t))^{\bot }}{|x- z(\beta ,t)|^2}\varpi (\beta ,t)d\beta , \end{aligned}$$

(1.3)

yielding

$$\begin{aligned} \partial _t z_i(\alpha ,t)&= \sum _j BR(z_j,\varpi _i)(z_i(\alpha ,t)) + c_i(\alpha ,t) \partial _\alpha z_i(\alpha ,t) \end{aligned}$$

(1.4)

$$\begin{aligned} \partial _t \varpi _i(\alpha ,t)&= \partial _\alpha (c_i(\alpha ,t) \varpi _i(\alpha ,t)), \end{aligned}$$

(1.5)

where the term $c_i(\alpha ,t)$ accounts for the reparametrization freedom of the curves. See the paper [19] by Izosimov–Khesin where they propose geodesic, group-theoretic, and Hamiltonian frameworks for their description.

The main goal of this paper is to establish radial symmetry properties of stationary/uniformly-rotating vortex sheets to (1.1). To do so, we first define what we mean by a stationary vortex sheet. Assume the initial data $\omega _0$ of (1.2) is supported on a finite number of curves parametrized by $z_i(\alpha )$, with strength $\varpi _i(\alpha )$ (with respect to the parametrization $z_i$) respectively. If there exists some reparametrization choice $c_i(\alpha )$ such that the right hand sides of (1.4)–(1.5) are both identically zero for every i, it gives that $\omega (\cdot ,t)$ is invariant in time, and we say $\omega (\cdot ,t)=\omega _0$ is a stationary vortex sheet.

For any $x\in {\mathbb {R}}^2$ and $\Omega \in {\mathbb {R}}$, let $R_{\Omega t} x$ denote the rotation of x counter-clockwise by angle $\Omega t$ about the origin. We say $\omega (x,t)=\omega _0(R_{\Omega t} x)$ is a uniformly-rotating vortex sheet with angular velocity $\Omega$ if $\omega _0$ is stationary in the rotating frame with angular velocity $\Omega$. (Note that in the special case $\Omega =0$, the uniformly-rotating sheet is in fact stationary.) In Lemma 2.1, we will derive the equations satisfied by a stationary/rotating vortex sheet.

It is easy to see that if the $z_i$’s are concentric circles with constant $\varpi _i$ (with respect to the constant-speed parametrization) for every i, the solution is stationary, and it is also uniformly-rotating with any $\Omega \in {\mathbb {R}}$. We would like to understand the reverse implication, namely:

Question 1

Under what conditions must a stationary/uniformly-rotating vortex sheet be radially symmetric?

This type of rigidity question has been very lately understood for different equations and different settings such as in the papers by Koch–Nadirashvili–Sverak [20] for Navier-Stokes, Hamel–Nadirashvili [16,17,18] for the 2D Euler equation on a strip, punctured disk or the full plane, Gómez-Serrano–Park–Shi–Yao [14] for the 2D Euler and modified SQG in the full plane and Constantin–Drivas–Ginsberg [8] for the 2D and 3D Euler, as well as the 2D Boussinesq and the 3D Magnetohydrostatic (MHS) equations.

The next theorem is the main result of the paper, solving it for the vortex sheet equations:

Theorem 1.1

Let $\omega (x,t)=\omega _0(R_{\Omega t} x)$ be a stationary/uniformly-rotating vortex sheet with angular velocity $\Omega$. Assume that $\omega _0$ is concentrated on $\Gamma$, which is a finite union of smooth curves, and $\omega _0$ has positive vorticity strength on $\Gamma$. (See (H1)–(H3) in Sect. 2 for the precise regularity and positivity assumptions.)

If $\Omega \le 0$, $\Gamma$ must be a union of concentric circles, and $\omega _0$ must have constant strength along each circle (with respect to the constant-speed parametrization). In addition, if $\Omega <0$, all circles must be centered at the origin.

Remark 1.2

Note that for any uniformly-rotating solution with $\Omega <0$, our theorem yields that $\omega _0$ must be concentrated on concentric circles centered at the origin, with constant strength on each circle. Such $\omega _0$ is actually stationary. As a result, there are no uniformly rotating solutions with negative angular velocity that are non-stationary.

We now go first over the history of the equations (1.4)–(1.5), focusing later on the case of steady solutions. The study of those solutions is important due to the ill-posedness of the vortex sheet equation, thus they represent (unstable) structures for which there is global existence.

1.1 Brief history of the dynamical problem

The existence of solutions to (1.4)–(1.5) has been widely studied. The seminal paper of Delort [9] proved global existence of weak solutions of (1.1) for an initial velocity in $L^{2}_{loc}$ and a vorticity a positive Radon measure. Majda [23] provided a simpler proof. See also the works by Schochet [33, 34] and Evans–Muller [13]. All of them use the hypothesis that the vorticity has a definite sign.

If the vorticity does not have a sign, Lopes Filho–Nussenzveig Lopes–Xin proved existence in [22], in the case where the system enjoys reflection symmetry. For the setting in which the curve $z_i$ is not closed and represented as a graph, Sulem–Sulem–Bardos–Frisch [35] proved local existence in the case of analytic initial data.

The first sign of singularities with analytic initial data goes back to Moore [26], where he demonstrated that the curvature may blow up in finite time. Ebin [11] showed ill-posedness in Sobolev spaces when $\gamma$ has a distinguished sign, and Duchon–Robert [10] proved global existence for a class of initial data in the unbounded setting. Caflisch–Orellana [6] also showed global existence for a class of initial data, as well as ill-posedness in $H^s$ for $s > \frac{3}{2}$ and simplified the analysis of Moore [5]. We also mention here the work of Wu [38], in which she proved the existence of solutions to (1.4)–(1.5) in spaces which are less regular than $H^s$. Székelyhidi [36] (resp. Mengual–Székelyhidi [25]) constructed infinitely many admissible weak solutions to (1.1) for vortex sheet initial data with (resp. without necessarily) a distinguished sign.

1.2 Stationary and rotating solutions

Relative equilibria are an important family of solutions of fluid equations since their structures persist for long times. This is specially important when the equations of motion are ill-posed. In the particular case of (1.4)–(1.5), our knowledge is very small and only very few explicit cases are known: the circle and the straight line (with constant $\gamma$), which are stationary, and the segment of length 2a and density

$$\begin{aligned} \gamma (x) = \Omega \sqrt{a^2 - x^2}, \qquad x \in [-a,a], \end{aligned}$$

(1.6)

which is a rotating solution with angular velocity $\Omega$ [2]. Protas–Sakajo [31] generalized this solution and proved the existence of several others made out of segments rotating about a common center of rotation with endpoints at the vertices of a regular polygon by solving a Riemann–Hilbert problem, even finding some of them analytically.

In the paper [15] we prove the existence of a family of vortex sheet rotating solutions with non-constant vorticity density supported on a non-radial curve, bifurcating from the circle with constant density.

Numerically, some solutions have been computed before. O’Neil [27, 28] used point vortices to approximate the vortex sheet and compute uniformly rotating solutions and Elling [12] constructed numerically self-similar vortex sheets forming cusps. O’Neil [29, 30] also found numerically steady solutions which are combinations of point vortices and vortex sheets.

1.3 Structure of the proof

The proof is inspired by our recent rigidity result in the paper [14] on stationary and rotating solutions of the 2D Euler equations both in the smooth and vortex patch settings. To prove it, we constructed an appropriate functional and showed, on one hand, that any stationary solution had to be a critical point, and on the other, for any curve which is not a circle there existed a vector field along which the first variation was non-zero. This vector field is defined in terms of an elliptic equation in the interior of the patch. In the case of the vortex sheet, this is not possible anymore. Instead, we desingularize the problem by considering patches of thickness $\sim \varepsilon$ which are tubular neighborhoods of the sheet. The drawback is that we lose the property that any stationary solution has to be a critical point if $\varepsilon > 0$ and very careful, quantitative estimates need to be done to show that indeed the first variation of a stationary solution tends to 0 as $\varepsilon \rightarrow 0$. This setup is also reminiscent of the numerical work by Baker–Shelley [1], where they approximate the motion of a vortex sheet by a vortex patch of very small width. In [3], Benedetto–Pulvirenti proved the stability (for short time) of vortex sheet solutions with respect to solutions to 2D Euler with a thin strip of vorticity around a curve. See also the work by Caflisch–Lombardo–Sammartino [4] for more stability results with a different desingularization.

1.4 Organization of the paper

In Sect. 2 the equations for the stationary/rotating vortex sheet are derived, and in Sect. 3 we perform the desingularization procedure. Section 4 is devoted to construct the aforementioned divergence free vector-field along which the first variation is non-zero. Finally in Sect. 5 we conclude the quantitative estimates and prove the symmetry result from Theorem 1.1.

1.5 Notations

For a bounded domain $D\subset {\mathbb {R}}^2$, we denote |D| by its area (i.e. its Lebesgue measure). For $x\in {\mathbb {R}}^2$ and $r>0$, denote by B(x, r) or $B_r(x)$ the open ball centered at x with radius r.

Through Sects 3–5 of this paper, we will desingularize the vortex sheet into a vortex layer with width $\sim \epsilon$, and obtain various quantitative estimates. In all these estimates, we say a term f is $O(g(\epsilon ))$ if $|f|\le Cg(\epsilon )$ for some constant C independent of $\epsilon$.

For a domain $U\subset {\mathbb {R}}^2$, in the boundary integral $\int _{\partial U}\mathbf {f}\cdot n d\sigma$, n denotes the outer normal of the domain U.

2 Equations for a Stationary/Rotating Vortex Sheet

Let $\omega (\cdot ,t)=\omega _0(R_{\Omega t})$ be a stationary/rotating vortex sheet solution to the incompressible 2D Euler equation, where $\omega _0\in {\mathcal {M}}({\mathbb {R}}^2) \cap H^{-1}({\mathbb {R}}^2)$ is a Radon measure. Here $\Omega =0$ corresponds to a stationary solution, and $\Omega \ne 0$ corresponds to a rotating solution. Assume $\omega _0$ is concentrated on $\Gamma$, which is a finite disjoint union of curves. Throughout this paper we assume $\Gamma$ satisfies the following:

(H1) Each connected component of $\Gamma$ is smooth and with finite length, and it is either a simple closed curve (denote them by $\Gamma _1,\dots ,\Gamma _n)$, or a non-self-intersecting curve with two endpoints (denote them by $\Gamma _{n+1},\dots , \Gamma _{n+m}$). Here we require $n+m\ge 1$, but allow either n or m to be 0.

Let us denote

$$\begin{aligned} d_{\Gamma }:= \min _{k\ne i} \text {dist}(\Gamma _i, \Gamma _k), \end{aligned}$$

(2.1)

which is strictly positive since we assume the curves $\{\Gamma _i\}_{i=1}^{n+m}$ are disjoint. For $i=1,\dots , n+m$, denote by $L_i$ the length of $\Gamma _i$. Let $z_i:S_i\rightarrow \Gamma _i$ denote a constant-speed parameterization of $\Gamma _i$ (in counter-clockwise direction if $\Gamma _i$ is a closed curve), where the parameter domain $S_i$ is given by

$$\begin{aligned} S_i{:}{=} {\left\{ \begin{array}{ll} {{\mathbb {R}}}/{\mathbb {Z}} &{} {\text {for }} i=1,\dots ,n,\\ {[}0,1{]} &{} {\text {for }} i=n+1,\dots , n+m. \end{array}\right. } \end{aligned}$$

Note that this gives $|z_i'|\equiv L_i$, and the arc-chord constant

$$\begin{aligned} F_\Gamma := \max _{i=1,\dots ,n+m}\sup _{\alpha \ne \beta \in S_i}\frac{|\alpha -\beta |}{|z_i(\alpha )-z_i(\beta )|} \end{aligned}$$

(2.2)

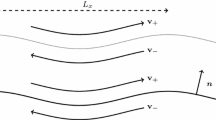
is finite, since $\Gamma$ is non-self-intersecting. Let ${\mathbf {s}}:\Gamma \rightarrow {\mathbb {R}}^2$ be the unit tangential vector on $\Gamma$, given by ${\mathbf {s}}(z_i(\alpha )) := \frac{z_i'(\alpha )}{|z_i'(\alpha )|} = \frac{z_i'(\alpha )}{L_i}$, and ${\mathbf {n}}:\Gamma \rightarrow {\mathbb {R}}^2$ be the unit normal vector, given by ${\mathbf {n}} = {\mathbf {s}}^\perp$. See Fig. 1 for an illustration.

Fig. 1

Illustration of the closed curves $\Gamma _1,\dots ,\Gamma _n$ and the open curves $\Gamma _{n+1},\dots ,\Gamma _{n+m}$, and the definitions of ${\mathbf {n}}$, ${\mathbf {s}}$, ${\mathbf {v}}^+$ and ${\mathbf {v}}^-$

For $i=1,\dots , n+m$, let us denote by $\gamma _i(\alpha )$ the vorticity strength at $z_i(\alpha )$ with respect to the arclength parametrization, which is related to $\varpi _i(\alpha )$ by

$$\begin{aligned} \gamma _i(\alpha ) = \frac{\varpi _i(\alpha )}{| z_i'(\alpha )|} \quad \text { for }\alpha \in S_i. \end{aligned}$$

(2.3)

Throughout this paper we will be working with $\gamma _i$, instead of $\varpi _i$. We impose the following regularity and positivity assumptions on $\gamma _i$:

(H2) Assume that $\gamma _i \in C^2(S_i)$ for $i=1,\dots ,n$ and $\gamma _i \in C^{b}(S_i) \cap C^1(S_i^\circ )$ for some $b\in (0,1)$ for $i=n+1,\dots ,n+m$.¹

(H3) For $i=1,\dots ,n$, assume $\gamma _i > 0$ in $S_i$. And for $i=n+1,\dots ,n+m$, assume $\gamma _i > 0$ in $S_i^\circ$, and $\gamma _i(0)=\gamma _i(1)=0$.

Note that for a closed curve, (H3) implies that $\gamma _i$ is uniformly positive; whereas for an open curve, $\gamma _i$ is positive in the interior of $S_i$ but vanishes at its endpoints. This is because any stationary/rotating vortex sheet with continuous $\gamma _i$ must have it vanishing at the two endpoints of any open curve: if not, one can easily check that $|BR(z_i(\alpha ))\cdot {\mathbf {n}}(z_i(\alpha ))|\rightarrow \infty$ as $\alpha$ approaches the endpoint, thus such a vortex sheet cannot be stationary in the rotating frame.

With the above notations of $z_i$ and $\gamma _i$, the Birkhoff–Rott integral (1.3) along the sheet can now be expressed as

$$\begin{aligned} BR(z_i(\alpha )) = \sum _{k=1}^{n+m} BR_k(z_i(\alpha )) := \sum _{k=1}^{n+m}PV \int _{S_k} K_2(z_i(\alpha ) - z_k(\alpha '))\, \gamma _k(\alpha ') |z_k'(\alpha ')| \,d\alpha ', \end{aligned}$$

(2.4)

with the kernel $K_2$ given by

$$\begin{aligned} K_2(x) := (2\pi )^{-1} \nabla ^\perp \log |x| = \frac{x^\perp }{2\pi |x|^2}, \end{aligned}$$

(2.5)

and the principal value in (2.4) is only needed for the integral with $k=i$.

Let ${\mathbf {v}}:{\mathbb {R}}^2\rightarrow {\mathbb {R}}^2$ be the velocity field generated by $\omega _0$, given by ${\mathbf {v}}:= \nabla ^\perp (\omega _0 * {\mathcal {N}})$. Note that ${\mathbf {v}} \in C^\infty ({\mathbb {R}}^2 \setminus \Gamma )$, but ${\mathbf {v}}$ is discontinuous across $\Gamma$. Let ${\mathbf {v}}^+,{\mathbf {v}}^-: \Gamma \rightarrow {\mathbb {R}}^2$ denote the two limits of ${\mathbf {v}}$ on the two sides of $\Gamma$ (with ${\mathbf {v}}^+$ being the limit on the side that ${\mathbf {n}}$ points into—see Fig. 1 for an illustration), and $[{\mathbf {v}}] := {\mathbf {v}}^- - {\mathbf {v}}^+$ the jump in ${\mathbf {v}}$ across the sheets. $[{\mathbf {v}}]$ is related to the vortex-sheet strength $\gamma$ as follows (see [24, Eq. (9.8)] for a derivation): $[{\mathbf {v}}]\cdot {\mathbf {n}}=0$, and

$$\begin{aligned}{}[{\mathbf {v}}] \times {\mathbf {n}} = [{\mathbf {v}}] \cdot {\mathbf {s}} = \gamma . \end{aligned}$$

In addition, the Birkhoff–Rott integral (2.4) is the the average of ${\mathbf {v}}^+$ and ${\mathbf {v}}^-$, namely

$$\begin{aligned} BR(z_i(\alpha )) =\frac{1}{2}({\mathbf {v}}^+(z_i(\alpha ))+{\mathbf {v}}^-(z_i(\alpha ))) \quad \text { for all }\alpha \in S_i, i=1,\dots ,n+m. \end{aligned}$$

In the following lemma, we derive the equation that the Birkhoff–Rott integral satisfies for a stationary/rotating vortex sheet.

Lemma 2.1

Assume $\omega (\cdot ,t)=\omega _0(R_{\Omega t} x)$ is a stationary/uniformly-rotating vortex sheet with angular velocity $\Omega \in {\mathbb {R}}$, and $\omega _0$ is concentrated on $\cup _{i=1}^{n+m}\Gamma _i$, with $z_i$ and $\gamma _i$ defined as above. Then the Birkhoff–Rott integral BR (2.4) and the strength $\gamma _i$ satisfy the following two equations:

$$\begin{aligned} (BR-\Omega x^\perp )\cdot {\mathbf {n}} ={\mathbf {v}}^+ \cdot {\mathbf {n}} = {\mathbf {v}}^- \cdot {\mathbf {n}} = 0 \quad \text { on } \Gamma , \end{aligned}$$

(2.6)

and

$$\begin{aligned} (BR(z_i(\alpha ))-\Omega z_i^\perp (\alpha )) \cdot {\mathbf {s}}(z_i(\alpha )) \,\gamma _i(\alpha )= {\left\{ \begin{array}{ll} C_i &{}\text { on } S_i \text { for } i = 1,\dots , n, \\ 0 &{} \text { on } S_i \text { for } i = n+1,\dots , n+m. \end{array}\right. } \end{aligned}$$

(2.7)

In particular, the above two equations imply that $BR(z_i(\alpha ))-\Omega z_i^\perp (\alpha ) \equiv {\mathbf {0}}$ for $i=n+1,\dots ,n+m$.

Proof

By definition of the stationary/uniformly-rotating solutions, $\omega _0$ is a stationary vortex sheet in the rotating frame with angular velocity $\Omega$. In this rotating frame, an extra velocity $-\Omega z_i^\perp$ should be added to the right hand side of (1.4). Therefore the evolution equations (1.4)–(1.5) become the following in the rotating frame (where we also use (2.4)):

$$\begin{aligned} \partial _t z_i(\alpha ,t)&= BR(z_i(\alpha ,t)) - \Omega z_i^\perp (\alpha ,t) + c_i(\alpha ,t) \partial _\alpha z_i(\alpha ,t) \end{aligned}$$

(2.8)

$$\begin{aligned} \partial _t \varpi _i(\alpha ,t)&=\partial _\alpha (c_i(\alpha ,t) \varpi _i(\alpha ,t)), \end{aligned}$$

(2.9)

where the term $c_i(\alpha ,t)$ accounts for the reparametrization freedom of the curves. Since $\omega _0$ is stationary in the rotating frame, $z_i(\cdot ,t)$ parametrizes the same curve as $z_i(\cdot ,0)$. Therefore $\partial _t z_i(\alpha ,t)$ is tangent to the curve $\Gamma _i$, and multiplying ${\mathbf {n}}(z_i(\alpha ,t))$ to (2.8) gives

$$\begin{aligned} 0=\partial _t z_i(\alpha ,t) \cdot {\mathbf {n}}(z_i(\alpha ,t)) = (BR(z_i(\alpha ,t))-\Omega z_i^\perp (\alpha ,t))\cdot {\mathbf {n}}(z_i(\alpha ,t)), \end{aligned}$$

(2.10)

where we use that ${\mathbf {n}}(z_i(\alpha ,t)) \cdot \partial _\alpha z_i(\alpha ,t)=0$. This proves (2.6).

Now we prove (2.7). Towards this end, let us choose

$$\begin{aligned} c_i(\alpha ,t) := -\frac{(BR(z_i(\alpha ,t))-\Omega z_i^\perp (\alpha ,t))\cdot {\mathbf {s}}(z_i(\alpha ,t))}{|\partial _\alpha z_i(\alpha ,t)|}, \end{aligned}$$

so that multiplying ${\mathbf {s}}(z_i(\alpha ,t))$ to (2.8) gives $\partial _t z_i(\alpha ,t) \cdot {\mathbf {s}}(z_i(\alpha ,t)) =0$, and combining it with (2.10) gives $\partial _t z_i(\alpha ,t) =0.$ In other words, with such choice of $c_i$, the parametrization $z_i(\alpha ,t)$ remains fixed in time. Since $\omega _0$ is stationary in the rotating frame, we know that with a fixed parametrization $z_i(\alpha ,t)=z_i(\alpha ,0)$, the strength $\varpi _i(\alpha ,t)$ must also remain invariant in time. Thus (2.9) becomes

$$\begin{aligned} c_i(\alpha ,t) \varpi _i(\alpha ,t) \equiv C_i. \end{aligned}$$

Plugging the definition of $c_i$ into the equation above and using the fact that $z_i$ is invariant in t, we have

$$\begin{aligned} \frac{(BR(z_i(\alpha ))-\Omega z_i^\perp (\alpha ))\cdot {\mathbf {s}}(z_i(\alpha )) \varpi _i(\alpha )}{|\partial _\alpha z_i(\alpha )| }\equiv -C_i\quad \text { for all }\alpha \in S_i, \end{aligned}$$

and finally the relationship between $\gamma _i$ and $\varpi _i$ in (2.3) yields (2.7) for $i=1,\dots , n$.

And for the open curves $i=n+1,\dots ,n+m$, note that we do not have any reparametrization freedom at the two endpoints $\alpha =0,1$, therefore the endpoint velocity $BR(z_i(0,t))-\Omega z_i^\perp (0,t)$ must be 0 to ensure that $\omega _0$ is stationary in the rotating frame. This immediately leads to $C_i=0$ for $i=n+1,\dots ,n+m$, finishing the proof of (2.7). $\square$

3 Approximation by a Thin Vortex Layer

Our aim in this section is to desingularize the vortex sheet $\omega _0$. Namely, for $0<\epsilon \ll 1$, we will construct a vorticity $\omega ^\epsilon \in L^\infty ({\mathbb {R}}^2) \cap L^1({\mathbb {R}}^2)$ that only takes values 0 and $\epsilon ^{-1}$, and is supported in an $O(\epsilon )$ neighborhood of $\Gamma$, such that $\omega ^\epsilon$ weakly converges to $\omega _0$ as $\epsilon \rightarrow 0^+$.

For each $i=1,\dots ,n+m$, we will describe a neighborhood of $\Gamma _i$ using the following change of coordinates: let $R^\epsilon _i: S_i\times {\mathbb {R}} \rightarrow {\mathbb {R}}^2$ be given by

$$\begin{aligned} R^\epsilon _i(\alpha , \eta ) := z_i(\alpha ) + \epsilon \gamma _i(\alpha ) {\mathbf {n}}(z_i(\alpha )) \eta , \end{aligned}$$

(3.1)

and let

$$\begin{aligned} D^\epsilon _i := \left\{ R^\epsilon _i(\alpha , \eta ) : \alpha \in S_i^\circ , \eta \in (-1, 0)\right\} . \end{aligned}$$

Note that each $D^\epsilon _i$ is a connected open set, and for all $\epsilon >0$ sufficiently small, the sets $(D^\epsilon _i)_{i=1}^{n+m}$ are disjoint. For $i=1,\dots ,n$, the domains $D_i^\epsilon$ are doubly-connected with smooth boundary, and its inner boundary coincides with $\Gamma _i$; see the left of Fig. 2 for an illustration. And for $i=n+1,\dots ,n+m$, the domains $D_i^\epsilon$ are simply-connected, and its boundary is smooth except at most two points; see the right of Fig. 2 for an illustration.

Fig. 2

Illustration of the definitions of $R_i^\epsilon$ and $D_i^\epsilon$ for a closed curve (left) and an open curve (right)

In addition, for $\epsilon >0$ that is sufficiently small, one can check that $R^\epsilon _i: S_i^\circ \times (-1,0) \rightarrow D_i^\epsilon$ is a diffeomorphism. Since $\gamma _i \in C^1(S_i)$ and $z_i\in C^2(S_i)$, we only need to show $R^\epsilon _i: S_i^\circ \times (-1,0) \rightarrow D_i^\epsilon$ is injective. Below we prove this fact in a stronger quantitative version, which will be used later.

Lemma 3.1

For any $i=1,\dots , n+m$, assume $\Gamma _i$ and $\gamma _i$ satisfy (H1)–(H2). Then the map $R^\epsilon _i: S_i^\circ \times (-1,0) \rightarrow D^\epsilon _i$ given by (3.1) is injective. In addition, there exist some $c_0,\epsilon _0>0$ depending on $\Vert z_i\Vert _{C^2(S_i)},$ $\Vert \gamma _i\Vert _{L^\infty (S_i)}$ and $F_\Gamma$, such that for all $\epsilon \in (0,\epsilon _0)$ we have

$$\begin{aligned} |R^\epsilon _i(\alpha ',\eta ')-R^\epsilon _i(\alpha ,\eta ) |\ge c_0\big (|\alpha '-\alpha | + \epsilon |\gamma _i(\alpha )\eta - \gamma _i(\alpha ')\eta '|\big ), \end{aligned}$$

(3.2)

for all $\alpha ,\alpha '\in S_i^\circ , ~\eta ,\eta ' \in (-1,0)$.²

Proof

To begin with, note that (3.2) immediately implies that $R^\epsilon _i:S_i^\circ \times (-1,0) \rightarrow D^\epsilon _i$ is injective, where we used the positivity assumption $\gamma _i>0$ in $S_i^\circ$ in (H2). Thus it suffices to prove (3.2). Throughout the proof, we fix any $i\in \{1,\dots , n+m\}$, and we will omit the subscript i for notational simplicity. Using the definition (3.1), let us break $R^\epsilon (\alpha ',\eta ') - R^\epsilon (\alpha ,\eta )$ into

$$\begin{aligned} R^\epsilon (\alpha ',\eta ') - R^\epsilon (\alpha ,\eta )= & {} \underbrace{z(\alpha ') - z(\alpha )}_{=:T_1} +\underbrace{\epsilon \left( \gamma (\alpha ')\eta ' - \gamma (\alpha )\eta \right) {\mathbf {n}}(z(\alpha '))}_{=:T_2} \nonumber \\&+ \underbrace{\epsilon \gamma (\alpha )\eta \left( {\mathbf {n}}(z(\alpha '))-{\mathbf {n}}(z(\alpha )) \right) }_{=:T_3}. \end{aligned}$$

(3.3)

For $T_1$ and $T_3$, we have

$$\begin{aligned} \begin{aligned} \left| T_1 - z'(\alpha ')(\alpha '-\alpha )\right|&\le \Vert z \Vert _{C^2(S)}|\alpha -\alpha '|^2, \\ \left| T_3 \right|&\le \epsilon \gamma (\alpha )\Vert z \Vert _{C^2(S)}|\alpha -\alpha '|. \end{aligned} \end{aligned}$$

(3.4)

Also, using that $z'(\alpha ')=L {\mathbf {s}}(z(\alpha '))$ is perpendicular to ${\mathbf {n}}(z(\alpha '))$, we have

$$\begin{aligned} \begin{aligned} |z'(\alpha ')(\alpha '-\alpha ) + T_2|&= \left| L(\alpha '-\alpha ) {\mathbf {s}}(z(\alpha ')) + \epsilon \left( \gamma (\alpha ')\eta ' - \gamma (\alpha )\eta \right) {\mathbf {n}}(z(\alpha '))\right| \\&\ge \frac{1}{2}L|\alpha '-\alpha | + \frac{1}{2}\epsilon \left| \gamma (\alpha ')\eta ' - \gamma (\alpha )\eta \right| , \end{aligned} \end{aligned}$$

where we use that $\sqrt{x^2+y^2}\ge \frac{1}{2}(|x|+|y|)$. Combining this with (3.4) gives

$$\begin{aligned} | T_1 + T_2 + T_3|&\ge |\alpha - \alpha '| \left( \frac{L}{2} - \Vert z\Vert _{C^2(S)}\left( |\alpha -\alpha '| + \epsilon \gamma (\alpha ) \right) \right) +\frac{1}{2} \epsilon | \gamma (\alpha ')\eta ' - \gamma (\alpha )\eta |, \end{aligned}$$

thus

$$\begin{aligned} |R^\epsilon (\alpha ',\eta ') - R^\epsilon (\alpha ,\eta )| \ge \frac{L}{4}|\alpha -\alpha '| + \frac{1}{2}\epsilon | \gamma (\alpha ')\eta ' - \gamma (\alpha )\eta | \end{aligned}$$

(3.5)

for all $0<\epsilon < L(8\Vert z \Vert _{C^2}\Vert \gamma \Vert _{L^\infty })^{-1}$ and $|\alpha -\alpha '| \le \frac{L}{8\Vert z \Vert _{C^2}}$.

For $|\alpha -\alpha '| > \frac{L}{8\Vert z \Vert _{C^2}}$, recall that the definition of $F_\Gamma$ in (2.2) gives $|z(\alpha ')-z(\alpha )| \ge F_\Gamma ^{-1}|\alpha '-\alpha |$. Thus a crude estimate gives

$$\begin{aligned} |R^\epsilon (\alpha ',\eta ') - R^\epsilon (\alpha ,\eta )|\ge |z(\alpha ')-z(\alpha )| -2\epsilon \Vert \gamma \Vert _{L^\infty (S)} \ge \frac{1}{2F_\Gamma } |\alpha '-\alpha | + \epsilon | \gamma (\alpha ')\eta ' - \gamma (\alpha )\eta | \end{aligned}$$

(3.6)

for $0<\epsilon <L(64F_\Gamma \Vert z\Vert _{C^2}\Vert \gamma \Vert _{L^\infty })^{-1}$. (Note that for such $\epsilon$ we have $4\epsilon \Vert \gamma \Vert _{L^\infty } \le \frac{1}{2F_\Gamma }|\alpha '-\alpha |$ due to our assumption that $|\alpha -\alpha '| > \frac{L}{8\Vert z \Vert _{C^2}}$).

Finally, combining (3.5) and (3.6), it follows that (3.2) holds for $c_0 = \min \{ \frac{L}{4}, \frac{1}{2F_\Gamma }, \frac{1}{2}\}$ and $\epsilon _0 = \min \{ L(8\Vert z \Vert _{C^2}\Vert \gamma \Vert _{L^\infty })^{-1}, L(64F_\Gamma \Vert z\Vert _{C^2}\Vert \gamma \Vert _{L^\infty })^{-1}\}$. This finishes the proof.

$\square$

In the next lemma we compute the partial derivatives and Jacobian of $R^\epsilon _i(\alpha ,\eta )$, which will be useful later.

Lemma 3.2

For any $i=1,\dots ,n+m$, let $z_i$ be a constant-speed parameterization of the curve $\Gamma _i$ (with length $L_i$), and let $R^\epsilon _i$ be given by (3.1). Then its partial derivatives are

$$\begin{aligned} \begin{aligned} \partial _\alpha R^\epsilon _i(\alpha ,\eta )&= z_i'(\alpha ) + \epsilon \left( \gamma _i'(\alpha ) \frac{z_i'(\alpha )^\perp }{L_i} \eta + \gamma _i(\alpha ) \frac{z_i''(\alpha )^\perp }{L_i} \eta \right) ,\\ \partial _\eta R^\epsilon _i(\alpha ,\eta )&= \epsilon \gamma _i(\alpha ) \frac{z_i'(\alpha )^\perp }{L_i}. \end{aligned} \end{aligned}$$

(3.7)

Moreover, its Jacobian is given by

$$\begin{aligned} \begin{aligned} \det (\nabla _{\alpha ,\eta } R^\epsilon _i)&= \epsilon L_i \gamma _i(\alpha ) - \epsilon ^2 L_i \gamma _i^2(\alpha ) \kappa _i(\alpha )\eta , \end{aligned} \end{aligned}$$

(3.8)

where $\kappa _i(\alpha )$ denotes the signed curvature of $\Gamma _i$ at $z_i(\alpha )$.

Proof

Since $z_i$ is the constant-speed parameterization of $\Gamma _i$ (which has length $L_i$), we have $|z_i'|\equiv L_i$ and ${\mathbf {n}}(z_i(\alpha ))=z_i'(\alpha )^\perp / L_i$. Taking the $\alpha$ and $\eta$ partial derivatives of (3.1) directly yields (3.7).

Putting the two partial derivatives into columns of a $2\times 2$ matrix and computing the determinant, we have

$$\begin{aligned} \begin{aligned} \det (\nabla _{\alpha ,\eta } R_i^\epsilon )&= \epsilon \gamma _i(\alpha ) \frac{|z_i'(\alpha )|^2}{L_i} + \epsilon ^2 \gamma _i^2(\alpha ) \frac{z_i''(\alpha )^\perp \cdot z_i'(\alpha )}{L_i^2}\eta \\&= \epsilon L_i \gamma _i(\alpha ) - \epsilon ^2 L_i \gamma _i^2(\alpha ) \kappa _i(\alpha )\eta , \end{aligned} \end{aligned}$$

where in the second equality we used that $z_i''(\alpha )=\kappa _i(\alpha ) {\mathbf {n}}(z_i(\alpha )) L_i^2$ (recall that $z_i$ has constant speed $L_i$). This finishes the proof. $\square$

Remark 3.3

We point out that for each $i=1,\dots ,n+m$, the determinant formula (3.8) immediately gives the following approximation of $|D^\epsilon _i|$, which will be helpful in the proofs later:

$$\begin{aligned} \frac{|D^\epsilon _i|}{\epsilon } =\frac{1}{\epsilon } \int _{D^\epsilon _i}1dx =\frac{1}{\epsilon }\int _{S_i}\int _{-1}^{0}\det (\nabla _{\alpha ,\eta } R^\epsilon _i(\alpha ,\eta ))\, d\eta d\alpha = L_i\int _{S_i}\gamma _i(\alpha )d\alpha + O(\epsilon ), \end{aligned}$$

(3.9)

where the $O(\epsilon )$ error term has its absolute value bounded by $C\epsilon$, with C only depending on $\Vert z_i\Vert _{C^2(S_i)}$ and $\Vert \gamma _i\Vert _{L^\infty (S_i)}$.

Finally, let $D^\epsilon := \cup _{i=1}^{n+m} D_i^\epsilon$, and $\omega ^\epsilon :{\mathbb {R}}^2\rightarrow {\mathbb {R}}$ is defined as

$$\begin{aligned} \omega ^\epsilon (x) := \epsilon ^{-1} 1_{D^\epsilon }(x) =\epsilon ^{-1} \sum _{i=1}^{n+m} 1_{D_i^\epsilon }(x), \end{aligned}$$

and let

$$\begin{aligned} {\mathbf {v}}^\epsilon = \nabla ^\perp (\omega ^\epsilon * {\mathcal {N}}) \end{aligned}$$

(3.10)

be the velocity field generated by $\omega ^\epsilon$.

In the next lemma we aim to obtain some fine estimate of ${\mathbf {v}}^\epsilon$ in the thin vortex layer $D^\epsilon$. Our goal is to show that along each cross section of the thin layer (i.e. fix i and $\alpha$, and let $\eta$ vary in $[-1,0]$), the function $\eta \mapsto {\mathbf {v}}^\epsilon (R_i^\epsilon (\alpha ,\eta ))$ is almost a linear function in $\eta$, with the endpoint values (at $\eta =-1$ and 0) being almost ${\mathbf {v}}^-(z_i(\alpha ))$ and ${\mathbf {v}}^+(z_i(\alpha ))$ respectively.

Lemma 3.4

For $i=1,\dots ,n+m$, assume $\Gamma _i$ and $\gamma _i$ satisfy (H1)–(H3). Let

$$\begin{aligned} g_i(\alpha , \eta ) := BR(z_i(\alpha )) - \Big (\eta +\frac{1}{2}\Big ) [{\mathbf {v}}](z_i(\alpha )) \quad \text { for }\alpha \in S_i, \end{aligned}$$

and note that $g_i(\alpha ,0) = {\mathbf {v}}^{+}(z_i(\alpha ))$ and $g_i(\alpha ,-1) = {\mathbf {v}}^{-}(z_i(\alpha ))$ (see Fig. 3 for an illustration of $g_i(\alpha ,\eta )$). Then for all sufficiently small $\epsilon >0$, for all $i = 1,\dots , n+m$ we have

$$\begin{aligned} |{\mathbf {v}}^\epsilon (R_i^\epsilon (\alpha ,\eta )) - g_i(\alpha ,\eta )| \le C\epsilon ^b |\log \epsilon | \quad \text { for all } \alpha \in S_i, \eta \in [-1,0], \end{aligned}$$

(3.11)

where $b\in (0,1)$ is as in (H2), and C depends on b, $\max _i\Vert z_i\Vert _{C^2(S_i)}$, $\max _{i}\Vert \gamma _i\Vert _{C^b(S_i)}$, $d_\Gamma$ and $F_\Gamma$.

Fig. 3

Illustration of the definition of $g_i(\alpha ,\cdot )$ (the orange arrows)

Proof

Let i be any fixed index in $1,\dots , n+m$. We begin with breaking ${\mathbf {v}}^\epsilon$ into contributions from different components $\{D_k^\epsilon \}_{k=1}^{n+m}$, namely

$$\begin{aligned} {\mathbf {v}}^\epsilon (x) = \sum _{k=1}^{n+m}{\mathbf {v}}_k^\epsilon (x) := \sum _{k=1}^{n+m}\epsilon ^{-1} \int _{D_i^\epsilon } K_2(x-y) dy, \end{aligned}$$

where the kernel $K_2$ is given by (2.5). Similarly, we can break $BR(z_i(\alpha ))$ into $\displaystyle BR(z_i(\alpha )) = \sum _{k=1}^{n+m} BR_k(z_i(\alpha )),$ where $BR_k$ is the contribution from the k-th integral in (2.4), and note that the PV symbol is only needed for $k= i$.

• Estimates for $k\ne i$ terms. For any $k\ne i$, we aim to show that

  $$\begin{aligned} |{\mathbf {v}}_k^\epsilon (R_i^\epsilon (\alpha ,\eta )) - BR_k(z_i(\alpha ))| \le C\epsilon , \end{aligned}$$

  (3.12)

  where C depends on $d_\Gamma , \max _k\Vert z_k\Vert _{C^2}$ and $\max _k\Vert \gamma _k\Vert _{L^\infty }$. Applying a change of variable $y=R_k^\epsilon (\alpha ',\eta ')$, we can rewrite ${\mathbf {v}}_k^\epsilon$ as

  $$\begin{aligned} \begin{aligned} {\mathbf {v}}_k^\epsilon (R_i^\epsilon (\alpha ,\eta ))&= \epsilon ^{-1} \int _{D_k^\epsilon } K_2(R_i^\epsilon (\alpha ,\eta )-y)\, dy \\&= \int _{S_k} \int _{-1}^0 \underbrace{K_2(R_i^\epsilon (\alpha ,\eta ) - R_k^\epsilon (\alpha ',\eta '))}_{=:T_1} \underbrace{\epsilon ^{-1}\det (\nabla _{\alpha ',\eta '} R_k^\epsilon (\alpha ',\eta '))}_{=:T_2} \, d\eta ' d\alpha '. \end{aligned} \end{aligned}$$

  (3.13)

  Using the facts that $R_i^\epsilon (\alpha ,\eta ) - R_k^\epsilon (\alpha ',\eta ') = z_i(\alpha )-z_k(\alpha ') + O(\epsilon )$ as well as $|z_i(\alpha )-z_k(\alpha ')|\ge d_{\Gamma }>0$ (recall that $d_{\Gamma }$ is as given in (2.1)), for all sufficiently small $\epsilon >0$ we have $T_1 = K_2(z_i(\alpha )-z_k(\alpha ')) + O(\epsilon ).$ For $T_2$, the explicit formula (3.8) for the determinant gives $T_2 = L_k \gamma _k(\alpha ') + O(\epsilon ).$ Plugging these into the above integral yields

  $$\begin{aligned} {\mathbf {v}}_k^\epsilon (R_i^\epsilon (\alpha ,\eta )) = \int _{S_k} K_2(z_i(\alpha )-z_k(\alpha ')) L_k \gamma _k(\alpha ')\, d\alpha ' + O(\epsilon ) = BR_k(z_i(\alpha ))+O(\epsilon ), \end{aligned}$$

  finishing the proof of (3.12).

• Estimates for the $k= i$ term. It will be more involved to control the $k=i$ term, and our goal is to show that

  $$\begin{aligned} \left| {\mathbf {v}}_i^\epsilon (R_i^\epsilon (\alpha ,\eta )) - BR_i(z_i(\alpha )) + \Big (\eta +\frac{1}{2}\Big ) [{\mathbf {v}}](z_i(\alpha )) \right| \le C\epsilon ^b|\log \epsilon |. \end{aligned}$$

  (3.14)

  To begin with, we again rewrite ${\mathbf {v}}_i^\epsilon$ as in (3.13) with $k=i$, and plug in the formula (3.8) for the determinant. This leads to

  $$\begin{aligned} \begin{aligned} {\mathbf {v}}_i^\epsilon (R_i^\epsilon (\alpha ,\eta ))&= \int _{S_k} \int _{-1}^0 K_2(R_i^\epsilon (\alpha ,\eta ) - R_i^\epsilon (\alpha ',\eta ')) \left( L_i \gamma _i(\alpha ') \right. \\&\left. \quad - \epsilon L_i \gamma _i^2(\alpha ') \kappa _i(\alpha ')\eta '\right) \, d\eta ' d\alpha '\\&=: I_1 + I_2, \end{aligned} \end{aligned}$$

  where $I_1, I_2$ are the contributions from the two terms in the last parenthesis respectively. Let us control $I_2$ first, and we claim that

  $$\begin{aligned} |I_2| \le C \epsilon |\log \epsilon |. \end{aligned}$$

  (3.15)

  Using (3.2) of Lemma 3.1 and the fact that $|K_2(x)|\le |x|^{-1}$, we can bound $I_2$ as

  $$\begin{aligned} |I_2|= & {} \left| \int _{S_k} \int _{-1}^0 K_2(R_i^\epsilon (\alpha ,\eta ) - R_i^\epsilon (\alpha ',\eta ')) \, \epsilon L_i \gamma _i^2(\alpha ') \kappa _i(\alpha ') \eta ' \, d\eta ' d\alpha ' \right| \nonumber \\\le & {} C \epsilon \int _{S_k} \int _{-1}^0 \frac{\gamma _i(\alpha ')}{|\alpha '-\alpha | + \epsilon |\gamma _i(\alpha ')\eta '-\gamma _i(\alpha )\eta |} \, d\eta ' d\alpha '\nonumber \\\le & {} C \epsilon \int _{S_k} \int _{-\Vert \gamma _i\Vert _{\infty }}^{\Vert \gamma _i\Vert _{\infty }} \frac{1}{|\alpha '-\alpha | + \epsilon |\theta '| }\, d\theta ' d\alpha ' \quad (\theta ':=\gamma _i(\alpha ')\eta '-\gamma _i(\alpha )\eta )\nonumber \\\le & {} C\epsilon \int _{-1/\epsilon }^{1/\epsilon } \int _{-\Vert \gamma _i\Vert _{\infty }}^{\Vert \gamma _i\Vert _{\infty }} \frac{1}{|\beta '| + |\theta '| }\, d\theta ' d\beta ' \quad (\beta ':=\epsilon ^{-1}(\alpha '-\alpha ))\nonumber \\\le & {} C\epsilon |\log \epsilon | \end{aligned}$$

  (3.16)

  where C depends on $\Vert z_i\Vert _{C^2}$ and $\Vert \gamma _i\Vert _{L^\infty }$.

  In the rest of the proof we focus on estimating $I_1 = \displaystyle \int _{S_k} \int _{-1}^0 K_2(R_i^\epsilon (\alpha ,\eta ) - R_i^\epsilon (\alpha ',\eta ')) L_i \gamma _i(\alpha ') \, d\eta ' d\alpha '.$ For $t \in [0,1]$, let us define

  $$\begin{aligned} f(\alpha ,\alpha ',\eta ,\eta ';t)&:= R_i^\epsilon (\alpha ,\eta -t\eta ') - R_i^\epsilon (\alpha ',\eta '-t\eta '), \nonumber \\ J(t)&:= \int _{S_k} \int _{-1}^0 K_2(f(\alpha ,\alpha ',\eta ,\eta ';t)) L_i \gamma _i(\alpha ') \, d\eta ' d\alpha '. \end{aligned}$$

  (3.17)

  Note that in the definition of f, the argument $\eta -t\eta '$ of $R_i^\epsilon$ belongs to $[-1,1]$, instead of $[-1,0]$ as in the original definition of (3.1). Here $R_i^\epsilon (\alpha ,\eta -t\eta ')$ is defined as in the formula (3.1), even though it might not belong to $D^\epsilon _i$. Clearly, $J(0) = I_1$. The motivation for us to define such f and J(t) is that at $t=1$, we have

  $$\begin{aligned} \begin{aligned} J(1)&= \int _{S_k} \int _{-1}^0 K_2(R_i^\epsilon (\alpha ,\eta {-}\eta ') {-}z_i(\alpha ')) L_i \gamma _i(\alpha ') \, d\eta ' d\alpha '{=} \int _{-1}^0 {\mathbf {v}}_i(R_i^\epsilon (\alpha ,\eta {-}\eta ')) \, d\eta ', \end{aligned} \end{aligned}$$

  (3.18)

  where ${\mathbf {v}}_i$ is the velocity field generated by the sheet $\Gamma _i$. Recall that ${\mathbf {v}}_i$ has a jump across $\Gamma _i$, where we denote its limits on two sides by ${\mathbf {v}}_i^\pm$. Using Lemma 3.5, which we will prove momentarily, we have

  $$\begin{aligned} {\mathbf {v}}_i(R_i^\epsilon (\alpha ,\eta -\eta ')) = {\left\{ \begin{array}{ll} {\mathbf {v}}_i^+(z_i(\alpha )) + O(\epsilon ^b |\log \epsilon |) &{}\text { if } \eta -\eta ' \in (0,2),\\ {\mathbf {v}}_i^-(z_i(\alpha ))+ O(\epsilon ^b |\log \epsilon |)&{} \text { if } \eta -\eta ' \in (-2,0). \end{array}\right. } \end{aligned}$$

  (3.19)

  We can then split the integration domain on the right hand side of (3.18) into $\eta '\in (-1,\eta )$ and $\eta '\in (\eta ,0)$, and use (3.19) to approximate the integrand in each interval. This gives

  $$\begin{aligned} \begin{aligned} J(1)&= (\eta +1) {\mathbf {v}}_i^+(z_i(\alpha )) - \eta {\mathbf {v}}_i^-(z_i(\alpha )) + O(\epsilon ^b |\log \epsilon |)\\&= BR_i(z_i(\alpha )) -\Big (\eta +\frac{1}{2}\Big ) [{\mathbf {v}}](z_i(\alpha ))+ O(\epsilon ^b |\log \epsilon |), \end{aligned} \end{aligned}$$

  (3.20)

  where in the last step we used that $[{\mathbf {v}}](z_i(\alpha )) = [{\mathbf {v}}_i](z_i(\alpha ))$, since all other ${\mathbf {v}}_k$ with $k\ne i$ are continuous across $\Gamma _i$.

  Finally, it remains to control $|J(0)-J(1)|$. Note that by (3.2), we have

  $$\begin{aligned} f(\alpha ,\alpha ',\eta ,\eta ';t) \ge c_0\big (|\alpha -\alpha '| + \epsilon |\gamma _i(\alpha ')\eta '-\gamma _i(\alpha )\eta |\big ). \end{aligned}$$

  In addition, we have

  $$\begin{aligned} \left| \frac{\partial }{\partial t} f(\alpha ,\alpha ',\eta ,\eta ';t)\right| = \left| \epsilon \big (\gamma _i(\alpha ) {\mathbf {n}}(z_i(\alpha ))-\gamma _i(\alpha ') {\mathbf {n}}(z_i(\alpha '))\big )\eta '\right| \le C\epsilon |\alpha -\alpha '|^b, \end{aligned}$$

  where the last inequality follows from (H2) and the fact that ${\mathbf {n}}(z_i(\alpha )) \in C^1(S_i)$. Therefore, for any $t\in (0,1)$, taking the t derivative of (3.17) and using that $|\nabla K_2(x)| \le |x|^{-2}$, we have

  $$\begin{aligned} \begin{aligned} |J'(t)|&\le C \int _{S_k} \int _{-1}^0 \frac{ \epsilon |\alpha -\alpha '|^b \gamma _i(\alpha ') }{\big (|\alpha -\alpha '| + \epsilon |\gamma _i(\alpha ')\eta '-\gamma _i(\alpha )\eta |\big )^{2}}d\eta ' d\alpha '\\&\le C \epsilon \int _{S_k} \int _{-1}^0 \frac{ \gamma _i(\alpha ') }{|\alpha -\alpha '|^{1-b}\left( |\alpha -\alpha '| + \epsilon |\gamma _i(\alpha ')\eta '-\gamma _i(\alpha )\eta |\right) }d\eta ' d\alpha ' \\&\le C \epsilon ^b \int _{-1/\epsilon }^{1/\epsilon } \int _{-\Vert \gamma _i\Vert _{\infty }}^{\Vert \gamma _i\Vert _{\infty }} \frac{1}{|\beta '|^{1-b}(|\beta '| + |\theta '|) }\, d\theta ' d\beta ' \\&\qquad (\theta ':=\gamma _i(\alpha ')\eta '-\gamma _i(\alpha )\eta ,\, \beta ':=\epsilon ^{-1}(\alpha '-\alpha ))\\&\le C \epsilon ^b \int _{-1/\epsilon }^{1/\epsilon } |\beta '|^{b-1}\log \left( 1+\frac{\Vert \gamma _i\Vert _{L^\infty }}{|\beta '|}\right) d\beta '\\&\le C\epsilon ^b, \end{aligned} \end{aligned}$$

  where C depends on b, $\Vert \gamma _i\Vert _{C^b(S_i)}$, $\Vert z_i\Vert _{C^2(S_i)}$ and $F_\Gamma$. This leads to

  $$\begin{aligned} |J(1)-I_1| = |J(1)-J(0)| \le C\epsilon ^b |\log \epsilon |. \end{aligned}$$

  Finally, combining this with (3.20) and (3.15) yields (3.14), finishing the proof of the $k=i$ case. We can then conclude the proof by taking the sum of this estimate with all the $k\ne i$ estimates in (3.12). $\square$

The following lemma proves (3.19). Let ${\mathbf {v}}_i$ be the velocity field generated by the sheet $\Gamma _i$, which is smooth in ${\mathbb {R}}^2\setminus \Gamma _i$, and has a discontinuity across $\Gamma _i$. It is known that ${\mathbf {v}}_i$ converges to ${\mathbf {v}}_i^\pm$ respectively on the two sides of $\Gamma _i$ [24]. However, we were unable to find a quantitative convergence rate (in terms of the distance from the point to $\Gamma _i$) in the literature, especially under the assumption that $\gamma _i$ is only in $C^b(S_i)$ for the open curves. Below we prove such an estimate.

Lemma 3.5

For $i=1,\ldots ,n+m$, let ${\mathbf {v}}_i$ be the velocity field generated by the sheet $\Gamma _i$, given by

$$\begin{aligned} {\mathbf {v}}_i(x) := \int _{S_i} K_2(x - z_i(\alpha '))\, \gamma _i(\alpha ') |z_i'(\alpha ')| \,d\alpha ' \quad \text { for }x\in {\mathbb {R}}^2\setminus \Gamma _i. \end{aligned}$$

Then there exist constants $C,\epsilon _0 >0$ depending on on b (as in (H2)), $\Vert z_i\Vert _{C^2(S_i)}$, $\Vert \gamma _i\Vert _{C^b(S_i)}$ and $F_\Gamma$, such that for all $\epsilon \in (0,\epsilon _0)$ and $\eta \in (-2,2)$ we have

$$\begin{aligned}&\left| {\mathbf {v}}_i(R^\epsilon _i(\alpha ,\eta )) - {\mathbf {v}}_i^+(z_i(\alpha )) \right| \le C \epsilon ^b|\log \epsilon | \quad \text { if }\eta \in (0,2), \end{aligned}$$

(3.21)

$$\begin{aligned}&\left| {\mathbf {v}}_i(R^\epsilon _i(\alpha ,\eta )) - {\mathbf {v}}_i^-(z_i(\alpha )) \right| \le C \epsilon ^b|\log \epsilon | \quad \text { if }\eta \in (-2,0), \end{aligned}$$

(3.22)

where

$$\begin{aligned} {\mathbf {v}}_i^{+} = BR_i(z_i(\alpha )) + \frac{{\mathbf {n}}(z_i(\alpha ))^\perp \gamma _i(\alpha )}{2},\quad {\mathbf {v}}_i^{-} = BR_i(z_i(\alpha )) - \frac{{\mathbf {n}}(z_i(\alpha ))^\perp \gamma _i(\alpha )}{2}, \end{aligned}$$

and $BR_i$ is the contribution from the i-th integral in (2.4).

Proof

We will show (3.21) only since (3.22) can be treated in the same way. From the definition of $R^\epsilon _i$ in (3.1), we have

$$\begin{aligned} {\mathbf {v}}_i(R^\epsilon _i(\alpha ,\eta ))&= \frac{L_i}{2\pi }\int _{S_i}\frac{\left( z_i(\alpha )-z_i(\alpha ') \right) ^{\perp } \gamma _i(\alpha ')}{\left| z_i(\alpha )-z_i(\alpha ')+\epsilon \eta {\mathbf {n}}(z_i(\alpha ))\gamma _i(\alpha )\right| ^2} \,d\alpha ' \\&\qquad + \frac{L_i}{2\pi }\int _{S_i}\frac{\epsilon \eta {\mathbf {n}}(z_i(\alpha ))^{\perp }\gamma _i(\alpha ) \gamma _i(\alpha ')}{\left| z_i(\alpha )-z_i(\alpha ')+\epsilon \eta {\mathbf {n}}(z_i(\alpha ))\gamma _i(\alpha )\right| ^2}\, d\alpha '\\&=: A_1 + A_2. \end{aligned}$$

We claim that for all $\epsilon >0$ sufficiently small and $\eta \in [0,2)$, we have

$$\begin{aligned} |A_1 - BR_i(z(\alpha )) |&\le C\epsilon ^b|\log \epsilon |, \end{aligned}$$

(3.23)

$$\begin{aligned} \left| A_2 - \frac{{\mathbf {n}}(z(\alpha ))^\perp \gamma (\alpha )}{2} \right|&\le C\epsilon ^b, \end{aligned}$$

(3.24)

and note that these two claims immediately yield (3.21). From now on, let us fix $i\in \left\{ 1,\ldots ,n+m\right\}$ and omit it in the notation for simplicity. Throughout this proof, let us denote

$$\begin{aligned} {\mathbf {y}}(\alpha ,\alpha '):= z(\alpha )-z(\alpha ') \quad \text { and }\quad {\mathbf {c}}(\alpha ):=\epsilon \eta {\mathbf {n}}(z(\alpha ))\gamma (\alpha ), \end{aligned}$$

so that

$$\begin{aligned} A_1 = \frac{L}{2\pi } \int _{S} \frac{{\mathbf {y}}^\perp (\alpha ,\alpha ') \gamma (\alpha ')}{|{\mathbf {y}}(\alpha ,\alpha ')+{\mathbf {c}}(\alpha )|^2} d\alpha ', \quad A_2 = \frac{L}{2\pi } \int _S \frac{{\mathbf {c}}^\perp (\alpha )\gamma (\alpha ')}{|{\mathbf {y}}(\alpha ,\alpha ')+{\mathbf {c}}(\alpha )|^2 } d\alpha '. \end{aligned}$$

Note that

$$\begin{aligned} F_\Gamma ^{-1} |\alpha -\alpha '| \le |{\mathbf {y}}(\alpha ,\alpha ')|\le \Vert z\Vert _{C^1}|\alpha -\alpha '|. \end{aligned}$$

(3.25)

For the closed curves with $i=1,\dots ,n$, since z has period 1, we can always set $\alpha -\alpha ' \in [-\frac{1}{2},\frac{1}{2})$ in this proof.

Applying (3.2) (with $\eta '=0$), we have

$$\begin{aligned} |{\mathbf {y}}(\alpha ,\alpha ')+{\mathbf {c}}(\alpha )|^2 \ge c_0(|\alpha -\alpha '|^2 + \epsilon ^2\eta ^2 \gamma ^2(\alpha )) = c_0(|\alpha -\alpha '|^2 +|{\mathbf {c}}(\alpha )|^2). \end{aligned}$$

(3.26)

Since $z'(\alpha )=L{\mathbf {s}}(z(\alpha ))$, let us define

$$\begin{aligned} \tilde{{\mathbf {y}}}(\alpha ,\alpha ') := L{\mathbf {s}}(z(\alpha ))(\alpha -\alpha '), \end{aligned}$$

which is a close approximation of ${\mathbf {y}}$ in the sense that

$$\begin{aligned} |{\mathbf {y}}(\alpha ,\alpha ')-\tilde{{\mathbf {y}}}(\alpha ,\alpha ')|\le \Vert z\Vert _{C^2}(\alpha -\alpha ')^2. \end{aligned}$$

(3.27)

Using ${\mathbf {s}}(z(\alpha )) \perp {\mathbf {n}}(z(\alpha ))$, we have

$$\begin{aligned} |\tilde{{\mathbf {y}}}(\alpha ,\alpha ')+{\mathbf {c}}(\alpha )|^2 = L^2|\alpha -\alpha '|^2 + \epsilon ^2\eta ^2 \gamma ^2(\alpha ) = L^2 |\alpha -\alpha '|^2 + |{\mathbf {c}}(\alpha )|^2. \end{aligned}$$

(3.28)

From now on, for notational simplicity, we compress the dependence of ${\mathbf {y}}(\alpha ,\alpha '), \tilde{{\mathbf {y}}}(\alpha ,\alpha '), {\mathbf {c}}(\alpha )$ on $\alpha$ and $\alpha '$ in the rest of the proof.

• Estimate (3.23). Note that $BR_i(z(\alpha ))$ can also be written using the above notations as

  $$\begin{aligned} BR_i(z(\alpha )) = \frac{L}{2\pi } PV\int _S \frac{{\mathbf {y}}^\perp }{|{\mathbf {y}}|^2} \gamma (\alpha ')d\alpha , \end{aligned}$$

  thus $A_1-BR_i(z(\alpha ))$ can be written as follows:

  $$\begin{aligned} \begin{aligned} A_1-BR_i(z(\alpha ))&= \frac{L}{2\pi } PV \int _S \underbrace{\left( \frac{{\mathbf {y}}^\perp }{|{\mathbf {y}}+{\mathbf {c}}|^2}-\frac{{\mathbf {y}}^\perp }{|{\mathbf {y}}|^2}\right) }_{=:{\mathbf {f}}({\mathbf {y}},{\mathbf {c}})}\gamma (\alpha ') d\alpha '\\&= \frac{L}{2\pi } \int _S {\mathbf {f}}({\mathbf {y}},{\mathbf {c}}) (\gamma (\alpha ')-\gamma (\alpha )) d\alpha ' + \frac{L\gamma (\alpha )}{2\pi } PV \int _S {\mathbf {f}}({\mathbf {y}},{\mathbf {c}}) d\alpha ' \\&=: A_{11}+A_{12}. \end{aligned} \end{aligned}$$

  A direct computation gives

  $$\begin{aligned} {\mathbf {f}}({\mathbf {y}},{\mathbf {c}}) = -\frac{{\mathbf {y}}^\perp }{|{\mathbf {y}}|^2}\,\frac{2{\mathbf {y}}\cdot {\mathbf {c}}+|{\mathbf {c}}|^2}{|{\mathbf {y}}+{\mathbf {c}}|^2}. \end{aligned}$$

  (3.29)

  Since ${\mathbf {y}}\cdot {\mathbf {c}}=({\mathbf {y}}-\tilde{{\mathbf {y}}})\cdot {\mathbf {c}} \le C|\alpha -\alpha '|^2 |{\mathbf {c}}|,$ (where we use $\tilde{{\mathbf {y}}}\perp {\mathbf {n}}(z(\alpha ))$ and (3.27)), combining this with (3.25) and (3.26) gives a crude bound

  $$\begin{aligned} |{\mathbf {f}}({\mathbf {y}},{\mathbf {c}})| \lesssim \frac{|\alpha -\alpha '|^2 |{\mathbf {c}}| + |{\mathbf {c}}|^2}{|\alpha -\alpha '| (|\alpha -\alpha '|^2+|{\mathbf {c}}|^2)}. \end{aligned}$$

  Plugging this into $A_{11}$ and using the Hölder continuity of $\gamma$, we have

  $$\begin{aligned} \begin{aligned} |A_{11}|&\lesssim \int _{S}\frac{|\alpha -\alpha '|^2 |{\mathbf {c}}| + |{\mathbf {c}}|^2}{|\alpha -\alpha '| (|\alpha -\alpha '|^2+|{\mathbf {c}}|^2)} |\alpha -\alpha '|^b d\alpha '\\&\lesssim \int _{|\theta |<|{\mathbf {c}}|}(|\theta |^{1+b}|{\mathbf {c}}|^{-1}+|\theta |^{b-1}) d\theta + \int _{|{\mathbf {c}}|\le |\theta |\le 1} (|{\mathbf {c}}| |\theta |^{b-1} \\&\quad + |{\mathbf {c}}|^2|\theta |^{b-3})d\theta \quad (\theta :=\alpha '-\alpha )\\&\lesssim |{\mathbf {c}}|^b \le C\epsilon ^b, \end{aligned} \end{aligned}$$

  where the last step follows from the fact that $|{\mathbf {c}}|\le 2\epsilon \Vert \gamma \Vert _\infty$. Now let us turn to $A_{12}$, which requires a more delicate estimate of ${\mathbf {f}}({\mathbf {y}},{\mathbf {c}})$. Let us break $A_{12}$ as

  $$\begin{aligned} \begin{aligned} A_{12}&= \frac{L\gamma (\alpha )}{2\pi } \int _S ({\mathbf {f}}({\mathbf {y}},{\mathbf {c}})-{\mathbf {f}}(\tilde{{\mathbf {y}}},{\mathbf {c}})) d\alpha ' + \frac{L\gamma (\alpha )}{2\pi }PV \int _S {\mathbf {f}}(\tilde{{\mathbf {y}}},{\mathbf {c}}) d\alpha '=: B_1 + B_2. \end{aligned} \end{aligned}$$

  For $B_1$, let us take the gradient of ${\mathbf {f}}({\mathbf {y}},{\mathbf {c}})$ (as in (3.29)) in the first variable. An elementary computation yields that

  $$\begin{aligned} |\nabla _{{\mathbf {x}}} {\mathbf {f}}({\mathbf {x}},{\mathbf {c}})| \le C|{\mathbf {x}}|^{-2}\min \Big \{1, \frac{|{\mathbf {c}}|}{|{\mathbf {x}}|}\Big \} \end{aligned}$$

  (3.30)

  as long as ${\mathbf {x}}$ satisfies

  $$\begin{aligned} |{\mathbf {x}} + {\mathbf {c}}|^2 \ge c_0(|{\mathbf {x}}|^2+|{\mathbf {c}}|^2). \end{aligned}$$

  (3.31)

  We point out that ${\mathbf {x}}=\xi {\mathbf {y}}+(1-\xi )\tilde{{\mathbf {y}}}$ indeed satisfies (3.31) for all $\xi \in [0,1]$: to see this, in the proof of Lemma 3.1, if we replace $T_1$ in (3.3) by $\xi {\mathbf {y}}+(1-\xi )\tilde{{\mathbf {y}}}$, one can easily check the proof still goes through for $\xi \in [0,1]$. In addition, for any $\xi \in [0,1]$ we also have

  $$\begin{aligned} |\xi {\mathbf {y}}+(1-\xi )\tilde{{\mathbf {y}}}| \ge c_0 |\alpha -\alpha '|. \end{aligned}$$

  (3.32)

  Thus the gradient estimate (3.30) together with (3.27) and (3.32) yields

  $$\begin{aligned} |f({\mathbf {y}}, {\mathbf {c}}) -f(\tilde{{\mathbf {y}}}, {\mathbf {c}})| \lesssim \min \{1, |{\mathbf {c}}||\alpha -\alpha '|^{-1}\}\lesssim \min \{1,\epsilon |\alpha -\alpha '|^{-1}\}, \end{aligned}$$

  and plugging this into $B_1$ gives

  $$\begin{aligned} \begin{aligned} |B_1|&\lesssim \epsilon + \int _{\epsilon<|\alpha -\alpha '|<1} \epsilon |\alpha -\alpha '|^{-1} d\alpha ' \lesssim \epsilon |\log \epsilon |. \end{aligned} \end{aligned}$$

  As for $B_2$, using the definition of $\tilde{{\mathbf {y}}}$, the identity (3.28) and the fact that $\tilde{{\mathbf {y}}}\cdot {\mathbf {c}}=0$, we have

  $$\begin{aligned} \begin{aligned} B_2&= \frac{L\gamma (\alpha )}{2\pi } PV \int _S -\frac{\tilde{{\mathbf {y}}}^\perp }{|\tilde{{\mathbf {y}}}|^2}\,\frac{|{\mathbf {c}}|^2}{|\tilde{{\mathbf {y}}}+{\mathbf {c}}|^2} d\alpha '\\&= \frac{L\gamma (\alpha )|{\mathbf {c}}|^2 {\mathbf {n}}(z(\alpha ))}{2\pi L } PV \int _S \frac{\alpha '-\alpha }{|\alpha '-\alpha |^2 (L^2 |\alpha '-\alpha |^2 + |{\mathbf {c}}|^2)}d\alpha '. \end{aligned} \end{aligned}$$

  For the closed curves $i=1,\dots ,n$, we immediately have $B_2=0$ since $\alpha -\alpha ' \in [-\frac{1}{2},\frac{1}{2})$, and the integrand is an odd function of $\alpha '-\alpha$.

For the open curves $i=n+1,\dots ,n+m$, the above integral becomes

$$\begin{aligned} \begin{aligned} B_2&= \frac{L\gamma (\alpha )|{\mathbf {c}}|^2 {\mathbf {n}}(z(\alpha ))}{2\pi L } PV \int _{-\alpha }^{1-\alpha } \frac{\theta }{|\theta |^2 (L^2 |\theta |^2 + |{\mathbf {c}}|^2)}d\theta \quad (\theta :=\alpha '-\alpha )\\&= \frac{L\gamma (\alpha )|{\mathbf {c}}|^2 {\mathbf {n}}(z(\alpha ))}{2\pi L } \int _{\alpha }^{1-\alpha } \frac{\theta }{\theta ^2 (L^2 \theta ^2 + |{\mathbf {c}}|^2)}d\theta , \end{aligned} \end{aligned}$$

where in the second inequality we used that the integral in $[-\alpha ,\alpha ]$ gives zero contribution to the principal value, since the integrand is odd.

Next we discuss two cases. If $\alpha > |{\mathbf {c}}|$, we bound the integrand by $C\theta ^{-3}$, which gives

$$\begin{aligned} |B_2| \le C \gamma (\alpha ) |{\mathbf {c}}|^2 \alpha ^{-2} \le C |{\mathbf {c}}|^2 \alpha ^{b-2} \le C |{\mathbf {c}}|^b \le C\epsilon ^b. \end{aligned}$$

where the second inequality follows from the assumption $\gamma (0)=0$ for an open curve in (H3), as well as the Hölder continuity of $\gamma$. And if $0<\alpha \le |{\mathbf {c}}|$, the integrand can be bounded above by $\theta ^{-1}|{\mathbf {c}}|^{-2}$, which immediately leads to

$$\begin{aligned} |B_2| \le C\gamma (\alpha )|\log \alpha | \le C|{\mathbf {c}}|^b|\log |{\mathbf {c}}|| \le C\epsilon ^b|\log \epsilon |. \end{aligned}$$

In both cases we have $|B_2| \le C\epsilon ^b|\log \epsilon |,$ and combining it with the $B_1$ and $A_{11}$ estimates gives (3.23).

• Estimate (3.24). We break $A_2$ into

  $$\begin{aligned} A_2&= \frac{L{\mathbf {c}}^\perp }{2\pi } \int _S \frac{\gamma (\alpha ')-\gamma (\alpha )}{|{\mathbf {y}}+{\mathbf {c}}|^2} d\alpha ' + \frac{L{\mathbf {c}}^\perp \gamma (\alpha )}{2\pi } \int _S \left( \frac{1}{|{\mathbf {y}}+{\mathbf {c}}|^2} - \frac{1}{|\tilde{{\mathbf {y}}}+{\mathbf {c}}|^2} \right) d\alpha ' \\&\quad +\frac{L{\mathbf {c}}^\perp \gamma (\alpha )}{2\pi } \int _S \frac{1}{|\tilde{{\mathbf {y}}}+{\mathbf {c}}|^2} d\alpha '\\&=: A_{21} + A_{22} + A_{23}. \end{aligned}$$

  For $A_{21}$, (3.26) and the Hölder continuity of $\gamma$ immediately lead to

  $$\begin{aligned} |A_{21}| \le C|{\mathbf {c}}|\int _{S} \frac{|\alpha -\alpha '|^b}{|\alpha -\alpha '|^2+|{\mathbf {c}}|^2} d\alpha ' \le |{\mathbf {c}}|^b \le C\epsilon ^b. \end{aligned}$$

  (3.33)

  For $A_{22}$, its integrand can be controlled as

  $$\begin{aligned} \left| \frac{1}{|{\mathbf {y}}+{\mathbf {c}}|^2} - \frac{1}{|\tilde{{\mathbf {y}}}+{\mathbf {c}}|^2}\right| \le \frac{|{\mathbf {y}}-\tilde{\mathbf {{{y}}}}| (|{\mathbf {y}}+{\mathbf {c}}|+|\tilde{{\mathbf {y}}}+{\mathbf {c}}|)}{|{\mathbf {y}}+{\mathbf {c}}|^2 |\tilde{{\mathbf {y}}}+{\mathbf {c}}|^2} \le \frac{C|\alpha -\alpha '|^2}{(|\alpha -\alpha '|^2+|{\mathbf {c}}|^2)^{3/2}}, \end{aligned}$$

  where the last step follows from (3.26), (3.27) and (3.28). This allows us to control $A_{22}$ as

  $$\begin{aligned} |A_{22}| \le C|{\mathbf {c}}| \int _{-1}^1 \frac{\theta ^2}{(\theta ^2 + |{\mathbf {c}}|^2)^{3/2}}d\theta \le C|{\mathbf {c}}| \,\big |\log |{\mathbf {c}}|\big | \le C\epsilon |\log \epsilon |. \end{aligned}$$

  (3.34)

  Finally, for the $A_{23}$ term, (3.28) gives

  $$\begin{aligned} A_{23}= & {} \frac{L{\mathbf {c}}^\perp \gamma (\alpha )}{2\pi } \int _S \frac{1}{L^2|\alpha '-\alpha |^2+|{\mathbf {c}}|^2} d\alpha ' = \frac{{\mathbf {n}}^\perp (\alpha )\gamma (\alpha )}{2\pi } \int _I \frac{1}{\theta ^2 + 1} d\theta \\&\quad (\text {set }\theta := \frac{L(\alpha '-\alpha )}{|{\mathbf {c}}|}), \end{aligned}$$

  where the integration interval $I{=}({-}\frac{L}{2|{\mathbf {c}}|},\frac{L}{2|{\mathbf {c}}|})$ for $i{=}1,\dots ,n$, and $I=(-\frac{L\alpha }{|{\mathbf {c}}|},\frac{L(1-\alpha )}{|{\mathbf {c}}|})$ for $i=n+1,\dots ,n+m$, and in the last equality we also used that $\frac{{\mathbf {c}}^\perp }{|{\mathbf {c}}|}={\mathbf {n}}^\perp$. For $i=1,\dots ,n$, one can easily check that

  $$\begin{aligned} \left| \int _I \frac{1}{\theta ^2 + 1} d\theta -\pi \right| = 2\int _{\frac{L}{2|{\mathbf {c}}|}}^\infty \frac{1}{\theta ^2+1} d\theta \le C|{\mathbf {c}}|\le C\epsilon , \end{aligned}$$

  which immediately leads to

  $$\begin{aligned} \left| A_{23}-\frac{{\mathbf {n}}(z(\alpha ))^\perp \gamma (\alpha )}{2}\right| =\left| \frac{{\mathbf {n}}^\perp (\alpha )\gamma (\alpha )}{2\pi } \left( \int _I \frac{1}{\theta ^2 + 1} d\theta -\pi \right) \right| \le C\epsilon \end{aligned}$$

  for $i=1,\dots ,n$. Next we turn to the open curves $i=n+1,\dots ,n+m$, and let us assume $\alpha \in [0,\frac{1}{2}]$ without loss of generality. In this case we have

  $$\begin{aligned} \left| \int _I \frac{1}{\theta ^2 + 1} d\theta -\pi \right| = \int ^{-\frac{L\alpha }{|{\mathbf {c}}|}}_{-\infty }\frac{1}{\theta ^2+1} d\theta +\int _{\frac{L(1-\alpha )}{|{\mathbf {c}}|}}^{\infty }\frac{1}{\theta ^2+1} d\theta \le \min \left\{ C\frac{|{\mathbf {c}}|}{\alpha },\frac{\pi }{2}\right\} +C\epsilon . \end{aligned}$$

  where we used $1-\alpha >\frac{1}{2}$ to control the second integral by $C\epsilon$. Using the above inequality as well as the fact that $\gamma (\alpha )\le C\alpha ^b$ due to (H3), we have

  $$\begin{aligned} \left| A_{23}-\frac{{\mathbf {n}}(z(\alpha ))^\perp \gamma (\alpha )}{2}\right|= & {} \frac{\gamma (\alpha )}{2\pi } \left| \int _I \frac{1}{\theta ^2 + 1} d\theta -\pi \right| \le C\alpha ^b \min \left\{ \frac{|{\mathbf {c}}|}{\alpha },1\right\} +C\epsilon \\\le & {} C(|{\mathbf {c}}|^b+\epsilon )\le C\epsilon ^b \end{aligned}$$

  for $i=n+1,\dots ,n+m$. Finally, combining the $A_{23}$ estimates together with (3.33) and (3.34) yields (3.24). $\square$

4 Constructing a Divergence-Free Perturbation

In this section, we aim to construct a divergence-free velocity field ${\mathbf {u}}^\epsilon :D^\epsilon \rightarrow {\mathbb {R}}^2$, such that $-{\mathbf {u}}^\epsilon$ tends to make each $D_i^\epsilon$ “more symmetric”. Let ${\mathbf {u}}^\epsilon : D^\epsilon \rightarrow {\mathbb {R}}^2$ be given by

$$\begin{aligned} {\mathbf {u}}^\epsilon := x + \nabla p^\epsilon \quad \text { in } D^\epsilon , \end{aligned}$$

(4.1)

where the function $p^\epsilon : \overline{D^\epsilon } \rightarrow {\mathbb {R}}$ is chosen such that

$$\begin{aligned} \nabla \cdot {\mathbf {u}}^\epsilon = 0\quad \text { in }D^\epsilon , \end{aligned}$$

(4.2)

and on each connected component l of $\partial D^\epsilon$, $u^\epsilon$ satisfies

$$\begin{aligned} \int _l {\mathbf {u}}^\epsilon \cdot n \,d\sigma = 0, \end{aligned}$$

(4.3)

where n is the unit normal of l pointing outwards of $D^\epsilon$. Note that $\partial D^\epsilon$ has a total of $2n+m$ connected components: $D_i^\epsilon$ is doubly-connected for $i=1,\dots ,n$ (denote its outer and inner boundaries by $\partial D_{i,\text {out}}^\epsilon$ and $\partial D_{i,\text {in}}^\epsilon$; note that $\partial D_{i,\text {in}}^\epsilon$ coincides with $\Gamma _i$), whereas it is simply-connected for $i=n+1,\dots ,n+m$ (denote its boundary by $\partial D_i^\epsilon$).

Next we show that there indeed exists a function $p^\epsilon$ so that ${\mathbf {u}}^\epsilon$ satisfies (4.2)–(4.3). Clearly, (4.2) requires that $p^\epsilon$ satisfies

$$\begin{aligned} \Delta p^\epsilon = -2 \quad \text { in }D^\epsilon . \end{aligned}$$

(4.4)

Once (4.2) is satisfied, the divergence theorem yields that ${\mathbf {u}}^\epsilon$ satisfies (4.3) for each $l = \partial D_i^\epsilon$ for $i=n+1,\dots ,n+m$.

Next let us set the boundary conditions as

$$\begin{aligned} p^\epsilon |_{\partial D_i^\epsilon } = 0 \quad \text {for }i=n+1,\dots ,n+m. \end{aligned}$$

(4.5)

For $i=1,\dots , n$, let

$$\begin{aligned} p^\epsilon = {\left\{ \begin{array}{ll} 0 &{} \text { on } \partial D_{i,\text {out}}^\epsilon \\ c_i^\epsilon &{} \text{ on } \partial D_{i,\text {in}}^\epsilon = \Gamma _i \end{array}\right. }\quad \text { for } i = 1,\dots , n, \end{aligned}$$

(4.6)

where $c_i^\epsilon >0$ is the unique constant such that

$$\begin{aligned} \int _{\partial U_i} \nabla p^\epsilon \cdot n d\sigma = -2|U_i| \quad \text { for } i = 1,\dots , n, \end{aligned}$$

(4.7)

where $U_i$ is the domain enclosed by $\partial D_{i,\text {in}}^\epsilon =\Gamma _i$ (thus $U_i$ is independent of $\epsilon$), and n is the outer normal of $U_i$ (thus the inner normal of $D_i^\epsilon$). The existence of $c_i^\epsilon$ is guaranteed by [14, Lemma 2.5]. One can then check that $\int _{\partial U_i} {\mathbf {u}}^\epsilon \cdot n d\sigma = 0$. Applying the divergence theorem in $D^\epsilon _i$ then gives us that $\int _{\partial D_{i,\text {out}}^\epsilon } {\mathbf {u}}^\epsilon \cdot n d\sigma = 0$ as well, thus ${\mathbf {u}}^\epsilon$ satisfies (4.3) for $i=1,\dots , n$.

In [14] we proved a rearrangement inequality for such $p^\epsilon$ in a similar spirit of Talenti’s rearrangement inequality for elliptic equations [37], which we state below.

Lemma 4.1

[14, Proposition 2.6]. The function $p^\epsilon : \overline{D^\epsilon }\rightarrow {\mathbb {R}}$ defined in (4.4)–(4.7) satisfies the following in each $D_i^\epsilon$ for $i=1,\dots ,n+m$:

$$\begin{aligned} \sup _{D_i^\epsilon } p^\epsilon \le \frac{|D_i^\epsilon |}{2\pi }, \end{aligned}$$

(4.8)

and

$$\begin{aligned} \int _{D_i^\epsilon } p^\epsilon (x) dx \le \frac{|D_i^\epsilon |^2}{4\pi }. \end{aligned}$$

(4.9)

Moreover, each inequality above achieves equality if and only $D_i^\epsilon$ is either a disk or an annulus.

Note that the inequalities (4.8)–(4.9) hold for any domain with $C^{1,\alpha }$ boundary. Even though the inequalities are strict when $D_i^\epsilon$ is non-radial, they are not strong enough to rule out non-radial vortex sheets, as we need quantitative versions of strict inequalities that are still valid in the $\epsilon \rightarrow 0^+$ limit. As we will see in the proof of Proposition 5.2, the key step is to show that if some $\Gamma _i$ is either not a circle or does not have a constant $\gamma _i$, then the following quantitative version of (4.9) holds: $\epsilon ^{-2}\left( \frac{|D_i^\epsilon |^2}{4\pi }-\int _{D_i^\epsilon } p^\epsilon (x) dx\right) \ge c_0>0$, where $c_0$ is independent of $\epsilon$.

In order to upgrade (4.9) into a quantitative version, we need to obtain some fine estimates for $p^\epsilon$ that take into account the shape of the thin domains $D^\epsilon _i$. For $i=n+1,\dots ,n+m$, since $p^\epsilon =0$ on $\partial D_i^\epsilon$, and the domain $D_i^\epsilon$ is a thin simply-connected domain with width $\epsilon \ll 1$, intuitively one would expect that $| p^\epsilon | \le C\epsilon ^2$. The next proposition shows that this crude estimate is indeed true, and its proof is postponed to Sect. 4.1.

Proposition 4.2

For any $i=n+1,\dots ,n+m$, let $p^\epsilon :\overline{D_i^\epsilon }\rightarrow {\mathbb {R}}$ be given by (4.4)–(4.5). Then there exist $\epsilon _1$ and C only depending on $\Vert z_i\Vert _{C^{2}(S_i)},\Vert \gamma _i \Vert _{L^\infty (S_i)}$ and $F_\Gamma$, such that

$$\begin{aligned} |p^\epsilon |\le C\epsilon ^2 \quad \text { in }D_i^\epsilon \end{aligned}$$

for all $\epsilon \in (0,\epsilon _1)$.

For $i=1,\dots , n$, the estimate is more involved, since $p^\epsilon$ takes different values $c^\epsilon _i$ and 0 on the inner and outer boundaries of $D^\epsilon _i$. Heuristically speaking, since $D^\epsilon _i$ is a doubly-connected thin tubular domain with width $\sim \epsilon$, we would expect that $p^\epsilon _i$ (in $\alpha ,\eta$ coordinate) changes almost linearly from 0 to $c^\epsilon _i$ as $\eta$ goes from $-1$ (outer boundary) to 0 (inner boundary). Next we will show that the error between $p^\epsilon (R^\epsilon _i(\alpha ,\eta ))$ and the linear-in-$\eta$ function $c^\epsilon _i(1+\eta )$ is indeed controlled by $O(\epsilon ^2)$. We will also obtain fine estimates of the gradient of the function $c^\epsilon _i(1+\eta )$, as well as the boundary value $c^\epsilon _i$. Again, its proof is postponed to Sect. 4.1.

Proposition 4.3

For any $i=1,\dots ,n$, let $p^\epsilon :\overline{D_i^\epsilon }\rightarrow {\mathbb {R}}$ and $c^\epsilon _i \in {\mathbb {R}}$ be given by (4.4) and (4.6)–(4.7). For such $p^{\epsilon }$, let us define ${\tilde{p}}^{\epsilon }$,$q^{\epsilon }:\overline{D_i^\epsilon }\mapsto {\mathbb {R}}$ as follows:

$$\begin{aligned} {\tilde{p}}^{\epsilon }(R^\epsilon _i(\alpha ,\eta ))&:= c^\epsilon _i(1+\eta ) \quad \text { for }\alpha \in S_i, \eta \in [0,-1], \nonumber \\ q^{\epsilon }&:= p^{\epsilon } - {\tilde{p}}^{\epsilon }\quad \quad \text { in }\overline{D^\epsilon _i}. \end{aligned}$$

(4.10)

Also let

$$\begin{aligned} \beta _i := \frac{2|U_i|}{L_i\int _{S_i}\gamma _i^{-1}(\alpha )d\alpha }. \end{aligned}$$

(4.11)

Then there exist $\epsilon _1$ and C only depending on $\Vert z_i\Vert _{C^{3}(S_i)},\Vert \gamma _i \Vert _{C^2(S_i)}$ and $F_\Gamma$, such that for all $\epsilon \in (0,\epsilon _1)$ we have the following:

$$\begin{aligned}&{\left\{ \begin{array}{ll} |q^{\epsilon }|\le C \epsilon ^2 &{} \text { in }D^{\epsilon }_i,\\ q^{\epsilon } = 0 &{} \text { on }\partial D^{\epsilon }_i, \end{array}\right. } \end{aligned}$$

(4.12)

$$\begin{aligned}&\left| \frac{c^\epsilon _i}{\epsilon }-\beta _i\right| \le C\epsilon , \end{aligned}$$

(4.13)

$$\begin{aligned}&\left| \nabla {\tilde{p}}^{\epsilon }(R^\epsilon _i(\alpha ,\eta ))- \frac{\beta _i}{\gamma _i(\alpha )}{\mathbf {n}}(z_i(\alpha ))\right| \le C\epsilon \quad \text { for }\alpha \in S_i, \eta \in [0,-1]. \end{aligned}$$

(4.14)

4.1 Proof of the quantitative lemmas for $p^\epsilon$

In this subsection we aim to prove Propositions 4.2 and 4.3 . We start with a technical lemma on estimating the solution of Poisson’s equation (with zero boundary condition) in the domain $D^\epsilon _i$.

Lemma 4.4

For any $i=1,\dots , n+m$, assume $\Gamma _i$ and $\gamma _i$ satisfy (H1)–(H3). Let $v^\epsilon \in C^2(D^\epsilon _i) \cap C(\overline{D^\epsilon _i})$ solve the Poisson’s equation with zero boundary condition:

$$\begin{aligned} {\left\{ \begin{array}{ll} \Delta v^\epsilon = -1 &{} \text { in }D^{\epsilon }_i, \\ v^{\epsilon } =0 &{} \text { on }\partial D^{\epsilon }_i. \end{array}\right. } \end{aligned}$$

(4.15)

Then there exist positive constants $\epsilon _0=C(\Vert z_i\Vert _{C^{2}(S_i)},\Vert \gamma _i\Vert _{L^\infty (S_i)},F_\Gamma )$ and $C_1, C_2 = C(\Vert \gamma _i\Vert _{L^\infty (S_i)})$, such that for all $\epsilon \in (0,\epsilon _0)$ we have

$$\begin{aligned} 0 \le v^\epsilon \le C_1 \epsilon ^2\quad \text { in } D^\epsilon _i \end{aligned}$$

(4.16)

and

$$\begin{aligned} \Vert \nabla v^\epsilon \Vert _{L^{\infty }(\Gamma _i)} \le C_2\epsilon \quad \text { for } i=1, \ldots , n. \end{aligned}$$

(4.17)

Proof

Throughout the proof, let $i\in \{1,\dots ,n+m\}$ be fixed. For notational simplicity, in the rest of the proof we omit the subscript i in $R^\epsilon _i$, $D^\epsilon _i$, $S_i$, $z_i$ and $\gamma _i$.

Step 1. We start with a simple geometric result that $D^\epsilon$ is “flat” in a small neighborhood of any interior $z(\alpha )$. For any $\alpha \in S^\circ$, let $V^\epsilon (\alpha ):= D^\epsilon \cap B_{6\epsilon \Vert \gamma \Vert _\infty }(z(\alpha ))$, where $\Vert \cdot \Vert _\infty$ denotes $\Vert \cdot \Vert _{L^\infty (S)}$. We will show that any $y\in V^\epsilon (\alpha )$ satisfies

$$\begin{aligned} \big |(z(\alpha )-y)\cdot {\mathbf {n}}(z(\alpha ))\big | \le 2\epsilon \Vert \gamma \Vert _\infty \end{aligned}$$

(4.18)

for all sufficiently small $\epsilon >0$ (to be quantified in (4.23)). See Fig. 4a for an illustration.

Since $y\in V^\epsilon (\alpha )\subset D^\epsilon$, there exist $\beta \in S$ and $\eta \in (-1,0)$ such that $y=R^\epsilon (\beta ,\eta ) = z(\beta ) + \epsilon \gamma (\beta ) {\mathbf {n}}(z(\beta ))\eta$. It follows that

$$\begin{aligned} \begin{aligned} \big |(z(\alpha )-y)\cdot {\mathbf {n}}(z(\alpha ))\big |&\le |(z(\alpha )-z(\beta ))\cdot {\mathbf {n}}(z(\alpha ))|+\epsilon \Vert \gamma \Vert _{\infty }\\&\le \Vert z'' \Vert _{\infty }(\alpha -\beta )^2+\epsilon \Vert \gamma \Vert _{\infty }, \end{aligned} \end{aligned}$$

(4.19)

where in the second inequality we used

$$\begin{aligned} |(z(\alpha )-z(\beta )) - z'(\alpha )(\alpha -\beta )| \le \Vert z''\Vert _{\infty } (\alpha -\beta )^2 \end{aligned}$$

(4.20)

and $z'(\alpha )\cdot {\mathbf {n}}(z(\alpha ))=0$. To bound $\alpha -\beta$ on the right hand side of (4.19), the fact that $y\in B_{6\epsilon \Vert \gamma \Vert _\infty }(z(\alpha ))$ gives

$$\begin{aligned} 6\epsilon \Vert \gamma \Vert _{\infty } \ge |z(\alpha )-y| \ge |z(\alpha )-z(\beta )| - \epsilon \gamma (\beta ), \end{aligned}$$

(4.21)

which implies $|z(\alpha )-z(\beta )| \le 7 \epsilon \Vert \gamma \Vert _{\infty }$. Since the arc-chord constant $F_\Gamma$ given in (2.2) is finite, this implies

$$\begin{aligned} |\alpha - \beta | \le 7 F_\Gamma \Vert \gamma \Vert _{\infty } \epsilon . \end{aligned}$$

(4.22)

Plugging this into the right hand side of (4.19), we know (4.18) holds for all

$$\begin{aligned} 0<\epsilon \le (49\Vert z''\Vert _\infty F_\Gamma ^2 \Vert \gamma \Vert _\infty )^{-1}. \end{aligned}$$

(4.23)

Fig. 4

a In Step 1, $V^\epsilon (\alpha )$ (the yellow set) must lie between the two dashed lines for small $\epsilon$. b In Step 2, $\partial V^\epsilon (\alpha _0)$ is decomposed into $\partial V_1^\epsilon (\alpha _0)$ (in dark green) and $\partial V_2^\epsilon (\alpha _0)$ (in purple)

Step 2. Next we prove (4.16). Note that $v^\epsilon$ is superharmonic in $D^{\epsilon }$ and vanishes on the boundary, thus it follows from the maximum principle that $v^\epsilon \ge 0$ in $D^\epsilon$. Denote $M:=\max _{x\in D^{\epsilon }}v^\epsilon (x)$, and pick $x_0=R(\alpha _0,\eta _0) \in D^{\epsilon }$ such that $v^\epsilon (x_0) = M$. Note that $\alpha _0\in S^\circ$. Without loss of generality, we can assume that $z(\alpha _0)=(0,0)$ and ${\mathbf {s}}(z(\alpha _0))={\mathbf {e}}_1:=(1,0)$, so that ${\mathbf {n}}(z(\alpha _0))=(0,1)$ and $x_0 =(0, \epsilon \gamma (\alpha _0)\eta _0)$. Let us consider a barrier function $b_1:{\mathbb {R}}^2 \mapsto {\mathbb {R}}$ given by

$$\begin{aligned} b_1(x_1,x_2) = x_2^2 - \frac{x_1^2}{2}. \end{aligned}$$

Clearly $\Delta b_1=1$, so $v^\epsilon +b_1$ is harmonic in $D^\epsilon$. It then follows from the maximum principle that $\max _{\overline{V^\epsilon (\alpha _0)}} (v^\epsilon +b_1)$ is achieved at some boundary point ${{\tilde{x}}}_0\in \partial V^\epsilon (\alpha _0)$. Let us break $\partial V^\epsilon (\alpha _0)$ into $\partial V^\epsilon _1(\alpha _0) \cup \partial V^\epsilon _2(\alpha _0)$ (see Fig. 4b for an illustration), given by

$$\begin{aligned} \partial V^\epsilon _1(\alpha _0):=\partial D^{\epsilon }\cap B_{6\epsilon \Vert \gamma \Vert _{\infty }}(z(\alpha _0)), \quad \partial V^\epsilon _2(\alpha _0):=\overline{D^{\epsilon }}\cap \partial B_{6\epsilon \Vert \gamma \Vert _{\infty }}(z(\alpha _0)). \end{aligned}$$

(4.24)

We claim that ${\tilde{x}}_0 \in \partial V^\epsilon _1(\alpha _0)$. To see this, note that any $y=(y_1,y_2)\in \partial V^\epsilon _2(\alpha _0)$ satisfies $|y|=6\epsilon \Vert \gamma \Vert _{\infty }$ and $|y_2|\le 2\epsilon \Vert \gamma \Vert _{\infty }$, where the latter follows from (4.18) and our assumptions that ${\mathbf {s}}(z(\alpha _0))= {\mathbf {e}}_1$ and $z(\alpha _0) = (0,0)$. This implies that $|y_1|\ge 4\epsilon \Vert \gamma \Vert _{\infty }>|y_2|$, thus $b_1(y)<0$. Using that $v^\epsilon (x_0) = M \ge v^\epsilon (y)$ and $b_1(x_0)= b_1(0, \epsilon \gamma (\alpha _0)\eta _0)\ge 0$, we have $(v^\epsilon +b_1)(y) < (v^\epsilon +b_1)(x_0).$ This shows that $\max _{\overline{V^\epsilon (\alpha _0)}}(v^\epsilon + b_1)$ cannot be achieved on $\partial V^\epsilon _2(\alpha _0)$, finishing the proof of the claim.

Since ${\tilde{x}}_0 \in \partial V^\epsilon _1(\alpha _0) \subset \partial D^\epsilon$, the boundary condition in (4.15) yields that $v^\epsilon ({\tilde{x}}_0)=0$. Thus

$$\begin{aligned} M+b_1(x_0)= v^\epsilon (x_0)+b_1(x_0) \le v^\epsilon ({\tilde{x}}_0)+b_1({\tilde{x}}_0) = b_1({\tilde{x}}_0). \end{aligned}$$

Using $b_1(x_0)= b_1(0, \epsilon \gamma (\alpha _0)\eta _0)\ge 0$, the above inequality becomes

$$\begin{aligned} M\le b_1({{\tilde{x}}}_0) \le |{{\tilde{x}}}_0|^2 \le 36 \Vert \gamma \Vert _{\infty }^2\epsilon ^2, \end{aligned}$$

(4.25)

where the second inequality follows from the definition of $b_1$. This proves (4.16) for $C_1=36 \Vert \gamma \Vert _{\infty }^2$.

Step 3. It remains to prove (4.17). First note that for $i\in \{1,\dots ,n\}$, the assumptions (H1)–(H3) yield that $D_i^\epsilon$ has $C^2$ boundary, therefore $v^\epsilon \in C^2(D_i^\epsilon )\cap C^1(\overline{D_i^\epsilon })$. Let us fix $i\in \left\{ 1, \ldots , n\right\}$ and any $\alpha \in S$, and we aim to show that $|\nabla v^\epsilon (z(\alpha ))|\le C_2 \epsilon$. Again, without loss of generality we can assume that $z(\alpha )=(0,0)$ and ${\mathbf {s}}(z(\alpha ))={\mathbf {e}}_1$. Let us consider a new barrier function $b_2:{\mathbb {R}}^2\rightarrow {\mathbb {R}}$

$$\begin{aligned} b_2(x_1,x_2) := x_2^2 + 4\epsilon \Vert \gamma \Vert _{\infty } x_2 - \frac{x_1^2}{2}, \end{aligned}$$

(4.26)

which satisfies $b_2(0,0)=0$, and one can easily check that its zero level set has horizontal tangent at (0, 0) (thus tangent to $\partial D^\epsilon$ at $z(\alpha )$).

Again, let us decompose $\partial V^\epsilon (\alpha )$ as $\partial V^\epsilon _1(\alpha ) \cup \partial V^\epsilon _2(\alpha )$ as in (4.24) (except that $\alpha _0$ now becomes $\alpha$). We claim that for all sufficiently small $\epsilon >0$, the new barrier function $b_2$ satisfies

$$\begin{aligned} \Delta b_2&= 1~~~\, \text { in }V^\epsilon (\alpha ), \end{aligned}$$

(4.27)

$$\begin{aligned} b_2&\le 0\quad ~~~ \text { on }\partial V^\epsilon _1, \end{aligned}$$

(4.28)

$$\begin{aligned} b_2&\le -\epsilon ^2 \quad \text { on } \partial V^\epsilon _2. \end{aligned}$$

(4.29)

Let us assume for a moment that (4.27)–(4.29) are true. Then it follows that

$$\begin{aligned} v^\epsilon +C_2b_2\le 0 \text { in } V^\epsilon (\alpha ), \end{aligned}$$

(4.30)

where $C_2:=\max \left\{ 1,C_1\right\}$ and $C_1$ is as in (4.16) (in the end of step 2 we have $C_1 = 36 \Vert \gamma \Vert _{\infty }^2$). To show (4.30), note that $v^\epsilon +C_2b_2$ is subharmonic in $V^\epsilon (\alpha )$ due to (4.27) and the definition of $C_2$, thus its maximum is attained on its boundary. The boundary conditions in (4.15) and (4.28) yield that $v^\epsilon +C_2 b_2 \le 0$ on $\partial V^\epsilon _1(\alpha )$; whereas (4.16), (4.29) and the definition of $C_2$ yield that $v^\epsilon +C_2b_2 \le 0$ on $\partial V^\epsilon _2(\alpha )$. Thus $v^\epsilon +C_2 b_2 \le 0$ on $\partial V^\epsilon _1(\alpha ) \cup \partial V^\epsilon _2(\alpha )$, implying (4.30).

However, $v^\epsilon +C_2b_2$ is actually zero at $z(\alpha ) \in \partial V^\epsilon (\alpha )$, therefore Hopf’s Lemma implies that $\nabla \left( v^\epsilon +C_2b_2\right) (z(\alpha )) \cdot \mathbf {n}(z(\alpha )) > 0$, where $\mathbf {n}(z(\alpha ))$ is the outer normal of $\partial D^{\epsilon }$ at $z(\alpha )$. Hence

$$\begin{aligned} | \nabla v^\epsilon (z(\alpha ))|= -\nabla v^\epsilon (z(\alpha ))\cdot \mathbf {n}(z(\alpha )) < C_2\nabla b_2(z(\alpha ))\cdot \mathbf {n}(z(\alpha )) = 4C_2\Vert \gamma \Vert _{\infty }\epsilon , \end{aligned}$$

(4.31)

where the first equality follows from the fact that $v^\epsilon$ is superharmonic in $D^{\epsilon }$ and constant on $\partial D^\epsilon$, and the second equality is a direct computation of $\nabla b_2$. Thus (4.31) proves (4.17).

To complete the proof, we only need to prove (4.27)–(4.29) for small $\epsilon >0$. Note that (4.27) follows immediately from computing the Laplacian of $b_2$. For (4.28), let us pick $y\in \partial V^\epsilon _1(\alpha )$, and we aim to show that $b_2(y)\le 0$. Note that $y=R^\epsilon (\beta ,0)$ or $R^\epsilon (\beta ,-1)$ for some $\beta \in S$. We first deal with the first case.

Let us denote $y=(y_1,y_2)$. Rewriting (4.20) into two inequalities for the two components, and using that $z(\alpha )=(0,0)$ and $z'(\alpha )=L{\mathbf {e}}_1$ (L is the length of the curve $\Gamma _i$), we have

$$\begin{aligned} |0-y_1 - L(\alpha -\beta )|&\le \Vert z''\Vert _\infty (\alpha -\beta )^2 \end{aligned}$$

(4.32)

$$\begin{aligned} |y_2| = |0-y_2|&\le \Vert z''\Vert _\infty (\alpha -\beta )^2. \end{aligned}$$

(4.33)

Also, (4.22) gives $|\alpha -\beta |\le 7 F_\Gamma \Vert \gamma \Vert _\infty \epsilon$. Applying it to (4.32), for all $\epsilon >0$ sufficiently small we have that

$$\begin{aligned} |y_1| \ge \frac{L}{2}|\alpha -\beta |. \end{aligned}$$

(4.34)

Plugging (4.34) and (4.33) into $b_2(y) = - \frac{1}{2} y_1^2 + y_2^2 + 4\epsilon \Vert \gamma \Vert _\infty y_2$, we have

$$\begin{aligned} \begin{aligned} b_2(y)&\le - \frac{L^2}{8}(\alpha -\beta )^2+ \Vert z''\Vert _\infty ^2 (\alpha -\beta )^4+ 4\epsilon \Vert \gamma \Vert _\infty \Vert z''\Vert _\infty (\alpha -\beta )^2 \\&\le \left( -\frac{L^2}{8} + C\epsilon ^2 + C\epsilon \right) (\alpha -\beta )^2 \le 0, \end{aligned} \end{aligned}$$

for all $\epsilon >0$ sufficiently small, where the second inequality follows from (4.22). This finishes the proof of (4.28) for the case $y=R^\epsilon (\beta ,0)$.

Before we deal with the case $y=R^\epsilon (\beta ,-1)$, let us prove (4.29) first. For any $y=(y_1,y_2)\in \partial V^\epsilon _2(\alpha )$, (4.18) gives $|y_2|\le 2\epsilon \Vert \gamma \Vert _\infty$. Combining this with $|y|=6\epsilon \Vert \gamma \Vert _\infty$ yields $|y_1|\ge \sqrt{32}\epsilon \Vert \gamma \Vert _{\infty }$. Thus

$$\begin{aligned} b_2(y) \le (2\epsilon \Vert \gamma \Vert _\infty )^2 + 4\epsilon \Vert \gamma \Vert _{\infty } (2\epsilon \Vert \gamma \Vert _\infty ) - \frac{(\sqrt{32}\epsilon \Vert \gamma \Vert _{\infty })^2}{2} \le -4\epsilon ^2 \Vert \gamma \Vert _\infty ^2. \end{aligned}$$

Finally we turn to the proof of (4.28) for the case $y=R^\epsilon (\beta ,-1)$. Note that the curve $\{R^\epsilon (\beta ,-1):\beta \in S\} \cap B_{6\epsilon \Vert \gamma \Vert _\infty }(z(\alpha ))$ lies in the interior of the region bounded by $\Gamma \cap B_{6\epsilon \Vert \gamma \Vert _\infty }(z(\alpha ))$ on the top, $\partial B_{6\epsilon \Vert \gamma \Vert _\infty }(z(\alpha ))$ on the sides, and $y_2 = -2\epsilon \Vert \gamma \Vert _\infty$ on the bottom. (The last one follows from (4.18) and our assumption that ${\mathbf {s}}(z(\alpha ))= {\mathbf {e}}_1$). We have already shown $b_2\le 0$ on $\Gamma \cap B_{6\epsilon \Vert \gamma \Vert _\infty }(z(\alpha ))$ and the lateral boundaries, and it is easy to check that $b_2\le 0$ on $y_2 = -2\epsilon \Vert \gamma \Vert _\infty$. Since the set $\{b_2\le 0\}$ is simply-connected, it implies that $b_2\le 0$ in the interior of this region, finishing the proof. $\square$

Note that (4.16) of Lemma 4.4 immediately implies Proposition 4.2. (The only difference is that $\Delta v^\epsilon =-1$ in Lemma 4.4 whereas $\Delta p^\epsilon =-2$ in Proposition 4.2, so the constant C in Proposition 4.2 is twice of that in (4.16)). The lemma also implies the following corollary, which will be helpful in the proof of Proposition 4.3.

Corollary 4.5

For any $i=1,\dots , n+m$, assume $\Gamma _i$ and $\gamma _i$ satisfy (H1)–(H3). Assume $v^\epsilon \in C^2(D^\epsilon _i) \cap C(\overline{D^\epsilon _i})$ satisfies that

$$\begin{aligned} {\left\{ \begin{array}{ll} \left| \Delta v^\epsilon \right| \le C_0 &{} \text { in }D^{\epsilon }_i, \\ v^\epsilon = 0 &{} \text { on }\partial D^{\epsilon }_i, \end{array}\right. } \end{aligned}$$

for some constant $C_0>0$. Then for the same constants $\epsilon _0, C_1, C_2$ as in Lemma 4.4, the following holds for all $\epsilon \in (0,\epsilon _0)$:

$$\begin{aligned} |v^\epsilon | \le C_0 C_1 \epsilon ^2\quad \text { in } D^\epsilon _i, \end{aligned}$$

(4.35)

and if $v^\epsilon \in C^2(D^\epsilon _i) \cap C^1(\overline{D^\epsilon _i})$, we have

$$\begin{aligned} \Vert \nabla v^\epsilon \Vert _{L^{\infty }(\Gamma _i)} \le C_0 C_2 \epsilon \quad \text { for }\quad i=1,\ldots ,n . \end{aligned}$$

(4.36)

Proof

Let ${\tilde{v}}$ be a solution to

$$\begin{aligned} {\left\{ \begin{array}{ll} \Delta {\tilde{v}} = -C_0 &{} \text { in }D^{\epsilon }_i, \\ {\tilde{v}} = 0 &{} \text { on }\partial D^{\epsilon }_i. \end{array}\right. } \end{aligned}$$

It is clear that $v^\epsilon +{\tilde{v}}$ is super-harmonic and $v^\epsilon -{\tilde{v}}$ is sub-harmonic in $D^{\epsilon }_i$, and they both vanish on the boundary. Thus the maximum principle implies that

$$\begin{aligned} -{\tilde{v}} \le v^\epsilon \le {\tilde{v}}\quad \text { in }D^\epsilon _i. \end{aligned}$$

(4.37)

Applying (4.16) of Lemma 4.4 to $\frac{{\tilde{v}}}{C_0}$, we obtain $0\le {{\tilde{v}}} \le C_0 C_1\epsilon ^2$ in $D^\epsilon _i$ for all $\epsilon \in (0,\epsilon _0)$, leading to (4.35). Furthermore, (4.37) and the fact that $v^\epsilon$ and v both have zero boundary condition imply that

$$\begin{aligned} |\nabla v^\epsilon |\le |\nabla {\tilde{v}}|\quad \text { on } \partial D^\epsilon _i. \end{aligned}$$

We then apply (4.17) of Lemma 4.4 to $\frac{{\tilde{v}}}{C_0}$ and obtain $\Vert \nabla v^\epsilon \Vert _{L^{\infty }(\Gamma _i)} \le C_0 C_2\epsilon ,$ which proves (4.36). $\square$

Now we are ready to prove Proposition 4.3.

Proof of Proposition 4.3

Throughout the proof, let $i\in \{1,\dots ,n\}$ be fixed. For notational simplicity, in the rest of the proof we omit the subscript i from all terms.

We claim that

$$\begin{aligned}&\left| \nabla {\tilde{p}}^{\epsilon }(R^\epsilon (\alpha ,\eta )) -\frac{c^\epsilon }{\epsilon \gamma (\alpha )}{\mathbf {n}}(z(\alpha )) \right| \le C\epsilon \quad \text { for all }\alpha \in S, \eta \in [0,-1], \end{aligned}$$

(4.38)

$$\begin{aligned}&\Vert \Delta q^{\epsilon }\Vert _{L^{\infty }(D^{\epsilon })} \le C \end{aligned}$$

(4.39)

for some constant $C>0$ only depending on $\Vert z_i\Vert _{C^{3}(S_i)},\Vert \gamma _i \Vert _{C^2(S_i)}$ and $F_\Gamma$. Assuming these are true, let us explain how they lead to (4.12)–(4.14). By (4.6) and (4.10), $p^\epsilon$ and ${{\tilde{p}}}^\epsilon$ have the same boundary condition, thus $q^{\epsilon }=0$ on $\partial D^{\epsilon }$. This and (4.39) allow us to apply Corollary 4.5 to $q^\epsilon$ to obtain the estimate (4.35), implying (4.12).

Due to (4.36) of Corollary 4.5, we also have

$$\begin{aligned} \Vert \nabla q^{\epsilon } \Vert _{L^{\infty }( \Gamma )} \le C\epsilon . \end{aligned}$$

(4.40)

Using (4.7) and $p^\epsilon = {{\tilde{p}}}^\epsilon + q^\epsilon$, we have

$$\begin{aligned} -2|U|&= \int _{\partial U} \nabla {\tilde{p}}^{\epsilon }\cdot {n}d\sigma + \int _{\partial U}\nabla q^{\epsilon }\cdot nd\sigma \\&= -\frac{c^{\epsilon }L}{\epsilon }\int _{S}\gamma ^{-1}(\alpha )d\alpha + O(\epsilon ), \end{aligned}$$

where the second equality follows from (4.38) for $\eta =0$, $n(z(\alpha ))=-{\mathbf {n}}(z(\alpha ))$ and $d\sigma = L d\alpha$, as well as (4.40). Rearranging the terms and using the definition of $\beta$ in (4.11) yields (4.13).

Finally, note that (4.13) and (4.38) directly lead to (4.14), where we are using the fact that $\gamma _i$ is uniformly positive for $i=1,\dots ,n$, due to (H3).

The rest of the proof is devoted to proving the claims (4.38) and (4.39). For (4.38), we compute the gradient of ${\tilde{p}}^{\epsilon }$. Differentiating (4.10) with respect to $\alpha$ and $\eta$, we obtain

$$\begin{aligned} (\nabla _{\alpha ,\eta }R^\epsilon (\alpha ,\eta ))^{t}\nabla {\tilde{p}}(R^\epsilon (\alpha ,\eta )) = \begin{pmatrix} 0 \\ c^{\epsilon } \end{pmatrix}, \end{aligned}$$

(4.41)

where $(\nabla _{\alpha ,\eta }R^\epsilon )^{t}$ denotes the transpose of the Jacobian matrix of $R^\epsilon$. Since $\nabla _{\alpha ,\eta }R^\epsilon = ( \partial _\alpha R^\epsilon , \partial _\eta R^\epsilon )$, using the formula for inverses of $2\times 2$ matrices, we have

$$\begin{aligned} \left( \left( \nabla _{\alpha ,\eta }R^\epsilon \right) ^{t}\right) ^{-1} = \frac{1}{J(\alpha ,\eta )}\big (\!-\!(\partial _\eta R^\epsilon )^{\perp },(\partial _\alpha R^\epsilon )^{\perp }\big ). \end{aligned}$$

(4.42)

where $J(\alpha ,\eta ) := \text {det}(\nabla _{\alpha ,\eta }R^\epsilon )$. Multiplying the inverse matrix on both sides of (4.41), we have

$$\begin{aligned} \nabla {\tilde{p}}^{\epsilon }(R^\epsilon (\alpha ,\eta )) = \frac{1}{J} \big (\!-\!(\partial _\eta R^\epsilon )^{\perp },(\partial _\alpha R^\epsilon )^{\perp }\big ) \begin{pmatrix} 0\\ c^{\epsilon } \end{pmatrix} =\frac{c^{\epsilon }}{J} (\partial _\alpha R^\epsilon )^{\perp }. \end{aligned}$$

(4.43)

Recall that Lemma 3.2 gives $(\partial _\alpha R^\epsilon )^{\perp } = z'(\alpha )^\perp +O(\epsilon ) = L{\mathbf {n}}(z(\alpha ))+O(\epsilon )$, and $J= \epsilon L \gamma + O(\epsilon ^2)$. Plugging these into (4.43) gives

$$\begin{aligned} \nabla {\tilde{p}}^{\epsilon }(R(\alpha ,\eta ))=\frac{c^\epsilon }{\epsilon }\left( \frac{{\mathbf {n}}(z(\alpha ))}{\gamma } + O(\epsilon )\right) . \end{aligned}$$

(4.44)

Note that it follows from (4.8) that $c^{\epsilon } \le \frac{|D^{\epsilon }|}{2\pi }$, where $|D^\epsilon |\le C\epsilon$ due to (3.9). These imply

$$\begin{aligned} \frac{c_\epsilon }{\epsilon }\le C, \end{aligned}$$

(4.45)

and applying it to (4.44) yields (4.38).

To prove (4.39), since $q^\epsilon =p^\epsilon -{{\tilde{p}}}^\epsilon$ and $\Delta p^\epsilon =-2$ in $D^\epsilon$, it suffices to show that

$$\begin{aligned} \left| \Delta {\tilde{p}}^{\epsilon } \right| \le C\quad \text { in } D^\epsilon , \end{aligned}$$

(4.46)

and we will begin with an explicit computation of $\partial _{x_1x_1} {{\tilde{p}}}^\epsilon$ and $\partial _{x_2x_2} {{\tilde{p}}}^\epsilon$. Let us denote $R^\epsilon =: (R^1, R^2)$. For notational simplicity, in the rest of the proof we will use subscripts on $R^\epsilon$, $R^1$, $R^2$ and J to denote their partial derivative, e.g. $R^1_\alpha := \partial _\alpha R^1$.

From (4.43), it follows that

$$\begin{aligned} \partial _{x_1}{\tilde{p}}^\epsilon (R^\epsilon (\alpha ,\eta )) = -\frac{c^{\epsilon }}{J} R^2_\alpha . \end{aligned}$$

Differentiating in $\alpha$ and $\eta$, we get

$$\begin{aligned} \begin{aligned}\nabla \left( \partial _{x_1}{\tilde{p}}^{\epsilon }\right) (R^\epsilon (\alpha ,\eta ))&= \left( \left( \nabla _{\alpha ,\eta }R^\epsilon \right) ^t\right) ^{-1}\nabla _{\alpha ,\eta }\left( -\frac{c^{\epsilon }}{J}R^2_\alpha \right) \\&= \frac{c^{\epsilon }}{J}\begin{pmatrix} R_\eta ^2 &{} -R_\alpha ^2\\ -R_\eta ^1 &{} R_\alpha ^1\end{pmatrix} \begin{pmatrix} \frac{J_\alpha }{J^2} R^2_\alpha - \frac{1}{J}R^2_{\alpha \alpha }\\ \frac{J_\eta }{J^2} R_\alpha ^2-\frac{1}{J}R^{2}_{\alpha \eta } \end{pmatrix}, \end{aligned} \end{aligned}$$

thus

$$\begin{aligned} \partial _{x_1x_1} {\tilde{p}}^{\epsilon }(R(\alpha ,\eta )) = \frac{c^\epsilon }{J}\left( \frac{ J_\alpha }{J^2} R^2_\eta R^2_\alpha - \frac{1}{J} R^2_\eta R^2_{\alpha \alpha }- \frac{J_\eta }{J^2} (R_\alpha ^2)^2 + \frac{1}{J}R^2_\alpha R^2_{\alpha \eta }\right) . \end{aligned}$$

Likewise, $\partial _{x_2x_2}{\tilde{p}}(R(\alpha ,\eta ))$ takes the same expression except every $R^2$ is changed into $R^1$. Adding them together gives

$$\begin{aligned} \Delta {\tilde{p}}^{\epsilon }(R(\alpha ,\eta )) = \frac{c^\epsilon }{J}\left( \frac{ J_\alpha }{J^2} R^\epsilon _\eta \cdot R^\epsilon _\alpha -\frac{1}{J} R_\eta ^\epsilon \cdot R^\epsilon _{\alpha \alpha } - \frac{J_\eta }{J^2} R^\epsilon _\alpha \cdot R^\epsilon _\alpha + \frac{1}{J} R^\epsilon _\alpha \cdot R^\epsilon _{\alpha \eta } \right) . \end{aligned}$$

(4.47)

Using the explicit formulae of $R_\alpha , R_\eta$ and J in Lemma 3.2, we directly obtain $|R^\epsilon _\alpha |, |R^\epsilon _{\alpha \alpha }|\le C$;  $|R^\epsilon _\eta |, |R^\epsilon _{\alpha \eta }|, |J_\alpha |\le C\epsilon$;  $|J_\eta |\le C\epsilon ^2$;  and $J^{-1}\le C\epsilon ^{-1}$ when $\epsilon$ is sufficiently small, where C depends on $\Vert z_i\Vert _{C^{3}(S_i)}$ and $\Vert \gamma _i \Vert _{C^2(S_i)}$. As a result, all the four terms in the parenthesis of (4.47) are bounded by some constant C independent of $\epsilon$. Finally, (4.45) yields $\frac{c_\epsilon }{J}\le C$ as well, thus $|\Delta {\tilde{p}}^{\epsilon }| \le C$, and this proves the second claim (4.39).

$\square$

5 Proof of the Symmetry Result

In this section we prove that a stationary vortex sheet with positive vorticity must be radially symmetric up to a translation, and a rotating vortex sheet with positive vorticity and angular velocity $\Omega <0$ must be radially symmetric. The key idea of the proof is to define the integral

$$\begin{aligned} \begin{aligned} I^\epsilon&:= \int _{D^\epsilon } \epsilon ^{-1} {\mathbf {u}}^\epsilon \cdot \nabla \left( \omega ^\epsilon * {\mathcal {N}}-\frac{\Omega }{2}|x|^2\right) dx \\ {}&= \int _{D^\epsilon } \epsilon ^{-1} (x+\nabla p^\epsilon ) \cdot \nabla \left( \omega ^\epsilon * {\mathcal {N}}-\frac{\Omega }{2}|x|^2\right) dx , \end{aligned} \end{aligned}$$

(5.1)

and compute it in two different ways. The motivation of the definition is as follows. As discussed in [14, Sect. 2.1], $I^\epsilon$ can be thought of as a first variation of an “energy functional”

$$\begin{aligned} {\mathcal {E}}[\omega ^\epsilon ]:=\int \frac{1}{2}\omega ^\epsilon (\omega ^\epsilon *{\mathcal {N}})-\frac{\Omega }{2}\omega ^\epsilon |x|^2 \,dx \end{aligned}$$

when we perturb $\omega ^\epsilon$ by a divergence free vector ${\mathbf {u}}^\epsilon$ in $D^\epsilon$. (This functional ${\mathcal {E}}$ only serves as our motivation, and will not appear in the proof.) On the one hand, using that $\omega _0$ is stationary in the rotating frame with angular velocity $\Omega$ and $\omega ^\epsilon$ is a close approximation of $\omega _0$, we will show in Proposition 5.1 that $I^\epsilon$ is of order $O(\epsilon |\log \epsilon |)$, thus goes to zero as $\epsilon \rightarrow 0$. On the other hand, using the particular ${\mathbf {u}}^\epsilon$ that we constructed in Sect. 4, we will prove in Proposition 5.2 that if $\Omega =0$, $I^\epsilon$ is strictly positive independently of $\epsilon$ unless all the vortex sheets are nested circles with constant density; and also prove a similar result in Corollary 5.3 for $\Omega <0$.

Proposition 5.1

Assume $\omega (\cdot ,t)=\omega _0(R_{\Omega t}\cdot )$ is a stationary/uniformly-rotating vortex sheet with angular velocity $\Omega \in {\mathbb {R}}$, where $\omega _0$ satisfies (H1)–(H3). Then there exists some $C>0$ only depending on b (as in (H2)), $\max _i \Vert z_i\Vert _{C^3(S_i)}$, $\max _{i\le n}\Vert \gamma _i\Vert _{C^2(S_i)}$, $\max _{i>n}\Vert \gamma _i\Vert _{C^b(S_i)}$, $d_\Gamma$ and $F_\Gamma$, such that $| I^\epsilon | < C \epsilon ^b |\log \epsilon |$ for all sufficiently small $\epsilon > 0$.

Proof

Let us decompose $I^\epsilon =: \sum _{i=1}^{n+m} I^\epsilon _i$, where $I_i^\epsilon := \int _{D^\epsilon _i} \epsilon ^{-1} (x+\nabla p^\epsilon ) \cdot \nabla (\omega ^\epsilon * {\mathcal {N}}-\frac{\Omega }{2}|x|^2)dx .$

We start with showing that $|I^\epsilon _i|\le C\epsilon ^b |\log \epsilon |$ for $i=n+1,\dots , n+m$. For such i, $p^\epsilon =0$ on $\partial D^\epsilon _i$, thus the divergence theorem (and the fact that $\omega ^\epsilon = \epsilon ^{-1}$ in $D^\epsilon _i$) gives

$$\begin{aligned} I^\epsilon _i = \underbrace{\int _{D^\epsilon _i} \epsilon ^{-1} x \cdot \nabla \left( \omega ^\epsilon *{\mathcal {N}}-\frac{\Omega }{2}|x|^2\right) dx}_{=:T_i^\epsilon }- \int _{D^\epsilon _i} \epsilon ^{-1}(\epsilon ^{-1}-2\Omega ) p^\epsilon (x) dx. \end{aligned}$$

Using the estimate $|p^\epsilon |\le C\epsilon ^2$ in Proposition 4.2 and the fact that $|D^\epsilon _i|\le C\epsilon$ from (3.9), we easily bound the second integral by $C\epsilon$. To control the first integral $T_i^\epsilon$, we rewrite it using the change of variables $x = R^\epsilon _i(\alpha ,\eta )$ and the definition ${\mathbf {v}}^\epsilon := \nabla ^\perp ( \omega ^\epsilon *{\mathcal {N}})$ in (3.10): (also note that on the right hand side we group $\epsilon ^{-1}$ with the determinant)

$$\begin{aligned} \begin{aligned} T_i^\epsilon {=} \int _{S_i} \int _{-1}^0 R_i^\epsilon (\alpha ,\eta ) {\cdot } \underbrace{\Big (\!{-}\!({\mathbf {v}}^\epsilon )^\perp (R_i^\epsilon (\alpha ,\eta )){-}\Omega R_i^\epsilon (\alpha ,\eta )\Big )}_{=:J_i^\epsilon } \underbrace{\epsilon ^{-1} \det (\nabla _{\alpha ,\eta } R_i^\epsilon (\alpha ,\eta ))}_{=:K_{i}^\epsilon } \,d\eta d\alpha , \end{aligned} \end{aligned}$$

and recall that the exact expression of the determinant was given in (3.8). Let us take a closer look at the integrand, which is a product of 3 terms. Clearly, the definition of $R_i^\epsilon$ gives $R_i^\epsilon (\alpha ,\eta ) = z_i(\alpha ) + O(\epsilon ).$ As for the middle term $J_i^\epsilon$, Lemma 3.4 yields

$$\begin{aligned} J_i^\epsilon (\alpha ,\eta )= - BR^\perp (z_i(\alpha )) + \left( \eta +\frac{1}{2}\right) [{\mathbf {v}}]^\perp (z_i(\alpha )) - \Omega z_i(\alpha ) + O(\epsilon ^b |\log \epsilon |). \end{aligned}$$

(5.2)

Using the fact that $BR(z_i(\alpha ))=\Omega z_i^\perp (\alpha )$ for $i=n+1,\dots ,n+m$ (which follows from (2.6) and (2.7)), it becomes

$$\begin{aligned} J_i^\epsilon (\alpha ,\eta )= \left( \eta +\frac{1}{2}\right) [{\mathbf {v}}]^\perp (z_i(\alpha )) + O(\epsilon ^b |\log \epsilon |). \end{aligned}$$

(5.3)

Also it follows from (3.8) that $K_i^\epsilon (\alpha ,\eta ) = L_i \gamma _i(\alpha ) + O(\epsilon ).$ Plugging these three estimates into the above integral gives

$$\begin{aligned} T_i^\epsilon = \int _{S_i} \int _{-1}^0 z_i(\alpha ) \cdot \left( \eta +\frac{1}{2}\right) [{\mathbf {v}}]^\perp (z_i(\alpha )) L_i \gamma _i(\alpha ) d\eta d\alpha + O(\epsilon ^b |\log \epsilon |) = O(\epsilon ^b |\log \epsilon |), \end{aligned}$$

where the last step follows from the fact that $\int _{-1}^0 (\eta +\frac{1}{2}) d\eta = 0$. This finishes the proof that $|I^\epsilon _i |\le C\epsilon ^b |\log \epsilon |$ for $i=n+1,\dots ,n+m$, where C depends on b, $\max _i\Vert z_i\Vert _{C^2(S_i)}$, $\max _{i}\Vert \gamma _i\Vert _{C^b(S_i)}$, $d_\Gamma$ and $F_\Gamma$.

In the rest of the proof we aim to show $|I^\epsilon _i|\le C\epsilon ^b |\log \epsilon |$ for $i=1,\dots , n$, which is slightly more involved. Recall that in Proposition 4.3 we defined ${{\tilde{p}}}^\epsilon$ and $q^\epsilon$ in $D_i^\epsilon$ for $i=1,\dots , n$, where they satisfy $p^\epsilon = {{\tilde{p}}}^\epsilon + q^\epsilon$ in $D_i^\epsilon$, and $q^\epsilon = 0$ on $\partial D_i^\epsilon$. This allows us to apply the divergence theorem (to the $q^\epsilon$ term only) and decompose $I_i^\epsilon$ as

$$\begin{aligned} I^\epsilon _i= & {} \int _{D^\epsilon _i} \epsilon ^{-1} (x+\nabla {{\tilde{p}}}_\epsilon ) \cdot \nabla \left( \omega ^\epsilon *{\mathcal {N}}-\frac{\Omega }{2}|x|^2\right) dx \\&- \int _{D^\epsilon _i} \epsilon ^{-1}(\epsilon ^{-1}-2\Omega ) q^\epsilon (x) dx =: I^\epsilon _{i,1} + I^\epsilon _{i,2}. \end{aligned}$$

We can easily show that $I^\epsilon _{i,2} = O(\epsilon )$: (4.12) of Proposition 4.3 gives $|q^\epsilon |\le C\epsilon ^2$, and combining it with $|D^\epsilon _i|\le C\epsilon$ in (3.9) immediately yields the desired estimate.

Next we turn to $I^\epsilon _{i,1}$. Again, the change of variables $x = R^\epsilon _i(\alpha ,\eta )$ and the definition ${\mathbf {v}}^\epsilon := \nabla ^\perp ( \omega ^\epsilon *{\mathcal {N}})$ gives

$$\begin{aligned} I_{i,1}^\epsilon= & {} \int _{S_i} \int _{-1}^0 \big (R_i^\epsilon (\alpha ,\eta )+\nabla {{\tilde{p}}}^\epsilon (R_i^\epsilon (\alpha ,\eta ))\big ) \cdot \underbrace{\Big (\!-\!({\mathbf {v}}^\epsilon )^\perp (R_i^\epsilon (\alpha ,\eta ))-\Omega R_i^\epsilon (\alpha ,\eta )\Big )}_{=:J_i^\epsilon } \\&\quad \underbrace{\epsilon ^{-1} \det (\nabla _{\alpha ,\eta } R_i^\epsilon (\alpha ,\eta ))}_{=:K_{i}^\epsilon } \,d\eta d\alpha . \end{aligned}$$

For the three terms in the product of the integrand, we will approximate the first term using the definition of $R_i^\epsilon$ and (4.14) of Proposition 4.3:

$$\begin{aligned} R_i^\epsilon (\alpha ,\eta )+\nabla {{\tilde{p}}}^\epsilon (R_i^\epsilon (\alpha ,\eta )) = z_i(\alpha ) + \frac{\beta _i}{\gamma _i(\alpha )}{\mathbf {n}}(z_i(\alpha )) + O(\epsilon ), \end{aligned}$$

where $\beta _i := \frac{2|U_i|}{L_i\int _{S_i}\gamma _i^{-1}(\alpha )d\alpha }$ is given by (4.11). Lemma 3.4 allows us to approximate the middle term $J_i^\epsilon$ as (5.2), however (5.3) no longer holds since for $i=1,\dots ,n$ we do not have $BR(z_i(\alpha ))=\Omega z_i^\perp (\alpha )$. As for $K_i^\epsilon$, we again use (3.8) to approximate it by $K_i^\epsilon (\alpha ,\eta ) = L_i \gamma _i(\alpha ) + O(\epsilon ).$ Plugging these three estimates into the integrand of $I_{i,1}^\epsilon$ gives

$$\begin{aligned} I_{i,1}^\epsilon= & {} \int _{S_i} \left( z_i(\alpha ) + \frac{\beta _i}{\gamma _i(\alpha )}{\mathbf {n}}(z_i(\alpha ))\right) \cdot \Big (-\!\!BR^\perp (z_i(\alpha )) - \Omega z_i(\alpha )\Big ) L_i\gamma _i(\alpha ) d\alpha \\&+ O(\epsilon ^b |\log \epsilon |), \end{aligned}$$

where we again use the fact that the $(\eta +\frac{1}{2})$ term gives zero contribution since $\int _{-1}^0 (\eta +\frac{1}{2}) d\eta =0$. Next we will show the integral on the right hand side is in fact 0. Since $\omega$ is a rotating solution with angular velocity $\Omega$, the conditions (2.6) and (2.7) yield that

$$\begin{aligned} -BR^\perp (z_i(\alpha )) - \Omega z_i(\alpha )= C_i \gamma _i^{-1}(\alpha ){\mathbf {n}}(z_i(\alpha )), \end{aligned}$$

for some constant $C_i$. Plugging this into the above integral gives

$$\begin{aligned} \begin{aligned} I_{i,1}^\epsilon&= C_i L_i \int _{S_i} \left( z_i(\alpha ) \cdot {\mathbf {n}}(z_i(\alpha )) + \frac{\beta _i}{\gamma _i(\alpha )}\right) d\alpha + O(\epsilon ^b |\log \epsilon |) \\ {}&= C_i L_i\left( \int _{S_i} z_i(\alpha ) \cdot {\mathbf {n}}(z_i(\alpha )) d\alpha + \frac{2|U_i|}{L_i}\right) + O(\epsilon ^b |\log \epsilon |), \end{aligned} \end{aligned}$$

where the second step follows from the definition of $\beta _i$ in (4.11). Let us compute the integral on the right hand side by changing to arclength parametrization and applying the divergence theorem:

$$\begin{aligned} \int _{S_i} z_i(\alpha ) \cdot {\mathbf {n}}(z_i(\alpha )) d\alpha = -\frac{1}{L_i}\int _{\partial U_i} x \cdot n d\sigma = -\frac{2|U_i|}{L_i}, \end{aligned}$$

which yields $I_{i,1}^\epsilon = O(\epsilon ^b |\log \epsilon |)$, and finishes the proof that $|I_i^\epsilon |\le C\epsilon ^b |\log \epsilon |$ for $i=1,\dots , n$, where C depends on b, $\Vert z_i\Vert _{C^{3}(S_i)},\Vert \gamma _i \Vert _{C^2(S_i)}$, $d_\Gamma$ and $F_\Gamma$.

Finally, summing the $I_i^\epsilon$ estimates for $i=1,\dots , n+m$ gives $|I^\epsilon | \le C\epsilon ^b |\log \epsilon |$ for all sufficiently small $\epsilon >0$, thus we can conclude. $\square$

Now we will use a different way to compute $I^\epsilon$. Let us first define a new integral ${{\tilde{I}}}^\epsilon$ that is the same as $I^\epsilon$ except with $\Omega$ set to zero:

$$\begin{aligned} \begin{aligned} {{\tilde{I}}}^\epsilon&:=\int _{D^\epsilon } \epsilon ^{-1} (x+\nabla p^\epsilon ) \cdot \nabla \left( \omega ^\epsilon * {\mathcal {N}}\right) dx. \end{aligned} \end{aligned}$$

(5.4)

Next we will prove that ${{\tilde{I}}}^\epsilon$ is strictly positive independently of $\epsilon$ unless all the vortex sheets are nested circles with constant density. As we will see in the proof, the key step is to show that if some $\Gamma _i$ is either not a circle or does not have a constant $\gamma _i$, then the estimates on $p^\epsilon$ in Propositions 4.2–4.3 lead to the following quantitative version of (4.9): $\epsilon ^{-2}\left( \frac{|D_i^\epsilon |^2}{4\pi }-\int _{D_i^\epsilon } p^\epsilon (x) dx\right) \ge c_0>0$, where $c_0$ is independent of $\epsilon$.

Proposition 5.2

Let ${{\tilde{I}}}^\epsilon$ be defined as in (5.4). Assume that $\Gamma _i$ and $\gamma _i$ satisfy (H1)–(H3) for $i=1,\dots ,n+m$. Then we have ${{\tilde{I}}}^\epsilon \ge 0$ for all sufficiently small $\epsilon >0$.

In addition, if $\Gamma$ is not a union of nested circles with constant $\gamma _i$’s on each connected component, there exists some $c_0>0$ independent of $\epsilon$, such that ${{\tilde{I}}}^\epsilon> c_0 > 0$ for all sufficiently small $\epsilon > 0$.

Proof

We start by decomposing ${{\tilde{I}}}^{\epsilon }$ as

$$\begin{aligned} {{\tilde{I}}}^{\epsilon } = \int _{D^{\epsilon }} \epsilon ^{-1}x\cdot \nabla (\omega ^{\epsilon }*{\mathcal {N}})dx + \int _{D^{\epsilon }}\epsilon ^{-1}\nabla p^\epsilon \cdot \nabla (\omega ^{\epsilon }*{\mathcal {N}})dx=:I^{\epsilon }_1 + I^{\epsilon }_2. \end{aligned}$$

$I^\epsilon _1$ can be easily computed as

$$\begin{aligned} \begin{aligned} I^\epsilon _1&= \frac{1}{2\pi \epsilon ^2} \int _{D^\epsilon }\int _{D^\epsilon }\frac{x\cdot (x-y)}{|x-y|^2}dxdy =\frac{|D^\epsilon |^2}{4\pi \epsilon ^2} = \frac{1}{4\pi \epsilon ^2}\left( \sum _{i=1}^{n+m} |D^\epsilon _i|\right) ^2 \end{aligned} \end{aligned}$$

(5.5)

where the second equality is obtained by exchanging x with y and taking the average with the original integral. As for $I^\epsilon _2$, we have

$$\begin{aligned} \begin{aligned} I^\epsilon _2&= \frac{1}{\epsilon }\int _{\partial D^\epsilon }p^\epsilon \nabla (\omega ^\epsilon * {\mathcal {N}})\cdot nd\sigma - \frac{1}{\epsilon }\int _{D^\epsilon }p^\epsilon \omega ^\epsilon dx \\&= -\frac{1}{\epsilon }\sum _{i=1}^nc^\epsilon _i\int _{\partial U_i}\nabla (\omega ^\epsilon * {\mathcal {N}})\cdot nd\sigma - \frac{1}{\epsilon ^2}\int _{D^\epsilon }p^\epsilon dx \\&\ge -\frac{1}{\epsilon ^2}\sum _{i=1}^n\sum _{j=1}^{n+m}\frac{|D^\epsilon _i|}{2\pi }\int _{U_i}1_{D^\epsilon _j} dx - \frac{1}{\epsilon ^2}\sum _{i=1}^{n+m}\int _{D^\epsilon _i}p^\epsilon dx, \end{aligned} \end{aligned}$$

(5.6)

where the first equality follows from the divergence theorem, the second equality follows from the boundary conditions (4.5) and (4.6) for $p^\epsilon$ (as well as the fact that $\partial U_i$ and $\partial D^\epsilon _i$ have opposite outer normals), and the last inequality follows from the divergence theorem as well as the inequality $c_i^\epsilon \le \sup _{D^\epsilon _i}p \le \frac{|D^\epsilon _i|}{2\pi }$ due to (4.8).

Let us denote $j\prec i$ if $i\in \left\{ 1,\ldots ,n\right\} , j\in \{1,\dots , n+m\}$, $j\ne i$ and $\Gamma _j$ lies in the interior of the domain enclosed by $\Gamma _i$ (that is, $\Gamma _j \subset U_i$). If not, we denote $j\nprec i$. Note that for sufficiently small $\epsilon >0$, we have

$$\begin{aligned} \int _{U_i} 1_{D^\epsilon _j} dx = {\left\{ \begin{array}{ll} |D^\epsilon _j| &{} \text { if } j \prec i, \\ 0 &{} \text { otherwise.} \end{array}\right. } \end{aligned}$$

(5.7)

Applying this to (5.6) yields

$$\begin{aligned} \begin{aligned} I^\epsilon _2&\ge -\frac{1}{2\pi \epsilon ^2} \sum _{i,j=1}^{n+m}\mathbb {1}_{j\prec i}\, |D^\epsilon _i| |D^\epsilon _j| - \frac{1}{\epsilon ^2}\sum _{i=1}^{n+m}\int _{D^\epsilon _i}p^\epsilon _i dx\\&= -\frac{1}{4\pi \epsilon ^2} \sum _{i,j=1}^{n+m}(\mathbb {1}_{j\prec i}+ \mathbb {1}_{i\prec j})\, |D^\epsilon _i| |D^\epsilon _j| - \frac{1}{\epsilon ^2}\sum _{i=1}^{n+m}\int _{D^\epsilon _i}p^\epsilon _i dx \end{aligned} \end{aligned}$$

(5.8)

where in the first step we used that the $i=n+1,\dots ,n+m$ terms have zero contribution in the first sum, due to the definition of $j\prec i$.

Adding (5.5) and (5.8) together, we obtain

$$\begin{aligned} {{\tilde{I}}}^\epsilon \ge \sum _{i=1}^{n+m} \underbrace{\frac{1}{\epsilon ^2}\left( \frac{|D^\epsilon _i|^2}{4\pi }-\int _{D^\epsilon _i}p^\epsilon _idx\right) }_{=:A_i^\epsilon } + \sum _{i,j=1}^{n+m}\underbrace{\frac{1}{\epsilon ^2}\left( \mathbb {1}_{i\ne j}-\left( \mathbb {1}_{j\prec i}+\mathbb {1}_{i\prec j}\right) \right) \frac{|D^\epsilon _i||D^\epsilon _j|}{4\pi }}_{=:B_{i,j}^\epsilon }, \end{aligned}$$

(5.9)

From (4.9), it follows that $A_i^\epsilon \ge 0$ for all $i =1,\dots ,n+m$, with equality achieved if and only if each $D^\epsilon _i$ is a disk or an annulus. Note that $B_{i,j}^\epsilon \ge 0$ as well for all i and j, since for any $i\ne j$, at most one of $i\prec j$ and $j\prec i$ can hold. Putting these together yields that ${{\tilde{I}}}^\epsilon \ge 0$ for any sufficiently small $\epsilon >0$.

In the rest of the proof, we assume $\Gamma$ is not a union of nested circles with constant $\gamma _i$’s on each connected component. Therefore at least one of the following 3 cases must be true. In each case we aim to show that ${{\tilde{I}}}_\epsilon \ge c_0>0$, where $c_0$ is independent of $\epsilon$ for all sufficiently small $\epsilon >0$.

Case 1. There exists some open curve $\Gamma _i$ that is not a loop. In this case $D^\epsilon _i$ is simply-connected, and $p^\epsilon =0$ on $\partial D^\epsilon _i$ by (4.5). Applying Proposition 4.2 to $p^\epsilon$ in $D^\epsilon _i$, we have $\sup _{D^\epsilon _i} p^\epsilon \le C\epsilon ^2$, where C is independent of $\epsilon$. This leads to $\int _{D^\epsilon _i} p^\epsilon dx \le C\epsilon ^3$, since $|D^\epsilon _i| = O(\epsilon )$ by (3.9). As a result, for the index i we have

$$\begin{aligned} A_i ^\epsilon = \frac{|D^\epsilon _i|^2}{4\pi \epsilon ^2}-\epsilon ^{-2} \int _{D^\epsilon _i}p^\epsilon _idx \ge \frac{L_i^2}{4\pi }\left( \int _{S_i}\gamma _i(\alpha )d\alpha \right) ^2 - C\epsilon , \end{aligned}$$

where we again used (3.9) in the second inequality. This gives that $A_i^\epsilon \ge \frac{L_i^2}{8\pi }(\int _{S_i}\gamma _i(\alpha )d\alpha )^2 > 0$ for all sufficiently small $\epsilon >0$.

Case 2. There exists some closed curve $\Gamma _i$ that is either not a circle, or $\gamma _i$ is not a constant. In this case we aim to show that $A_i^\epsilon \ge c_0>0$, and this will be done by finding good approximations (independent of $\epsilon$) for both terms in $A_i^\epsilon$. For the first term $\frac{|D^\epsilon _i|^2}{4\pi \epsilon ^2}$, using (3.9) we again have

$$\begin{aligned} \frac{|D^\epsilon _i|^2}{4\pi \epsilon ^2} \ge \frac{L_i^2}{4\pi }\left( \int _{S_i}\gamma _i(\alpha )d\alpha \right) ^2- C\epsilon =: J_i - C\epsilon , \end{aligned}$$

(5.10)

where $J_i>0$ is independent of $\epsilon$. For the second term $\epsilon ^{-2}\int _{D_i^\epsilon } p_i^\epsilon dx$, rewriting the integral using the change of variables $x=R_i^\epsilon (a,\eta )$ gives

$$\begin{aligned} \epsilon ^{-2}\int _{D_i^\epsilon } p_i^\epsilon dx = \int _{S_i}\int _{-1}^0 \frac{p^\epsilon (R_i^\epsilon (\alpha ,\eta ))}{\epsilon } \frac{\det (\nabla _{\alpha ,\eta }R_i^\epsilon )}{\epsilon } d\eta d\alpha . \end{aligned}$$

Recall that in Proposition 4.3 we defined ${\tilde{p}}^{\epsilon }(R^\epsilon _i(\alpha ,\eta )) := c^\epsilon _i(1+\eta )$ and $q_\epsilon$ such that $p^\epsilon - {{\tilde{p}}}_\epsilon = q_\epsilon$. By (4.12) and (4.13), for all $\alpha \in S_i$ and $\eta \in (-1,0)$ we have

$$\begin{aligned} \left| \frac{p^\epsilon (R_i^\epsilon (\alpha ,\eta ))}{\epsilon } - \beta _i (1+\eta )\right| \le \left| \frac{ p^\epsilon (R_i^\epsilon (\alpha ,\eta ))}{\epsilon } - \frac{c_i^\epsilon }{\epsilon }(1+\eta )\right| + \left| \frac{c_i^\epsilon }{\epsilon }-\beta _i\right| \le C\epsilon , \end{aligned}$$

where $\beta _i := \frac{2|U_i|}{L_i\int _{S_i}\gamma _i^{-1}(\alpha )d\alpha }$ is defined in (4.11). Combining this with the expression of the determinant in (3.8), we have

$$\begin{aligned} \begin{aligned} \epsilon ^{-2}\int _{D_i^\epsilon } p_i^\epsilon dx&= \int _{S_i}\int _{-1}^0 (\beta _i(1+\eta ) + O(\epsilon )) (L_i \gamma _i(\alpha ) + O(\epsilon )) d\eta d\alpha \\&\le \frac{|U_i|}{\int _{S_i} \gamma _i^{-1}(\alpha ) d\alpha } \int _{S_i} \gamma _i(\alpha ) d\alpha + C\epsilon =: K_i + C\epsilon , \end{aligned} \end{aligned}$$

where $K_i$ is independent of $\epsilon$. Putting this together with (5.10) yields the following:

$$\begin{aligned} \begin{aligned} A_i^\epsilon&\ge J_i - K_i - C\epsilon \\&= \frac{L_i^2}{4\pi } \frac{\int _{S_i}\gamma _i(\alpha )d\alpha }{\int _{S_i}\gamma _i^{-1}(\alpha )d\alpha }\left( \int _{S_i}\gamma _i^{-1}(\alpha )d\alpha \int _{S_i}\gamma _i(\alpha )d\alpha - \frac{4\pi |U_i|}{L_i^2}\right) - C\epsilon . \end{aligned} \end{aligned}$$

(5.11)

Let us take a closer look at the two terms inside the parenthesis. For the first term, Cauchy-Schwarz inequality gives

$$\begin{aligned} \int _{S_i}\gamma _i^{-1}(\alpha )d\alpha \int _{S_i}\gamma _i(\alpha )d\alpha \ge 1, \end{aligned}$$

with equality achieved if and only if $\gamma _i$ is a constant. For the second term, the isoperimetric inequality yields

$$\begin{aligned} \frac{4\pi |U_i|}{L_i^2} \le 1, \end{aligned}$$

(recall that $L_i = |\partial U_i|$), with equality achieved if and only $U_i$ is a disk. By the assumption of Case 2, at least one of the inequalities must be strict, thus the parenthesis on the right hand side of (5.11) is strictly positive (and independent of $\epsilon$). Therefore there exists some constant $c_0>0$ such that ${{\tilde{I}}}^\epsilon \ge A_i^\epsilon \ge c_0$ for all sufficiently small $\epsilon$.

Case 3. There exist $i\ne j$ such that $i\nprec j$ and $j\nprec i$. Then it is clear that for such i, j, $B_{i,j}^\epsilon$ in (5.9) is given by $B_{i,j}^\epsilon = \frac{|D^\epsilon _{i}||D^\epsilon _{j}|}{4\pi \epsilon ^2}$. Hence (3.9) gives

$$\begin{aligned} B_{i,j}^\epsilon \ge L_i L_j \bigg ( \int _{S_i}\gamma _i(\alpha )d\alpha \bigg )\bigg ( \int _{S_j} \gamma _j(\alpha )d\alpha \bigg ) - C\epsilon , \end{aligned}$$

which yields ${{\tilde{I}}}^\epsilon \ge \frac{1}{2}L_i L_j ( \int _{S_i}\gamma _i d\alpha )( \int _{S_j} \gamma _j d\alpha )>0$ for all sufficiently small $\epsilon >0$.

This finishes our discussion on all 3 cases. To conclude, since $\Gamma$ is not a union of nested circles with constant $\gamma _i$’s on each connected component, at least one of the 3 cases must hold, and all of them lead to ${{\tilde{I}}}^\epsilon \ge c_0>0$. $\square$

The above proposition immediately leads to the following corollary for the $\Omega <0$ case.

Corollary 5.3

Assume that $\Gamma _i$ and $\gamma _i$ satisfy (H1)–(H3) for $i=1,\dots ,n+m$. Let $I^\epsilon$ be defined as in (5.1), and assume $\Omega < 0$. Then we have $I^\epsilon \ge 0$ for all sufficiently small $\epsilon >0$. In addition, if $\Gamma$ is not a union of concentric circles all centered at the origin with constant $\gamma _i$’s, there exists some $c_0>0$ independent of $\epsilon$, such that $I^\epsilon> c_0 > 0$ for all sufficiently small $\epsilon > 0$.

Proof

Let us decompose $I^\epsilon$ as follows (recall the definition of ${{\tilde{I}}}^\epsilon$ in (5.4))

$$\begin{aligned} I^\epsilon = {{\tilde{I}}}^\epsilon + (-\Omega ) \left( \epsilon ^{-1} \int _{D^\epsilon } (|x|^2 + \nabla p^\epsilon \cdot x) dx\right) =: {{\tilde{I}}}^\epsilon + \underbrace{(-\Omega )}_{>0} J^\epsilon . \end{aligned}$$

(5.12)

Recall that Proposition 5.2 gives ${{\tilde{I}}}_\epsilon \ge c_0>0$ as long as $\Gamma$ is not a union of nested circles with constant $\gamma _i$’s. By [14, Lemma 2.11], we have

$$\begin{aligned} \int _{D_i^\epsilon } (|x|^2 + \nabla p^\epsilon \cdot x) dx\ge 0 \quad \text { for any } i=1,\dots ,n+m, \end{aligned}$$

thus $J^\epsilon \ge 0$. Putting them together, and using the fact that $\Omega <0$, we know $I^\epsilon \ge c_0>0$ if $\Gamma$ is not a union of nested circles with constant $\gamma _i$’s.

To finish the proof, we only need to focus on the case that the $\Gamma _i$’s are nested circles with constant $\gamma _i$’s, but not all of them are centered at the origin. Assume that there exists $k\in \{1,\dots ,n\}$ such that $\Gamma _k$ is a circle with radius $r_k$ centered at $x_k \ne 0$. Since $\gamma _k$ is a constant, $D_k^\epsilon$ is an annulus given by $B(x_k,r_k+\epsilon \gamma _k)\setminus B(x_k,r_k)$. The symmetry of $D_k^\epsilon$ about $x_k$ immediately leads to $p^\epsilon |_{D_k^\epsilon } = -\frac{1}{2}|x-x_k|^2 +\frac{1}{2} (r_k+\epsilon \gamma _k)^2.$ An elementary computation gives

$$\begin{aligned} \epsilon ^{-1}\int _{D^\epsilon _k} (|x|^2 + \nabla p^\epsilon \cdot x) dx= & {} \epsilon ^{-1} \int _{D^\epsilon _k} |x|^2 - (x-x_k)\cdot x dx = \epsilon ^{-1} |x_k|^2 |D_k^\epsilon | \\\ge & {} 2\pi r_k \gamma _k |x_k|^2>0, \end{aligned}$$

where in the second-to-last step we used that $|D_k^\epsilon | = 2\pi \epsilon r_k \gamma _k + \pi \epsilon ^2 \gamma _k^2$. Setting $c_0:=2\pi r_k \gamma _k |x_k|^2$ gives $I^\epsilon \ge c_0>0$, thus we can conclude.$\square$

Now we are ready to prove Theorem 1.1. Note that for $\Omega <0$, the symmetry result immediately follows from Proposition 5.1 and Corollary 5.3. For $\Omega =0$, Proposition 5.1–5.2 already imply that a stationary vortex sheet with positive strength must be a union of nested circles with constant strength on each of them. To finish the proof, we only need to show that these nested circles must be concentric.

Proof of Theorem 1.1

For a uniformly-rotating vortex sheet with $\Omega <0$, the symmetry result for $\Omega <0$ is a direct consequence of Proposition 5.1 and Corollary 5.3. Next we focus on the stationary (i.e. $\Omega =0$) case.

Combining Propsitions 5.1–5.2, we obtain that $\Gamma$ is a union of nested circles, and $\gamma _i$ is constant on $\Gamma _i$ for all $i=1\ldots ,n$. It remains to show that all $\Gamma _i$’s are concentric. Let us denote by ${\mathbf {v}}_i$ the contribution to the velocity field by $\Gamma _i$. Since $\Gamma _i$ is a circle with constant strength $\gamma _i$, a quick application of the divergence theorem yields that ${\mathbf {v}}_i \equiv 0$ in the open disk enclosed by $\Gamma _i$, whereas ${\mathbf {v}}_i(x) = \dfrac{\gamma _i L_i (x-x^0_i)^\perp }{2\pi |x-x^0_i|^2}$ in the open set outside $\Gamma _i$, where $x^0_i$ is the center of the circle $\Gamma _i$.

Without loss of generality, let us reorder the indices such that $\Gamma _i$ is nested inside $\Gamma _j$ for $i<j$. Towards a contradiction, let $k>1$ be such that $\Gamma _k$ is the first circle that is not concentric with $\Gamma _1$. From the above discussion, we know that ${\mathbf {v}}_i=0$ on $\Gamma _k$ for $i =k+1,\dots ,n$ (since $\Gamma _k$ is nested inside $\Gamma _i$), whereas for $i=1,\dots ,k-1$ we have ${\mathbf {v}}_i = \dfrac{\gamma _i L_i (x-x^0_1)^\perp }{2\pi |x-x^0_1|^2}$ on $\Gamma _k$, since all these $\Gamma _i$’s have the same center $x^0_1$ and are nested inside $\Gamma _k$. Summing them up (and also using the fact that $\Gamma _k$ contributes zero normal velocity on itself, since it is a circle with constant strength), we have

$$\begin{aligned} BR(x) \cdot {\mathbf {n}} = \sum _{i=1}^n {\mathbf {v}}_i(x) \cdot {\mathbf {n}}= \left( \sum _{i=1}^{k-1} \gamma _i L_i\right) \frac{(x-x^0_1)^\perp \cdot {\mathbf {n}}}{2\pi |x-x^0_1|^2} \quad \text { on }\Gamma _k, \end{aligned}$$

where the right hand side is not a zero function since $\Gamma _k$ has a different center from $x_1^0$. This causes a contradiction with the fact that $\omega = \omega _0$ is stationary. As a result, all $\Gamma _1,\dots , \Gamma _n$ must be concentric circles, finishing the proof. $\square$