Skip to main content
SpringerLink
Log in

Several Bifurcation Mechanisms for Limit Cycles in a Predator–Prey System

  • Published:
Qualitative Theory of Dynamical Systems Aims and scope Submit manuscript

Abstract

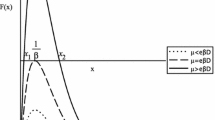
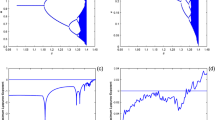
The research presented in this paper compares the occurrence of limit cycles under different bifurcation mechanisms in a simple system of two-dimensional autonomous predator–prey ODEs. Surprisingly two unconventional approaches, for a singular system and for a system with a center, turn out to produce more limit cycles than the traditional Andronov–Hopf bifurcation. The system has a functional response function which is a monotonically increasing cubic function of x for \(0\le x\le 1\) where x represents the prey density, and which is constant for \(x>1\). It acts as a proxy for investigating more general systems. The following results are obtained. For the Andronov–Hopf bifurcation the highest order of the weak focus is 2 and at most 2 small-amplitude limit cycles can be created. In the center bifurcation cases are shown to exist with at least 3 limit cycles. In the singular perturbation cases are shown to exist with at least 4 limit cycles and in some cases an exact upper bound of 2 limit cycles is obtained. Finally we indicate how the conclusions can be extended to more general systems. We show how an arbitrary number of limit cycles can be created by choosing an appropriate functional response function and growth function for the prey. One special situation is the system with group defense: the three bifurcation mechanisms typically produce less limit cycles if a group defense element is included.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24
Fig. 25
Fig. 26
Fig. 27
Fig. 28
Fig. 29

Similar content being viewed by others

References

  1. Andronov, A.A., et al.: Theory of Bifurcations of Dynamic Systems on a Plane. Halsted Press, New York (1973)

    Google Scholar 

  2. Arnold, V.I.: Experimental Mathematics, pp. 1–158. MSRI Mathematical Circles Library and the American Mathematical Society, Providence, Rhode Island (2015)

  3. De Maesschalck, P., Dumortier, F.: Canard solutions at non-generic turning points. Trans. Am. Math. Soc. 358(5), 2291–2334 (2006)

    Article  MathSciNet  Google Scholar 

  4. De Maesschalck, P., Dumortier, F.: Canard cycles in the presence of slow dynamics with singularities. Proc. R. Soc. Edinb. Sect. A 138(2), 265–299 (2008)

    Article  MathSciNet  Google Scholar 

  5. De Maesschalck, P., Dumortier, F.: Classical Liénard equation of degree \(n \ge 6\) can have \([\frac{n-1}{2}]+2\) limit cycles. J. Differ. Equ. 250, 2162–2176 (2011)

    Article  Google Scholar 

  6. De Maesschalck, P., Dumortier, F., Roussarie, R.: Cyclicity of common slow-fast cycles. Indag. Math. 22, 165–206 (2011)

    Article  MathSciNet  Google Scholar 

  7. De Maesschalck, P., Dumortier, F., Roussarie, R.: Canard cycle transition at a slow-fast passsage through a jump point. C. R. Math. Acad. Sci. Paris 352(4), 317–320 (2014)

    Article  MathSciNet  Google Scholar 

  8. Dumortier, F., Roussarie, R.: Canard cycles and center manifolds. Mem. Am. Math. Soc. 121(577) (1996)

  9. Dumortier, F., Roussarie, R.: Multiple canard cycles in generalized Liénard equations. J. Differ. Equ. 174(1), 1–29 (2001)

    Article  Google Scholar 

  10. Gause, G.F.: The Struggle for Existence. Williams and Wilkins, Baltimore (1934)

    Book  Google Scholar 

  11. Han, M., Wang, C.: On two stability problems of generalized Liénard equations (in Chinese). Appl. Math. JCU (Ser. A) 12(3), 273–278 (1997)

    MATH  Google Scholar 

  12. Han, M.: Bifurcation Theory of Limit Cycles, pp. 1–360. Alpha Science, Oxford (2017)

    Google Scholar 

  13. Holling, C.S.: The components of predation as revealed by a study of small-mammal predation of the European pine sawfly. Can. Entomol. 91, 293–320 (1959)

    Article  Google Scholar 

  14. Kooij, R.E., Zegeling, A.: Predator–prey models with non-analytical functional response. Chaos Solitons Fractals 123, 163–172 (2019)

    Article  MathSciNet  Google Scholar 

  15. Kooij, R.E., Zegeling, A.: Co-existence of a period annulus and a limit cycle in a class of predator-prey models with group defense. Int. J. Bif. Chaos (2021)

  16. Zegeling, A., Kooij, R.E.: Singular perturbations of the Holling I predator–prey system with a focus. J. Differ. Equ. 269, 5434–5462 (2020)

    Article  MathSciNet  Google Scholar 

  17. Zegeling, A., Kooij, R.E.: Uniqueness of limit cycles in polynomial systems with algebraic invariants. Bull. Aust. Math. Soc. 49, 7–20 (1994)

    Article  MathSciNet  Google Scholar 

  18. Zhang, Z., et al.: Qualitative Theory of Differential Equations, vol. 461. American Mathematical Society, Providence (1992)

    Google Scholar 

  19. Zhuo, L.: Periodic solutions for several types of certain planar differential equations (in Chinese). MSc. thesis, Shandong Inst. of Mining and Tech. (1996)

Download references

Author information

Authors and Affiliations

  1. Guilin University of Aerospace Technology, Jinji Road 2, Guilin, China

    André Zegeling

  2. Faculty of Electrical Engineering, Mathematics & Computer Science, Delft University of Technology, Mekelweg 4, 2628 CD, Delft, The Netherlands

    Robert E. Kooij

Authors
  1. André Zegeling
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Robert E. Kooij
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to André Zegeling.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zegeling, A., Kooij, R.E. Several Bifurcation Mechanisms for Limit Cycles in a Predator–Prey System. Qual. Theory Dyn. Syst. 20, 65 (2021). https://doi.org/10.1007/s12346-021-00501-w

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s12346-021-00501-w

Keywords

Mathematics Subject Classification

Search

Navigation