Analytical solutions for low-thrust orbit transfers

Abstract

This paper presents analytical solutions for the estimation of the $\Delta V$ cost of the transfer of a spacecraft subject to a low-thrust action. The equations represent an extension of solutions already available in the literature. Moreover, the paper presents novel analytical solutions for low-thrust transfers under the effect of the second-order zonal harmonics of the Earth’s gravitational potential. In particular, the paper is divided into two parts. The first part presents analytical expressions for the $\Delta V$ cost of transfers. All analytical equations were validated through numerical integration of the dynamics of the spacecraft. The second part of the paper introduces new analytical equations for low-thrust transfers between circular inclined orbits with different values of the right ascension of the ascending node, under the effect of the second-order zonal harmonic of the Earth’s gravitational potential. Both in the first and second parts, analytic solutions for the variation with time of the orbital elements during the transfer are presented. The proposed equations are applicable to low-thrust transfer realised through a long spiral trajectory.

1 Introduction

In the early stage of the definition of a space mission, it is often desirable to have a fast preliminary estimation of the $\Delta V$ cost of a low-thrust transfer. In particular, when the transfer is realised through a long spiral trajectory, a quick estimation of the total $\Delta V$ and transfer time can avoid potentially lengthy, albeit more accurate, calculations. For this reason a number of authors have proposed simple control laws for the variation of specific orbital elements, and, in some cases, analytical equations for the estimation of the $\Delta V$ associated to a given type of transfer. Burt (1967) presented the secular rates of change of the orbital elements for a thrust action having radial, transversal and normal components, constant in magnitude over one revolution. Burt showed that by reversing the thrust directions at certain points in the orbit, it is possible to change the orbital elements independently one from the others. In the work presented by Burt (1967), no closed-form expressions of the $\Delta V$ are provided. In addition, the integral of the secular rates of changes of the orbital elements was derived only for one of the proposed control laws. Edelbaum presented a solution for the minimum-time low-thrust transfer between inclined circular orbits (Edelbaum 1961). This solution was later reformulated by Kechichian (2010), where it was further extended in order to constrain the intermediate orbits during the transfer to remain below a given altitude. In addition, Kechichian presented the solution of the problem of a transfer between circular orbits with different values of the right ascension of the ascending node. In the work presented by Kéchichian (2010), the author derived some analytical expressions for the $\Delta V$ and for the variation of the orbital elements. Gao presented an analytic orbital averaging technique to obtain incremental changes of semi-major axis, eccentricity and inclination over an orbital revolution for specific control laws (Gao 2007). However, no closed-form expression of the $\Delta V$ was derived. In the work of Gao and Kluever (2005), the authors use approximated integrands in order to obtain an analytical solution for the variation of the orbital elements. Also in this case, no simple equation for the $\Delta V$ was derived. Hudson presented a method where the components of the thrust acceleration are represented by means of Fourier series in the eccentric anomaly (Hudson and Scheeres 2009). Analytic expressions for the secular rate of change of the orbital elements were given, but no simple equation for the $\Delta V$ or for the variation of the orbital elements with time was derived. Petropolous studied specific control laws for escape trajectories; he derived equations relating the average energy and eccentricity during the transfer, and for the approximated estimation of the $\Delta V$ (Petropolous 2002). Later, Petropoulos (2003) presented methods to determine the thrust direction to obtain specific changes in the orbital elements, leading to the definition of simple control laws. Simple control laws were also presented in Ruggiero et al. (2011). However, neither Petropoulos (2003) nor Ruggiero et al. (2011) report any analytical formula for the quick estimation of the $\Delta V$ or for the variation of the orbital elements. Finally, Pollard (2000) presented different pitch steering cases and their effect on the variation of the orbital elements. Of particular relevance, among the profiles presented by Pollard, are a steering profile that produces the simultaneous variation of the eccentricity and inclination, and one that produces a variation of the argument of the periapsis while holding semi-major axis and eccentricity constant. The control laws were applied on thrust arcs centred at pericentre and apocentre. For this specific case, an expression for the $\Delta V$ cost of the transfer is reported in Pollard (2000), but no equation is given for the variation of the orbital elements during the transfer.

Since not all the results available in the literature include analytical expressions for the $\Delta V$ to realise a transfer, or for the variation of the orbital elements, the first part of this paper extends the literature by introducing a number of analytical formulas for the quick estimation of the $\Delta V$ and for the evolution of the associated mean orbital elements. The novel equations presented in the first part of the paper have been obtained by extending the work of Burt (1967), Petropoulos (2003), Pollard (2000) and Ruggiero et al. (2011). For the control laws defined by Burt (1967), we now present analytical expression for the $\Delta V$ and for the variation of the orbital elements during the transfer. In addition, we extend the analytical expression for the $\Delta V$ given in Pollard (2000). While Pollard considered thrust applied on arcs centred at the apocentre and pericentre of an orbit, we now consider the same control law applied along the entire orbit. Finally, we have included the analytical expressions for the $\Delta V$ and for the variation of the orbital elements during the transfer, for some of the control laws presented by Petropoulos (2003) and Ruggiero et al. (2011) and for the case of circular orbits. While the time variation of the orbital parameters is presented for each considered control law, it is important to stress that the main focus of the paper remains the quick estimation of the $\Delta V$s through simple analytical formulas. The $\Delta V$s obtained using the analytical equations were compared against the $\Delta V$ resulting from a numerical integration of Gauss’ planetary equations.

For selected solution, a detailed analysis of the $\Delta V$ error, and of the error associated to the equations for the evolution of the mean orbital elements, is presented. When different formulas, associated to transfers characterised by different thrust profiles, can be used to define the same variation of orbital elements, we provide a comparative analysis of the $\Delta V$ cost of these formulas.

The solutions to the low-thrust motion presented in the first part of the paper do not consider perturbations to the orbital motion. However, gravity perturbations, such as the second zonal harmonic of the Earth’s gravitational potential, $J_2$, cause secular variations of the orbital elements of low Earth’s orbits. Thus, in this paper, new analytical solutions are derived for the two-point boundary value problem (TPBVP) associated to low-thrust transfers between inclined circular orbits with different values of the right ascension of the ascending node, under the effect of $J_2$. Analytical laws are derived for the variation of the orbital elements with time and for the cost of the transfer. The underlying assumption is that the thrust level is low, so that the transfer is represented by a long spiral.

The paper is structured as follows: Sect. 2 presents the relevant equations of motion; in the first part of the paper, Sects. 3 to 7 present the extensions to the available solutions for the variation of the semi-major axis (or combination of semi-major axis and other orbital elements), eccentricity (or combination of eccentricity and other orbital elements), inclination, right ascension of the ascending node, and argument of the periapsis. The analytical solutions presented in Sects. 3 to 7 are summarised at the end of the paper in “Appendix A”, where a taxonomy of the analytical solutions is also given. The second part of the paper is constituted by Sect. 8, which introduces new analytical solutions for the transfer between circular inclined orbits with different values of the right ascension, under the effect of $J_2$. To the authors’ best knowledge, similar solutions are not available in the literature. Finally, Sect. 9 concludes the paper.

2 Equations of motion

It is assumed that the spacecraft is subject to a low-thrust acceleration $\mathbf {f}$ that can be expressed in a radial–transverse–normal RTN reference frame (see Section 1.4.3., Vallado 2007 and Fig. 1) as

$$\begin{aligned} \mathbf {f} = \begin{bmatrix} f_{\mathrm{R}} \\ f_{\mathrm{T}} \\ f_{\mathrm{N}} \\ \end{bmatrix} = \begin{bmatrix} \epsilon \cos \beta \sin \alpha \\ \epsilon \cos \beta \cos \alpha \\ \epsilon \sin \beta \ \end{bmatrix} \ . \end{aligned}$$

(1)

Fig. 1

Low-thrust acceleration vector in a RTN reference frame and azimuth and elevation angles $\alpha$ and $\beta$

In Eq. (1) $\epsilon$ is the magnitude of the low-thrust acceleration, assumed to be constant, $\alpha$ is the azimuth angle, with respect to the transverse direction, and $\beta$ is the elevation angle with respect to the orbit plane. Gauss’ equations, expressing the time variation of the osculating classic orbital elements due to the low-thrust acceleration $\mathbf {f}$, are (see Section 10.3, page 484, Battin 1987)

$$\begin{aligned} \begin{aligned}&\frac{{\mathrm{d}}a}{{\mathrm{d}}t} = \frac{2 a^2}{h} \epsilon \cos \beta \left[ e \sin \theta \sin \alpha + \frac{p}{r} \cos \alpha \right] , \\&\frac{{\mathrm{d}}e}{{\mathrm{d}}t} = \frac{\epsilon \cos \beta }{h} \left\{ p \sin \theta \sin \alpha + \left[ \left( p+r \right) \cos \theta + r e \right] \cos \alpha \right\} , \\&\frac{{\mathrm{d}}i}{{\mathrm{d}}t} = \epsilon \frac{r}{h} \cos \nu \sin \beta , \\&\frac{{\mathrm{d}}\varOmega }{{\mathrm{d}}t} = \epsilon \frac{r}{h} \frac{\sin \nu }{\sin i} \sin \beta , \\&\frac{{\mathrm{d}}\omega }{{\mathrm{d}}t} = \frac{1}{h e} \epsilon \cos \beta \left[ - p \cos \theta \sin \alpha + \left( p+r \right) \sin \theta \cos \alpha \right] - \frac{r \sin \nu \cos i}{h \sin i} \sin \beta , \\&\frac{{\mathrm{d}} \theta }{{\mathrm{d}}t} = \frac{h}{r^2} + \frac{\epsilon }{e h} \cos \beta \left[ p \cos \theta \sin \alpha - \left( p+r\right) \sin \theta \cos \alpha \right] \approx \frac{h}{r^2}\ . \end{aligned} \end{aligned}$$

(2)

In Eq. (2), a is the semi-major axis, e the eccentricity, p the semilatus rectum, i the inclination, $\varOmega$ the right ascension of the ascending node, $\omega$ the argument of the periapsis, $\theta$ the true anomaly, h the magnitude of the angular momentum, $h = \sqrt{\mu \ p}$, and $\nu$ the argument of latitude, $\nu = \omega + \theta$.

The approximation in the last of Eq. (2) derives from the assumption that the perturbing forces are small enough to produce a negligible effect on ${\mathrm{d}}\theta /{\mathrm{d}}t$, compared to the term $h/r^2$, which is due to the Keplerian motion (a similar approximation is used also in Avanzini et al. 2015; Di Carlo et al. 2021; Zuiani and Vasile 2015). The variation with time of the argument of latitude is (Section 10.3, page 484, Battin 1987)

$$\begin{aligned} \frac{{\mathrm{d}}\nu }{{\mathrm{d}}t} = \frac{{\mathrm{d}}\omega }{{\mathrm{d}}t} + \frac{{\mathrm{d}}\theta }{{\mathrm{d}}t} = \frac{h}{r^2} - \frac{r \sin \nu \cos i}{h \sin i} \sin \beta \approx \frac{h}{r^2} \ . \end{aligned}$$

(3)

The approximation in Eq. (3) is based on the same assumptions used for the approximation in the last of Eq. (2). Another useful expression, used in the rest of this paper, is the time variation of the eccentric anomaly E (Burt 1967):

$$\begin{aligned} \frac{{\mathrm{d}}E}{{\mathrm{d}}t} = \sqrt{\frac{\mu }{a}} \frac{1}{r} + \frac{1}{e \sin E} \left[ \cos E \frac{{\mathrm{d}}e}{{\mathrm{d}}t} - \frac{r}{a^2} \frac{{\mathrm{d}}a}{{\mathrm{d}}t} \right] \approx \sqrt{\frac{\mu }{a}} \frac{1}{r} \ . \end{aligned}$$

(4)

The approximation in Eq. (4) holds when ${\mathrm{d}}a/{\mathrm{d}}t$ and ${\mathrm{d}}e/{\mathrm{d}}t$ are small (Burt 1967). In the rest of the paper, it is in fact assumed, unless otherwise specified, that the perturbing forces are small enough to produce negligible variations in the orbital elements over one orbital period.

3 Variation of the semi-major axis

In this section, we present two analytical solutions for the variation of the semi-major axis: the variation of the semi-major axis with constant tangential thrust and the variation of the semi-major axis with constant radial thrust. Both of them present no long-term variation of the eccentricity. Other solutions for the variation of the semi-major axis were presented by Edelbaum (1961) and Kéchichian (1997, 2010). In particular, Edelbaum (1961) and Kéchichian (1997, 2010) present solutions for the simultaneous variation of the semi-major axis and inclination, and of the semi-major axis and right ascension of the ascending node.

3.1 Variation of the semi-major axis with tangential thrust

The thrust angles that provide the maximum instantaneous rate of change of the orbital elements can be derived from the first derivatives of the Gauss’ equations with respect to $\alpha$ and $\beta$, as presented by Ruggiero et al. (2011). In particular, for the maximum variation of the semi-major axis:

$$\begin{aligned} \frac{\partial }{\partial \alpha }\left( \frac{{\mathrm{d}}a}{{\mathrm{d}}t} \right) = 0, \,\frac{\partial }{\partial \beta }\left( \frac{{\mathrm{d}}a}{{\mathrm{d}}t} \right) = 0 \ . \end{aligned}$$

(5)

Equation (5) provides the well-known result that the rate of change of the semi-major axis is maximum for planar thrust ($\beta =0$) and azimuth angle equal to the flight path angle $\gamma$:

$$\begin{aligned} \alpha = \arctan \left( \frac{e \sin \theta }{1 + e \cos \theta }\right) = \gamma , \, \beta = 0 \ . \end{aligned}$$

(6)

In particular, $\alpha = \gamma$ to increase the semi-major axis and $\alpha = \pi + \gamma$ to decrease the semi-major axis. Equations (5) and (6) are given by Ruggiero et al. (2011), while, to the authors’ best knowledge, the equations and derivations presented in the rest of this subsection have not been presented anywhere else in the literature.

Using Eq. (6), in the general case of non-circular orbits, the time variations of semi-major axis, eccentricity and argument of periapsis can be written as:

$$\begin{aligned} \begin{aligned}&\frac{{\mathrm{d}}a}{{\mathrm{d}}t} = \text {sgn}(\cos \alpha ) \frac{2 a^2 \epsilon }{\sqrt{\mu a (1-e^2)}} \sqrt{1 + e^2 + 2 e \cos \theta },\\&\frac{{\mathrm{d}}e}{{\mathrm{d}}t} = \text {sgn}(\cos \alpha ) \frac{2 \epsilon \sqrt{a (1-e^2)}}{\sqrt{\mu }} \frac{\left( e + \cos \theta \right) }{\sqrt{1+e^2 + 2 e \cos \theta }},\\&\frac{{\mathrm{d}}\omega }{{\mathrm{d}}t} = \text {sgn}(\cos \alpha ) \sqrt{\frac{p}{\mu }} \frac{\epsilon }{e} \frac{2 \sin \theta }{\sqrt{1+e^2+2 e \cos \theta }} \ . \end{aligned} \end{aligned}$$

(7)

Equations (7) are derived from Eq. (2) by expressing $\sin \alpha$ and $\cos \alpha$ as

$$\begin{aligned} \begin{aligned} \cos \alpha&= \text {sgn}(\cos \alpha ) \frac{1 + e \cos \theta }{\sqrt{1 + e^2 + 2 e \cos \theta }}, \\ \sin \alpha&= \text {sgn}(\cos \alpha ) \frac{e \sin \theta }{\sqrt{1 + e^2 + 2 e \cos \theta }} \ . \\ \end{aligned} \end{aligned}$$

(8)

The variations of a, e and $\omega$ with $\theta$ are thus given by

$$\begin{aligned} \begin{aligned} \frac{{\mathrm{d}}a}{{\mathrm{d}}\theta }&= \frac{{\mathrm{d}}a}{{\mathrm{d}}t} \frac{{\mathrm{d}}t}{{\mathrm{d}}\theta } = \text {sgn}(\cos \alpha ) \frac{2 \epsilon }{\mu } a^3 \left( 1-e^2 \right) \frac{\sqrt{1+ e^2 + 2\, e \, \cos \theta }}{\left( 1 + e \, \cos \theta \right) ^2},\\ \frac{{\mathrm{d}}e}{{\mathrm{d}}\theta }&= \frac{{\mathrm{d}}e}{{\mathrm{d}}t} \frac{{\mathrm{d}}t}{{\mathrm{d}}\theta } = \text {sgn}(\cos \alpha ) \frac{2 \epsilon }{\mu } a^2 \left( 1-e^2\right) \frac{e + \cos \theta }{\left( 1 + e\, \cos \theta \right) ^2 \sqrt{1+e^2 + 2\,e\, cos\theta }},\\ \frac{{\mathrm{d}}\omega }{{\mathrm{d}}\theta }&= \frac{{\mathrm{d}}\omega }{{\mathrm{d}}t} \frac{{\mathrm{d}}t}{{\mathrm{d}}\theta } =\text {sgn}(\cos \alpha ) \frac{2 \epsilon p^2}{e \mu } \frac{\sin \theta }{(1+e \cos \theta )^2\sqrt{1+e^2 + 2e \cos \theta }} \ . \end{aligned} \end{aligned}$$

(9)

We now introduce the assumption that the variations of a, e and $\omega$ are small within one revolution, since the thrust level is assumed to be small (Petropolous 2002). Therefore, they can be kept constant when computing the average quantities:

$$\begin{aligned} \Delta \bar{a}_{2\pi } = \int _{0}^{2\pi } \frac{{\mathrm{d}}a}{{\mathrm{d}}\theta }{\mathrm{d}}\theta \ ; \Delta \bar{e}_{2\pi } = \int _{0}^{2\pi } \frac{{\mathrm{d}}e}{{\mathrm{d}}\theta }{\mathrm{d}}\theta \ ; \Delta {\bar{\omega }}_{2\pi } = \int _{0}^{2\pi } \frac{{\mathrm{d}}\omega }{{\mathrm{d}}\theta }{\mathrm{d}}\theta \ , \end{aligned}$$

(10)

where $\bar{a}$, $\bar{e}$ and ${\bar{\omega }}$ are the mean values of the semi-major axis, eccentricity and argument of periapsis. The last two integrals in Eqs. (10) give $\Delta \bar{e}_{2\pi } = \Delta {\bar{\omega }}_{2\pi } = 0$, meaning that there is no secular variation of the eccentricity and argument of periapsis. The equation for the semi-major axis gives instead

$$\begin{aligned} \Delta \bar{a}_{2\pi } = \text {sgn}(\cos \alpha ) \frac{2 \epsilon \bar{a}^3 \left( 1-\bar{e}^2\right) }{\mu } f(\bar{e}). \end{aligned}$$

(11)

The expression for $f(\bar{e})$ is

$$\begin{aligned} f(\bar{e}) = \frac{2}{1-\bar{e}} E_{{\mathrm{Ic}}}\left( \frac{4\bar{e}}{(1+\bar{e})^2}\right) + \frac{2}{1+\bar{e}} F_{{\mathrm{Ic}}}\left( \frac{4\bar{e}}{(1+\bar{e})^2}\right) \ . \end{aligned}$$

(12)

In Eq. (12) $F_{{\mathrm{Ic}}}$ and $E_{{\mathrm{Ic}}}$ are, respectively, the complete elliptic integrals of the first and second kind:

$$\begin{aligned} \begin{aligned}&F_{{\mathrm{Ic}}}(m) = F_I \left( \frac{\pi }{2} , m \right) \ ,\\&E_{{\mathrm{Ic}}}(m) = E_I\left( \frac{\pi }{2} , m \right) \ , \end{aligned} \end{aligned}$$

(13)

and $F_I$ and $E_I$ are the elliptic integrals of the first and second kind (Section 1.5, page 68, Battin 1987). The value of the elliptic integrals was computed with the MATLAB function ellipke which implements the method of the arithmetic-geometric mean described by Abramowitz and Stegun (1965), Section 17.6. The tolerance default value of $2.2204\,\times \,10^{-16}$ was used. The variation with time of the semi-major axis is

$$\begin{aligned} \frac{{\mathrm{d}}\bar{a}}{{\mathrm{d}}t} = \frac{\Delta \bar{a}_{2\pi }}{T} = \text {sgn}(\cos \alpha ) \frac{\epsilon \bar{a}^{3/2}}{\pi \sqrt{\mu }} (1-\bar{e}^2) f(\bar{e}) \ , \end{aligned}$$

(14)

and depends on the eccentricity $\bar{e}$. In Eq. (14), T denotes the orbital period, $T=2\pi \sqrt{\bar{a}^3/\mu }$. Since there is no secular variation of the eccentricity during the transfer, the secular variation of the semi-major axis with time can be obtained by integrating Eq. (14) to have:

$$\begin{aligned} \bar{a}(t) = \left[ \frac{1}{\bar{a}_0} + \left( \frac{\epsilon (1-\bar{e}^2)f(\bar{e})}{2 \pi \sqrt{\mu }}\right) ^2 t^2- \text {sgn}(\cos \alpha )\frac{\epsilon (1-\bar{e}^2)f(\bar{e})}{\pi \sqrt{ \bar{a}_0\mu }} t\right] ^{-1} \ . \end{aligned}$$

(15)

Finally, integrating Eq. (14) from $t_0=0$ to ToF, with $\bar{a}(t_0)=\bar{a}_0$ and $\bar{a}({\mathrm{ToF}})=\bar{a}_f$, it is possible to state that:

Proposition 1

Given Eq. (15), the cost of a transfer to change the semi-major axis from $\bar{a}_0$ to $\bar{a}_f$, using the thrust profile defined in Eq. (6), and under the assumption that the variation of semi-major axis, eccentricity and argument of the periapsis is small within one revolution, is

$$\begin{aligned} \Delta V = \epsilon {\mathrm{ToF}} = \frac{2\pi \left|\sqrt{\frac{\mu }{\bar{a}_0}} - \sqrt{\frac{\mu }{\bar{a}_f}}\right|}{(1-\bar{e}^2) f(\bar{e})} \ . \end{aligned}$$

(16)

Equation (16) is not singular for circular orbits, since when $\bar{e}=0$, $f(\bar{e})\ne 0$. It is important to stress that Eqs. (16) and (15) provide only an approximation to the $\Delta V$ and to the variation of $\bar{a}$ during the transfer, and that the approximation is incorrect when the variation of the semi-major axis over one orbital period, or the variation of the eccentricity, cannot be neglected. The validity of this assumption is illustrated hereafter for Geocentric and Heliocentric, or interplanetary, transfers. Figure 2 shows the relative difference in the $\Delta V$ obtained using analytical Eq. (16) and computing the cost of the transfer by numerically integrating Gauss’ equations with Eq. (6), until the desired final semi-major axis is reached. More precisely, Fig. 2 shows the quantity $(\Delta V - \Delta V_{\mathrm{num}})/\Delta V_{\mathrm{num}}$, where $\Delta V$ is given by Eq. (16) and $\Delta V_ {num}$ is computed as $\Delta V_{\mathrm{num}} = \epsilon \ {\mathrm{ToF}}_{\mathrm{num}}$. The time of flight ${\mathrm{ToF}}_{\mathrm{num}}$ is obtained by integrating numerically the Gauss’ equations for a, e and $\omega$ using as initial conditions different values of $\bar{a}_0$ and $\bar{e}_0$, as shown in Fig. 2, and using ${\bar{\omega }}_0=0$. The numerical integration is performed in MATLAB using ode45 with absolute and relative tolerance equal to $10^{-12}$. The considered value of $\epsilon$ is $10^{-4} \text {m}/\text {s}^2$. The numerical integration is interrupted when the targeted final semi-major axis $\bar{a}_f$ is reached; the corresponding final time is ${\mathrm{ToF}}_{\mathrm{num}}$. Results show that the relative error is higher for higher values of the eccentricity but remains lower than 2$\%$ for Geocentric transfers with eccentricities up to 0.7. For the four points highlighted with a red mark in Fig. 2, the maximum relative errors in the expression for the variation of the orbital elements can be computed, by comparing the results of the analytical equations with those from the numerical integration. The errors are reported in Table 1, along with the values of $a_0$, $\Delta a$ and e.

Fig. 2

Relative difference between numeric and analytical $\Delta V$ for Geocentric transfers—variation of the semi-major axis with tangential thrust

Table 1 Values of $a_0$, $\Delta a$ and e and maximum relative errors for the four points highlighted with red marks in Fig. 2

It is important to stress that the control law presented in this section gives higher errors in the variation of the orbital elements, compared to the control laws presented in the rest of the paper. For conciseness, therefore, no further analysis of the error will be presented in the next sections. Figure 3 shows the relative difference in $\Delta V$ for Heliocentric transfers with initial semi-major axis $\bar{a}_0 \in \left[ 1, 1.5\right]$ AU and characterised by $\Delta \bar{a} \in \left[ 0.1, 0.5\right]$ AU; two different values of the eccentricity have been considered. The error between analytical and numerical $\Delta V$ is bigger for Heliocentric than for Geocentric transfers. The analytical equation for the $\Delta V$ can, therefore, be used to approximate the cost of Geocentric transfers for small values of the low-thrust acceleration. However, the analytical equation gives non-negligible errors for some interplanetary transfers. Heliocentric transfers are, in fact, characterised by longer orbital periods; over these long orbital revolutions, the value of the semi-major axis cannot be assumed to remain constant. Moreover, the ratio between the low-thrust acceleration and the local gravity field is bigger for Heliocentric than for Geocentric transfers.

Fig. 3

Relative difference between numeric and analytical $\Delta V$ for Heliocentric transfers—variation of semi-major axis with tangential thrust

3.2 Variation of semi-major axis with radial and transverse thrust

In Burt (1967), the author proposed a thrust profile with radial and transverse thrust that changes the semi-major axis of non-circular orbits, without any variation in the eccentricity. In order to obtain this thrust profile, the expressions for the variation of the orbital elements with respect to the eccentric anomaly E are required. From the Gauss’ equation for ${\mathrm{d}}a/{\mathrm{d}}t$ (Eq. 2), one can derive a relationship for da/dE:

$$\begin{aligned} \frac{{\mathrm{d}}a}{{\mathrm{d}}E} = \frac{{\mathrm{d}}a}{{\mathrm{d}}t} \frac{{\mathrm{d}}t}{{\mathrm{d}}E} = \frac{2 a^{5/2}}{\mu \sqrt{p}} \left[ f_{\mathrm{R}} \, a \, e \sqrt{1-e^2} \sin E + f_{\mathrm{T}}\, p\right] \ . \end{aligned}$$

(17)

Similarly, it is possible to obtain the equations for the variation of the eccentricity with respect to the eccentric anomaly,

$$\begin{aligned} \frac{{\mathrm{d}}e}{{\mathrm{d}}E} = \frac{\sqrt{a \, p}}{\mu } \left[ f_{\mathrm{R}} \, a\, \sqrt{1-e^2} \sin E + f_{\mathrm{T}} \, a \ \left( 2 \cos E - e - e \cos ^2 E \right) \right] \ , \end{aligned}$$

(18)

and, the variation of the argument of the periapsis with respect to the eccentric anomaly:

$$\begin{aligned} \begin{aligned}&\frac{{\mathrm{d}}\omega }{{\mathrm{d}}E} = \frac{a^2 \sqrt{1-e^2} }{\mu e} \left\{ -f_{\mathrm{R}} \left( \cos E - e\right) + f_{\mathrm{T}} \left[ 1 + \frac{a}{p}\left( 1 - e \cos E\right) \right] \left( \sqrt{1-e^2}\sin E \right) \right\} +\\&-f_{\mathrm{N}} \frac{a^2 \cot i}{\mu \sqrt{1-e^2}} \left\{ \sqrt{1-e^2} \cos \omega \sin E \left( 1 - e \cos E \right) + \right. \\&\left. \sin \omega \left[ -e + \cos E \left( 1+e^2\right) - e \cos ^2 E\right] \right\} \ . \end{aligned} \end{aligned}$$

(19)

The variation of a with no secular variation of e can be obtained with a radial acceleration that changes sign when $E=0$ and $E=\pi$ (Burt 1967). Integration of the equation for de/dE (Eq. 18) from $E=0$ to $E=2\pi$, under the assumption that the osculating elements during one orbital revolution remain equal to the elements at $E=0$, results in:

$$\begin{aligned} \Delta \bar{e}_{2\pi } = \frac{\sqrt{\bar{a} \, \bar{p}}}{\mu } \left[ \left( \text {sgn} f_{\mathrm{R}}\right) _{E=\pi /2} 4 \left|{f_{\mathrm{R}}} \right|\sqrt{1-\bar{e}^2} - 3 \pi \, \bar{e}\, f_{\mathrm{T}} \right] \ . \end{aligned}$$

(20)

From Eq. (20), imposing $\Delta \bar{e}_{2\pi }=0$, the following can be obtained:

$$\begin{aligned} \frac{\left|f_{\mathrm{R}} \right|}{f_{\mathrm{T}}} = \frac{3 \pi }{4} \frac{\bar{e}}{\sqrt{1-\bar{e}^2}} \ . \end{aligned}$$

(21)

Expressions for $f_{\mathrm{R}}$ and $f_{\mathrm{T}}$ can be obtained using Eq. (21) and considering that $\sqrt{f_{\mathrm{R}}^2 + f_{\mathrm{T}}^2} = \epsilon$. The expressions for the angles $\alpha$ and $\beta$ that satisfy Eq. (21), which are not given by Burt (1967), are

$$\begin{aligned} \alpha = {(\text {sgn} {f_{\mathrm{R}}})_{E=\pi /2}} \text {sgn}\left( \sin E\right) \arctan \left( \frac{3\pi }{4} \frac{\bar{e}}{\sqrt{1-\bar{e}^2}} \right) , \, \beta = 0 \ . \end{aligned}$$

(22)

By using the expression in Eq. (21) to derive $f_{\mathrm{R}}$, one can obtain the equation for the secular variations of a, as reported also by Burt (1967):

$$\begin{aligned} \frac{{\mathrm{d}}\bar{a}}{{\mathrm{d}}t} = \frac{\Delta \bar{a}_{2\pi }}{T} = \left[ \frac{2 }{\sqrt{\mu }} \sqrt{1-\bar{e}^2} + {\text {sgn}\left( f_{\mathrm{R}}\right) }_{E=\pi /2} \frac{3 \bar{e}^2}{\sqrt{\mu \left( 1-\bar{e}^2\right) }} \right] \bar{a}^ {3/2} \,f_{\mathrm{T}} \ . \end{aligned}$$

(23)

Analogously, it is possible to verify that:

$$\begin{aligned} \frac{{\mathrm{d}}\bar{e}}{{\mathrm{d}}t} = 0 \ . \end{aligned}$$

(24)

The rest of this subsection reports additional equations that are not available in the literature and that are derived here for the first time. The integration of Eq. (23) gives:

$$\begin{aligned} \sqrt{\frac{\mu }{\bar{a}_0}} - \sqrt{\frac{\mu }{\bar{a}(t)}} = \frac{1}{2}\left[ \frac{2+\bar{e}^2}{\sqrt{1-\bar{e}^2}} \right] \,f_{\mathrm{T}} \, t \ , \end{aligned}$$

(25)

from which it is possible to obtain an analytical expression for the variation of $\bar{a}$ with time :

$$\begin{aligned} \bar{a}(t) = \bar{a}_0 \left[ 1 - \sqrt{\frac{\bar{a}_0}{\mu }} \left( \frac{2+\bar{e}^2}{2\sqrt{1-\bar{e}}^2} \right) f_{\mathrm{T}} t \right] ^{-2} \ . \end{aligned}$$

(26)

From Eq. (26), and considering that $\bar{a}_f=\bar{a}({\mathrm{ToF}})$, it is then possible to state the following:

Proposition 2

Given Eq. (26), the cost of a transfer to change the semi-major axis from $\bar{a}_0$ to $\bar{a}_f$, with ${\mathrm{d}} \bar{e}/{\mathrm{d}}t = 0$, using the thrust profile defined in Eqs. (21) and (22), is:

$$\begin{aligned} \Delta V = f_{\mathrm{T}} \ ToF = 2 \left|\sqrt{\frac{\mu }{\bar{a}_0}} - \sqrt{\frac{\mu }{\bar{a}_f}}\right|\left[ \frac{\sqrt{1-\bar{e}^2}}{2+\bar{e}^2}\right] \ . \end{aligned}$$

(27)

Equation 27 shows no singularity for $\bar{e}=0$. It is important to stress that from the integration of Eq. (19), one can see that the proposed solution to the low-thrust motion does not cause any long-term variation of the argument of periapsis during the transfer: ${\mathrm{d}}{\bar{\omega }}/{\mathrm{d}}t=0$.

3.3 Comparison of analytical solutions for the variations of semi-major axis

Figure 4 compares the $\Delta V$ required for the variation of $\bar{a}$ using the two solutions presented in this section. The value of $\epsilon$ is set to $10^{-4} \text { m}/\text {s}^2$. In particular, Fig. 4 shows the difference in $\Delta V$ when using Eqs. (16) and (27); this difference increases with increasing eccentricity but is limited to very small values. For $e=0$, the two equations coincide.

Fig. 4

${\delta } \Delta V$ for the variation of $\bar{a}$ for different values of $\bar{a}_0$ and $\Delta \bar{a} = \bar{a}_f - \bar{a}_0$ (difference between Eqs. 16 and 27, that is $\Delta V$ from Eq. 16 minus $\Delta V$ from Eq. 27)

4 Variation of the eccentricity or combination of eccentricity and other orbital elements

In this section, analytical solutions for the variation of the eccentricity, or combinations of orbital elements including the eccentricity, are presented. Other thrust profiles, different from the ones presented in this section, have been proposed in the literature (Petropoulos 2003); however, they do not lead to a closed form analytical solution and, therefore, are not reported hereafter.

4.1 Variation of the eccentricity with no variations of semi-major axis and argument of periapsis

In this section two different strategies are presented to obtain a variation of the eccentricity without long-term variation of semi-major axis and argument of periapsis. One is based on the work presented by Pollard (2000), and the other is based on the work presented by Burt (1967).

4.1.1 Thrust perpendicular to the major axis of the orbit

Pollard (2000) presented a strategy to change the eccentricity keeping the semi-major axis constant, using thrusting arcs centred at the periapsis and apoapsis of the orbit. For consistency with the rest of this paper, the equations presented here have been derived for thrust continuously applied over the entire orbit; they are, therefore, to be considered a novel derivation. We consider the following thrust profile, perpendicular to the major axis of the orbit:

$$\begin{aligned} \alpha = \left\{ \begin{array}{ll} \theta &{} \text { if } \bar{e}_f > \bar{e}_0\\ \pi + \theta &{} \text { if } \bar{e}_f < \bar{e}_0 \end{array} \right. , \, \beta = 0 , \end{aligned}$$

(28)

where $\bar{e}_0$ is the initial eccentricity and $\bar{e}_f$ is the final eccentricity.

Substituting these values for $\alpha$ and $\beta$ in Eqs. (17), (18) and (19) results in:

$$\begin{aligned} \begin{aligned} \frac{{\mathrm{d}}a}{{\mathrm{d}}E}&= \text {sgn}(e_f - e_0) \frac{2 \epsilon a^3 \sqrt{1-e^2}}{\mu } \cos E ,\\ \frac{{\mathrm{d}}e}{{\mathrm{d}}E}&= \text {sgn}(e_f - e_0) \frac{\epsilon \, a \sqrt{a p}}{\mu } {\left( 1 - 2 e \cos E + \cos ^2 E\right) } , \\ \frac{{\mathrm{d}}\omega }{{\mathrm{d}}E}&= \text {sgn}(e_f - e_0) \frac{\epsilon a^2}{\mu e} {\sin E \left( \cos E - e \right) } \ . \end{aligned} \end{aligned}$$

(29)

The variations of semi-major axis and argument of periapsis over one orbital period are $\Delta \bar{a}_{2\pi } = \Delta {\bar{\omega }}_{2\pi } = 0$, while the secular variation of the eccentricity is

$$\begin{aligned} \frac{{\mathrm{d}}\bar{e}}{{\mathrm{d}}t}= \text {sgn}(\bar{e}_f - \bar{e}_0) \frac{\Delta \bar{e}_{2\pi }}{T} = \text {sgn}(\bar{e}_f - \bar{e}_0) \frac{3}{2} \epsilon \sqrt{\frac{\bar{p}}{\mu }} \ . \end{aligned}$$

(30)

The integration of Eq. 30 allows one to obtain the expression for the variation of the eccentricity with time:

$$\begin{aligned} \bar{e}(t) = \bar{e}_0 + \text {sgn}(\bar{e}_f - \bar{e}_0) \sin \left( \frac{3}{2}\sqrt{\frac{\bar{a}}{\mu }} \epsilon \ t \right) \ . \end{aligned}$$

(31)

Considering Eq. (31), it is then possible to state the following, regarding the $\Delta V$ required to realise the transfer:

Proposition 3

Given Eq. (31), the cost of the transfer to change the eccentricity from $\bar{e}_0$ to $\bar{e}_f$, with $\bar{a}_f=\bar{a}_0$ and ${\bar{\omega }}_f={\bar{\omega }}_0$, using the thrust profile defined in Eq. (28), is:

$$\begin{aligned} \Delta V = \frac{2}{3} \sqrt{\frac{\mu }{\bar{a}}} \left|\arcsin \left( \bar{e}_f -{{\bar{e}_0}} \right) \right|\ . \end{aligned}$$

(32)

Equation (32) presents no singularity for $\bar{e}_0=0$ or $\bar{e}_f=0$.

4.1.2 Transverse thrust

In the work presented by Burt (1967), it was proposed to change e, without secular variations of a and $\omega$, by applying a transverse acceleration $f_{\mathrm{T}}$ reversed in sign when $E = \pm \pi /2$ (crossing of the minor axis). The corresponding thrust angles are:

$$\begin{aligned} \alpha = \left\{ \begin{array}{ll} \left\{ \begin{array}{ll} 0 &{} \text { for } -\frac{\pi }{2} \le E< \frac{\pi }{2} \\ \pi &{} \text { for } \frac{\pi }{2} \le E< \frac{3\pi }{2} \end{array} \right. &{} \text { if } \bar{e}_f > \bar{e}_0\\ \left\{ \begin{array}{ll} \pi &{} \text { for } -\frac{\pi }{2} \le E< \frac{\pi }{2} \\ 0 &{} \text { for } \frac{\pi }{2} \le E< \frac{3\pi }{2} \end{array} \right. &{} \text { if } \bar{e}_f < \bar{e}_0\\ \end{array} \right. \, , \quad \beta = 0 \ . \end{aligned}$$

(33)

The variations of the orbital elements over one orbital period are

$$\begin{aligned} \begin{aligned}&\Delta \bar{a}_{2\pi } = \Delta {\bar{\omega }}_{2\pi } = 0 , \\&\Delta \bar{e}_{2 \pi } = \text {sgn} \left( \bar{e}_f - \bar{e}_0\right) \frac{8 \bar{a}^2 \sqrt{1-\bar{e}^2} \epsilon }{\mu } \ . \end{aligned} \end{aligned}$$

(34)

It is possible to obtain an analytical expression for the variation of $\bar{e}$ with time. The secular rate of change of the eccentricity is

$$\begin{aligned} \frac{{\mathrm{d}}\bar{e}}{{\mathrm{d}}t} =\frac{\Delta \bar{e}_{2\pi }}{T} = \text {sgn} \left( \bar{e}_f - \bar{e}_0\right) \frac{4}{\pi } \sqrt{\frac{\bar{{p}}}{\mu }} \epsilon \ . \end{aligned}$$

(35)

The integration of Eq. (35) results in:

$$\begin{aligned} \bar{e}(t) = \bar{e}_0 + \text {sgn} \left( \bar{e}_f - \bar{e}_0\right) \sin \left( \frac{4}{\pi } \sqrt{\frac{\bar{a}}{\mu }} \epsilon \ t \right) \ . \end{aligned}$$

(36)

Considering Eq. (36), and that $\bar{e}({\mathrm{ToF}}) = \bar{e}_f$, it is possible to obtain the following expression for the $\Delta V$:

Proposition 4

Given Eq. (36), the cost of a transfer to change the eccentricity from $\bar{e}_0$ to $\bar{e}_f$, with $\bar{a}_f=\bar{a}_0$ and ${\bar{\omega }}_f={\bar{\omega }}_0$, using the thrust profile defined in Eq. (33), is:

$$\begin{aligned} \Delta V = \epsilon \ ToF = \frac{\pi }{4}\sqrt{\frac{\mu }{{\bar{a}}}} \left|\arcsin \left( \bar{e}_f -{\bar{e}_0} \right) \right|\ . \end{aligned}$$

(37)

Equation (37) presents no singularity for $\bar{e}_0=0$ or $\bar{e}_f=0$.

4.2 Combined variation of eccentricity and inclination without variation of other orbital elements

According to Pollard (2000), the simultaneous variation of e and i can be obtained using the following thrust profile:

$$\begin{aligned} \alpha = \left\{ \begin{array}{ll} \theta &{} \text { if } \bar{e}_f > \bar{e}_0 \\ \pi + \theta &{} \text { if } \bar{e}_f< \bar{e}_0 \end{array} \right. \, , \quad \beta = \left\{ \begin{array}{ll} \text {sgn}\left( \bar{i}_f - \bar{i}_0 \right) |\beta |&{} \text { if } -\frac{\pi }{2} \le E< \frac{\pi }{2} \\ -\text {sgn}\left( \bar{i}_f - \bar{i}_0\right) |\beta |&{} \text { if } \frac{\pi }{2} \le E < \frac{3\pi }{2} \end{array} . \right. \end{aligned}$$

(38)

In Pollard (2000), the equations for this type of transfer are derived for the case of thrust applied on arcs centred at the periapsis and apoapsis of the orbit. In this paper, instead, a continuous thrust applied over the entire orbit is considered.

The equations for the secular variation of a, e and $\omega$ are derived from the results presented in Sect. 4.1.1, with the addition of the term $\cos \beta$ in the expressions for $f_{\mathrm{R}}$ and $f_{\mathrm{T}}$, and considering the addition of the term due to $f_{\mathrm{N}}$ in ${\mathrm{d}}{\bar{\omega }}/{\mathrm{d}}t$:

$$\begin{aligned} \begin{aligned}&\frac{{\mathrm{d}}\bar{a}}{{\mathrm{d}}t} = 0 , \\&\frac{{\mathrm{d}}\bar{e}}{{\mathrm{d}}t} = \text {sgn}(\bar{e}_f - \bar{e}_0) \frac{3}{2} \epsilon \cos \beta \sqrt{\frac{\bar{p}}{\mu }} ,\\&\frac{{\mathrm{d}}{\bar{\omega }}}{{\mathrm{d}}t} = -\sqrt{\frac{\bar{a}}{\mu }}\frac{\epsilon \sin \beta \cot \bar{i} \sin {\bar{\omega }}}{\pi \sqrt{1-\bar{e}^2}} 2 (1+\bar{e}^2) \ . \end{aligned} \end{aligned}$$

(39)

The variation of the inclination with the eccentric anomaly is

$$\begin{aligned} \begin{aligned}&{\frac{{\mathrm{d}}i}{{\mathrm{d}}E} =\frac{a^2}{\mu \sqrt{1-e^2}} \epsilon \sin \beta (1-e \cos E) \left[ \cos \omega (\cos E -e) -\sin \omega \sin E \sqrt{1-e^2}\right] }\\ \end{aligned} \end{aligned}$$

(40)

It is now possible to derive the secular variation of i by integrating Eq. (40) from 0 to $2\pi$ with the sign of $\beta$ flipping at the points along the orbit where the spacecraft is crossing the minor axis:

$$\begin{aligned} \frac{{\mathrm{d}}\bar{i}}{{\mathrm{d}}t} = \frac{\Delta \bar{i}_{2\pi }}{T} = {{\text {sgn}\left( \bar{i}_f - \bar{i}_0\right) }} \frac{\epsilon \sin \beta }{\pi } \sqrt{\frac{\bar{a}}{\mu }} \cos \omega \frac{2(1+\bar{e}^2)}{\sqrt{1-\bar{e}^2}} \ . \end{aligned}$$

(41)

Combining the equations for the secular variations of eccentricity and inclination provides:

$$\begin{aligned} \frac{{\mathrm{d}}\bar{i}}{{\mathrm{d}}e} = \text {sgn}(\bar{e}_f - \bar{e}_0) \ {{\text {sgn}\left( \bar{i}_f - \bar{i}_0\right) }} \frac{4}{3\pi } \frac{1+\bar{e}^2}{1-\bar{e}^2} \tan \beta \cos {\bar{\omega }} \ . \end{aligned}$$

(42)

It is possible to integrate Eq. (42) from $\bar{i}_0$ to $\bar{i}_f$ and from $\bar{e}_0$ to $\bar{e}_f$, under the assumption that ${\bar{\omega }}$ and $\beta$ are both constant. This is true when $\sin {\bar{\omega }} = 0$ (see Eq. 39 for ${\mathrm{d}}\bar{\omega }/{\mathrm{d}}t$), that is when $\bar{\omega }=0$ or $\bar{\omega }=\pi$. The integration provides an expression for the value of $\beta$:

$$\begin{aligned} \tan \beta = \text {sgn}(\bar{e}_f - \bar{e}_0) \ {{\text {sgn}\left( \bar{i}_f - \bar{i}_0\right) }} \frac{3\pi }{4} \frac{\bar{i}_f - \bar{i}_0}{\cos \bar{\omega }} \left[ \log \frac{\left( 1+\bar{e}_f \right) \left( 1-\bar{e}_0\right) }{\left( 1-\bar{e}_f \right) \left( 1+\bar{e}_0\right) } - \bar{e}_f + \bar{e}_0 \right] ^{-1} \ . \end{aligned}$$

(43)

The equation for the variation of the eccentricity with time is similar to Eq. (31), but for the term in $\beta$:

$$\begin{aligned} \bar{e}(t) = \sin \left( \arcsin \bar{e}_0 +\text {sgn}(\bar{e}_f - \bar{e}_0) \frac{3}{2}\cos \beta \sqrt{\frac{\bar{a}}{\mu }} \epsilon \ t \right) \ . \end{aligned}$$

(44)

From ${\mathrm{d}}\bar{i}/{\mathrm{d}}t$ one can derive an expression for the variation of the inclination $\bar{i}$ with time, which is not given in the literature:

$$\begin{aligned} \begin{aligned} \bar{i}(t) =&\ \bar{i}_0 + {{\text {sgn}\left( \bar{i}_f - \bar{i}_0\right) }} \frac{4}{3} \frac{\cos \bar{\omega } \tan \beta }{\pi } \left[ 2 \log \left( \frac{\cos \left( \frac{\arcsin \bar{e}_0}{2}\right) - \sin \left( \frac{\arcsin \bar{e}_0}{2}\right) }{\cos \left( \frac{\arcsin \bar{e}_0}{2}\right) + \sin \left( \frac{\arcsin \bar{e}_0}{2}\right) }\right) \right. \\&\left. + \bar{e}_0 - 2 \log \left( g(\bar{e}_0, \beta , \epsilon , \bar{a}, t)\right) {{-}} \sin \left( \arcsin \bar{e}_0 + {\text {sgn}(\bar{e}_f - \bar{e}_0)} \frac{3}{2} \cos \beta \epsilon \sqrt{\frac{\bar{a}}{\mu }} t\right) \right] \ , \end{aligned} \end{aligned}$$

(45)

where

$$\begin{aligned} \begin{aligned}&g(\bar{e}_0, \beta , \epsilon , \bar{a}, t) = \\&\frac{\cos \left[ \frac{1}{4} \left( 2 \arcsin \bar{e}_0 + 3 \ {\text {sgn}(\bar{e}_f - \bar{e}_0)} \epsilon \cos \beta \sqrt{\frac{\bar{a }}{\mu }} t \right) \right] - \sin \left[ \frac{1}{4} \left( 2 \arcsin \bar{e}_0 + 3 \ {\text {sgn}(\bar{e}_f - \bar{e}_0)} \epsilon \cos \beta \sqrt{\frac{\bar{a}}{\mu }} t \right) \right] }{\cos \left[ \frac{1}{4} \left( 2 \arcsin \bar{e}_0 + 3 \ {\text {sgn}(\bar{e}_f - \bar{e}_0)} \epsilon \cos \beta \sqrt{\frac{\bar{a}}{\mu }} t \right) \right] + \sin \left[ \frac{1}{4} \left( 2 \arcsin \bar{e}_0 + 3 \ {\text {sgn}(\bar{e}_f - \bar{e}_0)} \epsilon \cos \beta \sqrt{\frac{\bar{a}}{\mu }} t \right) \right] } \ . \end{aligned} \end{aligned}$$

(46)

Note that an analytic equation for $\bar{i}(t)$, corresponding to Eq. (45), was not derived in Pollard (2000). Considering Eq. (44), it is then possible to state the following:

Proposition 5

Given Eq. (44), the cost of a transfer to change the eccentricity from $\bar{e}_0$ to $\bar{e}_f$ and to change the inclination from $\bar{i}_0$ to $\bar{i}_f$, using the thrust profile defined in Eqs. (38) and (43), is:

$$\begin{aligned} \Delta V = \frac{2}{3} \sqrt{\frac{\mu }{\bar{a}}}\frac{ \left|\arcsin \bar{e}_f - \arcsin \bar{e}_0 \right|}{\cos \beta } \ . \end{aligned}$$

(47)

Equation (47) presents no singularity for $\bar{e}_0=0$ or $\bar{e}_f=0$. It is important to stress that this analytical solution, and the corresponding transfer, are valid only when there is a nonzero secular change of the eccentricity, because $\beta =0$ when $\bar{e}_0=\bar{e}_f$. Therefore, this thrust profile cannot be used to obtain a pure variation of the inclination. Another important point to stress is that, despite the out-of-plane component, this thrust profile causes no variation of the right ascension. This can be verified by looking at the expression for the variation of the right ascension with the eccentric anomaly, as presented in Pollard (2000):

$$\begin{aligned} \frac{{\mathrm{d}}\varOmega }{{\mathrm{d}}E} = \frac{f_{\mathrm{N}} a^2}{\mu } \frac{\left( 1-e \cos E\right) }{\sin i} \left[ \sin E \cos \omega + \frac{\left( \cos E - e\right) }{\sqrt{1-e^2}} \sin \omega \right] \ . \end{aligned}$$

(48)

It is easy to verify that the integral of Eq. (48) over one orbital period, with $\beta$ changing sign at the crossing of the minor axis, results in $\Delta \bar{\varOmega }_{2\pi } = 0$.

4.3 Comparison of laws for the variation of the eccentricity only

Figures 5 and 6 show the $\Delta V$ required for the variation of $\bar{e}$ without variation of the semi-major axis, for different values of the semi-major axis (7000 km, 8000 km, 9000 km and 10,000 km) and using $\epsilon =10^{-4} \text { m}/\text {s}^2$. In particular, Fig. 5 shows the $\Delta V$ relative to the thrust profile defined by Pollard (Eq. 32) and Fig. 6 shows the $\Delta V$ relative to the thrust profile defined by Burt (Eq. 37).

Fig. 5

$\Delta V$ (in [km/s]) for the variation of $\bar{e}$ for different values of $\bar{e}_0$, $\bar{e}_f$ and $\bar{a}$—Sect. 4.1.1

Fig. 6

$\Delta V$ (in [km/s]) for the variation of $\bar{e}$ for different values of $\bar{e}_0$, $\bar{e}_f$ and $\bar{a}$—Sect. 4.1.2

Figures 5 and 6 show that the $\Delta V$ cost is higher when the thrust profile defined by Burt is used.

5 Variation of inclination

Following the derivations presented by Ruggiero et al. (2011), the maximum instantaneous variation of inclination can be obtained using the following out of plane thrust profile:

$$\begin{aligned} \left|\beta \right|= \frac{\pi }{2} \ . \end{aligned}$$

(49)

Because of the term $\cos \nu$ in the Gauss’ equation for ${\mathrm{d}}i/{\mathrm{d}}t$, in order to obtain a nonzero variation of the inclination, $\beta$ has to change sign at $\nu =\pi /2$ and $\nu = 3 \pi /2$. Equation (49) can, therefore, be rewritten as

$$\begin{aligned} \beta = \text {sgn}\left( \cos \nu \right) \text {sgn} \left( \bar{i}_f - \bar{i}_0\right) \frac{\pi }{2} \ . \end{aligned}$$

(50)

Because of the term $\sin \nu$ in the equation for ${\mathrm{d}}\varOmega /{\mathrm{d}}t$, this thrust profile causes no variation of $\bar{\varOmega }$. There is, however, a variation of $\bar{\omega }$ due to $\beta$. No simple expression is available for the variation of $\bar{\omega }$ and $\bar{i}$ with time when $\bar{e}_0 \ne 0$.

For $\bar{e}_0=0$, instead, it is possible to find analytical equations for the variation of the orbital elements and for the cost of the transfer. The variation with time of the inclination is

$$\begin{aligned} \frac{{\mathrm{d}}\bar{i}}{{\mathrm{d}}t}= \text {sgn}(\bar{i}_f - \bar{i}_0)2 \frac{\epsilon }{\pi } \sqrt{\frac{\bar{a}}{\mu }} \ . \end{aligned}$$

(51)

The integration of Eq. (51) gives the expression for the variation of the inclination with time:

$$\begin{aligned} \bar{i}(t) = \bar{i}_0 + \text {sgn}(\bar{i}_f - \bar{i}_0) \frac{2 \epsilon }{\pi } \sqrt{\frac{\bar{a}}{\mu }} t \ . \end{aligned}$$

(52)

Considering Eq. (52), and $\Delta \bar{i} = \bar{i}_f - \bar{i}_0 = \bar{i}({\mathrm{ToF}}) - \bar{i}_0$, it is possible to state that:

Proposition 6

The cost of the transfer to change the inclination by $\Delta \bar{i}$ following the thrust profile defined in Eq. (50) is given by:

$$\begin{aligned} \Delta V = \frac{\pi }{2} \sqrt{\frac{\mu }{\bar{a}}} \Delta \bar{i} \ . \end{aligned}$$

(53)

6 Variation of the right ascension of the ascending node

Considering the Gauss’ equation for ${\mathrm{d}}\varOmega /{\mathrm{d}}t$, the instantaneous maximum variation of $\varOmega$ is obtained when

$$\begin{aligned} \beta = \text {sgn}(\bar{\varOmega }_f - \bar{\varOmega }_0) \text {sgn}\left( \sin \nu \right) \frac{\pi }{2} \ . \end{aligned}$$

(54)

This value of $\beta$ does not cause any variation of $\bar{i}$. No analytical expression is available for the time variation of $\bar{\varOmega }$, when using the values of $\beta$ given in Eq. (54), in the general case when $\bar{e}_0 \ne 0$. Analytical equations can be derived when $\bar{e}_0=0$. In this case:

$$\begin{aligned} {\frac{{\mathrm{d}}\bar{\varOmega }}{{\mathrm{d}}t}} = \text {sgn}(\bar{\varOmega }_f - \bar{\varOmega }_0) \frac{2 \epsilon }{\pi }\sqrt{\frac{\bar{a}}{\mu }} \frac{1}{\sin \bar{i}} \ . \end{aligned}$$

(55)

The expression for $\bar{\varOmega }(t)$, obtained from integration of Eq. (55), is:

$$\begin{aligned} \bar{\varOmega }(t) = \bar{\varOmega }_0 + \text {sgn}(\bar{\varOmega }_f - \bar{\varOmega }_0) \frac{2 \epsilon }{\pi } \sqrt{\frac{\bar{a}}{\mu }} \frac{1}{\sin \bar{i}} t \ . \end{aligned}$$

(56)

To the author’s best knowledge, Eq. (56) is not available in the literature. The cost of the transfer is Ruggiero et al. (2011)

$$\begin{aligned} \Delta V = \frac{\pi }{2}\sqrt{\frac{\mu }{\bar{a}}} \Delta \bar{\varOmega } \sin \bar{i} \ . \end{aligned}$$

(57)

Equation (57) is valid only for $\bar{i}\ne 0$. For $\bar{i}=0$, $\varOmega$ is not defined.

7 Variation of argument of the periapsis

Different solutions are available for the variation of the argument of periapsis. The ones that can provide analytical solutions are presented in this section. Other thrust profiles for the variation of $\omega$ that do not result in analytical solutions are presented by Petropoulos (2003) and Ruggiero et al. (2011). The results in this sections are valid only when $\bar{e}\ne 0$. When $\bar{e} = 0$, the argument of perigee is not defined.

7.1 Variation of the argument of the periapsis without variation of semi-major axis and eccentricity

The next subsections present thrust profiles that cause changes in the argument of the periapsis while keeping the secular variations of semi-major axis and eccentricity constant. We start from the work reported by Burt (1967) and derive analytical formulas for the secular variation of $\omega$ and for the associated $\Delta V$.

7.1.1 Transverse thrust

It is possible to change $\bar{\omega }$, without variations of $\bar{a}$ and $\bar{e}$, by using a thrust with nonzero transverse component $f_{\mathrm{T}}$, reversed in sign at the crossing of the major axis (that is, at $E = 0$ and $E = \pi$):

$$\begin{aligned} \left\{ \begin{array}{ll} \alpha = \left\{ \begin{array}{ll} 0 &{} \text { for } 0 \le E< \pi \\ \pi &{} \text { for } \pi \le E< 2\pi \end{array} \right. , \, \beta = 0 &{} \text { if } \text {sgn}(\bar{\omega }_f - \bar{\omega }_0) > 0 \ , \\ \alpha = \left\{ \begin{array}{ll} \pi &{} \text { for } 0 \le E< \pi \\ 0 &{} \text { for } \pi \le E< 2\pi \end{array} \right. , \, \beta = 0 &{} \text { if } \text {sgn}(\bar{\omega }_f - \bar{\omega }_0) < 0 \ .\\ \end{array} \right. \end{aligned}$$

(58)

If $f_{\mathrm{T}}$ is reversed in sign at the crossing of the major axis, Eqs. (17) and (18) give

$$\begin{aligned} \frac{{\mathrm{d}}\bar{a}}{{\mathrm{d}}t} = \frac{{\mathrm{d}}\bar{e}}{{\mathrm{d}}t} = 0 \ , \end{aligned}$$

(59)

while, Eq. (19) gives:

$$\begin{aligned} \frac{{\mathrm{d}}\bar{\omega }}{{\mathrm{d}}t} = \text {sgn}(\bar{\omega }_f - \bar{\omega }_0) \frac{2}{\pi } \sqrt{\frac{\bar{a}}{\mu }} \frac{(2-\bar{e}^2)}{\bar{e}} \epsilon \ . \end{aligned}$$

(60)

The integration of Eq. (60) gives a linear variation of $\bar{\omega }$ with time:

$$\begin{aligned} \bar{\omega }(t) = \bar{\omega }_0 + \text {sgn}(\bar{\omega }_f - \bar{\omega }_0) \frac{2}{\pi } \sqrt{\frac{\bar{a}}{\mu }} \frac{(2-\bar{e}^2)}{\bar{e}} \epsilon \ t \ . \end{aligned}$$

(61)

Then, from Eq. (61), one can derive an analytical expression for the $\Delta V$ cost of the transfer, as stated in the following proposition:

Proposition 7

Given Eq. (61), the cost required for a transfer to change the argument of periapsis from $\bar{\omega }_0$ to $\bar{\omega }_f$, with $\bar{a}_f=\bar{a}_0$ and $\bar{e}_f=\bar{e}_0$, and following the thrust profile defined in Eq. (58), is

$$\begin{aligned} \Delta V = \frac{\pi }{2} \sqrt{\frac{\mu }{\bar{a}}} \frac{\bar{e}}{(2-\bar{e}^2)} \left|\bar{\omega }_f - \bar{\omega }_0\right|\ . \end{aligned}$$

(62)

7.1.2 Radial thrust

Another possible thrust profile that changes $\bar{\omega }$ while giving no secular variation of $\bar{a}$ and $\bar{e}$ is the unidirectional radial acceleration (Burt 1967):

$$\begin{aligned} \alpha = \left\{ \begin{array}{ll} \pi /2 &{} \text { if } \bar{\omega }_f > \bar{\omega }_0 \\ 3 \pi /2 &{} \text { if } \bar{\omega }_f < \bar{\omega }_0 \end{array} \right. , \, \beta = 0 \ . \end{aligned}$$

(63)

In this case, the secular variations of $\omega$ are:

$$\begin{aligned} \frac{{\mathrm{d}}\bar{\omega }}{{\mathrm{d}}t} = \text {sgn}(\bar{\omega }_f - \bar{\omega }_0)\sqrt{\frac{\bar{p}}{\mu }} \epsilon \ , \end{aligned}$$

(64)

which gives the following expression for the time variation of $\bar{\omega }$:

$$\begin{aligned} \bar{\omega }(t) = \bar{\omega }_0 + \text {sgn}(\bar{\omega }_f - \bar{\omega }_0)\sqrt{\frac{\bar{p}}{\mu }} \epsilon t \ . \end{aligned}$$

(65)

Considering Eq. (65), it is possible to state that:

Proposition 8

The cost of a transfer to go from $\bar{\omega }_0$ to $\bar{\omega }_f$, with $\bar{a}_f=\bar{a}_0$ and $\bar{e}_f=\bar{e}_0$, using the thrust profile defined in Eq. (63) is:

$$\begin{aligned} \Delta V = \sqrt{\frac{\mu }{\bar{p}}} \left|\bar{\omega }_f - \bar{\omega }_0\right|\ . \end{aligned}$$

(66)

7.1.3 Thrust parallel to the major axis of the ellipse

The last thrusting strategy presented in this section was originally proposed by Pollard (2000); it is based on an in-plane acceleration parallel to the major axis of the ellipse:

$$\begin{aligned} \begin{aligned}&f_{\mathrm{R}} = - \text {sgn}(\omega _f - \omega _0) \epsilon \frac{(\cos E -e)}{1 - e \cos E} = - \text {sgn}(\omega _f - \omega _0) \epsilon \cos \theta , \\&f_{\mathrm{T}} = \text {sgn}(\omega _f - \omega _0)\epsilon \frac{\sqrt{1-e^2} \sin E}{1 - e \cos E} = \text {sgn}(\omega _f - \omega _0) \epsilon \sin \theta ,\\&f_{\mathrm{N}} = 0 \ . \end{aligned} \end{aligned}$$

(67)

This results in the following azimuth and elevation angles:

$$\begin{aligned} \tan \alpha = - \cot \theta , \, \beta = 0 \ . \end{aligned}$$

(68)

The derivation by Pollard (2000) considers a thrust applied over two symmetric arcs centred at the periapsis and apoapsis of the orbit. In the following, in order to be consistent with the rest of the paper, the thrust is assumed to be applied over the entire orbit. By using Eqs. (17) and (18) it is possible to verify that, with the thrust profile defined in Eq. (68), the secular variations of semi-major axis and eccentricity are both zero. The secular variation of the argument of the periapsis is:

$$\begin{aligned} \frac{{\mathrm{d}}\bar{\omega }}{{\mathrm{d}}t} = \text {sgn}(\bar{\omega }_f - \bar{\omega }_0) \frac{3 \epsilon }{2 \bar{e}} \sqrt{\frac{\bar{p}}{\mu }} \ . \end{aligned}$$

(69)

Equation (69) coincides with the equation given by Pollard (2000) when the two thrust arcs at periapsis and apoapsis have amplitude equal to $\pi$. From Eq. (69) one can derive the equation for the time variation of $\omega$:

$$\begin{aligned} \bar{\omega }(t) = \bar{\omega }_0 + \text {sgn}(\bar{\omega }_f - \bar{\omega }_0) \frac{3 \epsilon }{2 \bar{e}} \sqrt{\frac{\bar{p}}{\mu }} t \ . \end{aligned}$$

(70)

Considering Eq. (70), it is possible to state that:

Proposition 9

The cost of a transfer to go from $\bar{\omega }_0$ to $\bar{\omega }_f$, with $\bar{a}_f=\bar{a}_0$ and $\bar{e}_f=\bar{e}_0$, using the thrust profile of Eq. (68), is:

$$\begin{aligned} \Delta V = \frac{2 \bar{e}}{3} \sqrt{\frac{\mu }{\bar{p}}} \left|\Delta \bar{\omega } \right|\ . \end{aligned}$$

(71)

7.2 Comparison of laws for the variation of argument of the periapsis

Figures 7, 8 and 9 show the $\Delta V$ cost for the variation of $\bar{\omega }$, using the analytical solution defined in Sect. 7.1, for different values of $\Delta \bar{\omega }$, $\bar{e}$ and $\bar{a}$. The value of $\epsilon$ is set to $10^{-4} \text { m}/\text {s}^2$. Figures 7 and 8 show the results for transverse and radial low-thrust acceleration, respectively, as proposed in Burt (1967). Figure 9 presents instead the results for the case of low-thrust acceleration parallel to the major axis of the ellipse.

Fig. 7

$\Delta V$ (in [km/s]) for the variation of $\bar{\omega }$ with constant $\bar{a}$ and $\bar{e}$, for different values of $\Delta \bar{\omega }$, $\bar{e}$ and $\bar{a}$, using transverse acceleration

Fig. 8

$\Delta V$ (in [km/s]) for the variation of $\bar{\omega }$ with constant $\bar{a}$ and $\bar{e}$, for different values of $\Delta \bar{\omega }$, $\bar{e}$ and $\bar{a}$, using radial acceleration

Fig. 9

$\Delta V$ (in [km/s]) for the variation of $\bar{\omega }$ with constant $\bar{a}$ and $\bar{e}$ for different values of $\Delta \bar{\omega }$, $\bar{e}$ and $\bar{a}$, using acceleration parallel to the major axis of the ellipse

Results show that the law with acceleration parallel to the major axis of the ellipse is the most advantageous one in terms of $\Delta V$, while the law with radial acceleration is the most expensive.

The analytical solutions presented in Sects. 3 to 7 are summarised in “Appendix A”, where a taxonomy of the analytical solutions is also given.

8 Simultaneous variation of $a, i, \varOmega$ with $J_2$

The analytical solutions for low-thrust transfers presented in the previous sections are obtained assuming that the low-thrust acceleration is the only acceleration acting on the spacecraft; no other orbital perturbation is considered. In this section, new analytical solutions are derived for the Two-Point Boundary Value Problem (TPBVP) associated to the low-thrust transfer between inclined circular orbits, with different values of the initial and final right ascension of the ascending node, under the additional effect of the second order zonal harmonic of the Earth’s gravitational potential, $J_2$. Analytical laws are also derived for the variations of the orbital elements with time and for the cost of the transfer. As in the previous sections, it is assumed that the transfer trajectory is composed of several revolutions; during each revolution, the value of the considered orbital elements can be assumed to be constant. The proposed low-thrust transfers aim at realising the simultaneous variation of semi-major axis, inclination and right ascension of circular orbits, in a given time of flight ToF. The resulting TPBVP can be expressed as follows:

$$\begin{aligned} \begin{aligned}&\dot{\mathbf {x}} = \mathbf {F} \left( \mathbf {x}, \tilde{\mathbf {u}}, t \right) , \\&\mathbf {x}\left( t_0\right) = \mathbf {x}_0 , \\&\mathbf {x}\left( t_0 + {\mathrm{ToF}} \right) = \mathbf {x}_f ,\\&t \in \left[ t_0, t_0 + {\mathrm{ToF}} \right] . \end{aligned} \end{aligned}$$

(72)

The state $\mathbf {x}$ is:

$$\begin{aligned} \mathbf {x} = \left[ \bar{a}, \bar{i}, \bar{\varOmega }\right] ^T , \end{aligned}$$

(73)

and the initial and final conditions are expressed as

$$\begin{aligned} \begin{aligned}&\mathbf {x}_0 = \left[ \bar{a}_0, \bar{i}_0, \bar{\varOmega }_0\right] ^T , \\&\mathbf {x}_f = \left[ \bar{a}_f, \bar{i}_f, \bar{\varOmega }_f \right] ^T = \left[ \bar{a}_0+ \Delta \bar{a}, \bar{i}_0 + \Delta \bar{i}, \bar{\varOmega }_0 + \Delta \bar{\varOmega } \right] ^T .\\ \end{aligned} \end{aligned}$$

(74)

The right-hand side of the first equation in Eq. (72) is:

$$\begin{aligned} \mathbf {F}\left( \mathbf {x}, \tilde{\mathbf {u}}, t\right) = \begin{bmatrix} {{\mathrm{d}}\bar{a}}/{{\mathrm{d}}t} \\ {{\mathrm{d}} \bar{i}}/{{\mathrm{d}}t} \\ {{\mathrm{d}}\bar{\varOmega }}/{{\mathrm{d}}t} \\ \end{bmatrix} . \end{aligned}$$

(75)

The expressions for ${{\mathrm{d}}\bar{a}}/{{\mathrm{d}}t}$, ${{\mathrm{d}}\bar{i}}/{{\mathrm{d}}t}$ and ${{\mathrm{d}}\bar{\varOmega }}/{{\mathrm{d}}t}$ can be derived from the following set of Gauss’ planetary equations for $e=0$ (see Section 10.2.3 at page 262 in Mengali and Quarta 2006 for the terms in $J_2$):

$$\begin{aligned} \begin{aligned}&\frac{{\mathrm{d}}a}{{\mathrm{d}}t} = {2} {{\frac{a^2}{h}}} (\epsilon \cos \beta \cos \alpha -J_2{{\mu _{\oplus }}}\frac{R_{\oplus }^2}{a^4}3\sin ^2i\sin \nu \cos \nu ), \\&\frac{{\mathrm{d}}i}{{\mathrm{d}}t} = {{\frac{a}{h}}} \cos \nu (\epsilon \sin \beta -J_2{{\mu _{\oplus }}}\frac{R_{\oplus }^2}{a^4}3\sin i\cos i\sin \nu ), \\&\frac{{\mathrm{d}}\varOmega }{{\mathrm{d}}t} = \frac{a}{h} \frac{\sin \nu }{\sin i} (\epsilon \sin \beta -J_2{{\mu _{\oplus }}}\frac{R_{\oplus }^2}{a^4}3\sin i\cos i\sin \nu ) ,\\ \end{aligned} \end{aligned}$$

(76)

where $R_{\oplus }$ is the Earth’s radius. The control vector $\tilde{\mathbf {u}}$ in Eq. (72) defines the thrust orientation and the duration of each thrust phase, as specified more in details in the next subsections. In the following we will devise three strategies that exploit the secular drift in $\varOmega$ caused by $J_2$ in combination with the low-thrust action, to obtain the desired variation of $\bar{a}$, $\bar{i}$ and $\bar{\varOmega }$. The three strategies will be applied to the case in which $\bar{a}_0 < \bar{a}_f$; however, the same procedure can be used to define analogous strategies for $\bar{a}_0 > \bar{a}_f$.

8.1 Strategy 1: $\varDelta \bar{\varOmega }_{J_2}$ + $(\varDelta \bar{a}, \varDelta \bar{i})$

For the first strategy, the transfer from the initial to the final orbit is realised in two phases. During the first phase, denoted as $\Delta \bar{\varOmega }_{J_2}$ and characterised by a time of flight ${\mathrm{ToF}}_1$, $J_2$ is exploited to obtain a given variation of the right ascension. In the second phase, denoted as $(\Delta \bar{a}, \Delta \bar{i})$ and characterised by a time of flight ${\mathrm{ToF}}_2$, a low-thrust action is applied to change semi-major axis and inclination from their initial to their final values. In this phase, the low-thrust action is applied along two thrust arcs of constant angular span $2 \bar{\psi }$, with constant elevation angle $\bar{\beta }$. The variation of $\varOmega$, due to $J_2$ only, during the second phase is tuned in such a way that, starting from the value of $\varOmega$ reached at the end of phase one, the final targeted right ascension can be achieved. The vector of controls for Strategy 1 is $\tilde{\mathbf {u}} = [\bar{\psi }, \bar{\beta }, {\mathrm{ToF}}_1, {\mathrm{ToF}}_2]^T$. The symbols $\bar{\psi }$ and $\bar{\beta }$ are used in the rest of this section to denote constant control angles throughout the transfer. The two phases of Strategy 1 are schematically represented in Fig. 10.

Fig. 10

Representation of the two phases of Strategy 1. LT stands for low-thrust

The following subsections describe the two phases in more detail and derive the system of four equations required to compute the four components of $\tilde{\mathbf {u}}$ that solve the TPBVP (Problem (72)). Analytical equations for the variation of the orbital elements during the transfer and for the $\Delta V$ cost of the transfer are also provided.

8.1.1 First phase

During the first phase, the low-thrust engine is assumed to be off. The semi-major axis and inclination remain equal to their initial values, $\bar{a}_0$ and $\bar{i}_0$. This means that, considering the range of semi-major axes covered during the transfer $[\bar{a}_0, \bar{a}_f]$ and the assumption that $\bar{a}_0 < \bar{a}_f$, the drift of $\bar{\varOmega }$ due to $J_2$ is maximum and the resulting secular variation of $\varOmega$ with time is:

$$\begin{aligned} \bar{\varOmega }_1(t) = {{\bar{\varOmega }_0}}- \frac{3}{2} \sqrt{\mu _{\oplus }} J_2 R_{\oplus }^2 \cos \bar{i}_{0} \bar{a}_{0}^{-7/2} t \ , \ t \in [0, {\mathrm{ToF}}_1] \ , \end{aligned}$$

(77)

where the time of flight associated to this phase is ${\mathrm{ToF}}_{1}$ and $\bar{a}_1(t) = \bar{a}_0, \ \bar{i}_1(t) = \bar{i}_0 \ \forall t \in [0, {\mathrm{ToF}}_1]$. The right ascension of the ascending node at the end of the first phase is $\bar{\varOmega }_{1f}=\bar{\varOmega }_1({\mathrm{ToF}}_1)$. ${\mathrm{ToF}}_{1}$ and $\varOmega _{1f}$ satisfy the following relationship:

$$\begin{aligned} {\mathrm{ToF}}_{1} = \frac{\bar{\varOmega }_{1f} - \bar{\varOmega }_{0}}{\frac{3}{2} \sqrt{\mu _{\oplus }} J_2 R_{\oplus }^2 \cos \bar{i}_{0} \bar{a}_{0}^{-7/2}} . \end{aligned}$$

(78)

8.1.2 Second phase

During the second phase, the low-thrust engine is active during two thrust arcs per orbital revolution. During this phase, the semi-major axis and inclination change from their initial to their final values. Moreover, the drift of right ascension due to $J_2$ is such that, at the end of the transfer, the right ascension will have changed from $\bar{\varOmega }_{1f}$ to $\bar{\varOmega }_{f}$. Note that the variation of right ascension takes place only because of $J_2$ and not because of the low-thrust acceleration (as explained in more details later, see Eq. 85). The time of flight of the second phase is ${\mathrm{ToF}}_{2}$. The simultaneous variation of $\bar{a}$ and $\bar{i}$ in a given time of flight ${\mathrm{ToF}}_{2}$ can be obtained with two tangential thrust arcs of angular span $2 \bar{\psi }$ (constant during the transfer), constant azimuth angle $\bar{\alpha }=0$ and constant elevation angle $\bar{\beta }$, centred at the nodal points of the orbit, as shown in Fig. 11.

Fig. 11

Strategy 1, phase 2: thrust arcs centred at the nodal points of the orbit

The elevation angle $\bar{\beta }$ has equal and opposite values along the two thrust arcs. The relevant equations for this transfer can be obtained from Eq. (76), using $\alpha =0$:

$$\begin{aligned} \begin{aligned}&\frac{{\mathrm{d}}a}{{\mathrm{d}}\nu } = \frac{{\mathrm{d}}a}{{\mathrm{d}}t} \frac{{\mathrm{d}}t}{{\mathrm{d}}\nu } = \frac{2 a^3}{\mu } (\epsilon \cos \bar{\beta }-J_2{{\mu _{\oplus }}}\frac{R_{\oplus }^2}{a^4}3\sin ^3i\sin \nu \cos \nu ), \\&\frac{{\mathrm{d}}i}{{\mathrm{d}}\nu } = \frac{{\mathrm{d}}i}{{\mathrm{d}}t} \frac{{\mathrm{d}}t}{{\mathrm{d}}\nu }= \frac{ a^2 \cos \nu }{\mu }(\epsilon \sin \bar{\beta } -J_2{{\mu _{\oplus }}}\frac{R_{\oplus }^2}{a^4}3\sin i\cos i\sin \nu ) \ . \end{aligned} \end{aligned}$$

(79)

The resulting secular variations of a and i are computed as follows:

$$\begin{aligned} \begin{aligned}&\frac{{\mathrm{d}}\bar{a}}{{\mathrm{d}}t} = \frac{\Delta \bar{a}_{2\pi }}{T} =\frac{1}{T} \left[ \int _{-\bar{\psi }}^{\bar{\psi }} \frac{{\mathrm{d}}a}{{\mathrm{d}}\nu } {\mathrm{d}}\mathrm {\nu } +\int _{\pi -\bar{\psi }}^{\pi +\bar{\psi }} \frac{{\mathrm{d}}a}{{\mathrm{d}}\nu } {\mathrm{d}}\mathrm {\nu } \right] = \frac{4 \bar{a}^2 \bar{\psi } \ \epsilon \cos \bar{\beta }}{\pi \sqrt{\mu \bar{a}}} \ , \\&\frac{{\mathrm{d}}\bar{i}}{{\mathrm{d}}t} = \frac{1}{T} \left[ \int _{-\psi }^{\bar{\psi }} \frac{{\mathrm{d}}i}{{\mathrm{d}}\nu } {\mathrm{d}}\mathrm {\nu } +\int _{\pi -\bar{\psi }}^{\pi +\bar{\psi }} \frac{{\mathrm{d}}i}{{\mathrm{d}}\nu } {\mathrm{d}}\mathrm {\nu } \right] = \frac{2 \epsilon \bar{a} \sin \bar{\beta } \sin \bar{\psi }}{\pi \sqrt{\mu \bar{a}}} \ . \end{aligned} \end{aligned}$$

(80)

In Eq. (80) it is assumed that the variations of a and i in one revolution are negligible, so that they can be considered constant during the integration over $\nu$. In order for $\bar{a}$ and $\bar{i}$ to reach their final values simultaneously, the following equation is integrated from $\bar{a}_{0}$ to $\bar{a}_{f}$ and from $\bar{i}_{0}$ to $\bar{i}_{f}$:

$$\begin{aligned} \frac{{\mathrm{d}}\bar{a}}{{\mathrm{d}}\bar{i}} = \frac{{\mathrm{d}}\bar{a}}{{\mathrm{d}}t} \ \frac{{\mathrm{d}}t}{{\mathrm{d}}\bar{i}} = \frac{2 \ \bar{a} \ \bar{\psi } \cos \bar{\beta }}{\sin \bar{\psi } \sin \bar{\beta }} \ . \end{aligned}$$

(81)

From the integration of Eq. (81), one can derive the elevation angle $\bar{\beta }$ required to realise the transfer from $\bar{a}_0$ to $\bar{a}_f$ and from $\bar{i}_0$ to $\bar{i}_f$, as a function of $\bar{\psi }, \bar{a}_0, \bar{a}_f, \bar{i}_0$ and $\bar{i}_f$:

$$\begin{aligned} \tan \bar{\beta } = \frac{2 \bar{\psi } \left( \bar{i}_{f} - \bar{i}_{0}\right) }{\sin \bar{\psi } \log (\bar{a}_{f}/\bar{a}_{0})} \ . \end{aligned}$$

(82)

Finally, the expressions for the variation of $\bar{a}$ and $\bar{i}$ with time, during the second phase $(\Delta \bar{a}, \Delta \bar{i})$, are (see Eqs. 80 and 81):

$$\begin{aligned} \begin{aligned}&\bar{a}(t) = \mu \left[ \frac{\mu }{\bar{a}_0} + \left( \frac{2 \epsilon \cos \bar{\beta } \bar{\psi } (t - {\mathrm{ToF}}_1)}{\pi } \right) ^2 - 2 \sqrt{\frac{\mu }{\bar{a}_0}} \left( \frac{2 \epsilon \cos \bar{\beta } \bar{\psi } (t - {\mathrm{ToF}}_1)}{\pi } \right) \right] ^{-1} , \\&\bar{i}(t) = \bar{i}_0 + \frac{\tan \bar{\beta } \sin \bar{\psi }}{2 \bar{\psi }} \log \left( \frac{\bar{a}(t)}{\bar{a}_0} \right) \ , \end{aligned} \end{aligned}$$

(83)

with $t \in [{\mathrm{ToF}}_1, {\mathrm{ToF}}_1 + {\mathrm{ToF}}_2]$. From Eqs. (82) and (83), the time of flight of the second phase of the transfer can be expressed as a function of $\bar{\psi }$ and of the initial and final orbital elements:

$$\begin{aligned} {\mathrm{ToF}}_{2} = \frac{\pi }{2 \epsilon \bar{\psi }} \left( \sqrt{\frac{\mu }{\bar{a}_{0}}} - \sqrt{\frac{\mu }{\bar{a}_{f}}} \right) \sqrt{1 + \frac{4 \bar{\psi }^2 \left( \bar{i}_{f} - \bar{i}_{0}\right) ^2}{\sin ^2 \bar{\psi } \log ^2(\bar{a}_{f}/\bar{a}_{0})}} \ . \end{aligned}$$

(84)

During the second phase of the transfer, the right ascension changes because of $J_2$ and because of the variation of the semi-major axis and inclination with time. The rate of $\varOmega$ with time is given in the last equation in Eq. (76). The first term on the right-hand side of this equation cancels out when integrating in $\nu$ over one revolution, because $\bar{\beta }$ takes opposite values on the two thrust arcs. The secular variation of the right ascension is, therefore, due only to $J_2$:

$$\begin{aligned} \frac{{\mathrm{d}} \bar{\varOmega }}{{\mathrm{d}}t} = -\frac{3}{2} \sqrt{\mu } J_2 {R_{\oplus }}^2 \cos \bar{i}(t) \bar{a}(t)^{-7/2} \ . \end{aligned}$$

(85)

It is possible to write the expression of the variation of $\bar{\varOmega }$ with $\bar{i}$ as

$$\begin{aligned} \frac{{\mathrm{d}}\bar{\varOmega }}{{\mathrm{d}}\bar{i}} = \frac{{\mathrm{d}}\bar{\varOmega }}{{\mathrm{d}}t} \, \frac{{\mathrm{d}} t}{{\mathrm{d}}\bar{i}} = -\frac{3 \pi \mu J_2 R_{\oplus }^2 \bar{a}^{-4} \cos \bar{i}}{4 \epsilon {{\sin }} \bar{\beta } \sin \bar{\psi }} \ . \end{aligned}$$

(86)

Equation (86) can be integrated using the following expression for the variation of the semi-major axis with time (obtained from Eq. 83):

$$\begin{aligned} \bar{a}(t) = \bar{a}_0 \exp \left[ \frac{2 \bar{\psi } (\bar{i}(t) -\bar{i}_0)}{\tan \bar{\beta } \sin \bar{\psi }} \right] \ . \end{aligned}$$

(87)

Substituting Eqs. (87) in (86) and integrating from $\bar{\varOmega }_{1f}$ to $\bar{\varOmega }({\mathrm{ToF}}_1 + {\mathrm{ToF}}_2)$ and from $\bar{i}_0$ to $\bar{i}_f$ results in

$$\begin{aligned} \bar{\varOmega }({\mathrm{ToF}}_1 + {\mathrm{ToF}}_2) = \bar{\varOmega }_{1f} + \frac{k_1(\bar{\beta }, \bar{\psi })}{1+k_2^2} k_3 , \end{aligned}$$

(88)

where

$$\begin{aligned} \begin{aligned}&k_1(\bar{\beta }, \bar{\psi }) = -\frac{3 \pi \mu J_2 R_{\oplus }^2 }{4 \bar{a}_{0}^4 \epsilon \sin \bar{\beta } \sin \bar{\psi }} \exp \left[ \frac{4 \log (\bar{a}_{f}/\bar{a}_{0}) \bar{i}_{0}}{\left( \bar{i}_{f} - \bar{i}_{0} \right) }\right] ,\\&k_2 = {{-}} \frac{4 \log (\bar{a}_{f}/\bar{a}_{0})}{\left( \bar{i}_{f} - \bar{i}_{0} \right) },\\&k_3 = \exp (k_2 \bar{i}_{f}) (k_2 \cos \bar{i}_{f} + \sin \bar{i}_{f}) - \exp (k_2 \bar{i}_{0}) (k_2 \cos \bar{i}_{0} + \sin \bar{i}_{0}) \ . \end{aligned} \end{aligned}$$

(89)

In addition, it is required that $\bar{\varOmega } ({\mathrm{ToF}}_1 + {\mathrm{ToF}}_2) = \bar{\varOmega }_f$. Equation (89) becomes singular when $\left( \bar{i}_{f} - \bar{i}_{0}\right)$ is small. In the case $\bar{i}_{f} = \bar{i}_{0}$, an alternative, non-singular formulation is available. When $\bar{i}_{f} = \bar{i}_{0}$, $\bar{\beta } = 0$ and the expression for $\bar{\varOmega }_{2f}$ can be derived by integrating the expression of ${\mathrm{d}}\bar{\varOmega } /{\mathrm{d}}\bar{a}$ which is obtained from Eqs. (80) and (85):

$$\begin{aligned} { \bar{\varOmega }({\mathrm{ToF}}_1 + {\mathrm{ToF}}_2) = \bar{\varOmega }_{1f} + \frac{3}{32}\frac{\pi \mu J_2 R_{\oplus }^2 \cos \bar{i}}{\varepsilon \psi } \left( \frac{1}{\bar{a}_f^4} - \frac{1}{\bar{a}_0^4}\right) } \ . \end{aligned}$$

(90)

The cost of the transfer can be computed analytically considering that the engine is active during a fraction of the orbital period equal to

$$\begin{aligned} \frac{4 \bar{\psi }}{2 \pi } T = {4 \bar{\psi }} \sqrt{\frac{\bar{a}^3}{\mu }} ; \end{aligned}$$

(91)

therefore,

$$\begin{aligned} \frac{{\mathrm{d}} \Delta V}{{\mathrm{d}}t} = \frac{\epsilon {4 \bar{\psi }} \sqrt{\frac{\bar{a}^3}{\mu }}}{2 \pi \sqrt{\frac{\bar{a}^3}{\mu }}} = \frac{2 \epsilon \bar{\psi }}{\pi } \ . \end{aligned}$$

(92)

The final expression for the cost of the transfer is

$$\begin{aligned} \begin{aligned} \Delta V&= \int _{{\mathrm{ToF}}_1}^{\left( {\mathrm{ToF}}_1 + {\mathrm{ToF}}_2\right) } \frac{{\mathrm{d}} \Delta V}{{\mathrm{d}}t} {\mathrm{d}}\tau = \frac{2 \epsilon \bar{\psi } {\mathrm{ToF}}_2}{\pi } = \\&= \left( \sqrt{\frac{\mu }{\bar{a}_{0}}} - \sqrt{\frac{\mu }{\bar{a}_{f}}} \right) \sqrt{1 + \frac{4 \bar{\psi }^2 \left( \bar{i}_{f} - \bar{i}_{0}\right) ^2}{\sin ^2 \bar{\psi } \log ^2(\bar{a}_{f}/\bar{a}_{0})}} \ . \end{aligned} \end{aligned}$$

(93)

Equation (93) expresses the $\Delta V$ required to change semi-major and inclination under the effect of $J_2$. As such, it can be considered an extension to Eqs. (16), (27) and (53).

8.1.3 Solution method

Given the total time of flight (ToF), a complete solution for the transfer can be computed by solving the following system

$$\begin{aligned} \begin{aligned}&\tan \bar{\beta } = \frac{2 \bar{\psi } \left( \bar{i}_{f} - \bar{i}_{0}\right) }{\sin \bar{\psi } \log (\bar{a}_{f}/\bar{a}_{0})} , \\&\bar{\varOmega }_f = \bar{\varOmega }_0 - \frac{3}{2} \sqrt{\mu } J_2 R_{\oplus }^2 \cos \bar{i}_{0} \bar{a}_{0}^{-7/2} {\mathrm{ToF}}_1 + \frac{k_1(\bar{\beta },\bar{\psi })}{1+k_2^2} k_3 , \\&{\mathrm{ToF}}_{2} = \frac{\pi }{2 \epsilon \bar{\psi }} \left( \sqrt{\frac{\mu }{\bar{a}_{0}}} - \sqrt{\frac{\mu }{\bar{a}_{f}}} \right) \sqrt{1 + \frac{4 \bar{\psi }^2 \left( \bar{i}_{f} - \bar{i}_{0}\right) ^2}{\sin ^2 \bar{\psi } \log ^2(\bar{a}_{f}/\bar{a}_{0})}} ,\\&{\mathrm{ToF}}_1 + {\mathrm{ToF}}_2 = {\mathrm{ToF}}, \end{aligned} \end{aligned}$$

(94)

with respect to the vector $\tilde{\mathbf {u}}$, that is $\bar{\beta }$, $\bar{\psi }$, ${\mathrm{ToF}}_{1}$ and ${\mathrm{ToF}}_{2}$. In particular, substituting the first of Eqs. (94) into the second provides a nonlinear equation in $\bar{\psi }$ that can be solved using an algorithm based on a combination of bisection, secant and inverse quadratic interpolation methods, implemented in the function $\textit{fzero}$ in MATLAB. Once $\bar{\psi }$ is found, the rest of Eqs. (94) allows one to find $\bar{\beta }, {\mathrm{ToF}}_1$ and ${\mathrm{ToF}}_2$.

Figure 12 shows an example of transfer realised using Strategy 1, with time of flight of 600 days and low-thrust acceleration $\epsilon$ equal to $1.5 \ 10^{-4} \text { m}/\text {s}^2$. The variation of the semi-major axis is from 10,000 to 24,200 km, the inclination changes from 51 to $56^{\circ }$, and the right ascension changes from 0 to $150^{\circ }$. The relevant parameters of the solution for the low-thrust control are $\bar{\psi } = 67.02^{\circ }$ and $\bar{\beta } = 14.1^{\circ }$. The times of flight of the two phases are ${\mathrm{ToF}}_1 = 359.1$ days and ${\mathrm{ToF}}_2 = 240.9$ days. The cost of the transfer is $\Delta V = 2.32$ km/s. Figure 12 shows that, during the first phase, the semi-major axis and inclination stay constant, while the right ascension changes because of $J_2$. In the second phase, the semi-major axis and inclination change from their initial to their final values and the variation of the right ascension is such as to obtain, at the end of the transfer, and by means of $J_2$ only, the final desired value.

Fig. 12

Variation of $\bar{a}$, $\bar{i}$ and $\bar{\varOmega }$ (RAAN) during low-thrust transfer with Strategy 1

The evolution of the orbital elements shown in Fig. 12 is obtained using the expressions in Eqs. (77) and (83). For validation, the evolution of the orbital elements is compared to the numerical integration of the Gauss’ equations, using MATLAB ode45 with absolute and relative tolerance equal to $10^{-10}$. Results show that the absolute errors of the orbital elements were limited to the following values: semi-major axis error $< 31$ km; inclination error $< 0.03^{\circ }$; RAAN error $< 1.35^{\circ }$.

8.2 Strategy 2: $(\varDelta \bar{a}, \varDelta \bar{i})$ + $\varDelta \bar{\varOmega }_{\beta }$

Also in the second strategy the transfer is realised in two phases. The first phase, denoted as $(\Delta \bar{a}, \Delta \bar{i})$, is similar to the second phase of Strategy 1. The low-thrust action is applied over two thrust arcs of constant angular span $2 \bar{\psi _1}$, with constant elevation angle $\bar{\beta _1}$, for a time of flight equal to ${\mathrm{ToF}}_1$. In the second phase, of time length ${\mathrm{ToF}}_2$ and denoted as $\Delta \bar{\varOmega }_{\beta }$, an out-of-plane control thrust is used to change $\bar{\varOmega }$ to its final value. During the second phase, the low-thrust action is applied over two thrust arcs of constant angular span $2\bar{\psi _2}$. The vector $\tilde{\mathbf {u}}$ associated to the TPBVP is now $\tilde{\mathbf {u}} = \left[ \bar{\psi _1}, \bar{\beta _1}, \bar{\psi _2}, {\mathrm{ToF}}_1, {\mathrm{ToF}}_2\right] ^T$. The two phases of Strategy 2 are schematically represented in Fig. 13

Fig. 13

Representation of the two phases of Strategy 2. LT stands for low-thrust

The following subsections describe the two phases in more detail. Analytical equations for the variation of the orbital elements during the transfer and for the $\Delta V$ of the transfer are also provided.

8.2.1 First phase

During the first phase, $\bar{a}$ and $\bar{i}$ are changed from their initial values, $\bar{a}_{0}$ and $\bar{i}_{0}$, to their final values, $\bar{a}_f$ and $\bar{i}_f$, as described in Sect. 8.1. The engine is operated on two arcs per orbital revolution of amplitude $2 \bar{\psi }_1$ with elevation angle $\bar{\beta }_1$. The time of flight of the first phase is denoted as ${\mathrm{ToF}}_{1}$. The right ascension at the end of the first phase is computed from Eq. (88) as:

$$\begin{aligned} \bar{\varOmega }_{1f} = \bar{\varOmega }_{0} + \frac{k_1 \left( \bar{\psi _1}, \bar{\beta _1}\right) }{1+k_2^2} k_3 \ . \end{aligned}$$

(95)

The cost, $\Delta V_1$, is computed using Eq. (93).

8.2.2 Second phase

During the second phase, $\bar{\varOmega }$ is changed by applying an out-of-plane thrust action; two thrust arcs of angular span $2 \bar{\psi }_2$ and elevation angle $\left|\bar{\beta }_2 \right|= 90^{\circ }$ are centred at $\nu =90$ and $\nu =270^{\circ }$, as shown in Fig. 14. The sign of $\bar{\beta }$ is opposite on the two thrust arcs.

Fig. 14

Strategy 2, phase 2: thrust arcs centred at $\nu =90$ and $\nu =270^{\circ }$

Using the Gauss’ equation for $\varOmega$, Eqs. (2) and (3), it is possible to obtain the variation of $\varOmega$ with the argument of latitude $\nu$, due to the low-thrust action:

$$\begin{aligned} \frac{{\mathrm{d}}\varOmega }{{\mathrm{d}}\nu } = \frac{\epsilon a^2 \sin \nu }{\mu \sin i} \sin \beta \ . \end{aligned}$$

(96)

The variation of $\varOmega$ in one orbital period, due to the low-thrust action, is

$$\begin{aligned} \Delta \bar{\varOmega }_{2\pi }^{LT} = \int _{\frac{\pi }{2}-\bar{\psi }_2}^{\frac{\pi }{2}+\bar{\psi }_2} \frac{\epsilon a^2 \sin \nu }{\mu \sin i} {\mathrm{d}}\nu - \int _{\frac{3\pi }{2}-\bar{\psi }_2}^{\frac{3\pi }{2}+\bar{\psi }_2} \frac{\epsilon a^2 \sin \nu }{\mu \sin i} d \nu = \frac{4 \epsilon \bar{a}^2 \sin \bar{\psi }_2}{\mu \sin \bar{i}} \ . \end{aligned}$$

(97)

During the second phase, the variation of $\bar{\varOmega }$, due to both the out-of-plane thrust and $J_2$, is

$$\begin{aligned} \frac{{\mathrm{d}}\bar{\varOmega }}{{\mathrm{d}}t} = \frac{2 \epsilon \sin \bar{\psi }_2}{\pi \sin \bar{i}_f} \sqrt{\frac{\bar{a}_f}{\mu }} - \frac{3}{2} \sqrt{\mu } J_2 R_{\oplus }^2 \cos \bar{i}_f \bar{a}_f^{-7/2} \ . \end{aligned}$$

(98)

Equation (98) is obtained considering constant values for semi-major axis and inclination. The semi-major axis does not change because $\left|\bar{\beta } \right|= 90^{\circ }$, while the variation of the inclination is zero over one orbital period because the effect of the out-of-plane thrust on the inclination is equal and opposite on the two thrust arcs. The variation with time of $\bar{\varOmega }$ is

$$\begin{aligned} \bar{\varOmega }(t) = \bar{\varOmega }_{1f} + \left( \frac{2 \epsilon \sin \bar{\psi }_2}{\pi \sin \bar{i}_f} \sqrt{\frac{\bar{a}_f}{\mu }} - \frac{3}{2} \sqrt{\mu } J_2 R_{\oplus }^2 \cos \bar{i}_f a_f^{-7/2} \right) (t - {\mathrm{ToF}}_1) \ , \end{aligned}$$

(99)

with $t \in [{\mathrm{ToF}}_1, {\mathrm{ToF}}_1 + {\mathrm{ToF}}_2]$. The semi-amplitude of the thrust arcs can be computed from Eqs. (99) and (95) as:

$$\begin{aligned} \sin \bar{\psi }_2 = \left( \bar{\varOmega }_{f} - \bar{\varOmega }_{1f} + \frac{3}{2} \sqrt{\mu } J_2 R_{\oplus }^2 \cos \bar{i}_{f} \bar{a}_{f}^{-7/2} {\mathrm{ToF}}_2 \right) \left( \frac{2 \ \epsilon }{\pi \sin \bar{i}_{f}} \sqrt{\frac{\bar{a}_f}{\mu }} {\mathrm{ToF}}_2 \right) ^{-1} \ . \end{aligned}$$

(100)

The cost associated to the variation of $\bar{\varOmega }$ can be computed analytically, following a procedure similar to the one presented in Sect. 8.1, as

$$\begin{aligned} \Delta V_2 = \frac{2 \epsilon \bar{\psi }_2}{\pi } {\mathrm{ToF}}_2 , \end{aligned}$$

(101)

where ${\mathrm{ToF}}_2$ is derived from Eq. (100). The total cost is $\Delta V = \Delta V_1 + \Delta V_2$. Please note that Eq. (101) can be considered an extension to Eq. (57).

8.2.3 Solution method

When the combined transfer $(\Delta \bar{a}, \Delta \bar{i})$ + $\Delta \bar{\varOmega }_{\beta }$ has to be realised in a total time of flight ToF, the equations defined above are not in a sufficient number to define a unique solution. There are indeed five unknowns ($\bar{\psi }_1$, $\bar{\beta }_1$, $\bar{\psi }_2$, ${\mathrm{ToF}}_{1}$ and ${\mathrm{ToF}}_{2}$), while the available equations are four (Eqs. (82), (84), (100) and ${\mathrm{ToF}}_{1} + {\mathrm{ToF}}_{2} = {\mathrm{ToF}}$):

$$\begin{aligned} \begin{aligned}&\tan \bar{\beta _1} = \frac{2 \bar{\psi _1} \left( \bar{i}_{f} - \bar{i}_{0}\right) }{\sin \bar{\psi _1} \log (\bar{a}_{f}/\bar{a}_{0})} , \\&{\mathrm{ToF}}_{1} = \frac{\pi }{2 \epsilon \bar{\psi _1}} \left( \sqrt{\frac{\mu }{\bar{a}_{0}}} - \sqrt{\frac{\mu }{\bar{a}_{f}}} \right) \sqrt{1 + \frac{4 \bar{\psi _1}^2 \left( \bar{i}_{f} - \bar{i}_{0}\right) ^2}{\sin ^2 \bar{\psi _1} \log ^2(\bar{a}_{f}/\bar{a}_{0})}}, \\&\sin \bar{\psi }_2 = \left[ \left( \bar{\varOmega }_{f} - \bar{\varOmega }_{0} - \frac{k_1\left( \bar{\psi _1}, \bar{\beta _1}\right) }{1+k_2^2} k_3 + \frac{3}{2} \sqrt{\mu } J_2 R_{\oplus }^2 \cos \bar{i}_{f} \bar{a}_{f}^{-7/2} {\mathrm{ToF}}_2 \right) \right. \\&\left. \left( \frac{2 \ \epsilon }{\pi \sin \bar{i}_{f}} \sqrt{\frac{\bar{a}_f}{\mu }} {\mathrm{ToF}}_2 \right) ^{-1} \right] ,\\&{\mathrm{ToF}}_1 + {\mathrm{ToF}}_2 = {\mathrm{ToF}} .\\ \end{aligned} \end{aligned}$$

(102)

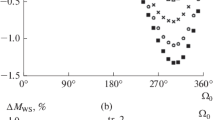
It is possible, however, to define different arbitrary values of ${\mathrm{ToF}}_{1} < {\mathrm{ToF}}$ and compute the corresponding values of $\bar{\psi }_1$, $\bar{\beta }_1$, $\bar{\psi }_2$ and ${\mathrm{ToF}}_{2}$. In particular, it is possible to find a ${\mathrm{ToF}}_1$ such that the $\Delta V$ of the transfer is the minimum possible value. An example of transfer realised with this strategy is shown in Fig. 15. The initial and final orbital elements are those used for the example reported in Sect. 8.1. The minimum $\Delta V$ transfer is realised with $\Delta V = 2.31$ km/s and the parameters of the low-thrust control are $\bar{\psi }_1 = 33.75^{\circ }$, $\bar{\beta }_1 = 11.82^{\circ }$ and $\bar{\psi }_2 = 0.29^{\circ }$. The times of flight of the two phases are ${\mathrm{ToF}}_1 = 474.07$ days and ${\mathrm{ToF}}_2 = 125.93$. The variation of the orbital elements is reported in Fig. 15. During the first phase, the semi-major axis and inclination change from their initial to their final values while the variation of the right ascension is due only to $J_2$. Note how the drift of $\bar{\varOmega }$ is slower than in the example reported in Fig. 12. This is because the semi-major axis increases considerably during the first phase, thus reducing ${\mathrm{d}}\bar{\varOmega }/{\mathrm{d}}t$. In the second phase the semi-major axis and inclination remain constant while the right ascension changes because of the out-of-plane thrust and because of $J_2$. The minimum $\Delta V$ transfer corresponds to a small value of $\bar{\psi }_2$, meaning that the out-of-plane thrust, more expensive than the in-plane thrust, is applied on very short arcs.

Fig. 15

Variation of $\bar{a}$, $\bar{i}$ and $\bar{\varOmega }$ during low-thrust transfer with Strategy 2

The transfer shown in Fig. 15 is the one characterised by the lowest value of $\Delta V$, among all the possible solutions. The $\Delta V$s obtained for different values of ${\mathrm{ToF}}_1$ are reported in Fig. 16. Figure 17 shows the variation of the right ascension during the transfer for two possible solutions: ${\mathrm{ToF}}_1 =$ 474.07 days and ${\mathrm{ToF}}_1$ = 505 days. The higher $\Delta V$ obtained when ${\mathrm{ToF}}_1=$ 505 days is due to the greater variation of $\bar{\varOmega }$ obtained with out-of-plane thrust during the second phase. $\bar{\psi }_2$ is indeed equal to $61.66^{\circ }$ when ${\mathrm{ToF}}_1=$ 505 days. For Strategy 2, the comparison with the numerical integration of the Gauss’ equations shows that the absolute errors of the orbital elements during the transfer are limited to the following values: semi-major axis error $< 8$ km; inclination error $< 3.4 \ 10^{-4}$deg; RAAN error $< 0.35^{\circ }$.

Fig. 16

$\Delta V$s for different values of ${\mathrm{ToF}}_1$

Fig. 17

Variation of $\bar{\varOmega }$ during the transfer for ${\mathrm{ToF}}_1=$ 474.07 days and ${\mathrm{ToF}}_1$ = 505 days

8.3 Strategy 3: $(\varDelta \bar{a}, \varDelta \bar{\varOmega }_{J_2})$ + $\varDelta \bar{i}$

Strategy 3 is composed of two phases: the first one changes semi-major axis and right ascension and is denoted as $(\Delta \bar{a}, \Delta \bar{\varOmega }_{J_2})$, while the second one uses the low-thrust acceleration to change the inclination, and is denoted as $\Delta \bar{i}$. During the second phase, $\bar{\varOmega }$ changes because of $J_2$. The first phase has time span ${\mathrm{ToF}}_1$ and makes use of a low-thrust action on two thrust arcs of constant semi-amplitude $\bar{\psi }_1$, while the second phase has time span ${\mathrm{ToF}}_2$ and uses arcs of constant semi-amplitude $\bar{\psi }_2$ per orbit. The vector of unknown variables is $\tilde{\mathbf {u}} = \left[ \bar{\psi _1}, \bar{\psi _2}, {\mathrm{ToF}}_1, {\mathrm{ToF}}_2\right] ^T$. The strategy is schematically shown in Fig. 18. More details are given hereafter.

Fig. 18

Representation of the two phases of Strategy 3. LT stands for low-thrust

8.3.1 First phase

The transfer in the first phase of Strategy 3 is analogous to the transfer during the second phase of Strategy 1, with $\bar{\beta }_1=0$. During the first phase, a tangential thrust is used to increase the semi-major axis from $\bar{a}_{0}$ to $\bar{a}_{f}$. The low-thrust engine is operated during two thrust arcs per revolution, of semi-amplitude $\bar{\psi }_1$. Considering Eq. (84) with $\bar{\beta }=0$, the time of flight for the first phase of the transfer is given by

$$\begin{aligned} {\mathrm{ToF}}_1 = \frac{\pi }{2 \epsilon \bar{\psi }_1} \left( \sqrt{\frac{\mu }{\bar{a}_{0}}} - \sqrt{\frac{\mu }{\bar{a}_{f}}} \right) \ . \end{aligned}$$

(103)

The cost of this phase can be computed analytically using Eq. (93) with $\bar{\beta }=0$:

$$\begin{aligned} \Delta V_1 = \sqrt{\frac{\mu }{\bar{a}_{0}}}- \sqrt{\frac{\mu }{\bar{a}_{f}}} \ . \end{aligned}$$

(104)

Equation (104) extends Eqs. (16), (27) and (57). The right ascension at the end of the transfer is derived by integrating the expression of ${\mathrm{d}}\bar{\varOmega }/{\mathrm{d}}\bar{a}$ which is obtained from the equations for ${\mathrm{d}}\bar{\varOmega }/{\mathrm{d}}t$ and ${\mathrm{d}}\bar{a}/{\mathrm{d}}t$ with $\bar{i}(t) = \bar{i}_0$ (refer to Sect. 2). This results in:

$$\begin{aligned} \bar{\varOmega }_{1f} = \bar{\varOmega }_{0} + \frac{3}{32} \frac{\mu J_2 R_{\oplus }^2 \cos \bar{i}_{0}}{\epsilon \bar{\psi }_1} \left( \frac{1}{\bar{a}_{f}^4} - \frac{1}{\bar{a}_{0}^4} \right) \ . \end{aligned}$$

(105)

8.3.2 Second phase

The transfer in the second phase of Strategy 3 is analogous to the transfer during the second phase of Strategy 1, with $\bar{\beta }=90^{\circ }$. The thrust is applied during two thrust arcs per revolution, of semi-amplitude $\bar{\psi }_2$, with elevation angle $\bar{\beta }_2 = 90^{\circ }$. This causes the inclination to change from $\bar{i}_{0}$ to $\bar{i}_{f}$, while the semi-major axis stays constant at $\bar{a}_f$. The time required can be computed integrating the equation for ${\mathrm{d}}\bar{i}/{\mathrm{d}}t$ (Eq. 80) from $\bar{i}_0$ to $\bar{i}_f$, using $\bar{a}=\bar{a}_f$:

$$\begin{aligned} {\mathrm{ToF}}_{2} = \frac{\pi }{2 \epsilon }\frac{\bar{i}_{f} - \bar{i}_{0}}{ \sin \bar{\psi }_2} \sqrt{\frac{\mu }{\bar{a}_f}} \ . \end{aligned}$$

(106)

The cost of this phase is derived from Eqs. (106) and (92):

$$\begin{aligned} \Delta V_2 = \frac{\bar{\psi }_2}{\sin \bar{\psi }_2} \sqrt{\frac{\mu }{\bar{a}_{f}}} \left( \bar{i}_{f} - \bar{i}_{0}\right) \ . \end{aligned}$$

(107)

Equation (107) extends Eq. (53). The variation of the right ascension is obtained from Eq. (86) with $\bar{a}=\bar{a}_f$:

$$\begin{aligned} \bar{\varOmega }_{2f} = \bar{\varOmega }_{1f} + \frac{3}{4} \frac{\pi \mu J_2 R_{\oplus }^2}{\epsilon \bar{a}_{f}^4 \sin \bar{\psi }_2} \left( \sin \bar{i}_{0} - \sin \bar{i}_{f}\right) \ . \end{aligned}$$

(108)

Fig. 19

Variation of $\bar{a}$, $\bar{i}$ and $\bar{\varOmega }$ (RAAN) during low-thrust transfer with Strategy 3

Fig. 20

Variation of $\bar{a}$, $\bar{i}$ and $\bar{\varOmega }$ during low-thrust transfer with strategies 1, 2 and 3

Fig. 21

$\Delta V$s for different values of ${\mathrm{ToF}}_{{\mathrm{total}}}$

8.3.3 Solution method

A complete transfer using Strategy 3 can be defined by solving the following system of equations, for a given time of flight ToF, with $\bar{\psi }_1$, $\bar{\psi }_2$, ${\mathrm{ToF}}_{1}$ and ${\mathrm{ToF}}_{2}$ as unknowns:

$$\begin{aligned} \begin{aligned}&{\mathrm{ToF}}_1 = \frac{\pi }{2 \epsilon \bar{\psi }_1} \left( \sqrt{\frac{\mu }{\bar{a}_{0}}} - \sqrt{\frac{\mu }{\bar{a}_{f}}} \right) , \\&{\mathrm{ToF}}_{2} = \frac{\pi }{2 \epsilon }\frac{\bar{i}_{f} - \bar{i}_{0}}{ \sin \bar{\psi }_2} \sqrt{\frac{\mu }{\bar{a}_f}} , \\&\bar{\varOmega }_{f} = \bar{\varOmega }_{0} + \frac{3}{32} \frac{\mu J_2 R_{\oplus }^2 \cos \bar{i}_{0}}{\epsilon \bar{\psi }_1} \left( \frac{1}{\bar{a}_{f}^4} - \frac{1}{\bar{a}_{0}^4} \right) + \frac{3}{4} \frac{\pi \mu J_2 R_{\oplus }^2}{\epsilon \bar{a}_{f}^4 \sin \bar{\psi }_2} \left( \sin \bar{i}_{0} - \sin \bar{i}_{f}\right) , \\&{\mathrm{ToF}}_1 + {\mathrm{ToF}}_2 = {\mathrm{ToF}} .\\ \end{aligned} \end{aligned}$$

(109)

An example of transfer realised with this strategy is shown in Fig. 19. The transfer requires $\Delta V = 2.6201$ km/s, $\bar{\psi }_1 = 34.21^{\circ }$, $\bar{\psi }_2 = 17.56^{\circ }$, ${\mathrm{ToF}}_1 =457.7$ days and ${\mathrm{ToF}}_2 = 142.3$ days. There is no variation of the inclination during the first phase, while during the second phase the semi-major axis stays constant and the inclination and right ascension change reaching their final values. For Strategy 3, the comparison with the numerical integration of the Gauss’ equations shows that the absolute errors of the orbital elements during the transfer are limited to the following values: semi-major axis error $< 8$ km; inclination error $< 3.4 \ 10^{-4}$deg; RAAN error $< 0.3^{\circ }$.

8.4 Comparison of the three strategies

Figure 20 shows the variation of the orbital elements during the example of transfer considered in the previous sections, for the three proposed strategies. Figure 21 shows the $\Delta V$ required to realise the transfer defined in Sect. 8.1.3, for different values of the times of flight and using the three proposed strategies. For Strategy 2, for which a unique solution does not exist, the solutions plotted are the ones corresponding to the values of ${\mathrm{ToF}}_1$ and ${\mathrm{ToF}}_2$ providing the lowest value of the $\Delta V$ for that transfer. The fact that, for Strategy 2, ${\mathrm{ToF}}_1$ and ${\mathrm{ToF}}_2$ are chosen to minimise the $\Delta V$, explains the noisy behaviour of the curve relative to Strategy 2 in Fig. 21.

Results show that the first and second strategies are those giving the lowest $\Delta V$s.

9 Conclusions

This paper has presented a number of analytical equations for the quick, approximated calculation of the $\Delta V$ cost of low-thrust orbital transfers. The same equations provide an approximation to the variation of the mean orbital elements with time.

In particular, the first part of the paper collects a number of analytical solutions, available in the literature, for the variation of the orbital elements with a low-thrust acceleration, in the absence of orbital perturbations. The formulae in this collection have been extended by adding new analytical expressions for the total transfer $\Delta V$ and the variations of the orbital elements. The most relevant novel equations have been presented as propositions. Two tables have been presented in Appendix to summarise the available analytical solutions. Results, on the range of case studies investigated in this paper, have shown that for most of the analytical solutions the maximum relative error in the $\Delta V$ estimate is 0.04 $\%$. Only in one case, the maximum error is higher than 0.04 $\%$. The low relative error and the fact that the computation of the $\Delta V$ simply requires the evaluation of an inexpensive analytical formula, allows one to rapidly analyse a large number of cases with good accuracy. The use of these formulae is limited by the working assumptions on the control laws and the use of standard Keplerian elements. Furthermore, the use of mean elements implies that these formulae are more appropriate to study long spirals than rendezvous where a precise calculation of the osculating elements is required.

Table 2 Summary of low-thrust analytical solutions

Table 3 Taxonomy of analytical low-thrust solutions. For solutions 6 and 7, $\bar{e}=0$ and therefore $\bar{\omega }$ is not defined

By capitalising on the formulae and methodology presented in the first part of the paper, the second part introduced three strategies to obtain the simultaneous variation of semi-major axis, inclination and right ascension of the ascending nodes of circular orbits, by combining the effect of a low-thrust acceleration with the one of the second zonal harmonic of the gravitational potential, $J_2$. Also in this case the validation of the formulae by direct numerical integration of Gauss’ equations has shown that the error remains contained in all the cases analysed in this paper. Thus, the three strategies, and associated analytical expressions, provide a quick and accurate estimation of the $\Delta V$ when a low-thrust spiral and natural dynamics can be combined to achieve the desired transfer.

In conclusion, the set of equations presented throughout this paper represent a fast and sufficiently accurate tool to obtain a preliminary estimation of the $\Delta V$ cost of low-thrust spiral transfers.

Summary of the analytical solutions with no perturbations

Table 2 summarises the analytical solutions presented in this paper for the orbit transfer from $(\bar{a}_0, \bar{e}_0, \bar{i}_0, \bar{\varOmega }_0, \bar{\omega }_0)$ to $(\bar{a}_f, \bar{e}_f, \bar{i}_f, \bar{\varOmega }_f,\bar{\omega }_f)$, without orbital perturbations. For each solution, the number of the equations which give the thrust angles, the time evolution of the orbital elements and the $\Delta V$ are given. When an orbital element does not change during the transfer this is directly reported in the table giving its initial value. The last column gives the number of the section where the solution is described in detail. N.A. stands for either not available or not applicable. Table 3 shows, for each analytical solution, if it was obtained computing the maximum instantaneous rate of change of the orbital elements or using other types of guidance laws. It shows, moreover, which orbital elements are to be changed and which ones stay constant during the transfer. The last column reports if new analytical equations were derived in this paper.