Computing Dynamic User Equilibrium on Large-Scale Networks Without Knowing Global Parameters

Abstract

Dynamic user equilibrium (DUE) is a Nash-like solution concept describing an equilibrium in dynamic traffic systems over a fixed planning period. DUE is a challenging class of equilibrium problems, connecting network loading models and notions of system equilibrium in one concise mathematical framework. Recently, Friesz and Han introduced an integrated framework for DUE computation on large-scale networks, featuring a basic fixed-point algorithm for the effective computation of DUE. In the same work, they present an open-source MATLAB toolbox which allows researchers to test and validate new numerical solvers. This paper builds on this seminal contribution, and extends it in several important ways. At a conceptual level, we provide new strongly convergent algorithms designed to compute a DUE directly in the infinite-dimensional space of path flows. An important feature of our algorithms is that they give provable convergence guarantees without knowledge of global parameters. In fact, the algorithms we propose are adaptive, in the sense that they do not need a priori knowledge of global parameters of the delay operator, and which are provable convergent even for delay operators which are non-monotone. We implement our numerical schemes on standard test instances, and compare them with the numerical solution strategy employed by Friesz and Han.

1 Introduction

This paper is concerned with a class of models known as Dynamic User Equilibrium (DUE). DUE problems have been studied within the broader context of Dynamic Traffic Assignment (DTA), which is concerned with modeling time-varying traffic flows consistent with established traffic flow theory. DTA models are greatly influenced by Wardrop’s equilibrium principle (Wardrop 1952), which is seen as a Nash-like equilibrium condition in an aggregative game:

• (a) Wardrop’s first principle, also known as the user optimality principle, states that road segments used in an equilibrium should display the same travel costs (i.e. delay);

• (b) Wardrop’s second principle, known as the system’s optimality principle, assumes that drivers behave cooperatively, in making travel decisions so that the over system costs (aggregate delays) are minimized.

Logically, the behavioral maxims (a) and (b) are disconnected, and a substantive literature in transportation research is concerned with the design of computational architectures aligning these potentially conflicting principles. Since the seminal work of Merchant and Nemhauser (1978a) and Merchant and Nemhauser (1978b), dynamic extensions of Wardrop’s principles have paved the way to the introduction of notions like DUE and Dynamic System Optimal (DSO) models. For comprehensive reviews of DTA models, we refer to Peeta and Ziliaskopoulos (2001), Jeihani (2007), and Wang et al. (2018).

In the last two decades there have been many efforts to develop a theoretically and sound formulation of DUE, acceptable to modelers and practitioners alike. Analytical DUE models tend to be of two varieties: (1) Route Choice (RC) DUE (Friesz et al. 1989; Merchant and Nemhauser 1978a; 1978b; Zhu and Marcotte 2000), and (2) Simultaneous Route and Departure Choice (SRDC) DUE (Friesz et al. 1993; Friesz et al. 2001; Friesz et al. 2011; Ran et al. 1996). Both types of DUE rest on two pillars:

• 1. A mathematical notion of equilibrium;

• 2. A model of network performance, based on some physical laws describing traffic flows.

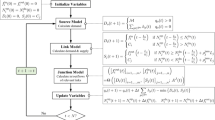
The second pillar is known in the literature as Dynamic Network Loading (DNL). Equilibrium is usually expressed in terms of Wardrop’s first principle. Mathematical approaches to describe equilibrium contain variational inequalities (VI) (Friesz et al. 1993; Zhu and Marcotte 2000), nonlinear complementarity problems (Pang et al. 2012; Han et al. 2011), differential variational inequalities (Pang and Stewart 2008; Friesz and Mookherjee 2006) and fixed point problems (Friesz et al. 2011). In this paper we choose the VI formulation of DUE, and our aim is to advance computational techniques for the practical solution of DUE. Our research builds on, and extends, recent advances in computational approaches to DUE reported in Han et al. (2019). As is well known computing user equilibrium is a challenging task; Its main complication arises since it constitutes an interconnected computational procedure, coupling equilibrium computation with DNL. The DNL, which could be understood as the first layer of the problem, aims at describing the spatial and temporal evolution of traffic flows on a network that is consistent with established route and departure choices of travelers. This is done by formulating appropriate dynamics to flow propagation, flow conservation, link delay, and path delay on a network level. In general, DNL models have the following components:

• 1. Some form of link and/or path dynamics;

• 2. An computationally-friendly relationship between flow/speed/density and link traversal time;

• 3. Flow propagation constraints;

• 4. A model of junction dynamics (Riemann Solvers) and delays;

• 5. A model of path traversal times, and

• 6. Appropriate initial conditions.

DNL generates the path delay operator, which is the key input when computing an equilibrium given the delays on user routes (travel costs). This is the second layer of the problem, and of main interest in this paper. At this layer one has to use some equilibrium solver, whose performance depends significantly on the information we have about the structural properties of the delay operator. However, since the delay operator is itself the result of a computational procedure, it is not available in closed form, and thus one is confronted essentially with a black-box upon which we can assume whatever we find useful, but the empirical validation of these assumptions is very hard. It is thus of utmost importance to have at our disposal efficiently implementable algorithms which are:

• (i) Adaptive to arrival of new information about unknown global parameters;

• (ii) Provably convergent under mild monotonicity assumptions.

We argue that, up to now, none of the perceived DUE solvers meet both of these criteria. To support this claim, we present Table 1, where the current state-of-the-art in DUE computation is summarized.¹

Table 1 Computational algorithms for DUE (adapted from Han et al. (2019))

We infer from Table 1 that known algorithmic strategies for solving the DUE problem require knowledge about the global Lipschitz constant and some sort of monotonicity of the path delay operator. Since the delay operator is not given to us in closed form, both assumptions are practically not verifiable. Algorithmic strategies which are provably convergent without explicit knowledge of these global properties, are thus to be seen as a very valuable contribution.

1.1 Our Contributions

This paper makes a significant step-ahead relative to the perceived computational literature on DUE, by describing two numerical algorithms acting directly in infinite-dimensional Hilbert spaces. Our algorithms share the following features:

• (i) Strong convergence to a single user equilibrium;

• (ii) Adaptive step-size choices without the need to know global Lipschitz parameters of the delay operator;

• (iii) Provably convergent under a plain pseudo-monotonicity assumption on the path delay operator.

• (iv) Include inertial and relaxation effects to potentially speed up the convergence.

While items (ii) and (iii) don’t need much motivation, our emphasis on strongly convergent methods seems to be somewhat pedantic at first sight, so it deserves some words of explanation.

In infinite-dimensional settings strongly convergent iterative schemes are much more desirable than weakly convergent ones since strong convergence translates the physically tangible property that the energy ∥h_n − h^∗∥² of the error between the iterate h_n and a solution h^∗ eventually becomes arbitrarily small. Of course, any numerical solution technique designed for solving a problem in infinite dimensions must be applied to a finite-dimensional approximation of the problem. Exactly in such situations strongly convergent methods are extremely powerful, because they guarantee stability with respect to numerical discretization. In fact, Güler (1991) demonstrated that strongly convergent schemes might even exhibit faster convergence rates as compared to their weakly convergent counterparts. It seems therefore fair to say that strong convergence is an extremely desirable property of solution schemes, with clearly observable physical consequences on the performance and stability of algorithms. As a matter of fact, Friesz et al. (2011) employs a projected gradient iteration of Halpern type (Halpern 1967; Bauschke and Combettes 2016), which forces trajectories to converge strongly to some DUE.

Adaptivity in the step-size policy frees us from any unavailable information about the global Lipschitz constant of the delay operator. It allows us to tune the step size on-the-fly and guarantees convergence for general pseudo-monotone operators with good performance properties.

Operator splitting methods with inertia and relaxation have received quite some attention in recent years, see e.g. Lorenz and Pock (2015), Iutzeler and Hendrickx (2019), and Attouch and Cabot (2019). These schemes are motivated by Nesterov’s accelerated method (Nesterov 2004), and therefore the main motivation for inertial methods is to speed up the convergence rate. To the best of our knowledge this is the first time that inertial and relaxation effects are investigated in the context of DUE computation and under weak pseudo-monotonicity assumptions.

Remark 1

In previous work (Duvocelle et al. 2019) investigated the DUE with a strongly convergent FBF variant. This paper replaces and significantly extends our previous work by the explicit consideration of inertial effects.

1.2 Organization of the Paper

Sections 2 and 3 describe user equilibrium and the DNL procedure we use in our numerical experiments. In setting up these two layers we follow closely Han et al. (2019). Section 4 describes the algorithms we construct and investigate in this paper. Building on the MATLAB toolbox publicly available at https://github.com/DrKeHan/DTA and documented in Han et al. (2019). We report the outcomes of our experiments in Section 5. Technical facts and proofs are organized in Sections 6.1 and 6.2.

2 Dynamic User Equilibrium

We introduce a few notations and terminologies for the ease of presentation below.

• $\mathcal {P}$: set of paths in the network.

• $\mathcal {W}$: set of origin-destination (O-D) pairs in the network.

• Q_w: fixed O-D demand between $w\in \mathcal {W}$.

• $\mathcal {P}_{w}$: subset of paths that connect O-D pair w.

• t: continuous time parameter in the fixed time horizon [t₀,t₁].

• h_p(t): departure rate along path p at time t.

• h(t): complete profile of departure rates $h(t)=\{h_{p}(t);p\in \mathcal {P}\}$.

• A_p(t,h): effective travel cost along path p with departure time t under the path profile h.

• ν_w(h): minimum travel cost between O-D pair $w\in \mathcal {W}$ for all paths and all departure times.

2.1 Formulation of DUE as a Variational Inequality

Let [t₀,t₁] be a fixed planning horizon. We are given a connected directed graph $G=(\mathcal {V},\mathcal {E})$ with finite set of vertices $\mathcal {V}$, representing traffic intersections (junctions) and arc set $\mathcal {E}$, representing road segments. A path p in the graph G is identified with a non-repeating finite sequence of links it traverses, i.e. p = {I₁,I₂,…,I_m(p)}, where m(p) is the number of links in this path. We denote the set of all paths by $\mathcal {P}$, and set $\mathsf {H}:= \mathbb {R}^{|{\mathcal {P}}|}$. We are interested in paths which connect a set of distinguished vertices acting as the origin-destination (O-D) pairs in our graph. We are given N distinct O-D pairs denoted as w₁,…,w_N, where each $w_{i}=(o_{i},d_{i})\in \mathcal {V}$. Call $\mathcal {W}:=\{w_{1},\ldots ,w_{N}\}$ the collection of all O-D pairs, and let us denote the set of paths connecting the O-D pair w by $\mathcal {P}_{w}\subseteq \mathcal {P}.$ For each O-D pair $w\in \mathcal {W}$ we are given an exogenous demand Q_w > 0; This represents the number of drivers who have to travel from the origin to the destination described by w. The list $Q=(Q_{w})_{w\in \mathcal {W}}$ is often called the trip table. In DUE modeling, the single most crucial ingredient is the path delay operator, which maps a given vector of departure rates (path flows) h to a vector of path travel times. We stipulate that path flows are square integrable functions over the planning horizon, so that $h_{p}\in L^{2}([t_{0},t_{1}];\mathbb {R}_{+})$ and $h=(h_{p};p\in \mathcal {P})\in {\mathscr{H}}:= L^{2}([t_{0},t_{1}];\mathsf {H})$. To measure the delay of drivers on paths, we introduce the operator $D:{\mathscr{H}}\to {\mathscr{H}},h\mapsto D(h)$, with the interpretation that D_p(t,h) is the path travel time of a driver departing at time t from the origin of path p, and following this path throughout. This operator is the result of some DNL procedure, which is an integrated subroutine in the dynamic traffic assignment problem. See Section 3 for a description of the DNL used in our computational experiments.

On top of path delays, we consider penalty terms of the form ϕ(t + D_p(t,h) − τ), penalizing all arrival times different from the target time τ > 0 (i.e. the usual time of a trip on the O-D pair w). The function $\phi :[-\infty ,\infty )\to [0,\infty ]$ should be monotonically increasing with ϕ(a) > 0 for a > 0 and ϕ(a) = 0 for a ≤ 0. Define the effective delay operator as

$$ A_{p}(t,h):=D_{p}(t,h)+\phi(t+D_{p}(t,h)-\tau). $$

(1)

We thus obtain an operator $A:{\mathscr{H}}\to {\mathscr{H}}$, mapping each profile of path departure rates h to effective delays $A(h)=\{A_{p}(t,h);t\in [t_{0},t_{1}]\}\in {\mathscr{H}}$.

We follow the perceived DUE literature, and stipulate that Wardrop’s first principle holds: Users of the network aim to minimize their own travel time, given the departure rates in the system. Thus, a user equilibrium is envisaged, where the delays (interpreted as costs) of all travelers in the same O-D pair are equal, and no traveler can lower his/her costs by unilaterally switching to a different route. To put this behavioral axiom into a mathematical framework, we first formulate the meaning of “minimal costs” in the present Hilbert space setting. Recall the essential infimum of a measurable function $g:[t_{0},t_{1}]\to \mathbb {R}$ as $\text {ess inf}\{g(t): t\in [t_{0},t_{1}]\}=\sup \left \{x\in \mathbb {R}: \mathsf {Leb}(\{s\in [t_{0},t_{1}]:g(s)<x\})=0\right \},$ where Leb(⋅) denoted the Lebesgue measure on the real line. Given a profile $h\in {\mathscr{H}}$, define

$$ \begin{array}{@{}rcl@{}} \nu_{p}(h)&:=&\text{ess inf}\{A_{p}(t,h): t\in[t_{0},t_{1}]\}\qquad\forall p\in\mathcal{P}, \text{ and } \end{array} $$

(2)

$$ \begin{array}{@{}rcl@{}} \nu_{w}(h)&:=& \underset{p\in\mathcal{P}_{w}}{\min}\nu_{p}(h)\qquad\forall w\in\mathcal{W}. \end{array} $$

(3)

On top of minimal costs, we have to restrict the set of departure rates to functions satisfying a basic flow conservation property. Specifically, insisting that all trips are realized, we naturally define the set of feasible flows as

$$ \mathcal{X}:=\left\{f\in\mathcal{H}: \underset{p\in\mathcal{P}_{w}}{\sum}{\int}_{t_{0}}^{t_{1}}f_{p}(t) d t=Q_{w}\quad\forall w\in\mathcal{W}\right\}. $$

(4)

The set of feasible flows $\mathcal {X}$ is sequentially closed and convex, but not sequentially compact (i.e. path departure rates are note a-priori assumed to be bounded as the above definition involves Lebesgue-integrable functions). We are now ready to give our first definition of user equilibrium.

Definition 1

A profile of departure rates $h^{\ast }\in {\mathscr{H}}$ is a DUE if

• $h^{\ast }\in \mathcal {X}$, and

• $h^{\ast }_{p}(t)>0,p\in \mathcal {P}_{w}\Rightarrow A_{p}(t,h^{\ast })=\nu _{w}(h^{\ast }).$

We denote by ${\varOmega }\subset \mathcal {X}$ the (possibly empty) set of DUE.

In Friesz et al. (1993) it is observed that the definition of DUE can be formulated equivalently as a variational inequality $\text {VI}(A,\mathcal {X})$: A flow $h^{\ast }\in \mathcal {X}$ is a DUE if

$$ \langle{A(h^{\ast}),h-h^{\ast}}\rangle\geq 0\qquad\forall h\in\mathcal{X} $$

(5)

This notion of equilibrium is very useful, since it allows us to apply a large variety of algorithms to solve $\text {VI}(A,\mathcal {X})$, and in fact it can be seen as the basis of most of the computational approaches to DUE. We now spell out sufficient conditions guaranteeing existence of DUE.

Assumption 1

• The penalty function $\phi :[t_{0},t_{1}]\to \mathbb {R}_{+}$ is continuous and there exists Δ > − 1 such that

  $$ \phi(a)-\phi(b)\geq{\varDelta}(a-b)\text{ for all }t_{0}\leq a<b\leq t_{1}. $$

  (6)

• The DNL satisfies the FIFO principle and each link has finite capacity.

• The effective delay operator is weak-to-weak continuous on bounded subsets of $\mathcal {X}$.

Theorem 1

Under Assumption 1 the DUE problem Eq. 5 has a solution, i.e. Ω≠∅.

Proof

See Han et al. (2013).

□

The construction of the delay operator requires a specification of a DNL (i.e. traffic flow generation). We focus in this work on a macroscopic model of network loading based on fluid dynamic approximations of traffic flow on networks, known as the Lighthill-Whitham-Richards (LWR) model (Lighthill and Whitham 1955; Richards 1956). The LWR model is able to describe the physics of kinematic waves (e.g. shock waves, rarefaction waves), and allows network extension that capture the formation and propagation of vehicle queues as well as vehicle spill-back. We will formulate the LWR-based DNL as a system of partial differential algebraic equations (PDAE), which uses vehicle density and queues as the unknown variables, and computes link dynamics, flow propagation, and path delay for any given vector of path departure rates.

2.2 The Differential Variational Inequality Formulation

It has been observed in Friesz et al. (2001) that DUE can be equivalently formulated as a differential variational inequality (Pang and Stewart 2008). From an algorithmic point-of-view this relation is interesting as it allows us to use time-stepping methods to compute approximate user equilibria Friesz et al. (2011) and Friesz and Mookherjee (2006). Independent of algorithmic considerations, we regard this identification as an important conceptual insight, and thus deserves some remarks here. The precise connection between DVI and DUE goes as follows:

Define the vector-valued function $x:[t_{0},t_{1}]\to \mathbb {R}^{|{\mathcal {W}}|},t\mapsto x(t)=\{x_{w}(t);w\in \mathcal {W}\}$ as the state trajectory of a controlled dynamical system with the interpretation that x_w(t) is the cumulative traffic up to time t on paths connecting the origin-destination pair $w\in \mathcal {W}$. The definition of this state-variable requires that its dynamic evolution is described by the linear differential equation

$$ \frac{ d}{ d t}x_{w}(t)=\underset{p\in\mathcal{P}_{w}}{\sum}h_{p}(t)\qquad\text{a.e. }t \in[t_{0},t_{1}]. $$

(7)

Additionally, it must satisfy the natural initial and boundary-value conditions

$$ (x_{w}(t_{0}),x_{w}(t_{1}))=(0,d_{w})\qquad\forall w\in\mathcal{W}. $$

(8)

The differential variational inequality describing DUE reads then as follows: Find $h\in {\mathscr{H}}$ such that Eq. 7, Eq. 8 and the instantaneous optimality condition

$$ h(t)\in\text{SOL}(\mathbb{R}^{|{\mathcal{P}}|}_{+},A(t,\cdot))\quad \text{a.e. }t\in[t_{0},t_{1}] $$

(9)

holds. Note that this defines a time-dependent complementarity system

$$ 0\leq h(t)\bot A(t,h(t))\geq 0\quad \text{a.e. }t\in[t_{0},t_{1}], $$

which has been used in a DUE model with a simplified bottleneck structure in Pang et al. (2012). See Friesz et al. (2011) for a formal proof on the correctness of this interpretation.

3 Dynamic Network Loading

The purpose of this section is to explain the dynamic network loading model used in our numerical investigation. We are considering the LWR model on networks, adopting the description in terms of a system of Differential Algebraic Equations (DAE). This formulation of the DNL procedure has the advantage over its mathematically equivalent description in terms of a system of partial differential algebraic equations that it avoids the use of partial differential operators, and thus is much more amenable to numerical discretization strategies.

3.1 The Lighthill-Whitham-Richards Link Model

Network loading acts on the same oriented graph $G=(\mathcal {V},\mathcal {E})$ as in Section 2, where links $I_{i}\in \mathcal {E}$ have a certain length measured by the interval [a_i,b_i]. The within-link dynamics are captured by the scalar conservation law

$$ \partial_{t}\rho_{i}(t,x)+\partial_{x}\left[\rho_{i}(t,x)v_{i}(\rho_{i}(t,x))\right]=0\quad (t,x)\in[t_{0},t_{1}]\times[a_{i},b_{i}]. $$

(10)

The fundamental diagram f_i(ρ) = ρ ⋅ v_i(ρ) is assumed to be continuous, concave and vanishes at $\rho \in \{0,\rho ^{jam}_{i}\}$, where $\rho ^{jam}_{i}$ is the jam density on link I_i. Moreover, there exists a unique global maximum of f_i at the value ${\rho _{i}^{c}}$. We focus on the triangular fundamental diagram

$$ f_{i}(\rho)=\left\{\begin{array}{ll} v_{i}\rho & \text{if }\rho\in[0,{\rho^{c}_{i}}],\\ -w_{i}(\rho-\rho^{jam}) & \text{if }\rho\in({\rho^{c}_{i}},\rho^{jam}_{i}] \end{array}\right. $$

(11)

where v_i,w_i > 0 denote the forward and backward kinematic wave speeds, respectively.

At junctions we need to make sure that relevant boundary conditions are satisfied to respect basic physical principles. Consider a junction with m incoming and n outgoing links. At each such junction, the following conservation property must hold:

$$ \sum\limits_{i=1}^{m}f_{i}(\rho_{i}(t,b_{i}))=\sum\limits_{j=1}^{n}f_{j}(\rho_{j}(t,a_{j}))\qquad\forall t\in[t_{0},t_{1}]. $$

(12)

This condition simply means that inflow into the junction equals outflow. However, this condition alone does not guarantee a unique flow profile at these m + n links. Additional conditions, usually formulated in terms of Riemann solvers and demand/supply conditions must be imposed. We refer to Bressan et al. (2014) and Garavallo et al. (2016) for reviews.

3.2 The Variational Representation of Link Dynamics

While Eq. 10 captures within-link dynamics, the inter-link propagation of congestion requires a careful treatment of junction dynamics. The overall system of PDEs leads to a complex system of junction dynamics and conservation laws which is very hard to handle computationally. We follow a different approach here, which is more amenable to numerical computations. We briefly introduce a variational representation of the link dynamics, based on the generalized Lax-Hopf formula, originally developed in Aubin et al. (2008), Claudel and Bayen (2010a), and Claudel and Bayen (2010b), which leads to a DNL procedure in terms of a system of differential algebraic equations (DAE). Compared to the flow-based approach described in Section 3.1, the DAE based formulation has the following main advantages: (1) the primary variable is flow instead of density); (2) no partial differential operators are involved; (3) it introduces simplified boundary conditions. We only give a high-level description of this approach, detailed enough so that the reader is able to understand the mechanics of the numerical solver. A rigorous description can be found in Garavallo et al. (2016).

Consider the Moskowitz function N_i(t,x) which measures the cumulative number of vehicles that have passed location x along link I_i by time t. The following identities hold:

$$ \partial_{t}N_{i}(t,x)=f_{i}(\rho_{i}(t,x)),\quad \partial_{x}N_{i}(t,x)=-\rho_{i}(t,x). $$

(13)

It follows immediately that N_i(t,x) satisfies the Hamilton-Jacobi equation

$$ \partial_{t}N_{i}(t,x)-f_{i}(-\partial_{x}N_{i}(t,x))=0\qquad x\in[a_{i},b_{i}],t\in[t_{0},t_{1}]. $$

(14)

Denote by $f^{in}_{i}(t)$ and $f^{out}_{i}(t)$ the link I_i inflow and outflow. The cumulative link entering and exiting vehicle counts are defined as

$$ \frac{ d}{ d t}N_{i}^{up}(t)=f_{i}^{in}(t),\quad \frac{ d}{ d t}N^{down}_{i}(t)=f_{i}^{out}(t), $$

where “up” and “down” represent the upstream and downstream boundaries of the link, respectively. Han et al. (2016b) derive explicit formulae for the link demand and supply based on a variational formulation known as the Lax-Hopf formula (Aubin et al. 2008, Claudel and Bayen 2010a, 2010b), as follows:

$$ D_{i}(t)=\left\{\begin{array}{cc} - f^{in}_{i}(t-L_{i}/v_{i}) & \text{if } N^{up}_{i}(t-L_{i}/v_{i})=N^{dn}_{i}(t)\\ C_{i} & \text{if } N_{i}^{up}(t-L_{i}/v)>N^{dn}_{i}(t) \end{array}\right. $$

and

$$ S_{i}(t)=\left\{\begin{array}{cc} f^{out}_{i}(t-L_{i}/w_{i}) & \text{if } N^{up}_{i}(t)=N^{dn}_{i}(t-L_{i}/w_{i})+\rho^{jam}_{i}L_{i}\\ C_{i} & \text{if } N^{up}_{i}(t)< N^{dn}_{i}(t-L_{i}/w_{i})+\rho^{jam}_{i}L_{i}. \end{array}\right. $$

where L_i = b_i − a_i is the length of the link I_i, $v_{i}=f^{\prime }_{i}(0+)$ and $w_{i}=f^{\prime }_{i}\left (\rho ^{jam}_{i}-\right )$. These two relations express the link demand and supply, which are inputs of the junction model, in terms of N^up and N^down. This means that one no longer has to compute the dynamics within the link, but focus instead on the cumulative counts at the two boundaries of the link. Note that, when discretizing the DNL in time, we immediately obtain the link transmission model Yperman et al. (2005). In general, the approach just described gives rise to the link-based formulation of DNL Han et al. (2016b).

Junction Dynamics

In a path-based DNL procedure one must incorporate established routing information into the junction model. Such information is usually formulated by some behavioral assumption on drivers’ preferences. In the numerical scheme we consider, such information is provided in terms of an endogenously given flow distribution matrix W(t) = [w_ij(t)], where w_ij(t) is the proportion of flow incoming into link i and continuing by following link j at a given junction. Abstractly, if Θ represents some junction model, we have the functional relationship

$$ (f^{out}(t),f^{in}(t))={\varTheta}(D(t),S(t),W(t)), $$

where $f^{out}(t)=(f_{i}^{out}(t))_{i=1,\ldots ,m}$ and $f^{in}(t)=(f_{j}^{in}(t))_{j=1,\ldots ,n}$, are the computed incoming and outgoing flows.

Dynamics at the origin nodes

At the origin nodes, we employ a simple point-queue model, in the spirit of Vickrey (1969). Let o be a given origin node, and denote by q_o(t) the volume of the point queue. Let link j be connected to the origin. We assume that

$$ \frac{ d }{ d t}q_{o}(t)=\underset{p\in\mathcal{P}_{o}}{\sum}h_{p}(t)-\min\{D_{0}(t),S_{j}(t)\}, $$

where $\mathcal {P}_{o}$ denotes the set of paths originating from o. The first term on the right represents the inflow into the queue, while the second term represents flow leaving the queue, modeling the demand at the origin as

$$ D_{o}(t)=\left\{\begin{array}{cc} M & \text{ if }q_{o}(t)>0,\\ {\sum}_{p\in\mathcal{P}_{o}}h_{p}(t) & \text{ else} \end{array}\right. $$

taking M to be a sufficiently large number, bigger than the flow capacity at link j.

Calculating path travel times

The DNL procedure calculates the path travel times with given path departure rates. The path travel time is defined as link travel time plus possible queuing at the origin. We define the link exit time function λ(t) implicitly as

$$ N^{up}(t)=N^{down}(\lambda(t)). $$

(15)

For a path enumerated as p = {1,2,…,m}, the path travel time D_p(t,h) is calculated as

$$ D_{p}(t,h)=\lambda_{s}\circ\lambda_{1}\circ {\ldots} \circ \lambda_{m}(t). $$

where (f ∘ g)(t) = f(g(t)) denotes the composition of two functions. λ_o(t) is the exit time function for the potential queuing at the origin o.

4 Strongly Convergent Fixed-Point Algorithms

4.1 Fixed Point Formulation of DUE

Once a DNL procedure has been fixed, the effective delay operator A(h) can be evaluated. The definition of DUE allows us to construct a suitable fixed-point problem which is the basis for the design of iterative numerical schemes for computing DUE. In fact, it is easy to see that $h^{\ast }\in {\mathscr{H}}$ is a path-departure rate profile corresponding to a DUE if and only if the residual

$$ r_{\tau}(h)=\|h-P_{\mathcal{X}}(h-\tau A(h))\| $$

is zero, i.e. r_τ(h^∗) = 0,τ > 0. Here, we call $P_{\mathcal {X}}(x)$ the orthogonal projection in L² onto the set $\mathcal {X}\subset {\mathscr{H}}$. A classical iterative scheme to find the roots of a nonlinear function is the Picard fixed-point iteration to localize a fixed point of the map $h\mapsto P_{\mathcal {X}}(h-\tau A(h))$. Under strong a-priori continuity and monotonicity assumptions on the effective delay operator A, the projected gradient (a.k.a. forward-backward) method, Algorithm 1, generates a sequence $\{h_{n}\}_{n\in \mathbb {N}}$ which will weakly converge to some DUE.

This iterative solver is used in the software package developed in Han et al. (2019), and has also been employed in many studies before. Weak convergence (see Definition 2 in Section 6.1) of the thus constructed sequence $\{h_{n}\}_{n\in \mathbb {N}}$ is known when the operator A is inverse strongly monotone (co-coercive) with modulus μ > 0

$$ \langle{A(x) - A(y),x-y}\rangle \ge \mu \|A(x)-A(y)\|^{2} \quad \forall x,y \in \mathcal{H}, $$

provided that the step sizes τ ∈ (0,2μ). Note that co-coercivity is equivalent to Lipschitz continuity with Lipschitz constant $\frac {1}{\mu }$. Thus, for making method (16) a provably convergent algorithm, we need to know the Lipschitz constant to pin down an upper bound on the step sizes. Strong convergence of $\{h_{n}\}_{n\in \mathbb {N}}$ requires even stronger uniform monotonicity assumption of the operator A over the set $\mathcal {X}$ (Theorem 25.8 Bauschke and Combettes (2016)),² or other modifications of the basic template (16) are needed. Friesz et al. (2011) present a strongly convergent variant of Eq. 16 using a Halpern-type modification of the basic scheme above. Both assumptions, Lipschitz continuity and uniform monotonicity, are very restrictive in the context of computing DUE. While continuity of the effective delay operator has been established in the context of the LWR network loading procedure Han et al. (2016a), monotonicity estimates are hardly available for realistic DNL procedures and not very likely to hold in practice. Therefore, strongly convergent algorithm which are provably convergent to a solution under mild monotonicity assumptions are highly desirable for modeling, optimization and simulation of traffic networks.

4.2 Computing DUE Under Weak Assumptions

Our aim is to design and study alternative numerical schemes for computing DUE, which require significantly less stringent a-priori assumptions on the delay operator, but still come with rigorous convergence guarantees. We summarize our working assumptions below, while Section 6.1 gathers precise mathematical definitions for the readers’ convenience.

Assumption 2

The delay operator $A:{\mathscr{H}}\to {\mathscr{H}}$ is sequentially weakly continuous and L-Lipschitz continuous on $\mathcal {X}$. However, we do not need to know L.

To cope with the unavailable information about the Lipschitz constant, we construct adaptive algorithms, and thus do not need information of this hardly available global parameter. Instead a simple and efficient update procedure of the step size parameters is proposed which depends on pointwise variations of the delay operator rather than global variations. This is a major advantage of the methods we propose here, both from a conceptual and practical point of view, as it allows us to decide step-sizes “online”.

The next assumption is concerned with the structural properties with impose on the delay operator.

Assumption 3

The delay operator A is pseudo-monotone on ${\mathscr{H}}$: For all $h_{1},h_{2}\in {\mathscr{H}}$, we have

$$ \langle{A(h_{1}),h_{2}-h_{1}}\rangle\geq 0\Rightarrow \langle{A(h_{2}),h_{2}-h_{1}}\rangle\geq 0 $$

(17)

Pseudo-monotonicity is a significant weakening of the (strict) monotonicity required when applying the fixed point iteration scheme (16). Some intuition for this concept can be given by considering the simpler case when the operator is integrable. Any smooth real-valued function $f:{\mathscr{H}}\to \mathbb {R}$ induces an operator $A:{\mathscr{H}}\to {\mathscr{H}}$ via its gradient A(h) = ∇f(h) (unique thanks to the Riesz representation theorem). Note that f is (strictly) convex if and only if the gradient map is a (strictly) monotone operator. If f is merely quasi-convex, the gradient operator is pseudo-monotone and vice versa. Assumptions 1-3 are the standing hypothesis for the rest of this paper. Building on them, we now describe the numerical schemes we analyze.

Our basic algorithmic design principle follows the forward-backward-forward (FBF) splitting scheme, originally due to Tseng (2000). In its original form, it ensures that path flows will weakly converge to a DUE, provided that the delay operator is monotone and Lipschitz continuous in the L² norm. In the special case of variational inequalities, it has been shown that pseudo-monotonicity suffices for weak convergence Bot and Mertikopoulos (2021). Actually, one can easily see that weak convergence holds for a large class of non-monotone VIs satisfying an angle property at the solution set Dang and Lan (2015), and this is the main reason why FBF is an attractive numerical solution scheme for DUE. FBF updates a current path departure rate profile h by first applying (16), in order to produce the extrapolated search point $y=P_{\mathcal {X}}(h-\tau A(h))$ (first forward-backward step). It then performs another forward step in path space, by calling the DNL procedure at the just constructed extrapolation point y, and shifts density into directions where the difference in the “travel costs” between the current path flow h and the new search point y is large. Algebraically, this leads to the correction step h⁺ = y + τ(A(h) − A(y)). We would like to emphasize that this correction step does not involve an additional projection onto the feasible set $\mathcal {X}$. This reduces the computational complexity of FBF relative to its close cousin the extragradient algorithm due to Korpelevich (1976), and speeds up the computations in practice whenever projections are expensive to implement (see Bot and Mertikopoulos (2021) for extensive numerical evidence supporting this claim).

In order to force strong convergence of the sequence of path departure rates $\{h_{n}\}_{n\in \mathbb {N}}$, we augment the scheme by an Halpern-type relaxation procedure. The pseudo-code of the resulting DUE solver is displayed in Algorithm 2.

Algorithm 2 has been analyzed in Duvocelle et al. (2019) in detail. In particular, we demonstrated strong convergence of the numerical scheme by proving Theorem 2 below.

Theorem 2 (Theorem 2, Duvocelle et al. (2019))

Suppose that Assumptions 1–3 are satisfied. Let $\{\alpha _{n}\}_{n\in \mathbb {N}}$ and $\{\beta _{n}\}_{n\in \mathbb {N}}$ be two real sequences in (0,1), satisfying conditions

$$ \{\beta_{n}\}_{n\in\mathbb{N}}\subseteq (b,1-\alpha_{n})\text{ for some }b>0, $$

(19)

and

$$ \underset{n\to\infty}{\lim}\alpha_{n}=0\text{ and }\sum\limits_{n=1}^{\infty}\alpha_{n}=\infty. $$

(20)

Then the sequence {h_n} generated by Algorithm 2 converges strongly to $h^{\ast }=\arg \min \limits \{\|{z}\|: z\in {\varOmega }\}$.

Departing from here, our aim in this paper is to significantly extend our previous work by designing a new FBF-based inertial algorithm, which meets all the desiderata spelled out in the introduction: i) Adaptive step-sizes, ii) Weak monotonicity, and iii) strong convergence.

To achieve a possible convergence acceleration and to meet conditions i)-iii), we include relaxation and inertial effects into our algorithm. To the best of our knowledge, this is the first available, provably convergent, relaxed-inertial splitting algorithm for computing DUE.

The basic idea behind inertial algorithms is to use information accumulated from past iterations in order to introduce momentum. This is achieved by computing the extrapolated point $z=h+\alpha (h-h^{\prime })$ in the first step of each iteration. The introduction of momentum is classical, and can be traced back to the heavy-ball method of Polyak Polyak (1964). We adapt momentum by injecting relaxations steps in a disciplined way to force the trajectory to converge strongly to a DUE. The so-constructed new strongly convergent method, to be called the inertial forward-backward-forward (IFBF) algorithm, is displayed in Algorithm 3.

In the convergence analysis of Algorithm 3 it turns out that any positive sequences $\{\epsilon _{n}\}_{n\in \mathbb {N}},\{\beta _{n}\}_{n\in \mathbb {N}}\subset (0,1)$, satisfying

$$ \underset{n\to\infty}{\lim}\beta_{n}=0, \quad{\sum}_{n=1}^{\infty} \beta_{n}=\infty \text{ and } \underset{n\to\infty}{\lim}\frac{\epsilon_{n}}{\beta_{n}}=0 $$

(23)

are admissible for strong convergence of the sequence of path flows $\{h_{n}\}_{n\in \mathbb {N}}$ generated by this Algorithm. The sequence $\{\tau _{n}\}_{n\in \mathbb {N}}$ has the same role as the step size λ in the basic fixed point iteration (16). Hence, we have to choose it small enough to ensure convergence (theoretically smaller than the reciprocal of the Lipschitz constant of the delay operator). Nevertheless we can realize IFBF without any a-priori knowledge of the Lipschitz constant by implementing the adaptive step-size policy (21). As we will see in Lemma 5, the step size sequence $\{\tau _{n}\}_{n\in \mathbb {N}}$ has a limit and

$$ \underset{n\to\infty}{\lim}\tau_{n} = \tau \geq \bar{\tau} :=\min\left\{\frac{\mu}{L},\tau_{0}\right\}. $$

The parameter α can be any constant in (0,1). The main theoretical result of this paper reads as follows.

Theorem 3

Let Assumptions 1-3 be in place. Then the sequence {h_n}_n≥ 0 generated by Algorithm 3 converges strongly to the minimum norm solution $h^{\ast }=\arg \min \limits \{\|{z}\|:z\in {\varOmega }\}$.

5 Numerical Experiments

We present preliminary computational examples of the simultaneous route-and-departure-time dynamic user equilibrium on the Nguyen network (Nguyen 1984) and the Sioux falls network. Detailed network parameters, including coordinates of nodes and link attributes, are sourced and adapted from Han et al. (2019). Given that our DUE and DNL formulations are path-based, enumeration of paths was applied to generate the path set using the Frank-Wolfe algorithm (Table 2).

Table 2 Key attributes of the test networks

We apply Algorithm 2 and Algorithm 3 with the embedded DNL procedure based on a time-stepping scheme discretizing the PDAE formulation described in Section 3. We compare our method with the projected gradient algorithm (16), as implemented in the MATLAB toolbox documented in Han et al. (2019).³

As remarked in Han et al. (2019), projected gradient requires strong monotonicity to ensure norm convergence, whereas all our methods are provably strongly convergent by means of Theorems 2 and 3. All computations reported in this section were performed using MATLAB (R2018a) on a Lenovo x64 Laptop with Intel Core i5 processor with 1.6 GHz and 8GB of RAM (Fig 1).

Fig. 1

The Nguyen and Sioux Falls network

5.1 Performance of the Algorithms

We run all three methods for fixed number of iterations and report the last iterate of the algorithm (h^Final), the corresponding effective delay operator (A(h^Final)), a numerical merit function (GAP), as well as a measure for the speed of convergence. The construction of our numerical merit function follows Han et al. (2019). It is designed to measures the distance to equilibrium via the following version of a gap function

$$ \begin{array}{@{}rcl@{}} \text{GAP}_{w}&=&\max\{A_{p}(t,h^{Final}):t\in[t_{0},t_{1}],p\in\mathcal{P}_{w}\text{ s.t. }h^{Final}_{p}(t)>0\}\\ &&-\min\{A_{p}(t,h^{Final}):t\in[t_{0},t_{1}],p\in\mathcal{P}_{w}\text{ s.t. }h^{Final}_{p}(t)>0\}, \end{array} $$

(24)

for all $w\in \mathcal {W}$. Hence, GAP_w represents the range of travel costs experienced by all drivers in the given O-D pair $w\in \mathcal {W}$. In fact, it is clear that GAP_w ≥ 0, and in an exact DUE, the gap should be zero for all O-D pairs, justifying the interpretation of GAP as a numerical merit function.

Table 3 contains a list of the global parameters employed in our numerical experiments. Here dt is regulating the mesh-size of the time grid in the numerical solution of the DNL. max. Iterations is the total number of iterations we let all three algorithms run on each test instance, and λ is the relaxation parameter in Algorithm 3. The construction of local parameters has been done in a simple way, without involving extensive search over the parameter space which would very likely improve the reported results. The FB Algorithm 1 has been implemented as in Han et al. (2019), using the constant step size τ = 10 on the Nguyen, and τ = 2 on the Sioux falls test network. FBF and IFBF (Algorithms 2 and 3) are implemented with the adaptive step-size (18) and (21), respectively. The relaxation and inertial sequences employed in FBF and IFBF are reported in Table 4.

Table 3 Global parameters for Algorithms 1, 2 and 3

Table 4 List of method-specific parameters. N.N. stands for “not needed”

Figure 2 shows the distribution of the values of our merit function (24) on the Nguyen network, and Fig. 3 displays the same statistic for the Sioux falls network.

Fig. 2

Distributions of O-D gaps to the DUE solutions in the Nguyen network, calculated according to Eq. 24

Fig. 3

Distributions of O-D gaps to the DUE solutions in the Sioux falls network, calculated according to Eq. 24

We see that in all our experiments the distribution of the O-D gaps is concentrated around 0.2 across all networks for FB and IFBF. This suggests that these algorithms preform similarly in terms of producing approximate equilibrium solutions. The decisive advantage of IFBF is however that it is guaranteed to converge strongly to the minimum norm solution, without requiring strict monotonicity of the delay operator.

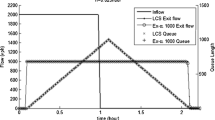
Figure 4 displays the path departure rates as well as the corresponding effective path delays on randomly selected paths in the considered test networks. We see from these plots that the path departure rates peak out around the minima of the effective delay, which reflects equilibrium behavior on the routes.

Fig. 4

Path departure rates and corresponding effective path delays for selected paths in the DUE solutions on the Nguyen network

We finally display a figure which gives some indication on the relative speed of convergence of each of the tested algorithms. We compute for each method the “relative energy” sequence

$$ e_{n} = \frac{\|{h_{n+1}-h_{n}}\|}{\|{h_{n}}\|} $$

(25)

which measures the decay of energy of the path departure rates generated by the algorithms. Han et al. (2019) call this the relative gap, and we follow this terminology in the labeling of the figures. For all our methods this sequence must converge to 0, and we can consider one method faster than the other if the rate of convergence of the energy sequence dominates the other. Figure 5 shows the evolution of the relative energy sequences for each method.

Fig. 5

The relative energy (25) on semi-log scale for both test networks

We see that already non-optimized step size parameters lead to some acceleration in the IFBF scheme when compared to other solvers.

6 Convergence Analysis

6.1 Preliminaries

The purpose of this section is to collect some standard concepts from real Hilbert spaces. Throughout this section we let ${\mathscr{H}}$ be a real Hilbert space with scalar product 〈⋅,⋅〉 and associated norm ∥⋅∥.

Definition 2 (Convergence in Hilbert spaces)

A sequence of points $\{x_{n}\}_{n\in \mathbb {N}}$ in a Hilbert space ${\mathscr{H}}$ converges weakly to a point $x\in {\mathscr{H}}$, denoted by $x_{n}\rightharpoonup x$, if

$$ \underset{n\to\infty}{\lim}\langle{x_{n},y}\rangle=\langle{x,y}\rangle $$

for all test vectors $y\in {\mathscr{H}}$. The sequence {x_n} converges strongly to x if

$$ \underset{n\to\infty}{\lim}\|{x_{n}-x}\|=0. $$

In order to prove our main convergence results, we need the following standard facts. For all $x,y\in {\mathscr{H}}$ and $\alpha \in \mathbb {R}$, we have

$$ \|x+y\|^{2}\le \|x\|^{2}+2\langle y,x+y\rangle. $$

(26)

Lemma 1

Let C be a nonempty closed convex set in ${\mathscr{H}}$ and $x\in {\mathscr{H}}$ arbitrary. Then

• langleP_C(x) − x,y − P_C(x)〉≥ 0 for all y ∈ C;

• ∥P_C(x) − y∥² ≤∥x − y∥² −∥x − P_C(x)∥² for all y ∈ C.

Definition 3

Let $A:{\mathscr{H}}\to {\mathscr{H}}$ be an operator. The operator A is called

• 1. L-Lipschitz continuous with L > 0 on $\mathcal {X}\subseteq {\mathscr{H}}$ if

  $$ \|{A(x)-A(y)}\|\leq L\|{x-y}\|\qquad\forall x,y\in\mathcal{X}. $$

• 2. pseudo-monotone on $\mathcal {X}\subseteq {\mathscr{H}}$ if

  $$ \langle{A(x),y-x}\rangle\geq 0\Rightarrow \langle{A(y),y -x}\rangle\geq 0\qquad\forall x,y\in\mathcal{X}. $$

  (27)

• 3. sequentially weakly continuous if $x_{n}\rightharpoonup x$ then $A(x_{n}) \rightharpoonup A(x)$.

The next classical fact shows that solutions of $\text {VI}(\mathcal {X},A)$ defined in terms of pseudo-monotone operators can be determined via “weak formulation”.

Lemma 2

(Cottle and Yao 1992) If $A: {\mathscr{H}} \to {\mathscr{H}}$ is pseudo-monotone and continuous, then x^∗ is a solution of $VI(\mathcal {X}, A)$ if and only if

$$ \langle{A(x), x - x^{\ast}}\rangle\geq 0 \ \ \forall x \in \mathcal{X}. $$

The next technical results are basic convergence guarantees for real-valued sequences.

Lemma 3

(Xu 2002) Let $\{a_{n}\}_{n\in \mathbb {N}}$ be a sequence of nonnegative real numbers, and $\{\beta _{n}\}_{n\in \mathbb {N}}$ be a sequence in (0,1) such that ${\sum }_{n}\beta _{n}=\infty$. Suppose that $\{b_{n}\}_{n\in \mathbb {N}}$ is a sequence with $\lim \sup _{n}b_{n}\leq 0$. If

$$ a_{n+1}\leq (1-\beta_{n})a_{n}+\beta_{n}b_{n}\qquad\forall n\in\mathbb{N} $$

then $\lim _{n\to \infty }a_{n}=0$.

Lemma 4

(Saejung and Yotkaew 2012) Let $\{a_{n}\}_{n\in \mathbb {N}}$ be a sequence of nonnegative real numbers, $\{\beta _{n}\}_{n\in \mathbb {N}}$ be a sequence of real numbers in (0,1) with ${\sum }_{n}\beta _{n}=\infty$ and $\{b_{n}\}_{n\in \mathbb {N}}$ be a sequence of real numbers. Assume that

$$ a_{n+1}\le (1-\beta_{n})a_{n}+\beta_{n} b_{n} \text{ for all } n\geq 1. $$

If $\limsup _{k\to \infty } b_{n_{k}} \le 0$ for every subsequence $\{a_{n_{k}}\}_{k=1}^{\infty }$ of $\{a_{n}\}_{n=1}^{\infty }$ satisfying $\liminf _{k\to \infty }(a_{n_{k}+1}-a_{n_{k}})\geq 0$ then $\lim _{n\to \infty }{a_{n}} = 0$.

Lemma 5

Let τ₀ > 0 and μ ∈ (0,1). Let $A:{\mathscr{H}}\to {\mathscr{H}}$ be a L-Lipschitz continuous operator. The sequence {τ_n}_n≥ 0 generated by Eq. 16 is non-increasing and satisfies

$$ \underset{n\to\infty}{\lim}\tau_{n} = \tau \geq \bar{\tau} :=\min\left\{\frac{\mu}{L},\tau_{0}\right\}. $$

(28)

Furthermore,

$$ \|{A(w_{n})-A(y_{n})}\|\leq \frac{\mu}{\tau_{n+1}}\|{w_{n}-y_{n}}\|\qquad\forall n\geq 1. $$

(29)

Proof

Since $\tau _{n+1}=\min \limits \left \{\frac {\mu \|{w_{n}-y_{n}}\|}{\|{A(w_{n})-A(y_{n})}\|},\tau _{n}\right \}$, it is clear that τ_n+ 1 ≤ τ_n for all n ≥ 0. Moreover, using the L-Lipschitz continuity of the operator A gives

$$ \frac{\mu\|{w_{n}-y_{n}}\|}{\|{A(w_{n})-A(y_{n})}\|}\geq\frac{\mu}{L}\quad \text{ if }A(w_{n})\neq A(y_{n}). $$

Hence, $\tau _{n+1}\geq \min \limits \{\frac {\mu }{L},\tau _{n}\}$ for all n. By induction, it follows that {τ_n}_n is bounded from below by $\min \limits \{\frac {\mu }{L},\tau _{0}\}.$ Therefore, $\lim _{n\to \infty }\tau _{n} = \tau \geq \bar {\tau } :=\min \limits \left \{\frac {\mu }{L},\tau _{0}\right \}.$□

6.2 Proof of Theorem 3

We start with an auxiliary technical result, which guarantees that weak cluster points of the algorithm produce solutions of DUE. It is based on techniques from Vuong (2018).

Lemma 6

Let {w_n} be a sequence generated by Algorithm 3. If there exists a subsequence $\{w_{n_{k}}\}$ convergent weakly to $z\in {\mathscr{H}}$ and $\lim _{k\to \infty }\|w_{n_{k}}-y_{n_{k}}\|=0$, then, having Assumptions 1-3 in place, we know z ∈Ω.

Proof

Recall that $y_{n}=P_{\mathcal {X}}(w_{n}-\tau _{n}A(w_{n}))$. By Lemma 1(i), we have

$$ \langle w_{n_{k}}-\tau_{n_{k}} A(w_{n_{k}})-y_{n_{k}},x-y_{n_{k}}\rangle \le 0, \forall x\in \mathcal{X}, $$

or, equivalently,

$$ \frac{1}{\tau_{n_{k}}}\langle w_{n_{k}}-y_{n_{k}},x-y_{n_{k}}\rangle \le \langle A(w_{n_{k}}),x-y_{n_{k}}\rangle, \forall x\in \mathcal{X}. $$

Consequently, we have

$$ \frac{1}{\tau_{n_{k}}}\langle w_{n_{k}}-y_{n_{k}},x-y_{n_{k}}\rangle +\langle A(w_{n_{k}}),y_{n_{k}}-w_{n_{k}}\rangle \le \langle A(w_{n_{k}}),x-w_{n_{k}}\rangle, \forall x\in \mathcal{X}. $$

(30)

Since $\{w_{n_{k}}\}$ is weakly convergent, it is bounded. Then, by the Lipschitz continuity of A, $\{A(w_{n_{k}})\}$ is bounded. As $\|w_{n_{k}}-y_{n_{k}}\|\to 0$, $\{y_{n_{k}}\}$ is also bounded and $\tau _{n_{k}} \geq \min \limits \{\tau _{0},\frac {\mu }{L}\}$. Passing (30) to the limit as $k\to \infty$, we get

$$ \underset{k\to\infty}{\liminf}\langle A(w_{n_{k}}),x-w_{n_{k}}\rangle \geq 0, \forall x\in \mathcal{X}. $$

(31)

Moreover, we have

$$ \begin{array}{@{}rcl@{}} \langle A(y_{n_{k}}),x-y_{n_{k}}\rangle&=&\langle A(y_{n_{k}})- A(w_{n_{k}}),x-w_{n_{k}}\rangle+\langle A(w_{n_{k}}),x-w_{n_{k}}\rangle \\ &&+\langle A(y_{n_{k}}),w_{n_{k}}-y_{n_{k}}\rangle\\ &\geq& -\|{A(y_{n_{k}})-A(w_{n_{k}})}\|\cdot\|{x-w_{n_{k}}}\|+\langle{A(w_{n_{k}}),x-w_{n_{k}}}\rangle\\ &&-\|{A(y_{n_{k}})}\|\cdot\|{w_{n_{k}}-y_{n_{k}}}\|. \end{array} $$

Since $\lim _{k\to \infty }\|w_{n_{k}}-y_{n_{k}}\|=0$ and A is L-Lipschitz continuous on H, we get from the above

$$ \lim_{k\to\infty}\|A(w_{n_{k}})-A(y_{n_{k}})\|=0. $$

Together with Eq. 31, we obtain

$$ \underset{k\to\infty}{\liminf}\langle A(y_{n_{k}}),x-y_{n_{k}}\rangle \geq 0\qquad\forall x\in\mathcal{X}. $$

Next, we show that z ∈Ω. We choose a sequence {𝜖_k} of positive numbers decreasing and tending to 0. For each k ≥ 1, we denote by N_k the smallest positive integer such that

$$ \langle A(y_{n_{j}}),x-y_{n_{j}}\rangle +\epsilon_{k} \geq 0, \forall j\geq N_{k}. $$

(32)

Since {𝜖_k} is decreasing, it is easy to see that the sequence {N_k} is increasing. Furthermore, for each k ≥ 1, since $\{y_{N_{k}}\}\subset \mathcal {X}$, we can suppose $A(y_{N_{k}})\ne 0$ (otherwise, $y_{N_{k}}$ is a solution) and, setting

$$ v_{N_{k}} = \frac{A(y_{N_{k}})}{\|A(y_{N_{k}})\|^{2} }, $$

we have $\langle A(y_{N_{k}}), v_{N_{k}}\rangle = 1$ for each k ≥ 1. Now, we can deduce from Eq. 32 that, for each k ≥ 1,

$$ \langle A(y_{N_{k}}), x+\epsilon_{k} v_{N_{k}}-y_{N_{k}}\rangle=\langle{A(y_{N_{k}}),x-y_{n_{k}}}\rangle+\epsilon_{k} \geq 0. $$

Since A is pseudo-monotone (Assumption 3) on ${\mathscr{H}}$, we get

$$ \langle A(x+\epsilon_{k} v_{N_{k}}), x+\epsilon_{k} v_{N_{k}}-y_{N_{k}}\rangle \geq 0. $$

This implies that

$$ \langle A(x), x-y_{N_{k}}\rangle \geq \langle A(x)-A(x+\epsilon_{k} v_{N_{k}}), x+\epsilon_{k} v_{N_{k}}-y_{N_{k}} \rangle-\epsilon_{k} \langle A(x), v_{N_{k}}\rangle. $$

(33)

Now, we show that $\lim _{k\to \infty }\epsilon _{k} v_{N_{k}}=0$. Indeed, since $w_{n_{k}}\rightharpoonup z$ and $\lim _{k\to \infty }\|w_{n_{k}}-y_{n_{k}}\|=0,$ we obtain $y_{N_{k}}\rightharpoonup z \text { as } k \to \infty$. Since $\{y_{n}\}\subset \mathcal {X}$, we clearly have $z\in \mathcal {X}$ as well. Since A is sequentially weakly continuous on $\mathcal {X}$, $\{ A(y_{n_{k}})\}$ converges weakly to A(z). We can suppose A(z)≠ 0 (otherwise, z is a solution). Since the norm mapping is sequentially weakly lower semi-continuous, we have

$$ 0 < \|A(z)\|\le \underset{k\to \infty}{\liminf}\|A(y_{n_{k}})\|. $$

Together with $\{y_{N_{k}}\}\subset \{y_{n_{k}}\}$ and 𝜖_k → 0 as $k \to \infty$, we readily conclude

$$ 0 \le \underset{k\to\infty}{\limsup} \|\epsilon_{k} v_{N_{k}} \|= \underset{k\to\infty}{\limsup} \left( \frac{\epsilon_{k}}{\|A(y_{n_{k}})\|}\right)\le \frac{\limsup_{k\to\infty}\epsilon_{k} } {\liminf_{k\to\infty}\|A(y_{n_{k}})\|}=0. $$

Hence, $\lim _{k\to \infty } \epsilon _{k} v_{N_{k}} = 0$.

Now, letting $k\to \infty$, then the right hand side of Eq. 33 tends to zero by A is uniformly continuous, $\{w_{N_{k}}\}, \{v_{N_{k}}\}$ are bounded and $\lim _{k\to \infty }\epsilon _{k} v_{N_{k}}=0$. Thus, we get

$$ \underset{k\to\infty}{\liminf}\langle A(x),x-y_{N_{k}}\rangle \geq 0. $$

Hence, for all $x\in \mathcal {X}$, we have

$$ \langle A(x), x-z\rangle=\lim_{k\to\infty} \langle A(x), x-y_{N_{k}}\rangle =\underset{k\to\infty}{\liminf} \langle A(x), x-y_{N_{k}}\rangle \geq 0. $$

By Lemma 2, z ∈Ω. This completes the proof. □

The next result established the boundedness of the sequence of path flows.

Lemma 7

Let Assumptions 1-3 hold. The sequence of path flows $\{h_{n}\}_{n=1}^{\infty }$ generated by Algorithm 3 is bounded. In addition,

$$ \|h_{n+1}-h^{*}\|^{2}\le \|w_{n}-h^{*}\|^{2}-\lambda\left( 1-\mu\frac{\tau_{n}}{\tau_{n+1}}\right)\left( 2-\lambda+\lambda\mu \frac{\tau_{n}}{\tau_{n+1}} \right)\|y_{n}-w_{n}\|^{2}. $$

(34)

Proof

We have

$$ \begin{array}{@{}rcl@{}} \|h_{n+1}-h^{*}\|^{2}&=& \|(1-\lambda)w_{n} +\lambda (y_{n}-\tau_{n}(A(y_{n})-A(w_{n})))-h^{*}\|^{2}\\ &=& \|(1-\lambda)(w_{n} -h^{*})+\lambda (y_{n}-h^{*})+\lambda\tau_{n}(A(w_{n})-A(y_{n})))\|^{2}\\ &=&(1-\lambda)^{2}\|w_{n}-h^{*}\|^{2}+\lambda^{2}\|y_{n}-h^{*}\|^{2}+\lambda^{2}{\tau_{n}^{2}}\|A(w_{n})-A(y_{n})\|^{2}\\ &&+2(1-\lambda)\lambda\langle w_{n}-h^{*},y_{n}-h^{*}\rangle +2(1-\lambda)\lambda\tau_{n}\langle w_{n}-h^{*},A(w_{n}) \\ &&-A(y_{n})\rangle +2\lambda^{2}\tau_{n}\langle y_{n}-h^{*},A(w_{n})-A(y_{n})\rangle. \end{array} $$

(35)

Combining

$$ 2\langle w_{n}-h^{*},y_{n}-h^{*}\rangle=\|w_{n}-h^{*}\|^{2}+\|y_{n}-h^{*}\|^{2}-\|w_{n}-y_{n}\|^{2}, $$

(36)

with the definition of {τ_n}, it is easy to see that

$$ \|A(w_{n})-A(y_{n})\|\le \frac{\mu}{\tau_{n+1}}\|w_{n}-y_{n}\|, \forall n\geq 0. $$

(37)

Substituting (36) and (37) into (35), we get

$$ \begin{array}{@{}rcl@{}} \|h_{n+1}-h^{*}\|^{2}&\le& (1-\lambda)\|w_{n}-h^{*}\|^{2}+\lambda\|y_{n}-h^{*}\|^{2}+\lambda^{2}\frac{{\tau_{n}^{2}}}{\tau^{2}_{n+1}}\mu^{2}\|w_{n}-y_{n}\|^{2}\\ &&-(1-\lambda)\lambda\| w_{n}-y_{n}\|^{2} +2(1-\lambda)\lambda\tau_{n}\langle w_{n}-h^{*},A(w_{n})-A(y_{n})\rangle\\ &&+2\lambda^{2}\tau_{n}\langle y_{n}-h^{*},A(w_{n})-A(y_{n})\rangle. \end{array} $$

(38)

Lemma 1(i) yields the estimate

$$ \begin{array}{@{}rcl@{}} \|y_{n}-h^{*}\|^{2}&=&\langle{y_{n}-h^{\ast},y_{n}-h^{\ast}}\rangle\\ &=&\langle{P_{\mathcal{X}}(w_{n}-\tau_{n}A(w_{n}))-P_{\mathcal{X}}(h^{\ast}),P_{\mathcal{X}}(w_{n}-\tau_{n}A(w_{n}))-P_{\mathcal{X}}(h^{\ast})}\rangle\\ &=&\langle{y_{n}-h^{\ast},w_{n}-\tau_{n}A(w_{n})-h^{\ast}}\rangle+\langle P_{\mathcal{X}}(w_{n}-\tau_{n}A(w_{n})-\\ &&P_{\mathcal{X}}(h^{\ast}),P_{\mathcal{X}}(w_{n}-\tau_{n}A(w_{n}))-w_{n}+\tau_{n}A(w_{n})\rangle\\ &\le& \langle y_{n}-h^{*},w_{n}-\tau_{n} A(w_{n})-h^{\ast}\rangle\\ &=&\frac{1}{2}\|y_{n}-h^{*}\|^{2}+\frac{1}{2}\|w_{n}-\tau_{n} A(w_{n})-h^{*}\|^{2}-\frac{1}{2}\|(w_{n}-h^{*})\\ &&-(w_{n}-\tau_{n} A(w_{n}))\|^{2}\\ &=&\!\frac{1}{2}\|y_{n}-h^{*}\|^{2} + \frac{1}{2}\|w_{n}-h^{*}\|^{2}-\frac{1}{2}\|y_{n} - w_{n}\|^{2}-\langle y_{n}-h^{*},\tau_{n} A(w_{n})\rangle, \end{array} $$

or equivalently

$$ \|y_{n}-h^{*}\|^{2} \le \|w_{n}-h^{*}\|^{2}-\|y_{n}-w_{n}\|^{2}-2\langle y_{n}-h^{*},\tau_{n} A(w_{n})\rangle. $$

(39)

Since h^∗∈Ω, we have 〈A(h^∗),y_n − h^∗〉≥ 0. It follows from the pseudo-monotonicity of A that

$$ 2\langle \tau_{n} A(y_{n}),y_{n} - h^{*}\rangle \geq 0. $$

(40)

Adding (39) and (40), we obtain

$$ \begin{array}{@{}rcl@{}} \|y_{n}-h^{*}\|^{2} \le \|w_{n}-h^{*}\|^{2}-\|y_{n}-w_{n}\|^{2}-2\tau_{n}\langle y_{n}-h^{*}, A(w_{n})-A(y_{n})\rangle. \end{array} $$

(41)

Substituting (41) into (38), we get

$$ \begin{array}{@{}rcl@{}} \|h_{n+1}-h^{*}\|^{2} &\le& (1-\lambda)\|w_{n}-h^{*}\|^{2}+\lambda\|w_{n}-h^{*}\|^{2}-\lambda\|y_{n}-w_{n}\|^{2}\\&&-2\lambda\tau_{n}\langle y_{n}-h^{*}, A(w_{n})-A(y_{n})\rangle\\ &&+\lambda^{2}\frac{{\tau_{n}^{2}}}{\tau^{2}_{n+1}}\mu^{2}\|w_{n}-y_{n}\|^{2}-(1-\lambda)\lambda\| w_{n}-y_{n}\|^{2} \\ &&+2(1-\lambda)\lambda\tau_{n}\langle w_{n}-h^{*},A(w_{n})-A(y_{n})\rangle\\&&+2\lambda^{2}\tau_{n}\langle y_{n}-h^{*},A(w_{n})-A(y_{n})\rangle\\ &=& (1-\lambda)\|w_{n}-h^{*}\|^{2}+\lambda\|w_{n}-h^{*}\|^{2}-\lambda\|y_{n}-w_{n}\|^{2}\\&&-2\lambda\tau_{n}\langle y_{n}-h^{*}, A(w_{n})-A(y_{n})\rangle\\ &&+\lambda^{2}\frac{{\tau_{n}^{2}}}{\tau^{2}_{n+1}}\mu^{2}\|w_{n}-y_{n}\|^{2}-(1-\lambda)\lambda\tau_{n}\| w_{n}-y_{n}\|^{2} \\ && +2(1-\lambda)\lambda\tau_{n}\langle y_{n}-h^{*},A(w_{n})-A(y_{n})\rangle\\ && +2(1-\lambda)\lambda\tau_{n}\langle w_{n}-y_{n},A(w_{n})-A(y_{n})\rangle\\ &&+2\lambda^{2}\tau_{n}\langle y_{n}-h^{*},A(w_{n})-A(y_{n})\rangle\\ &=& \|w_{n}-h^{*}\|^{2}\\ && +\lambda^{2}\frac{{\tau_{n}^{2}}}{\tau^{2}_{n+1}}\mu^{2}\|w_{n}-y_{n}\|^{2}-(2-\lambda)\lambda\| w_{n}-y_{n}\|^{2} \\ && +2(1-\lambda)\lambda\tau_{n}\langle w_{n}-y_{n},A(w_{n})-A(y_{n})\rangle\\ &\le& \|w_{n}-h^{*}\|^{2}\\ &&+\lambda^{2}\frac{{\tau_{n}^{2}}}{\tau^{2}_{n+1}}\mu^{2}\|w_{n}-y_{n}\|^{2}-(2-\lambda)\lambda\| w_{n}-y_{n}\|^{2} \\ &&+2(1-\lambda)\lambda\frac{\tau_{n}}{\tau_{n+1}}\mu \|w_{n}-y_{n}\|^{2}\\ &=& \|w_{n} - h^{*}\|^{2} - \lambda\left[2 - \lambda\! -\!\lambda \frac{{\tau^{2}_{n}}}{\tau^{2}_{n+1}}\mu^{2}-2(1-\lambda)\frac{\tau_{n}}{\tau_{n+1}}\mu\right]\|w_{n} - y_{n}\|^{2}\\ &=&\|w_{n}-h^{*}\|^{2}-\lambda\left( 1-\mu\frac{\tau_{n}}{\tau_{n+1}}\right)\left( 2-\lambda+\lambda\mu \frac{\tau_{n}}{\tau_{n+1}} \right)\|y_{n}-w_{n}\|^{2}\\ . \end{array} $$

(42)

Since

$$ \underset{n\to\infty}{\lim}\left( 1-\mu\frac{\tau_{n}}{\tau_{n+1}}\right)\left( 2-\lambda+\lambda\mu \frac{\tau_{n}}{\tau_{n+1}} \right)=(1-\mu)(2-\lambda+\lambda \mu)>0 $$

there exists $n_{0}\in \mathbb {N}$ such that

$$\left( 1-\mu\frac{\tau_{n}}{\tau_{n+1}}\right)\left( 2-\lambda+\lambda\mu \frac{\tau_{n}}{\tau_{n+1}} \right)>0 \ \ \forall n\geq n_{0}. $$

Hence

$$ \|h_{n+1}-h^{*}\|\le \|w_{n}-h^{*}\| \ \ \forall n\geq n_{0}. $$

(43)

On the one hand, using the definition of w_n, we obtain

$$ \begin{array}{@{}rcl@{}} \|w_{n}-h^{*}\|&=&\|(1-\beta_{n})(h_{n}+\alpha_{n}(h_{n}-h_{n-1}))-h^{*}\|\\ &=&\|(1-\beta_{n})(h_{n}-h^{*})+(1-\beta_{n})\alpha_{n}(h_{n}-h_{n-1})-\beta_{n} h^{*}\|\\ &\le& (1-\beta_{n})\|h_{n}-h^{*}\|+(1-\beta_{n})\alpha_{n}\|h_{n}-h_{n-1}\|+\beta_{n} \|h^{*}\|\\ &=&(1-\beta_{n})\|h_{n}-h^{*}\|+\beta_{n} [ (1-\beta_{n})\frac{\alpha_{n}}{\beta_{n}}\|h_{n}-h_{n-1}\|+\|h^{*}\|]. \end{array} $$

(44)

From Eqs. 16 and 23, we have

$$ \frac{\alpha_{n}}{\beta_{n}}\|h_{n}-h_{n-1}\|\le \frac{\epsilon_{n}}{\beta_{n}}\to 0. $$

Hence,

$$ \underset{n\to\infty}{\lim}\left[ (1-\beta_{n})\frac{\alpha_{n}}{\beta_{n}}\|h_{n}-h_{n-1}\|+\|h^{*}\|\right]=\|h^{*}\|, $$

Therefore, there exists M > 0 such that

$$ (1-\beta_{n})\frac{\alpha_{n}}{\beta_{n}}\|h_{n}-h_{n-1}\|+\|h^{*}\|\le M. $$

(45)

Combining (44) and (45) we obtain

$$ \|w_{n}-h^{*}\|\le (1-\beta_{n})\|h_{n}-h^{*}\|+\beta_{n} M. $$

(46)

Hence, from Eqs. 43 and 46, we have

$$ \begin{array}{@{}rcl@{}} \|h_{n+1}-h^{*}\|&\le &(1-\beta_{n})\|h_{n}-h^{*}\|+\beta_{n} M\\ &=&\max\{\|h_{n}-h^{*}\|, M \}\leq \ldots\le \max\{\|h_{n_{0}}-h^{*}\|,M\}. \end{array} $$

Therefore, the sequence $\{h_{n}\}_{n=1}^{\infty }$ is bounded. □

Lemma 8

It holds that

$$ \lambda\left( 1 - \mu\frac{\tau_{n}}{\tau_{n+1}}\right)\left( 2 - \lambda+\lambda\mu \frac{\tau_{n}}{\tau_{n+1}} \right)\|w_{n}-y_{n}\|^{2}\le\|h_{n}-h^{*}\|^{2}-\|h_{n+1}-h^{*}\|^{2}+\beta_{n} M_{1}. $$

Proof

Equation 46 yields

$$ \begin{array}{@{}rcl@{}} \|w_{n}-h^{*}\|^{2}&\le& (1-\beta_{n})^{2}\|h_{n}-h^{*}\|^{2}+2\beta_{n}(1-\beta_{n})M \|h_{n}-h^{*}\|+{\beta_{n}^{2}}M^{2}\\ &\le& \|h_{n}-h^{*}\|^{2}+\beta_{n} [2(1-\beta_{n})M \|h_{n}-h^{*}\|+\beta_{n} M^{2}]\\ &\le& \|h_{n}-h^{*}\|^{2}+\beta_{n} M_{1}, \end{array} $$

(47)

where $M_{1}:={\max \limits } \{2(1-\beta _{n})M \|h_{n}-h^{*}\|+\beta _{n} M^{2}:\ n\in \mathbb {N}\}$. Substituting (47) into (42) we get

$$ \|h_{n+1} - h^{*}\|^{2}\!\le\! \|h_{n}-h^{*}\|^{2}+\beta_{n} M_{1}-\lambda\left( 1-\mu\frac{\tau_{n}}{\tau_{n+1}}\right)\left( 2-\lambda+\lambda\mu \frac{\tau_{n}}{\tau_{n+1}} \right)\|w_{n}-y_{n}\|^{2}, $$

or equivalently

$$ \lambda\left( 1 - \mu\frac{\tau_{n}}{\tau_{n+1}}\right)\left( 2 - \lambda+\lambda\mu \frac{\tau_{n}}{\tau_{n+1}} \right)\|w_{n}-y_{n}\|^{2} \le\|h_{n}-h^{*}\|^{2}-\|h_{n+1}-h^{*}\|^{2}+\beta_{n} M_{1}. $$

□

Lemma 9

It holds that

$$ \begin{array}{@{}rcl@{}} \|h_{n+1}-h^{*}\|^{2}&\le &(1-\beta_{n})\|h_{n}-h^{*}\|^{2}+\beta_{n}\left[2(1-\beta_{n})\|h_{n}-h^{*}\|\frac{\alpha_{n}}{\beta_{n}} \|h_{n}-h_{n-1}\|\right.\\ &&+\left.\frac{{\alpha^{2}_{n}}}{\beta_{n}}\|h_{n} - h_{n-1}\|^{2} + 2 \|h^{*}\|\cdot \|w_{n} - h_{n+1}\| + 2 \langle -h^{*},h_{n+1}-h^{*} \rangle \right]. \end{array} $$

Proof

Using the inequalities (43) and then (26) as well as β_n ∈ (0,1), we get

$$ \begin{array}{@{}rcl@{}} \|h_{n+1}-h^{*}\|^{2}&\le& \|w_{n}-h^{*}\|^{2}\\ &=&\|(1-\beta_{n}) (h_{n}-h^{*})+(1-\beta_{n}) \alpha_{n} (h_{n}-h_{n-1})-\beta_{n} h^{*}\|^{2}\\ &\le& \|(1-\beta_{n})(h_{n}-h^{*})+(1-\beta_{n})\alpha_{n} (h_{n}-h_{n-1})\|^{2}\\&&+2\beta_{n} \langle -h^{*},w_{n}-h^{*}\rangle \\ &=&(1-{\beta_{n}^{2}}\|{h_{n}-h^{\ast}}\|^{2}+{\alpha^{2}_{n}}(1-\beta_{n})^{2}\|{h_{n}-h_{n-1}}\|^{2}\\&&+2\alpha_{n}(1-\beta_{n})^{2}\langle{h_{n}-h^{\ast},h_{n}-h_{n-1}}\rangle\\ &&+2\beta_{n}\langle{-h^{\ast},w_{n}-h^{\ast}}\rangle\\ &\leq& (1-\beta_{n})\|h_{n}-h^{*}\|^{2}+2(1-\beta_{n})\alpha_{n}\|h_{n}-h^{*}\| \|h_{n}-h_{n-1}\|\\&&+{\alpha_{n}^{2}}\|h_{n}-h_{n-1}\|^{2}\\ &&+2\beta_{n} \langle -h^{*},w_{n}-h_{n+1} \rangle+2\beta_{n} \langle -h^{*},h_{n+1}-h^{*} \rangle \\ &\le &(1-\beta_{n})\|h_{n}-h^{*}\|^{2}+\beta_{n}\left[2(1-\beta_{n})\|h_{n}-h^{*}\|\frac{\alpha_{n}}{\beta_{n}} \|h_{n}-h_{n-1}\|\right.\\ &&+\frac{{\alpha^{2}_{n}}}{\beta_{n}}\|h_{n}-h_{n-1}\|^{2}+2 \| h^{*}\| \cdot \|w_{n}-h_{n+1}\| \\ &&\left.+2 \langle -h^{*},h_{n+1}-h^{*} \rangle \vphantom{\frac{{\alpha^{2}_{n}}}{\beta_{n}}}\right]. \end{array} $$

□

Equipped with these preliminary result, we are now ready to proof the main result of this paper, Theorem 3. We restate the theorem below again, for the readers’ convenience.

Theorem 4

Let Assumptions 1-3 hold. The sequence of path flows $\{h_{n}\}_{n=1}^{\infty }$ generated by Algorithm 3 converges strongly to an element h^∗∈Ω, where h^∗ = argmin{∥z∥ : z ∈Ω}.

Proof

We split the proof in two cases. Let us call a_n := ∥h_n − h^∗∥² and

$$ \begin{array}{@{}rcl@{}} b_{n}&:=&2(1-\beta_{n})\|h_{n}-h^{*}\|\frac{\alpha_{n}}{\beta_{n}} \|h_{n}-h_{n-1}\|\\ &&+ \frac{{\alpha^{2}_{n}}}{\beta_{n}}\|h_{n}-h_{n-1}\|^{2}+2 \| h^{*}\| \cdot \|w_{n}-h_{n+1}\| +2 \langle -h^{*},h_{n+1}-h^{*} \rangle , \end{array} $$

so that Lemma 9 boils down to the recursion

$$ a_{n+1}\leq(1-\beta_{n})a_{n}+\beta_{n}b_{n}. $$

We split the proof in two case.

Case 1

There exists $N_{0}\in \mathbb {N}$ such that a_n+ 1 ≤ a_n for all n ≥ N₀. Then, $\lim \inf _{n\to \infty }(a_{n+1}-a_{n})=0$, and it follows $\lim \sup _{n}b_{n}\leq 0$. The conclusion follows from Lemma 3.

Case 2

By Lemma 4, it suffices to show that

$$ \underset{k\to\infty}{\limsup}\langle -h^{*}, h_{n_{k}+1}-h^{*}\rangle\le 0 $$

for every subsequence $\{\|h_{n_{k}}-h^{*}\|\}_{k=1}^{\infty }$ of $\{\|h_{n}-h^{*}\|\}_{n=1}^{\infty }$ satisfying

$$ \underset{k\to\infty}{\liminf}(\|h_{n_{k}+1}-h^{*}\|-\|h_{n_{k}}-h^{*}\|)\geq 0. $$

For this, suppose that $\{\|h_{n_{k}}-h^{*}\|\}_{k=1}^{\infty }$ is a subsequence of $\{\|h_{n}-h^{*}\|\}_{n=1}^{\infty }$ such that $\liminf _{k\to \infty }(\|h_{n_{k}+1}-h^{*}\|-\|h_{n_{k}}-h^{*}\|)\geq 0.$ Then

$$ \begin{array}{@{}rcl@{}} &&\underset{k\to\infty}{\liminf}(\|h_{n_{k}+1}-h^{*}\|^{2}-\|h_{n_{k}}-h^{*}\|^{2})\\ &=&\underset{k\to\infty}{\liminf}[(\|h_{n_{k}+1}-h^{*}\|-\|h_{n_{k}}-h^{*}\|)(\|h_{n_{k}+1}-h^{*}\|+\|h_{n_{k}}-h^{*}\|)]\geq 0. \end{array} $$

By Lemma 8 we obtain

$$ \begin{array}{@{}rcl@{}} &&\underset{k\to\infty}{\limsup}\left[\lambda\left( 1-\mu\frac{\tau_{n_{k}}}{\tau_{n_{k}+1}}\right)\left( 2-\lambda+\lambda\mu \frac{\tau_{n_{k}}}{\tau_{n_{k}+1}} \right)\|w_{n_{k}}-y_{n_{k}}\|^{2}\right]\\ &\le&\underset{k\to\infty}{\limsup}\left[ \|h_{n_{k}}-h^{*}\|^{2}-\|h_{{n_{k}}+1}-h^{*}\|^{2}+\beta_{n_{k}} M_{1}\right]\\ &\le& \underset{k\to\infty}{\limsup}\left[ \|h_{n_{k}}-h^{*}\|^{2}-\|h_{n_{k}+1}-h^{*}\|^{2}\right]+\underset{k\to\infty}{\limsup}\beta_{n_{k}} M_{1}\\ &=&- \underset{k\to\infty}{\liminf}\left[ \|h_{n_{k}+1}-h^{*}\|^{2}-\|h_{_{n_{k}}}-h^{*}\|^{2}\right] \le 0. \end{array} $$

This implies that

$$ \lim_{k\to\infty} \|y_{n_{k}}-w_{n_{k}}\|=0. $$

(48)

On the other hand, we have

$$ \begin{array}{@{}rcl@{}} \|h_{n+1}-y_{n}\|&=&\|(1-\lambda)(w_{n}-y_{n})+\lambda \tau_{n} (Ay_{n}-Aw_{n})\|\\ &\le& (1-\lambda)\|w_{n}-y_{n}\|+\lambda\tau_{n}\|Ay_{n}-Aw_{n}\|\\ &\le& (1-\lambda)\|w_{n}-y_{n}\|+\lambda \frac{\tau_{n}}{\tau_{n+1}}\|w_{n}-y_{n}\|\\ &=&\left( 1-\lambda+\lambda\mu\frac{\tau_{n}}{\tau_{n+1}}\right)\|w_{n}-y_{n}\|. \end{array} $$

(49)

Combining (48) and (49) we get

$$ \lim_{k\to\infty} \|h_{n_{k}+1}-y_{n_{k}}\|=0. $$

(50)

Also from Eqs. 48 and 50, it holds

$$ \lim_{k\to\infty} \|h_{n_{k}+1}-w_{n_{k}}\|=0. $$

(51)

Now, we show that

$$ \|h_{n_{k}+1}-h_{n_{k}}\| \to 0 \text{ as } n\to\infty. $$

(52)

Indeed, we have

$$ \|h_{n_{k}}-w_{n_{k}}\|=\alpha_{n_{k}} \|h_{n_{k}}-h_{n_{k}-1}\|=\beta_{n_{k}}\cdot\frac{\alpha_{n_{k}}}{\beta_{n_{k}}} \|h_{n_{k}}-h_{n_{k}-1}\|\to 0. $$

(53)

From Eqs. 51 and 53, we get

$$ \|h_{n_{k}+1}-h_{n_{k}}\|\le \|h_{n_{k}+1}-w_{n_{k}}\|+\|w_{n_{k}}-h_{n_{k}}\|\to 0. $$

Since the sequence $\{h_{n_{k}}\}_{k=1}^{\infty }$ is bounded, it follows that there exists a subsequence $\{h_{n_{k_{j}}}\}_{j=1}^{\infty }$ of $\{h_{n_{k}}\}_{k=1}^{\infty }$, which converges weakly to some z^∗∈ H, such that

$$ \limsup_{k\to \infty}\langle -h^{*},h_{n_{k}}-h^{*}\rangle =\lim_{j\to \infty}\langle -h^{*},h_{n_{k_{j}}}-h^{*}\rangle=\langle -h^{*},z^{*}-h^{*}\rangle. $$

(54)

From Eq. 53, we obtain

$$ w_{n_{k}} \rightharpoonup z^{*} \text{ as } k\to \infty. $$

Using Lemma 6, we conclude z^∗∈Ω. Next, since (54) and the definition of h^∗ = P_Ω(0), we have

$$ \limsup_{k\to \infty}\langle -h^{*},h_{n_{k}}-h^{*}\rangle =\langle -h^{*},z^{*}-h^{*}\rangle\le 0. $$

(55)

Combining (52) and (55), we have

$$ \begin{array}{@{}rcl@{}} \limsup_{k\to \infty}\langle -h^{*},h_{n_{k}+1}-h^{*}\rangle & \le& \limsup_{k\to \infty}\langle -h^{*},h_{n_{k}}-h^{*}\rangle\\ &=&\langle -h^{*},z^{*}-h^{*}\rangle\le 0. \end{array} $$

(56)

Hence, by Eq. 56, $\lim _{n\to \infty }\frac {\alpha _{n}}{\beta _{n}}\|h_{n}-h_{n-1}\|=0$, $\lim _{n\to \infty }\|h_{n+1}-w_{n}\|=0$, Lemmas 9 and 4, we obtain the desired result, $\lim _{n\to \infty }\|h_{n}-h^{*}\|=0$. □

7 Conclusion

This paper builds on recent advances in the computational theory of dynamic user equilibrium. Building on the network extension of the LWR model and its formulation in terms of a system of differential algebraic equations. Our aim is to advocate the use of strongly convergent fixed point iterations for computing dynamic user equilibrium which are provably convergent under mild a-priori monotonicity assumptions on the path delay operator, and which are adaptive in the sense that no global bound on the Lipschitz constant needs to be known. We focussed on the construction of new strongly convergent forward-backward-forward algorithms, augmented by relaxation and inertial modifications. We tested the performance of our algorithms in the Nguyen and the Sioux falls network, and provide thereby evidence that our methods improve upon pre-implemented solvers. In future research we aim to improve the fixed point iteration by reducing its complexity in terms of calls of the DNL subroutine. Indeed, the price to pay for provable convergence under weaker assumptions is that under FBF splitting we have to evaluate the delay operator twice per iterations, which is computationally costly. The FB iteration needs only a single call of the DNL, but converges only under strong monotonicity assumptions. In a future publication we will describe a single-call variant of the FBF, which still guarantees strong convergence under the same monotonicity assumptions as used in this paper.

Another very interesting direction of research we plan to pursue is to replace the costly DNL procedure by alternative approximation schemes motivated by machine learning approaches as commenced in Song et al. (2017).