Worked-out examples of the adequacy of Bayesian optional stopping

Abstract

The practice of sequentially testing a null hypothesis as data are collected until the null hypothesis is rejected is known as optional stopping. It is well known that optional stopping is problematic in the context of p value-based null hypothesis significance testing: The false-positive rates quickly overcome the single test’s significance level. However, the state of affairs under null hypothesis Bayesian testing, where p values are replaced by Bayes factors, has perhaps surprisingly been much less consensual. Rouder (2014) used simulations to defend the use of optional stopping under null hypothesis Bayesian testing. The idea behind these simulations is closely related to the idea of sampling from prior predictive distributions. Deng et al. (2016) and Hendriksen et al. (2020) have provided mathematical evidence to the effect that optional stopping under null hypothesis Bayesian testing does hold under some conditions. These papers are, however, exceedingly technical for most researchers in the applied social sciences. In this paper, we provide some mathematical derivations concerning Rouder’s approximate simulation results for the two Bayesian hypothesis tests that he considered. The key idea is to consider the probability distribution of the Bayes factor, which is regarded as being a random variable across repeated sampling. This paper therefore offers an intuitive perspective to the literature and we believe it is a valid contribution towards understanding the practice of optional stopping in the context of Bayesian hypothesis testing.

Introduction

Psychological science is living exciting and quickly changing days. From the midst of the crisis of confidence that afflicts our field, it has become clear that part of the solution is to reform null hypothesis significance testing (NHST). There are many literature sources stating the reasons supporting this decision. Here we refer to the recent special issue published in The American Statistician (Wasserstein et al., 2019), consisting of a set of 43 (!) articles that elaborate in detail on these issues.

One may question whether NHST is to be blamed for all the problems in our field. Arguably, some of the problems may be ascribed to practitioners misusing NHST. Questionable research practices (QRPs; John et al., 2012) such as post hoc removing of observations, performing multiple tests but reporting only the very few that ‘worked out’, and merging conditions are unfortunately all too common (Simmons et al., 2011). In this paper, we focus on another such QRP: Collecting more data while continuously testing for significance until rejection of the null hypothesis is possible. One aspect that QRPs make salient is that having the analysis depend on observing the outcome variables of interest (e.g., under optional stopping, or sequential testing, procedures) may have deleterious effects on the quality of the published research.

Proposed solutions to mitigate some of the problems alluded to above include the preregistration of experiments (Nosek et al., 2018), the use of registered reports (Nosek and Lakens, 2014), and the adoption of alternative statistical approaches to NHST. Here we explicitly consider one alternative to NHST and p values that has gained increased attention in the literature in recent years, namely, that of null hypothesis Bayesian testing (NHBT) and the Bayes factor (Jeffreys, 1961; Kass & Raftery, 1995; Tendeiro & Kiers, 2019; van de Schoot et al., 2017). Given two models ${\mathscr{M}}_{0}$ and ${\mathscr{M}}_{1}$, the Bayes factor BF₁₀ is the multiplicative term that updates the prior odds into posterior odds:

$$ \underset{\text{prior odds}}{\underbrace{\frac{p(\mathcal{M}_{1})}{p(\mathcal{M}_{0})}}} \times \underset{BF_{10}}{\underbrace{\frac{p(D|\mathcal{M}_{1})}{p(D|\mathcal{M}_{0})}}} = \underset{\text{posterior odds}}{\underbrace{\frac{p(\mathcal{M}_{1}|D)}{p(\mathcal{M}_{0}|D)}}}. $$

(1)

In other words, the Bayes factor quantifies the update in our relative belief about the two entertained models in light of the observed data D. Alternatively, the Bayes factor can be interpreted as the relative predictive value of each model. If, for instance, the observed data are better predicted under ${\mathscr{M}}_{1}$ then $p(D|{\mathscr{M}}_{1}) > p(D|{\mathscr{M}}_{0})$ and as a consequence BF₁₀ > 1. If ${\mathscr{M}}_{0}$ represents the null model and ${\mathscr{M}}_{1}$ an alternative model, the Bayes factor can be used to quantify evidence for ${\mathscr{M}}_{1}$ compared to ${\mathscr{M}}_{0}$; if a prior probability ratio is given, a posterior probability ratio can be computed. For a more thorough discussion of Bayes factors, including their merits and possible issues, see Tendeiro and Kiers (2019).

Goal of this paper

In this paper, we consider the problem of optional stopping by means of NHBT. It is well known that optional stopping is a real problem under p value-based NHST (Armitage et al., 1969); we will quickly illustrate the problem with a simple and well-known example. Interestingly, the optional stopping problem (or lack thereof) under the Bayesian framework has been far less consensual. In a provokingly titled paper (‘Optional stopping: No problem for Bayesians’), Rouder (2014) suggested that optional stopping is allowed under the Bayesian paradigm (he is not alone; see Edwards et al., 1963; Kadane et al., 1996). Rouder’s main premise is that the Bayesian optional stopping procedure leads to a well-calibrated decision rule in a particular sense: Given equal prior model probabilities, if for example BF₁₀ = 10, then it must happen that data randomly generated under ${\mathscr{M}}_{1}$ are ten times more likely to produce BF₁₀ = 10 than data randomly generated under ${\mathscr{M}}_{0}$. It is in this particular sense that Rouder (2014) claims that the Bayes factor is able to handle optional stopping (de Heide and Grünwald, 2017). Before proceeding, we note that other perspectives on the Bayesian optional stopping problem do exist. At the base of these alternatives is the multiplicity of ways of operationalizing the idea of being “able to handle optional stopping” (de Heide & Grünwald, 2017). And in fact, others have argued that the Bayesian optional stopping procedure can be problematic in some sense (e.g., Sanborn et al., 2014; Sanborn & Hills, 2014; Yu et al., 2014; de Heide & Grünwald, 2017). For the current paper, we will focus exclusively on Rouder’s perspective on the optional stopping problem (for those interested, see Rouder & Haaf, 2019 for a recent account of Rouder’s position on the aforementioned problems).

Recently, Deng et al. (2016) and especially Hendriksen et al. (2020) have offered mathematical proofs showing that the Bayesian optional stopping procedure is well calibrated in the sense of Rouder (2014). These papers further extended the realm of situations under which Bayesian optional stopping is expected to work (including in cases involving improper priors and nuisance parameters). Unfortunately, both of these papers are mathematically too technical for the common readership in the applied social sciences.

Rouder (2014) defended his assertions by means of simulated data. For fixed Bayes factors (called ‘nominal’ Bayes factors), many datasets were generated under either model and the ratio of cases under each model leading to (approximately) that Bayes factor was computed (this is the ‘observed’ Bayes factor). Our current contribution consists of offering worked-out examples that complement Rouder’s conjectures (which are proved in general terms by Hendriksen et al., 2020). Whenever possible, closed-form mathematical derivations of distributions of random variables which complement Rouder’s simulated distributions are provided. To the best of our knowledge, our contribution is unique in its modus operandi. Thus, we expect that our approach can offer help to further understand the optional stopping problem under the Bayesian framework, in the sense advocated by Rouder (2014).

The remainder of the paper is organized as follows. In the next section, we introduce the optional stopping procedure in detail, both under the frequentist and the Bayesian paradigms. We motivate Rouder’s reasoning by illustrating the connection between his idea and the definition of the Bayes factor as a ratio of two prior predictive distributions (e.g., Etz et al., 2018). Next, we show our results for the two hypotheses tests considered in Rouder (2014). Each section includes theoretical derivations of distributions of the Bayes factor. This is possible by looking at the Bayes factor as a function of randomly drawn data. Thus, effectively, what we offer is sampling distributions for the Bayes factor under either model under comparison. This approach complements that of Rouder, which is exclusively based on simulation. We compare our theoretically derived distributions with approximated distributions found by simulation, thus making clear that our precise results actually strengthen the simulation-based results by Rouder. We finish the paper with a discussion of the main theoretical findings in our derivations and some of the limitations of our approach. Most of the mathematical derivations are included in the Supplemental Material, to ease the reading of the paper. Furthermore, we provide all the R code that implements our results and produces all figures in OSF (https://osf.io/5z92h/).

Optional stopping

Under the frequentist paradigm

In this setting, the optional stopping (or sequential testing) procedure amounts to looking regularly at the statistical significance as data come in, and stopping once the p value falls below the critical threshold α (typically .05 or .01). The problem with this approach is that it leads to proportions of false-positive results above the nominal type I error rate α (typically .05). This is a well-known result (e.g., Armitage et al., 1969; Jennison and Turnbull, 1990). We used a simulation to illustrate the situation. The following procedure was replicated 1000 times: randomly draw n = 2 observations from $\mathcal {N}(0, 1)$ and compute the p value of a two-tailed one-sample t test (${\mathscr{M}}_{0}: \mu =0$ versus ${\mathscr{M}}_{1}: \mu \not =0$); stop if p is below α = .05, otherwise collect one more observation and recompute p; proceed until either p < α or n is 1,000,000. Figure 1 shows the cumulative proportion of replications that terminated due to statistical significance (i.e., a false positive) as a function of the sample size. As can be seen, the proportion of false positives increases¹ with n, and even at low sample sizes the error rates are already deemed unacceptably large (e.g., .36 at n = 50). Therefore, optional stopping under the frequentist paradigm leads to serious biases in favor of rejecting the null hypothesis.

Fig. 1

Proportion of false positives as a function of sample size under the frequentist optional stopping procedure, for a one-sample t test. The x-axis is in log-scale. The grayed area shows high agreement with results previously shown by Jennison and Turnbull (1990, Table 1)

Although there are proposals under the frequentist framework to try to remedy the situation (e.g., Armitage, 1960; Botella et al., 2006; Fitts, 2010; Frick, 1998; Jennison & Turnbull, 1999; Lakens, 2014; Pocock, 1983; Wald, 1945), these are largely ignored in psychology (Lakens, 2014). If such corrections are not used, researchers must adhere to designs based on predefined (i.e., fixed) sample sizes and sample until completion. Unfortunately, there is ample empirical evidence supporting the hypothesis that data collection decisions made by researchers are often dependent on the magnitude of the p value (John et al., 2012; Yu et al., 2014). For example, Yu et al. (2014) found evidence indicating that researchers are willing to prematurely terminate data collection upon observing either a low or a large p value. The problem is severe, and one may rightfully question whether similar limitations hold with Bayesian statistics.

Under the Bayesian paradigm

An optional stopping procedure similar to that under the frequentist paradigm is now considered. Unlike the frequentist procedure, now the p value is replaced by the Bayes factor BF₁₀. After observing the n-th datum and computing BF₁₀, one decides to stop data collection and retain ${\mathscr{M}}_{1}$ if BF₁₀ is larger than a threshold BF_U (thus, data evidence is deemed sufficiently compelling for ${\mathscr{M}}_{1}$). Alternatively, one decides to stop data collection and retain ${\mathscr{M}}_{0}$ if BF₁₀ is smaller than a threshold BF_L (data evidence is deemed sufficiently compelling for ${\mathscr{M}}_{0}$). Finally, data collection should proceed in case BF_L < BF₁₀ < BF_U.

The thresholds BF_U and BF_L should be chosen before data collection. In our analyses, we use the same threshold values as Rouder (2014): BF_U = 10 and $BF_{L} = \frac {1}{10}$ (see also Schönbrodt et al., 2017). These values can be considered as strong evidence, according to Jeffreys (1961).² Thus, similar amounts of evidence are required to terminate data collection in favor of either model when Bayesian optional stopping is employed. We notice that the Bayesian optional stopping procedure differs from the frequentist counterpart in one crucial aspect: The Bayesian procedure can stop due to sufficiently strong evidence in favor of ${\mathscr{M}}_{0}$. This is not possible by means of p value based NHST, where evidence can only be gathered against ${\mathscr{M}}_{0}$. Thus, the Bayesian optional stopping procedure has this one clear advantage over the frequentist method.

The Bayesian optional stopping procedure outlined above has been recurrently proposed in the literature (as early as Lindley, 1957; see also Kass and Raftery, 1995; Edwards et al., 1963). Several studies implemented and further extended this method (e.g., Matzke et al., 2015; Schönbrodt et al., 2017; Schönbrodt & Wagenmakers, 2018; Wagenmakers et al., 2012; Wagenmakers et al., 2015). There is general agreement that, under the Bayesian framework, the stopping rule is unrelated to the interpretation of the results (Rouder, 2014; Sanborn & Hills, 2014); this is a consequence of the likelihood principle (Berger & Wolpert, 1988). However, some have questioned frequentist properties related to the procedure, that is, how the procedure works in the long run (Sanborn et al., 2014; Yu et al., 2014). Therefore, the issue of whether the procedure ‘works as advertised’ has been a matter of contention.

In an attempt to clarify matters, Rouder (2014) presented an argument according to which the Bayes factor is said to be well calibrated under Bayesian optional stopping. To understand the reasoning behind Rouder’s simulation study, we make use of the concept of a prior predictive distribution (see e.g., Etz et al., 2018 for a more elaborate exposition). Assume entertaining two competing models in order to infer about the mean μ of a normally distributed population with known variance σ²: ${\mathscr{M}}_{0}: \mu =0$ versus ${\mathscr{M}}_{1}: \mu \sim \mathcal {N}(0, {\sigma _{1}^{2}})$ with σ₁ known (the corresponding Bayes factor is worked at length in this paper). We can generate values of μ from both of these models.³ Subsequently, we can generate sample data based on these μ parameters. The distributions of the resulting sample means (i.e., the prior predictive distributions) for 100,000 simulations, each simulation consisting of a sample of size 10, are shown in panel A of Fig. 2 (sample means larger than .25 in absolute value are not shown to ease the visualization).

Fig. 2

Prior predictive distributions (A and B) and the corresponding ratios (C and D), for normally distributed data ($X_{i}\sim \mathcal {N}(\mu ,\sigma ^{2})$ for i = 1,…,n and known variance σ²), when comparing ${\mathscr{M}}_{0}:\mu =0$ versus ${\mathscr{M}}_{1}: \mu \sim \mathcal {N}(0, {\sigma _{1}^{2}})$, with σ₁ known. In A and B, the prior predictive distributions for either model are plotted back-to-back for easier visual comparison. The (logarithm of) the Bayes factor is a mathematical function of the sample mean $\overline {X}$, thus we can think of it as being a random variable. The prior predictive distributions for $\overline {X}$ (A) and for $\ln (BF_{10})$ (B) under each model are closely related, as indicated by the absolute frequencies. Therefore, the ratios of both pairs of prior predictive distributions give the Bayes factor (C and D). See text for details

The Bayes factor BF₁₀ quantifies the relative probability of the observed data under ${\mathscr{M}}_{1}$ versus ${\mathscr{M}}_{0}$. In other words, the Bayes factor equals the ratio of the two prior predictive distributions (for an arbitrary sample mean $\overline {X}$). Thus, we can compare the relative heights of the two distributions for different points along the x-axis to get the corresponding Bayes factors; see panel C.

The two-sided alternative model ${\mathscr{M}}_{1}$ is symmetric in the sense that its within-model prior is symmetric around 0. The green arrows in panel A indicate the observed frequencies under either model of sample means of (about) .19 in magnitude. As shown in panel C, the associated Bayes factor is approximately the same (.63 at $\overline {X}=-.19$ and .59 at $\overline {X}=.19$; the exact value (solid line) is BF₁₀ = .63).

Observe that the Bayes factor is a mathematical function of the sample mean (for the running example, see Eq. 13). Panel B in Fig. 2 displays the frequencies of the (logarithm of) BF₁₀. Each bin in panel B (with a particular $\ln (BF_{10})$ value) is matched by the pair of bins in panel A with sample means corresponding to that BF₁₀ value via Eq. 13. For example, $\overline {X}=\pm .19$ corresponds to $\ln (BF_{10})=-.46$; the frequency associated to $\ln (BF_{10})=-.46$ is the sum of the frequencies associated to $\overline {X}=\pm .19$, under each model (see the green arrows in panel B). Their ratio should therefore also equal the Bayes factor; that is displayed in panel D.

More generally, let’s consider prior model odds of 1-to-1, thus assume that both models are equally likely a priori. In this case, the Bayes factor is equal to the posterior odds (by Eq. 1):

$$ \underset{BF_{10}}{\underbrace{\frac{p(D|\mathcal{M}_{1})}{p(D|\mathcal{M}_{0})}}} = \underset{\text{posterior odds}}{\underbrace{\frac{p(\mathcal{M}_{1}|D)}{p(\mathcal{M}_{0}|D)}}}. $$

(2)

The distribution of the left-hand side of Eq. 2 under either ${\mathscr{M}}_{0}$ or ${\mathscr{M}}_{1}$ for a given sample size can be approximated by simulation (as illustrated by panel B in Fig. 2). But the Bayes factor is equal to the posterior odds by Eq. 2. Thus, for each generated data set (under either model) we know that ${\mathscr{M}}_{1}$ is more likely than ${\mathscr{M}}_{0}$ by a factor corresponding to the resulting BF₁₀ for that data set. Rouder’s reasoning is the following (Assertion 1): The previous interpretation must hold even when one does not know under which model the data were generated. In other words, given a data set generated under either ${\mathscr{M}}_{0}$ or ${\mathscr{M}}_{1}$ (unknown to us), the Bayes factor can still be interpreted as the corresponding posterior odds. It is in this sense that Rouder claims that the Bayes factor (i.e., the posterior odds) is well calibrated (de Heide and Grünwald, 2017). Rouder used simulations to make his point. For any given BF₁₀ value, he tallied the number of simulations that resulted in approximately⁴ that Bayes factor, under either model (i.e., panel B in Fig. 2). The ratio of obtained Bayes factors under both models must then equal the Bayes factor itself under Rouder’s assertion (i.e., panel D in Fig. 2). For instance, the number of replicate experiments with a fixed sample size that produce BF₁₀ = 10 under ${\mathscr{M}}_{1}$ should be approximately ten times larger than the number of replicate experiments that produce BF₁₀ = 10 under ${\mathscr{M}}_{0}$.

Rouder then further suggested the following (Assertion 2): The above property also holds under optional stopping. Thus, using the Bayesian optional stopping procedure in each replication should preserve the property above of the Bayes factor. This goes beyond Assertion 1 in that it lets go of the fixed sample size. Instead, data gets continuously sampled until the BF₁₀ hits one of two thresholds (for instance, BF₁₀ = 10 or BF₁₀ = 1/10). Again, the number of replicate experiments under optional stopping that produce BF₁₀ = 10 under ${\mathscr{M}}_{1}$ should be approximately ten times larger than the number of replicate experiments that produce BF₁₀ = 10 under ${\mathscr{M}}_{0}$.

Our rationale

Rouder (2014) provided evidence for his statements by means of simulations and approximations. We now offer a mathematical view on this problem and derive probability distributions instead of approximate histograms of frequencies. We considered the same hypothesis testing procedures as Rouder. These are based on testing hypotheses about the mean of a normal distribution $\mathcal {N}(\mu , \sigma ^{2})$, for which the variance is assumed known. The first test is given by ${\mathscr{M}}_{0}:\mu =0$ versus ${\mathscr{M}}_{0}:\mu =\mu _{1}$, which tests two-point hypotheses; we refer to this case as the ‘point null versus point alternative test’. The second test is ${\mathscr{M}}_{0}:\mu =0$ versus ${\mathscr{M}}_{0}:\mu \sim \mathcal {N}(0, {\sigma _{1}^{2}})$ with ${\sigma _{1}^{2}}$ known; we refer to this case as the ‘point null versus interval alternative test’. In what follows, we will consider each of these two tests in turn. In our derivations, we provide a proof for Assertion 1 for a fixed sample size n. For Assertion 2, we only provide a proof for a particular situation, namely, that the assertion holds after exactly one step of the optional stopping procedure. For a general mathematical proof of the adequacy of the calibration of Bayes factors under Bayesian optional stopping we again refer the reader to Hendriksen et al. (2020).

Point null versus point alternative test

Suppose data are independently normally distributed: $X_{i}\sim \mathcal {N}(\mu ,\sigma ^{2})$ for i = 1,…,n and known variance σ². Our goal is to compare the predictive value of the following two models for parameter μ: ${\mathscr{M}}_{0}: \mu =0$ and ${\mathscr{M}}_{1}: \mu =\mu _{1}$. The Bayes factor BF₁₀ is given as follows (see Theorem 1 in the Supplemental Material for a derivation):

$$ BF_{10} = \exp \left[ \frac{n\mu_{1}(2\overline{X}-\mu_{1})}{2\sigma^{2}} \right]. $$

(3)

Working with logarithms simplifies the derivations, thus consider the following expression instead:

$$ \ln(BF_{10}) = \frac{n\mu_{1}(2\overline{X}-\mu_{1})}{2\sigma^{2}}. $$

(4)

We next derive the sampling distribution of $\ln (BF_{10})$ under each model, ${\mathscr{M}}_{0}$ and ${\mathscr{M}}_{1}$, and then divide both densities and show that it results in the Bayes factor. This proves Assertion 1.

Initial n observations

In general, the sampling distribution of $\overline {X}$ when the population mean is fixed (say, at μ_X) is given by

$$ \overline{X} \sim \mathcal{N}\left( \mu_{X}, \frac{\sigma^{2}}{n}\right). $$

(5)

$\ln (BF_{10})$ is a linear transformation of $\overline {X}$, thus the density of $\ln (BF_{10})$ can be found by means of the change of variable theorem (see Lemma 2 in the Supplemental Material for a derivation):

$$ f_{\ln(BF_{10})}(y) = \frac{\sigma}{\sqrt{n}\mu_{1}} \phi\left( \frac{\sigma}{\sqrt{n}\mu_{1}}y + \frac{\sqrt{n}\mu_{1}}{2\sigma} - \frac{\sqrt{n}}{\sigma}\mu_{X} \right), $$

(6)

where y is a realization of $\ln (BF_{10})$ and ϕ denotes the probability density function of the standard normal distribution. We therefore conclude that the sampling distribution of $\ln (BF_{10})$ under ${\mathscr{M}}_{0}$ and ${\mathscr{M}}_{1}$ is given by Eq. 6 for μ_X equal to 0 and μ₁, respectively.

Dividing the densities

The final step consists of showing that $\frac {f_{\ln (BF_{10})}^{{\mathscr{M}}_{1}}(y)}{f_{\ln (BF_{10})}^{{\mathscr{M}}_{0}}(y)} = \exp (y)$. Since y is a realization of $\ln (BF_{10})$, $\exp (y)$ is the realization of BF₁₀ for the corresponding observed data, which concludes the proof of Assertion 1.

$$ \begin{array}{@{}rcl@{}} \frac {f_{\ln(BF_{10})}^{\mathcal{M}_{1}}(y)} {f_{\ln(BF_{10})}^{\mathcal{M}_{0}}(y)} &=& \frac {\exp\left[ -\frac{1}{2}\left( \frac{\sigma}{\sqrt{n}\mu_{1}}y-\frac{\sqrt{n}\mu_{1}}{2\sigma}\right)^{2} \right]} {\exp\left[ -\frac{1}{2}\left( \frac{\sigma}{\sqrt{n}\mu_{1}}y+\frac{\sqrt{n}\mu_{1}}{2\sigma}\right)^{2} \right]} \\ &=& \exp\left[ -\frac{1}{2}(-4) \frac{\sigma}{\sqrt{n}\mu_{1}}y \frac{\sqrt{n}\mu_{1}}{2\sigma} \right] \\ &=& \exp(y). \end{array} $$

(7)

Proceed with optional stopping

We need a rule to decide whether the evidence provided by the first n observations is decisive (warranting the interruption of the optional stopping). As explained above, we set up the same rule as Rouder (2014): Stop if BF₁₀ > BF_U = 10 (retain ${\mathscr{M}}_{1}$) or $BF_{10} < BF_{L} = \frac {1}{10}$ (retain ${\mathscr{M}}_{0}$), otherwise proceed sampling. Equation 4 allows reexpressing the decision rule in terms of the observed sample mean. Let $\overline {X}_{0}$ and $\overline {X}_{1}$ denote the sample mean values associated with BF_L and BF_U, respectively. Solving Eq. 4 with respect to $\overline {X}$ gives

$$ \begin{array}{@{}rcl@{}} \overline{X} &=& \frac{1}{2}\mu_{1} + \frac{\sigma^{2}}{n\mu_{1}}\ln(BF_{10}). \end{array} $$

(8)

We conclude that $\overline {X}_{0} = \frac {1}{2}\mu _{1} - \frac {\sigma ^{2}}{n\mu _{1}}\ln (10)$ and $\overline {X}_{1} = \frac {1}{2}\mu _{1} + \frac {\sigma ^{2}}{n\mu _{1}}\ln (10)$. The sequential testing procedure stops after the first n observations when $\overline {X} \leq \overline {X}_{0}$ (retain ${\mathscr{M}}_{0}$) or $\overline {X} \geq \overline {X}_{1}$ (retain ${\mathscr{M}}_{1}$). The test is indecisive for all sample means in the interval $\mathcal {I}=(\overline {X}_{0}, \overline {X}_{1})$.

In case $\overline {X}\in \mathcal {I}$, we need to collect more data and reassess the relative evidence between both models. Suppose k (k ≥ 1) more observations are collected. It is important to distinguish between the first n observations (now fixed) from the k new observations (to be sampled). We therefore express the sample mean value of the (n + k) observations as follows:

$$ \overline{X}_{n+k} = \frac{n}{n+k} \left( \overline{X}_{n}+\frac{{\sum}_{i=n+1}^{n+k}X_{i}}{n}\right), $$

(9)

where we now introduce the general notation $\overline {X}_{t}$ to refer to the sample mean based on the first t observations. After the k new observations are available, we use Eq. 4 to recompute $\ln (BF_{10})$:

$$ \begin{array}{@{}rcl@{}} \ln(BF_{10}) &=& \frac{(n+k)\mu_{1}(2\overline{X}_{n+k}-\mu_{1})}{2\sigma^{2}} \\ &=& \frac{(n+k)\mu_{1}}{2\sigma^{2}} \left[ \frac{2n}{n+k} \left( \overline{X}_{n}+\frac{{\sum}_{i=n+1}^{n+k}X_{i}}{n}\right) - \mu_{1} \right]. \end{array} $$

(10)

The remaining of the proof consists of deriving the density of $\ln (BF_{10})$ given by Eq. 10 under each model, and then relate the ratio of both densities to the Bayes factor. We note that this is the distribution conditional on indecisive evidence after the first n observations. We first derive the distribution of the sum $S = \overline {X}_{n}+\frac {{\sum }_{i=n+1}^{n+k}X_{i}}{n}$; $\ln (BF_{10})$ is simply a linear transformation of S.

Firstly, and again assuming that the true population mean is μ_X (a general unknown quantity), we observe that $\overline {X}_{n}$ now follows a truncated normal distribution:

$$ \overline{X}_{n} \sim \mathcal{N}_{T}\left( \mu_{X}, \frac{\sigma^{2}}{n}; \mathcal{I}\right). $$

(11)

Moreover, from $X_{i}\sim \mathcal {N}(\mu _{X}, \sigma ^{2})$ it follows that

$$ \frac{{\sum}_{i=n+1}^{n+k}X_{i}}{n} \sim \mathcal{N}\left( \frac{k}{n}\mu_{X}, \frac{k}{n^{2}}\sigma^{2}\right). $$

(12)

Random variables $\overline {X}_{n}$ and $\frac {{\sum }_{i=n+1}^{n+k}X_{i}}{n}$ are independent, since sampling the k new observations is independent from the sampling of the first n observations. Hence, the distribution of S is given by the convolution of both densities (e.g., Blitzstein and Hwang, 2019, Section 8.2). We derive the closed form expression of the density of S in the Supplemental Material (see Theorem 3 for the general case, and Lemmas 3 and 4 for the particular cases under ${\mathscr{M}}_{0}$ and ${\mathscr{M}}_{1}$, resp.). Finally, the density of $\ln (BF_{10})$ is found by means of the change of variable theorem (Supplemental Material, Lemma 5).

Dividing the densities

Finally, we show that the ratio of the densities of $\ln (BF_{10})$ under either model, after (n + k) observations, leads to the Bayes factor (Supplemental Material, Lemma 6).

Unconditional distribution

What we just established above is the closed-form expression of the distribution of $\ln (BF_{10})$ under either model, conditional on an indecisive test result after the first n observations. Theorem 4 in the Supplemental Material can now be used to ascertain that the Bayes factor is well calibrated overall, that is, after the initial n observations (in case the first test was decisive) or after (n + k) observations (in case the first test was indecisive).

Example 1

We illustrate our derivations by means of an example. We use simulations as in Rouder (2014) and compare the approximate results from the simulations with our precise derivations. Let n = 10, k = 5, σ = .3, and μ₁ = .1. For each simulation (total = 100,000 simulations), we followed this procedure:

• 1. Randomly draw n observations from $\mathcal {N}(0, \sigma ^{2})$ (i.e., under ${\mathscr{M}}_{0}$). Compute $\overline {X}$ and $\ln (BF_{10})$; compare with the corresponding exact distributions (Eqs. 5 and 6 with μ_X = 0).

• 2. Randomly draw n observations from $\mathcal {N}(\mu _{1}, \sigma ^{2})$ (i.e., under ${\mathscr{M}}_{1}$). Compute $\overline {X}$ and $\ln (BF_{10})$; compare with the corresponding exact distributions (Eqs. 5 and 6 with μ_X = μ₁).

• 3. Approximate the ratio of the densities of $\ln (BF_{10})$ under either model and compare it to BF₁₀. The approximation is achieved by partitioning the support interval in small subintervals⁵ and then computing the ratio of the observed frequencies in each subinterval. This gives the observed (approximate) density ratio, which we compare to its exact counterpart (Eq. 7).

• 4. Stop in case BF₁₀ is larger than 10 or smaller than $\frac {1}{10}$, otherwise: Collect k more observations, recompute $\overline {X}$ and $\ln (BF_{10})$ under each model, and approximate the ratio of the densities of $\ln (BF_{10})$ under either model and compare it to BF₁₀.

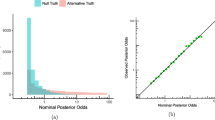
Panels A and B of Fig. 3 show the approximate distribution (histogram) and exact distribution (solid line) of $\overline {X}$ and $\ln (BF_{10})$ under ${\mathscr{M}}_{0}$ and ${\mathscr{M}}_{1}$, after the initial n observations. As can be seen, our exact distributions work as intended. In panel C we plot the approximate (points) and exact (solid line) density ratio. Our results imply that the line in panel C is the exponential function (see Eq. 7). The conclusion is that, as proved, the ratio of frequencies of observed Bayes factor values under either model (as also done by Rouder, 2014) is just an approximation to that very same nominal Bayes factor value.

Fig. 3

Distribution of various random variables after n observations, for the point null versus point alternative test. A: $\overline {X}$ under ${\mathscr{M}}_{0}$ (upper distribution; Eq. 5 with μ_X = 0) and under ${\mathscr{M}}_{1}$ (inverted distribution; Eq. 5 with μ_X = μ₁). B: $\ln (BF_{10})$ under ${\mathscr{M}}_{0}$ (upper distribution; Eq. 6 with μ_X = 0) and under ${\mathscr{M}}_{1}$ (inverted distribution; Eq. 6 with μ_X = μ₁). C: Relation between the nominal and observed $\ln (BF_{10})$ values based on approximation by simulation (points) and on the exact values (line) (Eq. 7)

Figures 4 and 5 show the distributions of $\overline {X}_{n}$, $\frac {{\sum }_{i=n+1}^{n+k}X_{i}}{n}$, and S under ${\mathscr{M}}_{0}$ and ${\mathscr{M}}_{1}$, respectively. Figure 6 illustrates the most relevant result for the point null versus point alternative test considered here: After optional stopping, the ratio of the densities of the Bayes factor values under each model does indeed lead to the Bayes factor, as proved above.

Fig. 4

Distribution of various random variables under ${\mathscr{M}}_{0}$ after (n + k) observations, for the point null versus point alternative test. These random variables correspond to intermediate results that facilitate the proof of Assertion 2 (Supplemental Material, Lemma 6). A: $\overline {X}_{n}$ (Eq. 11 with μ_X = 0). B: $\frac {{\sum }_{i=n+1}^{n+k}X_{i}}{n}$ (Eq. 12 with μ_X = 0). C: $S = \overline {X}_{n} + \frac {{\sum }_{i=n+1}^{n+k}X_{i}}{n}$ (Supplemental Material, Lemma 3)

Fig. 5

Distributions of various random variables under ${\mathscr{M}}_{1}$ after (n + k) observations, for the point null versus point alternative test. These random variables correspond to intermediate results that facilitate the proof of Assertion 2 (Supplemental Material, Lemma 6). A: $\overline {X}_{n}$ (Eq. 11 with μ_X = μ₁). B: $\frac {{\sum }_{i=n+1}^{n+k}X_{i}}{n}$ (Eq. 12 with μ_X = μ₁). C: $S = \overline {X}_{n} + \frac {{\sum }_{i=n+1}^{n+k}X_{i}}{n}$ (Supplemental Material, Lemma 4)

Fig. 6

Visualization of Assertion 2 for the point null versus point alternative test. A: $\ln (BF_{10})$ under ${\mathscr{M}}_{0}$ (upper distribution) and under ${\mathscr{M}}_{1}$ (lower distribution) (Supplemental Material, Lemma 5). B: Relation between the nominal and observed $\ln (BF_{10})$ values based on approximation by simulation (points) and on the exact values (line) (Supplemental Material, Lemma 6), after (n + k) observations for the point null versus point alternative test

Probability of interesting events

One added value of knowing the distribution of BF₁₀ under either model is that it allows quantifying the probability of interesting events. For example, by means of Eq. 8 we know that the procedure is inconclusive after n observations when $\overline {X}_{n}$ is in $\mathcal {I}=(-0.157, 0.257)$. We can quantify the probability of each possible outcome (i.e., retain ${\mathscr{M}}_{0}$, retain ${\mathscr{M}}_{1}$, or inconclusive) under each model through either the distribution of $\overline {X}$ (Eq. 5) or, equivalently, the distribution of $\ln (BF_{10})$ (Eq. 6); see Table 1 (top panel). Similarly, we can compute the overall probabilities of each event after the k extra observations are collected (Table 1, bottom panel). Because both hypotheses being tested are of the same type, the probabilities in Table 1 are symmetric (e.g., $p(\text {retain }{\mathscr{M}}_{0}|{\mathscr{M}}_{0}, n\text { obs.}) =$$p(\text {retain }{\mathscr{M}}_{1}|{\mathscr{M}}_{1}, n\text { obs.}) = .049$). It can be observed that, in this situation, the addition of k extra observations increases the probability of making a correct decision.

Table 1 Point null versus point alternative test, Example 1 (n = 10, k = 5, σ = .3, and μ₁ = .1): Probability of each decision after n observations (top panel) and overall after (n + k) observations (bottom panel), under either model

Point null versus interval alternative test

We now look at a different alternative model for μ and consider testing ${\mathscr{M}}_{0}:\mu =0$ versus ${\mathscr{M}}_{1}: \mu \sim \mathcal {N}(0, {\sigma _{1}^{2}})$, with σ₁ known. This test has been studied before (e.g., Berger and Delampady, 1987; Berger & Pericchi, 2001; Rouder, 2014; Rouder et al., 2018). The Bayes factor BF₁₀ is given by (for a derivation see, e.g., Tendeiro & Kiers, 2019, Appendix B):

$$ BF_{10} = \frac{\sigma}{\sqrt{\sigma^{2}+n{\sigma_{1}^{2}}}}\exp\left[\frac{n^{2}{\sigma_{1}^{2}}\overline{X}^{2}}{2\sigma^{2}(\sigma^{2}+n{\sigma_{1}^{2}})}\right], $$

(13)

or in terms of logarithms,

$$ \ln(BF_{10}) = \lambda + \frac{n^{2}{\sigma_{1}^{2}}\overline{X}^{2}}{2\sigma^{2}(\sigma^{2}+n{\sigma_{1}^{2}})}, $$

(14)

where $\lambda = \ln \left (\frac {\sigma }{\sqrt {\sigma ^{2}+n{\sigma _{1}^{2}}}}\right )$ does not depend on the observed data.

We will follow a similar strategy as for the point null versus point alternative test. First, we derive the sampling distribution of $\ln (BF_{10})$ under each model after the first n observations, and show that the ratio of both densities results in the Bayes factor. Second, we collect k more observations for the cases where evidence is inconclusive and reassess the distributions of $\ln (BF_{10})$ under each model. Once more, we will establish that the ratio of both densities results in the Bayes factor.

Under ${\mathscr{M}}_{0}$

When μ = 0, the sampling distribution of $\overline {X}$ is given by $\overline {X}|{\mathscr{M}}_{0} \sim \mathcal {N}\left (0, \frac {\sigma ^{2}}{n}\right )$ (Eq. 5 with μ_X = 0). It then follows that $\frac {\overline {X}-0}{\sigma /\sqrt {n}}\sim \mathcal {N}(0, 1)$ and $\left (\frac {\overline {X}-0}{\sigma /\sqrt {n}}\right )^{2} = \frac {n\overline {X}^{2}}{\sigma ^{2}}{\sim \chi ^{2}_{1}}$. Finally, observe that $\ln (BF_{10})$ (Eq. 14) is a linear function of $\frac {n\overline {X}^{2}}{\sigma ^{2}}$, thus the distribution $\ln (BF_{10})$ can be found by the change of variable theorem (see Lemma 7 in the Supplemental Material, with ${\sigma _{X}^{2}} = \frac {\sigma ^{2}}{n}$):

$$ f_{\ln(BF_{10})}^{\mathcal{M}_{0}}(y) = \frac{2(\sigma^{2}+n{\sigma_{1}^{2}})}{n{\sigma_{1}^{2}}} f_{{\chi^{2}_{1}}}\left[\frac{2(\sigma^{2}+n{\sigma_{1}^{2}})(y-\lambda)}{n{\sigma_{1}^{2}}}\right], \text{ for }y > \lambda. $$

(15)

Under ${\mathscr{M}}_{1}$

The sampling distribution of $\overline {X}$ is given by

$$ p(\overline{X}|\mathcal{M}_{1}) = {\int}_{-\infty}^{\infty} p(\overline{X}|\mu, \mathcal{M}_{1})p(\mu|\mathcal{M}_{1}) d\mu, $$

where $\overline {X}|\mu , {\mathscr{M}}_{1} \sim \mathcal {N}\left (\mu , \frac {\sigma ^{2}}{n}\right )$ and $\mu |{\mathscr{M}}_{1} \sim \mathcal {N}(0, {\sigma _{1}^{2}})$. In the Supplemental Material (Lemma 8) we solve the integral and conclude that

$$ \overline{X}|\mathcal{M}_{1} \sim \mathcal{N}\left( 0, \frac{\sigma^{2}}{n} + {\sigma_{1}^{2}}\right). $$

(16)

It then follows that $\frac {\overline {X}}{\sqrt {\frac {\sigma ^{2}}{n}+{\sigma _{1}^{2}}}} \sim \mathcal {N}(0, 1)$ and $\left (\frac {\overline {X}}{\sqrt {\frac {\sigma ^{2}}{n}+{\sigma _{1}^{2}}}}\right )^{2} = \frac {n\overline {X}^{2}}{\sigma ^{2}+n{\sigma _{1}^{2}}} \sim {\chi ^{2}_{1}}$. Again, observe that $\ln (BF_{10})$ (Eq. 14) can be expressed as a linear function of $\frac {n\overline {X}^{2}}{\sigma ^{2}+n{\sigma _{1}^{2}}}$, thus the distribution $\ln (BF_{10})$ can be found by the change of variable theorem (see Lemma 7 in the Supplemental Material, with ${\sigma _{X}^{2}} = \frac {\sigma ^{2}}{n}+{\sigma _{1}^{2}}$):

$$ f_{\ln(BF_{10})}^{\mathcal{M}_{1}}(y) = \frac{2\sigma^{2}}{n{\sigma_{1}^{2}}} f_{{\chi^{2}_{1}}}\left[\frac{2\sigma^{2}(y-\lambda)}{n{\sigma_{1}^{2}}}\right], \text{ for }y > \lambda. $$

(17)

Dividing the densities

As a final step, we show that $\frac {f_{\ln (BF_{10})}^{{\mathscr{M}}_{1}}(y)}{f_{\ln (BF_{10})}^{{\mathscr{M}}_{0}}(y)} = BF_{10}$, that is, the realization of BF₁₀ for the corresponding observed data (Supplemental Material, Lemma 9).

Proceed with optional stopping

More data are collected in case evidence from the first n observations is indecisive. Equation 14 allows reexpressing the decision rule in terms of the observed sample mean; solving Eq. 14 with respect to $\overline {X}$ gives

$$ \begin{array}{@{}rcl@{}} \overline{X}^{2} &=& \left[\ln(BF_{10})-\lambda\right] \frac{2\sigma^{2}(\sigma^{2}+n{\sigma_{1}^{2}})}{n^{2}{\sigma_{1}^{2}}} \\ \overline{X} &=& \pm\frac{\sigma}{n\sigma_{1}}\sqrt{2(\sigma^{2}+n{\sigma_{1}^{2}})\left[\ln(BF_{10})-\lambda\right]}, \end{array} $$

(18)

under the constraint that $\lambda < \ln (BF_{10})$. Let $\overline {X}_{0}$ and $\overline {X}_{1}$ denote the value of $\overline {X}$ when $BF_{10}=BF_{L}=\frac {1}{10}$ and BF₁₀ = BF_U = 10, respectively. Observe that $\overline {X}_{1}$ always exists because $\frac {\sigma }{\sqrt {\sigma ^{2}+n{\sigma _{1}^{2}}}} < 1 < 10 = BF_{10}$ and so $\lambda = \ln \left (\frac {\sigma }{\sqrt {\sigma ^{2}+n{\sigma _{1}^{2}}}}\right ) < \ln (BF_{10})$. $\overline {X}_{0}$ exists if $\lambda < \ln (BF_{10})=-\ln (10)$; this is possible when small enough absolute values of $\overline {X}$ are associated to values of BF₁₀ smaller than $\frac {1}{10}$, allowing to draw enough support for ${\mathscr{M}}_{0}$ and thus interrupting the optional stopping process. When $-\ln (10)<\lambda$ then even $\overline {X}=0$ is associated to a value of BF₁₀ not below $\frac {1}{10}$, which means that it is impossible to draw enough support for ${\mathscr{M}}_{0}$ after n observations. In this case we set $\overline {X}_{0}=0$, which is the limiting case of the first situation. Figure 7 shows the two possible situations that may arise. In particular, the test after the first n observations is indecisive when $\overline {X} \in \mathcal {J} = (-\overline {X}_{1}, -\overline {X}_{0}) \cup (\overline {X}_{0}, \overline {X}_{1})$.

Fig. 7

Data evidence for either model after assessing the first batch of n observations, for the point null versus interval alternative test. A: The case when $\lambda < -\ln (10)$. B: The case when $-\ln (10)<\lambda$

In case evidence is indecisive after the initial n observations, then the optional stopping procedure continues: Collect k more observations and reassess the evidence by means of the Bayes factor:

$$ \begin{array}{@{}rcl@{}} \ln(BF_{10}) &=& \lambda + \frac{(n+k)^{2}{\sigma_{1}^{2}}\overline{X}_{n+k}^{2}}{2\sigma^{2}\left[\sigma^{2}+(n+k){\sigma_{1}^{2}}\right]} \\ &=& \alpha + \beta\left( \overline{X}_{n}+\frac{{\sum}_{i=n+1}^{n+k}X_{i}}{n}\right)^{2}, \end{array} $$

(19)

where $\alpha = \ln \left [\frac {\sigma }{\sqrt {\sigma ^{2}+(n+k){\sigma _{1}^{2}}}}\right ]$ and $\beta = \frac {n^{2}{\sigma _{1}^{2}}}{2\sigma ^{2}\left [\sigma ^{2}+(n+k){\sigma _{1}^{2}}\right ]}$ do not depend on the observed data, and Eq. 9 was used to decompose $\overline {X}_{n+k}$. In what follows, we derive the distribution of $\ln (BF_{10})$ given by Eq. 19 under each model, and then relate the ratio of both densities to the Bayes factor.

Under ${\mathscr{M}}_{0}$

In this case, $\overline {X}_{n}$ follows a truncated normal distribution:

$$ \overline{X}_{n}|\mathcal{M}_{0} \sim \mathcal{N}_{T}\left( 0, \frac{\sigma^{2}}{n}; \mathcal{J}\right), $$

(20)

where the support for the truncation is the union of two intervals. Moreover, $\frac {{\sum }_{i=n+1}^{n+k}X_{i}}{n}$ is normally distributed (Eq. 12 with μ_X = 0). Therefore, the distribution of the sum, $S = \overline {X}_{n}+\frac {{\sum }_{i=n+1}^{n+k}X_{i}}{n}$, is given by the convolution of both densities; the closed-form expression for this density is given in the Supplemental Material (Lemma 11). Finally, observe that $\ln (BF_{10})$ in Eq. 19 is a linear function of the square of S. Hence, the density of $\ln (BF_{10})$ can be found in two steps: First find the density of S² (Supplemental Material, Lemma 13) and then find the density of the linear transformation of S² (Supplemental Material, Lemma 14).

Under ${\mathscr{M}}_{1}$

The distribution of the summation in Eq. 19 is more difficult to derive under ${\mathscr{M}}_{1}$. The reason is that the sampling distribution of a new observation is affected by conditioning on an indecisive test result after the initial n observations. Observe that, by Bayes’ rule,

$$ p(\mu|\overline{X}_{n}\in \mathcal{J}) = \frac{p(\mu)p(\overline{X}_{n}\in \mathcal{J}|\mu)}{p(\overline{X}_{n}\in \mathcal{J})}, $$

(21)

where $\mu \sim \mathcal {N}(0, {\sigma _{1}^{2}})$, $\overline {X}_{n}|\mu \sim \mathcal {N}\left (\mu , \frac {\sigma ^{2}}{n}\right )$, and $p(\overline {X}_{n}\in \mathcal {J}) = \displaystyle {\int \limits }_{\mathbb {R}} p(\mu )p(\overline {X}_{n}\in \mathcal {J}|\mu ) d\mu$. We derived the density of $\mu |\overline {X}_{n}\in \mathcal {J}$ (Supplemental Material, Lemma 15). This is the distribution of μ after the first optional stopping step, that is, after an inconclusive test result based on the first n data points.

Now consider the summation in Eq. 19, but conditional on μ. We have that $\overline {X}_{n}|\mu , {\mathscr{M}}_{1} \sim \mathcal {N}_{T}\left (\mu , \frac {\sigma ^{2}}{n};\mathcal {J}\right )$ and $\left .\frac {{\sum }_{i=n+1}^{n+k}X_{i}}{n}\right |\mu , {\mathscr{M}}_{1} \sim \mathcal {N}\left (\frac {k}{n}\mu , \frac {k}{n^{2}}\sigma ^{2}\right )$. The sum of these two independent conditional distributions, say $S|\mu = \overline {X}_{n}|\mu + \left .\frac {{\sum }_{i=n+1}^{n+k}X_{i}}{n}\right |\mu$, is the convolution of both densities; the distribution is given in the Supplemental Material, Lemma 16. To find the density of the unconditional sum we need to evaluate $f_{S}(s) = \displaystyle {\int \limits }_{\mathbb {R}}p(S=s|\mu ) p(\mu |\overline {X}_{n}\in \mathcal {J}) d\mu$. The exact closed form of this integral has evaded us. Instead, we resourced to numerical integration to approximate the integral. We next proceeded using numerical integration to approximate the density of S² and the density of $\ln (BF_{10})$ as a linear function of S². Finally, we numerically divided the densities of $\ln (BF_{10})$ (under ${\mathscr{M}}_{1}$ and ${\mathscr{M}}_{0}$) and compared the result with the Bayes factor. Also here, Theorem 4 in the Supplemental Material ascertains that the previous result holds overall (i.e., after the initial n observations or after (n + k) observations, depending on the first test result). The example below illustrates what is happening.

Example 2

Let n = 10, k = 5, σ = .3, and σ₁ = 1.1. For each simulation (total = 100,000 simulations), we followed this procedure:

• 1. Randomly draw n observations from $\mathcal {N}(0, \sigma ^{2})$ (i.e., under ${\mathscr{M}}_{0}$). Compute $\ln (BF_{10})$ and compare with the exact distribution (Eq. 15).

• 2. Sample one μ value from $\mathcal {N}(0, {\sigma _{1}^{2}})$. Randomly draw n observations from $\mathcal {N}(\mu , \sigma ^{2})$ (i.e., under ${\mathscr{M}}_{1}$). Compute $\ln (BF_{10})$ and compare with the exact distribution (Eq. 17).

• 3. Approximate the ratio of the densities of $\ln (BF_{10})$ under either model and compare it to BF₁₀ and compare to its exact counterpart (Supplemental Material, Lemma 9).

• 4. Stop in case BF₁₀ is larger than 10 or smaller than $\frac {1}{10}$, otherwise: Collect k more observations, recompute $\ln (BF_{10})$ under each model, and approximate the ratio of the densities of $\ln (BF_{10})$ under either model and compare it to BF₁₀.

Figure 8 shows the approximate distribution (histogram) and exact distribution (solid line) of $\overline {X}$ and $\ln (BF_{10})$ under ${\mathscr{M}}_{0}$ and ${\mathscr{M}}_{1}$, as well as the density ratio of the Bayes factors under either model, after the initial n observations. Figure 9 shows the distributions of $\overline {X}_{n}$, $\frac {{\sum }_{i=n+1}^{n+k}X_{i}}{n}$, S, and S² under ${\mathscr{M}}_{0}$, after (n + k) observations. Figure 10 shows the distributions of $\mu |\overline {X}_{n}\in \mathcal {J}$ (Eq. 21), $\overline {X}_{n}|\mu =.1$ (as one example of such a conditional distribution), $\frac {{\sum }_{i=n+1}^{n+k}X_{i}}{n}|\mu =.1$, S|μ = .1, and S under ${\mathscr{M}}_{1}$. Finally, Fig. 11 shows that the ratio of the densities of the Bayes factor values under each model is given by the Bayes factor.

Fig. 8

Distribution of various random variables after n observations, for the point null versus interval alternative test. A: $\overline {X}$ under ${\mathscr{M}}_{0}$ (upper distribution; $\mathcal {N}\left (0, \frac {\sigma ^{2}}{n}\right )$) and under ${\mathscr{M}}_{1}$ (inverted distribution; Eq. 16). B: $\ln (BF_{10})$ under ${\mathscr{M}}_{0}$ (Eq. 15). C: $\ln (BF_{10})$ under ${\mathscr{M}}_{1}$ (Eq. 17). D: Relation between the nominal and observed $\ln (BF_{10})$ values based on approximation by simulation (points) and on the exact values (line) (Supplemental Material, Lemma 9)

Fig. 9

Distribution of various random variables under ${\mathscr{M}}_{0}$ after (n + k) observations, for the point null versus interval alternative test. A: $\overline {X}_{n}$ (Eq. 20). B: $\frac {{\sum }_{i=n+1}^{n+k}X_{i}}{n}$ (Eq. 12 with μ_X = 0). C: $S = \overline {X}_{n} + \frac {{\sum }_{i=n+1}^{n+k}X_{i}}{n}$ (Supplemental Material, Lemma 11). D: S² (Supplemental Material, Lemma 13)

Fig. 10

Distributions of various random variables under ${\mathscr{M}}_{1}$ after (n + k) observations, for the point null versus interval alternative test. A: $\mu |\overline {X}_{n}\in \mathcal {J}$ (Eq. 21). B: $\overline {X}_{n}|\mu =.1$ ($\mathcal {N}_{T}\left (\mu ,\frac {\sigma ^{2}}{n};\mathcal {J}\right )$). C: $\frac {{\sum }_{i=n+1}^{n+k}X_{i}}{n}|\mu =.1$ ($\mathcal {N}\left (\frac {k}{n}\mu ,\frac {k}{n^{2}}\frac {\sigma ^{2}}{n}\right )$). D: $S = \overline {X}_{n} + \frac {{\sum }_{i=n+1}^{n+k}X_{i}}{n}|\mu =.1$ (Supplemental Material, Lemma 16). E: S, by means of numerical integration

Fig. 11

Visualization of Assertion 2 for the point null versus interval alternative test. A: $\ln (BF_{10})$ under ${\mathscr{M}}_{0}$ (upper distribution; Supplemental Material, Lemma 14) and under ${\mathscr{M}}_{1}$ (lower distribution, by means of numerical integration). B: Relation between the nominal and observed $\ln (BF_{10})$ values based on approximation by simulation (points) and on the exact values (line), after (n + k) observations for the point null versus interval alternative test

In the current setting, the sequential testing procedure is inconclusive after the initial n observations when $\overline {X}_{n}\in \mathcal {J}=(-.294, -.052)\cup (.052, .294)$ (Eq. 18). As before, we can quantify the probability of retaining ${\mathscr{M}}_{0}$, retaining ${\mathscr{M}}_{1}$, or proceeding data collection under each model, after n and after (n + k) observations (see Table 2). The conclusion is similar to that from the previous example, namely, increasing the sample size increased the probability of finding support for the correct model.

Table 2 Point null versus interval alternative test, Example 2 (n = 10, k = 5, σ = .3, and σ₁ = 1.1): Probability of each decision after n observations (top panel) and overall after (n + k) observations (bottom panel), under either model

Discussion

In this paper, we worked out two examples introduced by Rouder (2014) that were originally used to motivate why Bayes factors are well calibrated under Bayesian optional stopping (recently dubbed ‘Sequential Bayes Factor’ (SBF) by Schönbrodt et al., 2017). A completely general proof of this result is already offered by Hendriksen et al. (2020, Corollary 3), but the technical nature of this paper makes it rather inaccessible to less math-savvy readers. Our results offer a less ambitious but perhaps more insightful approach to understanding the findings presented in Rouder (2014), which were entirely simulation-based. Our contribution leaves us one step closer to understanding the Bayes factor and its properties under optional stopping.

Our results are limited in various ways. Firstly, we focused exclusively on the two tests used by Rouder (2014). Secondly, our approach is not easily generalizable to more complex cases. We note that we could not fully work out the last part of the mathematical derivation in the point null versus interval alternative case. Thirdly, our theoretical results apply to the first and second batches of data. If, as is often the case, the evidence is still inconclusive after the second data batch is taken into account, then the optional stopping procedure should be able to proceed. Our proof does not provide the full answer in this case. This could be the goal of a future extension of our results.

Our paper attempts to build a bridge between the practical simulation results offered by Rouder (2014), and the theoretical proofs provided by Hendriksen et al. (2020). We generalize Rouder’s simulation results such that they do not rely on specific values and present them in a way that are, hopefully, digestible to social scientists.