1 Introduction

As known, the nonlinear ordinary differential equations (ODEs) have an important role because of their applications in many fields of science and real life phenomena modeling for instance the logistic growth model in a population [1], the epidemic model [2], the kinetic model [3], the model of ozone decomposition [4], happiness dynamical models [5], the natural convection of Darcian fluid (NCDF) about a vertical full cone embedded in porous media (PM) with a prescribed wall temperature [6], and the Volterra population model [7]. The approximation and numerical techniques are used to treat the nonlinear ODEs, because getting the analytical exact solution is not easy in many cases. Several numerical methods have been given to solve nonlinear ODEs such as linearization method [8] and a sixth-degree B-spline method [9]. Moreover, the Chebshev collocation matrix method [10] is presented as a numerical solution of nonlinear ODEs. Also, the semi-analytical techniques, such as the Adomian decomposition method [11, 12], the homotopy perturbation method (HPM) [13, 14], and the decomposition method [15], are used to find the solution of nonlinear ODEs.

Many works considered solving differential equations in the finite [16–19] and infinite domain [20–22]. The rational Chebyshev (RC) functions are used in the domain \([ 0, L ]\), where \(0 \le L < \infty \), which provides great success in dealing with differential equations defined in the open domain \([ 0, L ]\). Many authors studied RC functions for solving different problems of differential, integro-differential equations, and some other physical problems with variable coefficients [23–25]. Saeid Abbasbandy et al. [26] investigated the use of the RC collocation method to get an approximate solution of magneto hydro dynamic flow of an incompressible viscous fluid over a stretching sheet. Parand et al. [27] and Ramadan et al. [28] introduced RC functions for solving natural convection of Darcian fluid about a vertical full cone embedded in porous media with a prescribed wall temperature. In [29] Ramadan et al. investigated the use of the RC collocation technique for approximating bio-mathematical problems of continuous population models for single and interacting species, systematically the logistic growth model in a population, prey-predator model: Lotka–Volterra system, the simple two-species Lotka–Volterra competition model, and the prey-predator model with limit cycle periodic behavior.

In this paper, the RC collocation method (RCC) as matrix discretization is introduced to obtain the solution of a general form of nonlinear ODEs defined on the semi-infinite domain. The order of convergence for RC functions is discussed. The validity and applicability of the method are tested through two examples. In addition, four applications as nonlinear real life models are solved using the proposed technique. On the other hand, the RC functions inherit many properties of Chebyshev polynomials as completeness, orthogonality, and strong convergence. The RC functions [23, 30–35] are defined as follows:

$$\begin{aligned} R_{n}(x) = \cos n\phi,\quad\text{where } \cos \phi = \biggl( \frac{x - 1}{x + 1} \biggr). \end{aligned}$$
(1.1)

The RC functions are orthogonal with respect to the weight function \(w(x)\) in the semi-infinite domain, where

$$\begin{aligned} w(x) = \frac{1}{(x + 1)\sqrt{x}}. \end{aligned}$$

If the substitution \(v = \frac{x - 1}{x + 1} \) is used in \(R_{n}(x)\), then we have the RC functions as polynomials in v, then \(R_{n}(x)\) takes the matrix form:

$$\begin{aligned} R(x) = V(x)C^{T}, \end{aligned}$$
(1.2)

where R (x) and V (x) are vector matrices of the form

$$\begin{aligned} &R(x) = \begin{bmatrix} R_{0}(x) & R_{1}(x) & \ldots & R_{N}(x) \end{bmatrix}, \\ &V(x) = \begin{bmatrix} v^{0}(x) & v^{1}(x) & \ldots & v^{N}(x) \end{bmatrix}, \end{aligned}$$

and C is a matrix given by

$$\begin{aligned} C = \begin{bmatrix} \begin{pmatrix} 0 \\ 0 \end{pmatrix} & 0 & 0 & 0 & \ldots & 0 & 0 \\ 0 & \begin{pmatrix} 1 \\ 0 \end{pmatrix} & 0 & 0 & \ldots & 0 & 0 \\ - \begin{pmatrix} 1 \\ 1 \end{pmatrix} & 0 & 2\begin{pmatrix} 2 \\ 0 \end{pmatrix} & 0 & \ldots & 0 & 0 \\ 0 & - \frac{3}{2}\begin{pmatrix} 2 \\ 1 \end{pmatrix} & 0 & 2^{2}\begin{pmatrix} 3 \\ 0 \end{pmatrix} & & 0 & 0 \\ . &. &. &. & &. &. \\ . &. &. &. & &. &. \\ . &. &. &. & &. &. \\ ( - 1)^{l}\begin{pmatrix} l \\ l \end{pmatrix} & 0 & ( - 1)^{l - 1}2\frac{2l}{l + 1}\begin{pmatrix} l + 1 \\ l - 1 \end{pmatrix} & 0 & \ldots & 2^{2l - 1}\begin{pmatrix} 2l \\ 0 \end{pmatrix} & 0 \\ 0 & ( - 1)^{l}\frac{2l}{l + 1}\begin{pmatrix} l + 1 \\ l \end{pmatrix} & 0 & ( - 1)^{l - 1}2^{2}\frac{2l + 1}{l + 2}\begin{pmatrix} l + 2 \\ l - 1 \end{pmatrix} & \ldots & 0 & 2^{2l}\begin{pmatrix} 2l + 1 \\ 0 \end{pmatrix} \end{bmatrix}. \end{aligned}$$

In the matrix C, if N is an odd number, the last row will be used, where \(N = 2l + 1\), while the second row from below is used for the even case of N and \(N = 2l\). For more instances of the RC functions and their properties, we provide some suggested references for the reader [23, 30, 31].

2 The order of convergence

Let us assume that

$$\begin{aligned} L_{w}^{2}(\Omega ) = \biggl\{ f: \Vert f \Vert _{w} = \biggl( \int _{0}^{\infty } \bigl\vert f(x) \bigr\vert ^{2} w(x) \,dx \biggr)^{\frac{1}{2}} < \infty \biggr\} , \end{aligned}$$
(2.1)

the space functions, and we denote the inner product as \(\langle v,u \rangle _{w}\) such that

$$\begin{aligned} \langle v,v \rangle _{w} = \bigl( \Vert v \Vert _{w} \bigr)^{2}. \end{aligned}$$
(2.2)

Therefore, from the orthogonality relation for RC functions

$$\begin{aligned} \int _{0}^{\infty } R_{n}(x)R_{m}(x)w(x) \,dx = \frac{c_{m}\pi }{2}\delta _{nm}, \end{aligned}$$
(2.3)

we note that the RC functions form a set of orthogonal bases for \(L_{w}^{2}(\Omega )\). Also, let us define the normed spaces \(H_{w}^{r}(\Omega )\) and \(H_{w,A}^{r}(\Omega )\) as follows:

$$\begin{aligned} &H_{w}^{r}(\Omega ) = \Biggl\{ f: \Vert f \Vert _{r,w} = \Biggl( \sum_{k = 0}^{r} \biggl\Vert \frac{d^{k}}{dx^{k}}f \biggr\Vert _{w} \Biggr)^{\frac{1}{2}} < \infty \Biggr\} , \end{aligned}$$
(2.4)
$$\begin{aligned} &H_{w,\theta }^{r}(\Omega ) = \Biggl\{ f: \Vert f \Vert _{r,w,\theta } = \Biggl( \sum_{k = 0}^{r} \biggl\Vert ( x + 1 )^{\frac{r}{2} + k}\frac{d^{k}}{dx^{k}}f \biggr\Vert _{w} \Biggr)^{\frac{1}{2}} < \infty \Biggr\} , \end{aligned}$$
(2.5)

where \(r \ge 0\) and k is a positive integer constant, and θ is the Sturm–Liouville operator in the following form:

$$\begin{aligned} \theta f = - w^{ - 1} \bigl( w^{ - 1}f' \bigr)^{\prime }. \end{aligned}$$
(2.6)

Let us define \(\Re _{N} = \operatorname{span}\{ R_{0}, R_{1}, \ldots, R_{N}\}\), N is a positive integer such that \(N < \infty \).

Theorem 2.1

For any \(r \ge 0\) and c a generic positive constant independent of any function, and \(\phi \in \Re _{N}\), then

$$\begin{aligned} \Vert \phi \Vert _{r,w} \le cN^{2r} \Vert \phi \Vert _{w}. \end{aligned}$$

The proof of Theorem 2.1 is found in [36].

Since the set of RC functions is orthogonal and complete, \(f(x)\) is defined over Ω, then it can be expanded in terms of RC functions as follows:

$$\begin{aligned} f(x) = \sum_{n = 0}^{\infty } a_{n}R_{n}(x), \end{aligned}$$
(2.7)

where

$$\begin{aligned} a_{n} = \frac{ \langle f,R_{n} \rangle _{w}}{ ( \Vert R_{n} \Vert _{w} )^{2}} = \frac{2}{c_{m}\pi } \int _{0}^{\infty } R_{n}(x)f(x) w(x)\,dx. \end{aligned}$$
(2.8)

Relation (2.7) may represent a spectral approximation in the following form:

$$\begin{aligned} f_{N}(x) = \sum_{n = 0}^{N} a_{n}R_{n}(x). \end{aligned}$$
(2.9)

To obtain the order of convergence of RC functions approximation, we need to investigate several orthogonal projections. From (2.9), it is evident that \(f_{N}\) is the orthogonal projection of f upon \(\Re _{N}\) with respect to the weighted inner product (2.2). According to Theorem 2.1, the following theorem contains the order of convergence of RC functions.

Theorem 2.2

For any \(f \in H_{w,\theta }^{r}(\Omega )\), \(r \ge 0\), and c is a positive constant, then

$$\begin{aligned} \Vert f_{N} - f \Vert _{r,w} \le cN^{ - r} \Vert f \Vert _{r,w,\theta }. \end{aligned}$$

The proof of Theorem 2.2 can be found in [26], and for more details see Ref [36]; this theorem shows that the RC approximation has exponential convergence.

3 Formulation of the problem

In this work, mth order nonlinear ODEs containing unknown \(y(x)\) and its derivatives with variable coefficients can be written in the following general form:

$$\begin{aligned} \sum_{k = 0}^{m} \sum _{r = 0}^{n} P_{k,r}(x)y^{r}(x)y^{(k)}(x) + \sum_{k = 1}^{m} \sum _{r = 1}^{m} Q_{k,r}(x)y^{(r)}(x)y^{(k)}(x) = g(x), \end{aligned}$$
(3.1)

where \(y(x)\) is the unknown function, \(y^{(k)}(x) = y(x)\) at \(k = 0, y(x) \in C^{m}[0,L]\), and L may tend to infinity. Also, \(Q_{k,r}(x), P_{k,r}(x)\), and g (x) are known functions that are defined on [\(0, \infty \)) and \(m, n \in {Z}^{ +} \), where m is the order of the differential equation and n represents the greatest power of unknown function \(y(x)\).

Equation (3.1) is subjected to the conditions

$$\begin{aligned} y^{ ( k )} ( a_{k} ) = \mu _{k}, \quad k = 0, 1, \ldots, m - 1, \end{aligned}$$
(3.2)

where \(a_{k}\) and \(\mu _{k}\) are real-valued constants.

The solution of (3.1) according to (2.9) takes the form

$$\begin{aligned} y(x) \approx \sum_{n = 0}^{N} a_{n}R_{n}(x), \end{aligned}$$
(3.3)

which is the truncated RC functions series, where N is any positive integer greater than the order of the proposed equation, i.e., \(N \geq m\) and \(a_{n}\) are the unknown RC coefficients.

4 Fundamental matrix relations

The solution \(y(x)\) of (3.1), according to the forms (1.2) and (3.3), can be written in the matrix form with its derivative \(y^{ ( k )}(x)\) in the following form:

$$\begin{aligned} y(x) = R(x)A = V(x)C^{T}A, \end{aligned}$$
(4.1)

where

$$\begin{aligned} A = \begin{bmatrix} a_{0} & a_{1} & \cdots & a_{N} \end{bmatrix}^{T}. \end{aligned}$$

And

$$\begin{aligned} y^{(k)}(x) = R^{(k)}(x)A,\quad k = 0,1, \ldots,m \le N, \end{aligned}$$
(4.2)

substituting relation (4.1) into Eq. (4.2), we get

$$\begin{aligned} y^{(k)}(x) = V^{(k)}(x)C^{T}A,\quad k = 0,1, \ldots,m \le N. \end{aligned}$$
(4.3)

The collocation points take the following form if the problem is defined in a semi-infinite domain:

$$\begin{aligned} x_{s} = \biggl( \frac{1 + \cos ( \frac{s\pi }{N} )}{1 - \cos ( \frac{s\pi }{N} )} \biggr),\quad s = 1, \ldots, N, \end{aligned}$$
(4.4a)

and at \(s = 0, x_{0} \to \infty \).

But if \(x \in [0,L]\), where \(L < \infty \), the collocation points will take the following form:

$$\begin{aligned} x_{s} = \frac{s}{N}L,\quad s = 0, 1, 2, \ldots, N. \end{aligned}$$
(4.4b)

Putting the collocation points \(x_{s}\) ((4.4a) or (4.4b)) in (4.3), we get

$$\begin{aligned} \bigl[y^{(k)}(x_{s})\bigr] = V^{(k)}(x_{s})C^{T}A, \end{aligned}$$

or briefly

$$\begin{aligned} {Y}^{(k)} = {V}^{(k)}C^{T}A, \end{aligned}$$
(4.5)

where

$$\begin{aligned} {V}^{(k)} = \begin{bmatrix} V^{k}(x_{0}) \\ V^{k}(x_{1}) \\ \vdots \\ V^{k}(x_{N}) \end{bmatrix} = \begin{bmatrix} (v^{0}(x_{0}))^{k} & (v^{1}(x_{0}))^{k} & \ldots & (v^{N}(x_{0}))^{k} \\ (v^{0}(x_{1}))^{k} & (v^{1}(x_{1}))^{k} & \ldots & (v^{N}(x_{1}))^{k} \\ \vdots & \vdots & \ddots & \vdots \\ (v^{0}(x_{N}))^{k} & (v^{1}(x_{N}))^{k} & \ldots & (v^{N}(x_{N}))^{k} \end{bmatrix}. \end{aligned}$$

Now, we turn to treat the matrix representation for the nonlinear terms in (3.1).

As previous, using the collocation points \(x_{s}\) into \(y^{r}(x)\), we get

$$\begin{aligned} \begin{bmatrix} y^{r}(x_{0}) \\ y^{r}(x_{1}) \\ \vdots \\ y^{r}(x_{N}) \end{bmatrix} = \begin{bmatrix} y(x_{0}) & 0 & \cdots & 0 \\ 0 & y(x_{1}) & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & y(x_{N}) \end{bmatrix}^{r - 1} \begin{bmatrix} y(x_{0}) \\ y(x_{1}) \\ \vdots \\ y(x_{N}) \end{bmatrix} = (\tilde{{Y}})^{r - 1}{Y} \end{aligned}$$

and

$$\begin{aligned} \tilde{{Y}} = \tilde{{V}} {C}^{T} {A}, \end{aligned}$$
(4.6)

where

$$\begin{aligned} &\tilde{{V}} = \begin{bmatrix} V(x_{0}) & 0 & \cdots & 0 \\ 0 & V(x_{1}) & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & V(x_{N}) \end{bmatrix}, \qquad {C}^{T} = \begin{bmatrix} C^{T} & 0 & \cdots & 0 \\ 0 & C^{T} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & C^{T} \end{bmatrix},\\ & {A} = \begin{bmatrix} A_{0} \\ A_{1} \\ \vdots \\ A_{k} \end{bmatrix}. \end{aligned}$$

In addition, substituting \(x_{s}\) into the nonlinear term \(y^{ ( r )}y^{ ( k )}\), we get

$$\begin{aligned} \begin{bmatrix} y^{(r)}(x_{0})y^{(k)}(x_{0}) \\ y^{(r)}(x_{1})y^{(k)}(x_{1}) \\ \vdots \\ y^{(r)}(x_{N})y^{(k)}(x_{N}) \end{bmatrix} = \begin{bmatrix} y^{(r)}(x_{0}) & 0 & \cdots & 0 \\ 0 & y^{(r)}(x_{1}) & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & y^{(r)}(x_{N}) \end{bmatrix} \begin{bmatrix} y^{(k)}(x_{0}) \\ y^{(k)}(x_{1}) \\ \vdots \\ y^{(k)}(x_{N}) \end{bmatrix} = \tilde{ {Y}}^{(r)}{Y}^{(k)}, \end{aligned}$$

by using (4.5), one gets

$$\begin{aligned} \tilde{{Y}}^{(r)}{Y}^{(k)} = \tilde{ {V}}^{(r)}{C}^{T}{AV}^{(k)}C^{T}A. \end{aligned}$$
(4.7)

Substituting \(x_{s}\) into Eq. (3.1), we get

$$\begin{aligned} \sum_{k = 0}^{m} \sum _{r = 0}^{n} {P}_{{k}, {r}}(\tilde{ {Y}})^{r}{Y}^{(k)} + \sum _{k = 1}^{m} \sum_{r = 1}^{m} {Q}_{{k}, {r}}\tilde{{Y}}^{(r)}{Y}^{(k)} = {G}, \end{aligned}$$
(4.8)

where

$$\begin{aligned} &{P}_{k,r} = \begin{bmatrix} P_{k}(x_{0}) & 0 & \ldots & 0 \\ 0 & P_{k}(x_{1}) & \ldots & 0 \\ 0 & 0 & \ddots & \vdots \\ 0 & 0 & \ldots & P_{k}(x_{N)} \end{bmatrix},\\ & {Q}_{k,r} = \begin{bmatrix} Q_{k,r}(x_{0}) & 0 & \ldots & 0 \\ 0 & Q_{k,r}(x_{1}) & \ldots & 0 \\ 0 & 0 & \ddots & \vdots \\ 0 & 0 & \ldots & Q_{k,r}(x_{N)} \end{bmatrix},\qquad {G} = \begin{bmatrix} g(x_{0}) \\ g(x_{1}) \\ \vdots \\ g(x_{N}) \end{bmatrix}. \end{aligned}$$

Using (4.5), (4.6), and (4.7) into (4.8), we get

$$\begin{aligned} \sum_{k = 0}^{m} \sum _{r = 0}^{n} {P}_{{k}, {r}}\bigl(\tilde{ {V}} {C}^{T}{A}\bigr)^{r} {V}^{(k)}C^{T}A + \sum_{k = 1}^{m} \sum_{r = 1}^{m} {Q}_{{k}, {r}} \tilde{{V}}^{(r)}{C}^{T}{AV}^{(k)}C^{T}A = {G}. \end{aligned}$$
(4.9)

Substituting the corresponding matrix \(y^{(k)}( a_{ k})\), which depends on the RC coefficients matrix A, into (3.2) and simplifying the result, we obtain

$$\begin{aligned} {V}^{(k)}( a_{ k})C^{T}A = \mu _{k}. \end{aligned}$$
(4.10)

5 Main results

The fundamental matrix Eq. (4.9) for problem (3.1) transforms to a system of nonlinear algebraic equations for (\(N+1\)) unknown.

Equation (4.9) can be written briefly as follows:

$$\begin{aligned} \psi A = G, \end{aligned}$$
(5.1)

where

$$\begin{aligned} \psi = \sum_{k = 0}^{m} \sum _{r = 0}^{n} {P}_{{k}, {r}}\bigl(\tilde{ {V}} {C}^{T}{A}\bigr)^{r} {V}^{(k)}C^{T} + \sum_{k = 1}^{m} \sum_{r = 1}^{m} {Q}_{{k}, {r}} \tilde{{V}}^{(r)}{C}^{T}{AV}^{(k)}C^{T}, \end{aligned}$$

the matrix form for the subjected conditions (3.2), by using (4.10), is in the following form:

$$\begin{aligned} U_{i}A = \mu _{i}; \quad\text{or}\quad [ U_{i};\mu _{i} ],\quad i = 0, 1, \ldots, m - 1, \end{aligned}$$
(5.2)

where

$$\begin{aligned} U_{i} = {V}^{(k)}( a_{ k}). \end{aligned}$$

Then the solution of (3.1) under the subjected conditions (3.2) can be found by replacing the produced Eqs. (5.2) with the last equations of system (5.1). Therefore, we get (\(N +1\)) nonlinear algebraic equations in terms of RC coefficient. This nonlinear system can be solved with the aid of a suitable solver. The well-known Newton iterative method can be used here with 100 iterations. Therefore, the corresponding approximate solution \(y(x)\) can be obtained.

6 Test examples

Two examples are considered to illustrate the effectiveness and accuracy properties of the proposed method. The calculations are carried out on the PC using our written codes using Mathematica 7.0.

Example 6.1

Consider the nonlinear equation

$$\begin{aligned} f^{(2)}(x) + f^{2}(x)f^{(1)}(x) + (x + 1)f^{5}(x) = \frac{2}{(1 + x)^{3}},\quad x \in [0,4], \end{aligned}$$
(6.1)

with the following subjected conditions:

$$\begin{aligned} f(0) = 1, \qquad f'(4) = - \frac{1}{25}. \end{aligned}$$

The collocation points at \(N =2\) are \(x_{0} = 0, x_{1} = 1.\bar{3}, x_{2} = 2.\bar{6}, x_{3} = 4\).

The fundamental matrix Eq. (4.9) corresponding to (6.1) becomes

$$\begin{aligned} \bigl\{ {V}^{(2)}C^{T} + \bigl(\tilde{{V}} {C}^{T}{A}\bigr)^{2}{V}^{(1)}C^{T} + {P}_{0,5}\bigl(\tilde{{V}} {C}^{T} {A}\bigr)^{4}{V}C^{T}\bigr\} A = {G}, \end{aligned}$$

where \(\tilde{{V}}, {C}^{{T}}, {A}, {V}^{(2)},C^{T},{V}^{(1)},{V}, {G}\), and \({P}_{0,5}\) are matrices given as follows:

$$\begin{aligned} &\tilde{{V}} = \begin{bmatrix} 1 & - 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & \frac{1}{3} & \frac{1}{9} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & \frac{3}{5} & \frac{9}{25} \end{bmatrix}, \qquad {V}^{(2)} = \begin{bmatrix} 0 & - 4 & 16 \\ 0 & \frac{ - 4}{27} & 0 \\ 0 & \frac{ - 4}{125} & \frac{ - 16}{625} \end{bmatrix}, \\ &{C}^{{T}} = \begin{bmatrix} 1 & 0 & - 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 2 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & - 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 2 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & - 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 2 \end{bmatrix},\qquad {A} = \begin{bmatrix} a_{0} & 0 & 0 \\ a_{1} & 0 & 0 \\ a_{2} & 0 & 0 \\ 0 & a_{0} & 0 \\ 0 & a_{1} & 0 \\ 0 & a_{2} & 0 \\ 0 & 0 & a_{0} \\ 0 & 0 & a_{1} \\ 0 & 0 & a_{2} \end{bmatrix},\\ &{G} = \begin{bmatrix} 2 \\ \frac{2}{27} \\ \frac{2}{127} \end{bmatrix},\qquad {P}_{0,5} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & 5 \end{bmatrix},\qquad C^{T} = \begin{bmatrix} 1 & 0 & - 1 \\ 0 & 1 & 0 \\ 0 & 0 & 2 \end{bmatrix},\\ & {V}^{(1)} = \begin{bmatrix} 0 & 2 & 4 \\ 0 & \frac{2}{9} & \frac{4}{27} \\ 0 & \frac{2}{25} & \frac{12}{125} \end{bmatrix},\qquad {V} = \begin{bmatrix} 1 & - 1 & 1 \\ 1 & \frac{1}{3} & \frac{1}{9} \\ 1 & \frac{3}{5} & \frac{9}{25} \end{bmatrix}. \end{aligned}$$

We get the RC coefficient as

$$\begin{aligned} {A} = \begin{bmatrix} \frac{1}{2} & - \frac{1}{2} & 0 \end{bmatrix}^{T}, \end{aligned}$$

therefore, the solution is

$$\begin{aligned} f(x) = \sum_{n = 0}^{5} a_{n}R_{n}(x) = \frac{1}{2}R_{0} - \frac{1}{2}R_{1}, \end{aligned}$$

after simplifying

$$\begin{aligned} f(x) = ( x + 1 )^{ - 1}, \end{aligned}$$

which represents the exact solution of (6.1).

Example 6.2

Consider the nonlinear ODE [37]

$$\begin{aligned} f'''(x) + f''(x) + f'(x)f(x) = - e^{ - 2x},\quad x \in [0, 1], \end{aligned}$$
(6.2)

subject to the initial conditions

$$\begin{aligned} f(0) = 1,\qquad f'(0) = - 1,\qquad f''(0) = 1. \end{aligned}$$

The exact solution of the present problem (6.2) is \(f(x) = e^{ - x}\). In Table 1 the comparison of absolute errors \(e_{N}\) of the presented method at \(N = 5\), 8, and 10 is listed. Also, Table 2 contains a comparison of the error norms (\(L_{2}\) and \(L_{\infty }\) [29]) for the RCC method and the shifted Chebyshev collocation method [37].

Table 1 Absolute errors for the RCC method at different N
Full size table
Table 2 Comparison of the \(L_{2}, L_{\infty } \) error norms
Full size table

7 Applications

In this section four applications are introduced as nonlinear real life models, solved using the proposed technique. The introduced applications are defined on finite and infinite domains as nonlinear differential equations. The proposed method deals with the boundary value problems defined on the semi-infinite domain without divergence.

Application 7.1

In this application the proposed method is introduced to solve NCDF about a vertical full cone embedded in PM with a prescribed wall temperature [6, 27]. Consider the governing equation of fluid flow and heat transfer of full cone embedded in PM that can be written by the following third-order nonlinear ODE, with boundary conditions that naturally have infinity:

$$\begin{aligned} f''' + \biggl( \frac{\lambda + 3}{2} \biggr)f f'' - \lambda \bigl(f' \bigr)^{2} = 0, \end{aligned}$$
(7.1)

for wall temperature the boundary conditions are

$$\begin{aligned} f(0) = 0,\qquad f'(0) = 1\quad\text{and}\quad f'(\eta ) = 0 \quad\text{at } \eta \to \infty. \end{aligned}$$

When the RCC method is applied for \(N= 26\), the approximate solution for \(f ( \eta )\) is given. Table 3 shows the comparison of the approximate values for \(f''(0)\) of the RCC method at \(N= 26\) with previous results obtained from different methods. Our obtained results are close to the ones of the following methods: fourth-order Runge–Kutta method, homotopy analysis method [6], and RCT method [27] along the given domain. Also, the results for \(f'(0)\) are shown in Tables 4 and 5 with two selected λ as 0 and 1/2, and the comparison between results of Runge–Kutta, [6], and [27] methods is given. Figure 1 shows the RCC approximation of \(f'(0)\) with different values for λ.

Figure 1
figure 1

RC approximation of \(f'(0)\) with different values for λ

Full size image
Table 3 A comparison between the RCC method and other existing methods with the values for \(f''(0)\)
Full size table
Table 4 Comparison between the RCC method and other existing methods for \(f'(0)\) with \(\lambda = 0\)
Full size table
Table 5 Comparison between RCC and other methods for \(f'(0)\) with \(\lambda = 1/2\)
Full size table

Application 7.2

The Riccati equation [39]

$$\begin{aligned} f'(x) - 2f(x) + f^{2}(x) = 1,\quad x \in [ 0, 1 ], \end{aligned}$$
(7.2)

with the subjected initial condition \(f(0) = 0\), and the exact analytical solution is

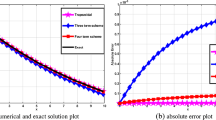
$$\begin{aligned} f(x) = 1 + \sqrt{2} \tanh \biggl[ \sqrt{2} x + \frac{1}{2}\log \biggl( \frac{\sqrt{2} - 1}{\sqrt{2} + 1} \biggr) \biggr]. \end{aligned}$$

By the RCC method, the solution of the Riccati equation is presented for deferent values of N. In Table 6 the comparison of the \(L_{2}\) error norm of the present technique for deferent values of N (\(N = 5\), 8, and 12) with the other methods is given. We substituted by the Chebyshev coefficient [40] and the relation, which give us Adomian and homotopy perturbation solutions [39]. The RCC method is compared with the exact solution at \(N= 5\), 8, and 12 in Fig. 2. Also, the RCC solution at \(N =5\) is compared with the exact solution, shifted Chebyshev collection method [40], Adomian and homotopy perturbation solutions [39] in Fig. 3. It is clear that present numeric results are more convergent to the exact solution, especially, when \(x > 1\), while the other methods are divergent.

Figure 2
figure 2

Comparison of the solution of Riccati equation for \(N= 5\), 8, and 12

Full size image
Figure 3
figure 3

Comparison of the solution of Riccati equation with other methods

Full size image
Table 6 Comparison of the \(L_{2}\), error norm
Full size table

We have to observe that the shifted Chebyshev domain is defined in the interval \([ 0, 1 ]\), therefore, we find it is divergent out from its domain [40]. Although, Adomian and homotopy perturbation methods defend in whole numbers, from Fig. 3 we see that the Adomian method is divergent when \(x > 1\). Also, the homotopy perturbation method diverges when \(x > 2\), while the RCC method is convergent along the interval.

Application 7.3

An application of the RCC method is approximating bio-mathematical problems of continuous population models for single and interacting species(CPM). The logistic growth model in a population of CPM [41] is nonlinear ODE of the following form:

$$\begin{aligned} \textstyle\begin{cases} \frac{df}{d\tau } = f ( 1 - f ), \\ f ( 0 ) = 2, \end{cases}\displaystyle \end{aligned}$$
(7.3)

with \(\frac{N_{0}}{K} = 2\), and the analytical solution is \(f ( \tau ) = \frac{2}{2 - e^{ - \tau }} \).

The approximate solution for \(f ( \tau )\) is obtained by applying the presented method at \(N = 10\) by the truncated RC series. Table 7 shows the comparison of the absolute errors for the presented method at \(N =10\) and other methods [42–45], where the comparison shows that our method obtains best accuracy along the interval \([ 0, 1 ]\). The error functions for the RCC method at \(N=10\) and 16 are compared with the Bessel collocation method [42] in Fig. 4; it is clear that our results are more accurate.

Figure 4
figure 4

Comparing error function for the RCC method and [42]

Full size image
Table 7 Comparing absolute errors for pervious work
Full size table

Application 7.4

We apply the RCC method for the Lane–Emden equation (LEE) which has the general form

$$\begin{aligned} y''(x) + \frac{\alpha }{x}y(x) + q(x)p(y) = g(x),\quad x \ge 0, \end{aligned}$$
(7.4)

with the initial conditions \(y(0) = \lambda, y'(0) = \beta \), where \(\alpha,\beta \), and λ are appropriate constants and \(q(x),p(y)\), and \(g(x)\) are given functions. The forms of \(p(y)\) give us various types of LEE which model several phenomena. In this application we study deferent cases of LEE types.

The standard LEE when \(q(x) = 1,p(y) = y^{m},\lambda = 1\), and \(\beta = 0\),we get the standard LEE that was used to model the thermal behavior of a spherical cloud of gas acting under the mutual attraction of its molecules and subject to the classical laws of thermodynamics [46–51]

$$\begin{aligned} y''(x) + \frac{2}{x}y'(x) + y^{m} = 0,\quad x \ge 0, \end{aligned}$$
(7.5)

with the initial conditions \(y(0) = 1, y'(0) = 0\), where m is a real constant \(m \ge 0\), if \(m = 0, 1\), and 5, we get the analytical solution

$$\begin{aligned} y(x) = 1 - \frac{1}{3!}x^{2},\qquad y(x) = \frac{\sin (x)}{x} \quad \text{and} \quad y(x) = \biggl( 1 + \frac{x^{2}}{3} \biggr)^{ - 1/2}, \end{aligned}$$

respectively, the other values of m have no analytical solution. Now, we apply the RCC method to deal with the standard LEE for \(m = 3\), 4, and 5. Table 8 shows the comparing of numerical results of the RCC method, the exact solution, and Runge–Kutta of fourth order at \(m=5\), while Table 9 compares absolute errors. Tables 10 and 11 compare the approximate solution of the RCC method with Runge–Kutta of fourth order at \(m=4\) and 3 respectively.

Table 8 Comparing numerical results of the RCC method with Runge–Kutta of fourth order at \(m=5\)
Full size table
Table 9 Comparing absolute errors at \(m= 5\)
Full size table
Table 10 Comparing approximate solution of the RCC method with Runge–Kutta of fourth order at \(m=4\)
Full size table
Table 11 Comparing approximate solution of the RCC method with Runge–Kutta of fourth order at \(m=3\)
Full size table

We note that the results at \(m=5\) with the exact solution for the proposed method are better than the given results by Runge–Kutta at \(N=25\) as Tables 8 and 9 show, so we expected that the results are also stable and better than those of fourth-order Runge–Kutta in other cases.

8 Conclusion

In this work, the rational Chebyshev collection method is applied to solve general nonlinear ordinary differential equations (ODEs) with variable coefficients and given conditions. The proposed method is applied as a matrix discretization to treat the nonlinear ODEs which take a block matrix form that is transformed to a nonlinear algebraic system of equations. The order of convergence for RC functions has been discussed. The technique has been tested and verified by two examples, then applied to natural convection of Darcian fluid (NCDF) about a vertical full cone embedded in porous media (PM) with a prescribed wall temperature which is a third-order nonlinear ODE with condition naturally tending to infinity. The second application is the Riccati equation, and the third one is continuous population models for single and interacting species (CPM). The standard Lane–Emden equation (LEE) is the last application, and we compare our results with other existing methods to study the applicability and accuracy.