Higher-order gravitational potential gradients by tensor analysis in spherical coordinates

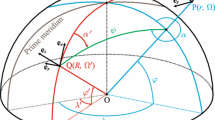
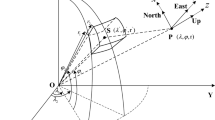
Abstract

Previous studies mainly focused on second- and third-order gravitational potential gradients that these values are already measurable or that appropriate measurement principles are being developed. Although the higher-order (i.e. the order is larger than or equal to four) gravitational potential gradients cannot be observed now, with the development of science and technology, it will be hoped to measure these parameters in the future. Once the values of higher-order gradients are observable, they can express the higher frequency of the Earth’s gravity field and have the higher sensitivity to the shallower structures of the Earth’s subsurface, which will be applied for the global and regional gravity field modelling and geoid determination in geodesy and the mass density mapping of the subsurface and shallower structures in geophysics. In this paper, the higher-order gravitational potential gradients in spherical coordinates are focused on by tensor analysis. Firstly, the rule of the covariant derivative of a tensor is revised based on Casotto and Fantino (2009). Secondly, the general expressions for the natural components of the fourth-order up to seventh-order gravitational potential gradients are derived based on the revised rule. Specifically, we derive the expressions for physical components of the fourth-order gravitational potential derivatives as an example. Thirdly, Laplace’s equation with a uniform tesseroid using the spherical integral kernels has been applied to validate these newly derived expressions’ correctness. The expressions for the physical components of higher-order gradients up to m order can theoretically be derived based on this paper’s research results.

Appendices

Appendix 1: Christoffel symbol of the second kind and its first-order up to fifth-order derivatives

In Casotto and Fantino (2009), the matrix forms of the Christoffel symbol of the second kind and first-order derivatives ($\varGamma ^{s}_{pq}$ and $\varGamma ^{s}_{pq,r}=\partial \varGamma ^{s}_{pq} / \partial u^{r}$ with $p, q, s, r \in \{1,2,3\}$) were provided. In order to maintain the integrity of the derivation process, the detailed expressions for the nonzero Christoffel symbol ($\varGamma ^{s}_{pq}$ with $p, q, s \in \{1,2,3\}$) and first-order derivatives ($\varGamma ^{s}_{pq,r}$ with $p, q, r, s \in \{1,2,3\}$) are expressed in Table 2 and 3, respectively. Other expressions for $\varGamma ^{s}_{pq}$ and $\varGamma ^{s}_{pq,r}$ are equal to zero. It should be noted that not only Christoffel symbol is symmetric in the lower indices ($\varGamma ^{s}_{pq} = \varGamma ^{s}_{qp}$), but also the same for first-order derivatives ($\varGamma ^{s}_{pq,r} = \varGamma ^{s}_{qp,r}$).

Table 2 Expressions for the nonzero Christoffel symbol of the second kind ($\varGamma ^{s}_{pq}$ with $p, q, s \in \{1,2,3\}$)

Table 3 Expressions for the nonzero first-order derivatives of Christoffel symbol of the second kind ($\varGamma ^{s}_{pq,r}$ with $p, q, r, s \in \{1,2,3\})$

In addition, the detailed expressions for the nonzero second-order up to fifth-order derivatives of Christoffel symbol of the second kind ($\varGamma ^{s}_{pq,rt}$ $=\partial \varGamma ^{s}_{pq} / (\partial u^{r} \partial u^{t})$, $\varGamma ^{s}_{pq,rtx}$ $=\partial \varGamma ^{s}_{pq} / (\partial u^{r} \partial u^{t} \partial u^{x})$, $\varGamma ^{s}_{pq,rtxy}$ $=\partial \varGamma ^{s}_{pq} / (\partial u^{r} \partial u^{t} \partial u^{x} \partial u^{y})$, and $\varGamma ^{s}_{pq,rtxyz}$ $=\partial \varGamma ^{s}_{pq} / (\partial u^{r} \partial u^{t} \partial u^{x} \partial u^{y} \partial u^{z})$ with p, q, r, s, t, x, y, z $\in \{1,2,3\}$) are expressed in Table 4 – 7, where other expressions are equal to zero. It can be interestingly found that the second-order up to fifth-order derivatives of Christoffel symbol have symmetry not only for the original lower indices of Christoffel symbol (e.g. $\varGamma ^{1}_{12,22} = \varGamma ^{1}_{21,22}$, $\varGamma ^{1}_{13,33} = \varGamma ^{1}_{31,33}$, $\varGamma ^{1}_{12,222}=\varGamma ^{1}_{21,222}$, $\varGamma ^{1}_{13,3333}=\varGamma ^{1}_{31,3333}$, and $\varGamma ^{1}_{12,22222}=\varGamma ^{1}_{21,22222}$), but also for the partial derivative parameters in the lower indices (e.g. $\varGamma ^{3}_{11,23}=\varGamma ^{3}_{11,32}$, $\varGamma ^{3}_{11,223} = \varGamma ^{3}_{11,232}=\varGamma ^{3}_{11,322}$, $\varGamma ^{3}_{11,2223}=\varGamma ^{3}_{11,2232} = \varGamma ^{3}_{11,2322}=\varGamma ^{3}_{11,3222}$, and $\varGamma ^{3}_{11,22223}=\varGamma ^{3}_{11,22232}=\varGamma ^{3}_{11,22322} = \varGamma ^{3}_{11,23222}=\varGamma ^{3}_{11,32222}$).

Table 4 Expressions for the nonzero second-order derivatives of Christoffel symbol of the second kind ($\varGamma ^{s}_{pq,rt}$ with $p, q, r, s, t \in \{1,2,3\}$)

Table 5 Expressions for the nonzero third-order derivatives of Christoffel symbol of the second kind ($\varGamma ^{s}_{pq,rtx}$ with $p, q, r, s, t, x \in \{1,2,3\}$)

Table 6 Expressions for the nonzero fourth-order derivatives of Christoffel symbol of the second kind ($\varGamma ^{s}_{pq,rtxy}$ with $p, q, r, s, t, x, y \in \{1,2,3\}$)

Table 7 Expressions for the nonzero fifth-order derivatives of Christoffel symbol of the second kind ($\varGamma ^{s}_{pq,rtxyz}$ with $p, q, r, s, t, x, y, z \in \{1,2,3\}$)

Appendix 2: Physical components of the fourth-order gravitational potential gradients in spherical coordinates in the topocentric ENU reference system

In order to keep the symbols consistent with Casotto and Fantino (2009), $V^{*}_{ijkl}$ = $V^{*}_{;pqrt}$ is adopted by dropping the colon sign (;), $\partial _{i} V$ = $V_{,p}$, $\partial _{ij} V$ = $V_{,pq}$, $\partial _{ijk} V$ = $V_{,pqr}$ and $\partial _{ijkl} V$ = $V_{,pqrt}$ are provided by dropping the comma sign (,), where $i, j, k, l \in \{\lambda , \varphi , r\}$.

Following the general rule of the properties of the potential field parameters (Deng and Ran 2020), the total number for the physical components of the fourth-order gravitational potential gradients is $3^4 = 81$ and the defining number is $(4+1)(4+2)/2 = 15$. Furthermore, the new notation for the physical components of the fourth-order gradients can be given as $V^{*}_{(\alpha ,\beta ,\gamma )}$ with $\alpha , \beta , \gamma \in \{0, 1, 2, 3, 4\}$ and $\alpha + \beta + \gamma = 4$, where $\alpha$ is the total number of $\lambda$, $\beta$ is the total number of $\varphi$, and $\gamma$ is the total number of r in the expression of $V^{*}_{ijkl}$.

The 15 defining physical components of the fourth-order gravitational potential gradients in spherical coordinates in the topocentric ENU reference system are expressed in Eqs. (33) – (47).

$$\begin{aligned} V^{*}_{(4,0,0)}= & {} V^{*}_{\lambda \lambda \lambda \lambda }\nonumber \\= & {} \frac{1}{r^4 \cos ^4 \varphi } \partial _{\lambda \lambda \lambda \lambda } V - \frac{6 \tan \varphi }{r^4 \cos ^2\varphi } \partial _{\lambda \lambda \varphi } V\nonumber \\&+ \frac{6}{r^3 \cos ^2\varphi } \partial _{\lambda \lambda r} V \nonumber \\&- \frac{8 }{r^4 \cos ^4\varphi } \partial _{\lambda \lambda } V + \frac{3 \tan ^2\varphi }{r^4} \partial _{\varphi \varphi } V \nonumber \\&- \frac{6 \tan \varphi }{r^3} \partial _{\varphi r} V + \frac{3}{r^2} \partial _{rr} V \nonumber \\&+ \frac{3 \tan \varphi }{r^4} (2+\frac{1}{\cos ^2\varphi }) \partial _\varphi V - \frac{3}{r^3} \partial _r V \end{aligned}$$

(33)

$$\begin{aligned} V^{*}_{(0,4,0)}= & {} V^{*}_{\varphi \varphi \varphi \varphi }\nonumber \\= & {} \frac{1}{r^4} \partial _{\varphi \varphi \varphi \varphi } V + \frac{6}{r^3} \partial _{\varphi \varphi r}V \nonumber \\&- \frac{8}{r^4} \partial _{\varphi \varphi } V + \frac{3}{r^2} \partial _{rr} V - \frac{3}{r^3} \partial _r V \end{aligned}$$

(34)

$$\begin{aligned} V^{*}_{(0,0,4)}= & {} V^{*}_{r r r r}= \partial _{rrrr} V \end{aligned}$$

(35)

$$\begin{aligned} V^{*}_{(3,1,0)}= & {} V^{*}_{\lambda \lambda \lambda \varphi }\nonumber \\= & {} \frac{1}{r^4 \cos ^3\varphi } \partial _{\lambda \lambda \lambda \varphi } V + \frac{3 \tan \varphi }{r^4 \cos ^3\varphi } \partial _{\lambda \lambda \lambda } V \nonumber \\&+ \frac{3}{r^3 \cos \varphi } \partial _{\lambda \varphi r} V - \frac{3 \tan \varphi }{r^4 \cos \varphi } \partial _{\lambda \varphi \varphi } \nonumber \\&+ \frac{1}{r^4 \cos \varphi }(3-\frac{8}{\cos ^2 \varphi }) \partial _{\lambda \varphi } V + \frac{3 \tan \varphi }{r^3 \cos \varphi } \partial _{\lambda r} V \nonumber \\&- \frac{6 \tan \varphi }{r^4 \cos ^3\varphi } \partial _{\lambda } V \end{aligned}$$

(36)

$$\begin{aligned} V^{*}_{(3,0,1)}= & {} V^{*}_{\lambda \lambda \lambda r}\nonumber \\= & {} \frac{1}{r^3 \cos ^3\varphi } \partial _{\lambda \lambda \lambda r} V - \frac{3}{r^4 \cos ^3\varphi } \partial _{\lambda \lambda \lambda } V \nonumber \\&- \frac{3 \tan \varphi }{r^3 \cos \varphi } \partial _{\lambda \varphi r} V + \frac{3 }{r^2 \cos \varphi } \partial _{\lambda r r} V \nonumber \\&+ \frac{9 \tan \varphi }{r^4 \cos \varphi }\partial _{\lambda \varphi } V \nonumber \\&- \frac{2}{r^3 \cos \varphi }(3+\frac{1}{\cos ^2 \varphi }) \partial _{\lambda r} V + \frac{6}{r^4 \cos ^3 \varphi } \partial _{\lambda } V \end{aligned}$$

(37)

$$\begin{aligned} V^{*}_{(1,3,0)}= & {} V^{*}_{\lambda \varphi \varphi \varphi }\nonumber \\= & {} \frac{1}{r^4 \cos \varphi } \partial _{\lambda \varphi \varphi \varphi } V + \frac{3}{r^3 \cos \varphi } \partial _{\lambda \varphi r} V\nonumber \\&+ \frac{3 \tan \varphi }{r^4 \cos \varphi } \partial _{\lambda \varphi \varphi } V \nonumber \\&+ \frac{2}{r^4 \cos \varphi }(\frac{3}{\cos ^2 \varphi }-4) \partial _{\lambda \varphi } V \nonumber \\&+ \frac{3 \tan \varphi }{r^3 \cos \varphi } \partial _{\lambda r} V \nonumber \\&+ \frac{6 \tan ^3 \varphi }{r^4 \cos \varphi }\partial _{\lambda } V \end{aligned}$$

(38)

$$\begin{aligned} V^{*}_{(1,0,3)}= & {} V^{*}_{\lambda r r r}= \frac{1}{r \cos \varphi } \partial _{\lambda r r r} V \nonumber \\&- \frac{3 }{r^2 \cos \varphi } \partial _{\lambda r r} V + \frac{6 }{r^3 \cos \varphi } \partial _{\lambda r} V\nonumber \\&- \frac{6 }{r^4 \cos \varphi } \partial _{\lambda } V \end{aligned}$$

(39)

$$\begin{aligned} V^{*}_{(0,3,1)}= & {} V^{*}_{\varphi \varphi \varphi r}\nonumber \\= & {} \frac{1}{r^3} \partial _{\varphi \varphi \varphi r} V - \frac{3}{r^4} \partial _{\varphi \varphi \varphi } V + \frac{3}{r^2} \partial _{\varphi r r} V\nonumber \\&- \frac{8}{r^3} \partial _{\varphi r} V + \frac{6}{r^4} \partial _{\varphi } V \end{aligned}$$

(40)

$$\begin{aligned} V^{*}_{(0,1,3)}= & {} V^{*}_{\varphi r r r}= \frac{1}{r} \partial _{\varphi r r r} V - \frac{3 }{r^2} \partial _{\varphi r r} V\nonumber \\&+ \frac{6 }{r^3} \partial _{\varphi r} V - \frac{6 }{r^4} \partial _{\varphi } V \end{aligned}$$

(41)

$$\begin{aligned} V^{*}_{(2,2,0)}= & {} V^{*}_{\lambda \lambda \varphi \varphi }\nonumber \\= & {} \frac{1 }{r^4 \cos ^2\varphi } \partial _{\lambda \lambda \varphi \varphi } V\nonumber \\&+ \frac{4 \tan \varphi }{r^4 \cos ^2\varphi } \partial _{\lambda \lambda \varphi } V + \frac{ 1 }{r^3 \cos ^2\varphi } \partial _{\lambda \lambda r} V\nonumber \\&- \frac{ \tan \varphi }{r^4} \partial _{\varphi \varphi \varphi } V \nonumber \\&+ \frac{1}{r^3} \partial _{\varphi \varphi r} V + \frac{6 \tan ^2\varphi }{r^4 \cos ^2\varphi } \partial _{\lambda \lambda } V \nonumber \\&- \frac{2 }{r^4 \cos ^2\varphi } \partial _{\varphi \varphi } V - \frac{ \tan \varphi }{r^3} \partial _{\varphi r} V + \frac{1}{r^2} \partial _{r r} V \nonumber \\&- \frac{2 \tan ^3\varphi }{r^4} \partial _{\varphi } V - \frac{1}{r^3} \partial _{r} V \end{aligned}$$

(42)

$$\begin{aligned} V^{*}_{(2,0,2)}= & {} V^{*}_{\lambda \lambda r r}= \frac{ 1 }{r^2 \cos ^2\varphi } \partial _{\lambda \lambda r r} V - \frac{4 }{r^3 \cos ^2\varphi } \partial _{\lambda \lambda r} V \nonumber \\&- \frac{ \tan \varphi }{r^2} \partial _{\varphi r r} V + \frac{1}{r} \partial _{rr r} V \nonumber \\&+ \frac{6 }{r^4 \cos ^2\varphi } \partial _{\lambda \lambda } V + \frac{4 \tan \varphi }{r^3} \partial _{\varphi r} V \nonumber \\&- \frac{2 }{r^2} \partial _{ r r} V - \frac{6 \tan \varphi }{r^4} \partial _{\varphi } V + \frac{2}{r^3} \partial _{r} V \end{aligned}$$

(43)

$$\begin{aligned} V^{*}_{(0,2,2)}= & {} V^{*}_{\varphi \varphi r r}= \frac{1}{r^2} \partial _{\varphi \varphi r r} V - \frac{4 }{r^3} \partial _{\varphi \varphi r} V \nonumber \\&+ \frac{1}{r} \partial _{r r r} V + \frac{6 }{r^4} \partial _{\varphi \varphi } V - \frac{2 }{r^2} \partial _{r r} V + \frac{2 }{r^3} \partial _{r} V \end{aligned}$$

(44)

$$\begin{aligned} V^{*}_{(2,1,1)}= & {} V^{*}_{\lambda \lambda \varphi r}= \frac{1}{r^3 \cos ^2\varphi } \partial _{\lambda \lambda \varphi r} V\nonumber \\&- \frac{3}{r^4 \cos ^2\varphi } \partial _{\lambda \lambda \varphi } V + \frac{2 \tan \varphi }{r^3 \cos ^2\varphi } \partial _{\lambda \lambda r} V \nonumber \\&- \frac{\tan \varphi }{r^3} \partial _{\varphi \varphi r} V + \frac{1}{r^2} \partial _{\varphi r r} V \nonumber \\&- \frac{6 \tan \varphi }{r^4 \cos ^2\varphi } \partial _{\lambda \lambda } V + \frac{3 \tan \varphi }{r^4} \partial _{\varphi \varphi } V\nonumber \\&- \frac{1}{r^3} (2+\frac{1}{\cos ^2\varphi }) \partial _{\varphi r} V + \frac{3}{r^4 \cos ^2\varphi } \partial _{\varphi } V \end{aligned}$$

(45)

$$\begin{aligned} V^{*}_{(1,2,1)}= & {} V^{*}_{\lambda \varphi \varphi r}= \frac{1}{r^3 \cos \varphi } \partial _{\lambda \varphi \varphi r} V \nonumber \\&+ \frac{2 \tan \varphi }{r^3 \cos \varphi } \partial _{\lambda \varphi r} V - \frac{3 }{r^4 \cos \varphi } \partial _{\lambda \varphi \varphi } V + \frac{1 }{r^2 \cos \varphi } \partial _{\lambda r r} V \nonumber \\&- \frac{6 \tan \varphi }{r^4 \cos \varphi } \partial _{\lambda \varphi } V + \frac{2}{r^3 \cos \varphi }(\tan ^2 \varphi -1) \partial _{\lambda r} V \nonumber \\&- \frac{6 \tan ^2 \varphi }{r^4 \cos \varphi } \partial _{\lambda } V \end{aligned}$$

(46)

$$\begin{aligned} V^{*}_{(1,1,2)}= & {} V^{*}_{\lambda \varphi r r}= \frac{ 1 }{r^2 \cos \varphi } \partial _{\lambda \varphi r r} V \nonumber \\&- \frac{4}{r^3 \cos \varphi } \partial _{\lambda \varphi r} V + \frac{ \tan \varphi }{r^2 \cos \varphi } \partial _{\lambda r r} V \nonumber \\&+ \frac{6 }{r^4 \cos \varphi } \partial _{\lambda \varphi } V - \frac{4 \tan \varphi }{r^3 \cos \varphi } \partial _{\lambda r} V \nonumber \\&+ \frac{6 \tan \varphi }{r^4 \cos \varphi } \partial _{\lambda } V \end{aligned}$$

(47)

It should be noted that $\partial _{ij} V$, $\partial _{ijk} V$, and $\partial _{ijkl} V$ are symmetrical, which means subscript symbols (i.e. i, j, k, and l) are interchangeable for the place. For example, $\partial _{ij} V$ = $\partial _{ji} V$ and $\partial _{ijk} V$ = $\partial _{ikj} V$ = $\partial _{jik} V$ = $\partial _{kij} V$ = $\partial _{jki} V$ = $\partial _{kji} V$. The same rule can be applied for the $\partial _{ijkl} V$.

Appendix 3: Expressions for the components of first-order up to fourth-order gravitational potential gradients of a uniform tesseroid using the spherical integral kernels

The 3 defining expressions of $\partial _{i} V$, 6 defining expressions of $\partial _{ij} V$, 10 defining expressions of $\partial _{ijk} V$, and 15 defining expressions of $\partial _{ijkl} V$ are the natural gravitational components. Due to the complex forms of these expressions, the Mathematica code (AppendixC.nb) is provided at https://www.github.com/xiaoledeng/higher-order-gravitational-potential-gradients. AppendixC.nb provides the expressions for the kernels of the different order derivatives of a uniform tesseroid using the spherical integral kernels, it should add the related triple integral symbols as $G \rho \int _{\lambda _{1}}^{\lambda _{2}} \int _{\varphi _{1}}^{\varphi _{2}} \int _{r_{1}}^{r_{2}} (kernels) \mathrm {d} r^{\prime } \mathrm {d} \varphi ^{\prime } \mathrm {d} \lambda ^{\prime }$.

Appendix 4: Validation with Laplace’s equation for physical components of the fourth-order gravitational potential gradients of a uniform tesseroid in spherical integral kernels

To demonstrate the detailed proof steps, the Mathematica code (AppendixD.nb) is provided at https://www.github.com/xiaoledeng/higher-order-gravitational-potential-gradients. After running all the codes in AppendixD.nb, the expressions for Laplace’s equation (i.e. Laplace1, Laplace2, Laplace3, Laplace4, Laplace5, and Laplace6) are all equal to zero. Thus, the expressions for the 15 defining physical components of the fourth-order gravitational potential gradients as Eqs. (33) – (47) in Appendix 2 are correct.