Introduction

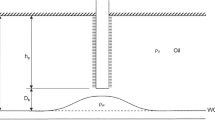
In near-wellbore regions, fluid flow can be significantly affected by the type of well completion applied. There are several different kinds of well completion. For example, open hole completion creates a radial flow pattern surrounding the wellbore, leaving a normal trajectory. However, this form of well completion may not in itself be sufficient, in which case other well completion approaches may be necessary. Other methods may be used for preventing water and gas coning, isolating or controlling wellbore fluid entry, or reducing sand production. Well completion applied on the part of a well is called a partially penetrated or restricted well. Unlike fully penetrated wells, the flow lines of partially completed wells proceed toward the wellbores perpendicularly, while flow pattern distortion due to partially penetrated completion increases pressure loss. Determining if stimulation of a partially penetrated well is warranted requires quantitatively calculating the various components in the total skin factor. For wells that are partially penetrated, the pseudo-skin factor needs to be evaluated as a primary component of the total skin. Furthermore, partially penetrated wells may have a one-dimensional radial flow that is more deeply formed at a distance from a wellbore. In this case, as the fluid nears the wellbore, there is a fluid convergence in the area immediately surrounding the open well. As shown in Fig. 1, partial penetration causes a field of flow surrounding the near-wellbore area that is two-dimensional. As a result of the fluid convergence along with the two-dimensional flow, the fluid at the wellbore region flows with higher velocity.

Fig. 1
figure 1

Schematic of partially penetrated well with formation damage

Full size image

Overall, partial penetration leads to increased pressure drop at near-wellbore regions. It also causes lower well productivity. Several researchers, e.g., Muskat (1949), Nisle (1958), Brons and Marting (1961), Odeh (1968, 1980), Gringarten and Ramey (1975), Jones and Watts (1971), Saidikowski (1979), Streltsova-Adams (1979), Papatzacos (1987), Yeh and Reynolds (1989), Vrbik (1991) have investigated how partial penetration at the wellbore affects pressure behavior as well as productivity. Their studies have yielded a number of analytical models that simulate flow in partially penetrating wells. Some of these models are generally quite complex and are based on many functions, for instance, infinite series and Bessel functions.

In two-dimensional analytical solutions, the models have been developed to calculate partial penetration skin using simpler and more straightforward approaches. The strategies presented by Odeh (1980), Papatzacos (1987) and Vrbik (1991) are especially popular due to their inherent ease of application. Also, analytical expressions pertaining to the skin factor were developed by Gomes and Ambastha (1993) for multilayered reservoirs featuring closed-bottom/-top boundaries in addition to bottom-water zones and gas caps. A year later, Ding and Reynolds (1994) expanded on Papatzacos’s (1987) research by modifying it and applying it to a multilayered reservoir, giving good results in simulations. Lee and Kyonggi (2001) proposed a novel approach for generating a pseudo-skin factor. The work is based on partial penetration of reservoirs that are either multilayered or single-layered at the cross-flow between layers.

Many different techniques and models have been used for calculating the partial penetration pseudo-skin factor. However, the results of some of these approaches tend to be inaccurate. The present study proposes experimental work, a numerical simulation model and statistical analysis for more accurate estimation of the skin factor for partially penetrated wells.

Methodology

Mathematical model

In porous media, fluid flow at low velocities typically obeys Darcy’s law. As the flow velocity increases, however, a non-Darcy flow regime begins to develop, caused by the increasingly nonlinear relationship between the local pressure gradient and in situ fluid velocity. Open hole well completion is both the simplest and most popular completion strategy used in the oil and gas hydrocarbon industry today. Constructing a productivity model of vertical open holes is also relatively straightforward. Through integrating the relevant data with Darcy’s equation, a well-productivity model can be built that describes open hole well production in steady-state flows.

$$~q = \frac{{~~2~\pi k_{{f~}} h~\Delta _{p} ~}}{{\mu \ln (r_{e} /r_{w} )}}$$
(1)

The productivity index is known as the ratio of flow rate to the pressure gradient.

$$~J_{o} = \frac{q}{{\Delta p}} = \frac{{~2~\pi k_{f} h}}{{\mu ~{\text{ln}}\left( {r_{e} /r_{w} } \right)}}$$
(2)

Hydrocarbon wells can be affected by a number of skin factors. These effects include mechanical skin as well as both geometrical and completion pseudo-skins. In other words, any difference between an actual well’s performances compared to that of an ideal vertical open hole is expressed as the total skin factor. In the literature, some studies calculate the total skin factor by adding together all of the abovementioned skin factors, as in eq given as follows(Yildiz 2006):

$$~~~~S_{t} = s_{d} + s_{{pp}} + s_{p} + s_{{cz}} + s_{\theta } + s_{{df}}$$
(3)

To better understand how skin factors can affect the productivity of a well, the productivity index for an ideal open hole is compared to that for a well with skin factors.

$$q = \frac{{~2~\pi k_{f} h~~\Delta p}}{{\mu \left[ {\ln (r_{e} /r_{w} ) + S_{t} } \right]}}$$
(4)
$$J_{d} = \frac{q}{{\Delta p}} = \frac{{~2~\pi k_{f} h}}{{\mu ~\left[ {\ln \left( {r_{e} /r_{w} } \right) + S_{t} } \right]}}$$
(5)

To quantify the comparison, the productivity ratio (PR) is applied, as expressed in eq:

$$PR = \frac{{J_{d} }}{{J_{o} }} = \frac{{\ln \left( {r_{e} /r_{w} } \right)}}{{\ln \left( {r_{e} /r_{w} } \right) + S_{t} }}$$
(6)

Using previous research as a foundation and reference point, the present study aims to compare and extend the investigations of near-wellbore region flow. This study is an extended work, conducting three investigative procedures of experimental, numerical, and statistical analysis for more accurate estimation of the pseudo-skin factor for partially penetrated wells. In some publications, a list of the partial penetration skin equations is given in Table 1.

Table 1 Summary of some studies' models that were conducted on partial completion wells
Full size table

The experimental approach was used to validate the numerical model results for single-phase flow through the perforation tunnel. Statistical analysis was coupled with numerical simulation to expand the investigation of fluid flow in the near-wellbore region that cannot be obtained experimentally, due to the limitations of the experimental setup, especially the small sample size.

Experimental procedure

In the present study, the experimental setup was initially designed and built by Ahammad et al. (Ahammad et al. 2018) and (Ahammad et al. 2019) as a radial flow cell (RFC). The RFC, which was constructed at Memorial University of Newfoundland’s Drilling Technology Laboratory, was created for the purpose of carrying out experiments under wellbore conditions. Figure 2 shows the setup, which features the three following main sections: flow lines extending from inlet to outlet; an inner chamber for holding samples with axial loads; and a data acquisition (DAQ) system.

Fig. 2
figure 2

Schematic diagram of the experiment: Water flow meter; Inlet and outlet pressure sensors; TS: Temperature sensor; and DAQ: Data Acquisition system

Full size image

Experiments carried out on perforation methods have primarily relied on rather simplistic assumptions, such as those presented by Rahman et al. (Rahman et al. 2007a), (Rahman et al. 2007b) (Rahman, Heidrick, Fleck, & Koksal, 2006) (Rahman M. A., 2008) (Zheng, Rahman, Ahammad, Butt, & Alam, 2016). Moreover, as a result of laboratory constraints, most experimental investigations have neglected key reservoir characteristics, such as thermal effects, drawdown pressure, and actual reservoir pressure. In the experimental portion of our work, we injected a measured volume of water into our core sample. As well, we used a geotechnical radial flow test setup to measure the differential pressure and single-phase flow rate of our perforated samples, with water being radially injected into our core sample within Darcy flow and the following boundary conditions: The outer side of the sample is considered an inlet while the perforation surface is an outlet. Furthermore, both inlet/outlet pressures were measured for our cylindrical samples using specified water flow rate.

Preparation of perforation tunnel was conducted by cutting a carbonate core sample from a rock from Nova Scotia, Canada. The geometry of the sample is cylindrical with a hole at the center as shown in Fig. 3. The dimensions of the geometry and the sample properties are listed in Table 2.

Fig. 3
figure 3

The dimensions and shape of carbonate sample used in the experimental work

Full size image
Table 2 The dimensions and properties of the carbonate sample that used in the experimental procedure
Full size table
Table 3 The dimensionless parameters of the near-wellbore region
Full size table

Numerical procedure

In the present work, we used ANSYS FLUENT 18.1 for our computational fluid dynamics (CFD) model. Our aim was to present a single-phase fluid flow simulation for a reservoir described as three-dimensional, vertical, and cylindrically layered. We created a sample that is vertical with a single layer of uniform thickness (\(h\)), and we assumed the well was centrally located and cast radius (\(r_{w}\)) throughout the formation. Furthermore, the well was partially completed at an open interval length \(~h_{p} ~\), in addition to the distance spanning the open interval’s top to the formation’s top (\(l\)); it also had vertical-to-horizontal permeability ratio (\(k_{v} /k_{h}\)). Hence, we could apply the conditions and assumptions enumerated below in developing our model:

  1. 1.

    The medium is anisotropic and porous, of uniform thickness, and is constantly permeable (i.e., features constant vertical permeability that is non zero).

  2. 2.

    The flow through the reservoir can be described as single-phase water, and either radial-vertical laminar or Darcy’s flow.

  3. 3.

    Any flux proceeding into the well features uniform distribution across perforated intervals.

  4. 4.

    Thermal effects are ignored.

  5. 5.

    Although partial penetration skin has been considered in the present research, other skin factors have not.

  6. 6.

    The present study modeled the flow as incompressible, as the applied pressure is low and thermal effect is also neglected in the numerical and experimental procedures; depending on that, the incompressible assumption valid for our study. Several researchers have investigated how partial penetration impacts well productivity loss and pressure behavior under the assumption that fluid is incompressible. In early work, Muskat & Boston (1982) and Vrbik (1986) examined the effect of partial completion in a single-layered reservoir by assuming fluid is incompressible; their models were provided an acceptable estimation for the partial penetration pseudo-skin factor.

In the numerical work, we injected a measured volume of water into the cylindrical sample. The conservation equations for mass and momentum describing single-phase flow in a porous region could be expressed, respectively, as

$$\frac{{\partial \gamma \rho }}{{\partial t}} + \nabla .\left( {\gamma \rho \vec{v}} \right) = 0$$
(7)
$$\frac{\partial }{{\partial t}}\left( {\gamma \rho \vec{v}} \right) + \nabla .\left( {\gamma \rho \vec{v}\vec{v}} \right) = - \gamma \nabla p{\text{+ }}\nabla .\left( {\gamma \vec{\tau }} \right) + \gamma \vec{B}_{f} - \left( {\frac{\mu }{k}\vec{v} + - \frac{{C_{2} }}{2}\rho \left| {\vec{v}} \right|\vec{v}} \right)$$
(8)

The last term in Eq. (8) represents the viscous and inertial loss imposed by the porous media on the fluid. The laminar flows in porous media generally feature a pressure drop proportional to permeability (\(k\).) and velocity (\(v\).). By ignoring out an inertial loss term, we can reduce the porous media model to Darcy’s law, as expressed in Equation:

$$\nabla p = - \frac{\mu }{k}\vec{v}$$
(9)

For the three coordinate directions (\(x{\text{}},{\text{}}y{\text{}}\) and \(z\)) of the porous region, the pressure drop calculated by ANSYS Fluent can be expressed as in eqs:

$$\Delta p_{x} = \mathop \sum \limits_{{j = 1}}^{3} \frac{\mu }{{k_{{xj}} }}v_{j} \Delta n_{x}$$
(10)
$$\Delta p_{y} = ~\mathop \sum \limits_{{j = 1}}^{3} \frac{\mu }{{k_{{yj}} }}v_{j} \Delta n_{y}$$
(11)
$$\Delta p_{z} = \mathop \sum \limits_{{j = 1}}^{3} \frac{\mu }{{k_{{zj}} }}v_{j} \Delta n_{z}$$
(12)

where \(v_{j}\) indicates velocity components for x, y and z directions, and \(n_{x}\), \(n_{y}\), and \(n_{z}\) denote the medium thickness for the x, y and z directions. In anisotropic porous materials, this measure represents a tensor in the second rank of nine components, with components \(k_{ij} = (i, j = x, y, z)\) indicating permeability in flows of the i direction, as channeled via gradients of the j direction. In other words, there are three main directions and as many positive principle values within the permeability tensor. Therefore, if we neglect the permeability tensor \(k_{ij}\) off-diagonal components, Equations. 10, 11 and 12 can be written as: with \(k_{xx}\) and \(k_{yy}\) denoting in plane permeability, and \(k_{zz}\) indicating transverse permeability.

Uniform mesh and cut mesh method (Fig. 4) were used to generate high-quality mesh. This configuration helped to predict a good quality, high density mesh close to perforation borders.

Fig. 4
figure 4

The shape of uniform configuration mesh that used in CFD simulations

Full size image

Statistical procedure

Various methods for examining how different parameters may affect experimental results are applied by using design of experiments (DoE) software. The initial step in DoE is the identification of independent variables and/or factors that may have an effect on the experimental outcomes. The next step involves identifying the dependent variables and/or factors (Davim 2016). The experiments usually run based on different factor values or levels, such that each run features a combination pertaining to the specific factor value(s) or level(s) being investigated. In the present work, we used design expert software with BBD in designing the runs needed for statistical analysis. The Box–Behnken design (BBD), described as a response surface methodology (RSM) design, requires only three levels in its experimental runs (Box & Cox 1964). The model is then statistically validated through analysis of variance (ANOVA) (Box & Behnken 1960) (Ferreira et al. 2007). Based on these initial processes, four parameters were investigated, including the length of the completed open interval (\(h_{p}\) ), wellbore radius (\(r_{w}\) ), and the distance from the top of the open interval to the top of the formation (\(l\) ) divided each one on the formation's thickness (\(h\) ) to make them dimensionless parameters as well as permeability ratio (\(k_{r}\) ):

$$h_{d} = \frac{{h_{p} }}{h}$$
(13)
$$r_{d} = \frac{{r_{w} }}{h}$$
(14)
$$l_{d} = \frac{l}{h}$$
(15)
$$k_{r} = \frac{{k_{v} }}{{k_{h} }}$$
(16)

Two boundary points were selected, and one midpoint was determined by BBD for the intervals of the parameters as presented in Table 3. Twenty-five numerical runs were performed and analyzed to obtain a suitable statistical analysis using the ANOVA analysis with the BBD model.

Results and discussion

This study investigates specific water flow rate \(Q_{w}\) = 2 cm3/s with viscosity µ = 0. 95 mPa.s that is injected into the sample to determine the differential pressure. The dimensions and properties of the perforation tunnel sample are the same as those used in the experimental procedure (see Table 1). The comparison between the experimental and numerical results of the pressure buildup with the same flow boundary conditions is shown in Fig. 5. The experimental data and numerical results are in good agreement.

Fig. 5
figure 5

The comparison between experimental data, numerical results at the same flow boundary condition

Full size image

The validation of numerical results with experimental ones has resulted in full confidence in using the numerical model to conduct huge investigations by creating the near-wellbore region with different dimensions. Therefore, partially penetrated well parameters were analyzed using statistical analysis coupled with the numerical simulation model. The statistical analysis results show that partial penetration completion increases the pressure drop and thus contributes to a reduction in the productivity index.

This research investigated a specific water volume that was injected into the samples to determine the differential pressure of these samples. Table 4 presents the results of 25 numerical runs that were analyzed with ANOVA and the BBD model; the partial penetration skin factor results are shown in the last column.

Table 4 Twenty-five numerical runs
Full size table

The primary assumption in using the DoE model was the normal distribution of numerical data with a constant variance of features. In looking at the residuals’ normal plot in Fig. 6, we can see that the numerical data follows a normal distribution pattern. Additionally, our results show that the predicted values derived from the model share strong similarities with the actual values derived numerically.

Fig. 6
figure 6

Normal plot of residuals

Full size image

This study provided correlation from the statistical analysis based on the numerical results. This correlation used to determine the relative impact of each factor for different scenarios on the partial penetration skin factor.

$$Spp = {\text{}}e^{{\left( {4 - 3.65h_{d} - 135r_{d} - 0.26k_{r} + 0.125l_{d} } \right)}}$$
(17)

For example (numerical run), the partial penetration skin factor can be calculated from the difference in the pressure drop between open hole completion and two partial completion ceases with isotropic permeability and anisotropic permeability (\(k_{r} = 1{\text{ and }}k_{r} = 0.1\)) at the same geometry dimensions and flow boundary conditions (Table 5). The numerical results showed the pressure distribution and increased pressure drop for partially penetrated cases compared to open hole completion and illustrated the anisotropic permeability effect on flow converging, as shown in Figs. 7 and 8. The fluid flow lines are started in the radial directions until the wellbore boundaries are reached; the spherical flow regime appears after that due to the flow convergence effect. A low vertical-to-horizontal permeability ratio creates a high-pressure drop and affects spherical flow shape due to the vertical resistance. Also, the numerical results showed the gradation in the pressure and flow shape from spherical to elliptical with decreasing the permeability ratio.

Table 5 The dimensions, dimensionless parameters of two partial completion cases, and flow boundary conditions
Full size table
Fig. 7
figure 7

The pressure gradient for open hole completion case

Full size image
Fig. 8
figure 8

The pressure gradient for the two partial completion case with isotropic permeability \(~\left( {k_{r} = 1} \right)\) and with anisotropic permeability \(~\left( {k_{r} = 0.1} \right)\)

Full size image

Based on the statistical analysis results, the partial penetration skin factor value increase with decreases the dimensionless parameter \((h_{d}\)). The pressure drop is more affected by a smaller area of perforation intervals; the smaller area makes a larger contribution to pressure drop; the higher inflow rate leads to energy consumption increases for accelerating the flow. In contrast, open hole or fully completed perforation interval, this effect does not exist. However, we must note that this represents an ideal case that may or may not be reproducible in practice. Also, the results showed the interaction effect of the two dimensionless parameters (\(h_{d}\) and \(r_{d}\)) on the partial penetration skin factor, as illustrated in Fig. 9. The results indicated that the wellbore radius has a significant impact on partial penetration skin factor.

Fig. 9
figure 9

The interaction between the dimensionless parameters (\(h_{d}\) and \(r_{d}\)) and their effect on partial penetration pseudo-skin factor with constant values for the two dimensionless parameters (\(l_{d} = 0.35\) and \(k_{r} = 0.1\))

Full size image

The results also showed a similar effect for the dimensionless parameter (\(k_{r}\)) on the partial penetration skin factor. Analyses of the impact of vertical-to-horizontal permeability ratio on partial penetration skin factor indicate productivity’s dependence on the permeability ratio. As shown in Fig. 10, the impact of the permeability ratio on the partial penetration skin factor is revealed by the positive slope curve. The reduction of productivity results from higher resistance to converging flow in very low vertical permeability cases, compared with horizontal permeability. Hence, we can assert that the permeability ratio is directly proportionate to the productivity ratio. In contrast, dimensionless parameter (\(l_{d}\)) has less effect on the partial penetration skin factor, whereas maximum value for pseudo-skin is achieved at a low and high value, while the middle values do not have any effect, as illustrated in Fig. 11. From these results, we can learn the effect of each parameter and, based on the results, choose a completion design that is optimal.

Fig. 10
figure 10

The interaction between the dimensionless parameters (\(h_{d}\) and \(k_{r}\)) and their effect on partial penetration pseudo-skin factor with constant values for the two dimensionless parameters (\(l_{d} = 0.35\) and \(r_{d} = 0.000833\))

Full size image
Fig. 11
figure 11

The interaction between the dimensionless parameters (\(h_{d}\) and \(l_{d}\)) and their effect on partial penetration pseudo-skin factor with constant values for the two dimensionless parameters (\(r_{d} = 0.000833\) and \(k_{r} = 0.1\)

Full size image

The optimal completion design led to a reduction in the pressure drop as a result of reduced resistance coupled with an enhanced inflow rate. This means choosing the best dimensions of parameter that will lead to a high flow rate and accelerate radial inflow. The overall outcome of these informed choices is an increase in the productivity index. The effects of the four dimensionless parameters (\(h_{d}\), \(k_{r} {\text{}},r_{d} {\text{ and }}l_{d}\)) on the productivity ratio are shown in Figs. 12, 13, 14, and 15.

Fig. 12
figure 12

Effect of the dimensionless parameter (\(h_{d}\)) on productivity ratio PR

Full size image
Fig. 13
figure 13

Effect of the dimensionless parameter (\(~r_{d}\)) on productivity ratio PR

Full size image
Fig. 14
figure 14

Effect of the dimensionless parameter (\(~k_{r}\)) on productivity ratio PR

Full size image
Fig. 15
figure 15

Effect of the dimensionless parameter (\(~l_{d}\)) on productivity ratio PR

Full size image

In order to compare the accuracy of our correlation, five models Brons and Marting (1961), Odeh (1980), (Vrbik J. 1991), Papatzacos (1987) and Yeh and Reynolds (1989) were selected and used to calculate the partial penetration skin factor. The five models were compared to our correlation. To perform a comprehensive test, the effects of three-dimensional parameters for \(h_{d}\) = 0.2–0.6, \(r_{d}\) = 0.00083–0.0025, \(k_{v} /k_{h}\) = 0.1–1, and \(l_{d}\) = 0.2 on partial penetration skin factor were compared. The novel correlation performs well by providing estimates for the pseudo-skin factor that are relatively close to those obtained by the tested models, as shown in Figs. 16, 17 and 18. In general, analytical solutions applied to partially penetrating wells take into consideration that fluid is admitted at each point along the surface of the open interval. In other words, existing models neglect to include any additional fluid convergence caused by perforations. However, our CFD model did consider the effect of this convergence. In the high length of the completed perforation cases, the novel correlation showed little deviation compared to other models, due to local fluid convergence caused by perforations. However, this deviation does not appear in the short length of the completed perforation cases.

Fig. 16
figure 16

The comparison of the five models and the proposed correlation results for the effect of dimensionless open interval length (\(h_{d}\)) on the partial pseudo-skin factor

Full size image
Fig. 17
figure 17

The comparison of the five models and the proposed correlation results for the effect of dimensionless wellbore radius (\(r_{d}\)) on the partial pseudo-skin factor

Full size image
Fig. 18
figure 18

The comparison of the five models and the proposed correlation results for the effect of permeabilty ratio (\(k_{r}\)) on the partial pseudo-skin factor

Full size image

Conclusions

The study has been conducted to expand the investigation on partially completed vertical wells, understand its effects on partial penetration skin factor, and choose the optimal dimensions and distribution of partial penetration parameters. Based on the results of investigative analysis, the following conclusions can be summarized:

  1. 1.

    The study showed a clear view of the effect of each penetration parameter on the partial penetration skin factor and productivity index.

  2. a)

    The results showed that perforated/completion interval, wellbore radius and permeability ratio have a significant effect on the partial penetration skin factor and productivity index.

  3. b)

    The results indicated the distance spanning the open interval’s top to the formation’s top has less effect on the partial penetration skin factor.

  4. 2.

    The novel correlation has been produced from the current study that simplifies the estimation of the skin factor in partially completed vertical wells for different dimensions and distributions of the completion parameters.

  5. 3.

    Compared to other approaches, the novel correlation performs well by providing estimates for the partial penetration skin factor that are relatively close to previous models.