1 Introduction

Let us consider the following multivariate model

$$\begin{aligned} \underset{num \times 1}{{\varvec{y}}} = {\mathrm{vec}}\left( \underset{um \times n}{{\varvec{Y}}}\right) \sim {\mathcal {N}}\big (({\varvec{1}}_{n} \otimes {\varvec{I}}_{um}) \varvec{\mu }, {\varvec{I}}_{n} \otimes \varvec{\Gamma }\big ), \end{aligned}$$
(1.1)

where \({\mathrm{vec}}\) is a vectorization operator that is a linear transformation which converts the matrix into a column vector obtained by stacking the columns of a matrix on top of one another, \({\varvec{I}}_{n}\) is \(n\times n\) identity matrix, \({\varvec{Y}}=\left( {\varvec{y}}_1,\ldots ,{\varvec{y}}_n\right) \) stands for data matrix, \({\varvec{y}}_j\) is \(um \times 1\)-dimensional vector of all measurements corresponding to the j-th individual, \({\varvec{1}}_{n}\) is n-vector of ones, \(\otimes \) denotes Kronecker product, \(\varvec{\mu }\) is \(um \times 1\)-dimensional unknown mean vector. Here the \((um \times um)\)-dimensional covariance matrix \(\varvec{\Gamma }\) has BCS structure which is defined as

$$\begin{aligned} \varvec{\Gamma }= & {} \left[ \begin{array}{cccc} \varvec{\Gamma }_{0} &{}\quad \varvec{\Gamma }_{1} &{}\quad \ldots &{}\quad \varvec{\Gamma }_{1} \\ \varvec{\Gamma }_{1} &{}\quad \ddots &{}\quad &{}\quad \varvec{\Gamma }_{1}\\ \vdots &{}\quad &{}\quad \ddots &{}\quad \vdots \\ \varvec{\Gamma }_{1} &{}\quad \varvec{\Gamma }_{1} &{}\quad \ldots &{}\quad \varvec{\Gamma }_{0} \end{array}\right] \nonumber \\= & {} {\varvec{I}}_{u}\otimes \left( \varvec{\Gamma }_{0}- \varvec{\Gamma }_{1}\right) + {\varvec{J}}_{u}\otimes \varvec{\Gamma }_{1}, \end{aligned}$$
(1.2)

where \({\varvec{J}}_{u}\) denotes the \(u\times u\) matrix of ones, the \(m \times m\) block diagonals \(\varvec{\Gamma }_{0}\) represent the covariance matrix of the m response variables at any given level of factor, while the \(m \times m\) block off diagonals \(\varvec{\Gamma }_{1}\) represent the covariance matrix of the m response variables between any two levels of factor.

The matrix \(\varvec{\Gamma }\) is positive definite if and only if \(\varvec{\Gamma }_{0}+(u-1)\varvec{\Gamma }_{1}\) and \(\varvec{\Gamma }_{0}-\varvec{\Gamma }_{1}\) are positive definite matrices. For the proof see Roy and Leiva (2011) or Zmyślony et al. (2018).

In the second section we deal with problem of testing simultaneous hypotheses both for the expectation vector and the covariance structure in model (1.1). In the next section we present simulation study to compare powers of considered tests. In the fourth section we deal with real data and calculate p-value for each presented test. The last section contains summary of all obtained results in the paper and some remarks.

2 Simultaneous ratio F test

In Zmyślony et al. (2018) test for single hypothesis about the mean vector is considered and in Fonseca et al. (2018) test for single hypothesis about the covariance matrix is constructed. More precisely, the null hypothesis for the mean vector is

$$\begin{aligned} H^{\varvec{\mu }}_0:\varvec{\mu }_1=\varvec{\mu }_2=\cdots =\varvec{\mu }_u \end{aligned}$$
(2.1)

what means that mean vectors stay unchanged between all levels of factor. Under the null hypothesis such structure of mean vector is called the structured mean vector. For more details about model with the structured mean structure see Kozioł et al. (2018).

The null hypothesis for the covariance matrix \(\varvec{\Gamma }_1\) is

$$\begin{aligned} H^{\varvec{\Gamma }_1}_0:\varvec{\Gamma }_1={\varvec{0}} \end{aligned}$$
(2.2)

what means that there is no correlation between any two levels of factor.

Now let us consider the following simultaneous hypothesis

$$\begin{aligned} H^{\varvec{\mu },\varvec{\Gamma }_1}_0:H^{\varvec{\mu }}_0\wedge H^{\varvec{\Gamma }_1}_0. \end{aligned}$$
(2.3)

For hypotheses (2.1) and (2.2) test statistics have been constructed in Zmyślony et al. (2018) and Fonseca et al. (2018), as a ratio of positive and negative parts of best unbiased estimators. Details about this framework can be found in Michalski and Zmyślony (1996, 1999). These two test statistics have F distribution under null hypotheses with different numbers of degrees of freedom in numerator and the same number of degrees of freedom in denominator.

Let \(\varvec{{\widetilde{\mu }}}_j^{(c)}\) be best unbiased estimator (BUE) of orthogonal normalized contrast vector of \(\varvec{\mu }_j\) for \(j=2,\ldots ,u\). This estimator can be obtained using Helmert matrices, see Zmyślony et al. (2018). Then \(\sum _{j=2}^{u}\varvec{{\widetilde{\mu }}}_j^{(c)}\varvec{{\widetilde{\mu }}}_j^{(c)'}\) is positive part of estimator of \(\sum _{j=2}^{u}\varvec{\mu }_j^{(c)}\varvec{\mu }_j^{(c)'}\). The best unbiased estimators for \(\varvec{\Gamma }_0\) and \(\varvec{\Gamma }_1\) are

$$\begin{aligned} \varvec{{\widetilde{\Gamma }}}_{0}= & {} \frac{1}{(n-1)u}{\varvec{C}}_{0},\\ \varvec{{\widetilde{\Gamma }}}_{1}= & {} \frac{1}{(n-1)u(u-1)}{\varvec{C}}_{1}, \nonumber \end{aligned}$$

while

$$\begin{aligned} {\varvec{C}}_{0}= & {} \sum _{s=1}^{u}\sum _{r=1}^{n}\left( {{\varvec{y}}_{r,s}-\varvec{\overline{y}}_{\bullet s}}\right) \left( {{\varvec{y}}_{r,s}-\varvec{\overline{y}}_{\bullet s} }\right) ^{\prime },\\ {\varvec{C}}_{1}= & {} \underset{s\ne s^{*}}{ \sum _{s=1}^{u}\sum _{s^{*}=1}^{u}}\sum _{r=1}^{n}\left( {{\varvec{y}} _{r,s}-\varvec{\overline{y}}_{\bullet s}}\right) \left( {{\varvec{y}}_{r,s^{*}}-\varvec{\overline{y}}_{\bullet s^{*}}}\right) ^{\prime }, \end{aligned}$$

where \(\varvec{\overline{y}}_{\bullet s}=\frac{1}{n}\sum _{r=1}^{n}{{\varvec{y}}_{r,s}}\) and \({\varvec{y}}_{r,s}\) is m-variate vector of measurements on the \(r-th\) individual at the sth level of factor, \(r=1,\ldots ,n,\) and \(s=1,\ldots ,u\). For details see Roy et al. (2016). Moreover, let \(\widetilde{\varvec{\Gamma }}_{1+}\) and \(\widetilde{\varvec{\Gamma }}_{1-}\) be positive and negative part of best unbiased estimator \(\widetilde{\varvec{\Gamma }}_{1}\) for \(\varvec{\Gamma }_1\) (see Fonseca et al. 2018), respectively.

Following the above mentioned idea we prove

Theorem 1

The test statistic

$$\begin{aligned} F^{\varvec{\mu },\varvec{\Gamma }_1}=\frac{(u-1) {\varvec{x}}'\widetilde{\varvec{\Gamma }}_{1+} {\varvec{x}}}{{\varvec{x}}'\sum _{j=2}^{u} \varvec{{\widetilde{\mu }}}_j^{(c)} \varvec{{\widetilde{\mu }}}_j^{(c)'}{\varvec{x}}} \end{aligned}$$
(2.4)

with \({\varvec{x}}\ne {\varvec{0}}\), under null hypothesis (2.3) has F distribution with \(n-1\) and \(u-1\) degrees of freedom.

Proof

Let \(\varvec{{\widetilde{\Gamma }}}_{0}\) and \(\varvec{{\widetilde{\Gamma }}}_{1}\) be BUE for \(\varvec{\Gamma }_0\) and \(\varvec{\Gamma }_1\), respectively (see Roy et al. 2016; Seely 1977; Zmyślony 1980). From Fonseca et al. (2018) we get that under null hypothesis (2.2):

$$\begin{aligned} (n-1)u\varvec{{\widetilde{\Gamma }}}_{1+}= & {} (n-1) \left( \varvec{{\widetilde{\Gamma }}}_{0}+(u-1) \varvec{{\widetilde{\Gamma }}}_{1}\right)&\sim {\mathcal {W}}_m \left( \varvec{\Gamma }_0,n-1\right) , \end{aligned}$$
(2.5)
$$\begin{aligned} (n-1)u(u-1)\varvec{{\widetilde{\Gamma }}}_{1-}= & {} (n-1)(u-1)\left( \varvec{{\widetilde{\Gamma }}}_{0} -\varvec{{\widetilde{\Gamma }}}_{1}\right)&\sim \mathcal W_m\left( \varvec{\Gamma }_0,(n-1)(u-1)\right) , \end{aligned}$$
(2.6)

and are independent. Throughout the paper \({\mathcal {W}}_m\left( \varvec{\Sigma },n\right) \) stands for Wishart distribution with covariance matrix \(\varvec{\Sigma }\) and number of degrees of freedom equal to n.

Moreover, under null hypothesis (2.1):

$$\begin{aligned}&\sum _{j=2}^{u}\varvec{{\widetilde{\mu }}}_j^{(c)} \varvec{{\widetilde{\mu }}}_j^{(c)'}&\sim {\mathcal {W}}_m \left( \varvec{\Gamma }_0,u-1\right) , \end{aligned}$$
(2.7)
$$\begin{aligned}&(n-1)(u-1)\left( \varvec{{\widetilde{\Gamma }}}_{0} -\varvec{{\widetilde{\Gamma }}}_{1}\right)&\sim \mathcal W_m\left( \varvec{\Gamma }_0,(n-1)(u-1)\right) , \end{aligned}$$
(2.8)

and are independent. Additionally, statistics given in (2.7) and (2.9) are independent. For the proof see Zmyślony et al. (2018)

From (2.5) and (2.6) we have that for any \({\varvec{x}}\ne {\varvec{0}}\) test statistics for testing hypothesis (2.2) about the covariance matrix \(\varvec{\Gamma }_1\) is

$$\begin{aligned} F^{\varvec{\Gamma }_1}=\frac{{\varvec{x}}'\varvec{{\widetilde{\Gamma }}}_{1+} {\varvec{x}}}{{\varvec{x}}'\varvec{{\widetilde{\Gamma }}}_{1-} {\varvec{x}}}=\frac{{\varvec{x}}'\left( \varvec{{\widetilde{\Gamma }}}_{0} +(u-1)\varvec{{\widetilde{\Gamma }}}_{1}\right) {\varvec{x}}}{{\varvec{x}} '\left( \varvec{{\widetilde{\Gamma }}}_{0}-\varvec{{\widetilde{\Gamma }}}_{1}\right) {\varvec{x}}}\sim F_{n-1,(n-1)(u-1)}. \end{aligned}$$
(2.9)

For details see Fonseca et al. (2018). On the other hand, using (2.7) and (2.8), we get that for any \({\varvec{x}}\ne {\varvec{0}}\) test statistic for testing hypothesis (2.1) about the mean vector \(\varvec{\mu }\) is

$$\begin{aligned} F^{\varvec{\mu }}=\frac{\frac{1}{(u-1)}{\varvec{x}}'\sum _{j=2}^{u} \varvec{{\widetilde{\mu }}}_j^{(c)}\varvec{{\widetilde{\mu }}}_j^{(c)'} {\varvec{x}}}{{\varvec{x}}'\left( \varvec{{\widetilde{\Gamma }}}_{0} -\varvec{{\widetilde{\Gamma }}}_{1}\right) {\varvec{x}}}\sim F_{u-1,(n-1)(u-1)}. \end{aligned}$$
(2.10)

The proof is given in Zmyślony et al. (2018). One should note that in denominators of (2.9) and (2.10) there are the same expression \({\varvec{x}}'(\varvec{{\widetilde{\Gamma }}}_{0} -\varvec{{\widetilde{\Gamma }}}_{1}){\varvec{x}}\). Thus taking ratio of \(F^{\varvec{\Gamma }_1}\) and \(F^{\varvec{\mu }}\) we get that under null hypothesis (2.3) for any \({\varvec{x}}\ne {\varvec{0}}\)

$$\begin{aligned} F^{\varvec{\mu },\varvec{\Gamma }_1}=\frac{F^{\varvec{\Gamma }_1}}{F^{\varvec{\mu }}}= & {} \frac{{\varvec{x}}'\left( \varvec{{\widetilde{\Gamma }}}_{0} +(u-1)\varvec{{\widetilde{\Gamma }}}_{1}\right) {\varvec{x}} \cdot {\varvec{x}}'\left( \varvec{{\widetilde{\Gamma }}}_{0} -\varvec{{\widetilde{\Gamma }}}_{1}\right) {\varvec{x}}}{{\varvec{x}}' \left( \varvec{{\widetilde{\Gamma }}}_{0} -\varvec{{\widetilde{\Gamma }}}_{1}\right) {\varvec{x}}\cdot \frac{1}{(u-1)} {\varvec{x}}'\sum _{j=2}^{u} \varvec{{\widetilde{\mu }}}_j^{(c)}\varvec{{\widetilde{\mu }}}_j^{(c)'}{\varvec{x}}}\nonumber \\= & {} \frac{(u-1){\varvec{x}}'\varvec{{\widetilde{\Gamma }}}_{1+} {\varvec{x}}}{{\varvec{x}}'\sum _{j=2}^{u}\varvec{{\widetilde{\mu }}}_j^{(c)} \varvec{{\widetilde{\mu }}}_j^{(c)'}{\varvec{x}}}\sim F_{n-1,u-1}. \end{aligned}$$

\(\square \)

Remark 1

Note that test statistic for ratio F test can be also obtained as a ratio of \(F^{\varvec{\mu }}\) and \(F^{\varvec{\Gamma }_1}\). In this case, under null hypothesis (2.3) for any fixed \({\varvec{x}}\ne {\varvec{0}}\) such test statistic has F distribution with \(u-1\) and \(n-1\) degrees of freedom.

3 Simulation study

In this section we compare powers of simultaneous ratio F test obtained in the previous section with two tests for single hypotheses i.e. (2.1) and (2.2) and also with simultaneous F test for (2.3) constructed in Zmyślony and Kozioł (2019), whose test statistic is convex combination of test statistics of single F tests. For simulation study we assume that vector \({\varvec{x}}={\varvec{1}}\), which means that in (2.4) in nominator and denominator we take a sum of elements of estimators. Regarding parameters, we choose \(n=15\), \(u=2\), \(m=3\) and in case when all elements in vector of contrasts and in \(\varvec{\Gamma }_1\) have the same sign, we take vector of contrast in the following form

$$\begin{aligned} \varvec{\mu }^{(c)}_{2}=\left[ \begin{array}{r} 1.23744\\ 1.76777\\ 2.09304 \end{array}\right] \end{aligned}$$

and the following matrices \(\varvec{\Gamma }_{0}\) and \(\varvec{\Gamma }_{1}\)

$$\begin{aligned} \varvec{\Gamma }_{0} = \left[ \begin{array}{rrr} 0.01234 &{} \quad 0.02204 &{} \quad 0.00907 \\ 0.02204 &{} \quad 0.07559 &{} \quad 0.01694 \\ 0.00907 &{} \quad 0.01694 &{} \quad 0.01105 \end{array}\right] \ \ \text{ and } \ \ \varvec{\Gamma }_{1} = \left[ \begin{array}{rrr} 0.01025 &{}\quad 0.01899 &{}\quad 0.00819 \\ 0.01899 &{}\quad 0.06610 &{}\quad 0.01517 \\ 0.00819 &{}\quad 0.01517 &{}\quad 0.00810 \end{array}\right] . \end{aligned}$$

For these matrices \(\varvec{\Gamma }_0\), \(\varvec{\Gamma }_1\) and value of u, we determined interval for positive values of multiplier \(\lambda \), so that the following two conditions are satisfied:

  1. 1.

    \(\varvec{\Gamma }_{0}+(u-1)\lambda \varvec{\Gamma }_{1}\) is positive definite matrix,

  2. 2.

    \(\varvec{\Gamma }_{0}-\lambda \varvec{\Gamma }_{1}\) is positive definite matrix.

These conditions ensure positive definite of matrix \(\varvec{\Gamma }\). Moreover, in each step of simulation in test for expectation vector we add randomly chosen vectors to the vector of contrasts multiplied by the same \(\lambda \) to obtain power function of the test. Note that for \(\lambda =0\) we have null hypotheses. The simulation study is given in the same manner as in Zmyślony and Kozioł (2019).

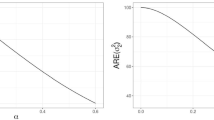
As can be seen from Fig. 1 in case when all elements in covariance matrix \(\varvec{\Gamma }_1\) and vector of contrasts \(\varvec{\mu }^{(c)}_{2}\) have the same sign, simultaneous ratio F test has bigger power than three other tests, both for single hypotheses and simultaneous convex combination F test.

Fig. 1
figure 1

Powers of tests in case when all elements in \(\varvec{\Gamma }_1\) and \(\varvec{\mu }^{(c)}_{2}\) are positive

Full size image

Now we consider case when elements in \(\varvec{\mu }^{(c)}_{2}\) have different signs. We take the following vector of contrasts

$$\begin{aligned} \varvec{\mu }^{(c)}_{2}=\left[ \begin{array}{r} 1.23744\\ -1.76777\\ 3.13955 \end{array}\right] . \end{aligned}$$

Matrices \(\varvec{\Gamma }_0\) and \(\varvec{\Gamma }_1\) have the same elements as in the previous case.

Figure 2 shows that this time simultaneous convex combination F test has the biggest power. Ratio F test close to null hypothesis has relatively small power but the farther away from the null hypothesis, the bigger increase power of this test, especially compared with power of F test for testing single hypothesis about covariance matrix. Power of test for testing single hypothesis about mean vector is poor which was predictable because in test statistic for this test is taken ratio of sum of elements of positive and sum of elements of negative part of BUE. For elements with different signs sum could be close to zero even if elements are far from 0.

Fig. 2
figure 2

Powers of tests in case when all elements in \(\varvec{\Gamma }_1\) are positive and elements in \(\varvec{\mu }^{(c)}_{2}\) have different signs

Full size image

In third case we take the same \(\varvec{\mu }^{(c)}_{2}\) as in the first case and matrices \(\varvec{\Gamma }_{0}\) and \(\varvec{\Gamma }_{1}\) of the following forms

$$\begin{aligned}&\varvec{\Gamma }_{0} = \left[ \begin{array}{rrr} 7.98767 &{}\quad -1.44727 &{}\quad 1.22910 \\ -2.44727 &{}\quad 12.25195 &{}\quad -4.18750 \\ 1.22950 &{}\quad -4.18750 &{}\quad 7.56094 \end{array}\right] \ \ \text{ and } \ \ \\&\varvec{\Gamma }_{1} = \left[ \begin{array}{rrr} 5.27860 &{}\quad -1.87846 &{}\quad 1.26189 \\ -1.87846 &{}\quad -3.19609 &{}\quad 1.11567 \\ 1.26189 &{}\quad 1.11567 &{}\quad -2.15724 \end{array}\right] . \end{aligned}$$

Thus now we consider case when elements in \(\varvec{\Gamma }_{1}\) have different signs and all elements in \(\varvec{\mu }^{(c)}_{2}\) have the same sign.

In Fig. 3 one can see different situation from two previous cases. Powers of simultaneous tests, both based on ratio and convex combination, are very low compared with the power of test for testing single hypothesis about \(\varvec{\mu }\). Nevertheless, ratio F test is better than convex combination F test in this comparison. Test for testing single hypothesis about \(\varvec{\Gamma }_{1}\) has the lowest power. The reason for this is the same as the one described in second case for test for \(\varvec{\mu }\). Poor power of simultaneous tests reveals fact that different signs of elements in the covariance matrix has big impact on power of these tests.

Fig. 3
figure 3

Powers of tests in case when elements in \(\varvec{\Gamma }_1\) have different signs and all elements in \(\varvec{\mu }^{(c)}_{2}\) are positive

Full size image

For the last considered case we take matrices \(\varvec{\Gamma }_0\) and \(\varvec{\Gamma }_1\) as in the previous case and vector of contrasts as in the second case. Thus elements in \(\varvec{\Gamma }_1\) and elements in \(\varvec{\mu }^{(c)}_{2}\) have different signs.

In Fig. 4 one can see that all four considered tests have low powers and this is clear from two previous cases. Thus in case when in the covariance matrix and in vector of contrasts there are both positive and negative elements, none of these tests are recommended for testing hypotheses about the mean vector \(\varvec{\mu }\) and the covariance matrix \(\varvec{\Gamma }_1\).

Fig. 4
figure 4

Powers of tests in case when elements in \(\varvec{\Gamma }_1\) and elements in \(\varvec{\mu }^{(c)}_{2}\) have different signs

Full size image

4 Data example

We consider clinical study data on mineral contents in bones of the upper arm and the forearm (radius, humerus and ulna) in 25 women. Measurements were taken on the dominant and non-dominant side of each woman. This data is taken from Johnson and Wichern (2007) on page 43 to give example of the use of the proposed test. For this data \(m=3\), \(u=2\) and \(n=25\). According to results given in Roy et al. (2016) the best unbiased estimators of \({\varvec{\Gamma }}_{0}\) and \({\varvec{\Gamma }}_{1}\) for model with unstructured mean vector are

$$\begin{aligned} \widetilde{\varvec{\Gamma }}_{0} = \left[ \begin{array}{rrr} 0.01221 &{}\quad 0.02172 &{}\quad 0.00901 \\ 0.02172 &{}\quad 0.07492 &{}\quad 0.01682 \\ 0.00901 &{}\quad 0.01682 &{}\quad 0.01108 \end{array}\right] \ \ \text{ and } \ \ \widetilde{\varvec{\Gamma }}_{1} = \left[ \begin{array}{rrr} 0.01038 &{}\quad 0.01931 &{}\quad 0.00824 \\ 0.01931 &{}\quad 0.06678 &{}\quad 0.01529 \\ 0.00824 &{}\quad 0.01529 &{}\quad 0.00807 \end{array}\right] , \end{aligned}$$

and the unbiased estimator of mean vector \(\varvec{\mu }\) is the following:

$$\begin{aligned} \widetilde{\varvec{\mu }} = \left[ \begin{array}{rrrrrr} 0.84380&1.79268&\quad 0.70440&\quad 0.81832&\quad 1.73484&\quad 0.69384 \end{array}\right] . \end{aligned}$$

We calculated p-values for F tests and LRTs for testing single hypotheses about matrix \(\varvec{\Gamma }_1\) and mean vector \(\varvec{\mu }\) and p-values for simultaneous F tests, both convex combination and ratio F test. Regarding mean structure p-value for F test is equal to 0.0363 and for LRT is equal to 0.1725, so that we make different conclusions on standard 5% level of significance (for details see Zmyślony et al. 2018). P-value for F test for testing hypothesis about covariance matrix is equal to \(1.0607\times 10^{-9}\) and for LRT is equal to \(1.8074\times 10^{-13}\), so in this case for both tests we make the same conclusions on any reasonable significance level. Finally p-values for simultaneous convex combination F test is equal to \(1.2832\times 10^{-9}\), while for ratio F test p-value is equal to 0.4126. The reason of difference between conclusions of those two simultaneous tests is that for single F test about mean structure p-value is relatively big comparing to p-value for F tests about covariance matrix \(\varvec{\Gamma }_1\). Thus ratio of these two single test statistics is relatively small what implies that p-value for ratio F test is quite high.

5 Conclusions

The test presented in this paper, whose statistic has explicit F distribution, provides a valid alternative to tests for single hypotheses about covariance components and mean vector in multivariate models with BCS covariance structure and convex combination F test for testing simultaneous hypotheses. Test statistic of proposed test is ratio of test statistics for single hypotheses mentioned in this paper. Simulation study shows good and bad sides of obtained ratio F test. In case when all elements in contrast vector and covariance matrix have the same sign proposed test is more powerful than all three other compared F tests. In the other cases it is recommended to use simultaneous convex combination F test or single F tests.