Abstract
In this paper, we aim to discuss the common fixed point of Proinov type mapping via simulation function. The presented results not only generalize, but also unify the corresponding results in this direction. We also consider an example to indicate the validity of the obtained results.
Similar content being viewed by others
1 Introduction and preliminaries
Fixed point theory is one of the dynamic research topics of the last decades due to its vast application potential on several distinct disciplines; see e.g. [1–4]. Very recently, Proinov [5] introduced new classes of auxiliary function to propose a new metric fixed point theorem that covers many existing fixed point theorems, mostly having appeared in the last decades. Proinov [5] also showed that recently declared theorems are in fact equivalent to the special cases of Skof’s theorem [6]. Recently, Proinov type contractions have attracted the attention of some authors; see e.g. [7–9] On the other hand, another interesting improvement was reported in 2015: simulation functions were proposed first by Khojasteh et al. [10] to unify some well-known fixed point theorems. This approach has been considered and improved by several authors; see e.g. [11–20].
In this paper, we combine the notions of simulation functions and Proinov type contraction to get a more general framework to guarantee the existence of a fixed point. We investigate the common fixed point of new types mapping under this construction in the context of complete metric space.
We shall first recall the notations we shall use: \(\mathbb{R},\mathbb{R}^{+},\mathbb{N}\) for the reals, nonnegative real numbers and natural numbers, \(\mathbb{R}^{+}_{0}=\mathbb{R}^{+} \cup \{0\}=[0,\infty )\) and \(\mathbb{N}_{0}=\mathbb{N} \cup \{0\}\) and \(\Theta = \{ \vartheta:(0,\infty )\rightarrow \mathbb{R} \} \).
Definition 1
(See [10])
A function \(\eta:\mathbb{R}^{+}_{0}\times \mathbb{R}^{+}_{0}\rightarrow \mathbb{R}\) is called a simulation function if the following conditions hold:
- \((\eta _{1})\):
-
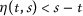 for all
for all 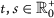 ;
; - \((\eta _{2})\):
-
if
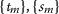 in \((0,\infty )\) are two sequences such that
in \((0,\infty )\) are two sequences such that 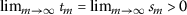 , then
, then 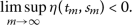 (1.1)
(1.1)
For the set of all functions simulation functions η, we employ the symbol Z.
Theorem 2
([5])
Let the metric space \((X, \mathsf {d})\) and the mapping \(P: X\rightarrow X\) such that

where \(\vartheta ,\psi:(0,\infty )\rightarrow \mathbb{R}\) are such that the following conditions hold:
-
(a)
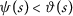 , for any
, for any 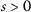 ;
; -
(b)
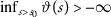 , for any
, for any 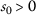 ;
; -
(c)
if the sequences \(\{ \vartheta (a_{m}) \} \) and \(\{ \psi (a_{m}) \} \) are convergent with the same limit and \(\{ \vartheta (a_{m}) \} \) is strictly decreasing, then \(a_{m}\rightarrow 0\) as \(m\rightarrow \infty \);
-
(d)
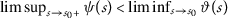 or
or 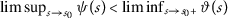 for any
for any 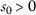 ;
; -
(e)
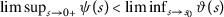 for any
for any 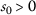 .
.
Then the mapping P possesses exactly one fixed point.
We mention here the following lemmas which will be useful in the sequel.
Lemma 3
([21])
Let  be a sequence in a metric space \((X,\mathsf {d})\) such that
be a sequence in a metric space \((X,\mathsf {d})\) such that  . If the sequence
. If the sequence  is not Cauchy then there exist \(\mathsf{e}_{0}>0\) and the sequences \(\{ m_{l} \} \), \(\{ p_{l} \} \) of positive integers such that \(m_{l}\) is the smallest index for which \(m_{l}>p_{l}>l\),
is not Cauchy then there exist \(\mathsf{e}_{0}>0\) and the sequences \(\{ m_{l} \} \), \(\{ p_{l} \} \) of positive integers such that \(m_{l}\) is the smallest index for which \(m_{l}>p_{l}>l\),  and
and

Lemma 4
([5])
For \(\vartheta:(0,\infty )\rightarrow \mathbb{R}\) the following conditions are equivalent:
-
(1)
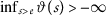 for every
for every 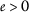 .
. -
(2)
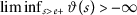 for every
for every 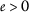 .
. -
(3)
\(\liminf_{m\rightarrow \infty }\vartheta (a_{m})=- \infty \) implies \(\lim_{m\rightarrow \infty }a_{m}=0\).
2 Main results
In what follows, we shall consider that \(P, Q: X\rightarrow X\) and \(\mathsf {m}, \mathsf {r}_{1}, \mathsf {r}_{2}:X\times X\rightarrow \mathbb{R}_{0}^{+}\) are defined as


and

for any  such that
such that  .
.
Theorem 5
Let \((X, \mathsf {d})\) be a complete metric space and two mappings \(P, Q: X\rightarrow X\). Assume that there exists a function \(\eta \in Z\) such that

where \(\vartheta ,\psi \in \Theta \). Then the mappings \(P,Q\) have a unique fixed point provided that the following conditions are satisfied:
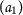 :
:-
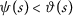 , for any
, for any 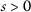 ;
; 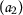 :
:-
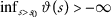 , for any
, for any 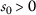 ;
; 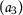 :
:-
if \(\{ a_{m} \} \), \(\{ b_{m} \} \) are two convergent sequences with \(\lim_{m\rightarrow \infty }a_{m}=\lim_{m \rightarrow \infty }b_{m}>0\) then the sequences \(\{ \vartheta (a_{m}) \} \), \(\{ \vartheta (b_{m}) \} \) are convergent and \(\lim_{m\rightarrow \infty }\vartheta (a_{m})= \lim_{m\rightarrow \infty }\vartheta (b_{m})>0\).
Proof
Let  be an arbitrary, but fixed point and the sequence
be an arbitrary, but fixed point and the sequence  defined as follows:
defined as follows:

for each \(m\in \mathbb{N}_{0}\). First of all, let us remark that, if there exists \(m_{0}\in \mathbb{N}\) such that  , then
, then  is a fixed point of P (in the case that \(m_{0}\) is even) or Q (if \(m_{0}\) is odd). Moreover, supposing, for example, that
is a fixed point of P (in the case that \(m_{0}\) is even) or Q (if \(m_{0}\) is odd). Moreover, supposing, for example, that  is a fixed point of the mapping P but is not a common fixed point of P and Q (this means
is a fixed point of the mapping P but is not a common fixed point of P and Q (this means  ), we get
), we get  and
and

since

and taking  into account we deduce that
into account we deduce that

which is a contradiction. Therefore, without loss of generality, we can suppose that  for any \(m\in \mathbb{N}_{0}\). Thus, supposing that \(m=2i\), we have
for any \(m\in \mathbb{N}_{0}\). Thus, supposing that \(m=2i\), we have  and from (2.4) and \((\eta _{1})\), we have
and from (2.4) and \((\eta _{1})\), we have

and using  we deduce
we deduce

In the case that there exists \(i_{0}\in \mathbb{N}\) such that  , the inequality (2.6) leads to
, the inequality (2.6) leads to  , which is a contradiction. Accordingly,
, which is a contradiction. Accordingly,

and then, for any even natural number m, the sequence  is non-increasing and positive. Of course, using the same argument, there follows a similar conclusion when m is an odd natural number. Therefore, we can find \(\mathsf{D}\geq 0\) such that
is non-increasing and positive. Of course, using the same argument, there follows a similar conclusion when m is an odd natural number. Therefore, we can find \(\mathsf{D}\geq 0\) such that  . Assuming that \(\mathsf{D}>0\) by (2.6) we have
. Assuming that \(\mathsf{D}>0\) by (2.6) we have

which shows us that the sequence  is decreasing and moreover, taking
is decreasing and moreover, taking  into account, it is bounded below. Thus, letting \(m\rightarrow \infty \) in (2.8), it follows that the sequences
into account, it is bounded below. Thus, letting \(m\rightarrow \infty \) in (2.8), it follows that the sequences  and
and  are convergent to the same limit. Therefore, by \((\eta _{2})\) we get
are convergent to the same limit. Therefore, by \((\eta _{2})\) we get

On the other hand, taking \((\eta _{1})\) into account, (2.4) implies

and

which contradicts (2.9). Thus,

Next, we claim that the sequence  is Cauchy. Reasoning by contradiction, if
is Cauchy. Reasoning by contradiction, if  is not Cauchy, by Lemma 3, we can find
is not Cauchy, by Lemma 3, we can find  and the sequences \(\{ m_{l} \} \), \(\{ p_{l} \} \) of positive integers such that the equalities (1.2) hold, where \(m_{l}\) is smallest index for which \(m_{l}>p_{l}>l\), for all \(l\geq 1\). Replacing in (2.1)
and the sequences \(\{ m_{l} \} \), \(\{ p_{l} \} \) of positive integers such that the equalities (1.2) hold, where \(m_{l}\) is smallest index for which \(m_{l}>p_{l}>l\), for all \(l\geq 1\). Replacing in (2.1)  by
by  and
and  by
by  we have
we have

and taking into account (2.1) and (2.10) it follows that

So,  and by
and by  we get
we get

Since by (2.4) we have

or, taking \((\eta _{1})\) and  into account,
into account,

Using (2.12) we get  . Thus, by (\(\eta _{2}\)) we have
. Thus, by (\(\eta _{2}\)) we have

which leads to a contradiction, since by (2.13), we have

Thereupon,  is a Cauchy sequence. Moreover, since X is a complete metric space, we can find
is a Cauchy sequence. Moreover, since X is a complete metric space, we can find  such that
such that

and we claim that this is a common fixed point of the mappings Q and P. From the point of view of a previous remark, it is enough to prove that  is a fixed point of Q (or P). Indeed, supposing
is a fixed point of Q (or P). Indeed, supposing  , we see that
, we see that  as \(m\rightarrow \infty \) and then
as \(m\rightarrow \infty \) and then  for infinitely many values of \(m\in \mathbb{N}\). Hence, from (2.4) we have
for infinitely many values of \(m\in \mathbb{N}\). Hence, from (2.4) we have

or

where

Thus,

and in view of  ,
,  . Therefore, letting \(m\rightarrow \infty \) in (2.16), we get
. Therefore, letting \(m\rightarrow \infty \) in (2.16), we get  and using \((\eta _{1})\) and \((\eta _{2})\) we obtain
and using \((\eta _{1})\) and \((\eta _{2})\) we obtain

a contradiction. Thereupon,  , which means that
, which means that  is a fixed point of Q and then a common fixed point of P and Q.
is a fixed point of Q and then a common fixed point of P and Q.
Finally, we have to show the uniqueness of this point. If on the contrary, there exists another point  , different by
, different by  , such that
, such that  , since
, since  , we have
, we have

which in view of \((\eta _{1})\) becomes

which is obviously a contradiction. □
Corollary 6
Let \((X, \mathsf {d})\) be a complete metric space and a mapping \(P: X\rightarrow X\). Assume that there exists a function \(\eta \in Z\) such that

for any  with
with  , where \(\vartheta ,\psi \in \Theta \). Then the mapping P has a unique fixed point provided that the following conditions are satisfied:
, where \(\vartheta ,\psi \in \Theta \). Then the mapping P has a unique fixed point provided that the following conditions are satisfied:
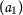 :
:-
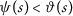 , for any
, for any 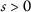 ;
; 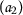 :
:-
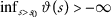 , for any
, for any 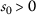 ;
; 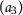 :
:-
if \(\{ a_{m} \} \), \(\{ b_{m} \} \) are two convergent sequences with \(\lim_{m\rightarrow \infty }a_{m}=\lim_{m \rightarrow \infty }b_{m}>0\) then the sequences \(\{ \vartheta (a_{m}) \} \), \(\{ \vartheta (b_{m}) \} \) are convergent and \(\lim_{m\rightarrow \infty }\vartheta (a_{m})= \lim_{m\rightarrow \infty }\vartheta (b_{m})>0\).
Proof
Put \(Q=P\) in Theorem 5. □
Theorem 7
Let \((X, \mathsf {d})\) be a complete metric space, two mappings \(P, Q: X\rightarrow X\) and a function \(\eta \in Z\) such that

where \(\vartheta ,\psi \in \Theta \). Suppose that
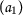 :
:-
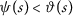 , for any
, for any 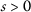 ;
; 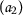 :
:-
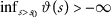 , for any
, for any 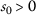 ;
; 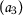 :
:-
if \(\{ a_{m} \} \), \(\{ b_{m} \} \) are convergent sequences with with \(\lim_{m\rightarrow \infty }a_{m}=\lim_{m \rightarrow \infty }b_{m}>0\) then the sequences \(\{ \vartheta (a_{m}) \} \), \(\{ \vartheta (b_{m}) \} \), are convergent and \(\lim_{m\rightarrow \infty }\vartheta (a_{m})= \lim_{m\rightarrow \infty }\vartheta (b_{m})\).
Then the mappings \(P,Q\) have a unique fixed point.
Proof
Let  be an arbitrary point and the sequence
be an arbitrary point and the sequence  in X, defined as follows:
in X, defined as follows:

for every \(m\in \mathbb{N}\). In what follows, we shall suppose that  for any \(m\in \mathbb{N}\) (using the same arguments as in the previous proof).
for any \(m\in \mathbb{N}\) (using the same arguments as in the previous proof).
Let  , \(m\in \mathbb{N}\). First of all, we claim that \(o_{m+1}< o_{m}\), for all \(m\in \mathbb{N}\). For this purpose, we shall distinguish two situations:
, \(m\in \mathbb{N}\). First of all, we claim that \(o_{m+1}< o_{m}\), for all \(m\in \mathbb{N}\). For this purpose, we shall distinguish two situations:
(1) If \(m=2i\), \(i\in \mathbb{N}\) we have

Since \(o_{m}>0\) for any \(m\in \mathbb{N}\), we see that  and by (2.18) we have
and by (2.18) we have

Moreover, from \((\eta _{1})\) and  it follows
it follows

If  for some \(i_{0}\in \mathbb{N}\), the inequality (2.20) leads to a contradiction. Therefore,
for some \(i_{0}\in \mathbb{N}\), the inequality (2.20) leads to a contradiction. Therefore,  for any \(i\in \mathbb{N}\).
for any \(i\in \mathbb{N}\).
(2) If \(m=2i-1\), \(i\in \mathbb{N}\),

and using the same arguments it follows that  , for any \(i\in \mathbb{N}\). Therefore, we conclude that the sequence \(\{ o_{m} \} \) is convergent with the limit \(\mathsf {D}\geq 0\) (being decreasing and bounded below by 0). Moreover, from (2.20) together with \((\eta _{1})\) and we get
, for any \(i\in \mathbb{N}\). Therefore, we conclude that the sequence \(\{ o_{m} \} \) is convergent with the limit \(\mathsf {D}\geq 0\) (being decreasing and bounded below by 0). Moreover, from (2.20) together with \((\eta _{1})\) and we get
From our considerations, we conclude that the sequence \(\{ \vartheta (o_{2i}) \} \) is convergent (being decreasing and taking  into account). Thereupon, by (2.21), the sequence \(\{ \psi (o_{2i}) \} )\) is convergent and has the same limit as \(\{ \vartheta (o_{2i}) \} )\). If we suppose that \(\mathsf {D}>0\), on the one hand, by \((\eta _{1})\) we have
into account). Thereupon, by (2.21), the sequence \(\{ \psi (o_{2i}) \} )\) is convergent and has the same limit as \(\{ \vartheta (o_{2i}) \} )\). If we suppose that \(\mathsf {D}>0\), on the one hand, by \((\eta _{1})\) we have
On the other hand, taking \((\eta _{2})\) into account we get
This is a contradiction. Therefore \(\mathsf {D}=0\), so,

We shall prove that  is a Cauchy sequence. Arguing by contradiction, if
is a Cauchy sequence. Arguing by contradiction, if  is not Cauchy, by Lemma 3, we can find two sequences \(\{ m_{l} \} \), \(\{ p_{l} \} \) of positive integers and
is not Cauchy, by Lemma 3, we can find two sequences \(\{ m_{l} \} \), \(\{ p_{l} \} \) of positive integers and  such that \(m_{l}\) is smallest index for which \(m_{l}>p_{l}>l\) and (1.2) hold. Letting
such that \(m_{l}\) is smallest index for which \(m_{l}>p_{l}>l\) and (1.2) hold. Letting  , respectively,
, respectively,  in (2.2) we have
in (2.2) we have

and then  . Moreover, by
. Moreover, by  ,
,

Plugging this into (2.18), we have

or, taking \((\eta _{1})\) and  into account
into account

Thus, by (2.23), we get

which implies, by \((\eta _{2})\),

On the other hand, letting \(l\rightarrow \infty \) in (2.24), we have

which contradicts the previous inequality. Therefore, the sequence  is Cauchy, and by the completeness of the space X it is a convergent sequence. Let
is Cauchy, and by the completeness of the space X it is a convergent sequence. Let  such that
such that  . We claim that
. We claim that  is a common fixed point of P and Q. First of all, we prove that
is a common fixed point of P and Q. First of all, we prove that  is a fixed point of Q. If for infinitely many values of m,
is a fixed point of Q. If for infinitely many values of m,  , then
, then

and  , so that
, so that  .
.
If  for any \(m\in \mathbb{N}\), by (2.18) we have
for any \(m\in \mathbb{N}\), by (2.18) we have

or, equivalently

Since  and
and

we see that  . Therefore, by
. Therefore, by  it follows that
it follows that  and taking \((\eta _{2})\) into account,
and taking \((\eta _{2})\) into account,

But, letting \(m\rightarrow \infty \) in (2.25),

This is a contradiction; consequently,  and
and  is a fixed point of Q and we assume, by “reductio ad absurdum”, that
is a fixed point of Q and we assume, by “reductio ad absurdum”, that  is not a fixed point of P. Then
is not a fixed point of P. Then  and (2.18) gives us
and (2.18) gives us

which is equivalent with

which is a contradiction. Therefore, by  it follows that
it follows that  and then
and then  is a common fixed point of P and Q.
is a common fixed point of P and Q.
As a last step in our proof, we shall prove the uniqueness of the common fixed point. Indeed, if there exists another point, for example  such that
such that  and
and  , then, since
, then, since  , from (2.18) we have
, from (2.18) we have

which is a contradiction. Thereupon,  , so the fixed point of the mappings Q and P is unique. □
, so the fixed point of the mappings Q and P is unique. □
Example 8
Let the set \(X= \{ \mathsf {a}_{1},\mathsf {a}_{2},\mathsf {a}_{3},\mathsf {a}_{4} \} \) and \(\mathsf {d}:X\times X\rightarrow [0,+\infty )\) be defined as follows:
Let \(Q,P: X\rightarrow X\) be two mappings where
and we choose the functions \(\eta \in Z\) and \(\vartheta ,\psi \in \Theta \), with

Of course, we can easily see that, with these choices, the assumptions  –
– of Theorem 7 are obviously satisfied. Thus, we shall check that (2.18) holds for any
of Theorem 7 are obviously satisfied. Thus, we shall check that (2.18) holds for any  , such that
, such that  . We discuss then the following situations:
. We discuss then the following situations:
-
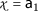 ,
, 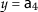 , $$\begin{aligned} &\mathsf {d}(P\mathsf {a}_{1}, Q\mathsf {a}_{4})=\mathsf {d}( \mathsf {a}_{1}, \mathsf {a}_{2})=2, \\ &\begin{aligned}[b] \mathsf {r}_{1}(\mathsf {a}_{1}, \mathsf {a}_{4})&=\max \biggl\{ \mathsf {d}( \mathsf {a}_{1},\mathsf {a}_{4}), \frac{(1+\mathsf {d}(\mathsf {a}_{1},P\mathsf {a}_{1}))\mathsf {d}(\mathsf {a}_{4}, Q\mathsf {a}_{4})}{1+\mathsf {d}(\mathsf {a}_{1}, \mathsf {a}_{4})}, \frac{\mathsf {d}(\mathsf {a}_{1},Q\mathsf {a}_{4})+\mathsf {d}(\mathsf {a}_{4},P\mathsf {a}_{1})}{2} \biggr\} \\ &=\max \biggl\{ \mathsf {d}(\mathsf {a}_{1},\mathsf {a}_{4}), \frac{(1+\mathsf {d}(\mathsf {a}_{1},\mathsf {a}_{1}))\mathsf {d}(\mathsf {a}_{4}, \mathsf {a}_{2})}{1+\mathsf {d}(\mathsf {a}_{1}, \mathsf {a}_{4})}, \frac{\mathsf {d}(\mathsf {a}_{1},\mathsf {a}_{2})+\mathsf {d}(\mathsf {a}_{4},\mathsf {a}_{1})}{2} \biggr\} \\ &=\max \biggl\{ 5, \frac{5}{6},\frac{7}{2} \biggr\} =5 \end{aligned} \end{aligned}$$
, $$\begin{aligned} &\mathsf {d}(P\mathsf {a}_{1}, Q\mathsf {a}_{4})=\mathsf {d}( \mathsf {a}_{1}, \mathsf {a}_{2})=2, \\ &\begin{aligned}[b] \mathsf {r}_{1}(\mathsf {a}_{1}, \mathsf {a}_{4})&=\max \biggl\{ \mathsf {d}( \mathsf {a}_{1},\mathsf {a}_{4}), \frac{(1+\mathsf {d}(\mathsf {a}_{1},P\mathsf {a}_{1}))\mathsf {d}(\mathsf {a}_{4}, Q\mathsf {a}_{4})}{1+\mathsf {d}(\mathsf {a}_{1}, \mathsf {a}_{4})}, \frac{\mathsf {d}(\mathsf {a}_{1},Q\mathsf {a}_{4})+\mathsf {d}(\mathsf {a}_{4},P\mathsf {a}_{1})}{2} \biggr\} \\ &=\max \biggl\{ \mathsf {d}(\mathsf {a}_{1},\mathsf {a}_{4}), \frac{(1+\mathsf {d}(\mathsf {a}_{1},\mathsf {a}_{1}))\mathsf {d}(\mathsf {a}_{4}, \mathsf {a}_{2})}{1+\mathsf {d}(\mathsf {a}_{1}, \mathsf {a}_{4})}, \frac{\mathsf {d}(\mathsf {a}_{1},\mathsf {a}_{2})+\mathsf {d}(\mathsf {a}_{4},\mathsf {a}_{1})}{2} \biggr\} \\ &=\max \biggl\{ 5, \frac{5}{6},\frac{7}{2} \biggr\} =5 \end{aligned} \end{aligned}$$and
$$\begin{aligned} \eta \bigl(\vartheta \bigl(\mathsf {d}(P\mathsf {a}_{1},Q\mathsf {a}_{4})\bigr), \psi \bigl(\mathsf {r}_{1}(\mathsf {a}_{1},\mathsf {a}_{4})\bigr) \bigr)=0.88\cdot 0.91 \cdot 5-2=2.004>0. \end{aligned}$$ -
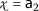 ,
, 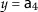 , $$\begin{aligned} &\mathsf {d}(P\mathsf {a}_{2}, Q\mathsf {a}_{4})=\mathsf {d}( \mathsf {a}_{1}, \mathsf {a}_{2})=2, \\ &\begin{aligned}[b] \mathsf {r}_{1}(\mathsf {a}_{2}, \mathsf {a}_{4})&=\max \biggl\{ \mathsf {d}( \mathsf {a}_{2},\mathsf {a}_{4}), \frac{(1+\mathsf {d}(\mathsf {a}_{2},P\mathsf {a}_{2}))\mathsf {d}(\mathsf {a}_{4}, Q\mathsf {a}_{4})}{1+\mathsf {d}(\mathsf {a}_{2}, \mathsf {a}_{4})}, \frac{\mathsf {d}(\mathsf {a}_{2},Q\mathsf {a}_{4})+\mathsf {d}(\mathsf {a}_{4},P\mathsf {a}_{2})}{2} \biggr\} \\ &=\max \biggl\{ \mathsf {d}(\mathsf {a}_{2},\mathsf {a}_{4}), \frac{(1+\mathsf {d}(\mathsf {a}_{2},\mathsf {a}_{1}))\mathsf {d}(\mathsf {a}_{4}, \mathsf {a}_{2})}{1+\mathsf {d}(\mathsf {a}_{2}, \mathsf {a}_{4})}, \frac{\mathsf {d}(\mathsf {a}_{1},\mathsf {a}_{2})+\mathsf {d}(\mathsf {a}_{4},\mathsf {a}_{1})}{2} \biggr\} \\ &=\max \biggl\{ 3, \frac{9}{4},\frac{7}{2} \biggr\} = \frac{7}{2} \end{aligned} \end{aligned}$$
, $$\begin{aligned} &\mathsf {d}(P\mathsf {a}_{2}, Q\mathsf {a}_{4})=\mathsf {d}( \mathsf {a}_{1}, \mathsf {a}_{2})=2, \\ &\begin{aligned}[b] \mathsf {r}_{1}(\mathsf {a}_{2}, \mathsf {a}_{4})&=\max \biggl\{ \mathsf {d}( \mathsf {a}_{2},\mathsf {a}_{4}), \frac{(1+\mathsf {d}(\mathsf {a}_{2},P\mathsf {a}_{2}))\mathsf {d}(\mathsf {a}_{4}, Q\mathsf {a}_{4})}{1+\mathsf {d}(\mathsf {a}_{2}, \mathsf {a}_{4})}, \frac{\mathsf {d}(\mathsf {a}_{2},Q\mathsf {a}_{4})+\mathsf {d}(\mathsf {a}_{4},P\mathsf {a}_{2})}{2} \biggr\} \\ &=\max \biggl\{ \mathsf {d}(\mathsf {a}_{2},\mathsf {a}_{4}), \frac{(1+\mathsf {d}(\mathsf {a}_{2},\mathsf {a}_{1}))\mathsf {d}(\mathsf {a}_{4}, \mathsf {a}_{2})}{1+\mathsf {d}(\mathsf {a}_{2}, \mathsf {a}_{4})}, \frac{\mathsf {d}(\mathsf {a}_{1},\mathsf {a}_{2})+\mathsf {d}(\mathsf {a}_{4},\mathsf {a}_{1})}{2} \biggr\} \\ &=\max \biggl\{ 3, \frac{9}{4},\frac{7}{2} \biggr\} = \frac{7}{2} \end{aligned} \end{aligned}$$and
$$\begin{aligned} \eta \bigl(\vartheta \bigl(\mathsf {d}(P\mathsf {a}_{2},Q\mathsf {a}_{4})\bigr), \psi \bigl(\mathsf {r}_{1}(\mathsf {a}_{2},\mathsf {a}_{4})\bigr) \bigr)=0.88\cdot 0,91 \cdot 3.5-2=0.8>0. \end{aligned}$$ -
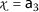 ,
, 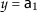 , $$\begin{aligned} &\mathsf {d}(P\mathsf {a}_{3}, Q\mathsf {a}_{1})=\mathsf {d}( \mathsf {a}_{2}, \mathsf {a}_{1})=2, \\ &\begin{aligned}[b] \mathsf {r}_{1}(\mathsf {a}_{3}, \mathsf {a}_{1})&=\max \biggl\{ \mathsf {d}( \mathsf {a}_{3},\mathsf {a}_{1}), \frac{(1+\mathsf {d}(\mathsf {a}_{3},P\mathsf {a}_{3}))\mathsf {d}(\mathsf {a}_{1}, Q\mathsf {a}_{1})}{1+\mathsf {d}(\mathsf {a}_{3}, \mathsf {a}_{1})}, \frac{\mathsf {d}(\mathsf {a}_{3},Q\mathsf {a}_{1})+\mathsf {d}(\mathsf {a}_{1},P\mathsf {a}_{3})}{2} \biggr\} \\ &=\max \biggl\{ \mathsf {d}(\mathsf {a}_{3},\mathsf {a}_{1}), \frac{(1+\mathsf {d}(\mathsf {a}_{3},\mathsf {a}_{2}))\mathsf {d}(\mathsf {a}_{1}, \mathsf {a}_{1})}{1+\mathsf {d}(\mathsf {a}_{2}, \mathsf {a}_{4})}, \frac{\mathsf {d}(\mathsf {a}_{3},\mathsf {a}_{1})+\mathsf {d}(\mathsf {a}_{1},\mathsf {a}_{1})}{2} \biggr\} \\ &=\max \biggl\{ 3, 0,\frac{3}{2} \biggr\} =3 \end{aligned} \end{aligned}$$
, $$\begin{aligned} &\mathsf {d}(P\mathsf {a}_{3}, Q\mathsf {a}_{1})=\mathsf {d}( \mathsf {a}_{2}, \mathsf {a}_{1})=2, \\ &\begin{aligned}[b] \mathsf {r}_{1}(\mathsf {a}_{3}, \mathsf {a}_{1})&=\max \biggl\{ \mathsf {d}( \mathsf {a}_{3},\mathsf {a}_{1}), \frac{(1+\mathsf {d}(\mathsf {a}_{3},P\mathsf {a}_{3}))\mathsf {d}(\mathsf {a}_{1}, Q\mathsf {a}_{1})}{1+\mathsf {d}(\mathsf {a}_{3}, \mathsf {a}_{1})}, \frac{\mathsf {d}(\mathsf {a}_{3},Q\mathsf {a}_{1})+\mathsf {d}(\mathsf {a}_{1},P\mathsf {a}_{3})}{2} \biggr\} \\ &=\max \biggl\{ \mathsf {d}(\mathsf {a}_{3},\mathsf {a}_{1}), \frac{(1+\mathsf {d}(\mathsf {a}_{3},\mathsf {a}_{2}))\mathsf {d}(\mathsf {a}_{1}, \mathsf {a}_{1})}{1+\mathsf {d}(\mathsf {a}_{2}, \mathsf {a}_{4})}, \frac{\mathsf {d}(\mathsf {a}_{3},\mathsf {a}_{1})+\mathsf {d}(\mathsf {a}_{1},\mathsf {a}_{1})}{2} \biggr\} \\ &=\max \biggl\{ 3, 0,\frac{3}{2} \biggr\} =3 \end{aligned} \end{aligned}$$and
$$\begin{aligned} \eta \bigl(\vartheta \bigl(\mathsf {d}(P\mathsf {a}_{3},Q\mathsf {a}_{1})\bigr), \psi \bigl(\mathsf {r}_{1}(\mathsf {a}_{3},\mathsf {a}_{1})\bigr) \bigr)=0.88\cdot 0,91 \cdot 3-2=0.4024>0. \end{aligned}$$ -
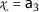 ,
, 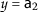 , $$\begin{aligned} &\mathsf {d}(P\mathsf {a}_{3}, Q\mathsf {a}_{2})=\mathsf {d}( \mathsf {a}_{2}, \mathsf {a}_{1})=2, \\ &\begin{aligned}[b] \mathsf {r}_{1}(\mathsf {a}_{3}, \mathsf {a}_{2})&=\max \biggl\{ \mathsf {d}( \mathsf {a}_{3},\mathsf {a}_{2}), \frac{(1+\mathsf {d}(\mathsf {a}_{3},P\mathsf {a}_{3}))\mathsf {d}(\mathsf {a}_{2}, Q\mathsf {a}_{2})}{1+\mathsf {d}(\mathsf {a}_{3}, \mathsf {a}_{2})}, \frac{\mathsf {d}(\mathsf {a}_{3},Q\mathsf {a}_{2})+\mathsf {d}(\mathsf {a}_{2},P\mathsf {a}_{3})}{2} \biggr\} \\ &=\max \biggl\{ \mathsf {d}(\mathsf {a}_{3},\mathsf {a}_{2}), \frac{(1+\mathsf {d}(\mathsf {a}_{3},\mathsf {a}_{2}))\mathsf {d}(\mathsf {a}_{1}, \mathsf {a}_{1})}{1+\mathsf {d}(\mathsf {a}_{2}, \mathsf {a}_{4})}, \frac{\mathsf {d}(\mathsf {a}_{3},\mathsf {a}_{1})+\mathsf {d}(\mathsf {a}_{1},\mathsf {a}_{1})}{2} \biggr\} \\ &=\max \biggl\{ 5, 0,\frac{3}{2} \biggr\} =5 \end{aligned} \end{aligned}$$
, $$\begin{aligned} &\mathsf {d}(P\mathsf {a}_{3}, Q\mathsf {a}_{2})=\mathsf {d}( \mathsf {a}_{2}, \mathsf {a}_{1})=2, \\ &\begin{aligned}[b] \mathsf {r}_{1}(\mathsf {a}_{3}, \mathsf {a}_{2})&=\max \biggl\{ \mathsf {d}( \mathsf {a}_{3},\mathsf {a}_{2}), \frac{(1+\mathsf {d}(\mathsf {a}_{3},P\mathsf {a}_{3}))\mathsf {d}(\mathsf {a}_{2}, Q\mathsf {a}_{2})}{1+\mathsf {d}(\mathsf {a}_{3}, \mathsf {a}_{2})}, \frac{\mathsf {d}(\mathsf {a}_{3},Q\mathsf {a}_{2})+\mathsf {d}(\mathsf {a}_{2},P\mathsf {a}_{3})}{2} \biggr\} \\ &=\max \biggl\{ \mathsf {d}(\mathsf {a}_{3},\mathsf {a}_{2}), \frac{(1+\mathsf {d}(\mathsf {a}_{3},\mathsf {a}_{2}))\mathsf {d}(\mathsf {a}_{1}, \mathsf {a}_{1})}{1+\mathsf {d}(\mathsf {a}_{2}, \mathsf {a}_{4})}, \frac{\mathsf {d}(\mathsf {a}_{3},\mathsf {a}_{1})+\mathsf {d}(\mathsf {a}_{1},\mathsf {a}_{1})}{2} \biggr\} \\ &=\max \biggl\{ 5, 0,\frac{3}{2} \biggr\} =5 \end{aligned} \end{aligned}$$and
$$\begin{aligned} \eta \bigl(\vartheta \bigl(\mathsf {d}(P\mathsf {a}_{3},Q\mathsf {a}_{2})\bigr), \psi \bigl(\mathsf {r}_{1}(\mathsf {a}_{3},\mathsf {a}_{2})\bigr) \bigr)=0.88\cdot 0,91 \cdot 5-2=2.004>0. \end{aligned}$$ -
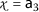 ,
, 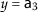 , $$\begin{aligned} &\mathsf {d}(P\mathsf {a}_{3}, Q\mathsf {a}_{3})=\mathsf {d}( \mathsf {a}_{2}, \mathsf {a}_{1})=2, \\ &\begin{aligned}[b] \mathsf {r}_{1}(\mathsf {a}_{3}, \mathsf {a}_{3})&=\max \biggl\{ \mathsf {d}( \mathsf {a}_{3},\mathsf {a}_{3}), \frac{(1+\mathsf {d}(\mathsf {a}_{3},P\mathsf {a}_{3}))\mathsf {d}(\mathsf {a}_{3}, Q\mathsf {a}_{3})}{1+\mathsf {d}(\mathsf {a}_{3}, \mathsf {a}_{3})}, \frac{\mathsf {d}(\mathsf {a}_{3},Q\mathsf {a}_{3})+\mathsf {d}(\mathsf {a}_{3},P\mathsf {a}_{3})}{2} \biggr\} \\ &=\max \biggl\{ \mathsf {d}(\mathsf {a}_{3},\mathsf {a}_{3}), \frac{(1+\mathsf {d}(\mathsf {a}_{3},\mathsf {a}_{2}))\mathsf {d}(\mathsf {a}_{3}, \mathsf {a}_{1})}{1+\mathsf {d}(\mathsf {a}_{3}, \mathsf {a}_{3})}, \frac{\mathsf {d}(\mathsf {a}_{3},\mathsf {a}_{1})+\mathsf {d}(\mathsf {a}_{3},\mathsf {a}_{1})}{2} \biggr\} \\ &=\max \biggl\{ 0, 18,\frac{6}{2} \biggr\} =18 \end{aligned} \end{aligned}$$
, $$\begin{aligned} &\mathsf {d}(P\mathsf {a}_{3}, Q\mathsf {a}_{3})=\mathsf {d}( \mathsf {a}_{2}, \mathsf {a}_{1})=2, \\ &\begin{aligned}[b] \mathsf {r}_{1}(\mathsf {a}_{3}, \mathsf {a}_{3})&=\max \biggl\{ \mathsf {d}( \mathsf {a}_{3},\mathsf {a}_{3}), \frac{(1+\mathsf {d}(\mathsf {a}_{3},P\mathsf {a}_{3}))\mathsf {d}(\mathsf {a}_{3}, Q\mathsf {a}_{3})}{1+\mathsf {d}(\mathsf {a}_{3}, \mathsf {a}_{3})}, \frac{\mathsf {d}(\mathsf {a}_{3},Q\mathsf {a}_{3})+\mathsf {d}(\mathsf {a}_{3},P\mathsf {a}_{3})}{2} \biggr\} \\ &=\max \biggl\{ \mathsf {d}(\mathsf {a}_{3},\mathsf {a}_{3}), \frac{(1+\mathsf {d}(\mathsf {a}_{3},\mathsf {a}_{2}))\mathsf {d}(\mathsf {a}_{3}, \mathsf {a}_{1})}{1+\mathsf {d}(\mathsf {a}_{3}, \mathsf {a}_{3})}, \frac{\mathsf {d}(\mathsf {a}_{3},\mathsf {a}_{1})+\mathsf {d}(\mathsf {a}_{3},\mathsf {a}_{1})}{2} \biggr\} \\ &=\max \biggl\{ 0, 18,\frac{6}{2} \biggr\} =18 \end{aligned} \end{aligned}$$and
$$\begin{aligned} \eta \bigl(\vartheta \bigl(\mathsf {d}(P\mathsf {a}_{3},Q\mathsf {a}_{3})\bigr), \psi \bigl(\mathsf {r}_{1}(\mathsf {a}_{3},\mathsf {a}_{3})\bigr) \bigr)=0.88\cdot 0,91 \cdot 18-2=12.41>0. \end{aligned}$$ -
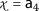 ,
, 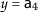 , $$\begin{aligned} &\mathsf {d}(P\mathsf {a}_{4}, Q\mathsf {a}_{4})=\mathsf {d}( \mathsf {a}_{1}, \mathsf {a}_{2})=2, \\ &\begin{aligned}[b] \mathsf {r}_{1}(\mathsf {a}_{4}, \mathsf {a}_{4})&=\max \biggl\{ \mathsf {d}( \mathsf {a}_{4},\mathsf {a}_{4}), \frac{(1+\mathsf {d}(\mathsf {a}_{4},P\mathsf {a}_{4}))\mathsf {d}(\mathsf {a}_{4}, Q\mathsf {a}_{4})}{1+\mathsf {d}(\mathsf {a}_{4}, \mathsf {a}_{4})}, \frac{\mathsf {d}(\mathsf {a}_{4},Q\mathsf {a}_{4})+\mathsf {d}(\mathsf {a}_{4},P\mathsf {a}_{4})}{2} \biggr\} \\ &=\max \biggl\{ \mathsf {d}(\mathsf {a}_{4},\mathsf {a}_{4}), \frac{(1+\mathsf {d}(\mathsf {a}_{4},\mathsf {a}_{1}))\mathsf {d}(\mathsf {a}_{4}, \mathsf {a}_{2})}{1+\mathsf {d}(\mathsf {a}_{4}, \mathsf {a}_{4})}, \frac{\mathsf {d}(\mathsf {a}_{4},\mathsf {a}_{2})+\mathsf {d}(\mathsf {a}_{4},\mathsf {a}_{1})}{2} \biggr\} \\ &=\max \{ 0, 18,4 \} =18 \end{aligned} \end{aligned}$$
, $$\begin{aligned} &\mathsf {d}(P\mathsf {a}_{4}, Q\mathsf {a}_{4})=\mathsf {d}( \mathsf {a}_{1}, \mathsf {a}_{2})=2, \\ &\begin{aligned}[b] \mathsf {r}_{1}(\mathsf {a}_{4}, \mathsf {a}_{4})&=\max \biggl\{ \mathsf {d}( \mathsf {a}_{4},\mathsf {a}_{4}), \frac{(1+\mathsf {d}(\mathsf {a}_{4},P\mathsf {a}_{4}))\mathsf {d}(\mathsf {a}_{4}, Q\mathsf {a}_{4})}{1+\mathsf {d}(\mathsf {a}_{4}, \mathsf {a}_{4})}, \frac{\mathsf {d}(\mathsf {a}_{4},Q\mathsf {a}_{4})+\mathsf {d}(\mathsf {a}_{4},P\mathsf {a}_{4})}{2} \biggr\} \\ &=\max \biggl\{ \mathsf {d}(\mathsf {a}_{4},\mathsf {a}_{4}), \frac{(1+\mathsf {d}(\mathsf {a}_{4},\mathsf {a}_{1}))\mathsf {d}(\mathsf {a}_{4}, \mathsf {a}_{2})}{1+\mathsf {d}(\mathsf {a}_{4}, \mathsf {a}_{4})}, \frac{\mathsf {d}(\mathsf {a}_{4},\mathsf {a}_{2})+\mathsf {d}(\mathsf {a}_{4},\mathsf {a}_{1})}{2} \biggr\} \\ &=\max \{ 0, 18,4 \} =18 \end{aligned} \end{aligned}$$and
$$\begin{aligned} \eta \bigl(\vartheta \bigl(\mathsf {d}(P\mathsf {a}_{4},Q\mathsf {a}_{4})\bigr), \psi \bigl(\mathsf {r}_{1}(\mathsf {a}_{4},\mathsf {a}_{4})\bigr) \bigr)=0.88\cdot 0.91 \cdot 18-2=12.41>0. \end{aligned}$$
Therefore, all the assumptions of Theorem 7 are satisfied; \(\mathsf {a}_{1}\) is the unique common fixed point of the mappings P and Q.
Corollary 9
Let \((X, \mathsf {d})\) be a complete metric space, a mapping \(P: X\rightarrow X\) and a function \(\eta \in Z\) such that

for any  with
with  , where \(\vartheta ,\psi \in \Theta \). Suppose that
, where \(\vartheta ,\psi \in \Theta \). Suppose that
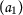 :
:-
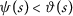 , for any
, for any 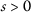 ;
; 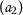 :
:-
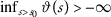 , for any
, for any 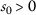 ;
; 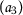 :
:-
if \(\{ a_{m} \} \), \(\{ b_{m} \} \) are convergent sequences with with \(\lim_{m\rightarrow \infty }a_{m}=\lim_{m \rightarrow \infty }b_{m}>0\) then the sequences \(\{ \vartheta (a_{m}) \} \), \(\{ \vartheta (b_{m}) \} \), are convergent and \(\lim_{m\rightarrow \infty }\vartheta (a_{m})= \lim_{m\rightarrow \infty }\vartheta (b_{m})\).
Then the mapping P possesses a unique fixed point.
Proof
Put \(Q=P\) in Theorem 7. □
Theorem 10
Let \((X, \mathsf {d})\) be a complete metric space, two mappings \(P, Q: X\rightarrow X\), the functions \(\vartheta ,\psi \in \Theta \) and a function such that

when  and
and  when
when  . Suppose that
. Suppose that
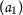 :
:-
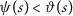 , for any
, for any 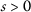 ;
; 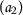 :
:-
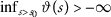 , for any
, for any 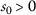 ;
; 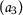 :
:-
if \(\{ a_{m} \} \), \(\{ b_{m} \} \) are convergent sequences with with \(\lim_{m\rightarrow \infty }a_{m}=\lim_{m \rightarrow \infty }b_{m}>0\) then the sequences \(\{ \vartheta (a_{m}) \} \), \(\{ \vartheta (b_{m}) \} \), are convergent and \(\lim_{m\rightarrow \infty }\vartheta (a_{m})= \lim_{m\rightarrow \infty }\vartheta (b_{m})\);
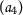 :
:-
if \(\{ \vartheta (a_{m}) \} \) is a strictly decreasing sequence and \(\{ \vartheta (a_{m}) \} \), \(\{ \psi (a_{m}) \} \) are convergent with the same limit then \(\lim_{m\rightarrow \infty }a_{m}=0\);
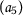 :
:-
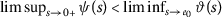 , for any
, for any 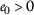 .
.
Then the mappings \(P,Q\) have a unique fixed point.
Proof
First of al, by (2.29) and taking \((\eta _{1})\) into account, we have

which can be rewritten as

Let  be the sequence defined by (2.19). Since
be the sequence defined by (2.19). Since  for any \(m\in \mathbb{N}_{0}\) (we have already shown this in the proof of Theorem 5), letting \(m=2i\), we have
for any \(m\in \mathbb{N}_{0}\) (we have already shown this in the proof of Theorem 5), letting \(m=2i\), we have

and letting \(m=2i-1\),

Thus, from (2.30) and keeping  in mind we get
in mind we get

and similarly

Denoting  by \(o_{m}\), we get
by \(o_{m}\), we get
and we conclude that
for any \(m\in \mathbb{N}\). Consequently, the sequence \(\{ \vartheta (o_{m}) \} \) is convergent, being strictly decreasing and bounded below(from  and Lemma 4). Thus, letting \(m\rightarrow \infty \) in (2.33) we see that \(\{ \psi (o_{m}) \} \) is convergent with the same limit as \(\{ \vartheta (o_{m}) \} \). Thereupon, by
and Lemma 4). Thus, letting \(m\rightarrow \infty \) in (2.33) we see that \(\{ \psi (o_{m}) \} \) is convergent with the same limit as \(\{ \vartheta (o_{m}) \} \). Thereupon, by  ,
,

We claim that the sequence  is Cauchy, reasoning by contradiction. Indeed, if we suppose that
is Cauchy, reasoning by contradiction. Indeed, if we suppose that  is not Cauchy, by Lemma 3, we can find
is not Cauchy, by Lemma 3, we can find  and the sequences \(\{ m_{l} \} \), \(\{ p_{l} \} \) of positive integers such that the equalities (1.2) hold, where \(m_{l}\) is the smallest index for which \(m_{l}>p_{l}>l\), for all \(l\geq 1\). We have
and the sequences \(\{ m_{l} \} \), \(\{ p_{l} \} \) of positive integers such that the equalities (1.2) hold, where \(m_{l}\) is the smallest index for which \(m_{l}>p_{l}>l\), for all \(l\geq 1\). We have

and setting  and
and  it follows that
it follows that  . Moreover, by
. Moreover, by  , \(\lim_{l\rightarrow \infty }\vartheta (u_{l})= \lim_{l\rightarrow \infty }\vartheta (v_{l})\). Consequently, by (2.33), \(\lim_{l\rightarrow \infty }\vartheta (u_{l})= \lim_{l\rightarrow \infty }\psi (v_{l})\) and using \((\eta _{2})\),
, \(\lim_{l\rightarrow \infty }\vartheta (u_{l})= \lim_{l\rightarrow \infty }\vartheta (v_{l})\). Consequently, by (2.33), \(\lim_{l\rightarrow \infty }\vartheta (u_{l})= \lim_{l\rightarrow \infty }\psi (v_{l})\) and using \((\eta _{2})\),
which is a contradiction, since by (2.29)

In this way we proved that  is a Cauchy sequence on a complete metric space, so there exists
is a Cauchy sequence on a complete metric space, so there exists  such that
such that  .
.
We shall show that  is a common fixed point of P and Q. First of all, we remark that, if
is a common fixed point of P and Q. First of all, we remark that, if  for infinitely many values of m, then
for infinitely many values of m, then

That means that  .
.
Therefore, we can suppose that  for infinitely many values of m, by (2.29) we have
for infinitely many values of m, by (2.29) we have

or equivalently, by 

where

as \(m\rightarrow \infty \). Let  . If we suppose that
. If we suppose that  , from (2.35) and
, from (2.35) and  we have
we have

which is a contradiction. Therefore,  .
.
Similarly, choosing  and
and  in (2.29), we can show that
in (2.29), we can show that  and we conclude that
and we conclude that  .
.
To prove the uniqueness of the common fixed point, we will assume that, on the contrary, there exists another point  such that
such that  and
and  . Since
. Since  , we have
, we have

which is a contradiction. Hence  . □
. □
Corollary 11
Let \((X, \mathsf {d})\) be a complete metric space, a mapping \(P: X\rightarrow X\), the functions \(\vartheta ,\psi \in \Theta \) and a function \(\eta \in Z\) such that

for any  with
with  , when
, when  and
and  when
when  . Suppose that
. Suppose that
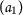 :
:-
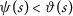 , for any
, for any 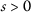 ;
; 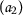 :
:-
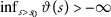 , for any
, for any 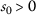 ;
; 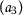 :
:-
if \(\{ a_{m} \} \), \(\{ b_{m} \} \) are convergent sequences with with \(\lim_{m\rightarrow \infty }a_{m}=\lim_{m \rightarrow \infty }b_{m}>0\) then the sequences \(\{ \vartheta (a_{m}) \} \), \(\{ \vartheta (b_{m}) \} \), are convergent and \(\lim_{m\rightarrow \infty }\vartheta (a_{m})= \lim_{m\rightarrow \infty }\vartheta (b_{m})\);
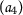 :
:-
if \(\{ \vartheta (a_{m}) \} \) is a strictly decreasing sequence and \(\{ \vartheta (a_{m}) \} \), \(\{ \psi (a_{m}) \} \) are convergent with the same limit then \(\lim_{m\rightarrow \infty }a_{m}=0\);
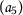 :
:-
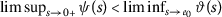 , for any
, for any 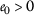 .
.
Then the mapping P has exactly one fixed point.
Proof
Put \(Q=P\) in Theorem 10. □
Availability of data and materials
Not applicable.
References
Karapınar, E.: A short survey on the recent fixed point results on b-metric spaces. Constr. Math. Anal. 1(1), 15–44 (2018)
Karapınar, E.: Ćirić types non-unique fixed point results: a review. Appl. Comput. Math. 1, 3–21 (2019)
Gulyaz-Ozyurt, S.: A note on Kannan type mappings with a F-contractive iterate. Res. Nonlinear Anal. 2(3), 143–146 (2019)
Rus, I.A.: Some variants of contraction principle in the case of operators with Volterra property: step by step contraction principle. Adv. Theory Nonlinear Anal. Appl. 3(3), 111–120 (2019)
Proinov, P.D.: Fixed point theorems for generalized contractive mappings in metric spaces. J. Fixed Point Theory Appl. 22(21), 1–27 (2020)
Skof, F.: Theoremi di punto fisso per applicazioni negli spazi metrici. Atti Accad. Sci. Torino, Cl. Sci. Fis. Mat. Nat. 111, 323–329 (1977)
Fulga, A.: On (\(\psi ,\phi \))-rational contractions. Symmetry 12(5), 723 (2020)
Karapınar, E., De la Sen, M., Fulga, A.: A note on the Górnicki–Proinov type contraction. J. Funct. Spaces 2021, Article ID 6686644 (2021)
Roldan Lopez de Hierro, A.F., Karapınar, E., Fulga, A.: Multiparametric contractions and related Hardy–Roger type fixed point theorems. Mathematics 8(6), 957 (2020)
Khojasteh, F., Shukla, S., Radenović, S.: A new approach to the study of fixed point theorems via simulation functions. Filomat 29, 1189–1194 (2015)
Alsubaie, R., Alqahtani, B., Karapınar, E., Roldan Lopez de Hierro, A.F.: Extended simulation function via rational expressions. Mathematics 8(5), 710 (2020)
Alqahtani, O., Karapınar, E.: A bilateral contraction via simulation function. Filomat 33(15), 4837–4843 (2019)
Alghamdi, M.A., Gulyaz-Ozyurt, S., Karapınar, E.: A note on extended Z-contraction. Mathematics 8(2), 195 (2020)
Agarwal, R.P., Karapınar, E.: Interpolative Rus–Reich–Ćirić type contractions via simulation functions. An. Ştiinţ. Univ. ‘Ovidius’ Constanţa, Ser. Mat. 27(3), 137–152 (2019)
Aydi, H., Karapınar, E., Rakocevic, V.: Nonunique fixed point theorems on b-metric spaces via simulation functions. Jordan J. Math. Stat. 12(3), 265–288 (2019)
Karapınar, E., Khojasteh, F.: An approach to best proximity points results via simulation functions. J. Fixed Point Theory Appl. 19(3), 1983–1995 (2017)
Asadi, M., Azhini, M., Karapınar, E., Monfared, H.: Simulation functions over M-metric spaces. East Asian Math. J. 33(5), 559–570 (2017)
Monfared, H., Asadi, M., Farajzadeh, A.: New generalization of Darbo’s fixed point theorem via α-admissible simulation functions with application. Sahand Commun. Math. Anal. 17(2), 161–171 (2020)
Asadi, M., Gabeleh, M., Vetro, C.: A new approach to the generalization of Darbo’s fixed point problem by using simulation functions with application to integral equations. Results Math. 74, Article ID 86 (2019)
Karapınar, E.: Fixed points results via simulation functions. Filomat 30(8), 2343–2350 (2016)
Radenović, S., Kadelburg, Z., Jandrlic, D., Jandrlic, A.: Some results on weak contraction maps. Bull. Iran. Math. Soc. 38, 625–645 (2012)
Acknowledgements
The authors extend their appreciation to the Deputyship for Research Innovation, “Ministry of Education” in Saudi Arabia for funding this research work through the project number IFKSURG-1441-420.
Funding
Not applicable.
Author information
Authors and Affiliations
Contributions
All authors contributed equally and significantly in writing this article. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Alqahtani, B., Alzaid, S.S., Fulga, A. et al. Common fixed point theorem on Proinov type mappings via simulation function. Adv Differ Equ 2021, 328 (2021). https://doi.org/10.1186/s13662-021-03482-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-021-03482-x



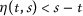 for all
for all 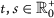 ;
;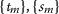 in
in 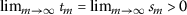 , then
, then 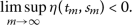
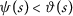 , for any
, for any 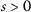 ;
;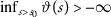 , for any
, for any 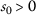 ;
;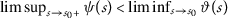 or
or 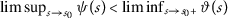 for any
for any 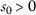 ;
;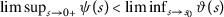 for any
for any 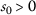 .
.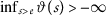 for every
for every 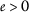 .
.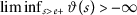 for every
for every 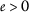 .
.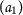 :
: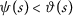 , for any
, for any 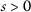 ;
;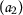 :
: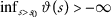 , for any
, for any 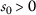 ;
;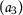 :
: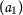 :
: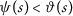 , for any
, for any 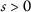 ;
;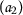 :
: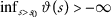 , for any
, for any 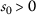 ;
;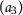 :
: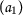 :
: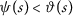 , for any
, for any  ;
; :
: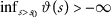 , for any
, for any 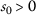 ;
;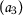 :
: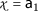 ,
, 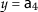 ,
, 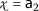 ,
, 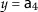 ,
, 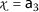 ,
, 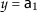 ,
, 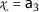 ,
, 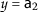 ,
, 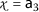 ,
, 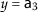 ,
, 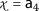 ,
, 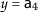 ,
, 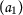 :
: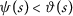 , for any
, for any 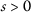 ;
; :
: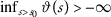 , for any
, for any 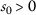 ;
;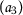 :
: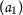 :
: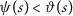 , for any
, for any 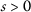 ;
;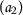 :
: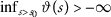 , for any
, for any 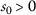 ;
;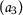 :
: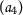 :
: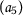 :
: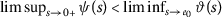 , for any
, for any 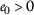 .
.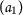 :
: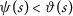 , for any
, for any 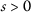 ;
;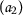 :
: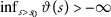 , for any
, for any 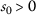 ;
;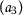 :
: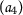 :
: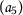 :
: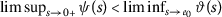 , for any
, for any 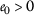 .
.