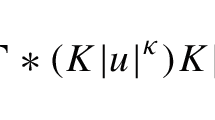Abstract
In this work, the relativistic particle with the action of the generalized exponential potential is studied in the Dirac equation in the context of minimum length, subsequently finding a suitable variable substitution and giving its wave function and explicit energy spectrum by using the Bethe ansatz method. Further, we will see that this research could be further extended to various special exponential potential, and the explicit energy spectrum and wave functions of various special exponential potential could be reproduced by selecting and adjusting the potential parameters. By observing the expressions of the exact solution of the generalized exponential potential, it can be found that for finite \(\beta \), its energy spectrum is not only related to the principal quantum number n, but also related to the square of n. Moreover, we will also see that this paper not only extends the study of Dirac equation with generalized exponential potential effect to the background of minimal length, but also provides an easier, alternative and valid method for solving the Dirac equation with exponential-type potential.
Similar content being viewed by others
References
P.A.M. Dirac, Proc. R. Soc. A 117, 610 (1928)
P.A.M. Dirac, Proc. R. Soc. A 126, 360 (1930)
P.A.M. Dirac, The Principles of Quantum Mechanics (Oxford University Press, London, 1966)
J.J. Peña, J. Morales, J. García-Ravelo, J. Math. Phys. 58, 043501 (2017)
S. Capozziello, G. Lambiase, G. Scarpetta, Int. J. Theor. Phys. 39, 15 (2000)
C.P. Burgess, Living Rev. Rel. 7, 5 (2004)
T. Clifton, P.G. Ferreira, A. Padilla, C. Skordis, Phys. Rep. 513, 1 (2012)
M. Ara, M. Moniruzzaman, S.B. Faruque, Phys. Scr. 82, 035005 (2010)
L.J. Garay, Int. J. Mod. Phys. A 10, 145 (1995)
J.B. Jimenez, L. Heisenberg, G.J. Olmo, D. Rubiera-Garcia, Phys. Rep. 727, 1 (2018)
S. Capozziello, M. De Laurentis, Phys. Rep. 509, 167 (2011)
S. Hossenfelder, Living Rev. Rel. 16, 2 (2013)
D. Amati, M. Ciafaloni, G. Veneziano, Phys. Lett. B 216, 41 (1989)
D. Amati, M. Ciafaloni, G. Veneziano, Nucl. Phys. B 403, 707 (1993)
D.J. Gross, P.F. Mende, Phys. Lett. B 197, 129 (1987)
S. Benczik et al., Phys. Rev. D 66, 026003 (2002)
D. Amati, M. Ciafaloni, G. Veneziano, Phys. Lett. B 197, 81 (1987)
M.B. Green, J.H. Schwarz, E. Witten, Superstring Theory (Cambridge University Press, Cambridge, 1987)
M.I. Park, Phys. Lett. B 659, 698 (2008)
S. Gangopadhyaya, D. Abhijit et al., EPL 112, 20006 (2015)
J. Magueijo, L. Smolin, Phys. Rev. Lett. 88, 190403 (2002)
J. Magueijo, L. Smolin, Phys. Rev. D 71, 026010 (2005)
J.L. Cortes, J. Gamboa, Phys. Rev. D 71, 065015 (2005)
W.S. Chung, H. Hassanabadi, Phys. Lett. B 785, 127 (2018)
A. Kempf, G. Mangano, R.B. Mann, Phys. Rev. D 52, 1108 (1994)
Y. Chargui, A. Trabelsi, L. Chetouani, Phys. Lett. A 374, 531 (2010)
T.K. Jana, P. Roy, Phys. Lett. A 373, 1239 (2009)
H. Shababi, W.S. Chung, Phys. Lett. B 770, 445 (2017)
J.Y. Bang, M.S. Berger, Phys. Rev. D 74, 125012 (2006)
A.F. Ali, S. Das, E.C. Vagenas, Phys. Lett. B 678, 497 (2009)
M.V. Battisti, G. Montani et al., Phys. Rev. D 77, 023518 (2008)
M.V. Battisti, G. Montani, Phys. Lett. B 656, 96 (2007)
A. Camacho, Gen. Relat. Gravit. 35, 1153 (2003)
F. Brau, F. Buisseret, Phys. Rev. D 74, 036002 (2006)
I. Kuntz, R. da Rocha, Eur. Phys. J. C 80, 478 (2020)
D. Park, Phys. Rev. D 101, 106013 (2020)
L.B. Castro, A.E. Obispo, J. Phys. A: Math. Theor. 50, 285202 (2017)
A. Kempf, J. Phys. A: Math. Gen. 30, 2093 (1997)
R.R. Sastry, J. Phys. A: Math. Gen. 33, 8305 (2000)
B. Gönül, O. Özer, Y. Cancelik, M. Kocak, Phys. Lett. A 275, 238 (2000)
D. Agboola, Phys. Scr. 80, 065304 (2009)
Y.P. Varshni, Phys. Rev. A 41, 4682 (1990)
A.I. Ahmadov, S.M. Aslanova, MSh. Orujova, S.V. Badalov, S.H. Dong, Phys. Lett. A 383, 3010 (2019)
F. Ungan, M.K. Bahar, Phys. Lett. A 384, 126400 (2020)
M. Deng, C.S. Jia, Eur. Phys. J. Plus 133, 258 (2018)
N. Rosen, P.M. Morse, Phys. Rev. 42, 210 (1932)
C. Eckart, Phys. Rev. 35, 1303 (1930)
H. Hassanabadi, E. Maghsoodi, A.N. Ikot, S. Zarrinkamar, Appl. Math. Comput. 219, 9388 (2013)
J.Y. Guo, Z.Q. Sheng, Phys. Lett. A 338, 90 (2005)
O. Aydoǧdu, R. Sever, Eur. Phys. J. A 43, 73 (2010)
M.F. Manning, N. Rosen, Phys. Rev. 44, 951 (1933)
X.Y. Chen, T. Chen, C.S. Jia, Eur. Phys. J. Plus 129, 75 (2014)
G.F. Wei, S.H. Dong, Phys. Lett. B 686, 288 (2010)
S.H. Dong, Commun. Theor. Phys. 55, 969 (2011)
Y.Z. Zhang, J. Phys. A: Math. Theor. 45, 065206 (2012)
P.B. Wiegmann, A.V. Zabrodin, Phys. Rev. Lett. 72, 1890 (1994)
R. Sasaki, W.L. Yang, Y.Z. Zhang, SIGMA 5, 104 (2009)
Z.L. Zhao, Z.W. Long, M.Y. Zhang, Adv. High Energy Phys. 2019, 3423198 (2019)
D. Agboola, Y.Z. Zhang, Ann. Phys. 330, 246 (2013)
H. Sobhani, H. Hassanabadi, D. Bonatsos, F. Pan, S. Cui, Z.W. Feng, J.P. Draayer, Eur. Phys. J. A 56, 29 (2020)
H. Sobhani, H. Hassanabadi, Nucl. Phys. A 983, 229 (2019)
S.H. Dong, Wave Equations in Higher Dimensions (Springer, Dordrecht, 2011)
S. Haouat, Phys. Lett. B 729, 33 (2014)
H. Hassanabadi, S. Zarrinkamar, E. Maghsoodi, Phys. Lett. B 718, 678 (2012)
Z.L. Zhao, C.Y. Long, Z.W. Long et al., Chin. Phys. B 26, 080301 (2017)
S. Ikhdair, M. Eshghi, Chin. Phys. B 23, 120304 (2014)
Acknowledgements
This paper is supported by the National Natural Science Foundation of China (Grant No. 11465006) and the Major Research Project of innovative Group of Guizhou province (2018-013).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix. Brief Review Functional Bethe Ansatz Method
Appendix. Brief Review Functional Bethe Ansatz Method
Now, we briefly review the functional Bethe ansatz method. For details, please refer to literature [55,56,57,58,59,60,61,62]. For second-order ordinary differential equations of the form
in which P(y), Q(y) and W(y) are polynomials with the highest degrees of 4, 5, and 4 respectively, and they could be given as follows
in which \({p_i}, {q_i}\) and \({w_i}\) are all constants. It is not difficult to find that the ordinary differential equation whose form satisfies (A.1) is quasi-exactly solvable, and whose corresponding exact solution can be given by n order polynomials of the variable y. Applying the functional Bethe ansatz method further, the polynomial solution of the ordinary differential equation with the form (A.1) can be written as
where the different roots \(y_1, y_2, \ldots , y_n\) could be determined. So, according to the ordinary differential equation (A.1), we have
It is not difficult to see that the left side of Eq. (A.4) is a constant, while its right is a meromorphic function which has simple poles \(y={y_i}\) and singularity at \(y=\infty \). Therefore, the precondition that the equation is always valid requires that its right side must also be constant, which is a sufficient and necessary condition that can be obtained from Liuville’s theorem. Thus, the constraints have
in which the different roots \(y_1, y_2, \ldots , y_n\) satisfy the Bethe ansatz equations
Rights and permissions
About this article
Cite this article
Zhao, ZL., Wu, H. & Long, ZW. Discussion on Exact Solution of Dirac Equation with Generalized Exponential Potential in the Presence of Generalized Uncertainty Principle. Few-Body Syst 62, 50 (2021). https://doi.org/10.1007/s00601-021-01643-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00601-021-01643-y