Abstract
Complex fuzzy (CF) sets (CFSs) have a significant role in modelling the problems involving two-dimensional information. Recently, the extensions of CFSs have gained the attention of researchers studying decision-making methods. The complex T-spherical fuzzy set (CTSFS) is an extension of the CFSs introduced in the last times. In this paper, we introduce the Dombi operations on CTSFSs. Based on Dombi operators, we define some aggregation operators, including complex T-spherical Dombi fuzzy weighted arithmetic averaging (CTSDFWAA) operator, complex T-spherical Dombi fuzzy weighted geometric averaging (CTSDFWGA) operator, complex T-spherical Dombi fuzzy ordered weighted arithmetic averaging (CTSDFOWAA) operator, complex T-spherical Dombi fuzzy ordered weighted geometric averaging (CTSDFOWGA) operator, and we obtain some of their properties. In addition, we develop a multi-criteria decision-making (MCDM) method under the CTSF environment and present an algorithm for the proposed method. To show the process of the proposed method, we present an example related to diagnosing the COVID-19. Besides this, we present a sensitivity analysis to reveal the advantages and restrictions of our method.
Similar content being viewed by others
Introduction
The fuzzy set (FS) theory was inaugurated by Zadeh [1] in 1965 to handle modelling of some problems containing uncertain data in real life. Since FS theory is a very useful tool for modelling uncertainty, it has many applications in the modelling and solving of the problems in many fields such as medical science, data mining and clustering. An FS is characterized by a membership function (MF) \(\mu \) from a set of the objects or elements considered in the universe to the interval [0,1]. In an FS, if the membership degree (MD) of an element x is \(\mu (x)\), then its non-membership degree (NMD) is \(1-\mu (x)\), that is, in the FS, hesitation degree of an element is “0”. This is one of the limited aspects of FS in modelling real-life problems. To overcome these limitations, the intuitionistic FS (IFS) was suggested by Atanassov [2] as a generalization of FSs. An IFS is identified by two functions from a universal set to the interval [0,1] called membership function (MF) (\(\mu \)) and non-membership function (NMF) (\(\nu \)). The summation of images under these two functions of an element cannot exceed 1. Therefore, IFS is not an appropriate tool for modeling in the situation \(\mu (x) + \nu (x) > 1\). To cope with this restriction, Yager [3, 4] introduced the concept of Pythagorean FS (PyFS) as an extension of IFS under condition \(\mu ^2(x)+\nu ^2(x)\le 1\). However, in the situation \(0.9^2+0.5^2=1.06>1\), a PyFS is not sufficient for modelling. To eliminate this type of limitation, Yager [5] put forward the concept of q-rung orthopair FS in which \(\mu ^q(x)+\nu ^q(x)\le 1\). The neutral situation is not taken into account in the set theories we have mentioned so far, but this situation is important for the representation of human thinking. For this, Cuong [6, 7] defined the concept of the Picture FS (PFS). A PFS is a useful tool for expressing how much an object provides a feature or how much a person has shared an idea because a PFS does a modelling considering cases of yes, abstention, no, and rejection. A PFS is characterized by three values from interval [0,1] for each element x belonging to set containing considered elements, called MD (\(\mu (x)\)), abstinence degree (AD) or neutral degree (\(\gamma (x)\)) and, NMD (\(\nu (x)\)) with the condition \(0\le \mu (x)+ \gamma (x)+ \nu (x)\le 1 \). Despite the fact that PFS structure is a useful tool in many applications such as decision-making (DM) [8,9,10,11,12,13,14], similarity measure [15,16,17,18,19], correlation coefficient [20, 21], and clustering [22, 23], it is not sufficient in modelling of some problems because of constrain \(0\le \mu (x)+ \gamma (x)+ \nu (x)\le 1\). Therefore, the notion of spherical FS (SFS), which is an extension of PFS, was initiated by Gungogdu and Kahraman [24, 25] and the applications of the SFS to decision-making was studied on. An SFS has the constrain \(0\le \mu ^2(x)+\gamma ^2(x)+\nu ^2(x)\le 1\). Kahraman et al. [24] developed a DM method based on the TOPSIS method under the SF environment and presented an application of the developed method in the selection of hospital location. In an SFS, when MD, NeD and NMD of an element are taken as 0.6, 0.9 and 0.5, respectively, since \(0.6^2+0.9^2+0.5^2=1.42>1\), condition \(0\le \mu ^2(x)+\gamma ^2(x)+\nu ^2(x)\le 1\) is not satisfied. To model such situations, the T-spherical FS (T-SFS) was introduced by Mahmood et al. [26] as an extension of the SFS under condition X and some applications in medical diagnosis and DM problems under T-SF and SF environments were given by same researchers. After the works of Mahmood et al. [26], many researchers have studied applications of T-SFS and SFS. For example, Ullah et al. [27] proposed some novel similarity measures including cosine similarity measures, grey similarity measures, and set theoretic similarity measures for SFS and T-SFSs. Garg et al. [28] defined some new improved aggregation operators for T-SFSs and developed a DM approach to solve the multi-attribute DM (MADM) problems. Ullah et al. [29] introduced the some ordered weighted aggregation operators and hybrid aggregation operators of T-SFS and proposed an MADM method. Wu et al. [30] studied divergence measure of T-SFSs and gave the application in pattern recognition. Ullah et al. [31] defined the concept of interval-valued T-SFSs and their basic operations. They also described two aggregation operators for interval-valued T-SF values and developed an MADM method for problem including evaluating companies to be made an investment. Liu et al. [32] proposed some novel operational laws for T-SPFNs and combine power average operator and with Murihead mean operator. They also developed some new aggregation operators. Guleria and Bajaj [33] defined some aggregation operations of T-Spherical fuzzy soft sets. Quek et al. [34] presented some new operational laws for T-spherical fuzzy sets and obtain some of their properties. Then, based on these new operations, they have proposed two types of Einstein aggregation operators called the Einstein interactive averaging aggregation operators and the Einstein interactive geometric aggregation operators. They also put forward a MADM method based on the defined aggregation operators. Munir et al. [35] studied on Einstein hybrid aggregation operators under T-SF environment and establish an MADM by integrating the proposed aggregation operators. Ullah et al. [36] establish the correlation coefficient formula for T-SF values and presented an application in clustering. Also, T-spherical Fuzzy Hamacher Aggregation Operators were defined Ullah et al. [37]. Furthermore, they put forward an MADM method and gave the application of the method in a problem including evaluation of the performance of search and rescue robots. Garg et al. [38] introduced power aggregation operators for the T-spherical fuzzy sets (T-SFSs). Ju et al. [39] defined the T-SF interaction aggregation operators and based on these operators they developed TODIM method under T-SF environment. Chen et al. [40] studied on some generalized T-Spherical and group-Generalized fuzzy geometric aggregation operators with MADM method. Associated immediate probability (interactive) geometric aggregation operators of for T-spherical fuzzy sets were introduced by Munir et al. [41].
As mentioned above, FS models are important tools for modelling uncertain and incomplete data. But mentioned FS models do not suffice to express the periodic information or two-dimension phenomenon. To cope with this issue, the concept of complex FS (CFS) was put forward by Ramot et al. [42, 43]. The basic idea in the definition given by Ramot is to extend the range of membership from [0, 1] to the unit circle in the complex plane. A CFS is characterized by membership function \(\mu =re^{i\omega }\) where r is called amplitude term and it takes values from the interval [0,1], and \(\omega \) is called phase term (periodic term) and it lies in the interval \([0, 2\pi ]\). The phase term has a very important role in defining the CF model. This is what makes the CF sets superior and distinct from other FS models. In a CFS, the membership value of an element is specified based on one amplitude term and one phase term. With this aspect, CFS is not enough to model the nonmembership degree. To avoid this restriction, Alkouri and Salleh [44] introduced complex intuitionistic FS (CIFS). A CIFS is identified by MF (\(\mu =re^{i\omega }\)) and NMF (\(\nu =ke^{i\eta }\)) such that \(0\le r+k\le 1\) and \(0\le \omega +\eta \le 2\pi \). Rani and Garg [45] developed a DM approach based on distance measure between CIFSs. Also, some researchers studied on aggregation operator of CIFS and DM methods [46,47,48,49,50,51]. Additionally, Ullah et al. [52] introduced the complex PyFS (CPFS) which is characterized by MF \(\mu =re^{i\omega }\), NeF \(\mu =se^{i\theta }\), and NMF \(\nu =ke^{i\eta }\) under the conditions \(0\le r+s+k\le 1\) and \(0\le \frac{\omega }{2\pi }+\frac{\theta }{2\pi }+\frac{\eta }{2\pi }\le 1\) as a generalization of CIFSs. Liu et al. [53] defined the complex q-ROFS (CqROFS) and studied on aggregation operator of them.
Akram et al. [54] presented some aggregation operators under CPF environment based on Hamacher operations and developed an MCDM method. Liu et al. [55] introduced CPF power averaging and CPF power geometric operators under CPFSs environment and constructed an MCDM method based on the proposed operators. Additionally, the complex SFS (CSFS) was defined by Akram et al. [56] as a generalization of CPFS. They also introduced some aggregation operation based on Dombi t-norm and t-conorm. Ali et al. [57] defined the concept of complex T-spherical FS (CTSFS) and their aggregation operators. They also proposed an MADM method in CTSFSs. Akram et al. [58] defined some aggregation operators of CSFSs and developed an MCGDM method called CSF-VIKOR. Nasir et al. [59] introduced the notion of CTSF relations and presented some applications related to the economy and international trade.
Since aggregation operators (AOs) convert the whole data into a single value, AOs have a vital importance in DM problems. Dombi [60] designated Dombi operators with flexible operational variables. In solving the DM problems, many researchers used Dombi operations of IFS [61], Pythagorean fuzzy [62,63,64], PF [66], bipolar fuzzy [65], spherical fuzzy [67], complex Pythagorean [68], and CSF [69].
As seen above, the studies on the theoretical aspects of SFSs, T-SFSs, CSFSs and CTSFSs and their applications in decision-making based on aggregation operators have increased rapidly. The following points motivate us to present this paper:
-
CFS and its generalizations have a very important role in decision-making problems containing two-dimensional information in real life. A TSFS comprehends a large amount of information as a generalization of the SFSs. However, it does not suffice in modelling an issue involving two-dimensional data. With this aspect, CTSFS has vital importance. A CTSFS is the generalization of theories like CFS, CIFS, CPFS, CPyFS and CSFS. Until now, there exists only one work [57] related to aggregation operators of CTSFS in the literature. Therefore, by considering the advantages of the Dombi operators, we develop some new aggregation operators based on Dombi t-norm and t-conorm to use in modelling a problem involving two-dimensional data.
-
Set-theoretical operators are an important tool for modelling some problems, in the literature, there is not any study related to set-theoretical operations of CTSFS. To fill this gap in the literature, we define the set-theoretical operations of CTSFSs.
-
In literature, there is only one study related to score and accuracy functions of CTSFNs and these functions have some drawbacks, we pointed out these drawbacks and define novel score and accuracy functions free from specified drawbacks.
-
We see that works related to aggregation operators of SFS, TSFS and CTSFSs are based on the hypothetical data in general. In this study, one of our aims is to develop a decision-making method by considering the advantages of the Dombi operators and presenting an application including real data that aims to diagnose COVID-19 patients.
This article is organized as follows: the next section recalls the required definitions in the following sections as SFS, TSFS, CTSFSs and Dombi operations. Also, new score and accuracy functions and set-theoretical operation are defined. The subsequent section defines Dombi operations of complex T-spherical fuzzy numbers and provides their examples, and related operations of these operators are obtained for introduced aggregation operators. Then the MCDM method and its application are presented. Before the final section, sensitivity analyses and discussion related to obtained results from the application of the proposed method are given. The final section mentions the conclusions and planned studies.
Preliminaries
This section reminds the definitions of CFS, CIFS, CPyFS, CPFS, SFS, T-SFS and CTSFSs.
Definition 1
[42] Let \({\mathfrak {X}}\) be a nonempty set. A complex fuzzy set (CFS) \(\mathfrak {I}\) is defined as
where \({\tilde{\alpha }}_{{\mathcal {F}}}({\mathfrak {x}})\) is called membership functions of CFS \({\mathcal {F}}\) and receive all lying within the unit circle in the complex plane. Thus, it can be expressed as \({\tilde{\alpha }}_{{\mathcal {F}}}({\mathfrak {x}})=\alpha _{{\mathcal {F}}}({\mathfrak {x}})e^{i2\pi \varpi _{\alpha _{{\mathcal {F}}}}({\mathfrak {x}})}\), and it denotes a complex-valued grade of membership of \({\mathfrak {x}}\in {\mathfrak {X}}\) to (CFS) \(\mathfrak {I}\). Here \(i=\sqrt{-1}\) and for all \({\mathfrak {x}}\in {\mathfrak {X}}\), \(0\le \alpha _{{\mathcal {F}}}({\mathfrak {x}}) \le 1\), and \(0\le \varpi _{\alpha _{{\mathcal {F}}}}({\mathfrak {x}})\le 1.\)
Definition 2
[44] Let \({\mathfrak {X}}\) be a nonempty set. A complex intuitionistic fuzzy set (CIFS) \({\mathcal {I}} \) is defined as:
where \({\tilde{\alpha }}_{{\mathcal {I}}}({\mathfrak {x}})\) and \({\tilde{\gamma }}_{{\mathcal {I}}}({\mathfrak {x}})\) are called membership function and non-membership function of CIFS \({\mathcal {I}}\), respectively. They receive all lying within the unit circle in the complex plane. Hence, they can be expressed as \({\tilde{\alpha }}_{{\mathcal {I}}}({\mathfrak {x}})= \alpha _{{\mathcal {I}}}({\mathfrak {x}})e^{i2\pi \varpi _{\alpha _{{\mathcal {I}}}}({\mathfrak {x}})}\), and \({\tilde{\gamma }}_{{\mathcal {I}}}({\mathfrak {x}})=\gamma _{{\mathcal {I}}}({\mathfrak {x}})e^{i2\pi \varpi _{\gamma _{{\mathcal {I}}}}({\mathfrak {x}})},\) where they denote the complex-valued grades of membership and non-membership of \({\mathfrak {x}}\in {\mathfrak {X}}\) to CIFS \({\mathcal {I}}\), respectively. Here \(i=\sqrt{-1}\), for all \({\mathfrak {x}}\in {\mathfrak {X}}\), \(0\le \alpha _{{\mathcal {I}}}({\mathfrak {x}})+\gamma _{{\mathcal {I}}}({\mathfrak {x}}) \le 1\), and \(0\le \varpi _{\alpha _{{\mathcal {I}}}}({\mathfrak {x}})+\varpi _{\gamma _{{\mathcal {I}}}}({\mathfrak {x}})\le 1.\)
Definition 3
[52] Let \({\mathfrak {X}}\) be a nonempty set. A complex pythagorean fuzzy set (CPyFS) \({\mathfrak {P}} \) is defined as
where \({\tilde{\alpha }}_{{\mathfrak {P}}}({\mathfrak {x}})\) and \({\tilde{\gamma }}_{{\mathfrak {P}} }({\mathfrak {x}})\) are called complex-valued membership function and non-membership function of CPyFS \({\mathfrak {P}}\), respectively. They receive all lying within the unit circle in the complex plane. Thus, they can be expressed as \({\tilde{\alpha }}_{{\mathfrak {P}}}({\mathfrak {x}})=\alpha _{{\mathfrak {P}} }({\mathfrak {x}})e^{i2\pi \varpi _{\alpha _{{\mathfrak {P}}}}({\mathfrak {x}})}\), and \({\tilde{\gamma }}_{{\mathfrak {P}} }({\mathfrak {x}})=\gamma _{{\mathfrak {P}}}({\mathfrak {x}})e^{i2\pi \varpi _{\gamma _{{\mathfrak {P}} }}({\mathfrak {x}})},\) where they denote the complex-valued grades of membership and non-membership of \({\mathfrak {x}}\in {\mathfrak {X}}\) to CPyFS \({\mathfrak {P}} \), respectively. Here \(i=\sqrt{-1}\) and for all \({\mathfrak {x}}\in {\mathfrak {X}}\), \(0\le \alpha _{{\mathcal {I}}}^2({\mathfrak {x}})+\gamma _{{\mathcal {I}}}^2({\mathfrak {x}}) \le 1\), and \(0\le \varpi _{\alpha _{{\mathfrak {P}} }}^2({\mathfrak {x}})+\varpi _{\gamma _{{\mathfrak {P}}}}^2({\mathfrak {x}})\le 1\) .
Definition 4
[54] Let \({\mathfrak {X}}\) be a nonempty set. A complex picture fuzzy set (CPFS) \({\mathcal {P}} \) is defined as
where \(\alpha _{{\mathcal {P}}}({\mathfrak {x}}), \beta _{{\mathcal {P}}}({\mathfrak {x}})\), and \(\gamma _{{\mathcal {P}}}({\mathfrak {x}})\) are called membership, neutral membership, and non-membership function of the CPFS \({\mathcal {P}}\), respectively. They receive all lying within the unit circle in the complex plane. Thus, they can be expressed as \({\tilde{\alpha }}_{{\mathcal {P}}}({\mathfrak {x}})=\alpha _{{\mathcal {P}}}({\mathfrak {x}})e^{i2\pi \varpi _{\alpha _{{\mathcal {P}}}}({\mathfrak {x}})}\), \({\tilde{\beta }}_{{\mathcal {P}}}({\mathfrak {x}})=\beta _{{\mathcal {P}}}({\mathfrak {x}})e^{i2\pi \varpi _{\beta _{{\mathcal {P}}}}({\mathfrak {x}})}\), and \({\tilde{\gamma }}_{{\mathcal {P}}}({\mathfrak {x}})=\gamma _{{\mathcal {P}}}({\mathfrak {x}})e^{i2\pi \varpi _{\gamma _{{\mathcal {P}}}}({\mathfrak {x}})},\) where they denote the complex-valued grades of membership and non-membership of \({\mathfrak {x}}\in {\mathfrak {X}}\) to CIFS \({\mathcal {P}}\), respectively. Here \(i=\sqrt{-1}\), and for all \({\mathfrak {x}}\in {\mathfrak {X}}\), \(0\le \alpha _{{\mathcal {P}}}({\mathfrak {x}})+\beta _{{\mathcal {P}}}({\mathfrak {x}})+\gamma _{{\mathcal {P}}}({\mathfrak {x}}) \le 1\), and \(0\le \varpi _{\alpha _{{\mathcal {P}}}}({\mathfrak {x}})+\varpi _{\beta _{{\mathcal {P}}}}({\mathfrak {x}})+\varpi _{\gamma _{{\mathcal {P}}}}({\mathfrak {x}})\le 1.\)
Definition 5
[24, 25] Let \({\mathfrak {X}}\) be a non-empty set. A spherical fuzzy set (SFS) \({\mathcal {A}}\) is defined over \({\mathfrak {X}}\) as follows:
Here the function \(\alpha _{{\mathcal {A}}}:{\mathfrak {X}} \rightarrow [0,1]\) expresses MF, \(\beta _{{\mathcal {A}}}:{\mathfrak {X}}\rightarrow [0,1]\) expresses NeMF, and \(\gamma _{{\mathcal {A}}}:X \rightarrow [0,1]\) expresses NMF of the SFS \({\mathcal {A}}\).
The concept of T-spherical fuzzy set was introduced by Mahmood et al. [26] as a generalization of the SFSs, as follows:
Definition 6
[26] Let \({\mathfrak {X}}\) be a nonempty set. A T-spherical fuzzy (TSF) set (TSFS) is defined over \({\mathfrak {X}}\) as follows:
Here the function \(\alpha _{{\mathcal {A}}}:{\mathfrak {X}} \rightarrow [0,1]\), \(\beta _{{\mathcal {T}}}:{\mathfrak {X}}\rightarrow [0,1]\), and \(\gamma _{{\mathcal {A}}}:{\mathfrak {X}} \rightarrow [0,1]\) express MF, NeMF, and NMF of the TSFS \({\mathcal {T}}\), respectively.
Definition 7
[57] Let \({\mathfrak {X}}\) be an initial universe different from empty set. A complex T-spherical fuzzy (CTSF) set (CTSFS) is defined as follows:
Here \(\alpha _\digamma ({\mathfrak {x}})=\alpha _\digamma ({\mathfrak {x}})e^{i2\pi \varpi _{\beta _\digamma ({\mathfrak {x}})}}\), \(\beta _\digamma ({\mathfrak {x}})=\beta _\digamma ({\mathfrak {x}})e^{i2\pi \varpi _{\beta _\digamma ({\mathfrak {x}})}}\), and \(\gamma _\digamma ({\mathfrak {x}})=\gamma _\digamma ({\mathfrak {x}})e^{i2\pi \varpi _{\gamma _\digamma ({\mathfrak {x}})}}\) denote the membership grades of truth, abstinence, and falsity such that \(0\le \alpha ^q_\digamma ({\mathfrak {x}})+\beta ^q_\digamma ({\mathfrak {x}})+\gamma ^q_\digamma ({\mathfrak {x}})\le 1\) and \(0\le \varpi ^q_{\alpha _\digamma ({\mathfrak {x}})}\) \(+\varpi ^q_{\beta _\digamma ({\mathfrak {x}})}+\varpi ^q_{\gamma _\digamma ({\mathfrak {x}})}\le 1.\) Furthermore,
\({\mathfrak {H}}_\digamma ({\mathfrak {x}})=\root q \of {1-\alpha _\digamma ({\mathfrak {x}})^q-\beta _\digamma ({\mathfrak {x}})^q-\alpha _\digamma ({\mathfrak {x}})^q} e^{\root q \of {(1-\varpi _{\alpha _\digamma ({\mathfrak {x}})}^q-\varpi _{\beta _\digamma ({\mathfrak {x}})}^q -\varpi _{\gamma _\digamma ({\mathfrak {x}})}^q)}}\) expresses the complex hesitancy grade of \({\mathfrak {x}}.\)
For convenience, \(\digamma =(\alpha _ke^{i2\pi \varpi _{\alpha _k}},\beta _ke^{i2\pi \varpi _{\beta _k}},\gamma _ke^{i2\pi \varpi _{\gamma _k}})\) is called complex T-spherical fuzzy number (CTSFN).
Ali et al. [57] defined the score functions for the CTSFNs by taking absolute value of formula given the following definitions.
When we consider the CTSFNs \((1e^{i2\pi 1},0e^{i2\pi 0},0e^{i2\pi 0})\) and \((0e^{i2\pi 1},0e^{i2\pi 0},1e^{i2\pi 1})\), their score values are 1. So, we need to use the accuracy function, but their accuracy values are 1. This is a weak aspect of the proposed score and accuracy functions. Therefore, we define the following score and accuracy functions.
Definition 8
Let \(\digamma =(\alpha e^{i2\pi \varpi _{\alpha }},\beta e^{i2\pi \varpi _{\beta }},\gamma e^{i2\pi \varpi _{\gamma }})\) is a CTSFN. The score function \(\Omega (\digamma )\) and accuracy function \(\mho (\digamma )\) of \(\digamma \) are formulated as follows:
Definition 9
Let \(\digamma _{1}=(\alpha _1e^{i2\pi \varpi _{\alpha _1}},\beta _1e^{i2\pi \varpi _{\beta _1}},\gamma _1e^{i2\pi \varpi _{\gamma _1}})\) and \(\digamma _{2}=(\alpha _2e^{i2\pi \varpi _{\alpha _2}},\beta _2e^{i2\pi \varpi _{\beta _2}},\gamma _2e^{i2\pi \varpi _{\gamma _2}})\) are two CTSFNs. For the comparison of \(\digamma _{1}\) and \(\digamma _{2}\),
-
\(\digamma _{1} \succeq \digamma _{2}\) (\(\digamma _{1}\) is superior to \(\digamma _{2}\)) if \(\Omega (\digamma _{1})> \Omega (\digamma _{2})\);
-
if \(\Omega (\digamma _{1}) = \Omega (\digamma _{2})\), then
-
\(\digamma _{1} \succeq \digamma _{2}\) (\(\digamma _{1}\) is superior to \(\digamma _{2}\)) if \(\mho (\digamma _{1})> \mho (\digamma _{2})\);
-
\(\digamma _{1} \sim \digamma _{2}\) (\(\digamma _{1}\) is equivalent to \(\digamma _{2}\)) if \(\mho (\digamma _{1}) = \mho (\digamma _{2})\).
-
Definition 10
Let \(\digamma _{1}=\Big \{\Big ({\mathfrak {x}},\alpha _1({\mathfrak {x}})e^{i2\pi \varpi _{\alpha _1}({\mathfrak {x}})}, \beta _1({\mathfrak {x}})e^{i2\pi \varpi _{\beta _1}({\mathfrak {x}})},\gamma _1({\mathfrak {x}})e^{i2\pi \varpi _{\gamma _1}({\mathfrak {x}})}\Big ):{\mathfrak {x}}\in {\mathfrak {X}}\Big \}\) and \(\digamma _2=\Big \{\Big ({\mathfrak {x}},\alpha _2({\mathfrak {x}})e^{i2\pi \varpi _{{\alpha _2}({\mathfrak {x}})}},\beta _2({\mathfrak {x}}) e^{i2\pi \varpi _{{\beta _2}({\mathfrak {x}})}},\gamma _2({\mathfrak {x}})e^{i2\pi \varpi _{{\gamma _2}({\mathfrak {x}})}}\Big ): {\mathfrak {x}}\in {\mathfrak {X}}\Big \}\) be any two CTSFSs. Then
-
1.
\(\digamma _{1} \preceq \digamma _{2}\) iff \(\alpha _1({\mathfrak {x}}) \le \alpha _2({\mathfrak {x}})\), \(\beta _1({\mathfrak {x}})\le \beta _2({\mathfrak {x}})\), \(\gamma _1({\mathfrak {x}}) \ge \gamma _2({\mathfrak {x}})\) and \(\varpi _{{\alpha _1}({\mathfrak {x}})}\le \varpi _{{\alpha _2}({\mathfrak {x}})}\),\(\varpi _{{\beta _1}({\mathfrak {x}}})\le \varpi _{{\beta _2}({\mathfrak {x}})}\),\(\varpi _{{\gamma _1}({\mathfrak {x}})}\ge \varpi _{{\gamma _2}({\mathfrak {x}})}\), for all \({\mathfrak {x}}\in {\mathfrak {X}}.\)
-
2.
\((\digamma _{1})^{c}=\{({\mathfrak {x}},\gamma _1({\mathfrak {x}})e^{i2\pi \varpi _{{\gamma _1}({\mathfrak {x}})}},\beta _1({\mathfrak {x}}) e^{i2\pi \varpi _{{\beta _1}({\mathfrak {x}})}},\alpha _1({\mathfrak {x}})e^{i2\pi \varpi _{{\alpha _1}({\mathfrak {x}})}}): {\mathfrak {x}}\in {\mathfrak {X}}\}.\)
-
3.
$$\begin{aligned} \digamma _{1} \cup \digamma _{2}= & {} \Big \{\Big ({\mathfrak {x}},\mathrm{max}\{\alpha _1({\mathfrak {x}}),\alpha _2({\mathfrak {x}})\}e^{i2\pi \mathrm{max}\{\varpi _{{\alpha _1}({\mathfrak {x}})},\varpi _{{\alpha _2}({\mathfrak {x}})}\}}, \\&\mathrm{min}\{\beta _1({\mathfrak {x}}), \beta _2({\mathfrak {x}})\}e^{i2\pi \mathrm{min}\{\varpi _{{\beta _1}({\mathfrak {x}})},\varpi _{{\beta _2}({\mathfrak {x}})}\}},\\&\mathrm{min}\{ \gamma _1({\mathfrak {x}}),\gamma _2({\mathfrak {x}})\}e^{i2\pi \mathrm{min}\{\varpi _{{\gamma _1}({\mathfrak {x}})},\varpi _{{\gamma _2}({\mathfrak {x}})}\}}\Big ):\\&{\mathfrak {x}}\in {\mathfrak {X}}\Big \}. \end{aligned}$$
-
4.
$$\begin{aligned} \digamma _{1} \cap \digamma _{2}= & {} \Big \{\Big ({\mathfrak {x}},\mathrm{min}\{\alpha _1({\mathfrak {x}}),\alpha _2({\mathfrak {x}})\}e^{i2\pi \mathrm{min}\{\varpi _{{\alpha _1}({\mathfrak {x}})},\varpi _{{\alpha _2}({\mathfrak {x}})}\}}, \\&\mathrm{min}\{\beta _1({\mathfrak {x}}), \beta _2({\mathfrak {x}})\}e^{i2\pi \mathrm{min}\{\varpi _{{\beta _1}({\mathfrak {x}})},\varpi _{{\beta _2}({\mathfrak {x}})}\}},\\&\mathrm{max}\{ \gamma _1({\mathfrak {x}}),\gamma _2({\mathfrak {x}})\}e^{i2\pi \mathrm{max}\{\varpi _{{\gamma _1}({\mathfrak {x}})},\varpi _{{\gamma _2}({\mathfrak {x}})}\}}\Big ):\\&{\mathfrak {x}}\in {\mathfrak {X}}\Big \}. \end{aligned}$$
Example 1
Let us consider CTSFSs \(\digamma _{1}\) and \(\digamma _{2}\) over universal set \({\mathfrak {X}}=\{{\mathfrak {x}}_{1},{\mathfrak {x}}_{2},{\mathfrak {x}}_{3}\}\) given as follows:
and
Then it is clear that \(\digamma _{1}\subseteq \digamma _{2}\). Also,
and
Dombi operations of complex T-spherical fuzzy numbers
In this section, we remind the definitions of Dombi t-norm (TN) and t-conorm (TCN) defined in [60] and we define the arithmetic operations of CTSFNs using Dombi TN and TCN.
Definition 11
[60] Let f and g be two real numbers. Then Dombi TN and Dombi TCN are defined by
Dombi t-conorm [60] is given by:
respectively.
Definition 12
Let \({\mathfrak {X}}\) be a universe and \(\digamma _1=\Big (\alpha _1e^{i2\pi \varpi _{\alpha _1}},\beta _1e^{i2\pi \varpi _{\beta _1}},\gamma _1e^{i2\pi \varpi _{\gamma _1}}\Big )\)and \(\digamma _2=\Big (\alpha _2e^{i2\pi \varpi _{\alpha _2}},\beta _2e^{i2\pi \varpi _{\beta _2}},\gamma _2e^{i2\pi \varpi _{\gamma _2}}\Big )\) are two CTSFNs on \({\mathfrak {X}}\). Then some Dombi operations between \(\digamma _{1}\) and \(\digamma _{2}\) are given as follows:
-
1.
\(\digamma _1\bigoplus \digamma _2=\left( \begin{array}{c} \left( \begin{array}{c} \root q \of {1-\frac{1}{1+\big (\big (\frac{(\alpha _1)^q}{1-(\alpha _1)^q}\big )^{\eta }+\big (\frac{(\alpha _2)^q}{1-(\alpha _2)^q}\big )^{\eta }\big )^{\frac{1}{\eta }}}} e^{{i2\pi \root q \of {1-\frac{1}{1+\big (\frac{(\varpi _{\alpha _{1}})^q}{1-(\varpi _{\alpha _{1}})^q}\big )^{\eta }+ (\big (\frac{(\varpi _{\alpha _{2}})^q}{1-(\varpi _{\alpha _{2}})^q}\big )^{\eta }\big )^{\frac{1}{\eta }}}}}} \end{array} \right) ,\\ \left( \begin{array}{c} \root q \of {\frac{1}{1+\big (\big (\frac{1-(\beta _1)^q}{(\beta _1)^q}\big )^{\eta }+\big (\frac{1-(\beta _2)^q}{(\beta _2)^q}\big )^{\eta }\big )^{\frac{1}{\eta }}}} e^{i2\pi \root q \of {\frac{1}{1+\big (\frac{1-(\varpi _{\beta _{1}})^q}{(\varpi _{\beta _{1}})^q}\big )^{\eta }+ (\big (\frac{1-(\varpi _{\beta _{2}})^q}{(\varpi _{\beta _{2}})^q}\big )^{\eta }\big )^{\frac{1}{\eta }}}}} \end{array} \right) ,\\ \left( \begin{array}{c} \root q \of {\frac{1}{1+\big (\big (\frac{1-(\gamma _1)^q}{(\gamma _1)^q}\big )^{\eta }+\big (\frac{1-(\gamma _2)^q}{(\gamma _2)^q}\big )^{\eta }\big )^{\frac{1}{\eta }}}} e^{i2\pi \root q \of {\frac{1}{1+\big (\frac{1-(\varpi _{\gamma _{1}})^q}{(\varpi _{\gamma _{1}})^q}\big )^{\eta }+ (\big (\frac{1-(\varpi _{\gamma _{2}})^q}{(\varpi _{\gamma _{2}})^q}\big )^{\eta }\big )^{\frac{1}{\eta }}}}} \end{array} \right) , \end{array} \right) .\)
-
2.
\(\digamma _1\bigotimes \digamma _2=\left( \begin{array}{c} \left( \begin{array}{c} \root q \of {\frac{1}{1+\big (\big (\frac{1-(\alpha _1)^q}{(\alpha _1)^q}\big )^{\eta }+\big (\frac{1-(\alpha _2)^q}{(\alpha _2)^q}\big )^{\eta }\big )^{\frac{1}{\eta }}}} e^{i2\pi \root q \of {\frac{1}{1+\big (\frac{1-(\varpi _{\alpha _{1}})^q}{(\varpi _{\alpha _{1}})^q}\big )^{\eta }+ (\big (\frac{1-(\varpi _{\alpha _{2}})^q}{(\varpi _{\alpha _{2}})^q}\big )^{\eta }\big )^{\frac{1}{\eta }}}}} \end{array} \right) ,\\ \left( \begin{array}{c} \root q \of {\frac{1}{1+\big (\big (\frac{1-(\beta _1)^q}{(\beta _1)^q}\big )^{\eta }+\big (\frac{1-(\beta _2)^q}{(\beta _2)^q}\big )^{\eta }\big )^{\frac{1}{\eta }}}} e^{i2\pi \root q \of {\frac{1}{1+\big (\frac{1-(\varpi _{\beta _{1}})^q}{(\varpi _{\beta _{1}})^q}\big )^{\eta }+ (\big (\frac{1-(\varpi _{\beta _{2}})^q}{(\varpi _{\beta _{2}})^q}\big )^{\eta }\big )^{\frac{1}{\eta }}}}} \end{array} \right) ,\\ \left( \begin{array}{c} \root q \of {1-\frac{1}{1+\big (\big (\frac{(\gamma _1)^q}{1-(\gamma _1)^q}\big )^{\eta }+\big (\frac{(\gamma _2)^q}{1-(\gamma _2)^q}\big )^{\eta }\big )^{\frac{1}{\eta }}}} e^{i2\pi \root q \of {1-\frac{1}{1+\big (\frac{(\varpi _{\gamma _{1}})^q}{1-(\varpi _{\gamma _{1}})^q}\big )^{\eta }+ (\big (\frac{(\varpi _{\gamma _{2}})^q}{1-(\varpi _{\gamma _{2}})^q}\big )^{\eta }\big )^{\frac{1}{\eta }}}}} \end{array} \right) , \end{array} \right) .\)
-
3.
\(\tau \digamma =\left( \begin{array}{c} \left( \begin{array}{c} \root q \of {1-\frac{1}{1+\big (\tau \big (\frac{(\alpha _1)^q}{1-(\alpha _1)^q}\big )^{\eta }\big )^{\frac{1}{\eta }}}} e^{i2\pi \root q \of {1-\frac{1}{1+\big (\tau \big (\frac{(\varpi _{\alpha _{1}})^q}{1-(\varpi _{\alpha _{1}})^q}\big )^{\eta }\big )^{\frac{1}{\eta }}}}} \end{array} \right) ,\\ \left( \begin{array}{c} \root q \of {\frac{1}{1+\big (\tau \big (\frac{1-(\beta _1)^q}{(\beta _1)^q}\big )^{\eta }\big )^{\frac{1}{\eta }}}} e^{(i2\pi (\root q \of {\frac{1}{1+\big (\tau \big (\frac{1-(\varpi _{\beta _{1}})^q}{(\varpi _{\beta _{1}})^q}\big )^{\eta }\big )^{\frac{1}{\eta }}}}} \end{array} \right) ,\\ \left( \begin{array}{c} \root q \of {\frac{1}{1+\big (\tau \big (\frac{1-(\gamma _1)^q}{(\gamma _1)^q}\big )^{\eta }\big )^{\frac{1}{\eta }}}} e^{i2\pi \root q \of {\frac{1}{1+\big (\tau \big (\frac{1-(\varpi _{\gamma _{1}})^q}{(\varpi _{\gamma _{1}})^q}\big )^{\eta }\big )^{\frac{1}{\eta }}}}} \end{array} \right) \end{array}\right) ;\tau \ge 0.\)
-
4.
\(\digamma ^{\tau }=\left( \begin{array}{c} \left( \begin{array}{c} \root q \of {\frac{1}{1+\big (\tau \big (\frac{1-(\alpha _1)^q}{(\alpha _1)^q}\big )^{\eta }\big )^{\frac{1}{\eta }}}} e^{\i 2\pi \root q \of {\frac{1}{1+\big (\tau \big (\frac{1-(\varpi _{\alpha _{1}})^q}{(\varpi _{\alpha _{1}})^q}\big )^{\eta }\big )^{\frac{1}{\eta }}}}} \end{array} \right) ,\\ \left( \begin{array}{c} \root q \of {\frac{1}{1+\big (\tau \big (\frac{1-(\beta _1)^q}{(\beta _1)^q}\big )^{\eta }\big )^{\frac{1}{\eta }}}} e^{i2\pi \root q \of {\frac{1}{1+\big (\tau \big (\frac{1-(\varpi _{\beta _{1}})^q}{(\varpi _{\beta _{1}})^q}\big )^{\eta }\big )^{\frac{1}{\eta }}}}} \end{array} \right) ,\\ \left( \begin{array}{c} \root q \of {1-\frac{1}{1+\big (\tau \big (\frac{(\gamma _1)^q}{1-(\gamma _1)^q}\big )^{\eta }\big )^{\frac{1}{\eta }}}} e^{i2\pi \root q \of {1-\frac{1}{1+\big (\tau \big (\frac{(\varpi _{\gamma _{1}})^q}{1-(\varpi _{\gamma _{1}})^q}\big )^{\eta }\big )^{\frac{1}{\eta }}}}} \end{array} \right) \end{array}\right) ; \tau \ge 0.\)
Example 2
Consider two CTSFNs given by
Then for \(\eta =1\) and \(q=6\)
Dombi weighted aggregation operators of CTSFNs
In this part, we introduce two operators called complex T-spherical Dombi fuzzy weighted arithmetic averaging (CTSDFWAA) operator and complex T-spherical Dombi fuzzy weighted geometric averaging (CTSDFWGA) operator. We also obtain some pivotal properties of the introduced operators.
Complex T-spherical Dombi fuzzy weighted arithmetic averaging operator
Definition 13
Let \({\mathfrak {X}}\) be a universe and \(\digamma _k=\Big (\alpha _ke^{i2\pi \varpi _{\alpha _k}},\beta _ke^{i2\pi \varpi _{\beta _k}},\gamma _ke^{i2\pi \varpi _{\gamma _k}}\Big )\) \((k=1,2,\ldots ,u)\) be a set of CTSFNs with weight vector \({\mathcal {W}}=({\mathcal {W}}_1,{\mathcal {W}}_2,\ldots ,{\mathcal {W}}_u)^T\), where \({\mathcal {W}}_k>0\), \(\sum _{k=1}^{u}{\mathcal {W}}_k=1\). Then (CTSDFWAA) operator is defined by a mapping \(\mathrm{CTSDFWAA}:\digamma ^u \rightarrow \digamma \), where
Theorem 1
Let \({\mathfrak {X}}\) be a universe and \(\digamma _k=\Big (\alpha _ke^{i2\pi \varpi _{\alpha _k}},\beta _ke^{i2\pi \varpi _{\beta _k}},\gamma _ke^{i2\pi \varpi _{\gamma _k}}\Big )\) \((k=1,2,\ldots ,u)\) be a set of CTSFNs of with weight vector \({\mathcal {W}}=({\mathcal {W}}_1,{\mathcal {W}}_2,\ldots ,{\mathcal {W}}_u)^T\), where \(\mathcal {W_i}>0\) \((k=1,2,3,\ldots ,u)\) and \(\sum _{k=1}^{u}{\mathcal {W}}_k=1\). Then, aggregated value of set using CTSDFWAA is a CTSFN defined as follows:
Proof
We can simply prove the theory using the mathematical induction method. Using Dombi operations of CTSFNs for \(u = 2\), we have
Assume that the equation holds, when \(u = \sigma \), i.e.
If \(u=\sigma +1\), then we have
Hence, the theory 3.1 is true for \(u=\sigma +1\). Then the equation is true for all \(u \in \mathbb {N}.\) \(\square \)
Example 3
Consider three CTSFNs with weight vector \(\mathbb {W}=(0.5,0.3,0.2)^{\tau }\) and operational parameter \(\eta =1\) and \(q=6\) given as follows:
Using the CTSDFWAA operator, we can aggregate the three CTSFNs and find an aggregate value as shown below:
\(=(0.488e^{i2\pi 0.493},0.534e^{i2\pi 0.553},0.666e^{i2\pi 0.683}).\)
The values when \(\eta \ne 1\) are shown in Table 1.
Theorem 2
(Idempotency) Let \(\digamma _k=\Big (\alpha _ke^{i2\pi \varpi _{\alpha _k}},\beta _ke^{i2\pi \varpi _{\beta _k}},\gamma _ke^{i2\pi \varpi _{\gamma _k}}\Big )\) \((k=1,2,\ldots ,u)\) be a set of CTSFNs such that \(\digamma _k=\digamma \). Then
Proof
Assume that \(\digamma _k = \digamma \) for all \(k=1,2,\ldots ,u\). Using Eq. 3, we have
\(\square \)
Theorem 3
(Monotonicity) Let \(\digamma _k=\Big (\alpha _ke^{i2\pi \varpi _{\alpha _k}},\beta _ke^{i2\pi \varpi _{\beta _k}},\gamma _ke^{i2\pi \varpi _{\gamma _k}}\Big )\) and \(\digamma _k'=\Big (\alpha _k'e^{i2\pi \varpi _{\alpha '_k}}, \beta _k'e^{i2\pi \varpi _{\beta '_k}},\gamma '_ke^{i2\pi \varpi _{\gamma '_k}}\Big )\) \((k=1,2,\ldots ,u)\) be two sets of CTSFNs. If \(\alpha _k\le \alpha '_k, \beta _k\ge \beta '_k, \gamma _k\ge \gamma '_k\), \(\varpi _{\alpha _k}\le \varpi _{\alpha '_k}, \varpi _{\beta _k}\ge \varpi _{\beta '_k},\) and \(\varpi _{\gamma _k}\ge \varpi _{\gamma '_k}\) for all \(k=1,2,\ldots ,u\). Then
Proof
Let CTSDFWAA\(\digamma _k=\Big (\alpha _ke^{i2\pi \varpi _{\alpha _k}},\beta _ke^{i2\pi \varpi _{\beta _k}},\gamma _ke^{i2\pi \varpi _{\gamma _k}}\Big )\) and
CTSDFWAA \(\digamma _k'=\Big (\alpha _k'e^{i2\pi \varpi _{\alpha '_k}},\beta _k'e^{i2\pi \varpi _{\beta '_k}},\gamma '_ke^{i2\pi \varpi _{\gamma '_k}}\Big ),k=\{1,2,3,\ldots ,u\}\) since \(\alpha _{\digamma _{1}}\le \alpha _{\acute{\digamma _{1}}}\), \(\frac{\alpha ^{q}_{\digamma _{1}}}{1-\alpha ^{q}_{\digamma _{1}}}\le \frac{\alpha ^{q}_{\acute{\digamma _{1}}}}{1-\alpha ^{q}_{\acute{\digamma _{1}}}}\). We show first that \(\alpha \le \acute{\alpha } \). So, we have
Hence, \(\alpha \le \acute{\alpha }\) Similarly, it is easy to show that \(\beta \le \acute{\beta }\) , \(\gamma \le \acute{\gamma }\), \(\varpi _{\alpha } \le \varpi _{\acute{\alpha }}\),\(\varpi _{\beta } \le \varpi _{\acute{\beta }} \),\(\varpi _{\gamma }\le \varpi _{\acute{\gamma }}\). Thus, the proof of the theorem is completed. \(\square \)
Theorem 4
(Boundedness) Let \(\digamma _k=\Big (\alpha _ke^{i2\pi \varpi _{\alpha _k}},\beta _ke^{i2\pi \varpi _{\beta _k}}, \gamma _ke^{i2\pi \varpi _{\gamma _k}}\Big ),(k=1,2,3,\ldots ,u)\) a set of CTSFNs with \(\digamma _{min}=min\left( \digamma _1,\digamma _2,\digamma _3,\ldots ,\digamma _u\right) \) and \(\digamma _{max}=max\left( \digamma _1,\digamma _2,\digamma _3,\ldots ,\digamma _u\right) \). Then
Proof
Let
and
Therefore,
The inequality for amplitude term of membership grade is given as follows:
Similarly, the inequality for phase term of membership grade is given as follows:
In a similar manner, we can get the results for the amplitude and phase terms of abstinence and non-membership grades. Thus,
\(\square \)
Complex T-spherical Dombi fuzzy weighted geometric averaging operator
Definition 14
Let \(\digamma _k=\Big (\alpha _ke^{i2\pi \varpi _{\alpha _k}},\beta _ke^{i2\pi \varpi _{\beta _k}},\gamma _ke^{i2\pi \varpi _{\gamma _k}}\Big )\) \((k=1,2,\ldots ,u)\) be a set of CTSFNs of with weight vector \({\mathcal {W}}=({\mathcal {W}}_1,{\mathcal {W}}_2,\ldots ,{\mathcal {W}}_u)^T\), where \({\mathcal {W}}_k>0\), \(\sum _{k=1}^{u}{\mathcal {W}}_k=1\). Then (CTSDFWGA) operator is defined by a mapping CTSDFWGA\(:\digamma ^u \rightarrow \digamma \), where
Theorem 5
If \(\digamma _k=\Big (\alpha _ke^{i2\pi \varpi _{\alpha _k}},\beta _ke^{i2\pi \varpi _{\beta _k}},\gamma _ke^{i2\pi \varpi _{\gamma _k}}\Big )\) \((k=1,2,\ldots ,u)\) be a set of CTSFNs of with weight vector \({\mathcal {W}}=({\mathcal {W}}_1,{\mathcal {W}}_2,\ldots ,{\mathcal {W}}_u)^T\), where \({\mathcal {W}}_k>0\), \(\sum _{k=1}^{u}{\mathcal {W}}_k=1\). Then (CTSDFWGA) operator the clumped value of these CTSFNs is again a CTSFN. This clumped value can be obtained by the following formula:
Proof
The proof can be made by similar way to the proof of Theorem 9. \(\square \)
Example 4
Let us consider three CTSFNs given as follows:
with the weight vector \(\mathbb {W}=(0.5,0.3,0.2)^{\tau }\) and operational parameter \(\eta =1\) and \(q=6\). Using the CTSDFWGA operator, we can aggregate the three CTSFNs and find a clumped value as given below:
\(=\left( 0.788e^{i2\pi 0.801},0.534e^{i2\pi 0.553},0.443e^{i2\pi 0.461}\right) \).
The values when \(\eta \ne 1\) are shown in Table 2.
Theorem 6
(Idempotency) Let \(\digamma _k=\Bigg (\alpha _ke^{i2\pi \varpi _{\alpha _k}},\beta _ke^{i2\pi \varpi _{\beta _k}},\gamma _ke^{i2\pi \varpi _{\gamma _k}}\Bigg )\) \((k=1,2,\ldots ,u)\) be a set of CTSFNs such that \(\digamma _k=\digamma \). Then
Proof
The proof is similar to the proof of Theorem 2. \(\square \)
Theorem 7
(Monotonicity) Let \(\digamma _k=\Big (\alpha _ke^{i2\pi \varpi _{\alpha _k}},\beta _ke^{i2\pi \varpi _{\beta _k}},\gamma _ke^{i2\pi \varpi _{\gamma _k}}\Big )\) and \(\digamma _k'=\Big (\alpha _k'e^{i2\pi \varpi _{\alpha '_k}}, \beta _k'.e^{i2\pi \varpi _{\beta '_k}},\gamma '_ke^{i2\pi \varpi _{\gamma '_k}}\Big )\) \((k=1,2,\ldots ,u)\) be two sets of CTSFNs. If \(\alpha _k\le \alpha '_k, \beta _k\ge \beta '_k, \gamma _k\ge \gamma '_k\), \(\varpi _{\alpha _k}\le \varpi _{\alpha '_k}, \varpi _{\beta _k}\ge \varpi _{\beta '_k},\) and \(\varpi _{\gamma _k}\ge \varpi _{\gamma '_k}\) for all k, then
Proof
The proof can be made by the similar way to Theorem 3. \(\square \)
Theorem 8
(Boundedness) Let \(\digamma _k=\Big (\alpha _ke^{i2\pi \varpi _{\alpha _k}},\beta _ke^{i2\pi \varpi _{\beta _k}}, \gamma _ke^{i2\pi \varpi _{\gamma _k}}\Big ), (k=1,2,3,\ldots ,u)\) be a set of CTSFNs with \(\digamma _{min}=min(\digamma _1,\digamma _2,\digamma _3,\ldots ,\digamma _u)\) and \(\digamma _{max}=max(\digamma _1,\digamma _2,\digamma _3,\ldots ,\digamma _u)\). Then
Proof
The proof can be made by the similar way to proof of Theorem 4. \(\square \)
Dombi ordered weighted aggregation operators of CTSFNs
In this part, we propose two operators, namely, complex T-spherical Dombi fuzzy ordered weighted arithmetic averaging (CTSDFOWAA) operator and complex T-spherical Dombi fuzzy weighted ordered geometric averaging (CTSDFOWGA) operator. Moreover, we also discuss some pivotal properties of these operators.
Complex T-spherical Dombi fuzzy ordered weighted arithmetic averaging operator
Definition 15
Let \(\digamma _k=\Big (\alpha _ke^{i2\pi \varpi _{\alpha _k}},\beta _ke^{i2\pi \varpi _{\beta _k}},\gamma _ke^{i2\pi \varpi _{\gamma _k}}\Big )\) \((k=1,2,\ldots ,u)\) be a set of CTSFNs of with weight vector \({\mathcal {W}}=({\mathcal {W}}_1,{\mathcal {W}}_2,\ldots ,{\mathcal {W}}_u)^T\), where \({\mathcal {W}}_k>0\), \(\sum _{k=1}^{u}{\mathcal {W}}_k=1\). Then (CTSDFOWAA) operator is defined by a mapping
\(\mathrm{CTSDFOWAA}:\digamma ^u \rightarrow \digamma \), where
and \(\left( \sigma _{1},\sigma _{2},\ldots ,\sigma _{u}\right) \) are the permutations of \(\sigma (k)\) having the condition \(|\digamma _{\sigma (k-1)}| \ge |\digamma _{\sigma (k)}|\) for all \((k=1,2,\ldots ,u).\)
Theorem 9
If \(\digamma _k=\Big (\alpha _ke^{i2\pi \varpi _{\alpha _k}},\beta _ke^{i2\pi \varpi _{\beta _k}},\gamma _ke^{i2\pi \varpi _{\gamma _k}}\Big )\) \((k=1,2,\ldots ,u)\) be a set of CTSFNs of with weight vector \({\mathcal {W}}=({\mathcal {W}}_1,{\mathcal {W}}_2,\ldots ,{\mathcal {W}}_u)^T\), where \({\mathcal {W}}>0\) and \(\sum _{k=1}^{u}{\mathcal {W}}_k=1\).
Then aggregated value of set using CTSDFOWAA is a CTSFN defined as follows:
Example 5
Let us consider three CTSFNs given as follows:
having the weight vector \({\mathcal {W}}=(0.5,0.3,0.2)^{\tau }\) with operational parameter \(\eta =1\) and \(q=6\). Using the CTSDFOWAA operator, we can aggregate the three CTSFNs. We can find the values of the score function of this CTSFNs
Hence, \(\Omega (\digamma _{2}) \ge \Omega (\digamma _{3}) \ge \Omega (\digamma _{1})\), we will also find that
\(=\left( 0.488e^{i2\pi 0.493},0.489e^{i2\pi 0.508},0.682e^{i2\pi 0.696}\right) .\)
Theorem 10
(Idempotency) Let \(\digamma _k=\Bigg (\alpha _ke^{i2\pi \varpi _{\alpha _k}},\beta _ke^{i2\pi \varpi _{\beta _k}},\gamma _ke^{i2\pi \varpi _{\gamma _k}}\Bigg )\) \((k=1,2,\ldots ,u)\) be a set of CTSFNs such that \(\digamma _k=\digamma \). Then
Theorem 11
(Monotonicity) Let \(\digamma _k=\Big (\alpha _ke^{i2\pi \varpi _{\alpha _k}},\beta _ke^{i2\pi \varpi _{\beta _k}},\gamma _ke^{i2\pi \varpi _{\gamma _k}}\Big )\) and \(\digamma _k'=\Big (\alpha _k'e^{i2\pi \varpi _{\alpha '_k}}, \beta _k'.e^{i2\pi \varpi _{\beta '_k}},\gamma '_ke^{i2\pi \varpi _{\gamma '_k}}\Big )\) \((k=1,2,\ldots ,u)\) be two sets of CTSFNs. If \(\alpha _k\le \alpha '_k, \beta _k\ge \beta '_k, \gamma _k\ge \gamma '_k\), \(\varpi _{\alpha _k}\le \varpi _{\alpha '_k}, \varpi _{\beta _k}\ge \varpi _{\beta '_k},\) and \(\varpi _{\gamma _k}\ge \varpi _{\gamma '_k}\) for all k. Then
Theorem 12
(Boundedness) Let \(\digamma _k=\Big (\alpha _ke^{i2\pi \varpi _{\alpha _k}},\beta _ke^{i2\pi \varpi _{\beta _k}},\gamma _ke^{i2\pi \varpi _{\gamma _k}}\Big ),k=\{1,2,3,\ldots ,u\}\) a set of CTSFNs with \(\digamma _{min}=min(\digamma _1,\digamma _2,\digamma _3,\ldots ,\digamma _u)\) and \(\digamma _{max}=max(\digamma _1,\digamma _2,\digamma _3,\ldots ,\digamma _u)\). Then
Complex T-spherical Dombi fuzzy ordered weighted geometric averaging operator
Definition 16
Let \(\digamma _k=\Big (\alpha _ke^{i2\pi \varpi _{\alpha _k}},\beta _ke^{i2\pi \varpi _{\beta _k}},\gamma _ke^{i2\pi \varpi _{\gamma _k}}\Big )\) \((k=1,2,\ldots ,u)\) be a set of CTSFNs of with weight vector \({\mathcal {W}}=({\mathcal {W}}_1,{\mathcal {W}}_2,\ldots ,{\mathcal {W}}_u)^T\), where \({\mathcal {W}}_k>0\), \(\sum _{k=1}^{u}{\mathcal {W}}_k=1\). Then (CTSDFOWGA) operator is defined by a mapping \(CTSDFOWGA:\digamma _u \rightarrow \digamma \), where
and \(\left( \sigma _{1},\sigma _{2},\ldots ,\sigma _{u}\right) \) are the permutations of \(\sigma (k)\) having the condition \(|\digamma _{\sigma (k-1)}| \ge |\digamma _{\sigma (k)}|\) for all \((k=1,2,\ldots ,u)\)
Theorem 13
If \(\digamma _k=\Bigg (\alpha _ke^{i2\pi \varpi _{\alpha _k}},\beta _ke^{i2\pi \varpi _{\beta _k}},\gamma _ke^{i2\pi \varpi _{\gamma _k}}\Bigg )\) \((k=1,2,\ldots ,u)\) be a set of CTSFNs of with weight vector \({\mathcal {W}}=({\mathcal {W}}_1,{\mathcal {W}}_2,\ldots ,{\mathcal {W}}_u)^T\), where \({\mathcal {W}}_k>0\), \(\sum _{k=1}^{u}{\mathcal {W}}_k=1\). Then (CTSDFWGA) operator the clumped value of these CTSFNs is again a CTSFN. This clumped value can be obtained by the following formula:
Example 6
Consider CTSFNs given in Example 3.4. Then
Theorem 14
(Idempotency) Let \(\digamma _k=\Bigg (\alpha _ke^{i2\pi \varpi _{\alpha _k}},\beta _ke^{i2\pi \varpi _{\beta _k}},\gamma _ke^{i2\pi \varpi _{\gamma _k}}\Bigg )\) \((k=1,2,\ldots ,u)\) be a set of CTSFNs such that \(\digamma _k=\digamma \). Then
Theorem 15
(Monotonicity) Let \(\digamma _k=\Bigg (\alpha _ke^{i2\pi \varpi _{\alpha _k}},\beta _ke^{i2\pi \varpi _{\beta _k}},\gamma _ke^{i2\pi \varpi _{\gamma _k}}\Bigg )\) and \(\digamma _k'=\Bigg (\alpha _k'e^{i2\pi \varpi _{\alpha '_k}}, \beta _k'e^{i2\pi \varpi _{\beta '_k}},\gamma '_ke^{i2\pi \varpi _{\gamma '_k}}\Bigg )\) \((k=1,2,\ldots ,u)\) be two sets of CTSFNs. If \(\alpha _k\le \alpha '_k, \beta _k\ge \beta '_k, \gamma _k\ge \gamma '_k\), \(\varpi _{\alpha _k}\le \varpi _{\alpha '_k}, \varpi _{\beta _k}\ge \varpi _{\beta '_k},\) and \(\varpi _{\gamma _k}\ge \varpi _{\gamma '_k}\) for all k. Then
Theorem 16
(Boundedness) Let \(\digamma _k=\Big (\alpha _ke^{i2\pi \varpi _{\alpha _k}},\beta _ke^{i2\pi \varpi _{\beta _k}}, \gamma _ke^{i2\pi \varpi _{\gamma _k}}\Big ),\) \((k=1,2,3,\ldots ,u)\) a set of CTSFNs with \(\digamma _\mathrm{min}=\mathrm{min}\left( \digamma _1,\digamma _2,\digamma _3,\ldots \ldots ,\digamma _u\right) \) and \(\digamma _\mathrm{max}=\mathrm{max}\left( \digamma _1,\digamma _2,\digamma _3,\ldots ,\digamma _u\right) \). Then
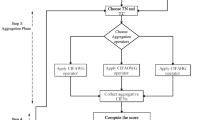
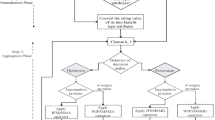
MCDM method under CTSF environment
In this section, we present an MCDM method under CTSF environment.
Let \(\kappa =\{\kappa _1,\kappa _2,\ldots ,\kappa _l\}\) be set of alternatives, \(\epsilon =\{\epsilon _1,\epsilon _2,\ldots ,\epsilon _s\}\) be a set of criteria. Let us consider \({\mathcal {W}}=\left( {\mathcal {W}}_1,{\mathcal {W}}_2,\ldots ,{\mathcal {W}}_s\right) \) such that \({\mathcal {W}}_j\in (0,1]\) and \(\sum _{j=1}^{s}{\mathcal {W}}_j=1\) as the weight vector of the criteria which is determined by decision-makers. The steps of the MCDM method are given as follows:
Step 1: The evaluation of the alternative \(\kappa _i\) according to criteria \(\epsilon _j\) performed by decision-maker. It can be written as \(\zeta _{yj} (j=1,2,\ldots ,s; y=1,2,\ldots ,t)\). Hence, CTSF-decision matrix \(\mathcal {DM}=[\zeta _{yj}]_{t\times s}\) can be constructed as follows:
Here \(\zeta _{yj}=\Big (\alpha _{yj} e^{i2\pi \varpi _{yj}},\beta _{yj} e^{i2\pi \varpi _{yj}},\gamma _{yj} e^{i2\pi \varpi _{yj}}\Big )\).
Step 2: Find the aggregated value denoted by \({\mathbb {A}}_y\) \((y=1,2,3,\ldots ,l)\) using the CTSDFWAA operators.
Step 3: Find the score values, for each \({\mathbb {A}}_y y=1,2,3,\ldots ,l\)
Step 4: Choose the alternative which has a maximum score value.
Application
The COVID-19 outbreak first appeared in Wuhan city of China in December 2019 and spread rapidly all over the world [70, 71]. Until May 5, 2021, 153,790,183 people were infected with the COVID-19 and 3,218,080 people died [72]. Also, the spread of COVID-19 still continuous. In some papers, mathematical analysis revealing the spread of such a deathly disease have been presented [73,74,75].
In this section, an application of the proposed method to determine a patient infected by COVID-19 is presented. In this application, after we discuss by infectious diseases physician, we determine the criteria as a basic symptoms of COVID-19. Set of the symptoms is considered as \(\epsilon =\{\epsilon _1=\text { Fever } ,\epsilon _2=\text { headache }, \epsilon _3=\text { dyspnea }, \epsilon _4=\text { cough }\}\). Also, we consider the five patients \(p_1,p_2,p_3,p_4\) and \(p_5\). For each of patients, data measured along with 14 days according to symptoms are given in Tables 3, 4, 5 and 6.
Here we transform data given in tables to CTSFN. We will only explain transforming process of data given in Table 3. Other transforming of the tables will not be showed.
We establish amplitude terms and phase terms according to fever degree and days, respectively. First, we classify the degree of fever for MD (38.6-39.5 ), NeD(37.6-38.5 ), and NMD (36.5-37.5). Then we assign values from 0.1 to 0.9 for fever intervals. This is shown in Table 7.
For each of MD, NeD and NMD, we find the arithmetic mean of the fever values. Then we assign a value from 0.1 to 0.9.
and
We divide the number of MD, NeD and NMD days by 14 for each patient to obtain the phase terms. For example, according to Table 3, we see that fever of \(p_1\) is in MD for 6 days, in NeD for 5 days and in NMD for 3 days. Then phase terms for MD, NeD and NMD are \(\frac{6}{14}=0.43, \frac{5}{14}=0.36,\) and \(\frac{3}{14}=0.21\). All of phase terms for patients are shown in Table .
In a similar way, we can obtain all of the CTSF values for each of the patients with respect to symptoms using following classification tables for other symptoms.
Here we use the steps of the proposed method.
Step 1: \(\mathcal {DM}\) matrix is constructed by taking into consideration the above data.
Here we consider \(q=9\).
Step 2: Aggregated values are found for each of the patients by applying CTSDFWAA and CTSDFWGA operators to rows of the \(\mathcal {MD}\).
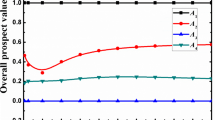
Step 3: Using Eq. 1, score values of the aggregated values are obtained as follows:
SVs according to CTSDFWAA op. | SVs according to CTSDFWGA op. | |
|---|---|---|
\(p_{1}\) | 0.505 | 0.447 |
\(p_{2}\) | 0.460 | 0.449 |
\(p_{3}\) | 0.528 | 0.489 |
\(p_{4}\) | 0.559 | 0.518 |
\(p_{5}\) | 0.511 | 0.451 |
Step 4: According to Table 4.1, \(p_4\) is suffer from COVID-19.
Sensitivity analyses and discussion
In this section, we compute the score values of the patients according to CTSDFWAA and CTSDFWGA values for “\(\eta =1,2,\ldots ,10\)”.
According to Tables 18 and 19, we see that for \(\eta =1,2,\ldots ,10\), results obtained using CTSDFWAA operator match by medical results. By results, \(P_4\) was infected by COVID-19. For \(\eta =1,2\) results from both operators are consistent. For \(\eta =3,4,\ldots ,10\) according to results obtained using CTSDFWGA operator \(P_3\) was infected by COVID-19. Also, this matches the medical results made by a medical doctor. In this study, we consider only four symptoms. However, the epidemic of the COVID-19 continue all over the worlds and medical researchers encounter some new symptoms of COVID-19. Here we give a simple example to show the trueness of the proposed method, this is a restriction of our study. We think that this study may be a reference point for researchers who want to study clustering and medical diagnosis with large data.
Conclusion
In this paper, weakness of score and accuracy function defined by Ali et al. [57] was pointed out and new score and accuracy functions were defined for CTSFNs. Set theoretical operations was introduced and some aggregation operators based on Dombi t-norms and t-conorms were defined under CTSF environment with their examples. Also, some properties of the proposed aggregation operators were investigated. Furthermore, an MCDM method was developed based on proposed aggregation operators and score function. Moreover, an application of the developed method, including determining the COVID-19, was presented by transforming the real data to CTSF data. We see that obtained results match real results. We also pointed out some restrictions and their reasons. In future, our targets are to study other aggregation operators such as Hamacher and Bonferroni, similarity measures, distance measures and decision-making methods based on TOPSIS, VIKOR, AHP, etc. By transferring the algorithm of the proposed method to the computer program, our analysis for a limited number of patients can be made under big data and by considering more parameters. We hope that this study will provide a useful perspective for researchers working on decision-making.
References
Zadeh LA (1965) Fuzzy sets. Inf Control 8(3):338–353
Atanassov KT (1986) Intuitionistic fuzzy sets. Fuzzy Sets Syst 20(1):87–96
Yager RR (2013) Pythagorean fuzzy subsets. IEEE 2013:57–61
Yager RR (2013) Pythagorean membership grades in multi-criteria decision making. IEEE Trans Fuzzy Syst 22(4):958–965
Yager RR (2017) Generalized orthopair fuzzy sets. IEEE Trans Fuzzy Syst 25:1222–1230
Cuong BC (2013) Picture fuzzy sets-First results, Part 1. In: Seminar Neuro-Fuzzy Systems with Applications; Institute of Mathematics, Vietnam Academy of Science and Technology: Hanoi, Vietnam (2013)
Cuong BC (2013) Picture fuzzy sets-First results, Part 2. In: Seminar Neuro-Fuzzy Systems with Applications; Institute of Mathematics, Vietnam Academy of Science and Technology: Hanoi, Vietnam (2013)
Garg H (2017) Some picture fuzzy aggregation operators and their applications to multicriteria decision-making. Arab J Sci Eng 42(12):5275–5290
Peng X, Dai J (2017) Algorithm for picture fuzzy multiple attribute decision-making based on new distance measure. Int J Uncertain Quantif 7(2):177–187
Wei G (2017) Picture fuzzy aggregation operators and their application to multiple attribute decision making. J Intell Fuzzy Syst 33(2):713–724
Wei G (2018) TODIM method for picture fuzzy multiple attribute decision making. Informatica 29:555–566
Cao G (2020) A multi-criteria picture fuzzy decision-making model for green supplier selection based on fractional programming. Int J Comput Commun Control 15(1):1–14
Joshi R (2020) A novel decision-making method using r-norm concept and VIKOR approach under picture fuzzy environment. Expert Syst Appl 147:113228
Tian C, Peng J, Zhang W, Zhang S, Wang J (2020) Tourism environmental impact assessment based on improved AHP and picture fuzzy PROMETHEE II methods. Technol Econ Dev Econ 26(2):355–378
Wei G (2017) Some cosine similarity measures for picture fuzzy sets and their applications to strategic decision making. Informatica 28(3):547–564
Wei G, Gao H (2018) The generalized Dice similarity measures for picture fuzzy sets and their applications. Informatica 29(1):107–124
Wei G (2018) Some similarity measures for picture fuzzy sets and their applications. Iran J Fuzzy Syst 15(1):77–89
Rafiq M, Ashraf S, Abdullah S, Mahmood T, Muhammad S (2019) The cosine similarity measures of spherical fuzzy sets and their applications in decision making. J Intell Fuzzy Syst 36(6):6059–6073
Thao NX (2020) Similarity measures of picture fuzzy sets based on entropy and their application in MCDM. Pattern Anal Appl 23(3):1203–1213
Singh P (2015) Correlation coefficients for picture fuzzy sets. J Intell Fuzzy Syst 28(2):591–604
Ganie AH, Singh S, Bhatia PK (2020) Some new correlation coefficients of picture fuzzy sets with applications. Neural Comput Appl 32:12609–12625
Son LH (2016) Generalized picture distance measure and applications to picture fuzzy clustering. Appl Soft Comput 46(C):284–295
Hao ND, Son LH, Thong PH (2016) Some improvements of fuzzy clustering algorithms using picture fuzzy sets and applications for geographic data clustering. VNU J Sci Comput Sci Commun Eng 32(3):32–38
Gündogdu FK, Kahraman C (2019) Spherical fuzzy sets and spherical fuzzy TOPSIS method. J Intell Fuzzy Syst 36(1):337–352
Gündogdu FK, Kahraman C (2019) Spherical fuzzy sets and decision making applications. In: Kahraman C, Cebi S, Cevik Onar S, Oztaysi B, Tolga A, Sari I (eds) Intelligent and fuzzy techniques in big data analytics and decision making. INFUS 2019. Advances in Intelligent Systems and Computing, p 1029. Springer, Cham
Mahmood T, Ullah K, Khan Q, Jan N (2019) An approach toward decision-making and medical diagnosis problems using the concept of spherical fuzzy sets. Neural Comput Appl 31:7041–7053
Ullah K, Mahmood T, Jan N (2018) Similarity Measures for T-Spherical Fuzzy Sets with Applications in Pattern Recognition. Symmetry 10(6):193
Garg H, Munir M, Ullah K, Mahmood T, Jan N (2018) Algorithm for T-spherical fuzzy multi-attribute decision making based on improved interactive aggregation operators. Symmetry 10(12):670
Ullah K, Mahmood T, Jan N, Ali Z (2018) A note on geometric aggregation operators in T-spherical fuzzy environment and their applications in multi-attribute decision making. J Eng Appl Sci 37(2):75–86
Wu M, Chen T, Fan J (2020) Divergence measure of T-spherical fuzzy sets and its applications in pattern recognition. IEEE Access 8:10208–10221
Ullah K, Hassan N, Mahmood T, Jan N, Hassan M (2019) Evaluation of investment policy based on multi-attribute decision-making using interval valued T-spherical fuzzy aggregation operators. Symmetry 11(3):357
Liu P, Khan Q, Mahmood T, Hassan N (2019) T-spherical fuzzy power muirhead mean operator based on novel operational laws and their application in multi-attribute group decision making. IEEE Access 7:22613–22632
Guleria A, Bajaj RK (2019) T-spherical fuzzy soft sets and its aggregation operators with application in decision making. Sci Iran. https://doi.org/10.24200/SCI.2019.53027.3018
Quek SG, Selvachandran G, Munir M, Mahmood T, Ullah K, Son LH, Thong PH, Kumar R, Priyadarshini I (2019) Multi-attribute multi-perception decision-making based on generalized t-spherical fuzzy weighted aggregation operators on neutrosophic sets. Mathematics 7:780
Munir M, Kalsoom H, Ullah K, Mahmood T, Chu YM (2020) T-spherical fuzzy Einstein hybrid aggregation operators and their applications in multi-attribute decision making problems. Symmetry 12(3):365
Ullah K, Garg H, Mahmood T, Jan N, Ali Z (2020) Correlation coefficients for T-spherical fuzzy sets and their applications in clustering and multi-attribute decision making. Soft Comput 24(3):1647–1659
Ullah K, Mahmood T, Garg H (2020) Evaluation of the performance of search and rescue robots using t-spherical fuzzy hamacher aggregation operators. Int J Fuzzy Syst 22(2):570–582
Garg H, Ullah K, Mahmood T, Hassan N, Jan N (2021) T-spherical fuzzy power aggregation operators and their applications in multi-attribute decision making. J Ambient Intell Hum Comput. https://doi.org/10.1007/s12652-020-02600-z
Ju Y, Liang Y, Lu C, Dong P, Gonzalez EDS, Wang A (2021) T-spherical fuzzy TODIM method for multi-criteria group decision-making problem with incomplete weight information. Soft Comput 25(4):2981–3001
Chen Y, Munir M, Mahmood T, Hussain A (2021) Zeng S (2021) some generalized t-spherical and group-generalized fuzzy geometric aggregation operators with application in MADM problems. J Math
Munir M, Mahmood T (2021) Hussain A (2021) Algorithm for T-spherical fuzzy MADM based on associated immediate probability interactive geometric aggregation operators. Artif Intell Rev. https://doi.org/10.1007/s10462-021-09959-1
Ramot D, Milo R, Fiedman M, Kandel A (2002) Complex fuzzy sets. IEEE Trans Fuzzy Syst 10(2):171–186
Ramot D, Friedman M, Langholz G, Kandel A (2003) Complex fuzzy logic. IEEE Trans Fuzzy Syst 11(4):450–461
Alkouri A, Salleh A (2012) Complex intuitionistic fuzzy sets. In: International conference on fundamental and applied sciences, AIP conference proceedings, vol 1482, pp 464–470
Rani D, Garg H (2017) Distance measures between the complex intuitionistic fuzzy sets and their applications to the decision-making process. Int J Uncertainty Quant 7:5
Rani D, Garg H (2018) Complex intuitionistic fuzzy power aggregation operators and their applications in multicriteria decision-making. Expert Syst 35(6):e12325
Garg H, Rani D (2019) Some generalized complex intuitionistic fuzzy aggregation operators and their application to multicriteria decision-making process. Arab J Sci Eng 44(3):2679–2698
Garg H, Rani D (2019) Novel aggregation operators and ranking method for complex intuitionistic fuzzy sets and their applications to decision-making process. Artif Intell Rev 2019:1–26
Garg H, Rani D (2019) Exponential, logarithmic and compensative generalized aggregation operators under complex intuitionistic fuzzy environment. Group Decis Negot 28(5):991–1050
Garg H, Rani D (2019) Multi-criteria decision making method based on Bonferroni mean aggregation operators of complex intuitionistic fuzzy numbers. J Ind Manag Optim. https://doi.org/10.3934/jimo.2020069
Garg H, Rani D (2020) Generalized geometric aggregation operators based on t-norm operations for complex intuitionistic fuzzy sets and their application to decision-making. Cogn Comput 12:679–698
Ullah K, Mahmood T, Ali Z, Jan N (2019) On some distance measures of complex Pythagorean fuzzy sets and their applications in pattern recognition. Complex Intell Syst 6:15–27
Liu P, Mahmood T, Ali Z (2020) Complex q-Rung orthopair fuzzy aggregation operators and their applications in multi-attribute group decision making. Information 11(5):2–28. https://doi.org/10.3390/info11010005
Akram M, Bashir A, Garg H (2020) Decision-making model under complex picture fuzzy Hamacher aggregation operators. Comput Appl Math 39(3):1–38
Liu P, Akram M, Bashir A (2021) Extensions of power aggregation operators for decision making based on complex picture fuzzy knowledge. J Intell Fuzzy Syst 40(1):1107–1128
Akram M, Garg H, Zahid K (2020) Extensions of ELECTRE-I and TOPSIS methods for group decision-making under complex Pythagorean fuzzy environment. Iran J Fuzzy Syst 17(5):147–164
Ali Z, Mahmood T, Yang MS (2020) Complex T-spherical fuzzy aggregation operators with application to multi-attribute decision making. Symmetry 12(8):1311
Akram M, Kahraman C, Zahid K (2021) Group decision-making based on complex spherical fuzzy VIKOR approach. Knowl-Based Syst 216:106793
Nasir A, Jan N, Yang MS, Khan SU (2021) Complex T-spherical fuzzy relations with their applications in economic relationships and international trades. IEEE Access. https://doi.org/10.1109/ACCESS.2021.3074557
Dombi J (1982) A general class of fuzzy operators, the De Morgan class of fuzzy operators and fuzziness measures induced by fuzzy operators. Fuzzy Sets Syst 8(2):149–163
Liu P, Liu J, Chen SM (2018) Some intuitionistic fuzzy Dombi Bonferroni mean operators and their application to multi-attribute group decision making. J Oper Res Soc 69(1):1–24
Akram M, Dudek WA, Dar JM (2019) Pythagorean Dombi fuzzy aggregation operators with application in multicriteria decision-making. Int J Intell Syst 34(11):3000–3019
Waseem N, Akram M, Alcantud JCR (2019) Multiattribute decision-making based on m-polar fuzzy Hamacher aggregation operators. Symmetry 11(12):1498
Shahzadi G, Akram M, Al-Kenani AN (2020) Decision making approach under Pythagorean fuzzy Yager weighted operators. Mathematics 8(1):70
Jana C, Pal M, Wang JQ (2019) Bipolar fuzzy Dombi aggregation opeartors and its application in multiple-attribute decision-making process. J Ambient Intell Hum Comput 10:3533–3549
Jana C, Senapati T, Pal M, Yager RR (2019) Picture fuzzy Dombi aggregation operators; application to MADM process. Appl Soft Comput 74:99–109
Ashraf S, Abdullah S, Mahmood T (2020) Spherical fuzzy Dombi aggregation operators and their application in group decision making problems. J Ambient Intell Hum Comput 11:2731–2749
Akram M, Khan A (2020) Complex Pythagorean Dombi fuzzy graphs for decision making. Granul Comput. https://doi.org/10.1007/s41066-020-00223-5
Akram M, Khan A, Karaaslan F (2021) Complex spherical Dombi fuzzy aggregation operators for decision-making. J Multiple-valued Logic Soft Comput (Accepted)
Wu Y-c, Chen C-s, Chan Y-j (2020) The outbreak of COVID-19: an overview. J Chin Med Assoc 83(3):217–220
Rafiq M, Macías-Díaz JE, Raza A, Ahmed N (2021) Design of a nonlinear model for the propagation of COVID-19 and its efficient nonstandard computational implementation. Appl Math Model 89:1835–1846
Center for systems science and engineering at Johns Hopkins university, COVID-19 dashboard, (2020) https://gisanddata.maps.arcgis.com/apps/opsdashboard/index.html#/bda7594740fd40299423467b48e9ecf6
Shatanawi W, Raza A, Arif MS, Abodayeh K, Rafiq M, Bibi M (2020) Design of nonstandard computational method for stochastic susceptible-infected-treated-recovered dynamics of coronavirus model. Adv Differ Equ 1:505. https://doi.org/10.1186/s13662-020-02960-y
Macías-Díaz JE, Raza A, Ahmed N (2021) Rafiq M (2021) Analysis of a nonstandard computer method to simulate a nonlinear stochastic epidemiological model of coronavirus-like diseases. Comput Methods Programs Biomed. https://doi.org/10.1016/j.cmpb.2021.106054
Akgül A, Ahmed N, Ali Raza, Iqbal Z, Rafiq M, Baleanu D, Aziz-ur Rehman M (2021) New applications related to Covid-19. Result Phys 20:103663
Acknowledgements
We thank Dr. Ahmed Qasim Al-Rawi who the manager of Heet hospital in Al-Anbar, Iraq, and Dr. Omer Moayed Al-Bayati who is a doctor in Al Mahmoodia hospital in Baghdad for real data and information. In this study, we got patients’ permissions and attached the signed documents that allow the use of patient data.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Karaaslan, F., Dawood, M.A.D. Complex T-spherical fuzzy Dombi aggregation operators and their applications in multiple-criteria decision-making . Complex Intell. Syst. 7, 2711–2734 (2021). https://doi.org/10.1007/s40747-021-00446-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40747-021-00446-2