Skip to main content
SpringerLink
Log in

Extension with log-canonical measures and an improvement to the plt extension of Demailly–Hacon–Păun

  • Published:
Mathematische Annalen Aims and scope Submit manuscript

Abstract

With a view to proving the conjecture of “dlt extension” related to the abundance conjecture, a sequence of potential candidates for replacing the Ohsawa measure in the Ohsawa–Takegoshi \(L^2\) extension theorem, called the “lc-measures”, which hopefully could provide the \(L^2\) estimate of a holomorphic extension of any suitable holomorphic section on a subvariety with singular locus, are introduced in the first half of the paper. Based on the version of \(L^2\) extension theorem proved by Demailly, a proof is provided to show that the lc-measure can replace the Ohsawa measure in the case where the classical Ohsawa–Takegoshi \(L^2\) extension works, with some improvements on the assumptions on the metrics involved. The second half of the paper provides a simplified proof of the result of Demailly–Hacon–Păun on the “plt extension” with the superfluous assumption “\({{\,\mathrm{supp}\,}}D \subset {{\,\mathrm{supp}\,}}\left( S+B\right) \)” in their result removed. Most arguments in the proof are readily adopted to the “dlt extension” once the \(L^2\) estimates with respect to the lc-measures of holomorphic extensions of sections on subvarieties with singular locus are ready.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Notes

  1. The notation is chosen by mimicking the reduced Planck constant \(\hbar = \frac{h}{2\pi }\).

  2.  “\({\text {lcv}}\)” is used in the lc-measure to suggest “lc-centre-volume”. It also looks like the mirror image of “\({\text {vol}}\)”.

  3. This is usually named as the “Riemann extension theorem”. The current naming “Riemann continuation theorem” is used just to distinguish this theorem from the Ohsawa–Takegoshi-type extension theorem which is studied in this paper. The use of “continuation” is found in Grauert–Remmert’s book [20, Section A.3.8] (English translation by Huckleberry), but “extension” is used in [19, Section 7.1], a later publication of the same authors.

  4. Thanks to Chen-Yu Chi for pointing out to the authors that the converse is not true. An example is provided by taking \(\psi = \log \left( \left|x^3\right|^2 +\left|y^2\right|^2\right) -1\) and \(\varphi _L=0\) on \(X = \Delta ^2 \subset \mathbb {C}^2_{(x,y)}\), the unit 2-disc centred at the origin, and considering the standard principalisation of the ideal \((x^3,y^2)\) given by blowing-up 3 times. In this case, \(\frac{5}{6}\) and \(\frac{7}{6}\) are consecutive jumping numbers of \(\left\{ \mathscr {I}_{X}\left( m\psi \right) \right\} _{m\in \mathbb {R}_{\ge 0}}\), but \(\left\{ \mathscr {I}_{\widetilde{X}}\left( m\pi ^*\psi -\phi _R\right) \right\} _{m\in \mathbb {R}_{\ge 0}}\) also has 1 as a jumping number.

  5. See footnote 3.

  6. Note that \(\varphi _L+\psi \) is, being psh by Remark 3.3.2, locally bounded from above, so the weight in the norm \(\left\Vert \cdot \right\Vert _{X^\circ ,\omega ,\varphi }\) is everywhere positive on \(X^\circ \) even though \(\varphi _L\) itself may go to \(+\infty \).

  7. Here f is abused to mean its image under the map .

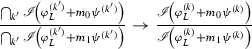  8. This is precisely the place where \(\delta > 0\) is needed, and thus the use of [15, Lemma 5.5] cannot be avoided.

References

  1. Andersson, M., Samuelsson Kalm, H., Wulcan, E., Yger, A.: Segre numbers, a generalized King formula, and local intersections. J. Reine Angew. Math. 728, 105–136 (2017). https://doi.org/10.1515/crelle-2014-0109

    Article  MathSciNet  MATH  Google Scholar 

  2. Berndtsson, B., Lempert, L.: A proof of the Ohsawa–Takegoshi theorem with sharp estimates. J. Math. Soc. Jpn. 68(4), 1461–1472 (2016). https://doi.org/10.2969/jmsj/06841461

    Article  MathSciNet  MATH  Google Scholar 

  3. Björk, J.-E., Samuelsson, H.: Regularizations of residue currents. J. Reine Angew. Math. 649, 33–54 (2010). https://doi.org/10.1515/CRELLE.2010.087

    Article  MathSciNet  MATH  Google Scholar 

  4. Błocki, Z.: Suita conjecture and the Ohsawa–Takegoshi extension theorem. Invent. Math. 193(1), 149–158 (2013). https://doi.org/10.1007/s00222-012-0423-2

    Article  MathSciNet  MATH  Google Scholar 

  5. Cao, J.Y., Demailly, J.-P., Matsumura, S.: A general extension theorem for cohomology classes on non reduced analytic subspaces. Sci. China Math. 60(6), 949–962 (2017). https://doi.org/10.1007/s11425-017-9066-0

    Article  MathSciNet  MATH  Google Scholar 

  6. Cao, J., Păun, M.: On the Ohsawa–Takegoshi extension theorem, arXiv:2002.04968 [math.CV], 36, 2020, with an appendix by Bo Berndtsson

  7. Chi, C.-Y.: On the extension of holomorphic sections from reduced unions of strata of divisors. 28 (2019). arXiv:1905.06481v3 [math.AG]

  8. Demailly, J.-P.: Estimations \(L^{2}\) pour l’opérateur \(\bar{\partial }\) d’un fibré vectoriel holomorphe semi-positif au-dessus d’une variété kählérienne complète, Ann. Sci. École Norm. Sup. (4) 15(3), 457–511 (1982) (French)

  9. Demailly, J.-P.: Regularization of closed positive currents and intersection theory. J. Algebra Geom. 1(3), 361–409 (1992)

    MathSciNet  MATH  Google Scholar 

  10. Demailly, J.-P.: Analytic methods in algebraic geometry, Surveys of Modern Mathematics, 1, International Press, Somerville. MA; Higher Education Press, Beijing (2012)

  11. Demailly, J.-P.: Complex analytic and differential geometry, OpenContent Book. http://www-fourier.ujf-grenoble.fr/~demailly/manuscripts/agbook.pdf (2012)

  12. Demailly, J.-P.: Extension of holomorphic functions defined on non reduced analytic subvarieties, The legacy of Bernhard Riemann after one hundred and fifty years. Vol. I, Adv. Lect. Math. (ALM), 35, Int. Press, Somerville, MA, 191–222 (2016). arXiv:1510.05230 [math.CV]

  13. Demailly, J.-P., Peternell, T., Schneider, M.: Compact complex manifolds with numerically effective tangent bundles. J. Algebra Geom. 3(2), 295–345 (1994)

    MathSciNet  MATH  Google Scholar 

  14. Demailly, J.-P., Peternell, T., Schneider, M.: Pseudo-effective line bundles on compact Kähler manifolds. Internat. J. Math. 12(6), 689–741 (2001). https://doi.org/10.1142/S0129167X01000861

    Article  MathSciNet  MATH  Google Scholar 

  15. Demailly, J.-P., Hacon, C.D., Păun, M.: Extension theorems, non-vanishing and the existence of good minimal models. Acta Math. 210(2), 203–259 (2013). https://doi.org/10.1007/s11511-013-0094-x

    Article  MathSciNet  MATH  Google Scholar 

  16. Fujino, O.: On abundance theorem for semi log canonical threefolds. Proc. Japan Acad. Ser. A Math. Sci. 75(6), 80–84 (1999)

    MathSciNet  MATH  Google Scholar 

  17. Fujino, O., Gongyo, Y.: Log pluricanonical representations and the abundance conjecture. Compos. Math. 150(4), 593–620 (2014). https://doi.org/10.1112/S0010437X13007495

    Article  MathSciNet  MATH  Google Scholar 

  18. Gongyo, Y., Matsumura, S.: Versions of injectivity and extension theorems, Ann. Sci. Éc. Norm. Supér. (4), 50(2), 479–502 (2017). https://doi.org/10.24033/asens.2325 (English, with English and French summaries)

  19. Grauert, H., Remmert, R.: Coherent analytic sheaves, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], 265, Springer, Berlin (1984). https://doi.org/10.1007/978-3-642-69582-7

  20. Grauert, H., Remmert, R.: Theory of Stein spaces, Classics in Mathematics, Translated from the German by Alan Huckleberry; Reprint of the 1979 translation, Springer, Berlin (2004). https://doi.org/10.1007/978-3-642-18921-0

  21. Guan, Q., Zhou, X.: A solution of an \(L^2\) extension problem with an optimal estimate and applications. Ann. Math. (2) 181(3), 1139–1208 (2015). https://doi.org/10.4007/annals.2015.181.3.6

    Article  MathSciNet  MATH  Google Scholar 

  22. Guan, Q., Zhou, X.: Effectiveness of Demailly’s strong openness conjecture and related problems. Invent. Math. 202(2), 635–676 (2015). https://doi.org/10.1007/s00222-014-0575-3

    Article  MathSciNet  MATH  Google Scholar 

  23. Guenancia, H.: Toric plurisubharmonic functions and analytic adjoint ideal sheaves. Math. Z. 271(3–4), 1011–1035 (2012). https://doi.org/10.1007/s00209-011-0900-0

    Article  MathSciNet  MATH  Google Scholar 

  24. Hacon, C.D., McKernan, J.: Boundedness of pluricanonical maps of varieties of general type. Invent. Math. 166(1), 1–25 (2006). https://doi.org/10.1007/s00222-006-0504-1

    Article  MathSciNet  MATH  Google Scholar 

  25. Hacon, C.D., McKernan, J.: Existence of minimal models for varieties of log general type. II. J. Am. Math. Soc. 23(2), 469–490 (2010). https://doi.org/10.1090/S0894-0347-09-00651-1

    Article  MathSciNet  MATH  Google Scholar 

  26. Hiep, P.H.: The weighted log canonical threshold. C. R. Math. Acad. Sci. Paris, 352(4), 283–288 (2014). https://doi.org/10.1016/j.crma.2014.02.010 (English, with English and French summaries)

  27. Hironaka, H.: Resolution of singularities of an algebraic variety over a field of characteristic zero. I, II. Ann. Math. (2) 79, 109–203 (1964)

    Article  MathSciNet  Google Scholar 

  28. Hironaka, H.: Resolution of singularities of an algebraic variety over a field of characteristic zero. I, II. Ann. Math. (2) 79, 205–326 (1964)

    Article  MathSciNet  Google Scholar 

  29. Hörmander, L.: An introduction to complex analysis in several variables, Second revised edition, North-Holland Mathematical Library, Vol. 7, North-Holland Publishing Co., Amsterdam-London; American Elsevier Publishing Co., Inc., New York, (1973)

  30. Kim, D.: Extension of pluriadjoint sections from a log-canonical center. Thesis (Ph.D.)–Princeton University, ProQuest LLC, Ann Arbor, MI (2007)

  31. Kim, D.: \(L^2\) extension of adjoint line bundle sections. Ann. Inst. Fourier (Grenoble) 60(4), 1435–1477 (2010) (English, with English and French summaries)

  32. Kim, D.: Themes on non-analytic singularities of plurisubharmonic functions, Complex analysis and geometry. Spring Proc. Math. Stat., 144, Springer, Tokyo, 197–206 (2015). https://doi.org/10.1007/978-4-431-55744-9_14

  33. Koike, T.: On the minimality of canonically attached singular Hermitian metrics on certain nef line bundles. Kyoto J. Math. 55(3), 607–616 (2015). https://doi.org/10.1215/21562261-3089091

    Article  MathSciNet  MATH  Google Scholar 

  34. Kollár, J.: Annals of Mathematics Studies. Lectures on resolution of singularities, vol. 166. Princeton University Press, Princeton, NJ (2007)

    Google Scholar 

  35. Kollár, J.: Singularities of the minimal model program, Cambridge Tracts in Mathematics, 200, With a collaboration of Sándor Kovács, Cambridge University Press, Cambridge (2013). https://doi.org/10.1017/CBO9781139547895

  36. Lempert, L.: Modules of square integrable holomorphic germs. Analysis meets geometry, Trends Math., Birkhäuser/Springer, Cham, pp. 311–333 (2017). arXiv:1404.0407 [math.CV]

  37. Matsumura, S.: An injectivity theorem with multiplier ideal sheaves of singular metrics with transcendental singularities. J. Algebra Geom. 27(2), 305–337 (2018). https://doi.org/10.1090/jag/687

    Article  MathSciNet  MATH  Google Scholar 

  38. McNeal, J.D., Varolin, D.: Analytic inversion of adjunction: \(L^2\) extension theorems with gain, Ann. Inst. Fourier (Grenoble), 57(3), 703–718, (2007) (English, with English and French summaries)

  39. Mustaţă, M.: Introduction to resolution of singularities. Analytic and algebraic geometry, IAS/Park City Math. Ser., 17, Amer. Math. Soc., Providence, RI, pp. 405–449 (2010)

  40. Ohsawa, T.: On the extension of \(L^2\) holomorphic functions. V. Effects of generalization. Nagoya Math. J. 161, 1–21 (2001). https://doi.org/10.1017/S0027763000022108

    Article  MathSciNet  MATH  Google Scholar 

  41. Ohsawa, T.: On a curvature condition that implies a cohomology injectivity theorem of Kollár-Skoda type. Publ. Res. Inst. Math. Sci. 41(3), 565–577 (2005)

    Article  MathSciNet  Google Scholar 

  42. Ohsawa, T., Takegoshi, K.: On the extension of \(L^2\) holomorphic functions. Math. Z. 195(2), 197–204 (1987). https://doi.org/10.1007/BF01166457

    Article  MathSciNet  MATH  Google Scholar 

  43. Samuelsson, H.: Analytic continuation of residue currents. Ark. Mat. 47(1), 127–141 (2009). https://doi.org/10.1007/s11512-008-0086-9

    Article  MathSciNet  MATH  Google Scholar 

  44. Siu, Y.T.: Complex-analyticity of harmonic maps, vanishing and Lefschetz theorems. J. Differ. Geom. 17(1), 55–138 (1982)

    Article  MathSciNet  Google Scholar 

  45. Siu, Y.-T.: Invariance of plurigenera. Invent. Math. 134(3), 661–673 (1998). https://doi.org/10.1007/s002220050276

    Article  MathSciNet  MATH  Google Scholar 

  46. Siu, Y.-T.: Extension of twisted pluricanonical sections with plurisubharmonic weight and invariance of semipositively twisted plurigenera for manifolds not necessarily of general type, Complex geometry, Göttingen, 2000, pp. 223–277. Springer, Berlin (2002)

    MATH  Google Scholar 

  47. Tian, G.: On Kähler-Einstein metrics on certain Kähler manifolds with \(C_1(M)>0\). Invent. Math. 89(2), 225–246 (1987). https://doi.org/10.1007/BF01389077

    Article  MathSciNet  MATH  Google Scholar 

  48. Varolin, D.: Minischool on \(L^2\) extension, lecture note distributed in the “Workshop on \(L^2\) Extensions” at the University of Tokyo from 13 to 17 February, 2016, 46 (2016). https://www.math.stonybrook.edu/~dror/L2-minischool.pdf

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Pusan National University, Busan, 46241, South Korea

    Tsz On Mario Chan & Young-Jun Choi

Authors
  1. Tsz On Mario Chan
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Young-Jun Choi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Tsz On Mario Chan.

Ethics declarations

Conflict of interest

On behalf of all authors, the corresponding author states that there is no conflict of interest. Data sharing is not applicable to this article as no datasets were generated or analysed during the current study.

Additional information

Communicated by Ngaiming Mok.

Dedicated to Prof. Fabrizio Catanese on the occasion of his 71st birthday.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Most part of this project was done when the first author was under the support of the National Center for Theoretical Sciences (NCTS) in Taiwan and while the second author had a short term visit there. The first author is thankful for the trust from Director Jungkai Chen of the NCTS and the second author would like to thank Director Chen for his hospitality. Both authors are in debt to Jean-Pierre Demailly who shared his ideas around the subject of extension and a lot more unreservedly with the authors, especially during their stay at the Institut Fourier which was supported by the ERC grant ALKAGE (No. 670846). The authors are grateful to Bo Berndtsson and Mihai Păun for their comments on the lc-measures and the potential extension theorem in the higher codimensional cases. Many thanks also to Chen-Yu Chi for drawing the first author’s attention to the study of analytic adjoint ideal sheaves as well as pointing out several mistakes in the first draft of this paper, and to Dano Kim for the advice on the development of \(L^2\) extension theorems. This work was supported by the National Research Foundation (NRF) of Korea grant funded by the Korea government (No. 2018R1C1B3005963).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chan, T.O.M., Choi, YJ. Extension with log-canonical measures and an improvement to the plt extension of Demailly–Hacon–Păun. Math. Ann. 383, 943–997 (2022). https://doi.org/10.1007/s00208-021-02152-3

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00208-021-02152-3

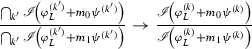Mathematics Subject Classification

Search

Navigation