Information-theoretic regularization for learning global features by sequential VAE

Abstract

Sequential variational autoencoders (VAEs) with a global latent variable z have been studied for disentangling the global features of data, which is useful for several downstream tasks. To further assist the sequential VAEs in obtaining meaningful z, existing approaches introduce a regularization term that maximizes the mutual information (MI) between the observation and z. However, by analyzing the sequential VAEs from the information-theoretic perspective, we claim that simply maximizing the MI encourages the latent variable to have redundant information, thereby preventing the disentanglement of global features. Based on this analysis, we derive a novel regularization method that makes z informative while encouraging disentanglement. Specifically, the proposed method removes redundant information by minimizing the MI between z and the local features by using adversarial training. In the experiments, we trained two sequential VAEs, state-space and autoregressive model variants, using speech and image datasets. The results indicate that the proposed method improves the performance of downstream classification and data generation tasks, thereby supporting our information-theoretic perspective for the learning of global features.

1 Introduction

Uncovering the global factors of variation from high-dimensional data is a significant and relevant problem in representation learning (Bengio et al. 2013). For example, a global representation of images that presents only the identity of the objects and is invariant to the detailed texture would assist in downstream semi-supervised classification (Ma et al. 2019). In addition, the representation is useful for the controlled generation of data. Obtaining the representation allows us to manipulate the voice of a speaker (Yingzhen and Mandt 2018), or generate images that share similar global structures (e.g., structure of objects) but varying details (Razavi et al. 2019).

Sequential variational autoencoders (VAEs) with a global latent variable z play an important role in the unsupervised learning of global features. Specifically, we consider the sequential VAEs with a structured data-generating process in which an observation x at time t (denoted as $x_t$) is generated from a global z and local latent variable $s_t$. Then, the z of these sequential VAEs can only acquire global features invariant to t. For example, Yingzhen and Mandt (2018) demonstrated that disentangled sequential autoencoders (DSAEs), which combine state-space models (SSMs) with a global latent variable z, can uncover the speaker information from speeches. Furthermore, Chen et al. (2017), Gulrajani et al. (2017) proposed VAEs with a PixelCNN decoder (denoted as PixelCNN-VAEs), which combines autoregressive models (ARMs) and z. In both methods, the hidden state of the sequential model (either SSMs or ARMs) is designed to capture local information, whereas an additional latent variable z captures the global information.

Unfortunately, the design of a structured data-generating process alone is insufficient to uncover global features in practice. A typical issue is that the latent variable z is ignored by a decoder (SSMs or ARMs) and becomes uninformative, which is referred to as posterior collapse (PC). This phenomenon occurs as follows: with expressive decoders, such as SSMs or ARMs, the additional latent variable z cannot assist in improving the evidence lower bound (ELBO), which is the objective function of VAEs; therefore, the decoders will not use z (Chen et al. 2017; Alemi et al. 2018). To alleviate this issue, existing approaches regularize the mutual information (MI) between x and z to be large by using $\beta$-VAE (Alemi et al. 2018) or adversarial training (Makhzani and Frey 2017), for example. Because a higher MI I(x; z) indicates that z consists of significant information regarding x, this regularization prevents z from becoming uninformative.

Fig. 1

Comparison of a MI-maximizing regularization and b the proposed method, using a Venn diagram of information-theoretic measures of x, z, and s

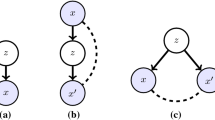
In this study, we further analyze the MI-maximizing approach and claim that merely maximizing I(x; z) is insufficient to uncover the global features. Figure 1a summarizes the issue of MI-maximization. As illustrated in the Venn diagram, the MI can be decomposed into ${I(x; z)} = {I(x; z|s)} + {I(x; z; s)}$. Although maximizing the first term I(x; z|s) is beneficial, maximizing the second term I(x; z; s) may cause a negative effect because the latter results in increasing I(z; s). Obtaining a large I(z; s) is undesirable because it indicates that the latent variables z and $s = [s_1, ..., s_T]$ consist of redundant information. For example, when I(x; z) increases to the point where z retains all the (local and global) information of x, that is, z has redundant information, the downstream classification performance is degraded. Also, when s remains to contains global information, that is, s has redundant information, the decoder can extract global information either from z and s; thereby, it becomes difficult to control the decoder output using z (e.g., control speaker information in speech). In Sect. 6.2, we provide the empirical evidence indicating that MI maximization increases I(z; s).

Based on this analysis, we propose a new information-theoretic regularization term for disentangling global features. Specifically, the regularization term not only maximizes I(x; z), but also minimizes I(z; s), as illustrated in Fig. 1b. As I(z; s) measures the dependence between z and s, our method encourages z and s to contain different information, that is, the disentanglement of global and local factors. We call the term CMI-maximizing regularization, because it is the lower bound of the conditional mutual information (CMI) I(x; z|s). In practice, because this term is difficult to compute analytically, we estimate it using adversarial training (Ganin et al. 2016). Specifically, we approximate the upper bound of I(z; s) using a density ratio trick (DRT) (Nguyen et al. 2008), where an adversarial classifier models the density ratio. Once we estimate the bound, I(z; s) can be minimized via backpropagation through the classifier.

In our experiments, we used DSAEs and PixelCNN-VAEs as illustrative examples of SSMs and ARMs. DSAEs and PixelCNN-VAEs are trained on speech and image datasets, respectively. The experiment regarding the speech domain demonstrates that CMI-maximizing regularization yields z and s that have more and less global (speaker) information than MI-maximizing regularization, respectively. In the image domain, we first evaluate the quality of z, similar to previous studies, and demonstrate that CMI-maximizing regularization yields z that have more global information (class label information). In addition, we evaluated the ability of controlled generation using a novel evaluation method inspired by Ravuri and Vinyals (2019), and confirmed that CMI-maximizing regularization consistently outperformed MI-maximizing regularization. These results support (1) our information-theoretic view of learning global features: the sequential VAEs can suffer from obtaining redundant features when merely maximizing the MI. The results also support that (2) regularizing I(x; z) and I(z; s) are complementary: learning global features can be facilitated by not only making z informative, but also by controlling which aspect of the x information (global or local) goes into z.

Our contribution can be summarized as follows: (1) Through our analysis and experiments, we reveal a problem in MI-maximizing regularization that was overlooked, although the regularization has been commonly employed in learning global representation with sequential VAEs. (2) To learn a global representation, we proposed regularizing I(x; z) and I(z; s) simultaneously. I(x; z) and I(z; s) are shown to work complementarily in our experiments using two models and two domains (speech and image datasets), indicating that it would help improve various sequential VAEs proposed previously.

2 Preliminary

2.1 Sequential VAEs for learning global representations

Here, we first present the standard VAE, followed by the overviews of two types of sequential VAEs. Namely, this study considers the SSMs and ARMs with a global latent variable z, using DSAE and PixelCNN-VAEs as illustrative examples. Both models are interpreted as having two types of latent variables, global z and local $s_t$; although it is not explicitly stated for PixelCNN-VAE. Here, $s_t$ is designed to influence particular timesteps or dimensions of x (e.g., a single frame in a speech or a small area of pixels in an image). However, z influences all the timesteps of x. Then, when successfully trained, z and $s_t$ capture only the global and local features of the data, respectively.

2.1.1 Variational autoencoder (VAE)

Let $p(x) :=\int p(z)p(x|z) \hbox {d}z$ be a latent variable model whose decoder p(x|z) is parameterized by deep neural networks (DNNs). Using an encoder distribution q(z|x), which is also parameterized by DNNs, the VAEs maximize the ELBO:

$$\begin{aligned} \mathcal {L}_{\mathrm {ELBO}} :=\mathbb {E}_{p_d(x)} \bigr [ \mathbb {E}_{q(z|x)} [\log p(x|z)] - D_{\mathrm {KL}} (q(z|x)||p(z)) \bigl ]. \end{aligned}$$

(1)

Here, $p_d(x)$ denotes the data distribution. ELBO contains the following two terms: the reconstruction error and the Kullback-Leibler (KL) divergence between encoder q(z|x) and the prior p(z).

Fig. 2

Graphical models for a SSMs with a global latent variable z, and b ARMs with z

2.1.2 State space model with global latent variable

This study considers SSMs that have a global latent variable z and a local latent variable $s_t$ to model the global and local features of the data, respectively. It generates an observation $x_t$ at time t from z and $s_t$. In addition, it uses encoder distributions to infer latent variables similar to the standard VAEs. Then, the ELBO can be expressed as follows:

$$\begin{aligned} \mathcal {L}_{\mathrm {SSM}}&:=- \mathrm {Recon} - \mathrm {KL(}z\mathrm {)} - \mathrm {KL(}s\mathrm {)}, \nonumber \\ \mathrm {where} \;\;&\mathrm {Recon} = - \mathbb {E}_{q(x, z, s)} \left[ \sum _{t=1}^T \log p(x_t|s_t, z)\right] , \nonumber \\&\mathrm {KL(}z\mathrm {)} = \mathbb {E}_{q(x, z, s)} [D_{\mathrm {KL}} (q(z|x_{\le T})||p(z))], \nonumber \\&\mathrm {KL(}s\mathrm {)} = \mathbb {E}_{q(x, z, s)} \left[ \sum _{t=1}^T D_{\mathrm {KL}}(q(s_t|x_{\le T}, z, s_{t-1})||p(s_t|s_{t-1}))\right] . \end{aligned}$$

(2)

Here, T is the sequence length, $p(s_t|s_{t-1})$ is the prior, $q(z|x_{\le T})$ and $q(s_t|x_{\le T}, z, s_{t-1})$ are the encoders, $p(x_t|s_t, z)$ is a decoder, and $q(x, z, s) :=p_d(x)q(z|x)q(s|x, z)$. Furthermore, $x_{<t}$ denotes all the elements of the sequences up to t, and x denotes $x :=x_{\le T}$. Figure 2a illustrates the data generating process. One of the SSM variants is DSAE (Yingzhen and Mandt 2018), which has demonstrated being useful in controlling the outputs (e.g., performing voice conversion) using the disentangled latent variables.

2.1.3 Autoregressive model with global latent variable

In addition to the SSMs, this study considers ARMs that have a global latent variable z. These ARMs can also be interpreted as a structured VAE in which $x_t$ is generated from the global latent variable z and local variable $s_t$ as follows. First, the autoregressive decoder is expressed as $p(x_{\le T} | z) = \Pi _{t=1}^T p(x_t|z, x_{<t})$. This implies that for every time step t, $x_t$ is sampled from $p(x_t|z, x_{<t})$ using previous observations $x_{<t}$ and the latent variable z. Second, we assume that the decoder can be decomposed as $p(x_t|z, x_{<t}) = p(x_t|z, s_t) \delta (s_t - f(x_{<t}))$, where f denotes a deterministic function parameterized by neural networks, $s_t$ denotes a random variable, and $\delta$ denotes the Dirac delta. In other words, the decoder $p(x_t|z, x_{<t})$ can be decomposed into two parts: an embedding part $s_t = f(x_{<t})$ and a decoding part $p(x_t|z, s_t)$. For the rest of the paper, we denote $\delta (s_t - f(x_{<t})) = q(s_t|x_{<t}) = p(s_t|x_{<t})$ to simplify the notation. With this notation, $x_t$ can be regarded as being generated from z and $s_t$, which is sampled from $p(s_t | x_{<t})$ (see Fig. 2b). Furthermore, the ELBO is given as follows:

$$\begin{aligned} \mathcal {L}_{\mathrm {ARM}} =&- \mathrm {Recon} - \mathrm {KL(}z\mathrm {)}. \end{aligned}$$

(3)

One of the ARM variants is PixelCNN-VAEs, whose z is intended to maintain only the global information by discarding local information, such as the textures and sharp edges of images (Gulrajani et al. 2017). Details regarding the data-generating process for PixelCNN-VAEs are provided in Appendix 1.

2.2 Mutual information-maximizing regularization for sequential VAEs

Sequential VAEs with a global latent variable z can, in principle, uncover the global representation of data by exploiting its structured data-generating process. However, despite the intentional data-generating process of sequential VAEs, the global latent variable z often becomes uninformative owing to the PC. To alleviate this issue and encourage z to obtain x information, prior studies regularized the MI I(x; z), which is defined by the encoder distribution as follows:

$$\begin{aligned} I(x; z) = \mathbb {E}_{p_d(x)q(z|x)} \left[ \log \frac{p_d(x)q(z|x)}{p_d(x)q(z)} \right] . \end{aligned}$$

(4)

Note that I(x; z) here is not defined in terms of the true posterior, but is defined with the product of data distribution $p_d(x)$ and the variational posterior q(z|x).

In practice, prior studies regularized I(x; z) by optimizing it along with ELBO ${\mathcal{L}}_{{{\text{ELBO}}}}$ as follows:

$$\max {\mathcal{L}}_{{{\text{ELBO}}}} + \alpha I(x;z),$$

(5)

where $\alpha$ is a weighting parameter. Because I(x; z) is difficult to analytically compute, prior studies have proposed various approaches to approximate it [e.g., using variational bounds (Alemi et al. 2018) or adversarial training (Zhao et al. 2019)], which will be presented in Sect. 5.

3 Problem in MI-maximizing regularization

In this section, we claim that the MI-maximizing regularization for sequential VAEs remains insufficient to uncover the global features. More precisely, we claim that compared to optimizing only the ELBO ${\mathcal{L}}_{{{\text{ELBO}}}}$, optimizing Eq.5provides the same or larger I(z; s) value. Here, I(z; s) is defined as follows:

$$\begin{aligned} I(z; s) =&\mathbb {E}_{q(z, s)} [\log \frac{q(z)q(s|z)}{q(z)q(s)}], \\ \mathrm {where}\;\;&q(z; s) :=\int p_d(x) q(z|x) q(s|x, z) \hbox {d}x. \end{aligned}$$

The increase in I(z; s) is undesirable because this indicates that the latent variables z and s have redundant information, which contradicts the original intention of disentangling the global features of data.

Note that, although the graphical model of the SSMs (Fig. 2a) is designed such that z and s are independent, I(z; s) is not necessarily zero because $p(z, s) = p(z)p(s)$ (independence of prior distribution) does not definitely indicate that $q(z, s) = q(z)q(s)$ (independence of encoder distribution). For example, although $p(z, s) = q(z, s)$ enables $q(z, s)=q(z)q(s)$, it needs certain conditions. Namely, since q(z, s) is defined as $q(z, s) = \int q(z, s|x) p_d(x) dx$ and p(z, s) is defined as $p(z, s) = \int p(z, s|x) p(x) dx$, the sufficient condition for $p(z, s) = q(z, s)$ is $q(z, s|x) = p(z, s|x)$ and $p_d(x) = p(x)$. Here, (i) $p_d(x) = p(x)$ holds only if the latent variable model p(x) matches data distribution $p_d(x)$, which is often impractical when the data is high-dimensional. Also, (ii) $q(z, s|x) = p(z, s|x)$ means that the approximation error of the posterior is null, which is difficult although some recent studies have tackled to reduce the error in standard VAE settings (Kingma et al. 2016; Park et al. 2019).

Prior to discussing the validity of the claim, an intuitive explanation of why the phenomenon occurs is presented. This would also facilitate a better understanding of why the increase in I(z; s) is undesirable. Namely, regularizing I(x; z) to be large may cause either of the following two phenomena:

• (Case 1) If global information is encoded into z, I(x; z) becomes larger. However, it also increases I(z; s) if s has all (local and global) the information regarding x.

• (Case 2) If all (local and global) information is encoded into z, I(x; z) remains to become larger. However, it also increases I(z; s) despite s having only local information.

Case 1 and Case 2 indicate that a larger I(x; z) value would result in redundant s and z, respectively. One of the possible factors that determines which case occurs is the neural network architecture, which controls the retrieval of information from z. For example, z of PixelCNN-VAEs is input to the decoder after being linearly transformed into time-dependent feature maps (see Appendix 1). In contrast, z of DSAEs is input into the decoder without this linear transformation. Then, the z of PixelCNN-VAEs can easily have local (time-dependent) information, and Case 2 could occur. However, the z of the DSAEs is constrained to have no local information; therefore, Case 1 is likely to occur.

Next, we identify the concrete problems which large I(z; s) induces in the DSAEs and PixelCNN-VAEs. For DSAEs, z and s are expected to express only the speaker and linguistic information in speech sequences, respectively. However, if s still contains speaker information due to redundancy (i.e., Case 1 occurs), the decoder can extract speaker information from either s or z, and there is no guarantee that z will be used. For PixelCNN-VAE, previous studies (Alemi et al. 2018; Razavi et al. 2019) have shown that by stochastically sampling x from PixelCNN-VAE with a given z, one can obtain images with different local patterns but similar global characteristics (e.g., color background, scale, and structure of objects). However, when I(x; z) becomes significantly large, making z have all (local and global) the information (i.e., Case 2 occurs), the diversity of the generated images decreases because the decoder resembles one-to-one mapping from z to x.

Finally, we discuss the validity of our claim. From a theoretical perspective, the following decomposition of I(x; z) illustrates the issue:

$$\begin{aligned} I(x; z) =&I(z; s) - I(z; s|x) + I(x; z|s). \nonumber \\ proof: \mathrm {r.h.s.} =&\mathbb {E}_{q(x, z, s)} \left[ \log \frac{q(z, s)}{q(z)q(s)} (\frac{q(x, z, s)q(x)}{q(x, z)q(x, s)})^{-1} \frac{q(x, z, s)q(s)}{q(x, s)q(z, s)} \right] \nonumber \\ =&\mathbb {E}_{q(x, z, s)} \left[ \log \frac{q(x, z)}{q(z)q(x)}\right] \nonumber \\ =&I(x; z) , \end{aligned}$$

(6)

where we denote $p_d (x) q(z, s|x) = q(x, z, s)$ for better visibility. Then, simply maximizing I(x; z) indicates increasing I(z; s) on the right-hand side of Eq. 6, assuming the remaining term ($- I(z; s|x) + I(x; z|s)$) does not increase. Although our claim relies on this assumption, we leave its generality excluded from the scope of this study. Instead, in Sect. 6.2, we experimentally confirm that the regularization of I(x; z) and the increase in I(z; s) are linked. In addition, in Sects. 6.3 and 6.4, we present empirical evidence indicating that Case 1 and Case 2 occur in DSAEs and PixelCNN-VAEs, respectively.

4 Proposed method

4.1 Conditional mutual information-maximizing regularization

Considering the limitations of MI regularization, we need a method that can encourage both (i) an increase in I(x; z) to prevent z from becoming uninformative, and (ii) the decrease of I(z; s) to prevent z and s from having information that is irrelevant to the global and local structures, respectively. Therefore, we propose maximizing the following objective:

$$\max {\mathcal{L}}_{{{\text{ELBO}}}} + \alpha I(x;z) - \gamma I(z;s),$$

(7)

where $\alpha I(x; z) - \gamma I(z; s)$ is a regularization term with weights $\alpha \ge 0$ and $\gamma \ge 0$. As I(z; s) measures the mutual dependence between s and z, minimizing I(z; s) encourages z and s to avoid redundant information. Then, the induced global variable z would have more x information, whereas z and s maintain only the global and local information, respectively.

We refer to the proposed method as the CMI-maximizing regularization for convenience because it closely relates to CMI I(x; z|s). Specifically, when assuming $\gamma \ge \alpha$,

$$\begin{aligned} I(x; z|s)&= I(x; z) - I(z; s) + I(z; s|x) \nonumber \\&\ge I(x; z) - I(z; s) \nonumber \\&\ge \frac{1}{\alpha } \bigl (\alpha I(x; z) - \gamma I(z; s)\bigr ). \end{aligned}$$

(8)

It indicates that the proposed regularization term $\alpha I(x; z) - \gamma I(z; s)$ is a constant multiple of a lower bound of I(x; z|s); therefore, Eq. 7 is the weighted sum of ELBO and the lower bound. Here, the approximation error becomes smallest when $\alpha =\gamma$ (further discussed in Appendix 2). In addition, the relation between I(x; z), I(z; s), and I(x; z|s) is intuitively provided in the Venn diagram in Fig. 1: while I(x; z|s) comprises of I(x; z), it is irrelevant to I(z; s).

4.2 Estimation method of the regularization term

In this section, we present one of the tractable instances for estimating $\alpha I(x; z) - \gamma I(z; s)$. A simple way to estimate $\alpha I(x; z) - \gamma I(z; s)$ may be to estimate I(x; z) and I(z; s) separately, and tune the strength of them independently. However, because both I(x; z) and I(z; s) are difficult to compute analytically, this approach must approximate both, which may complicate optimization. Therefore, we derive a lower bound of $\alpha I(x; z) - \gamma I(z; s)$ to reduce the number of terms to be approximated to only one. By setting the weights as $\gamma \ge \alpha$, we can derive the bound as follows:

$$\begin{aligned} \alpha I(x; z) - \gamma I(z; s) =&\alpha \mathbb {E}_{p_d(x)} \bigl [D_{\mathrm {KL}} (q(z|x)||p(z)) \bigr ] - \alpha D_{\mathrm {KL}} (q(z)||p(z)) \nonumber \\&- \gamma D_{\mathrm {KL}} (q(z, s) || q(z)q(s)) \nonumber \\ =&\alpha \mathbb {E}_{p_d(x)} \bigl [D_{\mathrm {KL}} (q(z|x)||p(z)) \bigr ] - \alpha D_{\mathrm {KL}} (q(z)||p(z)) \nonumber \\&- \gamma D_{\mathrm {KL}} (q(z, s) || p(z)q(s)) + \gamma D_{\mathrm {KL}} (q(z) || p(z)) \nonumber \\ =&\alpha \mathbb {E}_{p_d(x)} \bigl [D_{\mathrm {KL}} (q(z|x)||p(z)) \bigr ] + (\gamma - \alpha ) D_{\mathrm {KL}} (q(z)||p(z)) \nonumber \\&- \gamma D_{\mathrm {KL}} (q(z, s) || p(z)q(s)) \nonumber \\ \ge&\alpha \mathbb {E}_{p_d(x)} \bigl [D_{\mathrm {KL}} (q(z|x)||p(z)) \bigr ] - \gamma D_{\mathrm {KL}} (q(z, s) || p(z)q(s)), \end{aligned}$$

(9)

where the first term is the upper bound of I(x; z), and the second term is the lower bound of $-I(z; s)$. Here, $\gamma \ge \alpha$ indicates that the second term is weighted more. In addition, the lower bound of Eq. 9 becomes the tightest when $\gamma = \alpha$. Note that, $\gamma = \alpha$ also minimizes the approximation error in Eq. 8, which makes the connection between the CMI I(x; z|s) and Eq. 9 clearer.

While the first term is the same as KL(z) in Eq. 1 and is simple to calculate, the second KL term is difficult to calculate analytically. However, we provide options to approximate it. For example, it can be replaced with other distances, such as the maximum mean discrepancy (MMD) (Zhao et al. 2019), minimized via the Stein variational gradient (Zhao et al. 2019), or approximated with DRT (Nguyen et al. 2008; Sugiyama et al. 2012). Among these options, we chose to utilize DRT, as performed in generative adversarial networks (GANs) (Mohamed and Lakshminarayanan 2017) and infoNCE (van den Oord et al. 2019). A possible advantage of using DRT is the scalability to the dimension size. Scalability could be significant because the dimension size of $s = [s_1, ..., s_T]$ depends on the sequence length T and the dimension size of $s_t$. However, a comparison of these methods is excluded from the scope of this study because our main proposal aims to regularize I(x; z) and I(z; s) simultaneously.

Here, we present how the second term can be approximated with the DRT. By introducing the labels $y=1$ for samples from q(z, s) and $y=0$ for those from p(z)q(s), we re-express these distributions in a conditional form, that is, $q(z, s) =:p(z, s|y=1)$ and $p(z)q(s) =:p(z, s|y=0)$. The density ratio between q(z, s) and p(z)q(s) can be computed using these conditional distributions as follows:

$$\begin{aligned} \frac{q(z, s)}{p(z)q(s)}&= \frac{p(z, s|y=1)}{p(z, s|y=0)} \nonumber \\&= \frac{p(y=1|z, s)}{p(y=0|z, s)} \nonumber \\&= \frac{p(y=1|z, s)}{1 - p(y=1|z, s)}, \end{aligned}$$

(10)

where we used Bayes’ rule and assumed that the marginal class probabilities were equal, that is, $p(y = 0) = p(y = 1)$. The condition $p(y=0)=p(y=1)$ can be easily satisfied by sampling the same number of z and s from q(z, s) and p(z)q(s) because p(y) represents the frequency of sampling from q(z, s) and p(z)q(s). Here, $p(y=1|z, s)$ can be approximated with a discriminator D(z, s), which outputs $D=1$ when $z, s \sim _{i.i.d.} q(z, s)$, and $D=0$ when $z, s \sim _{i.i.d.} q(s) p(z)$. Then, Eq. 9 can be approximated as follows:

$$\begin{aligned} \alpha I(x; z) - \gamma I(z; s)&\approx \alpha \mathbb {E}_{p_d(x)} \left[ D_{\mathrm {KL}} (q(z|x)||p(z))\right] - \gamma \mathbb {E}_{q(z, s)} \left[ \log \frac{D(z, s)}{1-D(z, s)} \right] \nonumber \\&=:I_{\mathrm {CMI-DRT}}. \end{aligned}$$

(11)

We parameterize D(z, s) with DNNs and train it alternately with the VAE objectives. Specifically, we train D to maximize the following objective using Monte Carlo estimates:

$$\begin{aligned} \mathbb {E}_{q(z, s)} [ \log D(z, s) ] + \mathbb {E}_{p(z)q(s)} \left[ \log \bigr (1 - D(z, s) \bigl ) \right] . \end{aligned}$$

(12)

In Eqs. 10 and 11, we need to sample z and s from $q(z, s) = \int p_d (x) q(z, s|x) dx$. Therefore, we first sample x from $p_{d}(x)$, and then sample z and s from q(z, s|x) using the sampled data x.

4.3 Objective function for DSAEs and PixelCNN-VAEs

In this section, we introduce the concrete objectives of the DSAEs and PixelCNN-VAEs with a CMI regularization term. Adding $I_{\mathrm {CMI-DRT}}$ as a regularization term to Eqs. 2 and 3, we obtain the objective functions of our proposed method as follows:

$$\begin{aligned} \max \mathcal {J}_{\mathrm {SSM}} :=&\mathcal {L}_{\mathrm {SSM}} + I_{\mathrm {CMI-DRT}} \nonumber \\ =&- \mathrm {Recon} - \mathrm {KL(}s\mathrm {)} - (1-\alpha ) \mathrm {KL(}z\mathrm {)} - \gamma I^\prime (z; s), \end{aligned}$$

(13)

$$\begin{aligned} \max \mathcal {J}_{\mathrm {ARM}} :=&\mathcal {L}_{\mathrm {ARM}} + I_{\mathrm {CMI-DRT}} \nonumber \\ =&- \mathrm {Recon} - (1-\alpha ) \mathrm {KL(}z\mathrm {)} - \gamma I^\prime (z; s), \nonumber \\ \mathrm {where}&\;\; I^\prime (z; s) = \mathbb {E}_{q(z, s)} \left[ \log \frac{D(z, s)}{1-D(z, s)}\right] . \end{aligned}$$

(14)

Note that, Eqs. 13 and 14 are alternately optimized with Eq. 12 because the approximation of Eq. 11 requires the assumption that $\frac{D}{1-D}$ approximates the true density ratio, as well as GANs.

Comparison with $\beta$-VAE Our objective functions (Eqs. 13, 14) are similar to those of $\beta$-VAE. $\beta$-VAE is a representative example of MI-maximizing regularization, which was shown to be a simple and effective method for PC (Alemi et al. 2018) and also used as a baseline method in He et al. (2019). The concrete $\beta$-VAE objectives for DSAE and PixelCNN-VAE are:

$$\begin{aligned}&\max \mathcal {V}_{\mathrm {SSM}} :=-\mathrm {Recon} - \beta \mathrm {KL(}z\mathrm {)} - \mathrm {KL(}s\mathrm {)}, \end{aligned}$$

(15)

$$\begin{aligned}&\max \mathcal {V}_{\mathrm {ARM}} :=-\mathrm {Recon} - \beta \mathrm {KL(}z\mathrm {)}. \end{aligned}$$

(16)

Because $\mathrm {KL(}z\mathrm {)}$ is an upper bound of I(x; z), we can control I(x; z) to some extent by varying the weighting parameter $\beta$ (Alemi et al. 2018; He et al. 2019). Note that, Alemi et al. (2018), He et al. (2019) used $\beta < 1$ to regularize I(x; z) to be large, although $\beta$-VAE was originally invented to encourage the independence of each dimension of z with $\beta > 1$ by Higgins et al. (2017).

When setting $1-\alpha = \beta$, the first and second terms of the objective functions (Eqs. 13 and 14) equal to those of $\beta$-VAE (Eqs. 15, 16). This indicates that our objective function requires only one modification (minimizing $I^\prime (z; s)$) from $\beta$-VAE, simplifying optimization. Here, the additional term for minimizing $I^\prime (z, s)$ is employed to decrease the redundancy of z and s.

5 Related works

Sequential VAEs with a global latent variable have been studied for disentangling global and local features of data in various domains: topics and details of texts (Bowman et al. 2016), object identities and the detailed textures of images (Chen et al. 2017), content and motion of movies (Hsieh et al. 2018), and speaker and linguistic information of speeches (Hsu et al. 2017; Yingzhen and Mandt 2018). Although this study uses DSAE and PixelCNN-VAE as examples in the experiment, our method could also be combined with them. In addition, these models are closely related to the literature regarding disentangled representation. Locatello et al. (2019) claimed that pure unsupervised disentangling (Chen et al. 2016; Higgins et al. 2017; Kim and Mnih 2018) is fundamentally impossible, whereas using rich supervision (Kulkarni et al. 2015) can be costly. Thus, the use of inductive bias or weak supervision (Shu et al. 2020) has been encouraged. The assumption that data are generated from global and local factors is a representative example of a inductive bias. The sequential VAEs leverage the bias by utilizing the carefully designed data-generating process.

Unfortunately, the design of structured data-generating processes alone is often insufficient to learn the global features. To address this issue, Bowman et al. (2016); Chen et al. (2017) initially proposed to weaken the decoder because PC often occurs when using highly expressive decoders. Subsequently, various methods have been proposed to control the MI I(x; z) with a regularization term, which does not require the problem-specific architectural constraints of Bowman et al. (2016); Chen et al. (2017). Concrete examples of MI-maximizing regularization methods are as follows:

• InfoVAE: Zhao et al. (2019) regularizes I(x; z) to be large by using the MMD, Stein variational gradient, or adversarial training.

• $\beta$-VAE: Alemi et al. (2018) demonstrate that because the ELBO (Eq. 1) contains a positive lower bound and a negative upper bound of I(x; z), the MI can be controlled by balancing the two terms using a weighting parameter $\beta$. They then observed that the objective with $\beta <1$ alleviates the PC. $\beta$-VAE is simpler than InfoVAE because it does not require an approximation of I(x; z).

• Auxiliary loss: Lucas and Verbeek (2018) uses the auxiliary tasks of predicting x from z, which approximates the minimization of conditional entropy H(x|z). The minimization of H(x|z) is equivalent to maximizing I(x; z) because the data entropy H(x) is constant.

• Discriminative objective: Hsu et al. (2017) predicts a sequence index from z, which also approximates H(x|z) minimization in the finite sample case.

Additionally, studies (He et al. 2019; Lucas et al. 2019) have proposed methods for alleviating PC, which are complementary to MI maximization. Our study differs from these studies for alleviating PC in that it aims to obtain information and disentangled representations with sequential VAEs, and are complementary to them.

Similar to our method, Zhu et al. (2020) proposed to regularize I(z; s) to be small for DSAEs. Furthermore, apart from the studies regarding sequential VAEs, various studies have attempted to separate relevant from irrelevant information via information-theoretic regularization, which is similar to our regularization term of minimizing I(z; s). Specifically, the studies regarding domain-invariant representation have been proposed to learn the invariant representation using adversarial training (Ganin et al. 2016; Xie et al. 2017; Liu et al. 2018), variational information bottleneck frameworks (Moyer et al. 2018), or Hilbert-Schmidt independence criterion (Jaiswal et al. 2019). Our regularization term differs from the methods of these studies in considering PC, that is, maximizing I(x; z), at the same time.

Also, the separation of global and local information may be achieved by using some network architectures other than sequential VAE. For example, VQ-VAE2 (Razavi et al. 2019) uses a multi-scale hierarchical encoder to separate global and local information. However, since our purpose is to improve the existing approach of learning global representation by sequential VAEs, we leave the comparison between sequential VAEs and such methods out of the scope of this study. Moreover, note that VQ-VAE2 and the sequential VAEs have different goals and applications. For example, while sequential VAEs can handle variable-length data, VQ-VAE2 cannot handle them. Also, as the latent representation of VQ-VAE2 has a spatial structure, it might not be suitable for downstream classification and verification tasks that we employed in Sect. 6.

From a technical perspective, our study also relates to a feature selection technique based on CMI (Fleuret 2004). CMI is useful for selecting features that are both individually informative and two-by-two weakly dependent. Then, the CMI-based technique is different from the MI-based technique in considering the independence of the features. Moreover, it is different from the previous studies for disentangled representation learning, for example, Higgins et al. (2017), Kim and Mnih (2018), Liu et al. (2018) controlled only the independence of latent factors. Also, Mukherjee et al. (2019) first proposed the estimation of CMI using DNNs; however, our method is different in that it utilizes the encoder distribution of VAEs similar to Zhao et al. (2019), which might improve the estimation (Poole et al. 2019).

6 Experiments

6.1 Settings

In the experiments, we provide empirical evidence that MI-maximizing regularization causes the problem discussed in Sect. 3. Also, we confirmed that CMI-maximizing regularization can alleviate the problem. The base model architectures used in our experiment were chosen as follows. Firstly, although this paper targets two sequential models, the SSM and the ARM, there are several possible options for the network architecture that parameterizes these data generating processes. Then, we chose to use DSAE (Yingzhen and Mandt 2018) as an instance of the SSM because, to our knowledge, it is the first and representative VAE-based SSM with a global latent variable. Also, we adopted PixelCNN-VAEs (He et al. 2019) as an instance of the ARM, which is a representative VAE-based ARM with a global variable in the literature on image modeling. However, note that the proposed regularization method is applicable regardless of the architecture choice as long as the model has the data generating process shown in Fig. 2.

In addition, we used the speech corpus TIMIT (Garofolo et al. 1992) for the DSAE, and evaluated the representation quality using a speaker verification task, as performed in previous studies (Hsu et al. 2017; Yingzhen and Mandt 2018). For PixelCNN-VAE, we trained the VAE with a 13-layer PixelCNN decoder on the statically binarized MNIST and Fashion-MNIST (Xiao et al. 2017) datasets. Using the trained models, we performed linear classification from z to class labels to evaluate the representation quality, as performed in Razavi et al. (2019), and then evaluated the ability of controlled generation. z, which has a dimensional size of 32, was concatenated with the feature map output from the fifth layer of the PixelCNN (which corresponds to s, see Appendix 1), and was passed to the sixth layer. Further experimental details are provided in Appendix 3.

As the proposed method, we employed the objective functions $\mathcal {J}_{\mathrm {SSM}}$ and $\mathcal {J}_{\mathrm {ARM}}$ in Eqs. 13 and 14 (denoted as CMI-VAE). We implemented a discriminator D as a CNN that receives s and z as inputs (Appendix 5) and trained it alternately with the VAEs. As baseline methods, we employed two MI-maximizing regularization methods: $\beta$-VAE and AdvMI-VAE. $\beta$-VAE is a representative example of MI-maximizing regularization. The objectives of the $\beta$-VAE are provided in Eqs. 15 and 16, and are equal to CMI-VAE, except for not having the $I^\prime (z; s)$ term. Moreover, we employed the regularization method denoted as AdvMI-VAE, which was proposed in Makhzani and Frey (2017), Zhao et al. (2019). AdvMI-VAE estimates I(x; z) in Eq. 5 with adversarial training. Details regarding AdvMI-VAE can be found in Appendix 4.

The hyperparameters $\gamma$ and $\alpha$ are set as follows. A naive way to choose these parameters would be to use grid search. However, grid search for multiple hyperparameters requires exponential computational costs. Therefore, we set $\gamma =\alpha$ in our experiments. Although $\gamma =\alpha$ is a heuristic choice and tuning the strength of them independently is left as future work, it has the advantage that it does not break the balance of I(x; z) and I(z; s) significantly, and also minimizes the approximation error of Eqs. 8 and 9. Then, we trained the methods with various values of $\gamma$: $\gamma \in \{0, 0.4, 0.8, 0.9, 0.99\}$ for DSAEs, $\gamma \in \{0, 0.1, 0.2, ..., 0.7\}$ for PixelCNN-VAEs on MNIST, $\gamma \in \{0, 0.1, 0.2, ..., 0.9\}$ for PixelCNN-VAEs on Fashion-MNIST. The reason for not setting $\gamma =\alpha > 1$ is to avoid a significant change from the original VAE objective function due to flipping the sign of the KL term in Eqs. (13) and (14). Also, we will report the performance for various values of $\gamma$ rather than reporting only the performance for “the best” $\gamma$ after hyperparameter search in order to confirm that the proposed method robustly outperforms the baseline performance for various hyperparameters. The baseline models ($\beta$-VAE and AdvMI-VAE) were also trained with various values of hyperparameter $\gamma$. Here, instead of using $\beta$ for $\beta$-VAE, we use the notation $\gamma = 1 - \beta$ to match the notation of the proposed method.

6.2 Comparing estimated I(z; s) values

In this section, we evaluate the I(z; s) values of the DSAE (trained on TIMIT) and PixelCNN-VAEs (trained on Fashion-MNIST). Because I(z; s) is intractable, we reported the estimated value (denoted as $\hat{I}(z; s)$) with DRT in the same manner as indicated in Sect. 4.2. Here, all methods are trained with various values of the weighting parameter $\gamma$. For $\beta$-VAE and AdvMI-VAE, a larger $\gamma$ indicates that I(x; z) is regularized to be larger.

From the results in Table 1, we can make the following observations: (1) the table shows that I(z; s) can be larger than 0. It is worth noting that, for DSAEs, the MI defined in terms of true posterior p(z, s|x) must be null because z and s are defined as independent random variables. Therefore, the result indicates that even though the MI defined in terms of the true posterior is null, the MI I(z; s), which is defined by approximated posterior q(z, s|x), is not necessarily null, which supports the need for regularizing I(z; s). (2) Also, when using the MI-maximizing regularization ($\beta$-VAE and AdvMI-VAE), a larger $\gamma$ tends to result in larger $\hat{I}(z; s)$ values. This indicates that when we simply regularize I(x; z) to be larger, z and s have more redundant information. In contrast, when we do not regularize I(x; z) (i.e., $\gamma =0$), $\hat{I}(z; s)$ becomes small; however, it is also undesirable because, in this case, z is uninformative regarding x owing to the PC. Contrastingly, CMI-VAE tends to suppress the increase in $\hat{I}(z; s)$ compared to $\beta$-VAE and AdvMI-VAE, especially when the regularization becomes stronger (e.g., $\gamma \ge 0.9$ for DSAEs and $\gamma \ge 0.3$ for PixelCNN-VAEs). This may be because CMI-VAE regularizes I(z; s) to be small at the same time when $\gamma$ becomes larger. Also, note that the difference between AdvMI-VAE and CMI-VAE’s performance seems negligible for small $\gamma$ values (e.g., $\gamma =0.4$ for DSAEs) probably because the regularization for I(z; s) was not enough to offset the increase in I(z; s) caused by the side effect of increasing I(x; z). This problem could be mitigated by carefully choosing $\alpha$ values, and is left as future work.

Table 1 Estimated values of I(z; s) with the DRT

6.3 Speaker verification experiment with disentangled sequential autoencoders

To quantitatively assess the global representation of DSAE, we evaluate whether z can uncover speaker individualities, which are the global features of speech. Specifically, we extract z and $s_{\le T}$ from the test utterances using the mean of the encoders of the learned DSAE. Subsequently, we performed speaker verification by measuring the cosine similarity of the variables and evaluated the equal error rate (EER). Here, EER is measured for both z and s (denoted as EER(z) and EER(s), respectively), and $s_{\le T}$ is averaged over each utterance prior to its measurement. A lower EER(z) is preferable because it indicates that the model has an improved global representation, containing sufficient information of the speakers in a linearly separable form. Furthermore, a higher EER(s) is preferable because it indicates that s does not have redundant speaker information. In addition, we report KL(z) (see Eq. 2), which approximates the amount of information in z.

Table 2 presents the values of KL(z) and EER for the vanilla DSAE, $\beta$-VAE, and CMI-VAE. For a comparison with AdvMI-VAE, please refer to Appendix 6.1. Note that, our results for vanilla DSAE differ from those reported in Yingzhen and Mandt (2018) (DSAE${}^*$ in the table), which may be due to differences in the unreported training settings. Although it is difficult to tell the difference because an official implementation cannot be obtained, a possible factor is the difference in calculation way of the three terms in Eq. 2. For example, if one uses the average over time and features to calculate $\mathrm {Recon}$ and $\mathrm {KL(}s\mathrm {)}$, instead of using the sum as we did, the balance of the three terms would change. However, the balance is a significant factor on EER as the results for $\beta$-VAE show in the next paragraph. Also, differences in optimizers, early stopping criteria, and data preprocessing such as silence removal could have affected the performance.

Table 2 KL term and EER values of DSAE trained using TIMIT

The table presents that (1) $\beta$-VAE with a smaller $\gamma$ (such as 0) provides a lower EER(s), which indicates that s has global information instead of z owing to the PC. Furthermore, (2) $\beta$-VAE with a larger $\gamma$ (such as 0.99) provides an EER(s) value of approximately 38%, which remains substantially different from random chance. Therefore, although MI-maximizing regularization was employed, s remained to have global information, indicating that Case 1 in Sect. 3 may occur. In addition, (3) given a fixed $\gamma$, CMI-VAE consistently achieved a lower EER(z) and a higher EER(s), while having the same level of KL(z) compared to $\beta$-VAE. This indicates that regularizing I(z; s) is complementary to MI maximization ($\beta$-VAE), yielding a better z and s that have sufficient global or local information, but are well compressed.

One may wonder why $\gamma \ge 0.8$ yields a higher EER(z) than $\gamma =0.4$. This may be due to the fact that the independence of each dimension of z is worsened by increasing $\gamma$, as indicated in Higgins et al. (2017), and the induced non-linear relation cannot be measured by the cosine similarity. In fact, $\gamma \ge 0.8$ presented a better performance in our supplementary experiment using the voice conversion task in Appendix 7, indicating that z with $\gamma \ge 0.8$ has more global information, although the EER(z) is worse. In addition, note that the EER(z) value lower than our results here is reported in Hsu et al. (2017). However, we believe that our claim, “regularizing I(x; z) and I(z; s) is complementary” is defended, despite not achieving state-of-the-art results.

6.4 Experiments with PixelCNN-VAEs

6.4.1 Unsupervised learning for image classification

For a quantitative assessment of the representation z of PixelCNN-VAEs, we performed a logistic regression from z to the class labels y on MNIST and Fashion-MNIST. Specifically, we first extracted z from 1000 training samples using the mean of q(z|x), where each of the 10 classes had 100 samples, and trained the classifier with a total of 1000 samples. We then evaluated the accuracy of the logistic regression (AoLR) on the test data. A high AoLR indicates that z succeeds in capturing the label information in a linearly separable form. Note that we use a small sample size (1000 samples) in order to mimic the settings of semi-supervised learning. In other words, we assumed that a large amount of unlabeled data and a small amount of labeled data are available, and evaluated whether the methods can learn good representation with the unlabeled data to facilicate downstream classification task.

Figure 3a, b present AoLR for $\beta$-VAE, AdvMI-VAE, and CMI-VAE, along with the ELBO (3a) or KL(z) (3b); the upper left curve indicates that the method balances better compression (low KL(z)) and high downstream task performance. As shown in the figures, given a fixed $\gamma$, the AoLRs for CMI-VAE are consistently better than those for $\beta$-VAE and AdvMI-VAE, although all methods have the same level of KL(z). This indicates that CMI-VAE can extract more global information when compressing data to the same size as $\beta$-VAE. Note that, a small $\gamma$ (such as $\gamma =0$) and a significantly large $\gamma$ degrade the AoLRs, which may be attributed to the same reason indicated in Sect. 6.3. Furthermore, the AoLRs of AdvMI-VAE are lower than those of $\beta$-VAE, which may be owing to the adversarial training in AdvMI-VAE causing optimization difficulties, as stated in Alemi et al. (2018).

Fig. 3

Comparison of CMI-VAE with $\beta$-VAE and AdvMI-VAE. In each figure, the inverted triangle markers (i.e., the markers for $\beta$-VAE) are annotated with the value of $\gamma$ like 0.0, 0.1, etc. In the figures, an upper left curve is desirable because it indicates that the method balances better compression (low KL(z)) and high downstream task performances (AoLR and mCAS; see explanations in Sect. 6.4). In addition, detailed results can be found in Appendix 6.2

6.4.2 Controlled generation

Most previous studies Yingzhen and Mandt (2018), He et al. (2019) have primarily focused on evaluating the quality of global representation. However, a better representation does not necessarily improve the performance of the controlled generation, as claimed by Nie et al. (2020). To evaluate the ability of the controlled generation, we propose a modified version of the classification accuracy score (CAS) (Ravuri and Vinyals 2019), called mCAS. CAS trains a classifier that predicts class labels only from the samples generated from conditional generative models, and then evaluates the classification accuracy on real images, thus measuring the sample quality and diversity of the model. CAS is not directly applicable to non-conditional models such as PixelCNN-VAEs. Instead, mCAS measures the ability of the model to produce high-quality, diverse, but globally coherent (i.e., belonging to the same class) images for a given z.

In mCAS, we first prepared 100 real images $\{x_{i}\}_{i=1}^{100}$, along with their class labels $\{y_{i}\}_{i=1}^{100}$, where each of the 10 classes had 10 samples. Then, using the trained VAEs, we encoded each $x_{i}$ into $z_{i}$ and decoded $z_{i}$ to obtain 10 images $\{\hat{x}_{i, j}\}_{j=1}^{10}$ for every $z_{i}$, thereby resulting in 1000 generated images (sample images $\hat{x}$ can be found in Appendix 6.3). Finally, we trained the logistic classifier with pairs $\{(\hat{x}_{i, j}, y_{i}) | i \in \{1, ..., 100\}, j \in \{1, ..., 10\} \}$, and evaluated the performance on real test images. Intuitively, when the decoder ignores z, the generated samples may belong to a class different from the original ones, which produces label errors. Moreover, when z has excessive information regarding x and the VAE resembles an identity mapping, the diversity of the generated samples decreases (recall that 10 samples are generated for every $z_i$), which induces overfitting of the classifier. Therefore, to achieve a high mCAS, z should capture only global (label) information.

Figure 3c, d compare the mCAS along with KL(z) on MNIST and Fashion-MNIST. In addition, the black horizontal line indicates the classification accuracy when the classifier is trained on 100 real samples $\{ (x_{i}, y_{i}) \}_{i=1}^{100}$, and evaluated on real test images, which are referred to as the baseline score. The following can be observed from the figures: (1) The mCAS of the three methods outperformed the baseline score, despite using only 100 labeled samples, as well as in the baseline score, indicating that properly regularized PixelCNN-VAEs could be used for data augmentation. (2) As expected, a significantly low KL(z) results in a low mCAS because the decoder of the VAE does not utilize z. Moreover, a significantly high KL(z) also tends to degrade mCAS because the decoder may resemble a one-to-one mapping from z to x, and therefore, degrade the diversity. This indicates that Case 2 in Sect. 3 may have occurred. This phenomenon can also be observed in the sample images in Appendix 6.3: there seems to be less diversity in the samples drawn from $\beta$-VAE and CMI-VAE with $\gamma =0.6$ than $\gamma =0.3$. (3) Finally, the curves for CMI-VAE are consistently left to those for $\beta$-VAE, indicating that regularizing I(z; s) is also complementary to regularizing I(x; z) at the controlled generation.

7 Discussions and future works

Based on the experimental results, it was confirmed that MI-maximizing regularization could cause the problems stated in Sect. 3. It was also confirmed that regularizing I(z; s) is complementary to regularizing I(x; z) and leads to an improvement in the learning of global features. Here, we chose to extend $\beta$-VAE to construct the proposed objective function (recall that our regularization term needs only one modification from $\beta$-VAE). It is because we believe that $\beta$-VAE is the simplest MI-maximization method that requires fewer hyperparameters, which is widely used in the (sequential) VAE community (e.g., He et al. 2019; Alemi et al. 2018). However, other MI estimation methods, such as AdvMI-VAE and the discriminative objective, can be extended to CMI regularization by the addition of the I(z; s) minimization term (see Sect. 4.2). Leveraging these MI maximization methods into the estimation of CMI, or stabilizing adversarial training with certain techniques (Miyato et al. 2018) may improve the performance, and this remains an issue to be addressed in future work. It would also be noteworthy to tune the strength of I(x; z) and I(z; s) independently. Future studies may also apply the proposed method to encourage the learning of representations that capture the global factors of the environment, such as maps, to support reinforcement learning, as suggested in Gregor et al. (2019).

Appendices

Appendix 1: Data generating process of PixelCNN-VAEs

Here we show the detailed data generating process of PixelCNN-VAEs. Especially, we show how the autoregressive data generating process $\Pi _{t = 1}^T p(x_t|z, x_{<t}) = \Pi _{t = 1}^T p(x_t|z, s_t) q(s_t | x_{<t})$ is applied to PixelCNN-VAEs. We consider the 13-layer PixelCNN used in He et al. (2019), which has five (7 × 7)-kernel-size layers, followed by, four (5 × 5) layers, and then four (3 × 3) layers. Each layer has 64 feature maps with dimensions 28 × 28 dimensions. The latent variable z is extracted by an encoder, linearly transformed into (28, 28, 4) feature maps, and then concatenated to the each layer of the PixelCNN feature maps after the sixth layer. We denote the output of the i-th ($i \in \{1, ..., 13\}$) layer as $h_{i, t}$, where t denotes the timestep (that is, x and y coordinates; here, $t \in \{1, ..., 28 \times 28 = 784\}$). Then, we can put $s_t :=h_{6, <t}$ and the decomposition $\Pi _{t = 1}^T p(x_t|z, x_{<t}) = \Pi _{t = 1}^T p(x_t|z, s_t) q(s_t | x_{<t})$ holds because only $h_{6, <t}$ (not $h_{6, \ge t}$) are used to generate $x_t$ with causal convolution.

One might wonder whether the activations of the PixelCNN, which is the deterministic function of x, can be treated as random variables. However, because we regularize s only via minimizing I(z; s) (Sect. 4.1) and z and s have no deterministic relation, s can be meaningfully referred to as random variables. Furthermore, it is common to treat the activations of hidden layers as random variables and to consider their MI (or conditional entropy) in other literature, e.g., domain-invariant representation learning (Xie et al. 2017).

Note that, the definition of s is an important factor for the “control” of what will be learned in z. For example, Chen et al. (2017) proposed improving global representation z by using smaller receptive fields for $q(s_t|x_{<t})$ and constraining $s_t$ to more local information. Although this architectural constraint can make z informative, it requires weakening the expressiveness of PixelCNN and can degrade ELBO (Chen et al. 2017). By contrast, our method can be applied regardless of the size of the receptive fields because it prevents s from having global information with an information theoretic regularization term. Therefore, in our experiments, the architectural change of Chen et al. (2017) was not employed and large receptive fields were used to balance sufficient ELBO and representation quality.

Appendix 2: The lower bound of I(x; z|s)

Here we derive Eq. 8 and discuss the approximation error between I(x; z|s) and its lower bound. Firstly, we can take the lower bound as follows:

$$\begin{aligned} I(x; z|s)&= I(x; z) - I(z; s) + I(z; s|x) \ge I(x; z) - I(z; s), \end{aligned}$$

(17)

since the MI I(z; s|x) is positive. Then, the lower bound $I(x; z) - I(z; s)$ has approximation error I(z; s|x). Note that the error can be small under a particular condition. Namely, the error can be decomposed as:

$$\begin{aligned} I(z; s|x) = H(z|x) - H(z|x, s). \end{aligned}$$

Here, both H(z|x) and H(z|x, s) is thought to be small when x is high-dimensional data such as images, movies, and audios, because observing such x would enable us to predict z accurately. Also, empirically, it has been shown that the performance of inference model did not drop much even if the encoders of DSAE are decomposed into $q(z, s|x)=q(z|x)q(s|x)$ (Yingzhen and Mandt 2018), which indicates the error is small.

In addition, as long as $\lambda \ge 1$, the following condition holds:

$$\begin{aligned} I(x; z) - I(z; s) \ge I(x; z) - \lambda I(z; s), \end{aligned}$$

(18)

because the MI I(z; s) is positive. This approximation error becomes the smallest when $\lambda =1$.

Appendix 3: Details of experimental settings

1.1 Appendix 3.1: Disentangled sequential autoencoder

Data preprocessing We use the TIMIT data (Garofolo et al. 1992), which contains broadband 16 kHz recordings of phonetically-balanced read speech. A total of 6300 utterances (5.4 h) are presented with 10 sentences from each of the 630 speakers (70% male and 30% female). The data have split by Garofolo et al. (1992) into train/test subset. We followed Hsu et al. (2017); Yingzhen and Mandt (2018) for data preprocessing: the raw speech waveforms are first split into sub-sequences of 200 ms, and then preprocessed with sparse fast Fourier transform to obtain a 201 dimensional log-magnitude spectrum, with the window size 25ms and shift size 10 ms. This results in $T=20$ for the observation $x_{1:T}$.

Optimization we follow Yingzhen and Mandt (2018) for model architecture, data preprocessing, and evaluation procedures. The dimensionality of $s_t$ and z were fixed at 64; we set $T=20$ for the observation $x_{\le T}$. We used Adam optimizer with learning rate 2e−4 for the VAE and 2e−3 for the discriminator, and trained the models for 6000 epochs to get good convergence on the training set. The batch size is set to 32. The VAE architecture followed full model in Yingzhen and Mandt (2018), and the discriminator architecture is described in Appendix 5. The discriminator is updated twice while the VAE is updated once. The results are averaged over three random seed trials.

1.2 Appendix 3.2: PixelCNN-VAE

Data preprocessing We use the statically binarized version of MNIST and Fashion-MNIST datasets: each pixel value $\in [0, 1]$ is binarized with the threshold 0.5. The datasets are originally split into train/test subsets, and we further split the train subsets into 80% of train and 20% of validation subsets.

Optimization Regarding the optimization of VAEs, we used the Adam optimizer with a learning rate of 0.0001, trained for 300 epochs. The batch size is set to 50. We reported the values for the test data when the objective function for the validation data was maximized. Regarding the discriminators, we used the Adam optimizer with learning rate 0.001. The discriminator architecture is described in Appendix 5, and is updated twice while the VAE is updated once.

Appendix 4: Details of AdvMI-VAE in our experiments

We employ I(x; z) maximization method proposed by Makhzani and Frey (2017), Zhao et al. (2019) as a baseline method in our experiment. Briefly, we add I(x; z) to the standard VAE objectives as a regularization term with weighting term $\gamma$ as in Eq. 5. Here, to estimate I(x; z), Makhzani and Frey (2017) utilize the follwing relation based on the DRT:

$$\begin{aligned} \frac{q(z)}{p(z)} =:\frac{p(z|y=1)}{p(z|y=0)} = \frac{p(y=1|z)}{p(y=0|z)}, \end{aligned}$$

(19)

where $p(y=0)=\frac{1}{2}$ and $p(y=1) = \frac{1}{2}$. Then, although conditional probability p(y|z) cannot be obtained, it can be approximated with a discriminator D(z), which outputs $D=1$ when $z \sim _{i.i.d.} q(z)$ and $D=0$ when $z \sim _{i.i.d.} p(z)$. Then, I(x; z) can be approximated as follows:

$$\begin{aligned}&I(x; z) = \mathbb {E}_{p_d(x)} [D_{KL} [q(z|x)||p(z)] - D_{KL} (q(z) || p(z)) ] \\&\approx \mathbb {E} [D_{KL} [q(z|x)||p(z)] - \log \frac{D(z)}{1-D(z)} ]. \end{aligned}$$

D(z) is parameterized with some DNN, and trained alternately with VAEs’ objectives. Namely, D is trained to maximize the following objective with Monte Carlo sampling:

$$\begin{aligned} \mathbb {E}_{q(z)} [ \log D(z) ] + \mathbb {E}_{p(z)} [\log \bigr (1 - D(z) \bigl ) ]. \end{aligned}$$

Appendix 5: Discriminator settings

We have used discriminators for CMI-VAE and AdvMI-VAE. For the discriminator of CMI-VAE, to obtain the embedding of $s_{1:T}$, we first applied convolutional encoder and took mean pooling along time axis. Then, in PixelCNN-VAE, we took innner product of the embedding and z and treated it as logit of the discriminator. On the other hand, in DSAE, we took cosine similarity of the embedding and z, multiplied the similarity by a learnable scale parameter, and treated it as logit of the discriminator. The encoder architectures for PixelCNN-VAE and DSAE are summarized as follows, with the format Conv (depth, kernel size, stride, padding):

PixelCNN-VAE

• Input (28, 28, 1)

• Conv2D (256, 4, 2, 1)

• BatchNorm

• ReLU

• Conv2D (256, 4, 2, 1)

• BatchNorm

• ReLU

• Conv2D (z-dim, 4, 2, 1)

DSAE

• Input (20, 201)

• Conv1D (256, 4, 2, 1)

• BatchNorm

• ReLU

• Conv1D (256, 4, 2, 1)

• BatchNorm

• ReLU

• Conv1D (z-dim, 4, 2, 1)

AdvMI-VAE The discriminator architecture for AdvMI-VAE is summarized as follows, with the format Linear (input size, output size):

• Input (z-dim)

• Linear (z-dim, 400)

• ReLU

• Linear (400, 1)

• Softmax

Appendix 6: Detailed experimental results

1.1 Appendix 6.1: Detailed experimental results for DSAE

In this section, we present detailed experimental results for DSAEs, including the comparison with AdvMI-VAE. Table 3 presents the ELBO, KL, Recon, EER, and $\hat{I}(z; s)$ values of DSAE on TIMIT corpus. The ELBO, Recon, and KL(S) values are not divided by $T=20$. Also, the Recon values can be nevative because the variance of our decoder are learnable parameters. Here, note that KL(z) approximates I(x; z) because it upper bounds I(x; z), and can be used for the metric to assess whether a decoder ignores z or not (Bowman et al. 2016; Alemi et al. 2018; He et al. 2019).

Table 3 The ELBO, KL, Recon, EER, and $\hat{I}(z; s)$ values of DSAE on TIMIT corpus

Comparison with $\beta$-VAE Please see Sect. 6.3 for the explanations of main results. Also, note that, even for large $\gamma$, there is still reasonable reconstruction performance for the both methods.

1.1.1 Comparison with AdvMI-VAE

As shown in the table, given a fixed $\gamma$, AdvMI-VAE has the smallest EER(z) and the smallest EER(s) compared to $\beta$-VAE and CMI-VAE. The reason of the smallest EER(z) might be attributed to the independence of each dimension of z; since MI-VAE encourages p(z) and q(z) to be the same, the independence would improve and z would become a linear-separable form. The smallest EER(z) is apparentaly preferable; however, the smallest EER(s) indicates that s has redundant global (speaker) information. As we discussed in Sect. 3, such s is undesirable because the decoder can extract global information either from z and s; thereby it becomes difficult to control decoder’s output using z. As evidence of this, our supplementary experiment in Appendix 7 shows that AdvMI-VAE has the worset performance in voice conversion task.

1.1.2 Statistical test

We conducted statistical tests to investigate whether the values of $\hat{I}(z; s)$ and EER differ between the methods. Since we used only three random seeds due to the high computational costs of training DNNs, we did not verify whether the results for a fixed $\gamma$ value differed between the methods. Instead, we performed paired samples t tests, in which we regarded the results of two methods with a fixed $\gamma$ and fixed seed as a pair, and verify whether the results for all $\gamma$ values differed between the methods. More specifically, we set a null hypothesis as follows: regarding two groups (CMI-VAE v.s. $\beta$-VAE or CMI-VAE v.s. AdvMI-VAE), the mean value of the difference between pairs equals zero. As a result, we obtained p-values smaller than 0.05 for all the tests, indicating that the difference of the values of $\hat{I}(z; s)$, EER(s), and EER(z) between the methods is statistically significant.

1.2 Appendix 6.2: Detailed experimental results for PixelCNN-VAE

In this section, we present detailed experimental results for PixelCNN-VAEs. Tables 4 and 5 present the ELBO, KL(z), Recon, $\hat{I}(z; s)$, mCAS, and AoLR values of PixelCNN-VAEs on MNIST and Fashion-MNIST. Moreover, these tables present mCAS(SVM) and AoSVM, which are the same with mCAS and AoLR except for using a support vector machine (SVM) with RBF kernel, i.e., a more powerful non-linear classifier, instead of the logistic classifier. Also, note that KL(z) approximates I(x; z) because it upper bounds I(x; z), and has been used for the metric to assess whether a decoder ignores z or not (Bowman et al. 2016; Alemi et al. 2018; He et al. 2019). Here, the ELBO and Recon values are not divided by $T=28 \times 28$.

For the explanations of main results in the tables, please see Sect. 6.4. Also, as shown in the tables, even when we used a non-linear classifier SVM to calculate mCAS(SVM) and AoSVM, CMI-VAE achieved competitive or higher performance than the baselines in most cases. Note that, the exception is that given a $\gamma > 0.4$, there were not much differences in mCAS(SVM) for Fashion-MNIST within the three methods. One possible reason is that using the non-linear classifier increases the number of factors to be considered, such as overfitting, and makes fair comparisons difficult. Also, we note that using a very large $\gamma$ for PixelCNN-VAEs might not be a good idea. It is because when $\gamma$ becomes too large, the decoder of PixelCNN tends to resemble an identity mapping from z to its output, regardless of the regularization method (e.g., see, generated samples for $\gamma =0.6$ in Appendix 6.3). To improve performance while avoiding this phenomenon, it might be useful to using a weighting parameter $\gamma > \alpha$ in Eq. 7, and this remains an issue to be addressed in a future work.

Table 4 The ELBO, KL(z), Recon, mCAS, AoLR, mCAS(SVM), and AoSVM values of PixelCNN-VAEs on MNIST

Table 5 The ELBO, KL(z), Recon, mCAS, AoLR, mCAS(SVM), and AoSVM values of PixelCNN-VAEs on fashion-MNIST each model was trained with a weighting parameter $\gamma$

1.3 Appendix 6.3: Sample images for PixelCNN-VAE

Figures 4 present the generated images with PixelCNN-VAEs.

Fig. 4

Real images (the first column) and generated images by PixelCNN-VAEs (the other 10 columns). The images in each row are stochastically sampled from the decoder p(x|z) using the same z, which is extracted from x in the first column. The figures present that the diversity of the images in $\gamma =0.3$ is better than that in $\gamma =0.6$, which may be because PixelCNN-VAE would resemble an identity mapping with a large $\gamma$. In contrast, $\gamma =0.3$ apparently produces more label errors than $\gamma =0.6$ because the decoder ignores z with a small $\gamma$ (see, e.g., the rows for 3 and 4). Furthermore, when comparing a (CMI-VAE with $\gamma =0.3$) and b ($\beta$-VAE with $\gamma =0.3$), apparently, a produces less label errors (see, e.g., the rows for 2 and 3). This result is consistent with the mCAS scores in Fig. 3 (Sect. 6.4), which indicates that CMI-VAE achieved better diversity and less label errors than $\beta$-VAE

Appendix 7: Supplementary Experiment: voice conversion using disentangled sequential autoencoder

See Table 6.

Table 6 VC-mCAS for $\beta$-VAE, AdvMI-VAE, and CMI-VAE

For a quantitative assessment of controlled generation by DSAE, we performed voice conversion and evaluated the models with a score similar to mCAS (see, Sect. 6.4), which we call VC-mCAS. First, we prepared 500 real speeches (spectrograms with $T=20$) $\{x_{i}\}_{i=1}^{500}$, along with their gender labels (male or female) $\{y_{i}\}_{i=1}^{500}$, where each of the 2 classes had 250 samples. Then, we randomly created 250 pairs $\{(x_i, x_j) | y_i \ne y_j\}$, i.e., each pair consists of one male and one female speech. Using the trained DSAE, we encoded each x into z and s, created the pairs $\{(z_{i}, s_{i}, z_{j}, s_{j}) | y_i \ne y_j\}$, and decoded $z_i$ and $s_j$ ($z_j$ and $s_i$) to obtain $\hat{x}_{i, j}$ ($\hat{x}_{j, i}$), which ideally has the speaker characteristics of $x_i$ and the linguistic contents of $x_j$. Thus, we obtain 500 generated samples, where each $\hat{x}_{i, j}$ was labeled with $y_i$, assuming that the characteristics that tend to depend on gender (such as pitch) were successfully converted. Finally, we trained a logistic classifier with the 500 pairs $\{(\hat{x}_{i, j}, y_{i})\}$ and evaluated the performance on real test speeches. Note that, because the raw $\hat{x}_{i, j}$ has an excessively high dimension ($20\mathrm {(}T\mathrm {)} \times 201\mathrm {(features)}$) for the logistic classifier, $\hat{x}$ was averaged over the time-axis prior to its measurement. Intuitively, when the decoder ignores z, the generated samples might belong to a class different from the labeled ones, which produces label errors. Therefore, to achieve a high VC-mCAS, z should capture global information but s should not. Also, the generated samples should be realistic to reduce the domain gap between train (generated) and test (real) data.

Table 6 presents the values of VC-mCAS for the objectives of $\beta$-VAE, AdvMI-VAE, and CMI-VAE. Note that we report the mean and best scores within three random seed trials for each $\gamma$. The table illustrates that (1) given a fixed $\gamma$, CMI-VAE nearly consistently achieved a higher VC-mCAS compared to the baseline methods, indicating that regularizing $I^\prime (z; s)$ is complementary to MI-maximizing regularization. Furthermore, (2) although $\gamma =0.8$ yields a higher EER(z) than those with $\gamma =0.4$ in Table 2, it yields a higher VC-mCAS. Also, (3) given a fixed $\gamma$, although AdvMI-VAE yields the smallest EER(z) among the three methods (Appendix 6.1), it yields the lowest performance in VC-mCAS. The observations (2) and (3) indicates that EER(z), which was used in previous studies (Hsu et al. 2017; Yingzhen and Mandt 2018) for evaluating the quality of global representation, does not always be suitable for evaluating the “usefulness” of the representation. Therefore, we recommend that future studies should evaluate the performance of the controlled generation in addition to measuring EER.