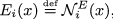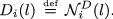Metrics and methods for robustness evaluation of neural networks with generative models

Abstract

Recent studies have shown that modern deep neural network classifiers are easy to fool, assuming that an adversary is able to slightly modify their inputs. Many papers have proposed adversarial attacks, defenses and methods to measure robustness to such adversarial perturbations. However, most commonly considered adversarial examples are based on perturbations in the input space of the neural network that are unlikely to arise naturally. Recently, especially in computer vision, researchers discovered “natural” perturbations, such as rotations, changes of brightness, or more high-level changes, but these perturbations have not yet been systematically used to measure the performance of classifiers. In this paper, we propose several metrics to measure robustness of classifiers to natural adversarial examples, and methods to evaluate them. These metrics, called latent space performance metrics, are based on the ability of generative models to capture probability distributions. On four image classification case studies, we evaluate the proposed metrics for several classifiers, including ones trained in conventional and robust ways. We find that the latent counterparts of adversarial robustness are associated with the accuracy of the classifier rather than its conventional adversarial robustness, but the latter is still reflected on the properties of found latent perturbations. In addition, our novel method of finding latent adversarial perturbations demonstrates that these perturbations are often perceptually small.

1 Introduction

Unlike in more conventional software engineering, the problem of ensuring reliability of machine learning (ML) based software is complicated by the fact that ML-based models, such as artificial neural networks (ANNs), are not programmed explicitly. Instead, they significantly depend on the data on which they are trained. The traditional form of assessing model performance based on validation/test data (e.g., a holdout set) and measures such as accuracy or F-score, become insufficient when the models interact with the real world, such as in the cases of aircraft and unmanned vehicle control. This is proven by the discovery of adversarial examples (Szegedy et al., 2014)—slightly perturbed inputs that cause ANNs to malfunction, for example by misclassifying an image. For a human, adversarial examples may be even indistinguishable from original, unperturbed inputs. Adversarial examples are often produced in a rather artificial environment, by adopting special algorithms that perturb the input until a certain criterion is reached, but recent evidence (Akhtar and Mian, 2018; Gilmer et al., 2018) suggests that they may transfer to the material world.

The classic framework of empirical risk minimization (ERM) (Vapnik, 2013), where the classifier is trained on available data samples, is used to achieve high values of sample-based metrics such as accuracy or F-score. However, if the classifier must be protected from adversarial examples, ERM is insufficient, and robust optimization (Madry et al., 2018) with projected gradient descent (PGD) can be used instead. This corresponds to enforcing adversarial robustness (Anderson et al., 2019; Bastani et al., 2016; Fawzi et al., 2018; Huang et al., 2017; Katz et al., 2017; Moosavi-Dezfooli et al., 2016; Singh et al., 2019), which is often treated either as a metric (Bastani et al., 2016; Fawzi et al., 2018; Moosavi-Dezfooli et al., 2016) specifying the minimum magnitude of an adversarial perturbation, or as a specification (Anderson et al., 2019) stating that the decision of the ANN must be invariant to perturbations of input of a certain form. Adversarial robustness can be local (Anderson et al., 2019; Fawzi et al. 2018; Huang et al., 2017; Katz et al., 2017; Singh et al., 2019) or global (Katz et al., 2017).

Traditional adversarial examples are based on perturbations in the input space of the ANN that are constrained with $\ell _p$ (e.g., $\ell _2$ or $\ell _\infty$) norms. The resulting adversarial examples are highly improbable to arise naturally (Song et al., 2018a), but it was shown that even natural adversarial examples (i.e., the ones plausible under the data distribution) exist (Amadou Dia et al., 2019; Dreossi et al., 2018; Engstrom et al., 2019; Gu et al., 2019; Hendrycks et al., 2019; Jalal et al. 2019; Song et al., 2018b; Zhao et al., 2017). While conventional adversarial examples often require 2D or 3D printing of precomputed images (Akhtar and Mian, 2018) to be applied in the real world, a natural adversary could be seen as a manipulator of high-level features of classified objects. The plausibility of natural adversarial examples makes statistical attack detection and defense approaches, such as (Song et al., 2018a; Samangouei et al., 2018), less reliable. At the same time, these examples are theoretically interesting: unlike traditional adversarial examples, they show the failures of ANNs on the distribution on which they were trained.

Construction of a subclass (Amadou Dia et al., 2019; Jalal et al., 2019; Song et al., 2018b; Zhao et al., 2017) of natural adversarial examples is possible with the help of generative models, such as generative adversarial networks (GANs) (Goodfellow et al., 2014) and generative autoencoders (Makhzani et al., 2015). Previous works that considered natural adversarial examples mostly focused on attacks and defenses rather than assessing the performance of classifiers. In addition, Jalal et al. (2019) applied adversarial examples for ANN training, although the focus so far has been on adversarial robustness in the input space of the ANN. This paper utilizes generative models as a means of capturing real-world data distributions in order to specify and evaluate performance metrics for ANN classifiers in terms of probabilities, likelihood and distances in latent spaces of generative models. As a result, our metrics capture the robustness of classifiers to natural adversarial examples. More precisely, the contributions of the paper are as follows:

• 1. We propose a framework to evaluate the performance of deep feed-forward ANN classifiers on natural adversarial examples with the help of generative models and their latent spaces. The implementation of the framework is publicly available online.

• 2. Within this framework, we propose latent space performance metrics—novel performance metrics for feed-forward ANN classifiers that are based on probabilistic reasoning in latent spaces of generative models, and, informally speaking, measure the “resistance” of the classifier to natural adversarial examples. The naturality of adversarial examples is achieved by (1) operating in the latent space of the generative model, (2) considering a distribution-preserving model of noise, and (3) generating adversarial examples by adding random noise, or by searching for worst-case examples that are bounded by the likelihood of noise.

• 3. We propose methods to approximately evaluate these metrics in a white-box setting using (1) sampling and (2) gradient-based search of adversarial perturbations in the latent space. The latter method is a form of untargeted attack based on PGD. We show that such a search is possible not only with GANs (Zhao et al., 2017), but also with generative autoencoders.

• 4. With the proposed framework, metrics and methods, we reveal interesting properties of ANN classifiers with respect to natural adversarial examples, which contributes to understanding the latter better. On four image classification case studies, we examine classifiers trained traditionally and in a way that achieves adversarial robustness, and evaluate their performance according to latent space performance metrics. Our PGD-based untargeted attack yields perceptually smaller latent perturbations than reported earlier (Zhao et al., 2017), and we find positive association between latent counterparts of adversarial robustness and the accuracy of a classifier on clean images. Moreover, we did not identify a similar association for latent space performance metrics and conventional adversarial robustness, but we found that the latter leads to minimum latent adversarial perturbations being further from the original image in the original (non-latent) space as well as perceptually.

The rest of the paper is structured as follows. Section 2 presents background material. Section 3 motivates the use of generative models to measure ANN classifier performance, and proposes corresponding metrics. In Sect. 4, approaches are given to evaluate these metrics. Evaluation of deep convolutional neural network (CNN) classifiers with these approaches is performed in Sect. 5. Section 6 reviews related work, and Sect. 7 concludes the paper.

2 Preliminaries

2.1 Artificial neural networks

A feed-forward artificial neural network (ANN) ${\mathcal {N}}$ is a parametric model that predicts some outcome y (a single number or a vector) based on some input vector x of dimension $n_I$. By feed-forward, we mean that the input is supplied to the network at once and is passed through a predefined computation graph with a finite number of computation nodes. When the input is an image, ${\mathcal {N}}$ is usually a convolutional neural network (CNN). In this paper, we focus on the classification task, where ${\mathcal {N}}$ must assign its input to one of $m > 1$ classes. Thus, we have ${\mathcal {N}}: {\mathbb {R}}^{n_I} \rightarrow \{1, ..., m\}$. We assume that class prediction is done as follows: ${\mathcal {N}}$ first produces real-valued scores of each class i, to which we will refer as the values of the scoring function $S_{\mathcal {N}}(x, i)$, and the actually predicted class is the one with the maximum score: ${\mathcal {N}}(x) = \arg \max _i S_{\mathcal {N}}(x, i)$. In addition, we require that $S_{\mathcal {N}}(x, i)$ is continuous and almost everywhere differentiable with respect to x.

ANN classifiers are typically trained in a supervised way with some form of gradient descent (e.g., stochastic gradient descent), using samples $x_1, ..., x_k \in {\mathbb {R}}^{n_I}$, which are paired with respective reference class labels $y_1, ..., y_k \in \{1, ..., m\}$. These pairs $(x_1, y_1), ..., (x_k, y_k)$ are assumed to come from joint distribution ${\mathcal {J}}$, whose marginals are the input data distribution ${\mathcal {X}}$ and the class label distribution ${\mathcal {Y}}$.

2.2 Generative models

A generative adversarial network (GAN) (Goodfellow et al., 2014), which consists of two feed-forward ANNs called the discriminator and the generator ${\mathcal {G}}$, is trained to make ${\mathcal {G}}$ generate elements of some target data distribution ${\mathcal {X}}$ of $n_I$-dimensional vectors (in the simplest case, without sample labels). Data generation is done by applying ${\mathcal {G}}$ to a low-dimensional vector $l \in {\mathbb {R}}^{n_L}$ sampled from the latent code distribution ${\mathcal {L}}$ (typically, N(0, I)). If $l \sim {\mathcal {L}}$, then for a well-trained GAN we may assume that ${\mathcal {G}}(l) \sim {\mathcal {X}}$. Often, the dimension of ${\mathcal {L}}$ is made smaller than the dimension of ${\mathcal {X}}$: $n_L < n_I$. The set of all latent codes (usually, just ${\mathbb {R}}^{n_L}$) is called the latent space. By contrast, we will refer to the input space of an ANN classifier (${\mathbb {R}}^{n_I}$) as the original space. With some enhancements, GANs may be also capable of reconstruction—finding latent representation $l \in {\mathbb {R}}^{n_L}$ for the given original vector $x \in {\mathbb {R}}^{n_I}$ such that ${\mathcal {G}}(l)$ is close to x (e.g., according to some norm in the original space). For example, this may be done by training an additional ANN ${\mathcal {I}}: {\mathbb {R}}^{n_I} \rightarrow {\mathbb {R}}^{n_L}$ called an inverter (Hendrycks et al., 2019). However, obtaining good inversions, especially for GANs that generate high-resolution images, requires more effort: for example, Bau et al. (2019) performed layer-wise inversion and combined it with gradient-based optimization.

An autoencoder $({\mathcal {N}}^E, {\mathcal {N}}^D)$, where ${\mathcal {N}}^E$ and ${\mathcal {N}}^D$ are feed-forward ANNs called the encoder and the decoder respectively, is a model whose goal is to compress (encode) its inputs $x \in {\mathbb {R}}^{n_I}$ to low-dimensional vectors $l = {\mathcal {N}}^E\left( x\right) \in {\mathbb {R}}^{n_L}$ (again, $n_L < n_I$) such that approximate decompression (decoding, reconstruction) can be achieved: ${\mathcal {N}}^D\left( l\right)$ is close to x. A generative autoencoder, such as in (Heljakka et al., 2020; Makhzani et al., 2015), is an autoencoder whose decoder is additionally trained to sample from the original distribution ${\mathcal {X}}$—thus, essentially, a generative autoencoder performs both the tasks of an autoencoder and a GAN. For a well-trained generative autoencoder, we may assume both $l \sim {\mathcal {L}} \Rightarrow {\mathcal {N}}^D(l) \sim {\mathcal {X}}$ and $x \sim {\mathcal {X}} \Rightarrow {\mathcal {N}}^E(x) \sim {\mathcal {L}}$.

To summarize, generative models are capable of data generation from low-dimensional vectors. By using special types of generative models or enhancing existing generative models, it is also possible to achieve data reconstruction.

2.3 Adversarial examples and perturbations

Suppose that ${\mathcal {N}}$ is an ANN classifier. An adversarial example is an input $x'$ to ${\mathcal {N}}$ such that $x' \in A(x)$ and ${\mathcal {N}}(x') \ne {\mathcal {N}}(x)$, where x is a real data sample, A(x) is the set of allowed changes of x (often, it is taken as the $\varepsilon$-ball around x according to the $\ell _p$ norm: $A(x) = \{x' \, | \left\Vert x' - x\right\Vert _p \le \varepsilon \}$). $\Delta x = x' - x$ is the corresponding adversarial perturbation.

Adversarial examples and adversarial perturbations have been first found to exist by Dalvi et al. (2004) and Globerson and Roweis (2006), but were publicized by Szegedy et al. (2014), who presented human-indistinguishable ImageNet perturbations. Since 2013, many adversarial attacks and defenses have been proposed (Akhtar and Mian, 2018). While many proposed defenses were shown to be ineffective (Gilmer et al., 2018), attacks were transported to the real world (Akhtar and Mian, 2018), raising concerns regarding the safety and security of deep ANNs.

For adversarial perturbations bounded with $\ell _2$ and $\ell _\infty$ norms, projected gradient descent (PGD) has been shown (Madry et al., 2018) to be the best adversary that has access only to $\nabla _x S_{\mathcal {N}}(x, \cdot )$. The most common method of defense is robust optimization with PGD, where training is done on adversarial examples for the current version of the ANN. Gilmer et al. (2019) showed that it is possible to train the classifier on samples with added visible Gaussian noise instead of specially crafted adversarial examples.

Recent works explain adversarial examples through the peculiarities of the multidimensional geometry (Gilmer et al., 2019) and the fact that conventional ERM-based training does not introduce human priors to the training process (Ilyas et al., 2019). Samangouei et al. (2018) and Song et al. (2018a) also hypothesized that adversarial examples do not lie on the data manifold of the training distribution, but several works show that even natural adversarial examples exist, such as the ones that come from the real world (Hendrycks et al., 2019), are made by rotations and translations (Engstrom et al., 2019), color distortions (Gu et al., 2019), semantic changes (Dreossi et al., 2018), looping over consequent video frames (Gu et al., 2019), and created with generative models (Amadou Dia et al., 2019; Jalal et al., 2019; Song et al., 2018b; Zhao et al., 2017). Latent space adversarial examples, or adversarial examples that correspond to some latent codes of a generative model, may be based on perturbations (Amadou Dia et al., 2019; Zhao et al., 2017) or generated from scratch (Song et al., 2018b). Jalal et al. (2019) showed that latent space adversarial examples can be used to enhance robust optimization and increase the overall robustness of the classifier.

2.4 Performance metrics for adversarial robustness

Often, the set of possible adversarial examples is defined locally for each input x—for example, as an $\ell _p$ $\varepsilon$-ball, or as a set of rotations of x (Engstrom et al., 2019). The robustness of the classifier is then measured as its accuracy on worst-case inputs taken from such sets. For the $\ell _\infty$ norm, Bastani et al. (2016) formalized this metric as adversarial frequency. Adversarial frequency, however, depends on $\varepsilon$. A different way to measure robustness, which is free from this hyperparameter, is adversarial severity (Bastani et al., 2016)—the expected (with $x \sim {\mathcal {X}}$) minimum distance from x to an adversarial example. The corresponding local metric is pointwise robustness, which is the minimum distance to an adversarial example for a particular x. In this paper, we will define metrics that are based on pointwise robustness, adversarial frequency and severity but operate with different norms in different spaces. Known metrics that are defined in the original space will be referred to as conventional metrics.

3 Latent space performance metrics

In this paper, we are interested in specifying and evaluating performance metrics for ANN classifiers with the help of generative models. In addition, we would like to evaluate these metrics given the original training and validation data. This section will propose several such latent space performance metrics, and methods to evaluate them will be proposed in Sect. 4.

3.1 Preliminary definitions

Suppose that ${\mathcal {N}}: {\mathbb {R}}^{n_I} \rightarrow \{1, ..., m\}$, $m > 1$, is a feed-forward ANN classifier with scoring function $S_{\mathcal {N}}$. The goal of ${\mathcal {N}}$ is to correctly classify input vectors drawn from distribution ${\mathcal {X}}$. In the most general case, there may be no unique correct label for an input vector, but rather there is a joint distribution ${\mathcal {J}}$ of pairs (x, y) of an input vector x and its label y. For simplicity, we assume that ${\mathcal {N}}$ is validated on samples drawn exactly from ${\mathcal {J}}$, although the training might have been performed on a distribution induced by data augmentation of input vectors x.

Suppose that ${\mathcal {L}}_{i}$, $1 \le i \le m$, are $n_L$-dimensional ($n_L < n_I$) class-conditional latent distributions (often assumed to be N(0, I)) such that we have trained transformations $D_i {: {\mathbb {R}}^{n_L} \rightarrow {\mathbb {R}}^{n_I}}$ that generate samples from class-conditional data distributions ${\mathcal {X}}_{i}$: $l \sim {\mathcal {L}}_{i} \Rightarrow D_i(l) \sim {\mathcal {X}}_{i}$. In certain cases (see models capable of reconstruction in Sect. 2.2), we may additionally have transformations $E_i {: {\mathbb {R}}^{n_I} \rightarrow {\mathbb {R}}^{n_L}}$ that return latent code approximations of $n_I$-dimensional vectors. We would like $D_i$ to be compatible with gradient descent, i.e., continuous and almost everywhere differentiable, but we do not require the same from $E_i$.

3.2 Motivation for latent space performance metrics

With both $D_i$ and $E_i$, we can convert vectors to the latent space and back. Assuming that the latent space corresponds to a well-trained generative model, working in it has the following benefits compared to the original space:

• 1. For a random vector $l \sim {\mathcal {L}}_{i}$, $D_i(l)$ has a distribution that was trained to approximate ${\mathcal {X}}$.

• 2. Changes of the vector in the latent space are high-level in terms of the original representation.

• 3. For each class i, the image $D_i({\mathbb {R}}^{n_L})$ contains an infinite number of diverse data samples, which may be useful to evaluate ${\mathcal {N}}$ or train it further.

• 4. The aforementioned samples can not only be generated at random, but also can be optimized with gradient-based techniques to optimize a certain objective (e.g., $S_{\mathcal {N}}$).

As many performance metrics, such as accuracy, adversarial frequency and severity, will remain meaningful when the original space is replaced with the latent one, in this paper we will mainly move conventional performance metrics to the latent space. We will do it in a way that provides additional benefits related to the probabilistic interpretation of the latent space—for example, while considering adversarial perturbations, we will take care that the data remains plausible according to ${\mathcal {X}}$.

3.3 Possible scenarios

Intuitively, sampling from ${\mathcal {L}}_{i}$ gives latent vectors l such that $D_i(l)$ are instances of class i. Previous works on natural adversarial examples obtained latent vectors based on generation (Song et al. 2018b) and reconstruction (Zhao et al., 2017). These two scenarios of obtaining $D_i(l)$ (see the upper part of Fig. 1, paths 1a and 1b) directly correspond to two operations that generative models are capable of (see Sect. 2.4):

• 1. Sample $l \sim {\mathcal {L}}_{i}$ and generate $x = D_i(l)$.

• 2. Take a random real sample ${\hat{x}} ~ \sim {\mathcal {X}}_{i}$, encode it as $l = E_i({\hat{x}})$, and reconstruct it as $x = D_i(l).$

Fig. 1

Overview of considered scenarios

In this paper, we are interested in finding latent space counterparts for the following metrics (each of them will correspond to one of three scenarios in the lower part of Fig. 1):

• 1. Accuracy, as well as similar metrics based on counting success frequencies (Fig. 1, path 2a). This is the simplest case: it is sufficient to calculate the success frequency of ${\mathcal {N}}$ on reconstructed or generated samples. This will be formalized in Sect. 3.4.

• 2. Corruption robustness to random noise (Gilmer et al., 2019; Hendrycks and Dietterich, 2019) (Fig. 1, path 2b). While in the original space the addition of noise is a form of data corruption, in the latent space this noise will introduce high-level changes to the input, and we could measure the success frequency of ${\mathcal {N}}$ on such inputs. In Sect. 3.5, we will introduce a family of noise-adding distributions $N_{\epsilon , l}$ that retain the transformed data plausible even for large noise, and define a corresponding performance metric.

• 3. Adversarial robustness (Anderson et al., 2019; Fawzi et al., 2018; Huang et al., 2017; Katz et al., 2017; Singh et al., 2019) (Fig. 1, path 2c). Adversarial robustness in the latent space can be treated as “resistance” to worst-case noise additions that are bounded according to noise likelihood and optimized to degrade the performance of ${\mathcal {N}}$. The connection between noise corruption robustness and adversarial robustness exists already in the original space: for example, if the noise is Gaussian, its likelihood is determined by its $\ell _2$ norm, a threshold on which is a common constraint on adversarial perturbations. What is more, noise corruption robustness and adversarial robustness were found to be highly related (Gilmer et al., 2019). The corresponding latent space metrics will be formalized in Sect. 3.6.

3.4 Accuracy in the latent space

Probably the simplest thing that can be done with generative models is to evaluate the accuracy of the classifier on generated and reconstructed data items. This situation corresponds to the absence of any adversary. These ideas are formalized in the following definitions:

Definition 1

The latent generation accuracy (LGA) of ${\mathcal {N}}$ is:

Definition 2

The latent reconstruction accuracy (LRA) of ${\mathcal {N}}$ is:

In LGA, which requires $D_i$ but not $E_i$, compared to regular accuracy on the holdout set, we have replaced real data samples with generated samples, following class probabilities in ${\mathcal {J}}$ (also note that it is possible to consider similar metrics for each class separately). As a result, an unlimited number of samples can be used to estimate LGA. In addition, misclassified samples found during the check of this specification can be used to train ${\mathcal {N}}$ further. In LRA, instead of generating new samples, we take the approximations of real ones computed with both $D_i$ and $E_i$. This resembles the Defense-GAN (Samangouei et al., 2018) approach.

While LGA can be measured by sampling latent codes, LRA can be estimated based on samples from the holdout set (see Sect. 4.2). The main purpose of LGA and LRA in this paper is to serve as baselines for other metrics proposed in the following subsections, which, in addition to generation or reconstruction, assume the presence of an adversary.

3.5 Noise corruption robustness in the latent space

In this subsection, we consider a randomized noise-adding adversary. Suppose that $N_{\epsilon , l}$ is some noise-adding distribution that operates on latent vectors l, where parameter $\epsilon \ge 0$ controls the magnitude of the noise. Below, we will use the same notation for the probability density function (PDF) of this distribution. We would like the following conditions to be satisfied:

• 1. Distribution preservation: for all $\epsilon$, sampling $l' \sim N_{\epsilon , l}$ with $l \sim {\mathcal {L}}_{i}$ is equivalent to sampling $l' \sim {\mathcal {L}}_{i}$. This condition ensures the “naturality” of noise: its addition does not shift the distribution of input vectors, meaning that it will not produce vectors that are not plausible according to ${\mathcal {L}}_{i}$ (compared, e.g., with addition of noise to each component of the original data item).

• 2. Support of small noise: if $\epsilon \rightarrow 0$, random vectors ${\lambda _\epsilon } \sim N_{\epsilon , l}$ converge in distribution to $\lambda \equiv l$, i.e., the added noise becomes negligible. This condition ensures that small $\epsilon$ corresponds to small noise.

• 3. Support of large noise: if $\epsilon \rightarrow +\infty$, random vectors ${\lambda _\epsilon } \sim N_{\epsilon , l}$ converge in distribution to ${\lambda } \sim {\mathcal {L}}_{i}$, i.e., the unperturbed latent vector l becomes irrelevant. This condition ensures that large $\epsilon$ corresponds to large noise. Convergence to ${\mathcal {L}}_{i}$ is needed to comply with the first condition.

• 4. Connection with perturbation magnitude: there exists a distance $\nu$ and a continuous, strictly decreasing function $q_\epsilon$ such that the likelihood of the noise is given by $N_{\epsilon , l}(l') = q_\epsilon (\nu (l', l))$. This requirement is needed to make the magnitude of perturbations measurable by their likelihood. In addition, it guarantees that $N_{\epsilon , l}$ has an upper bound $q_\epsilon (0)$.

We will propose a concrete family of distributions satisfying these properties in Sect. 4.3. Now, we look at the case where the input to be classified is a perturbed version of the reconstruction of a real data element:

Definition 3

The local latent noise accuracy (LLNA) of ${\mathcal {N}}$ in point $x \in {\mathbb {R}}^{n_I}$ of known class i with noise magnitude $\epsilon$ is:

LLNA is similar to LRA, except that checks are performed on noisy reconstructions of a fixed real data sample x. LLNA can be evaluated based on sampling noise vectors (see Sect. 4.3).

3.6 Adversarial robustness in the latent space

Next, instead of checking the classifier’s resistance to random noise, we consider perturbations chosen by an adversary. In terms of $N_{\epsilon , l}$, we can assume that the adversary can choose the worst case input within bounded likelihood. Given fixed x and i, $l' \sim N_{\epsilon , E_i(x)}$ is a random $n_L$-dimensional vector. Then:

Definition 4

The local latent adversarial robustness (LLAR) of ${\mathcal {N}}$ in point $x \in {\mathbb {R}}^{n_I}$ with known class i, with noise magnitude $\epsilon$, is:

This defines LLAR as the maximum likelihood of a latent adversarial perturbation, with low LLAR corresponding to high robustness. Condition 4 on the noise distribution makes the value of LLAR correspond to some value of a distance between the original and the perturbed vectors, giving it an intuitive interpretation. Also, due to the boundedness of $N_{\epsilon , E_i(x)}$, which follows from the same condition, this expression may not give positive infinity. Negative infinity may be obtained in a peculiar case of all the latent space being classified into class i, which, for example, may be caused by the trained models being inadequate. Still, our definitions below tolerate this case.

LLAR captures proximity in the latent space and is similar to known definitions of local robustness checked in the input space of the ANN (Anderson et al., 2019; Bastani et al., 2016; Fawzi et al., 2018; Huang et al., 2017; Katz et al., 2017; Singh et al., 2019), for example, to pointwise robustness (Bastani et al., 2016). However, the likelihood $\tau$ of a multivariate random vector may be inconvenient to operate with, and thus we allow it to be post-processed with some decreasing function $g_\epsilon (\tau )$. In Sect. 4.7, we will propose an approach that views LLAR as $\ell _2$ robustness in the latent space (i.e., $g_\epsilon$ will convert the likelihood to this norm) and either finds its approximate value or checks whether it is above a given threshold.

Next, we transform LLAR to global performance metrics, returning to the ideas of sampling latent vectors and looping through reconstructed data items:

Definition 5

The latent adversarial generation severity (LAGS) of ${\mathcal {N}}$ with noise magnitude $\epsilon$ is:

Definition 6

The latent adversarial reconstruction severity (LARS) of ${\mathcal {N}}$ with noise magnitude $\epsilon$ is:

Definition 7

The latent adversarial generation accuracy (LAGA) of ${\mathcal {N}}$ with noise magnitude $\epsilon$ and bound $\rho$ on its transformed likelihood is:

Definition 8

The latent adversarial reconstruction accuracy (LARA) of ${\mathcal {N}}$ with noise magnitude $\epsilon$ and bound $\rho$ on its transformed likelihood is:

LAGS and LARS are similar to adversarial severity as defined by Bastani et al. (2016), and LAGA and LARA are similar to adversarial frequency as defined by the same authors. Intuitively, LAGS and LARS are average LLAR values, while LAGA and LARA are average success rates of passing a specification of being resistant to sufficiently likely latent perturbations. In Sect. 4.7, we will approximately evaluate all these metrics with sampling and PGD. The overview of all considered latent space performance metrics is given in Table 1.

Table 1 Overview of the proposed latent space performance metrics

4 Evaluating latent space performance metrics

This section proposes concrete approaches to calculate the values of the metrics defined in Sect. 3. The general idea is to work with the standard multivariate Gaussian distribution as the latent one due to its well-known properties. This is especially important for addressing latent adversarial robustness in Sect. 4.7.

4.1 Choice of generative models

To be able to work with probability densities in the latent spaces ${\mathcal {L}}_{i}$, we need to fix the selection of these spaces. We achieve this by taking ${\mathcal {L}}_{i} = N(0, I)$. Then, to evaluate all metrics proposed in Sect. 3, transformations $D_i$ and, for reconstruction-based metrics, $E_i$ must be defined for all classes $1 \le i \le m$. The following techniques can be applied:

• 1. For each i, train a generative autoencoder $({\mathcal {N}}_i^E, {\mathcal {N}}_i^D)$ and take

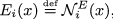
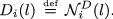
• 2. For each i, train a GAN with generator ${\mathcal {G}}_i$ and take $E_i$ can be obtained by enhancing these GANs with encoding procedures, e.g., by training inverters (Hendrycks et al., 2019), performing gradient-based optimization of latent codes, or both (Bau et al., 2019). Instead of training models for each class separately, it is possible to train class-conditional models (Odena et al., 2017).

4.2 Measuring latent accuracy

With $D_i$ and $E_i$ defined, LGA can be measured by repeatedly sampling a class label $i \sim {\mathcal {Y}}$ and a latent code $l \sim N(0, I)$, calculating $o_g = [{\mathcal {N}}(D_i(l)) = i]$,¹ which is a Bernoulli random variable, and averaging the obtained values of $o_g$, which gives an unbiased estimate of LGA. Similarly, LRA can be measured by sampling validation data items (x, i) and averaging $o_r = [{\mathcal {N}}(D_i(E_i(x)) = i]$.

4.3 Noise model and measuring local latent noise accuracy

Suppose that we sample $(x, i) \sim {\mathcal {J}}$ by enumerating over $(x_1, y_1), ..., (x_k, y_k)$. In this case $l = E_i(x) \sim N(0, I)$. At this point, we can inject a random perturbation into the latent code. We define the noise-adding distribution $N_{\epsilon , l}$ as follows:

(1)

Note that, given the previous choice ${\mathcal {L}}_{i} = N(0, I)$, this choice of $N_{\epsilon , l}$ complies with the constraints stated in Sect. 3.2 (point 1 is easy to check, the proofs of points 2 and 3 are given in Appendix B, and point 4 will be clarified in Sect. 4.4), and it would not be distribution-preserving either (1) with a non-Gaussian $\delta l$, or (2) without the denominator $\sqrt{1 + \epsilon ^2}$. Furthermore, the definition (1) is equivalent to:

$$\begin{aligned} N_{\epsilon , l} = N\left( \frac{l}{\sqrt{1 + \epsilon ^2}}, \frac{\epsilon ^2}{1 + \epsilon ^2}I\right) . \end{aligned}$$

(2)

LLNA can be measured by finding the latent vector $l = E_i(x)$, then repeatedly sampling $l' \sim N_{\epsilon , l}$ and calculating $o_n = [{\mathcal {N}}(l') = i]$, which is again a Bernoulli random variable. The rest is similar to checking LGA and LRA.

4.4 Likelihood of perturbations and perturbed vectors

In the rest of this section, to check LLAR and its derivatives, we will optimize latent perturbations—adversarially chosen perturbations that are bounded by the likelihood of the outcomes of $N_{\epsilon , l}$. They are similar to the ones considered in (Zhao et al., 2017). Noise addition $N_{\epsilon , l}$ (2) can be interpreted as a composition of two transformations:

• 1. Decay (reduction) of the unperturbed latent vector l by $\sqrt{1 + \epsilon ^2}$.

• 2. Addition of Gaussian noise $\Delta l \sim N\left( 0, \epsilon ^2 I / (1 + \epsilon ^2)\right)$.

Below, we will refer to $\Delta l$ as a latent adversarial perturbation rather than noise, emphasizing that $\Delta l$ will be produced with directed search rather than sampling. What perturbations $\Delta l$ are more likely? The log-likelihood of $\Delta l$ having a standard Gaussian distribution is determined by the $\ell _2$ norm of $\Delta l$:

$$\begin{aligned} \log f_{N\left( 0, \epsilon ^2 I / (1 + \epsilon ^2) \right) }(\Delta l) = \log \prod _{j = 1}^{n_L} \sqrt{\frac{1 + \epsilon ^2}{2 \pi \epsilon ^2}} \exp \left( -\frac{1 + \epsilon ^2}{2 \epsilon ^2}\Delta l_j^2\right) \nonumber \\ = n_L \log \sqrt{\frac{1 + \epsilon ^2}{2 \pi \epsilon ^2}} - \frac{1 + \epsilon ^2}{2 \epsilon ^2}\sum _{j = 1}^{n_L} \Delta l_j^2 = c_1(\epsilon ) - c_2(\epsilon ) \left\Vert \Delta l\right\Vert _2^2. \end{aligned}$$

(3)

The distribution of the perturbed vector $l' = l / \sqrt{1 + \epsilon ^2} + \Delta l$, which is of interest in the definition of LLAR, differs from the one of $\Delta l$ only by its mean, and thus its log-likelihood as a function of $\Delta l$ is the same. Also, (3) shows that the condition 4 (Sect. 3.5) on the noise distribution is satisfied with $\nu$ being the Euclidean distance.

4.5 Optimization problem for bounded latent perturbation search

To measure LAGA and LARA (Sect. 3.6), it is sufficient to check whether LLAR at the current latent point is bounded with a defined likelihood $\tau$ (according to the noise model from Sect. 4.3): that is, any perturbation whose likelihood is at least $\tau$, is class-preserving. According to Eq. 3, each positive value $\tau$ uniquely corresponds to a particular value of the $\ell _2$ norm of the perturbation $\Delta l$ around $l / \sqrt{1 + \epsilon ^2}$. For convenience, we will measure perturbation likelihood with its scaled norm $\left\Vert \cdot \right\Vert _2^s = \left\Vert \cdot \right\Vert _2 / \sqrt{n_L}$. With this scaling, the expected squared scaled norm of a multidimensional vector distributed according to N(0, I) is one. The following function transforms the likelihood of $\Delta l$ to $\left\Vert \Delta l\right\Vert _2^s$:

$$\begin{aligned} g_\epsilon (\tau ) = \sqrt{\frac{c_1(\epsilon ) - \log \tau }{n_L \cdot c_2(\epsilon )}}. \end{aligned}$$

We also introduce the following auxiliary definitions:

• $l_0$ is the initial latent vector, where a LLAR specification should be checked. It corresponds to some input vector x with its available label i: $l_0 = E_i(x)$.

• The decay factor $d = 1 - 1 / \sqrt{1 + \epsilon ^2}$ ($0 \le d \le 1$) is the amount of reducing the vector l prior to the search of a perturbation.

• $l_1 = (1 - d) l_0 = l_0 / \sqrt{1 + \epsilon ^2}$ is the reduced vector, which is the mean of the perturbation $\Delta l$.

Thus, we need to check whether there is an adversarial perturbation $\Delta l$ with $\left\Vert \Delta l\right\Vert _2^s \le \rho$, where $\rho = g_\epsilon (\tau )$, that makes the classifier ${\mathcal {N}}$ classify $D_i(l_1 + \Delta l)$ as not belonging to class i. Suppose that an objective function ${\mathcal {O}}: {\mathbb {R}}^{n_L} \rightarrow {\mathbb {R}}$ is available such that ${\mathcal {O}}(\Delta l) > 0$ implies correct classification and ${\mathcal {O}}(\Delta l) < 0$ implies misclassification. We take

$$\begin{aligned} {\mathcal {O}}(\Delta l) = s(i) - \max _{1 \le j \le m, j \ne i} s(j), \text {~where~} s(j) = S_{\mathcal {N}}(D_i(l_1 + \Delta l), j). \end{aligned}$$

It is almost everywhere differentiable due to the corresponding assumptions on $S_{\mathcal {N}}$ and $D_i$. Then we can solve the following constrained optimization problem with gradient-based techniques:

$$\begin{aligned} {{\,\mathrm{minimize}\,}}_{\Delta l : \, \left\Vert \Delta l\right\Vert _2^s \le \rho } {\mathcal {O}}(\Delta l). \end{aligned}$$

(4)

4.6 Intuition for non-zero decay factor

At first glance, viewing latent perturbations as a perturbation of $l_1$ but not $l_0$ (which equals $l_1$ only in the case of zero noise) may be confusing. The intuitive explanation, on the other hand, is in line with the purpose of division by $\sqrt{1 + \epsilon ^2}$ in (1), which is needed to reduce the covariance matrix of the distribution of perturbed vectors (with unperturbed vectors $l \sim N(0, I)$) back to I. Decay moves the search region to the area of more likely (having a smaller norm) vectors. Again, we remind that the likelihood in ${\mathcal {L}}_{i}$ in the general case does not correspond to the likelihood in ${\mathcal {X}}_{i}$. Still, in our experiments, decay moves latent vectors towards “averaged” representatives of each class.

4.7 Latent perturbation search with PGD

The constrained problem (4), considered for an approximation $E_y(x)$ of a data element (x, y), corresponds to checking a threshold specification on LLAR. Our proposed untargeted attack that solves this problem is a variant of PGD (Madry et al., 2018). PGD is started from a random latent perturbation within the allowed $\rho$-ball and is run until a misclassification is achieved, i.e., ${\mathcal {O}}(\Delta l) < 0$, but no longer than for a predetermined number of steps. The learning rate is set to ensure that the boundary of the $\rho$-ball can be reached from any point inside it. To avoid exploding or vanishing gradients, as in (Madry et al., 2018), we scale $g = \nabla {\mathcal {O}}(\Delta l)$ with its $\ell _2$ norm (specifically, we divide g by $\left\Vert g\right\Vert _2^s$). The optimization procedure is illustrated in Fig. 2.

Fig. 2

Graphical interpretation of latent perturbation search with PGD. The grey circle is the region where the adversarial perturbation $\Delta l$ is searched, and l is the current candidate solution

Next, we consider evaluation of performance metrics that are based on LLAR. The process is similar to evaluation of conventional adversarial robustness, with the only essential differences being the search of perturbations in the latent space instead of the original one and the replacement of the original image with its decayed version. Accordingly, evaluation of LAGA and LARA differs from the one of LGA and LRA by using the PGD adversary with the corresponding $\rho$ to alter the generated or approximated image prior to submitting it to the classifier. To increase reliability, PGD should be run multiple times. To evaluate LAGS and LARS, minimum perturbation bounds $\rho$ need to be calculated and averaged. To approximately find the minimum norm $\rho$ of a class-changing perturbation without pre-setting it, we apply the following techniques:

• Set $\rho$ to a large value (we use $\rho = 2.5$) and start PGD with a small learning rate at $\Delta l = 0$. It will reach some solution, whose norm could be used as an approximation for minimum $\rho$.

• The solution above might be prone to reaching local optima, which can be mitigated by several restarts from different points. In this case, to enforce norm minimization, each new restart is done with $\rho$ set to the scaled norm of the previously found solution, and the learning rate is reduced proportionally to the shrinkage of $\rho$.

To evaluate LAGS and LARS, we also tried DeepFool (Moosavi-Dezfooli et al., 2016), which is an algorithm to find minimum $\ell _p$ adversarial perturbations. Essentially, it is a variant of gradient descent with specifically chosen step magnitudes that are intended for fast convergence to a perturbation lying on the decision boundary of the classifier. Unfortunately, we observed its frequent divergence on our optimization problem. Gradient clipping resumed convergence, although it often cannot be achieved in just a few steps as in (Moosavi-Dezfooli et al., 2016). Thus, for the lack of apparent benefits of using DeepFool, in our experiments we apply only PGD.

5 Experimental evaluation

5.1 Implementation and experimental setup

The proposed framework of evaluating feed-forward ANN classifier performance with generative models was implemented in Python with PyTorch. The code and models used to obtain the results described in this section are publicly available online.² As the case studies, we considered the following image classification problems:

• 1. MNIST (LeCun, 1998) digit classification ($m = 10$ classes). As generative models, for MNIST, we trained a WGAN (Arjovsky et al., 2017) with $n_L = 64$ for each class, and implemented $E_i$ with gradient descent (Adam with 4 restarts) over latent codes. Examples of images reconstructed and generated by these models are given in Fig. 6 (top).

• 2. Gender predictions based on face photos, using the CelebA (Liu et al., 2015) dataset ($m = 2$ classes: 1 = “female”, 2 = “male”; images were center-cropped and resized to 128$\times$128 pixels). For CelebA, we trained PIONEER (Heljakka et al., 2018, 2020) generative autoencoders for each dataset and class with $n_L = 511$. Examples of images produced by the models are given in Fig. 6 (middle)—note that the visual quality of reconstructed images is somewhat better compared to generated images.

• 3. Scene type prediction using the LSUN (Yu et al., 2015) dataset ($m = 2$ classes: 1 = “bedroom”, 2 = “church outdoor”; images were center-cropped and resized to 128$\times$128 pixels). For LSUN scene types, we also trained PIONEER models with $n_L = 511$. However, as seen from Fig. 6 (bottom), except for bedroom reconstructions, the visual quality of images produced by PIONEER models for LSUN is worse compared to CelebA images.

For each of these classification problems, we trained fifteen deep CNN classifiers (see "Appendix C" for details) divided into five groups with three classifiers in each:

• 1. ${\mathcal {N}}_\text {UT}$ (“undertrained”): classifiers trained in a usual way, without data augmentation, but only for one epoch (to intentionally achieve lower accuracy);

• 2. ${\mathcal {N}}_\text {NR}$ (“non-robust”): the same as above, but trained for several epochs;

• 3. ${\mathcal {N}}_\text {CA}$ (“conventional augmentation”): classifiers trained in a usual way, with conventional data augmentation;

• 4. ${\mathcal {N}}_\text {R}$ (“robust”): classifiers trained on images corrupted with visible Gaussian noise (Gilmer et al., 2019);³

• 5. ${\mathcal {N}}_\text {B}$ (“both”): classifiers trained with both conventional data augmentation and noise corruption.

In addition, a limited evaluation on several pretrained classifiers was performed on ImageNet (Russakovsky et al., 2015). The details of these experiments will be reported separately in Sect. 5.4. Finally, for all the considered generative models, we report the values of their reconstruction and generation performance metrics in Table 2.

Table 2 Performance metrics of used generative models

5.2 Performance evaluation using original space metrics

The performance metrics of the above deep CNN classifiers in the original space are reported in Table 3. From this table, it is visible that, as expected, training with Gaussian noise achieved not only noise corruption robustness but also adversarial robustness, and the latter two are associated. In addition, a trade-off is visible between the accuracy of the classifiers on clean images (hereinafter, clean accuracy) and adversarial robustness, which is in agreement with previous observations (Tsipras et al., 2018).

Table 3 Performance metrics of considered CNN classifiers measured in the original space

5.3 Performance evaluation using the proposed latent space metrics

We calculated the values of the proposed latent space performance metrics for all aforementioned classifiers. The corresponding results are provided in Table 4 and Fig. 3. We start interpreting these results from LGA and LRA, which can be regarded as quality measures of generation and reconstruction capabilities of generative models that are complementary to the ones reported in Table 2. For CelebA and LSUN, in Fig. 3, plots 1 and 4, it is visible that clean accuracy is correlated with both LGA and LRA. The stronger correlation of LRA and clean accuracy can be explained by better reconstruction capabilities of our PIONEER models compared to their generation capabilities. On MNIST, the associations of clean accuracy with LGA and LRA are roughly the same (Pearson’s $r = 0.5$). Based on these observations, we conclude that the used generative models are suitable for evaluation of other proposed metrics.

Table 4 Latent space performance metrics of considered CNN classifiers

Fig. 3

Correlation plots for some of the data presented in Table 4 (plots 1–6, 8–9, 11–12) and additional data (plots 7 and 10). Plots are made for CelebA (blue crosses) and LSUN (orange circles) data combined (MNIST data is not shown). Plots 1 and 4 show the relation between clean accuracy, LRA and LGA. Plots 2–3 and 5–6 show an association between clean accuracy and latent adversarial robustness (measured as LAGS, LAGA, LARS, LARA). Plots 7 and 10 show an association between conventional adversarial robustness (measured as adversarial severity with respect to perturbations bounded by scaled $\ell _2$ norm) and the averaged scaled $\ell _2$ norm of found approximately minimum latent perturbations. Plots 8–9 and 11–12 demonstrate the inconclusive results regarding the association between conventional adversarial robustness and latent adversarial robustness. For each plot, Pearson’s and Spearman’s correlation coefficients (r and $\rho$, respectively) are given

Next, we comment on LLNA, which is a local metric, unlike the others. We computed its values on particular images and show several noise-based perturbations used in these computations in Fig. 4. Noise addition appeared to be a very sample-inefficient adversary, but the values of LLNA can be treated as prediction stability measures. For example, for the reconstructed (second) image in the second row of Fig. 4, the prediction of ${\mathcal {N}}_\text {NR}$ is incorrect, and this also reflects in low accuracy of perturbed images (e.g., for $\epsilon = 0.5$, the LNNA on this image is 82.5%). The same image is also somewhat difficult for ${\mathcal {N}}_\text {R}$ (for $\epsilon = 0.5$, LLNA = 92.0%).

Fig. 4

Examples of perturbations for CelebA and LSUN images of each class (left: “female”, “bedroom”, right: “male”, “church outdoor”) that were generated as latent Gaussian noise. In each row: the original image, the image reconstructed by PIONEER ($\epsilon = 0$), then four perturbed reconstructed images with increasing noise magnitudes $\epsilon = 0.25, 0.5, 0.75, 1$. Green labels show classification outcomes of ${\mathcal {N}}_\text {NR}$ (on the first line) and ${\mathcal {N}}_\text {R}$ (on the second line). All images in this figure have resolution 128$\times$128

The following findings, which are more prominent, are related to metrics that evaluate adversarial robustness in latent spaces:

• 1. We found association between clean accuracy and latent adversarial robustness measured as LAGS, LAGA, LARS, and LARA—see Fig. 3, plots 2–3 and 5–6. In addition, distribution plots of approximately minimum perturbations found with PGD that were used in computing LAGS and LARS are given in Fig. 10. For LARS, examples of such perturbations are shown in Figs. 5, 7 and 8 . This finding implies that latent space perturbations may be valuable in training ANN classifiers further.

• 2. The results regarding the association of the traditional and conventional adversarial robustness are inconclusive. While the measured values of conventional adversarial severity have a small correlation with LARS and LAGS, they have a negative correlation with LARA and LAGA—the corresponding plots are given in Fig. 3, plots 8–9 and 11–12. This pattern is similar regardless of the dataset, $\epsilon$ or the choice of the norm to evaluate conventional adversarial severity. This outcome might have been caused by the difference in PGD search strategies used to evaluate these two kinds of metrics. In addition, these correlations are not required to be identical as the precise values of both these metrics are different statistics of the real minimum norms of adversarial perturbations (mean for LARS and LAGA and percentile rank for LARA and LAGA). Overall, we did not find evidence that increasing conventional adversarial robustness increases latent adversarial robustness metrics, but it is not possible to conclude that they are not associated.

• 3. As visible from Figs. 5, 7, and 8, latent adversarial perturbations are surprisingly small on CelebA and LSUN and result in adversarial images that are perceptually close to the originals. Even though we do not have consistent results regarding the influence of conventional robustness on latent space robustness, the adversarial images computed for robust classifiers are, on average, further away from the original ones (despite having similar distances in the latent space). This distance was measured with $\ell _1$ and $\ell _2$ norms in the original space, and the increase of this distance is visible in Fig. 10, columns 3 and 4.

Fig. 5

Examples of approximately minimum latent CelebA and LSUN image perturbations with $\epsilon = 1~(d = 0.293)$, each found with a single run of PGD from $\Delta l = 0$, for classifiers ${\mathcal {N}}_\text {NR}$ and ${\mathcal {N}}_\text {R}$. In each row, images are given in the following order: x, the real image (with classification outcomes of ${\mathcal {N}}_\text {NR}$ and ${\mathcal {N}}_\text {R}$ shown in green); $x_0 = D_i(l_0)$, the reconstructed image (with both classification outcomes); $x_1 = D_i(l_1)$, the decayed image (with both classification outcomes); $\Delta x = x_1 - x_0$, the difference between two previous images; $x'_\text {NR} = D_i(l'_\text {NR})$, the perturbed image for ${\mathcal {N}}_\text {NR}$ (with the classification outcome of ${\mathcal {N}}_\text {NR}$); $\Delta x^{}_\text {NR} = x'_\text {NR} - x_1$, the perturbation for ${\mathcal {N}}_\text {NR}$; $x'_\text {R} = D_i(l'_\text {R})$, the perturbed image for ${\mathcal {N}}_\text {R}$ (with the classification outcome of ${\mathcal {N}}_\text {R}$); $\Delta x^{}_\text {R} = x'_\text {R} - x_1$, the perturbation for ${\mathcal {N}}_\text {R}$. All images in this figure have resolution 128$\times$128

As for the validity of our study, the small size of the found latent space perturbations indicates that our proposed PGD-based untargeted attack is successful. At the same time, generated images require smaller latent space perturbations—this can be explained by lower quality of generated images, which makes classifiers less confident in their initial predictions. On the other hand, on MNIST, perturbations are very large (Fig. 10, two topmost plots in the first column), significantly raise the norm of the perturbed vector (Fig. 10, two topmost plots in the second column) and thus exploit the part of the latent space where the generative models were not trained to work. This can be explained by the simplicity of the MNIST classification problem.

Finally, we confirmed the meaning of decay in the latent space as a countermeasure against the increase of the norm of the latent vector by the adversary: as visible from Fig. 10, column 2, perturbed vectors typically exceed unperturbed vectors by norm. This phenomenon is explained by (1) the lower probability density of vectors with large latent space norms and the associated lack of classifier training on such less plausible input images, and (2) a higher ease to exploit a weakness of a generative model with the same sort of vectors. In particular, the second explanation applies to CelebA, where roughly half of approximately minimum latent space perturbations found with $\epsilon = 0.5~(d = 0.106)$ contained visual artifacts, even though the likelihood of perturbed images in ${\mathcal {L}}_i$ was actually higher than the one of unperturbed images. With $\epsilon = 1~(d = 0.293)$, the visual quality of perturbed images was higher. On the other hand, on all datasets, even with $\epsilon = 1~(d = 0.293)$, decayed images were visually close to the originals (this is visible on Figs. 5, 7, and 8, columns 2–4).

5.4 Experiments on ImageNet

To demonstrate the possibility of evaluating the proposed metrics for larger classifiers and more challenging classification problems, we also considered ImageNet-1k image classification with a reduced experimental setup. As a generative model, we used a pretrained⁴ class-conditional BigGAN (Brock et al., 2018) with $n_L = 128$ and image size of 128$\times$128. The details of our experimental setup are:

• 1. We only computed latent generation metrics since we do not have a corresponding inverter model, and decoding the image with gradient-based search, like we did on MNIST, would have slowed the experiments significantly. To increase the visual quality of generated images, we sampled latent vectors with a built-in decay of 0.25.

• 2. For the same reason of computational complexity, we evaluate pretrained ImageNet classifiers and considered a smaller number of them. We took four non-robust models from PyTorch Model Zoo⁵ and one robust classifier by Santurkar et al. (2019). All these classifiers accept input images of sizes 256$\times$256 or 224$\times$224, so we upsampled the generated images with bicubic interpolation.

• 3. Adversarial examples used to evaluate conventional adversarial severity were searched for in the 128$\times$128 original space, i.e., the interpolation layer was regarded as the first layer of a classifier. This was done to make the results comparable between classifiers with different input sizes.

The results of experiments are shown in Table 5 and examples of approximately minimum adversarial perturbations are given in Fig. 9. Although the amount of data is small to give definite conclusions, we find a correlation between the accuracy and all latent space adversarial robustness metrics (Pearson’s correlation coefficients $0.47 \le r \le 0.68$), and an even stronger correlation of LGA with these metrics ($0.79 \le r \le 0.97$). Unlike our previous findings, latent space adversarial robustness is now positively correlated with conventional adversarial robustness ($0.16 \le r \le 0.57$). However, while having notably larger conventional robustness, the robust classifier is not very different from others in terms of latent space adversarial robustness.

Table 5 Results of experiments on ImageNet

5.5 Threats to validity

Below, we list the identified threats to the validity of our study and comment on them:

• 1. To keep the time required to perform the experiments manageable, most of them were done on CNN classifiers of small size (17—497 thousand trainable parameters), recognizing a small number of classes—it may appear that state-of-the-art classifiers have different patterns of latent space performance metric values. Our evaluation of ImageNet classifiers is limited and only demonstrates the possibility of applying the proposed methods to complex classification tasks. Yet, we have checked that (1) for the classifiers that we have studied, a connection between adversarial robustness and noise corruption robustness (Gilmer et al., 2019) exists, (2) on MNIST and CelebA, our robust classifiers have limited capabilities of image generation (Santurkar et al., 2019). On LSUN, we have seen that optimizing class activation of robust classifiers adds qualitatively different features to the image compared to non-robust classifiers, but we have not recognized the resulting images as bedrooms nor outdoors.

• 2. As we measure latent space adversarial robustness (LAGS, LARS, LAGA, LARA) with imprecise attack approaches, we overestimate the values of these metrics. This bias might have resulted in our classifiers ranked wrongly according to the computed values. PGD was shown to work well in the original space (Madry et al., 2018), but there is so far no similar set of experiments that confirm this property in latent spaces. We used PGD with 12 restarts to compensate for the possibility of such a bias. In certain cases (search of minimum adversarial perturbations on CelebA and LSUN), we used a single PGD run with a smaller learning rate, but in these cases, we had ensured that such runs differ insignificantly from the ones of PGD with restarts in terms of the resulting metric values.

• 3. On LSUN, the small size of the validation set (600 images) may have resulted in prematurely early stopping of training and imprecise accuracy estimates. In addition, the corresponding generative models produced random images with visible flaws. Yet, our observations for this dataset are not very different from the ones for CelebA, and perfect generative models might be hard to achieve on custom datasets.

• 4. PIONEER (CelebA and LSUN) models are designed to be trained to generate images from normalized latent vectors, and the latent distribution is actually the uniform distribution on the unit sphere instead of the Gaussian. In this paper, this has led to all reconstructed and generated images having unit scaled norm. Nonetheless, the decoder was capable of accepting unnormalized latent vectors, and decay still worked intuitively, i.e., by softening prominent features of images. This effect might have been caused by N(0, I) and the uniform distribution on the unit sphere being very similar in multidimensional spaces: $\ell _2$ norms of high-dimensional standard Gaussians are concentrated around $\sqrt{n_L}$.

• 5. As the adversarial examples considered in this paper are generated images, it is impossible to conclude that the classifiers actually make a mistake when classifying the generated adversarial examples differently. For example, the problem of determining the gender of a person who does not exist is not well-defined, but this also applies to other real-world object classification problems. Our definitions of metrics only require that the classification decision is changed, so this problem does not influence the soundness of these definitions. However, this also means that the values of the proposed metrics are not proven to be indicators of good classifier performance according to human judgment. A possible solution to address this problem would be to get manual labels of generated adversarial examples (Song et al., 2018b).

• 6. All the proposed latent space performance models rely on the generative models, and thus the computed values of these metrics depend on the quality of approximation of the original training/validation distribution and the choice of the generative model. In particular, due to a lower quality of the used generative models for LSUN (especially low generation quality for outdoors), our results for this dataset may be less reliable. Yet, we considered several datasets and kinds of generative models, and the correlation of the accuracy with latent space robustness metrics was found in each of these cases.

6 Related work

6.1 Adversarial examples in latent spaces

A number of works used generative models to create adversarial attacks and/or defenses. Zhao et al. (2017) proposed an approach to search adversarial examples in the latent space of a GAN, also measuring them with $\ell _2$ norms. This approach is white-box and is based on directed sampling rather than gradient descent, which makes it applicable to discrete input data, such as in natural language processing tasks. By contrast, our techniques operate in a black-box setting and only with feed-forward ANNs accepting continuous data. Nonetheless, (1) being based on gradient descent, our latent perturbation search approach is able to find perceptually smaller perturbations compared to the ones presented by Zhao et al. (2017), (2) we consider a more general framework of transforming data to the latent space and back, (3) we connect latent adversarial robustness to a “natural” model of noise in the latent space and this way motivate the use of the $\ell _2$ norm, (4) we search adversarial examples for larger classification tasks (128$\times$128 instead of 64$\times$64) and latent spaces (511 dimensions instead of 128), and (5) we focus on computing performance metrics for classifiers and not on finding adversarial examples per se.

Song et al. (2018b) created latent space adversarial examples from scratch. This was done using a class-conditional AC-GAN, and evaluation was in particular done on the CelebA (gender classification) and MNIST datasets. We also search for adversarial examples based on generated data items, however, (1) again, we do it for images larger than 64$\times$64, (2) we consider the untargeted attack scenario and use a different approach to generate adversarial examples, (3) our approach is not restricted to AC-GANs, and (4) we focus on computing performance metrics rather than finding adversarial examples.

Mirman et al. (2020) developed an approach to formally verify properties of one-dimensional interpolations in the latent space of a generative model. The idea is to consider a set of images that correspond to a line segment in the latent space associated with a meaningful high-level change in the image, and determine whether adversarial examples exist on this line, or the probability of getting an adversarial example given a distribution on the input line segment. In our work, we search for adversarial examples in a multidimensional setting, without focusing on specific high-level features, and do this with imprecise approaches.

Generative models were used as defenses against adversarial attacks (Samangouei et al., 2018; Song et al., 2018a). For example, the Defense-GAN (Samangouei et al. 2018) approach protects image classifiers from adversarial attacks by replacing their input with an approximation in the latent space of a GAN (similarly to what is done when computing LRA in our work). This defense was broken by Jalal et al. (2019) with an optimization procedure in the latent space subject to a norm constraint in the original space. Our results are in line with this work, since we similarly approximate input images using a latent space of a generative model, and are able to find perceptually small perturbations that change the prediction of the classifier. Jalal et al. (2019) also proposed a defense approach based on the search of pairs of examples that are close in the latent space but are scored completely differently by the classifier, and subsequent augmentation of robust optimization with training on these pairs.

6.2 Robustness metrics for ANNs and their evaluation

Usually robustness of ANNs to adversarial attacks is measured relatively to a specific attack success. Yu et al. (2019) proposed an improvement over the default accuracy-based approach. By analyzing the decision surfaces of models, they note that robust models have smooth decision boundaries. The proposed metric reflects this by rewarding models with smooth decision surfaces.

The first authors to formalize the notion of adversarial robustness were Bastani et al. (2016), who proposed several metrics quantifying the network robustness, namely, pointwise robustness, adversarial frequency and adversarial severity (see Sect. 2.4). The authors compute the latter two through pointwise robustness, which is measured by approximation.

Exact pointwise robustness calculations was performed by Boopathy et al. (2019), although they refer to the measure as to the “lower bound on the image distortion.” Also, the notion of pointwise robustness was explored by Fawzi et al. (2018), who derived theoretical upper bounds for it. Weng et al. (2018) proposed an effective proxy measure of network robustness based on measuring Lipschitz constants, although it has received some criticism (Goodfellow, 2018). An alternative method to quantifying global robustness properties of networks was proposed by Gopinath et al. (2017), who developed a clustering algorithm that outputs a set of verified regions—a collection of hyperspheres where the network is guaranteed to produce the same label.

7 Discussion and conclusions

In this paper, we presented a framework to evaluate the performance of feed-forward ANN classifiers with the help of generative models. Within the framework, we proposed several performance metrics, the most interesting of which are related to measuring the robustness of classifiers to perturbations in latent spaces of these generative models. In addition, we presented techniques to evaluate these metrics for classifiers, including a novel PGD-based untargeted attack. The main motivation of our work is the property of generative models of mimicking the data distribution. This property implies that the adversarial perturbations that we consider result in natural data changes.

The proposed metrics allowed us to make several interesting observations regarding the performance of deep ANN classifiers on natural adversarial examples. We computed the values of these metrics on several CNN image classifiers and found an association between the accuracy of the classifiers on clean images and adversarial robustness in latent spaces. This implies that latent adversarial examples might be useful for further classifier training. We also did not reveal a notable impact of conventional adversarial robustness on its latent counterparts, except for the influence on the norms of latent adversarial perturbations in the original space.

A speculative explanation of the found connection between the accuracy and latent adversarial robustness is that the latter measures the vulnerability of the classifier to natural adversarial examples, while the accuracy measures the same for random natural examples. A similar interdependence of accuracy and robustness to natural adversarial examples of a different kind was experimentally found by Gu et al. (2019). An alternative explanation is based on the work by Gilmer et al. (2019), who demonstrated a connection between conventional adversarial robustness and robustness to corruption with Gaussian noise. When we move to latent spaces, the former becomes LARS/LARA, and the latter becomes the averaged version of LLNA, which, due to our noise model, is just LRA. In turn, for a generative model with good reconstruction quality, LRA is highly associated with accuracy. The finding of Gilmer et al. (2019) is exact for linear models and was shown to hold on CIFAR-10 and ImageNet nonlinear classifiers. In our case, we can imagine that the classifier accepts latent representations of class i, and is actually a composition of $D_i$ and the original classifier ${\mathcal {N}}$. Unfortunately, the same properties were not confirmed to hold for classifiers of this kind, and hence this explanation is speculative as well.

The majority of the proposed metrics relies on the choices of latent distributions as Gaussians and the corresponding Gaussian noise model for this distribution (Eq. 1) that together (1) make the noise preserve the distributions of unperturbed vectors ${\mathcal {L}}_i$ and (2) result in simple likelihood bounds as $\ell _2$ norms. The choice of Gaussians is very conventional, and there is at least one different possible choice: consider the uniform distribution on the unit sphere and the noise model that adds a random Gaussian vector and then normalizes the resulting vector to unit norm. This solution would still result in $\ell _2$ vector distances monotonically corresponding to noise likelihood. Some other choices would not achieve both properties (1) and (2). For example, a Gamma-distributed latent vector would sum with a Gamma-distributed noise vector and still remain Gamma-distributed, but the likelihood of such vectors is more difficult. Conversely, taking Laplace distributions would result in $\ell _1$ norm likelihood bounds, but summing the unperturbed vector and the noise would not preserve the distribution family.

The following research directions may be explored in future work:

• Check experimentally whether the findings of Gilmer et al. (2019) are also satisfied in latent spaces—this would further clarify the relationship between the accuracy and latent adversarial robustness.

• Perform robust manifold defense (Jalal et al., 2019) or other form of training with latent adversarial examples, and explore the impact of this training on the values of performance metrics.

• Perform a more thorough evaluation of ImageNet classifiers.

• The proposed latent space adversarial robustness metrics (LAGS, LARS, LAGA, LARA) can be treated as specifications for ANN classifiers, given a threshold on their values to be satisfied. Gradient-based approaches of checking them are imprecise, and verification of even simpler ANN properties was proven to be NP-hard (Katz et al., 2017). A precise, but more computationally intensive way of checking ANN specifications is formal verification (Anderson et al., 2019; Dutta et al., 2017; Huang et al., 2017; Katz et al., 2017, 2019; Ruan et al., 2018; Singh et al., 2019; Elboher et al., 2020).

• The approach could be modified to be applicable to evaluate safety and security of classifiers. First, a practical view on a “natural” adversary must account for the variability in the difficulty of real-world manipulation of high-level features of the classified objects (e.g., changing the tilt on one’s head is easier than changing facial features). Second, latent adversarial metrics should be shown to be related to the actual classification mistakes, at least according to human judgment.

Appendices

Appendix A: additional figures

Fig. 6

Examples of images reconstructed and generated by considered generative models. All CelebA and LSUN images in this figure and other images produced by PIONEER in the figures below have resolution 128$\times$128

Fig. 7

Additional examples of approximately minimum latent CelebA image perturbations with $\epsilon = 1~(d = 0.293)$. Images are arranged as in Fig. 5

Fig. 8

Additional examples of approximately minimum latent LSUN image perturbations with $\epsilon = 1~(d = 0.293)$. Images are arranged as in Fig. 5

Fig. 9

Examples of approximately minimum latent ImageNet image perturbations with $\epsilon = 1~(d = 0.293)$. Images are arranged as in Fig. 5 except that all the original images are generated and there is no reconstruction phase. The class labels used to generated the images are: “vestment”, “dog sled”, “jacamar”, “cannon”, “mailbox”, “Vizsla”, “projectile”, “canoe”, “wallaby”, “red fox.” To produce this figure, we used resnext as the non-robust (NR) classifier (see Sect. 5.4)

Fig. 10

Distribution plots (with Gaussian kernel density estimation) with statistics on approximately minimum latent image perturbations with $\epsilon = 1~(d = 0.293)$ found by PGD (600 images for each row of plots). l is the decayed latent vector, $\Delta l$ is the found perturbation, and $\Delta x$ is the change of the original image as a vector of pixel intensities. Colors correspond to classifiers as follows: ${\mathcal {N}}_\text {UT}$ is blue, ${\mathcal {N}}_\text {NR}$ is orange, ${\mathcal {N}}_\text {CA}$ is green, ${\mathcal {N}}_\text {R}$ is red, ${\mathcal {N}}_\text {B}$ is purple

B Appendix: proofs of convergence properties of the noise-adding distribution

Below, we prove that the points 2 and 3 of the properties of a noise-adding distribution (Sect. 3.5) are satisfied for $N_{\epsilon , l}$ defined according to (1) and ${\mathcal {L}}_i = N(0, I)$.

Theorem B.1

If ${\mathcal {L}}_i = N(0, I)$, $N_{\epsilon , l}$ is defined according to (1) and $\epsilon \rightarrow 0$, then random vectors $\lambda _\epsilon \sim N_{\epsilon , l}$ converge in distribution to $\lambda \equiv l$.

Proof

We will prove convergence in distibution according to the Cramér-Wold theorem. We need to show that for all vectors t, $t^\top \lambda _\epsilon$ converges in distribution to $t^\top \lambda$. That is, $\lim \limits _{\epsilon \rightarrow 0} {\mathbb {P}}(t^\top \lambda _\epsilon \le u) = F(u)$ for all $u \in {\mathbb {R}}$ where $F(u) = {\mathbb {P}}(t^\top \lambda \le u)$ is continuous. This is trivial for $t = 0$. Otherwise, we have:

$$\begin{aligned}&\begin{aligned} \lambda _\epsilon&\sim N\left( \frac{l}{\sqrt{1 + \epsilon ^2}}, \frac{\epsilon ^2}{1 + \epsilon ^2} I\right) ,\\ t^\top \lambda _\epsilon&\sim N\left( \frac{t^\top l}{\sqrt{1 + \epsilon ^2}}, \frac{\left\Vert t\right\Vert _2^2 \epsilon ^2}{1 + \epsilon ^2}\right) , \end{aligned} \\&\begin{aligned} \left| {\mathbb {P}}(t^\top \lambda _\epsilon \le u) - F(u)\right|&= \left| \frac{1}{2} + \frac{1}{2}\text {erf}\left( \frac{u - \frac{t^\top l}{\sqrt{1 + \epsilon ^2}}}{\frac{\left\Vert t\right\Vert _2 \epsilon }{\sqrt{1 + \epsilon ^2}}\sqrt{2}}\right) - \left[ t^\top l \le u \right] \right| \\&= \left| \frac{1}{2} + \frac{1}{2}\text {erf}\left( \frac{\sqrt{1 + \epsilon ^2}u - t^\top l}{\left\Vert t\right\Vert _2 \epsilon \sqrt{2}}\right) - \left[ t^\top l \le u \right] \right| \\&= \left| \frac{1}{2} + \frac{1}{2}\text {erf}\left( \frac{u - t^\top l + \left( \sqrt{1 + \epsilon ^2} - 1\right) u}{\left\Vert t\right\Vert _2 \epsilon \sqrt{2}}\right) - \left[ u - t^\top l \ge 0 \right] \right| . \end{aligned} \end{aligned}$$

If $u > t^\top l$, then the nominator inside $\text {erf}$ is positive for sufficiently small $\epsilon$, and $\text {erf}$ will approach one, making the limit of the entire expression zero. The case of $u < t^\top l$ is similar. Finally, $u = t^\top l$ is a point of discontinuity of F(u). $\square$

Theorem B.2

If ${\mathcal {L}}_i = N(0, I)$, $N_{\epsilon , l}$ is defined according to (1) and $\epsilon \rightarrow +\infty$, then random vectors $\lambda _\epsilon \sim N_{\epsilon , l}$ converge in distribution to $\lambda \sim {\mathcal {L}}_{i}$.

Proof

We follow the outline of the previous proof. Now, for all vectors t and scalars u, we need to show that $\lim \limits _{\epsilon \rightarrow +\infty } {\mathbb {P}}(t^\top \lambda _\epsilon \le u) = F(u)$, where $F(u) = {\mathbb {P}}(t^\top \lambda \le u)$. This is trivial for $t = 0$. Otherwise, $t^\top \lambda \sim N\left( 0, \left\Vert t\right\Vert _2^2\right)$ and we have:

$$\begin{aligned} F(u) = \frac{1}{2} + \text {erf}\left( \frac{u}{\left\Vert t\right\Vert _2 \sqrt{2}}\right) , \\ \begin{aligned} \left| {\mathbb {P}}(t^\top \lambda _\epsilon \le u) - F(u)\right|&= \left| \frac{1}{2} + \frac{1}{2}\text {erf}\left( \frac{\sqrt{1 + \epsilon ^2}u - t^\top l}{\left\Vert t\right\Vert _2 \epsilon \sqrt{2}}\right) - \frac{1}{2} - \frac{1}{2}\text {erf}\left( \frac{u}{\left\Vert t\right\Vert _2 \sqrt{2}}\right) \right| \\&= \frac{1}{2}\left| \text {erf}\left( \frac{\sqrt{1 + \epsilon ^2}u - t^\top l}{\left\Vert t\right\Vert _2 \epsilon \sqrt{2}}\right) - \text {erf}\left( \frac{u}{\left\Vert t\right\Vert _2 \sqrt{2}}\right) \right| \\&= \frac{1}{2}\left| \text {erf}\left( \frac{\sqrt{1 + \epsilon ^2}}{\epsilon }\frac{u}{\left\Vert t\right\Vert _2 \sqrt{2}} - \frac{1}{\epsilon }\frac{t^\top l}{\left\Vert t\right\Vert _2 \sqrt{2}}\right) - \text {erf}\left( \frac{u}{\left\Vert t\right\Vert _2 \sqrt{2}}\right) \right| . \end{aligned} \end{aligned}$$

The last expression approaches zero when $\epsilon \rightarrow +\infty$. $\square$

C Appendix: classifier training procedure

All classifiers listed in Sect. 5.1 were trained as follows. We considered three slightly different CNN architures. Two of them are based on the script https://github.com/keras-team/keras/blob/f295e8ee39d4ba841ac281a9337d69c7bc5e0eb6/examples/cifar10_cnn.py and differ in their depth. Essentially, these are simple CNN architectures composed of convolutional blocks, ReLU nonlinearities, batch normalization, max-pooling, dropout, and a fully connected layer with ${{\,\mathrm{softmax}\,}}$ on top. One more architecture used the same operations, but was based on residual blocks. Training was done with RMSprop. In each epoch, we took 100 thousand random images from the training set. The learning rate was set to 0.0004 and multiplied by 0.75 after each epoch. Training continued for up to 8 epochs, but was stopped prematurely if validation accuracy had not increased during the previous epoch. The following was specific to different classifier types:

• 1. ${\mathcal {N}}_\text {UT}$: No data augmentation was used. Training was stopped after one epoch.

• 2. ${\mathcal {N}}_\text {NR}$: No data augmentation was used. Training was done for the remaining 7 epochs starting from ${\mathcal {N}}_\text {UT}$.

• 3. ${\mathcal {N}}_\text {CA}$: Training images were augmented with conventional approaches: small affine transformations, color distortions and erasures of small image parts.

• 4. ${\mathcal {N}}_\text {R}$: Training images were augmented with Gaussian noise of magnitude $\sigma = 0.8$ (pixel intensities belong to $[-1, 1]$). Note that this is different from the work (Gilmer et al. 2019), where for each image first $\sigma$ was selected uniformly at random and then noise was added. Training was started from ${\mathcal {N}}_\text {NR}$.

• 5. ${\mathcal {N}}_\text {B}$: Training images were first augmented conventionally (as in the case of ${\mathcal {N}}_\text {CA}$), and then with Gaussian noise (as in the case of ${\mathcal {N}}_\text {R}$). Training was started from ${\mathcal {N}}_\text {CA}$.