1 Introduction

Strong field phenomena have been widely studied using the strong field approximation (SFA) which gives an approximate analytic solution to the time-dependent Schrödinger equation (TDSE) [1]. Contrary to a fully numerical treatment of the TDSE, such an approximate analytical treatment provides valuable information about the underlying interaction mechanisms as in the case of high-order harmonic generation [2]. Within the standard SFA however, the Coulomb potential is neglected once the electron reaches the continuum through tunneling. This means that high-order processes in the Coulomb potential such as frustrated tunneling [3, 4], Coulomb focusing [5] or low energy structures in above-threshold ionization (ATI) spectra [6], which are caused by the residual ion’s Coulomb potential, are not described by the usual SFA. As a result, attempts have been made to include the Coulomb potential through a Born series. However, given the complexity of the analytical calculations, only the first two terms of this series have been evaluated, at least approximately [7]. In this context, the question of the convergence properties of this Born series inevitably arises.

This question has been addressed by Galstyan et al. in [8]. Through a reformulation of the SFA, they have developed a numerically stable approach that allows one to generate high-order terms of this Born series. In the case of the interaction of atomic hydrogen with a short laser pulse, they showed that for photon energies exceeding the ionization potential, where convergence is expected, the Born series actually diverges. A deeper analysis indicates that this divergence does not result from the infinite range of the Coulomb potential. For photon energies below the ionization potential, the convergence of the series is much more difficult to probe since many high-order terms must be evaluated. However, it is clear that the inclusion of the first high-order terms strongly affects, not only quantitatively but also qualitatively the results for the electron energy spectrum.

Several alternative approaches have been developed to modify the SFA in order to take into account the effect of the Coulomb potential. Perelomov and Popov introduced a first-order correction in the Coulomb potential through the classical action [9]. Torlina and Smirnova [10] generalized their ideas and developed a semi-analytical R-matrix approach. Coulomb corrections have also been treated through WKB-like approximations [11, 12] and through a semiclassical quantum trajectory approach [13,14,15]. Faisal [16, 17] developed an S-matrix theory in which final state Coulomb interactions are taken into account at all orders. More recently, we have developed a Faddeev-like iterative approach to generate a new Born-like series in the Coulomb potential of the ionic core and the dipole potential due to the external field [18]. The first-order term of this series coincides with the standard SFA. This new series has been used to calculate ionization properties such as the electron energy spectrum resulting from the interaction of atomic hydrogen with a high-frequency (photon energy larger than the ionization potential) electric field. Contrary to the SFA Born series, this new series converges rapidly to the results obtained by solving numerically the TDSE.

In this paper, we continue our work presented in [18]. We further examine the convergence properties of our Faddeev-like iterative approach as a function of frequency and intensity and show how this approach can also be used to calculate the excitation probability to individual excited states and the total excitation yield in addition to the ionization yield. Such an excitation process cannot be described by the usual SFA since, by nature, it is of high order in the Coulomb potential of the ionic core. For high frequencies and pulse durations in the attosecond regime, the convergence of the new Born series is fast making this approach particularly well adapted. For intermediate frequencies, \(\omega = 0.1\) a.u., we show that the series converges by calculating many orders and comparing the results with those obtained from the TDSE.

For low frequencies and few cycle pulses, experimental studies indicate that in the tunnel ionization regime, atomic excited states play a significant role. Nubbemeyer et al. [3] have shown that in the case of helium and for a broad range of field intensities up to \(10^{15}\) W/cm\(^2\), a substantial fraction of atoms survive the laser pulse in many excited states. To explain their experimental data, they proposed a mechanism whereby electrons returning to the parent ion are recaptured in excited states following a re-collision with the parent ion. They called this mechanism, frustrated tunneling. Later, Landsman et al. [4] studied in detail this frustrated tunneling process by means of a purely classical approach. They showed that although the recapture process into a Rydberg state following a re-collision of an electron with the parent ion does occur, the dominant process leading to Rydberg state creation came from slow electrons, which having tunneled through the barrier, do not return to the ion but are captured by the weak long range Coulomb field. Very recently, Hu et al. [19] have developed a SFA-based quantum model that includes a first-order correction in the Coulomb potential in order to study re-collision-based frustrated tunneling. We apply our Faddeev-like treatment to the excitation yield for hydrogen as a function of intensity at a frequency of 0.057 a.u. to compare the first-order term of our Faddeev-like series to their theory and to address the problem of the convergence of the series. We also analyze the excited state angular momentum distribution in order to improve our understanding of the recombination mechanism.

The present contribution is organized as follows. First and for the sake of clarity, we present briefly our Faddeev-like treatment. We analyze in more detail the expression of the first three terms of our Born-like series and discuss the physical processes that these terms describe. We subsequently discuss our numerical approach based on the solution of the coupled time-dependent inhomogeneous Schrödinger equations. In the Results section, we consider the interaction of atomic hydrogen with a radiation pulse for a range of frequencies and intensities. Our results for the excitation yield, the ionization yield and the population of given bound states are compared with those obtained by directly solving numerically the time-dependent Schrödinger equation (TDSE). We analyze the convergence of our Faddeev-like series for the probability of excitation to a given state. We discuss for low frequencies the pertinence of limiting in that case, our Faddeev-like expansion to the first-order term in the Coulomb potential in the spirit of the recently developed quantum model of Hu et al. [19] and we end with our conclusions.

Atomic units are used throughout unless otherwise specified.

2 Theory

2.1 Basic definitions

We consider a linearly polarized pulsed field and assume that the dipole approximation is valid. The vector potential \(\mathbf {A}(t)\) and the electric field \(\mathbf {{\mathcal {E}}}(t)\) at a given time t are defined as follows:

$$\begin{aligned} \mathbf {A}(t)= & {} -cb'(t)\mathbf {e}, \end{aligned}$$
(1)
$$\begin{aligned} \mathbf {{\mathcal {E}}}(t)= & {} b''(t)\mathbf {e}, \end{aligned}$$
(2)

where \('\) is the derivative with respect to time and \(\mathbf {e}\) is the unit vector along the polarization axis which we assume to coincide with the z-axis. c is the velocity of light and \(b'(t)\) is given by

$$\begin{aligned} b'(t)=\frac{1}{\omega }\sqrt{\frac{I}{I_0}}\sin ^2(\pi \frac{t}{T})\sin (\omega t), \end{aligned}$$
(3)

with I the pulse peak intensity, \(I_0\) the atomic unit of intensity, and \(\omega \) the photon energy. The pulse vanishes for \(t\le 0\) and \(t \ge T\) where \(T=2\pi N/\omega \) is the total pulse duration, N being the total number of optical cycles within the pulse. It is also convenient to define the following field-related expression:

$$\begin{aligned} \zeta (t)=\frac{1}{2}\int ^t_0\mathrm {d}\xi \left[ b'(\xi )\right] ^2. \end{aligned}$$
(4)

2.2 Faddeev-like treatment of interactions of lasers with one active electron systems

We consider the interaction of atomic hydrogen with the above-defined radiation pulse. The corresponding TDSE is:

$$\begin{aligned} \left[ i\frac{\partial }{\partial t}-H(t)\right] |\Psi (t)\rangle =0, \end{aligned}$$
(5)

where

$$\begin{aligned} H(t)=H_0+V_c+V_d(t). \end{aligned}$$
(6)

\(H_0\) is the kinetic energy operator, \(V_c\) is the Coulomb potential, and \(V_d(t)\) is the dipole interaction potential. Depending on the gauge, \(V_d\) takes two forms:

$$\begin{aligned} V_d^{(v)}=ib'(t)(\mathbf {e}\cdot \mathbf {\nabla }_r)+\zeta '(t), \end{aligned}$$
(7)

in the velocity gauge and

$$\begin{aligned} V_d^{(l)}=b''(t)(\mathbf {e}\cdot \mathbf {r}), \end{aligned}$$
(8)

in the length gauge. The initial condition is \(|\Psi (0)\rangle =|\varphi _0\rangle \) with \(|\varphi _0\rangle \) being the atomic hydrogen ground state.

We now take into account the fact that we have two potentials. Inspired by Faddeev’s approach, we write

$$\begin{aligned} |\Psi (t)\rangle =|\Psi _1(t)\rangle +|\Psi _2(t)\rangle , \end{aligned}$$
(9)

and replace Eq. (5) by the two following equations :

$$\begin{aligned}&\left[ i\frac{\partial }{\partial t}-H_0-V_c\right] |\Psi _1(t)\rangle =V_c|\Psi _2(t)\rangle , \end{aligned}$$
(10)
$$\begin{aligned}&\left[ i\frac{\partial }{\partial t}-H_0-V_d(t)\right] |\Psi _2(t)\rangle =V_d(t)|\Psi _1(t)\rangle . \end{aligned}$$
(11)

The initial conditions are \(|\Psi _1(0)\rangle = |\varphi _0\rangle \) and \(\quad |\Psi _2(0)\rangle = 0. \) Equations (10) and (11) may be solved, by iteration. At the zero iteration, we write \(|\Psi _1^{(0)}(t)\rangle = e^{-i\varepsilon _0 t}|\varphi _0\rangle \), where \(\varepsilon _0\) is the ground-state energy and \(\ |\Psi _2^{(0)}(t)\rangle = 0\). The first iteration consists in inserting \(|\Psi _1^{(0)}(t)\rangle \) in (11). This gives the equation satisfied by \(|\Psi _2^{(1)}(t)\rangle \) which in turn is inserted in (10) to obtain the equation for \(|\Psi _1^{(1)}(t)\rangle \):

$$\begin{aligned}&\left[ i\frac{\partial }{\partial t}-H_0-V_d(t)\right] |\Psi _2^{(1)}(t)\rangle =V_d(t)e^{-i\varepsilon _0 t}|\varphi _0\rangle , \end{aligned}$$
(12)
$$\begin{aligned}&\left[ i\frac{\partial }{\partial t}-H_0-V_c\right] |\Psi _1^{(1)}(t)\rangle =V_c|\Psi _2^{(1)}(t)\rangle , \end{aligned}$$
(13)

and so on.

The wave function associated with \(|\Psi (t)\rangle \) has to be normalized. Hence, we impose \(\langle \Psi (t)|\Psi (t)\rangle =1\) for any time t. In practice, we truncate our series and normalize the partial sum \(|\Psi ^{(n)}(t)\rangle =|\Psi ^{(0)}_1(t)\rangle + |\Psi ^{(1)}_2(t)\rangle + |\Psi ^{(1)}_1(t)\rangle + ... \).

To generate our series expansion, it is convenient to rewrite the differential Eqs. (10) and (11) in integral form:

$$\begin{aligned} |\Psi _1(t)\rangle= & {} e^{-\mathrm {i}\varepsilon _0t}|\varphi _0\rangle -\mathrm {i}\int _0^\infty \mathrm {d}\xi G^-_c(t,\xi )V_c|\Psi _2(\xi )\rangle ,\nonumber \\ |\Psi _2(t)\rangle= & {} -\mathrm {i}\int _0^\infty \mathrm {d}\xi G_{d}(t,\xi )V_{d}(\xi )|\Psi _1(\xi )\rangle . \end{aligned}$$
(14)

The Coulomb Green’s function \(G_c^-(\mathbf {r},t;\mathbf {r}',\xi )\) is expressed as a sum/integral of the Coulomb bound/continuum wave functions \({\tilde{\varphi }}^-_\alpha (\mathbf {r})\) in the configuration space

$$\begin{aligned}&G_c^-(\mathbf {r},t;\mathbf {r}',\xi )=\theta (t-\xi )\sum _\alpha {\tilde{\varphi }}^-_\alpha (\mathbf {r})e^{-i\varepsilon _\alpha (t-\xi )}{\tilde{\varphi }}^{-*}_\alpha (\mathbf {r}'), \nonumber \\&G_c^-(\mathbf {r},t;\mathbf {r}',t)=\delta (\mathbf {r}-\mathbf {r}'). \end{aligned}$$
(15)

The superscript − in \({\tilde{\varphi }}^-_\alpha (\mathbf {r})\) indicates that the Coulomb continuum wave function behaves asymptotically as an ingoing spherical wave. The Green’s function associated with the dipole interaction is expressed in terms of the Volkov wave functions \({\tilde{\chi }}_g(\mathbf {r},\mathbf {p},t)\) in a given gauge g (\(g\equiv V\) for the velocity gauge and \(g\equiv L\) for the length gauge)

$$\begin{aligned}&G_{d}(\mathbf {r},t;\mathbf {r}',\xi )=\theta (t-\xi )\int \frac{\mathrm {d}^3p}{(2\pi )^3}{\tilde{\chi }}_g(\mathbf {r},\mathbf {p},t){\tilde{\chi }}_g^*(\mathbf {r}',\mathbf {p},\xi ),\nonumber \\&G_{d}(\mathbf {r},t;\mathbf {r}',t)=\delta (\mathbf {r}-\mathbf {r}'). \end{aligned}$$
(16)

let us recall the expression of a Volkov wave function

$$\begin{aligned}&{\tilde{\chi }}_V(\mathbf {r},\mathbf {p},t)= e^{[\mathrm {i}\mathbf {p}\cdot \mathbf {r}-\mathrm {i}p^2t/2+\mathrm {i}b(t)(\mathbf {e}\cdot \mathbf {p})-\mathrm {i}\zeta (t)]}=e^{\mathrm {i}\mathbf {p}\cdot \mathbf {r}-\mathrm {i}S(\mathbf {p},t)}, \end{aligned}$$
(17)
$$\begin{aligned}&{\tilde{\chi }}_L(\mathbf {r},\mathbf {p},t)= e^{-\mathrm {i}b'(t)(\mathbf {e}\cdot \mathbf {r})}{\tilde{\chi }}_V(\mathbf {r},\mathbf {p},t)=e^{\mathrm {i}\mathbf {P}(t)\cdot \mathbf {r}-\mathrm {i}S(\mathbf {p},t)}.\;\;\; \end{aligned}$$
(18)

In these equations,

$$\begin{aligned} \mathbf {P}(t)= & {} \mathbf {p}-b'(t)\mathbf {e}, \\ S(\mathbf {p},t)= & {} \frac{1}{2}\int _0^t P^2(\xi )\mathrm {d}\xi . \end{aligned}$$

\(\mathbf {P}(t)\) is the canonical momentum of the electron and \(S(\mathbf {p},t)\) is the classical action.

Note that both Green’s functions alternate in the successive high-order terms. Furthermore, the presence of the Coulomb Green’s function allows us to consider different intermediate Coulomb transitions within the iterative scheme. For illustration, let us write the full ket \(|\Psi (t)\rangle \), i.e., the sum of \(|\Psi _1(t)\rangle \) and \(|\Psi _2(t)\rangle \) after the second iteration:

$$\begin{aligned}&|\Psi ^{(2)}(t)\rangle = e^{-\mathrm {i}\varepsilon _0t}|\varphi _0\rangle -\mathrm {i}\int _0^\infty \mathrm {d}\xi \ e^{-\mathrm {i}\varepsilon _0\xi }G_{d}(t,\xi ) V_{d}(\xi )|\varphi _0\rangle \nonumber \\&\quad -\int _0^{\infty }\mathrm {d}\xi _1\int _0^{\infty }\mathrm {d}\xi _2G_c(t,\xi _1)V_ce^{-i\varepsilon _0\xi _2}G_d(\xi _1,\xi _2)V_d(\xi _2)|\varphi _0\rangle . \end{aligned}$$
(19)

In this way, the first two terms of the above expansion coincide with that of the SFA expansion, when the potential \(V_c\) is chosen as a perturbation once the electron is ejected [8]. The last term of expression (19) for \(|\Psi ^{(2)}(t)\rangle \) describes the following process. The electron initially in the ground state of the atom absorbs a virtual photon creating a wavepacket consisting of bound and continuum states of the field-free atom (tunnel ionization) at time \(t=\xi _2\); it then propagates freely in the electric field until time \(t=\xi _1\) where it is scattered by the Coulomb potential; this scattering is followed by a propagation of the electron in the Coulomb potential without any influence of the external field until time t where it ends up in any bound or continuum state of the atom. If the final state of the atom is an excited state, this term is the lowest-order one that describes the so-called re-collision-based frustrated tunneling. Many higher-order terms in this Faddeev-like series expansion are expected to contribute to the treatment of frustrated tunneling and in particular to the re-collision-free recapture process . Whether or not the calculation of \(|\Psi ^{(2)}(t)\rangle \) is sufficient to describe qualitatively or/and quantitatively re-collision-based frustrated tunneling is a pertinent question that will be addressed later on in this paper. It is interesting to note that the first two terms in (19), namely \(|\Psi ^{(1)}(t)\rangle \), may be written in a different form. After some simple algebraic manipulations (see [8], Eq. (36) and also [20]), we have

$$\begin{aligned} |\Psi ^{(1)}(t)\rangle =G_d(t,0)|\varphi _0\rangle -\mathrm {i}\int _0^{\infty }\mathrm {d}\xi e^{-\mathrm {i}\varepsilon _0\xi }G_d(t,\xi )V_c|\varphi _0\rangle . \nonumber \\ \end{aligned}$$
(20)

Let us now address a few important points. The first one is related to the perturbative character of the expansion and its convergence. This point is difficult since both potentials participate equally preventing to define a clear perturbation parameter. It is the reason why, in the spirit of Faddeev’s approach in scattering theory, we prefer to qualify the present approach as iterative instead of perturbative. Let us remark that the expression (3) for \(b'(t)\) depends only on the variable \(\tau =\omega t\), where \(0\le \tau <\tau _N=2\pi N\) with N being the number of optical cycles. In this case, each successive iteration in (14) introduces an additional factor \(1/\omega \). So, we can expect that the convergence of this expansion is connected with the value of \(\omega \).

It is important to note that the wave function \(|\Psi ^{(1)}(t)\rangle \) depends on the gauge. Let us remember that two wave functions which are solutions of Eq. (5) for different forms of \(V_{d}(t)\) are connected with the well-known Göppert–Mayer (GM) phase transformation [21] (see also interesting remarks on the validity of this transformation in [22]). The approximate solutions of the system of coupled Eqs. (14) are not gauge invariant, because the zeroth-order term \(\exp (-\mathrm {i}\varepsilon _0t)|\varphi _0\rangle \) is the same for both gauges. We can make these terms gauge-invariant connecting them by GM phase-factor. In such a way, we obtain two families of gauge invariant approximate solutions up to any iterative order, but still, the L-gauge approximate solution of one family is not equal to the L-gauge approximate solution of the other family. A detailed discussion of this point is given in [18].

Finally, it is interesting to remark that Keldysh in his famous paper [23] wrote: “So far we have considered a transition from the ground state directly to the continuous-spectrum state. Let us consider now, in the next higher order of perturbation theory, a process in which the electron first goes over into an excited state, and then into the continuous spectrum”. The first term in Keldysh approach is nothing else than the usual SFA. What is remarkable is the fact that the next high-order term he is mentioning, involves the Coulomb Green’s function (see Eqs. (22)–(24) of his paper). This is possible to do self-consistently only within the scheme that is considered here.

2.3 Numerical implementation

In order to describe the numerical solution, we introduce a compact notation to generate the successive terms of our Faddeev-like series. Let us write the full ket \(|\Psi (t)\rangle \) as follows:

$$\begin{aligned} |\Psi (t)\rangle =|\varphi _0\rangle e^{-\mathrm {i}\varepsilon _0t}+|F(t)\rangle , \end{aligned}$$
(21)

with

$$\begin{aligned} |F(t)\rangle =\sum _{s=1}|F^{(s)}(t)\rangle , \end{aligned}$$
(22)

and the initial condition \(|F(0)\rangle = 0.\) The ket \(|F^{(s)}\rangle \) is obtained for \(s=1, 2, 3, \ldots \) by solving iteratively a system of coupled non-homogeneous time-dependent Schrödinger equations:

$$\begin{aligned}&\left[ \mathrm {i}\frac{\partial }{\partial t}-H_0-V_d(t)\right] |F^{(1)}(t)\rangle =V_d(t)e^{-\mathrm {i}\varepsilon _0t}|\varphi _0\rangle ,\nonumber \\&\quad \left[ \mathrm {i}\frac{\partial }{\partial t}-H_0-V_c\right] |F^{(2)}(t)\rangle =V_c|F^{(1)}(t)\rangle ,\nonumber \\&\quad \left[ \mathrm {i}\frac{\partial }{\partial t}-H_0-V_d(t)\right] |F^{(3)}(t)\rangle =V_d(t)|F^{(2)}(t)\rangle ,\nonumber \\&\quad \mathrm {etc}\ldots . \end{aligned}$$
(23)

Hence, for example, \(|F^{(1)}(t)\rangle = |\Psi ^{(1)}_2(t)\rangle ,\) and \(|F^{(2)}(t)\rangle = |\Psi ^{(1)}_1(t)\rangle \) in our earlier discussion on the iterative solution after Eqs. (10) and (11). Furthermore, \(|\Psi ^{(2)}(t)\rangle \) in Eq. (19) is \(|\Psi ^{(2)}(t)\rangle = |\varphi _0\rangle e^{-\mathrm {i}\varepsilon _0t} + |F^{(1)}(t)\rangle + |F^{(2)}(t)\rangle .\)

In order to numerically solve these equations, we use a spectral method which consists of expanding each \(|F^{(s)}(t)\rangle \) in a basis of a product of Coulomb Sturmian radial functions [24] and spherical harmonics. Let us note that most of the time propagation methods such as Arnoldi method or the Crank–Nicolson method are based on the well-known ansatz for the time evolution operator

$$\begin{aligned} U(t+\Delta t,t)\approx e^{-\mathrm {i}\Omega (t+\Delta t)}, \end{aligned}$$
(24)

where \(\Omega (t+\Delta t)\) is approximated for small \(\Delta t\) by using a Magnus expansion [25, 26] of the correct expression of \(U(t+\Delta t,t)\). However, these methods can no longer be used in the case of non-homogeneous equations. In the present case, we use a diagonally implicit Runge–Kutta method of order 2 [27] to determine the time-dependent coefficients in our basis expansion and hence the \(|F^{(s)}(t)\rangle \). Furthermore, at the end of the propagation, the solution to a given order has to be normalized.

Unexpectedly, the present numerical scheme turns out to be extremely stable. If we go back to Eqs. (23), we see that solving the first equation amounts to acting on the right-hand side of this equation with the Green operator associated with the dipole potential. Similarly, solving the second equation amounts to acting on the right-hand side of this equation with the Coulomb–Green operator. The fact that these Green operators depend on time and that the interaction time is finite implies that all the possible poles are no longer on the real axis of the complex energy plane. This prevents singularities to occur and facilitates the numerical integration.

In our spectral method, we take into account 64 values of \(\ell \), the angular quantum number (\(\ell =0\;\mathrm {to}\;63\)) and 2000 Coulomb Sturmian functions for each value of \(\ell \). Diagonalizing the atomic Hamiltonian matrix shows that more than 80 atomic bound states are well described for each value of \(\ell \). In particular, the energy of these states is obtained with a relative error of the order of \(10^{-13}\). The modulus square of the coefficient in front of these atomic states in the final wave packet gives the probability of excitation to these states. We checked that the convergence of these excitation probabilities as a function of \(\ell \) and n, the principal quantum number, is reached for values of \(\ell \) and n much smaller than their maximum value in the present calculations. As a result, the probability of ionization or the ionization yield is obtained by subtracting from one the sum of the probabilities of transition to excited states (the excitation yield) and the probability to stay in the ground state. It is important to note that our direct method to solve numerically the TDSE, which differs from the present Faddeev-like approach, is based on a complex dilation of the total Hamiltonian.

3 Results

3.1 High and intermediate frequencies: convergence of the series

The convergence of our Faddeev-like expansion is expected to be fast for high photon energies (above the ionization potential) and as we show below, this approach is particularly convenient to treat the interaction of atoms with high-frequency attosecond pulses. We consider a pulse with \(\omega = 0.7\) a.u., and we initially study the ionization yield and the excitation yield as a function of the maximal order of the terms taken into account in our Faddeev-like expansion in the case of the interaction of atomic hydrogen, in its ground state with a two optical cycle pulse and various peak intensities. We compare our results to the ‘exact’ results obtained by numerically integrating the TDSE.

Fig. 1
figure 1

Ionization yield resulting from the interaction of atomic hydrogen, initially in its ground state, with a two optical cycle pulse of \(\omega =0.7\) a.u. photon energy and of various peak intensities, as a function of the maximal order of the terms taken into account in our Faddeev-like expansion. The horizontal red lines give the value of the ionization yield obtained by solving the corresponding TDSE

Full size image
Fig. 2
figure 2

The same as in Fig. 1 for the excitation yield

Full size image

In Figs. 1 and 2, we clearly observe a fast convergence of the series even for the very high peak intensities. In fact, at low intensities, around \(10^{14}\) W/cm\(^2\), the SFA plus the first-order correction in the Coulomb potential is sufficient to calculate both the ionization and excitation yields. Instead of considering various peak intensities and a fixed pulse duration of 2 optical cycles, let us now fix the peak intensity to \(10^{14}\) W/cm\(^2\) and let us consider various pulse durations from 2 to 14 optical cycles. Our results for the ionization yield and the excitation yield are shown in Fig. 3 and in Fig. 4, respectively. As in the previous case, the SFA plus the first-order correction in the Coulomb potential are sufficient to obtain the correct ionization yield, even for relatively long pulses. In the case of the excitation yield, higher-order corrections in the Coulomb potential become significant once the duration of the pulse increases above 6 optical cycles. It is interesting to note that unlike the ionization yield, the excitation yield decreases rapidly for long pulse durations. In fact, at 0.7 a.u. photon energy, excited states are populated thanks to the bandwidth of the pulse.

Fig. 3
figure 3

Ionization yield resulting from the interaction of atomic hydrogen, initially in its ground state, with a pulse of \(\omega =0.7\) a.u. photon energy, \(10^{14}\) W/cm\(^2\) peak intensity and various durations, as a function of the maximal order of the terms taken into account in our Faddeev-like expansion. The horizontal red lines give the value of the ionization yield obtained by solving the corresponding TDSE

Full size image
Fig. 4
figure 4

The same as in Fig. 3 for the excitation yield

Full size image
Fig. 5
figure 5

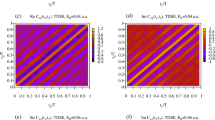
Population of the first low-lying s-states after the interaction of atomic hydrogen, initially in its ground state, with a two optical cycle pulse of \(10^{14}\) W/cm\(^2\) peak intensity and \(\omega =0.1\) a.u. photon energy, as a function of the order of the iteration taken into account in our Faddeev-like expansion. The horizontal lines give the value of the s-state populations obtained by solving the corresponding TDSE

Full size image
Fig. 6
figure 6

Population of the first low-lying p-states after the interaction of atomic hydrogen, initially in its ground state, with a two optical cycle pulse of \(10^{14}\) W/cm\(^2\) peak intensity and \(\omega =0.1\) a.u. photon energy, as a function of the order of the iteration taken into account in our Faddeev-like expansion. The horizontal lines give the value of the p-state populations obtained by solving the corresponding TDSE

Full size image

To consider whether such rapid convergence is observed at lower frequencies, we present results for an intermediate frequency of \(\omega =0.1\) a.u. which is much lower than the ionization potential. We consider the interaction of atomic hydrogen with a two optical cycle pulse of \(10^{14}\) W/cm\(^2\) peak intensity and 0.1 a.u. photon energy and study the excitation probabilities of individual states at the end of the pulse as a function of the iterative order. In Figs. 5 and 6, we show the population, at the end of the pulse, of the low lying s- and p-states as a function of the maximal order of the terms taken into account in our Faddeev-like expansion. One notes immediately that the first 2 orders are no longer adequate to obtain a reasonable estimate for the final population and only beyond 30 orders do the populations converge toward a value that coincides within two or three digits with the results obtained with a full TDSE calculation. Remarkably, our numerical calculation up to such high orders is stable and yields the correct final result. A photon energy of 0.1 in atomic units is actually the lowest one for which we observe perfect convergence. For lower photon energies, the convergence is much slower thereby requiring the calculation of terms of much higher order which leads to the accumulation of round off errors.

For strong field processes at low frequency, our results show that any study based on only the first-order terms of a series expansion, as is often the case in the literature, may lead to incorrect conclusions.

3.2 Low frequency: Dynamics of excitation of H exposed to a low frequency laser pulse

As we have seen above, for frequencies below about 0.1 a.u. we are unable to find numerical convergence of our series. Nevertheless, we will examine now the total excitation yield as a function of the iteration order for a frequency of 0.057 or wavelength of 800 nm to compare with the ‘exact’ TDSE results to see what conclusions can be drawn.

Fig. 7
figure 7

Excitation yield as a function of the peak intensity for atomic hydrogen exposed to a 8 optical cycle sine square pulse of 800 nm wave length. These results have been obtained by solving numerically the TDSE. The red lines indicate the positions of the n-photon thresholds

Full size image
Fig. 8
figure 8

Excitation yield as a function of the peak intensity for the same case as in Fig. 7. The results (light blue curve) obtained by solving numerically the TDSE are presented together with those obtained by taking into account the first-order term (red curve), the first two terms (green curve), the first three terms (blue curve) and the four first terms (brown curve) of our Faddeev-like Born series

Full size image

We consider here the excitation of atomic hydrogen by a 8 optical cycle laser pulse of 800 nm wave length. We first solve the TDSE numerically, and in Fig. 7, we show the excitation probability as a function of the peak intensity of the pulse. The vertical red lines indicate the position of the n-photon thresholds the calculation of which takes into account the ac-Stark shift of both the ground state and high lying Rydberg states at the peak intensity of the pulse. The probability of excitation exhibits a series of maxima the position of which are not clearly correlated to the position of the n-photon thresholds except for peak intensities above \(2.5\times 10^{14}\) W/cm\(^2\) where each maximum of the excitation probability is at the right but very close to a n-photon threshold as predicted by Floquet theory. The fact that for low peak intensities the maxima of the excitation probability are not regularly spaced is known to result from the pulse shape and duration [30]. In the non-adiabatic tunneling regime [31], it is not expected that the excited states play a role and yet, there is a significant population which is trapped in many excited states at the end of the interaction with the pulse. Nubbemeyer et al. [3] have proposed a re-collision-based frustrated tunneling mechanism to explain this trapping of population in excited states. In this process, an electron, emitted by tunneling, is driven back by the oscillating electric field to the ionic core where it is recaptured in an excited state. Numerical simulations based on Monte Carlo-type calculations have been used to show that such a process does occur. Recently, Hu \(\textit{et al.}\) [19] proposed a first fully quantum-mechanical model based on the SFA which takes into account a first correction in the Coulomb potential to the traditional SFA. By means of the usual saddle-point method, they calculated the probability of excitation of atomic hydrogen by a 10 optical laser pulse of 800 nm wave length and found a result which is in relatively good qualitative agreement with those obtained by solving numerically the TDSE. It turns out that their expression for the excitation probability amplitude to a given excited state coincides exactly with the first two terms of our Faddeev-like Born series. There is, however, a difference regarding the gauge since unlike us, they use the length gauge.

Fig. 9
figure 9

Bar chart of the excited-state population resulting from the interaction of atomic hydrogen with the same 8 optical cycle sine square pulse of 800 nm wave length. These populations are given as a function of the angular momentum quantum number for four values of the peak intensity

Full size image

In Fig. 8, we compare our results presented in Fig. 7 to what we obtain with our Faddeev-like Born series, keeping the first term as well as the first two, three and four terms. The first term of this Born Series is the traditional SFA. Although all excited states are neglected within the SFA, the projection of the SFA wave packet on excited states is not zero. In the present case, this contribution, although artificial, is rather significant. The second-order term which is equivalent to Hu \({et al's.}\) quantum model contributes very significantly since it reduces the excitation probability by two orders of magnitude. Similarly, the next two terms contribute also significantly. This means that the convergence of this Faddeev-like Born series is far from being reached, indicating that the excitation dynamics is very complex. In particular, the description of the re-scattering-free frustrated tunneling mechanism, which according to Landsman et al. [4] is the most important mechanism leading to significant population in excited states of the atom at the end of its interaction with the pulse, is expected to involve the contribution of many high order terms. It is interesting to note that the excitation probability as a function of the pulse peak intensity exhibits some structure only when our Faddeev-like Born series is truncated to an odd number of terms. In that case, the dipole potential is acting an even number of times, while the Coulomb potential acts an odd number of times.

In their quantum model, Hu et al. analyzed in detail the quantum orbits in order to explain why, in their case, the angular momentum components of each peak of the excitation probability are odd or even. The fact that the parity alternates from peak to peak has been observed in [30] in the case of a very long pulse where Floquet theory applies. In fact, just above a n-photon threshold, all the Rydberg states that are populated have the same value \(\ell \) of the angular momentum, \(\ell \) having the same parity as n. For short pulses as in the present case, the problem is much more complicated. In Fig. 9, we show a bar chart of the excited-state population as a function of the angular quantum number for 4 different values of the pulse peak intensity. It is only for the highest peak intensity that we clearly see that odd values of the angular momentum dominate. Interestingly, it is precisely for the highest values of the peak intensities that we observe a clear correlation between the positions of the n-photon thresholds and the peaks of the excitation probability as is the case when Floquet theory applies. For lower values of the peak intensities, we do not observe any dominant parity.

4 Conclusions and perspectives

We have shown how a Faddeev-like iterative approach can be used to generate a Born-like series which takes into account the Coulomb potential in laser–atom interactions in a consistent way. We have shown how the series can be calculated, in principle, to arbitrary order to evaluate observables such as the ionization yield and the excitation probability to a given final excited state. Although remarkably for intermediate frequencies like \(\omega = 0.1\) a.u. one can obtain exact results, one requires an impractically large number of orders to be calculated for lower frequencies. The approach is therefore best suited to high-frequency attosecond pulses where only the first 2 terms in the series may suffice. We have shown that for long wavelengths (800 nm) the first 2 terms in the series are inadequate which means that one should proceed with extreme caution in using them to either quantitatively or qualitatively interpret strong field effects at this frequency. (There may be some way of effectively resuming the terms in the series but that remains unproven.)

This approach can be readily extended to multi-electron atoms and in the first place, to helium. As for atomic Hydrogen, Eqs. (10) and (11) stay valid with the Coulomb potential replaced by the full binding potential of the atom. In this context, it is more convenient to use hyperspherical coordinates since the stationary Schrödinger for the atom has the same structure as the corresponding equation for atomic Hydrogen except that the nuclear charge in the expression of the Coulomb potential is replaced by an angle-dependent effective charge. Note that the well-known problem of the slow convergence of the expansion of the solution of the corresponding TDSE in terms of hyperspherical harmonics has been solved recently by Abdouraman et al. [28] who further developed an approach due to Macek and Ovchinnikov [29].