Dynamic Response of Stiffened Bridge Decks Subjected to Moving Loads

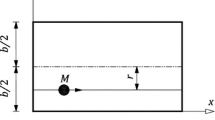
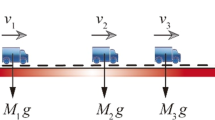
Abstract

Background

Dynamic analysis of structures under moving load excitation has been one of the most critical challenges for engineers during the last few years. The vast applications of this type of loading in many fields of the industry have intensified the importance of evaluating the dynamic response of vibrant structures under moving loads.

Purpose

This paper investigates the dynamic response of stiffened bridge decks subjected to moving loads for various constant velocities. The plates’ strength is improved by the placement of the stiffeners either concentrically or eccentrically. The stiffeners’ orientation, size, and shape play an important role in strengthening the plates, keeping the structure's weight low. Also, the number of loads and load traversing paths significantly affect the plate's response behaviour. Hence, an attempt has been made to present a parametric study for the dynamic response characteristics of stiffened bridge decks under single and multiple moving loads considering all the aforementioned parameters.

Methods

An in-house finite element MATLAB code is developed for the dynamic response study of the stiffened bridge decks. The plate and stiffener elements’ stiffness and mass matrices have been obtained separately and assembled to form the entire structure’s global matrices. Newmark integration method is used for computing the displacement, velocity, and acceleration for each time step. Some example results have been verified with previously published results and the FEAST (Finite Element Analysis of STructures) software to show the method’s efficacy.

Results

The frequency and the dynamic deflection results of bridge decks with various eccentrically and concentrically attached stiffeners are reported. The dynamic responses under single and multiple loads moving with different constant velocities are also addressed. The dynamic deflection results at various points of the bridge deck and the deflections due to the load moving in an arbitrary path are also assessed.

Conclusions

The attachment of I-beam stiffeners makes the bridge deck stiffer and depicts higher frequencies and lesser deflections than the attachment of T-beam or R-beam type stiffeners. The central deflection of the stiffened bridge deck is directly proportional to the distance traversed by the load. The maximum deflection value increases with an increment of dimension and load velocity.

Appendix

The torsional stiffness matrix is given by:

$$\begin{aligned} \begin{Bmatrix} m_{sxi} \\ m_{sxk} \end{Bmatrix}= \dfrac{G_{sx}J_x}{a}\begin{bmatrix} 1 &{} -1 \\ -1 &{} 1 \end{bmatrix}\begin{Bmatrix} \theta _{sxi} \\ \theta _{sxk} \end{Bmatrix}. \end{aligned}$$

The stiffness matrix is given by

$$\begin{aligned}{}[k]_s=\begin{bmatrix} \dfrac{E_sA_x}{a} &{} 0 &{} 0 &{} 0 &{} 0 &{} -\dfrac{E_sA_x}{a} &{} 0 &{} 0 &{} 0 &{} 0 \\ &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ &{} &{} K3 &{} 0 &{} K4 &{} 0 &{} 0 &{} -K3 &{} 0 &{} K4 \\ &{} &{} &{} \dfrac{G_{sx}J_x}{a} &{} 0 &{} 0 &{} 0 &{} 0 &{} -\dfrac{G_{sx}J_x}{a} &{} 0 \\ &{} &{} &{} &{} K1 &{} 0 &{} 0 &{} -K4 &{} 0 &{} K2 \\ &{} &{} &{} &{} &{} \dfrac{E_sA_x}{a} &{} 0 &{} 0 &{} 0 &{} 0 \\ &{} &{} &{} \mathrm{symm.} &{} &{} &{} 0 &{} 0 &{} 0 &{} 0 \\ &{} &{} &{} &{} &{} &{} &{} K3 &{} 0 &{} -K4 \\ &{} &{} &{} &{} &{} &{} &{} &{} \dfrac{G_{sx}J_x}{a} &{} 0\\ &{} &{} &{} &{} &{} &{} &{} &{} &{} K1 \end{bmatrix}, \end{aligned}$$

where

$$\begin{aligned} K1&=\dfrac{4E_sI_{ox}}{a}-\dfrac{e_c^2 E_s A_x}{a} \\ K2&=\dfrac{2E_sI_{ox}}{a}+\dfrac{e_c^2 E_s A_x}{a} \\ K3&=\dfrac{12E_sI_{ox}}{a^3}\\ K4&=\dfrac{6E_sI_{ox}}{a^2}\\ I_{ox}&=I_x+A_xe_c^2. \end{aligned}$$

The mass matrix is given by

$$\begin{aligned}{}[m]_s=\rho _s\;A_x\;a \begin{bmatrix} \dfrac{1}{J_x} &{} 0 &{} \dfrac{e_c}{2a} &{} 0 &{} \dfrac{e_c}{4} &{} \dfrac{1}{6} &{} 0 &{} -\dfrac{e_c}{2a} &{} 0 &{} \dfrac{e_c}{4} \\ &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ &{} &{} S1 &{} 0 &{} S2 &{} \dfrac{e_c}{2a} &{} 0 &{} S5 &{} 0 &{} -S4 \\ &{} &{} &{} S7 &{} 0 &{} 0 &{} 0 &{} 0 &{} \dfrac{S7}{2} &{} 0 \\ &{} &{} &{} &{} S3 &{} \dfrac{e_c}{4} &{} 0 &{} S4 &{} 0 &{} S6 \\ &{} &{} &{} &{} &{} \dfrac{1}{J_x} &{} 0 &{} 0 &{} 0 &{} \dfrac{e_c}{4} \\ &{} &{} &{} &{} &{} &{} 0 &{} 0 &{} 0 &{} 0 \\ &{} &{} symm. &{} &{} &{} &{} &{} S1 &{} 0 &{} -S2 \\ &{} &{} &{} &{} &{} &{} &{} &{} S7 &{} 0 \\ &{} &{} &{} &{} &{} &{} &{} &{} &{} \, S3 \end{bmatrix}, \end{aligned}$$

where

$$\begin{aligned} S1&=\dfrac{13}{35}+\dfrac{6}{5}\dfrac{I_{ox}}{A_xa^2} \\ S2&=\dfrac{11a}{210}+\dfrac{I_{ox}}{10A_xa}+\dfrac{e_c^2}{2a} \\ S3&=\dfrac{a^2}{105}+\dfrac{2}{15}\dfrac{I_{ox}}{A_x}+\dfrac{e_c^2 }{6} \\ S4&=\dfrac{13a}{420}-\dfrac{I_{ox}}{10A_xa}-\dfrac{e_c^2}{2a}\\ S5&=\dfrac{9}{70}-\dfrac{6}{5}\dfrac{I_{ox}}{A_xa^2} \\ S6&=-\dfrac{a^2}{140}-\dfrac{I_{ox}}{30A_x}+\frac{e_c^2}{3}\\ S7&= \dfrac{J_x}{3A_x}. \end{aligned}$$