Abstract
Based on the predator–prey system with a Holling type functional response function, a diffusive predator–prey system with digest delay and habitat complexity is proposed. Firstly, the stability of the equilibrium of diffusion system without delay is studied. Secondly, under the Neumann boundary conditions, taking time delay as the bifurcation parameter, by analyzing the eigenvalues of linearized operator of the system and using the normal form theory and center manifold method of partial functional differential equations, the effect of time delay on the stability of the system is studied and the conditions under which Hopf bifurcation occurs are given. In addition, the calculation formulas of the bifurcation direction and the stability of bifurcating periodic solutions are derived. Finally, the accuracy of theoretical analysis results is verified by numerical simulations and the biological explanation is given for the analysis results.
Similar content being viewed by others
1 Introduction
1.1 Development of the population model
In the ecosystem, the functional response function can reflect the optimal feeding behavior of the predator with the maximum energy intake per unit time in order to achieve the maximum growth capacity of the population. Holling proposed three kinds of different functional response functions, later, a Holling IV functional response function was proposed to describe the interaction between zooplankton and phytoplankton. In addition, scholars have also intensively studied on predator–prey models with Beddington–DeAngelis functional response function [1], a ratio-dependent functional response function [2], the Ivelev functional response function [3] and the Crowley–Martin functional response function [4].
At the same time, more and more biological effects are applied to the predator–prey systems when studying the stability of the equilibrium, such as Allee effect [5], prey refuge effect [6–11], habitat complexity effect [12–14], and harvesting effect [28]. Habitat usually refers to the area where organisms live, in which the organism can find food, shelter and breed. Homogeneous habitat means that the habitat has the same resource level. However, in fact, the living environment of natural habitats is spatial heterogeneous, and existing studies have shown that most of habitats have complexity due to heterogeneity [15–17]. A large number of experimental studies have shown that the complexity of habitats reduces the meeting rate between predator and prey, thus reduces the predation rate of predators [18–23]. Therefore, the effect of habitat complexity on the interaction between predator and prey cannot be ignored. However, the habitat complexity effect reduces the predation probability of prey, and the prey is not absolutely safe, while prey with refuge effect are absolutely safe.
In the natural environment, because of the limited resources, the spatial distribution of the population is heterogeneous, the biology will search for food everywhere in order to survive, then migration and diffusion will occur. Therefore, considering the heterogeneity of spatial distribution of the population, the corresponding reaction–diffusion system can be obtained. Different boundary conditions represent different biological significance in the study of predator–prey systems with diffusion term. For example, the homogeneous Neumann boundary condition means that neither prey nor predator can cross the boundary, the homogeneous Dirichlet boundary means that the number of both prey and predator is zero at the boundary, the homogeneous Robin boundary condition means that prey or predator can cross the boundary.
1.2 Establishment of the model
In [24], the author introduced habitat complexity into the ordinary differential equation system with Holling type functional response function and delay. The model is as follows:
where \(x ( t )\), \(y ( t )\), respectively, represents the density of prey population and predator population at time t, and the other parameters are all positive. The biological significance is expressed as follows: r is the intrinsic growth rate of prey population; K is the maximum environmental capacity of prey population; \(\frac{c(1-\beta ){{x}^{\alpha }}}{1+ch(1-\beta ){{x}^{\alpha }}}\) represents Holling type functional response function, in which, \(\alpha \geq 1\) and represents a kind of aggregation efficiency, when \(\alpha =1\), it becomes Holling II type functional response, when \(\alpha =2\), it becomes Holling III type functional response; c represents the attack rate of the predator on the prey; h is the handing time; e (\(0< e<1\)) is the conversion efficiency; d represents per capita death rate of predators; β (\(0<\beta <1\)) represents the intensity of the habitat complexity effect.
Considering that the habitat is heterogeneous, we introduce the diffusion term in the model (1.1), and obtain the reaction–diffusion system with homogeneous Neumann boundary conditions, the model is as follows:
Next, we will study the stability of the equilibrium point of the system, give the existence conditions of Hopf bifurcation, and derive the properties of Hopf bifurcation using the central manifold theory and normal form method proposed by Hassar [25], Wu [26], Faria [27], including the direction of Hopf bifurcation and the stability of bifurcating periodic solutions.
1.3 Existence of the constant equilibria
In order to ensure the biological significance of the model (1.2), we make the following hypothesis:
- (\(\mathbf{H_{0}}\)):
-
\(h < e/d\) and \(\alpha \geq 1 \).
Three equilibria of the system (1.2) can be obtained:
where
\({{u}^{*}}\) can be regarded as a function of habitat complexity effect β, let \({{u}^{*}}=u(\beta )\). For convenience, denote \(\beta ^{*}=1-\frac{d}{ck^{\alpha }(e-dh)}\) and make the following assumption:
- (\(\mathbf{H_{1}}\)):
-
\(\beta <\beta ^{*} \).
Theorem 1.1
If (\(\mathbf{H_{0}}\)) and (\(\mathbf{H_{1}}\)) hold, then the system (1.2) has a unique positive equilibrium point \({{P}^{*}}=({{u}^{*}},{{v}^{*}})\).
2 Stability analysis of diffusion system without time delay
When \(\tau =0\), the system (1.2) becomes
Define the real-valued Sobolev space
and let the complexification of X be
Let
then the system (2.1) can be written in the form of an abstract equation
We use \(J ( F )\) to represent the Jacobian matrix of F, then the linearization of the steady state system corresponding to the system (2.1) at \(( \beta ,0,0 )\) is
2.1 Stability of positive equilibrium
Let the Jacobian matrix corresponding to system (2.1) at the positive equilibrium point \({{P}^{*}}=({{u}^{*}},{{v}^{*}})\) be
where
We assume
then the characteristic equation of \({{L}_{n}}\) is
the characteristic roots of Eq. (2.2) are
Theorem 2.1
Suppose (\(\mathbf{H_{0}}\)) and (\(\mathbf{H_{1}}\)) are true, then we can obtain
-
(i)
If \(1-(1-{{\beta }^{*}}){{ ( 1+\frac{e}{e+\alpha (e-dh)} )}^{ \alpha }}<\beta <{{\beta }^{*}}\), then the system (2.1) is locally asymptotically stable at \({{P}^{*}}=({{u}^{*}},{{v}^{*}})\).
-
(ii)
If \(\beta <1-(1-{{\beta }^{*}}){{ ( 1+\frac{e}{e+\alpha (e-dh)} )}^{\alpha }}\), then the system (2.1) is unstable at \({{P}^{*}}=({{u}^{*}},{{v}^{*}})\).
2.2 Stability of boundary equilibria
At the equilibrium point \({{P}_{0}}= ( 0,0 )\), the corresponding characteristic roots are \(\lambda _{01}^{n}=r-{{d}_{1}}\frac{{{n}^{2}}}{{{l}^{2}}}\), \(\lambda _{02}^{n}=-d-{{d}_{1}} \frac{{{n}^{2}}}{{{l}^{2}}}<0\). At the equilibrium point \({{P}_{1}}= ( K,0 )\), the corresponding characteristic roots are \(\lambda _{11}^{n}=-r-{{d}_{1}}\frac{{{n}^{2}}}{{{l}^{2}}}<0\), \(\lambda _{12}^{n}= \frac{ec ( 1-\beta ){{K}^{\alpha }}}{1+ch ( 1-\beta ){{K}^{\alpha }}}-d-{{d}_{2}} \frac{{{n}^{2}}}{{{l}^{2}}}\).
Theorem 2.2
For the system (2.1), the following statements are true.
-
(i)
\({{P}_{0}}= ( 0,0 )\) is unstable.
-
(ii)
If \(\beta >{{\beta }^{*}}\), then \({{P}_{1}}= ( K,0 )\) is locally asymptotically stable; if \(\beta <{{\beta }^{*}}\), \({{P}_{1}}= ( K,0 )\) is unstable.
Theorem 2.3
Suppose (\(\mathbf{H_{0}}\)) and (\(\mathbf{H_{1}}\)) are true, for the system (2.1), if \(\beta >{{\beta }^{*}}\), then the equilibrium \({{P}_{1}}= ( K,0 )\) is globally asymptotically stable.
Proof
Under hypotheses (\(\mathbf{H_{0}}\)) and (\(\mathbf{H_{1}}\)), \(u\geq 0\), \(v \geq 0\). By the first equation of the system (2.1),
Using the comparison principle, we know \(\lim_{t\to \infty } \max_{x\in [ 0,l\pi ]} u ( x,t )\le K \). From the second equation,
we can obtain \(\frac{ec(1-\beta ){{u}^{\alpha }}v}{1+ch(1-\beta ){{u}^{\alpha }}}-dv<0\). Therefore, for any \(\varepsilon >0\), there exist \(T>0\), \(v ( x,t )\le \varepsilon \) so that
Applying the comparison principle again, we have \(u ( x,t )\ge K ( 1- \frac{c ( 1-\beta ){{K}^{\alpha }}\varepsilon }{r} )\), \(t>T\), \(x\in [ 0,l\pi ]\), so \(\lim_{t\to \infty } \max_{x\in [ 0,l\pi ]} u ( x,t )=K\). That is, the equilibrium point \({{P}_{1}}= ( K,0 )\) is globally asymptotically stable. □
3 Hopf bifurcation property analysis of time-delay system
When \(\tau \ne 0\), we will study the time-delay effect on dynamic properties of the diffusion system (1.2).
3.1 Existence of Hopf bifurcation induced by time delay
Assuming that (\(\mathbf{H_{0}}\)) and (\(\mathbf{H_{1}}\)) are true, the system (1.2) has a unique positive equilibrium \({{P}^{*}}=({{u}^{*}},{{v}^{*}})\). For convenience, we make transformations \(\hat{u}=u-{{u}^{*}}\), \(\hat{v}=v-{{v}^{*}}\) to move \({{P}^{*}}\) to the origin. We still use u, v to represent û, v̂, and then the system (1.2) becomes
Let
in phase space \({{\mathbb{C}}_{\tau }}=C ( [ -\tau ,0 ],X )\), (3.1) can be abstracted as
where \(\phi ={{ ( {{\phi }_{1}},{{\phi }_{2}} )}^{T}}\), \(D=\operatorname{diag}({{d}_{1}},{{d}_{2}}). L:{{\mathbb{C}}_{\tau }}\to X\), \(F:{{\mathbb{C}}_{\tau }}\to X\) are defined as follows:
with
The linearized equation of (3.1) at the origin is
where
It is well known that the eigenvalue of \(-{\varphi }''=\mu \varphi \), \(x\in ( 0,l\pi ) \), \({\varphi }' ( 0 )={\varphi }' ( l\pi )=0 \) is \({{\mu }_{n}}={{{n}^{2}}}/{{{l}^{2}},n\in {{\mathbb{N}}_{0}}}\), the characteristic function is \({{\varphi }_{n}}=\cos \frac{n\pi }{l}\), \(n\in {{ \mathbb{N}}_{0}}\), λ is the eigenvalue of (3.3). Substituting into \(\lambda y-d\Delta y-L({{e}^{\lambda }}y)=0\), we can obtain
the corresponding characteristic equation is
It is equivalent to
where
Make the assumptions:
- (\(\mathbf{H_{2}}\)):
-
\({{a}_{1}}<0\),
- (\(\mathbf{H_{3}}\)):
-
\({{a}_{2}}{{c}_{1}}-2{{a}_{1}}d<0\),
- (\(\mathbf{H_{4}}\)):
-
\({{a}_{2}}{{c}_{1}}-2{{a}_{1}}d\geq 0\).
We have the following lemmas.
Lemma 3.1
If (\(\mathbf{H_{0}}\))–(\(\mathbf{H_{2}}\)) are true, the following conclusions can be drawn.
-
(i)
When \(\tau =0\), all the characteristic roots of Eq. (3.4) have negative real parts, and the system (3.1) is locally asymptotically stable at the positive equilibrium point \({{P}^{*}}=({{u}^{*}},{{v}^{*}})\);
-
(ii)
\(\lambda =0\) is not the root of Eq. (3.4).
Lemma 3.2
Assume (\(\mathbf{H_{0}}\))–(\(\mathbf{H_{2}}\)) are true, we have the following conclusions.
-
(i)
If (\(\mathbf{H_{3}}\)) holds, when \(n>{{N}_{1}}\), Eq. (3.4) has no pure imaginary roots. When \(0\leq n \leq {{N}_{1}}\), Eq. (3.4) has a pair of pure imaginary roots \(\pm i\omega _{n}^{+}\) at \(\tau =\tau _{n}^{j,+}\).
-
(ii)
If (\(\mathbf{H_{4}}\)) holds, Eq. (3.4) has no pure imaginary roots.
We have
where
Proof
We seek the critical value of τ which makes for the characteristic equation (3.4) exist a pair of pure imaginary roots. Let \(\lambda =i\omega\) (\(\omega >0 \)) be the root of (3.4), and for some \(n\in {{\mathbb{N}}_{0}}\), ω satisfies \(-{{\omega }^{2}}+i\omega {{A}_{n}}+{{B}_{n}}+[({{a}_{1}}-{{d}_{1}}{{ \mu }_{n}}-i\omega )d-{{a}_{2}}{{c}_{1}}] ( \cos \omega \tau -i \sin \omega \tau )=0\). Separate the real part and the imaginary part,
Let \({{D}_{n}}={{a}_{1}}d-d{{d}_{1}}{{\mu }_{n}}-{{a}_{2}}{{c}_{1}}\), then we have
Let \(z={{\omega }^{2}}\), then (3.6) can be rewritten as
where
under hypothesis (\(\mathbf{H_{3}}\)), when \(0\le n\le {{N}_{1}}\), \({{B}_{n}}-{{D}_{n}}<0\), \({{B}_{n}}^{2}-{{D}_{n}}^{2}< 0\); when \(n>{{N}_{1}}\), \({{B}_{n}}-{{D}_{n}}\ge 0\), \({{B}_{n}}^{2}-{{D}_{n}}^{2} \geq 0\). If hypothesis (\(\mathbf{H_{4}}\)) holds, \({{B}_{n}}-{{D}_{n}}>0\), \({{B}_{n}}^{2}-{{D}_{n}}^{2}> 0\) for \(n\in {{\mathbb{N}}_{0}}\).
In summary, the conclusions are true. The roots of Eq. (3.7) are
Thus Eq. (3.7) has one positive root \(z_{n}^{+}\). If all parameter values of the system (3.1) are given, the roots of Eq. (3.6) can be easily calculated, and \(\omega _{n}^{+}=\sqrt{z_{n}^{+}}\). □
Lemma 3.3
If hypothesis (\(\mathbf{H_{2}}\)) is true, then \({\alpha }' ( \tau _{n}^{j,+} )=\frac{d\lambda }{d\tau } | _{\tau =\tau _{n}^{j,+}}> 0\).
Proof
Taking the derivative of Eq. (3.4) with respect to τ, we can obtain
then
□
Let \(\lambda ( \tau )=\alpha ( \tau )+i\beta ( \tau )\) be the root of Eq. (3.4) when τ is sufficiently close to \(\tau _{n}^{j,+}\) \((0\leq n\leq {{N}_{1}})\), which satisfies \(\alpha ( \tau _{n}^{j,+} )=0\), \(\beta ( \tau _{n}^{j,+} )=\omega _{n}^{+}\), \(j\in {{\mathbb{N}}_{0}}\). According to the Rouche theorem, as τ changes from a value less than \(\tau _{n}^{j,+}\) to a value greater than \(\tau _{n}^{j,+}\), the characteristic root of (3.4) transverses the imaginary axis. Therefore, when \(\tau =\tau _{n}^{j,+}\), the system (3.1) satisfies the condition for a Hopf bifurcation to occur.
Obviously, \(\tau _{n}^{0}=\min_{j\in \mathbb{N}_{0}} \{ \tau _{n}^{j,+} \} \), denote \(\tau _{*}^{0}=\min_{0\leq n\leq {{N}_{1}}} \{ \tau _{n}^{0} \} \), we have the following theorem.
Theorem 3.1
Assume that (\(\mathbf{H_{0}}\))–(\(\mathbf{H_{2}}\)) are true, if (\(\mathbf{H_{3}}\)) (\(0\leq n \leq {{N}_{1}}\)) is also satisfied, we have the following conclusions for the system (3.1).
-
(i)
When \(\tau \in [0,\tau _{*}^{0})\), the equilibrium \({{P}^{*}}=({{u}^{*}},{{v}^{*}})\) is locally asymptotically stable.
-
(ii)
When \(\tau >\tau _{*}^{0}\), the equilibrium \({{P}^{*}}=({{u}^{*}},{{v}^{*}})\) is unstable.
-
(iii)
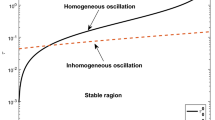
When \(\tau =\tau _{0}^{j,+}\), \(j\in {{\mathbb{N}}_{0}}\), Hopf bifurcation occurs at the equilibrium \({{P}^{*}}=({{u}^{*}},{{v}^{*}})\) and the bifurcating periodic solutions are homogeneous; When \(\tau \in \{\tau _{n}^{j,+}:\tau _{n}^{j,+}\ne \tau _{m}^{i,+},m\ne n,0 \le m,n\leq {{N}_{1}},j,i\in {\mathbb{N}_{0}}\}/\{\tau _{0}^{k,+} | k\in {\mathbb{N}_{0}} \}\), the system undergoes Hopf bifurcation at \({{P}^{*}}=({{u}^{*}},{{v}^{*}})\) and the bifurcating periodic solutions are inhomogeneous.
3.2 Direction and periodic solutions of Hopf bifurcation
In this section, we shall study the direction of Hopf bifurcation and the stability of bifurcating periodic solutions. For fixed \(j\in \mathbb{N}_{0}\) and \(0\le n \le N_{1}\), we denote \(\tilde{\tau }=\tau _{n}^{j,+}\), \(\omega_{n}=\omega_{n}^{+}\), and let \(\tilde{u}(x,t)=u(x,\tau t)-{{u}^{*}}\) and \(\tilde{v}(x,t)=v(x,\tau t)-{{v}^{*}}\). For convenience, we drop the tilde, then the system (1.2) can be transformed into
for \(x \in (0, l\pi )\), and \(t>0\). Let
Then (3.8) can be rewritten in an abstract form in the phase space \({{\mathbb{C}}_{\tau }}:=C([-1,0],X)\)
in which
with
respectively, for \(\phi =(\phi _{1}, \phi _{2})^{T} \in {{\mathbb{C}}_{\tau }}\). Consider the linearized equation
According to the results in Sect. 3.1, \(\pm i \omega _{n} \) are eigenvalues of the system (3.12) and the linearized functional differential equation is
By the Riesz representation theorem, there exists a \(2\times 2\) matrix function \(\eta ^{n}(\sigma , \tilde{\tau })\), \(-1\le \sigma \le 0\), whose elements are bounded variation functions such that
for \(\phi \in C([-1,0],{{\mathbb{R}}^{2}})\).
We select
in which
Denote by \(A(\tilde{\tau })\) the infinitesimal generators of semigroup included by the solutions of Eq. (3.13) and let \(A^{*}\) be the formal adjoint of \(A(\tilde{\tau })\) under the bilinear paring
for \(\phi , \psi \in C([-1,0],{{\mathbb{R}}^{2}})\). \(A(\tilde{\tau })\) and \(A^{*}\) both have a pair of simple purely imaginary eigenvalues \(\pm i \omega _{n} \tilde{\tau }\). Let P and \(P^{*}\) be the center subspace, i.e., the generalized eigenspace of \(A(\tilde{\tau })\) and \(A^{*}\) connected with \(\Lambda _{n}\), respectively. Then \(P^{*}\) is the adjoint space of P, and \(\operatorname{dim}P=\operatorname{dim}P^{*}=2\).
We can verify that \(p_{1}(\theta )=(1,\xi )^{T}e^{i\omega _{n} \tilde{\tau } \sigma } \) (\(\sigma \in [-1,0]\)), \(p_{2}(\sigma )=\overline{p_{1}(\sigma )} \) is a basis of \(A(\tilde{\tau })\) with \(\Lambda _{n}\) and \(q_{1}(r)=(1,\eta )e^{-i\omega _{n} \tilde{\tau } r} \) (\(r \in [0,1]\)), \(q_{2}(r)= \overline{q_{1}(r)}\) is a basis of \(A^{*}\) with \(\Lambda _{n}\), where
Let \(\Phi =(\Phi _{1},\Phi _{2})\) and \(\Psi ^{*}=(\Psi ^{*}_{1},\Psi ^{*}_{2})^{T}\) with
for \(\theta \in [-1,0]\), and \(r \in [0,1]\). According to (3.16), we can calculate
Define and construct a basis Ψ of \(P^{*}\) by
then \((\Psi ,\Phi )=I_{2}\).
Furthermore, we define \(f_{n}:=(\beta ^{1}_{n},\beta ^{2}_{n})\) with
and
Thus the center subspace of the linear equation (3.12) is given by \(P_{CN} {{\mathbb{C}}_{\tau }} \oplus P_{S} {{\mathbb{C}}_{\tau }}\) and \(P_{S} {{\mathbb{C}}_{\tau }}\) is the complement subspace of \(P_{CN} {{\mathbb{C}}_{\tau }}\) in \({{\mathbb{C}}_{\tau }}\),
for \(u=(u_{1},u_{2})\), \(v=(v_{1},v_{2})\), \(u,v\in X\) and \(\langle \phi ,f_{0}\rangle=(\langle \phi ,f^{1}_{0}\rangle, \langle\phi ,f^{2}_{0}\rangle)^{T}\).
Let \(A_{\tilde{\tau }}\) be the infinitesimal generator of an analytic semigroup induced by the linear system (3.12), and Eq. (3.8) can be rewritten as
where
By the decomposition of \({{\mathbb{C}}_{\tau }}\), the solution above can be written as
where
and
Specially, the solution of (3.9) on the center manifold is given by
Let \(z=x_{1}-i x_{2}\), and because \(p_{1}=\Phi _{1}+i\Phi _{2}\), we have
and
Therefore, Eq. (3.19) can be transformed into
in which
z satisfies
where
Let
from Eqs. (3.20) and (3.23), we have
and
with
Therefore,
with
and
Denote
and because
we can obtain
then, by (3.23), (3.24) and (3.31), we get \(g_{20}=g_{11}=g_{02}=0\), for \(n\in {{\mathbb{N}}}\). When \(n=0\), \(g_{20}=\gamma _{1}\tilde{\tau } \chi _{20} + \gamma _{2}\tilde{\tau } \varsigma _{20}\), \(g_{11}=\gamma _{1}\tilde{\tau }\chi _{11}+ \gamma _{2} \tilde{\tau }\varsigma _{11}\), \(g_{02}=\gamma _{1}\tilde{\tau } \overline{\chi }_{20} + \gamma _{2}\tilde{\tau }\overline{\varsigma }_{20} \). When \(n\in \mathbb{N}_{0}\), \(g_{21}=\tilde{\tau }( \gamma _{1} \kappa _{1} +\gamma _{2} \kappa _{2})\).
Next, we shall compute \(W_{20}(\theta )\) and \(W_{11}(\theta )\) (\(\theta \in [-1,0]\)) to get \(g_{21}\). We have
and \(W(z,\overline{z})\) satisfies
where
Hence, we can obtain
that is,
By (3.31), we obtain, for \(\theta \in [-1,0)\),
According to (3.32), for \(\theta \in [-1,0)\),
and
where
By the definition of \(A_{\tilde{\tau }}\) and (3.33), for \(-1\le \theta <0\), we have
That is,
in which
Also using the definition of \(A_{\tilde{\tau }}\) and (3.33), for \(-1\le \theta <0\), we have
According to
and
we can obtain
That is,
in which
Similarly, from (3.34), we can obtain
That is,
Similar to the procedure of computing \(W_{20}\), we have
where
Thus, the following quantities which determine the direction and the stability of bifurcating periodic solutions can be obtained:
Theorem 3.2
For any critical value \(\tau _{n}^{j,+}\), we have
-
(i)
If \(\mu _{2}>0\) (\(\mu _{2}<0\)), then Hopf bifurcation is forward (backward), that is, the bifurcating periodic solutions exists for \(\tau >\tau _{n}^{j,+}\) (\(\tau <\tau _{n}^{j,+}\)).
-
(ii)
If \(\beta _{2}<0\) (\(\beta _{2}>0\)), then the bifurcating periodic solutions are orbitally asymptotically stable (unstable).
-
(iii)
If \(T_{2}>0\) (\(T_{2}<0\)), then the period increases (decreases).
4 Numerical simulation
In model (2.1), if \(\beta =0\), i.e., the habitat complexity effect is 0, it means that all prey may be caught by the predator. When \(\beta \to 1\), it means that only little of preys can be caught, i.e., most prey are protected.
1. Stability of the system without delay.
In the system (2.1), select the parameters as
At \({{P}^{*}}=({{u}^{*}},{{v}^{*}})\), when \(0<\beta <0.467\), the system (2.1) is unstable, when \(0.467<\beta <0.834\), the system is locally asymptotically stable. Fix \(\beta =0.5\), by calculation, \({{P}^{*}}=({{u}^{*}},{{v}^{*}})=(99.568,5.787)\) (see Figs. 1–4).
2. Stability of the system with delay.
(1) For the system (2.1), let \(\alpha =1\), we choose other parameters:
By Theorem 2.1, we know that when \(0<\beta <0.0895\), the equilibrium \({{P}^{*}}=({{u}^{*}},{{v}^{*}})\) is unstable; when \(0.0895<\beta <{{\beta }^{*}}=0.6789\), the equilibrium \({{P}^{*}}=({{u}^{*}},{{v}^{*}})\) is locally asymptotically stable. We choose \(\beta =0.18\), by direct computation, \({{P}^{*}}=({{u}^{*}},{{v}^{*}})=(117.47,18.78)\), \(\tau _{0} ^{0} \approx 0.2236\). By the theorem, when \(\tau \in (0,\tau _{0} ^{0}]\), the equilibrium \({{P}^{*}}=({{u}^{*}},{{v}^{*}})\) is locally asymptotically stable. When τ crosses \(\tau _{0} ^{0}\), the equilibrium \({{P} ^{*}} = ({{u} ^{*}}, {v ^{*}})\) loses stability and a Hopf bifurcation occurs (see Figs. 5–7).
(2) For the system (2.1), let \(\alpha =2\), we choose the other parameters:
By Theorem 2.1, we know that when \(0<\beta <0.3743\), the equilibrium \({{P}^{*}}=({{u}^{*}},{{v}^{*}})\) is unstable; when \(0.3743<\beta <{{\beta }^{*}}=0.998\), the equilibrium \({{P}^{*}}=({{u}^{*}},{{v}^{*}})\) is locally asymptotically stable. We choose \(\beta =0.7\), by direct computation, \({{P}^{*}}=({{u}^{*}},{{v}^{*}})=(40.87,11.68)\), \(\tau _{0} ^{0} \approx 2.1563\). By the theorem, when \(\tau \in (0,\tau _{0} ^{0}]\), the equilibrium \({{P}^{*}}=({{u}^{*}},{{v}^{*}})\) is locally asymptotically stable. When τ crosses \(\tau _{0} ^{0}\), the equilibrium \({{P} ^{*}} = ({{u} ^{*}}, {v ^{*}})\) loses stability and a Hopf bifurcation occurs (see Figs. 8–10).
(3) In the system (2.1), let \(\alpha =3\), we choose other parameters:
By Theorem 2.1, we know that when \(0<\beta <0.6376\), the equilibrium \({{P}^{*}}=({{u}^{*}},{{v}^{*}})\) is unstable; when \(0.6376<\beta <{{\beta }^{*}}=0.9757\), the equilibrium \({{P}^{*}}=({{u}^{*}},{{v}^{*}})\) is locally asymptotically stable. We choose \(\beta =0.8\), by direct computation, \({{P}^{*}}=({{u}^{*}},{{v}^{*}})=(12.71,1.17)\), \(\tau _{0} ^{0} \approx 3.8624\). By the theorem, when \(\tau \in (0,\tau _{0} ^{0}]\), the equilibrium \({{P}^{*}}=({{u}^{*}},{{v}^{*}})\) is locally asymptotically stable. When τ crosses \(\tau _{0} ^{0}\), the equilibrium \({{P} ^{*}} = ({{u} ^{*}}, {v ^{*}})\) loses stability and a Hopf bifurcation occurs (see Figs. 11–13).
5 Biological significance
From the biological standpoint, when the intensity of habitat complexity effect is higher, the magnitude of the predator population will decrease with the increase of habitat complexity effect. This is due to a lower predation rate causing predators to starve to death because of lacking sufficient food. However, when the intensity of habitat complexity effect is relatively low, the population equilibrium density of the predator will increase with the increase of habitat complexity effect, because when the habitat complexity effect is lower, the predator still has not enough food to survive continuously.
The existence of equilibrium \({{P}_{0}}= ( 0,0 )\) means the extinction of predator and prey populations. This is so because, when the intensity of habitat complexity effect is lower, the prey are quickly eaten by the predator, leading to a sharp reduction in the number of prey to extinction, and finally the predators are extinct without food.
The existence of equilibrium \({{P}_{1}}= ( K,0 )\) means the extinction of predators, which means that when the intensity of habitat complexity effect is higher, the predators cannot get food, the mortality rate of predators is higher than the growth rate, and the predators eventually die. The prey are absolutely safe and the number of prey eventually stabilizes at the maximum carrying capacity of the environment. Compared with the refuge effect, it is not difficult to find that they have the same effect on the equilibrium density of predator and prey populations. However, the difference is that the habitat complexity effect reduces the predation rate by reducing the meeting rate between predator and prey, prey are not absolutely safe. Under the refuge effect, prey are perfectly safe.
The stability of coexistence equilibrium \({{P}^{*}}=({{u}^{*}},{{v}^{*}})\) means that the system may have spatially homogeneous or inhomogeneous periodic solutions due to the existence of a diffusion term and time delay. That is to say, if the intensity of habitat complexity effect is higher, the predator’s ability is higher and there is a short digestion delay, then the predator and prey can coexist in time and space, and the population quantity will remain near the stable value. When the digest delay is close to the Hopf bifurcation value, the system may have stable periodic solutions. In this case, predators and preys can coexist, but the population quantity may show stable periodic solutions.
Availability of data and materials
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
References
Melese, D., Gakkhar, S.: Stability analysis of a prey–predator model with Beddington–DeAngelis functional response. J. Int. Acad. Phys. Sci. 15, 1–6 (2011)
Lajmiri, Z., Khoshsiar Ghaziani, R., Orak, I.: Bifurcation and stability analysis of a ratio-dependent predator–prey model with predator harvesting rate. Chaos Solitons Fractals 106, 193–200 (2018)
Wang, X., Wei, J.: Dynamics in a diffusive predator–prey system with strong Allee effect and Ivlev-type functional response. J. Math. Anal. Appl. 422(2), 1447–1462 (2015)
Yang, R.: Bifurcation analysis of a diffusive predator–prey system with Crowley–Martin functional response and delay. Chaos Solitons Fractals 95, 131–139 (2017)
Verma, M., Misra, A.K.: Modeling the effect of prey refuge on a ratio-dependent predator–prey system with the Allee effect. Bull. Math. Biol. 80(3), 626–656 (2018)
Kar, T.: Modelling and analysis of a harvested prey–predator system incorporating a prey refuge. J. Comput. Appl. Math. 185, 19–33 (2006)
Ko, W., Ryu, K.: Qualitative analysis of a prey–predator model with Holling TypeII functional response incorporating a prey refuge. J. Differ. Equ. 231, 534–550 (2006)
Ma, Z., Li, W., Zhao, Y., et al.: Effects of prey refuges on a predator–prey model with a class of functional responses: the role of refuges. Math. Biosci. 218(2), 73–79 (2009)
Chen, L., Chen, F., Chen, L.: Qualitative analysis of a predator–prey model with Holling type II functional response incorporating a constant prey refuge. Nonlinear Anal., Real World Appl. 11(1), 246–252 (2010)
Ji, L., Wu, C.: Qualitative analysis of a predator–prey model with constant-rate prey harvesting incorparating a constant prey refuge. Nonlinear Anal., Real World Appl. 11(4), 2285–2295 (2010)
Guan, X., Wang, W., Cai, Y.: Spatiotemporal dynamics of a Leslie–Gower predator–prey model incorporating a prey refuge. Nonlinear Anal., Real World Appl. 12(4), 2385–2395 (2011)
Bairagi, N., Jana, D.: Age-structured predator–prey model with habitat complexity: oscillations and control. Dyn. Stab. Syst. 27(4), 475–499 (2012)
Debaldev, J., Bairagi, N.: Habitat complexity, dispersal and metapopulations: macroscopic study of a predator–prey system. Ecol. Complex. 17(3), 131–139 (2014)
Bartholomew, A., Diaz, R., Cicchetti, G.: New dimensionless indices of structural habitat complexity: predicted and actual effects on a predator’s foraging success. Mar. Ecol Prog. 206(1), 45–58 (2000)
Wang, W., Mulone, G., Salemi, F., Salone, V.: Permanence and stability of a stage-structured predator–prey model. J. Math. Anal. Appl. 262(2), 499–528 (2001)
Kar, T., Jana, S.: Stability and bifurcation analysis of a stage structured predator prey model with time delay. Appl. Math. Comput. 219(8), 3779–3792 (2012)
Carroll, L.J., Jackson, J.M.: The effect of increasing habitat complexity on bay scallop survival in the presence of different decapod crustacean predators. Estuar. Coast. 38(5), 1569–1579 (2015)
Bell, S.S.: Habitat complexity of polychaete tubecaps: influence of architecture on dynamics of a meioepibenthic assemblage. J. Mar. Res. 43(3), 647–671 (1985)
Bell, S.S., McCoy, E.D., Mushinsky, H.: Habitat structure: the physical arrangement of objects in space. Biochem. Syst. Ecol. 19(6), 526–527 (1991)
Kuang, Y., Takeuchi, Y.: Predator–prey dynamics in models of prey dispersal in two-patch environments. Math. Biosci. 120(1), 77–98 (1994)
Kar, T., Pahari, U.K.: Modelling and analysis of a prey–predator system with stage-structure and harvesting. Nonlinear Anal., Real World Appl. 8(2), 601–609 (2007)
Michalko, R., Petrakova, L., Sentenska, L., Pekar, S.: The effect of increased habitat complexity and density-dependent non-consumptive interference on pest suppression by winter-active spiders. Agric. Ecosyst. Environ. 242, 26–33 (2017)
Church, K.D.W., Grant, J.W.: Does increasing habitat complexity favour particular personality types of juvenile Atlantic salmon, Salmo salar. Anim. Behav. 135, 139–146 (2018)
Ma, Z., Wang, S.: A delay-induced predator–prey model with Holling type functional response and habitat complexity. Nonlinear Dyn. 93, 1519–1544 (2018)
Hassard, B., Kazarino, N., Wan, Y.: Theory and Applications of Hopf Bifurcation. Cambridge University Press, Cambridge (1981)
Wu, J.: Theory and Applications of Partial Functional Differential Equations. Springer, New York (1996)
Faria, T.: Normal forms and Hopf bifurcation for partial differential equations with delays. Trans. Am. Math. Soc. 352(5), 2217–2238 (2000)
Belkhodja, K., Moussaoui, A., Alaoui, M.A.A.: Optimal harvesting and stability for a prey–predator model. Nonlinear Anal., Real World Appl. 39, 321–336 (2018)
Acknowledgements
The authors wish to express their gratitude to the editors and the reviewers for the helpful comments.
Funding
Not applicable.
Author information
Authors and Affiliations
Contributions
The idea of this research was introduced by YL and HL. All authors contributed to the main results and numerical simulations. RY contributed to revising the manuscript. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Li, Y., Liu, H. & Yang, R. Time-delay effect on a diffusive predator–prey model with habitat complexity. Adv Differ Equ 2021, 320 (2021). https://doi.org/10.1186/s13662-021-03473-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-021-03473-y