Dynamics of SIR model with vaccination and heterogeneous behavioral response of individuals modeled by the Preisach operator

Abstract

We study global dynamics of an SIR model with vaccination, where we assume that individuals respond differently to dynamics of the epidemic. Their heterogeneous response is modeled by the Preisach hysteresis operator. We present a condition for the global stability of the infection-free equilibrium state. If this condition does not hold true, the model has a connected set of endemic equilibrium states characterized by different proportion of infected and immune individuals. In this case, we show that every trajectory converges either to an endemic equilibrium or to a periodic orbit. Under additional natural assumptions, the periodic attractor is excluded, and we guarantee the convergence of each trajectory to an endemic equilibrium state. The global stability analysis uses a family of Lyapunov functions corresponding to the family of branches of the hysteresis operator.

1 Introduction

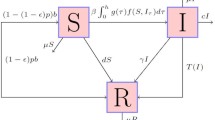
In the classical compartmental models of epidemiology, the key parameters such as the transmission and vaccination rates are assumed to remain the same during an epidemic. As an example, consider a SIR model with vaccination of the form

$$\begin{aligned} \begin{aligned} \dot{S}&= - \frac{\beta S I}{N} -v S - \mu S +\mu N,\\ \dot{I}&=\frac{\beta S I}{N} - \gamma I-\mu I, \\ \dot{R}&= \gamma I +v S- \mu R,\\ \end{aligned} \end{aligned}$$

(1)

where S, I and R are densities of the populations of susceptible, infected and recovered individuals, respectively; $N=S+I+R$ is the total population density; $\beta$ is the transmission rate, which can be expressed as the product of the average number of daily contacts a susceptible individual has with other individuals and the probability of transmission during each contact; v is the vaccination rate; $\gamma$ is the recovery rate; and, $\mu$ is the birth/mortality rate (or immigration/emigration rate; for childhood infections, individuals leave the group at a certain age). The recovered individuals are assumed to be immune to the disease. In this particular model setup, the equality of the birth and mortality rates ensures the conservation of the total population density, i.e. N is constant. A simpler version of this model without vaccination was first published in Kermack (1927); (1932; 1933).

The key parameter is the so-called basic reproduction number $R_0$. For model (1) it equals $R_0=\beta \mu /((\gamma +\mu )(\mu +v))$. If $R_0 < 1$, the infection dies out in the long run; if $R_0 > 1$, the infection spreads in the population (Korobeinikov and Wake 2002; Korobeinikov and Maini 2004; Ullah et al. 2013)

Due to their simplicity, the standard SIR model and its variants, including (1), assume that the hosts are unable to respond in any way to the advent of an epidemic and disregard the ability of the community to adapt its behavior to the danger. Humans, however, are able to intelligently respond to a threat as they receive and perceive information regarding the epidemic from the “outside” world, the government and health authorities, and can adjust their behavior to avoid or to reduce the risk of being infected. Typical aspects of this adaptability may include simple precautionary measures, such as refraining from potentially dangerous contacts, increasing hygiene, using hand sanitizer and disinfectants, adjusting a general life style, taking an extra portion of vitamin C in a case of a common cold, using vaccination in the case of influenza or face covering in public places (Javid and Balaban 2020). At the threat of epidemics, the government and health authorities can intervene by promoting immunizations, if available, raising awareness in the population about the current severity of the epidemic, providing access to effective and affordable medicines and tests, working with school authorities, using media and/or administrative pressure, etc. During the covid-19 epidemics we have seen such interventions imposed by the authorities on an unprecedented scale including massive quarantine and social distancing measures, business restrictions, gathering limitations, stay-at-home and shelter-in-place orders and closing the state borders (Marquioni and de Aguiar 2020).

In order to account for the adaptability of the population, the assumptions of the standard SIR models, which postulate constant transmission and vaccination rates during the whole time period in question, was revisited in several different ways. The incidence rate of the modified form ${\beta S I}/({1 + a I})$ or ${\beta S I}/({1 + a S})$ was used to account for the saturation effect with saturation rate a. The first form is based on the assumption that an increase in the number of infective individuals leads to a reduction of the incidence rate; the second form is associated with protective measures taken by susceptible individuals against the infection. The two effects were also combined into the incidence rate of the form ${\beta S I}/({1 + a S + bI})$ (Dubey et al. 2015; Kaddar 2010) for an overview of several models. Their extensions of these models include non-pharmaceutical intervention factors such as quarantine and isolation of patients (Hou et al. 2020; Davies et al. 2020; Volpert et al. 2020; Wearing et al. 2005). Time-dependent transmission rates were used to account for seasonal effects and varying weather conditions (Grassly and Fraser 2006; Liu and Stechlinski 2012).

Immunization is a proven and probably the most effective tool for controlling and eliminating infectious diseases (Chauhan et al. 2014). It was hypothesized that a vaccination effort can be more efficient when it is pulsed in time rather than uniform. The effect of pulsed vaccination policy has been studied quite extensively (Agur et al. 1993; Lu et al. 2002) where a detailed comparison of models with constant and pulsed vaccination rate is provided. Piecewise smooth epidemiological models of switched vaccination, implemented once the number of people exposed to a virus reaches a critical level, were studied in Wang et al. (2014). In yet another class of epidemiological models with adaptive switching behavior, a stochastic switching model was combined with an economic optimal stopping problem to determine the optimal timings for public health interventions (Sims et al. 2016). Models studied in Chladná et al. (2020) assume that intervention measures are implemented when the number of infected individuals exceeds a critical level, and the intervention stops when this number drops below a different (lower) threshold. Implications of such two-threshold intervention strategies for dynamics of an SIR model were considered both in the case of switched vaccination rate (see Sect. 2.1) and switched transmission rate.

Multiple factors can influence the willingness of an individual to receive immunization depending on the perceived risk of contracting the disease, risk of possible complications, personal beliefs, etc. These risks vary with age, health conditions, lifestyle and profession (Guidry et al. 2021; Lazarus et al. 2021). Further, interventions of the health authorities and administrative measures at the level of a county or state can vary in scale depending on the availability of resources, the local economic situation and other factors. All these variations lead to the heterogeneity of the response of the population to the advent of an epidemic.

Hysteresis effect in adopting a ‘healthy behavior’, with the associated two switching thresholds, can result form social interaction, social reinforcement and social imitation (Su et al. 2017). In particular, in the presence of imperfect vaccine, hysteresis loops of vaccination rate arise with respect to changes in the perceived cost of vaccination (Chen and Fu 2019). This cost changes dynamically as individuals revisit their vaccination decision in response to dynamics of the epidemic and through a social learning processes under peer influence, through which process they try to learn vaccination strategies that are more successful. One of the findings in (Chen and Fu 2019) is that hysteresis becomes more pronounced with increasing heterogeneity of the population.

In this paper, we propose a variant of the SIR model with a heterogeneous response and analyze how the heterogeneity affects the dynamics. We focus on the scenario when interventions of the health authorities affect the vaccination rate (assuming vaccines are available) while the transmission rate remains constant; the case of variable transmission rate will be considered elsewhere. As a starting point, we adopt the approach of Chladná et al. (2020) to modeling the homogeneous switched response of a subpopulation to the varying number of infected individuals by a two-threshold two-state relay operator (as described in Sect. 2.1). To reflect the heterogeneity, multiple subpopulations are considered, each characterized by a different pair of switching thresholds. In order to keep the model relatively simple, we apply averaging under further simplifying assumptions. The main simplification is that perfect mixing of the population is assumed. This leads to a differential model with just two variables, S and I, but with a complex operator relationship between the vaccination rate v and the density of the infected individuals I. As such, this operator relationship, known as the Preisach operator, accounts for the heterogeneity of the response. Heterogeneity of intervention policies can be modeled in a similar fashion (see Sect. 2.2).

We show that the system with the Preisach operator is amenable to analysis when interpreted as a switched system (Bernardo et al. 2008) associated with a one-parameter family of nonlinear planar vector fields $\varPhi _u=\varPhi _u(I,S)$ (where $u\in {\mathbb {R}}$ is a parameter). Between the switching moments, a trajectory of the system is an integral curve of a particular vector field. The Preisach operator imposes non-trivial rules for switching from one vector field to another. Some intuition can be drawn from dynamics of systems with dry friction such as models of presliding friction behavior (Al-Bender et al. 2004; Ruderman 2011), and population models with thresholds (Meza and Bhaya 2009).

Using the switched systems approach, we show that if $R_0\le 1$, then the infection-free equilibrium is globally stable. In the case of $R_0>1$, the bi-stable nature of an individual response leads to multi-stability in the aggregated model. Namely, the system has a connected set of endemic equilibrium states characterized by different proportion of infected and immune individuals¹. In this case, we show that every trajectory converges either to one of the endemic equilibrium states or to a periodic orbit corresponding to the recurrence of the disease. Under additional natural assumptions, we prove the global stability of the set of endemic equilibrium states by adapting the method of Lyapunov functions. Each vector field $\varPhi _u$ has a global Lyapunov function $V_u=V_u(I,S)$. We establish the global stability of the switched system by controlling the increment $V_u(I_1,S_1)-V_u(I_2,S_2)$ of the Lyapunov function along a trajectory between the switching points, and the difference $V_{u_1}(I,S)-V_{u_2}(I,S)$ of the Lyapunov functions at those points. Numerical analysis of SIR models with the Preisach operator was previously performed in (Pimenov et al. 2010, 2012).

The paper is organized as follows. In the next section we present the model and recall the definition of the Preisach operator. In Sect.3 some preliminary properties of the Preisach operator and the model are discussed, including hysteresis loops, equilibrium states and the global stability of the infection-free equilibrium in the case $R_0\le 1$. Sects. 4 and 5 present the main results on dynamics in the case $R_0>1$ and their proofs.

2 Model

We consider the following SIR model

$$\begin{aligned} \dot{I}= & {} \beta IS -(\gamma +\mu )I,\nonumber \\ \dot{S}= & {} -\beta IS -v(t)S-\mu S+\mu ,\nonumber \\ \dot{R}= & {} \gamma I +v(t) S -\mu R \end{aligned}$$

(2)

with an additional feedback loop, which relates the variable vaccination rate $v=v(t)$ to the concurrent and past values of the density $I=I(t)$ of the infected population. In the main part of the paper, it is assumed that the function $I: {\mathbb {R}}_+\rightarrow {\mathbb {R}}$ is mapped to the function $v: {\mathbb {R}}_+\rightarrow {\mathbb {R}}$ by the so-called continuous Preisach operator, which is described in the following sections. In order to motivate and explain the nature of the assumed operator relationship between I and v, we first briefly discuss the non-ideal relay operator in the same context. Regardless of the specific form of the feedback, one can see that the sum $I+S+R$ is conserved by system (2), and the last equation is redundant. Without loss of generality, we can interpret S, I, R as relative densities assuming that $I+S+R=1$

at all times. We denote $\delta = \mu + \gamma$ and rewrite the system as

$$\begin{aligned} \begin{array}{l} \dot{I}=\beta IS - \delta I,\\ \dot{S}= -\beta IS -v(t)S-\mu S+\mu . \end{array} \end{aligned}$$

(3)

Note that the domain

$$\begin{aligned} {\mathfrak {D}}=\{ (I,S): I>0, S>0, S+I \le 1\} \end{aligned}$$

(4)

is flow-invariant for this system. Indeed, in this region, $\dot{I}\le (\beta -\delta )I$ and

$$\begin{aligned} \begin{array}{c}\dot{I}=0 \quad \text {for} \quad I=0, \ \dot{S}=\mu >0 \quad \text {for} \quad S=0,\\ \dot{I} + \dot{S} = - \delta I - v(t) S + \mu (1-S) \le -\delta I + \mu - \mu S < 0 \quad \text {for} \quad {I+S=1} \end{array} \end{aligned}$$

(where we use $\delta >\mu$),

which implies the statement.

We will consider trajectories from the domain ${\mathfrak {D}}$ only.

2.1 Switched model with one non-ideal relay operator

In Chladná et al. (2020), the relationship between the density of the infected population, $I=I(t)$, and the vaccination rate was modeled by the simplest hysteretic operator called the non-ideal relay, which is also known as a rectangular hysteresis loop or a lazy switch (Visintin 1994). The relay operator is characterized by two scalar parameters $\alpha _1$ and $\alpha _2$, the threshold values, with $\alpha _1<\alpha _2$. We will use the notation $\alpha =(\alpha _1,\alpha _2)$. The input of the relay is an arbitrary continuous function of time, $I: {\mathbb {R}}_+\rightarrow {\mathbb {R}}$. The state $\nu _{\alpha }(\cdot )$ equals either 0 or 1 at any moment $t\in {\mathbb {R}}_+$. If the input value at some instant is below the lower threshold value $\alpha _1$, then the state at this instant is 0 and it remains equal to 0 as long as the input is below the upper threshold value $\alpha _2$. When the input reaches the value $\alpha _2$, the state switches instantaneously to the value 1. Then, the state remains equal to 1 as long as the input stays above the lower threshold value $\alpha _1$. When the input reaches the value $\alpha _1$, the state switches back to 0. This dynamics is captured by the input-state diagram shown in Fig. 1. In particular, the input-state pair $(I(t),\nu _{\alpha }(t))$ belongs to the union of the two horizontal rays shown in bold in Fig. 1 at all times.

The above description results in the following definition. Given any continuous input $I: {\mathbb {R}}_+\rightarrow {\mathbb {R}}$ and an initial value of the state, $\nu _{\alpha }(0)=\nu _{\alpha }^0$, satisfying the constraints

$$\begin{aligned}&\nu _{\alpha }^0\in \{0,1\} \quad \text {if} \quad \alpha _1<I(0)< \alpha _2; \end{aligned}$$

(5)

$$\begin{aligned}&\nu _{\alpha }^0=0 \quad \text {if} \quad I(0)\le \alpha _1;\qquad \nu _{\alpha }^0=1 \quad \text {if} \quad I(0)\ge \alpha _2, \end{aligned}$$

(6)

the state of the relay at the future moments $t>0$ is defined by

$$\begin{aligned} \nu _{\alpha }(t)= \left\{ \begin{array}{cl} 0 &{} \hbox {if there is } t_1\in [0,t] \hbox { such that} I(t_1)\le \alpha _1\\ &{} \text {and }I(\tau )<\alpha _2 \text { for all }\tau \in (t_1, t];\\ 1 &{} \hbox {if there is } t_1\in [0,t] \hbox { such that } I(t_1)\ge \alpha _2\\ &{} \hbox {and } I(\tau )>\alpha _1 \hbox { for all } \tau \in (t_1, t];\\ \nu _{\alpha }(0) &{} \text {if }\alpha _1<I(\tau )<\alpha _2 \text { for all } \tau \in [0,t]. \end{array}\right. \end{aligned}$$

(7)

This time series of the state, which depends both on the input I(t) $(t\ge 0)$ and the initial state $\nu _{\alpha }(0)=\nu _{\alpha }^0$ of the relay, will be denoted by

$$\begin{aligned} \nu _{\alpha }(t)=({{\mathcal {R}}}_{\alpha }[\nu _{\alpha }^0]I)(t),\qquad t\ge 0. \end{aligned}$$

(8)

By definition, the state satisfies the constraints

$$\begin{aligned} \nu _{\alpha }(t)=1 \quad \text {whenever} \quad I(t)\ge \alpha _2; \quad \nu _{\alpha }(t)=0 \quad \text {whenever} \quad I(t)\le \alpha _1 \end{aligned}$$

(9)

at all times. Further, the function (7) has at most a finite number of jumps between the values 0 and 1 on any finite time interval $t_{0}\le t\le t_{1}$. If the input oscillates between two values $I_1,I_2$, such that $I_1<\alpha _1<\alpha _2<I_2$, then the point $(I(t),\nu _{\alpha }(t))$ moves counterclockwise along the rectangular hysteresis loop shown in Fig. 1.

Fig. 1

The non-ideal relay operator defined by (7) maps the pair $(I(t),\nu _{\alpha }(0))$, where I(t) ($t\ge 0$) is the input and $\nu _{\alpha }(0)$ is the initial state, to the time series of the state $\nu _{\alpha }(t)$ for $t>0$. The input-state pair $(I,\nu _{\alpha })$ belongs to the union of the two bold (open) horizontal rays at all times. Initially, it belongs to the upper ray if $\nu _{\alpha }(0)=1$ and to the lower ray if $\nu _{\alpha }(0)=0$. The point $(I,\nu _{\alpha })$ moves horizontally left whenever $\dot{I}<0$ and right whenever $\dot{I}>0$. Further, when $(I,\nu _{\alpha })$ reaches the end of either ray, it transits vertically to the other ray. This transition is instantaneous

In Chladná et al. (2020), it was assumed that interventions of the health authority change the vaccination rate according to the following rules. The vaccination rate is switched from a lower rate $v_{nat}$ to a higher rate ${v_{int}:=v_{nat}+ q_0}$, ${q_0 > 0}$, when the density of the infected population reaches a threshold value $\alpha _2$. The intervention stops when the number of infected individuals drops below a lower threshold value $\alpha _1$, at which point the vaccination rate returns to its lower value $v_{nat}$. Using the definition (7) of the non-ideal relay operator (8), this leads to the formula

$$\begin{aligned} v(t)= v_{nat} + q_0\cdot ({{\mathcal {R}}}_{\alpha }[\nu _{\alpha }^0]I)(t). \end{aligned}$$

(10)

Coupling of this operator equation with dynamic Eq. (3) results in a switched system.

As shown in Chladná et al. (2020), switched system (3), (10) exhibits different dynamic scenarios depending on its parameters. In particular, it can have a globally stable endemic equilibrium. Alternatively, a locally stable endemic equilibrium coexists with a stable periodic orbit. Along this orbit, the vaccination rate (10) switches between the values $v_{nat}$ and $v_{nat}+ q_0$ twice per period.

2.2 Model with heterogeneous vaccination rate

Now, we consider a model, in which several vaccination laws of the form (10), with different thresholds $\alpha$, are combined either because the health authority employs multiple intervention strategies or because different individuals respond differently to the advent of an epidemic.

Assume that the health authority has multiple intervention policies (numbered $n=1,\ldots ,N$) in place, each increasing the vaccination rate by a certain amount $q_n$ while the intervention is implemented, in order to provide a response, which is adequate to the severity of the epidemic. Further, assume that each intervention policy is guided by the two-threshold start/stop rule, such as in (10), associated with a particular pair of thresholds $\alpha ^n=(\alpha _1^n,\alpha _2^n)$. Under these assumptions, the vaccination rate in system (3) is given by

$$\begin{aligned} v(t)= v_{nat} + \sum _{n=0}^{N-1} q_n\cdot ({{\mathcal {R}}}_{\alpha ^n}[\nu _{\alpha ^n}^0]I)(t). \end{aligned}$$

(11)

This formula defines a mapping from the space of continuous inputs $I:{\mathbb {R}}_+\rightarrow {\mathbb {R}}$ to the space of piecewise constant outputs $v:{\mathbb {R}}_+\rightarrow {\mathbb {R}}$, which is known as the discrete Preisach operator (Krasnosel’skii and Pokrovskii 1989), see Fig. 2. In particular, the vaccination rate (11) is set to change at multiple thresholds $\alpha _1^n, \alpha _2^n$.

Fig. 2

Preisach model as the parallel connection of non-ideal relays with weights. Relays $R_{\alpha }$ with different pairs of thresholds respond to a common input I(t). These relays function independently of each other and contribute to the output v(t) of the model, which is defined as the weighted sum (integral) of the outputs of the individual relays $R_{\alpha }$

On the other hand, individuals can respond differently to dynamics of the epidemic and interventions of the health authority. In particular, the willingness to receive vaccination can vary significantly from individual to individual for the same level of threat of contracting the disease. In order to account for the heterogeneity of the individual response, let us divide the susceptible population into non-intersecting subpopulations parameterized by points $\alpha$ of a subset $\varPi \subset \{\alpha =(\alpha _1,\alpha _2): \alpha _1<\alpha _2\}$ of the $\alpha$-plane. Assuming that the vaccination rate for a subpopulation labeled $\alpha$ is given by (10) with $q=q(\alpha )$, the total vaccination rate equals

$$\begin{aligned} v(t)= v_{nat} + \iint _{\varPi } q(\alpha )\, ({{\mathcal {R}}}_{\alpha }[\nu _{\alpha }^0]I)(t)\, d F(\alpha ), \end{aligned}$$

(12)

where the probability measure F describes the distribution of the susceptible population over the index set $\varPi$ (the set of threshold pairs). As a simplification, let us assume that this measure is independent of time (in particular, the distribution does not change with variations of I). Then, the mapping of the space of continuous inputs $I:{\mathbb {R}}_+\rightarrow {\mathbb {R}}$ to the space of outputs $v:{\mathbb {R}}_+\rightarrow {\mathbb {R}}$ defined by (12) is known as the general Preisach operator, which includes the discrete Preisach operator (11) and a continuous Preisach model (corresponding to an absolutely continuous measure F) as particular cases. In either case, the Preisach operator is referred to as a superposition (or parallel connection) of weighted non-ideal relays.

2.3 Continuous Preisach model

Let us consider a rigorous definition of the Preisach operator (12) with an absolutely continuous measure F (Krasnosel’skii and Pokrovskii 1989). It involves a collection of non-ideal relays ${{\mathcal {R}}}_{\alpha }$, which respond to the same continuous input $I=I(t)$ independently. The relays contributing to the system have different pairs of thresholds $\alpha =(\alpha _1,\alpha _2)\in \varPi$, where we assume that $\varPi$ is measurable and bounded; the $\alpha$-plane is called the Preisach plane. The output of the continuous Preisach model is the scalar-valued function

$$\begin{aligned} v(t)=v_{nat}+\iint _{\varPi } q(\alpha )\, \bigl ({{\mathcal {R}}}_{\alpha }[\nu _{\alpha }^0]I\bigr )(t) \,d\alpha _1 d\alpha _2,\qquad t\ge 0, \end{aligned}$$

(13)

where $q:\varPi \rightarrow {\mathbb {R}}$ is a positive bounded measurable function (measure density) representing the weights of the relays; and, $\nu _{\alpha }^0$ is the initial state of the relay ${{\mathcal {R}}}_{\alpha }$ for any given $\alpha \in \varPi$. The function $\nu ^0=\nu _{\alpha }^0:\varPi \rightarrow \{0,1\}$ of the variable $\alpha =(\alpha _1,\alpha _2)$ is referred to as the initial state of the Preisach operator. It is assumed to be measurable and satisfy the constraints (5), (6), in which case the initial state-input pair is called compatible. These requirements ensure that the integral in (13) is well-defined for each $t\ge 0$ and, furthermore, the output $v(\cdot )$ of the Preisach model is continuous. The input-output operator of the Preisach model defined by (13) will be denoted by

$$\begin{aligned} v(t)=({{\mathcal {P}}}[\nu ^0]I)(t),\qquad t\ge 0, \end{aligned}$$

(14)

where both the input $I:{\mathbb {R}}_+\rightarrow {\mathbb {R}}$ and the initial state $\nu ^0=\nu ^0_{\alpha }$ (which is compatible with the input) are the arguments; the value of this operator is the output $v:{\mathbb {R}}_+\rightarrow {\mathbb {R}}$.

In what follows we consider system (3) with the vaccination rate defined by equation (13).

3 Preliminaries

We begin by discussing some of the properties of the Preisach operator and system (3), (13).

3.1 Global Lipschitz continuity

The Preisach operator (14) is globally Lipschitz continuous (Krasnosel’skii and Pokrovskii 1989). More precisely, the relations

$$\begin{aligned} v_k(t)=({{\mathcal {P}}}[\nu ^0_k]I_k)(t),\qquad t\ge 0, {\qquad k=1,2,} \end{aligned}$$

imply

$$\begin{aligned} \Vert v_1-v_2\Vert _{C([0,\tau ];{\mathbb {R}})} \le K \Big ( \Vert \nu ^0_1-\nu ^0_2\Vert _{L_1(\varPi ;{\mathbb {R}})} + \Vert I_1-I_2\Vert _{C([0,\tau ];{\mathbb {R}})}\Big ) \end{aligned}$$

(15)

for any $\tau \ge 0$ with

$$\begin{aligned} K := \max _{0\le \alpha _1\le 1} \int _{\alpha _1}^1 q(\alpha _1,\alpha _2) \,\mathrm {d}\alpha _2. \end{aligned}$$

(16)

Let us denote by ${\mathfrak {U}}$ the set of all triplets $(I_0,S_0,\nu ^0)$, where $(I_0,S_0)\in {\mathfrak {D}}$ (see (4)) and the initial state $\nu ^0$ of the Preisach operator is compatible with $I_0$. The global Lipschitz estimate (15) ensures (for example, using the Picard-Lindelöf type of argument) that for given $(I_0,S_0,\nu ^0)\in {\mathfrak {U}}$, system (3) with the Preisach operator (14) has a unique local solution with the initial data $I(0)=I_0, S(0)=S_0$ and the initial state $\nu ^0$ (see, for example, the survey in Leonov et al. 2017). Further, the invariance of ${\mathfrak {D}}$ implies that each solution is extendable to the whole semi-axis $t\ge 0$. These solutions induce a semi-flow in the set ${\mathfrak {U}}$, which is considered to be the phase space of system (3) and is endowed with a metric by the natural embedding into the space ${\mathbb {R}}^2\times L_1(\varPi ;{\mathbb {R}})$. This leads to the standard definition of local and global stability including stability of equilibrium states and periodic solutions. In particular, an equilibrium is a triplet $(I_0,S_0,\nu ^0)\in {\mathfrak {U}}$ and a periodic solution is a periodic function $(I(\cdot ),S(\cdot ),\nu (\cdot )): {\mathbb {R}}_+\rightarrow {\mathfrak {U}}$ where the last component viewed as a function $\nu :{\mathbb {R}}_+\times \varPi \rightarrow \{0,1\}$ of two variables $t\in {\mathbb {R}}_+$ and $\alpha \in \varPi$ is given by (8).

The vaccination rate (13) at an equilibrium is constant, while for a periodic solution the vaccination rate is also periodic with the period of I and S.

3.2 Hysteresis loops

We call a periodic input $I=I(t)$ simple if each local minimum of this input is its global minimum and each local maximum is its global maximum. That is, the input increases from its global minimum value to its global maximum value and then decreases back to its global minimum value over one period. Let us consider inputs $I:{\mathbb {R}}_+\rightarrow [0,1]$.

The following property of the Preisach operator is called monocyclicity: for any T-periodic input I(t), $t\ge 0$, and any admissible initial state of the Preisach operator, the corresponding output $v(t)=({\mathcal {P}}[\nu ^0]I)(t)$ satisfies $v(t+T)=v(t)$ for all $t\ge T$. Further, for a simple periodic input, the output is defined by

$$\begin{aligned} v(t)=\left\{ \begin{array}{lll} {{\bar{v}}} (I(t)) &{} \text {as }I(t) \text { increases},\\ {{\hat{v}}} (I(t)) &{} \text {as }I(t)\text { decreases} \end{array} \right. \end{aligned}$$

(17)

for $t\ge T$, where the Lipschitz continuous functions ${{\bar{v}}}(\cdot ), {{\hat{v}}}(\cdot )$ increase and satisfy

$$\begin{aligned}&{{\bar{v}}}(I)< {{\hat{v}}}(I) \ \ \text {for} \ \ I_1<I<I_2; \end{aligned}$$

(18)

$$\begin{aligned}&{{\bar{v}}}(I_1) = {{\hat{v}}}(I_1); \qquad {{\bar{v}}}(I_2) = {{\hat{v}}}(I_2) \end{aligned}$$

(19)

with

$$\begin{aligned} I_1:=\min _{t\ge 0} I(t), \qquad I_2:=\max _{t\ge 0} I(t). \end{aligned}$$

(20)

In other words, a simple periodic input produces a closed (hysteresis) loop formed by the graphs of the functions ${{\bar{v}}}(\cdot ), {{\hat{v}}}(\cdot )$ on the input-output diagram (after the moment T), see Fig. 3a.

Fig. 3

Hysteresis loops on the (I, v) diagram

Importantly, these functions depend on the initial state of the Preisach operator. However, their difference does not. Indeed, for a simple periodic input satisfying (20), for all the threshold pairs $\alpha =(\alpha _1,\alpha _2)$ such that either $\alpha _1<I_1$ or $\alpha _2>I_2$ formula (7) implies

$$\begin{aligned} \nu _\alpha (t)=\nu _\alpha (T) \quad \text {for all} \quad t\ge T. \end{aligned}$$

Further, according to (7), on each time interval where I increases, the state of any relay ${\mathcal {R}}_\alpha$ with $\alpha =(\alpha _1,\alpha _2)$ from the triangle $I_1<\alpha _1<\alpha _2<I_2$ is related to the input value $I=I(t)$ by the formula

$$\begin{aligned} {\bar{\nu }}_\alpha (I)={\left\{ \begin{array}{ll} 1 &{} \text {for} \ \,\ I_1<\alpha _1<\alpha _2<I, \\ 0 &{} \text {for} \ \,\ I_1<\alpha _1<\alpha _2,\ I<\alpha _2<I_2. \end{array}\right. } \end{aligned}$$

Similarly, on each time interval where I decreases, the states of such relays are related to the input value $I=I(t)$ by

$$\begin{aligned} {\hat{\nu }}_\alpha (I)={\left\{ \begin{array}{ll} 1 &{} \text {for} \ \,\ I_1<\alpha _1<I,\ \alpha _1<\alpha _2<I_2, \\ 0 &{} \text {for} \ \,\ I<\alpha _1<\alpha _2<I_2. \end{array}\right. } \end{aligned}$$

Therefore, for each $I\in [I_1,I_2]$,

$$\begin{aligned} {\hat{\nu }}_\alpha (I)-{\bar{\nu }}_\alpha (I)= {\left\{ \begin{array}{ll} 1 &{} \text {for} \ \,\ I_1<\alpha _1<I,\ I<\alpha _2<I_2, \\ 0 &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

Multiplying this equation by the density function $q(\alpha )$ and integrating the product with respect to $\alpha$ over the set $\varPi$ (cf. (13)), we obtain

$$\begin{aligned} {\hat{v}}(I) - {{\bar{v}}}(I) = \int _I^{I_2}\,\mathrm {d}\alpha _2 \int _{I_1}^{I} q(\alpha _1, \alpha _2) \,\mathrm {d}\alpha _1. \end{aligned}$$

(21)

Thus, for a simple periodic input, the difference $\varDelta v= {{\hat{v}}}-{{\bar{v}}}$ is a nonnegative function of three scalar variables, $\varDelta v=\varDelta v(I,I_1,I_2)$, defined on the domain $0\le I_1\le I\le I_2\le 1$. Since $q=q(\alpha _1,\alpha _2)$ is bounded, the following quantity is well-defined and finite:

$$\begin{aligned} L:=\max _{0\le I_1 < I_2\le 1} \frac{1}{I_2 - I_1} \left( \max _{I_1 \le I\le I_2}{\bigl ({\hat{v}}(I) - {{\bar{v}}}(I)\bigr )}\right) . \end{aligned}$$

(22)

The quantity (22) measures the maximal width of the hysteresis loops of the Preisach operator relative to their length. Thus, L can be considered as a measure of the amount of hysteresis in the adaptive response with larger values of L corresponding to wider hysteresis loops. In particular, L is smaller if the excess vaccination rate (above the base vaccination rate $v_{nat}$) defined by the hysteretic component of the response (13) is smaller, and $L\rightarrow 0$ as $\max _{\alpha \in \varPi } q(\alpha )\rightarrow 0$. More generally, L decreases as the proportion of individuals with a wide separation of switching thresholds, $\alpha _2-\alpha _1$, decreases and the proportion of individuals with a small separation of switching thresholds increases. The vaccination rate defined by any single-valued function $v=v(I)$ corresponds to $L=0$. This case is technically included with the general Preisach operator (12) and corresponds to the absence of hysteresis in the response. In the particular case when the vaccination rate is defined by the continuous Preisach operator (13), the relation $L=0$ is equivalent to $v=v_{nat}$, i.e. simply a constant vaccination rate, hence one recovers the classical model. In other words, $L=0$ if and only if the density function $q=q(\alpha )$ in (13) is identically zero. The results presented in the following sections focus on system (3), (13) with $L>0$, i.e. the case when $q=q(\alpha )$ is not identically zero, hence the response exhibits hysteresis. The limit $q(\alpha )\rightarrow q_0 \delta (\alpha -\alpha ^*)$ of the Dirac measure concentrated at a point $\alpha ^*=(\alpha _1^*,\alpha _2^*)$ with $\alpha _1^*<\alpha _2^*$ corresponds to system (3), (10) with one non-ideal relay operator. This system models a perfectly homogeneous response of the population to a two-threshold hysteretic intervention policy. A uniform density $q(\alpha )=q_0$ with a $q_0>0$ corresponds to the most heterogeneous response.

The value of the quantity L plays an important role for the following results. Note that $L\le K$ (cf. (16)). We will assume that

$$\begin{aligned} L < \beta . \end{aligned}$$

(23)

We will also need to consider the response to a wider class of inputs. Let $0\le t_0<t'<t''$ and let an input $I=I(t)$ increase on the interval $[t_0,t']$ and then decrease on the interval $[t',t'']$. Such inputs will be also called simple on the interval $[t_0,t'']$. Suppose that the input values $I_0=I(t_0)$, $I_2=I(t')$ and $I_1=I(t'')$ satisfy $I_0\le I_1<I_2$. Then it follows from the definition of the Preisach operator that formula (17) is valid, where the increasing functions ${{\bar{v}}}(\cdot ), {{\hat{v}}}(\cdot )$ satisfy (18), but relations (19) and (21) do not necessarily hold. Formulas (17) and (18) are also true if the input $I=I(t)$ first decreases on the interval $[t_0,t']$ and then increases on the interval $[t',t'']$, and the input values $I_0=I(t_0)$, $I_1=I(t')$ and $I_2=I(t'')$ satisfy $I_1<I_2\le I_0$, see Fig. 3b. Functions ${{\bar{v}}}={{\bar{v}}}(I)$, ${{\hat{v}}}={{\hat{v}}}(I)$ in (17) will be referred to as an ascending branch and a descending branch of the Preisach operator. It is important to notice that these functions depend on the states $\nu _\alpha (t_0)$, $\alpha \in \varPi$, of the relays at the moment $t_0> 0$, which in turn depend on the initial states $\nu _\alpha ^0$ of the relays at the moment $t=0$ and the value of the input I on the interval $[0,t_0]$ (cf. (8)). As such, on any interval of monotonicity of the input, the input-output pair (I, v) follows one of infinitely many possible branches of the Preisach operator, and a particular branch followed by the input-output pair is uniquely defined by the prior history of the input variations and the initial states of the relays.

3.3 Equilibrium points

We will assume that

$$\begin{aligned} \varPi = \{\alpha =(\alpha _1,\alpha _2): 0\le \alpha _1<\alpha _2\le 1 \}. \end{aligned}$$

(24)

Due to this assumption and the compatibility constraint (9), the inclusion $\alpha \in \varPi$ implies that all the relays are in state $\nu _\alpha =0$ when $I=0$. Therefore, system (3), (13) has a unique infection-free equilibrium

$$\begin{aligned} (I_*,S_*,\nu ^0)=\left( 0,\frac{\mu }{\mu +v_{nat}},0\right) \in {\mathfrak {U}}, \end{aligned}$$

(25)

in which the state $\nu ^0=\nu _\alpha ^0: \varPi \rightarrow \{0,1\}$ of the Preisach operator is the identical zero. According to (13), the vaccination rate at this equilibrium is minimal and equals $v_{nat}$.

In addition, if

$$\begin{aligned} R_0:=\frac{\beta \mu }{\delta (\mu +v_{nat})}>1, \end{aligned}$$

(26)

then system (3), (13) also has a family of endemic equilibrium states

$$\begin{aligned} (I^*,S^*,\nu ^0)=\left( \frac{\mu }{\delta }-\frac{\mu +v^0}{\beta }, \frac{\delta }{\beta },\nu ^0\right) \in {\mathfrak {U}} \end{aligned}$$

(27)

with $(I^*,S^*)\in {\mathfrak {D}}$, where the vaccination rate $v^0$ is related to the state $\nu ^0=\nu _\alpha ^0: \varPi \rightarrow \{0,1\}$ of the Preisach operator by

$$\begin{aligned} v^0=v_{nat}+\iint _{\varPi } \nu _{\alpha }^0 \,q(\alpha ) \,d\alpha _1 d\alpha _2. \end{aligned}$$

(28)

These equilibria form a connected set in ${\mathfrak {U}}$. Further, the set (27) includes equilibrium states with different vaccination rates $v^0$ and different proportions of the infected and recovered populations, while the fraction of the susceptible individuals is the same at all these states.

Remark 1

If $\varPi$ is different from (24) and includes points $(\alpha _1,\alpha _2)$ with $\alpha _1<0, \ 0\le \alpha _2\le 1$, then the set of infection-free equilibrium states is also infinite and connected. Depending on the parameters, it can be either an attractor or repeller or include equilibrium states with different stability properties (this is not unlike the classical SIR model with zero mortality rate). Further, in this case, a solution which starts from small infected population and converges to an infection-free equilibrium is characterized by higher vaccination rate at the end than at the beginning. This is because the relays with $\alpha _1<0$ switch from state 0 to state 1 but never switch back due to the positivity of the input I.

Trajectories of system (3), (13) lie in the infinite-dimensional phase space ${\mathfrak {U}}$ of triplets $(I,S,\nu ^0)$. Slightly abusing the notation, we will sometimes also refer to the two-dimensional curve (I(t), S(t)) as to a trajectory, omitting the component (8) in the state space of the Preisach operator.

Proposition 1

If

$$\begin{aligned} R_0=\frac{\beta \mu }{\delta (\mu +v_{nat})}\le 1, \end{aligned}$$

(29)

then the infection-free equilibrium (25) is the global attractor of system (3), (13). If the opposite inequality (26) holds, then any trajectory of system (3), (13), which has at most finite number of intersections with the nullcline $\dot{I}=0$ (the line $S=S^*=\delta /\beta$),

converges to an endemic equilibrium.

In particular, according to (29), if the base vaccination rate $v_{nat}$ is greater than or equal to $(\beta - \delta )\mu /\delta$, then the infection-free equilibrium is attained globally.

Proof

If $\delta /\beta \ge 1$, then the first equation of (3) implies that $\dot{I}<0$ in ${\mathfrak {D}}$.

Therefore, on any given trajectory of (3), (13), the vaccination rate is defined by $v(t)={{{\hat{v}}}(I(t))}$ (cf. (17)), where the function ${{{\hat{v}}}(I)}$ is a continuous descending branch of the Preisach operator; this branch depends on the initial state $\nu ^0=\nu ^0_\alpha$. Thus, a trajectory of (3), (13) is simultaneously a trajectory of the ordinary differential system

$$\begin{aligned} \begin{array}{l} \dot{I}=\beta IS - \delta I,\\ \dot{S}= -\beta IS - {\tilde{v}}(I)S-\mu S+\mu \end{array} \end{aligned}$$

(30)

with ${\tilde{v}}(\cdot )={{{\hat{v}}}(\cdot )}$ depending on $\nu ^0=\nu ^0_\alpha$. Since $\dot{I}<0$, each trajectory of (30) converges to the infection-free equilibrium $(I_*,S_*)$ for any branch ${\tilde{v}}(\cdot )={{{\hat{v}}}(\cdot )}$, and the result follows.

Now, assume that $1>\delta /\beta$ and (29) holds. Let us consider the intersection of the region

$S\ge \delta /\beta =S^*$ and the domain ${\mathfrak {D}}$. In this region, the first equation of (3) implies $\dot{I}\ge 0$ and hence $I(t)\ge I(0)>0$. Therefore, the second equation of (3) implies

$$\begin{aligned} \dot{S}=-S(\beta I + v +\mu )+\mu \le -S(\beta I(0) + v_{nat} +\mu )+\mu \end{aligned}$$

and due to (29),

$$\begin{aligned} \dot{S} \le -S\left( \beta I(0)+\frac{\beta \mu }{\delta }\right) +\mu = -S\left( \beta I(0)+\frac{\mu }{S^*}\right) +\mu \le -\beta I(0)S^* \quad \text {if}\quad S\ge S^*. \end{aligned}$$

Since $I(0)>0,$ we conclude that all trajectories of (3), (13) enter the region $\{(I,S)\in {\mathfrak {D}}: S<S^*\}$ and remain there for all sufficiently large t. Therefore, the same argument as we used in the case $\delta /\beta \ge 1$ above shows that all the trajectories of system (3), (13) converge to the infection-free equilibrium (25).

Finally, assume that (26) holds, and suppose that a trajectory of system (3), (13) has at most finite number of intersections with the line $S=S^*$ where $\dot{I}=0$. Then, after the last intersection, the I-component of the trajectory either strictly decreases or strictly increases with t. In either case, the monotonicity of I(t) implies that the trajectory of the (3), (13) (after its last intersection with the line $S=S^*$) is simultaneously a trajectory of the ordinary differential system (30) where ${\tilde{v}}(\cdot )$ is either a descending or an ascending branch of the Preisach operator. Due to the fact that any branch ${\tilde{v}}(I)$ increases, relation (26) implies that system (30) has a unique endemic equilibrium $(I^*,S^*)$ given by

$$\begin{aligned} \mu (1-S^*)-\beta S^* I^* = S^* {\tilde{v}}(I^*), \qquad S^*=\delta /\beta . \end{aligned}$$

(31)

Furthermore, system (30) has a global Lyapunov function (Korobeinikov and Wake (2002); Korobeinikov and Maini (2004))

$$\begin{aligned} V(I,S)= S - S^* \ln \frac{S}{S^*} + I - I^* \ln \frac{I}{I^*} + \frac{1}{\beta }\int _{I^*}^I \frac{{\tilde{v}}(i)-{\tilde{v}}(I^*)}{i}\,d i. \end{aligned}$$

(32)

Indeed,

$$\begin{aligned} \dot{V}&= \left( S- {S^*}\right) \left( -\beta I -{\tilde{v}}(I)-\mu +\frac{\mu }{S}\right) + \left( I- {I^*}\right) (\beta S-\delta ) \\&\quad +({\tilde{v}}(I)-{\tilde{v}}(I^*)) \left( S-\frac{\delta }{\beta }\right) , \end{aligned}$$

where we replace $\mu =-\beta I^* -{\tilde{v}}(I^*) +{\mu }/{S^*}$, $\delta =\beta S^*$ to obtain

$$\begin{aligned} \dot{V}= & {} \left( S- {S^*}\right) \left( -\beta (I-I^*) -{\tilde{v}}(I) +{\tilde{v}}(I^*)-\frac{\mu }{S^*} +\frac{\mu }{S}\right) + \beta \left( I- {I^*}\right) (S-S^*) \nonumber \\&+({\tilde{v}}(I)-{\tilde{v}}(I^*)) \left( S-S^*\right) =-\frac{\mu (S-S^*)^2}{S^* S}<0. \end{aligned}$$

(33)

This implies convergence to the endemic equilibrium point. $\square$

4 Main results

4.1 Poincaré-Bendixson type alternative

Proposition 1 does not cover those trajectories that have infinitely many intersections with the nullcline $S=S^*$ in the case when relation (26) holds.

Theorem 1

Let (26) hold. Any trajectory of system (3), (13) (starting from any initial values from the region $I>0$, $S>0$, $S+I \le 1$ and any admissible initial state of the Preisach operator) converges either to an endemic equilibrium or to a simple periodic orbit.

Proof

Consider a trajectory (I(t), S(t)) which does not converge to an equilibrium point. Due to Proposition 1, it has infinitely many intersections with the line $S=S^*$ at points $I(t_k)=I_k$, $k=1,2,...$ with $t_k<t_{k+1}$ (where we can assume without loss of generality that $I_1> I_2$).

If for some $k'$ we have $I_{k'}< I_{k'+2} < I_{k'+1}$, then let us compare the arc $\varGamma _{k'+2}$ of the trajectory (I(t), S(t)) connecting the points $(I_{k'+2}, S^*)$ and $(I_{k'+3},S^*)$ with its arc $\varGamma _{k'}$ connecting the points $(I_{k'},S^*)$ and $(I_{k'+1},S^*)$. Note that on each arc $\varGamma _{k'}$ the vaccination rate follows a particular branch of the Preisach operator, which we will denote as ${{\bar{v}}}_{k'}$ (cf. (17)).

Both arcs $\varGamma _{k'+2}$ and $\varGamma _{k'}$ lie above the nullcline $S=S^*$, both go from left to right (hence $I_{k'+3}> I_{k'+2}$), and $\varGamma _{k'}$ starts to the left of $\varGamma _{k'+2}$. Since for the internal points of these arcs,

$$\begin{aligned} \frac{dS}{dI}=\frac{\dot{S}}{\dot{I}}= \frac{-\beta IS -{{\bar{v}}}_i(I)S-\mu S+\mu }{\beta IS - \delta I},\qquad (I,S)\in \varGamma _i, \ i=k', k'+2, \end{aligned}$$

and ${{\bar{v}}}_{k'+2}(I)>{{\bar{v}}}_{k'}(I)$, we see that $\varGamma _{k'}$ and $\varGamma _{k'+2}$ cannot intersect except at the end point, hence $I_{k'}<I_{k'+2}< I_{k'+3}\le I_{k'+1}$ as required. Further, if $I_{k'+3}= I_{k'+1}$, then due to forward uniqueness the trajectory becomes periodic starting from the moment $t=t_{k'+1}$, i.e. $I_{k'+2j+1}=I_{k'+1}$, $I_{k'+2j+2}=I_{k'+2}$ for all $j=1,2,\ldots$

Similarly, relations $I_{k'+1}> I_{k'+3} > I_{k'+2}$ imply $I_{k'+1}> I_{k'+3} > I_{k'+4}\ge I_{k'+2}$, and if $I_{k'+4}= I_{k'+2}$, then the trajectory becomes periodic after the moment $t=t_{k'+2}$.

Combining the above two results, we see that if either $I_{k'}< I_{k'+2} < I_{k'+1}$ or $I_{k'+1}> I_{k'+3} > I_{k'+2}$ for some $k'$, and the trajectory does not become periodic, then

$$\begin{aligned} {I_{k'}< } I_{k'+2}< I_{k'+4}< I_{k'+6}< \cdots< I_{k'+5}< I_{k'+3} < I_{k'+1}. \end{aligned}$$

Therefore, the trajectory converges to a periodic orbit oscillating between the points $(I',S^*)$ and $(I'',S^*)$ with $I'=\lim _{j\rightarrow \infty } I_{k'+2j}$ and $I''=\lim _{j\rightarrow \infty } I_{k'+2j+1}$ (or an equilibrium if the two limits coincide).

The only remaining alternative to this scenario is to have either

$$\begin{aligned} \cdots> I_5> I_3> I_{1}> I_{2}> I_{4}> I_6 > \cdots \end{aligned}$$

or

$$\begin{aligned} \cdots< I_5< I_3< I_{1}< I_{2}< I_{4}< I_6 < \cdots \end{aligned}$$

for all $I_k$. In this case, again, the limit is a periodic trajectory oscillating between the points $(I',S^{*})$ and $(I'',S^*)$ unless $\inf I_k=0$. However, it is easy to see that actually $\inf I_k\ge \varepsilon >0$. Indeed, on each arc $\varGamma _k$ which lies below the line $S=S^*$, the component I(t) of the solution decreases, and the vaccination rate is given by $v(t)={{\hat{v}}}_k(I(t))$ for some descending branch ${{\hat{v}}}_k(\cdot )$ of the Preisach operator. Therefore, the Lyapunov function $V_k(I,S)$ given by (31), (32) with ${\tilde{v}}(\cdot )={{\hat{v}}}_k(\cdot )$ decreases along the segment $\varGamma _k$ of the trajectory, hence the value of $V_k(\cdot ,\cdot )$ at the left end of $\varGamma _k$ is less than at the right end. But the functions $V_k(\cdot ,S^*): (0,1]\rightarrow {\mathbb {R}}$ are uniformly bounded for $I\in [\delta ^{*},1]$, $\delta ^{*} > 0$, and satisfy $V_k(I,S^*)\ge -I^*_k \ln ({I}/{I^*_k})$, where $I^*_k$ is the solution of (31) for ${\tilde{v}}(\cdot )={{\bar{v}}}_k(\cdot )$. Relation (26) ensures that $\inf I_k^*\ge \varepsilon _0>0$, hence $\inf _k V_k(I ,S^*)\rightarrow \infty$ as $I\rightarrow 0+$, and consequently the fact that the set of values of $V_k(\cdot ,\cdot )$ at the right ends of the arcs $\varGamma _k$ is bounded implies that the left ends satisfy $\inf I_k\ge \varepsilon >0$. $\square$

4.2 Sufficient conditions for global stability of the set of endemic equilibrium states.

In the rest of the paper, we derive sufficient conditions which ensure the global convergence to endemic equilibrium states.

We make the following assumption:

(A) Each input-output loop of the Preisach operator corresponding to a simple periodic input is convex. In other words, the function ${{{\bar{v}}}(\cdot )}$ in (17) is convex and the function ${{\hat{v}}}(\cdot )$ in (17) is concave.

Assumption (A) is satisfied if the distribution of the population over the set of threshold pairs is uniform or sufficiently close to uniform, i.e. the density $q(\alpha )$ in (13) is sufficiently close to a constant. In other words, the adaptive response, which defines the excess vaccination rate (over the base rate $v_{nat}$), is sufficiently heterogeneous.

Lemma 1

Let ${{\bar{I}}}^*>0$ and the function ${{\bar{V}}}(I,S)$ be defined by formulas (31), (32) with ${\tilde{v}}(i)={{\bar{v}}}(i)$, and let ${{\hat{I}}}^*$, ${{\hat{V}}}(I,S)$ be defined by the same formulas with ${\tilde{v}}(i)={{\hat{v}}}(i)$. Assumption (A) guarantees that all the sets $\{(I,S): {{\bar{V}}}(I,S)\le c\}$ are convex and the intersection of every such set with the half plane $I\le {{\hat{I}}}^*$ is convex.

Proof

The curvature of the level line of the function V(I, S) is given by

$$\begin{aligned} \kappa = - \frac{V_{SS} (V_I)^2 + V_{II} (V_S)^2 - 2 V_{IS} V_I V_S}{(V_S^2 + V_I^2)^{3/2}}, \end{aligned}$$

where $V_{IS}=0$ by the definition of V. We need to show that $\kappa < 0$, i.e. $V_{SS} (V_I)^2 + V_{II} (V_S)^2 > 0$, which for the function (32) is equivalent to

$$\begin{aligned} 0 < \frac{S^*}{S^2} \, V_I^2 + \frac{ \beta I^* + I {\tilde{v}}'(I)-{\tilde{v}}(I) + {\tilde{v}}(I^*)}{ \beta I^2} \, V_S^2. \end{aligned}$$

(34)

For ${\tilde{v}}(\cdot )={{\bar{v}}}(\cdot )$, the convexity of ${{\bar{v}}}$ implies

$$\begin{aligned} ({I-{{\bar{I}}}^*}){{\bar{v}}}'(I)\ge {{{\bar{v}}}(I)-{{\bar{v}}}({{\bar{I}}}^*)}, \end{aligned}$$

hence

$$\begin{aligned} I {{\bar{v}}}'(I) \ge {{\bar{v}}}(I)-{{\bar{v}}}({{{\bar{I}}}^*}) \end{aligned}$$

(because ${{\bar{v}}}$ increases) and (34) follows. For ${\tilde{v}}(\cdot )={{\hat{v}}}(\cdot )$, relation (34) holds in the region $I\le {{\hat{I}}}^*$ because ${{\hat{v}}}(\cdot )$ is an increasing function. $\square$

Theorem 2

Let assumptions (A) and (26) be satisfied. Let the quantity L defined by (22) be sufficiently small. Then, system (3), (13) has no periodic solutions, and every trajectory converges to an endemic equilibrium point.

In Theorem 2, condition (A) ensures a sufficiently heterogeneous adaptive response, and simultaneously we assume a sufficiently small overall amount of hysteresis in the response, i.e. sufficiently narrow hysteresis loops as measured by the quantity L. For example, both conditions are satisfied for the uniform distribution of individuals over the set of switching threshold pairs corresponding to a constant density function $q(\alpha )=q_0$ with a sufficiently small $q_0>0$ in (13). Small perturbations of such densities also satisfy the conditions of Theorem 2. On the other hand, system (3) with the vaccination rate (10) corresponding to the perfectly homogeneous response (modeled by a single non-ideal relay) can exhibit a periodic attractor, see Chladná et al. (2020). Further, as shown in the next section, a periodic attractor is also possible in the heterogeneous model (3), (13), if the density is concentrated near one point, in which case the response is close to homogeneous and the hysteresis loops are non-convex. Therefore, a sufficient heterogeneity degree of the hysteretic response might be required for the global stability of the equilibrium set. However, assumption (A) is not a necessary condition for the global stability. There might be other conditions that ensure a heterogeneous response and the convergence of trajectories to the equilibrium set.

Due to Theorem 1, to prove Theorem 2 it suffices to show that system (3), (13) has no simple periodic solutions if the quantity L defined by (22) is sufficiently small. An explicit estimate for L will be established in the proof.

Extensions of Theorem 2 to system (3) with the response (12), which is more general than in (13), are beyond the scope of this paper. In particular, as mentioned above, in the case $L=0$ the vaccination rate in this system is a nonlinear single-valued function $v=v(I)$. In other words, there is no hysteresis because the degenerate hysteresis loops have zero width, i.e. ${{\hat{v}}}(I)={{\bar{v}}}(I)=v(I)$. These degenerate loops are generally non-convex (unless v is linear). On the other hand, the adaptive response is heterogeneous (unless v is constant), and the set of equilibrium states is the global attractor (Korobeinikov and Maini 2004). It would be interesting to find sufficient conditions for the global stability when some hysteresis is present, i.e. L is positive, but the hysteresis loops remain non-convex.

4.3 Discussion

To explore how the heterogeneity of the response of the susceptible population to the advent of an epidemic can affect dynamics of system (3), we first consider the aggregate vaccination rate (13) with the Gaussian density

$$\begin{aligned} q(\alpha _1,\alpha _2) = A e^{-\frac{(\alpha _1-\alpha _{m_1})^2 + (\alpha _2-\alpha _{m_2})^2}{2\sigma ^2}}, \end{aligned}$$

(35)

where the normalizing parameter $A=A(\alpha _{m_1},\alpha _{m_2},\sigma )$ ensures that the integral of q over the domain (24) equals 1. Due to this normalization condition, the quantity (22) satisfies $L=L(\alpha _{m_1},\alpha _{m_2},\sigma )\ge 1$, i.e. the response is hysteretic for any parameter values of the density (35). The limit $\sigma \rightarrow 0$ corresponds to the perfectly homogeneous response (10), i.e. the vaccination rate switches from the value $v_{nat}=0$ to the value $v_{int}=1$ at the switching threshold $I=\alpha _{m_2}$ and switches backwards at the threshold $I=\alpha _{m_1}$. In this limit, $L\rightarrow 1/(\alpha _{m_2}-\alpha _{m_1})$. Increasing the variance $\sigma ^2$ of the (truncated) Gaussian distribution corresponds to increasing the heterogeneity of the response within the susceptible population and, simultaneously, decreasing the quantity L.

Figure 4 presents an example of the convergence to a periodic cyclic behavior for small $\sigma >0$. This scenario for system (3), (10) with one non-ideal relay was studied in Chladná et al. (2020). Further, Fig. 4 shows that the periodic behavior replaces the convergence to an endemic equilibrium state as $\sigma$ decreases. This is in agreement with Theorem 2 because the quantity (22) increases and the heterogeneity of the response decreases with decreasing $\sigma$. The attracting periodic orbit bifurcates from the continuum of equilibrium states indicating that the system undergoes a supercritical Hopf bifurcation as L increases and the heterogeneity decreases. This type of the Hopf bifurcation in systems with the Preisach operator was studied in Appelbe et al. (2008), Balanov et al. (2012).

Fig. 4

A solution of system (3) with the vaccination rate defined by relations (10) and (35). The parameters are $\mu = 0.0006$, $\delta = 0.6$, $\beta = 10.8$ ($\hbox {week}^{-1}$), $\alpha _{m_1} = 0.0002$, $\alpha _{m_2} = 0.0055$. The corresponding basic reproduction number is $R_0=18$. (a) The green and blue trajectories correspond to $\sigma = 0.0009$ and $\sigma = 0.01$, respectively. The initial conditions for both trajectories, $I(0)=10^{-5}, S(0)=1-I(0)$, correspond to a small number of infected individuals in a fully susceptible population. (b) Zoom into the region marked by the red box on panel (a). The green trajectory converges to a cycle; the blue trajectory converges to an endemic equilibrium. (c) Hysteresis loops on the (I, v)-plane for both trajectories using the same color code. (d, e) Time traces of the infected population and the vaccination rate. The time unit is one week. (f) Zoom into one pulse of the infected population for the green trajectory

The trajectory corresponding to a more heterogeneous response ($\sigma =0.01$) in Fig. 4 converges to an endemic equilibrium state with the densities $I^*=0.00063$, $S^*=0.056$ of the infected and susceptible populations, respectively. The vaccination rate at this equilibrium is $v^*=0.0041$ ($\hbox {week}^{-1}$). The trajectory corresponding to a more homogeneous response and a larger L ($\sigma =0.0009$) converges to the periodic orbit and exhibits a lower initial peak of the infected population during the transient than the trajectory of the heterogeneous system. The average density of the susceptible population for the periodic trajectory, ${{\bar{S}}}=0.057$, is close to $S^*$. The density of the infected population along the periodic trajectory is much higher than $I^*$ at its peaks, but the average density ${{\bar{I}}}=0.00016$ is significantly lower than $I^*$. This agrees with the fact that the average vaccination rate ${{\bar{v}}}=0.023$ ($\hbox {week}^{-1}$) is significantly higher than $v^*$.

Let us now consider a set of densities

$$\begin{aligned} q(\alpha _1,\alpha _2)= {\left\{ \begin{array}{ll} q_0 \ \ \text {for} \ \ 0< \alpha _2- \alpha _1 < c,\\ 0 \ \ \ \text {for} \ \ c\le \alpha _2- \alpha _1 \le 1, \end{array}\right. } \end{aligned}$$

(36)

where $q_0>0$ and $c\in [0,1]$. Here the parameter c defines the maximal separation of thresholds for the non-ideal relays contributing to the integral (13), and the susceptible population is assumed to be distributed uniformly over the set of threshold pairs $(\alpha _1,\alpha _2)$ with the difference $\alpha _2-\alpha _1$ not exceeding c. Thus, the hysteresis effect increases with c and $q_0$. One can show that all the hysteresis loops of the Preisach operator (13) with the density (36) are convex, i.e. assumption (A) is satisfied. Further, the quantity (22) can be obtained explicitly, namely

$$\begin{aligned} L=q_0 c \left( 1-\frac{1}{\sqrt{2}}\right) \quad \text {for} \quad c<\frac{1}{\sqrt{2}}; \qquad L=q_0 \left( c-\frac{c^2}{2}-\frac{1}{4}\right) \quad \text {for} \quad c\ge \frac{1}{\sqrt{2}}, \end{aligned}$$

hence Theorem 2 can be easily applied to this setting. The parameters of the density function (36) can be related to measurements of the infection rate $I=I(t)$ and vaccination rate $v=v(t)$. In particular, if I starts at zero and monotonically increases, then the excess vaccination rate first increases quadratically and then linearly:

$$\begin{aligned} v=v_{nat}+{\left\{ \begin{array}{ll}\frac{q_0}{2} I^2, &{} 0\le I\le c,\\ q_0 c(I-\frac{c}{2}), &{} c\le I \le 1. \end{array}\right. } \end{aligned}$$

More generally, the density function $q=q(\alpha )$ can be estimated from simultaneous observations of $I=I(t)$ and $v=v(t)$ using the Mayergoyz identification theorem (Mayergoyz 2003). If I increases from zero to a value $I_1$, then drops back to zero, then increases to a value $I_2$, then drops back to zero again, etc., and if the local maximum values $\{I_1, I_2,\ldots , I_N\}$ of I form an $\varepsilon$-net of the interval $0\le I\le 1$, then the identification theorem provides an $O(\varepsilon )$-approximation of the density function from measurements of I and v. In the epidemiological context, this scenario corresponds to several waves of the epidemic. A number of practical identification algorithms can deal with measurement noise and limited amount of data, see e.g. Hoffmann et al. (1989); Cirrincione et al. (2002); Rachinskii et al. (2016). They include both non-parametric and parametric identification methods, where the latter assume a particular form of the density function such as in (35), (36) or that in Appelbe et al. 2009. The quantity (22) can be evaluated either directly from the measurements of I and v along the hysteresis loops or from an estimate of the density function $q(\alpha )$ using formula (21). For this purpose, it is sufficient to use measurements of large hysteresis loops (which correspond to larger values of the local maxima $I_n$ of the infection I), while measurements along small loops can be ignored because L is the maximal relative width of the loops, and the relative width of small loops increases linearly with their length due to (21):

$$\begin{aligned} \frac{1}{I_n}\max _{0 \le I\le I_n}{\bigl ({\hat{v}}(I) - {{\bar{v}}}(I)\bigr )}=O(I_n) \quad \text {as}\quad I_n\rightarrow 0. \end{aligned}$$

5 Proof of theorem 2

The following inequalities will be systematically used:

$$\begin{aligned}&\ln (1 + x) \ge \frac{x}{1+x}, \qquad x \ge -1; \end{aligned}$$

(37)

$$\begin{aligned}&\frac{x(2+x)}{2(1+x)}\ge \ln (1 + x) , \qquad x \ge 0; \end{aligned}$$

(38)

$$\begin{aligned}&\ln (1 + x) \le \frac{2x}{2+x}, \qquad -1< x \le 0. \end{aligned}$$

(39)

We prove the theorem by contradiction. Let us assume that there exists a simple periodic solution (I(t), S(t)), for which I(t) increases from $I_1$ to $I_2$ and then decreases from $I_2$ to $I_1$ on a period with $I_1 <I_2$. Let us denote by ${{\bar{v}}}(I)$ and ${{\hat{v}}}(I)$ the two branches of the Preisach operator corresponding to the increasing I and decreasing I of this solution, respectively, hence relations (17) – (20) hold. Then system (3), (13) has an endemic equilibrium $({{\bar{I}}}^*,S^*)$ defined by Eq. (31) with ${\tilde{v}}(\cdot )={{\bar{v}}}(\cdot )$ and an endemic equilibrium $({{\hat{I}}}^*,S^*)$ defined by Eq. (31) with ${\tilde{v}}(\cdot )={{\hat{v}}}(\cdot )$. Further, since $(I_1, S^*)$ and $(I_2, S^*)$ are the turning points of the periodic solution,

$$\begin{aligned} {{\bar{v}}}(I_1)={{\hat{v}}}(I_1)< \mu \left( \frac{\beta }{\delta } - 1\right) - \beta I_1; \quad \ \ \mu \left( \frac{\beta }{\delta } - 1\right) - \beta I_2 < {{\bar{v}}}(I_2)={{\hat{v}}}(I_2). \end{aligned}$$

Introducing the functions

$$\begin{aligned} {{\bar{f}}}(I)={{\bar{v}}}(I)+ \beta I-\mu \left( \frac{\beta }{\delta } - 1\right) , \qquad {{\hat{f}}}(I)={{\hat{v}}}(I)+ \beta I-\mu \left( \frac{\beta }{\delta } - 1\right) , \end{aligned}$$

this means that

$$\begin{aligned} {{\bar{f}}}(I_1)={{\hat{f}}}(I_1)<0, \qquad {{\bar{f}}}(I_2)={{\hat{f}}}(I_2)>0. \end{aligned}$$

(40)

On the other hand, according to (31),

$$\begin{aligned} {{\bar{f}}}({{\bar{I}}}^*)={{\hat{f}}}({{\hat{I}}}^*)=0. \end{aligned}$$

(41)

Also, according to (18),

$$\begin{aligned} {{\bar{f}}}(I)<{{\hat{f}}}(I), \qquad I_1<I<I_2. \end{aligned}$$

(42)

Since the functions ${{\bar{v}}}$ and ${{\hat{v}}}$ increase, so do the functions ${{\hat{f}}}$ and ${{\bar{f}}}$, hence combining relations (40) – (42), we obtain

$$\begin{aligned} I_1< {{\hat{I}}}^*< {{\bar{I}}}^* < I_2. \end{aligned}$$

(43)

Recall the definition of the functions ${{\bar{V}}}(I,S)$ and ${{\hat{V}}}(I,S)$, see Lemma 1. We now consider the following trivial identity

$$\begin{aligned}&\bigl ( {\bar{V}}(I_1,S^*)- {\bar{V}}(I_2,S^*) \bigr ) + \bigl ({\hat{V}}(I_2,S^*) - {\hat{V}}(I_1,S^*) \bigr ) \\&\quad = \bigl ( {\hat{V}}(I_2,S^*)-{\bar{V}}(I_2,S^*) \bigr )+ \bigl ( {\bar{V}}(I_1,S^*) - {\hat{V}}(I_1,S^*) \bigr ) \end{aligned}$$

and estimate the differences participating in it to establish a lower bound for L.

5.1 Estimation of ${\bar{V}}(I_1,S^*)-{\bar{V}}(I_2,S^*)$.

Dividing (33) by the first equation of (3), we obtain

$$\begin{aligned} \frac{d {\bar{V}}}{d I} = -\mu \frac{S - S^*}{\beta I S S^*}= - \frac{\mu }{\beta I S^*}\left( 1- \frac{S^*}{S}\right) \end{aligned}$$

(44)

along the trajectory. For the part ${\bar{\varGamma }}$ of the periodic trajectory with increasing I and $S>S^*$, this relation implies

$$\begin{aligned} \frac{d {\bar{V}}}{d I}<0, \qquad I_1<I<I_2, \ (I,S)\in {\bar{\varGamma }}. \end{aligned}$$

(45)

Therefore, this segment of the trajectory lies outside the set $\{(I,S): {\bar{V}}(I,S)\le {\bar{V}}(I_2, S^*)\}$. The top point (with the largest S) of the level line ${\bar{V}}(I,S)= {\bar{V}}(I_2, S^*)$ is defined by $\partial {\bar{V}}/ \partial I = 0$, i.e. $\beta I+ {{\bar{v}}}(I) = \beta {{\bar{I}}}^*+ {{\bar{v}}}({{\bar{I}}}^*),$ which by monotonicity of ${{\bar{v}}}$ implies $I = {{\bar{I}}}^*$. Denoting the S-component of this point as $S_M$, we see that

$$\begin{aligned} {\bar{V}}(I_2, S^*)= {\bar{V}}({{\bar{I}}}^*, S_M) = S_M - S^* \ln \frac{S_M}{S^*} + {{\bar{I}}}^*. \end{aligned}$$

(46)

Let us fix a positive $h < S_M - S^*$. By Lemma 1, there is a unique point $(I_b,S_b)$ on the level line ${{\bar{V}}}(I,S)={\bar{V}}(I_2, S^*)$ of the function ${{\bar{V}}}$ with $S_b=S^*+h$, $I_b\ge {{\bar{I}}}^*$. The convexity of the set $\{(I,S):{{\bar{V}}}(I,S)\le {\bar{V}}(I_2, S^*)\}$ also implies that the point $(I_b,S^*+h)$ lies above the line segment connecting the points $({{\bar{I}}}^*,S_M)$ and $(I_2,S^*)$ because all three points lie on the boundary of this set. Therefore,

$$\begin{aligned} I_b - {{\bar{I}}}^* \ge \left( 1 - \frac{h}{S_M - S^*}\right) (I_2 - {{\bar{I}}}^*). \end{aligned}$$

(47)

Since the part ${\bar{\varGamma }}$ of the periodic trajectory lies outside the set $\{(I,S):{{\bar{V}}}(I,S)\le {\bar{V}}(I_2, S^*)\}$ and the line segment $S=S^*+h$, ${{\bar{I}}}^*\le I\le I_b$ belongs to this set, we have $S\ge S^*+h$ for $(I,S)\in {\bar{\varGamma }}$, ${{\bar{I}}}^*\le I\le I_b$. Therefore, on the interval $[{{\bar{I}}}^*,I_b]$, relation (44) implies

$$\begin{aligned} \frac{d {\bar{V}}}{d I} = - \frac{\mu }{\beta I S^*}\left( 1- \frac{S^*}{S}\right) \le - \frac{\mu }{\beta I S^*}\left( 1- \frac{S^*}{S^* + h}\right) = - \frac{\mu h}{\beta S^* (S^* + h) I}. \end{aligned}$$

We integrate this inequality along the trajectory over the interval $I \in [{{\bar{I}}}^*,I_b]$ and using the monotonicity of ${\bar{V}}$ which follows from (45), we obtain

$$\begin{aligned} {\bar{V}}(I_2, S^*) - {\bar{V}}(I_1, S^*) \le {\bar{V}}(I_b, S^*) - {\bar{V}}({{\bar{I}}}^*, S^*) \le - \frac{\mu h}{\beta S^* (S^* + h)} \ln \frac{I_b}{{{\bar{I}}}^*}, \end{aligned}$$

hence

$$\begin{aligned} {\bar{V}}(I_1, S^*) - {\bar{V}}(I_2, S^*) \ge \frac{\mu }{\beta S^*} \max _{h\le S_M - S^*}\frac{h}{S^* + h} \ln \frac{I_b}{{{\bar{I}}}^*}. \end{aligned}$$

(48)

Using inequality (37) and relation (47), we estimate the right hand side of (48) as follows:

$$\begin{aligned}&\frac{\mu }{\beta S^*} \max _{h\le S_M - S^*}\frac{h}{S^* + h} \ln \frac{I_b}{{{\bar{I}}}^*} \ge \frac{\mu }{\beta S^*} \max _{h\le S_M - S^*}\frac{h}{S^* + h}\cdot \frac{I_b - {{\bar{I}}}^*}{I_b}\\&\ge \frac{\mu }{\beta S^*} \max _{h\le S_M - S^*}\frac{h}{S_M}\left( 1-\frac{h}{S_M - S^*}\right) \frac{I_2 - {{\bar{I}}}^*}{I_b} \\&= \frac{\mu }{\beta S^*S_M {I_b} } (I_2 - {{\bar{I}}}^*) (S_M - S^*) \max _{h\le S_M - S^*}\frac{h}{S_M-S^*}\left( 1-\frac{h}{S_M - S^*}\right) \\&= \frac{\mu }{4\beta S^*S_M {I_b}} (I_2 - {{\bar{I}}}^*) (S_M - S^*). \end{aligned}$$

Therefore,

$$\begin{aligned} {\bar{V}}(I_1, S^*) - {\bar{V}}(I_2, S^*) \ge \frac{\mu }{4\beta S^*S_M {I_b}} (I_2 - {{\bar{I}}}^*) (S_M - S^*). \end{aligned}$$

(49)

In order to estimate $S_M - S^*$, we evaluate the function ${\bar{V}}$ at the point $(I_2,S^*)$ using (32) and substitute the result into (46) to obtain

$$\begin{aligned} S_M - S^* - S^* \ln \frac{S_M}{S^*} = I_2 - {{\bar{I}}}^* - {{\bar{I}}}^* \ln \frac{I_2}{{{\bar{I}}}^*} + \frac{1}{\beta } \int _{{{\bar{I}}}^*}^{I_2} \frac{{{\bar{v}}}(i) - {{\bar{v}}}({{\bar{I}}}^*)}{i} \,\mathrm {d}i. \end{aligned}$$

(50)

We estimate the left hand side of (50) from above using

$$\begin{aligned}&S_M - S^* - S^* \ln \frac{S_M}{S^*} = S^* \left[ \frac{S_M}{S^*} -1 -\ln \left( 1 + \frac{S_M}{S^*} -1\right) \right] \\&\le S^*\frac{\left( \frac{S_M}{S^*} -1\right) ^2}{\frac{S_M}{S^*} } = \frac{(S_M - S^*)^2}{S_M}. \end{aligned}$$

Further, we find a lower bound of the right hand side of (50) using estimate (38):

$$\begin{aligned} I_2 - {{\bar{I}}}^* - {{\bar{I}}}^* \ln \frac{I_2}{{{\bar{I}}}^*} + \frac{1}{\beta } \int _{{{\bar{I}}}^*}^{I_2} \frac{{{\bar{v}}}(i) - {{\bar{v}}}({{\bar{I}}}^*)}{i} \,\mathrm {d}i \ge I_2 - {{\bar{I}}}^* - {{\bar{I}}}^* \ln \frac{I_2}{{{\bar{I}}}^*}\\ = {{{\bar{I}}}^*}\left[ \frac{I_2}{{{\bar{I}}}^*} - 1 - \ln \left( 1 + \frac{I_2}{{{\bar{I}}}^*} - 1\right) \right] \ge {{\bar{I}}}^* \frac{\left( \frac{I_2}{{{\bar{I}}}^*} - 1\right) ^2}{2\frac{I_2}{{{\bar{I}}}^*}} = \frac{(I_2 - {{\bar{I}}}^*)^2}{2I_2}. \end{aligned}$$

Combining the last two inequalities with (50), we obtain

$$\begin{aligned} \frac{(S_M - S^*)^2}{S_M} \ge \frac{(I_2 - {{\bar{I}}}^*)^2}{2I_2}, \end{aligned}$$

hence

$$\begin{aligned} S_M - S^* \ge \sqrt{\frac{S_M}{2I_2}}(I_2 - {{\bar{I}}}^*). \end{aligned}$$

Substituting this relation into (49), we finally arrive at

$$\begin{aligned} {\bar{V}}(I_1, S^*) - {\bar{V}}(I_2, S^*) \ge \frac{\mu }{4\beta S^* I_b \sqrt{2 S_M I_2}} (I_2 - {{\bar{I}}}^*)^2 \ge \frac{\mu }{4\sqrt{2}\,\delta } (I_2 - {{\bar{I}}}^*)^2,\nonumber \\ \end{aligned}$$

(51)

where the last inequality holds due to $I_b\le I_2\le 1$, $S_M\le 1$ and $S^*=\delta /\beta$.

5.2 Estimation of ${\hat{V}}(I_1,S^*)-{\hat{V}}(I_2,S^*)$.

Now we consider the lower part ${\hat{\varGamma }}$ of the trajectory with decreasing I and $S<S^*$. We slightly modify the above argument. The relation

$$\begin{aligned} \frac{d {\hat{V}}}{d I} = -\mu \frac{S - S^*}{\beta I S S^*}= - \frac{\mu }{\beta I S^*}\left( 1- \frac{S^*}{S}\right) , \end{aligned}$$

(52)

which is similar to (44), implies

$$\begin{aligned} \frac{d {\hat{V}}}{d I}>0, \qquad I_1<I<I_2, \ (I,S)\in {\hat{\varGamma }}. \end{aligned}$$

(53)

Hence, ${\hat{\varGamma }}$ lies outside the set $\{(I,S):{\hat{V}}(I,S)\le {\hat{V}}(I_1, S^*)\}$. The bottom point (with the smallest S) of the level line ${\hat{V}}(I,S)= {\hat{V}}(I_1, S^*)$ of the function ${{\hat{V}}}$ is defined by $\partial {\hat{V}}/ \partial I = 0$, therefore $I = {{\hat{I}}}^*$ at this point. Denoting its S-component by $S_m$, we obtain

$$\begin{aligned} {\hat{V}}(I_1, S^*)= {\hat{V}}({\hat{I}}^*, S_m) = S_m - S^* \ln \frac{S_m}{S^*} + {\hat{I}}^*, \end{aligned}$$

(54)

which is similar to (46). We fix a positive $h < S^* - S_m$. Using the convexity of the intersection of the set $\{(I,S):{\hat{V}}(I,S)\le {\hat{V}}(I_1, S^*)\}$ with the half-space $I\le {{\hat{I}}}^*$ (see Lemma 1), we establish the existence of a unique point on the level line ${{\hat{V}}}(I,S)={\bar{V}}(I_1, S^*)$ with the coordinates $(I_c,S_c)$ satisfying $S_c=S^*-h$, $I\le {{\hat{I}}}^*$. Arguing as before (cf. (47)), we obtain

$$\begin{aligned} {\hat{I}}^* - I_c \ge \left( 1 - \frac{h}{S^* - S_m}\right) ({\hat{I}}^* - I_1). \end{aligned}$$

(55)

Since ${\hat{\varGamma }}$ lies outside the set $\{(I,S):{{\hat{V}}}(I,S)\le {\hat{V}}(I_1, S^*)\}$, the S-coordinate of the points $(I,S)\in {\hat{\varGamma }}$ with $I\in [I_c, {{\hat{I}}}^*]$ satisfies $S\le S^*-h$, hence (52) implies

$$\begin{aligned} \frac{d {\hat{V}}}{dI} \ge \frac{\mu h}{\beta S^* I (S^* - h)} , \end{aligned}$$

which after integration over $[I_c, {\hat{I}}^*]$, using also (53), gives

$$\begin{aligned} {\hat{V}}(I_2, S^*) - {\hat{V}}(I_1, S^*) \ge {\hat{V}}({\hat{I}}^*, S^*) - {\hat{V}}(I_c, S^*) \ge \frac{\mu h}{\beta S^* (S^* - h)} \ln \frac{{\hat{I}}^*}{I_c}. \end{aligned}$$

Therefore,

$$\begin{aligned} {\hat{V}}(I_2, S^*) - {\hat{V}}(I_1, S^*) \ge \frac{\mu }{\beta S^*} \max _{h\le S^*-S_m}\frac{h}{S^* - h} \ln \frac{{\hat{I}}^*}{I_c}. \end{aligned}$$

(56)

Using relation (37) and (55), the right hand side of Eq. (56) can be estimated as follows:

$$\begin{aligned}&\frac{\mu }{\beta S^*} \max _{h\le S^*-S_m}\frac{h}{S^* - h} \ln \frac{{\hat{I}}^*}{I_c} \ge \frac{\mu }{\beta S^*} \max _{h\le S^*-S_m} \frac{h}{S^*} \ln \left( 1 + \frac{{\hat{I}}^* - I_c}{I_c}\right) \\&\ge \frac{\mu }{\beta S^*} \max _{h\le S^*-S_m}\frac{h({\hat{I}}^* - I_c)}{S^* {\hat{I}}^*} = \frac{\mu }{\beta S^*} \max _{h\le S^*-S_m}\frac{h}{S^*{\hat{I}}^*} \left( 1-\frac{h}{S^*-S_m}\right) ({\hat{I}}^* - I_1)\\&= \frac{\mu }{\beta (S^*)^2{\hat{I}}^* } ({\hat{I}}^* - I_1) (S^* - S_m) \max _{h\le S^*-S_m}\frac{h}{S^* - S_m}\left( 1-\frac{h}{S^* - S_m}\right) \\&= \frac{\mu }{4\beta (S^*)^2 {\hat{I}}^*} ({\hat{I}}^* - I_1) (S^* - S_m). \end{aligned}$$

Hence,

$$\begin{aligned} {\hat{V}}(I_2, S^*) - {\hat{V}}(I_1, S^*) \ge \frac{\mu }{4\beta (S^*)^2 {\hat{I}}^*} ({\hat{I}}^* - I_1) (S^* - S_m). \end{aligned}$$

(57)

In order to estimate $S^* - S_m$, we evaluate ${{\hat{V}}}(I_1,S^*)$ using (32) and rewrite (54) equivalently as

$$\begin{aligned} S^* - S_m + S^* \ln \frac{S_m}{S^*} = {\hat{I}}^* - I_1 + {\hat{I}}^* \ln \frac{I_1}{{\hat{I}}^*} - \frac{1}{\beta } \int _{{\hat{I}}^*}^{I_1} \frac{{\hat{v}}(i) - {\hat{v}}({\hat{I}}^*)}{i} \,\mathrm {d}i. \end{aligned}$$

(58)

A lower bound of the left hand side of (58) using (37) is

$$\begin{aligned} S^* - S_m + S^* \ln \frac{S_m}{S^*} \ge S^* - S_m + S^* - \frac{(S^*)^2}{S_m} = -\frac{(S^* - S_m)^2}{S_m}. \end{aligned}$$

An upper estimate of the right hand side of (58) using (39) and the monotonicity of ${{\hat{v}}}$ is

$$\begin{aligned}&{\hat{I}}^* - I_1 + {\hat{I}}^* \ln \frac{I_1}{{\hat{I}}^*} - \frac{1}{\beta } \int _{{\hat{I}}^*}^{I_1} \frac{{\hat{v}}(i) - {\hat{v}}({\hat{I}}^*)}{i} \,\mathrm {d}i \le {\hat{I}}^* - I_1 + {\hat{I}}^* \ln \frac{I_1}{{\hat{I}}^*} \\&\le {\hat{I}}^* - I_1 + {\hat{I}}^* \frac{2\left( \frac{I_1}{{\hat{I}}^*}-1\right) }{1+\frac{I_1}{{\hat{I}}^*}}=-\frac{({\hat{I}}^* - I_1)^2}{I_1 + {\hat{I}}^*}. \end{aligned}$$

Combining the previous two inequalities with (58), we obtain

$$\begin{aligned} \frac{(S^* - S_m)^2}{S_m} \ge \frac{({\hat{I}}^* - I_1)^2}{I_1 + {\hat{I}}^*}, \end{aligned}$$

hence

$$\begin{aligned} S^* - S_m \ge ({\hat{I}}^* - I_1)\sqrt{\frac{S_m}{I_1 + {\hat{I}}^*}}, \end{aligned}$$

and (57) implies

$$\begin{aligned} {\hat{V}}(I_2, S^*) - {\hat{V}}(I_1, S^*) \ge \frac{\mu }{4\beta (S^*)^2 {\hat{I}}^*}\sqrt{\frac{S_m}{I_1 + {\hat{I}}^*}}\, ({\hat{I}}^* - I_1)^2 \ge \frac{\mu \sqrt{S_m}}{4 \sqrt{{2}}\, \delta } ({\hat{I}}^* - I_1)^2,\nonumber \\ \end{aligned}$$

(59)

where we also use that $I_1\le {{\hat{I}}}^*\le 1$, $S^*\le 1$ and $\beta S^*=\delta$.

5.3 Estimation of ${\bar{V}}(I_1,S^*) - {\bar{V}}(I_2,S^*) + {\hat{V}}(I_2,S^*)- {\hat{V}}(I_1,S^*)$.

Using the definition (32) of the Lyapunov function, we can write

$$\begin{aligned}&{\bar{V}}(I_1,S^*) - {\bar{V}}(I_2,S^*) + {\hat{V}}(I_2,S^*)- {\hat{V}}(I_1,S^*) = \nonumber \\&= - {{\bar{I}}}^* \ln \frac{I_1}{{{\bar{I}}}^*}+\frac{1}{\beta } \int _{{{\bar{I}}}^*}^{I_1} \frac{{{\bar{v}}}(i) - {{\bar{v}}}({{\bar{I}}}^*)}{i} \,\mathrm {d}i + {{\bar{I}}}^* \ln \frac{I_2}{{{\bar{I}}}^*}-\frac{1}{\beta } \int _{{{\bar{I}}}^*}^{I_2} \frac{{{\bar{v}}}(i) - {{\bar{v}}} ({{\bar{I}}}^*)}{i} \,\mathrm {d}i \nonumber \\&\quad - {\hat{I}}^*\ln \frac{I_2}{{\hat{I}}^*}+\frac{1}{\beta } \int _{{\hat{I}}^*}^{I_2} \frac{{\hat{v}}(i) - {\hat{v}}({\hat{I}}^*)}{i} \,\mathrm {d}i + {\hat{I}}^* \ln \frac{I_1}{{\hat{I}}^*}-\frac{1}{\beta } \int _{{\hat{I}}^*}^{I_1} \frac{{\hat{v}}(i) - {\hat{v}}({\hat{I}}^*)}{i} \,\mathrm {d}i \nonumber \\&= {{\bar{I}}}^* \ln \frac{I_2}{I_1} - {\hat{I}}^*\ln \frac{I_2}{I_1} -\frac{1}{\beta } \int _{I_1}^{I_2} \frac{{{\bar{v}}}(i) - {{\bar{v}}}({{\bar{I}}}^*)}{i} \,\mathrm {d}i + \frac{1}{\beta } \int _{I_1}^{I_2} \frac{{\hat{v}}(i) - {\hat{v}}({\hat{I}}^*)}{i} \,\mathrm {d}i \nonumber \\&= \left[ ({{\bar{I}}}^* - {\hat{I}}^*) + \frac{1}{\beta } {{\bar{v}}}({{\bar{I}}}^*) -\frac{1}{\beta } {\hat{v}}({\hat{I}}^*)\right] \ln \frac{I_2}{I_1} + \frac{1}{\beta } \int _{I_1}^{I_2} \frac{{\hat{v}}(i) - {{\bar{v}}}(i)}{i} \,\mathrm {d}i = \nonumber \\&= \frac{1}{\beta } \int _{I_1}^{I_2} \frac{{\hat{v}}(i) - {{\bar{v}}}(i)}{i} \,\mathrm {d}i, \end{aligned}$$

(60)

where we use the fact that

$$\begin{aligned} \beta ({{\bar{I}}}^* - {\hat{I}}^*) + {{\bar{v}}}({{\bar{I}}}^*) - {\hat{v}}({\hat{I}}^*) = 0. \end{aligned}$$

(61)

Indeed, the fixed points $({{\hat{I}}}^*,S^*)$, $({{\bar{I}}}^*,S^*)$ of (3), (13) (with $v={{\hat{v}}}, {{\bar{v}}}$, respectively) satisfy the equations

$$\begin{aligned} -\beta S^* {\hat{I}}^* - {\hat{v}}({\hat{I}}^*)S^* + \mu (1-S^*) = 0,\nonumber \\ -\beta S^* {{\bar{I}}}^* - {{\bar{v}}}({{\bar{I}}}^*)S^* + \mu (1-S^*) = 0, \end{aligned}$$

(62)

and therefore taking their difference gives (61). Equations (60) imply

$$\begin{aligned} {\bar{V}}(I_1,S^*) - {\bar{V}}(I_2,S^*) + {\hat{V}}(I_2,S^*)- {\hat{V}}(I_1,S^*) \le \frac{I_2-I_1}{\beta I_1} \max _{I_1 \le I \le I_2}({\hat{v}}(I) - { {{\bar{v}}}(I)}). \end{aligned}$$

Now, we combine this relation with (51) and (59) to obtain

$$\begin{aligned} 0 \le -\frac{\mu }{4 \sqrt{2}\,\delta } (I_2 - {{\bar{I}}}^*)^2 - \frac{\mu \sqrt{S_m} }{4\sqrt{2}\,\delta } ({\hat{I}}^* - I_1)^2 + \frac{I_2-I_1}{\beta I_1} \max _{I_1 \le I \le I_2}({\hat{v}}(I) - {{\bar{v}}}(I)) \end{aligned}$$

and further,

$$\begin{aligned} A (I_2 - {{\bar{I}}}^*)^2 +B ({\hat{I}}^* - I_1)^2 \le \frac{L(I_2-I_1)^2}{\beta I_1}, \end{aligned}$$

(63)

where L is defined by (22) and

$$\begin{aligned} A := \frac{\mu }{4\sqrt{2}\,\delta }, \qquad B := \frac{\mu \sqrt{S_m}}{4 \sqrt{2} \,\delta }. \end{aligned}$$

Relation (61) implies that

$$\begin{aligned} {{\bar{I}}}^* - {\hat{I}}^* = \frac{1}{\beta } ({\hat{v}}({ {{\hat{I}}}^*}) - {{\bar{v}}}({{\bar{I}}}^*)), \end{aligned}$$

and since the function ${{\hat{v}}}$ increases, it follows from (43) that

$$\begin{aligned} {{\bar{I}}}^* - {\hat{I}}^* \le \frac{1}{\beta } ({\hat{v}}({ {{\bar{I}}}^*}) - {{\bar{v}}}({{\bar{I}}}^*)) \le \frac{1}{\beta } \max _{I_1 \le I \le I_2} ({\hat{v}}(I) - {{\bar{v}}}(I)) \le \frac{L}{\beta }(I_2 - I_1) , \end{aligned}$$

i.e.

$$\begin{aligned} I_2-{{\bar{I}}}^*\ge 0, \quad \ \ {{\hat{I}}}^*-I_1\ge 0, \quad \ \ I_2-{{\bar{I}}}^* + {{\hat{I}}}^*-I_1\ge \Big (1-\frac{L}{\beta }\Big )(I_2-I_1),\nonumber \\ \end{aligned}$$

(64)

where $L/\beta <1$ according to (23).

Let us find the minimum value $F_{min}$ of the function $F(x, y)=Ax^2+By^2$ under the constraints $x, y\ge 0$ and $x+y \ge (1- L/\beta )(I_2-I_1).$ Clearly, the minimum value is achieved for $x+y = (1- L/\beta )(I_2-I_1)$ and equals

$$\begin{aligned} F_{min}=\frac{AB}{A+B}\left( 1-\frac{L}{\beta }\right) ^2 (I_2-I_1)^2. \end{aligned}$$

Hence, due to (64), the left hand side of (63) satisfies

$$\begin{aligned} A(I_2 - {{\bar{I}}}^*)^2 + B(I_1 - {\hat{I}}^*)^2 \ge F_{min} \end{aligned}$$

and (63) implies

$$\begin{aligned} \frac{AB}{A+B}\left( 1-\frac{L}{\beta }\right) ^2 \le \frac{L}{\beta I_1}. \end{aligned}$$

Recalling the definition of A and B, this is equivalent to

$$\begin{aligned} I_1\,\frac{\beta }{L} \left( 1-\frac{L}{\beta }\right) ^2 \le \frac{4\sqrt{2}\,\delta }{\mu } \left( 1+ \frac{1}{\sqrt{S_m}} \right) . \end{aligned}$$

(65)

5.4 Estimates of $I_1$, $S_m$.

Denote

$$\begin{aligned} v_{max}:= \iint _{0\le \alpha _1 < \alpha _2\le 1} q(\alpha _1,\alpha _2) \,\mathrm {d}\alpha _1 \,\mathrm {d}\alpha _2. \end{aligned}$$

It follows from (53) that ${\hat{V}}(I_1, S^*) \le {\hat{V}}(I_2, S^*)$. Using formula (32) for ${{\hat{V}}}$, this implies

$$\begin{aligned} I_1 - {\hat{I}}^* \ln \frac{I_1}{{\hat{I}}^*} \le I_2 - {\hat{I}}^* \ln \frac{I_2}{{\hat{I}}^*} + \frac{v_{max}}{\beta }\ln \frac{I_2}{{\hat{I}}^*} - \frac{{\hat{v}}({\hat{I}}^*)}{\beta }\ln \frac{I_2}{{\hat{I}}^*}, \end{aligned}$$

(66)

where we use that

$$\begin{aligned} {{\hat{v}}}(i) \le v_{max} \end{aligned}$$

and the estimate

$$\begin{aligned} \int _{{{\hat{I}}}^*}^{I_1}\frac{{{\hat{v}}}(i)-{{\hat{v}}} ({{\hat{I}}}^*)}{i} \,\mathrm {d}i\ge 0, \end{aligned}$$

which follows from the monotonicity of ${{\hat{v}}}$. Since $0<I_1<I_2 \le 1$, relation (66) implies

$$\begin{aligned} - {\hat{I}}^* \ln \frac{I_1}{{\hat{I}}^*} \le 1+ \left( - {\hat{I}}^* + \frac{v_{max}}{\beta } - \frac{{\hat{v}}({\hat{I}}^*)}{\beta }\right) \ln \frac{I_2}{{\hat{I}}^*}, \end{aligned}$$

where due to (62),

$$\begin{aligned} {\hat{I}}^* + \frac{{\hat{v}}({\hat{I}}^*)}{\beta }=\frac{\mu (1-S^*)}{\beta S^*}, \end{aligned}$$

hence

$$\begin{aligned} - {\hat{I}}^* \ln \frac{I_1}{{\hat{I}}^*} \le 1 + \left( \frac{v_{max}}{\beta } - \frac{\mu (1-S^*)}{\beta S^*}\right) \ln \frac{I_2}{{\hat{I}}^*}. \end{aligned}$$

Therefore,

$$\begin{aligned} I_1 \ge {\hat{I}}^* \exp {\left( -\frac{1}{{\hat{I}}^*} - \frac{v_{max} S^*-\mu (1-S^*)}{\beta S^* {{\hat{I}}^*}}\ln \frac{I_2}{{\hat{I}}^*}\right) }. \end{aligned}$$

(67)

From relations (62) and

$$\begin{aligned} {{\bar{v}}}(I)\le {{\hat{v}}}(I) \le v_{nat} + K I \end{aligned}$$

(68)

(where (68) follows from (15)) it follows that

$$\begin{aligned} \frac{\mu (1-S^*)}{S^*} =\beta {{\hat{I}}}^*+{{\hat{v}}}({{\hat{I}}}^*)\le \beta {{\hat{I}}}^* +K {{\hat{I}}}^* +v_{nat}, \end{aligned}$$

hence

$$\begin{aligned} \rho _0:=\frac{\mu (1-S^*)-v_{nat} S^* }{(\beta +K) S^*}\le {{\hat{I}}}^*, \end{aligned}$$

(69)

where, due to assumption (26),

$$\begin{aligned} \rho _0>0. \end{aligned}$$

If $v_{max} S^*\le \mu (1-S^*)$, then relations (67), (69) imply

$$\begin{aligned} I_1 \ge {\hat{I}}^*e^{-\frac{1}{{\hat{I}}^*}} \ge \rho _0 e^{-\frac{1}{\rho _0}}. \end{aligned}$$

On the other hand, if $v_{max} S^* > \mu (1-S^*)$, then

$$\begin{aligned} I_1&\ge {\hat{I}}^* \exp {\left( -\frac{\beta S^*+\bigr (v_{max}S^*-\mu (1-S^*)\bigl )\ln \frac{I_2}{{\hat{I}}^*}}{ \beta S^*{\hat{I}}^*}\right) } \\&\ge \rho _0 \exp {\left( -\frac{\beta S^*+\bigl (v_{max}S^*-\mu (1-S^*)\bigr )\ln \frac{1}{\rho _0}}{\beta S^* \rho _0}\right) }. \end{aligned}$$

Combining the two cases,

$$\begin{aligned} I_1 \ge \rho _1:= \rho _0 \exp {\left( -\frac{1}{\rho }_0+ \frac{\ln {\rho _0}}{\beta S^* \rho _0}\big \lfloor v_{max}S^*-\mu (1-S^*)\big \rfloor _+ \right) }, \end{aligned}$$

(70)

where $\lfloor a\rfloor _+ = a$ for $a> 0$ and $\lfloor a\rfloor _+ = 0$ for $a\le 0$.

Finally, we obtain a lower bound for $S_m.$ From (58) and (62) it follows that

$$\begin{aligned} -S^{*} \ln \frac{S_m}{S^*}&\le S^* -S_m +I_1- {\hat{I}}^* -{\hat{I}}^* \ln \frac{I_1}{{\hat{I}}^*} - \frac{{\hat{v}}({\hat{I}}^*)}{\beta }\ln \frac{I_1}{{\hat{I}}^*} \\&\le S^* - \frac{\mu (1- S^*)}{\beta S^*} \ln \frac{I_1}{{\hat{I}}^*}. \end{aligned}$$

Therefore,

$$\begin{aligned} S_m \ge S^{*} \exp \left\{ -1 + \frac{\mu (1- S^*)}{{\beta (S^*)}^{2}} \ln \frac{I_1}{{\hat{I}}^*}\right\} \end{aligned}$$

and using (70) we arrive at

$$\begin{aligned} S_m \ge S^{*} \exp \left\{ -1 + \frac{\mu (1- S^*)}{{\beta (S^*)}^{2}} \ln \rho _1\right\} . \end{aligned}$$

(71)

Thus, we have shown that the existence of a simple periodic orbit implies estimates (65), (70) and (71), which establish a lower bound $L\ge L_0>0$ on the quantity (22). This completes the proof.

6 Conclusions

We considered an SIR model with vaccination, where we assumed that the vaccination rate changes in response to dynamics of the epidemic. We modeled the adaptive response of an individual to the varying number of active cases by a two-state two-threshold switch; the individual response exhibits hysteresis. The aggregate response of the susceptible population was modeled by the Preisach operator. This operator relationship between the vaccination rate and the number of active cases accounts for the heterogeneity of the response among the susceptible individuals.

Both hysteresis and some heterogeneity of the response can be expected. Hysteresis effect arises as a feature of two-threshold (or multi-threshold) intervention policies and two-threshold (multi-threshold) response of the public to such policies when the thresholds are different. In a more general epidemiological context, hysteresis is associated with permanent (or long-lasting) effects of temporary stimuli (Pimenov et al. 2010). For example, one can expect that covid-19 epidemics will lead to some permanent social changes, which will remain in effect after the epidemic ends. Such changes may include annual seasonal vaccination coverage, maintaining a certain number of hospital beds allocated for covid-19 patients, continued development of tests, a wider use of face covering by general public in public places, a significant permanent shift from face-to-face towards online business and education services, wider use of web conferencing, etc.

If the basic reproduction number satisfies $R_0<1$, then the infection-free equilibrium of the proposed heterogeneous SIR model is globally stable. On the other hand, if $R_0>1$, then the system has a connected infinite set of endemic equilibrium states. In this case, we showed that each trajectory converges either to an endemic equilibrium or to a periodic orbit. This is in agreement with Chladná et al. (2020) where a simpler system with the homogeneous response modeled by a single two-state two-threshold switch was considered. Further, we showed that the set of endemic equilibrium states is the global attractor if two conditions are satisfied. The first condition limits the magnitude of the hysteresis effect by requiring hysteresis loops of the Preisach operator to be sufficiently narrow (relative to their length). The second condition ensures sufficient heterogeneity of the adaptive response by requiring hysteresis loops to be convex. Based on these results, one can conclude that the heterogeneity of the hysteretic response promotes the convergence to an endemic equilibrium state, while the homogeneous hysteretic response may result in recurrent periodic outbreaks of the epidemic.