Abstract
We provide a survey of so-called shot-noise queues: queueing models with the special feature that the server speed is proportional to the amount of work it faces. Several results are derived for the workload in an M/G/1 shot-noise queue and some of its variants. Furthermore, we give some attention to queues with general workload-dependent service speed. We also discuss linear stochastic fluid networks, and queues in which the input process is a shot-noise process.
Similar content being viewed by others
1 Introduction
This paper aims to present a survey of queueing models with the special feature that the server speed is proportional to the amount of work it faces. If the workload in a single server queue equals x, then the server processes work at speed \(rx, ~x >0\). We call such a queue a shot-noise queue. We shall also pay some attention to queues with more general workload-dependent service speeds.
The term “shot noise” stems from physics. Campbell [33, 34] pioneered the study of discontinuous noise, conveyed by pulses, in continuous-time physical systems. The discontinuous nature stems from the discreteness of the carriers: electrons in electrical systems, photons in optical systems. Schottky performed fundamental experiments with ideal vacuum tubes, and reported in 1918 [94] that he observed two types of noise: the thermal effect (Wärme-effekt) being the continuously fluctuating thermal white noise, and what he called the shot effect (Schroteffekt) of discontinuous pulses.
Shot-noise phenomena have received much attention in the physics literature, but were also treated in several probability textbooks, including the classics by Doob [41], Feller [44] and Parzen [83]. In the fifties, some leading queueing theorists like Keilson and Takács (cf. [60, 97, 99,100,101]) began the study of shot-noise models for physical phenomena like electron multiplier counters. In his celebrated book Introduction to the Theory of Queues [102], Takács devoted a chapter to shot-noise counter models. He assumed that particles are emitted according to a Poisson process, and that these particles are detected using an electron multiplier. To the i-th particle corresponds an electronic pulse whose amplitude is a random variable \(B_i\), \(i=1,2,\dots \). These random variables are i.i.d. (independent and identically distributed). Each electronic pulse has an exponential decay in the RC (Resistance/Capacitance) circuit in which the electron multiplier is included, with a time constant \(r = 1/RC\): the voltage V(t) decays according to \(\mathrm{d}V(t)/\mathrm{d}t = -V(t)/RC\), where R is the resistance and C the capacitance. The measured voltage process \(\{V(t), t \ge 0\}\) is the main stochastic process under consideration. If one now replaces particles by customers, pulse amplitudes by service requirements, decay by service, and voltage by workload, one has an M/G/1 queue with the special feature that the service speed is proportional to the workload — the M/G/1 shot-noise queue. This queue and various generalizations form the subject of our survey.
Motivation Our motivation for writing this survey is twofold. Firstly, we would like to draw the reader’s attention to a class of queueing models with some very attractive properties, which allow one to obtain quite explicit workload results; a class of queueing models, on the other hand, for which not that many results have been obtained, and for which there are also numerous interesting open problems. We shall mention some of them at the end of each section; for example, the very intriguing problem of obtaining queue length results in shot-noise queues.
Secondly, it is almost invariably assumed in the queueing literature that servers work at constant speed. However, there are many situations where this assumption does not hold. We mention three examples. These should be viewed as motivation for the study of queues with workload-dependent service speed, and not specifically the more narrow class of shot-noise queues. (i) In systems where the server represents a human being, the amount of work present may directly affect the speed of the server [16]. (ii) Dams, serving as storage area for water, are often studied as queues. Inflowing water, caused by rainfall, is temporarily stored, and released according to a release rule that is state-dependent [48]. (iii) In data centers with huge numbers of servers, it is crucial to have mechanisms, like autoscaling techniques, to balance energy consumption and performance. An autoscaling algorithm adjusts the processing speed of the processors (servers) according to their workload. At the data center level, it controls the number of active servers; at the individual computer level, a CPU is able to adjust the processing speed by either dynamic frequency scaling or dynamic voltage scaling techniques [105]. The processing speed is scaled up when the workload of the server is high, and scaled down under a low workload.
Related literature While focusing on queueing models with workload-dependent service speed, we would like to briefly point out in this paragraph that there is a much larger literature on stochastic aspects of shot-noise processes. We refer to [19] for a compact account of shot-noise processes and shot-noise distributions, and to [53] for a comprehensive overview of several variants of shot-noise processes. Quite a large number of papers is devoted to the study of convergence results and scaling limits of Poisson shot-noise processes. After appropriate centerings and scalings, such processes approximate a Gaussian process, fractional Brownian motion or a stable Lévy process; see, for example, [32, 52, 68, 69, 75, 76]. In [54], which considers limit theorems for renewal shot-noise processes, various other limiting results are mentioned.
Applications of shot-noise processes are found in many areas besides queueing, covering, for example, the occurrence of earthquakes [82, 103], water flows [104], financial models [90, 93] and insurance risk [68]. In the latter case, some results can immediately be translated from the insurance to the queueing setting by using specific duality relations between the two classes of models.
Another large bulk of related literature is formed by studies concerning growth-collapse processes and autoregressive processes, and more generally particular recursive sequences of stochastic processes. We have tried to keep the focus as much as possible on shot-noise queues, now and then briefly indicating relations to other stochastic processes – and undoubtedly our choices were sometimes biased towards models and results that are close to our own research interests. Throughout the paper we present derivations of a few key results. In presenting those results and derivations, we aim for accessibility rather than generality and abstraction. For example, on several occasions one could have generalized from a compound Poisson input process to a Lévy subordinator, or have considered a multi-class vector version, but we have mostly refrained from this.
Structure of the paper Section 2 is devoted to a detailed study of the classical M/G/1 shot-noise queue: an M/G/1 queue with the special feature that its service speed is proportional to the workload. In Sect. 3 we discuss the generalization to the case of a more general service speed r(x) when the workload equals x. In addition, we allow a workload-dependent arrival rate. In Sect. 4 we consider several variants of the M/G/1 shot-noise queue. Linear stochastic fluid networks are discussed in Sect. 5. Section 6 focuses on a quite different aspect of shot noise; it studies queues in which the input process is a shot-noise process.
2 The M/G/1 shot-noise queue
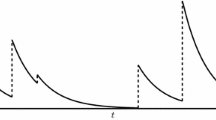
In this section we consider what is perhaps the most basic shot-noise queue: the M/G/1 queue with the special feature that the server works at a speed which is proportional to the amount of work present. Let us first specify the model under consideration. Customers arrive at a single server queue according to a Poisson process \(\{N(t), ~ t \ge 0\}\) with rate \(\lambda \). The service requirements \(B_1,B_2,\dots \) of the arriving customers are i.i.d. random variables with distribution \(B(\cdot )\) and LST (Laplace–Stieltjes transform) \(\beta (\cdot )\). Hence the input process to the single server queue is a compound Poisson process, which we denote by \(\{J(t), ~t \ge 0\}\). We further introduce the offered load per time unit \(\rho := \lambda {{\,\mathrm{\mathbb {E}}\,}}[B]\). Let X(t) denote the amount of work in the system at time t. Contrary to the usual assumption in queueing theory, the server speed is not constant but proportional to the workload, viz., if \(X(t) = y\) then the server speed r(X(t)) at time t equals \(r(X(t)) = ry\), with \(r>0\) some constant; see Figure 1.
It is readily seen that \(\{X(t), ~t \ge 0\}\) is a Markov process (cf. p. 393 of [87]). Considering this Markov process during an infinitesimal length of time h shows that
Dividing by h and letting \(h \downarrow 0\) yields
Alternatively, one can define the workload process by the following stochastic integral equation:
It can be shown (see, for example, Section 4 of [66]) that the unique solution to this integral equation is given by
Indeed, that X(t) as given in (4) is a solution to (3) follows by integrating both sides of (4) and changing the order of integration in the resulting double integral. To show the uniqueness, observe that the difference \(\Delta X(t)\) of two solutions satisfies \(\Delta X(t) = - r \int _0^t \Delta X(s) \mathrm{d}s\) with \(\Delta X(0)=0\). It follows that \(\Delta X(t)\) is continuous and differentiable, and differentiation shows that it satisfies \({\mathrm{d} \Delta X(t)}/{\mathrm{d}t} = - r \Delta X(t)\) with \(\Delta X(0)=0\). Hence \(\Delta X(t) \equiv 0\). We refer to [67] for a general treatment of such uniqueness issues for a more general class of stochastic integral equations that covers the shot-noise process, as well as related growth-collapse and clearing processes, as special cases.
Realizing that \(\{J(t), ~t \ge 0\}\) is a compound Poisson process, we can rewrite (4) as follows:
where \(t_1,t_2,\dots , t_{N(t)}\) denote the successive arrival epochs of customers in [0, t]. This expression has an important interpretation, that plays a role of paramount importance in the analysis of shot-noise queues: During an interval of any length v, each quantum of work that has size \(\Delta \) at the beginning of that interval, is at the end of that interval reduced to the amount \(\Delta \mathrm{e}^{-rv}\), independent of any other unit of work. That is of course not what is really happening when, for example, customers are served FCFS (actually, we do not specify the service discipline), but it is a valid interpretation when just considering the workload. The implication is that, for the analysis of the workload process in a shot-noise queue, one can treat different amounts of work, and in particular service requirements of different customers, as quantities which are processed independently of other workload quantities – very much the same as customers in an infinite-server queue are treated independently of each other. This similarity to the infinite-server queue was already observed by Kella and Whitt [66]. Moreover, De Graaf et al. [49] argue that the M/G/1 shot-noise queue can be seen as a limit of a certain class of infinite-server queues; we get back to this in Remark 2.2.
Another implication of (5) is that the workload never becomes zero, each contribution to the workload decreasing exponentially. These two properties of shot-noise queues make the analysis of their workload relatively easy. In the next theorem, we obtain the LST of X(t); see, for example, Ross [87, p. 394].
Theorem 2.1
The LST of the workload X(t) in the M/G/1 shot-noise queue is, for \(t \ge 0\), given by
Proof
Our starting point is the representation (5). Conditioning on N(t) and exploiting the fact that the jump epochs are uniformly distributed on (0, t) we have
The substitution \(w = s \mathrm{e}^{-ru}\) yields (6). \(\square \)
Remark 2.2
We could have obtained the same result by taking Laplace transforms already in Equation (1), thus arriving at the following partial differential equation for \(\phi (s,t) := {{\,\mathrm{\mathbb {E}}\,}}[\mathrm{e}^{-sX(t)}]\):
De Graaf et al. [49] have followed this approach for a more general M/G/1 shot-noise queue, also allowing a time-dependent arrival rate \(\lambda (t)\) and time-dependent service requirement B(t) for an arrival at t, with LST \(\beta (s,t)\). In the right-hand side of the above PDE, \(\lambda (1-\beta (s))\) is then replaced by \(\lambda (t) (1 - \beta (s,t))\), and solving the PDE yields (7) with the exponent in its last line replaced by \(- \int _0^t \lambda (u) (1 - \beta (s \mathrm{e}^{-r(t-u)},u)) \mathrm{d}u\). In addition, it is through this PDE that [49] explores the above-mentioned relationship between the M/G/1 shot-noise queue and the infinite-server queue. More concretely, they introduce a sequence of \(M^{H_k(t)}/M/\infty \) infinite-server queues, \(k=1,2,\dots ,\) with batches arriving at rate \(\lambda (t)\) and with size \(H_k(t) = \lceil kB(t) \rceil \); each individual customer has a service requirement that has an exponential distribution with parameter \(k \mu \), where it turns out that they need to choose \(\mu = r\). They derive a PDE for the transform of the number of customers in the k-th system at time t, and prove convergence of these PDEs, as \(k \rightarrow \infty \), to the PDE for the corresponding shot-noise queue. Their approach eventually leads to a proof of process-level convergence.\(\Diamond \)
Remark 2.3
Theorem 2.1 is a special case of the following well-known result:
where \(J(\cdot )\) is a non-decreasing Lévy process, \(\eta (s) = - \log {{\,\mathrm{\mathbb {E}}\,}}[\mathrm{e}^{-sJ(1)}]\), and \(h(\cdot )\) is Borel and nonnegative. The latter result has in fact been further generalized in Subsection 2.3 of the recent paper [22]. \(\Diamond \)
Remark 2.4
As it turns out, the result of Theorem 2.1 can also be extended in other ways. One such extension, proven in pp. 44,45 of [72], is the following: If \(f(\cdot ,\cdot )\) is piecewise continuous in its first argument, with at most a countable number of discontinuities, then
This result will be used later in this survey, in the context of infinite-server queues with a shot-noise arrival rate. \(\Diamond \)
The fact that the server speed becomes proportionally higher with increasing workload makes it intuitively clear that the stationary distribution of the workload exists for all values of the offered load \(\rho \). This property, proven in [37], concretely means that no condition needs to be imposed to make the M/G/1 shot-noise queue stable. Letting t tend to infinity in (6), we obtain the following expression for the LST of the steady-state workload X.
Theorem 2.5
The LST of the steady-state workload X in the M/G/1 shot-noise queue is given by
This result can already be found in [60]. It is instructive to derive (10) in a different way. Consider the workload process \(\{X(t), ~t \ge 0\}\) as depicted in Fig. 1 and apply the level crossing technique (cf. [29, 38]), which uses the fact that, in steady state, each level \(x>0\) is just as often crossed from above as from below. This implies that, with v(x) the steady-state density of X,
Here the left-hand side represents the rate of downcrossing x and the right-hand side represents the rate of upcrossing x. Introducing \(\phi (s) := {{\,\mathrm{\mathbb {E}}\,}}[\mathrm{e}^{-sX}]\), multiplying both sides of (11) by \(\mathrm{e}^{-sx}\) and integrating over x from zero to infinity yields
Here we have used the following well-known facts: (i) \({{{\,\mathrm{\mathbb {P}}\,}}(B>z)}/{{{\,\mathrm{\mathbb {E}}\,}}[B]}\) is the density of the residual \(B^{\mathrm{res}}\) of a service requirement B, (ii) the integral in the right-hand side of (11) (when divided by \({{\,\mathrm{\mathbb {E}}\,}}[B]\)) is a convolution of two densities, (iii) the Laplace transform of such a convolution is the product of their two Laplace transforms, and (iv) the Laplace transform of the density \({{{\,\mathrm{\mathbb {P}}\,}}(B>z)}/{{{\,\mathrm{\mathbb {E}}\,}}[B]}\) equals (applying integration by parts)
Solving the first-order differential equation (12), with initial condition \(\phi (0)=1\), immediately gives (10).
Remark 2.6
The first few moments of X can be easily obtained from (10), by differentiation, or from (11), by integration:
A recursion for the moments can be set up in the standard way.
Also, the time-dependent moments can be found. When \({{\,\mathrm{\mathbb {E}}\,}}[X(0)] < \infty \), then \({{\,\mathrm{\mathbb {E}}\,}}[X(t)]\) may be computed in the following way, cf. Lemma 2.1 of [69]: By (3),
and the same reasoning that led from (3) to (4) gives
which of course again yields the above expression for \({{\,\mathrm{\mathbb {E}}\,}}[X]\). Higher time-dependent moments can be found along similar lines. \(\Diamond \)
Remark 2.7
In the special case of exponentially distributed service requirements with parameter \(\mu \), \(\phi (s)\) is easily seen to reduce to
Hence X is in this case Gamma(\(\lambda /r,\mu \)) distributed; the density of X now is
Observe that, from the form of (11), it is already clear that \(\lambda \) and r only appear as a ratio in the expressions for v(x) and its Laplace transform. In the special case \(\lambda = r\), X turns out to be exp(\(\mu \)) distributed.\(\Diamond \)
Remark 2.8
Let us take another look at the Gamma(\(\lambda /r,\mu \)) result. Because of pasta (Poisson Arrivals See Time Averages), the density of the workload just before arrivals is also \(v(\cdot )\). If we denote the workload just before the n-th arrival by \(W_n\) and the workload just after the n-th arrival by \(Y_n = W_n + B_n\), and the interarrival time between the n-th and (\(n+1\))-st arrival by \(A_{n}\), then we can write
Now the fact that \(W_n\) has a Gamma(\(\lambda /r,\mu \)) density makes sense; \(Y_n=W_n+B_n\) then has a Gamma(\(\lambda /r + 1,\mu \)) density, and integrating in (18) with respect to this density is readily seen to result in a Gamma(\(\lambda /r,\mu \)) distribution. In particular, with \(\mathrm{U}(0,x)\) denoting a random variable that is uniformly distributed on (0, x), for \(\lambda =r\) one has \(W_{n+1} \sim \mathrm{U}(0,Y_n)\), and in steady state
where \({\mathop {=}\limits ^{d}}\) denotes equality in distribution and where W and B are generic random variables having the same distribution as \(W_n\) and \(B_n\), respectively. It is obvious from (19) that W and B have the same distribution, and hence W is exp(\(\mu \)) distributed as well (cf. [15]). In this context we would like to mention that Chamayou [35] has pointed out that the steady-state workload can be represented as
where \(K_i = \prod _{j=1}^i U_j^{r/\lambda }\) and \(U_j\) are i.i.d. Uniform(0, 1) random variables. In [35] also a procedure is presented to efficiently simulate the workload process. \(\Diamond \)
Remark 2.9
We briefly discuss weak convergence results under a diffusion scaling. Suppose we work with arrival rate \(n\lambda \) rather than \(\lambda ,\) focusing on the steady-state workload, say \(X_n\), it can be shown that \((X_n-{{\mathbb {E}}}[X_n])/\sqrt{n}\) converges to a zero-mean normal random variable as n to \(\infty .\) Indeed, from (10) and the expression for \({{\mathbb {E}}}[X_n]=n{{\mathbb {E}}}[X]\) that follows from (13), we obtain, as \(n\rightarrow \infty \),
Recognize in the limiting LST the expression for the variance \({{\,\mathrm{Var}\,}}X\) that follows from (13) and the LST of a zero-mean normal random variable, and finally apply the Lévy convergence theorem. In line with this asymptotic normality, using the martingale central-limit theorem, it can be proven that the process \(X_n(t)\) converges to an Ornstein–Uhlenbeck process.
Such an Ornstein–Uhlenbeck limiting result is also known to hold for the \(M/G/\infty \) queue. This agreement is not surprising: the shot-noise queue and the infinite-server queue exhibit a very similar so-called mean-reverting behavior, i.e., the further the process is away from its mean, the stronger, proportionally, is the drift towards that equilibrium – which is the defining feature of the Ornstein–Uhlenbeck diffusion process. Eliazar and Klafter [42] obtained an Ornstein–Uhlenbeck limiting process after scaling particular growth-collapse processes, which in turn are related to shot noise (see also Remark 4.11). \(\Diamond \)
For the case of the M/M/1 shot-noise queue, Kella and Stadje [62] determined the LST \({{\,\mathrm{\mathbb {E}}\,}}_x [\mathrm{e}^{-sT_a}]\) of the hitting time \(T_a\) of level a, starting from level x. They distinguished between the cases \(a \le x\) and \(a > x\). Using a martingale argument they showed that, for \(a \le x\), one has \({{\,\mathrm{\mathbb {E}}\,}}_x [\mathrm{e}^{-sT_a}] = f_s(x)/f_s(a)\), where \(f_s(x)\) satisfies the following second-order differential equation, called Kummer’s equation:
When \(a>x\), the hitting time can be written as the sum of two independent components: the time until level a is upcrossed (the overshoot of course is exp(\(\mu \))), and the subsequent time to downcross a. With the appropriate boundary conditions to solve (21), this yields the following result.
Theorem 2.10
For the M/M/1 shot-noise queue,
if \( 0<a \le x\), and
if \( 0<x < a.\)
Even in this M/M/1 setting, the expression for the mean hitting time turns out to be rather complicated, as seen from the following result.
Corollary 2.11
For the M/M/1 shot-noise queue,
Tail asymptotics One can readily surmise the tail behavior of X for the following case of heavy-tailed service times, using a technique that extracts this tail behavior from the behavior of the LST around zero. Suppose that the service times are regularly varying of index \(-\nu \) (usually abbreviated to: \(B \in \mathrm{RV}(-\nu )\)), i.e.,
with \(L(\cdot )\) a slowly varying function at infinity, i.e., \({L(bx)}/{L(x)} \rightarrow 1\) when \(x \rightarrow \infty \), for all \(b>0\). In the ordinary M/G/1 queue with constant service speed, it is known that the workload and waiting time are now regularly varying of index \(1-\nu \), so their tail is one degree heavier. In the shot-noise case, one can apply the above-mentioned relation between the tail behavior of X and the behavior of its LST near zero, so as to prove that \(X \in \mathrm{RV}(-\nu )\) if \(B \in \mathrm{RV}(-\nu )\): notably, for the M/G/1 shot-noise queue the tails of B and X are equally heavy.
In particular, if (25) holds with \(\nu \in (1,2)\) then, according to Theorem 8.1.6 of [17], with \(\Gamma (\cdot )\) the Gamma function,
and hence, using (10) and (13),
Another application of Theorem 8.1.6 of [17] (now in the reverse direction) implies that
Of course, the fact that a very large jump upward results in a very fast service speed is instrumental in this; and the fact that \({{\,\mathrm{\mathbb {E}}\,}}[X]\) only involves the first moment of B already is an indication that both tails might be equally heavy. The above result was first obtained, in the dual setting of insurance risk, by Klüppelberg and Stadtmüller [70]. Asmussen [6] has proved, for the more general case of service speed r(x) and B subexponential, with v(x) the workload density, that
showing that the workload tail depends crucially on the rate at which the system decreases from high levels, since this strongly affects the time spent above a high level x.
We close the section with a number of unsolved problems which could be of considerable interest.
Open Problem 2.12
One of the most challenging problems which we have encountered in shot-noise queues is the determination of the queue length distribution. We restrict ourselves to the FCFS discipline. The M/D/1 shot-noise queue in that case forms an exception, as the number of customers can immediately be inferred from the workload. But even for the M/M/1 FCFS shot-noise queue hardly any queue length result appears to be known. Koops (pp. 11–12 of [72]) has proven for this queue that the steady-state probability of having \(N=1\) customer in the system equals
which reduces to \({{\,\mathrm{\mathbb {P}}\,}}(N=1) = 1/2\) for \(\lambda = r\). Remarkably, this probability appears not to depend on the service rate \(\mu \).
What makes the queue length problem hard? Although the service requirement is memoryless, this is not the case for the service time. The service time strongly depends on future arrival intervals and future service requirements, which seems to be the main complication. In this context, remember that the system never gets empty, so that there is always at least one customer present. Hence the service time of a customer who is the only customer in the system will at least be extended until the next arrival. In particular, if \(\lambda =0\) and at time zero there is one customer, then its service time is infinite, regardless of its actual service requirement or its distribution. A more tractable open problem might be to study the conditional queue length distribution, given that the workload exceeds some large value x. Here one should distinguish between light-tailed and heavy-tailed service requirement distributions. \(\bigcirc \)
Open Problem 2.13
Just like service time is a significantly more complex quantity than service requirement, waiting (sojourn) time is intrinsically more complex than workload just before (just after) an arrival epoch. We are not aware of any sojourn time distribution results in non-trivial shot-noise models. See [31] for sufficient conditions for the delay and the sojourn time to have a finite k-th moment, in a class of shot-noise queues which is far more general than the one of the present section; they allow a general service speed function r(x) and work modulation.
When it comes to sojourn time calculations in shot-noise queues, D/G/1 might be the most accessible case. Taking the arrival times to be nT, and denoting the amount of work just after time nT by \(Y_n\), the amount of work done at time nT by \(D_n\), \(n=1,2,\dots \), and the amount of work at time \(0+\) by u, we have
with \(Y_n+D_n = u + \sum _{j=1}^n B_j\). We always have \(D_1 < u\), and for \(n \ge 2\) we have that \(D_n < u\) iff
or equivalently, with \(a := \mathrm{e}^{-rT}\), iff
If \(B_j \equiv b\) (i.e., the D/D/1 shot-noise queue!) we thus have \(D_n < u\) iff
Now suppose that
Then \(Y_n-nb\) work needs to be served until u has been completely served. Starting at \(Y_n\) this takes time \(\Delta := {r}^{-1} \mathrm{ln} [{Y_n}/({nb})]\); cf. (31) below, and the sojourn time T(u) to remove the initial work u equals \(T(u) = nT + \Delta \).
If \(B_j \sim \mathrm{exp}(\mu )\) then the terms \(B_j(1-a^j)\) in (30) are exponentially distributed with parameter \({\mu }/({1-a^j})\). Their sum is hypo-exponentially distributed, with a density as given in, for example, Section 5.2 of [88]. So this is another case for which the sojourn time distribution can be obtained.\(\bigcirc \)
Open Problem 2.14
In terms of workload analysis, the above-mentioned D/G/1 shot-noise queue is a very easy variant of the M/G/1 shot-noise queue. It is readily verified that, with interarrival time T, the steady-state workload W just before an arrival satisfies
Introducing \(\omega (s) := {{\,\mathrm{\mathbb {E}}\,}}[\mathrm{e}^{-sW}]\), and again taking \(a = \mathrm{e}^{-rT}\), this leads to the recursion \(\omega (s) = \beta (as) \omega (as)\). Hence, after iteration,
Here the i-th term in the infinite product represents the contribution to W from an arrival that occurred i arrivals before the present one. In contrast to this D/G/1 case, and the M/G/1 case, almost any other interarrival time distribution seems to lead to a challenging functional equation for \(\omega (s)\). The case in which the interarrival time \(A_i\) equals one of M different constants \(T_1,\dots ,T_M\) appears to be tractable [1], adapting an idea of [2]. \(\bigcirc \)
3 Workload-dependent service speed and arrival rate
In this section we consider a fundamental extension of the M/G/1 shot-noise queue discussed in the previous section, by allowing a more general service speed function (Sect. 3.1) and, in addition, a workload-dependent arrival rate (Sect. 3.2).
3.1 Workload-dependent service speed
Consider the M/G/1 queue with service speed r(x) when the workload equals x. We assume that \(r(0)=0\) and that otherwise \(r(\cdot )\) is strictly positive; \(r(\cdot )\) is further assumed to be left-continuous and to have a strictly positive right limit on \((0,\infty )\). If there is no arrival in (0, t), then the workload process decreases according to the formula \(X(t) = X(0) - \int _0^t r(X(u)) \mathrm{d}u\). It is readily verified that the time to go from level x to level \(y<x\), in the absence of arrivals, is
In particular, it follows that the origin can be reached in finite time if \(R(x,0) < \infty \). An influential early paper on dams with content-dependent release rate is the one by Gaver and Miller [48]. They constructed the Kolmogorov forward equations for several model variants. In one of their variants, the release rate was \(r_1\) when \(X(t)<R\) and \(r_2\) otherwise. For this case they presented a beautiful approach towards determining the steady-state workload distribution, based on an idea for the inversion of the product of two Laplace transforms. A second variant was the shot-noise case \(r(x) = rx\) of the previous section, which had already been treated by Keilson and Mermin [60].
Moran [81] proved that sample paths of the workload process \(\{X(t), ~t \ge 0\}\) satisfy the so-called storage equation (see also (3))
with \(\{J(t), ~t \ge 0\}\) the compound Poisson input process. For the special case of constant service speed, Reich [86] had obtained a similar equation. Çinlar and Pinsky [37] have studied (32) and proved that, under certain conditions (a finite jump rate and a continuous non-decreasing \(r(\cdot )\)), the sample paths of \(\{X(t), ~t \ge 0\}\) are uniquely defined by (32). They also proved that a limiting distribution exists if \(\mathrm{sup_{x>0}} ~ r(x) > {{\mathbb {E}}}J(1)\).
Harrison and Resnick [50] relaxed the assumption on \(r(\cdot )\). Under the assumption that \(R(x,0) < \infty \), so that the workload has an atom V(0) at zero, they provided necessary and sufficient conditions for the existence of a stationary workload distribution. In view of the importance and general applicability of their study, we provide some details. The starting point is the following relation for the steady-state workload density which can, for example, be obtained using the level crossing technique, and which is a straightforward generalization of (11):
Introducing \(Q(x) := \lambda {{\,\mathrm{\mathbb {P}}\,}}(B>x)\) and the kernel \(K(x,y) := {Q(x-y)}/{r(x)}\) for \(0 \le y<x< \infty \), we have
Introducing \(K_1(x,y):= K(x,y)\) and \(K_n(x,y) := \int _y^x K_{n-1}(x,z) K(z,y) \mathrm{d}z\) for \(0 \le y< x < \infty \) and \(n \ge 2\), the well-known Picard iteration applied to the second-order Volterra integral equation (34) gives
The convergence of the sum follows by observing that
hence \(K^*(x,y) := \sum _{n=1}^{\infty } K_n(x,y)\) is well-defined. Harrison and Resnick [50] concluded that the workload process has a stationary distribution iff
Brockwell et al. [30] extended the work of [50] in various ways. These extensions include cases in which level 0 is never reached, so that the workload does not have an atom at zero, as is for example the case when \(r(x) = rx\). They proved that, if \(R(x,0) = \infty \) (for any, and hence for all, \(x>0\)), the workload process is positive recurrent iff \(\int _a^{\infty } K^*(x,a) \mathrm{d}x < \infty \) for some (and then for all) \(a>0\); see also the exposition in Section XIV.1 of [7]. Kaspi and Perry [59] considered a storage/production model that is in a sense dual to the model of Harrison and Resnick: the process level increases gradually in a state-dependent way, in between jumps downward (demands). They also employed the Picard iteration procedure to determine the steady-state process level. Miyazawa [80] used rate conservation laws to describe the time-dependent behavior of storage models with state-dependent release rate and with a stationary marked point process as input. Asmussen and Kella [9] studied a shot-noise queue in which the service speed depends both on the workload and on a background state. They used duality with a risk process to obtain conditions for the existence of a limiting distribution. We conclude this brief literature overview by mentioning that Eliazar and Klafter [43] have introduced a different class of nonlinear shot-noise models that is amenable to mathematical analysis.
In special cases, like \(r(x) \equiv r\) (the classical M/G/1 queue) or exponentially distributed service times, Formula (35) can be rewritten into a more explicit expression for the steady-state workload density. Below we follow a more straightforward approach for the latter case. Taking \(B_i \sim \mathrm{exp}(\mu )\), (33) reduces to
Introducing \(z(x) := r(x) v(x)\mathrm{e}^{\mu x}\), we obtain by multiplying both sides by \(\mathrm{e}^{\mu x}\) that
Differentiation with respect to x yields
and hence
Remember that \(R(x,0) < \infty \) is the condition to have an atom at zero. To leave the “no atom” option open, we wrote R(x, 1) and introduced a constant C. Harrison and Resnick [50] concluded that, in the “atom at zero” case, and with \(\rho (x) := {\lambda }/({\mu r(x)})\), one has
and that a necessary and sufficient condition for existence of a stationary workload distribution is, cf. (36),
If there is no atom at zero, like in the case \(r(x)=rx\), then it follows from (40), using the normalization condition, that
When \(r(x) = rx\), this simplifies to
in agreement with (17).
3.2 Workload-dependent service speed and arrival rate: Proportionality relations
Next, to the assumptions on the workload-dependent service speed \(r(\cdot )\), which were discussed in the previous subsection, we now also assume the following about the arrival rate: If A is the time until the next arrival, starting from some initial workload w, then \({{\,\mathrm{\mathbb {P}}\,}}(A>t) = \mathrm{exp}(-\int _0^t \lambda (X(s)) \mathrm{d}s)\), where (as before) X(s) decreases deterministically from level w. We assume that \(\lambda (\cdot )\) is nonnegative, left-continuous, and has a right limit on \([0,\infty )\). Of course, if \(\lambda (x) \equiv \lambda \), then the arrival process is the Poisson(\(\lambda \)) process of the previous subsection. In the present subsection, we assume that the workload process is ergodic and has a stationary distribution.
The following discussion is based on [15]. The starting point is the following integral equation for the steady-state workload density – a generalization of (33) to the \(\lambda (x)\) case, that again can be obtained via the level crossing technique:
Alternatively, this relation can be obtained by extending an argument of Takács [98] for workload-dependent arrival rates to the case in which also the service speed is workload-dependent.
Let us now consider two model variants, which only differ from each other by having \(\lambda _1(x)\) and \(r_1(x)\) as rate functions in Model 1, and \(\lambda _2(x)\) and \(r_2(x)\) in Model 2. We use indices 1 and 2 for all quantities in these two model variants. Now assume that
We consider both the case
for all \(0<x<\infty \) (which here is the condition for having an atom at zero) and the case in which h(x) is infinite for some \(0<x<\infty \). The following theorem is proven in [15].
Theorem 3.1
For all \(x>0\),
with \(C := \frac{\lambda _1(0) V_1(0)}{\lambda _2(0) V_2(0)}\) if \(h(x)< \infty \) for all \(0<x<\infty \) and else \(C:=1\).
Proof
This result is proven by defining \(z_i(x) := r_i(x) v_i(x)\), \(i=1,2\), and applying the Picard iteration procedure (cf. (35)) to
Because of (44), the resulting kernel
is the same for both model variants. This directly leads to the conclusion that \(z_1(x)\) and \(z_2(x)\) only differ by a multiplicative constant C, giving (45). More intuitively, switching between models 1 and 2 is essentially a matter of rescaling time. If in model variant i the speed of time is \(1/r_i(x)\) when the workload is x, for \(i=1,2\), then model variants 1 and 2 are equivalent. Actually we had already seen something similar in the special case of constant rates \(\lambda \) and r: they only appear in the workload expressions as a ratio. \(\square \)
One implication of (45) is that it becomes possible to translate results for a particular model to results for a class of related models. For example, the steady-state workload density for the M/G/1 shot-noise model of Sect. 2, with \(\lambda (x) \equiv \lambda \) and \(r(x) = rx\), immediately gives us the steady-state workload density when \(\lambda (x)\) becomes \(\lambda x^{\alpha }\) and simultaneously r(x) becomes \(r x^{\alpha + 1}\) (divide by \(x^{\alpha }\)).
We now turn to the workload W just before an arrival – which would be a waiting time if \(r(x) \equiv 1\). Denote its steady-state density by \(w(\cdot )\) and its atom at zero (if there is one) by W(0); and for the two model variants, use \(w_i(\cdot )\) and \(W_i(0)\). One has the following recursion for the workloads at two successive arrival epochs:
with \(A_{n,y}\) the workload decrement between the n-th and (\(n+1\))-st arrival, when the workload equals y after the n-th arrival. This is a Lindley recursion, but with a dependence structure between \(W_n+B_n\) and \(A_{n,W_n+B_n}\). It is readily seen [15] that the distribution of \(A_{n,W_n+B_n}\) only depends on \(\lambda (\cdot )\) and \(r(\cdot )\) via their ratio; in fact,
One thus arrives at the following theorem.
Theorem 3.2
and if there is an atom at zero, then \(W_1(0)=W_2(0)\).
Finally, there is the following relation between w(x) and v(x).
Theorem 3.3
with
Notice that (50) is consistent with (45) and (49). In [15] one finds a rigorous proof of (50), and also the following intuitive argument:
Differentiation gives (50). We finally observe that \(w(x) = v(x)\) when \(\lambda (x) \equiv \lambda \), which is in agreement with the pasta property; one could view (50) as a generalization of pasta.
In [15] also an alternative method for deriving relations between V and W is outlined, for the M/G/1 shot-noise queue with general \(r(\cdot )\) and \(\lambda (\cdot )\). Based on Palm-theoretic principles, applying Campbell’s formula (see [11], Sects. 1.2 and 1.3), one obtains the following stochastic mean-value formula:
with A an arbitrary interarrival time and \(f(\cdot )\) such that the considered expectations exist and are finite. In [15] this is shown to imply that, for such functions \(f(\cdot )\),
Taking \(f(x) = \lambda (x)\) gives
and taking \(f(x) = \lambda (x) g(x)\) subsequently implies that
Subsequently taking \(g(x) = \mathrm{e}^{-sx}\) yields
in agreement with (50). In [15], this Palm-theoretic approach is extended to obtain some relations between V and W in the case of general interarrival intervals.
We finally mention that (i) Browne and Sigman [31] have obtained new and simplified stability proofs for queueing models with workload-dependent arrival rates and service speeds, and that (ii) Stadje [96] has also studied the model with state-dependent arrival rate and service speed, in addition allowing for state-dependent service requirements. He focused on the number of arrivals, and the number of workload record values, before a certain level x is first reached.
Open Problem 3.4
From a design point of view, it would be interesting to develop methods for selecting the service speed \(r(\cdot )\) such that the system exhibits certain desirable behavior. One could think of objective functions that somehow minimize the fluctuations of the workload level.\(\bigcirc \)
4 Variants and generalizations of the M/G/1 shot-noise queue
This section contains five subsections in which we discuss the following variants and generalizations of the M/G/1 shot-noise queue:
- \(\circ \):
-
Subsection 4.1: Insurance risk models with interest rate r when the insurance company invests its money.
- \(\circ \):
-
Subsection 4.2: a two-sided shot-noise model of a bloodbank.
- \(\circ \):
-
Subsection 4.3: shot-noise models with a finite buffer.
- \(\circ \):
-
Subsection 4.4: shot-noise vacation and polling models.
- \(\circ \):
-
Subsection 4.5: fluid queues with state-dependent rates.
4.1 Affine storage models and insurance risk models
The main reason for devoting a subsection of this paper to insurance risk models is that an important connection, a form of duality, has been established between a class of insurance risk models and a class of queueing and storage models. In its most simple form, it relates the ordinary M/G/1 queue and the Cramér–Lundberg model (which has a Poisson arrival process of claims, general claim size distribution and in between claims a linear increase of the capital due to a constant insurance premium rate), under the assumptions that both models feature the same arrival rates and same jump distributions (of service requirements and of claims, respectively), and with service speed equaling the insurance premium rate. The duality result then states that, for any u, the steady-state complementary cumulative workload distribution \({{\,\mathrm{\mathbb {P}}\,}}(X>u)\) in the queueing model equals the ruin probability in the insurance risk model with initial capital u. Harrison and Resnick [51] have proven that this steady-state duality also holds when generalizing the service speed (insurance premium rate, respectively) to the level-dependent function r(x).
We refer to Section III.2 of [8] for a beautiful exposition of the duality concept, based on sample path arguments, and an extension of the above-mentioned duality results to the time-dependent case (equating the complementary cumulative workload distribution at some time t, when starting from an empty system, and the probability of ruin before t). See also [10] for the first proof of that time-dependent duality in the case of service speed (premium rate, respectively) r(x).
The implication of the above is that several results from queueing, as mentioned in the present survey, are relevant to the insurance risk community – and vice versa. For the latter, we mainly refer to Chapter VIII of [8]. In particular, the case \(r(x) = rx+ \alpha \) is studied in some detail in its Section VIII.2; importantly, taking \(\alpha > 0\) complicates matters substantially. Here \(\alpha \) can be interpreted as the fixed premium rate, and r as the interest rate when the insurance company invests its money. This particular case was already studied in [95] and in [84]. The latter paper not only allowed exponential claim sizes, finding an explicit expression for the ruin probability in terms of an incomplete gamma function; it also provided the ruin probability for the cases of Erlang-2 claim sizes (in terms of Bessel functions) and hyperexponential-2 claim sizes (in terms of confluent hypergeometric functions). Albrecher et al. [5] obtained the finite-time ruin probability in the case of exponential claim sizes and the arrival rate being an integer times r. Knessl and Peters [71] studied the asymptotic behavior of that finite-time ruin probability, again in the case of exponential claim sizes. In [4], among other things, special choices of r(x) were considered for which the ruin probability can be calculated in an explicit way when the claim sizes are exponentially distributed: \(r(x) = c(1 + \mathrm{e}^{-x})\), \(r(x) = c + 1/(1+x)\) and \(r(x) = c + x^2\). Via duality, this also gives workload results for specific M/M/1 shot-noise queues; see (42) for a different representation.
In [26] the duality between queueing/storage and insurance risk models with speed/rate \(r(x) = rx + \alpha \) was extended to the case of two-sided jumps: the queueing/storage model and the risk model both have an additional compound Poisson input process, now with exponentially distributed downward (upward) jumps in the storage (risk) model. For the risk model the joint transform of the time to ruin, the capital just before ruin and the loss at ruin was determined. See the graphical illustration of Fig. 2; here \(\tau _x\) is the time to ruin given the initial level X(0) is x. It was also shown how some of the exponentiality assumptions of the paper can be relaxed. We further point out that Jacobsen and Jensen [55] also have allowed both positive and negative jumps, for the case \(r(x)=rx\).
Open Problem 4.1
In [25], a reflected autoregressive process of the following form is studied:
with \(C_n\) the difference of two positive random variables and \(S_n(t)\) a sequence of i.i.d. subordinators with \({{\,\mathrm{\mathbb {E}}\,}}[S_n(1)] < 1\), \(n=1,2,\dots \); \(S_n(Y_n)\) performs a “Lévy thinning” of \(Y_n\). The analysis of this autoregressive process, so as to obtain its steady-state distribution, bears similarities to that of the above-described affine storage process with two-sided jumps, just after the n-th jump:
where \(C_{n}\) denotes the size of the n-th jump (up or down). It would be interesting to explore this relation further, perhaps linking reflected autoregressive processes to generalizations of shot-noise queues. See also Remark 4.11 below for relations between shot-noise queues in which the origin is never reached, growth-collapse processes and autoregressive processes.\(\bigcirc \)
4.2 A two-sided shot-noise model
In [12] the following model for a blood bank with perishable blood and demand impatience was studied: Amounts of blood and demands for blood arrive at a blood bank according to two independent compound Poisson processes with jump rates \(\lambda _b\), \(\lambda _d\) and with the offered amounts and demanded amounts generically denoted by B and D. If there is enough blood in inventory for a demand, then that demand is instantaneously satisfied; otherwise it is partially satisfied, and not at all if the inventory is empty. Blood has a finite expiration date. Because of this, it was assumed in [12] that blood is discarded at a rate \(r_bx+\alpha _b\) if the amount present is x. Furthermore, because blood demands have a finite patience, blood disappears from the inventory at a rate \(r_dx+\alpha _d\) when the total amount of demand is x.
The process \(\{X(t), ~t \ge 0\}\) \(= \{(X_b(t),X_d(t)), ~ t \ge 0\}\) of total amount of blood present and total amount of blood demand present at time t is a two-sided process. At most one of \(X_b(t)\) and \(X_d(t)\) is nonzero at any time t. The level crossing technique was used to show that the densities \(v_b(\cdot )\) and \(v_d(\cdot )\) of amounts of blood in inventory and of demand satisfy the following two integral equations: firstly, for level x of the amount of blood in inventory:
and a completely symmetrical equation for the total amount of demand. These equations were solved for the case of Coxian distributed B, D, tackling these two integral equations with Laplace transforms. For exponentially distributed B, D, and \(\alpha _b=\alpha _d=0\), a more explicit solution was obtained, without resorting to Laplace transforms. A second-order Kummer differential equation was derived, similarly to (21), where it featured in the case of first-exit probabilities of an M/M/1 shot-noise queue. The Kummer second-order differential equation appears to be a natural differential equation for the M/M/1 shot-noise queue, just like a specific Bessel differential equation is natural for the ordinary M/M/1 queue. Finally, [12] also studied the model variant with \(\alpha _b=\alpha _d=0\) from an asymptotic perspective, obtaining the fluid and diffusion limits of the blood inventory process. It was shown that the process after an appropriate centering and scaling converges to an Ornstein–Uhlenbeck process; cf. our account of the weak convergence results under a diffusion scaling, in Sect. 2.
Open Problem 4.2
In the above model it is assumed that there is only one type of blood. It would be interesting to extend the above model and its analysis to the realistic case of several blood types.\(\bigcirc \)
4.3 Finite buffer
Bekker [14] has considered a class of M/G/1-type queues with workload-dependent arrival and service rates, with restricted accessibility. When a customer arrives to find an amount of work y, this customer is only fully accepted if the sum of y and her service time B does not exceed a value K. If \(y+B > K\), there are various options. In the case of partial rejection, \(K-y\) is accepted and the remainder of the service requirement is rejected; in the case of complete rejection, such a customer is not at all admitted to the system; and in the case of impatience, it is assumed that the full service requirement is accepted if \(y<K\). Introducing the function g(y, B, K) as min(\(y+B,K\)) for the case of partial rejection, as \(y + BI(y+B \le K)\) with \(I(\cdot )\) an indicator function for the case of complete rejection, and as \(y + BI(y \le K)\) for the case of impatience, Bekker [14] extended (43) to the following integral equation:
Subsequently two model variants were compared, with arrival rate \(\lambda _i(x)\) and service speed \(r_i(x)\) in model variant i, \(i=1,2\), and with \({\lambda _1(x)}/{r_1(x)} = {\lambda _2(x)}/{r_2(x)}\), \(\forall x > 0\); cf. (44). Replacing the kernel \(K(x,y) = {{\,\mathrm{\mathbb {P}}\,}}(B>x-y) {\lambda (y)}/{r(y)}\) as introduced below (46) by
a Picard iteration procedure could be used, just as it was applied to (46), thus showing that Theorems 3.1-3.3 still hold. The implication is that, if one is able to prove a workload result for, say, a restricted accessibility model variant with constant arrival rate \(\lambda \) and shot-noise service speed \(r(x) = rx\), then one can easily translate that to a workload result for another model variant with \(\lambda (x)/r(x) = \lambda /(rx)\).
One example is the following result, which can also be found in [14]: Consider the partial-rejection rule, and let \(X^K\) denote the steady-state workload in the M/G/1 queue with finite buffer K, arrival rate \(\lambda \) and service speed \(r(x)=rx\). X denotes the workload in the corresponding model with infinite buffer. The LST of X was derived in Sect. 2; for \(B \sim \mathrm{exp}(\mu )\), X was shown to have a Gamma(\(\lambda /r,\mu \)) distribution. Bekker [14] proved that
The proof is based on a sample path argument, in which, in the infinite buffer model, the parts of the sample path are deleted between each upcrossing of level K and the subsequent downcrossing of that level.
We finally remark that in [14] also the loss probability of an arbitrary customer is determined, which is then related to the probability \({{\,\mathrm{\mathbb {P}}\,}}(C_{\mathrm{{max}}} \ge K)\) that the cycle maximum in the corresponding infinite buffer model exceeds K. Furthermore, first-exit probabilities in infinite buffer queues are obtained, by combining (i) the fact that one may restrict oneself to a model variant with constant arrival rate \(\lambda \) with (ii) first-exit results from [50] for the latter case, in addition exploiting a clever relation to finite buffer queues. Another first-exit result was obtained by Yeo [106]: for the M/D/1 and M/M/1 shot-noise queue he derived the first-passage time distribution of a barrier K when starting from an empty system.
4.4 Vacation queues and polling
In this subsection we consider an M/G/1 shot-noise queue with workload-dependent speed \(r(x)=rx\), with the special feature that the server alternately spends a visit time at the queue and takes a vacation. All visit times and vacation times are independent. \(C_1\) denotes a generic visit time, and \(C_2\) a generic vacation time. As before the customer Poisson arrival process has intensity \(\lambda \), and \(\beta (s)\) is the LST of an arbitrary service requirement. We focus on the steady-state workload Z at the start of a visit. We first consider the case of exponentially distributed visit times, and then the case of constant visit times. See [89] for another vacation queue with workload-dependent service speed r(x).
Case 1: \(C_1 \sim \mathrm{exp}(c)\). We generalize the approach of Subsect. 7.1 of [27] from exponential vacation times to generally distributed vacation times with LST \(\gamma (\cdot )\), and prove the following theorem.
Theorem 4.3
For \(C_1 \sim \mathrm{exp}(c)\), the steady-state workload LST at the start of visit periods is given by
Proof
We determine the marginal workload LST in the following four steps.
(i) During a vacation, the workload in the queue increases according to a compound Poisson process; hence
(ii) Using (6),
Simplifying the above equation by substituting \(s e^{-rt} = v\) yields
(iii) Combining parts (i) and (ii) above, we can look one cycle — consisting of a visit and a vacation — ahead:
(iv) Deconditioning on \(X(0)=x\) and observing that, in steady state, \(X(C_1+C_2)\) has the same distribution as X(0), we conclude that \(G(s) := {{\,\mathrm{\mathbb {E}}\,}}[\mathrm{e}^{-sZ}] = {{\,\mathrm{\mathbb {E}}\,}}[\mathrm{e}^{-sX(0)}]\) satisfies the following relation:
Differentiating with respect to s yields
The theorem follows by solving this standard first-order differential equation. \(\square \)
Remark 4.4
Theorem 4.3 yields the steady-state workload LST in a straightforward way, by averaging over a visit period and a vacation period with weight factors \({{\,\mathrm{\mathbb {E}}\,}}[C_i]/({{\,\mathrm{\mathbb {E}}\,}}[C_1]+{{\,\mathrm{\mathbb {E}}\,}}[C_2])\), \(i=1,2\). The workload LST at an arbitrary epoch during a visit period is, by pasta, the same as the workload LST \({\tilde{G}}(s)\) at the end of a visit period, and the latter LST follows from \(G(s) = {\tilde{G}}(s) \gamma (\lambda (1-\beta (s)))\). Also the workload LST at an arbitrary epoch during a vacation period can be determined, using a stochastic mean value argument. \(\Diamond \)
Remark 4.5
Theorem 4.3 reveals that G(s) is the product of three LSTs of nonnegative random variables. Hence Z can be written as the sum of these, independent, random variables: \(Z=Z_1+Z_2+Z_3\). \(Z_1\) is the steady-state amount of work in the shot-noise queue without vacation periods; cf. (10). With this in mind, it is readily seen that \(Z_2\) is the steady-state amount of work in a shot-noise queue with arrival rate c (corresponding to the occurrence of a vacation) and service requirement LST \(\gamma (\lambda (1-\beta (s)))\). The latter term denotes the LST of the amount of service requirement that enters the system during a vacation; and that amount also equals \(Z_3\). This kind of decomposition is reminiscent of the well-known Fuhrmann–Cooper decompositions [45] for queues with constant service speed. \(\Diamond \)
Remark 4.6
In [27], the joint workload LST in a two-queue polling model with exponential visit times and workload-dependent service speeds at both queues is also studied. A two-dimensional Volterra integral equation for this LST is formulated, and it is shown that this equation can be solved by a fixed-point iteration. \(\Diamond \)
Case 2: \(C_1\) is constant. Assume that the length of each visit time \(C_1 \equiv T\), a constant. In that case we have the following result for the steady-state workload LST at the beginning of visits.
Theorem 4.7
For \(C_1 \equiv T\), the steady-state workload LST at the start of visit periods is given by
Proof
We follow the same steps (i)-(iv) as in the proof of Theorem 4.3.
(i) and (ii) are basically the same, replacing (63) in Step (ii) by
(iii) Combining (i) and (ii) we can again look one cycle ahead:
(iv) Just like in the proof of Theorem 4.3, we now decondition on \(X(0)=x\) and observe that, in steady state, \(X(C_1+C_2)\) has the same distribution as X(0). Hence \(H(s) := {{\,\mathrm{\mathbb {E}}\,}}[\mathrm{e}^{-sZ}] = {{\,\mathrm{\mathbb {E}}\,}}[\mathrm{e}^{-sX(0)}]\) satisfies the following relation:
The theorem follows by iterating the above relation; in [27] it is shown that this iteration converges. \(\square \)
Remark 4.8
It is readily seen that Theorems 4.3 and 4.7 can be generalized to the case in which the compound Poisson input process is replaced by a Lévy subordinator. In the final expressions, just replace \(\lambda (1-\beta (\cdot ))\) everywhere by the Laplace exponent \(\eta (\cdot )\) of the Lévy process.\(\Diamond \)
Remark 4.9
In the infinite product in Theorem 4.7, the j-th term gives the contribution to the LST of Z from \(j+1\) vacations ago. Furthermore, observe that actually
again an infinite product. The j-th term gives the contribution to the LST of Z from j visits ago.\(\Diamond \)
Let us now make the step from vacation queues to polling, i.e., we assume that a single server cyclically visits N queues, with constant visit time \(T_i\) at \(Q_i\), and with independent compound Poisson input processes \((\lambda _i,\beta _i(s))\) at \(Q_i\), and with workload-dependent service speed \(r_i(x) = r_i x\) at \(Q_i\), \(i=1,\dots ,N\). A little thought will convince the reader that, at visit completion epochs, all N workloads are independent, and the LST of the steady-state workload at \(Q_i\) at the start of its visit can be obtained via Theorem 4.7. At an arbitrary epoch, the various workloads are not independent, because the length of time since the start of the present visit affects all N queues; but it is easy to determine the steady-state joint workload LST from the workload LST at a visit completion epoch [27]. This is a rare example of an N-queue polling system for which the joint workload can be determined, even though the service discipline is not of so-called branching type. Crucial for this are the constant visit periods and the attractive features of shot noise that we stressed before, viz., no queue can ever become empty, and each quantity of work \(\Delta _i\) at \(Q_i\) reduces to \(\Delta _i \mathrm{e}^{-rT_i}\) during a visit to that queue.
Open Problem 4.10
It would be highly interesting to provide an analytic solution to the two-dimensional Volterra integral equation for the joint workload LST in the case of the polling model of Remark 4.6. Another open problem concerns the extension of the Fuhrmann–Cooper decompositions to shot-noise queues. \(\bigcirc \)
4.5 Fluid queues with state-dependent rates
So far we have focused on systems with jumps, which mostly represent an instantaneous input of work. However, both in communication systems and in production/storage settings, it is often natural to have a gradual input. There is a sizable literature on such models, in which the content of a buffer (of fluid, or stored material, or data bits) increases during off periods and decreases during on periods of the server. We mention some studies in which that decrease is level-dependent. Kaspi, Kella and Perry [58] have considered an on/off model with generally distributed on- and off periods, and level-dependent release rates as well as level-dependent production rates. They mainly focused on stability issues, and also considered the model variant in which the off periods are compressed to a point, replacing the total increment during an off period by a state-dependent jump. In [23], that compression idea was applied to a fluid queue in which the content level decreases in a level-dependent way during exponentially distributed on periods. During off periods, an underlying Markov process moves between K different states, and the content level increases at rate \(a_j\) when the state is j. By compressing the off periods and replacing the total increment in an off period by a jump, one arrives at the model of Harrison and Resnick [50], and for \(r(x)=rx\) one has the M/G/1 shot-noise queue.
In [21] an on/off model is studied with not only level-dependent (\(r_0(x)\)) gradual increase during off periods and level dependent (\(r_1(x)\)) decrease during on periods; the lengths of the off- and on periods are also dependent on the content level. The system switches from off to on with rate \(\lambda _0(x)\), and from on to off with rate \(\lambda _1(x)\). The stationary distribution of the two-dimensional process \(\{(X(t),I(t)), ~t \ge 0\}\) and conditions for its existence and uniqueness were determined, where X(t) denotes the buffer content and I(t) the state of a background process (on or off). If, for some \(\epsilon >0\),
then the stationary densities \(g_0(x), ~g_1(x)\) (respectively conditioned on being off and on) are given by
with \(C_0,C_1\) constants, while there is also an atom at zero. The similarity with (42) should be noticed. If the above finiteness condition does not hold, then there is no atom at zero, but the \(g_i(x)\) take a very similar form. We remark in passing that the proportionality of \(r_0(x) g_0(x)\) and \(r_1(x) g_1(x)\) immediately follows via a level crossing argument.
The above model is called a Markov modulated feedback fluid queue. In feedback fluid queues, not only is the buffer content determined by the state of a background process, but also the background process is influenced by the content process. Feedback fluid queues are also studied in [78, 79, 92]. In [92] the object of study was a fluid queue with a finite buffer and a background process governed by a continuous-time Markov chain whose generator, and the traffic rates, depend continuously on the buffer level. For the case of two background states, an explicit solution for the stationary buffer content distribution was derived.
Remark 4.11
The idea of compressing off periods to a single instant and replacing the increment by a jump can also be applied to on periods, and then gives rise to so-called growth-collapse models. These are models where, after a certain period of growth of the process, its level jumps downward with the jump size being dependent on the level just before the jump. Kella [61] considered the case in which, at the n-th collapse, for \(n=1,2,\dots \), the process level \(Y_n\) is reduced by a random factor \(X_n \in [0,1]\) to \(W_n = X_nY_n\), while between the (\(n-1\))-st and n-th collapse the process increases with \(B_n\). Hence \(Y_n = (Y_{n-1}+B_n)X_n\), representing an autoregressive process with random coefficients. Iteration yields
The latter relation should be compared with (20) for the M/G/1 shot-noise queue. In fact, Kella [61] explicitly pointed out the relation to shot-noise models, stating the following: if \(X_n\) does not have an atom at zero, and \(-{{\,\mathrm{\mathbb {E}}\,}}\mathrm{log} X_n < \infty \), then the above-described growth-collapse process and the G/G/1 shot-noise queue with interarrival intervals \(\xi _n = -{r}^{-1} \,\mathrm{log} X_n\) have the same dynamics just before, and just after, jump epochs. The relation between growth-collapse processes and shot-noise queues is further explored in [24, 28]. In the latter paper the intervals between collapses have a general distribution, and the random reduction factor at collapses has a minus-log phase-type distribution, i.e., minus its natural logarithm has a phase-type distribution. This corresponds to a G/G/1 shot-noise queue with phase-type distributed intervals \(A_i\) between generally distributed jumps. \(\Diamond \)
Open Problem 4.12
An interesting research direction concerns the extension of the results of [21] to the case of more than two background states. \(\bigcirc \)
5 Linear stochastic fluid networks
In this section we discuss the network version of the M/G/1 shot-noise queue that was analyzed in Sect. 2. Such networks are usually called linear stochastic fluid networks. In this brief discussion we mainly focus on deriving the transient and stationary joint workload distribution, providing network counterparts of Theorems 2.1 and 2.5. We refer to Chapter 7 of [36] for a more extensive discussion of linear stochastic fluid networks, to [57, 65] for stability discussions, to [64, 66] for calculations in the stationary regime, to [63] for a Markov-modulated network and to [85] for moment calculations.
We begin with a model description. Now there are m resources, rather than just one, whose evolutions are recorded by the m-dimensional Markov process \(\{{{\varvec{X}}}(t), t\ge 0\}\). Customers arrive at the network according to a Poisson process \(\{N(t), t\ge 0\}\) with rate \(\lambda \). The service requirements, denoted by \({{\varvec{B}}_1},{{\varvec{B}}_2},\ldots \) are m-dimensional vectors now: the i-th component of these vectors is instantaneously fed into resource i. We let \(\beta (\cdot )\) be the corresponding LST, whose argument, say \({{\varvec{s}}}\), is an element of \({{\mathbb {R}}}_+^m\). The corresponding vector-valued input process is called \(\{{{\varvec{J}}}(t), t\ge 0\}\). We work with proportional service speeds given by the m-dimensional vector \({{\varvec{r}}}\), in that the service rate of resource i at time t is \(r_iy\) if \(X_i(t)=y\). When being served at resource i, a fraction \(p_{ij}\) of the output is fed into resource j. We throughout assume the matrix \(P=(p_{ij})_{i,j=1}^m\) to be substochastic, with \(P^n\rightarrow 0\) as \(n\rightarrow \infty \). As a consequence \((I-P)^{-1}\) is well-defined, and can be represented by \(\sum _{n=0}^\infty P^n.\) We call the resulting system a linear stochastic fluid network, which can be seen as the genuine multivariate extension of the single-dimensional shot-noise model discussed before.
Observe that the setup introduced above is rather general. It in particular covers cases in which there are, for subsets S of \(\{1,\ldots ,m\}\), Poisson arrival streams of customers (with arrival rate, say, \(\lambda _S\)) at the resources in S only. For instance, the setup covers the case that with rate \(\lambda _i\) work arrives at resource i only, for \(i=1,\ldots ,m\); then we have to pick \(\lambda :=\lambda _1+\ldots +\lambda _m\), while \({{\varvec{B}}}_i\) equals with probability \(\lambda _i/\lambda \) an m-dimensional vector with a positive entry on the i-th position and zeroes elsewhere.
This system’s time-dependent and stationary distribution can be found, as was argued in Sects 4 and 5 of [66]. It is noted that [66] considers various generalizations and ramifications, for example, one in which our driving compound Poisson process has been replaced by a non-decreasing Lévy process.
As a first step in the analysis, observe that the counterpart of (1) becomes, with \(R=\mathrm{diag}({{\varvec{r}}})\), as \(h\downarrow 0\),
leading to the differential form
where \(Q=R(I-P)\). This equation can be written in the corresponding integral form
which, cf. (4), is solved by
where it is noted that the two terms on the right-hand side are independent. This representation allows us to state and prove the counterpart of Theorem 2.1, i.e., the multivariate version of (7).
Theorem 5.1
The LST of the workload \({{\varvec{X}}}(t)\) in the M/G/1 shot-noise network is, for \(t\ge 0\), given by
Proof
First consider a nonnegative m-dimensional “pulse” \({{\varvec{x}}}_0\) that is fed into the system at time 0. Our objective is to describe how it has evolved at time \(t\ge 0\), which we call \({{\varvec{x}}}(t)\). Observe that, as \(h\downarrow 0\),
so that \({{\varvec{x}}}(t) = \mathrm{e}^{-Q^\top t}{{\varvec{x}}}_0\); cf. (74).
Now follow the line of the proof of Theorem 2.1; see also Section 3.1 of [20]. The number of “pulses” N(t) arriving in (0, t] is Poisson distributed with parameter \(\lambda t\), and each of them has an arrival epoch that is uniformly distributed over (0, t].
This completes the proof. \(\square \)
We also have the counterpart of Theorem 2.5, found by letting t grow large in the result of Theorem 5.1. As before, to guarantee stability no additional assumptions need to be imposed.
Theorem 5.2
The LST of the steady-state workload \({{\varvec{X}}}\) in the M/G/1 shot-noise network is given by
Remark 5.3
The setting considered lends itself well to performing rare event analysis, as discussed in great detail in [20]. Suppose that, for some scaling parameter n, the arrival rate is \(\lambda n\) and that \({{\varvec{X}}}(0) = n{{\varvec{x}}}_0.\) Then \({{\varvec{X}}}(t)\equiv {{\varvec{X}}}_n(t)\) can be seen as the sum of n i.i.d. contributions. As a consequence, standard large deviations techniques can be used to compute, for any set \(A\subset {{\mathbb {R}}}^m\), the corresponding logarithmic tail asymptotics. Indeed, under mild regularity conditions, we have that as a direct consequence of the multivariate version of Cramér’s theorem,
where, applying Theorem 5.1 to find the cumulant generating function \(\log {{\mathbb {E}}}[\mathrm{e}^{{\varvec{\theta }}^\top {{\varvec{X}}}(t)}]\),
denotes the corresponding Legendre transform. In [20] it is also pointed out how insights from large deviations theory can be used to efficiently estimate the probability \({{\mathbb {P}}}({{\varvec{X}}}_n(t) \in nA)\) by importance sampling-based simulation. More concretely, a logarithmically efficient algorithm is proposed, meaning that the number of runs required to obtain an estimate with a given precision (defined as the ratio of the width of the confidence interval and the estimate) grows subexponentially in the scaling parameter n, whereas this number would grow exponentially when using conventional simulation.
\(\Diamond \)
Remark 5.4
Another topic covered in [20, 64] concerns the extension of the model to a setting in which the arrival rate, the service requirement vector and the routing matrix are modulated by an external, autonomously evolving Markov process (often referred to as the background process). In the first place, with techniques similar to the ones we have applied above, the Laplace transform of \({{\varvec{X}}}(t)\) can be characterized, jointly with the state of the background process, in terms of a system of partial differential equations. It allows the evaluation of moments as well; these require intricate matrix multiplications, involving various types of Kronecker matrices. In [20] an algorithm is presented that can estimate rare-event probabilities in a logarithmically efficient manner. \(\Diamond \)
Open Problem 5.5
It is tempting to believe that under the scaling of Remark 5.3 the process converges, after centering and normalizing by \(\sqrt{n}\), to a multivariate Ornstein–Uhlenbeck process; cf. the discussion above (25). This is likely to carry over to the modulated setting of Remark 5.4, when also speeding up the background process, in line with results found for networks of modulated infinite-server queues in [18, 56]. In more general terms, it would also be interesting to further explore the relationship between linear stochastic fluid networks and infinite-server queueing networks; see already, for example, [49, 66].\(\bigcirc \)
6 Infinite-server queues with shot-noise arrival rates
This last section has a different flavor than the previous ones: shot noise here does not enter the picture in the form of workload-dependent service speed, but in the form of an arrival rate that evolves as shot noise. In insurance mathematics, a claim arrival process with a stochastically varying intensity given by a shot-noise process was introduced in [68], see also [3, 39]. A shot up in the shot-noise process is viewed as a disaster that triggers a number of claims, with decaying intensity. The main object of study in [3] was the asymptotic behavior of the ruin probability. In [82], a shot-noise arrival process was used to model the occurrence of earthquakes. Ganesh et al. [46] have studied sample path large deviations for Poisson shot-noise processes, with a view towards applications in queueing and teletraffic theory. Their results include the identification of the most likely path to exceedance of a large buffer level in a single server queue fed by Poisson shot noise.
In the present section we primarily focus on networks of infinite-server queues, with the distinguishing feature that the arrival rates are not constant but rather evolve as shot noise; i.e., the arrival process is a Poisson process with the stochastic arrival rate \(\Lambda (t)\) at time t, with \(\{\Lambda (t), t \ge 0\}\) a shot-noise process. Such an arrival process is called a shot-noise Cox process. We start with just one infinite-server queue. Customers arrive according to a shot-noise Cox process that is characterized by the shot rate \(\nu \), the jump size LST \(\beta (\cdot )\) and the decay rate r. The customer service requirements are i.i.d., and distributed as a generic nonnegative random variable S. We first present an analysis for the time-dependent and stationary number of customers in the system, based on Sect. 3 of [73].
Our first objective is to find the distribution of the number of customers in the system at time t, in the sequel denoted by M(t). This can be found in several ways; because of the appealing underlying intuition, we here provide a limiting argument. The idea is that we approximate the arrival rate on intervals of length \(\Delta \) by a constant, and then let \(\Delta \downarrow 0\), as follows: Consider an arbitrary sample path \(\Lambda (t)\) of the driving shot-noise process. Given this \(\Lambda (t)\), the number of customers that arrived in the interval \([k\Delta ,(k+1)\Delta )\) and are still in the system at time t has a Poisson distribution with parameter \({{\,\mathrm{\mathbb {P}}\,}}(S>t-(k\Delta +\Delta U_k))\cdot \Delta \Lambda (k\Delta ) + o(\Delta )\), where \(U_1, U_2,\ldots \) are i.i.d. standard uniform random variables. Summing over k yields that the number of customers in the system at time t has a Poisson distribution with parameter
which converges, as \(\Delta \downarrow 0\), to
Since \(\Lambda (\cdot )\) is actually a stochastic process, we conclude that the number of customers has a mixed Poisson distribution, i.e., Poisson with a random parameter, viz. the expression in Eqn. (77). As a consequence, we find by conditioning on the filtration \({\mathcal {F}}_t\) to which \(\Lambda (t)\) is adapted,
here \(\Xi (t,z) :=(z-1) {{\mathbb {P}}}(S>t)\). We have found the following result.
Theorem 6.1
Let \(\Lambda (\cdot )\) be a shot-noise process with \(\Lambda (0)=0\). Then
Proof
The result follows directly from Eqns. (9) and (78). \(\square \)
This result allows the evaluation of moments of M(t). In particular, it is easily verified that the mean satisfies the intuitively appealing expression
Higher moments can be found as well. By the law of total variance,
The latter expression we can further evaluate: as pointed out in [73],
where, for \(u\ge v\), \({{\,\mathrm{Cov}\,}}(\Lambda (u),\Lambda (v)) = e^{-r(u-v)} {{\,\mathrm{Var}\,}}\Lambda (v)\). It thus follows that (81) equals
We can make this more explicit using the closed-form formulas for \({{\,\mathrm{\mathbb {E}}\,}}\Lambda (u)\) and \({{\,\mathrm{Var}\,}}\Lambda (v)\). For the special case of S being exponentially distributed, Example 3.2 in [73] presents expressions for \({{\,\mathrm{\mathbb {E}}\,}}M(t)\) and \({{\,\mathrm{Var}\,}}\,M(t)\).
Under a specific scaling, and again assuming that the service durations are exponentially distributed, it can be shown that an appropriately centered and normalized version of the queue length process M(t) converges to a Gaussian limit. More concretely, after blowing up the shot-rate of the driving shot-noise process by a factor n, the queue length process M(t), which now depends on n, subtracted by its mean and divided by \(\sqrt{n}\) converges to an Ornstein–Uhlenbeck process with the appropriate parameters. This functional central-limit theorem extends to non-exponential service durations. In that case, however, the (non-Markovian) limiting process, a so-called Kiefer process, is considerably more involved.
Our setting with just a single infinite-server queue can be directly generalized to various types of networks. In Section 4.1 of [73] tandem networks are treated. Below we focus on the two-node tandem case, but the underlying principle carries over to tandem networks of any length. Let \(S_1\) be the generic service duration at node 1, and \(S_2\) its counterpart at node 2, and let \(M_1(t)\), \(M_2(t)\) be the queue lengths in the two nodes at time t. Above we established that \(M_1(t)\) is mixed Poisson, with the random parameter given by (77), but \(M_2(t)\) is mixed Poisson as well, with the random parameter corresponding to \(M_2(t)\) being
This formula has appealing intuition: a job that arrives at node 1 at time u should have left node 1 at time t (hence its duration should be shorter than \(t-u\)), but should still be present at node 2 (hence the duration of both service times together should be longer than \(t-u\)). Also the joint distribution of all queue lengths in the system can be explicitly characterized through its joint probability generating function.
Various more involved types of networks can be handled as well; notably, general feedforward networks are covered by Theorem 4.6 of [73]. In addition, [22] provides a detailed account of networks of infinite-server queues in which the arrival rate is a vector-valued linear transformation of a multivariate generalized shot-noise process (i.e., being driven by a general subordinator Lévy process rather than a compound Poisson process); cf. Remark 4.8. Moments and asymptotic results for such a network are derived in [91]. In another branch of the literature, the shot-noise arrival rate process is replaced by a Hawkes arrival rate process, a “self-exciting” process that bears some similarity to shot noise; see the studies on (infinite-server) queues fed by a Hawkes driven arrival process [40, 47, 74].
Open Problem 6.2
Coxian and Hawkes arrival processes offer interesting possibilities for modeling overdispersed input to a queue. In this section we have mentioned some results in this area for infinite-server queues. In terms of open problems, there is the embarrassment of choice: for the single server queue we only mentioned a few asymptotic results, because exact results seem lacking, even for the single server queue with exponential service times. \(\bigcirc \)
References
Adan, I.J.B.F., Boxma, O.J., Resing, J.A.C.: (2021). Paper in preparation
Adan, I.J.B.F., Hathaway, B., Kulkarni, V.G.: On first-come, first-served queues with two classes of impatient customers. Queueing Syst. 91, 113–142 (2019)
Albrecher, H., Asmussen, S.: Ruin probabilities and aggregate claims distributions for shot noise Cox processes. Scandinavian Actuarial J. 2006, 73–85 (2006)
Albrecher, H., Constantinescu, C., Palmowski, Z., Regensburger, C., Rosenkrantz, M.: Exact and asymptotic results for insurance risk models with surplus-dependent premiums. SIAM J. Appl. Math. 73, 47–66 (2013)
Albrecher, H., Teugels, J.L., Tichy, R.F.: On a gamma series expansion for the time-dependent probability of collective ruin. Insurance: Mathematics and Economics 29, 345-355 (2001)
Asmussen, S.: Subexponential asymptotics for stochastic processes: extremal behavior, stationary distributions and first passage probabilities. The Ann. Appl. Probability 8, 354–374 (1998)
Asmussen, S.: Applied Probability and Queues, 2nd edn. Springer, New York (2003)
Asmussen, S., Albrecher, H.: Ruin Probabilities, 2nd edn. World Scientific, London (2010)
Asmussen, S., Kella, O.: Rate modulation in dams and ruin problems. J. Appl. Probability 33, 523–535 (1996)
Asmussen, S., Schock Petersen, S.: Ruin probabilities expressed in terms of storage processes. Adv. Appl. Probability 20, 913–916 (1989)
Baccelli, F., Brémaud, P.: Elements of Queueing Theory. Springer-Verlag, Berlin (2003)
Bar-Lev, S.K., Boxma, O.J., Mathijsen, B., Perry, D.: A blood bank model with perishable blood and demand impatience. Stochastic Syst. 7(2), 237–263 (2017)
Bekker, R.: Queues with State-Dependent Rates. PhD thesis, Technische Universiteit Eindhoven. http://pure.tue.nl/ws/files/1755140/200513578.pdf (2005)
Bekker, R.: Finite-buffer queues with workload-dependent service and arrival rates. Queueing Syst. 50, 231–253 (2005)
Bekker, R., Borst, S.C., Boxma, O.J., Kella, O.: Queues with workload-dependent arrival and service rates. Queueing Syst 46(3–4), 537–556 (2004)
Bertrand, J.W.M., van Ooijen, H.P.G.: Workload based order release and productivity: a missing link. Produc. Plann. Cont. 13, 665–678 (2002)
Bingham, N.H., Goldie, C.M., Teugels, J.L.: Regular Variation. Cambridge University Press, Cambridge (1987)
Blom, J., De Turck, K., Mandjes, M.: Analysis of Markov-modulated infinite-server queues in the central-limit regime. Prob. Eng. Inf. Sci. 29(3), 433–459 (2015)
Bondesson, L.: Shot-noise processes and shot-noise distributions. In: Kotz, S. (ed.) Encyclopedia of Statistical Sciences, vol. 8, pp. 448–452. Wiley, New York (1988)
Boxma, O.J., Cahen, E., Koops, D., Mandjes, M.: Linear stochastic fluid networks: rare-event simulation and Markov modulation. Methodol. Comput. Appl. Prob. 21, 125–153 (2005)
Boxma, O.J., Kaspi, H., Kella, O., Perry, D.: On/off storage systems with state dependent input, output and switching rates. Prob. Eng. Inf. Sci. 19, 1–14 (2005)
Boxma, O.J., Kella, O., Mandjes, M.: Infinite-server systems with Coxian arrivals. Queueing Syst. 92, 233–255 (2019)
Boxma, O.J., Kella, O., Perry, D.: An intermittent fluid system with exponential on-times and semi-Markov input rates. Prob. Eng. Inf. Sci. 15, 189–198 (2001)
Boxma, O.J., Kella, O., Perry, D.: On some tractable growth collapse processes with renewal collapse epochs. J. of Appl. Prob. 48A, 401–405 (2011)
Boxma, O.J., Löpker, A., Mandjes, M.R.H.: On two classes of reflected autoregressive processes. J. of Appl. Prob. 57, 657–678 (2020)
Boxma, O.J., Mandjes, M.R.H.: Affine storage and insurance risk models. Eurandom report 2019-009; to appear in Mathematics of Operations Research (2021)
Boxma, O.J., Mayank, M., Janssen, A.J.E.M.: Two queues with time-limited polling and workload-dependent service speeds. Eurandom Report 2019-011; to appear in Stochastic Models (2021)
Boxma, O.J., Perry, D., Stadje, W., Zacks, S.: A Markovian growth collapse model. Adv. Appl. Probab. 38, 221–243 (2006)
Brill, P.H.: Level Crossing Methods in Stochastic Models. Springer, New York (2008)
Brockwell, P., Resnick, S., Tweedie, R.: Storage processes with general release rule and additive inputs. Adv. Appl. Probab. 14, 392–433 (1982)
Browne, S., Sigman, K.: Work-modulated queues with applications to storage processes. J. Appl. Probab. 29, 699–712 (1992)
Çağlar, M.: A Poisson shot-noise scaling process of pulses and its scaling limit. Commun. on Stochastic Analy. 9(4), 503–527 (2020)
Campbell, N.: The study of discontinuous phenomena. Proc. Cambridge Philos. Soc. 15, 117–136 (1909)
Campbell, N.: Discontinuities in light emission. Proc. Cambridge Philos. Soc. 15, 310–328 (1909)
Chamayou, J.M.F.: On the simulation of shot noise and some other random variables. Stoch. Proc. Appl. 6, 305–316 (1978)
Chen, H., Yao, D.D.: Fundamentals of Queueing Networks. Springer, New York (2001)
Çinlar, E., Pinsky, M.: A stochastic integral in storage theory. Zeitschrift für Wahrscheinlichkeitstheorie und Verwandte Gebiete 17, 227–240 (1971)
Cohen, J.W.: On up- and downcrossings. J. Appl. Probab. 14, 405–410 (1977)
Dassios, A., Jang, J.W.: Pricing of catastrophe reinsurance and derivatives using the Cox process with shot noise intensity. Finance Stochast. 7(1), 73–95 (2003)
Daw, A., Pender, J.: Queues driven by Hawkes processes. Stoch. Syst. 8, 192–229 (2018)
Doob, J.L.: Stochastic Processes. Wiley, New York (1953)
Eliazar, I., Klafter, J.: A growth-collapse model: Lévy inflow, geometric crashes, and generalized Ornstein-Uhlenbeck dynamics. Phys. A 334, 1–21 (2004)
Eliazar, I., Klafter, J.: On the nonlinear modeling of shot noise. PNAS 102, 13779–13782 (2005)
Feller, W.: An Introduction to Probability Theory and its Applications, vol. 2. Wiley, New York (1971)
Fuhrmann, S.W., Cooper, R.B.: Stochastic decompositions in the \(M/G/1\) queue with generalized vacations. Oper. Res. 33, 1117–1129 (1985)
Ganesh, A., Macci, C., Torrisi, G.L.: Sample path large deviations principles for Poisson shot noise processes, and applications. Elect. J. Probab. 10, 1026–1043 (2005)
Gao, X., Zhu, L.: Functional central limit theorems for stationary Hawkes processes and application to infinite-server queues. Queueing Syst. 90, 161–206 (2018)
Gaver, D., Miller, R.: Limiting distributions for some storage problems. In: Arrow, K., Karlin, S., Scarf, H. (eds.) Studies in applied probability and management science, pp. 110–126. Stanford University Press, CA (1962)
de Graaf, W., Scheinhardt, W., Boucherie, R.: Shot-noise fluid queues and infinite-server systems with batch arrivals. Perform. Eval. 116, 143–155 (2017)
Harrison, J.M., Resnick, S.I.: The stationary distribution and first exit probabilities of a storage process with general release rule. Mathematics of Operations Research 1, 347–358 (1976)
Harrison, J.M., Resnick, S.I.: The recurrence classification of risk and storage processes. Mathematics of Operations Research 3, 57–66 (1978)
Heinrich, L., Schmidt, V.: Normal convergence of multidimensional shot noise and rates of this convergence. Adv. Appl. Probab. 17, 709–730 (1985)
Iksanov, A., Jurek, Z.: Shot noise distributions and selfdecomposability. Stochastic Anal. Appl. 21, 593–609 (2003)
Iksanov, A., Marynych, A., Meiners, M.: Limit theorems for renewal shot noise processes with decreasing response function. Eurandom Report 2012-023. Extended preprint version at arXiv:1212:1583v2, (2012)
Jacobsen, M., Jensen, A.: Exit times for a class of piecewise exponential Markov processes with two-sided jumps. Stoch. Proc. Appl. 117, 1330–1356 (2007)
Jansen, H.M., Mandjes, M., De Turck, K., Wittevrongel, S.: Diffusion limits for networks of Markov-modulated infinite-server queues. Performance Evaluation 135, article number 102039 (2019)
Kaspi, H., Kella, O.: Stability of feed-forward fluid networks with Lévy input. J. Appl. Probab. 33, 513–522 (1996)
Kaspi, H., Kella, O., Perry, D.: Dam processes with state dependent batch sizes and intermittent production processes with state dependent rates. Queueing Syst. 24, 37–57 (1996)
Kaspi, H., Perry, D.: On a duality between a non-Markovian storage/production process and a Markovian dam process with state-dependent input and output. J. Appl. Probab. 27, 835–844 (1989)
Keilson, J., Mermin, N.: The second-order distribution of integrated shot noise. IRE Transac. Inf. Theory 5(2), 75–77 (1959)
Kella, O.: On growth collapse processes with stationary structure and their shot-noise counterparts. J. Appl. Probab. 46, 363–371 (2009)
Kella, O., Stadje, W.: On hitting times for compound Poisson dams with exponential jumps and linear release rate. J. Appl. Probab. 38(3), 781–786 (2001)
Kella, O., Stadje, W.: Exact results for a fluid model with state-dependent flow rates. Probab. Eng. Inf. Sci. 16, 389–402 (2002)
Kella, O., Stadje, W.: Markov modulated linear fluid networks with Markov additive input. J. Appl. Probab. 39, 413–420 (2002)
Kella, O., Whitt, W.: Stability and structural properties of stochastic fluid networks. J. Appl. Probab. 33, 1169–1180 (1996)
Kella, O., Whitt, W.: Linear stochastic fluid networks. J. Appl. Probab. 36, 244–260 (1999)
Kella, O., Yor, M.: A new formula for some linear stochastic equations with applications. The Ann. Appl. Probab. 20, 367–381 (2010)
Klüppelberg, C., Mikosch, T.: Explosive Poisson shot noise processes with applications to risk reserves. Bernoulli 1, 125–147 (1995)
Klüppelberg, C., Mikosch, T., Schärf, A.: Regular variation in the mean and stable limits for Poisson shot noise. Bernoulli 9, 467–496 (2003)
Klüppelberg, C., Stadtmüller, U.: Ruin probabilities in the presence of heavy tails and interest rates. Scandinavian Actuar. J. 1995, 49–58 (1995)
Knessl, C., Peters, C.: Exact and asymptotic solutions for the time-dependent probability of collective ruin II. SIAM J. Appl. Math. 56, 1471–1521 (1996)
Koops, D. T.: Queueing Systems with Nonstandard Input Processes. PhD thesis, University of Amsterdam. http://pure.uva.nl/ws/files/32459480/Thesis.pdf (2019)
Koops, D.T., Boxma, O.J., Mandjes, M.: Networks of \(\cdot /G/\infty \) queues with shot-noise-driven arrival intensities. Queueing Syst. 86, 301–325 (2017)
Koops, D.T., Saxena, M., Boxma, O.J., Mandjes, M.: Infinite-server queues with Hawkes input. J. Appl. Probab. 55, 920–943 (2018)
Kurtz, T.: Limit theorems for workload input models. In: Kelly, F.P., Zachary, S., Ziedins, I. (eds.), Stochastic Networks: Theory and Applications, Oxford University Press, Oxford, pp. 119-140 (1996)
Lane, J.A.: The central limit theorem for the Poisson shot-noise process. J. Appl. Probab. 21, 287–301 (1984)
van Leeuwaarden, J.S.H., Löpker, A.H., Ott, T.J.: TCP and iso-stationary transformations. Queueing Syst. 63, 459–475 (2009)
Mandjes, M.R.H., Mitra, D., Scheinhardt, W.R.W.: A simple model of network access: feedback adaptation of rates and admission control. Proc. INFOCOM 2002, 3–12 (2002)
Mandjes, M.R.H., Mitra, D., Scheinhardt, W.R.W.: Models of network access using feedback fluid queues. Queueing Syst. 44, 365–398 (2003)
Miyazawa, M.: Time-dependent rate conservation laws for a process defined with a stationary marked point process and their applications. J. Appl. Probab. 31, 114–129 (1994)
Moran, P.A.P.: A theory of dams with continuous input and a general release rule. J. Appl. Probab. 6, 88–98 (1969)
Ogata, Y.: Statistical models for earthquake occurrences and residual analysis for point processes. J. Am. Stat. Assoc. 84, 9–27 (1988)
Parzen, E.: Stochastic Processes. Holden-Day, Oakland (Calif.) (1962)
Paulsen, J., Gjessing, H.K.: Ruin theory with stochastic return on investments. Adv. Appl. Probab. 29, 965–985 (1997)
Rabehasaina, L.: Moments of a Markov-modulated irreducible network of fluid queues. J. Appl. Probab. 43, 510–522 (2006)
Reich, E.: On the integrodifferential equation of Takács I. Ann. Math. Statis. 29, 563–570 (1958)
Ross, S.M.: Stochastic Processes. Wiley, New York (1996)
Ross, S.M.: Introduction to Probability Models, 12th edn. Academic Press, New York (2019)
Sakuma, Y., Boxma, O. J., Phung-Duc, T.: A single server queue with workload-dependent service speed and vacations. In Proceedings of Queueing Theory and Network Applications (QTNA). Springer-Verlag, Berlin, pp. 112-128 (2019)
Samorodnitsky, G.: A class of shot noise models for financial applications. In: Heyde, C.C., Prohorov, Y.V., Pyke, R., Rachev, S.T. (eds.), Athens Conference on Applied Probability and Time Series Analysis, Vol.I (Springer, New York), pp. 332-353 (1996)
Saxena, M., Boxma, O.J., Mandjes, M.: An infinite-server system with Lévy shot-noise modulation: moments and asymptotics. Markov Proces. Related Fields 26, 757–778 (2020)
Scheinhardt, W.R.W., van Foreest, N., Mandjes, M.R.H.: Continuous feedback fluid queues. Oper. Res. Lett. 33, 551–559 (2004)
Schmidt, T.: Shot-noise processes in finance. Chapter 18 of: Ferger, D., González Mantelga, W., Schmidt, T., Wang J.-L. (eds.) From Statistics to Mathematical Finance, (Springer, New York) (2017)
Schottky, W.: Ueber spontane Stromschwankungen in verschiedenen Elektrizitätsleitern. Annalen Physik 57, 541–567 (1918)
Segerdahl, C.: Ueber einige risikotheoretische Fragestellungen. Skandinavisk Aktuaritidsskrift 25, 43–83 (1942)
Stadje, W.: Some structural properties of a Markovian storage/production system. Queueing Syst. 25, 339–350 (1997)
Takács, L.: On secondary stochastic processes generated by a Poisson process and their application in physics. Act. Math. Sci. Hung. 5, 203–236 (1954)
Takács, L.: Investigation of waiting time problems by reduction to Markov processes. Acta Math. Sci. Hung. 6, 101–129 (1955)
Takács, L.: On stochastic processes connected with certain physical recording apparatuses. Act. Math. Sci. Hung. 6, 363–380 (1955)
Takács, L.: On secondary stochastic processes generated by recurrent processes. Act. Math. Sci. Hung. 7, 17–28 (1956)
Takács, L.: Über die wahrscheinlichkeitstheoretische Behandlung der Anodenstromschwankungen von Elektronenröhren. Act. Phys. Acad. Sci. Hung. 7, 25–50 (1957)
Takács, L.: Introduction to the Theory of Queues. Oxford University Press, New York (1962)
Vere-Jones, D.: Stochastic models for earthquake occurrence. J. Roy. Stat. Soc. B 32, 1–62 (1970)
Weiss, G.: Shot noise models for the generation of synthetic streamflow data. Water Resour. Res. 13, 101–108 (1977)
Wierman, A., Andrew, L.L.H., Lin, M.: Speed scaling: An algorithmic perspective. In: Handbook of Energy-Aware and Green Computing. Chapman & Hall/CRC Computing and Information Science Series, pp. 385-406 (2012)
Yeo, G.F.: A finite dam with exponential release. J. Appl. Probab. 11, 122–133 (1974)
Acknowledgements
We gratefully acknowledge valuable comments and suggestions made by René Bekker and Offer Kella. The research for this paper has been supported by the NWO Gravitation Programme Networks (Grant Number 024.002.003).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Boxma, O., Mandjes, M. Shot-noise queueing models. Queueing Syst 99, 121–159 (2021). https://doi.org/10.1007/s11134-021-09708-9
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11134-021-09708-9