Abstract
We study the discrete-to-continuum variational limit of the antiferromagnetic XY model on the two-dimensional triangular lattice. The system is fully frustrated and displays two families of ground states distinguished by the chirality of the spin field. We compute the \(\Gamma \)-limit of the energy in a regime which detects chirality transitions on one-dimensional interfaces between the two admissible chirality phases.
Similar content being viewed by others
1 Introduction
Ordering problems in magnetism have been extensively studied by both the physics and the mathematics communities. Researchers have been attracted by the rich phase diagrams and critical behaviors of magnetic models which are often the result of difficult-to-detect optimization effects taking place at several energy and length scales. The reason for such a complex behavior can be traced back to the presence of many competing mechanisms which give rise to frustration. Frustration in the context of spin systems (here, as it is customary in the statistical mechanics literature, we will often refer to magnets as to spins) refers to the situation where spins cannot find an orientation that simultaneously minimizes all the pairwise exchange interactions. Such interactions are said to be ferromagnetic or antiferromagnetic if they favour alignment or antialignment, respectively. Often frustration occurs in those systems where spins are subject to conflicting short range ferromagnetic and long range antiferromagnetic interactions, as when modulated phases appear (see, e.g. the expository paper [37]). For antiferromagnetic lattice systems, that is systems of lattice spins subject to only antiferromagnetic interactions, frustration can also stem from the relative spatial arrangement of spins induced by the geometry of the lattice. In this case frustration is often referred to as geometric frustration. As a consequence of geometric frustration magnetic compounds show complex geometric patterns that induce often unexpected effects whose understanding is one of the primary subjects in statistical and condensed matter physics as it can help to better explain the nature of phase transitions in magnetic materials [30, 32, 33]. From a mathematical perspective, several interesting questions can be addressed. In this paper we are interested in the variational coarse graining of the system, in the line of what is by now addressed to as the “discrete-to-continuum variational analysis of discrete systems”. Within this line of investigation the analysis of spin systems turns out to be a difficult nonlinear optimization problem requiring the combination of several methods ranging from simple discrete optimization procedures to sophisticated techniques in geometric measure theory and the calculus of variations. While models where frustration is induced by the competition of ferromagnetic/antiferromagnetic interactions have been already studied from a variational perspective (see, e.g. [1, 12, 20, 24, 28, 36]), what we present here is the first discrete-to-continuum result for a geometrically frustrated system.
We carry out the discrete-to-continuum variational analysis (at zero temperature) of a geometrically frustrated spin model in a specific energetic regime and we characterize the effective behavior of its low-energy states, that is states that can deviate from the global minimizers (ground states) by a certain small amount of energy. More precisely we consider a 2-dimensional nearest-neighbors antiferromagnetic planar spin model on the triangular lattice, cf. [30, Chapter 1]. Despite being considered one of the most elementary geometrically frustrated spin models, its variational analysis turns out to be quite a delicate task. More in detail, we let \(\varepsilon > 0\) be a small parameter and we consider the triangular lattice \({\mathcal {L}}_\varepsilon \) with spacing \(\varepsilon \) (see Subsection 2.2 for the precise definition). To every spin field \(u :{\mathcal {L}}_\varepsilon \rightarrow {\mathbb {S}}^1\) we associate the energy
where \(\langle \cdot , \cdot \rangle \) denotes the scalar product. (Below, the energy will be restricted to bounded regions in the plane.) This model is antiferromagnetic since the interaction energy between two neighboring spins is minimized by two opposite vectors. Such an order in the magnetic alignment, also known as antiferromagnetic order, is frustrated by the geometry of the triangular lattice, which inhibits a configuration where each pair of neighboring spins are opposite or, equivalently, where each interaction is minimized. This suggests that the antiferromagnetic XY model depends substantially on the geometry of the lattice, which affects the structure of the ground states, the choice of the relevant variables and of the energy scalings. Notice, for example, that on a square lattice the system would not be frustrated, as opposite vectors distributed in a checkerboard structure minimize each interaction. In fact, on the square lattice a straightforward change of variable allows one to recast the antiferromagnetic XY model into the ferromagnetic XY model [2, Remark 3], which is driven by an energy with neighboring interactions \(- \langle u(\varepsilon \sigma ), u(\varepsilon \sigma ')\rangle \). The latter model has been thoroughly investigated in the last decade both on the square lattice [2, 3, 5, 21, 22] and on the triangular lattice [18, 29]. Independently of the geometry of the lattice, it has been proved that spin fields that deviate from the ground states by an amount of energy which diverges logarithmically as \(\varepsilon \) vanishes form of topological charges (vortex-like singularities of the spin field as those arising in the Ginzburg-Landau model [10, 35]), when subject to boundary conditions or external magnetic fields. In [9] we show how such a phenomenon also occurs in the antiferromagnetic XY model on the triangular lattice.
We now come back to our model (1.1). In order to identify the relevant variable of the system, we first need to characterize the ground states of the antiferromagnetic XY system in (1.1). To this end it is convenient to rearrange the indices of the sum in (1.1) and to recast the energy as a sum over all triangular plaquettes T with vertices \(\varepsilon i, \varepsilon j, \varepsilon k \in {\mathcal {L}}_\varepsilon \)
In each triangle T the energy is minimized (and is equal to \(-\frac{3}{2}\)) if and only if \(u(\varepsilon i) + u(\varepsilon j) + u(\varepsilon k) = 0\), namely, when the vectors of a triple \((u(\varepsilon i),u(\varepsilon j),u(\varepsilon k))\) point at the vertices of an equilateral triangle. By the \({\mathbb {S}}^1\)-symmetry, every rotation of a minimizing triple \((u(\varepsilon i),u(\varepsilon j),u(\varepsilon k))\) is minimizing, too. The ground states in this model feature an additional symmetry, usually referred to as \({\mathbb {Z}}_2\)-symmetry: triple obtained by from a minimizing triple via a permutation of negative sign as \((u(\varepsilon i),u(\varepsilon k),u(\varepsilon j))\) is also minimizing. This determines two families of ground states, i.e., spin fields for which the energy is minimized in each plaquette, see Fig. 1. These two families can be distinguished through the chirality, a scalar which quantifies the handedness of a certain spin structure. To define the chirality of a spin field u in a triangle T, we need a consistent ordering of its vertices \(\varepsilon i\), \(\varepsilon j\), \(\varepsilon k\). We assume that \(\varepsilon i \in {\mathcal {L}}^1_\varepsilon \), \(\varepsilon j \in {\mathcal {L}}^2_\varepsilon \), \(\varepsilon k \in {\mathcal {L}}^3_\varepsilon \), where \({\mathcal {L}}^1_\varepsilon \), \({\mathcal {L}}^2_\varepsilon \), \({\mathcal {L}}^3_\varepsilon \) are the sublattices as in Fig. 1, and we set (see (2.1) for the precise definition)
where the symbol \(\times \) stands for the cross product. We denote by \(\chi (u) \in L^\infty ({\mathbb {R}}^2)\) the function equal to \(\chi (u,T)\) on the interior of each plaquette T. The ground states are exactly those configurations u that satisfy either \(\chi (u) \equiv 1\) or \(\chi (u) \equiv - 1\), cf. Remark 2.2.
A ground state \(u_\varepsilon ^\mathrm {pos}\) with positive chirality and a ground state \(u_\varepsilon ^\mathrm {neg}\) with negative chirality. Any other ground state of the system is obtained by composing one of these two configurations with a constant rotation. In the center: three points of the sublattices \({\mathcal {L}}^1_\varepsilon \), \({\mathcal {L}}^2_\varepsilon \), and \({\mathcal {L}}^3_\varepsilon \) in black, gray, and white, respectively
In this paper we analyze the energy regime at which the two families of ground states coexist and at the same time the energy of the system concentrates at the interface between the two chiral phases \(\{\chi =1\}\) and \(\{\chi =-1\}\). We fix \(\Omega \subset {\mathbb {R}}^2\) open, bounded, and with Lipschitz boundary and we consider the energy (1.2) restricted to \(\Omega \), i.e., computed only on plaquettes of \({\mathcal {L}}_\varepsilon \) contained in \(\Omega \). We refer the energy to its minimum by removing the energy of the ground states (\(-\frac{3}{2}\) for each plaquette) and we divide it by the number of lattice points in \(\Omega \) (of order \(1/\varepsilon ^{2}\)). We obtain (up to a multiplicative constant) the energy per particle given by
We are interested to the asymptotic behavior of the energy above as \(\varepsilon \rightarrow 0\) on sequences of spin fields \(u_\varepsilon :{\mathcal {L}}_\varepsilon \rightarrow {\mathbb {S}}^1\) that can deviate from ground states yet satisfying a bound \(E_\varepsilon (u_\varepsilon ) \le C \varepsilon \). To this end we define the energy \(F_\varepsilon (u) := \frac{1}{\varepsilon } E_\varepsilon (u)\) and study sequences of spin fields with equibounded \(F_{\varepsilon }\) energy. Due to the \({\mathbb {S}}^1\)-symmetry, the energy at this regime cannot distinguish ground states with the same chirality, so that the relevant order parameter of the model is, in fact, not the spin field but its chirality: in Proposition 3.1 we prove that a sequence \((u_\varepsilon )\) satisfying \(F_\varepsilon (u_\varepsilon ) \le C\) admits a subsequence (not relabeled) such that \(\chi (u_\varepsilon ) \rightarrow \chi \) strongly in \(L^1(\Omega )\) for some \(\chi \in BV(\Omega ;\{-1,1\})\), i.e., the admissible chiralities in the continuum limit are \(-1\) and 1 and the chirality phases \(\{\chi = -1\}\) and \(\{\chi = 1\}\) have finite perimeter in \(\Omega \). This suggests that the model shares similarities with systems having finitely many phases, such as Ising models [1, 17, 34] or Potts models [23]. However, a crucial difference consists in the fact that in our case the variable that shows a phase transition is not the spin variable itself, but the chirality, which depends on the spin field in a nonlinear way. This is a source of difficulties that will be explained below.
To describe the asymptotic behavior of the system it is convenient to introduce the functionals depending only on functions \(\chi \in L^1(\Omega )\) defined by \({\mathscr {F}}_\varepsilon (\chi ) := \inf \{ F_\varepsilon (u) :\ u :{\mathcal {L}}_\varepsilon \rightarrow {\mathbb {S}}^1 \text { such that } \chi = \chi (u,T) \text { on every } T \subset \Omega \}\) (equal to \(+\infty \) if \(\chi \) is not the chirality of a spin field). The main result in this paper is Theorem 2.5, where we prove that the \(\Gamma \)-limit of \({\mathscr {F}}_\varepsilon \) with respect to the \(L^1\)-convergence is an anisotropic surface energy given by
extended to \(+\infty \) otherwise in \(L^1(\Omega )\), where \(J_\chi \) is the interface between \(\{\chi = -1\}\) and \(\{\chi = 1\}\) and \(\nu _\chi \) is the normal to \(J_\chi \). The density \(\varphi \) is given by the following asymptotic formula
where \(Q^\nu \) is the square with one side orthogonal to \(\nu \), \(u_\varepsilon ^\mathrm {pos}\) and \(u_\varepsilon ^\mathrm {neg}\) are the ground states depicted in Fig. 1, and \(\partial _\varepsilon ^\pm Q^\nu \) are a discrete version of the top/bottom parts of \(\partial Q^\nu \). Asymptotic formulas like (1.3) are common in discrete-to-continuum variational analyses and are often used to represent \(\Gamma \)-limits of discrete energies [6, 8, 12, 14, 15, 31]. However, proving an asymptotic lower bound with the density (1.3) for this model requires additional care and is the technically most demanding contribution of this paper. We conclude this introduction by describing the main difficulties that arise in the proof.
Via a classical blow-up argument (see Proposition 4.1) we obtain an asymptotic lower bound with the surface density
where \(\chi _\nu \) is the pure-jump function which takes the values \(\chi _\nu (x)=\pm 1\) for \(\pm \langle x, \nu \rangle > 0\). Hence, the proof of the asymptotic lower bound boils down to the proof of the inequality \(\psi (\nu ) \ge \varphi (\nu )\). To obtain the latter inequality, we need to modify sequences \((u_\varepsilon )\) with \(\chi (u_\varepsilon )\rightarrow \chi _\nu \) in \(L^1(Q^\nu )\) without increasing their energy in such a way that they attain the boundary conditions required in (1.3). A common approach to deal with this modification consists in selecting (via a well-known slicing/averaging argument due to De Giorgi) a low-energy frame contained in \(Q^\nu \) and close to \(\partial Q^\nu \) where the sequence can be modified using a cut-off function that interpolates to the boundary values. In our problem, instead, a cut-off modification of \(\chi (u_\varepsilon )\) may generate a sequence of functions that are not chiralities of spin fields (and thus have infinite energy \({\mathscr {F}}_\varepsilon \)). Consequently, we have to operate directly on the sequence \((u_\varepsilon )\), on whose convergence we have no information due to the invariance of the system under rotation of the spin field (the \({\mathbb {S}}^1\)-symmetry discussed above). We turn however the \({\mathbb {S}}^1\)-symmetry to our advantage to define the needed modification. Inside a one-dimensional slice of \({\mathcal {L}}_\varepsilon \), a spin field close to a ground state in one triangle can be slowly rotated to reach any other ground state with the same chirality by paying an amount of energy proportional to the energy in the starting triangle (see Lemma 4.5). This one-dimensional construction can then be reproduced in the whole \(Q^{\nu }\) starting from triangles in a low-energy frame close to \(\partial Q^\nu \) in such a way that the modified spin field attains the fixed ground states \(u_\varepsilon ^\mathrm {pos}\) and \(u_\varepsilon ^\mathrm {neg}\) at the (discrete) boundary. However, for this procedure to be successful, the usual slicing/averaging method to find a low-energy frame close to \(\partial Q^\nu \) is not enough. We need to improve it and to find a frame with a better (smaller) energy bound. To this end, we proceed as follows. In Lemma 4.3 we show that \(\psi (\nu )\) can be equivalently defined using in place of \(Q^\nu \) any rectangle coinciding with \(Q^\nu \) along the interface, but with arbitrarily small height (similar results appeared in different contexts, e.g. [16, 17, 19, 25,26,27, 31]). Hence the energy of any sequence \((u_\varepsilon )\) admissible for (1.4) concentrates arbitrarily close to the jump set of \(\chi _\nu \), i.e., the interface \(\{\langle x,\nu \rangle =0\}\). (This is, in general, not true for discrete systems, as observed in [11].) With this result at hand, in Lemma 4.4 we can apply the averaging method with the advantage of knowing that in most of the space the total energy is going to vanish, thus finally deducing the existence of a frame close to \(\partial Q^\nu \) with the wished (small enough) energy bound. Even at this point, to reproduce the one-dimensional interpolation along this frame requires additional care. In fact, to conclude the argument one still needs to prove that the winding number of the spin field in the low-energy frame can be properly controlled (Step 3 of Proposition 4.2).
2 Setting of the problem and statement of the main result
2.1 General notation
Throughout this paper \(\Omega \subset {\mathbb {R}}^2\) is an open, bounded set with Lipschitz boundary. For every \(A\subset {\mathbb {R}}^2\) measurable we denote by |A| its 2-dimensional Lebesgue measure. With \({\mathcal {H}}^1\) we indicate the 1-dimensional Hausdorff measure in \({\mathbb {R}}^2\). Given two points \(x,y \in {\mathbb {R}}^2\) we use the notation \([x;y] := \{ \lambda x + (1-\lambda ) y :\lambda \in [0,1] \}\) for the segment joining x and y. The set \({\mathbb {S}}^1:=\{\nu \in {\mathbb {R}}^2:|\nu |=1\}\) is the set of all 2-dimensional unit vectors. For every such vector \(\nu =(\nu _1,\nu _2)\in {\mathbb {S}}^1\) we denote by \(\nu ^\perp :=(-\nu _2,\nu _1)\in {\mathbb {S}}^1\) the unit vector orthogonal to \(\nu \) obtained by rotating \(\nu \) counterclockwise by \(\pi /2\). Given \(v,w \in {\mathbb {S}}^1\) we denote by \(\langle v, w\rangle \) their scalar product and by \(v {\times }w =-\langle v, w^\perp \rangle \) their cross product. We denote by \(\iota \) the imaginary unit in the complex plane. It will be often convenient to write vectors in \({\mathbb {S}}^1\) as \(\exp (\iota \theta )\), \(\theta \in {\mathbb {R}}\). We denote by \(R_{\ell ,h}^\nu \) the rectangle of length \(\ell >0\) and height \(h>0\) with two sides orthogonal to \(\nu \in {\mathbb {S}}^1\) given by
extending the definition to the case \(\ell = +\infty \) by setting \(R_{\infty ,h}^\nu :=\{x\in {\mathbb {R}}^2:|\langle x,\nu \rangle |<h/2\}\). Given \(\rho >0\) we define the cube centered at the origin with side length \(\rho \) and one face orthogonal to \(\nu \) by \(Q_\rho ^\nu :=R_{\rho ,\rho }^\nu \). For \(\rho =1\) we simply write \(Q^\nu \) instead of \(Q_1^\nu \). By \(L^\nu :=\{x\in {\mathbb {R}}^2:\langle x,\nu \rangle =0\}\) we denote the line orthogonal to \(\nu \) passing through the origin, while \(H^\nu _+:=\{x\in {\mathbb {R}}^2:\langle x,\nu \rangle \ge 0\}\) and \(H^\nu _-:={\mathbb {R}}^2\setminus H^\nu _+\) stand for the two half spaces separated by \(L^\nu \). Given \(x_0\in {\mathbb {R}}^2\) we set \(Q_\rho ^\nu (x_0):=x_0+Q_\rho ^\nu \), \(R_{\ell ,h}^\nu (x_0):=x_0+R_{\ell ,h}^\nu \), \(L^\nu (x_0):=x_0+L^\nu \) and \(H^\nu _\pm (x_0):=x_0+H^\nu _\pm \).
2.2 Triangular lattices and discrete energies
In this paragraph we define the discrete energy functionals we consider in this paper. To this end we first define the triangular lattice \({\mathcal {L}}\). It is given by
with \({\hat{e}}_1=(1,0)\), and \({\hat{e}}_2=\frac{1}{2}(1,\sqrt{3})\). For later use, we find it convenient here to introduce \({\hat{e}}_3:=\tfrac{1}{2}(-1,\sqrt{3})\) as a further unit vector connecting points of \({\mathcal {L}}\) and to define three pairwise disjoint sublattices of \({\mathcal {L}}\), denoted by \({\mathcal {L}}^1\), \({\mathcal {L}}^2\), and \({\mathcal {L}}^3\) (see Fig. 1), by
Eventually, we define the family of triangles subordinated to the lattice \({\mathcal {L}}\) by setting
where \({{\,\mathrm{conv}\,}}\{i,j,k\}\) denotes the closed convex hull of i, j, k. It is also convenient to introduce the families of upward/downward facing triangles
For \(\varepsilon >0\), we consider rescaled versions of \({\mathcal {L}}\) and \({\mathcal {T}}({\mathbb {R}}^2)\) given by \({\mathcal {L}}_\varepsilon :=\varepsilon {\mathcal {L}}\) and \({\mathcal {T}}_\varepsilon ({\mathbb {R}}^2):=\varepsilon {\mathcal {T}}({\mathbb {R}}^2)\), \({\mathcal {T}}^\pm _\varepsilon ({\mathbb {R}}^2) :=\varepsilon {\mathcal {T}}^\pm ({\mathbb {R}}^2)\). With this notation every \(T\in {\mathcal {T}}_\varepsilon ({\mathbb {R}}^2)\) has vertices \(\varepsilon i,\varepsilon j,\varepsilon k\in {\mathcal {L}}_\varepsilon \). The same notation applies to the sublattices, namely \({\mathcal {L}}_\varepsilon ^\alpha :=\varepsilon {\mathcal {L}}^\alpha \) for \(\alpha \in \{1,2,3\}\). Given a Borel set \(A\subset {\mathbb {R}}^2\) we denote by \({\mathcal {T}}_\varepsilon (A):=\{T\in {\mathcal {T}}_\varepsilon ({\mathbb {R}}^2):T\subset A\}\) the subfamily of triangles contained in A. Eventually, we introduce the set of admissible configurations as the set of all spin fields
In the case \(\varepsilon =1\) we set \(\mathcal {SF}:=\mathcal {SF}_1\). For \(u\in \mathcal {SF}_\varepsilon \) we now define the discrete energies \(F_\varepsilon (u)\) as follows: for every \(T\in {\mathcal {T}}_\varepsilon ({\mathbb {R}}^2)\) we set
and we extend the energy to any Borel set \(A\subset {\mathbb {R}}^2\) by setting
If \(A=\Omega \) we omit the dependence on the set and write \(F_\varepsilon (u):=F_\varepsilon (u,\Omega )\).
2.3 Chirality
In this section we introduce the relevant order parameter to analyze the asymptotic behavior of \(F_\varepsilon \), namely the chirality \(\chi \). More in detail, given \(u\in \mathcal {SF}_\varepsilon \) and \(T={{\,\mathrm{conv}\,}}\{\varepsilon i,\varepsilon j,\varepsilon k\}\in {\mathcal {T}}_\varepsilon ({\mathbb {R}}^2)\) with \(i\in {\mathcal {L}}^1\), \(j\in {\mathcal {L}}^2\) and \(k\in {\mathcal {L}}^3\) we set
Moreover, we define \(\chi (u):\Omega \rightarrow {\mathbb {R}}\) by setting \(\chi (u)(x):=\chi _\varepsilon (u,T)\) if \(x\in {{\,\mathrm{int}\,}}T\). Given \(u\in \mathcal {SF}_\varepsilon \) and \(T={{\,\mathrm{conv}\,}}\{\varepsilon i,\varepsilon j,\varepsilon k\}\in {\mathcal {T}}_\varepsilon ({\mathbb {R}}^2)\) it is sometimes convenient to rewrite \(\chi _\varepsilon (u,T)\) and \(F_\varepsilon (u,T)\) in terms of the angular lift of u. More precisely, let \(\theta (\varepsilon i),\theta (\varepsilon j),\theta (\varepsilon k)\in {\mathbb {R}}\) be such that \(u(\varepsilon \alpha )=\exp (\iota \theta (\varepsilon \alpha ))\), \(\alpha \in \{i,j,k\}\). Then
The next lemma is useful to relate the chirality and the energy in a triangle.
Lemma 2.1
Let \(f,g:[0,2\pi ){\times }[0,2\pi )\rightarrow {\mathbb {R}}\) be given by
Then f and g have the following properties:
-
(i)
\(f(\theta _1,\theta _2)\in [-\tfrac{3\sqrt{3}}{2},\tfrac{3\sqrt{3}}{2}]\) for every \(\theta _1,\theta _2\in [0,2\pi )\). Moreover, \(f(\theta _1,\theta _2)\in \{-\tfrac{3\sqrt{3}}{2},\tfrac{3\sqrt{3}}{2}\}\) if and only if \(g(\theta _1,\theta _2)=-\tfrac{3}{2}\).
-
(ii)
\(f(\theta _1,\theta _1)=f(\theta _1,0)=f(0,\theta _2)=0\) for every \(\theta _1,\theta _2\in [0,2\pi )\). In addition, for every \(\theta _2\in (0,2\pi )\) there holds \(f(\, \cdot \, ,\theta _2)>0\) on \((0,\theta _2)\) and \(f(\, \cdot \, ,\theta _2)<0\) on \((\theta _2,2\pi )\).
Proof
Since there obviously holds \(f(\theta _1,\theta _1)=f(\theta _1,0)=f(0,\theta _2)=0\), we only need to prove (i) and the second part of (ii). To prove (i) we show that \(\min f=-\tfrac{3\sqrt{3}}{2}\) and \(\max f=\tfrac{3\sqrt{3}}{2}\) and we relate minimizers and maximizers of f to minimizers of g. To this end we start computing
A direct calculation shows that \(\nabla f(\theta _1,\theta _2)=0\) for some \((\theta _1,\theta _2)\in (0,2\pi ){\times }(0,2\pi )\) if and only if
For \((\theta _1,\theta _2)\in (0,2\pi ){\times }(0,2\pi )\) this can only be satisfied if
Then, since \(f=0\) on the boundary of \([0,2\pi ){\times }[0,2\pi )\), we deduce that
Moreover, \(g((\tfrac{2\pi }{3},\tfrac{4\pi }{3}))=g((\tfrac{4\pi }{3},\tfrac{2\pi }{3}))=-\tfrac{3}{2}\), which shows one direction of the second part of (i). To prove the opposite direction, let us assume that \(({\overline{\theta }}_1,{\overline{\theta }}_2)\in (0,2\pi ){\times }(0,2\pi )\) is such that \(g(({\overline{\theta }}_1,{\overline{\theta }}_2)=\min g\). Then necessarily \(\nabla g({\overline{\theta }}_1,{\overline{\theta }}_2)=0\), from which we deduce that \(({\overline{\theta }}_1,{\overline{\theta }}_2)\) must satisfy (2.4) (the possibility that \({\overline{\theta }}_1 = \pi \) or \({\overline{\theta }}_2 = \pi \) are ruled out by the fact that \(g(\, \cdot \, ,\pi )=g(\pi ,\, \cdot \, )=-1\)). The pairs \(({\overline{\theta }}_1,{\overline{\theta }}_2)\) satisfying (2.4) are either \(({\overline{\theta }}_1,{\overline{\theta }}_2)=(\tfrac{2\pi }{3},\tfrac{4\pi }{3})\) or \(({\overline{\theta }}_1,{\overline{\theta }}_2)=(\tfrac{4\pi }{3},\tfrac{2\pi }{3})\) and in both cases it holds \(g({\overline{\theta }}_1,{\overline{\theta }}_2)=-\tfrac{3}{2}\). This yields that \(\min g=-\tfrac{3}{2}\) and that the opposite direction of (i) holds, upon noticing that \(g\ge -1\) on the boundary of \([0,2\pi ){\times }[0,2\pi )\). To complete the proof of (ii) let us fix \(\theta _2\in (0,2\pi )\) and consider \(f(\, \cdot \, ,\theta _2)\) as a function of \(\theta _1\). Then (2.4) shows that \(\tfrac{\partial f}{\partial \theta _1}(\theta _1,\theta _2)=0\) if and only if \(\theta _1\in \{\theta _2^{\mathrm{pos}},\theta _2^{\mathrm{neg}}\}\), where
Moreover, upon extending \(f(\, \cdot \, ,\theta _2)\) to an open interval containing \((0,2\pi )\), we get
In particular, from the intermediate value theorem we deduce that \(f(\, \cdot \, ,\theta _2)\) is strictly increasing on \((0,\theta _2^{\mathrm{pos}})\) and strictly decreasing on \((\theta _2^{\mathrm{pos}},\theta _2)\). Since in addition \(f(0,\theta _2)=f(\theta _2,\theta _2)=0\) this implies that \(f(\, \cdot \, ,\theta _2)>0\) on \((0,\theta _2)\). Arguing similarly on the intervals \((\theta _2,\theta _2^{\mathrm{neg}})\) and \((\theta _2^{\mathrm{neg}},2\pi )\) we obtain \(f(\, \cdot \, ,\theta _2)<0\) on \((\theta _2,2\pi )\), which proves (ii). \(\square \)
Remark 2.2
Using the expressions of \(\chi (u,T)\) and \(F_\varepsilon (u,T)\) in (2.2)–(2.3) one can show that \(\chi (u,T)\in [-1,1]\) and \(\chi (u,T)\in \{-1,1\}\) if and only if \(F_\varepsilon (u,T)=0\), i.e., configurations that maximize or minimize \(\chi (\, \cdot \, ,T)\) are at the same time minimizers for \(F_\varepsilon (\, \cdot \, ,T)\). This follows from Lemma 2.1 (i) upon noticing that in (2.2)–(2.3) it is not restrictive to assume that \(\theta (\varepsilon i)=0\), since both \(\chi _\varepsilon \) and \(F_\varepsilon \) are invariant under rotations in u. We observe that also a quantitative version of this property holds. Namely, a continuity argument shows that for every \(\delta >0\) there exists \(C_\delta >0\) such that for every \(u\in \mathcal {SF}_\varepsilon \) and every \(T\in {\mathcal {T}}_\varepsilon ({\mathbb {R}}^2)\) the following implication holds:
Remark 2.3
As a consequence of Lemma 2.1 (ii) one obtains the following characterization of the sign of the chirality. Let \(\theta (\varepsilon j) \in [0,2\pi )\) be the angle between \(u(\varepsilon i)\) and \(u(\varepsilon j)\) and let \(\theta (\varepsilon k) \in [0,2\pi )\) the angle between \(u(\varepsilon i)\) and \(u(\varepsilon k)\). Then \(\chi (u,T)>0\) if and only if \(\theta (\varepsilon j)<\theta (\varepsilon k)\) and \(\chi (u,T)< 0\) if and only if \(\theta (\varepsilon j)>\theta (\varepsilon k)\). In other words, a positive chirality on \(T={{\,\mathrm{conv}\,}}\{\varepsilon i,\varepsilon j,\varepsilon k\}\) corresponds to a counterclockwise ordering of \((u(\varepsilon i), u(\varepsilon j), u(\varepsilon k))\) on \({\mathbb {S}}^1\), while a negative chirality corresponds to a clockwise ordering on \({\mathbb {S}}^1\) (Fig. 2).
On the left: a configuration of vectors with positive chirality which shows the criterion explained in Remark 2.3. On the right: negative chirality
2.4 Statement of the main result
Notice that \(\chi (u)\in L^1(\Omega )\). We then extend \(F_\varepsilon \) to \(L^1(\Omega )\) by setting
with the convention \(\inf \emptyset =+\infty \).
Remark 2.4
If \(\chi \in L^1(\Omega )\) is such that \(\chi =\chi (u)\) for some \(u\in \mathcal {SF}_\varepsilon \), then the infimum in (2.8) is actually a minimum.
To state the main theorem we need to introduce two ground states, that we name \(u_\varepsilon ^{\mathrm{pos}},u_\varepsilon ^{\mathrm{neg}}\in \mathcal {SF}_\varepsilon \) which have a uniform chirality equal to \(+1\) and \(-1\), respectively. They are given by
for every \(x\in {\mathcal {L}}_\varepsilon \). We also set \(u^\mathrm {pos}:=u_1^\mathrm {pos}\), \(u^\mathrm {neg}:=u_1^\mathrm {neg}\). The ground states \(u^\mathrm {pos}\) and \(u^\mathrm {neg}\) will be used as boundary conditions on the discrete boundary of the square \(Q^\nu \) given by (see Fig. 3)
Theorem 2.5
The energies \({\mathscr {F}}_\varepsilon :L^1(\Omega )\rightarrow [0,+\infty ]\) defined by (2.8) \(\Gamma \)-converge in the strong \(L^1(\Omega )\)-topology to the functional \({\mathscr {F}} :L^1(\Omega )\rightarrow [0,+\infty ]\) given by
where \(\varphi :{\mathbb {S}}^1\rightarrow [0,+\infty )\) is defined by
The proof of Theorem 2.5 will be carried out in Sections 4 and 5 , where we prove separately the asymptotic lower bound (Proposition 4.1) and the asymptotic upper bound (Proposition 5.1), respectively.
Remark 2.6
By standard arguments in the analysis of asymptotic cell formulas (see e.g. [4, Proposition 4.6]) one can show that the limit in (2.11) actually exists, so that \(\varphi \) is well defined. Note that, by the symmetries of the interaction energies, there holds \(\varphi (-\nu )=\varphi (\nu )\). Moreover, one can show (cf. [4, Proposition 4.7]) that the one-homogeneous extension of \(\varphi \) is convex, hence continuous.
Remark 2.7
By a scaling argument we note that for all \(\rho >0\) there holds
where \(\partial _\varepsilon ^\pm Q_\rho ^\nu \) are defined according to (2.9) with \(Q_\rho ^\nu \) in place of \(Q^\nu \).
3 Compactness
Proposition 3.1
Let \((u_\varepsilon )\) be a sequence of spin fields \(u_\varepsilon \in \mathcal {SF}_\varepsilon \) satisfying
Then there exists \(\chi \in BV(\Omega ;\{-1,1\})\) such that up to subsequences \(\chi (u_\varepsilon )\rightarrow \chi \) in \(L^1(\Omega )\).
To prove Proposition 3.1 we first estimate from below the energy of a spin field u on two neighboring triangles where \(\chi (u)\) changes sign. Given a triangle \(T\in {\mathcal {T}}_{\varepsilon }({\mathbb {R}}^{2})\) we introduce the class \({\mathcal {N}}_\varepsilon (T)\) of its neighboring triangles, namely those triangles in \({\mathcal {T}}_{\varepsilon }({\mathbb {R}}^{2})\) that share a side with T. More precisely, we define
Lemma 3.2
Let \(u\in \mathcal {SF}_\varepsilon \) and suppose that \(T^{\mathrm{pos}}, T^{\mathrm{neg}}\in {\mathcal {T}}_\varepsilon ({\mathbb {R}}^2)\) with \(T^\mathrm {neg}\in {\mathcal {N}}_\varepsilon (T^\mathrm {pos})\) are such that \(\chi (u,T^{\mathrm{pos}})\ge 0\) and \(\chi (u,T^{\mathrm{neg}})\le 0\). Then \(F_\varepsilon (u,T^{\mathrm{pos}}\cup T^{\mathrm{neg}})\ge \tfrac{5}{3}\varepsilon \).
Proof
It is not restrictive to assume that \(T^{\mathrm{pos}}={{\,\mathrm{conv}\,}}\{\varepsilon i,\varepsilon j,\varepsilon k\}\) and \(T^{\mathrm{neg}}={{\,\mathrm{conv}\,}}\{\varepsilon i,\varepsilon j',\varepsilon k\}\) with \(i\in {\mathcal {L}}^1\), \(j,j'\in {\mathcal {L}}^2\) and \(k\in {\mathcal {L}}^3\). Moreover, we can assume that \(u(\varepsilon i)={\hat{e}}_1\), that is, \(\theta (\varepsilon i)=0\) according to the notation in (2.2)–(2.3). Then, using the function \(g:[0,2\pi )\times [0,2\pi )\rightarrow {\mathbb {R}}\) defined in Lemma 2.1, we can rewrite \(F_\varepsilon (u,T^{\mathrm{pos}}\cup T^{\mathrm{neg}})\) as
Moreover, thanks to Lemma 2.1 (ii) the chirality constraint reads \(0\le \theta (\varepsilon j)\le \theta (\varepsilon k)\le \theta (\varepsilon j')\). Thus, the statement is proved if we show that for all \(\theta _1\), \(\theta _2\), \(\theta _3\in [0,2\pi )\) with \(0\le \theta _1\le \theta _2\le \theta _3\) there holds
We first observe that (3.3) trivially holds if \(\theta _2=0\) or \(\theta _2=\pi \). Indeed, if \(\theta _2=0\), then also \(\theta _1=0\), hence \(g(\theta _1,\theta _2)+g(\theta _3,\theta _2)=4+2\cos (\theta _3)\ge 2\), thus (3.3) is satisfied. If, instead, \(\theta _2=\pi \), then a direct computation shows that \(g(\theta _1,\theta _2)+g(\theta _3,\theta _2)= -2\) for every \(\theta _1,\theta _3\in [0,2\pi )\), which directly gives (3.3).
Suppose now that \(\theta _2\in (0,2\pi )\setminus \{\pi \}\) and let us minimize \(g(\, \cdot \, ,\theta _2)\) on the two intervals \([0,\theta _2]\) and \([\theta _2,2\pi )\). As in the proof of Lemma 2.1 we obtain that \(\frac{\partial g}{\partial _{\theta _1}}(\theta _1,\theta _2)=0\) if and only if \(\theta _1\in \{\theta _2^{\mathrm{pos}},\theta _2^{\mathrm{neg}}\}\) with \(\theta _2^{\mathrm{pos}}\), \(\theta _2^{\mathrm{neg}}\) as in (2.6). Moreover, we have
Thus, either \(\theta _2^{\mathrm{pos}}\in (0,\theta _2)\) or \(\theta _2^{\mathrm{neg}}\in (\theta _2,2\pi )\) is a minimizer for \(g(\, \cdot \, ,\theta _2)\), depending on wether \(\theta _2\in (0,\pi )\) or \(\theta _2\in (\pi ,2\pi )\). Suppose first that \(\theta _2\in (\pi ,2\pi )\). Then (3.4) implies that \(g(\, \cdot \, ,\theta _2)\) is minimized in \([0,\theta _2)\) by \(\theta _2^{\mathrm{pos}}\), while in \([\theta _2,2\pi )\) it attains its minimum on the boundary, that is at \(\theta _2\). This yields
for every \(\theta _1\in [0,\theta _2]\) and \(\theta _3\in [\theta _2,2\pi )\). Using the equality \(\cos (\theta _2)=2\cos ^2(\tfrac{\theta _2}{2})-1\), the estimate in (3.5) can be continued via
Since the mapping \(t\mapsto 6t^2+2t-2\) admits its minimum at \(t=-1/6\), from (3.6) we finally deduce that
which is equivalent to (3.3). Eventually, the case \(\theta _2\in (0,\pi )\) follows similarly by exchanging the roles of \(\theta _1\) and \(\theta _3\) and replacing \(\theta _2^\mathrm {pos}\) by \(\theta _2^\mathrm {neg}\). \(\square \)
Based on Lemma 3.2 we now prove Proposition 3.1.
Proof of Proposition 3.1
We divide the proof in two steps. First, we construct a sequence \(({\hat{\chi }}_\varepsilon )\) of auxiliary functions \({\hat{\chi }}_\varepsilon : \Omega \rightarrow \{-1,1\}\) whose level sets \(\{{\hat{\chi }}_\varepsilon =1\}\) have uniformly bounded perimeter. Second, we show that the constructed auxiliary functions are close in \(L^1(\Omega )\) to the original chirality functions \(\chi (u_\varepsilon )\) defined according to (2.1).
Step 1. (Compactness of the auxiliary functions) Let \(\varepsilon >0\) and define \({\hat{\chi }}_\varepsilon : \Omega \rightarrow \{-1,1\}\) by
We claim that for every \(\Omega '\subset \subset \Omega \) we have
Then the uniform bound (3.1) together with [7, Theorem 3.39 and Remark 3.37] yields the existence of a function \(\chi \in BV(\Omega ;\{-1,1\})\) and a subsequence (not relabelled) such that \({\hat{\chi }}_\varepsilon \rightarrow \chi \) in \(L^1(\Omega )\). To prove (3.7) it is convenient to consider the class of triangles
where \({\mathcal {N}}_\varepsilon (T)\) is as in (3.2). Let \(\Omega '\subset \subset \Omega \). By the very definition of \({\hat{\chi }}_\varepsilon \) and of \(\chi (u_\varepsilon )\) we have
provided \(\sqrt{3}\varepsilon <{{\,\mathrm{dist}\,}}(\Omega ', \partial \Omega )\). Estimating the \({\mathcal {H}}^1\)-measure of the latter set in terms of the cardinality of \({\mathcal {T}}_\varepsilon ^\mathrm {pos}\) we thus infer
The last term in (3.8) can be bounded using Lemma 3.2. Indeed, from Lemma 3.2 we deduce that
where the additional factor 3 comes from the fact that each triangle is counted 3 times. Thus, (3.7) follows from (3.8) and (3.9).
Step 2. (Closeness to \(\chi (u_\varepsilon )\)) We claim that for every \(\delta >0\) and every \(\Omega '\subset \subset \Omega \) there holds
i.e., the functions \({\hat{\chi }}_\varepsilon -\chi (u_\varepsilon )\) converge to 0 locally in measure. Since \(\Vert {\hat{\chi }}_\varepsilon -\chi (u_\varepsilon )\Vert _\infty \le 2\), this implies that \(({\hat{\chi }}_\varepsilon -\chi (u_\varepsilon ))\rightarrow 0\) in \(L^1(\Omega )\), which concludes the proof of the Proposition 3.1 thanks to Step 1. It remains to prove the claim (3.10). Let \(\Omega '\subset \subset \Omega \) and \(\delta >0\) and let \(C_\delta \) be given by (2.7). Setting
for \(\varepsilon \) sufficiently small we deduce that
Hence, (3.10) follows from the uniform bound (3.1).
\(\square \)
4 Lower bound
In this section we start proving the main result of our paper, namely Theorem 2.5 by presenting the optimal lower bound estimate on the energy \({\mathscr {F}}_{\varepsilon }\), the technically most demanding part of our contribution. We begin with a blow-up argument that gives us a first asymptotic lower bound.
Proposition 4.1
Let \({\mathscr {F}}_\varepsilon \) be as in (2.8). Then for every \(\chi \in L^1(\Omega )\) we have
where \({\mathscr {F}}\) is given by (2.10) and the \(\Gamma \hbox {-}\liminf \) is with respect to the strong topology in \(L^1(\Omega )\).
Proof
Let \(\chi _\varepsilon \rightarrow \chi \) in \(L^1(\Omega )\). We assume that \(\liminf _{\varepsilon }{\mathscr {F}}_\varepsilon (\chi _\varepsilon ) < +\infty \), otherwise we have nothing to prove. Moreover, upon extracting a (not relabeled) subsequence we can assume the liminf to be a limit and hence \(\sup _\varepsilon {\mathscr {F}}_\varepsilon (\chi _\varepsilon )<+\infty \). In view of Remark 2.4 we can find a sequence of spin fields \(u_\varepsilon \in \mathcal {SF}_\varepsilon \) with \(\chi (u_\varepsilon )=\chi _\varepsilon \) and \({\mathscr {F}}_\varepsilon (\chi _\varepsilon )=F_\varepsilon (u_\varepsilon )\). In particular, \(\sup _\varepsilon F_\varepsilon (u_\varepsilon )<+\infty \). Thus, from Proposition 3.1 we deduce that \(\chi \in BV(\Omega ;\{-1,1\})\). As a consequence, to prove the statement of the proposition it suffices to show that
where \(\varphi \) is as in (2.11). To prove (4.1) we consider the sequence of non-negative finite Radon measures \(\mu _\varepsilon \) given by
where \(\delta _{\varepsilon i}\) denotes the Dirac delta in \(\varepsilon i\). From the condition \(\sup _\varepsilon F_\varepsilon (u_\varepsilon )<+\infty \) it follows that \(\sup _\varepsilon \mu _\varepsilon (\Omega )<+\infty \), hence there exists a non-negative finite Radon measure \(\mu \) such that up to subsequences (not relabeled) \(\mu _\varepsilon \overset{*}{\rightharpoonup }\mu \). By the Radon-Nikodým Theorem the measure \(\mu \) can be decomposed in the sum of two mutually singular non-negative measures as

Then, to establish (4.1) it is sufficient to show that
where \(\nu _\chi (x_0)\) denotes the measure theoretic normal to \(J_{\chi }\) at \(x_0\). To verify (4.2) we choose \(x_0\in J_{\chi }\) satisfying
-
(i)
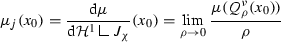 , where we have set \(\nu :=\nu _\chi (x_0)\),
, where we have set \(\nu :=\nu _\chi (x_0)\), -
(ii)
\(\displaystyle \lim _{\rho \rightarrow 0}\frac{1}{\rho ^2}\int \limits _{Q_\rho ^\nu (x_0)\cap H^\nu _+(x_0)}|\chi _\varepsilon (x)-1|\, \mathrm{d}x=0=\lim _{\rho \rightarrow 0}\frac{1}{\rho ^2}\int \limits _{Q_\rho ^\nu (x_0)\cap H^\nu _-(x_0)}|\chi _\varepsilon (x)+1|\, \mathrm{d}x\),
and we notice that (i) and (ii) are satisfied for \({\mathcal {H}}^1\)-a.e. \(x_0\in J_{\chi }\) thanks to the Besicovitch derivation Theorem and the definition of approximate jump point, respectively. Moreover, since \(\mu \) is a finite Radon measure, we can choose a sequence \(\rho _n\rightarrow 0\) along which \(\mu (\partial Q_{\rho _n}^\nu (x_0)) = 0\). Thanks to [7, Proposition 1.62 (a)], the convergence \(\mu _\varepsilon \overset{*}{\rightharpoonup }\mu \) together with (i) implies that
where the last inequality follows from the positivity of the energy. Notice that for every \(n\in {\mathbb {N}}\) there exist sequences \((\rho _n^\varepsilon )\) and \((x_0^\varepsilon )\) with \(\lim _\varepsilon \rho _n^\varepsilon =\rho _n\), \(\lim _\varepsilon x_0^\varepsilon =x_0\), \(x_0^\varepsilon \in {\mathcal {L}}_\varepsilon \), and
In fact, if we write \(x_0\) in terms of the basis \({\hat{e}}_1,{\hat{e}}_2\) as \(x_0=a_1{\hat{e}}_1+a_2{\hat{e}}_2\) for some \(a_1,a_2\in {\mathbb {R}}\), we obtain the required sequence \((x_0^\varepsilon )\) by setting
Then, upon noticing that \(|x_0^\varepsilon -x_0|\le 2\varepsilon \), it suffices to set \(\rho _n^\varepsilon :=\rho _n-4\varepsilon \). Indeed, if \(T\in {\mathcal {T}}_\varepsilon (Q_{\rho _n^\varepsilon }^\nu (x_0^\varepsilon ))\), by definition we have that for every \(x\in T\)
so that for any \(x\in T\) there also holds
and similarly \(|\langle x-x_0,\nu ^\perp \rangle |<\rho _n/2\), hence \(T\in {\mathcal {T}}_\varepsilon (Q_{\rho _n}^\nu (x_0))\). As a consequence, (4.4) holds true. In particular, we obtain the following estimate
where we have set \(\sigma _n^\varepsilon :=\varepsilon /\rho _n^\varepsilon \) and \(v_{\varepsilon ,n}(z):=u_\varepsilon (x_0^\varepsilon +\rho _n^\varepsilon z)\) for every \(z\in {\mathcal {L}}_{\sigma _n^\varepsilon }\). Let \(\chi _\nu :{\mathbb {R}}^2\rightarrow \{-1,1\}\) be given by
Then (ii) ensures that \(\chi (v_{\varepsilon ,n})\rightarrow \chi _\nu \) in \(L^1(Q^\nu )\) as first \(\varepsilon \rightarrow 0\) and then \(n\rightarrow +\infty \). Thus, gathering (4.3)–(4.5) and applying a diagonal argument we find a sequence \(\sigma _m:=\varepsilon _m/\rho _{n_m}\) converging to 0 as \(m\rightarrow +\infty \) such that for \(v_m:=v_{\varepsilon _m,n_m}\) there holds \(\chi (v_m)\rightarrow \chi _\nu \) in \(L^1(Q^\nu )\) and
For \(\ell ,h>0\) let us finally introduce the minimization problem
so that the sequence \((v_m)\) is admissible for \(\psi (1,1,\nu )\). Then (4.2) follows from Proposition 4.2 below, concluding the proof of Proposition 4.1. \(\square \)
Proposition 4.2
Let \(\psi \) be the function defined in (4.6). Then \(\psi (1,1,\nu )\ge \varphi (\nu )\) for every \(\nu \in {\mathbb {S}}^1\).
To prove Proposition 4.2 it is necessary to modify admissible sequences for the infimum problem defining \(\psi (1,1,\nu )\) in such a way that they satisfy the boundary conditions required in the minimum problem defining \(\varphi (\nu )\), without essentially increasing the energy. This will be done by a careful interpolation procedure based on several auxiliary results and estimates that we prefer to state in separate lemmas below. As a first step towards the proof of Proposition 4.2 we show that \(\psi (\ell ,h,\nu )\) is independent of \(\ell \) and h, which in turn will allow us to conclude that the energy of admissible functions for \(\psi (1,1,\nu )\) concentrates close to the line segment \(L^\nu \) (see Lemma 4.4 below).
Lemma 4.3
Let \(\psi :(0,+\infty ){\times }(0,+\infty ){\times }{\mathbb {S}}^1\rightarrow [0,+\infty ]\) be given by (4.6); then \(\psi (\cdot ,\cdot ,\nu )\) is independent of \(\ell ,h\) for every \(\nu \in {\mathbb {S}}^1\).
Proof
Let \(\nu \in {\mathbb {S}}^1\) be fixed. To show that \(\psi (\cdot ,\cdot ,\nu )\) does not depend on \(\ell ,h\) it suffices to show that for every \(\ell ,h,\lambda >0\) the following identities hold
Let us fix \(\ell ,h>0\). We first observe that
since \(F_\varepsilon \) is increasing as a set function. The proof of (4.7) is now divided into three steps.
Step 1. \(\psi \) is invariant under dilations, i.e.,
Let \((u_\varepsilon )\) be any sequence of spin fields \(u_\varepsilon :{\mathcal {L}}_\varepsilon \rightarrow {\mathbb {S}}^1\) with \(\chi (u_\varepsilon )\rightarrow \chi _{\nu }\) in \(L^1(R_{\lambda \ell ,\lambda h}^\nu )\). We define the rescaled functions \(v_\varepsilon :{\mathcal {L}}_{\varepsilon /\lambda }\rightarrow {\mathbb {S}}^1\) by setting \(v_\varepsilon (z):=u_\varepsilon (\lambda z)\) for every \(z\in {\mathcal {L}}_{\varepsilon /\lambda }\). Then \(\chi (v_\varepsilon )\rightarrow \chi _\nu \) in \(L^1(R_{\ell ,h}^{\nu })\) and
Setting \(\eta :=\varepsilon /\lambda \rightarrow 0\) as \(\varepsilon \rightarrow 0\) and passing to the infimum over all admissible sequences \((u_\varepsilon )\) we deduce that
The opposite inequality and hence (4.10) follow by observing that
Note that thanks to (4.10) it suffices to show the first equality in (4.7). In fact, if the first equality in (4.7) is true, from (4.10) we directly deduce that
Step 2. We continue establishing the first equality in (4.7) by showing that
For \(N\in {\mathbb {N}}\) fixed let \((u_\varepsilon )\) be a sequence of spin fields satisfying \(\chi (u_\varepsilon )\rightarrow \chi _\nu \) in \(L^1(R_{N\ell ,h}^\nu )\). We subdivide the rectangle \(R_{N\ell ,h}^\nu \) in N open rectangles of the form
Notice that \(x\in R_{\ell ,h}^\nu (x_m)\) if and only if
and therefore \(R_{\ell ,h}^\nu (x_m)\subset R_{N\ell ,h}^\nu \) for all \(m \in \{0,\ldots ,N-1\}\). By choosing \(m_0\in \{0,\ldots ,N-1\}\) such that \(F_\varepsilon (u_\varepsilon ,R_{\ell ,h}^\nu (x_{m_0}))\le F_\varepsilon (u_\varepsilon ,R_{\ell ,h}^\nu (x_m))\) for every \(m\in \{0,\ldots ,N-1\}\) we obtain the estimate
We now define a suitable shifted version of \(u_\varepsilon \) whose energy is concentrated in a rectangle centered at zero. To this end, as in the proof of Proposition 4.1 it is convenient to write the vector \(\nu ^\perp \) in terms of the basis \(\{{\hat{e}}_1,{\hat{e}}_2\}\) as \(\nu ^\perp =a_1{\hat{e}}_1+a_2{\hat{e}}_2\) for some \(a_1,a_2\in {\mathbb {R}}\) and to introduce the vector \(x_{m_0}^\varepsilon \in {\mathcal {L}}_\varepsilon \) given by
We then define spin fields \(v_\varepsilon :{\mathcal {L}}_\varepsilon \rightarrow {\mathbb {S}}^1\) by setting \(v_\varepsilon (z):=u_\varepsilon (z+x_{m_0}^\varepsilon )\). As in the proof of Proposition 4.1 we notice that \(|x_{m_0}^\varepsilon -x_{m_0}|\le 2\varepsilon \), \(\chi (v_\varepsilon )\rightarrow \chi _\nu \) in \(L^1(R_{\ell ,h}^\nu )\) and \(R_{\ell -4\varepsilon ,h-4\varepsilon }^\nu (x_{m_0}^\varepsilon )\subset R_{\ell ,h}^\nu (x_{m_0})\). Let us fix \(\lambda \in (0,1)\) and \(\varepsilon _\lambda >0\) sufficiently small such that \(\ell -4\varepsilon _\lambda >\lambda \ell \), \(h-4\varepsilon _\lambda >\lambda h\). Then for every \(\varepsilon \in (0,\varepsilon _\lambda )\) there holds \({\mathcal {T}}_\varepsilon (R_{\lambda \ell ,\lambda h}^\nu (x_{m_0}^\varepsilon ))\subset {\mathcal {T}}_\varepsilon (R_{\ell ,h}^\nu (x_{m_0}))\), hence
Moreover, since \(v_\varepsilon \) is admissible for \(\psi (\lambda \ell ,\lambda h,\nu )\), we have
Combining (4.10) in Step 1 with (4.12)–(4.13), in view of the arbitrariness of \(u_\varepsilon \) we finally obtain
Thus, by letting \(\lambda \rightarrow 1\) we deduce that \(\psi (\ell ,h,\nu )\le \psi (N\ell ,h,\nu )\). Finally, (4.11) follows from (4.10) and (4.9) by observing that
Step 3. We prove the first equality in (4.7). Suppose first that \(\lambda \in (0,+\infty )\cap {\mathbb {Q}}\). Then \(\lambda =N/M\) for some \(N,M\in {\mathbb {N}}\), hence applying twice (4.11) yields
Suppose now that \(\lambda \in (0,+\infty )\) and let \((\lambda _n)\subset (0,+\infty )\cap {\mathbb {Q}}\) with \(\lambda _n\rightarrow \lambda \) as \(n\rightarrow +\infty \), \(\lambda _n>\lambda \) for every \(n\in {\mathbb {N}}\). Thanks to (4.10) and (4.14) we deduce that
where the last inequality follows from (4.8), since \(\lambda _n/\lambda >1\). To prove the opposite inequality it suffices to take a sequence \((\lambda _n)\subset (0,+\infty )\cap {\mathbb {Q}}\) converging to \(\lambda \) with \(\lambda _n<\lambda \). Then, arguing as before and now applying (4.8) we obtain
hence equality follows.
\(\square \)
On account of Lemma 4.3 we show that for a sequence \((u_\varepsilon )\) realizing the infimum in the definition of \(\psi (1,1,\nu )\) the energy concentrates close to the line \(L^\nu \). As a consequence, we obtain that outside a small neighborhood of \(L^\nu \) there exists a suitable strip on which the energy is of order \(o(\varepsilon )\). To be more precise, for fixed \(\nu \in {\mathbb {S}}^1\), \(\delta >0\), and every \(\varepsilon >0\) we introduce the class \({\mathscr {S}}_{\varepsilon ,\delta }^\nu \) of strips
We denote the elements of \({\mathscr {S}}_{\varepsilon ,\delta }^\nu \) by \(S_{\varepsilon ,r}\) (see Fig. 4). Then the following result holds true.
Lemma 4.4
Let \(\nu \in {\mathbb {S}}^1\) and let \((u_\varepsilon )\) be a sequence such that \(\chi (u_\varepsilon )\rightarrow \chi _\nu \) in \(L^1(Q^\nu )\) and \(F_\varepsilon (u_\varepsilon ,Q^\nu )\rightarrow \psi (1,1,\nu )\). Then for every \(\delta >0\) there exists a sequence \(\sigma _\varepsilon \rightarrow 0\) (depending on \(\delta \)) and a strip \(S_\varepsilon =S_{\varepsilon ,r_\varepsilon }\in {\mathscr {S}}_{\varepsilon ,\delta }^\nu \) such that
Proof
Let \(\nu \in {\mathbb {S}}^1\) and \((u_\varepsilon )\) be as in the statement and let \(\delta >0\) be fixed. For every Borel set \(A\subset Q^\nu \) set
We consider for \(\varepsilon \) small enough the family of pairwise disjoint strips \(S_{\varepsilon ,r_\varepsilon ^m}\in {\mathscr {S}}_{\varepsilon ,\delta }^\nu \) with \(r_\varepsilon ^m=1-3\delta +12m\varepsilon \) and \(m\in \{0,\ldots ,\lfloor \tfrac{\delta }{12\varepsilon }\rfloor -1\}\) and we notice that
This implies in particular that
Averaging over \(m\in \{0,\dots ,\lfloor \tfrac{\delta }{12\varepsilon }\rfloor -1\}\) we thus find \(m(\varepsilon )\) such that the strip \(S_{\varepsilon ,r_\varepsilon ^{m(\varepsilon )}}\) satisfies
Notice that \(F_\varepsilon (u_\varepsilon ,Q^\nu \setminus {\overline{R}}_{1,\delta }^\nu )\rightarrow 0\) as \(\varepsilon \rightarrow 0\). In fact, Lemma 4.3 together with the choice of \((u_\varepsilon )\) yields
from which we readily deduce that \(F_\varepsilon (u_\varepsilon ,R_{1,\delta }^\nu )\rightarrow \psi (1,1,\nu )\) as \(\varepsilon \rightarrow 0\), hence
Thus, in view of (4.17), it suffices to set \(\sigma _\varepsilon :=\tfrac{13}{\delta }(F_\varepsilon (u_\varepsilon ,Q^\nu \setminus {\overline{R}}_{1,\delta }^\nu )+\Vert \chi (u_\varepsilon )-\chi _\nu \Vert _{L^1(Q^\nu )})\) and \(r_\varepsilon :=r_\varepsilon ^{m(\varepsilon )}\) to find the required strip \(S_{\varepsilon , r_\varepsilon }\in {\mathscr {S}}_{\varepsilon ,\delta }^\nu \) satisfying (4.16). \(\square \)
We are now in a position to start with the interpolation procedure mentioned before. The final interpolation procedure will be based on a one-dimensional construction that we introduce below.
4.1 One-dimensional interpolation
To define the one-dimensional interpolation we consider slices in the triangular lattice. To this end, let \({\hat{e}}_1\), \({\hat{e}}_2\), and \({\hat{e}}_3\) be as in Section 2.2. Given \(\alpha \in \{1,2,3\}\) we consider the orthogonal vector \({\hat{e}}_\alpha ^\perp \) to \({\hat{e}}_\alpha \) and we define the slice in the direction \({\hat{e}}_\alpha \) by
Given \(z \in {\mathbb {Z}}\), we define
Finally, for every \(\varepsilon \) we set
We shall define the one-dimensional interpolation in a slice \(\Sigma ^{\alpha }\) starting from a triangle \(T_0\in {\mathcal {T}}({\mathbb {R}}^2)\) such that \(T_0 \subset \Sigma ^{\alpha }\). Let us denote by \(i_0 \in {\mathcal {L}}^1\), \(j_0 \in {\mathcal {L}}^2\), \(k_0 \in {\mathcal {L}}^3\) the vertices of \(T_0\). Note that \(\langle i_0, {\hat{e}}_\alpha ^\perp \rangle , \langle j_0, {\hat{e}}_\alpha ^\perp \rangle , \langle k_0, {\hat{e}}_\alpha ^\perp \rangle \in \{0,\tfrac{\sqrt{3}}{2}\}\). We define the lattice points \(i_h \in {\mathcal {L}}^1\), \(j_h \in {\mathcal {L}}^2\), \(k_h\in {\mathcal {L}}^3\) and the triangle \(T_h\) with the following recursive formula: we set \(\tau (0) := 1\), \(\tau (\tfrac{\sqrt{3}}{2}) := -1\) and for \(h\in {\mathbb {N}}\)
(see Fig. 5). Observe that \(\tau (\langle i_{h+1} , {\hat{e}}_\alpha ^\perp \rangle ) = -\tau (\langle i_h , {\hat{e}}_\alpha ^\perp \rangle )\), the analogous equality being true also for \(j_h\) and \(k_h\). Moreover, \(T_{2h} = T_0 + 3 h {\hat{e}}_\alpha \).
We define the half-slice \(\Sigma ^\alpha (T_0)\) of the lattice \({\mathcal {L}}\) starting from \(T_0\) by
Given \(u:{\mathcal {L}}\rightarrow {\mathbb {S}}^1\) and \(N,m\in {\mathbb {N}}\), we now define in the half-slice \(\Sigma ^\alpha (T_0)\) a one-parameter family (parametrized by m) of spin fields which coincides with u on \(T_0\) and with the fixed ground state \(u^\mathrm {pos}\) on \(T_h\) for \(h \ge N\). We construct the interpolation in such a way that the configuration of spins rotates a fixed amount of times by \(2\pi \). To make the construction precise, we first say that the three angles \(\theta (i_0)\in {\mathbb {R}}\) (not necessarily in \([0,2\pi )\)), \(\theta (j_0)\in [\theta (i_0)-\pi ,\theta (i_0)+\pi )\) and \(\theta (k_0)\in [\theta (j_0)-\pi ,\theta (j_0)+\pi )\) represent a lifting of u in \(T_{0}\) if \(u(i_0)=\exp (\iota \theta (i_0))\), \(u(j_0)=\exp (\iota \theta (j_0))\) and \(u(k_0)=\exp (\iota \theta (k_0))\). We then define the interpolated angles \(\theta (i_h),\theta (j_h),\theta (k_h)\) for \(h=0,\dots ,N\) by
and \(\theta (i_h) := 2\pi m\), \(\theta (j_h) := 2\pi m+\frac{2\pi }{3}\), \(\theta (k_h) := 2\pi m+\frac{4\pi }{3}\) for \(h \ge N+1\) (see Fig. 5). Eventually, we define \(u^{N,m}:{\mathcal {L}}\cap \Sigma ^\alpha (T_0)\rightarrow {\mathbb {S}}^1\) by setting
Note that \(u^{N,m} = u^\mathrm {pos}\) on \(T_h\) for \(h \ge N\).
In the next lemma we estimate the energy of the interpolation on \(\Sigma ^\alpha (T_0)\) in terms of the energy on the initial triangle \(T_0\) plus an error depending on the number of steps N and on m. We assume that the configuration of spins in the initial triangle is sufficiently close to a ground state with chirality 1 (not necessarily \(u^\mathrm {pos}\)).
Lemma 4.5
Let \(T_0\in {\mathcal {T}}({\mathbb {R}}^2)\) be a triangle of vertices \(i_{0}\in {\mathcal {L}}^{1}\), \(j_{0}\in {\mathcal {L}}^{2}\), and \(k_{0}\in {\mathcal {L}}^{3}\). Let \(u:{\mathcal {L}}\rightarrow {\mathbb {S}}^1\) and let \(\theta (i_0) \in {\mathbb {R}}\), \(\theta (j_0) \in [\theta (i_0) - \pi , \theta (i_0) + \pi )\) and \(\theta (k_0) \in [\theta (j_0)-\pi , \theta (j_0)+\pi )\) be three angles representing a lifting of u in \(T_{0}\) satisfying
Let \(N,m \in {\mathbb {N}}\) and assume that
Let \(u^{N,m}\) be the interpolation on \(\Sigma ^\alpha (T_0)\) defined according to (4.22). Then there exists a constant \(C>0\) independent of N and m such that
Proof
It is not restrictive to assume that \(j_0-i_0={\hat{e}}_\alpha \) as in Fig. 5. We shall estimate each of the terms in the sum
where we used that for \(h \ge N\) we have that
being \(u^\mathrm {pos}\) a ground state. Adopting the notation for the angles used in the construction in (4.22), we recast the energy in the first term of the sum as
Note that, by (4.21) and (4.23),
By Taylor’s formula, there exists \(\zeta \in [\phi ,2\pi /3]\) such that \(1 + 2\cos (\phi ) = - \sqrt{3} (\phi -\frac{2\pi }{3}) + \frac{1}{2} (\phi -\frac{2\pi }{3})^2 + \frac{1}{3} \sin (\zeta ) (\phi -\frac{2\pi }{3})^3\). As a result we obtain the estimates
Analogously,
Then by (4.26), (4.27), and the two previous estimates we infer that
This proves that
Let us now consider the second term in the sum in the right-hand side of (4.25). For every \(h=0,\dots ,N-1\) we have
The first term is estimated as via \(2F_1(u,T_0)\). As for \(|u^{N,m}(i_{h+1}) - u^{N,m}(i_h)|^2\), by (4.21) we have that
Using the fact that \(1-\cos (t)\le \tfrac{t^2}{2}\) we deduce
since \(|\theta (i_0)| \le 2 \pi m\). Hence
The third term in the right-hand side in (4.25) is treated analogously using the inequality
where we used (4.23) to get that \(|\theta (k_0)|+\frac{4\pi }{3} \le |\theta (i_0)|+\frac{1}{2}+\frac{4\pi }{3} \le |\theta (i_0)| + 2 \pi \le 2 \pi (m+1)\). \(\square \)
We are now in a position to prove Proposition 4.2 and thus conclude the proof of the lower bound in Proposition 4.1.
Proof of Proposition 4.2
For the reader’s convenience, we recall here the definitions of \(\varphi (\nu )\) and \(\psi (1,1,\nu )\):
Let us fix a sequence \((u_\varepsilon )\) such that \(\chi (u_\varepsilon )\rightarrow \chi _\nu \) in \(L^1(Q^\nu )\) and \(F_\varepsilon (u_\varepsilon ,Q^\nu ) \rightarrow \psi (1,1,\nu )\). The aim of this proof is to define a modification \({{\widetilde{u}}}_\varepsilon \) of \(u_\varepsilon \) such that
This allows us to conclude that \(\varphi (\nu ) \le \psi (1,1,\nu )\).
The construction of the modified sequence \(({\widetilde{u}}_\varepsilon )\) is divided in several steps.
Step 1. (Choosing a strip with low energy). We begin the construction by exploiting the property that the energy of \((u_\varepsilon )\) concentrates close to the interface \(Q^\nu \cap L^\nu \) in order to choose a strip with low energy. Given \(\delta \in (0,\tfrac{1}{3})\), we consider the family of strips \({\mathscr {S}}^\nu _{\varepsilon ,\delta }\) defined in (4.15) and we apply Lemma 4.4 to deduce the existence of a strip \(S_\varepsilon = S_{\varepsilon ,r_\varepsilon } = Q_{r_\varepsilon +12\varepsilon }^\nu \setminus \left( {\overline{Q}}_{r_\varepsilon }^\nu \cup {\overline{R}}_{1,\delta }^\nu \right) \in {\mathscr {S}}^\nu _{\varepsilon ,\delta }\) such that
where \(\sigma _\varepsilon \rightarrow 0\). The modification \({\widetilde{u}}_\varepsilon \) of \(u_\varepsilon \) will coincide with \(u^\mathrm {pos}_\varepsilon \) and \(u^\mathrm {neg}_\varepsilon \) in \(Q^{\nu } \setminus ({{\overline{Q}}}^\nu _{1-\delta } \cup {{\overline{R}}}^{\nu }_{1,\delta })\) (notice that the square \(Q^\nu _{1-\delta }\) contains the closure of \(S_\varepsilon \), cf. (4.15)). In the triangles contained in \(S_\varepsilon \) the energy is low and thus \(u_\varepsilon \) is close to ground states, yet not necessarily \(u_\varepsilon ^\mathrm {pos}\) or \(u_\varepsilon ^\mathrm {neg}\). There \({\widetilde{u}}_\varepsilon \) will start to interpolate from the configuration \(u_\varepsilon \) until it reaches the fixed ground state \(u_\varepsilon ^\mathrm {pos}\) or \(u_\varepsilon ^\mathrm {neg}\) close to the boundary.
We shall describe in detail how to define \({\widetilde{u}}_\varepsilon \) in the top part of the cube given by \(Q_+^\nu = Q^\nu \cap \{x :\langle x, \nu \rangle > 0\}\), where the chirality of \(u_\varepsilon \) converges to 1. The construction in \(Q_-^\nu \cap \{x :\langle x, \nu \rangle < 0\}\) is completely analogous.
Step 2. (Choosing triangles with low energy). We show here how to choose the triangles with low energy where to start the modification of \(u_\varepsilon \). Let us consider the line
which cuts in two the top part of the strip given by the rectangle
We describe now how to start the modification in \(S_\varepsilon ^{\mathrm {top}}\). The modification in the other parts
cf. Figure 6, will be only sketched since it is completely analogous.
We consider now the slices \((\Sigma ^{\alpha ,z}_\varepsilon )_{z \in {\mathbb {Z}}}\) of the \(\varepsilon \)-triangular lattice defined in (4.18). We choose \(\alpha \in \{1,2,3\}\) such that \(|\langle {\hat{e}}_\alpha , \nu \rangle | \ge \frac{\sqrt{3}}{2}\), namely the best approximation of \(\nu \) in the set \(\{{\hat{e}}_1,{\hat{e}}_2,{\hat{e}}_3\}\). Equivalently, \(|\langle {\hat{e}}_\alpha , \nu ^\perp \rangle | \le \frac{1}{2}\), where \(\nu ^\perp \) is the direction of \(L_\varepsilon \). (For \(S^{\mathrm {right}}_\varepsilon \) and \(S^{\mathrm {left}}_\varepsilon \) we consider a different direction, namely \(\beta \in \{1,2,3\}\) such that \(|\langle {\hat{e}}_\beta , \nu ^\perp \rangle | \ge \frac{\sqrt{3}}{2}\).)
We can find a chain of closed triangles which intersect \(L_\varepsilon \) such that each slice in the direction \({\hat{e}}_\alpha \) contains only one triangle of the chain. Specifically, there exist \((T_z)_{z \in {\mathbb {Z}}}\), satisfying
for every \(z \in {\mathbb {Z}}\), cf. Fig. 7. We prove this statement in Lemma 4.6 below, since the geometric argument is irrelevant for the present discussion.
The modification of \(u_\varepsilon \) starts in the triangles \(T_z\) of the chain contained in \(S_\varepsilon ^{\mathrm {top}}\). For this reason it is convenient to consider
For future purposes we observe that
for some positive constant \(C_1\) and for \(\varepsilon \) small enough.
Step 3. (Estimating the maximal winding number). The energy regime we are working in does not rule out the possibility that inside the strip \(S_\varepsilon \) the configuration of spin field displays global rotations. However, the bound of the energy in \(S_\varepsilon \) allows us to estimate the maximal number of complete turns of \(2\pi \). To present precisely the estimate, we define in the triangles chosen in Step 2 the liftings \(\theta _\varepsilon \in {\mathbb {R}}\) of \(u_\varepsilon \) according to the following recursive argument. Given \(z \in {\mathcal {Z}}^{\mathrm {top}}_\varepsilon \) we denote by \(i_z \in {\mathcal {L}}^1\), \(j_z \in {\mathcal {L}}^2\), \(k_z \in {\mathcal {L}}^3\) the points in the sublattices such that \(\varepsilon i_z, \varepsilon j_z, \varepsilon k_z\) are the vertices of the triangle \(T_z\) (some points might have multiple labels). We now define recursively angles \(\theta _\varepsilon (\varepsilon i_z), \theta _\varepsilon (\varepsilon j_z), \theta _\varepsilon (\varepsilon k_z)\) in suitably chosen intervals of length \(2\pi \) satisfying \(u_\varepsilon (\varepsilon i_{z}) = \exp \left( \iota \theta _\varepsilon (\varepsilon i_{z})\right) , u_\varepsilon (\varepsilon j_{z}) = \exp \left( \iota \theta _\varepsilon (\varepsilon j_{z})\right) , u_\varepsilon (\varepsilon k_{z}) = \exp \left( \iota \theta _\varepsilon (\varepsilon k_{z})\right) \) as follows. We choose
The choice of \(\theta _\varepsilon (\varepsilon j_z)\) and \(\theta _\varepsilon (\varepsilon k_z)\) is made according to the same recursive procedure above, but taking as starting point (instead of \(\theta _\varepsilon (\varepsilon i_{z_0})\)) the angles \(\theta _\varepsilon (\varepsilon j_{z_0})\) and \(\theta _\varepsilon (\varepsilon k_{z_0})\), respectively. We claim that
for some positive constant \(C_2\). To prove the claim, let us fix \(z_* \in {\mathcal {Z}}^{\mathrm {top}}_\varepsilon \), \(z_* \ge z_0\). Note that \(z_* - z_0 \le \frac{C_1}{\varepsilon }\) by (4.33). Jensen’s inequality implies that
for some positive constants C, where we used the fact that \(1 - \cos (\phi ) \ge \frac{1}{12} \phi ^2\) for every \(|\phi | \le \pi \). We start observing that the regular hexagon \(H_z\) containing \(T_z\) and \(T_{z+1}\) is contained in \(S_\varepsilon \). Indeed, let \(x \in H_z\) and let \(y \in T_z \cap L_\varepsilon \subset S_\varepsilon ^\mathrm {top}\). Then \({{\,\mathrm{dist}\,}}(x,L_\varepsilon ) \le |x - y| \le {{\,\mathrm{diam}\,}}H_z = 2 \varepsilon < 3 \varepsilon \). Hence, cf. (4.31), \(x \in (L_\varepsilon + B_{3\varepsilon }(0)) \cap R^\nu _{r_\varepsilon + 6 \varepsilon ,1} \subset S_\varepsilon \). Let us show that
Indeed, if \(T_z \cap T_{z+1} = \{\varepsilon i_z\} = \{\varepsilon i_{z+1}\}\), then \(|u_\varepsilon (\varepsilon i_{z+1}) - u_\varepsilon (\varepsilon i_{z})|^2 = 0\); if \(T_z \cap T_{z+1} = \{\varepsilon j_z\} = \{\varepsilon j_{z+1}\}\) (and analogously if \(T_z \cap T_{z+1} = \{\varepsilon k_z\} = \{\varepsilon k_{z+1}\}\)), then we let \(T'\) be the third triangle in \({{\,\mathrm{conv}\,}}\{T_z, T_{z+1}\}\). The triangle \(T'\) is either \({{\,\mathrm{conv}\,}}\{\varepsilon i_z, \varepsilon j_z, \varepsilon k_{z+1}\}\) or \({{\,\mathrm{conv}\,}}\{\varepsilon i_{z+1}, \varepsilon j_z, \varepsilon k_z\}\) and is always contained in \(H_z\), see Fig. 8. Letting \(\varepsilon k\) be its vertex in \({\mathcal {L}}^3_\varepsilon \) (either \(\varepsilon k_z\) or \(\varepsilon k_{z+1}\)) we have that
Then we estimate the last sum in (4.35) using (4.36) by
for some positive constant C. In conclusion, by (4.35) we have that
Arguing in an analogous way for \(|\theta _\varepsilon (\varepsilon j_{z_*}) - \theta _\varepsilon (\varepsilon j_{z_0})|\) and \(|\theta _\varepsilon (\varepsilon k_{z_*}) - \theta _\varepsilon (\varepsilon k_{z_0})|\), we conclude the proof of the claim (4.34).
We consider the bound on the maximal winding number given by
where \(\lceil \, C_2 \sqrt{\frac{\sigma _\varepsilon }{\varepsilon }} \, \rceil \) is the smallest natural number grater than or equal to \( C_2 \sqrt{\frac{\sigma _\varepsilon }{\varepsilon }}\) and \(C_2\) is the constant given in (4.34).
Step 4. (Modification on slices). We define the modification on the slices \(\Sigma ^{\alpha ,z}_\varepsilon \) starting from triangles \(T_z\) with \(z \in {\mathcal {Z}}^{\mathrm {top}}_\varepsilon \) by reproducing the construction in Lemma 4.5. Here we make precise the choice of the parameters for this construction and the notation. Let us assume, without loss of generality, that \(\langle {\hat{e}}_\alpha , \nu \rangle \ge \frac{\sqrt{3}}{2}\) (if, instead, \(\langle {\hat{e}}_\alpha , \nu \rangle \le - \frac{\sqrt{3}}{2}\) we work with \(- {\hat{e}}_\alpha \)). For \(z\in {\mathcal {Z}}^{\mathrm {top}}_\varepsilon \) we let \(i_z^0 := i_z \in {\mathcal {L}}^1\), \(j_z^0 := j_z \in {\mathcal {L}}^2\), \(k_z^0 := k_z \in {\mathcal {L}}^3\) where \(\varepsilon i_z\), \(\varepsilon j_z\), \(\varepsilon k_z\) are the vertices of \(T_z\). As in (4.19), we define the lattice points \(i_z^h \in {\mathcal {L}}^1\), \(j_z^h \in {\mathcal {L}}^2\), \(k_z^h\in {\mathcal {L}}^3\) and the triangle \(T_z^h\) with the following recursive formula: for \(h\in {\mathbb {N}}\) we set
where \(\tau (0) := 1\), \(\tau (\tfrac{\sqrt{3}}{2}) := -1\). As in (4.20), we define the half-slice \(\Sigma ^{\alpha ,z}_\varepsilon (T_z)\) of the lattice \({\mathcal {L}}_\varepsilon \) starting from \(T_z\) by \(\Sigma ^{\alpha ,z}_\varepsilon (T_z) :={{\,\mathrm{conv}\,}}\{T_z^h :h \in {\mathbb {N}}\}\).
Number of interpolation steps. The number of interpolation steps will be defined by finding the first shifted triangle \(T_{z_0}^{2 h}\) in the half-slice \(\Sigma ^{\alpha ,z_0}_\varepsilon (T_{z_0})\) that is well contained in \(R^\nu _{\infty ,1-\delta } \setminus {{\overline{R}}}^{\nu }_{\infty , 1-2\delta }\). Specifically, we define
Given another \(z \in {\mathcal {Z}}^{\mathrm {top}}_\varepsilon \), we have that
Indeed, let \(y = y_0 + 3\varepsilon \frac{N_\varepsilon }{2} {\hat{e}}_\alpha \in T_{z}^{N_\varepsilon }\) with \(y_0 \in T_z\). Let \(x_0 \in T_{z_0} \cap L_\varepsilon \), cf. (4.32), and let \(x:= x_0+3\varepsilon \frac{N_\varepsilon }{2} {\hat{e}}_\alpha \in T_{z_0}^{N_\varepsilon }\). Since \(y_0 \in L_\varepsilon + B_{3\varepsilon }(0)\), we have that \(|\langle y_0-x_0,\nu \rangle | < 3 \varepsilon \) and thus \(|\langle y-x,\nu \rangle | < 3 \varepsilon \), i.e., y belongs to the \(3 \varepsilon \)-neighborhood of \(R^\nu _{\infty , 1-5\delta /4} \setminus {{\overline{R}}}^{\nu }_{\infty , 1-7 \delta /4}\), which is contained in \(R^\nu _{\infty ,1- \delta } \setminus {{\overline{R}}}^{\nu }_{\infty , 1-2\delta }\).
Observe that
for some positive constant \(C_3\). To prove this, let \(x_0 \in T_{z_0}\) and \(x := x_0+3\varepsilon \frac{N_\varepsilon }{2} {\hat{e}}_\alpha \in T_{z_0}^{N_\varepsilon }\). The segment \([x_0;x]\) is fully contained in \(R^\nu _{\infty ,1-\delta } \setminus {{\overline{R}}}^\nu _{\infty ,1-3\delta }\) and thus \(\delta \ge |\langle x-x_0 , \nu \rangle | = 3\varepsilon \frac{N_\varepsilon }{2} \langle {\hat{e}}_\alpha , \nu \rangle \ge 3\varepsilon \frac{N_\varepsilon }{2} \frac{\sqrt{3}}{2}\).
Winding number. We choose \(m_\varepsilon \) given by (4.37). We consider the angles \(\theta _\varepsilon (\varepsilon i_{z})\), \(\theta _\varepsilon (\varepsilon j_{z})\), \(\theta _\varepsilon (\varepsilon k_{z})\) introduced in Step 3. By (4.37) and (4.34) we infer that
hence (4.24) is satisfied.
Checking the assumptions on the angles. We check that the assumptions (4.23) are satisfied. First, we claim that for \(\varepsilon \) small enough the configuration \(u_\varepsilon \) has positive chirality in every triangle \(T \in {\mathcal {T}}_\varepsilon ({\mathbb {R}}^2)\) contained in \(S_\varepsilon ^{\mathrm {top}}\). To prove it, let us start by showing that the sign of the chirality is constant arguing by contradiction. Assume that there exist two triangles \(T',T'' \subset S_\varepsilon ^{\mathrm {top}}\) with a common side such that \(\chi (u_\varepsilon ) \le 0\) in \(T'\) and \(\chi (u_\varepsilon ) \ge 0\) in \(T''\). Then by (4.30) and Lemma 3.2 we would get
which contradicts the condition \(\sigma _\varepsilon \rightarrow 0\). Therefore \(\chi (u_\varepsilon )\) has constant sign in \(S_\varepsilon ^{\mathrm {top}}\). In fact, \(\chi (u_\varepsilon ) > 0\) in \(S_\varepsilon ^{\mathrm {top}}\). If instead \(\chi (u_\varepsilon ) \le 0\) in \(S_\varepsilon ^{\mathrm {top}}\), by (4.30) we would have that
which contradicts \(\sigma _\varepsilon \rightarrow 0\). In conclusion, \(\chi (u_\varepsilon ) > 0\) in \(S_\varepsilon ^{\mathrm {top}}\).
Let now \(z \in {\mathcal {Z}}^{\mathrm {top}}_\varepsilon \). We have
Since \(\chi (u_\varepsilon ) > 0\) in \(T_z\), for \(\varepsilon \) small enough \(u_\varepsilon \) is close to a ground state with chirality 1 and therefore, using (2.3) and Lemma 2.1 (see also (2.5)),
Definition of the interpolation. We are in a position to define the interpolation. We reproduce the one-dimensional construction of Lemma 4.5 by suitably translating and scaling it, providing the precise notation as it will be useful for later estimates. We shall define the interpolation only on slices starting from every other triangle \(T_z\), for the constructions on two slices \(\Sigma ^{\alpha ,z}_\varepsilon \) and \(\Sigma ^{\alpha ,z+2}_\varepsilon \) completely determine the values of the modified spin configuration in \(\Sigma ^{\alpha ,z+1}_\varepsilon \). For this reason, let \(z \in {\mathcal {Z}}^{\mathrm {top}}_\varepsilon \) be such that \(z \equiv z_0 \!\! \mod 2\). We then define the interpolated angles \(\theta (\varepsilon i_z^h)\), \(\theta (\varepsilon j_z^h)\), \(\theta (\varepsilon k_z^h)\) for \(h=0,\dots ,N_\varepsilon \) as in (4.21) by (recall that \(i_z^0 = i_z\), \(j_z^0 = j_z\), \(k_z^0 = k_z\))
and \(\theta _\varepsilon (\varepsilon i_z^h) := 2\pi m_\varepsilon \), \(\theta _\varepsilon (\varepsilon j_z^h) := 2\pi m_\varepsilon +\frac{2\pi }{3}\), \(\theta _\varepsilon (\varepsilon k_z^h) := 2\pi m_\varepsilon +\frac{4\pi }{3}\) for \(h \ge N_\varepsilon +1\).
Eventually, we define \(u_\varepsilon ^\mathrm {top}:{\mathcal {L}}_\varepsilon \cap \Sigma ^{\alpha ,z}_\varepsilon (T_z) \rightarrow {\mathbb {S}}^1\) by setting
By (4.39) we have that
Estimate on “even” slices. We observe that the construction of \(u_\varepsilon ^\mathrm {top}\) is simply a translation and a scaling of the construction in Lemma 4.5. As the assumption (4.23) is satisfied, cf. (4.41), we can apply Lemma 4.5 to deduce that
Estimate on “odd” slices. We estimate the energy on the missing half-slices. Let us fix \(z, z+1, z+2 \in {\mathcal {Z}}^{\mathrm {top}}_\varepsilon \) with \(z \equiv z_0 \! \mod 2\). Let T be a triangle contained in \(\Sigma ^{\alpha ,z+1}_\varepsilon (T_{z+1})\). Then T shares two vertices with one triangle contained in \(\Sigma ^{\alpha ,z}_\varepsilon (T_{z})\) or with one triangle contained in \(\Sigma ^{\alpha ,z+2}_\varepsilon (T_{z+2})\). Let us assume, without loss of generality, that the two shared vertices are the vertices \(\varepsilon j'\in {\mathcal {L}}^2_\varepsilon \) and \(\varepsilon k' \in {\mathcal {L}}^3_\varepsilon \) of some triangle \(T' \subset \Sigma ^{\alpha ,z}_\varepsilon (T_{z})\). The third vertex of \(T'\) is of the type \(\varepsilon i_z^{h'} \in {\mathcal {L}}^1_\varepsilon \) for some \(h' \in {\mathbb {N}}\). Moreover, the third vertex of T is shared with a triangle \(T_{z+2}^{h}\), \(h \in {\mathbb {N}}\), and is of the type \(\varepsilon i_{z+2}^{h}\in {\mathcal {L}}^3_\varepsilon \). We remark that \(|h'-h| \le 2\). Indeed, by (4.38) we have that
From the assumptions on the position of the two triangles together with the definition of \(i_z^{h'}, i_{z+2}^{h}\) it follows that
where in the last inequality we used the fact that \(T_z \cap T_{z+1} \ne \emptyset \) and \(T_{z+1} \cap T_{z+2} \ne \emptyset \).
We estimate the energy in the triangle T by
Note that (4.34) and (4.37) imply
From (4.42), from the previous estimate, and since \(|h'-h|\le 2\) it follows that
It remains to estimate \(\big | \theta _\varepsilon (\varepsilon i_z) - \theta _\varepsilon (\varepsilon i_{z+2})\big |^2\). Using the fact that \(1 - \cos (\phi ) \ge \frac{1}{12} \phi ^2\) for every \(|\phi | \le \pi \) and by (4.36) we obtain that
where \(H_z\) is an hexagon containing \(T_z\) and \(T_{z+1}\) and \(H_{z+1}\) is an hexagon containing \(T_{z+1}\) and \(T_{z+2}\). In conclusion, we have that
Summing over all triangles in \(\Sigma ^{\alpha ,z}_\varepsilon (T_{z+1})\) (their number is \(C N_\varepsilon \)) we deduce that
Final estimate on top part. By (4.45), (4.44), summing over z and by (4.30), (4.33), (4.37), and (4.40) we conclude thatFootnote 1
Step 5. (parts of the square). The modification starting from \(S_\varepsilon ^\mathrm {left}\) and \(S_\varepsilon ^\mathrm {right}\) is completely analogous. We recall that \(\beta \in \{1,2,3\}\) is such that \(|\langle {\hat{e}}_\beta , \nu ^\perp \rangle | \ge \frac{\sqrt{3}}{2}\). We consider chains of triangles contained in \(S_\varepsilon ^\mathrm {left}\) and \(S_\varepsilon ^\mathrm {right}\) given by Lemma 4.6 (suitably adapted). In half-slices in the direction \({\hat{e}}_\beta \) starting from triangles of these chains and approaching the boundary \(\partial Q^\nu \), we define \(u_\varepsilon ^\mathrm {left}\) and \(u_\varepsilon ^\mathrm {right}\) as in Step 4.
We are finally in a position to define \({\widetilde{u}}_\varepsilon \) in \(Q^\nu _+\). We fix \(\delta \in (0,\tfrac{1}{8})\) and we consider the two-barred cross-shaped set (the white region in Fig. 9)
Given \(T \in {\mathcal {T}}_\varepsilon ({\mathbb {R}}^2)\) such that \(T \subset Q^\nu \), we distinguish some cases.
Definition of \({\widetilde{u}}_\varepsilon \) in \(Q^\nu _+\): in the hatched regions it is equal to \(u^\mathrm {pos}\); in the white region enclosed by \(Q^\nu _{r_\varepsilon +6\varepsilon }\) it is equal to \(u_\varepsilon \); outside of \(Q^\nu _{r_\varepsilon }\) it is defined through the interpolation \(u^\mathrm {top}_\varepsilon \), \(u^\mathrm {left}_\varepsilon \), and \(u^\mathrm {right}_\varepsilon \) constructed with the slices in the lattice directions \({\hat{e}}_\alpha \) and \({\hat{e}}_\beta \)
Case \(T \subset P_\delta \cap Q^\nu _{r_\varepsilon +6\varepsilon }\): We set
Case \(T \subset R^\nu _{1-5\delta ,1} \setminus {{\overline{Q}}}^\nu _{r_\varepsilon }\) (part of the cross-shaped set \(P_\delta \) aligned with \(\nu \)): We give the definition in the case \(T \subset Q^\nu _+\) (the case \(T \subset Q^\nu _-\) being analogous). Let \(y_0 \in T\). Let us consider the slice \(\Sigma ^{\alpha ,z}_\varepsilon \) such that \(T \subset \Sigma ^{\alpha ,z}_\varepsilon \) and let us show that \(z \in {\mathcal {Z}}^{\mathrm {top}}_\varepsilon \). Let \(x \in T_z\) and first of all note that \(x \in L_\varepsilon + B_{3 \varepsilon }(0)\). Since T and \(T_z\) are contained in the same slice, by definition of \(\Sigma ^{\alpha ,z}_\varepsilon \) we can find \(s \in {\mathbb {R}}\) such that \(x_0 := y_0 + s {\hat{e}}_\alpha \in T_z\). Since \(y_0 \notin {{\overline{Q}}}^\nu _{r_\varepsilon }\), the segment \([x_0;y_0]\) is contained in \(R^\nu _{\infty ,1} \setminus {{\overline{R}}}^\nu _{\infty ,r_\varepsilon }\), thus \(|s| \frac{\sqrt{3}}{2} \le |s| |\langle {\hat{e}}_\alpha , \nu \rangle |=|\langle x_0-y_0,\nu \rangle | \le \tfrac{1}{2}(1- r_\varepsilon )\), i.e., \(|s| \le \frac{1}{\sqrt{3}} (1-r_\varepsilon ) < \sqrt{3} \delta \). Then, using that \(|\langle {\hat{e}}_\alpha , \nu ^\perp \rangle | \le \frac{1}{2}\),
i.e., \(x \in R^\nu _{r_\varepsilon ,1}\) and hence \(x \in (L_\varepsilon + B_{3 \varepsilon }(0)) \cap R^\nu _{r_\varepsilon ,1} = S_\varepsilon ^\mathrm {top}\). We set
The definition is consistent with the previous case: if \(T \subset Q^\nu _{r_\varepsilon + 6\varepsilon } \setminus {{\overline{Q}}}^\nu _{r_\varepsilon }\), then T is not contained in any half-slice \(\Sigma ^{\alpha ,z}_\varepsilon (T_{z})\) (because \(T_z \cap \partial Q^\nu _{r_\varepsilon + 6\varepsilon } \ne \emptyset \)) and thus \({\widetilde{u}}_\varepsilon |_T = u_\varepsilon |_T\), in accordance with (4.47). If \(T \subset R^\nu _{1-5\delta ,1} \setminus {{\overline{Q}}}^\nu _{r_\varepsilon }\) but T is not contained in any half-slice \(\Sigma ^{\alpha ,z}_\varepsilon (T_{z})\), then \(T \subset S_\varepsilon \). In particular, by (4.46) and (4.30) we infer that
Case \(T \subset (R^\nu _{1,1-5\delta } \setminus {{\overline{R}}}^\nu _{1,3\delta }) \setminus {{\overline{Q}}}^\nu _{r_\varepsilon }\) (part of the cross-shaped set \(P_\delta \) aligned with \(\nu ^\perp \)): As in the previous case, assuming \(T \subset Q^\nu _+\), we define \({\widetilde{u}}_\varepsilon |_T := u_\varepsilon ^\mathrm {left}|_T\) if T is contained in a half-slice starting from a triangle in \(S_\varepsilon ^\mathrm {left}\), \({\widetilde{u}}_\varepsilon |_T := u_\varepsilon ^\mathrm {right}|_T\) if T is contained in a half-slice starting from a triangle in \(S_\varepsilon ^\mathrm {right}\), and \({\widetilde{u}}_\varepsilon |_T := u_\varepsilon |_T\) otherwise. As before, the definition is compatible with (4.47). Similarly to (4.49) we obtain that
Case \(T \cap ({\mathbb {R}}^2 \setminus P_\delta ) \ne \emptyset \): let x be a vertex of T and assume that x is not the vertex of a triangle \(T'\) covered by the previous cases. Then we set \({\widetilde{u}}_\varepsilon (x):=u_\varepsilon ^\mathrm {pos}(x)\) if \(\langle x, \nu \rangle \ge 0\) and \({\widetilde{u}}_\varepsilon (x):=u_\varepsilon ^\mathrm {neg}(x)\) if \(\langle x, \nu \rangle < 0\). In particular,
We remark that
and
Let us check that \({\widetilde{u}}_\varepsilon \) attains the desired boundary conditions (4.28). Let \(T \subset Q^\nu _+ \setminus {{\overline{Q}}}^\nu _{1-\delta }\). If \(T \subset (Q^\nu _+ \setminus {{\overline{Q}}}^\nu _{1-\delta }) \cap R^\nu _{1-5\delta ,1}\) (and similarly if \(T \subset (Q^\nu _+ \setminus {{\overline{Q}}}^\nu _{1-\delta }) \cap (R^\nu _{1,1-5\delta } \setminus {{\overline{R}}}^\nu _{1,3\delta })\)), then we are in the case covered by (4.48). By (4.43) we have \({\widetilde{u}}_\varepsilon |_T = u_\varepsilon ^\mathrm {top}|_T = u_\varepsilon ^\mathrm {pos}|_T\). Otherwise, if \(T \cap ({\mathbb {R}}^2 \setminus P_\delta ) \ne \emptyset \), let x be a vertex of T and assume that x is not the vertex of a triangle \(T'\) covered by the previous cases. Then, by definition, \({\widetilde{u}}_\varepsilon (x):=u_\varepsilon ^\mathrm {pos}(x)\). We argue analogously if \(T \subset Q^\nu _- \setminus {{\overline{Q}}}^\nu _{1-\delta }\). Finally, if \(T \cap L^\nu \ne \emptyset \), then \(T \subset L^\nu + B_{2\varepsilon }(0)\) and thus it is not relevant for the boundary conditions by the definition of discrete boundary \(\partial _\varepsilon ^\pm Q^\nu \).
Step 6. (Energy estimate). By (4.52), (4.51), and (4.53) we have that
Moreover, by (4.47), (4.49), and (4.50) we deduce that
In conclusion,
Eventually, letting \(\delta \rightarrow 0\) and with a diagonal argument, we construct a sequence which satisfies (4.29).
\(\square \)
In the proof of Proposition 4.2 we applied the following lemma.
Lemma 4.6
Let \(\Sigma ^{\alpha ,z}_\varepsilon \) be the slices of the triangular lattice defined in (4.18). Let L be a line in \({\mathbb {R}}^2\) orthogonal to \(\nu \) and assume that \(|\langle {\hat{e}}_\alpha , \nu ^\perp \rangle | \le \frac{1}{2}\). Then there exists a chain of triangles \((T_z)_{z \in {\mathbb {Z}}}\) satisfying for every \(z \in {\mathbb {Z}}\)
Proof
It is enough to prove the following:
Claim: Let \(z \in {\mathbb {Z}}\) and let \(T_z \in {\mathcal {T}}^+_\varepsilon ({\mathbb {R}}^2)\) be such that \(T_z \subset \Sigma ^{\alpha ,z}_\varepsilon \) and \(T_z \cap L \ne \emptyset \). Then there exists \(T_{z+1} \in {\mathcal {T}}^+_\varepsilon ({\mathbb {R}}^2)\) such that \(T_{z+1} \subset \Sigma ^{\alpha ,z+1}_\varepsilon \), \(T_{z+1} \cap L \ne \emptyset \), and \( T_z \cap T_{z+1}\ne \emptyset \). (The analogous statement with \(\Sigma ^{\alpha ,z-1}_\varepsilon \) in place of \(\Sigma ^{\alpha ,z+1}_\varepsilon \) holds true.)
With the proven claim at hand it is immediate to define a chain of triangles \((T_z)_{z \in {\mathbb {Z}}}\) which satisfies the properties in (4.54) by initializing the construction from a triangle \(T_{z_0} \in {\mathcal {T}}^+_\varepsilon ({\mathbb {R}}^2)\) which satisfies \(T_{z_0} \cap L \ne \emptyset \) and \(T_{z_0} \subset \Sigma ^{\alpha ,z_0}_\varepsilon \). Such a triangle always exists since the set \({\mathbb {R}}^2 \setminus \bigcup _{T \in {\mathcal {T}}^+_\varepsilon ({\mathbb {R}}^2)} T\) is the union of disjoint open triangles, thus cannot contain L.
To prove the claim let us denote be \({\hat{e}}_\beta ,{\hat{e}}_\gamma \) the remaining two unit vectors connecting points of \({\mathcal {L}}\) and introduced in Section 2.2 and let us set \(\tau _\beta :={{\,\mathrm{sign}\,}}\langle {\hat{e}}_\beta ,{\hat{e}}_\alpha ^\perp \rangle \), \(\tau _\gamma :={{\,\mathrm{sign}\,}}\langle {\hat{e}}_\gamma ,{\hat{e}}_\alpha ^\perp \rangle \). For later use we observe that \(\tau _\beta =\tau _\gamma \) if and only if \(\alpha \ne 2\), that is if and only if \(\langle {\hat{e}}_\beta ,{\hat{e}}_\alpha \rangle =-\langle {\hat{e}}_\gamma ,{\hat{e}}_\alpha \rangle \). In particular, we always have
Suppose now that \(T_z \in {\mathcal {T}}^+_\varepsilon ({\mathbb {R}}^2)\), \(T_z\subset \Sigma _\varepsilon ^{\alpha ,z}\) with \(T_z\cap L\ne \emptyset \). The triangles \(T^\beta :=T_z+\varepsilon \tau _\beta {\hat{e}}_\beta \in {\mathcal {T}}^+_\varepsilon ({\mathbb {R}}^2)\) and \(T^\gamma :=T_z+\varepsilon \tau _\gamma {\hat{e}}_\gamma \in {\mathcal {T}}^+_\varepsilon ({\mathbb {R}}^2)\) satisfy \( T_z\cap T^\beta \ne \emptyset \) and \(T_z\cap T^\gamma \ne \emptyset \). Moreover, they are contained in \(\Sigma _\varepsilon ^{\alpha ,z+1}\). Indeed, for \(x \in T_z\) we have \(\langle {\hat{e}}_\alpha ^\perp , x + \varepsilon \tau _\beta {\hat{e}}_\beta \rangle = \langle {\hat{e}}_\alpha ^\perp , x \rangle + \varepsilon \tau _\beta \langle {\hat{e}}_\alpha ^\perp , {\hat{e}}_\beta \rangle = \langle {\hat{e}}_\alpha ^\perp , x \rangle + \varepsilon \frac{\sqrt{3}}{2} \in [\varepsilon \frac{\sqrt{3}}{2} (z+1), \varepsilon \frac{\sqrt{3}}{2} (z+2)]\), hence \(T^\beta \subset \Sigma ^{\alpha ,z+1}_\varepsilon \) (analogously \(T^\gamma \subset \Sigma ^{\alpha ,z+1}_\varepsilon \)).
The triangle \(T_z\) has one side contained in \(\partial \Sigma ^{\alpha ,z}_\varepsilon \), i.e., either in \(s_z^{\alpha } := {\mathbb {R}}{\hat{e}}_\alpha + \varepsilon \frac{\sqrt{3}}{2} z {\hat{e}}_\alpha ^\perp \) or in \(s_{z+1}^{\alpha } := {\mathbb {R}}{\hat{e}}_\alpha + \varepsilon \frac{\sqrt{3}}{2} (z+1) {\hat{e}}_\alpha ^\perp \). Let us assume, without loss of generality, that the side is contained in \(s_z^\alpha \). The line L intersects \(s_z^\alpha \) in a point x. We claim that \(x \in T_z\). Indeed, if \(x \notin T_z\), then the angle in \([0,\frac{\pi }{2}]\) between the lines L and \(s_z^\alpha \) belongs to \([0,\frac{\pi }{3})\), since L intersects also \(T_z\), see Fig. 10. Let us fix \(y \in T_z \cap L \ne \emptyset \). Then we have \(|\langle x-y, {\hat{e}}_\alpha \rangle | > \frac{1}{2} |x-y|\). This contradicts the fact that \(|\langle x-y, {\hat{e}}_\alpha \rangle | = |x-y| |\langle \nu ^\perp , {\hat{e}}_\alpha \rangle | \le \frac{1}{2} |x-y|\) since \(|\langle \nu ^\perp , {\hat{e}}_\alpha \rangle | \le \frac{1}{2}\). In conclusion \(x \in T_z \cap s_z^\alpha \). Then \(x_\beta :=x+\varepsilon \tau _\beta {\hat{e}}_\beta \in T^\beta \cap s_{z+1}^\alpha \), \(x_\gamma :=x+\varepsilon \tau _\gamma {\hat{e}}_\gamma \in T^\gamma \cap s_{z+1}^\alpha \). The line L intersects the segment \([x_\beta ;x_\gamma ]\), and thus either \(T^\beta \) or \(T^\gamma \). To see this, we let \({y_\lambda :=\lambda x_\beta +(1-\lambda )x_\gamma }\) for \(\lambda \in [0,1]\). Note that
and analogously \(\langle y_1-x,\nu \rangle =\varepsilon \left( \tfrac{\sqrt{3}}{2}\langle {\hat{e}}_\alpha ^\perp ,\nu \rangle +\tau _\beta \langle {\hat{e}}_\beta ,{\hat{e}}_\alpha \rangle \langle {\hat{e}}_\alpha ,\nu \rangle \right) \). In combination with (4.55), this yields
where we used that \(\langle {\hat{e}}_\alpha ^\perp ,\nu \rangle ^2=\langle {\hat{e}}_\alpha ,\nu ^\perp \rangle ^2\le \tfrac{1}{4}\) and \(\langle {\hat{e}}_\alpha ,\nu \rangle ^2\ge \tfrac{3}{4}\). Now (4.56) together with the continuity of the mapping \(\lambda \mapsto \langle y_\lambda -x,\nu \rangle \) implies that there exists \(\lambda \in [0,1]\) with \(\langle y_\lambda -x,\nu \rangle =0\), hence \(y_\lambda \in (T^\beta \cup T^\gamma )\cap L\).
\(\square \)
5 Upper bound
It remains to prove the \(\Gamma \)-limsup inequality to complete the proof of Theorem 2.5.
Proposition 5.1
Let \({\mathscr {F}}_\varepsilon \) be as in (2.8). Then for every \(\chi \in L^1(\Omega )\) we have
where \({\mathscr {F}}\) is given by (2.10) and the \(\Gamma \hbox {-}\limsup \) is with respect to the strong topology in \(L^1(\Omega )\).
Proof
It is not restrictive to assume that \(\chi \in BV(\Omega ;\{-1,1\})\). Moreover, thanks to Remark 2.6, the density result [13, Corollary 2.4], and the \(L^1\)-lower semicontinuity of the \(\Gamma \)-limsup it suffices to prove (5.1) for \(\chi \in BV(\Omega ;\{-1,1\})\) such that \(J_{\chi }\) is polygonal, i.e., \(J_{\chi }=\bigcup _{n=1}^N\Gamma _n\), where \(\Gamma _n\) are line segments satisfying \({\mathcal {H}}^1(\Gamma _n\cap \partial \Omega )=0\). To simplify the exposition we restrict ourselves to the case \(J_{\chi }=\Gamma _1\cup \Gamma _2\) with \(\Gamma _1=[x_0;x_1]\), \(\Gamma _2=[x_1;x_2]\), \(x_0,x_1,x_2\in {\mathbb {R}}^2\), i.e., the two segments have one common endpoint. The general case then follows by repeating the construction on each line segment.
Step 1. (Construction of a recovery sequence) Denoting by \(\ell _1,\ell _2\) the length of \(\Gamma _1\), \(\Gamma _2\) and by \(\nu _1,\nu _2\) the outer unit normal to the set \(\{\chi =1\}\) on \(\Gamma _1\), \(\Gamma _2\), upon relabeling we can assume that \(x_1=x_0+\ell _1\nu _1^\perp \), \(x_2=x_1+\ell _2\nu _2^\perp \). Moreover, we have
where \(\varphi \) is as in (2.12). Let \(\rho >0\) be sufficiently small and let \(u_{\varepsilon ,\rho }^1\in \mathcal {SF}_\varepsilon \) and \(u_{\varepsilon ,\rho }^2\in \mathcal {SF}_\varepsilon \) be admissible for the minimum problems defining \(\varphi (\nu _1)\), \(\varphi (\nu _2)\), respectively with
We now start constructing a recovery sequence for \(\chi \) by subdividing \(\Gamma _1\) and \(\Gamma _2\) into segments of length of order \(\rho \) and suitable shifting \(u_{\varepsilon ,\rho }^1\), \(u_{\varepsilon ,\rho }^2\) along these segments. In doing so we need to leave out a small region close to the common endpoint \(x_1\). Namely, denoting by \(\theta \in (0,\pi ]\) the angle between \(\Gamma _1\) and \(\Gamma _2\) we choose \(c=c(\nu _1,\nu _2)>0\) with \(c\ge \frac{1}{2}+\frac{1}{2}\cot (\frac{\theta }{2})\) and we only subdivide the smaller segments \([x_0;x_1-c\rho \nu _1^\perp ]\) and \([x_1+c\rho \nu _2^\perp ;x_2]\) as follows. We set \(M_{\varepsilon ,\rho }^1:=\lfloor \frac{\ell _1-c\rho }{\rho +5\varepsilon }\rfloor \), \(M_{\varepsilon ,\rho }^2:=\lfloor \frac{\ell _2-c\rho }{\rho +5\varepsilon }\rfloor \) and we choose lattice points
Note that the constant c and the lattice points \(x_{m,1}^\varepsilon \), \(x_{m,2}^\varepsilon \) are chosen in such a way that, for \(\varepsilon \) small enough,
is a union of pairwise disjoint cubes, see Fig. 11. This allows us to define \(u_{\varepsilon ,\rho }\in \mathcal {SF}_\varepsilon \) by setting
We observe that since \(x_{m,1}^\varepsilon ,x_{m,2}^\varepsilon \) belong to the sublattice \({\mathcal {L}}_\varepsilon ^1\), the boundary conditions satisfied by the shifted functions \(u_{\varepsilon ,\rho }^1(\,\cdot -x_{m,1}^\varepsilon )\), \(u_{\varepsilon ,\rho }^2(\,\cdot -x_{m,2}^\varepsilon )\) are compatible one with each other and with \(u_\varepsilon ^\mathrm {pos}\) and \(u_\varepsilon ^\mathrm {neg}\) on \(\Omega \setminus U_\rho \). In particular, if \(x\in \Omega \) is such that \({{\,\mathrm{dist}\,}}(x,J_{\chi })\ge \rho /2\) then \(\chi (u_{\varepsilon ,\rho })(x)=\chi (x)\), which implies that \(\Vert \chi (u_{\varepsilon ,\rho })-\chi \Vert _{L^1(\Omega )}\le C\rho {\mathcal {H}}^1(J_{\chi })\rightarrow 0\) as \(\rho \rightarrow 0\).
Step 2. (Energy estimate) In order to estimate \(F_\varepsilon (u_{\varepsilon ,\rho })\) we start by rewriting the energy as
and we estimate the terms on the right-hand side of (5.4) separately. Let us first consider the energy on triangles \(T\in {\mathcal {T}}_\varepsilon (\Omega )\) with \(T\cap (\Omega \setminus U_\rho )\ne \emptyset \). Suppose that \({{\,\mathrm{dist}\,}}(T,J_{\chi })>5\varepsilon \). Then, if \(T\subset \Omega \setminus U_\rho \) we have \(u_{\varepsilon ,\rho }=u_\varepsilon ^\mathrm {pos}\) or \(u_{\varepsilon ,\rho }=u_\varepsilon ^\mathrm {neg}\) on T, so that \(F_\varepsilon (u_{\varepsilon ,\rho },T)=0\). If instead \(T\cap U_\rho \ne \emptyset \), the fact that \({{\,\mathrm{dist}\,}}(T,J_{\chi })>5\varepsilon \) ensures that T intersects a cube in \(U_\rho \) in a region where the boundary conditions are prescribed. Thus, using once more the compatibility of the boundary conditions, we infer that \(F_\varepsilon (u_{\varepsilon ,\rho },T)=0\). This implies that
where to obtain the first inequality we used \(F_\varepsilon (u_{\varepsilon ,\rho },T)\le 9\varepsilon \), while the second inequality follows by counting triangles contained either in \(\left( [x_1-c\rho \nu _1^\perp ;x_1]\cup [x_1;x_1+c\rho \nu _2^\perp ]\right) +B_{6\varepsilon }(0)\) or in \(\left( \partial U_\rho \cap J_{\chi }\right) +B_{6\varepsilon }(0)\).
Combining (5.4), (5.5), and (5.3) we deduce that
Since the latter term converges to \(\ell _1\varphi (\nu _1)+\ell _2\varphi (\nu _2)\) as \(\rho \rightarrow 0\), thanks to (5.2) and (5.6), a diagonal argument provides us with a sequence \((u_\varepsilon )=(u_{\varepsilon ,\rho (\varepsilon )})\) with \(\chi (u_\varepsilon )\rightarrow \chi \) in \(L^1(\Omega )\) and satisfying \(\limsup _\varepsilon F_\varepsilon (u_\varepsilon )\le {\mathscr {F}}(\chi )\), from which we finally deduce (5.1).
\(\square \)
Notes
In this estimate it becomes evident that it was crucial to prove that the energy concentrates close to the interface. A classical averaging/slicing argument would only provide a bound on the strip \(S_\varepsilon \) of the type \(F_\varepsilon (u_\varepsilon ,S_\varepsilon ) \le C \varepsilon \). This would not suffice to conclude that the modified sequence does not increase the energy, as the right-hand side in this estimate would end up to be a constant.
References
Alicandro, R., Braides, A., Cicalese, M.: Phase and antiphase boundaries in binary discrete systems: a variational viewpoint. Netw. Heterog. Media 1, 85–107 (2006)
Alicandro, R., Cicalese, M.: Variational analysis of the asymptotics of the XY model. Arch. Ration. Mech. Anal. 192, 501–536 (2009)
Alicandro, R., Cicalese, M., Ponsiglione, M.: Variational equivalence between Ginzburg-Landau, \(XY\) spin systems and screw dislocations energies. Indiana Univ. Math. J. 60, 171–208 (2011)
Alicandro, R., Cicalese, M., Sigalotti, L.: Phase transitions in presence of surfactants: from discrete to continuum. Interf. Free Bound. 14, 65–103 (2012)
Alicandro, R., De Luca, L., Garroni, A., Ponsiglione, M.: Metastability and dynamics of discrete topological singularities in two dimensions: a \(\Gamma \)-convergence approach. Arch. Ration. Mech. Anal. 214, 269–330 (2014)
Alicandro, R., Gelli, M.S.: Local and nonlocal continuum limits of Ising-type energies for spin systems. SIAM J. Math. Anal. 48, 895–931 (2016)
Ambrosio, L., Fusco, N., Pallara, D.: Functions of Bounded Variation and Free Discontinuity Problems. The Clarendon Press, Oxford University Press, New York, Oxford Mathematical Monographs (2000)
Bach, A., Braides, A., Cicalese, M.: Discrete-to-continuum limits of multi-body systems with bulk and surface long-range interactions. SIAM J. Math. Anal. 52, 3600–3665 (2020)
Bach, A., Cicalese, M., Kreutz, L., Orlando, G.: The antiferromagnetic XY model on the triangular lattice: topological singularities. Indiana Univ. Math. J. (to appear)
Bethuel, F., Brezis, H., Hélein, F.: Ginzburg-Landau Vortices. Springer (1994)
Braides, A.: An example of non-existence of plane-like minimizers for an almost-periodic Ising system. J. Stat. Phys. 157, 295–302 (2014)
Braides, A., Cicalese, M.: Interfaces, modulated phases and textures in lattice systems. Arch. Ration. Mech. Anal. 223, 977–1017 (2017)
Braides, A., Conti, S., Garroni, A.: Density of polyhedral partitions. Calc. Var. Partial Differ. Equ. 56, 28 (2017)
Braides, A., Kreutz, L.: Design of lattice surface energies. Calc. Var. Partial Differ. Equ. 57, 97 (2018)
Braides, A., Piatnitski, A.: Homogenization of surface and length energies for spin systems. J. Funct. Anal. 264, 1296–1328 (2013)
Caffarelli, L.A., de la Llave, R.: Planelike minimizers in periodic media. Comm. Pure Appl. Math. 54, 1403–1441 (2001)
Caffarelli, L.A., de la Llave, R.: Interfaces of ground states in Ising models with periodic coefficients. J. Stat. Phys. 118, 687–719 (2005)
Canevari, G., Segatti, A.: Defects in nematic shells: a \(\Gamma \)-convergence discrete-to-continuum approach. Arch. Ration. Mech. Anal. 229, 125–186 (2018)
Chambolle, A., Goldman, M., Novaga, M.: Plane-like minimizers and differentiability of the stable norm. J. Geom. Anal. 24, 1447–1489 (2014)
Cicalese, M., Forster, M., Orlando, G.: Variational analysis of a two-dimensional frustrated spin system: emergence and rigidity of chirality transitions. SIAM J. Math. Anal. 51, 4848–4893 (2019)
Cicalese, M., Orlando, G., Ruf, M.: Emergence of concentration effects in the variational analysis of the \(N\)-clock model. Comm. Pure Appl. Math. (to appear)
Cicalese, M., Orlando, G., Ruf, M.: The \(N\)-clock model: Variational analysis for fast and slow divergence rates of \(N\). Preprint (2020)
Cicalese, M., Orlando, G., Ruf, M.: Coarse graining and large-\(N\) behavior of the \(d\)-dimensional \(N\)-clock model. Interf. Free Bound. (to appear)
Cicalese, M., Solombrino, F.: Frustrated ferromagnetic spin chains: a variational approach to chirality transitions. J. Nonlinear Sci. 25, 291–313 (2015)
Conti, S., Fonseca, I., Leoni, G.: A \(\Gamma \)-convergence result for the two-gradient theory of phase transitions. Comm. Pure Appl. Math. 55, 857–936 (2002)
Conti, S., Garroni, A., Massaccesi, A.: Modeling of dislocations and relaxation of functionals on 1-currents with discrete multiplicity. Calc. Var. Partial Differ. Equ. 54, 1847–1874 (2015)
Conti, S., Schweizer, B.: Rigidity and gamma convergence for solid-solid phase transitions with \(SO(2)\) invariance. Comm. Pure Appl. Math. 59, 830–868 (2006)
Daneri, S., Runa, E.: Exact periodic stripes for minimizers of a local/nonlocal interaction functional in general dimension. Arch. Ration. Mech. Anal. 231, 519–589 (2019)
De Luca, L.: \(\Gamma \)-convergence analysis for discrete topological singularities: the anisotropic triangular lattice and the long range interaction energy. Asymptot. Anal. 96, 185–221 (2016)
Diep, H., et al.: Frustrated spin systems. World Scientific (2013)
Friedrich, M., Kreutz, L., Schmidt, B.: Emergence of rigid polycrystals from atomistic systems with heitmann-radin sticky disc energy. Arch. Ration. Mech. Anal. (to appear)
Lee, D., Joannopoulos, J., Negele, J., Landau, D.: Discrete-symmetry breaking and novel critical phenomena in an antiferromagnetic planar (XY) model in 2 dimensions. Phys. Rev. Lett. 52, 433–436 (1984)
Miyashita, S., Shiba, H.: Nature of the phase-transition of the two-dimensional antiferromagnetic plane rotator model on the triangular lattice. J. Phys. Soc. Jpn 53, 1145–1154 (1984)
Presutti, E.: Scaling Limits in Statistical Mechanics and Microstructures in Continuum Mechanics. Theoretical and Mathematical Physics. Springer, Berlin (2009)
Sandier, E., Serfaty, S.: Vortices in the Magnetic Ginzburg-Landau Model. Springer Science & Business Media (2008)
Scilla, G., Vallocchia, V.: Chirality transitions in frustrated ferromagnetic spin chains: a link with the gradient theory of phase transitions. J. Elast. 132, 271–293 (2018)
Seul, M., Andelman, D.: Domain shapes and patterns: the phenomenology of modulated phases. Science 267, 476–483 (1995)
Acknowledgements
The work of A. Bach and M. Cicalese was supported by the DFG Collaborative Research Center TRR 109, “Discretization in Geometry and Dynamics”. G. Orlando has received funding from Alexander von Humboldt Foundation and the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No 792583. The work of L. Kreutz was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy EXC 2044 -390685587, Mathematics Münster: Dynamics–Geometry–Structure. A. Bach and G. Orlando thank the TU München, where they were affiliated while working on the paper.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by J. M. Ball.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bach, A., Cicalese, M., Kreutz, L. et al. The antiferromagnetic XY model on the triangular lattice: chirality transitions at the surface scaling. Calc. Var. 60, 149 (2021). https://doi.org/10.1007/s00526-021-02016-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00526-021-02016-3


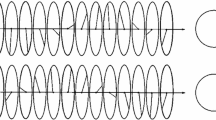




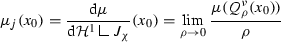 , where we have set
, where we have set 






