1 Introduction

Methods of complex function theory provide various tools to construct exact solutions to differential equations, especially in the case of singularities, such as, e.g. crack tip problems in linear elastic fracture mechanics. In particular, with the introduction of the famous Kolosov–Muskhelishvili formulae, methods of complex function theory became indispensable to handle problems of linear elasticity [23]. The classical Kolosov–Muskhelishvili formulae enable us to represent displacements and stresses of a two-dimensional elastic body in terms of two holomorphic functions \(\varPhi (z)\) and \(\varPsi (z)\), \(z\in \mathbb {C}\). Because of obvious advantages of the function-theoretic approach, such as exact singular behaviour near the crack tip and preservation of all basic physical assumptions, methods of complex function theory constituted the foundation of classical fracture mechanics [20, 28].

A known disadvantage of function-theoretic methods is the fact that a complete boundary value problem can be solved explicitly only for some elementary (simple) domains, such as, e.g. the unit disk or half-plane. Considering that domains coming from real-world engineering problems generally have more complicated geometry, numerical methods, such as e.g. extended finite element method [21], are frequently used to solve static and dynamic fracture mechanics problems nowadays. The idea of modern numerical methods used in fracture mechanics applications is to enrich classical finite element shape functions with known analytical solution, e.g. Westergaard solution and partition of unity [21], to obtain correct asymptotic behaviour near the crack tip. The drawback of such methods is the lost continuity between enriched and standard elements, since the modified shape functions do not satisfy the interpolation conditions. Thus, the methods obtained in this way do not satisfy basic assumptions of the classical theory of the finite element method [6], and therefore, it is difficult to perform a rigorous convergence analysis.

In this context, utilising advantages of both function-theoretic methods and the finite element method, coupled analytical–numerical methods could be alternative approaches towards higher accuracy of solutions in the region near the singularity. While a coupling between the analytical solution obtained by function-theoretic methods and the finite element solution can be introduced in several ways (see e.g. [25, 26]), we focus on a continuous coupling in this paper. The idea of a continuous analytical–numerical coupling is to introduce a special interpolation operator preserving \(C^{0}\) continuity of the displacement field on the interface between the function-theoretic solution and the classical finite elements. Construction of such an interpolation operator has been presented in [12, 13], and convergence analysis of the coupled method has been performed in [14, 18], where the coupling error has been also estimated explicitly. However, only problems of fracture mechanics with static cracks have been considered so far. Therefore, in this paper, we present an extension of the coupled approach to crack propagation problems in two-dimensional domains.

The crack propagation approach presented in this paper is within the framework of linear elastic fracture mechanics. The main result of this theory of fracture is that linear elastic calculations are sufficient to estimate the fracture energy release rate, or equivalently the stress intensity factor, to determine whether a crack propagates or not. However, a prediction of the crack propagation path with bifurcation points cannot be obtained only by considering the fracture energy release rate. Therefore, additional bifurcation criteria have been introduced for computing the crack propagation path, e.g. the maximum hoop stress criterion [9], the maximum-energy-release-rate criterion [29] or an asymptotic expansion of the stress intensity factor [17]. Moreover, one of the most elegant and physically consistent approaches is the variational formulation proposed in [10]. In this approach, at each time, and for any boundary condition, the crack propagation path is obtained by finding the global minimum of the total energy, which is the sum of potential energy and dissipated energy, under the constraint of the irreversibility of the crack growth. One of the main advantages of the energetic formulation is its correspondence to a quasi-static evolution of the crack, implying that a succession of stable states is simulated without referring to the detailed mechanisms arising between two stable states. Thus, the energetic approach authorises discontinuous evolutions, practically meaning that, for instance, the crack length increase is not infinitesimal but may be finite between two time steps. However, the minimisation procedure may be time-consuming as numerical methods (that should be sufficiently refined to obtain acceptable accuracy) are repeatedly used to minimise the total energy.

In this paper, an approach combining a coupled analytical–numerical method and an energetic approach in order to model crack propagation is proposed. The expected advantage of such an approach is a reduced computation time on the finite element side, since the analytical solution near the crack tip is used. However, since the original coupled analytical–numerical method is limited to cracks without bifurcation points [14], the analytical solution at first must be extended to the case of kinked cracks. This extension is done by using a conformal mapping approach, and therefore, the linear elastic problem in the region near the crack tip is reduced to a Riemann–Hilbert problem for holomorphic functions in the unit disk. Therefore, our aim here is to extend the conformal mapping approach to the case of the coupled analytical–numerical method. As will be discussed in the paper, practical (numerical) realisation of this approach still needs to be addressed properly due to known difficulties with numerical conformal mappings. Therefore, this paper aims at presenting a general strategy for modelling crack propagation based on a continuous coupling of function-theoretic methods and the finite element method. Moreover, we present an explicit solution of the Riemann–Hilbert problem and provide a detailed discussion on future steps for practical realisation of the proposed method along with first numerical calculations for the Riemann–Hilbert problem.

2 Modelling Crack Propagation Via the Coupling of Function-Theoretic and Finite Element Methods

In this section we present a general description of the method to model crack propagation via a continuous coupling of complex function theory and the finite element method. To support the reader, we start with a general overview of the coupled method underlying only the essential steps relevant for the crack propagation modelling. After that, we discuss the mechanical point of view on the propagation process and outline the idea using a conformal mapping approach leading to the formulation of a Riemann–Hilbert problem, which is discussed in detail in the upcoming sections.

2.1 Continuous Analytical–Numerical Coupling for Static Cracks

Let \(G\subset \mathbb {C}\) be a simply connected bounded domain containing a crack. Further, let \(\varGamma \) be a boundary of G, which is assumed to be sufficiently smooth except for the turning point given by a crack tip, which causes a well-known crack-tip singularity. We consider now the classical boundary value problem of linear elasticity formulated as follows

$$\begin{aligned} \left\{ \begin{array}{rcll} -\mu \,\varDelta \mathbf {u}-(\lambda +\mu )\,\mathrm {grad}\,\mathrm {div}\,\mathbf {u} &{} = &{} \mathbf {f} &{} \text{ in } G,\\ \mathbf {u} &{} = &{} \mathbf {g}_{0} &{} \text{ on } \varGamma _{0},\\ \displaystyle \varvec{\sigma }\cdot \overline{n} &{} = &{} \mathbf {g}_{1} &{} \text{ on } \varGamma _{1}, \end{array}\right. \end{aligned}$$
(1)

where \(\lambda \) and \(\mu \) are classical Lamé constants, and \(\mathbf {f}\) is the density of volume forces, \(\mathbf {u}\) is the unknown displacement vector, \(\varvec{\sigma }\) is the Cauchy stress tensor, \(\overline{n}\) is the unit outer normal vector, and \(\varGamma _{0}\) and \(\varGamma _{1}\) are parts of the boundary with Dirichlet and Neumann boundary conditions (\(\mathbf {g}_{0}\) and \(\mathbf {g}_{1}\)), respectively.

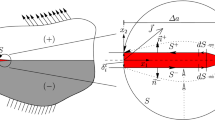
To provide an exact description of the solution behaviour near the singularity, we introduce a local coupling region surrounding the crack tip (see Fig. 1, left). The right side of Fig. 1 illustrates the coupling region with more details. In particular, the coupling region is further subdivided into analytical domain \(\varOmega _{\mathrm {A}}\) circled by curved triangular elements \(\mathbb {T}_{i}\) (8 in Fig. 1), which are called coupling elements. The interface \(\varGamma _{\mathrm {AD}}\) between \(\varOmega _{\mathrm {A}}\) and coupling elements is called the coupling interface. The remaining part of the domain G is triangulated by standard finite elements.

Fig. 1
figure 1

Left: domain G containing a crack and the coupling region. Right: further subdivision of the coupling region into analytical domain \(\varOmega _{\mathrm {A}}\) and coupling elements \(\mathbb {T}_{i}, i=1,\ldots ,8\)

Full size image

Introducing the coupling region enables us to couple continuously the exact solution to the differential equation of linear elasticity in \(\varOmega _{\mathrm {A}}\) with the finite element solution in the remaining part of the domain. This continuous coupling is provided by help of a special interpolation operator, which is based on the analytical solution. A detailed construction of such an interpolation operator and its invariance property have been discussed in [12, 13]. Because of the continuous coupling, a variational problem as in the classical finite element method (FEM) theory, see [6] for details, can be formulated in our case. Since the goal of this paper is not to discuss finite element aspects of the coupled method, but rather focus on function-theoretic tools to model crack propagation, we omit all further technical details on the FEM part of the method and refer to [19] for a complete construction.

An analytical solution to the differential equation in \(\varOmega _{\mathrm {A}}\) is constructed by the Kolosov–Muskhelishvili formulae [23]; in polar coordinates these formulae allow us to represent components of the displacement field and stress tensor in the following form

$$\begin{aligned} \displaystyle 2\mu (u_{r}+i\,u_{\varphi })= & {} \displaystyle e^{-i\varphi }\left( \kappa \,\varPhi (z)-z\,\overline{\varPhi '(z)}-\overline{\varPsi (z)}\right) , \\ \displaystyle \sigma _{rr}+\sigma _{\varphi \varphi }= & {} \displaystyle 2\left[ \varPhi '(z)+\overline{\varPhi '(z)}\right] , \\ \displaystyle \sigma _{\varphi \varphi }-\sigma _{rr}+2i\,\sigma _{r\varphi }= & {} \displaystyle 2e^{2i\,\varphi }\left[ \bar{z}\,\varPhi ''(z)+\varPsi '(z)\right] , \end{aligned}$$

where \(\varPhi (z)\) and \(\varPsi (z)\) are two holomorphic functions, and \(\kappa \in (1,3)\) is the Kolosov’s constant. For static cracks, the holomorphic function \(\varPhi (z)\) and \(\varPsi (z)\) have been written in terms of a power series expansion [12]

$$\begin{aligned} \varPhi (z)=\sum _{k=0}^{\infty }a_{k}z^{\lambda _{k}},\quad \varPsi (z)=\sum _{k=0}^{\infty }b_{k}z^{\lambda _{k}}, \, \text{ with } \, a_{k},b_{k}\in \mathbb {C}, \lambda _{k}\in \mathbb {R}. \end{aligned}$$

Using these series expansions in the Kolosov–Muskhelishvili formulae and applying traction free boundary conditions on the crack faces, exponents \(\lambda _{k} = k/2\), \(k=1,2,\ldots \), are found, which correspond to the classical crack tip singularity, see [20] for details. Moreover, relations between complex coefficients \(a_{k}\) and \(b_{k}\) are also identified, and therefore, the displacement field can be written now as follows

$$\begin{aligned} 2\mu (u_{1}+i\,u_{2})= & {} \displaystyle \sum \limits _{n=0,2,\ldots }^{\infty }r^{n/2}\left[ a_{n} \left( \kappa \,e^{i\varphi n/2}+e^{-i\varphi n/2}\right) \right. \nonumber \\&\displaystyle + \left. \frac{n}{2}\bar{a}_{n}\left( e^{-i\varphi n/2}-e^{-i\varphi (n/2-2)}\right) \right] \nonumber \\&\displaystyle + \sum \limits _{n=1,3,\ldots }^{\infty }r^{n/2}\left[ a_{n} \left( \kappa \,e^{i\varphi n/2}-e^{-i\varphi n/2}\right) \right. \nonumber \\&\displaystyle \left. + \frac{n}{2}\bar{a}_{n}\left( e^{-i\varphi n/2}-e^{-i\varphi (n/2-2)}\right) \right] , \end{aligned}$$
(2)

where unknown coefficients \(a_{n}\) are still to be identified by solving the global boundary value problem (1) via the coupled finite element procedure.

Finally, the continuity of the displacement field through the entire coupling interface \(\varGamma _{\mathrm {AD}}\) in the finite element procedure is preserved by constructing finite element basis functions based on the truncated exact solution (2). Let us consider n nodes on the interface \(\varGamma _{\mathrm {AD}}\) belonging to the interval \([-\pi ,\pi ]\), then the interpolation function \(f_{n}(\varphi )\) restricted to \(\varGamma _{\mathrm {AD}}\), i.e. \(r=r_{\mathrm {A}}\), has the following form

$$\begin{aligned} f_{n}(\varphi )= & {} \displaystyle \sum \limits _{k=0,2,\ldots }^{N_{1}}r_{\mathrm {A}}^{k/2}\left[ a_{k} \left( \kappa \,e^{i\varphi k/2}+e^{-i\varphi k/2}\right) +\frac{k}{2}\bar{a}_{k}\left( e^{-i\varphi k/2}-e^{-i\varphi (k/2-2)}\right) \right] \nonumber \\&+\displaystyle \sum \limits _{k=1,3,\ldots }^{N_{2}}r_{\mathrm {A}}^{k/2}\left[ a_{k} \left( \kappa \,e^{i\varphi k/2}-e^{-i\varphi k/2}\right) +\frac{k}{2}\bar{a}_{k}\left( e^{-i\varphi k/2}-e^{-i\varphi (k/2-2)}\right) \right] ,\nonumber \\ \end{aligned}$$
(3)

where the numbers of basis functions \(N_{1}\) and \(N_{2}\) are related to n as follows:

$$\begin{aligned} \begin{array}{ll} N_{1} = \left\{ \begin{array}{ll} n-2 &{} \text{ for } \text{ even } n,\\ n-1 &{} \text{ for } \text{ odd } n,\end{array}\right. &{} N_{2} = \left\{ \begin{array}{ll} n-1 &{} \text{ for } \text{ even } n,\\ n-2 &{} \text{ for } \text{ odd } n.\end{array}\right. \end{array} \end{aligned}$$

The basis functions for finite element approximation are then obtained by interpolating the unknown displacements \(\mathbf {U}_{j}\), \(j=0,\ldots ,n-1\), on the coupling interface \(\varGamma _{\mathrm {AD}}\), see [14, 18, 19] for all further details.

In summary, this paper aims at extending this coupling strategy to crack propagation, which allows us to consider more complex crack paths and therefore to develop an adapted analytical solution in the analytical domain \(\varOmega _{\mathrm {A}}\).

2.2 Strategy to Model Crack Propagation

A typical approach to model crack propagation by help of the finite element method is based on the idea of a local or global remeshing at each step of the crack propagation. Although this approach can be immediately adapted to our setting, it is well-known that remeshing is computationally costly and inefficient. Alternatively, we prefer to utilise the advantage of the coupled method enabling us to work with a fixed size of the analytical domain \(\varOmega _{\mathrm {A}}\) without involving a global refinement. In this case, we allow the crack to propagate only inside the analytical domain that should be taken as large as possible, while performing refinement on the mesh around \(\varOmega _{\mathrm {A}}\).

Let us now consider more precisely the analytical domain \(\varOmega _{\mathrm {A}}\). At the initial moment, the crack tip is located inside \(\varOmega _{\mathrm {A}}\), and the crack faces are going along the negative direction of the \(x_{1}\)-axis of a Cartesian coordinate system. After the first loading step, the crack is allowed to propagate inside the analytical domain. We assume that the crack propagates with a finite length at one loading step, i.e. the crack tip moves along the propagation direction defined by the angle \(\theta _{i}\) for a finite length \(d_{i}\) with \(i=1,2,\ldots \), denoting the loading step, see Fig. 2. To evaluate the angle \(\theta _{i}\) and the length \(d_{i}\) we have to solve a minimisation problem according to [10], and therefore, to construct an analytical solution to the crack tip problem in \(\varOmega _{\mathrm {A}}\).

Fig. 2
figure 2

Development of the crack inside the analytical domain \(\varOmega _{\mathrm {A}}\) for first few loading steps

Full size image

As already mentioned, the analytical solution (2) cannot be used to calculate the displacement field for the next loading steps, since the basic assumptions of the model are no longer satisfied due to the presence of a kinked crack. This problem can be solved by application of a conformal mapping, which allows us to map the analytical domain after several loading steps (see Fig. 2) to the unit disk. The solution of a boundary value problem in the unit disk can be obtained again by the Kolosov–Muskhelishvili formulae. According to [23], these the Kolosov–Muskhelishvili formulae under a conformal mapping are written as follows

$$\begin{aligned} \displaystyle \sigma _{rr}+\sigma _{\varphi \varphi }= & {} \displaystyle 2\left[ \varPhi (\zeta )+\overline{\varPhi (\zeta )}\right] , \nonumber \\ \displaystyle \sigma _{rr}+i\,\sigma _{r\varphi }= & {} \displaystyle \varPhi (\zeta )+\overline{\varPhi (\zeta )} - \frac{\bar{\zeta }^{2}}{r^{2}\omega '(\zeta )}\left[ \omega (\zeta )\overline{\varPhi '(\zeta )} + \overline{\omega '(\zeta )}\,\overline{\varPsi (\zeta )}\right] ,\nonumber \\ \displaystyle 2\mu |\omega '(\zeta )|(u_{r}+i\,u_{\varphi })= & {} \displaystyle \frac{\bar{\zeta }}{r}\overline{\omega '(\zeta )}\left[ \kappa \,\eta (\zeta ) - \omega (\zeta )\overline{\varPhi (\zeta )}-\overline{\chi (\zeta )}\right] , \end{aligned}$$
(4)

where \(r,\varphi \) denote polar coordinates in the unit disk, \(\zeta =r\exp (i\varphi )\), \(\varPhi (\zeta )\) and \(\varPsi (\zeta )\) are two holomorphic functions defined on the unit disk and, and \(\eta (\zeta )\) and \(\chi (\zeta )\) are functions related to \(\varPhi (\zeta )\), \(\varPsi (\zeta )\) by help of the expressions

$$\begin{aligned} \eta '(\zeta )=\varPhi (\zeta )\omega '(\zeta ), \qquad \chi '(\zeta )=\varPsi (\zeta )\omega '(\zeta ), \end{aligned}$$
(5)

and \(\omega (\zeta )\) is a mapping from the original geometry to the unit disk. Solution of a boundary value in the unit disk and construction of a mapping \(\omega (\zeta )\) is described in detail in Sect. 3.

In addition, if 1, 2 denote Cartesian directions in the original geometry, displacements \(u_{1}\), \(u_{2}\) read according to [23] as follows

$$\begin{aligned} 2\mu (u_{1}+i\,u_{2}) = \kappa \,\eta (\zeta ) - \omega (\zeta )\overline{\varPhi (\zeta )}-\overline{\chi (\zeta )}. \end{aligned}$$
(6)

3 Conformal Mapping for a Cracked Disk and the Riemann–Hilbert Problem

In this section, we discuss the application of conformal mapping to construct an analytical solution for a crack disk and formulation of the corresponding Riemann–Hilbert problem in the unit disk. Moreover, to keep construction general, we do not specify the corresponding conformal mapping explicitly, although the classical Schwarz–Christoffel mapping is the first candidate [8]. We come back to this point later during the discussion in Sect. 5.

3.1 Application of the Conformal Mapping to a Cracked Disk

The idea of using conformal mapping for studying crack propagation within the domain \(\varOmega _{\mathrm {A}}\) is motivated by several facts: (i) analytical solution (2) is not valid for the case of a propagated crack, since the distance between the crack tip and the kinking point is too small to validate the assumptions of the classical crack tip solution; (ii) remeshing is not necessary if the propagating crack does not intersect the coupling interface \(\varGamma _{\mathrm {AD}}\); (iii) analytical constructions are expected to provide higher flexibility and accuracy in calculating mechanical quantities of interest relevant for propagation process [28].

Looking at the crack propagation process from the mechanical point of view, it is known that depending on the specific loading conditions the crack can propagate in different directions controlled by the angle \(\theta _{i}\) with the propagation length \(d_{i}\), where  i is the number of the loading step. Practically it implies, that conformal mappings need to be calculated for all possible directions and lengths, which is a computationally expensive operation to perform online. However, considering that the crack propagates only inside \(\varOmega _{\mathrm {A}}\), conformal mappings can be pre-calculated for different values of the angle \(\theta _{i}^{(k)}\in \left[ -\pi /2,\pi /2\right] \) with i denoting the propagation step and \(k=0,\ldots ,N\) being the number of a specific angle with parameter N controlling the angular discretisation, and having the lengths d as a free parameter in the mapping, see Fig. 3. Note that the crack tip is located at the centre of \(\varOmega _{\mathrm {A}}\) in Fig. 3 only for clarity reasons. In practice, it is better to place the crack tip sufficiently close to the boundary of \(\varOmega _{\mathrm {A}}\) (taking into account the fact that traction-free assumptions on the crack faces must be still satisfied) for addressing more propagation steps inside \(\varOmega _{\mathrm {A}}\) without remeshing.

Fig. 3
figure 3

Mapping between the unit disk and a cracked disk with different possible directions for crack propagation

Full size image

3.2 Boundary Value Problem of Linear Elasticity as a Riemann–Hilbert Problem

Now we will show how a boundary value problem of elasticity can be transformed into a Riemann–Hilbert problem for a piecewise holomorphic function. Let now \(\mathbb {D}=\left\{ \zeta \in \mathbb {C}:|\zeta |<1\right\} \) be the unit disk with the boundary \(\gamma =\left\{ \zeta \in \mathbb {C},\ |\zeta |=1\right\} \), and as a positive direction we choose the counter-clockwise direction, as usual. Let S be a finite domain in the complex z plane bounded by a simple smooth closed contour L, and let

$$\begin{aligned} \omega : \zeta \in \mathbb {D}\mapsto z=\omega (\zeta )\in S \end{aligned}$$

be a mapping, which maps S onto \(\mathbb {D}\) in the plane \(\zeta \). The function \(\omega (\zeta )\) is a holomorphic function inside of \(\gamma \).

By taking complex conjugation of the second equation in Kolosov–Muskhelishvili formulae (4), the following relation is obtained:

$$\begin{aligned} \sigma _{rr}-i\,\sigma _{r\varphi } = \varPhi (\zeta )+\overline{\varPhi (\zeta )} - \frac{\zeta ^{2}}{r^{2}\overline{\omega '(\zeta )}}\left[ \overline{\omega (\zeta )}\varPhi '(\zeta ) + \omega '(\zeta )\,\varPsi (\zeta )\right] . \end{aligned}$$
(7)

For transforming the boundary value problem of linear elasticity in the unit disk of the \(\zeta \)-plane into a Riemann–Hilbert boundary value problem for a holomorphic function, discontinuities of holomorphic functions defined on \(\mathbb {C}{\setminus }\gamma \) need to be described. Therefore, we consider the exterior of the unit disk \(\mathbb {E}:=\mathbb {C}{\setminus }\mathbb {D}\), and we introduce holomorphic reflections as follows

$$\begin{aligned} l_{R} :\zeta \in \mathbb {E}\mapsto \overline{l\left( \frac{1}{\overline{\zeta }}\right) }, \end{aligned}$$
(8)

where the index R stays for reflection of a function and will be used in the sequel. The function \(l_{R}(\zeta )\) is holomorphic in \(\mathbb {E}\), if the function \(l(\zeta )\) is holomorphic in \(\mathbb {D}\).

Let now \(t=e^{i\varphi }\in \gamma \) be a point of the unit circle, and let \(t^+\) and \(t^-\) tend to t from the interior and exterior of the unit disk, respectively. Thus, \(t^+\) and \(t^-\) can be defined as follows

$$\begin{aligned} \left\{ \begin{array}{l} t^{+} := r^{+}e^{i\varphi }\in \mathbb {D} \text{ for } r^+\underset{r^{+}<1}{\rightarrow } 1, \\ \displaystyle {t^{-} := \frac{1}{\overline{t^{+}}}}\in \mathbb {E}. \end{array}\right. \end{aligned}$$
(9)

Let now \(\gamma _{\sigma }\) denotes the part of boundary \(\gamma \), where traction boundary conditions are defined. Note that \(\gamma _{\sigma }\) can be a union of several disjoint arcs, see [22, 23] for details. Considering relations \(\overline{l(t^+)}=\overline{l(1/\overline{t^-})}=l_R(t^-)\), Eq.  (7) can be now rewritten for a point \(t\in \gamma _{\sigma }\) as follows

$$\begin{aligned} \displaystyle \overline{\omega '(t)}\left[ \sigma ^*_{rr}-i\,\sigma ^*_{r\varphi }\right]= & {} \displaystyle \omega _R'(t^-)\varPhi _R(t^-)+\omega _R'(t^-)\varPhi (t^+) \nonumber \\&\displaystyle - t^2\left[ \omega _R(t^-)\varPhi '(t^+) + \omega '(t^+)\,\varPsi (t^+)\right] , \end{aligned}$$
(10)

where \(\omega _R'\) is the reflection of the derivative function, and the left-hand side represents a known stress function on the boundary \(\gamma _{\sigma }\) with \(\sigma ^*_{rr}\) and \(\sigma ^*_{r\varphi }\) being imposed stresses on \(\gamma _{\sigma }\).

To formulate a classical Riemann–Hilbert problem for a holomorphic function we need to rewrite Eq. (10) in terms of only one holomorphic function, rather than a combination of several functions as it is written at the moment. For that we need to introduce an additional assumption: the conformal mapping has to be holomorphic on the entire complex plane \(\mathbb {C}\) and not only on the unit disk \(\mathbb {D}\)

$$\begin{aligned} \omega :\zeta \in \mathbb {C}\mapsto \omega (\zeta ). \end{aligned}$$

Consequently, \(\omega _R(\zeta )\) is also defined on the entire complex plane and, in particular, in the interior of the unit disk \(\mathbb {D}\). Hence, \(\omega _R(t^-)\) and \(\omega _R'(t^-)\) can be replaced by \(\omega _R(t^+)\) and \(\omega _R'(t^+)\) in (10), respectively. It should be noted that if \(\omega (\zeta )\) has a pole at infinity of order not higher than N, then the asymptotic expansion \(\omega (\zeta )\) at the infinity can be written as follows

$$\begin{aligned} \omega (\zeta )\underset{\left| z\right| \rightarrow +\infty }{=}\sum _{k=0}^N\omega _k\zeta ^k. \end{aligned}$$

In addition, if \(\omega (\zeta )\) has a pole at infinity, then \(\omega _R(\zeta )\) has a pole at zero and the asymptotic expansion have the form

$$\begin{aligned} \omega _R(\zeta )\underset{\left| z\right| \rightarrow 0}{=}\sum _{k=0}^N\frac{\overline{\omega }_k}{\zeta ^k}. \end{aligned}$$
(11)

Let us consider the following holomorphic function on \(\mathbb {C}{\setminus }\gamma \)

$$\begin{aligned} \varOmega :\zeta \in \mathbb {C}{\setminus }\gamma \mapsto \left\{ \begin{array}{ll} \displaystyle {\omega _R'(\zeta )\varPhi (\zeta )-\zeta ^2\left[ \omega _R(\zeta )\varPhi '(\zeta ) + \omega '(\zeta )\,\varPsi (\zeta )\right] }, &{} \text{ if } \left| \zeta \right| <1,\\ \\ \displaystyle -\omega _R'(\zeta )\varPhi _R(\zeta ), &{} \text{ if } \left| \zeta \right| >1, \end{array} \right. \end{aligned}$$
(12)

where the origin has been removed from the domain for the case if \(\omega _R(\zeta )\) has a pole at zero. However, if \(\omega _R(\zeta )\) does not have a pole at the origin, then the origin should be added to the domain. The boundary condition (10) can now be written as

$$\begin{aligned} \overline{\omega '(t)}\left[ \sigma ^*_{rr}(t)-i\,\sigma ^*_{r\varphi }(t)\right] =\varOmega (t^+)-\varOmega (t^-). \end{aligned}$$
(13)

Similar to \(\gamma _{\sigma }\), we denote by \(\gamma _{u}\) the part of \(\gamma \), where displacements are prescribed. Again, \(\gamma _{u}\) can be a union of several disjoint arcs. From (6) and by help of variables \(t^+\) the formula for displacement boundary condition for a point \(t\in \gamma _{u}\) can be written as follows

$$\begin{aligned} 2\mu (u^*_1-iu^*_2)=\kappa \overline{\eta (t^+)}-\overline{\omega (t^+)}\varPhi (t^+)-\chi (t^+), \end{aligned}$$

where \(u^*_1\) and \(u^*_2\) are known displacements along Cartesian directions in the original domain S imposed on \(\gamma _u\) considered as a function of \(\varphi \). Finally, we need a formula for \(\left( u_{1}^{*}\right) ' - i\left( u_{2}^{*}\right) '\) with

$$\begin{aligned} \left( u_{1}^{*}\right) ' = \frac{\partial u_{1}^{*}}{\partial \varphi }, \qquad \left( u_{2}^{*}\right) ' = \frac{\partial u_{2}^{*}}{\partial \varphi }. \end{aligned}$$

Differentiating the previous formula we obtain

$$\begin{aligned} \displaystyle -2\mu i t\left[ \left( u_{1}^{*}\right) '-i\left( u_{2}^{*}\right) '\right]= & {} \displaystyle \overline{\omega '(t^+)}\varPhi (t^+)- \kappa \overline{\omega '(t^+)}\overline{\varPhi (t^+)} \nonumber \\&\displaystyle - t^2\left( \overline{\omega (t^+)}\varPhi '(t^+)+\omega '(t^+)\varPsi (t^+)\right) , \end{aligned}$$
(14)

where the relations \(\eta '(\zeta )=\omega '(\zeta )\varPhi (\zeta )\) and \(\chi '(\zeta )=\omega '(\zeta )\varPsi (\zeta )\) have been used. Taking into account the assumption that \(\omega (\zeta )\) is defined on \(\mathbb {C}\), we finally get

$$\begin{aligned} \displaystyle -2\mu i t\left[ \left( u_{1}^{*}\right) '-i\left( u_{2}^{*}\right) '\right]= & {} \displaystyle \omega _R'(t^+)\varPhi (t^+)-\kappa \omega _R'(t^-)\varPhi _R(t^-) \\&\displaystyle - t^2\left( \omega _R(t^+)\varPhi '(t^+)+\omega '(t^+)\varPsi (t^+)\right) , \end{aligned}$$

or in terms of function (12),

$$\begin{aligned} -2\mu i t\left[ \left( u_{1}^{*}\right) '-i\left( u_{2}^{*}\right) '\right] = \varOmega (t^+)+\kappa \varOmega (t^-). \end{aligned}$$
(15)

Thus, we get the following Riemann–Hilbert problem for the holomorphic function \(\varOmega \)

$$\begin{aligned} \left\{ \begin{array}{rcl} \displaystyle \varOmega (t^+)-\varOmega (t^-)&{} = &{} f(t) \text{ on } \gamma _{\sigma },\\ \displaystyle \varOmega (t^+)+\kappa \varOmega (t^-) &{} = &{} f(t) \text{ on } \gamma _u, \end{array} \right. \end{aligned}$$
(16)

with boundary function f(t) defined by

$$\begin{aligned} f(t):=\left\{ \begin{array}{lcl} \overline{\omega '(t)}\left[ \sigma ^*_{rr}-i\,\sigma ^*_{r\varphi }\right] &{}\text {on}&{}\gamma _{\sigma },\\ \displaystyle {-2\mu i t\left[ \left( u_{1}^{*}\right) '-i\left( u_{2}^{*}\right) '\right] }&{}\text {on}&{}\gamma _u. \end{array} \right. \end{aligned}$$
(17)

It should be noted that the imposed normal and tangential stresses \(\sigma ^*_{rr}\) and \(\sigma ^*_{r\varphi }\) on \(\gamma _{\sigma }\) correspond to polar directions in the \(\zeta \)-plane, although the imposed displacements \(u^*_1\) and \(u^*_2\) on \(\gamma _u\) correspond to Cartesian directions in the z-plane. However, both imposed stresses and displacements are seen as functions of \(\varphi \), or equivalently t, in the \(\zeta \)-plane.

3.3 Solution of the Riemann–Hilbert Boundary Value Problem in the Unit Disk for a General Case

In this section we describe at first the solution of the Riemann–Hilbert problem (16) for a general case, and later we specify it for the considered problem. Consider that \(\gamma _{u}\) is the union of n arcs such as \(\gamma _u =\bigcup _{k=1}^n(a_k,b_k)\). Let us consider the following holomorphic function on \(\mathbb {C}{\setminus }\gamma _u\)

$$\begin{aligned} X_{0}:\zeta \in \mathbb {C}{\setminus }\gamma _u\mapsto \prod \limits _{k=1}^{n}(\zeta -a_{k})^{-1/2+i\beta }(\zeta -b_{k})^{-1/2-i\beta }, \text{ with } \beta =\frac{\log \kappa }{2\pi }. \end{aligned}$$
(18)

Taking into account displacement and traction boundary conditions given on \(\gamma _{u}\) and \(\gamma _{\sigma }\), it is well known that the following classical relations hold [22]:

$$\begin{aligned} \frac{X_0(t^+)}{X_0(t^-)}=-\kappa \text { on }\gamma _{u} \text{ and } \frac{X_0(t^+)}{X_0(t^-)}=1\text { on }\gamma _{\sigma }. \end{aligned}$$

Thus, the mixed boundary value problem (16) can be reduced to the following problem for \(\frac{\varOmega (\zeta )}{X_0(\zeta )}\)

$$\begin{aligned} \frac{\varOmega (t^+)}{X_0(t^+)}-\frac{\varOmega (t^-)}{X_0(t^-)}=\frac{f(t)}{X_0(t^+)} \text{ on } \gamma =\gamma _{\sigma }\cup \gamma _{u}. \end{aligned}$$
(19)

Solution of (19) requires describing the asymptotic behaviour of \(\varOmega (\zeta )/X_0(\zeta )\). For that, we recall that the function \(\varPhi (\zeta )\) is holomorphic in \(\mathbb {D}\), and therefore, we have

$$\begin{aligned} \left\{ \begin{array}{rcl} \displaystyle \varPhi (\zeta ) &{} = &{} \displaystyle \sum _{k=0}^{+\infty }A_k\zeta ^k, \text{ if } \left| \zeta \right| <1,\\ \\ \displaystyle \varPhi _R(\zeta ) &{} = &{} \displaystyle \sum _{k=0}^{+\infty }\frac{\overline{A}_k}{\zeta ^k}, \text{ if } \left| \zeta \right| >1,\\ \end{array}\right. \end{aligned}$$

where \(A_{k},k=0,1,\ldots \), are unknown coefficients of the decomposition. Next, using the fact that \(\omega '_R(\zeta )\underset{\left| \zeta \right| \rightarrow +\infty }{\rightarrow }\omega '(0)\) and definition of \(\varOmega (\zeta )\), we obtain the following asymptotic expansion

$$\begin{aligned} \varOmega (\zeta )\underset{\left| \zeta \right| \rightarrow +\infty }{=} B_{0}+\frac{B_{1}}{\zeta }+\frac{B_{2}}{\zeta ^2}+\cdots , \end{aligned}$$

where \(B_{0},B_{1},\ldots \) are unknown coefficients. The asymptotic expansion of \(1/X_0(\zeta )\) is obtained from (18) as follows

$$\begin{aligned} \frac{1}{X_0(\zeta )}\underset{\left| \zeta \right| \rightarrow +\infty }{=}\zeta ^n+D_{n-1}\zeta ^{n-1}+\cdots +D_{1}\zeta +D_0+\frac{D_{-1}}{\zeta }+\cdots , \end{aligned}$$
(20)

where \(D_{n-1},\ldots ,D_{0},\ldots \) are known coefficients obtained by an asymptotic expansion of \(1/X_0(\zeta )\). Finally, it is evident that there exists a polynomial of degree not higher than n

$$\begin{aligned} P_{n}(\zeta )=\widehat{C}_{0} + C_{1}\zeta + \ldots + C_{n}\zeta ^{n}, \end{aligned}$$
(21)

such that

$$\begin{aligned} \frac{\varOmega (\zeta )}{X_0(\zeta )}-P_{n}(\zeta )\underset{\left| \zeta \right| \rightarrow +\infty }{\rightarrow }0. \end{aligned}$$
(22)

If \(\omega _R(\zeta )\) has a pole at the origin, then the asymptotic expansion of \(\varOmega (\zeta )/X_0(\zeta )\) at the origin has to be determined. If the order of this pole of \(\omega _R(\zeta )\) is not higher than N, as it has been shown in (11), then the pole of \(\omega _R'(\zeta )\) at the origin is not higher than \(N-1\). Considering that the value of \(X_{0}(\zeta )\) at the origin is a non-zero constant, it follows from (12) that there exists a function \(Q_N(\zeta )\) of the form

$$\begin{aligned} Q_N(\zeta )=\widetilde{C}_0+\frac{C_{-1}}{\zeta }+\cdots +\frac{C_{-(N-1)}}{\zeta ^{N-1}}, \end{aligned}$$

such that

$$\begin{aligned} \frac{\varOmega (\zeta )}{X_0(\zeta )}-Q_{N}(\zeta )\underset{\left| \zeta \right| \rightarrow 0}{\rightarrow }0. \end{aligned}$$
(23)

Introducing a new constant \(C_0:=\widehat{C}_0+\widetilde{C}_0\), we finally obtain:

$$\begin{aligned} R(\zeta )=P_n(\zeta )+Q_N(\zeta )=C_n\zeta ^n+\cdots +C_0+\frac{C_{-1}}{\zeta } +\cdots +\frac{C_{-(N-1)}}{\zeta ^{N-1}}. \end{aligned}$$

Thus, the general solution of (16) is given now by

$$\begin{aligned} \varOmega (\zeta )=\varOmega _0(\zeta )+X_0(\zeta )R(\zeta ) \text{ with } \varOmega _0(\zeta )=\frac{X_0(\zeta )}{2i\pi }\int _{\gamma }\frac{f(t)\text {d}t}{X_0(t^+)(t-\zeta )}, \end{aligned}$$
(24)

where the integration is taken over the whole boundary \(\gamma \). The coefficients \(C_{-(N-1)},\ldots ,C_0,\ldots ,C_n\) should be identified by ensuring displacement continuity at ends of the arcs \(a_k\) and \(b_k\) and by ensuring that there is no stress and displacement singularities at zero.

Finally, holomorphic functions \(\varPhi (\zeta )\) and \(\varPsi (\zeta )\) can be easily derived from (24) and therefore displacements and stresses are obtained in S.

3.4 Solution of the Riemann–Hilbert Boundary value Problem in the Unit Disk for the Considered Crack Configuration

Next, we discuss the construction of an explicit solution of the Riemann–Hilbert problem for the crack propagation process shown in Fig. 2. Domain \(\varOmega _{\mathrm {A}}\) with a kinked crack can be considered as a circular-arc polygon with vertices \(w_{i}\), \(i=1,\ldots n\), which are located along the crack path, and we keep the convention that vertex \(w_{(n+1)/2}\) is located at the crack tip. Since according to the coupling idea, displacements are interpolated on the whole coupling interface \(\varGamma _{\mathrm {AD}}\), no extra vertices are required on \(\varGamma _{\mathrm {AD}}\), and the fact of having several coupling elements will be addressed by piecewise definition of the boundary function f(t) in (16). Thus, vertices \(w_{i}\), \(i=1,\ldots n\), are mapped to the corresponding pre-vertices at the unit circle \(\gamma \) denoted by \(z_{i}\), \(i=1,\ldots n\), see Fig. 4.

Fig. 4
figure 4

Vertices and pre-vertices for the mapping between the unit disk and a cracked disk during the crack propagation process

Full size image

Thus, in the case of analytical–numerical coupling the unit circle \(\gamma \) is subdivided into arcs \(\gamma _{u}=z_{n}z_{1}\) with unknown displacement boundary conditions given by the interpolation function (3), and \(\gamma _{\sigma } = \bigcup _{i=1}^{n-1} z_{i}z_{i+1}\) with traction-free conditions on the crack faces. Therefore, considering that only one arc with displacement boundary conditions is given and assuming that \(\omega _R(\zeta )\) has no pole at the origin, a general solution (16) can be written as follows

$$\begin{aligned} \varOmega (\zeta ) = \frac{X_{0}(\zeta )}{2\pi i\kappa }\int \limits _{\gamma }\frac{f(t)dt}{X_{0}^{+}(t)(t-\zeta )} + X_{0}(\zeta )\left[ C_{0}+C_{1}\zeta \right] , \end{aligned}$$
(25)

where

$$\begin{aligned} X_{0}(\zeta )=(\zeta -z_{1})^{-1/2-i\beta }(\zeta -z_{n})^{-1/2+i\beta }, \text{ with } \beta =\frac{\log \kappa }{2\pi }. \end{aligned}$$

Applying displacement boundary conditions on \(\varGamma _{\mathrm {AD}}\) and traction-free conditions on the crack faces, the following system of equations for unknown coefficients is obtained

$$\begin{aligned} \left\{ \begin{array}{rcl} \displaystyle (\kappa +1)\int \limits _{z_{n}z_{1}}\varOmega _{0}(t_{0})\omega '(t_{0})dt_{0} \\ \\ \displaystyle + (\kappa +1)\int \limits _{z_{n}z_{1}}\omega '(t_{0})X_{0}(t_{0})(C_{0} + C_{1}t_{0})dt_{0} &{} = &{} \displaystyle 2\mu [f(z_{1})-f(z_{n})], \\ \\ \displaystyle \frac{X_{0}(0)}{2\pi \,i\kappa }\int \limits _{\gamma }\frac{f(t)}{X_{0}^{+}(t)}\frac{dt}{t} + C_{0}X_{0}(0) + \overline{C}_{1} &{} = &{} 0, \end{array}\right. \end{aligned}$$
(26)

with

$$\begin{aligned} \varOmega _{0}(t_{0}) = \frac{X_{0}(t_{0})}{2\pi \,i\kappa }\int \limits _{\gamma }\frac{f(t)dt}{X_{0}^{+}(t)(t-t_{0})}, \end{aligned}$$

and

$$\begin{aligned} \displaystyle X_{0}(0) = \lim \limits _{\zeta \rightarrow 0}\left[ (\zeta -z_{1})^{-1/2-i\beta }(\zeta -z_{n})^{-1/2+i\beta }\right] = e^{-i\pi }e^{-i(\varphi _{1}+\varphi _{n})/2}e^{-\beta (\varphi _{n}-\varphi _{1})}, \end{aligned}$$

where the fact that \(\ln |z_{1}|\) and \(\ln |z_{n}|\) are zero on the unit disk has been taken into account. Denoting by \(\varphi _{0}\) the argument of the middle of the arc \(z_{n}z_{1}\), and by \(\omega _{0}\) its central angle, the expression for \(X_{0}(0)\) can be simplified to

$$\begin{aligned} X_{0}(0)=-e^{-i\varphi _{0}-\beta \omega _{0}}. \end{aligned}$$

To identify constants \(C_{0}\) and \(C_{1}\), system (26) can be transformed into its real form and solved explicitly. To avoid bulky expressions, we omit the presentation of the explicit solution of the corresponding real 4 by 4 system here. Nonetheless, the whole procedure remains the same at each step of the crack propagation process as long as the boundary conditions of the Riemann–Hilbert problem are kept as described in this section. The main computational complexity is related to numerical calculation of the conformal mapping.

4 Energetic Approach to Crack Propagation

In this section, the mechanical point of view on the crack propagation based on the energetic formulation proposed in [10] is described. Similar to previous sections, we describe a general setting of the energetic approach at first, and after that, we specify it for the problem considered in the paper.

Consider now time-dependent Neumann boundary conditions \(\mathbf {F}(t)\) given on \(\varGamma _{1}\), then for any time t, the crack geometry \(\varGamma _{c}(t)\) is obtained by finding the global minimum of the total energy \(\mathcal {E}^{\text {tot}}\) under the assumption of irreversibility of the crack growth, i.e. the crack can only grow. The total energy for the Neumann boundary conditions \(\mathbf {F}^{*}\) on \(\varGamma _{1}\) and for any crack geometry \(\varGamma _{c}^{*}\) is expressed as follows

$$\begin{aligned} \mathcal {E}^{\text {tot}}(\mathbf {F}^{*},\varGamma _{c}^{*}) := \mathcal {E}(\mathbf {F}^{*},\varGamma _{c}^{*})-\mathcal {W}(\mathbf {F}^{*},\varGamma _{c}^{*})+\mathcal {D}(\varGamma _{c}^{*}), \end{aligned}$$

where the stored elastic energy \(\mathcal {E}(\mathbf {F}^{*},\varGamma _{c}^{*})\), the work of external forces \(\mathcal {W}(\mathbf {F}^{*},\varGamma _{c}^{*})\), and the dissipated energy \(\mathcal {D}(\varGamma _{c}^{*})\), are given by

$$\begin{aligned} \displaystyle \mathcal {E}(\mathbf {F}^{*},\varGamma _{c}^{*})= & {} \displaystyle \frac{1}{2}\int _{G}\varvec{\sigma }(\mathbf {F}^{*},\varGamma _{c}^{*}):\varvec{\varepsilon }(\mathbf {F}^{*},\varGamma _{c}^{*})\text {d}V, \\ \displaystyle \mathcal {W}(\mathbf {F}^{*},\varGamma _{c}^{*})= & {} \displaystyle \int _{\varGamma _{1}}\mathbf {F}^{*}\cdot \mathbf {u}(\mathbf {F}^{*},\varGamma _{c}^{*})\text {d}S, \quad \mathcal {D}(\varGamma _{c}^{*})=G_{c}\int _{\varGamma _{c}^{*}}\text {d}l, \end{aligned}$$

where \(\varvec{\sigma }\) is the stress tensor, \(\varvec{\varepsilon }\) the strain tensor and \(\mathbf {u}\) the displacement vector. Based on the above consideration, the energetic criterion can now be formulated as follows [10]:

$$\begin{aligned} \left\{ \begin{array}{ll} (a): &{} \displaystyle \forall \, s<t,\,\varGamma _c(s)\subset \varGamma _{c}(t),\\ \\ (b): &{} \displaystyle \forall \, \varGamma _{c}(t)\subset \varGamma _{c}^{*},\,\mathcal {E}^{\text {tot}}(\mathbf {F}(t),\varGamma _{c}(t))\le \mathcal {E}^{\text {tot}}(\mathbf {F}(t),\varGamma _{c}^{*}), \\ \\ (c): &{} \displaystyle {\forall \, s<t,\,\mathcal {E}^{\text {tot}}(\mathbf {F}(t),\varGamma _{c}(t))\le \mathcal {E}^{\text {tot}}(\mathbf {F}(t),\varGamma _{c}(s))}. \end{array}\right. \end{aligned}$$
(27)

Let us make some remarks regarding the criterion: condition (a) corresponds to the constraint of irreversibility of the crack growth; the condition (b) ensures that the total energy for the actual crack is lower than for any longer crack; and condition (c) ensures that the total energy of the actual crack is lower than for any previous real crack considering the actual boundary conditions.

Energetic criterion (27) is formulated for a continuous time, in practice, however, a time discretisation \(t_{1}< \ldots <t_{n}\) is introduced with \(t_{1}\) corresponding to the initial configuration. Thus, according to (27), knowing the crack geometry \(\varGamma _{c}(t_{j-1})\) at the time step \(j-1\), the crack geometry \(\varGamma _{c}(t_j)\) at the time step j (with \(1\le j\le n\)) is determined as follows

$$\begin{aligned} \varGamma _c(t_j)=\underset{\varGamma _{c}(t_{j-1})\subset \varGamma _{c}^{*}}{\text {argmin}} \left[ \mathcal {E}^{\text {tot}}(\mathbf {F}(t_{j}),\varGamma _{c}^{*})\right] \end{aligned}$$
(28)

Indeed, for any time discretisation, (28) clearly implies (27).

In general, the total energy \(\mathcal {E}^{\text {tot}}(\mathbf {F}(t_{j}),\varGamma _{c}^{*})\) depends on the stress and displacement field in the whole domain \(\varOmega \). However, under the assumption that the crack can propagate only inside the analytical domain \(\varOmega _{\mathrm {A}}\), minimisation problem (28) can be formulated locally. In this case of local formulation, Neumann boundary conditions \(\mathbf {F}_{\mathrm {A}}\) on the coupling interface \(\varGamma _{\mathrm {AD}}\) are considered. These Neumann boundary conditions are obtained at each step of propagation j and for each trial of new crack geometry by solving the continuous coupling with finite element method. Indeed, as the crack growth tends to relax strain and stress, the Neumann boundary conditions \(\mathbf {F}_{\mathrm {A}}\) needs to be re-computed for any tested evolution of the crack geometry. However, as the analytical domain \(\varOmega _{\mathrm {A}}\) is chosen to cover the largest possible area in the elastic body, the computational cost is expected to be reduced. Such a local formulation would not be possible in the classical finite element setting without using elements of higher regularity, since traces of generalised derivatives of basis functions are needed in order to obtain Neumann data on \(\varGamma _{\mathrm {AD}}\). However, this problem does not appear in the case of analytical–numerical coupling described in previous sections, since a strong solution to the differential equation in \(\varOmega _{\mathrm {A}}\) is constructed. Thus, Neumann data on \(\varGamma _{\mathrm {AD}}\) can be obtained straightforwardly.

So, to formulate the minimisation problem, we consider Neumann boundary conditions \(\mathbf {F}_{\mathrm {A}}\), which are formally determined as a function of \(\mathbf {F}(t)\) and \(\varGamma _{c}^{*}\), on the coupling interface \(\varGamma _{\mathrm {AD}}\) for any crack \(\varGamma _{c}^{*}\). Then, minimisation problem (28) can be reduced to:

$$\begin{aligned} \varGamma _c(t_j)=\underset{\varGamma _{c}(t_{j-1})\subset \varGamma _{c}^{*}}{\text {argmin}}\left[ \mathcal {E}_{\mathrm {A}}^{\text {tot}}(\mathbf {F}_{\mathrm {A}} \left[ \mathbf {F}(t_{j}),\varGamma _{c}^{*}\right] ,\varGamma _{c}^{*})\right] , \end{aligned}$$
(29)

where the local total energy \(\mathcal {E}_{\mathrm {A}}^{\text {tot}}(\mathbf {F}^{*}_{\mathrm {A}},\varGamma _{c}^{*})\) is given by

$$\begin{aligned} \mathcal {E}_{\mathrm {A}}^{\text {tot}}(\mathbf {F}^{*}_{\mathrm {A}},\varGamma _{c}^{*}) =\mathcal {E}_{\mathrm {A}}(\mathbf {F}^{*}_{\mathrm {A}},\varGamma _{c}^{*}) -\mathcal {W}_{\mathrm {A}}(\mathbf {F}^{*}_{\mathrm {A}},\varGamma _{c}^{*})+\mathcal {D}(\varGamma _{c}^{*}), \end{aligned}$$

with the elastic energy \(\mathcal {E}_{\mathrm {A}}(\mathbf {F}^{*}_{\mathrm {A}},\varGamma _{c}^{*})\) stored in the analytical domain \(\varOmega _{\mathrm {A}}\), and the work of forces \(\mathcal {W}_{\mathrm {A}}(\mathbf {F}^{*}_{\mathrm {A}},\varGamma _{c}^{*})\) on the coupling interface \(\varGamma _{\mathrm {AD}}\) are given by

$$\begin{aligned} \displaystyle \mathcal {E}_{\mathrm {A}}(\mathbf {F}^{*}_{\mathrm {A}},\varGamma _{c}^{*})= & {} \displaystyle \frac{1}{2}\int _{\varOmega _{\mathrm {A}}}\varvec{\sigma }(\mathbf {F}^{*}_{\mathrm {A}},\varGamma _{c}^{*}):\varvec{\varepsilon }(\mathbf {F}^{*}_{\mathrm {A}},\varGamma _{c}^{*})\text {d}V, \nonumber \\ \displaystyle \mathcal {W}_{\mathrm {A}}(\mathbf {F}^{*}_{\mathrm {A}},\varGamma _{c}^{*})= & {} \displaystyle \int _{\varGamma _{\mathrm {AD}}}\mathbf {F}^{*}_{\mathrm {A}}\cdot \varvec{u}(\mathbf {F}^{*}_{\mathrm {A}},\varGamma _{c}^{*})\text {d}S. \end{aligned}$$
(30)

Thus, formulation (29) presents the advantage that the analytical solution of the Riemann–Hilbert problem described in Sect. 3 is used to compute at each time step j the total energy \(\mathcal {E}_{\mathrm {A}}^{\text {tot}}\). Indeed, for all \(\mathbf {F}^{*}_{\mathrm {A}}\) and \(\varGamma _{c}^{*}\) one can compute analytically \(\varvec{\sigma }(\mathbf {F}^{*}_{\mathrm {A}},\varGamma _{c}^{*})\), \(\varvec{\varepsilon }(\mathbf {F}^{*}_{\mathrm {A}},\varGamma _{c}^{*})\) and \(\varvec{u}(\mathbf {F}^{*}_{\mathrm {A}},\varGamma _{c}^{*})\) involved in (30).

5 First Example Towards a Complete Numerical Scheme

The aim of this section is twofold: first, we briefly discuss the difficulties related to practical implementation of the complete solution strategy presented in this paper, and recall some of possible approaches to overcome these difficulties, which will constitute the future work; after that, we present a small numerical example focusing only on the use of conformal mapping and the Riemann–Hilbert problem, since these are the crucial parts of the complete algorithm to model crack propagation in elastic bodies. Moreover, we outline clearly all problems related to the numerical stability of the method, since overcoming these problems constitute the major part of future work.

The analytical domain \(\varOmega _{\mathrm {A}}\) containing a crack is a circular-arc polygon, with crack-faces representing the polygonal part and the coupling interface \(\varGamma _{\mathrm {AD}}\) being the circular arc. The idea of the method presented in this paper is to map the circular-arc polygon to the unit disk, because Riemann–Hilbert problems in the unit disk are well studied in the context of linear elasticity, see for example [11, 22]. While there are several classical works studying conformal mappings of circular arc-polygon regions, see for example [4, 8] and references therein, it is well-known that an explicit representation of a mapping function between a circular-arc polygon and the unit disk does not exist. The classical approach to construct a mapping function for such type of domains is to work with the Schwarz–Christoffel differential equation.

Because the Schwarz–Christoffel differential equation is ill-posed due to non-linear constrains for the parameters of the map, it is known that its numerical solution is a challenging task, although some methods for numerical calculations of such mappings exist [2, 5, 16]. An alternative approach would be to directly use algorithms for numerical conformal mapping, such as for example the osculation algorithms [15, 27]. However, the main obstacle for the use of numerical conformal mapping in the context of coupled method is the fact, that not only the geometry must be mapped, as typically addressed in the field of numerical conformal mappings, but the differential equation and its solution procedure as well. Thus, it must be studied how the solution of Riemann–Hilbert problem in our case will behave under a numerical conformal mapping.

Because of difficulties discussed above in the way of implementing the complete numerical procedure presented in this paper, we present an illustrative example focusing only on the crack propagation based on the solution of the Riemann–Hilbert problem. Thus, instead of considering a global boundary value problem in a domain G, we consider a boundary value problem formulated directly in the analytical domain \(\varOmega _{\mathrm {A}}\) and boundary conditions on the coupling interface \(\varGamma _{\mathrm {AD}}\). Additionally, to avoid a circular-arc polygon mapping, we consider a square domain centred at the crack tip of the initial configuration.

Let us consider an infinite plane containing a single crack of length 2a with constant stresses \(\mathbf {p}\) applied at infinity (Fig. 5, left). To formulate a boundary value problem, we consider a square domain of length L located around one of the crack tips (Fig. 5, right) representing the analytical domain \(\varOmega _{\mathrm {A}}\). To keep the illustrative example closer to the setting discussed in Sect. 3, displacement boundary conditions are considered on the interface \(\varGamma _{\mathrm {AD}}\) and traction-free conditions on the crack faces \(\varGamma _{\mathrm {c}}\). Thus, we consider the following boundary value problem

$$\begin{aligned} \left\{ \begin{array}{rcll} -\mu \,\varDelta \mathbf {u}-(\lambda +\mu )\,\mathrm {grad}\,\mathrm {div}\,\mathbf {u} &{} = &{} 0, &{} \text{ in } \varOmega _{\mathrm {A}},\\ \mathbf {u} &{} = &{} u_{1}+iu_{2}, &{} \text{ on } \varGamma _{\mathrm {AD}},\\ \displaystyle \varvec{\sigma }\cdot \overline{n} &{} = &{} 0, &{} \text{ on } \varGamma _{\mathrm {c}}, \end{array}\right. \end{aligned}$$

where the displacements components \(u_{1}\) and \(u_{2}\) are chosen according to the well-known analytical solution, see for example [20], and are given by the following formulae:

$$\begin{aligned} \begin{array}{rcl} \displaystyle u_{1} &{} = &{} \displaystyle \frac{p\sqrt{2ra}}{8\mu }\left[ (2\kappa -1)\cos \left( \frac{\varphi }{2}\right) - \cos \left( \frac{3\varphi }{2}\right) \right] , \\ \\ \displaystyle u_{2} &{} = &{} \displaystyle \frac{p\sqrt{2ra}}{8\mu }\left[ (2\kappa +1)\sin \left( \frac{\varphi }{2}\right) - \sin \left( \frac{3\varphi }{2}\right) \right] , \end{array} \end{aligned}$$

with r, \(\varphi \) being polar coordinates with the coordinate origin located at the crack tip, and \(\kappa \) and \(\mu \) being material parameters.

Fig. 5
figure 5

Setting for the illustrative example: crack in an infinite body (left), representation of the analytical domain \(\varOmega _{\mathrm {A}}\) with the coupling interface \(\varGamma _{\mathrm {AD}}\) as a square (right)

Full size image

For a numerical conformal mapping of the domain \(\varOmega _{\mathrm {A}}\), in general, the classical Schwarz–Christoffel toolbox for Matlab developed by Driscoll [7] can be used. However, using this toolbox implies the necessity to work with the inverse Schwarz–Christoffel mapping in all constructions presented in Sect. 3, which complicates the numerical part. Therefore, instead of the Schwarz–Christoffel toolbox, the PlgCirMap Matlab toolbox will be used, which has been introduced recently in [24]. The PlgCirMap toolbox allows mapping of polygonal multiply connected domains onto circular domains by using Koebe’s iterative method. Fig. 6 shows the domain \(\varOmega _{\mathrm {A}}\) and the unit disk together with the conformal grid calculated by the PlgCirMap toolbox.

Fig. 6
figure 6

Domain \(\varOmega _{\mathrm {A}}\) together with the conformal grid (left), and the unit disk with the conformal grid obtained after calculating the conformal mapping from \(\varOmega _{\mathrm {A}}\) by using the PlgCirMap toolbox

Full size image

The advantage of using the PlgCirMap toolbox is the fact that the direct mapping from the polygonal domain \(\varOmega _{\mathrm {A}}\) to the unit disk can be used in all constructions presented in Sect. 3, which significantly simplifies all related calculations. Nonetheless, although the PlgCirMap toolbox provides a lot of useful functions for numerical conformal mapping, it is also not free of geometrical restrictions: polygonal domains with slits and cusps are not allowed. To overcome this restriction, we model the crack in a domain as a cut with width of order \(10^{-4}\). In this case, the conformal mapping to the unit disk can be calculated with the relative residual of order \(10^{-5}\). The vertices calculated during the conformal mapping, as well as pre-vertices of the original domain, are listed in Table 1. Because some vertices are located very close to each other, we list the coordinates of vertices in a long format provided by Matlab.

Table 1 Vertices and pre-vertices for the conformal mapping
Full size table

Let us now outline the general procedure for constructing a solution of the Riemann–Hilbert problem:

  1. Step 1.

    Map the domain \(\varOmega _{\mathrm {A}}\) to the unit disk.

  2. Step 2.

    Map boundary conditions from \(\varOmega _{\mathrm {A}}\) to the unit disk.

  3. Step 3.

    Create and solve linear system of Eqs. (26).

  4. Step 4.

    Compute the general solution of Riemann–Hilbert problem in the unit disk by help of formula (25).

Figure 7 shows the solution of Riemann–Hilbert problem in the unit disk with respect to \(\varphi \in [-\pi ,\pi ]\) and for \(r=1/2\). It is also important to remark, that the solution of a linear system in Step 3 can be written explicitly in our case, implying that no numerical procedure is necessary to solve the linear system. Nonetheless, computing the solution is still numerically difficult, because several singular integrals need to be calculated in Step 3, since they appear in the coefficients of the system and in the right-hand side. Thus, the quality of the solution of the Riemann–Hilbert problem (and further computations with it) strongly depends on calculation of these singular integrals. However, because four of the eight vertices are located very close to each other, see Table 1, they cause numerical stability issues during computing the singular integrals. In the example presented in this section, the singular integrals could be computed only with the accuracy of order \(10^{-1}\) by using built-in Matlab adaptive quadratures. Evidently, this accuracy is not sufficient for further calculations of stresses and displacements. Therefore, one of the tasks for future work is finding a numerical quadrature for computing singular integrals with the accuracy of the same order as provided by numerical conformal mapping.

Fig. 7
figure 7

Domain \(\varOmega _{\mathrm {A}}\) together with the conformal grid (left), and the unit disk with the conformal grid obtained after calculating the conformal mapping from \(\varOmega _{\mathrm {A}}\) by using the PlgCirMap toolbox

Full size image

6 Summary and Outlook

In this paper, we have presented the theoretical background of a coupled analytical–numerical approach to model a crack propagation process in two-dimensional bounded domains. The main idea of the method is to obtain the correct solution behaviour near the crack tip by help of the analytical solution constructed by using tools of the complex function theory and couple it continuously with the finite element solution in the region far from singularity. To calculate possible directions of crack growth, the idea is to utilise the conformal mapping techniques and to transform a problem of linear elasticity into a Riemann–Hilbert problem in the unit disk for holomorphic functions. In the paper, we have presented the analytical solution of the Riemann–Hilbert problem, as well as discussed numerical stability issues appearing on the way of practical realisation of the method, proposed in this paper.

As has been discussed in Sect. 5, the main difficulty of the method is related to the need of having a conformal mapping between a circular-arc polygon and the unit disk. Unfortunately, this mapping cannot be expressed explicitly by help of known conformal mappings. Therefore, we have considered a simplified version of a problem in Sect. 5, where a circular domain has been replaced by a rectangular domain. Nonetheless, even in that case, further studies are necessary for finding a numerical quadrature enabling calculating of singular integrals with a higher accuracy, which is necessary for calculating stresses and displacements.

In summary, this paper presents a work-in-progress, rather than a final result. The scope of future work consists in studying different approaches for practical calculations of circular-arc polygon mappings in the context of the coupling method, as well as analysing of different advanced methods for computing singular integrals. Additionally, further theoretical studies of the method, such as for example unique solvability of the interpolation problem under conformal mapping, must also be made.

Finally, it is worth mentioning, that some recent works dealing with analysis of kinked cracks proposed to work with a mapping from a half-space [1, 3]. Considering that different conformal mappings can be used on different propagation steps, as well as a composition of several conformal mappings can also be helpful in practice, the use of the mapping from a half-space needs also to be studied in the context of the coupled method, presented in this paper. Perhaps a new setting for the complete methods can be found in this way.