High-Order Data-Driven Spatial Simulation of Categorical Variables

Abstract

Modern approaches for the spatial simulation of categorical variables are largely based on multi-point statistical methods, where a training image is used to derive complex spatial relationships using relevant patterns. In these approaches, simulated realizations are driven by the training image utilized, while the spatial statistics of the actual sample data are ignored. This paper presents a data-driven, high-order simulation approach based on the approximation of high-order spatial indicator moments. The high-order spatial statistics are expressed as functions of spatial distances that are similar to variogram models for two-point methods, while higher-order statistics are connected with lower-orders via boundary conditions. Using an advanced recursive B-spline approximation algorithm, the high-order statistics are reconstructed from the available data and are subsequently used for the construction of conditional distributions using Bayes’ rule. Random values are subsequently simulated for all unsampled grid nodes. The main advantages of the proposed technique are its ability to (a) simulate without a training image to reproduce the high-order statistics of the data, and (b) adapt the model’s complexity to the information available in the data. The practical intricacies and effectiveness of the proposed approach are demonstrated through applications at two copper deposits.

1 Introduction

Geostatistical simulations are often required in reservoir modeling, as well as in the quantification of geological uncertainty, pollutants in contaminated areas, and other spatially dependent geological and environmental phenomena. During the past few decades, geostatistical simulations of categorical variables, such as geological units with complex spatial geometries of mineral deposits and petroleum reservoirs, have largely been modeled within the framework of multiple-point spatial simulation (MPS) methods that were introduced in the 1990s and have been further developed since then (Guardiano and Srivastava 1993; Journel 1993; Strebelle 2002, 2021; Journel 2003; Zhang et al. 2006; Chugunova and Hu 2008; Remy et al. 2009; Mariethoz and Renard 2010; Straubhaar 2011; Stien and Kolbjørnsen 2011; Toftaker and Tjelmeland 2013; Strebelle and Cavelius 2014; Zhang et al. 2017; Gómez-Hernández and Srivastava 2021, others). The MPS framework is based on the use of training images (TI) or analogues of the attributes of interest being modeled and contains additional information about the complex spatial relations of the attributes to be simulated; however, the TIs are not conditioned to the available data and their spatial statistics. To retrieve and use the pertinent information from a TI, the similarity between the local neighborhood of an unsampled location to be simulated and the TI is calculated in an explicit or implicit form. Based on this similarity measure, the value of a node from the TI with the most similar neighborhood is assigned to the unsampled location being simulated. Generally, most of the multi-point simulation techniques are a Monte Carlo sampling of values from the TI in some form. No spatial models are used and, importantly, no spatial information is retrieved from the available sample data. As a result, simulated realizations of attributes of interest reflect the TI and its spatial aspects. In cases where there are relatively large data sets, conflict between the available data and the TI statistics is observed, and the resulting simulated realizations do not reproduce the spatial statistics of the data (Goodfellow et al. 2012; Osterholt and Dimitrakopoulos 2007; Dimitrakopoulos et al. 2010; Pyrcz and Deutsch 2014). Several attempts have been made to incorporate more information from the available data. Some authors suggest using replicates from the data in addition to TI (Mariethoz and Renard 2010); however, in practice, it is difficult to find any replicates for three-point relations when data are sparse. Others (Mariethoz and Kelly 2011) apply affine transformations to better condition to the data; however, a TI remains the main source of information.

Dimitrakopoulos et al. (2010) and Mustapha and Dimitrakopoulos (2010a, b) propose the use of high-order spatial cumulants to capture complex multi-point relations during the simulation of non-Gaussian random fields. The proposed high-order simulation approach estimates the third- and fourth-order spatial statistics from data and complements them with higher-order statistics from the TI. Further developments in algorithmic performance (Yao et al. 2018, 2020), generalization using splines (Minniakhmetov et al. 2018), a high-order decorrelation method (Minniakhmetov and Dimitrakopoulos 2017a), and efficient block simulations (de Carvalho et al. 2019), and training-image-free simulations (Yao et al. 2021) have made the approach more practical. These approaches are based on the approximation of a conditional distribution using Legendre polynomials, which are smooth functions and are incapable of an adequate approximation of the discrete distribution of categorical variables.

The topic of describing complex multi-point relations of categorical variables is addressed in Vargas-Guzman (2011) and Vargas-Guzman and Qassab (2006), who use high-order indicator statistics to characterize spatially distributed rock units, while Minniakhmetov and Dimitrakopoulos (2017b) develop this further by introducing the connection between different orders to the related mathematical model for the two-dimensional case. For example, consider a third-order spatial indicator moment of a stationary random field, which is a function of two lags. When one of the lags is equal to zero, the third-order indicator moment becomes the second-order indicator moment. In addition, instead of exponential functions, the B-spline functions are used to estimate high-order spatial indicator moments. It is known that B-splines provide an optimal (in terms of accuracy) estimation of equi-continuous functions defined on compacts (Evans et al. 2009; Babenko 1986). Based on the above, a new recursive algorithm is proposed for the better approximation of high-order spatial statistics with nested boundary conditions of lower-level relations. Then, the conditional distribution for the given neighborhood is calculated from high-order indicator moments and the related category is simulated. In addition to extending previous developments mentioned above, the present study also explores practical aspects of the proposed method through applications at two major, real-world copper deposits: Olympic Dam, Australia, and Escondida, Chile (the world’s largest copper mine). Furthermore, the paper highlights the importance of high-order spatial statistics as the useful tool for the analysis of spatial contact relations between categories. Contrary to indicator variograms (Journel and Alabert 1990; Goovaerts 1997) that provide information about pair-wise relationships between categories, the third- and fourth-order spatial indicator moments reflect three- and four-wise relations between multiple categories in space. It should be noted that, as shown in the subsequent sections, the proposed method works without a TI; however, additional information from a TI can be incorporated as a secondary condition, ensuring that the high-order spatial indicator moments are driven by the available data.

The paper is organized as follows. First, high-order spatial indicator moments are introduced as a function of distances between points for two-point and multi-point cases. Then, a mathematical model for recursive approximation of high-order spatial indicator moments is presented, followed by the proposed high-order, data-driven, categorical simulation method. Subsequently, the proposed simulation algorithm is applied in two case studies to simulate the geological units of copper deposits. Discussion and conclusions follow.

2 High-Order Spatial Indicator Simulation

Let $(\Omega ,F,P)$ be a probability space. Consider a stationary ergodic random vector ${\mathbf{Z}} = (Z_{1} ,Z_{2} , \ldots ,Z_{N} )^{{\text{T}}} ,\,\,{\mathbf{Z}}:\Omega \to S^{N} ,$ defined on a regular grid $D = \{ {\mathbf{x}}_{1} ,{\mathbf{x}}_{2} , \ldots ,{\mathbf{x}}_{N} \}$, ${\mathbf{x}} \in R^{n} ,n = 2,3$, where $\Omega$ is a space of all possible outcomes, $F$ contains all combinations of $\Omega$, $S^{N}$ is a set of states represented by categories $S = \{ s_{1} ,s_{2} , \ldots ,s_{K} \}$, and ${\text{P}}$ is the probability measure, or probability. For example, the probability of $Z_{1}$ being at a state $s_{k}$ is defined as

$$ P(Z_{1} = s_{k} ) \equiv P(\{ \omega \in \, \Omega : {\mathbf{Z}}(\omega ) \, \in s_{k} \otimes S^{N - 1} \} ) $$

(1)

Without loss of generality, assume that $s_{k} = k,k = 1 \ldots K$. Let ${\mathbf{d}}_{n} = \{ z_{\alpha } ,\alpha = 1 \ldots n\}$ be a given set of conditioning data, where lowercase $z$ stands for outcomes of random variable $Z$. The focus of high-order simulation techniques is to simulate the realization of the random vector ${\mathbf{Z}}$ for all nodes of a grid $D$ with a given set of conditioning data ${\mathbf{d}}_{n}$.

Similarly to Minniakhmetov and Dimitrakopoulos (2017b), the high-order categorical simulation method is based on the concept of sequential simulation (Journel and Alabert 1990; Journel 1993), where the joint probability distribution $P(Z_{1} = k_{1} ,Z_{2} = k_{2} , \ldots ,Z_{N} = k_{N} |{\mathbf{d}}_{{\mathbf{n}}} )$ of the random vector ${\mathbf{Z}}$ can be decomposed into the product of conditional univariate distributions

$$ \begin{aligned} P(Z_{1} = k_{1} , \ldots ,Z_{N} = k_{N} |{\mathbf{d}}_{{\mathbf{n}}} ) & = P(Z_{2} = k_{2} , \ldots ,Z_{N} = k_{N} |Z_{1} = k_{1} ,{\mathbf{d}}_{{\mathbf{n}}} )P(Z_{1} = k_{1} |{\mathbf{d}}_{{\mathbf{n}}} ) \\ & = \prod\limits_{i = 2}^{N} {P(Z_{i} = k_{i} |Z_{1} = k_{1} , \ldots ,Z_{i - 1} = k_{i - 1} ,{\mathbf{d}}_{{\mathbf{n}}} )} P(Z_{1} = k_{1} |{\mathbf{d}}_{{\mathbf{n}}} ) \\ \end{aligned}. $$

(2)

According to Eq. (2), simulation of categorical variables can be done sequentially by visiting a grid node at a time and calculating $P(Z_{i} = k_{i} |Z_{1} = k_{1} , \ldots ,Z_{i - 1} = k_{i - 1} ,{\mathbf{d}}_{{\mathbf{n}}} )$. However, in practice (Dimitrakopoulos and Luo 2004), instead of considering all previously simulated nodes and data $\{ Z_{1} , \ldots ,Z_{i - 1} ,{\mathbf{d}}_{{\mathbf{n}}} \}$, only those in local neighborhood of $Z_{i}$ are considered, i.e.

$$ P(Z_{i} = k_{i} |Z_{1} = k_{1} , \ldots ,Z_{i - 1} = k_{i - 1} ,{\mathbf{d}}_{{\mathbf{n}}} ) \approx P(Z_{i} = k_{i} |\Lambda_{i} ), $$

(3)

where $\Lambda_{i}$ is the set of previously simulated nodes and data within the local neighborhood of $Z_{i}$.

Similarly to Mustapha and Dimitrakopoulos (2010a, b), the conditional distribution in Eq. (3) can be calculated from the joint distribution. Without loss of generality, consider conditional distribution $P(Z_{0} = k_{0} |Z_{1} = k_{1} , \ldots ,Z_{n} = k_{n} )$; it can then be calculated using Bayes’ rule (Ripley 1987)

$$ P(Z_{0} = k_{0} |Z_{1} = k_{1} , \ldots ,Z_{n} = k_{n} ) = P(Z_{0} = k_{0} ,Z_{1} = k_{1} , \ldots ,Z_{n} = k_{n} )/P(Z_{1} = k_{1} , \ldots ,Z_{n} = k_{n} ), $$

(4)

where $P(Z_{1} = k_{1} , \ldots ,Z_{n} = k_{n} )$ can be considered as a normalization coefficient due to the relations

$$ P(Z_{1} = k_{1} , \ldots ,Z_{n} = k_{n} ) = \sum\limits_{{k_{0} = 1}}^{K} {P(Z_{0} = k_{0} ,Z_{1} = k_{1} , \ldots ,Z_{n} = k_{n} )}, $$

(5)

It can be shown that the probability is equivalent to spatial indicator moment (Vargas-Guzman 2011)

$$ P(Z_{{i_{0} }} = k_{0} ,Z_{{i_{1} }} = k_{1} , \ldots ) = E\left[ {I_{{k_{0} }} (Z_{{i_{0} }} )I_{{k_{1} }} (Z_{{i_{1} }} ) \ldots } \right],\,\,\,\forall i_{0} ,i_{1} \ldots = 1 \ldots N,\quad \forall k_{0} ,k_{1} , \ldots = 1 \ldots K $$

(6)

where $E$ is the expected value operator and $I_{k} (Z_{i} )$ is an indicator function

$$ I_{k} (Z_{i} ) = \left\{ {\begin{array}{*{20}c} {1,} & {Z_{i} = k} \\ {0,} & {Z_{i} \ne k_{0} } \\ \end{array} } \right.. $$

(7)

From here on, indicator moments are denoted as

$$ M_{{\mathbf{k}}} (Z_{{i_{0} }} ,Z_{{i_{1} }} , \ldots ) = M_{{k_{0} k_{1} , \ldots }} (Z_{{i_{0} }} ,Z_{{i_{1} }} , \ldots ) = E\left[ {I_{{k_{0} }} (Z_{{i_{0} }} )I_{{k_{1} }} (Z_{{i_{1} }} ) \ldots } \right]. $$

(8)

Finally, Eqs. (2–5) define simulation algorithm of categorical random vector ${\mathbf{Z}}$.

Algorithm A.1

• 1. Define a random path visiting all the unsampled nodes.

• 2. For each node ${\mathbf{x}}_{{i_{0} }}$ in the path:

  • a. Find the closest data samples ${\mathbf{x}}_{{i_{1} }} ,{\mathbf{x}}_{{i_{2} }} , \ldots {\mathbf{x}}_{{i_{n} }}$. The categories at these nodes are denoted by $k_{1} , \ldots k_{n}$.

  • b. For all $k_{0} = 1 \ldots K$, calculate the high-order spatial indicator moments $M_{{\mathbf{k}}} (Z_{{i_{0} }} ,Z_{{i_{1} }} , \ldots ,Z_{{i_{n} }} )$

  • c. Calculate the conditional distribution from joint distribution

    $$ P\left( {Z_{{i_{0} }} = k_{0} |Z_{{i_{1} }} = k_{1} \ldots ,Z_{{i_{n} }} = k_{n} } \right) = AM_{{\mathbf{k}}} (Z_{{i_{0} }} ,Z_{{i_{1} }} , \ldots ,Z_{{i_{n} }} ), $$

    (9)

    where coefficient $A$ is the normalization coefficient as in Eq. (4)

    $$ A = 1/\sum\limits_{{k_{0} = 1}}^{K} {M_{{\mathbf{k}}} (Z_{{i_{0} }} ,Z_{{i_{1} }} , \ldots ,Z_{{i_{n} }} )} $$

    (10)

  • d. Draw a random value $z_{{i_{0} }}$ from this conditional distribution (10) and assign it to the unsampled location ${\mathbf{x}}_{{i_{0} }}$.

  • e. Add $z_{{i_{0} }}$ to the set of sample hard data and the previously simulated values.

  • f. Repeat Steps 2a–e for all the points along the random path defined in Step 1.

The next section presents a new method to calculate high-order spatial indicator moments for Eqs. (9–10).

3 High-Order Spatial Indicator Moments

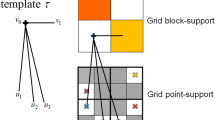
Similarly to second-order statistics such as variograms, high-order spatial moments are calculated by discretizing distances between data samples into lags and finding all pairs, triplets, or multiplets separated by the same lags. To define lags in the two-dimensional case, the local neighborhood of each data sample is divided into eight sectors (${\text{oct}} = 1 \ldots 8$) and concentric circles with radius ($r = \{ r_{1} ,r_{2} , \ldots r_{\max } \}$) increasing by logarithmic law (Fig. 1). The choice of logarithmically increasing lags is driven mainly by computational resource limits. For example, to cover extents of 400 m (with 200 m typical continuity range for the deposits under consideration), the constant lag division with resolution at first lags of about 20 m requires 20 lags, which correspond to 20⁴ = 160,000 bins in a fourth-order map for each possible combination of categories in four points, whereas logarithmically increasing lags {20, 30, 40, 70, 160, 400} require 6⁴ = 1296 bins, i.e. 123 times fewer calculations. In Fig. 1, data samples are denoted by $x_{0}$ (central point), $x_{1}$, $x_{2}$, and $x_{3}$. Data sample $x_{1}$ is located in octant $o = 7$ and lag $h = r_{3}$, $x_{2}$ is in octant $o = 1$ and lag $h = r_{2}$, and $x_{3}$ is in octant $o = 5$ and lag $h = r_{2}$. Any point located in the central circle belongs to all octant and lag 0. Thus, high-order moments can be expressed as functions of octant index and lags, e.g. $M_{{k_{0} k_{1} k_{2} }} (Z_{0} ,Z_{1} ,Z_{2} ) \approx M_{{k_{0} k_{1} k_{2} }} (o_{1} = 7,o_{2} = 1;h_{1} = r_{3} ,h_{2} = r_{2} )$, where $Z_{0} ,Z_{1} ,Z_{2}$ are random variables at locations $x_{0} ,x_{1} ,x_{2}$. From here on, calculated indicator moments are denoted as

$$ M_{{\mathbf{k}}} ({\mathbf{o}};\,{\mathbf{h}}) = M_{{k_{0} k_{1} , \ldots ,k_{n} }} (o_{1} , \ldots o_{n} ;\,h_{1} , \ldots h_{n} ) = M_{{\mathbf{k}}} (Z_{{i_{0} }} ,Z_{{i_{1} }} , \ldots Z_{{i_{n} }} ), $$

(11)

and are calculated using sampling average

$$ \hat{M}_{{\mathbf{k}}} ({\mathbf{o}};\,{\mathbf{h}}) = \frac{1}{{N_{{{\mathbf{o}},{\mathbf{h}}}} }}\sum\limits_{j = 1}^{{N_{{{\mathbf{o}},{\mathbf{h}}}} }} {I_{{k_{0} }} (z_{{i_{0} }}^{j} ) \ldots I_{{k_{n} }} (z_{{i_{n} }}^{j} )} , $$

(12)

where $\wedge$ denotes statistics calculated from data samples, i.e. sampling statistics, and $N_{{{\mathbf{o}},{\mathbf{h}}}}$ is the number of all data samples $z_{{i_{0} }}^{j} \ldots z_{{i_{n} }}^{j} ,j = 1 \ldots N_{{{\mathbf{o}},{\mathbf{h}}}}$ falling in the octants ${\mathbf{o}} = \{ o_{1} , \ldots ,o_{n} \}$ and lags ${\mathbf{h}} = \{ h_{1} , \ldots ,h_{n} \}$.

Fig. 1

Octant division of local neighborhood with logarithmically increasing lags. $x_{0}$ (central point), $x_{1}$, $x_{2}$, and $x_{3}$ are data samples

The data samples in Fig. 1 contribute to experimental high-order spatial statistics from order 2 to 4: second-order indicator moments $\hat{M}_{{k_{0} k_{1} }} (o = 7;\,h = r_{3} )$, $\hat{M}_{{k_{0} k_{2} }} (o = 1;\,h = r_{2} )$, $\hat{M}_{{k_{0} k_{3} }} (o = 5;\,h = r_{2} )$, third-order indicator moments $\hat{M}_{{k_{0} k_{1} k_{2} }} (o_{1} = 7,o_{2} = 1;\,h_{1} = r_{3} ,h_{2} = r_{2} )$, $\hat{M}_{{k_{0} k_{1} k_{3} }} (o_{1} = 7,o_{2} = 5;\,h_{1} = r_{3} ,h_{2} = r_{2} )$, $\hat{M}_{{k_{0} k_{2} k_{3} }} (o_{1} = 7,o_{2} = 5;\,h_{1} = r_{3} ,h_{2} = r_{2} )$, and fourth-order indicator moment $\hat{M}_{{k_{0} k_{1} k_{2} k_{3} }} (o_{1} = 7,o_{2} = 1,o_{3} = 5;\,h_{1} = r_{3} ,h_{2} = r_{2} ,h_{3} = r_{2} )$. It should be noted that during simulation Step 2a, only one data sample per octant is used as conditional data to avoid calculation of high-order moments with repetitive random variables, e.g. $\hat{M}_{{k_{0} k_{1} k_{1} }} (Z_{0} ,Z_{1} ,Z_{1} )$, $\hat{M}_{{k_{0} k_{1} k_{3} k_{3} }} (Z_{0} ,Z_{1} ,Z_{3} ,Z_{3} )$. This is quite similar to the octant search approach for second-order statistics methods (Remy et al. 2009). If several data samples fall in the same octant, the choice is made randomly.

In the three-dimensional case, instead of octants, the quadraginta octant division (Biswas and Bhowmick 2017) with 48 sectors (6 sectors per quadrant) is used (Fig. 2).

Fig. 2

Quadraginta octant division for the tree-dimensional case (Biswas and Bhowmick 2017)

Following the logic of fitting theoretical variograms to variogram models (Journel and Huijbregts 1978), the sampling statistics (12) are not used directly to calculate joint distributions, but they are used to model high-order indicator moments.

The quadraginta octant division is the critical part of step 2b, which entails the calculation of high-order spatial indicator moment $M_{{\mathbf{k}}} (Z_{{i_{0} }} ,Z_{{i_{1} }} , \ldots ,Z_{{i_{n} }} )$ of Algorithm A1 above. For the sake of simplicity, consider three possible categories $k \in \{ 0,1,2\}$ and three points: central point random value $Z_{0}$ to be simulated at location ${\mathbf{x}}_{0}$ and two neighborhood data samples $z_{1}$ and $z_{2}$ in arbitrary directions ${\mathbf{x}}_{1}$ and ${\mathbf{x}}_{2}$. First, the octants $(o_{1} ,o_{2} )$ and lag distances $(h_{1} ,h_{2} )$ are calculated from lags ${\mathbf{h}}_{1} = {\mathbf{x}}_{1} - {\mathbf{x}}_{0}$ and ${\mathbf{h}}_{2} = {\mathbf{x}}_{2} - {\mathbf{x}}_{0}$ centered at point ${\mathbf{x}}_{0}$. Next, the two-dimensional surfaces $\hat{M}_{{k_{0} = 0,k_{1} ,k_{2} }} (o_{1} ,o_{2} ;\,u,v)$, $\hat{M}_{{k_{0} = 1,k_{1} ,k_{2} }} (o_{1} ,o_{2} ;\,u,v)$, $\hat{M}_{{k_{0} = 2,k_{1} ,k_{2} }} (o_{1} ,o_{2} ;\,u,v)$ are approximated using all available data and the nested algorithm presented in Sect. 3.1. Note that $(k_{1} ,k_{2} )$ and $(o_{1} ,o_{2} )$ are fixed and known from neighborhood data at ${\mathbf{x}}_{1}$ and ${\mathbf{x}}_{2}$; $(u,v)$ are distances along directions $(o_{1} ,o_{2} )$—the only variable part of $\hat{M}_{{k_{0} = 0,k_{1} ,k_{2} }} (o_{1} ,o_{2} ;\,u,v)$.

It should be noted that using quadraginta octant search in Algorithm A1 is quite different from the search in the classical MPS methods, such as SNESIM (Strebelle and Cavelius 2014). Firstly, MPS methods reduce the number of neighborhood data when no exact replicates are found for a particular spatial configuration, whereas octant search provides all possible replicates at different lags with the fixed angles; for example, for the third-order moments (3-point statistics) for the fixed octants $(o_{1} ,o_{2} )$ defined by neighborhood data, all replicates at different lag distances $(h_{1} ,h_{2} )$ are found and used in the simulation of a value in a node. Secondly, octant search does not look for exact spatial replicates, but replicates within tolerances of lags and angles, which dramatically increases the number of replicates used in the simulation process. Lastly, there is no restriction on the “regularity” of the data sample locations or TI (if used), as the octant search works on points rather than on a grid.

3.1 Approximating High-Order Indicator Moments

Data available in some applications can be dense in space and give the impression that the high-order spatial statistics in Eq. (10) can be directly calculated from samples. However, the dimension of space in high-order spatial statistics grows exponentially as the order increases, such that even dense drilling is insufficient for the direct calculation of high-order statistics from the data. For example, in the fourth-order indicator moments, there are 17,296 possible combinations of directions (all possible three neighbor directions from 48 quadraginta octant division) and 2⁴ possible combinations of indicators, for the case with two categories only, which results in 2⁴ × 17,296 = 138,368 fourth-order spatial indicator moments. Figure 3 and Table 1 show the histogram and percentiles, respectively, of the number of replicates for fourth- and fifth-order spatial indicator moments found in the Olympic Dam data set described in Sect. 4.1. Replicates have been calculated using quadraginta octant division and 20 m lag tolerance. Overall, 80% of all possible spatial configurations from the drill-hole data had fewer than eight samples to calculate the fourth-order indicator moment and fewer than six samples for the fifth-order indicator moments. Such a small number of replicates is not sufficient to provide a robust calculation of high-order moments for Eq. (10) of Algorithm A.1.

Fig. 3

Histogram of number of replicates for a fourth- and b fifth-order spatial indicator moments found in the Olympic Dam data set

Table 1 Percentiles of number of replicates for (a) fourth-order and (b) fifth-order spatial indicator moments found in the Olympic Dam data set

To increase the amount of information and, consequently, the quality of approximation of high-order moments, Minniakhmetov and Dimitrakopoulos (2017a, b) show that high-order indicator moments are bound by low-order moments

$$ M_{{\mathbf{k}}} ({\mathbf{o}};\,h_{1} , \ldots ,h_{p} = 0, \ldots ,h_{n} ) = M_{{{\mathbf{k}}\backslash k_{p} }} ({\mathbf{o}};\,{\mathbf{h}}\backslash h_{p} )\delta_{{k_{0} ,k_{p} }} ,\forall p \in 1 \ldots n, $$

(13)

where ${\mathbf{h}}\backslash h_{p}$ denotes all the lags ${\mathbf{h}}$ excluding the lag $h_{p}$, and ${\mathbf{k}}\backslash k_{p}$ denotes all the categories ${\mathbf{k}}$ excluding the category $k_{p}$. If the directions are close to orthogonal, then additional boundary conditions are valid

$$ M_{{\mathbf{k}}} ({\mathbf{o}};\,h_{1} , \ldots ,h_{p} \to \infty , \ldots ,h_{n} ) = M_{{{\mathbf{k}}\backslash k_{p} }} ({\mathbf{o}};\,{\mathbf{h}}\backslash h_{p} )M_{{k_{p} }} ,\forall p \in 1 \ldots n. $$

(14)

where $M_{k}$ is first-order statistics, i.e. proportion of category $k$ in the data. Using the boundary conditions Eqs. (13–14) and sampling statistics (12), high-order indicator moments are approximated by

$$ M_{{\mathbf{k}}} ({\mathbf{o}};\,{\mathbf{h}}) = M_{{\mathbf{k}}}^{0} ({\mathbf{o}};\,{\mathbf{h}}) + \delta M_{{\mathbf{k}}} ({\mathbf{o}};\,{\mathbf{h}}), $$

(15)

where $M_{{\mathbf{k}}}^{0} ({\mathbf{o}},{\mathbf{h}})$ is a trend defined just by boundary conditions, and $\delta M_{{\mathbf{k}}} ({\mathbf{o}};\,{\mathbf{h}})$ is the B-spline regression of the mismatch between sampling statistics and trend $M_{{\mathbf{k}}}^{0} ({\mathbf{o}};\,{\mathbf{h}})$.

The trend $M_{{\mathbf{k}}}^{0} ({\mathbf{o}};\,{\mathbf{h}})$ connects lower-order moments with high-order moment by recursive formula

$$ \begin{aligned} M_{{\mathbf{k}}}^{0} ({\mathbf{o}};\,{\mathbf{h}}) & = \frac{1}{{\sum\nolimits_{p = 1}^{n} {e^{{ - ah_{p} }} + } e^{{ - a(1 - h_{p} )}} }}\left[ {\sum\limits_{p = 1}^{n} {M_{{k_{0} \ldots k_{n} }} ({\mathbf{o}};\,h_{1} , \ldots ,h_{p} = 0 \ldots ,h_{n} )e^{{ - ah_{p} }} } } \right. \\ & \quad \left. { + \sum\nolimits_{p = 1}^{n} {M_{{k_{0} \ldots k_{n} }} ({\mathbf{o}};\,h_{1} , \ldots ,h_{p} \to \infty \ldots ,h_{n} )e^{{ - a(1 - h_{p} )}} } } \right],\,\,\forall p = 1 \ldots n, \\ \end{aligned} $$

(16)

where $a = c/r_{\max }$, $r_{\max }$ is the radius that defines the local neighborhood, and $c$ is the user-defined parameter that controls the influence of boundary conditions, i.e. small values of c force the approximation to use lower-order statistics close to boundaries ($h_{p} = 0,r_{\max }$) and sampling statistics in the area far from boundaries, whereas large values of c increase the influence of low-order statistics on high-order statistics. For data-rich environments, such as mining of mineral deposits, the use of smaller values of c is suggested, and for sparse data, large values.

As the term $M_{{\mathbf{k}}}^{0} ({\mathbf{o}};\,{\mathbf{h}})$ incorporates the connection between low and high orders, the $\delta M_{{\mathbf{k}}} ({\mathbf{o}};\,{\mathbf{h}})$ is only responsible for approximation of sampling statistics with zero boundary conditions.

The approximation of the multidimensional function $\delta M_{{\mathbf{k}}} ({\mathbf{o}};\,{\mathbf{h}})$ is the classical linear regression problem with constraints. In the present work, the multidimensional cardinal B-spline regression is used (Friedman et al. 2001), where $\delta M_{{\mathbf{k}}} ({\mathbf{o}};\,{\mathbf{h}})$ is approximated using a linear combination of B-splines defined on uniform intervals.

$$ \delta M_{{\mathbf{k}}} ({\mathbf{o}};\,{\mathbf{h}}) = \sum\limits_{{i_{1} = 1}}^{\omega } { \cdots \sum\limits_{{i_{n} = 1}}^{\omega } {\alpha_{{i_{1} , \ldots ,i_{n} }} } } B_{{i_{1} ,r}} (h_{1} ) \ldots B_{{i_{n} ,r}} (h_{n} ), $$

(17)

where $\alpha_{{i_{1} , \ldots ,i_{n} }}$ are coefficients of B-spline approximation, and $B_{i,r} (t)$ is the $i$th B-splines of order $r$ on uniformly divided knot sequence $\{ 0,dr,2dr \ldots r_{\max } \}$, which are separated by step $dr$ that increases with the order of moment $\delta M_{{\mathbf{k}}} ({\mathbf{o}};\,{\mathbf{h}})$, thus providing more regularized approximation for higher orders and detailed approximation for lower orders. In practice, only orders up to 5 can be adequately calculated from the data; therefore, $dr = r_{\max } /6$, $dr = r_{\max } /4$, and $dr = r_{\max } /2$ are used for moments of order 3, 4, 5, respectively. For second-order moments, standard variogram modeling is utilized (David 1988).

The coefficients $\alpha_{{i_{1} , \ldots ,i_{n} }}$ are found using a least-squares algorithm to fit points, which are the residual of high-order moments calculated from the data samples and trend $M_{{\mathbf{k}}}^{0} ({\mathbf{o}};\,{\mathbf{h}})$ from Eq. (16)

$$ \delta M_{{\mathbf{k}}} ({\mathbf{o}};\,{\mathbf{h}}^{d} ) = \hat{M}_{{\mathbf{k}}} ({\mathbf{o}};\,{\mathbf{h}}^{d} ) - M_{{\mathbf{k}}}^{0} ({\mathbf{o}};\,{\mathbf{h}}^{d} ), $$

(18)

under zero boundary constraints

$$ \begin{gathered} \delta M_{{\mathbf{k}}} ({\mathbf{o}};\,h_{1} , \ldots ,h_{p} = 0, \ldots ,h_{n} ) = 0, \hfill \\ \delta M_{{\mathbf{k}}} ({\mathbf{o}};\,h_{1} , \ldots ,h_{p} \to \infty , \ldots ,h_{n} ) = 0,\forall p = 1 \ldots n, \hfill \\ \end{gathered} $$

(19)

where ${\mathbf{h}}^{d}$ are centers of lags used to calculate high-order statistics from the data (12).

Using all the above, the high-order moments are recursively constructed by starting from the second-order indicator moments. Figure 4 illustrates the approximation process. First, second-order indicator moments $M_{{k_{0} k_{p} }} (o_{p} ;\,h_{p} ),p = 1 \ldots n$, depicted by red solid lines in Fig. 4(a), are calculated from the basic variogram model. Then, the trend $M_{{k_{0} ,k_{1} ,k_{2} }}^{0} ({\mathbf{o}};\,{\mathbf{h}})$, which is the surface in Fig. 4(a), is calculated using these boundary conditions and Eq. (16). Next, the residuals $\delta M_{{k_{0} ,k_{1} ,k_{2} }}^{{}} ({\mathbf{o}};\,{\mathbf{h}}^{d} )$, which are the black points in Fig. 4(b), are estimated by subtracting the trend $M_{{k_{0} ,k_{1} ,k_{2} }}^{0} ({\mathbf{o}};\,{\mathbf{h}})$ from the sampling statistics $\hat{M}_{{k_{0} ,k_{1} ,k_{2} }} ({\mathbf{o}};\,{\mathbf{h}}^{d} )$ using Eq. (18). Then, residual spatial moments $\delta M_{{k_{0} ,k_{1} ,k_{2} }}^{{}} ({\mathbf{o}};\,{\mathbf{h}})$, depicted as the surface in Fig. 4(c), are approximated from residuals $\delta M_{{k_{0} ,k_{1} ,k_{2} }}^{{}} ({\mathbf{o}};\,{\mathbf{h}}^{d} )$ and zero boundary conditions (red lines in Fig. 4c), using the B-spline regression in Eq. (17). Finally, the third-order spatial indicator moments, shown as the surface in Fig. 4(d), are retrieved by adding residual spatial moments $\delta M_{{k_{0} ,k_{1} ,k_{2} }}^{{}} ({\mathbf{o}};\,{\mathbf{h}})$ to the trend $M_{{k_{0} ,k_{1} ,k_{2} }}^{0} ({\mathbf{o}};\,{\mathbf{h}})$ using Eq. (15).

Fig. 4

Approximation of the third-order spatial indicator moments $M_{{k_{0} ,k_{1} ,k_{2} }}^{{}} ({\mathbf{o}};\,{\mathbf{h}})$: a calculating the trend $M_{{k_{0} ,k_{1} ,k_{2} }}^{0} ({\mathbf{o}};\,{\mathbf{h}})$ from boundary conditions shown by red lines, b residuals $\delta M_{{k_{0} ,k_{1} ,k_{2} }}^{{}} ({\mathbf{o}};\,{\mathbf{h}}^{d} )$ with sampling statistics and zero boundary conditions, c B-spline regression of the residual third-order map $\delta M_{{k_{0} ,k_{1} ,k_{2} }}^{{}} ({\mathbf{o}};\,{\mathbf{h}})$, d the final reconstructed third-order spatial indicator moments $M_{{k_{0} ,k_{1} ,k_{2} }}^{{}} ({\mathbf{o}};\,{\mathbf{h}})$

The calculated third-order spatial indicator moments $M_{{k_{0} ,k_{1} ,k_{2} }}^{{}} ({\mathbf{o}};\,{\mathbf{h}})$ are used as the boundary conditions for the fourth-order spatial indicator moments $M_{{k_{0} ,k_{1} ,k_{2} ,k_{3} }}^{{}} ({\mathbf{o}};\,{\mathbf{h}})$ (Fig. 5). Note that the fourth-order moment is a three-dimensional function that requires eight boundary conditions. The same procedure is recursively repeated for the fourth and fifth orders.

Fig. 5

The third-order indicator moments (left) $M_{{k_{0} ,k_{1} ,k_{2} }} ({\mathbf{o}};\,{\mathbf{h}})$ as the boundary condition for the fourth-order indicator moments $M_{{k_{0} ,k_{1} ,k_{2} ,k_{3} }} ({\mathbf{o}};\,{\mathbf{h}})$

4 Applications

4.1 Olympic Dam Copper Deposit, Australia

Olympic Dam, located in South Australia, is the fourth largest copper deposit in the world. A part of the Olympic Dam deposit covering an area 1 km by 1 km is used here to demonstrate the application of the proposed simulation method in a case study. The grade cut-off of 1% Cu is applied to the available drillhole data to define two categories to be simulated; then results are validated using high-order spatial indicator moments. Data are available in 515 exploration drill-holes shown in Fig. 6. Three-dimensional simulated realizations are generated on a regular grid with $100 \times 100 \times 50$ grid nodes and a block of $10 \times 10 \times 10$ m³. Figure 7 depicts vertical sections from a simulated realization of the deposit. The figure shows that the proposed method generates spatially complex geometric structures that honor the drill-hole data. The spatial statistics and contacts are validated using high-order spatial indicator moments.

Fig. 6

Drill-holes from Olympic Dam copper deposit. Red represents grades above 1% Cu and blue below

Fig. 7

Vertical sections of a simulated realization. Red represents grades above 1% Cu and blue below. Drill-holes are traced by black outlines, and white sections represent missing values

It should be noted that the simulations are performed using all possible directions from the quadraginta octant division. For the third-order indicator moments, there are 1,128 possible combinations of directions, and each of the combinations has 2³ possible combinations of categories 0 and 1. Thus, the total number of indicator maps is 9,024. For the fourth-order indicator moments, there are 17,296 possible combinations of directions, which results in 138,368 forth-order indicator maps. Without a doubt, the information in these indicator maps is quite similar, and the complex high-order relations can be expressed using a smaller number of moments. Therefore, only the orthogonal directions, so-called L-shape templates, are used for validation purposes.

The third-order indicator moment maps $\hat{M}_{111} ({\mathbf{h}}_{1} ,{\mathbf{h}}_{2} )$ are calculated using the L-shape template (Mustapha and Dimitrakopoulos 2010a) with lags ${\mathbf{h}}_{1} = (i{\text{d}}x,0)$ ${\mathbf{h}}_{2} = (0,j{\text{d}}y)$, indexed by $i = 0 \ldots 8$, $j = 0 \ldots 8$, where ${\text{d}}x$ and ${\text{d}}y$ are 50 m × 50 m. The moment map $\hat{M}_{111} ({\mathbf{h}}_{1} ,{\mathbf{h}}_{2} )$ shows the probability of having category 1 in three points separated from each-other by lags along X and Y (L-shape). Note that validation of high-order moments is done with an approach with regular steps and two directions as in Mustapha and Dimitrakopoulos (2010a, b), in contrast to the octant approach with logarithmically increasing lags in Sect. 3. The logarithmically increasing lags with small steps close to the origin are helpful to better inform the approximation of high-order moments close to the central node, whereas for validation it is important to visualize both short-range and long-range connectivity. The moment map shows the probability of having copper grades above 1% at three points separated by lags along X and Y, that is, the continuity of high grades. As can be seen in Fig. 8, the simulated realization generated by the proposed method (Fig. 8b) reproduces red and yellow areas in the moment map of the hard data (Fig. 8a), that is, continuity ranges. As shown above, values along axes are indicator moments of order 2, that is the conventional indicator covariances. The third-order indicator moment maps $\hat{M}_{101} ({\mathbf{h}}_{1} ,{\mathbf{h}}_{2} )$ are shown in Fig. 9. The moment map shows the probability of having copper grades above 1% at two points in the Y direction and copper grade below 1% at one point in the X direction. $\hat{M}_{101} ({\mathbf{h}}_{1} ,{\mathbf{h}}_{2} )$ reflects the contact plane between the copper grades above and below 1%, respectively, in the east–west direction. As can be seen in Fig. 9, the simulation using the proposed method (Fig. 9b) reproduces the spatial characteristics of the data between copper grades above and below 1% (Fig. 9a), represented by the yellow–red cone in the lower right part of the moment maps in Fig. 9.

Fig. 8

The third-order indicator moment maps $\hat{M}_{111} ({\mathbf{h}}_{1} ,{\mathbf{h}}_{2} )$ of a the available data, and b a simulated realization generated with the proposed method

Fig. 9

The third-order indicator moment maps $\hat{M}_{101} ({\mathbf{h}}_{1} ,{\mathbf{h}}_{2} )$ of a the data, and b a simulation using the proposed method

The third-order indicator moment maps ${\hat{\mathbf{M}}}_{110} (h_{1} ,h_{2} )$ are shown in Fig. 10. Similarly to the above, the moment map shows the probability of having copper grades above 1% at two points in the X direction and copper grade below 1% at one point in the Y direction. $\hat{M}_{101} ({\mathbf{h}}_{1} ,{\mathbf{h}}_{2} )$ reflects the contact plane between copper grades above and below 1%, respectively, in the north–south direction. As can be seen in Fig. 10, the realization generated using the proposed method (Fig. 10b) reproduces the contact between copper grades above and below 1% as found in the data (Fig. 10a), represented by the yellow–red cone in the upper left part of the moment maps in Fig. 10.

Fig. 10

The third-order indicator moment maps ${\hat{\mathbf{M}}}_{110} (h_{1} ,h_{2} )$ of a the data, and b a simulation using the proposed method

The fourth-order spatial indicator moment $\hat{M}_{1000} ({\mathbf{h}}_{1} ,{\mathbf{h}}_{2} ,{\mathbf{h}}_{3} )$ (Fig. 11) is calculated with lags ${\mathbf{h}}_{1} = (i{\text{d}}x,0)$, ${\mathbf{h}}_{2} = (0,j{\text{d}}y)$, and ${\mathbf{h}}_{3} = (0,k{\text{d}}z)$ indexed by $i,j,k = 1 \ldots 8$, where ${\text{d}}x$, ${\text{d}}y$, and ${\text{d}}z$ are 50 m × 50 m × 50 m. The moment $\hat{M}_{1000} ({\mathbf{h}}_{1} ,{\mathbf{h}}_{2} ,{\mathbf{h}}_{3} )$ reflects the complex contact between copper grades above and below 1%, where grades with values above 1% are surrounded by grades below 1% in the X, Y, and Z directions. The fourth-order moment map of the simulation using the proposed method (Fig. 11b) reproduces the yellow–red area in the moment map of the data (Fig. 11a). All other spatial indicator moments, that is, $\hat{M}_{{k_{1} k_{2} k_{3} }} ({\mathbf{h}}_{1} ,{\mathbf{h}}_{2} )$, $\hat{M}_{{k_{1} k_{2} k_{3} k_{4} }} ({\mathbf{h}}_{1} ,{\mathbf{h}}_{2} ,{\mathbf{h}}_{3} )$,$\forall k_{1} ,k_{2} ,k_{3} ,k_{4} = 0,1$, were analyzed and found consistent with the spatial indicator moments from the drill-hole data.

Fig. 11

The fourth-order indicator moment maps $\hat{M}_{1000} ({\mathbf{h}}_{1} ,{\mathbf{h}}_{2} ,{\mathbf{h}}_{3} )$ of a the data, and b a simulation using the proposed method

To highlight the importance of high-order calculations, a realization from the sequential indicator simulation method (SISIM) is analyzed in terms of third-order spatial indicator moments $\hat{M}_{{k_{1} k_{2} k_{3} }} ({\mathbf{h}}_{1} ,{\mathbf{h}}_{2} )$. A section of the realization, shown in Fig. 12(a), exhibits low nonlinear connectivity and a high number of small disconnected shapes. This is confirmed by third-order indicator moments $\hat{M}_{111} ({\mathbf{h}}_{1} ,{\mathbf{h}}_{2} )$, $\hat{M}_{101} ({\mathbf{h}}_{1} ,{\mathbf{h}}_{2} )$, $\hat{M}_{110} ({\mathbf{h}}_{1} ,{\mathbf{h}}_{2} )$ in Fig. 12b–d, respectively. In contrast to Figs. 8, 9, and 10, the third-order indicator moments from the SISIM method have low values for non-zero lags $({\mathbf{h}}_{1} ,{\mathbf{h}}_{2} )$ and a high contrast between values along axes, i.e. second-order statistics and values away from the axes. This indicates that the realization from the SISIM method does not reproduce complex relations of data and exhibits lower nonlinear connectivity of related categories.

Fig. 12

Section of a realization from the SISIM method a and corresponding third-order indicator moment maps. b–d $\hat{M}_{111} ({\mathbf{h}}_{1} ,{\mathbf{h}}_{2} )$, $\hat{M}_{101} ({\mathbf{h}}_{1} ,{\mathbf{h}}_{2} )$, $\hat{M}_{110} ({\mathbf{h}}_{1} ,{\mathbf{h}}_{2} )$

4.2 Escondida Norte Copper Deposit, Chile

Escondida is a large porphyry copper deposit in Chile consisting of two open-pit mines, Escondida and Escondida Norte. A part of Escondida Norte, 2.5 km by 2.5 km by 0.5 km, is used in this section to present a case study. Four mineralization zones are simulated using the proposed approach: oxides, sulfides, mix of oxides and sulfides, and waste. Complex geometrical shapes of mineralization zones and geological contacts are validated here using high-order spatial indicator moments. High-order spatial indicator moments allow us to analyze cross-categorical relations and take into account geological aspects of mineral deposits, such as which category is always embedded within another, which categories cannot be in contact, and so on.

The drill-holes available are shown in Fig. 13. In general, mineralization zones are quite variable, and the uncertainty of related contacts need to be quantified. The three-dimensional simulated realizations generated are defined on $115 \times 107 \times 55$ grid of blocks of $25 \times 25 \times 15$ m³ size. Sulfides are predominantly located in the bottom part and are covered by layers of mix and oxide zones. The upper part of the deposit consists mostly of waste materials. Vertical and horizontal sections of two simulated realizations using the proposed method are shown in Figs. 14 and 15, respectively. The simulations honor the layered structure of the mineralization zones and demonstrate higher variability of oxides and mix mineralization zones.

Fig. 13

Drill-holes from Escondida Norte copper mine; colors represent the mineralization zones

Fig. 14

Vertical section from two simulated realizations; colors represent mineralization, and drill-hole locations are represented by black outlines

Fig. 15

Horizontal section from two simulated realizations; colors represent mineralization, and drill-hole locations are represented by black outlines

The third-order indicator moment maps $\hat{M}_{OSS} ({\mathbf{h}}_{1} ,{\mathbf{h}}_{2} )$ (O stands for oxides, S for sulfides, M for mix, and W for waste) are calculated using lags ${\mathbf{h}}_{1} = (i{\text{d}}x,0)$ ${\mathbf{h}}_{2} = (0,j{\text{d}}y)$ indexed by $i = 0 \ldots 8$, $j = 0 \ldots 8$, where ${\text{d}}x$ and ${\text{d}}y$ are 50 m × 50 m. The moment map shows the probability of having oxide separated from sulfides by lags along X and Y, that is, a complex contact between oxides and sulfides. As can be seen in Fig. 16, the simulated realization generated with the proposed method (Fig. 16b) reproduces the red and yellow areas in the moment map of the data (Fig. 16a). The third-order indicator moment maps $\hat{M}_{SSW} ({\mathbf{h}}_{1} ,{\mathbf{h}}_{2} )$ are shown in Fig. 17. The moment map shows the probability of having sulfides at two points in the X direction and waste in the Y direction. $\hat{M}_{SSW} ({\mathbf{h}}_{1} ,{\mathbf{h}}_{2} )$ reflects the contact plane between sulfides and waste with a north to north–south direction. As can be seen in Fig. 17, the simulation using the proposed method (Fig. 17b) reproduces the corresponding spatial relations found in the data (Fig. 17a).

Fig. 16

The third-order indicator moment maps $\hat{M}_{OSS} ({\mathbf{h}}_{1} ,{\mathbf{h}}_{2} )$ of (a) the data, and (b) a simulated realization generated with the proposed method

Fig. 17

The third-order indicator moment maps $\hat{M}_{SSW} ({\mathbf{h}}_{1} ,{\mathbf{h}}_{2} )$ of a the hard data, and b the simulation using the proposed method

The fourth-order spatial indicator moments $\hat{M}_{MOWM} ({\mathbf{h}}_{1} ,{\mathbf{h}}_{2} ,{\mathbf{h}}_{3} )$ (Fig. 18) are calculated with lags ${\mathbf{h}}_{1} = (i{\text{d}}x,0)$, ${\mathbf{h}}_{2} = (0,j{\text{d}}y)$, and ${\mathbf{h}}_{3} = (0,k{\text{d}}z)$ indexed by $i,j = 1 \ldots 8$, $k = 1 \ldots 5$, where ${\text{d}}x$, ${\text{d}}y$, and ${\text{d}}z$ are 50 m × 50 m × 50 m. The moment $\hat{M}_{MOWM} ({\mathbf{h}}_{1} ,{\mathbf{h}}_{2} ,{\mathbf{h}}_{3} )$ reflects the spatial aspects of the contact between mixed oxides and waste zones. The fourth-order moment maps of the simulation using the proposed method (Fig. 18b) reproduce the yellow–red area in the moment map of the data (Fig. 18a).

Fig. 18

The fourth-order indicator moment maps $\hat{M}_{MOWM} ({\mathbf{h}}_{1} ,{\mathbf{h}}_{2} ,{\mathbf{h}}_{3} )$ of a the hard data and b the simulation using the proposed method

Similarly to the above, all other spatial indicator moments, that is, $\hat{M}_{{k_{1} k_{2} k_{3} }} ({\mathbf{h}}_{1} ,{\mathbf{h}}_{2} )$, $\hat{M}_{{k_{1} k_{2} k_{3} k_{4} }} ({\mathbf{h}}_{1} ,{\mathbf{h}}_{2} ,{\mathbf{h}}_{3} )$,$\forall k_{1} ,k_{2} ,k_{3} ,k_{4} = \{ S,O,M,W\}$, of the simulated realizations were analyzed and found consistent with the spatial indicator moments from the drill-hole data.

5 Conclusions

This paper presents a new data-driven, high-order sequential method for the simulation of categorical random fields. The sequential algorithm is based on the B-spline approximation of high-order spatial indicator moments that are consistent with each other. The main distinction from commonly used MPS methods is that in the proposed approach, conditional distributions are constructed using high-order spatial indicator moments as functions of distances based on hard data. Thus, simulated realizations can be generated without a TI. Note that in applications with relatively large data sets, such as the simulation of mineral deposits, the higher-order statistics are deduced from hard data. However, the option of adding a TI to a data set is available only if sparse data sets are available, as is the case with petroleum reservoirs.

The basic concept of the method presented is to use recursive approximation models with enclosed boundary conditions, which are derived from the nested nature of high-order spatial indicator moments, as presented herein. To provide a robust estimation, the regularized B-splines are used. An additional critical aspect of the proposed approach is that different amounts of information can be retrieved for different levels of relations. Each order of spatial statistics is approximated using the appropriate number of B-splines to provide robustness to the approach and to avoid overfitting. Thus, lower-order statistics are estimated with a higher resolution than the higher-order statistics.

The simulation algorithm presented was tested at two real copper deposits, without using TIs. The results of the applications demonstrate that the proposed method reproduces complex spatial patterns and preserves the high-order spatial statistics in the data. While the proposed technique is fully data-driven, information from a TI can be incorporated with the proposed model as a trend to capture high-frequency features when available in the TI. Further research may consider improving the approximation methods.

Appendix

Consider an arbitrary spatial configuration of three points in space. Using Eqs. (7) and (8), the third-order spatial indicator moment can be expressed as

$$ M_{{k_{0} ,k_{1} ,k_{2} }} (Z_{0} ,Z_{1} ,Z_{2} ) = E\left[ {I_{{k_{0} }} (Z_{0} )I_{{k_{1} }} (Z_{1} )I_{{k_{2} }} (Z_{2} )} \right]. $$

(20)

Let us consider that $Z_{0}$ has the same location as $Z_{1}$, i.e. $h_{1} = x_{1} - x_{0} = 0$. Then, $Z_{0}$ has the same value as $Z_{1}$

$$ M_{{k_{0} ,k_{1} ,k_{2} }} (Z_{0} ,Z_{1} ,Z_{2} ) = E\left[ {I_{{k_{0} }} (Z_{0} )I_{{k_{1} }} (Z_{1} )I_{{k_{2} }} (Z_{2} )} \right] = E\left[ {I_{{k_{0} }} (Z_{0} )I_{{k_{1} }} (Z_{0} )I_{{k_{2} }} (Z_{2} )} \right],{\text{ when }}x_{0} = x_{1} . $$

(21)

It is not hard to see that the term $I_{{k_{0} }} (Z_{0} )I_{{k_{1} }} (Z_{0} )$ is zero when $k_{1} \ne k_{0}$, and otherwise equal to $\left[ {I_{{k_{0} }} (Z_{0} )} \right]^{2} = I_{{k_{0} }} (Z_{0} )$. Therefore,

$$ M_{{k_{0} ,k_{1} ,k_{2} }} (Z_{0} ,Z_{1} ,Z_{2} ) = E\left[ {I_{{k_{0} }} (Z_{0} )I_{{k_{2} }} (Z_{2} )} \right]\delta_{{k_{0} ,k_{1} }} = M_{{k_{0} ,k_{2} }} (Z_{0} ,Z_{2} )\delta_{{k_{0} ,k_{1} }} ,{\text{ when }}x_{0} = x_{1} . $$

(22)

Thus, Eq. (22) connects third-order spatial statistics with second-order statistics and can be generalized for high-order spatial statistics in the form of Eq. (13)

$$ M_{{\mathbf{k}}} ({\mathbf{o}};\,h_{1} , \ldots ,h_{p} = 0, \ldots ,h_{n} ) = M_{{{\mathbf{k}}\backslash k_{p} }} ({\mathbf{o}};\,{\mathbf{h}}\backslash h_{p} )\delta_{{k_{0} ,k_{p} }} ,\forall p \in 1 \ldots n, $$

In Eq. (20), let us consider the other extreme $h_{1} \to \infty$; then, under the assumption of finite spatial correlation length of the random field ${\mathbf{Z}}$, the random variable $Z_{1}$ can be considered as independent from random variables $Z_{0}$ and $Z_{2}$. Then, using Eq. (3),

$$ M_{{k_{0} ,k_{1} ,k_{2} }} (Z_{0} ,Z_{1} ,Z_{2} ) = P(Z_{0} = k_{0} ,Z_{1} = k_{1} ,Z_{2} = k_{2} ) = P(Z_{0} = k_{0} ,Z_{2} = k_{2} )P(Z_{1} = k_{1} ) $$

$$ M_{{k_{0} ,k_{1} ,k_{2} }} (Z_{0} ,Z_{1} ,Z_{2} ) = M_{{k_{0} ,k_{2} }} (Z_{0} ,Z_{2} )M_{{k_{1} }} (Z_{1} ). $$

(23)

Thus, Eq. (23) connects third-order spatial statistics with second-order statistics and can be generalized for high-order spatial statistics in the form of Eq. (14)

$M_{{\mathbf{k}}} ({\mathbf{o}};\,h_{1} , \ldots ,h_{p} \to \infty , \ldots ,h_{n} ) = M_{{{\mathbf{k}}\backslash k_{p} }} ({\mathbf{o}};\,{\mathbf{h}}\backslash h_{p} )M_{{k_{p} }} ,\forall p \in 1 \ldots n$

.Graphically, for the third-order spatial indicator moments, the boundary conditions, i.e. second-order spatial indicator moments, are show on Fig. 19. The three-point spatial indicator moment $M_{000} ({\mathbf{o}};\,h_{1} ,h_{2} )$ with $k_{0} = k_{1} = k_{2} = 0$ is considered. The solid violet lines represent second-order spatial statistics at $h_{1} = 0$ or $h_{2} = 0$, i.e. $M_{000} ({\mathbf{o}};\,h_{1} = 0,h_{2} ) = M_{00} (o_{2} ;\,h_{2} )$ and $M_{000} ({\mathbf{o}};\,h_{1} ,h_{2} = 0) = M_{00} (o_{1} ;\,h_{1} )$, respectively. The red solid lines represent second-order spatial statistics when either $h_{1} \to \infty$ or $h_{2} \to \infty$, i.e. $M_{000} ({\mathbf{o}};\,h_{1} \to \infty ,h_{2} ) = M_{00} (o_{2} ;\,h_{2} )M_{0} (Z_{1} )$ and $M_{000} ({\mathbf{o}};\,h_{1} ,h_{2} \to \infty ) = M_{00} (o_{1} ;\,h_{1} )M_{0} (Z_{2} )$, respectively.

Fig. 19

The three-point spatial indicator moment map $M_{000} ({\mathbf{o}};\,h_{1} ,h_{2} )$. The solid violet lines represent second-order spatial statistics at $h_{1} = 0$ or $h_{2} = 0$, and the solid red lines represent second-order spatial statistics when either $h_{1} \to \infty$ or $h_{2} \to \infty$

In summary, all-order moments are connected via boundary conditions:

• 1. Marginal distribution ${\mathrm{P}\left({Z}_{0}={k}_{0}\right)=M}_{{k}_{0}}({Z}_{0})$, i.e. the first-order moment is the boundary for the second-order moment ${M}_{{k}_{0},{k}_{1}}({Z}_{0},{Z}_{1})$

  $$ { }M_{{k_{0} ,k_{1} }} \left( {Z_{0} ,Z_{1} } \right) = E\left[ {I_{{k_{0} }} \left( {Z_{0} } \right)I_{{k_{1} }} \left( {Z_{1} } \right)} \right] = E\left[ {I_{{k_{0} }} \left( {Z_{0} } \right)} \right]\delta_{{k_{0} ,k_{1} }} = { }M_{{k_{0} }} \left( {Z_{0} } \right)\delta_{{k_{0} ,k_{1} }} ,{\text{ when }}x_{0} = x_{1} $$

• 2. The second-order moment is the boundary for the third-order moment. For example,

  $$ M_{{k_{0} ,k_{1} ,k_{2} }} (Z_{0} ,Z_{1} ,Z_{2} ) = E\left[ {I_{{k_{0} }} (Z_{0} )I_{{k_{2} }} (Z_{2} )} \right]\delta_{{k_{0} ,k_{1} }} = M_{{k_{0} ,k_{2} }} (Z_{0} ,Z_{2} )\delta_{{k_{0} ,k_{1} }} ,{\text{ when }}x_{0} = x_{1} . $$

• 3. The third-order moment is the boundary for the fourth-order moment. For example,

  $$ \begin{aligned} M_{{k_{0} ,k_{1,} k_{2,} k_{3} }} \left( {Z_{0} ,Z_{1} ,Z_{2} ,Z_{3} } \right) & = E\left[ {I_{{k_{0} }} \left( {Z_{0} } \right)I_{{k_{1} }} \left( {Z_{1} } \right)I_{{k_{2} }} \left( {Z_{2} } \right)I_{{k_{3} }} \left( {Z_{3} } \right)} \right] \\ & = E\left[ {I_{{k_{0} }} \left( {Z_{0} } \right)I_{{k_{1} }} \left( {Z_{1} } \right)I_{{k_{2} }} \left( {Z_{2} } \right)} \right]\delta_{{k_{0} ,k_{3} }} \\ & = { }M_{{k_{0} ,k_{1,} k_{2} }} \left( {Z_{0} ,Z_{1} ,Z_{2} } \right)\delta_{{k_{0} ,k_{3} }} ,{\text{ when }}x_{0} = x_{3} . \\ \end{aligned} $$