Dynamic analysis of a belt transmission with the GMS friction model

Abstract

The paper presents a certain method of analysing the dynamics of a belt transmission. A flat transmission model developed by us was presented. For the analysis, it assumed the transmission 5PK belt. A discrete belt model, being a system of rigid beams interconnected with flexible and shock-absorbing elements, was used. To account for the mutual influence between the belt and pulleys, the Kelvin–Voigt contact model was used. The GMS friction model was also implemented, which allows all basic known friction phenomena to be taken into account. For this purpose, the vector of generalized coordinates was expanded with additional sub-systems of coordinates modelling the flexible belt-pulley connection. Moreover, two additional cases of a sudden transmission start were presented: with values of driving and resistance torque not causing a significant slip in the transmission as well as values of torque that cause slip.

1 Introduction

Leonard Euler [1] was the first to initiate research on the phenomena occurring in belt transmission systems. The first paper discussing the existence of micro-displacements in belt transmissions was written by Reynolds [2]. The research objectives, which changed over the centuries together with some more important works, were presented by Fawcett in [3]. What also deserves a mention are papers in which friction between rubber and other materials was modeled. The most well-known examples include works related to automotive engineering, especially those dealing with the modelling of friction between the tire and the road, e.g. a frequently cited work by [4]. The proposed friction model, also presented in the paper above, included the Dahl friction model [5]. The paper [4] also introduced another dynamic friction model, the LuGre model, which allows accounting for the Stribeck effect. Belt models can be divided into continuous models where the belt is modeled as an elastic rod [6] or a string with some longitudinal stiffness and sometimes with bending stiffness [7,8,9,10], and discrete [11,12,13,14] models, most commonly assuming rigid beam elements joined together by translational and sometimes additionally by torsional spring-damping elements.

The papers [13, 14] presented belt transmission models with a linear friction model with the possibility of predicting belt creep. This is called the Coulomb-like tri-linear creep-rate-dependent friction model. In [15], a model taking into account the elastic/perfectly-plastic friction law (EPP) was presented.

What also deserves a mention is a group of papers in which the Dahl friction model is applied as a way of modelling friction in the revolute joint in a belt tensioner, e.g. [16, 17].

In his papers, the authors developed two-dimensional models of belt transmissions using the Dahl friction model [18], the Threlfall friction model [19], and a model that included a microslip [20]. In [20], the assumptions and requirements made during the process of model development were presented.

The Generalized Maxwell-Slip friction model (hereinafter referred to as GMS friction model) was used to take into account the friction between the belt and the pulleys of the belt transmission under consideration. The application of the GMS friction model to the belt transmission model is a novel approach to the problem. The GMS model has been developed as an expansion of the Leuven friction model [21, 22] and the earlier LuGre model [23], in turn, based on the Dahl model. The GMS friction model has been described in several basic publications, which are chronologically [24,25,26,27]. This is a universal model, as it allows to take into account all known friction phenomena i.e. preliminary displacement (first described in [28]), together with the interdependence between the static friction coefficient and the tangential loading rate [29, 30] and hysteresis with non-local frictional memory [31, 32], the Stribeck effect (for the first time described in [33]) and the phenomenon of time delay in the case of dynamic friction characteristics (described for the first time in [34]). Because of these properties, the analysed model may be successfully used for the analysis of the “stick-slip” phenomenon occurring in various mechanical systems, including belt transmissions.

The stick-slip phenomenon occurring in belt transmissions was analysed, among others, in [35,36,37,38].

2 Method of dynamic analysis

2.1 Application of the generalized Maxwell-slip friction model to account for friction between the belt and pulleys of the belt transmission

To analyse the presented friction model, it is necessary to consider the system of $n_{GMS}$ bodies presented in Fig. 1 and known from physics. It is a system of interconnected parallel, weightless Maxwell elements [39, 40].

Fig. 1

Maxwell’s system of elements

For considerations presented in this paper Maxwell’s elements correspond to local frictional contacts at the places where individual unevenness of the surfaces sliding on top of each other interact. These surfaces constitute contact surfaces for the individual discrete rigid element modelling the belt together with relevant pulleys. These elements move in such a way that the slip phase under kinetic friction conditions is separated by a short-term standstill phase under static friction conditions.

The input value for the system under consideration is the displacement $x_{T_i}$ in the global contact under consideration. Element k, where $k=1,\ldots ,n_{GMS}$ (its number is equivalent to the number of the relevant local frictional contact), whose displacement is determined by the coordinate $x_{T_{i,k}}$, has its own individual initial value $T_{i,k}$ of the friction force acting on it.

As shown in the Fig. 1, positive or negative spring deformation k is determined by the formula:

$$\begin{aligned} \varDelta x_{T_{i,k}}=x_{T_i}-x_{T_{i,k}}, \end{aligned}$$

(1)

with the spring deformation $\varDelta x_{T_{i,k}}$ (representing the state variable) being equivalent to the deformation of the local friction contact k modeled by the spring in the direction tangential to the direction of movement.

The value $T_{i,k}$ of the friction force acting on the element k, equivalent to the force exerted by in by the spring under consideration, with either positive or negative sign, is proportional to the change $\varDelta x_{T_{i,k}}$:

$$\begin{aligned} T_{i,k}=\sigma _k \varDelta x_{T_{i,k}}, \end{aligned}$$

(2)

where the spring coefficient of stiffness $\sigma _k$ is the same as the coefficient of the stiffness of the local friction contact k modelled by it in a direction tangential to the direction of movement. This coefficient takes the same value, regardless of the rigid body (RB) considered.

Taking into account Coulomb’s formula, the value of the friction force acting on element i can be expressed as:

$$\begin{aligned} T_{i,k}=\mu ^*_{i,k}N_{i,k}, \end{aligned}$$

(3)

where $N_{i,k}$—value of normal reaction force in the local frictional contact k under consideration.

The value of $N_{i,k}$ can be expressed as:

$$\begin{aligned} N_{i,k}=\nu _kN_i, \end{aligned}$$

(4)

where $N_i$—the value of the normal of the reaction force in global frictional contact i, i.e. contact of the discrete rigid element i with the relevant pulley, $\nu _k$—weight coefficient meeting $\sum _{k=1}^{n_{GMS}} \nu _k=1$.

The computational friction coefficient $\mu _{i,k}^*$ in the local frictional contact k under consideration is expressed by the formula:

$$\begin{aligned} \mu _{i,k}^*=\text {sgn}\dot{x}_{T_i}\mu _{i,k}, \end{aligned}$$

(5)

where $\mu _{i,k}$—friction coefficient in this contact (taking the same value regardless of the RB under consideration).

Taking into account the relations (2) and (3), the computational friction coefficient can be presented as:

$$\begin{aligned} \mu _{i,k}^*=\sigma _{\mu _k} \varDelta x_{T_{i,k}}, \end{aligned}$$

(6)

with the following coefficient being taken into account:

$$\begin{aligned} \sigma _{\mu _k}=\frac{\sigma _{k}}{N_{i,k}}. \end{aligned}$$

(7)

If element k stays immobile, then the following condition is met:

$$\begin{aligned} \dot{x}_{T_{i,k}}=0, \end{aligned}$$

(8)

thus, based on formula (1) it may be written:

$$\begin{aligned} \varDelta \dot{x}_{T_{i,k}}=\dot{x}_{T_i}. \end{aligned}$$

(9)

If element k stays in motion, the differential equation expressing the time derivative of the computational friction coefficient is true:

$$\begin{aligned} \frac{d \mu _{i,k}^*}{dt}=\text {sgn}\dot{x}_{T_i}\nu _kc \left( 1-\frac{\mu _{i,k}^*}{s(\dot{x}_{T_i})} \right) , \end{aligned}$$

(10)

where c—attraction parameter, expressed in s^-1, determining the convergence speed of the computational friction coefficient $\mu _{i,k}^*$ to the value of the expression $s(\dot{x}_{T_i})$.

This equation was implemented after a slight modification of the original relationship presented in paper [25] in which there are values of friction forces and not its coefficients.

The expression $s(\dot{x}_{T_i})$, determining the course of the computational kinetic friction coefficient in the global contact i as a function of the constant slip velocities $\dot{x}_{T_i}$, is presented by a formula illustrating the so-called Stribeck effect (Fig. 2) taken from [41]. This formula has the form:

$$\begin{aligned} s(\dot{x}_{T_i})=\text {sgn}\dot{x}_{T_i} \left( \mu _C+(\mu _s-\mu _C)e^{- \left( \frac{\dot{x}_{T_i}}{v_S} \right) ^2} \right) , \end{aligned}$$

(11)

where $\mu _C$—Coulomb friction coefficient independent of the slip velocities $\dot{x}_{T_i}$, $\mu _s$—static friction coefficient, $v_S$—Stribeck velocity.

Fig. 2

Graphical representation of the expression $s(\dot{x}_{T_i})$ presenting Stribeck effect (for $\dot{x}_{T_i}>0$)

Taking into account the relationship (6), (10) can be transformed into:

$$\begin{aligned} \varDelta \dot{x}_{T_{i,k}}=\text {sgn}\dot{x}_{T_i} \frac{\nu _kc}{\sigma _{\mu _k}} \left( 1-\frac{\mu _{i,k}^*}{s(\dot{x}_{T_i})} \right) . \end{aligned}$$

(12)

Variables $\varDelta \dot{x}_{T_{i,k}}$ in any movement moment t are determined by integrating differential equations (9) and (12). Then, based on formula (6), computational friction coefficients $\mu _{i,k}^*$ can be determined.

The element k stays immobile as long as the condition $\vert \mu _{i,k}^* \vert \le \vert s(\dot{x}_{T_i}) \vert$ is met, and it remains in motion as long as slip velocity $\dot{x}_{T_{i,k}}$ does not change its sign.

Now, the value of friction force $T_i$ in the global contact i under consideration can be calculated using the equation:

$$\begin{aligned} T_i=N_i \sum _{k=1}^{n_{GMS}} \mu _{i,k}^* \nu _k. \end{aligned}$$

(13)

2.2 The model of transmission with discrete belt model

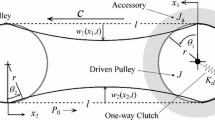
It assumed a discrete belt model, divided into $n_b$ rigid bodies (RB) connected by spring damping elements (SDE) with longitudinal stiffness, damping and bending stiffness also being assumed. Every belt element, shown in Fig. 3, is described by the position vector:

$$\begin{aligned} \mathbf{P} _i=\left[ \begin{array}{c} x_i \\ y_i \\ 0 \end{array} \right] , \end{aligned}$$

(14)

and the rotation $\theta _i$. In the transmission model, it also assumed $n_p$ pulleys.

Fig. 3

Assumed belt bodies and spring damping element

The GMS model of friction with the number of $n_{GMS}$ of the assumed bodies is connected with the ith belt body by spring elements. The vector of generalized coordinates can be therefore written as:

$$\begin{aligned} \mathbf{q} =\left[ \begin{array}{ccc} \mathbf{q} _b&\mathbf{q} _p&\mathbf{q} _{GMS} \end{array} \right] ^T, \end{aligned}$$

(15)

where $\mathbf{q} _b=\left[ \begin{array}{ccccc} x_1y_1\varphi _1&\ldots&x_iy_i\varphi _i&\ldots&x_{n_b}y_{n_b}\varphi _{n_b} \end{array} \right] ^T$—vector of coordinates of $n_b$ bodies, $\mathbf{q} _p=\left[ \begin{array}{ccccc} \theta _1&\ldots&\theta _j&\ldots&\theta _{n_p} \end{array} \right] ^T$—vector of coordinates of $n_p$ pulleys, $\mathbf{q} _{GMS}=\left[ \begin{array}{ccccc} \mathbf{q} _{1GMS}&\ldots&\mathbf{q} _{iGMS}&\ldots&\mathbf{q} _{n_b GMS} \end{array} \right] ^T$—vector of coordinates of all elements k, $\mathbf{q} _{iGMS}=\left[ \begin{array}{ccccc} z_{i,1}&\ldots&z_{i,k}&\ldots&z_{i,n_{GMS}} \end{array} \right] ^T$—vector of coordinates of element $n_{GMS}$ connected to ith RB, $i=1 \ldots n_b$, $j=1 \ldots n_p$, $k=1 \ldots n_{GMS}$.

The number of generalized coordinates can be therefore calculated with the formula: $n=3n_b+n_p+n_bn_{GMS}$.

Coordinates of belt bodies can be derived from vector $\mathbf{q}$ in the following manner:

$$\begin{aligned} x_i=\mathbf{q} [3i-2], y_i=\mathbf{q} [3i-1], \varphi _i=\mathbf{q} [3i]. \end{aligned}$$

(16)

Coordinates of pulleys can be also calculated from:

$$\begin{aligned} \theta _j=\mathbf{q} [3n_b+j]. \end{aligned}$$

(17)

and also coordinates of elements k from:

$$\begin{aligned} z_{i,k}=\mathbf{q} [3n_b+n_p+(i-1) \cdot n_{GMS}+k]. \end{aligned}$$

(18)

Equations of motion of belt bodies can be formulated as the following system:

$$\begin{aligned} \left\{ \begin{array}{ccl} m_i\ddot{x}_i &{} = &{} \hat{\mathbf{X }}^T(\mathbf{F} _i+\mathbf{R} _i+\mathbf{F} _{gi}) \\ m_i\ddot{y}_i &{} = &{} \hat{\mathbf{Y }}^T(\mathbf{F} _i+\mathbf{R} _i+\mathbf{F} _{gi}) \\ I_{zi}\ddot{\varphi }_i &{} = &{} \hat{\mathbf{Z }}^T\mathbf{M} _i \end{array}, \right. \end{aligned}$$

(19)

where $\hat{\mathbf{X }}$—the unit vector along the x axis, $\hat{\mathbf{Y }}$—the unit vector along the y axis, $\hat{\mathbf{Z }}$—the unit vector along the z axis.

In the equations above, the vector $\mathbf{F} _i$ is the sum of forces from neighbouring spring-damping elements:

$$\begin{aligned} \mathbf{F} _i=\mathbf{F} _i^L+\mathbf{F} _i^R. \end{aligned}$$

(20)

The vector $\mathbf{R} _i$ is the resultant reaction force acting from the pulleys:

$$\begin{aligned} \mathbf{R} _i=\sum _{j=1}^{n_p}(\mathbf{N} _{i,j}+\mathbf{T} _{i,j}), \end{aligned}$$

(21)

where $\mathbf{N} _{i,j}$—the normal force between the ith belt body and the jth pulley, $\mathbf{T} _{i,j}$—the friction force between the ith belt body and the jth pulley.

The normal force $\mathbf{N} _{i,j}$ can be calculated from the formula:

$$\begin{aligned} \mathbf{N} _{i,j}=N_{i,j}\hat{\mathbf{r }}_{i,j}, \end{aligned}$$

(22)

where $\hat{\mathbf{r }}_{i,j}$—the versor (unit vector) of the $\mathbf{r} _{i,j}$.

The vector $\mathbf{r} _{i,j}$ can be calculated from the formula:

$$\begin{aligned} \mathbf{r} _{i,j}=\mathbf{P} _i-\mathbf{P} _j^p, \end{aligned}$$

(23)

where $\mathbf{P} _j^p$—position vector of the jth pulley.

The value of normal force $\mathbf{N} _{i,j}$ assumed from the same Kelvin–Voigt contact model as in [18]:

$$\begin{aligned} N_{i,j}=c_{con1}p_{i,j}^2+c_{con2}p_{i,j}+b_{con}\dot{p}_{i,j}, \end{aligned}$$

(24)

where $p_{i,j}=r_{j}-\vert \mathbf{r} _{i,j} \vert$, $r_j$—radius of the jth pulley, $c_{con1}$, $c_{con1}$—belt-pulley contact stiffness coefficients, $b_{con}$—belt-pulley contact damping coefficients.

The value of normal force $N_i$ can be derived from:

$$\begin{aligned} \mathbf{N} _i=\sum _{j=1}^{n_p}{} \mathbf{N} _{i,j}. \end{aligned}$$

(25)

The gravity force can be calculated from:

$$\begin{aligned} \mathbf{F} _{gi}=m_i\mathbf{g} , \end{aligned}$$

(26)

where $m_i$—mass of the ith belt body.

The torque $\mathbf{M} _i$ acting on the ith belt body is the sum of torques from neighbouring spring-damping elements:

$$\begin{aligned} \mathbf{M} _i=\mathbf{M} _i^L+\mathbf{M} _i^R, \end{aligned}$$

(27)

where

$$\begin{aligned} \mathbf{M} _i^L= & {} \mathbf{M} _i^{Ltra}+\mathbf{M} _i^{Lben}, \end{aligned}$$

(28)

$$\begin{aligned} \mathbf{M} _i^R= & {} \mathbf{M} _i^{Rtra}+\mathbf{M} _i^{Rben}. \end{aligned}$$

(29)

The components of the formulas presented above include translational and bending stiffness torques, from left and right spring-damping elements and can be calculated from:

$$\begin{aligned} \mathbf{M} _i^{Ltra}= & {} -\mathbf{d} _i \times \mathbf{F} _i^L, \end{aligned}$$

(30)

$$\begin{aligned} \mathbf{M} _i^{Rtra}= & {} \mathbf{d} _i \times \mathbf{F} _i^R, \end{aligned}$$

(31)

$$\begin{aligned} \mathbf{d} _i= \,& {} \left[ \begin{array}{c} \frac{l_i}{2} \cos \varphi _i \\ \frac{l_i}{2} \sin \varphi _i \\ 0 \end{array} \right] . \end{aligned}$$

(32)

The forces $\mathbf{F} _i^L=-\mathbf{F} _{i-1}^R$ have the same direction as the vector:

$$\begin{aligned} \mathbf{P} _i^{LR}=\mathbf{P} _i+\mathbf{d} _i-\mathbf{P} _{i-1}-\mathbf{d} _{i-1}, \end{aligned}$$

(33)

whereas direction of the torques $\mathbf{M} _i^{Lben}=-\mathbf{M} _i^{Rben}$ conforms with the z axis. The values of these vectors can be calculated from:

$$\begin{aligned} F_i^L= & {} F_{i-1}^R=c_{tra} \varDelta l_i^L+b_{tra} \varDelta \dot{l}_i^L, \end{aligned}$$

(34)

$$\begin{aligned} M_i^{Lben}= & {} M_{i-1}^{Rben}=c_{ben}\varDelta \varphi _i+b_{tra}\varDelta \dot{\varphi }_i, \end{aligned}$$

(35)

where $c_{tra}=\frac{n_bc_{tra}^b}{l}$, $b_{tra}=\frac{n_bb_{tra}^b}{l}$, $c_{ben}=\frac{n_bc_{ben}^b}{l}$, $b_{ben}=\frac{n_bb_{ben}^b}{l}$, $\varDelta \varphi _i=\varphi _i-\varphi _{i-1}$, $\varDelta \dot{\varphi }_i=\dot{\varphi }_i-\dot{\varphi }_{i-1}$, $c_{tra}^b$—translational stiffness per one unit length of the belt, $b_{tra}^b$—translational damping per one unit length of the belt, $c_{ben}^b$—bending stiffness per one unit length of the belt, $b_{ben}^b$—bending damping per one unit length of the belt, l—assumed length of the belt (calculated from geometric dependences).

The longitudinal deflection of the spring-damping elements can be calculated from:

$$\begin{aligned} \varDelta l_i^L=\varDelta l_{i-1}^R=P_i^{LR}. \end{aligned}$$

(36)

Equations of motion of pulleys described as:

$$\begin{aligned} I_{zj}\ddot{\theta }_j=-M_j-\sum _{i=1}^{n_b}{\hat{\mathbf{Z }}}^T\mathbf{M} _{T_{i,j}}, \end{aligned}$$

(37)

where $\mathbf{M} _{T_{i,j}}=\hat{\mathbf{r }}_{i,j}\times \mathbf{T} _{i,j}$—torque from friction force of ith belt body.

Components of the formula presented above have been shown in Fig. 4.

Fig. 4

The positions of the ith belt body and the jth pulley

The relative velocity between the ith body and the jth pulley is:

$$\begin{aligned} \mathbf{v} _{i,j}=\mathbf{v} _{i,j}^p-\mathbf{v} _{i}^t, \end{aligned}$$

(38)

where $\mathbf{v} _{i,j}^p={\hat{\mathbf{Z }}}\cdot \dot{\theta }_j \times \hat{\mathbf{r }}_{i,j}$—the tangent pulley velocity vector, applied to the point of contact, $\mathbf{v} _{i}^t$—velocity vector of the ith belt body tangent to the pulley.

The value of velocity $\mathbf{v} _{i}^t$ can be calculated from the following scalar product:

$$\begin{aligned} v_{i}^t=\mathbf{v} _{i}^T\cdot \mathbf{t} _{i,j}. \end{aligned}$$

(39)

The direction of the vector $\mathbf{v} _{i}^t$ is the same as $\mathbf{t} _{i,j}$:

$$\begin{aligned} \mathbf{t} _{i,j}=\frac{\hat{\mathbf{Z }} \times \hat{\mathbf{r }}_{i,j}}{\vert \hat{\mathbf{Z }} \times \hat{\mathbf{r }}_{i,j} \vert }. \end{aligned}$$

(40)

3 Results of simulations

For analysis, it assumed transmission with poly-V belt 5PK, presented schematically in Fig. 5. The transmission consists of two pulleys with identical radiuses equal to $r=0.2$ m. The distance between the pulleys was $l=1$ m. The centre of the first pulley was accepted as the origin of the system of coordinates $O_1$. It assumed that a driving torque of the arbitrary value of $M_d$ will be applied to the first pulley and a resistance torque of $M_{res}$ to the second pulley. Friction and contact parameters have been assumed based on data proposed in [42, 43]. The presented equations have been implemented in the C++ programming language. Runge–Kutta of the fourth order method was used for numerical integration of differential equations of motion. The multithreading of the processor was used to speed up the calculations, using the OpenMP library for this purpose. Table 1 presents the assumed parameter values.

Fig. 5

The analysed transmission

Table 1 Assumed values of parameters

3.1 First simulation

In the first analysed case, arbitrary drive torque values of $M_d=20$ N m and resistance values of $M_{res}=15$ N m were assumed. The course of the torques $M_1$ and $M_2$, acting on the pulleys have been assumed based on the following relations:

$$\begin{aligned} M_1 &= \left\{ \begin{array}{lll} 50t &{} \text {for} &{} t=0\ldots0.4\,\text {s,} \\ 20 &{} \text {for} &{} t=0.4\ldots2\,\text {s,} \\ -50t+120 &{} \text {for} &{} t=2\ldots2.4\,\text {s,}\\ 0 &{} \text {for} &{} t>2.4\,\text {s.} \end{array} \right. \end{aligned}$$

(41)

$$\begin{aligned} M_2= & {} \left\{ \begin{array}{lll} 50t &{} \text {for} &{} t=0\ldots0.3\,\text {s,} \\ 15 &{} \text {for} &{} t>0.3\,\text {s.} \end{array} \right. \end{aligned}$$

(42)

As can be noticed from the formulas above, torque $M_1$ can achieve arbitrary value $M_d$ ($t=0.4\ldots2\,\text {s,}$) whereas torque $M_2$ can achieve arbitrary value $M_{res}$ ($t>0.3\,\text {s}$). Figure 6 presents the resulting course of torques $M_1$ and $M_2$ applied to the pulleys. Figure 7 presents the resulting angular velocities of the pulleys.

As can be seen with the resulting torque courses, until 0.3 s the values of these torques compensate. From this moment on, the torque $M_1$ dominates over torque $M_2$ and the transmission accelerates. From 2 s, the value of $M_1$ starts decreasing to reach zero at 2.4 s. As a result of this, the transmission starts decelerating. The simulation finishes when both pulleys come to a stop, i.e. after ca. 2.8 s.

Sudden start results in the generation of relatively large reaction forces in the belt and friction forces between the belt and the pulley. The transmission deceleration is also quite sudden. Despite the sudden course of these torques in Fig. 7, no major differences between the angular velocity of the drive pulley and angular velocity of the driven pulley were observed, which means that the transmission operates with only a slight slip. The transmission achieves its maximum velocity after ca. 2.1 s. At this moment, the angular velocity of the driven pulley is ca. 155 rad/s, whereas the angular velocity of the drive pulley is ca. 153 rad/s (slip was ca. 1.3%).

Fig. 6

The courses of drive and driven torque

Fig. 7

The courses of angular velocities of drive and driven pulleys

Figure 8 presents the course of normal force $N_{i}$ acting on the selected ith RB. The zero values of this force mean that the selected ith RB is between the pulley in the tensioned or loose part of the belt.

Normal force directly influences the values of the friction force. The course of this force, for the same ith RB has been presented in Fig. 9. Figure 10 presents the resulting course of the reaction force in SDE directly neighbouring the analysed ith RB. Initially, this element is located on the driven pulley. At ca. 0.58 s, it moves towards the tensioned part of the belt between the driven and the drive pulley. The course presented in Fig. 10 clearly shows a significant increase in the reaction force in SDE. At ca. 0.76 s, repeated contact with a pulley, the drive pulley this time, takes place, which results in a quick drop in the reaction force. Then, at 0.83 s, the analysed ith RB separates from the pulley and moves along the loose part of the belt. Lower values of the reaction force are observed. Together with an increase in the pulley rotational speed, the transition phases between the driven pulley, tensioned part of the belt, drive pulley and lose part of the belt become increasingly shorter.

Fig. 8

The course of contact normal force $N_{i}$ acting on selected ith RB from pulleys

Fig. 9

The course of friction force $T_{i}$ acting on selected ith RB from pulleys

Fig. 10

The course of reaction force acting on selected ith RB from neighbouring SDE

Figure 11 presents the values of friction forces calculated for each of the elements k. Figure 12, in turn, presents the corresponding value of the friction coefficient.

Because the coefficient $\sigma _{\mu _1}$, being the measure of stiffness, is the lowest, the calculated component of the friction force is also the lowest. Force values for elements $k=2$ and $k=3$ are proportionally larger. Insignificant disproportions between these force values may result from the fact that elements k do not move in synchrony.

The short-term drop in the value of these forces to zero at the moment of transmission start-up, although part of the belt with the analysed ith RB is located on the driven pulley, results from a temporary loss of adhesion ith RB (thus indirectly from relatively small flexibility of the assumed parameters of the contact model and the neighbouring SDE). It was also noted that the remaining neighbouring ith RB, which are also located on the pulley, do not detach from it in these moments.

In Fig. 12, it can be seen that the values of individual coefficients $\mu _{i,k}^*$ did not approach the arbitrary values of coefficients $\mu _s$ and $\mu _d$.

Fig. 11

The courses of friction force components calculated for elements k

Fig. 12

The courses of friction coefficient values calculated for elements k

Figures 13 and 14 present respectively the course of the displacement $x_{T_i}$ and velocity $\dot{x}_{T_i}$ in friction connection between the analysed ith RB and the pulleys. As can be seen from the course presented in Fig. 13, the displacement values slightly exceed $3\times 10^{-4}$ m. The largest value is observed at first contact with the drive pulley, when the transmission accelerates. On the other hand, from Fig. 14, it can be concluded that the values of slip velocities are influenced by the rotational speed of the transmission and the values of drive torque and resistance. At the very moment when the disproportion between these elements is the greatest, just before the assumed reduction in drive torque, the largest velocity value of ca. 0.53 m/s was observed.

Fig. 13

The course of displacement $\varDelta x_{T_{i,k}}$ of selected ith RB

Fig. 14

The course of displacement velocity $\varDelta \dot{x}_{T_{i,k}}$ of selected ith RB

3.2 Second simulation

In the second analysed case, twice as large arbitrary values of the drive torque $M_d=40$ N m and resistance $M_{res}=30$ N m were assumed. Courses of the torques $M_1$ and $M_2$ were thus assumed to meet the following relations:

$$\begin{aligned} M_1= & {} \left\{ \begin{array}{lll} 100t &{} \text {for} &{} t=0\ldots0.4\,\text {s,} \\ 40 &{} \text {for} &{} t=0.4\ldots2\,\text {s,} \\ -100t+240 &{} \text {for} &{} t=2\ldots2.4\,\text {s,}\\ 0 &{} \text {for} &{} t>2.4\,\text {s.} \end{array} \right. \end{aligned}$$

(43)

$$\begin{aligned} M_2= & {} \left\{ \begin{array}{lll} 100t &{} \text {for} &{} t=0\ldots0.3\,\text {s,} \\ 30 &{} \text {for} &{} t>0.3\,\text {s.} \end{array} \right. \end{aligned}$$

(44)

Figure 15 presents the resulting courses of torques $M_1$ and $M_2$ applied to the pulleys obtained in the second simulation. Whereas, Fig. 16 presents analogical resulting angular velocities of pulleys. As can be seen, at ca. 0.9 s, belt slip occurred. What is interesting is that this slip did not occur directly at the moment of achieving the maximum values of torques $M_1$ and $M_2$. Thus, without any doubt, an increase in the centrifugal force acting on the pulley also played a role. It increased under the influence of increasingly larger values of pulley angular velocities. Increasing values of this force lead to the reduction in normal force $N_{i}$. Maximum pulley angular velocities, in this case, were 835rad/s for the drive pulley and 102 rad/s for the driven pulley. Moreover, shortly after the occurrence of slip, the driven pulley reduced its speed close to zero. The simulation was interrupted once the drive pulley stopped.

Fig. 15

The courses of drive and driven torque

Fig. 16

The courses of angular velocities of drive and driven pulleys

Figures 17 and 18 present the resulting values of normal force $N_{i}$ and friction $T_{i}$ obtained for the second simulation. Comparing these courses with the base courses presented in Figs. 8 and 9, the previously mentioned reduction in the value of normal force together with a slight increase in friction force can be observed, especially in the final phase of the simulation. After 2.5 s, the analysed ith RB slipped considerably on the driven pulley. At the previous stage, when the belt cooperated with the driven pulley (in the time interval ca. 1.41... 1.84 s) smaller friction values were observed as the belt was trying to follow the pulley.

Fig. 17

The course of contact normal force $N_{i}$ acting on selected ith RB from pulleys

Fig. 18

The course of friction force $T_{i}$ acting on selected ith RB from pulleys

When comparing the course of the reaction force in SDE presented in Fig. 19 with the course presented in Fig. 10, no major changes in the values of reaction forces in SDE neighbouring the analysed ith RB were observed.

Fig. 19

The course of reaction force acting on selected ith RB from neighbouring SDE

Comparing the courses of friction forces for specific elements k presented in Fig. 20 with the courses presented in Fig. 11, the above-mentioned significant increase in friction force is also noticeable, but the disproportions between specific courses are smaller. The same short-lived moment when the ith RB detached from the driven pulley at the initial simulation stage was also observed. An analysis of the value of friction coefficients for specific elements k (Fig. 21) allows us to see that in the final transmission movement phase values close to $\mu _s$ and $\mu _d$ have been observed.

Fig. 20

The courses of friction force components calculated for elements k

Fig. 21

The courses of friction coefficient values calculated for elements k

When analysing the course of the values $\varDelta x_{T_{i,k}}$ (Fig. 22) and $\varDelta \dot{x}_{T_{i,k}}$ (Fig. 23) at contact with the drive pulley (in time interval 1.41..1.84 s), relatively similar values of displacement of the individual elements k were observed. The reason for similar values includes the relatively large belt slip of ca. 141 m/s, which can be seen in the second course. Finally, when the analysed ith RB cooperates with the driven pulley, the situation gets reversed. The values of displacement increase proportionally with each element k, and the slip becomes negligible.

Fig. 22

The course of displacement $\varDelta x_{T_{i,k}}$ of selected ith RB

Fig. 23

The course of displacement $\varDelta \dot{x}_{T_{i,k}}$ velocity of selected ith RB

4 Conclusions

As already mentioned, the GMS friction model, which takes into account all the basic known friction phenomena, allows for reflecting the continuous, i.e. the real nature of friction consisting in smooth, unnoticeable transmission from the phase of standstill (under static friction conditions) to phase of motion (under dynamic friction conditions) and the other way round. Similarly to earlier dynamic friction models such as the above-mentioned Dahl, LuGre, and Leuven models, this model is based on the same mathematical formulas regardless of the current phase. It constitutes a significant simplification of the computational process. This makes it different from the switching friction models, e.g. [44, 45], previously used in the dynamics of mechanical systems, where standstill and motion phases are analysed separately. Switching friction models are based on different mathematical formulas describing the friction phenomenon in both friction phases. This poses a major difficulty in the implementation of the computational process. It was necessary to develop a special control procedure allowing us to determine the transition conditions between the friction phases. It might lead to a hypothesis that despite using a complex mathematical apparatus, switching friction models becomes obsolete as they model both phases of friction separately thus failing to depict the continuous nature of friction. To achieve more realistic results in the future by using the GMS friction model, detailed identification of parameters of friction occurring in belt transmissions between the belt and the pulleys would be needed. It needs to be stressed that the GMS friction model is the latest and the most advanced of all the dynamic friction models used in the dynamics of mechanical systems but due to its complexity, it is hardly ever used in calculations. Therefore, in our opinion, this work, based on this model, may be perceived as truly novel.