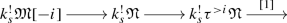Correction to: Generalized Springer theory for D-modules on a reductive Lie algebra

1 Correction to: Selecta Mathematica (2018) 24:4223–4277 https://doi.org/10.1007/s00029-018-0443-x

2 Summary of errata and revisions

The source of the problem is the incorrect [4] Proposition B.5.¹ This error invalidates Proposition B.7, which is also false as stated.² This, in turn, invalidates the proof of Lemma 3.5, which gives a bound on the singular support of parabolic restriction. Lemma 3.5 was used to give a characterization of the kernel of the parabolic restriction functor in terms of singular support (Theorem 3.14). This in turn was used to prove the t-exactness of parabolic restriction (Proposition 3.20), and thus the remainder of the generalized Springer decomposition was proved in Sect. 4.

In this note we will provide an alternative proof of the t-exactness of parabolic restriction (and induction) which doesn’t make reference to singular support (see Sect. 3).³ With the t-exactness of parabolic induction and restriction in hand, we can go about proving the generalized Springer decomposition as in Section 4 of [4]. The only trouble is that the definition of the subcategories $\mathbf {D}({\underline{\mathfrak {g}}})_{\nleq (L)}$ (and their relatives) in [4] was in terms of singular support conditions and it was shown (erroneously) that they were characterized in terms of parabolic restriction (see Theorem 3.14 and the subsequent paragraph in loc. cit.). While we will eventually see that both these characterizations are indeed equivalent, it will be more convenient for us to take parabolic restriction characterization as a definition, prove the generalized Springer decomposition using that definition, then finally prove the characterization in terms of singular support.

Thus the revised logic of the paper [4] now reads as follows.⁴ We may expunge Subsections 3.2, 3.4, 3.5, and 3.6. After Subsection 3.7 we may insert the proof of t-exactness given in Sect. 3 below. At the beginning of Sect. 4, insert the following.

Definition 1.1

For a given parabolic subgroup P of G and Levi factor $L \subseteq P$, we define $\mathbf {M}({\underline{\mathfrak {g}}})_{\nless (L)}$ to be the full subcategory of $\mathbf {M}({\underline{\mathfrak {g}}})$ consisting of objects ${\mathfrak {M}}$ for which $\mathbf{Res}^G_{P,L}({\mathfrak {M}})$ is cuspidal. We define $\mathbf {M}({\underline{\mathfrak {g}}})_{\nleq (L)}$ to be the further subcategory consisting of objects such that $\mathbf{Res}^G_{P,L}({\mathfrak {M}})$ is zero (recall that the zero object is considered cuspidal here).⁵

With these definitions, the rest of Sect. 4 of [4] goes through unchanged, except for the “Proof of Theorem C” near the end of the section. In particular, we recover proofs of Theorem A and Theorem B. Finally, we insert the content of Sect. 4 below, thus finishing the proof of Theorem C.

In the remainder of this note we will give the promised proof of t-exactness (Sect. 3) and prove the characterization of the blocks $\mathbf {M}({\underline{\mathfrak {g}}})_{(L)}$ in terms of singular support (Sect. 4).

3 Review of notation from [4]

• Throughout this note, G denotes a connected complex reductive algebraic group and ${\mathfrak {g}}$ its Lie algebra. The quotient stack ${\mathfrak {g}}/G$ is denoted by ${\underline{\mathfrak {g}}}$. Analogous notation is used for parabolic subgroups P and Levi factors L.

• Given a Levi subgroup L of G we write $W_{G,L} = N_G(L)/L$ for the relative Weyl group.

• For a given stack X, we write $\mathbf {D}(X)$ for the (unbounded) derived category of D-modules on X and $\mathbf {M}(X)$ for the corresponding abelian category sitting as the heart of the natural t-structure. We write $\mathbf {D}(X)^{\ge 0}$ (respectively $\mathbf {D}(X)^{\le 0}$) for the subcategory consisting of complexes concentrated in non-negative (respectively, non-positive) degrees (we use cohomological conventions).

• Given an element $x\in {\mathfrak {g}}$ we write $H_G(x)$ for the centralizer $C_G(x_s)$ of the semisimple part $x_s$ of x with respect to the Jordan decomposition. Thus $H_G(x)$ is a Levi subgroup of G.

• Recall that ${\mathfrak {g}}$ is partitioned in to locally closed subsets ${\mathfrak {g}}_{(L)}$ defined by the property that $x\in {\mathfrak {g}}_{(L)}$ if and only if $H_G(x)$ is conjugate to L. More generally, we have subsets of the form ${\mathfrak {g}}_{\le (L)}$, ${\mathfrak {g}}_{\ngeq (L)}$, etc. defined as the appropriate unions of ${\mathfrak {g}}_{(M)}$ for Levi subgroups M of G.

• We write ${\mathfrak {g}}_\heartsuit$ for ${\mathfrak {g}}_{(G)}$. This is isomorphic to ${\mathfrak {z}}({\mathfrak {g}}) \times {\mathcal {N}}_G$ where ${\mathcal {N}}_G$ denotes the nilpotent cone.

• Given a Levi subgroup L of G, we write ${\mathfrak {l}}^\mathrm{reg}$ for the open locus consisting of elements $x\in {\mathfrak {l}}$ with $H_G(x) \subseteq L$.

• We fix a non-degenerate G-invariant symmetric bilinear form on ${\mathfrak {g}}$. Given an object ${\mathfrak {M}}\in \mathbf {M}({\underline{\mathfrak {g}}})$ its singular support $SS({\mathfrak {M}})$ is considered as a G-stable closed subset of the commuting variety ${\mathfrak {comm}}({\mathfrak {g}}) \subseteq {\mathfrak {g}}\times {\mathfrak {g}}$ which is contained in the commuting variety ${\mathfrak {comm}}({\mathfrak {g}})$. It is conic with respect to the scaling action on the second factor. Given $x\in {\mathfrak {g}}$ we write $SS({\mathfrak {M}})_x$ for $\{y\in {\mathfrak {g}}\mid (x,y) \in SS({\mathfrak {M}})\}$. Note that this is non-empty if and only if $x\in Supp({\mathfrak {G}})$.

• For a pair $(x,y) \in {\mathfrak {comm}}({\mathfrak {g}})$ we define $H_G(x,y)$ as $H_G(x) \cap H_G(y)$ (this is again a Levi subgroup of G). Similarly, ${\mathfrak {comm}}({\mathfrak {g}})_{(L)}$ consists of elements (x, y) with $H_G(x,y)$ conjugate to L.

• Given a parabolic subgroup P of G with a corresponding Levi subgroup L, we denote as follows the functors of parabolic induction for derived categories:

  

  After the proving Theorems A and B in [4], we know that these functors restrict to exact functors on the corresponding abelian categories which are independent of the choice of parabolic P. These are denoted:

  

4 Exactness of parabolic restriction

The goal of this section is to prove the following result.

Theorem 3.1

([1, Theorem 5.6]) The functors $\mathbf{Res}^G_{P,L}$ and $\mathbf{Ind}^G_{P,L}$ are t-exact.

Bezrukavnikov and Yom-Din first prove the exactness of the corresponding induction and restriction functors in the group case, i.e. for G-equivariant D-modules or sheaves on G [1, Theorem 5.4]. Using a combination of adjunction relations and Verdier duality, their proof reduces to showing that parabolic induction is left t-exact (this reduction is somewhat more subtle for the case of not-necessarily holonomic D-modules). The left t-exactness of parabolic restriction is proved using dimension estimates on the intersection of certain G-invariant subsets of G with cosets of the unipotent radical of the parabolic. The authors then observe that the same argument works in the Lie algebra case (Theorem 5.6).

The proof of Theorem 3.1 in this note follows the same argument as [1] to reduce to the left exactness of parabolic restriction, Proposition 3.2. However, the proof of Proposition 3.2 in this note is slightly different (at least at first glance), using an inductive argument with respect to a stratification of ${\mathfrak {g}}$ to reduce to orbital D-modules.

Here is a brief outline of the reduction argument from [1]. As $\mathbf{Res}^G_{P,L}$ is left t-exact, $\mathbf{Ind}^G_{P,L}$ is right t-exact. But $\mathbf{Ind}^G_{P,L}$ commutes with Verdier duality (it is the composite of a smooth pullback and proper pushforward). It follows that $\mathbf{Ind}^G_{P,L}$ is also left t-exact. This is clear in the context of holonomic D-modules (where Verdier duality is a t-exact anti-auto-equivalence) but needs further justification in general—see [1, Proof of Theorem 5.4]. By [4, Theorem 3.24] (Second Adjunction), we have that $\mathbf{Res}^G_{P^-,L}$ is right t-exact. But this argument holds for any parabolic P, and thus $\mathbf{Res}^G_{P,L}$ is right t-exact as required.

Thus we are reduced to proving the following result, and the remainder of the section is devoted to this proof.

Proposition 3.2

If ${\mathfrak {G}}\in \mathbf {D}({\underline{\mathfrak {g}}})^{\ge 0}$, then for any parabolic P with Levi factor L, $\mathbf{Res}^G_{P,L}({\mathfrak {M}}) \in \mathbf {D}({\underline{\mathfrak {l}}})^{\ge 0}$.

Let ${\mathfrak {L}}= \mathbf{Res}^G_{P,L}({\mathfrak {G}}) \in \mathbf {D}({\underline{\mathfrak {l}}})$ as in Proposition 3.2. According to Lemma A.1, to show that ${\mathfrak {L}}$ is concentrated in non-negative degrees it is enough to show that the !-restriction to ${\underline{\mathfrak {l}}}_{(K)}$ is concentrated in non-negative degrees for each Levi subgroup K of L (with ${\mathfrak {k}}= {{\,\mathrm{Lie}\,}}(K)$). Fix such a subgroup K and let

$$\begin{aligned} {\mathfrak {L}}' := ({\underline{\mathfrak {l}}}_{(K)} \rightarrow {\underline{\mathfrak {l}}})^!{\mathfrak {L}}\end{aligned}$$

denote the restriction. By [4, Proposition 2.13], we have an étale covering of stacks

$$\begin{aligned} d^K_L:{\underline{\mathfrak {k}}}_{\heartsuit }^{L-\mathrm{reg}} \rightarrow {\underline{\mathfrak {l}}}_{(K)} \end{aligned}$$

where ${\underline{\mathfrak {k}}}_\heartsuit ^{L-\mathrm{reg}} \cong {\mathfrak {z}}({\mathfrak {k}})^{L-\mathrm{reg}} \times \underline{\mathcal {N}}_K$. It follows that ${\mathfrak {L}}'$ is concentrated in non-negative degrees if and only if

$$\begin{aligned} {\mathfrak {L}}'' := ({\underline{\mathfrak {k}}}_{\heartsuit }^{L-\mathrm{reg}} \rightarrow {\underline{\mathfrak {l}}}_{(K)})^! {\mathfrak {L}}' \end{aligned}$$

is concentrated in non-negative degrees. Note that

$$\begin{aligned} {\underline{\mathfrak {k}}}_\heartsuit ^{L-\mathrm{reg}} = {\mathfrak {z}}({\mathfrak {k}})^{L-\mathrm{reg}} \times \underline{\mathcal {N}}_K \end{aligned}$$

is partitioned in to locally closed subsets of the form

$$\begin{aligned} {\mathfrak {k}}_\heartsuit ^M := {\mathfrak {z}}(\mathfrak {m})^\mathrm{reg}\times {\mathcal {N}}_K \end{aligned}$$

where $\mathfrak {m}= {{\,\mathrm{Lie}\,}}(M)$ and M ranges over the (finite) set of Levi subgroups of M containing L such that $L\cap M = K$. Thus, applying Lemma A.1 again, we see that ${\mathfrak {L}}''$ is concentrated in non-negative degrees if and only if for each such M

$$\begin{aligned} {\mathfrak {L}}''' = ({\underline{\mathfrak {k}}}_\heartsuit ^M \rightarrow {\underline{\mathfrak {k}}}_\heartsuit ^{L-\mathrm{reg}})^!{\mathfrak {L}}'' \end{aligned}$$

is concentrated in non-negative degrees.

In summary we have shown the following:

Lemma 3.3

Let ${\mathfrak {L}}\in \mathbf {D}({\underline{\mathfrak {l}}})$ be a bounded below complex. Then ${\mathfrak {L}}$ is concentrated in non-negative degrees if and only if $({\underline{\mathfrak {k}}}_\heartsuit ^M \rightarrow {\underline{\mathfrak {l}}})^!({\mathfrak {L}})$ is concentrated in non-negative degrees for each Levi subgroup M of G and K of L such that $K=M\cap L$.

Now fix K, M Levi subgroups of G with $L \cap M = K$ as above. Let $Q = M\cap P$; this is a parabolic subgroup of M with Levi factor K. We write $\underline{\mathfrak {q}}_\heartsuit ^M$ for the substack ${\mathfrak {z}}(\mathfrak {m})^\mathrm{reg}\times \underline{\mathcal {N}}_Q$ of $\underline{\mathfrak {q}}$. Consider the diagram of stacks:

(1)

Lemma 3.4

The right hand square in Diagram 1 is cartesian.

Proof

Concretely, the lemma states that the following P-equivariant morphism of varieties is an isomorphism.⁶

Here, the overline notation denotes the projection from a parabolic subgroup or subalgebra to its Levi quotient. We will show that $\rho$ is bijective; we phrase the argument in terms of ${\mathbb {C}}$-points, but the same argument shows that $\rho$ is bijective on R-points for any commutative ${\mathbb {C}}$-algebra R (alternatively, one could note that the source is connected and the target is normal, so bijection on ${\mathbb {C}}$-points implies isomorphism).

Let us first note that the morphism $\rho$ is surjective. In other words, given an element $x\in \mathfrak {p}$ such that its image $y:=\overline{x} \in {\mathfrak {l}}$ lies in some L-conjugate of ${\mathfrak {k}}_\heartsuit ^M$, then we must show that x lies in some P-conjugate of $\mathfrak {q}_\heartsuit ^M$. But we can always conjugate x by an element of P so that $x_s$ lies in the Levi subalgebra ${\mathfrak {l}}$ and thus $x_s= y_s$. Conjugating further by an element of L, we may assume that $y_s \in {\mathfrak {z}}(\mathfrak {m})^\mathrm{reg}$. Thus $x_n \in C_{\mathfrak {p}}(x_s) = \mathfrak {p}\cap \mathfrak {m}= \mathfrak {q}$, so $x = x_s + x_n \in \mathfrak {q}_\heartsuit ^M$ as required. Similarly, to check that $\rho$ is injective boils down to the fact that if we have $(g,x) \in P \times \mathfrak {q}_\heartsuit ^M$ such that $^{g}x = x$, then $g\in C_P(x) = P \cap C_G(x) \subseteq P \cap M = Q$. Thus $\rho$ is bijective at the set-theoretic level. As the target is normal and the source connected, it follows that $\rho$ is an isomorphism as required. $\square$

We are now ready to finish the proof of Proposition 3.2. Let ${\mathfrak {G}}\in \mathbf {D}({\underline{\mathfrak {g}}})^{\ge 0}$ and ${\mathfrak {L}}:= \mathbf{Res}^G_{P,L}({\mathfrak {G}})$. We must show that ${\mathfrak {L}}$ is concentrated in non-negative degrees. By Lemma 3.3 it is enough to show that $({\underline{\mathfrak {k}}}_\heartsuit ^M \rightarrow {\underline{\mathfrak {l}}})^!{\mathfrak {L}}$ is concentrated in non-negative degrees for each pair M, K of Levis with $M\cap L = K$. Then by Lemma 3.4 and base-change, we are reduced to showing that

$$\begin{aligned} \left( \mathbf{Res}^M_{Q,K}\right) ^\mathrm{reg}_\heartsuit ({\underline{\mathfrak {m}}}_\heartsuit ^\mathrm{reg}\rightarrow {\underline{\mathfrak {g}}})^! {\mathfrak {G}}\end{aligned}$$

(2)

is concentrated in non-negative degrees, where $\left( \mathbf{Res}^M_{Q,K}\right) ^\mathrm{reg}_\heartsuit$ denotes the functor given by pull-push with respect to the bottom row of Diagram 1. Note that ${\underline{\mathfrak {m}}}_\heartsuit ^\mathrm{reg}\rightarrow {\underline{\mathfrak {g}}}$ is a composition of an étale covering and a locally closed embedding, thus the corresponding !-pullback is left t-exact. Thus we are reduced to showing that $\left( \mathbf{Res}^M_{Q,K}\right) ^\mathrm{reg}_\heartsuit$ is left t-exact.

The bottom row of Diagram 1 can also be written as

Thus $\left( \mathbf{Res}^M_{Q,K}\right) ^\mathrm{reg}_\heartsuit$ is an external product of the identity functor on $\mathbf {D}({\mathfrak {z}}(\mathfrak {m})^\mathrm{reg})$ and the usual parabolic restriction functor between $\mathbf {D}(\underline{\mathcal {N}}_M)$ and $\mathbf {D}(\underline{\mathcal {N}}_K)$. Thus we are reduced to showing that parabolic restriction is left t-exact for nilpotent orbital D-modules.

At this point, we may appeal to one of the various proofs of (left) t-exactness for parabolic restriction of orbital (or character) sheaves in the literature, e.g. [3, Theorem 4.1], [8, Theorem 7.3]. Alternatively, we may run the above argument again but now for the Fourier transform ${\mathbb {F}}_{{\underline{\mathfrak {g}}}} {\mathfrak {G}}$, where ${\mathfrak {G}}$ is now assumed to be a nilpotent orbital D-module. In this way, we reduce to the situation where both ${\mathfrak {G}}$ and its Fourier transform are supported on the nilpotent cone. Such a D-module is readily seen to be cuspidal (see e.g. [8, Theorem 4.7]) from which the result follows.

5 Singular support and parabolic restriction

The goal of this section is to prove the following result.

Theorem 4.1

Let ${\mathfrak {G}}\in \mathbf {M}({\underline{\mathfrak {g}}})_{(L)}$ be a non-zero object. Then we have

• (1)
  $$\begin{aligned} SS({\mathfrak {G}}) \subseteq {\mathfrak {comm}}({\mathfrak {g}})_{\ge (L)} \end{aligned}$$
• (2)
  $$\begin{aligned} SS({\mathfrak {G}}) \cap {\mathfrak {comm}}({\mathfrak {g}})_{\le (L)} \ne \emptyset \end{aligned}$$

The first part of the theorem is relatively straightforward. It is a consequence of the standard bounds on singular support with respect to a smooth pullback and proper pushforward (see e.g. [5, Theorem 4.7, Theorem 4.27]). Indeed, parabolic induction is a composite of such functors, and by [4, Lemma 3.8] we have $SS({\mathfrak {L}}) \subseteq {\mathfrak {comm}}({\mathfrak {l}})_\heartsuit$ from which the required bound on $SS({\mathfrak {G}})$ follows (using that ${\mathfrak {G}}$ is a direct summand of ${\mathbf {ind}}^G_L({\mathfrak {L}})$). Alternatively, it follows from the “if” direction of the proof of Lemma 3.19 in [4] (which does not make use of the erroneous results). Indeed, by assumption we have ${\mathbf {res}}^G_M({\mathfrak {G}})\cong 0$ for all Levis M with $(M) \ngeq (L)$. Then loc. cit. states that

$$\begin{aligned} SS({\mathfrak {M}}) \subseteq \bigcap _{(M)\ngeq (L)} {\mathfrak {comm}}({\mathfrak {g}})_{\nleq (M)} = {\mathfrak {comm}}({\mathfrak {g}})_{\ge (L)} \end{aligned}$$

The second part of Theorem 4.1 is more tricky, as singular support is hard to control under parabolic restriction. The remainder of the subsection is devoted to its proof. Let us first note that singular support is preserved by parabolic restriction once we restrict to the regular locus:

Lemma 4.2

Let be as above, and take $x\in {\mathfrak {l}}^\mathrm{reg}$. Then

$$\begin{aligned} SS({\mathbf {res}}^G_L({\mathfrak {G}}))_x = SS({\mathfrak {G}})_x. \end{aligned}$$

Proof

Recall that ${\mathbf {res}}^G_L({\mathfrak {G}})|_{{\underline{\mathfrak {l}}}^\mathrm{reg}}$ is identified with $(d^\mathrm{reg})^!{\mathfrak {G}}$ where $d^\mathrm{reg}:{\underline{\mathfrak {l}}}^\mathrm{reg}\rightarrow {\underline{\mathfrak {g}}}$ is an étale morphism. The lemma follows from the fact that singular support is preserved by étale (or more generally, smooth) morphisms. Alternatively, in non-stacky terms the result follows from the fact that the inclusion ${\mathfrak {l}}^\mathrm{reg}\hookrightarrow {\mathfrak {g}}$ is non-characteristic with respect to G-equivariant D-modules on ${\mathfrak {g}}$. $\square$

The following key lemma relates the singular support of a nilpotent orbital D-module and its Fourier transform.

Lemma 4.3

Suppose ${\mathfrak {G}}\in \mathbf {M}({\underline{\mathfrak {g}}})$ is supported on the nilpotent cone and ${\mathfrak {L}}:= {\mathbf {res}}^G_L({\mathfrak {G}})$ is non-zero. Then

$$\begin{aligned} SS({\mathfrak {G}})_0 \cap {\mathfrak {g}}_{\le (L)} \ne \emptyset \end{aligned}$$

Proof

Note that ${\mathfrak {L}}$ is supported in the nilpotent cone ${\mathcal {N}}_L$ (and in particular, is ${\mathbb {G}}_m$-monodromic and regular holonomic). Consider the decomposition ${\mathfrak {l}}= {\mathfrak {z}}({\mathfrak {l}}) \oplus [{\mathfrak {l}},{\mathfrak {l}}]$. As ${\mathfrak {L}}$ is supported on ${\mathcal {N}}_L \subseteq [{\mathfrak {l}},{\mathfrak {l}}]$, its Fourier transform takes the form

$$\begin{aligned} {\mathbb {F}}_{\mathfrak {l}}({\mathfrak {L}}) \cong {\mathcal {O}}_{{\mathfrak {z}}({\mathfrak {l}})} \boxtimes {\mathbb {F}}_{[{\mathfrak {l}},{\mathfrak {l}}]}({\mathfrak {L}}) \end{aligned}$$

where in the second factor we consider ${\mathfrak {L}}$ as a D-module on $[{\mathfrak {l}},{\mathfrak {l}}]$. In particular, any $y\in {\mathfrak {z}}({\mathfrak {l}})^\mathrm{reg}$ is contained in $Supp({\mathcal {O}}_{{\mathfrak {z}}({\mathfrak {l}})})$ and thus in $Supp({\mathbb {F}}_{{\mathfrak {l}}} {\mathfrak {L}})$ (note that ${\mathbb {F}}_{[{\mathfrak {l}},{\mathfrak {l}}]}{\mathfrak {L}}$ is ${\mathbb {G}}_m$-monodromic, so 0 is contained in its support).

Now recall that Fourier transform commutes with parabolic restriction (see e.g. [4, Lemma 3.7]). Thus we can apply Lemma 4.2 to ${\mathbb {F}}_{\mathfrak {g}}({\mathfrak {G}})$ and ${\mathbb {F}}_{\mathfrak {l}}({\mathfrak {L}})$ to deduce that

$$\begin{aligned} SS({\mathbb {F}}_{{\mathfrak {g}}}{\mathfrak {G}})_y = SS({\mathbf {res}}^G_L {\mathbb {F}}_{{\mathfrak {g}}}{\mathfrak {G}}) = SS({\mathbb {F}}_{{\mathfrak {l}}}{\mathfrak {L}})_y \end{aligned}$$

By assumption, the right hand side is a non-empty conical closed subset of ${\mathfrak {g}}$, and thus contains the element 0. Finally, by Proposition A.2, we have that $(0,y) \in SS({\mathfrak {G}}) \cap {\mathfrak {g}}_{\le (L)}$ as required. $\square$

Proof of Theorem 4.1

It remains to prove part 2 of the theorem. By assumption we have ${\mathfrak {G}}= {\mathbf {ind}}^G_L({\mathfrak {L}})^{W_{G,L}}$ for some cuspidal ${\mathfrak {L}}\in \mathbf {M}({\underline{\mathfrak {l}}})_{cusp}$. Recall that ${\mathfrak {L}}$ is supported in ${\mathfrak {l}}_\heartsuit = {\mathfrak {z}}({\mathfrak {l}}) \times {\mathcal {N}}_L$. We must find $(x,y) \in SS({\mathfrak {G}})$ with $H_G(x,y) \subseteq L$ (or equivalently, $H_G(x,y)=L$).

If $Supp({\mathfrak {L}})$ intersects ${\mathfrak {l}}^\mathrm{reg}$ non-trivially, we are done by Lemma 4.2. On the other hand if $Supp({\mathfrak {L}}) \subseteq {\mathcal {N}}_L$ we are done by Lemma 4.3. In general, we consider the locally closed partition of ${\mathfrak {z}}({\mathfrak {l}}) \times {\mathcal {N}}_L$ given by ${\mathfrak {z}}(\mathfrak {m})^\mathrm{reg}\times {\mathcal {N}}_L$ as $\mathfrak {m}$ ranges over the (finitely many) Levi subalgebras of ${\mathfrak {g}}$ containing ${\mathfrak {l}}$. By Lemma A.1 we can find such a Levi subalgebra $\mathfrak {m}$ such that ${\mathfrak {L}}' := R^0\Gamma _{{\mathfrak {z}}(\mathfrak {m}) \times {\mathcal {N}}_L} {\mathfrak {L}}$ is a non-zero submodule of ${\mathfrak {L}}$ and there exists $x\in Supp({\mathfrak {L}}')\cap {\mathfrak {z}}(\mathfrak {m})^\mathrm{reg}\times {\mathcal {N}}_L$. Let M denote the Levi subgroup of G corresponding to $\mathfrak {m}$ and consider the object

$$\begin{aligned} {\mathfrak {M}}:= {\mathbf {res}}^G_M({\mathfrak {G}}) \cong {\mathbf {ind}}^M_L({\mathfrak {L}})^{W_{M,L}} \in \mathbf {M}({\underline{\mathfrak {m}}}) \end{aligned}$$

As ${\mathfrak {z}}(\mathfrak {m}) \times {\mathcal {N}}_L$ is $W_{M,L}$-stable, ${\mathfrak {L}}'$ is still $W_{M,L}$-equivariant (though not in general $W_{G,L}$-equivariant) and we obtain a non-zero submodule

$$\begin{aligned} {\mathfrak {M}}' = {\mathbf {ind}}^M_L({\mathfrak {L}})^{W_{M,L}} \hookrightarrow {\mathfrak {M}}\end{aligned}$$

with $x\in Supp({\mathfrak {M}}') \cap \mathfrak {m}^\mathrm{reg}$. We have now reduced to finding $y\in SS({\mathfrak {M}}')_x$ with $H_M(y)\subseteq L$ (in that case, by Lemma 4.2, $y\in SS({\mathfrak {G}})_x$ and $H_G(x,y) = H_G(x) \cap H_G(y) = G_M(y) \subseteq L$ as required).

Let us split off the copy of ${\mathfrak {z}}(\mathfrak {m})$ from ${\mathfrak {l}}$ using our fixed invariant form; that is, we consider an orthogonal decomposition:

$$\begin{aligned} {\mathfrak {l}}= {\mathfrak {z}}(\mathfrak {m}) \oplus {\mathfrak {l}}' \end{aligned}$$

We have a corresponding decomposition $\mathfrak {m}= {\mathfrak {z}}(\mathfrak {m}) \oplus \mathfrak {m}'$. Note that ${\mathfrak {l}}'$ can be considered as a Levi subalgebra of the Lie algebra $\mathfrak {m}' = [\mathfrak {m},\mathfrak {m}]$. Recall that ${\mathfrak {L}}'$ can be written as external tensor products with respect to this decomposition

$$\begin{aligned} {\mathfrak {L}}' \cong {\mathfrak {L}}'_s \boxtimes {\mathfrak {L}}'_n \end{aligned}$$

where ${\mathfrak {L}}'_n$ is supported on the nilpotent cone of ${\mathfrak {l}}'$ (see e.g. [4, Proposition 4.21]). As in the proof of [4, Lemma 4.19], we have that parabolic induction and restriction between L and M acts as the identity on the ${\mathfrak {z}}(\mathfrak {m})$ factor. Thus ${\mathfrak {M}}$ is also an external tensor product (with the first factor unchanged)

$$\begin{aligned} {\mathfrak {M}}' \cong {\mathfrak {L}}'_s \boxtimes {\mathfrak {M}}'_n \end{aligned}$$

Applying Lemma 4.3 (with G replaced by M and ${\mathfrak {G}}$ replaced by ${\mathfrak {M}}'_n$) we deduce that there exists $y\in SS({\mathfrak {M}}'_n)_0$ with $H_M(y) \subseteq L$. We claim that $(x,y) \in SS({\mathfrak {M}}')$. Indeed, note that $SS({\mathfrak {M}}')$ can be identified with $SS({\mathfrak {L}}'_s) \times SS({\mathfrak {M}}'_n)$, and under this identification, the element (x, y) corresponds to (x, 0) in the first factor and (0, y) in the second. Thus we have found the required element $y \in SS({\mathfrak {M}}')_x$ completing the proof of Theorem 4.1. $\square$

Appendix A. Generalities on D-modules

The following elementary lemma is probably well-known, but we include a proof for completeness.

Lemma A.1

Let X be a variety with a finite partition in to locally closed subsets indexed by a poset $({\mathcal {S}},\le )$

$$\begin{aligned} X = \bigcup _{s\in {\mathcal {S}}} X_s \end{aligned}$$

with the property that the closure of a stratum is the union of smaller strata:⁷

$$\begin{aligned} \overline{X_s} = X_{\ge s} = \bigcup _{t\ge s} X_t \end{aligned}$$

We write $k_s:X_s \hookrightarrow X$ for the corresponding locally closed embedding.

• (1) If ${\mathfrak {M}}\in \mathbf {M}(X)$ is a non-zero object, then there exists $s\in {\mathcal {S}}$ such that $H^0 k_s^!({\mathfrak {M}})$ is non-zero.

• (2) If $\mathfrak {N}\in \mathbf {D}(X)$ is a bounded below complex, then $\mathfrak {N}\in \mathbf {D}(X_s)^{\ge 0}$ if and only if $k_s^!(\mathfrak {N}) \in \mathbf {D}(X_s)^{\ge 0}$ for all s.

Proof

By way of notation, given the inclusion of a locally closed subvariety $f:V\hookrightarrow Y$ we write $R\Gamma _V$ for the (derived) functor $f_*f^!$ and $R^0\Gamma _V$ for $H^0 f_*f^!$.

• (1) Let $s\in {\mathcal {S}}$ be maximal such that $R^0\Gamma _{X_{\ge s}} {\mathfrak {M}}$ is non-zero. Then we have a left exact sequence

  $$\begin{aligned} 0 \rightarrow R^0\Gamma _{X_{>s}} {\mathfrak {M}}\rightarrow R^0\Gamma _{X_{\ge s}} {\mathfrak {M}}\rightarrow R^0\Gamma _{X_s} {\mathfrak {M}}\end{aligned}$$

  The maximality of s means that the left hand term vanishes, so the middle term must inject in to the right. Thus $R^0\Gamma _{X_s} {\mathfrak {M}}$ is non-zero or equivalently $H^0 k_s^! {\mathfrak {M}}$ is non-zero as required.

• (2) One direction is clear: if $\mathfrak {N}\in \mathbf {D}(X)^{\ge 0}$ then $k_s^! {\mathfrak {M}}\in \mathbf {D}(X_s)^{\ge 0}$ for all $s \in {\mathcal {S}}$, as the functors $k_s^!$ are left t-exact. For the converse, suppose $\mathfrak {N}$ has a non-zero negative cohomology module. We must show that $k_s^!(\mathfrak {N})$ has a non-zero negative cohomology module for some s. Let ${\mathfrak {M}}= H^i(\mathfrak {N})$ be the smallest non-zero cohomology object (by assumption i is negative). By the first part of this lemma, we can find $s\in {\mathcal {S}}$ such that $H^0k_s^!{\mathfrak {M}}\ne 0$. Now by inspection of the long exact sequence associated to the triangle

  

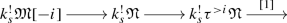
  we see that $H^i k_s^!\mathfrak {N}\ne 0$ as required. $\square$

We will also need the following result.

Proposition A.2

([2, Corollaire 7.25]) Let V be a vector space, and suppose $\mathfrak {F}\in \mathbf {M}(V)$ is regular holonomic and ${\mathbb {G}}_m$-monodromic (that is, the Euler vector field induced by the ${\mathbb {G}}_m$-action on V acts locally finitely on $\mathfrak {F}$). Then $SS(\mathfrak {F})$ and $SS({\mathbb {F}}_V(\mathfrak {F}))$ are identified under the natural identification of $T^*V$ and $T^*V^*$.

Remark A.3

The proposition fails if $\mathfrak {F}$ is not assumed regular holonomic or monodromic. For example if $\mathfrak {F}$ is the D-module of delta functions $\delta _a$ supported at some non-zero $a\in V$ (which is not ${\mathbb {G}}_m$-monodromic), then its Fourier transform ${\mathbb {F}}_V \delta _a = {\mathcal {E}}^a$ is an exponential D-module (which is not regular). We have $SS(\delta _a) = \{a\} \times V^*\subseteq V\times V^*$, but $SS({\mathcal {E}}^a) = V^*\times \{0\}$.