Introduction

The accurate determination of the rheological behaviour of highly concentrated suspensions in pressure driven flows is relevant for many processing operations and industries. Examples include the extrusion of ceramics (Powell et al. 2013), molten plastics (Rueda et al. 2017) and food materials (Alam et al. 2016), but also the pumping of oil-cement slurries (Tao et al. 2020) and even the flow of blood through stenosed arteries (Mandal 2005). It is important to know and understand the rheological behaviour, in order to model and predict the influence of compositional variations of the suspension and changes in flow conditions.

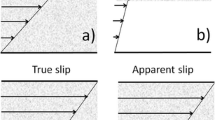
The rheological characterization of materials generally focusses on the shear viscosity, which is ratio between the imposed shear stress and the resulting shear rate. For pure liquids and dilute suspensions, the material and resulting flow profile are homogeneous and the shear viscosity can be directly determined using classical rheological measurements (Barnes 2000). Unfortunately, the characterization of the shear viscosity of highly concentrated suspensions is complicated by the heterogeneous nature of their flow profile. Instead of pure shear flow, regions of slip-, shear- and plug flow can co-exist (Fig. 1A) (Bertola et al. 2003; Cloitre and Bonnecaze 2017). As the relative contribution of these regions varies depending on the flow conditions, it is important to accurately discriminate between them and increase our understanding of their individual dynamics. This understanding will improve the generality of resulting flow models and increase their accuracy when applied to practical situations.

Fig. 1
figure 1

Schematic representation of the velocity profile of a concentrated suspension through a die with radius R, (A) with apparent wall slip for a channel wall with a smooth surface and (B) without wall slip for a rough surface. τ is the shear stress, τy the yield stress, Ra the surface roughness, D4,3 the diameter of the solid particles and \({{\delta }}_{{p}{l}m{u}{g}}\) the thickness of the plug flow layer. Adapted from Wilms et al. (2020)

Full size image

The slip region of highly concentrated suspensions is thought to originate from a reduced local concentration of particles close to a rigid surface and is often referred to as the wall slip layer (Barnes 1995). The particles are not able to occupy the space close to an enclosing surface as effectively as in the bulk, thus leading to a particle-depleted layer. Although the thickness of this layer is expected to be only a fraction of the average particle size, it has a significantly lower viscosity than the bulk and acts as a sort of lubricant (Kalyon 2005). This lubrication effect manifests itself as an apparent velocity jump that can lead to the misinterpretation of experimental data (Cloitre and Bonnecaze 2017). The importance of wall slip increases with increasing ratio between the bulk- and slip layer viscosity and the ratio between the slip layer thickness and flow gap (Kalyon 2005). Note that for highly concentrated suspensions, the wall slip is actually apparent wall slip, as true slip would mean a velocity discontinuity at the wall.

A classical way to prevent wall slip and determine the true viscosity of suspensions is to make use of a serrated or grooved surface, thereby preventing the formation of a slip layer (Barnes 1995). When the grooves are larger than the average particle diameter, the material will move into the cavities and create a surface on which no particle-depleted layer is formed (Fig. 1B). The use of grooved surfaces has become the standard for rotational and oscillation rheometry that is used to measure the viscosity of suspensions with solid volume fractions well below their maximum packing (Mezger 2006). Elimination of wall slip is sufficient, as the flow curve satisfactorily describes the flow behaviour for the target process operation, such as mixing. In the case of pressure-driven, Poiseuille-like, flow of concentrated suspensions, however, wall slip is an integral part of the overall flow and the goal is not to eliminate, but to characterize. The characterization of the slip layer is of great practical importance, as it can be beneficial from a processing perspective to have a lubrication effect that reduces the required flow pressure (Barnes 1995).

The quantification of wall slip is often performed by inferring it from rheometry data that is obtained using different flow gaps (Cloitre and Bonnecaze 2017). This indirect method was originally proposed by Mooney (1931) and has since been applied to numerous materials and flow geometries (Kalyon 2005). Despite its apparent success, the Mooney method has often failed to quantify the slip of complex fluids (Martin and Wilson 2005). Attempts are made to modify the indirect method (Jastrzebski 1967; Crawford et al. 2005; Wilms et al. 2020), yet they still lack a theoretical foundation and are subject to an ongoing debate. Although direct measurement methods to quantify wall slip have been developed, including nuclear magnetic resonance (Rofe et al. 1996) and particle image velocimetry (Jesinghausen et al. 2016), these methods generally require complex equipment, which limits their universal use.

In this contribution, we have quantified the wall slip velocity of highly concentrated non-Brownian suspensions using a commercially available high-pressure capillary rheometer (HPCR). A dedicated 3D-printed die is made with a grooved interior surface to prevent wall slip and allow for a direct determination of the shear viscosity. Results are compared to a smooth die with an identical flow gap, which allows for the quantification of the slip contribution to the overall flow. This is a similar procedure as proposed by Mourniac et al. (1992) and Halliday and Smith (1995). As the slip layer is often assumed to consist of pure liquid phase, i.e. being a particle-depleted layer, the flow index of the slip velocity and liquid phase should be identical. The validity of this assumption is tested for suspensions that are made with thickeners that show different flow indices and the calculated wall slip velocities are compared to the liquid phase rheology. Measurements are performed at shear rates between 101 and 103 s−1, as typically observed in pumping and extrusion processes (Barnes et al. 1989).

Materials and methods

Materials

To prepare the liquid phases, three different thickeners were used, polyethylene glycol (PEG) (ROTIPURAN® 20,000, Carl Roth GmbH & Co. KG, Germany), sodium alginate (Algogel™, Cargill, Germany) with a molecular weight of 151 kg/mol and a M/G ratio of 0.64 and hydroxypropyl methyl cellulose (HPMC) (Mantrocel® K100M, Gustav Parmentier GmbH, Germany), kindly provided by Gustav Permentier GmbH. Limestone was added as a solid phase (Ulmer Weiss 15H, Edouard Merkle GmbH, Germany), kindly provided by Edouard Merkle GmbH, with a D4,3 of 4.91 µm (10 v% below 1 µm and < 10 v% above 10 µm) that is measured using static light scattering (Mastersizer 2000, Malvern Instruments GmbH, Germany) using the dry dispersion unit at a dispersion pressure of 1.5 × 105 Pa. The density of limestone was determined using a helium pycnometer (AccuPyc II 1340, Micromeritics Instrument Corp. USA) and was 2.73 × 103 kg/m3. Limestone did not dissolve in water and no gelation effects have been observed between calcium and alginate. All samples are prepared using regular tap water.

Suspension preparation

PEG solutions with a concentration of 40 wt.% and sodium alginate solution with a concentration of 60 g/L were made by dispersing the material in cold water and gently stirring for 4 h. Solutions containing 30 g/L HPMC were made by first dispersing the powder into half of the desired amount of water (warm, ~ 75 °C), before adding the remaining water (cold, ~ 20 °C). For all thickeners, clear solutions were obtained after 48 h at 8 °C. The density of the solutions was measured using the helium pycnometer, as their viscosity was too high for measurements on a regular pycnometer. Suspensions (150 mL) with solid volume fractions between 0.55 and 0.60 were made by adding limestone to the liquid phase inside a KitchenAid (Artisan 5KSM150, Whirlpool Company, USA), operated at speed 1. After 5 min of mixing, the homogeneity of the suspensions was increased by subjecting them to 5 s of high shear inside a hand blender (Multiquick 5, Braun GmbH, Germany) equipped with a chopper. The suspensions were immediately covered in two layers of plastic to prevent them from drying out and allowed to rest for 24 h before performing rheological measurements. To account for production variation, two batches were produced of each suspension.

Suspension composition

To quantify the volume of air that is incorporated into the paste during production, density measurements were performed on suspensions with a solid volume fraction above 0.57. The density of the paste was measured using the Archimedes principle. A small cage, suspended from a laboratory stand was lowered into a beaker glass that is filled with water and standing on a laboratory balance. Between 5 and 10 g of paste was weighed and subsequently put into the cage, ensuring complete submersion. The density of the paste was then calculated from the original weight of the sample and the weight of the displaced water. The measurement is performed in fivefold. The volume fraction of air in the paste was calculated using the densities of the limestone and liquid phase (Table 1). Note that we were unable to measure suspensions with volume fractions below 0.58 and assume that the air volume fraction decreases with decreasing solid volume fraction (Table 1).

Table 1 Density measurements of the suspensions with a solid volume fraction > 0.58
Full size table

Rheological measurements

Rotational rheometry

The viscosity of the liquid phase was measured using a rotational rheometer (Kinexus ultra, Malvern Instruments GmbH, Germany) equipped with a Couette geometry consisting of a serrated cup (diameter, 27.5 mm) and serrated bob (diameter, 25.0 mm) with a conical tip (15°) at a gap height of 9.15 mm. The samples were pre-heated to 22 °C for 15 min, before being pre-sheared at 400 s−1 for 30 s. The flow curve was then determined using a shear rate ramp with a stepwise reduction of shear rates (500 s−1–0.01 s−1), with 10 measurement points per decade. Each step was maintained until a steady state was reached, with a minimum time of 1 / \(\dot{\gamma }\), where \(\dot{\gamma }\) is the shear rate (Mezger 2006). No thixotropic effects were observed. A maximum shear rate of 500 s−1 was chosen, as it approached the torque limit of the rheometer and rod climbing of the HPMC-introduced measurement errors at higher shear rates. The flow index was determined by describing the flow curve with an Ostwald-de Waele relationship (Eq. (1)) (Ostwald 1929).

$$\tau =K{\left(\frac{\partial v}{\partial y}\right)}^{n}$$
(1)

where \(\tau\) is the shear stress, \(K\) is the consistency coefficient, \(\frac{\partial v}{\partial y}\) the shear rate and \(n\) the flow index. Since sodium alginate was still in its first Newtonian plateau around 10 s−1, the fit was performed between 50 and 500 s−1.

Oscillation rheometry

To know the relative importance of the plug flow region (Fig. 1), the yield stress was measured using oscillation rheometry (Kinexus ultra, Malvern Instruments GmbH, Germany), using parallel plates (diameter of 40.0 mm) with a serrated surface. A gap height of 1 mm was used and the sample exterior was coated with silicon oil (10,000 cSt) to prevent water evaporation. After a 5-min waiting step, stress sweeps were performed between 0.1 and 1000 Pa at a frequency of 10 rad/s (~ 1.6 Hz). The yield stress was defined as the point at which the storage modulus has decreased by 30% from that observed in the linear viscoelastic regime.

Capillary rheometry

To measure the pressure driven flow, a twin-bore high-pressure capillary rheometer (HPCR) (RH 2000; Malvern Instruments GmbH, Germany) was used. The barrels were equipped with a 10 MPa (left) and 1.5 MPa (right) pressure transducer. Three types of die were used to perform the measurements, all having a radius, \(R\), of 0.50 mm; a smooth and a rough die, both with a length, \(L\), to radius ratio of 32 and an orifice die, with an \(L/R\) ratio of ~ 0. The rough die was made using Direct Metal Laser Sintering (DMLS) of stainless steel (GP1) (Speedpart GmbH, Germany). The internal surface of the die consisted of an equilateral saw tooth pattern along the die length (Fig. 1B), having a depth of 0.4 mm and a distance of 0.4 mm between successive teeth. The radius of the internal flow channel was inspected prior to every set of measurements using a drilling tip with a thickness of 1.00 mm and a metal thread with a thickness of 1.005 mm (Malvern Instruments GmbH, Germany). The drilling tip could penetrate the die prior to every measurement, whereas the metal thread did not, indicating little to no surface wear. The orifice die was used to correct for the entry pressure loss and the pressure drop is thus assumed to be linearly related to the length of the die, i.e. all Bagley plots are assumed to be linear (Bagley 1957). Material is filled into 20 mL disposable syringes by punching, thereby minimizing the inclusion of air, before transferring them into the temperature-controlled barrel (22 °C). The sample is pre-compressed at a rate of 10 mm s−1 until material discharge is observed at the die, followed by a 5-min waiting step. A table of apparent shear rates (\({\dot{\gamma }}_{a}\)) was used (10, 20, 40, 80, 160, 320, 640, 960, 1280 s−1) for the measurement, which was controlled by the volumetric flow rate, \(\dot{Q}\), through the die, following Eq. (2).

$${\dot{\gamma }}_{a}=\frac{4\dot{Q}}{\pi {R}^{3}}$$
(2)

In the case of the rough die, the constricted radius is chosen for \(R\), as indicated in Fig. 1. The use of the constricted radius is discussed later in this document. For the PEG suspensions, the shear rate was increased until the maximum extrusion pressure (10 MPa) was reached, e.g. for 59 v% the maximum shear rate was 960 s−1. Each shear rate stage was maintained until a pressure plateau was observed. For the measurements on the rough die, the relative standard deviations of the final 10 values (corresponding to 5 s) at each plateau never exceeded 3.0% and was on average 0.24% and for measurements on the smooth die it never exceeded 1.8% and was on average also 0.24%. As all suspensions were prepared in duplicate, they are separately measured once. For the rough die, the relative standard deviation between two different batches never exceeded 15% and was on average 3.3% for each shear rate, whereas for the smooth die, the relative standard deviation between batches never exceeded 22% and was on average also 3.3%. A small layer of oil was applied to the orifice die’s surface using a brush prior to every measurement to prevent sticking of the paste to the orifice die and consequently an increase in pressure loss. Note that the rough die was cleaned between every measurement using an interdental brush. The final 10 values (corresponding to 5 s) at each shear rate stage were averaged and used for further calculations. The results from the orifice die were then subtracted from the smooth and rough die data, to obtain the true pressure drop over the dies. All data was analysed in Origin (OriginPro 2020, OriginLab, USA).

Results and discussion

Liquid phase rheology

The rheological behaviour of the liquid phases follows from the gradient of their flow curves (Fig. 2). PEG shows Newtonian behaviour, as the shear stress increases linearly with shear rate and the resulting flow index of the Ostwald-de Waele fit (Eq. (1)) is equal to 1.00. Both sodium alginate and HPMC are shear thinning, with flow indices of 0.50 and 0.20 respectively.

Fig. 2
figure 2

Flow curves of the liquid phases, measured using rotational rheometry (cup bob) with a decreasing shear rate ramp (500–0.01 s−1) at 22 °C, of which only part (500 to 50 s−1) is shown. As duplicates did not show a visible difference, only a single measurement is included. Solid lines indicate the fit to the Ostwald-de Waele equation, of which the function and fit parameters are shown in the legend

Full size image

Although the effective shear rate of the liquid phase can be a few orders of magnitude higher than the apparent shear rate of the bulk (Pal 2015), we assume that the Ostwald-de Waele function can be extrapolated and is valid within the entire range of experimental conditions. Note that the possible influence of viscoelastic behaviour of the liquid phase on the suspension rheology is not considered in this manuscript, for the current status of this topic, please refer to Tanner (2019).

Yield stress

As the shear stress linearly increases from the centre of the die towards the wall, a central plug develops for yield stress fluids in regions where the shear stress is below the yield stress (Fig. 1). The material inside this plug region has a constant flow velocity, thus affecting the velocity profile and consequently the equations that are required to determine the rheological parameters from the pressure drop (Kelessidis et al. 2006). Although it is possible to determine the rheological parameters from the pressure drop using constitutive equations that include the yield stress (Kelessidis et al. 2006; Ardakani et al. 2011; Ahuja et al. 2018), this involves a numerical approximation rather than being directly obtained from the analytical solution of the velocity profile that is used for materials described by Eq. (1). To see if the simplified, more practical Ostwald-de Waele approach is justified, the yield stress has to be quantified separately.

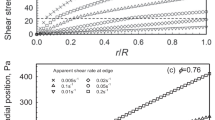
A yield stress may arise when particles form a percolating network that is able to resist gravitational forces. This percolating network is stabilized by either soft interactions (e.g. depletion attraction) or direct contact between suspended particles (Coussot 2005; Bessaies-bey et al. 2018). The strength of this network increases with increasing solid volume fraction (Fig. 3). The PEG and HPMC suspensions show yield stress values that are in the same order of magnitude as observed for spherical particles by Heymann and Peukert (2002), using polymethylmethacrylate particles in polydimethylsiloxane, and by Mueller et al. (2010), using glass beads in silicon oil. Heymann and Peukert (2002) found that the yield stress, τ0, as a function of solid volume fraction,\(\varphi\), can be described by a modified Maron-Pierce relationship;

Fig. 3
figure 3

Yield stress of concentrated suspensions made using different thickeners as measured using oscillation rheometry with a stress sweep (0.01–1000 Pa) at 22 °C. Solid lines indicate the fit to the modified Maron-Pierce equation, of which the function and fit parameters are shown in the legend. The star indicates a sodium alginate suspension with a waiting time of 30 min, instead of 10, between measurement loading and start

Full size image
$${\tau }_{0}={\tau }^{*}\left[{\left(1-\frac{\varphi }{{\varphi }_{m}}\right)}^{-2}-1\right]$$
(3)

where \({\tau }^{*}\) and \({\varphi }_{m}\) are fitting paramters. \({\tau }^{*}\) describes the yield stress at \(\varphi\) = \({\varphi }_{m}\) (1-½√2) and \({\varphi }_{m}\) the maximum particle packing. The solid lines in Fig. 3 show the fit of Eq. (3) to the experimental data. \({\tau }^{*}\) is thought to decrease with increasing particle size (Heymann and Peukert 2002) and found values fit the trend that is previously reported in literature, despite the anisotropy of the limestone particles (Table 2). The aspect ratio is estimated to be ~ 1.55 ± 0.38 following shape analysis of approximately 4000 particles using images made with a scanning electron microscope (JSM-IT100, Jeol Ltd., Japan) and analysed using a Matlab script (Matlab R2020b, MathWorks, USA) with an advanced watershed function described by (Koster et al. 2011). A direct comparison of the absolute values of \({\varphi }_{m}\) is difficult, as the limestone was not completely monomodal, in contrast to the materials used by the other authors in Table 2. For sodium alginate suspensions, the yield stress values are significantly lower and found to be dependent on the relaxation time between gap adjustment and measurement start. After increasing the waiting step to 30 min, the yield stress of the sodium alginate suspension with a solid volume fraction of 0.60 resembles the values found for the other suspensions (star, Fig. 3). It is assumed that, in order for the extrusion to be successful, the majority of the material has experienced stresses greater than the yield stress during the converging flow into the die (Ardakani et al. 2011). Thus, the waiting time of 5 min is already a strong overestimation of the relaxation time of the material within the die and the yield stress values for sodium alginate are not investigated further.

Table 2 Comparison of model yield stress (τ*) and particle properties of concentrated suspensions
Full size table

Shear viscosity

A first impression on the difference of the apparent rheology of concentrated suspensions with and without slip follows from Fig. 4. Figure 4 includes the data from a measurement with a rough, smooth and orifice die and shows the incremental increase of pressure over time during a measurement, i.e. with each increase in apparent shear rate. At identical apparent shear rates, the pressure that is required for the flow through the rough die is significantly larger than for the smooth die. The pressure shows few fluctuations after reaching a steady state at each shear rate, indicating a homogeneous suspension. Sticking of material to the inside of the orifice die could not be completely prevented, despite the addition of an oil layer prior to every measurement (Fig. 4). As the relative contribution of the entry pressure to the overall flow is limited and the effect of sticking on the entry pressure drop did not exceed 30%, no further corrections are made.

Fig. 4
figure 4

Pressure profile for a sodium alginate suspension with 58 v% solids at incrementally increased apparent shear rates (secondary y-axis) at 22 °C, as measured with a high-pressure capillary rheometer. The results of the three different dies are shown; rough (solid), smooth (dotted) and orifice (dashed). The shear rate (green, thin) is shown for the rough die and the orifice die follows the same shear rate as the rough die. The increase of the pressure as a result of sticking in the orifice die is highlighted

Full size image

The shear viscosity can directly be determined from the rough- and smooth die data, after correcting for the entry pressure loss, i.e. using the orifice die. The wall shear stress (\({\tau }_{w}\)) is calculated from the pressure drop (\(\Delta P\)) using Eq. (4);

$${\tau }_{w}=\frac{R\Delta P}{2L}$$
(4)

The calculation of the shear rate depends on the used constitutive equation to describe rheology of the material and, in this case, on the possible incorporation of a yield stress. The relative thickness of the central plug (\({\delta }_{plug}\)) depends on the ratio between the wall shear stress and the yield stress \(\left({\delta }_{plug}=R\left({\tau }_{y}/{\tau }_{w}\right)\right)\). As the wall shear stress varied between 103 and 105 Pa during the measurements and the maximum yield stress of the suspensions was 60 Pa (Fig. 3), the thickness of the central plug (Fig. 1) did not exceed 0.05 \(R\). As a result, following the proposed calculations for Herschel-Bulkley fluids in pipes from Kelessidis et al. (2006) and using the suspension with the largest value of \({\tau }_{y}/{\tau }_{w}\) (the PEG suspension with a solid volume fraction of 0.55), the determined consistency coefficient would only vary by less than 0.5% if the yield stress is not accounted for. The influence of the yield stress is therefore assumed to be negligible and the rheology of the material and corresponding velocity profile are assumed to follow the Ostwald-de Waele relationship (Eq. (1)). The wall shear rate is then calculated from the apparent shear rate (Eq. (2)) using the Weissenberg-Rabinowitsch correction (Eq. (5)) (Rabinowitsch 1929). This correction is required to account for the non-parabolic velocity profile as a result of non-Newtonian behaviour of the material.

$${\dot{\gamma }}_{w}={\dot{\gamma }}_{a}\left[\frac{1}{4}\left(3+\frac{d\mathrm{ln}({\dot{\gamma }}_{a})}{d\mathrm{ln}({\tau }_{w})}\right)\right]$$
(5)

The term ‘apparent shear rate’ indicates that the corresponding value is the expected shear rate, when assuming Poiseuille flow without wall slip. Thus, the apparent shear rate does not have to be the same as the true shear rate of the material.

Although \({{d\ln \left( {\dot{\gamma }_{a} } \right)} \mathord{\left/ {\vphantom {{d\ln \left( {\dot{\gamma }_{a} } \right)} {d\ln \left( {\tau _{w} } \right)}}} \right. \kern-\nulldelimiterspace} {d\ln \left( {\tau _{w} } \right)}}\) was constant for most samples, some results that are obtained using smooth dies indicated an increase in gradient with increasing wall shear stress. To account for this non-linearity, the gradient was calculated by differentiating the second order polynomial function that describes the logarithm of the apparent shear rate as a function of the logarithm of the wall shear stress.

The shear viscosity then follows from;

$$\eta =\frac{{\tau }_{w}}{{\dot{\gamma }}_{w}}$$
(6)

Similar to the liquid phase rheology, the shear viscosity can be described by the Ostwald-de Waele relationship, which can be written as;

$$\eta =K{\left(\frac{\partial v}{\partial y}\right)}^{n-1}$$
(7)

In this document, we will refer to the shear viscosity as calculated from the smooth die as the apparent viscosity and from the rough die as the true viscosity. The apparent viscosity describes all flow regions as a continuum, whereas the true viscosity describes the flow inside the shear flow region (Fig. 1).

The influence of solid volume fraction on the true viscosity of the sodium alginate suspensions is visualized in Fig. 5A. The consistency factor \(K\) increases in an exponential fashion (inset Fig. 5A), as expected from established suspension rheology (Krieger and Dougherty 1959; Rueda et al. 2017). The same is true for PEG (Fig. 5B) and HPMC (Fig. 5C). The sodium alginate and PEG suspensions (Fig. 5A and B) show a significantly lower flow index compared to the pure liquid phase (Fig. 2). In the case of sodium alginate, the flow index decreases from 0.50 to 0.35–0.38, and in the case of PEG from 1.00 to 0.71–0.77. This decrease of the flow index has been observed for other non-Brownian suspensions and its origin remains an open question (Mueller et al. 2010; Vázquez-Quesada et al. 2017). Hypotheses regarding the underlying physics vary from a hydrodynamic origin, e.g. viscous heating (Mueller et al. 2010) or slip at the particle’s surface (Kroupa et al. 2017; Vázquez-Quesada et al. 2018), to a frictional origin, e.g. nonlinear dependency of friction coefficients on the normal load (Chatté et al. 2018; Lobry et al. 2019).

Fig. 5
figure 5

True viscosity as a function of corrected shear rate for suspensions with different solid volume fractions, using different thickeners; (A) Sodium alginate, (B) PEG and (C) HPMC. Solid lines indicate the fit to viscosity function following an Ostwald-de Waele relationship, of which the function and fit parameters are shown in the legend. The inset shows corresponding K values as a function of solid volume fraction, the solid line indicates an exponential fit to guide the eye (y = aebx)

Full size image

One important assumption of the current analysis is the choice of effective radius that is used to determine the shear stress and shear rate. Recent studies with parallel plate geometries show that an additional slip velocity can develop when using roughened surfaces, leading to lower measured viscosities than expected (Carotenuto and Minale 2013; Pawelczyk et al. 2020). To correct for this additional slip phenomenon, a correction has been proposed that increases the effective gap height that is used in subsequent calculations. This correction can be determined by interpolating data that is obtained from measurements at different gap heights or by using a porous medium approach (Carotenuto and Minale 2013; Carotenuto et al. 2015). The value of this correction depends on the geometry of the roughness elements (e.g. pyramid-shaped, cross-hatched or columnar) and could even increase the effective gap height with a value that is in the order of the depth of the roughness elements(Carotenuto et al. 2015; Pawelczyk et al. 2020). For the parallel plate geometries that were investigated, it has been assumed that the roughness elements present obstacles that hinder, but not completely block, the flow of the material. The fluid is still able to flow in between the actual roughness elements, similar to flow through a porous medium. Comparable observations are made for pressure driven flows with a brush-like roughness on the wall (Agelinchaab et al. 2006). However, in the case of the die that is used within this study, i.e. with the sawtooth pattern along the length of the die (Fig. 1B), the roughness elements prevent any parallel flow between the roughness elements to extend over more than the distance between successive ‘teeth’. Such roughness does not provide a porous structure. Similar sawtooth patterns were studied in microchannels, having channel radii within the same order of magnitude as used in this study (Kandlikar et al. 2005; Liu et al. 2019). Kandlikar et al. (2005) showed that, in the laminar flow regime, the constricted flow diameter, i.e. the diameter that is free from surface roughness, shows the same relation between mass flow rate and pressure loss as a smooth channel. The good correlation of using the constricted flow diameter has been explained by the inability of the flow to reattach to the surface of the wall when flowing over the roughness elements (Webb et al. 1971; Kandlikar et al. 2005). Instead, it creates a new flow boundary at a specific distance from the wall. Although Kandlikar et al. (2005) performed measurements in the laminar regime, a direct comparison is difficult as they operated at significantly higher Reynolds numbers, i.e. Re > 200 compared to Re <  < 1 as observed in this study.

Figure 6 shows the flow curves that are determined using the rough die and with rotational rheometry using the same parallel plate setup as for the oscillation measurements. The results suggest that if an additional slip correction is indeed required, it would be in the same order of magnitude for the conventional parallel-plate setup as for the rough die. As this additional slip velocity directly affects the measured viscosity, its quantification for rough dies with similar annular grooves provides an interesting topic for future studies. It is, however, out of scope for this contribution and the validity of using the constricted radius is an adequate assumption to calculate shear stress and shear rate, considering the good agreement to the conventional analysis with rough parallel plates (Fig. 6). Note that in Fig. 6, the range with overlapping shear rates is between 10 and 30 s−1, as the parallel plate measurements were stopped as soon as edge fracture occurred and material was expelled from the measurement gap.

Fig. 6
figure 6

Flow curves of a 40 wt.% PEG suspension with a solid volume fraction of 0.55, measured with a high-pressure capillary rheometer equipped with a rough die (squares) and measured with a rotational rheometer equipped with parallel plates (circles). The parallel plate measurements are performed in a controlled shear stress mode from 300 Pa until edge fracture occurred. The same geometry is used as described for oscillation rheometry, with a gap height of 1 mm. The torque and angular velocity are converted to shear stress and shear rate according to Steffe (1996). Filled and open symbols indicate duplicates and the shaded area indicates overlapping shear rates

Full size image

Wall slip velocity

The wall slip velocity is the apparent velocity jump at the wall (\({v}_{s}\), Fig. 1) and is generally described as a function of wall shear stress. It can be calculated from the difference between the apparent shear rates of the smooth and rough die, at identical wall shear stress. As the measurements were shear rate controlled (Fig. 4), an interpolation was performed for the apparent shear rate as a function of wall shear stress, by fitting an exponential function (\(y={y}_{0}+A{e}^{Bx}\)). An exception was made for the HPMC suspensions, where the data of the rough die showed poor fits at lower shear rates and a power function (\(y=A{x}^{B}\)) was used instead. The goal was to adequately describe the data and not use an equation with a physical origin. If the shear rates are known at a specific wall shear stress, the wall slip velocity can be calculated from the difference in the apparent shear rates using Eq. (8);

$${v}_{s}=\frac{\left({\dot{\gamma }}_{a,s}-{\dot{\gamma }}_{a,r}\right)R}{4}$$
(8)

With \({v}_{s}\) the slip velocity, \({\dot{\gamma }}_{a,s}\) the apparent shear rate determined using the smooth die and \({\dot{\gamma }}_{a,r}\) the apparent shear rate determined using the rough die. For sodium alginate and PEG the wall slip velocity was only determined for wall shear stresses that were measured for both the smooth and rough die, i.e. within the range that is indicated by the striped area in Fig. 7. For HPMC extrapolation was required, as the wall slip was so pronounced that, for all suspensions, the wall shear stress at the highest shear rate of the smooth die (\({\dot{\gamma }}_{a,s}\) = 1280 s−1) was lower than the wall shear stress at the lowest shear rate of the rough die (\({\dot{\gamma }}_{a,r}\) = 10 s−1). The data obtained from the rough die measurements was therefore extrapolated to lower shear rates.

Fig. 7
figure 7

Apparent shear rate as a function of wall shear stress for a 60 g/L sodium alginate suspension with a solid volume fraction of 0.60, measured using a rough and smooth die. The striped area indicates the area that is used for slip velocity estimation

Full size image

The slip velocity is often expressed as a function of wall shear stress, following a generalized Navier slip law;

$${v}_{s}=\beta {\tau }_{w}^{\alpha }$$
(9)

where \(\beta\) is the slip coefficient and \(\alpha\) the slip exponent (Kalyon 2005). Equation (9) can also be written as

$${v}_{s}=\beta {\tau }_{w}^{\frac{1}{{n}_{s}}}$$
(10)

where \({n}_{s}\) will be referred to as the slip index. As the slip layer is thought to consist of pure liquid, of which the rheological behaviour follows an Ostwald-de Waele relationship (Eq. (1)), \(\alpha\) is often assumed to be \(1/{n}_{l}\), with \({n}_{l}\) the flow index of the liquid phase (Fig. 2) (Cohen and Metzner 1985; Kalyon 2005). If this assumption regarding the slip layer is true, the slip index should be similar to the flow index, i.e. ns = nl. This is confirmed for all suspensions with a solid volume fraction of 0.60 (Fig. 8). The slip index of the PEG suspension was 1.12, compared to a flow index of 1.00 that of sodium alginate 0.42, compared to 0.50 and that of HPMC 0.19, compared to 0.20.

Fig. 8
figure 8

Wall slip velocity as a function of wall shear stress for suspensions with a solid volume fraction of 0.60, made using different thickeners. Solid lines indicate fit to the slip equation, of which the function and fit parameters are presented in the legend

Full size image

Found values are consistent with other studies on concentrated suspensions and polymers, with the majority reporting slightly lower slip indices (ns < nl). Examples include, glass- and aluminium beads in hydroxyl-terminated polybutadiene (Soltani and Yilmazer 1998), coal water slurries (Chen et al. 2009), PMMA particles in a blend of cassia and castor oil (Jesinghausen et al. 2016) and a variety of polymer solutions (Cohen and Metzner 1985). The variation of the slip index can be explained by looking at the underlying physics of the slip layer formation. It is generally thought that steric depletion is the main cause of the formation of a slip layer in concentrated suspensions (Barnes 1995; Cloitre and Bonnecaze 2017). However, in addition to steric depletion, the inhomogeneous shear field along the radius of the flow channel can lead to a migration of particles from high to low shear rate and down the shear stress gradient (Leighton and Acrivos 1987). This shear-induced migration has been observed in particulate (Ramachandran 2007) and macromolecular flows (Agarwal et al. 1994), reducing the local concentration of particles and macromolecules at the channel wall.

From a solid’s perspective, the area close to the wall can be roughly divided into two regions, differentiating between steric depletion and shear induced migration. At the wall, the steric depletion leads to a region of reduced solid concentration with a fixed thickness (the steric layer). Directly adjacent, the shear induced migration leads to a region with a transient nature of which the (average) thickness depends on, among others, the shear stress and shear rate gradient (the diffuse layer). Of these two regions, the formation of a steric layer is prevented by the roughened surface, whereas the diffuse layer is inherent to flow and cannot be avoided.

At identical wall shear stress, it is reasonable to assume that the diffuse layer is similar in both the rough and smooth die. As the slip layer is expected to be only a fraction of the average particle size (Kalyon 2005), the stress at the outer edge of the shear flow region (\(R-\delta\), Fig. 1) is similar for both dies. The resulting flow profiles of the shear flow region are thus independent of the surface roughness of the die and the influence of shear-induced migration on the shear flow should be similar. Consequently, any difference between \({n}_{s}\) and \({n}_{l}\) should be related to something that occurs within steric layer. Within this layer, the macromolecules can show a similar migration as the particles in the diffuse layer, i.e. the macromolecules migrate away from the wall (Agarwal et al. 1994; Ma and Graham 2005). The migration increases with increasing shear stress- and shear rate gradient, leading to lower local viscosities, larger slip velocities and a smaller slip index (ns < nl). The effect is most pronounced in the case of shear-thinning matrices as the non-parabolic velocity profile leads to a steep shear rate gradient within the slip layer and thus to a large driving force for migration (Reddy et al. 2019). Knowing that the thickness of the particle depleted layer depends on the solid volume fraction (Kalyon 2005), the slip index should decrease with decreasing solid volume fraction. This is confirmed for sodium alginate, decreasing from 0.43 at a solid volume fraction of 0.60 to 0.34 for \(\varphi\) = 0.55 (Fig. 9A), and for HPMC, decreasing from 0.19 for \(\varphi\) = 0.60 to 0.14 for \(\varphi\) = 0.58 (Fig. 9B).

The shear rate gradient is significantly less steep in the case of a Newtonian matrix and the driving force for the shear-induced migration of macromolecules in the steric layer is thus smaller, reducing its effect on the slip index (PEG, Fig. 8). Interestingly, the slip index further increases with decreasing solid volume fraction and shows a clear drop at \(\varphi\) < 0.58 (Fig. 9C). This decrease in slip velocity with increasing wall shear stress suggests that the original assumption of identical shear induced migration of particles in the diffuse layer for rough and smooth dies is incorrect. Instead, the shear-induced migration appears to be more pronounced for a roughened surface, compared to a smooth surface. This difference only becomes visible at high wall shear stress and low slip velocity (compare Fig. 9A and B to Fig. 9C), as the shear stress is a driving force for shear induced migration (Leighton and Acrivos 1987). Considering that the relative contribution of wall slip to the overall flow decreases with decreasing difference between the bulk- and slip layer viscosity (Kalyon 2005), the effect is most pronounced for suspensions with lower solid volume fractions in a Newtonian matrix. To improve the measurement accuracy for such suspensions, more research is required regarding the physical origin of the influence of surface roughness on shear-induced migration.

Fig. 9
figure 9

Wall slip velocity as a function of wall shear stress for suspensions with different solid volume fractions, using different thickeners; (A) Sodium alginate, (B) HPMC and (C) PEG. Solid lines indicate fit to the slip equation, of which the function and fit parameters are presented in the legend. For clarity, the error bars in (C) are not shown for the solid volume fractions 0.55 and 0.56

Full size image

Slip layer thickness

An estimation can be made regarding the slip layer thickness (\(\delta\)) based on the slip velocity, if one knows the liquid phase consistency (\({K}_{l}\)) and flow index (\({n}_{l}\)), following;

$$\delta =\frac{{v}_{s}{K}_{l}^{1/{n}_{l}}}{{\tau }_{w}^{{1/n}_{l}}}$$
(11)

as presented by Kalyon (2005). The slip layer thickness was calculated for the suspensions with a solid volume fraction of 0.60, i.e. the slip velocities from Fig. 8 and using the liquid phase rheology as presented in Fig. 2, as a function of wall shear stress (Fig. 10). For PEG and sodium alginate, the calculated slip layer thickness is similar and varies between 0.17 and 0.30 µm. This is just a fraction (0.035–0.061) of the average particle size (D4,3 = 4.91 µm), which is in the same order of magnitude as reported in literature (Soltani and Yilmazer 1998; Jesinghausen et al. 2016). Soltani and Yilmazer (1998), for instance, determined the ratio of slip layer thickness over average particle diameter to be 0.037 for glass beads and 0.071 for aluminium powder in hydroxyl-terminated polybutadiene.

In the case of HPMC suspensions, the calculated slip layer thickness is in the same order of magnitude as the radius of single atoms (10−10 µm), which is physically impossible. This low value could be the result of three assumptions that are made for the current analysis;

  1. (i)

    The slip layer consists of pure liquid

  2. (ii)

    The rheological behaviour of the liquid phase that is measured in the rotational rheometer can be extrapolated to shear rates within the slip layer

  3. (iii)

    The rough die measurements can be extrapolated to lower shear rates

Fig. 10
figure 10

Slip layer thickness as a function of wall shear stress for suspensions with a solid volume fraction of 0.60, made using different thickeners. The inset shows a close-up of HPMC

Full size image

The slip layer thickness that is calculated according to Eq. (11) can be considered as the lower limit estimate, as it assumes that the slip layer consists of pure liquid phase and thus to be completely devoid of particles. Although the local solid volume fraction might approach 0 at the wall, it immediately increases in the radial direction, as known from powder mechanics and, for instance, shown by Benenati and Brosilow (1962) for packed beds of lead spheres. In reality, the solid volume fraction shows a gradient over the apparent slip layer and the (average) consistency within the slip layer is higher than what is used in Eq. (11). As the slip layer thickness scales with the consistency to the power of the inverse of the flow index (Eq. (11)), the error is most pronounced in the case of HPMC. The notion of pure liquid also assumes a homogeneity with respect to the macromolecules. However, macromolecules show both steric depletion and shear-induced migration themselves (Cohen and Metzner 1985). In addition, the high shear rates within the slip layer could result in errors when extrapolating the rheological behaviour of the liquid phase. If the rheological behaviour of HPMC can indeed be described by Eq. (1) and the constants shown in Fig. 2, a wall shear stress of 104 Pa (Fig. 8) will result in a shear rate in the order of 107 s−1 and an effective viscosity (0.4 mPas) that is lower than water. It is likely that the liquid phase tends towards an infinite-shear viscosity at such high shear rates (Dakhil et al. 2019), but no information is available for the thickeners that are used in this study. Because the wall slip of HPMC suspensions was so pronounced, extrapolation of the rough die measurements was required to apply the subtractive method of slip analysis. Considering the possibility of a change in the flow curve at low shear rates (Fig. 6), this could also introduce an error. The use of Eq. (11) is, therefore, not recommended for suspensions with a strongly shear thinning liquid phase, such as HPMC.

Shear- or slip-dominated flow

It is of practical use to approach a concentrated suspension as a continuum and describe its rheological behaviour using a single flow function (Benbow and Bridgwater 1993). By knowing the relative contribution of the shear and slip regions (Fig. 1) to the overall flow, the correctness of the continuum approach can be assessed. It would, furthermore, give an indication of the relative error of measurements and simulations where either wall slip or shearing of the bulk is not accounted for. The relative contribution can be visualized by plotting the normalized consistency (\({K}_{apparent}/{K}_{true}\)), i.e. the ratio between the determined consistencies with and without wall slip, as a function of solid volume fraction (Fig. 11). The normalized consistency linearly decreases with increasing solid volume fraction, with both the slope and intercept depending on the used thickener. The decrease in normalized consistency can be explained from a wall slip perspective, as its influence depends on the ratio between the liquid phase viscosity and the true viscosity of the suspension (Kalyon 2005). Since the latter follows an exponential increase with solid volume fraction (e.g. inset Fig. 5A), the relative contribution of wall slip increases with increasing solid volume fraction. As only the apparent consistency is affected by wall slip, the normalized consistency decreases. Figure 11 does not include the HPMC suspensions with solid volume fractions below 0.58, as the pressure readings of the smooth die were significantly below the accuracy limit of the pressure sensor (< < 10% of the maximum pressure). Note that the difference between the thickeners in Fig. 11 originates from the difference between the flow index of the liquid phase and the flow index of the suspension, but is out of scope for this contribution.

Fig. 11
figure 11

Normalized consistency (Kapparent/Ktrue) as a function of solid volume fraction for PEG, sodium alginate (SA) and HPMC suspensions. The solid line indicates the fit to a linear function of which the fit parameters are shown in the legend

Full size image

When extrapolating Fig. 11 and assuming a threshold value for the normalized consistency of 0.9, the flow will be shear dominated for suspensions with a solid volume fraction below 0.52 (PEG) and 0.54 (sodium alginate), at given measurement conditions. Similarly, assuming a threshold value of 0.1, the majority of the deformation will be in the slip layer and the bulk material will move as a plug for suspensions with a solid volume fraction above 0.61 (PEG) and 0.63 (sodium alginate). The dominance of wall slip is an important assumption for equations such as that proposed by Benbow and Bridgwater (1993), allowing it to describe the flow through dies using a simple Herschel-Bulkley-like equation. The application of the Benbow-Bridgwater model has proven useful to calculate pressure drops for several extrusion applications (Cheyne et al. 2005; Wilson and Rough 2012). The validity of extrapolating Fig. 11 to higher and lower solid volume fractions has to be verified in future studies.

Conclusion

Quantifying the flow behaviour of concentrated suspensions in pressure-driven flows is complicated by the heterogeneous nature of the flow profile. Slip, shear and plug flow regions co-exist, with their relative contributions depending on the flow conditions. Especially the quantification of wall slip has proven to be difficult, as indirect methods are often unsuccessful (Martin and Wilson 2005) and direct methods are not universely applicable (Sochi 2011).

In this contribution, a subtractive method is used to quantify the shear viscosity and wall slip velocity of highly concentrated suspensions in pressure driven flows. The shear viscosity was determined by equipping a commercially available high-pressure capillary rheometer with a 3D-printed die with a grooved surface of the internal flow channel. The grooved surface prevents wall slip and allows for a direct quantification of the shear viscosity, which was shown to increase exponentially with solid volume fraction (0.55–0.60). The constricted radius was used to calculate the shear stress and shear rate, assuming there was no additional flow of material between the roughness elements, unlike recent observations in parallel plate geometries (Carotenuto and Minale 2013). Verifying this assumption is an interesting topic for future research.

The wall slip velocity was quantified from the difference between the apparent shear rates through a rough and smooth die, at identical wall shear stress. This is a similar procedure as proposed by Mourniac et al. (1992) and Halliday and Smith (1995). The wall slip velocities of suspensions with a solid volume fraction of 0.60 were shown to scale with the flow index of the liquid phase, which was verified for Newtonian (PEG) and non-Newtonian shear-thinning matrices (sodium alginate and HPMC). Increasingly large deviations were observed with decreasing solid volume fraction. In the case of sodium alginate and HPMC, it is hypothesized that the origin of these deviations is related to shear-induced migration of macromolecules due to the large shear rate gradient within the slip layer. The slip behaviour of PEG suspensions is more complex and further research is required to understand the influence of surface roughness on shear-induced migration.

The estimated slip layer thickness of the PEG and sodium alginate suspensions with a solid volume fraction of 0.60 was found to be a fraction of the average particle size. The values ranged between 0.035 and 0.061, which is in good agreement with results that are previously reported in literature (Soltani and Yilmazer 1998; Kalyon 2005). Physically unreasonable results were obtained in the case of HPMC. The assumptions that the slip layer consists of pure liquid, that the rheological behaviour of the liquid matrix can be extrapolated to shear rates within the slip layer and that the rough die measurements can be extrapolated to lower shear rates will lead to significant errors in the case of strongly shear thinning liquid matrices.

The use of smooth and rough dies presents a quick and universally applicable alternative to quantify the shear viscosity and wall slip velocity of highly concentrated suspensions in pressure driven flows. It provides the opportunity to increase the understanding of these complex flows and develop new- or improve on exisiting flow models.