Skip to main content
SpringerLink
Log in

Energy minimization versus criteria-based methods in discrete cohesive fracture simulations

  • Original Paper
  • Published:
Computational Mechanics Aims and scope Submit manuscript

Abstract

We highlight the ability of a proposed energy-based cohesive interface method to produce stable and convergent solutions where methods based on failure criteria at similar discretization levels fail. The key feature of the method is the smooth transition from “uncracked” to “cracked” states, i.e., internal forces remain continuous functions of the deformation at initiation of failure. This property is missing in methods based on stress criteria. In explicit time stepping calculations, lack of continuity gives rise to spurious crack opening velocity fields. This issue is particularly significant in multiphysics problems such as hydraulic fracturing due to the coupling of the unknown fields and may lead to instability of the computational algorithm. In implicit time stepping calculations, lack of continuity introduces challenges in obtaining convergence of Newton iterations. Often the issue is circumvented by keeping cracks fixed within the iterative solver; the configuration of cracks is only updated at the end of a time step in such algorithms. This approach leads to the dependence of the crack-tip velocity on temporal and spatial discretization parameters. We present various simulation results to show that the energy approach is free of all such undesirable behaviors.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

Notes

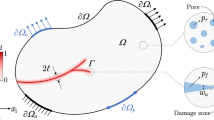
  1. In derivation of (18), the flow rate is taken to be zero at a crack-tip within \(\Gamma _p\) due to the assumption of an impermeable medium and zero fluid-lag conditions

  2. It has been pointed out that sequential (staggered) schemes sometimes suffer from convergence issues especially in viscosity dominated regimes. A thorough analysis of these issues can be found in [39, 71]. The present solution algorithm assumes that the time steps used are sufficiently small that a reasonably accurate solution is obtained after one passing of a staggered iteration.

References

  1. Xu X-P, Needleman A (1994) Numerical simulations of fast crack growth in brittle solids. J Mech Phys Solids 42:1397–1434

    Article  MATH  Google Scholar 

  2. Camacho GT, Ortiz M (1996) Computational modeling of impact damage in brittle materials. Int J Solids Struct 33:2899–2938

    Article  MATH  Google Scholar 

  3. Khoei A, Azadi H, Moslemi H (2008) Modeling of crack propagation via an automatic adaptive mesh refinement based on modified superconvergent patch recovery technique. Eng Fract Mech 75:2921–2945

    Article  Google Scholar 

  4. Paulino GH, Park K, Celes W, Espinha R (2010) Adaptive dynamic cohesive fracture simulation using nodal perturbation and edge-swap operators. Int J Numer Meth Eng 84:1303–1343

    Article  MATH  Google Scholar 

  5. Wells GN, Sluys L (2001) A new method for modelling cohesive cracks using finite elements. Int J Numer Meth Eng 50:2667–2682

    Article  MATH  Google Scholar 

  6. Moës N, Belytschko T (2002) Extended finite element method for cohesive crack growth. Eng Fract Mech 69:813–833

    Article  Google Scholar 

  7. Khoei A, Vahab M, Hirmand M (2018) An enriched FEM technique for numerical simulation of interacting discontinuities in naturally fractured porous media. Comput Methods Appl Mech Eng 331:197–231

    Article  MathSciNet  MATH  Google Scholar 

  8. Armero F, Linder C (2009) Numerical simulation of dynamic fracture using finite elements with embedded discontinuities. Int J Fract 160:119

    Article  MATH  Google Scholar 

  9. Armero F, Linder C (2008) New finite elements with embedded strong discontinuities in the finite deformation range. Comput Methods Appl Mech Eng 197:3138–3170

    Article  MathSciNet  MATH  Google Scholar 

  10. Radovitzky R, Seagraves A, Tupek M, Noels L (2011) A scalable 3D fracture and fragmentation algorithm based on a hybrid, discontinuous Galerkin, cohesive element method. Comput Methods Appl Mech Eng 200:326–344

    Article  MathSciNet  MATH  Google Scholar 

  11. Nguyen VP (2014) Discontinuous Galerkin/extrinsic cohesive zone modeling: Implementation caveats and applications in computational fracture mechanics. Eng Fract Mech 128:37–68

    Article  Google Scholar 

  12. Hansbo P, Salomonsson K (2015) A discontinuous Galerkin method for cohesive zone modelling. Finite Elem Anal Des 102:1–6

    Article  MathSciNet  Google Scholar 

  13. Abedi R, Petracovici B, Haber RB (2006) A space-time discontinuous Galerkin method for linearized elastodynamics with element-wise momentum balance. Comput Methods Appl Mech Eng 195:3247–3273

    Article  MathSciNet  MATH  Google Scholar 

  14. Dimitri R, De Lorenzis L, Wriggers P, Zavarise G (2014) Nurbs-and t-spline-based isogeometric cohesive zone modeling of interface debonding. Comput Mech 54:369–388

    Article  MathSciNet  MATH  Google Scholar 

  15. Song J-H, Belytschko T (2009) Cracking node method for dynamic fracture with finite elements. Int J Numer Meth Eng 77:360–385

    Article  MathSciNet  MATH  Google Scholar 

  16. Rabczuk T, Belytschko T (2004) Cracking particles: a simplified meshfree method for arbitrary evolving cracks. Int J Numer Meth Eng 61:2316–2343

    Article  MATH  Google Scholar 

  17. Remmers JJ, de Borst R, Needleman A (2003) A cohesive segments method for the simulation of crack growth. Comput Mech 31:69–77

    Article  MATH  Google Scholar 

  18. Khoei A, Barani O, Mofid M (2011) Modeling of dynamic cohesive fracture propagation in porous saturated media. Int J Numer Anal Meth Geomech 35:1160–1184

    Article  MATH  Google Scholar 

  19. Schrefler BA, Secchi S, Simoni L (2006) On adaptive refinement techniques in multi-field problems including cohesive fracture. Comput Methods Appl Mech Eng 195:444–461

    Article  MATH  Google Scholar 

  20. Moës N, Dolbow J, Belytschko T (1999) A finite element method for crack growth without remeshing. Int J Numer Meth Eng 46:131–150

    Article  MathSciNet  MATH  Google Scholar 

  21. Thomas RN, Paluszny A, Zimmerman RW (2020) Growth of three-dimensional fractures, arrays, and networks in brittle rocks under tension and compression. Comput Geotech 121:103447

    Article  Google Scholar 

  22. Li S, Ghosh S (2006) Multiple cohesive crack growth in brittle materials by the extended voronoi cell finite element model. Int J Fract 141:373–393

    Article  MATH  Google Scholar 

  23. Erdogan F, Sih G (1963) On the crack extension in plates under plane loading and transverse shear

  24. Menouillard T, Belytschko T (2010) Smoothed nodal forces for improved dynamic crack propagation modeling in XFEM. Int J Numer Meth Eng 84:47–72

    Article  MathSciNet  MATH  Google Scholar 

  25. Song J-H, Wang H, Belytschko T (2008) A comparative study on finite element methods for dynamic fracture. Comput Mech 42:239–250

    Article  MATH  Google Scholar 

  26. Hirmand MR, Papoulia KD (2018) A continuation method for rigid-cohesive fracture in a discontinuous Galerkin finite element setting. Int J Numer Meth Eng 115:627–650

    Article  Google Scholar 

  27. Sam C-H, Papoulia KD, Vavasis SA (2005) Obtaining initially rigid cohesive finite element models that are temporally convergent. Eng Fract Mech 72:2247–2267

    Article  Google Scholar 

  28. Hirmand M, Vahab M, Papoulia K, Khalili N (2019) Robust simulation of dynamic fluid-driven fracture in naturally fractured impermeable media. Comput Methods Appl Mech Eng 357:112574

    Article  MathSciNet  MATH  Google Scholar 

  29. Papoulia KD, Sam C-H, Vavasis SA (2003) Time continuity in cohesive finite element modeling. Int J Numer Meth Eng 58:679–701

    Article  MATH  Google Scholar 

  30. Ortiz M, Pandolfi A (1999) Finite-deformation irreversible cohesive elements for three-dimensional crack-propagation analysis. Int J Numer Meth Eng 44:1267–1282

    Article  MATH  Google Scholar 

  31. Klein P, Foulk J, Chen E, Wimmer S, Gao H (2001) Physics-based modeling of brittle fracture: cohesive formulations and the application of meshfree methods. Theoret Appl Fract Mech 37:99–166

    Article  Google Scholar 

  32. Hirmand M (2019) Nondifferentiable energy minimization for cohesive fracture in a discontinuous Galerkin finite element framework

  33. Verhoosel CV, Scott MA, De Borst R, Hughes TJ (2011) An isogeometric approach to cohesive zone modeling. Int J Numer Meth Eng 87:336–360

    Article  MATH  Google Scholar 

  34. Peruzzo C, Cao TD, Milanese E, Favia P, Pesavento F, Hussain F, Schrefler BA (2018) Dynamics of fracturing saturated porous media and self-organization of rupture. J Mech Phys Solids 111:113–133

    MathSciNet  MATH  Google Scholar 

  35. Peruzzo C, Simoni L, Schrefler B (2019) On stepwise advancement of fractures and pressure oscillations in saturated porous media. Eng Fract Mech 215:246–250

    Article  Google Scholar 

  36. Fathima KP, de Borst R (2019) Implications of single or multiple pressure degrees of freedom at fractures in fluid-saturated porous media. Eng Fract Mech 213:1–20

    Article  Google Scholar 

  37. Areias PM, Rabczuk T (2008) Quasi-static crack propagation in plane and plate structures using set-valued traction-separation laws. Int J Numer Meth Eng 74:475–505

    Article  MATH  Google Scholar 

  38. Areias P, Rabczuk T, Camanho P (2013) Initially rigid cohesive laws and fracture based on edge rotations. Comput Mech 52:931–947

    Article  MATH  Google Scholar 

  39. Giovanardi B, Serebrinsky S, Radovitzky R (2019) A fully-coupled computational framework for large-scale simulation of fluid-driven fracture propagation on parallel computers, arXiv preprint arXiv:1911.10275

  40. Ferté G, Massin P, Moës N (2016) 3D crack propagation with cohesive elements in the extended finite element method. Comput Methods Appl Mech Eng 300:347–374

    Article  MathSciNet  MATH  Google Scholar 

  41. Aduloju SC, Truster TJ (2019) A variational multiscale discontinuous Galerkin formulation for both implicit and explicit dynamic modeling of interfacial fracture. Comput Methods Appl Mech Eng 343:602–630

    Article  MathSciNet  MATH  Google Scholar 

  42. Truster TJ, Masud A (2013) A discontinuous/continuous Galerkin method for modeling of interphase damage in fibrous composite systems. Comput Mech 52:499–514

    Article  MathSciNet  MATH  Google Scholar 

  43. Bruggi M, Venini P (2009) Modeling cohesive crack growth via a truly-mixed formulation. Comput Methods Appl Mech Eng 198:3836–3851

    Article  MathSciNet  MATH  Google Scholar 

  44. Wang Y, Waisman H (2018) An arc-length method for controlled cohesive crack propagation using high-order XFEM and irwin’s crack closure integral. Eng Fract Mech 199:235–256

    Article  Google Scholar 

  45. Wang Y, Waisman H (2016) From diffuse damage to sharp cohesive cracks: A coupled XFEM framework for failure analysis of quasi-brittle materials. Comput Methods Appl Mech Eng 299:57–89

    Article  MathSciNet  MATH  Google Scholar 

  46. Zeng X, Li S (2010) A multiscale cohesive zone model and simulations of fractures. Comput Methods Appl Mech Eng 199:547–556

    Article  MATH  Google Scholar 

  47. Li S, Zeng X, Ren B, Qian J, Zhang J, Jha AK (2012) An atomistic-based interphase zone model for crystalline solids. Comput Methods Appl Mech Eng 229:87–109

    Article  MathSciNet  MATH  Google Scholar 

  48. Silling SA (2000) Reformulation of elasticity theory for discontinuities and long-range forces. J Mech Phys Solids 48:175–209

    Article  MathSciNet  MATH  Google Scholar 

  49. Francfort GA, Marigo J-J (1998) Revisiting brittle fracture as an energy minimization problem. J Mech Phys Solids 46:1319–1342

    Article  MathSciNet  MATH  Google Scholar 

  50. Bourdin B, Francfort GA, Marigo J-J (2000) Numerical experiments in revisited brittle fracture. J Mech Phys Solids 48:797–826

    Article  MathSciNet  MATH  Google Scholar 

  51. Nguyen VP, Wu J-Y (2018) Modeling dynamic fracture of solids with a phase-field regularized cohesive zone model. Comput Methods Appl Mech Eng 340:1000–1022

    Article  MathSciNet  MATH  Google Scholar 

  52. Geelen RJ, Liu Y, Hu T, Tupek MR, Dolbow JE (2019) A phase-field formulation for dynamic cohesive fracture. Comput Methods Appl Mech Eng 348:680–711

    Article  MathSciNet  MATH  Google Scholar 

  53. Lorentz E, Cuvilliez S, Kazymyrenko K (2011) Convergence of a gradient damage model toward a cohesive zone model. Comptes Rendus Mécanique 339:20–26

    Article  MATH  Google Scholar 

  54. Lorentz E (2008) A mixed interface finite element for cohesive zone models. Comput Methods Appl Mech Eng 198:302–317

    Article  MATH  Google Scholar 

  55. Papoulia KD (2017) Non-differentiable energy minimization for cohesive fracture. Int J Fract 204:143–158

    Article  Google Scholar 

  56. Bourdin B, Chukwudozie CP, Yoshioka K, et al., A variational approach to the numerical simulation of hydraulic fracturing, in: SPE Annual Technical Conference and Exhibition, Society of Petroleum Engineers

  57. Khisamitov I, Meschke G (2018) Variational approach to interface element modeling of brittle fracture propagation. Comput Methods Appl Mech Eng 328:452–476

    Article  MathSciNet  MATH  Google Scholar 

  58. Mandal TK, Nguyen VP, Wu J-Y (2020) Evaluation of variational phase-field models for dynamic brittle fracture. Eng Fract Mechan 235:107169

    Article  Google Scholar 

  59. Fraternali F (2007) Free discontinuity finite element models in two-dimensions for in-plane crack problems. Theoret Appl Fract Mech 47:274–282

    Article  Google Scholar 

  60. Papoulia KD, Vavasis SA, Ganguly P (2006) Spatial convergence of crack nucleation using a cohesive finite-element model on a pinwheel-based mesh. Int J Numer Meth Eng 67:1–16

    Article  MathSciNet  MATH  Google Scholar 

  61. Charlotte M, Laverne J, Marigo J-J (2006) Initiation of cracks with cohesive force models: a variational approach. Eur J Mech A/Solids 25:649–669

    Article  MathSciNet  MATH  Google Scholar 

  62. Bourdin B, Francfort GA, Marigo J-J (2008) The variational approach to fracture. J Elast 91:5–148

    Article  MathSciNet  MATH  Google Scholar 

  63. Hirmand MR, Papoulia KD (2019) Block coordinate descent energy minimization for dynamic cohesive fracture. Comput Methods Appl Mech Eng 354:663–688

    Article  MathSciNet  MATH  Google Scholar 

  64. Petrie JIM, Hirmand MR, Papoulia KD (2021) Quasistatic cohesive fracture with an alternating direction method of multipliers (ADMM). In review

  65. Vavasis SA, Papoulia KD, Hirmand MR (2020) Second-order cone interior-point method for quasistatic and moderate dynamic cohesive fracture. Comput Meth Appl Mech Eng 358:112633

    Article  MathSciNet  MATH  Google Scholar 

  66. Grote MJ, Schneebeli A, Schötzau D (2006) Discontinuous galerkin finite element method for the wave equation. SIAM J Numer Anal 44:2408–2431

    Article  MathSciNet  MATH  Google Scholar 

  67. Barenblatt GI (1962) The mathematical theory of equilibrium cracks in brittle fracture. Adv Appl Mech 7:55–129

    Article  MathSciNet  Google Scholar 

  68. Detournay E (2004) Propagation regimes of fluid-driven fractures in impermeable rocks. Int J Geomech 4:35–45

    Article  Google Scholar 

  69. Vahab M, Khalili N (2018) Computational algorithm for the anticipation of the fluid-lag zone in hydraulic fracturing treatments. Int J Geomech 18:04018139

    Article  Google Scholar 

  70. Garagash DI (2019) Cohesive-zone effects in hydraulic fracture propagation. J Mech Phys Solids 133:103727

    Article  MathSciNet  Google Scholar 

  71. Parcheis Efahani M, Gracie R (2019) On the undrained and drained hydraulic fracture splits. Int J Numer Meth Eng 118:741–763

    Article  MathSciNet  Google Scholar 

  72. Garagash D, Detournay E (2000) The tip region of a fluid-driven fracture in an elastic medium. J Appl Mech 67:183–192

    Article  MATH  Google Scholar 

  73. Desroches J, Detournay E, Lenoach B, Papanastasiou P, Pearson JRA, Thiercelin M, Cheng A (1994) The crack tip region in hydraulic fracturing. In: Proceedings of the Royal Society of London. Series A: Mathematical and Physical Sciences, vol 447, pp 39–48

  74. Khoei A, Hirmand M, Vahab M, Bazargan M (2015) An enriched FEM technique for modeling hydraulically driven cohesive fracture propagation in impermeable media with frictional natural faults: numerical and experimental investigations. Int J Numer Meth Eng 104:439–468

    Article  MathSciNet  MATH  Google Scholar 

  75. Boone TJ, Ingraffea AR (1990) A numerical procedure for simulation of hydraulically-driven fracture propagation in poroelastic media. Int J Numer Anal Meth Geomech 14:27–47

    Article  Google Scholar 

  76. Courant R, Friedrichs K, Lewy H (1967) On the partial difference equations of mathematical physics. IBM J Res Dev 11:215–234

    Article  MathSciNet  MATH  Google Scholar 

  77. M. Vahab, N. Khalili, X-FEM modeling of multizone hydraulic fracturing treatments within saturated porous media, Rock Mechanics and Rock Engineering (2018) 1–21

  78. ICOLD, Fifth International Benchmark Workshop on Numerical Analysis of dams, Them A2, Denver, Colorado

  79. Khoei A, Vahab M, Haghighat E, Moallemi S (2014) A mesh-independent finite element formulation for modeling crack growth in saturated porous media based on an enriched FEM technique. Int J Fract 188:79–108

    Article  Google Scholar 

  80. Sharon E, Fineberg J (1996) Microbranching instability and the dynamic fracture of brittle materials. Phys Rev B 54:7128

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. CanmetMATERIALS, Natural Resources Canada, Hamilton, ON, L8P 0A5, Canada

    M. R. Hirmand

  2. Department of Mechanical and Mechatronics Engineering, University of Waterloo, Waterloo, ON, N2L 3G1, Canada

    M. R. Hirmand

  3. School of Civil and Environmental Engineering, The University of New South Wales, Sydney, 2052, Australia

    M. Vahab & N. Khalili

  4. Department of Civil Engineering, York University, Toronto, ON, M3J 1P3, Canada

    K. D. Papoulia

Authors
  1. M. R. Hirmand
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. Vahab
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. K. D. Papoulia
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. N. Khalili
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to M. R. Hirmand.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Hirmand, M.R., Vahab, M., Papoulia, K.D. et al. Energy minimization versus criteria-based methods in discrete cohesive fracture simulations. Comput Mech 68, 845–860 (2021). https://doi.org/10.1007/s00466-021-02049-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00466-021-02049-7

Keywords

Search

Navigation