1 Introduction

A dislocation is the elementary carrier of plasticity in crystals and the most important crystal defect. Therefore, plasticity is based on dislocations, in particular on the glide of dislocations. The natural scale of the mechanics of dislocations is the Ångström scale, which is the characteristic scale in crystallography. However, all fields of dislocations using classical dislocation theory possess singularities, like the 1/r-type singularity in the stress and elastic strain fields of dislocations, because the classical approach is not valid at small scales like the Ångström scale (see, e.g., [6, 12, 17, 41]).

Generalized continuum theories, like gradient elasticity and nonlocal elasticity, are continuum theories valid at small scales (see, e.g., [7, 27, 30]). Mindlin [32] (see also [33]) derived the theory of compatible first strain gradient elasticity. Compatible first strain gradient elasticity incorporates the gradient of the elastic strain tensor in the elastic energy in addition to the elastic strain tensor. For an isotropic material, this framework is characterized by the two Lamé constants and five strain gradient parameters leading to two characteristic lengths. Mindlin’s first strain gradient elasticity theory respects the invariance under the group SO(3) and their irreducible representations (see [26]). Already, Toupin and Grazis [47] and Mindlin [34] (see also [13]) pointed out that first strain gradient elasticity, sometimes called gradient elasticity of grade-2, can be considered as the continuum version of a lattice theory with up to second-neighbor interactions (nearest and next-nearest neighbor interactions). Using ab initio density functional theory (DFT) calculations, Shodja et al. [45] showed that the characteristic lengths of Mindlin’s compatible strain gradient elasticity theory are in the order of \(\sim 10^{-10}\) m (Ångström) for several fcc and bcc materials. The elements of the Hessian matrix, obtained by taking the second derivatives of the total energy with respect to the atomic positions, are related to the strain gradient material constants. Nowadays, the material parameters of first strain gradient elasticity can be computed from interatomic potentials to be a self-consistent and parameter-free field theory of materials [1, 40]. Moreover, the atomistic representation of the constitutive tensors in first strain gradient elasticity was given by Admal et al. [1]. The atomistic representations are analytical expressions in terms of the first and second derivatives of the interatomic potential with respect to interatomic distances, and dyadic products of relative atomic positions (see [1]).

First efforts toward dislocations in the framework of Mindlin’s strain gradient elasticity were carried out by Lardner [16] and Rogula [42], who considered screw and edge dislocations in the framework of Mindlin’s compatible strain gradient elasticity [32]. Considering neither plastic distortion nor dislocation density, Lardner [16] and Rogula [42] constructed solutions to a compatible elastic boundary value problem and consequently failed to remove the classical singularities.

More than two decades later, using a simplified theory of gradient elasticity with only one characteristic length scale parameter, non-singular elastic strain fields of screw and edge dislocations were given, for the first time, by Gutkin and Aifantis [8, 9]. Non-singular stress and strain fields of screw and edge dislocations based on a simplified gradient elasticity (or gradient elasticity of Helmholtz type) were given by Lazar and Maugin [18] (see also [19]). Simplified strain gradient elasticity is a particular version of Mindlin’s strain gradient elasticity where the double stress tensor can be expressed in a particular form in terms of the gradient of the Cauchy stress tensor (see, e.g., [18, 26]). Moreover, Lazar and Maugin [20] have shown for straight dislocations that the gradient terms with the characteristic length scale parameter lead to a smoothing of the displacement profile, in contrast with the jump occurring in the classical displacement field. Simplified incompatible gradient elasticity (gradient elasticity of Helmholtz type) provides robust non-singular solutions including one length scale parameter for the elastic distortion, plastic distortion, stress and displacement fields of screw and edge dislocations. An important mathematical property of gradient elasticity is that it provides a regularization based on partial differential equations (PDEs) of higher order where the characteristic length scale parameter plays the role of a regularization parameter. Afterward, the non-singular expressions of all dislocation key equations were given by Lazar [23,24,25] for dislocation loops using simplified gradient elasticity. For dislocations, the incompatible version of simplified gradient elasticity including plastic distortion and dislocation density tensors is used leading to an incompatible strain gradient elasticity of defects. These non-singular dislocation key equations (Burgers formula, Mura–Willis equation, and Peach–Koehler stress formula) have been implemented in the UCLA Discrete Dislocation Dynamics (DD) code called “model” [35] and used for applications [39]. The results of the dislocation fields in simplified gradient elasticity endow DD with a level of maturity that is necessary for computer simulations of three-dimensional dislocation ensembles with near atomic resolution. Therefore, the use of strain gradient elasticity theory for micromechanical problems of dislocations leads to non-singular and smooth dislocation fields, and in this way to an Ångström-mechanics of dislocations (see also [30]). Nevertheless, for a more realistic and physically based modeling of an edge dislocation due to its inherent asymmetry more than one characteristic length scale parameter is necessary, and this is exactly what Mindlin’s strain gradient elasticity offers.

Using an incompatible version of Mindlin’s strain gradient elasticity and the technique of Fourier transform, non-singular and smooth displacement fields of screw and edge dislocations have been recently reported by Delfani and Tavakol [3] and Delfani et al. [4], respectively. Delfani and Tavakol [3] and Delfani et al. [4] have reproduced the smoothing of the displacement profile of screw and edge dislocations. However, a systematic and complete study of screw and edge dislocations (including the elastic strain and stress fields) in the incompatible framework of Mindlin’s strain gradient elasticity is still missing in the literature. Therefore, the present work aims to close this gap in the literature of dislocations in strain gradient elasticity.

The purpose of the present work is to find solutions for the displacement, plastic distortion, dislocation density, stress and elastic distortion fields of screw and edge dislocations within the framework of incompatible isotropic strain gradient elasticity theory of Mindlin type. This is an unsolved fundamental problem for more than half a century. We will formulate the eigenstrain problem of dislocations in Mindlin’s isotropic gradient elasticity. Dislocation problems are typical examples of eigenstrain problems (see, e.g., [31, 36]). We will use the two-dimensional Green tensors (fundamental solutions of the Mindlin operator) to find non-singular dislocation fields for a given eigenstrain (or plastic distortion). Furthermore, we clarify the question of the influence on the dislocation solutions of different characteristic length scale parameters and the five gradient parameters of the incompatible isotropic strain gradient elasticity theory of Mindlin type and the similarities and differences to the dislocation solutions obtained in the framework of simplified incompatible strain gradient elasticity. For the numerical computations, the values of the five gradient parameters for aluminum will be used given by Shodja [45, 46] using atomistic ab initio DFT calculations.

The paper is organized as follows. In Sect. 2, we give the basics of incompatible strain gradient elasticity of Mindlin type including the relevant Green’s functions which are necessary to solve the field equations for prescribed plastic distortion of a dislocation. Using the technique of Green’s functions and convolution, solutions of screw and edge dislocations are presented in Sects. 3 and 4, respectively. The limit of the solutions of screw and edge dislocations in incompatible strain gradient elasticity of Mindlin type toward simplified incompatible gradient elasticity is given in Sect. 5. In Sect. 6, conclusions are given. Some technical details are reported in the “Appendix.”

2 Incompatible strain gradient elasticity of Mindlin type

In this Section, we present the structure and framework of the theory of incompatible strain gradient elasticity of Mindlin type, which is the incompatible generalization of Mindlin’s compatible first strain gradient elasticity and is suitable as defect theory at small scales down to the Ångström scale.

2.1 General form

Consider an infinite elastic body. In Mindlin’s theory of first strain gradient elasticity [32, 33], the strain energy density for centrosymmetric materials reads as

$$\begin{aligned} \mathcal {W}(\varvec{e},\varvec{\nabla }\varvec{e}) =\frac{1}{2}\, \mathbb {C}_{ijkl}e_{ij}e_{kl}+\frac{1}{2}\, \mathbb {D}_{ijmkln}\partial _m e_{ij} \partial _n e_{kl}\, . \end{aligned}$$
(1)

Here \(e_{ij}\) denotes the incompatible elastic strain tensor which is given by

$$\begin{aligned} e_{ij}=\frac{1}{2}\left( \beta _{ij}+\beta _{ji}\right) \, \end{aligned}$$
(2)

and is nothing but the symmetric part of the incompatible elastic distortion tensor

$$\begin{aligned} \beta _{ij}=\partial _j u_{i}-\beta ^{\mathrm {P}}_{ij}\,, \end{aligned}$$
(3)

which is given in terms of the gradient of the displacement vector \(u_i\) and the plastic distortion (or eigendistortion) tensor \(\beta ^{\mathrm {P}}_{ij}\).

Moreover, \(\mathbb {C}_{ijkl}\) is the fourth-rank matter tensor (constitutive tensor) of the elastic constants possessing the minor symmetries

$$\begin{aligned} \mathbb {C}_{ijkl}=\mathbb {C}_{jikl}=\mathbb {C}_{ijlk} \end{aligned}$$
(4)

and the major symmetry

$$\begin{aligned} \mathbb {C}_{ijkl}=\mathbb {C}_{klij}\,, \end{aligned}$$
(5)

whereas \(\mathbb {D}_{ijmkln}\) is the sixth-rank matter tensor (constitutive tensor) of the gradient elastic constants possessing the minor symmetries

$$\begin{aligned} \mathbb {D}_{ijmkln}=\mathbb {D}_{jimkln}=\mathbb {D}_{ijmlkn} \end{aligned}$$
(6)

and the major symmetry

$$\begin{aligned} \mathbb {D}_{ijmkln}=\mathbb {D}_{klnijm}\,. \end{aligned}$$
(7)

The quantities conjugate to the elastic strain tensor \(e_{ij}\) and the gradient of the elastic strain tensor \(\partial _m e_{ij}\) are the Cauchy stress tensor \(\sigma _{ij}\) and the double stress tensor \(\tau _{ijm}\), respectively. They are defined as

$$\begin{aligned} \sigma _{ij}&=\frac{\partial \mathcal {W}}{\partial e_{ij}} =\mathbb {C}_{ijkl}e_{kl}\, , \end{aligned}$$
(8)
$$\begin{aligned} \tau _{ijm}&=\frac{\partial \mathcal {W}}{\partial (\partial _m e_{ij})} = \mathbb {D}_{ijmkln} \partial _n e_{kl}\,. \end{aligned}$$
(9)

In dislocation theory, the dislocation density tensor is defined in terms of the incompatible plastic distortion tensor (see, e.g., [15, 25])

$$\begin{aligned} \alpha _{ij}=-\epsilon _{jkl}\partial _k\beta _{il}^{\mathrm {P}}\,, \end{aligned}$$
(10)

and in terms of the incompatible elastic distortion tensor

$$\begin{aligned} \alpha _{ij}=\epsilon _{jkl}\partial _k\beta _{il} \,, \end{aligned}$$
(11)

where \(\epsilon _{jkl}\) denotes the Levi-Civita tensor. In other words, the dislocation density tensor is the incompatibility tensor due to dislocations, and it gives the characteristic shape and size of the dislocation core. The dislocation density tensor satisfies the Bianchi identity of dislocations,

$$\begin{aligned} \partial _j\alpha _{ij}=0\,, \end{aligned}$$
(12)

which means that dislocations cannot end inside the body.

The condition of static equilibrium is expressed by the Euler–Lagrange equation, and it reads in first strain gradient elasticity

$$\begin{aligned} \frac{\delta \mathcal {W}}{\delta u_i}=\frac{\partial \mathcal {W}}{\partial u_i} -\partial _j\, \frac{\partial \mathcal {W}}{\partial (\partial _j u_i)} +\partial _k \partial _j\, \frac{\partial \mathcal {W}}{\partial (\partial _k \partial _j u_i)}=0\,. \end{aligned}$$
(13)

In terms of the Cauchy stress and double stress tensors, Eq. (13) takes the form [32]

$$\begin{aligned} \partial _j\big (\sigma _{ij}-\partial _k\tau _{ijk}\big )=0\, . \end{aligned}$$
(14)

Because dislocations cause self-stresses, no physical body forces are present in the equilibrium condition for dislocations. Dislocations belong to the category of eigenstrain problems (see [6, 36]).

2.2 Isotropic form

Consider now the isotropic version of Mindlin’s strain gradient elasticity theory of form II. Using SO(3)-invariance arguments, an isotropic matter tensor of rank 4, satisfying Eqs. (4) and (5), reads as

$$\begin{aligned} \mathbb {C}_{ijkl}=\lambda \delta _{ij}\delta _{kl} +\mu \big (\delta _{ik}\delta _{jl}+\delta _{il}\delta _{jk}\big )\,, \end{aligned}$$
(15)

where \(\lambda \) and \(\mu \) are the Lamé constants (elastic constants) and \(\delta _{ij}\) is the Kronecker symbol, and an isotropic matter tensor of rank 6, satisfying Eqs. (6) and (7), reads as

$$\begin{aligned} \mathbb {D}_{ijmkln}&=\frac{a_1}{2}\big (\delta _{ij}\delta _{km}\delta _{ln} +\delta _{ij}\delta _{kn}\delta _{lm} +\delta _{kl}\delta _{im}\delta _{jn} +\delta _{kl}\delta _{in}\delta _{jm}\big ) +2a_2\, \delta _{ij}\delta _{kl}\delta _{mn} \nonumber \\&\quad +\frac{a_3}{2}\big (\delta _{jk}\delta _{im}\delta _{ln} +\delta _{ik}\delta _{jm}\delta _{ln} +\delta _{il}\delta _{jm}\delta _{kn} +\delta _{jl}\delta _{im}\delta _{kn}\big ) +a_4\big (\delta _{il}\delta _{jk}\delta _{mn} +\delta _{ik}\delta _{jl}\delta _{mn}\big ) \nonumber \\&\quad +\frac{a_5}{2}\big (\delta _{jk}\delta _{in}\delta _{lm} +\delta _{ik}\delta _{jn}\delta _{lm} +\delta _{jl}\delta _{km}\delta _{in} +\delta _{il}\delta _{km}\delta _{jn}\big ) , \end{aligned}$$
(16)

where \(a_1\), \(a_2\), \(a_3\), \(a_4\), \(a_5\) are the five strain gradient parameters (or gradient elastic constants) in Mindlin’s isotropic first strain gradient elasticity theory [32] (see also [26, 33]).

For the isotropic case, the Cauchy stress tensor is given by

$$\begin{aligned} \sigma _{ij}= 2 \mu \, e_{ij} +\lambda \, \delta _{ij} e_{ll}, \end{aligned}$$
(17)

and the double stress tensor is given by

$$\begin{aligned} \tau _{ijk}&=\frac{a_1}{2} \big (\delta _{ik}\partial _j e_{ll}+\delta _{jk} \partial _i e_{ll}+2\delta _{ij} \partial _l e_{kl}\big ) +2 a_2 \delta _{ij} \partial _k e_{ll} \nonumber \\&\quad +a_3\big (\delta _{ik}\partial _l e_{jl}+\delta _{jk}\partial _l e_{il}\big ) +2 a_4 \partial _k e_{ij} +a_5 \big (\partial _i e_{jk}+\partial _j e_{ki}\big ) . \end{aligned}$$
(18)

Using Eqs. (2), (8), and (9), Eq. (14) can be cast in the following equation in terms of the displacement vector and the plastic distortion tensor:

$$\begin{aligned} L^{\text {M}}_{ik}\, u_k=\mu \big [1-\ell _2^2\Delta \big ]\big (\partial _l \beta ^{\mathrm {P}}_{il}+\partial _l \beta ^{\mathrm {P}}_{li}\big ) +\big [\lambda -(a_1+2a_2)\Delta \big ] \partial _i \beta ^{\mathrm {P}}_{ll} -(a_1+a_3+a_5) \partial _i \partial _k\partial _l \beta ^{\mathrm {P}}_{kl} \,, \end{aligned}$$
(19)

where \(L^{\text {M}}_{ik}\) denotes the tensorial linear partial differential operator arising in Mindlin’s first strain gradient elasticity called the Mindlin operator. The isotropic Mindlin operator (differential operator of fourth order) is given by

$$\begin{aligned} L_{ik}^\text {M}&= (\lambda +2\mu )\big [1-\ell _1^2\Delta \big ]\partial _i\partial _k +\mu \big [1-\ell _2^2\Delta \big ](\delta _{ik}\Delta -\partial _i\partial _k)\,, \end{aligned}$$
(20)

where \(\Delta \) indicates the Laplace operator (differential operator of second order) and the two characteristic lengths, defined in terms of the five gradient elastic constants and the two elastic constants (Lamé constants), which are known in isotropic compatible strain gradient elasticity of Mindlin type,

$$\begin{aligned} \ell _1^2&=\frac{2(a_1+a_2+a_3+a_4+a_5)}{\lambda +2\mu }\,, \end{aligned}$$
(21)
$$\begin{aligned} \ell _2^2&=\frac{a_3+2a_4+a_5}{2\mu }\,. \end{aligned}$$
(22)

The two characteristic lengths \(\ell _1\) and \(\ell _2\) are the length scales appearing in the isotropic Mindlin operator (20), and they are the characteristic length scales for the displacement vector \(u_k\). Therefore, the two characteristic lengths \(\ell _1\) and \(\ell _2\) are the length scales appearing in Mindlin’s isotropic compatible gradient elasticity (see [28, 32]). Also, it can be observed on the right-hand side of Eq. (19) that the gradient elastic constants \(a_1\), \(a_3\), and \(a_5\) play a particular role for the plastic distortion.

Now, we decompose the plastic distortion tensor \(\beta ^{\mathrm {P}}_{ij}\) into its deviatoric (traceless) part \(\mathring{\beta }_{ij}^{\mathrm {P}}\), which we call deviatoric plastic distortion tensor, and its trace \(\beta _{ll}^{\mathrm {P}}\), which is the plastic dilatation:

$$\begin{aligned} \beta _{ij}^{\mathrm {P}}=\mathring{\beta }_{ij}^{\mathrm {P}}+\frac{1}{3}\, \delta _{ij}\beta _{ll}^{\mathrm {P}}\end{aligned}$$
(23)

with \(\mathring{\beta }_{ll}^{\mathrm {P}}=0\). If we substitute the decomposition (23) into Eq. (19), the mathematical structure of the right-hand side of Eq. (19) becomes more visible,

$$\begin{aligned} L^{\text {M}}_{ik}\, u_k=\mu L_2 \big (\partial _l \mathring{\beta }^{\mathrm {P}}_{il}+\partial _l \mathring{\beta }^{\mathrm {P}}_{li}\big ) +\frac{1}{3}\, (2\mu +3\lambda ) L_3 \, \partial _i \beta ^{\mathrm {P}}_{ll} +2\mu (\ell _2^2 -\ell _4^2) \partial _i \partial _k\partial _l \mathring{\beta }^{\mathrm {P}}_{kl}\,, \end{aligned}$$
(24)

where the isotropic scalar Helmholtz operator (differential operator of second order) is defined by

$$\begin{aligned} L_j=1-\ell _j^2\Delta \,, \qquad \ell _j>0\,. \end{aligned}$$
(25)

Here, \(\ell _j\) are positive real length scale parameters. Sometimes, the differential operator (25) is called modified Helmholtz operator [49] or metaharmonic operator [37]. In Eq. (24), it becomes obvious that in isotropic incompatible strain gradient elasticity of Mindlin type, two additional characteristic lengths can be defined in terms of the five gradient elastic constants and the two elastic constants (Lamé constants), namely

$$\begin{aligned} \ell _3^2&=\frac{2(2a_1+3a_2+a_3+a_4+a_5)}{3\lambda +2\mu }\,, \end{aligned}$$
(26)
$$\begin{aligned} \ell _4^2&=\frac{a_1+2a_3+2a_4+2a_5}{2\mu }\,. \end{aligned}$$
(27)

The two characteristic lengths \(\ell _3\) and \(\ell _4\) are additional length scales due to the plastic distortion tensor appearing on the right-hand side of Eq. (24). The length scale \(\ell _3\) is the characteristic length of the plastic dilatation. On the other hand, the divergence of Eq. (24) gives

$$\begin{aligned} (2\mu +\lambda ) L_1 \Delta \partial _k u_k =\frac{1}{3}(2\mu +3\lambda ) L_3 \Delta \beta ^{\mathrm {P}}_{ll}+ 2\mu L_4 \partial _k\partial _l \mathring{\beta }^{\mathrm {P}}_{kl}\,. \end{aligned}$$
(28)

Moreover, Eq. (24) can be cast in the following form:

$$\begin{aligned} L^{\text {M}}_{ik}\, u_k+f_i=0 \end{aligned}$$
(29)

with the fictitious body force due to the plastic distortion

$$\begin{aligned} f_i= -\Big [ \mu L_2 \big (\partial _l \mathring{\beta }^{\mathrm {P}}_{il}+\partial _l \mathring{\beta }^{\mathrm {P}}_{li}\big ) +\frac{1}{3}\, (2\mu +3\lambda ) L_3 \, \partial _i \beta ^{\mathrm {P}}_{ll} +2\mu (\ell _2^2 -\ell _4^2) \partial _i \partial _k\partial _l \mathring{\beta }^{\mathrm {P}}_{kl} \Big ]\,. \end{aligned}$$
(30)

The difficulty in the theory of incompatible strain gradient elasticity of Mindlin type is that both fields, the displacement field \(u_k\) on the left-hand side and the plastic distortion \(\beta ^{\mathrm {P}}_{il}\) on the right-hand side of Eq. (19), are “a priori” unknown, and an operator decomposition of the Mindlin operator (20) might be helpful, which is given in the next Section.

2.3 Decomposition of the isotropic Mindlin operator

The operator decomposition used in incompatible strain gradient elasticity of Helmholtz type  [25] or in simplified strain gradient elasticity [43] is based on the decomposition of a partial differential equation (PDE) of higher order into a system of PDEs of lower order and on the property that the appearing differential operator can be decomposed into a product of differential operators of lower order. Here, we present such an operator decomposition valid in incompatible strain gradient elasticity of Mindlin type.

Because the Mindlin operator (20) is a decomposable linear partial differential operator, it can be decomposed into an inner product of two tensorial linear partial differential operators,

$$\begin{aligned} L^{\text {M}}_{ik}=L^{(0)}_{il}L^{\text {H}}_{lk}=L^{\text {H}}_{il}L^{(0)}_{lk}\,, \end{aligned}$$
(31)

where \(L^{(0)}_{il}\) is the isotropic Navier operator (differential operator of second order)

$$\begin{aligned} L^{(0)}_{ik}=(\lambda +2\mu )\partial _i\partial _k +\mu (\delta _{ik}\Delta -\partial _i\partial _k) \end{aligned}$$
(32)

and \(L^{\text {H}}_{lk}\) is a tensorial Helmholtz type operator (differential operator of second order) given by

$$\begin{aligned} L_{lk}^\text {H}=\delta _{lk}-\ell _1^2\partial _l\partial _k -\ell _2^2 (\delta _{lk}\Delta -\partial _l\partial _k) \,, \end{aligned}$$
(33)

which is the tensorial generalization of the scalar Helmholtz operator \(L=1-\ell ^2\Delta \). In the case that \(\ell _1=\ell _2=\ell \), it reduces to: \(L_{lk}^\text {H}=\delta _{lk}\big (1-\ell ^2\Delta \big )=\delta _{lk}L\).

Using the operator decomposition (31), the inhomogeneous PDE (29) of fourth order

$$\begin{aligned} L^{(0)}_{il}L^{\text {H}}_{lk}\, u_k+f_i=0\, \end{aligned}$$
(34)

might be decomposed into a system of PDEs of second order, namely the inhomogeneous tensorial Helmholtz type equation,

$$\begin{aligned} L^{\text {H}}_{lk}\, u_k=u_l^{(0)}, \end{aligned}$$
(35)

and the classical inhomogeneous Navier equation of incompatible elasticity or eigenstrain theory,

$$\begin{aligned} L^{(0)}_{il} u^{(0)}_l+f_i=0\,, \end{aligned}$$
(36)

where \(u^{(0)}_l\) is the classical displacement field and \(f_i\) is the fictitious body force due to the classical plastic distortion \(\beta ^{{\mathrm {P}}, 0}_{il}\) (see also [5])

$$\begin{aligned} f_i&=-\big [ \mu \big (\partial _l \beta ^{{\mathrm {P}},0}_{il}+\partial _l \beta ^{{\mathrm {P}},0}_{li}\big )+\lambda \partial _i \beta ^{{\mathrm {P}},0}_{ll}\big ] \nonumber \\&=-\Big [ \mu \big (\partial _l \mathring{\beta }^{{\mathrm {P}},0}_{il}+\partial _l \mathring{\beta }^{{\mathrm {P}},0}_{li}\big ) +\frac{1}{3}\, (2\mu +3\lambda ) \partial _i \beta ^{{\mathrm {P}},0}_{ll} \Big ] \,. \end{aligned}$$
(37)

Thus, Eq. (37) represents the body force equivalent for dislocations in the framework of eigenstrain.

By combining Eqs. (30) and (37), the following PDE results for the plastic distortion tensorFootnote 1:

$$\begin{aligned}&\mu L_2 \big (\partial _l \mathring{\beta }^{\mathrm {P}}_{il}+\partial _l \mathring{\beta }^{\mathrm {P}}_{li}\big ) +\frac{1}{3}\, (2\mu +3\lambda ) L_3\, \partial _i \beta ^{\mathrm {P}}_{ll} +2\mu (\ell _2^2 -\ell _4^2) \partial _i \partial _k\partial _l \mathring{\beta }^{\mathrm {P}}_{kl} \nonumber \\&\quad =\mu \big (\partial _l \mathring{\beta }^{{\mathrm {P}},0}_{il}+\partial _l \mathring{\beta }^{{\mathrm {P}},0}_{li}\big ) +\frac{1}{3} \,(2\mu +3\lambda ) \partial _i \beta ^{{\mathrm {P}},0}_{ll}\,. \end{aligned}$$
(38)

If the deviatoric plastic distortion is zero, then Eq. (38) simplifies for the plastic dilatation \(\beta ^{\mathrm {P}}_{ll}\) to an inhomogeneous Helmholtz equation with characteristic length scale \(\ell _3\):

$$\begin{aligned} L_3 \beta ^{\mathrm {P}}_{ll}=\beta ^{{\mathrm {P}},0}_{ll}\,. \end{aligned}$$
(39)

For instance, the length scale \(\ell _3\) is important for the plastic dilatation of a dilatation point defect (see, e.g., [29]). Substituting Eq. (38) into Eq. (24), we obtain the fundamental equation where the displacement vector \(u_k\) is determined by the classical plastic distortion tensor, which acts as prescribed plastic distortion,

$$\begin{aligned} L^{\text {M}}_{ik}\, u_k= \mu \big (\partial _l \beta ^{{\mathrm {P}},0}_{il}+\partial _l \beta ^{{\mathrm {P}},0}_{li}\big )+\lambda \partial _i \beta ^{{\mathrm {P}},0}_{ll}\,. \end{aligned}$$
(40)

The important consequence of the operator decomposition is that the displacement field \(u_k\) and the plastic distortion \(\beta ^{\mathrm {P}}_{ij}\) are obtained by the prescribed classical plastic distortion by solving the PDEs (40) and (38), respectively.

2.4 Green tensors of linear partial differential operators in incompatible strain gradient elasticity

In this Section, we present the Green tensors which arise from the dislocation problem in incompatible strain gradient elasticity of Mindlin type.

2.4.1 Green tensor of the isotropic Mindlin operator

First, we give the Green tensor of the Mindlin operator (20) for the case of an infinite isotropic medium needed for the solutions of the screw and edge dislocation problems. The Green tensor, which is the fundamental solution of the isotropic Mindlin operator (20), is defined by (see, e.g., [28])

$$\begin{aligned} L^{\text {M}}_{ik}G^{\text {M}}_{kj}(\varvec{R}) =-\delta _{ij} \delta (\varvec{R})\,, \end{aligned}$$
(41)

where \(\delta (.)\) is the Dirac delta function.

The two-dimensional Green tensor of the plane strain problem in Mindlin’s strain gradient elasticity is given by (see [14, 28, 42])

$$\begin{aligned} G^{\text {M}}_{ij}(\varvec{R})= \frac{1}{8\pi \mu }\, \Big [ \big (\delta _{ij}\Delta -\partial _i\partial _j\big ) A(R,\ell _2) +\frac{1-2\nu }{2(1-\nu )}\, \partial _i\partial _j A(R,\ell _1) \Big ] \end{aligned}$$
(42)

with the two scalar auxiliary functions

$$\begin{aligned} A(R,\ell _1)&=-\Big \{R^2\ln R -R^2+4\ell _1^2\, \big [\ln R+K_0\big (R/\ell _1\big )\big ]\Big \}\,, \end{aligned}$$
(43)
$$\begin{aligned} A(R,\ell _2)&=-\Big \{R^2\ln R -R^2+4\ell _2^2\, \big [\ln R+K_0\big (R/\ell _2\big )\big ]\Big \} \,, \end{aligned}$$
(44)

where \(i,j=x,y\) and \(\varvec{R}\in \mathbb R^2\). Here \(K_n\) is the modified Bessel function of the second kind of order n, and \(\nu \) indicates Poisson’s ratio.

For the anti-plane strain problem in Mindlin’s strain gradient elasticity, the Green function is defined by (see, e.g., [28])

$$\begin{aligned} L^{\text {M}}_{zz}G^{\text {M}}_{zz}(\varvec{R}) =-\delta (\varvec{R}) \end{aligned}$$
(45)

with the Mindlin operator of anti-plane strain depending only on the length \(\ell _2\),

$$\begin{aligned} L_{zz}^\text {M}&=\mu \big [1-\ell _2^2\Delta \big ] \Delta \,. \end{aligned}$$
(46)

For anti-plane strain, the two-dimensional Mindlin operator simplifies to the two-dimensional Laplace-Helmholtz operator. The two-dimensional Green tensor of the anti-plane strain problem in Mindlin’s strain gradient elasticity is given by (see [28])

$$\begin{aligned} G^{\text {M}}_{zz}(\varvec{R})=-&\frac{1}{2\pi \mu }\, \big [\ln R+K_0\big (R/\ell _2\big )\big ]\,, \end{aligned}$$
(47)

which is non-singular and finite. The gradient of the Green’s function (47) reads as

$$\begin{aligned} \partial _k G^{\text {M}}_{zz}(\varvec{R})=-&\frac{1}{2\pi \mu }\, \frac{R_k}{R^2} \Big (1-\frac{R}{\ell _2}K_1\big (R/\ell _2\big )\Big )\,, \end{aligned}$$
(48)

being non-singular, continuous and zero at \(R=0\).

2.4.2 Two-dimensional Green’s functions of the Helmholtz and bi-Helmholtz operators

The Green’s function of the Helmholtz operator (25) is defined by

$$\begin{aligned} L_j G^{L_j}=\delta (\varvec{R}), \end{aligned}$$
(49)

and its solution reads

$$\begin{aligned} G^{L_j}=\frac{1}{2\pi \ell _j^2}\, K_0(R/\ell _j)\,. \end{aligned}$$
(50)

The Green’s function of the bi-Helmholtz operator, which is the product of two Helmholtz operators, is defined by

$$\begin{aligned} L_i L_j G^{L_i L_j}=\delta (\varvec{R}) \end{aligned}$$
(51)

and reads (see, e.g., [21])

$$\begin{aligned} G^{L_i L_j}=\frac{1}{2\pi }\, \frac{1}{\ell _i^2-\ell _j^2}\, \big [K_0(R/\ell _i)-K_0(R/\ell _j)\big ] \end{aligned}$$
(52)

for \(i\ne j\). Of course, it yields

$$\begin{aligned} G^{L_i L_j}=G^{L_i}*G^{L_j}\,, \end{aligned}$$
(53)

where \(*\) denotes the convolution.

2.5 Solutions for the displacement vector and the plastic distortion tensor

Using the technique of Green’s functions, the solution of Eq. (40) reads for the displacement vector

$$\begin{aligned} u_i=-\mu \partial _k G^\text {M}_{ij}*\big (\beta ^{{\mathrm {P}},0}_{jk}+\beta ^{{\mathrm {P}},0}_{kj}\big ) -\lambda \partial _j G^\text {M}_{ij}*\beta ^{{\mathrm {P}},0}_{kk}\,. \end{aligned}$$
(54)

For the plastic distortion, Eq. (38) must be solved. The divergence of Eq. (38) yields

$$\begin{aligned} 2\mu L_4 \partial _k\partial _l \mathring{\beta }^{\mathrm {P}}_{kl} +\frac{1}{3}(2\mu +3\lambda ) L_3 \Delta \beta ^{\mathrm {P}}_{ll} = 2\mu \partial _k\partial _l \mathring{\beta }^{{\mathrm {P}},0}_{kl}+\frac{1}{3}(2\mu +3\lambda ) \Delta \beta ^{{\mathrm {P}},0}_{ll}\,. \end{aligned}$$
(55)

We consider dislocations that incur no volume change (dislocations of glide mode), so that the plastic dilatation must be zero,

$$\begin{aligned} \beta ^{\mathrm {P}}_{ll}=0\,, \end{aligned}$$
(56)

and the classical plastic dilatation must be zero,

$$\begin{aligned} \beta ^{{\mathrm {P}},0}_{ll}=0\,. \end{aligned}$$
(57)

That means that the plastic dilatation must be zero for dislocations of glide mode. Then, Eq. (55) reduces to

$$\begin{aligned} L_4 \partial _k\partial _l \mathring{\beta }^{\mathrm {P}}_{kl}&=\partial _k\partial _l \mathring{\beta }^{{\mathrm {P}},0}_{kl}, \end{aligned}$$
(58)

and the solution of Eq. (58) can be written as

$$\begin{aligned} \partial _k\partial _l \mathring{\beta }^{\mathrm {P}}_{kl}&=G^{L_4}*\partial _k\partial _l \mathring{\beta }^{{\mathrm {P}},0}_{kl}\,. \end{aligned}$$
(59)

If we substitute Eq. (59) into Eq. (38), under consideration of Eqs. (56) and (57), we obtain the following solution:

$$\begin{aligned} \partial _l \mathring{\beta }^{\mathrm {P}}_{il}+\partial _l \mathring{\beta }^{\mathrm {P}}_{li} =G^{L_2}*(\partial _l \mathring{\beta }^{{\mathrm {P}},0}_{il}+\partial _l \mathring{\beta }^{{\mathrm {P}},0}_{li}) -2(\ell _2^2-\ell _4^2) G^{L_2L_4}*\partial _i\partial _k\partial _l \mathring{\beta }^{{\mathrm {P}},0}_{kl}\,. \end{aligned}$$
(60)

Therefore, the solution for the divergence of the deviatoric plastic strain tensor is given by Eq. (60).

2.6 Material parameters

It is important to point out that both the elastic constants (\(\mu \), \(\lambda \)) and the gradient elastic constants (\(a_1\), \(a_2\), \(a_3\), \(a_4\), \(a_5\)) are characteristic material parameters which can be computed from interatomic potentials (e.g., [44]) or via ab initio DFT calculations (e.g., [45]). Therefore, the characteristic length scale parameters are also characteristic material parameters given in terms of the elastic constants and gradient elastic constants by Eqs. (21), (22), (26), and (27).

For the numerical analysis of the elastic and plastic fields produced by screw and edge dislocations, we choose aluminum (Al) which is a nearly isotropic material [2]. The Lamé constants, gradient elastic constants, characteristic lengths, equilibrium lattice parameter and Poisson’s ratio of aluminum, which have been calculated via ab initio DFT by Shodja et al. [45] and Shodja [46], are given in Table 1. It is interesting to note that the characteristic length \(\ell _2\) is the smallest one of the four characteristic lengths for aluminum given in Table 1. For the numerical analysis of screw and edge dislocations in Sects. 3, 4, and 5, we are using the material parameters given in Table 1.

Table 1 Lamé constants, gradient elastic constants, characteristic lengths, equilibrium lattice parameter and Poisson’s ratio for aluminum (Al) computed via ab initio DFT [45, 46]
Full size table

3 Screw dislocation

Consider a screw dislocation at the position \((x,y)=(0,0)\) whose Burgers vector \(b_z\) and dislocation line coincide with the z-axis of a Cartesian coordinate system. The problem of a screw dislocation is of anti-plane strain type.

For a screw dislocation, Eqs. (19), (38), and (40) simplify to

$$\begin{aligned} L^{\text {M}}_{zz} u_z&=\mu L_2 \partial _y \beta _{zy}^{{\mathrm {P}}}\,, \end{aligned}$$
(61)
$$\begin{aligned} L_2 \beta _{zy}^{{\mathrm {P}}}&=\beta _{zy}^{{\mathrm {P}},0}\ \end{aligned}$$
(62)

and

$$\begin{aligned} L^{\text {M}}_{zz} u_z&=\mu \partial _y \beta _{zy}^{{\mathrm {P}},0}\,, \end{aligned}$$
(63)

respectively.Footnote 2

For the classical plastic distortion of a screw dislocation, we choose the expression given by deWit [6] (see also [36])

$$\begin{aligned} \beta _{zy}^{{\mathrm {P}},0} =b_z \delta (y) H(-x)=b_z \delta (y)\int _x^{\infty } \delta (X)\,{\mathrm {d}}X\,, \end{aligned}$$
(64)

possessing a discontinuity at \(y=0\) for \(x<0\). Here H(.) is the Heaviside step function. The plastic distortion (64) is caused by a relative slip \(b_z\) on the half-plane (\(y=0\), \(x<0\)) in the z-direction. The classical plastic distortion (64) is concentrated on the slip plane (the semi-infinite part of the xz-plane for negative x). This causes singularities and discontinuities.

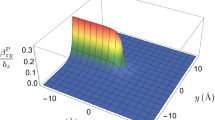
If we substitute Eq. (64) into Eq. (62) and use the Green’s function (50), the plastic distortion reads in incompatible strain gradient elasticity of Mindlin type

$$\begin{aligned} \beta _{zy}^{{\mathrm {P}}}&=G^{L_2}*\beta _{zy}^{{\mathrm {P}},0}\nonumber \\&=\frac{b_z}{2\pi \ell _2^2}\int _x^{\infty } K_0\big (\sqrt{X^2+y^2}/\ell _2\big )\, {\mathrm {d}}X\,, \end{aligned}$$
(65)

which is non-singular and finite as observed in Fig. 1. Unlike the classical plastic distortion (64), the plastic distortion (65) is a smooth and continuous function in strain gradient elasticity. In gradient elasticity, the plastic distortion is distributed, and as a result, singularities and discontinuities are avoided (see Fig. 1).

Fig. 1
figure 1

Plastic distortion \(\beta ^{\mathrm {P}}_{zy}\) of a screw dislocation in incompatible strain gradient elasticity of Mindlin type near the dislocation line

Full size image

The corresponding dislocation density of a screw dislocation reads as

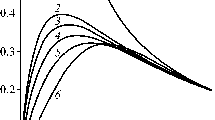
$$\begin{aligned} \alpha _{zz}&=-\partial _x \beta _{zy}^{{\mathrm {P}}}\nonumber \\&=G^{L_2}*\alpha _{zz}^{0}\nonumber \\&=\frac{b_z}{2\pi \ell _2^2}\, K_0\big (r/\ell _2\big )\,, \end{aligned}$$
(66)

where \(\alpha _{zz}^0=b_z\delta (x)\delta (y)\) is the classical dislocation density of a screw dislocation and \(r=\sqrt{x^2+y^2}\). The dislocation density (66) is plotted in Fig. 2, and it gives the shape and the size of the dislocation core of a screw dislocation. It can be seen that the dislocation core of a screw dislocation possesses a cylindrical symmetry. Such a shape of the dislocation core of a screw dislocation is physical because the Burgers vector, which is in z-direction, does not break the cylindrical symmetry of the dislocation core of a screw dislocation. Note that the dislocation density (66) possesses a logarithmic singularity at the dislocation line.

Fig. 2
figure 2

Contour plot of the dislocation density of a screw dislocation \(\alpha _{zz}\) (normalized by the Burgers vector \(b_z\)) in incompatible strain gradient elasticity of Mindlin type

Full size image

Substituting Eq. (64) into Eq. (63) and using the Green’s function (47), the displacement field \(u_z\) is calculated as

$$\begin{aligned} u_{z}&=-\mu \, \partial _y G^{\text {M}}_{zz}*\beta _{zy}^{{\mathrm {P}},0}\nonumber \\&=-\frac{b_z}{2\pi } \partial _y \int _x^{\infty } \left[ \ln \sqrt{X^2+y^2} +K_0\left( \sqrt{X^2+y^2}/\ell _2\right) \right] \, {\mathrm {d}}X\nonumber \\&=\frac{b_z}{2\pi } \left( \arctan \frac{y}{x}+\pi H(-x)\, \text {sgn}(y) +\partial _y \int _x^{\infty } K_0\left( \sqrt{X^2+y^2}/\ell _2\right) \, {\mathrm {d}}X \right) \,, \end{aligned}$$
(67)

where the first part in Eq. (67) is the angle \(\varphi \) with range (\(-\pi \), \(\pi \)], that is \(-\pi <\varphi \le \pi \), and discontinuity of \(2\pi \) across the negative x-axis (see also [6, 38])Footnote 3,

$$\begin{aligned} \varphi =\arctan \frac{y}{x}+\pi H(-x)\, \text {sgn}(y) \,. \end{aligned}$$
(68)

The displacement field (67) is plotted in Fig. 3. It is interesting to note that the displacement field (67) is non-singular and has a smooth form due to the superposition of the classical jump discontinuity (first term) and the gradient term (second term). This superposition gives a smoothing of the classical jump discontinuity present in Eq. (68). Therefore, while the displacement field of a screw dislocation in classical dislocation theory possesses a jump discontinuity at the branch cut or dislocation surface (\(y=0\) and \(x<0\)), the jump discontinuity has been smoothed out in strain gradient elasticity. This smoothing of the classical jump discontinuity (68) strongly depends on the value of the length scale parameter \(\ell _2\) and, in particular, on the ratio \(\ell _2/a\) and is a result of the convolution in Eq. (67). In the limit as \(\ell _2\rightarrow 0\), we recover the classical discontinuity in the displacement field. Note that the displacement field (67) is in agreement with the expression given in [3].

Fig. 3
figure 3

Displacement field \(u_z\) of a screw dislocation in incompatible strain gradient elasticity of Mindlin type near the dislocation line

Full size image
Fig. 4
figure 4

Elastic distortion of a screw dislocation in incompatible strain gradient elasticity of Mindlin type near the dislocation line: a \(\beta _{zx}\) and b \(\beta _{zy}\)

Full size image

For a screw dislocation, the non-vanishing components of the elastic distortion are calculated as

$$\begin{aligned} \beta _{zx}&=\mu b_z\partial _y G^\text {M}_{zz}=-\frac{b_z}{2\pi }\,\frac{y}{r^2}\bigg [1-\frac{r}{\ell _2}\, K_1(r/\ell _2 )\bigg ]\, , \end{aligned}$$
(69)
$$\begin{aligned} \beta _{zy}&=-\mu b_z\partial _x G^\text {M}_{zz}=\frac{b_z}{2\pi }\,\frac{x}{r^2}\bigg [1-\frac{r}{\ell _2}\, K_1(r/\ell _2 )\bigg ]\, . \end{aligned}$$
(70)

The components of the elastic distortion tensor, Eqs. (69) and (70), are plotted in Fig. 4a, b. It is evident that they are non-singular. The components (69) and (70) of the incompatible elastic distortion tensor satisfy the relation: \(\alpha _{zz}=\partial _x\beta _{zy}-\partial _y\beta _{zx}\). In the limit \(\ell _2\rightarrow 0\), the classical expressions given by deWit [6] are recovered in Eqs. (69) and (70). The non-vanishing components of the Cauchy stress tensor are given by: \(\sigma _{zx}=\mu \beta _{zx}\) and \(\sigma _{zy}=\mu \beta _{zy}\). All fields (displacement, elastic distortion, plastic distortion, stress, dislocation density) of a screw dislocation depend only on the characteristic length \(\ell _2\).

4 Edge dislocation

Consider an edge dislocation at the position \((x,y)=(0,0)\) whose Burgers vector \(b_x\) lies in x-direction and the dislocation line coincides with the z-axis of a Cartesian coordinate system. The problem of an edge dislocation is of plane strain type.

For the classical plastic distortion of an edge dislocation of glide mode, the expression given by deWit [6] (see also [36]) reads as

$$\begin{aligned} \beta _{xy}^{{\mathrm {P}},0} =b_x \delta (y) H(-x)=b_x \delta (y)\int _x^{\infty } \delta (X)\,{\mathrm {d}}X\,. \end{aligned}$$
(71)

The plastic distortion (71) is caused by a relative slip \(b_x\) on the half-plane (\(y=0\), \(x<0\)) in the x-direction.

Using Eq. (60), the non-vanishing component of the plastic distortion tensor can be written for an edge dislocation,

$$\begin{aligned} \beta ^{\mathrm {P}}_{xy}&=G^{L_2}*\beta ^{{\mathrm {P}},0}_{xy} -2(\ell _2^2-\ell _4^2) G^{L_2L_4}*\partial ^2_x \beta ^{{\mathrm {P}},0}_{xy}\nonumber \\&=G^{L_2}*\beta ^{{\mathrm {P}},0}_{xy} +2(\ell _2^2-\ell _4^2) \partial _x G^{L_2L_4}* \alpha ^{0}_{xz}, \end{aligned}$$
(72)

and the corresponding non-vanishing component of the dislocation density tensor reads

$$\begin{aligned} \alpha _{xz}&=-\partial _x\beta ^{\mathrm {P}}_{xy}\nonumber \\&=G^{L_2}*\alpha ^{0}_{xz} -2(\ell _2^2-\ell _4^2) \partial ^2_x G^{L_2L_4}* \alpha ^{0}_{xz} \,, \end{aligned}$$
(73)

where \(\alpha _{xz}^0=b_x\delta (x)\delta (y)\) is the classical dislocation density of an edge dislocation.

On the one hand, if we substitute Eq. (71) into Eq. (72) and use the Green’s functions (50) and (52), the plastic distortion of the edge dislocation reads in incompatible gradient elasticity of Mindlin type

$$\begin{aligned} \beta ^{\mathrm {P}}_{xy}&=\frac{b_x}{2\pi \ell _2^2}\int _x^{\infty } K_0\big (\sqrt{X^2+y^2}/\ell _2\big )\, {\mathrm {d}}X - \frac{b_x}{\pi } \, \frac{x}{r} \bigg [ \frac{1}{\ell _2}\, K_1(r/\ell _2)-\frac{1}{\ell _4}\, K_1(r/\ell _4) \bigg ] \,. \end{aligned}$$
(74)

Note that the plastic distortion (74) is non-singular and finite as observed in Fig. 5. It depends on the two characteristic lengths \(\ell _2\) and \(\ell _4\). Unlike the classical plastic distortion (71), the plastic distortion (74) is a smooth and continuous function in strain gradient elasticity. The first part in Eq. (74) has the same characteristic form as the plastic distortion of a screw dislocation given in Eq. (65).

Fig. 5
figure 5

Plastic distortion \(\beta ^{\mathrm {P}}_{xy}\) of an edge dislocation in incompatible strain gradient elasticity of Mindlin type near the dislocation line

Full size image

On the other hand, if we substitute Eq. (71) into Eq. (73) and use the Green’s functions (50) and (52), the dislocation density of the edge dislocation reads in incompatible gradient elasticity of Mindlin type

$$\begin{aligned} \alpha _{xz}=\frac{b_x}{2\pi \ell _2^2}\, K_0\big (r/\ell _2\big )&- \frac{b_x}{\pi } \bigg [ \frac{x^2}{r^2} \bigg (\frac{1}{\ell ^2_2}\,K_0(r/\ell _2)-\frac{1}{\ell ^2_4}\,K_0(r/\ell _4)\bigg ) \nonumber \\&\quad +\frac{x^2-y^2}{r^3} \bigg (\frac{1}{\ell _2}\, K_1(r/\ell _2)-\frac{1}{\ell _4}\, K_1(r/\ell _4)\bigg ) \bigg ] \,. \end{aligned}$$
(75)

The dislocation density (75) is plotted in Fig. 6, and it gives the shape and the size of the dislocation core of an edge dislocation. It depends on the two characteristic lengths \(\ell _2\) and \(\ell _4\). It can be seen that the dislocation core of an edge dislocation does not possess a cylindrical symmetry. Such a shape of the dislocation core of an edge dislocation is physical because the Burgers vector, which is in x-direction, breaks the cylindrical symmetry of the dislocation core of an edge dislocation toward an asymmetric dislocation core shape. Therefore, an edge dislocation possesses an inherent asymmetry. The first part in Eq. (75) has the same characteristic form as the dislocation density of a screw dislocation given in Eq. (66), whereas the second part in Eq. (75) produces the asymmetric form of the dislocation core of an edge dislocation. For the first time, the asymmetry of the dislocation core inherent in an edge dislocation is modeled in a generalized continuum theory with symmetric stresses revealing the advantage of the considered gradient theory. Until now, the modeling of an asymmetric dislocation core of an edge dislocation was only possible in the framework of the translation gauge theory of dislocations with asymmetric stresses (see [22]).

Fig. 6
figure 6

Contour plot of the dislocation density of an edge dislocation \(\alpha _{xz}\) (normalized by the Burgers vector \(b_x\)) in incompatible strain gradient elasticity of Mindlin type

Full size image

In order to get the displacement fields of an edge dislocation, the Green tensor (42) is used in Eq. (54) in addition to some mathematical manipulations like Eq. (A.4) and \(\alpha ^0_{xz}=-\partial _x\beta ^{{\mathrm {P}},0}_{zy}\). In this manner, the displacement fields may be expressed in terms of the auxiliary functions (43) and (44), and the Green’s function (47),

$$\begin{aligned} u_{x}&=-\mu \, \partial _y G_{zz}^\text {M}*\beta _{xy}^{{\mathrm {P}},0} -\frac{b_x}{4\pi } \bigg (\partial _y\partial _x A(r,\ell _2)-\frac{1-2\nu }{2(1-\nu )}\, \partial _y \partial _x A(r,\ell _1)\bigg ) \,, \end{aligned}$$
(76)
$$\begin{aligned} u_{y}&=\mu b_xG_{zz}^\text {M} -\frac{b_x}{4\pi } \bigg (\partial ^2_y A(r,\ell _2)-\frac{1-2\nu }{2(1-\nu )}\, \partial ^2_yA(r,\ell _1)\bigg )\,. \end{aligned}$$
(77)

Substituting Eq. (71) into Eq. (76) and using Eqs. (47) and (A.3) in Eqs. (76) and (77), the non-vanishing components of the displacement vector of an edge dislocation read explicitly

$$\begin{aligned} u_x&=\frac{b_x}{2\pi } \bigg [ \arctan \frac{y}{x}+\pi H(-x)\, \text {sgn}(y) +\partial _y \int _x^{\infty } K_0\big (\sqrt{X^2+y^2}/\ell _2\big ) \, {\mathrm {d}}X \nonumber \\&\quad +\frac{xy}{r^2} \bigg (1-\frac{4\ell _2^2}{r^2}+2K_2(r/\ell _2)\bigg ) -\frac{1-2\nu }{2(1-\nu )}\, \frac{xy}{r^2} \bigg (1-\frac{4\ell _1^2}{r^2}+2K_2(r/\ell _1)\bigg ) \bigg ] \,, \end{aligned}$$
(78)
$$\begin{aligned} u_{y}&=-\frac{b_x}{4\pi } \bigg [\frac{1-2\nu }{1-\nu } \bigg \{\ln r+K_0(r/\ell _1) -\frac{x^2-y^2}{r^2} \bigg (1-\frac{4\ell _1^2}{r^2}+2K_2(r/\ell _1)\bigg ) \bigg \} \nonumber \\&\qquad \qquad +\frac{x^2-y^2}{r^2} \bigg (1-\frac{4\ell _2^2}{r^2}+2K_2(r/\ell _2)\bigg ) \bigg ] \,. \end{aligned}$$
(79)

The displacement fields (78) and (79) are plotted in Fig. 7a, b. It is interesting to note that the displacement fields (78) and (79) are non-singular and smooth functions. The first part of Eq. (78) has the same characteristic form as the displacement field of a screw dislocation given in Eq. (67). The displacement fields (78) and (79) depend on the two characteristic lengths \(\ell _1\) and \(\ell _2\). Note that the displacement fields (78) and (79) agree with the expressions given in [4].

Fig. 7
figure 7

Displacement fields of an edge dislocation in incompatible strain gradient elasticity of Mindlin type near the dislocation line: a \(u_x\) and b \(u_y\)

Full size image

Substituting the plastic distortion (72), the gradient of the displacement fields (76) and (77) into Eq. (3), the incompatible elastic distortion follows as

$$\begin{aligned} \beta _{xx}&=\mu b_x\partial _y G_{zz}^\text {M} -\frac{b_x}{4\pi } \bigg (\partial _y\partial ^2_x A(r,\ell _2)-\frac{1-2\nu }{2(1-\nu )}\, \partial _y\partial ^2_x A(r,\ell _1)\bigg ) \,, \end{aligned}$$
(80)
$$\begin{aligned} \beta _{yy}&=\mu b_x \partial _y G_{zz}^\text {M} -\frac{b_x}{4\pi } \bigg (\partial ^3_y A(r,\ell _2)-\frac{1-2\nu }{2(1-\nu )}\, \partial _y^3 A(r,\ell _1)\bigg ) \,, \end{aligned}$$
(81)
$$\begin{aligned} \beta _{xy}&=-\mu b_x\partial _x G_{zz}^\text {M} -\frac{b_x}{4\pi } \bigg (\partial ^2_y \partial _x A(r,\ell _2)-\frac{1-2\nu }{2(1-\nu )}\, \partial ^2_y \partial _x A(r,\ell _1)\bigg ) -2b_x \big (\ell _2^2-\ell _4^2\big ) \partial _x G^{L_2L_4} \,, \end{aligned}$$
(82)
$$\begin{aligned} \beta _{yx}&=\mu b_x\partial _x G_{zz}^\text {M} -\frac{b_x}{4\pi } \bigg (\partial ^2_y \partial _x A(r,\ell _2)-\frac{1-2\nu }{2(1-\nu )}\, \partial ^2_y \partial _x A(r,\ell _1)\bigg ) \,. \end{aligned}$$
(83)

Using now Eq. (A.5) for the third-order derivatives, Eq. (48) for the gradient of the Green’s function \(G^\text {M}_{zz}\) and the Green’s function of the bi-Helmholtz operator (52), the non-vanishing components (80)–(83) of the incompatible elastic distortion tensor of an edge dislocation are found to be

$$\begin{aligned} \beta _{xx}&=-\frac{b_x}{4\pi (1-\nu )}\, \frac{y}{r^2} \bigg [(1-2\nu )+\frac{2x^2}{r^2}\nonumber \\&\quad -\,2(1-\nu )\bigg \{ \frac{3x^2-y^2}{r^2} \bigg (\frac{4\ell _2^2}{r^2}-2K_2(r/\ell _2)\bigg ) -\frac{x^2-y^2}{\ell _2 r}\,K_1(r/\ell _2)\bigg \} \nonumber \\&\quad +(1-2\nu )\bigg \{ \frac{3x^2-y^2}{r^2} \bigg (\frac{4\ell _1^2}{r^2}-2K_2(r/\ell _1)\bigg ) -\frac{2x^2}{\ell _1 r}\,K_1(r/\ell _1)\bigg \} \bigg ], \end{aligned}$$
(84)
$$\begin{aligned} \beta _{yy}&=-\frac{b_x}{4\pi (1-\nu )}\, \frac{y}{r^2} \bigg [(1-2\nu )-\frac{2x^2}{r^2}\nonumber \\&\quad +\,2(1-\nu )\bigg \{ \frac{3x^2-y^2}{r^2} \bigg (\frac{4\ell _2^2}{r^2}-2K_2(r/\ell _2)\bigg ) -\frac{x^2-y^2}{\ell _2 r}\,K_1(r/\ell _2)\bigg \} \nonumber \\&\quad -\,(1-2\nu )\bigg \{ \frac{3x^2-y^2}{r^2} \bigg (\frac{4\ell _1^2}{r^2}-2K_2(r/\ell _1)\bigg ) +\frac{2y^2}{\ell _1 r}\,K_1(r/\ell _1)\bigg \} \bigg ], \end{aligned}$$
(85)
$$\begin{aligned} \beta _{xy}&=\frac{b_x}{4\pi (1-\nu )}\, \frac{x}{r^2} \bigg [(3-2\nu )-\frac{2y^2}{r^2} +4(1-\nu ) \bigg \{ \frac{r}{\ell _2}\, K_1(r/\ell _2)-\frac{r}{\ell _4}\, K_1(r/\ell _4) \bigg \} \nonumber \\&\quad -\,2(1-\nu )\bigg \{ \frac{x^2-3y^2}{r^2} \bigg (\frac{4\ell _2^2}{r^2}-2K_2(r/\ell _2)\bigg ) +\frac{x^2+3y^2}{\ell _2 r}\,K_1(r/\ell _2)\bigg \} \nonumber \\&\quad +\,(1-2\nu )\bigg \{ \frac{x^2-3y^2}{r^2} \bigg (\frac{4\ell _1^2}{r^2}-2K_2(r/\ell _1)\bigg ) +\frac{2y^2}{\ell _1 r}\,K_1(r/\ell _1)\bigg \} \bigg ], \end{aligned}$$
(86)
$$\begin{aligned} \beta _{yx}&=-\frac{b_x}{4\pi (1-\nu )}\, \frac{x}{r^2} \bigg [(1-2\nu )+\frac{2y^2}{r^2}\nonumber \\&\quad +\,2(1-\nu )\bigg \{ \frac{x^2-3y^2}{r^2} \bigg (\frac{4\ell _2^2}{r^2}-2K_2(r/\ell _2)\bigg ) -\frac{x^2-y^2}{\ell _2 r}\,K_1(r/\ell _2)\bigg \} \nonumber \\&\quad -\,(1-2\nu )\bigg \{ \frac{x^2-3y^2}{r^2} \bigg (\frac{4\ell _1^2}{r^2}-2K_2(r/\ell _1)\bigg ) +\frac{2y^2}{\ell _1 r}\,K_1(r/\ell _1)\bigg \} \bigg ] . \end{aligned}$$
(87)

The components of the elastic distortion tensor, Eqs. (84)–(87), are plotted in Fig. 8a–d. It can be observed that they are non-singular and zero at the dislocation line. The elastic distortion fields, Eqs. (84)–(87), depend on the three characteristic lengths \(\ell _1\), \(\ell _2\), and \(\ell _4\). The component \(\beta _{xy}\) is larger than the other three components in the near field (see Fig. 8c). Note that the components (84) and (86) of the incompatible elastic distortion tensor satisfy the relation: \(\alpha _{xz}=\partial _x\beta _{xy}-\partial _y\beta _{xx}\).

Fig. 8
figure 8

Elastic distortion components of an edge dislocation in incompatible strain gradient elasticity of Mindlin type near the dislocation line: a \(\beta _{xx}\), b \(\beta _{yy}\), c \(\beta _{xy}\) and d \(\beta _{yx}\)

Full size image

The elastic dilatation, which is the trace of the elastic distortion tensor, reads

$$\begin{aligned} \beta _{ll}&=-\frac{b_x(1-2\nu )}{2\pi (1-\nu )}\, \frac{y}{r^2}\bigg [1-\frac{r}{\ell _1}\, K_1(r/\ell _1 )\bigg ]\,. \end{aligned}$$
(88)

The elastic rotation, which is the skew-symmetric part of the elastic distortion tensor, reads

$$\begin{aligned} \omega _{xy}&=\frac{b_x}{2\pi }\, \frac{x}{r^2}\bigg [1-\frac{r}{\ell _4}\, K_1(r/\ell _4 )\bigg ]\,. \end{aligned}$$
(89)

In Eqs. (88) and (89), one can see that in the case of an edge dislocation \(\ell _1\) and \(\ell _4\) are the characteristic lengths for the elastic dilatation and elastic rotation, respectively. The non-vanishing components of the elastic strain tensor are given by: \(e_{xx}=\beta _{xx}\), \(e_{yy}=\beta _{yy}\), and \(e_{xy}=\sigma _{xy}/(2\mu )\).

Substituting the symmetric part of the elastic distortion tensor given in Eqs. (84)–(87) and the elastic dilatation (88) into the Hooke’s law (17) and using the relation \(\lambda =2\mu \nu /(1-2\nu )\), the non-vanishing components of the Cauchy stress tensor of an edge dislocation are obtained as

$$\begin{aligned} \sigma _{xx}&=-\frac{\mu b_x}{2\pi (1-\nu )}\, \frac{y}{r^2} \bigg [\frac{3x^2+y^2}{r^2}-\frac{2\nu r}{\ell _1}\,K_1(r/\ell _1) \nonumber \\&\quad -2(1-\nu )\bigg \{ \frac{3x^2-y^2}{r^2} \bigg (\frac{4\ell _2^2}{r^2}-2K_2(r/\ell _2)\bigg ) -\frac{x^2-y^2}{\ell _2 r}\,K_1(r/\ell _2)\bigg \} \nonumber \\&\quad +(1-2\nu )\bigg \{ \frac{3x^2-y^2}{r^2} \bigg (\frac{4\ell _1^2}{r^2}-2K_2(r/\ell _1)\bigg ) -\frac{2x^2}{\ell _1 r}\,K_1(r/\ell _1)\bigg \} \bigg ] \,, \end{aligned}$$
(90)
$$\begin{aligned} \sigma _{yy}&=\frac{\mu b_x}{2\pi (1-\nu )}\, \frac{y}{r^2} \bigg [\frac{x^2-y^2}{r^2}+\frac{2\nu r}{\ell _1}\,K_1(r/\ell _1)\nonumber \\&\quad -2(1-\nu )\bigg \{ \frac{3x^2-y^2}{r^2} \bigg (\frac{4\ell _2^2}{r^2}-2K_2(r/\ell _2)\bigg ) -\frac{x^2-y^2}{\ell _2 r}\,K_1(r/\ell _2)\bigg \} \nonumber \\&\quad +(1-2\nu )\bigg \{ \frac{3x^2-y^2}{r^2} \bigg (\frac{4\ell _1^2}{r^2}-2K_2(r/\ell _1)\bigg ) +\frac{2y^2}{\ell _1 r}\,K_1(r/\ell _1)\bigg \} \bigg ] \,, \end{aligned}$$
(91)
$$\begin{aligned} \sigma _{xy}&=\frac{\mu b_x}{2\pi (1-\nu )}\, \frac{x}{r^2} \bigg [\frac{x^2-y^2}{r^2} +2(1-\nu ) \bigg \{ \frac{r}{\ell _2}\, K_1(r/\ell _2)-\frac{r}{\ell _4}\, K_1(r/\ell _4)\bigg \} \nonumber \\&\quad -2(1-\nu )\bigg \{ \frac{x^2-3y^2}{r^2} \bigg (\frac{4\ell _2^2}{r^2}-2K_2(r/\ell _2)\bigg ) +\frac{2y^2}{\ell _2 r}\,K_1(r/\ell _2)\bigg \} \nonumber \\&\quad +(1-2\nu )\bigg \{ \frac{x^2-3y^2}{r^2} \bigg (\frac{4\ell _1^2}{r^2}-2K_2(r/\ell _1)\bigg ) +\frac{2y^2}{\ell _1 r}\,K_1(r/\ell _1)\bigg \} \bigg ] \,, \end{aligned}$$
(92)
$$\begin{aligned} \sigma _{zz}&= -\frac{\mu \nu b_x}{\pi (1-\nu )}\, \frac{y}{r^2}\bigg [1-\frac{r}{\ell _1}\, K_1(r/\ell _1 )\bigg ] \,. \end{aligned}$$
(93)

The components of the Cauchy stress tensor, Eqs. (90)–(93), are plotted in Fig. 9a–d. It can be seen that they are non-singular. At the dislocation line, the stress is zero. The stress components, Eqs. (90)–(93), depend on the three characteristic lengths \(\ell _1\), \(\ell _2\), and \(\ell _4\). The component \(\sigma _{xx}\) is larger than the other three components in the near field (see Fig. 9a). Moreover, the contours of the non-zero components of the Cauchy stress tensor, Eqs. (90)–(93), are given in Fig. 10a–d. Using incompatible strain gradient elasticity of Mindlin type, the contours, as shown in Fig. 10a–d, are the non-singular versions of the classical contours (see, e.g., Hirth and Lothe [12]) in terms of three characteristic lengths. The component \(\sigma _{xx}\) possesses the characteristic butterfly shape (see Fig. 10a). Of course, the non-singular stresses caused by an edge dislocation are more “complex” due to the inherent asymmetry. Moreover, it is important to note that the non-singular stresses of an edge dislocation, Eqs. (90)–(93), are in good agreement with the stress fields of an edge dislocation in Al computed in atomistic simulations by Webb III et al. [48] using the discrete and Hardy expressions for \(\sigma _{ij}\).

Fig. 9
figure 9

Stress components of an edge dislocation in incompatible strain gradient elasticity of Mindlin type near the dislocation line: a \(\sigma _{xx}\), b \(\sigma _{yy}\), c \(\sigma _{xy}\), and d \(\sigma _{zz}\)

Full size image
Fig. 10
figure 10

Contours of equal stress about an edge dislocation in incompatible strain gradient elasticity of Mindlin type: a \(\sigma _{xx}/b_x\), b \(\sigma _{yy}/b_x\), c \(\sigma _{xy}/b_x\), and d \(\sigma _{zz}/b_x\)

Full size image

Last but not least, concerning the gradient of the elastic strain tensor and the double stress tensor, it should be noted that some components are non-singular and some other ones are singular, for instance, the gradient of elastic dilatation, \(\partial _i \beta _{ll}\), appearing in the double stress tensor (18), is still singular.

5 Screw and edge dislocations in simplified incompatible strain gradient elasticity

Now, we perform the limit from incompatible strain gradient elasticity of Mindlin type to simplified incompatible strain gradient elasticity (gradient elasticity of Helmholtz type) for the fields of screw and edge dislocations in order to check if the solutions in incompatible strain gradient elasticity of Mindlin type recover the correct ones in simplified incompatible strain gradient elasticity known in the literature. The limit to simplified incompatible strain gradient elasticity is given by [18, 28]

$$\begin{aligned} a_1=0\,,\quad a_2=\frac{\lambda \ell ^2}{2}\,,\quad a_3=0\,,\quad a_4=\mu \ell ^2\,,\quad a_5=0 \end{aligned}$$
(94)

and therefore

$$\begin{aligned} \ell _1=\ell _2=\ell _3=\ell _4=\ell \,. \end{aligned}$$
(95)

For the case of a screw dislocation, the limit reads as \(\ell _2=\ell \) in Eqs. (65), (66), (67), (69), and (70) leading to known results in the literature (see, e.g., [8, 11, 18, 24, 27]). Therefore, the dislocation fields of a screw dislocation in incompatible strain gradient elasticity of Mindlin type agree with the dislocation fields of a screw dislocation in simplified incompatible strain gradient elasticity.

In the limit to simplified incompatible gradient elasticity for an edge dislocation, the plastic distortion (74) simplifies to

$$\begin{aligned} \beta ^{\mathrm {P}}_{xy}&=\frac{b_x}{2\pi \ell ^2}\int _x^{\infty } K_0\big (\sqrt{X^2+y^2}/\ell \big )\, {\mathrm {d}}X, \end{aligned}$$
(96)

and the dislocation density (75) reduces to

$$\begin{aligned} \alpha _{xz}=\frac{b_x}{2\pi \ell ^2}\, K_0\big (r/\ell \big ) \,. \end{aligned}$$
(97)

Of course, Eq. (97) is in agreement with the expression given by Lazar and Maugin [20], Lazar [24, 27]. Equation (96) corresponds to the plastic field given in [20, 27] with a different branch cut.

The displacement fields (76) and (77) reduce to

$$\begin{aligned} u_x&=\frac{b_x}{4\pi (1-\nu )} \bigg [ 2(1-\nu )\bigg ( \arctan \frac{y}{x}+\pi H(-x)\, \text {sgn}(y) +\partial _y \int _x^{\infty } K_0\big (\sqrt{X^2+y^2}/\ell \big ) \, {\mathrm {d}}X \bigg ) \nonumber \\&\qquad \qquad +\frac{xy}{r^2} \bigg (1-\frac{4\ell ^2}{r^2}+2K_2(r/\ell )\bigg ) \bigg ] \,, \end{aligned}$$
(98)
$$\begin{aligned} u_{y}&=-\frac{b_x}{4\pi (1-\nu )} \bigg [ (1-2\nu ) \Big (\ln r+K_0(r/\ell )\Big ) +\frac{x^2-y^2}{2r^2} \bigg (1-\frac{4\ell ^2}{r^2}+2K_2(r/\ell )\bigg ) \bigg ]\,. \end{aligned}$$
(99)

Equation (98) is in agreement with the displacement field given in [20, 27] up to a different branch cut (see also [11]) and in full agreement with the displacement field given in [4]. Equation (99) agrees with the expression given in [4, 9, 11, 20, 27] up to a constant displacement. Note that the component (99) is the non-singular gradient version of the classical displacement field given in [12, 41].

Moreover, the incompatible elastic distortion fields (84)–(87) simplify to

$$\begin{aligned} \beta _{xx}&=-\frac{b_x}{4\pi (1-\nu )}\, \frac{y}{r^2} \bigg [(1-2\nu )+\frac{2x^2}{r^2} -\frac{3x^2-y^2}{r^2} \bigg (\frac{4\ell ^2}{r^2}-2K_2(r/\ell )\bigg ) -\frac{2(y^2-\nu r^2)}{\ell r }\, K_1(r/\ell ) \bigg ] \, , \end{aligned}$$
(100)
$$\begin{aligned} \beta _{yy}&=-\frac{b_x}{4\pi (1-\nu )}\, \frac{y}{r^2} \bigg [(1-2\nu )-\frac{2x^2}{r^2} +\frac{3x^2-y^2}{r^2} \bigg (\frac{4\ell ^2}{r^2}-2K_2(r/\ell )\bigg ) -\frac{2(x^2-\nu r^2)}{\ell r}\,K_1(r/\ell )\bigg ] \, , \end{aligned}$$
(101)
$$\begin{aligned} \beta _{xy}&=\frac{b_x}{4\pi (1-\nu )}\, \frac{x}{r^2} \bigg [(3-2\nu )-\frac{2y^2}{r^2} -\frac{x^2-3y^2}{r^2} \bigg (\frac{4\ell ^2}{r^2}-2K_2(r/\ell )\bigg ) -\frac{2\big (y^2+(1-\nu ) r^2\big )}{\ell r}\,K_1(r/\ell ) \bigg ] \, , \end{aligned}$$
(102)
$$\begin{aligned} \beta _{yx}&=-\frac{b_x}{4\pi (1-\nu )}\, \frac{x}{r^2} \bigg [(1-2\nu )+\frac{2y^2}{r^2} +\frac{x^2-3y^2}{r^2} \bigg (\frac{4\ell ^2}{r^2}-2K_2(r/\ell )\bigg ) -\frac{2\big (x^2-\nu r^2\big )}{\ell r}\,K_1(r/\ell ) \bigg ] \,, \end{aligned}$$
(103)

which agree with the formulas given by Lazar and Maugin [20], Lazar [24, 27]. The comparison of the non-zero components of the elastic distortion tensor of an edge dislocation in strain gradient elasticity of Mindlin type (Eqs. (84)–(87)), simplified strain gradient elasticity (Eqs. (100)–(103)), and classical incompatible elasticity is given in Fig. 11a–d. It is interesting to observe that all four components of the elastic distortion tensor of an edge dislocation using strain gradient elasticity of Mindlin type and simplified strain gradient elasticity are in good agreement, even the “strange" behavior (with two additional zeros) of the near field of the component \(\beta _{yy}\) is reproduced in both gradient theories (see Fig. 11b).

The stress fields (90)–(93) reduce to

$$\begin{aligned} \sigma _{xx}&=-\frac{\mu b_x}{2\pi (1-\nu )}\, \frac{y}{r^4} \bigg [(3x^2+y^2) -(3x^2-y^2) \bigg (\frac{4\ell ^2}{r^2}-2K_2(r/\ell )\bigg ) -\frac{2y^2r}{\ell }\, K_1(r/\ell ) \bigg ] \, , \end{aligned}$$
(104)
$$\begin{aligned} \sigma _{yy}&=\frac{\mu b_x}{2\pi (1-\nu )}\, \frac{y}{r^4} \bigg [(x^2-y^2) -(3x^2-y^2) \bigg (\frac{4\ell ^2}{r^2}-2K_2(r/\ell )\bigg ) +\frac{2x^2 r}{\ell }\, K_1(r/\ell ) \bigg ] \, , \end{aligned}$$
(105)
$$\begin{aligned} \sigma _{xy}&=\frac{\mu b_x}{2\pi (1-\nu )}\, \frac{x}{r^4} \bigg [(x^2-y^2) -(x^2-3y^2) \bigg (\frac{4\ell ^2}{r^2}-2K_2(r/\ell )\bigg ) -\frac{2y^2 r}{\ell }\, K_1(r/\ell ) \bigg ] \, , \end{aligned}$$
(106)
$$\begin{aligned} \sigma _{zz}&= -\frac{\mu \nu b_x}{\pi (1-\nu )}\, \frac{y}{r^2}\bigg [1-\frac{r}{\ell }\, K_1(r/\ell )\bigg ]\,, \end{aligned}$$
(107)

which are in agreement with the formulas given by Gutkin and Aifantis [10], Gutkin [11], Lazar and Maugin [18], and Lazar [27]. The contours of the non-zero components of the stress tensor, Eqs. (104)–(107), are given in Fig. 12a–d. If we compare Figs. 12a–c and 10a–c, it can be seen that the stress components \(\sigma _{xx}\), \(\sigma _{yy}\), and \(\sigma _{xy}\) possess a slightly different shape in the dislocation core region. In the dislocation core region, the stress components in Fig. 10a–c are weaker than the corresponding ones in Fig. 12a–c. Using simplified incompatible strain gradient elasticity, the contours, as shown in Fig. 12a–d, are the non-singular versions of the classical contours (see, e.g., Hirth and Lothe [12]) in terms of only one length scale \(\ell \). The characteristic butterfly shape of the component \(\sigma _{xx}\) is changing slightly its form in the dislocation core region (see Fig. 12a). If we compare Figs. 10b and 12b for the component \(\sigma _{yy}\), and Figs. 10c and 12c for the component \(\sigma _{xy}\), the Cauchy stress components, Eqs. (91) and (92), obtained in incompatible strain gradient elasticity of Mindlin type look more realistic and physical in the dislocation core region than the Cauchy stress components, Eqs. (105) and (106), obtained in simplified incompatible strain gradient elasticity. In particular, the “classical” contours of the stress components \(\sigma _{yy}\) and \(\sigma _{xy}\) at \(|x|=|y|\) of zero stress are slightly modified in the dislocation core region (see Fig. 12b, c).

Last but not least, the limit from simplified incompatible strain gradient elasticity to classical incompatible elasticity is given by \(\ell \rightarrow 0\) leading to the well-known results of screw and edge dislocations given by deWit [6].

Fig. 11
figure 11

Plots of the elastic distortion components of an edge dislocation in incompatible strain gradient elasticity of Mindlin type (Mindlin), simplified incompatible strain gradient elasticity (SGE) for \(\ell =\ell _2\) and classical incompatible elasticity (Classical): a \(\beta _{xx}/b_x\), b \(\beta _{yy}/b_x\), c \(\beta _{xy}/b_x\), and d \(\beta _{yx}/b_x\)

Full size image
Fig. 12
figure 12

Contours of equal stress about an edge dislocation in simplified incompatible strain gradient elasticity for \(\ell =\ell _2\): a \(\sigma _{xx}/b_x\), b \(\sigma _{yy}/b_x\), c \(\sigma _{xy}/b_x\), and d \(\sigma _{zz}/b_x\)

Full size image

6 Conclusions

The present paper solves the long-standing problem of dislocations in incompatible isotropic strain gradient elasticity theory of Mindlin type. Exact analytical solutions for the displacement fields, elastic distortions, Cauchy stresses, plastic distortions, and dislocation densities of screw and edge dislocations have been derived. The technique of Green’s functions for PDEs of higher order has been used. For the numerical study of the dislocation fields, elastic constants and strain gradient parameters for Al have been used taken from ab initio DFT calculations. As characteristic fact of incompatible gradient elasticity, the analytical solutions for the displacement fields, elastic distortions, stresses, plastic distortions of screw and edge dislocations are non-singular and finite and depend on the characteristic lengths of incompatible isotropic strain gradient elasticity of Mindlin type. The characteristic fields of a screw dislocation depend on one characteristic length \(\ell _2\), whereas the characteristic fields of an edge dislocation depend on up to three characteristic lengths \(\ell _1\), \(\ell _2\), and \(\ell _4\). The most important length for the characteristic dislocation profile of the displacement, plastic distortion and dislocation density fields of screw and edge dislocations is the characteristic length \(\ell _2\). The dependence of the dislocation fields on the characteristic length scale parameters is as follows:

Screw dislocation:

  • displacement field: \(u_z=u_z(\varvec{r}, \ell _2)\)

  • plastic distortion: \(\beta ^{\mathrm {P}}_{zy}=\beta ^{\mathrm {P}}_{zy}(\varvec{r}, \ell _2)\)

  • dislocation density: \(\alpha _{zz}=\alpha _{zz}(\varvec{r}, \ell _2)\)

  • incompatible elastic distortion: \(\beta _{ij}=\beta _{ij}(\varvec{r}, \ell _2)\)

  • Cauchy stress: \(\sigma _{ij}=\sigma _{ij}(\varvec{r}, \ell _2)\)

Edge dislocation:

  • displacement field: \(u_i=u_i(\varvec{r}, \ell _1, \ell _2)\)

  • plastic distortion: \(\beta ^{\mathrm {P}}_{xy}=\beta ^{\mathrm {P}}_{xy}(\varvec{r}, \ell _2, \ell _4)\)

  • dislocation density: \(\alpha _{xz}=\alpha _{xz}(\varvec{r}, \ell _2, \ell _4)\)

  • incompatible elastic distortion: \(\beta _{ij}=\beta _{ij}(\varvec{r}, \ell _1, \ell _2, \ell _4)\)

  • Cauchy stress: \(\sigma _{ij}=\sigma _{ij}(\varvec{r}, \ell _1, \ell _2, \ell _4)\).

The main feature of the obtained solutions of screw and edge dislocations is the absence of any singularity in the displacement, elastic distortion, plastic distortion and stress fields. For a screw dislocation, all the dislocation fields (displacement, elastic distortion, Cauchy stress, plastic distortion, and dislocation density) obtained in incompatible strain gradient elasticity of Mindlin type agree with the corresponding ones in simplified incompatible strain gradient elasticity. In the case of an edge dislocation, all the dislocation fields (displacement, elastic distortion, Cauchy stress, plastic distortion, and dislocation density) obtained in incompatible strain gradient elasticity of Mindlin type are different, presenting more features than the corresponding ones in simplified incompatible strain gradient elasticity. For instance, the Cauchy stress of an edge dislocation obtained in incompatible isotropic strain gradient elasticity of Mindlin type looks more physical and more realistic in the dislocation core region than the Cauchy stress obtained in simplified incompatible strain gradient elasticity and is in agreement with the stress around the core of an edge dislocation in Al computed in atomistic simulations. In general, the dislocation core appears naturally in incompatible strain gradient elasticity and is characterized by the dislocation density tensor, which has the physical meaning of a dislocation core tensor. The most exciting fact is that the shape of the dislocation core of an edge dislocation has a more realistic asymmetric form due to its inherent asymmetry in incompatible isotropic strain gradient elasticity of Mindlin type than the dislocation core shape possessing cylindrical symmetry in simplified incompatible strain gradient elasticity. Incompatible isotropic strain gradient elasticity of Mindlin type is a generalized continuum theory with symmetric stress which gives an asymmetric dislocation core for an edge dislocation, and it captures the plastic phenomenon more realistically. Therefore, incompatible strain gradient elasticity of Mindlin type with several characteristic length scale parameters is able to model an edge dislocation more realistically in the dislocation core region than simplified incompatible gradient elasticity with only one length scale. Moreover, incompatible strain gradient elasticity of Mindlin type delivers a better physical based regularization than the regularization with only one regularization parameter in simplified incompatible gradient elasticity. From the dislocation fields obtained in incompatible isotropic strain gradient elasticity theory of Mindlin type, the correct limits for the dislocation fields obtained in simplified incompatible gradient elasticity have been recovered.