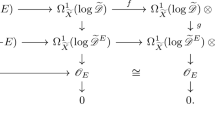Framed sheaves on projective space and Quot schemes

Abstract

We prove that, given integers $m\ge 3$, $r\ge 1$ and $n\ge 0$, the moduli space of torsion free sheaves on ${\mathbb {P}}^m$ with Chern character $(r,0,\ldots ,0,-n)$ that are trivial along a hyperplane $D \subset {\mathbb {P}}^m$ is isomorphic to the Quot scheme $\mathrm{Quot}_{{\mathbb {A}}^m}({\mathscr {O}}^{\oplus r},n)$ of 0-dimensional length n quotients of the free sheaf ${\mathscr {O}}^{\oplus r}$ on ${\mathbb {A}}^m$. The proof goes by comparing the two tangent-obstruction theories on these moduli spaces.

1 Introduction

This paper builds an identification between two classical moduli spaces in algebraic geometry: the moduli space of framed sheaves on projective space ${\mathbb {P}}^m$ and Grothendieck’s Quot scheme. Unless stated otherwise, we work over an algebraically closed field $\mathbf {k}$ of characteristic 0. If $D\subset Y$ is a divisor on a projective variety Y, a D-framed sheaf on Y is a pair $(E,\phi )$ where E is a torsion free sheaf on Y and $\phi$ is an isomorphism $E|_D \,\widetilde{\rightarrow }\,\mathscr {O}_D^{\oplus r}$, where $r = \text {rk}E$. Such pairs $(E,\phi )$ are a special case of the more general notion of framed modules introduced by Huybrechts–Lehn [16].

For a fixed coherent sheaf V on Y, the Quot scheme $\mathrm{Quot}_Y(V,P)$ parametrises quotients $V\twoheadrightarrow Q$ such that Q has Hilbert polynomial P. If P is a constant polynomial, the Quot scheme also exists (as a quasiprojective scheme) for quasiprojective varieties. For instance, if $P=n \in {\mathbb {Z}}_{\ge 0}$, we have a natural open immersion $\mathrm{Quot}_{{\mathbb {A}}^m}(\mathscr {O}^{\oplus r},n) \hookrightarrow \mathrm{Quot}_{{\mathbb {P}}^m}(\mathscr {O}^{\oplus r},n)$.

The following is the main result of this paper, proved in Theorem 2.7 in the main body of the text.

Theorem A

Fix integers $m\ge 2,$ $r\ge 1$ and $n\ge 0$. Fix a hyperplane $D\subset {\mathbb {P}}^m$. Let ${\mathrm {Fr}}_{r,n}({\mathbb {P}}^m)$ be the moduli space of D-framed sheaves on ${\mathbb {P}}^m$ with Chern character $(r,0,\ldots ,0,-n)$. There is an injective morphism

$$\begin{aligned} \eta :\mathrm{Quot}_{{\mathbb {A}}^m}(\mathscr {O}^{\oplus r},n) \rightarrow {\mathrm {Fr}}_{r,n}({\mathbb {P}}^m) \end{aligned}$$

which is an isomorphism if and only if $m\ge 3$ or $(m,r)=(2,1)$.

The map $\eta$, constructed in Proposition 2.3, is defined on closed points by

where Q is a 0-dimensional coherent sheaf on ${\mathbb {P}}^m$ supported away from D. The fact that $\eta$ is not an isomorphism for $m=2$ (unless $r=1$) ultimately depends on the fact that on ${\mathbb {P}}^2$ there are nontrivial vector bundles that are trivial on a line: this says that given a framed sheaf $(E,\phi )$ of rank $r>1$ on ${\mathbb {P}}^2$, one may not be able to reconstruct an embedding $i:E \hookrightarrow \mathscr {O}_{{\mathbb {P}}^2}^{\oplus r}$, and this prevents $\eta$ from being surjective. In fact, the moduli space ${\mathrm {Fr}}_{r,n}({\mathbb {P}}^2)$ is a smooth variety of dimension 2nr containing $\mathrm{Quot}_{{\mathbb {A}}^2}(\mathscr {O}^{\oplus r},n)$ as an irreducible subvariety of dimension $(r+1)n$, which is singular as soon as $r,n>1$ (Example 3.3).

Donaldson [10] constructed a canonical identification between the moduli space of instantons on $S^{4}={\mathbb {R}}^4 \cup \{\infty \}$ with SU(r)-framing at $\infty$ and the moduli space of rank r holomorphic vector bundles on ${\mathbb {P}}^2$ trivial on a line $\ell _{\infty }$. He defined a partial compactification of the moduli space on the 4-manifold side of the correspondence by allowing connections acquiring singularities. This in turn corresponds to considering torsion free sheaves on the algebro-geometric side, leading to the study of ${\mathrm {Fr}}_{r,n}({\mathbb {P}}^2)$.

The 3-dimensional analogue of Donaldson’s construction has attracted lots of attention in string theory and hence, after translating in the language of algebraic geometry, in Donaldson–Thomas theory. For instance, in the work of Cirafici–Sinkovics–Szabo [8, Sec. 4.1], the authors construct a correspondence between non-commutative U(r)-instantons on ${\mathbb {A}}^3$ and the 3-dimensional analogue of Donaldson’s construction, namely the moduli space ${\mathrm {Fr}}_{r,n}({\mathbb {P}}^3)$. They relate the construction to the quiver gauge theory of the ‘r-framed 3-loop quiver’ (Fig. 1), which corresponds to $\mathrm{Quot}_{{\mathbb {A}}^3}(\mathscr {O}^{\oplus r},n)$ in a precise sense [2]. We briefly review this story in Sect. 3. Moreover, the very same quiver gauge theory can be derived from the rank r Donaldson–Thomas theory of ${\mathbb {A}}^4$, as shown by Nekrasov and Piazzalunga in [19]. Theorem A formalises this correspondence from an algebraic perspective in the 3-dimensional case, and extends it to higher dimensions.

Framed sheaves and framed modules were mostly studied on surfaces. We do not aim at giving an exhaustive list of references, but we refer the reader to [4, 26] for a more complete bibliography. Framed sheaves were also studied on 3-folds by Oprea [20], where a symmetric obstruction theory on their moduli space is constructed—we end Sect. 2 with a conjecture suggesting that Oprea’s obstruction theory might take a very explicit form (Conjecture 2.12). Quot schemes also received a lot of attention lately in enumerative geometry [13, 21, 23, 25], and in the context of motivic invariants [9, 17, 24].

2 Framed modules and framed sheaves

In this section we briefly review the notion of stability on framed modules introduced by Huybrechts–Lehn [16], and we show that D-framed sheaves on ${\mathbb {P}}^m$ (Definition 1.4) are stable with respect to a suitable choice of stability parameters (Lemma 1.7). This implies the representability of their moduli functor.

2.1 Framed modules after Huybrechts–Lehn

Let Y be a smooth projective variety over an algebraically closed field $\mathbf {k}$ of characteristic 0, and let H be an ample divisor on Y. Fix a coherent sheaf G on Y. A framed module on Y, with ‘framing datum’ G, is a pair $(E,\alpha )$, where E is a coherent sheaf on Y and $\alpha :E \rightarrow G$ is a homomorphism of $\mathscr {O}_Y$-modules. The map $\alpha$ is called the framing, whereas $\ker \alpha$ (resp. $\text {rk}E$) is called the kernel (resp. the rank) of the framed module. Set $\epsilon (\alpha ) = 1$ if $\alpha \ne 0$ and $\epsilon (\alpha )=0$ otherwise.

The Hilbert polynomial of a coherent sheaf E, with respect to H, is defined as $P_E(k) = \chi (E(k))$, where $E(k) = E\otimes \mathscr {O}_Y(kH)$. Fix a polynomial $\delta \in {\mathbb {Q}}[k]$ with positive leading coefficient. The framed Hilbert polynomial of a framed module $(E,\alpha )$, depending on the pair $(H,\delta )$, is defined as

$$\begin{aligned} P_{(E,\alpha )} = P_E - \epsilon (\alpha )\delta . \end{aligned}$$

(1.1)

If $j:E'\hookrightarrow E$ is an $\mathscr {O}_Y$-submodule, there is an induced framing $\alpha ' = \alpha \circ j:E' \rightarrow G$. Note that

$$\begin{aligned} \epsilon (\alpha ') = {\left\{ \begin{array}{ll} 1 &{} \text {if }E' \nsubseteq \ker \alpha \\ 0 &{} \text {if }E' \subseteq \ker \alpha . \end{array}\right. } \end{aligned}$$

Definition 1.1

[16, Def. 1.1] A framed module $(E,\alpha )$ of rank r is $\delta$-semistable if for every submodule $E' \hookrightarrow E$ of rank $r'$, with induced framing $\alpha '$, one has $rP_{(E',\alpha ')}\le r'P_{(E,\alpha )}$. We say that $(E,\alpha )$ is $\delta$-stable if the same holds with ‘<’ replacing ‘$\le$’.

Huybrechts and Lehn defined moduli functors

$$\begin{aligned} {\mathcal {M}}_\delta ^{{\mathrm {st}}}(Y;G,P)\,\subseteq \,{\mathcal {M}}_\delta ^{{\text {ss}}}(Y;G,P) \end{aligned}$$

parametrising isomorphism classes of flat families of $\delta$-(semi)stable framed modules with framing datum G and framed Hilbert polynomial $P \in {\mathbb {Q}}[k]$.

As proved in [16, Lemma 1.7], if $\deg \delta \ge m = \dim Y$ then in every semistable framed module $(E,\alpha )$ the framing $\alpha$ either vanishes or is injective, thus the study of $\delta$-semistable framed modules reduces to Grothendieck’s theory of the Quot scheme. Thus one focuses on the case $\deg \delta = m-1$, writing

$$\begin{aligned} \delta (k) = \delta _1\frac{k^{m-1}}{(m-1)!} + \delta _2\frac{k^{m-2}}{(m-2)!} + \cdots + \delta _m,\quad \delta _1>0. \end{aligned}$$

(1.2)

Huybrechts and Lehn defined the $(H,\delta )$-slope of a framed module $(E,\alpha )$ with positive rank as the ratio

$$\begin{aligned} \mu _{(H,\delta )}(E,\alpha ) = \frac{c_1(E) \cdot H^{m-1}-\epsilon (\alpha )\delta _1}{\text {rk}E}. \end{aligned}$$

(1.3)

Definition 1.2

[16, Def. 1.8] A framed module $(E,\alpha )$ of positive rank $r = \text {rk}E$ is said to be $\mu$-semistable with respect to $\delta _1$ if $\ker \alpha$ is torsion free and for every submodule $E' \hookrightarrow E$, with $0< \text {rk}E' < r$, one has $\mu _{(H,\delta )}(E',\alpha ')\le \mu _{(H,\delta )}(E,\alpha )$. Stability is defined replacing ‘$\le$’ with ‘<’.

For framed modules of positive rank, such as those studied in this paper, one has that $\mu$-stability with respect to $\delta _1$ implies $\delta$-stability. Also note that a rank 1 framed module $(E,\alpha )$ with E torsion free is $\mu$-stable for any choice of $(H,\delta )$.

The notion which behaves best in the sense of moduli is $\delta$-stability. We now recall the part of the main theorem of [16] which is relevant for our paper.

Theorem 1.3

[16, Thm. 0.1] Let $\delta \in {\mathbb {Q}}[k]$ be as in (1.2). Fix $G \in \mathrm{Coh}\, Y$ and $P \in {\mathbb {Q}}[k]$. There exists a quasiprojective fine moduli scheme $M_{\delta }^{{\mathrm {st}}}(Y;G,P)$ representing the functor ${\mathcal {M}}_\delta ^{{\mathrm {st}}}(Y;G,P)$ of isomorphism classes of $\delta$-stable framed modules with framing datum G and framed Hilbert polynomial P.

2.2 Framed sheaves on projective spaces

Fix a hyperplane $\iota :D \hookrightarrow {\mathbb {P}}^m$, with $m\ge 2$, and the polarisation $H=\mathscr {O}_{{\mathbb {P}}^m}(1)$. Of course D is linearly equivalent to H, so in particular we have $D\cdot H^{m-1} = 1$, but we distinguish them as they play different roles.

Indeed, as framing datum we fix the coherent sheaf

$$\begin{aligned} G = \iota _*\mathscr {O}_D^{\oplus r}, \end{aligned}$$

for a fixed integer $r\ge 1$. Note that the framings $\alpha \in {\text {Hom}}(E,G)$ naturally correspond to morphisms $\phi _\alpha :E|_D \rightarrow \mathscr {O}_D^{\oplus r}$ via the adjunction $\iota ^*\dashv \iota _*$.

Fix an integer $n \ge 0$. Consider the Chern character

$$\begin{aligned} v_{r,n} = (r,0,\ldots ,0,-n)\,\in \,{\mathrm {H}}^{*}({\mathbb {P}}^m,{\mathbb {Z}}). \end{aligned}$$

Definition 1.4

Let $m\ge 2$ be an integer. A D-framed sheaf of rank r on ${\mathbb {P}}^m$ is a framed module $(E,\alpha )$ on ${\mathbb {P}}^m$ with framing datum $G=\iota _*\mathscr {O}_D^{\oplus r}$, such that E is torsion free with Chern character ${\mathrm {ch}}(E) = v_{r,n}$ for some $n\ge 0$, and the morphism $\phi _\alpha :E|_D \rightarrow \mathscr {O}_D^{\oplus r}$ induced by the framing $\alpha$ is an isomorphism.

Note that, for a D-framed sheaf $(E,\alpha )$, the torsion free sheaf E is locally free in a neighborhood of D, and the canonical map $E \hookrightarrow E^{\vee \vee }$ is an isomorphism in a neighborhood of D.

We will make crucial use of the following result due to Abe and Yoshinaga.

Theorem 1.5

[1, Thm. 0.2] Let F be a reflexive sheaf of positive rank on ${\mathbb {P}}^{m},$ where $m\ge 3$. Then F splits into a direct sum of line bundles if and only if there exists a hyperplane $D \subset {\mathbb {P}}^m$ such that $F|_{D}$ splits into a direct sum of line bundles.

Corollary 1.6

Let $(E,\alpha )$ be a D-framed sheaf of rank r on ${\mathbb {P}}^{m},$ with $m\ge 3,$ such that ${\mathrm {ch}}(E) = v_{r,n}$. Then there is a natural short exact sequence of sheaves

$$\begin{aligned} 0 \rightarrow E \rightarrow \mathscr {O}_{{\mathbb {P}}^{m}}^{\oplus r} \rightarrow Q \rightarrow 0 \end{aligned}$$

(1.4)

where Q has finite support contained in ${\mathbb {A}}^{m}={\mathbb {P}}^{m}{\setminus } D$.

Proof

Since E is torsion free, the natural map $E \rightarrow E^{\vee \vee }$ to its double dual is injective. Moreover, $E^{\vee \vee }$ is reflexive and $\alpha$ induces a canonical isomorphism $E^{\vee \vee }|_{D}\cong \mathscr {O}_{D}^{\oplus r}$. By Theorem 1.5 we have that $E^{\vee \vee }$ splits as a direct sum of line bundles, and it is immediate to see that these line bundles are necessarily trivial. This yields an isomorphism $E^{\vee \vee }\cong \mathscr {O}_{{\mathbb {P}}^{m}}^{\oplus r}$, and since $E|_{D}\cong \mathscr {O}_{D}^{\oplus r}$ it follows that the quotient $Q = \mathscr {O}_{{\mathbb {P}}^{m}}^{\oplus r}/E$ is supported on finitely many points lying in ${\mathbb {P}}^{m}{\setminus } D$. $\square$

In the case of projective surfaces it has been proved by Bruzzo and Markushevich that $\mu _{(H,\delta )}$-stability is automatically implied when considering a “good framing” [4, Thm. 3.1]. The strategy of the proof does not extend in full generality to higher dimensional varieties, as observed by Oprea [20]. We shall now provide a new argument for the particular case at hand, but it is still an open question whether it is possible to extend the result to more general settings.

Lemma 1.7

Fix integers $m\ge 3,$ and $r\ge 1$. Let $(E,\alpha )$ be a D-framed sheaf of rank r on ${\mathbb {P}}^{m},$ and consider a polynomial $\delta$ as in (1.2),  such that $0< \delta _1 < r$. Then $(E,\alpha )$ is $\mu$-stable with respect to $\delta _1,$ thus in particular it is $\delta$-stable.

Proof

First of all, since $c_1(E) = 0$ and $\epsilon (\alpha )=1$, the $(H,\delta )$-slope of $(E,\alpha )$ defined in Eq. (1.3) is

$$\begin{aligned} \mu _{(H,\delta )}(E,\alpha ) = - \frac{\delta _1}{r}. \end{aligned}$$

(1.5)

Clearly $\ker \alpha \hookrightarrow E$ is torsion free because E is torsion free by definition. Moreover, by means of the diagram

we deduce that $\ker \alpha = E(-D)$.

If $r=1$ there is nothing left to prove, so we can assume $r>1$. Fix a submodule $E' \hookrightarrow E$ of rank $r'$, where $0<r'<r$. By Corollary 1.6, we have an inclusion $E' \hookrightarrow E \hookrightarrow \mathscr {O}_{{\mathbb {P}}^m}^{\oplus r}$. Since $\mathscr {O}_{{\mathbb {P}}^m}^{\oplus r}$ is $\mu _H$-semistable of slope 0, we have $\mu _H(E') \le 0$. We now have to distinguish two cases:

• (1) $E'\nsubseteq \ker \alpha$. This means $\epsilon (\alpha ') = 1$, where $\alpha ' :E' \hookrightarrow E \rightarrow \iota _*\mathscr {O}_D^{\oplus r}$ is the induced framing on $E'$. We have the sought after inequality

  $$\begin{aligned} \mu _{(H,\delta )}(E',\alpha ') = \frac{c_1(E')\cdot H^{m-1}-\delta _1}{r'} = \mu _H(E')-\frac{\delta _1}{r'} < -\frac{\delta _1}{r} \end{aligned}$$

  if and only if $\mu _H(E') < \delta _1(1/r'-1/r)$. But since $\delta _1>0$ and $r'<r$ we have $\delta _1(1/r'-1/r)>0$. Since $E'$ embeds in the $\mu _H$-semistable module $\mathscr {O}_{{\mathbb {P}}^m}^{\oplus r}$, necessarily $\mu _H(E') \le 0 < \delta _1(1/r'-1/r)$, as claimed.

• (2) $E' \subseteq \ker \alpha =E(-D)$. This means $\epsilon (\alpha ')=0$. We compute the ordinary H-slope

  $$\begin{aligned} \mu _H(E'(D)) = \frac{c_1(E'(D))\cdot H^{m-1}}{r'} = \frac{(r'D + c_1(E'))\cdot H^{m-1}}{r'} = 1+\mu _H(E') \le 0 \end{aligned}$$

  where the inequality is induced by the inclusion $E'(D) \hookrightarrow E \hookrightarrow \mathscr {O}_{{\mathbb {P}}^m}^{\oplus r}$. So we obtain

  $$\begin{aligned} \mu _{(H,\delta )}(E',\alpha ') = \frac{c_1(E')\cdot H^{m-1}}{r'} = \mu _H(E')\le -1 < - \frac{\delta _1}{r} = \mu _{(H,\delta )}(E,\alpha ), \end{aligned}$$

  by our assumption $\delta _1<r$ and Eq. (1.5).

The proof is complete. $\square$

2.3 The moduli functor of framed sheaves

Fix integers $m\ge 2$, $r\ge 1$, and $n\ge 0$. Also fix a hyperplane $\iota :D \hookrightarrow {\mathbb {P}}^m$. Consider the moduli functor of D-framed sheaves of rank r on ${\mathbb {P}}^m$ with Chern character $v_{r,n} = (r,0,\ldots ,0,-n)$, i.e. the functor ${\mathsf {Fr}}_{r,n}({\mathbb {P}}^m):\text {Sch}_{\mathbf {k}}^{\text {op}} \rightarrow \text {Sets}$ sending

$$\begin{aligned} B \mapsto \left\{ ({\mathscr {E}},\Phi )\,\Bigg | \begin{array}{c} {\mathscr {E}} \in \mathrm{Coh}({\mathbb {P}}^m\times _{\mathbf {k}} B)\text { is a }B\text {-flat family of torsion free sheaves} \\ \text { with }{\mathrm {ch}}({\mathscr {E}}_b) = v_{r,n}\text { for all }b\in B, \text { and }\Phi :{\mathscr {E}}|_{D\times _{\mathbf {k}} B} \,\widetilde{\rightarrow }\,\mathscr {O}^{\oplus r}_{D\times _{\mathbf {k}} B} \end{array} \right\} \Bigg {/}\sim \end{aligned}$$

where $({\mathscr {E}},\Phi ) \sim ({\mathscr {F}},\Psi )$ if and only if there is an isomorphism $\theta :{\mathscr {E}} \,\widetilde{\rightarrow }\,{\mathscr {F}}$ such that $\Psi \circ \theta |_{D\times _{\mathbf {k}} B} = \Phi$. We have defined the functor using the map ${\mathscr {E}}|_{D\times _{\mathbf {k}} B} \rightarrow \mathscr {O}_{D\times _{\mathbf {k}} B}^{\oplus r}$, but we could have used ${\mathscr {E}} \rightarrow (\iota \times {\text {id}}_B)_*\mathscr {O}_{D\times _{\mathbf {k}} B}^{\oplus r}$ instead.

Let $\delta$ be a rational polynomial as in (1.2). If $(E,\alpha )$ is a D-framed sheaf with ${\mathrm {ch}}(E)=v_{r,n}$ then, since $\epsilon (\alpha )=1$, according to Eq. (1.1) we have

$$\begin{aligned} P_{(E,\alpha )}(k) = P_{r,n}(k)-\delta (k)\in {\mathbb {Q}}[k], \end{aligned}$$

where $P_{r,n}(k) = \chi (E(k))$ is the Hilbert polynomial of a coherent sheaf E with Chern character $v_{r,n}$.

Proposition 1.8

Fix integers $m\ge 2,$ $r\ge 1,$ and $n\ge 0$. Let $\delta$ be a polynomial as in (1.2),  with $0<\delta _1<r$. Set $G=\iota _*\mathscr {O}_D^{\oplus r}$ and $P=P_{r,n}-\delta$. Then the moduli functor ${\mathsf {Fr}}_{r,n}({\mathbb {P}}^m)$ is represented by an open subscheme ${\mathrm {Fr}}_{r,n}({\mathbb {P}}^m) \subset M^{{\mathrm {st}}}_\delta ({\mathbb {P}}^m;G,P)$.

Proof

The case of ${\mathbb {P}}^2$ is well known [4, 18]. Hence, we can restrict to the case $m\ge 3$. The locus of framed modules $(E,\alpha ) \in M^{{\mathrm {st}}}_\delta ({\mathbb {P}}^m;G,P)$ such that E is torsion free, and the map $\phi _\alpha :E|_D \rightarrow \mathscr {O}_D^{\oplus r}$ induced by the framing $\alpha$ is an isomorphism, is open. But by Lemma 1.7, all D-framed sheaves are $\delta$-stable. $\square$

3 Moduli of framed sheaves and Quot schemes

In this section we review the notion of tangent-obstruction theory on a deformation functor [12], and we compare the tangent-obstruction theory on the local Quot functor with that on the D-framed sheaves local moduli functor. This leads to the proof of Theorem A.

3.1 Comparing tangent-obstruction theories

We refer the reader to [12, Ch. 6] for a thorough exposition on tangent-obstruction theories on deformation functors.

Let $\text {Art}_{\mathbf {k}}$ be the category of local artinian ${\mathbf {k}}$-algebras with residue field ${\mathbf {k}}$.¹ A deformation functor is a covariant functor ${\mathrm {D}}:\text {Art}_{\mathbf {k}}\rightarrow \text {Sets}$ such that ${\mathrm {D}}(\mathbf {k})$ is a singleton. A tangent-obstruction theory on a deformation functor ${\mathrm {D}}$ is defined to be a pair $(T_1,T_2)$ of finite dimensional ${\mathbf {k}}$-vector spaces such that for any small extension $I \hookrightarrow B\twoheadrightarrow A$ in $\text {Art}_{\mathbf {k}}$ there is an ‘exact sequence of sets’

$$\begin{aligned} T_1\otimes _{\mathbf {k}}I \rightarrow {\mathrm {D}}(B) \rightarrow {\mathrm {D}}(A) \xrightarrow {\text {ob}} T_2\otimes _{\mathbf {k}}I, \end{aligned}$$

(2.1)

which would be decorated with an additional ‘0’ on the left whenever $A=\mathbf {k}$, and is moreover functorial in small extensions in a precise sense [12, Def. 6.1.21]. We spell out here what exactness of a short exact sequence of sets such as (2.1) means. Exactness at ${\mathrm {D}}(A)$ means that an element $\alpha \in {\mathrm {D}}(A)$ lifts to ${\mathrm {D}}(B)$ if and only if $\text {ob}(\alpha )=0$. Exactness at ${\mathrm {D}}(B)$ means that, if there is a lift, then $T_1\otimes _{\mathbf {k}}I$ acts transitively on the set of lifts. If the sequence started with a ‘0’, it would mean that lifts form an affine space under $T_1\otimes _{\mathbf {k}}I$.

The tangent space of the tangent-obstruction theory is $T_1$, and is canonical, in the sense that it is determined by the deformation functor as $T_1={\mathrm {D}}(\mathbf {k}[t]/t^2)$. The obstruction space, $T_2$, is not canonical: any larger $\mathbf {k}$-linear space $U_2\supset T_2$ yields a new tangent-obstruction theory $(T_1,U_2)$. A deformation functor ${\mathrm {D}}$ is pro-representable if ${\mathrm {D}}\cong {\text {Hom}}_{\mathbf {k}\text {-alg}}(R,-)$ for some local ${\mathbf {k}}$-algebra R with residue field ${\mathbf {k}}$. A tangent-obstruction theory on a pro-representable deformation functor is always decorated with a ‘0’ on the left in the sequences (2.1), for any small extension $I\hookrightarrow B \twoheadrightarrow A$.

Example 2.1

Let V be a coherent sheaf on a projective ${\mathbf {k}}$-scheme Y, and fix a polynomial P. The Quot functor

$$\begin{aligned} {\mathsf {Q}} = {\mathsf {Quot}}_Y(V,P):\text {Sch}_{\mathbf {k}}^{\text {op}} \rightarrow \text {Sets}\end{aligned}$$

sends a $\mathbf {k}$-scheme B to the set of isomorphism classes of surjections $\pi _Y^*V \twoheadrightarrow {\mathscr {Q}}$, where $\pi _Y:Y\times _{\mathbf {k}} B \rightarrow Y$ is the projection and ${\mathscr {Q}}$ is a coherent sheaf on $Y\times _{\mathbf {k}}B$, flat over B, whose fibres ${\mathscr {Q}}_b = {\mathscr {Q}}|_{Y\times _{\mathbf {k}} \{b\}}$ have Hilbert polynomial P. Two surjections are ‘isomorphic’ if they have the same kernel. The Quot functor is represented by a projective ${\mathbf {k}}$-scheme ${\mathrm {Q}} = \mathrm{Quot}_Y(V,P)$. We refer the reader to [12, Ch. 5] for a complete, modern discussion on Quot schemes. Fix a point $x_0 \in {\mathrm {Q}}(\mathbf {k})$ corresponding to a quotient $V \twoheadrightarrow Q$ with kernel E. One can consider the local Quot functor at $x_0$, namely the subfunctor ${\mathsf {Q}}_{x_0} \subset \mathsf {Q}|_{\text {Art}_{\mathbf {k}}}:{\text {Art}_{\mathbf {k}}} \rightarrow \text {Sets}$ sending a local artinian ${\mathbf {k}}$-algebra A to the set of families $x \in \mathsf {Q}({\text {Spec}}A)$ such that $x|_{\mathfrak {m}}=x_0$, where $\mathfrak {m}$ is the closed point of ${\text {Spec}}A$. By representability of ${\mathsf {Q}}$, the functor ${\mathsf {Q}}_{x_0}$ is pro-representable, isomorphic to ${\text {Hom}}_{\mathbf {k}\text {-alg}}(\mathscr {O}_{{\mathrm {Q}},x_0},-)$. By [12, Thm. 6.4.9], the pair of $\mathbf {k}$-vector spaces

$$\begin{aligned} T_1 = {\text {Hom}}(E,Q),\quad T_2 = {\text {Ext}}^1(E,Q) \end{aligned}$$

(2.2)

form a tangent-obstruction theory on the deformation functor ${\mathsf {Q}}_{x_0}$.

The proof of the following result is included for the sake of completeness (and for lack of a suitable reference).

Proposition 2.2

Let ${\mathrm {D}}$ and ${\mathrm {D}}'$ be two pro-representable deformation functors carrying tangent-obstruction theories $(T_1,T_2)$ and $(T'_1,T'_2),$ respectively. Let $\eta :{\mathrm {D}}\rightarrow {\mathrm {D}}'$ be a natural transformation inducing a $\mathbf {k}$-linear isomorphism ${\mathrm {d}}:T_1 \,\widetilde{\rightarrow }\,T_1'$ and a $\mathbf {k}$-linear embedding $T_2\hookrightarrow T_2'$. Then $\eta$ is a natural equivalence.

Proof

We already know that $\eta _B:{\mathrm {D}}(B) \rightarrow {\mathrm {D}}'(B)$ is bijective when $B = \mathbf {k}$ and when $B = \mathbf {k}[t]/t^2$, by assumption. We then proceed by induction on the length of the artinian rings $A\in \text {Art}_{\mathbf {k}}$. Fix a small extension $I\hookrightarrow B \twoheadrightarrow A$ in $\text {Art}_{\mathbf {k}}$ and form the commutative diagram

where the leftmost vertical map is ${\mathrm {d}}\otimes _{\mathbf {k}} {\text {id}}_I$ and the isomorphism ${\mathrm {D}}(A) \,\widetilde{\rightarrow }\,{\mathrm {D}}'(A)$ is the induction hypothesis. We have to show that $\eta _B$ is bijective. The statement is reminiscent of the Five Lemma, but since we are dealing with the (non-standard) concept of short exact sequence of sets, we include full details.

To prove injectivity, pick two elements $\beta _1\ne \beta _2\in {\mathrm {D}}(B)$. We may assume their images in ${\mathrm {D}}(A)$ agree, for otherwise there is nothing to prove. Then, by pro-representability of ${\mathrm {D}}$, we have $\beta _2 = v\cdot \beta _1$ for a unique nonzero $v \in T_1\otimes _{\mathbf {k}}I$. Then, after setting $v' = ({\mathrm {d}}\otimes _{\mathbf {k}} {\text {id}}_I)(v)$, we find $\eta _B(\beta _2) = v'\cdot \eta _B(\beta _1) \ne \eta _B(\beta _1)$ since $v'\ne 0$ and ${\mathrm {D}}'$ is pro-representable.

To prove surjectivity, pick $\beta '\in {\mathrm {D}}'(B)$. It maps to $0\in T_2'\otimes _{\mathbf {k}} I$, and its image $\alpha '$ in ${\mathrm {D}}'(A)$ lifts uniquely to an element $\alpha \in {\mathrm {D}}(A)$ such that $\text {ob}(\alpha )$ goes to $0\in T_2'\otimes _{\mathbf {k}} I$. But by the injectivity assumption, we have $\text {ob}(\alpha ) = 0$, i.e. $\alpha$ lifts to some $\beta \in {\mathrm {D}}(B)$. But $\eta _B(\beta )$ is a lift of $\alpha ' \in {\mathrm {D}}(A)$, so $\beta ' = v'\cdot \eta _B(\beta )$ for a unique $v'$, as above. Then, if $v \in T_1\otimes _{\mathbf {k}} I$ is the preimage of $v'$, we conclude that $v\cdot \beta \in {\mathrm {D}}(B)$ is a preimage of $\beta '$ under $\eta _B$. $\square$

3.2 Relating Quot scheme and framed sheaves

Let $\mathbf {k}$ be an algebraically closed field of characteristic 0. Let $M=M_{\delta }^{{\mathrm {st}}}(Y;G,P)$ be a fine moduli space of $\delta$-stable framed modules (with framing datum G and framed Hilbert polynomial P) on a smooth projective $\mathbf {k}$-variety Y, as in Theorem 1.3. Fix a closed point $y_0 \in M(\mathbf {k})$ corresponding to a framed module $(E,\alpha )$. Consider the deformation functor

$$\begin{aligned} \mathsf {M}_{y_0}:\text {Art}_{\mathbf {k}} \rightarrow \text {Sets}\end{aligned}$$

defined as the subfunctor of ${\mathcal {M}}_{\delta }^{{\mathrm {st}}}(Y;G,P)|_{\text {Art}_{\mathbf {k}}}$ sending a local artinian $\mathbf {k}$-algebra A to the set of isomorphism classes of families of $\delta$-stable framed modules $y \in {\mathcal {M}}_{\delta }^{{\mathrm {st}}}(Y;G,P)({\text {Spec}}A)$ such that $y|_{\mathfrak {m}} = y_0$, where $\mathfrak {m}$ is the closed point of ${\text {Spec}}A$. It is the local moduli functor attached to $y_0 \in M(\mathbf {k})$. By representability of ${\mathcal {M}}_{\delta }^{{\mathrm {st}}}(Y;G,P)$, the functor $\mathsf {M}_{y_0}$ is pro-representable: it is isomorphic to ${\text {Hom}}_{\mathbf {k}\text {-alg}}(\mathscr {O}_{M,y_0},-)$.

Fix $m\ge 2$. If $Y={\mathbb {P}}^m$, $\iota :D\hookrightarrow {\mathbb {P}}^m$ is a hyperplane and $y_0 \in {\mathrm {Fr}}_{r,n}({\mathbb {P}}^m)(\mathbf {k})\subset M_\delta ^{{\mathrm {st}}}({\mathbb {P}}^m;G,P)(\mathbf {k})$ corresponds to a D-framed sheaf $(E,\alpha )$ for a choice of $(\delta ,G,P)$ as in Proposition 1.8, we denote by ${\mathsf {Fr}}_{y_0} \subset \mathsf {M}_{y_0}$ the corresponding open subfunctor. By [16, Thm. 4.1], the pair of vector spaces

$$\begin{aligned} T_1 = {\text {Ext}}^1(E,E(-D)),\quad T_2 = {\text {Ext}}^2(E,E(-D)) \end{aligned}$$

form a natural tangent-obstruction theory on the deformation functor ${\mathsf {Fr}}_{y_0}$.

On the other hand, we have Grothendieck’s Quot functor

$$\begin{aligned} {\mathsf {Q}}={\mathsf {Quot}}_{{\mathbb {P}}^m}(\mathscr {O}^{\oplus r},n):\text {Sch}_{\mathbf {k}}^{\text {op}}\rightarrow \text {Sets}. \end{aligned}$$

It contains as an open subfunctor the Quot functor

$$\begin{aligned} {\mathsf {Quot}}_{{\mathbb {A}}^m}(\mathscr {O}^{\oplus r},n) \hookrightarrow {\mathsf {Q}}, \end{aligned}$$

parametrising quotients $\mathscr {O}_{{\mathbb {P}}^m\times _{\mathbf {k}} B}^{\oplus r} \twoheadrightarrow {\mathscr {Q}}$ such that the projection ${\text {Supp}}{\mathscr {Q}} \rightarrow {\mathbb {P}}^m$ factors through ${\mathbb {A}}^m = {\mathbb {P}}^m {\setminus } D$.

Proposition 2.3

Fix integers $m\ge 2,$ $r\ge 1$ and $n\ge 0$. Then there is a morphism of $\mathbf {k}$-schemes

$$\begin{aligned} \eta :\mathrm{Quot}_{{\mathbb {A}}^m}(\mathscr {O}^{\oplus r},n) \rightarrow {\mathrm {Fr}}_{r,n}({\mathbb {P}}^m) \end{aligned}$$

which is injective on geometric points,  and is a bijection if $m\ge 3$ or $(m,r) = (2,1)$.

Proof

Fix a $\mathbf {k}$-scheme B. Consider a short exact sequence

$$\begin{aligned} 0 \rightarrow {\mathscr {E}} \xrightarrow {i} \mathscr {O}^{\oplus r}_{{\mathbb {P}}^m \times _{\mathbf {k}} B} \rightarrow {\mathscr {Q}} \rightarrow 0 \end{aligned}$$

defining an element of ${\mathsf {Quot}}_{{\mathbb {A}}^m}(\mathscr {O}^{\oplus r},n)(B) \subset {\mathsf {Q}}(B)$. This means that the image of ${\text {Supp}}{\mathscr {Q}} \subset {\mathbb {P}}^m \times _{\mathbf {k}} B \rightarrow {\mathbb {P}}^m$ is disjoint from D, in particular ${\mathscr {Q}}|_{D\times _{\mathbf {k}} B} = 0$. Then we define $\eta _B:{\mathsf {Quot}}_{{\mathbb {A}}^m}(\mathscr {O}^{\oplus r},n)(B) \rightarrow {\mathsf {Fr}}_{r,n}({\mathbb {P}}^m)(B)$ by sending such an exact sequence to the pair $({\mathscr {E}},\Phi )$, where

$$\begin{aligned} \Phi = i|_{D\times _{\mathbf {k}} B} :{\mathscr {E}}|_{D\times _{\mathbf {k}} B} \,\widetilde{\rightarrow }\,\mathscr {O}^{\oplus r}_{D \times _{\mathbf {k}} B}. \end{aligned}$$

Note that ${\mathscr {E}}$ is B-flat since ${\mathscr {Q}}$ is B-flat.

Such a map is easily seen to be injective on geometric points, by definition of the Quot functor. If $m\ge 3$, we can construct the inverse of $\eta _{\mathbf {k}}$ as follows. Given a D-framed sheaf $(E,\phi )$, with trivialisation $\phi :E|_D \,\widetilde{\rightarrow }\,\mathscr {O}_D^{\oplus r}$, we know by the proof of Corollary 1.6 how to construct a canonical isomorphism $E^{\vee \vee } \,\widetilde{\rightarrow }\,\mathscr {O}^{\oplus r}_{{\mathbb {P}}^m}$. Thus the inverse of $\eta _{\mathbf {k}}$ will send $(E,\phi )$ to the isomorphism class of the surjection

$$\begin{aligned} \mathscr {O}^{\oplus r}_{{\mathbb {P}}^m} \twoheadrightarrow \mathscr {O}^{\oplus r}_{{\mathbb {P}}^m} / E. \end{aligned}$$

The same argument works in the isolated case $(m,r) = (2,1)$. Indeed, in that case $E = {\mathscr {I}}_Z$ is an ideal sheaf of a 0-dimensional subscheme $Z \subset {\mathbb {A}}^2 = {\mathbb {P}}^{2} {\setminus } D$ of length n, and again we have ${\mathscr {I}}_Z^{\vee \vee } \,\widetilde{\rightarrow }\,\mathscr {O}_{{\mathbb {P}}^2}$, canonically. The proof is complete. $\square$

We will use an infinitesimal method based on Proposition 2.2 to prove that the map $\eta$ of Proposition 2.3 is an isomorphism as long as $m\ge 3$.

3.3 Infinitesimal method

Let $y_0 = \eta (x_0) \in {\mathrm {Fr}}_{r,n}({\mathbb {P}}^m)$ be the image of a point $x_0 \in \mathrm{Quot}_{{\mathbb {A}}^m}(\mathscr {O}^{\oplus r},n)$ under the morphism $\eta$. We obtain an induced natural transformation

$$\begin{aligned} \eta _0:{\mathsf {Q}}_{x_0} \rightarrow {\mathsf {Fr}}_{y_0} \end{aligned}$$

between the local moduli functors—${\mathsf {Q}}_{x_0}$ was defined in Example 2.1. Both functors are pro-representable and carry a tangent-obstruction theory, cf. (2.2) for the case of the Quot scheme. Our next goal is to show that $\eta _0$ is an equivalence when $m\ge 3$, using Proposition 2.2. This will be achieved by means of the following two lemmas.

Lemma 2.4

Fix $m\ge 3$ and a hyperplane $D\subset {\mathbb {P}}^m$. Let E be a torsion free sheaf on ${\mathbb {P}}^{m}$ such that $E|_{D}\cong \mathscr {O}_{{\mathbb {P}}^m}^{\oplus r}$. Then

$$\begin{aligned} {\mathrm {H}}^{m-1}\left( {\mathbb {P}}^{m}, E(-m)\right)&\,=\, 0\\ {\mathrm {H}}^{m}\left( {\mathbb {P}}^{m}, E(-m)\right)&\,=\, 0. \end{aligned}$$

If the strict inequality $m>3$ holds,  then

$$\begin{aligned} {\mathrm {H}}^{m-2}\left( {\mathbb {P}}^{m}, E(-m)\right) = 0. \end{aligned}$$

Proof

Consider the short exact sequence of sheaves

$$\begin{aligned} 0 \rightarrow E(k-1) \rightarrow E(k) \rightarrow \iota _*\iota ^*E(k) \rightarrow 0 \end{aligned}$$

(2.3)

obtained from the ideal sheaf short exact sequence of the hyperplane $D\subset {\mathbb {P}}^m$. The map $E(k-1)\rightarrow E(k)$ is injective because it is locally given as multiplication by the defining equation of D, and the sheaf E is torsion-free. Notice first that

$$\begin{aligned} {\mathrm {H}}^\ell ({\mathbb {P}}^m,\iota _*\iota ^*E(k)) = {\mathrm {H}}^\ell (D,\iota ^*E(k)) = {\mathrm {H}}^\ell (D,\mathscr {O}_D(k))^{\oplus r}. \end{aligned}$$

Since $D \cong {\mathbb {P}}^{m-1}$, we have

$$\begin{aligned} {\mathrm {H}}^{m-2}\left( D, \mathscr {O}_{D}(k)\right)&= 0 \quad \text {for all } k,\\ {\mathrm {H}}^{m-1}\left( D, \mathscr {O}_{D}(k)\right)&= 0 \quad \text {if } k>-m,\\ {\mathrm {H}}^{m}\left( D, \mathscr {O}_{D}(k)\right)&= 0 \quad \text {for all } k. \end{aligned}$$

The first vanishing follows by our assumption $m\ge 3$. For any $k>-m$ we then deduce the following isomorphisms from the long exact sequence in cohomology associated to (2.3):

$$\begin{aligned} {\mathrm {H}}^{m-1}\left( {\mathbb {P}}^{m}, E(k-1)\right) \,\widetilde{\rightarrow }\,&{\mathrm {H}}^{m-1}\left( {\mathbb {P}}^{m}, E(k)\right) ,\\ {\mathrm {H}}^{m}\left( {\mathbb {P}}^{m} , E(k-1)\right) \,\widetilde{\rightarrow }\,&{\mathrm {H}}^{m}\left( {\mathbb {P}}^{m}, E(k)\right) . \end{aligned}$$

Since both cohomology groups on the right hand side of the isomorphisms vanish for k large enough by Serre’s vanishing theorem, we deduce ${\mathrm {H}}^{m-1}\left( {\mathbb {P}}^{m}, E(-m)\right) = {\mathrm {H}}^{m}\left( {\mathbb {P}}^{m}, E(-m)\right) = 0$.

If $m>3$, then

$$\begin{aligned} {\mathrm {H}}^{m-3}\left( D, \mathscr {O}_{D}(k)\right) = 0\quad \text {for all } k, \end{aligned}$$

and applying analogously Serre’s vanishing theorem we deduce ${\mathrm {H}}^{m-2}\left( {\mathbb {P}}^{m}, E(-m)\right) =0$. $\square$

Lemma 2.5

Fix $m\ge 3$ and a hyperplane $D\subset {\mathbb {P}}^m$. Let $(E,\alpha )$ be a D-framed sheaf of rank r on ${\mathbb {P}}^{m},$ and let $Q = \mathscr {O}_{{\mathbb {P}}^m}^{\oplus r}/E$ be as in (1.4). Then there is a $\mathbf {k}$-linear isomorphism

$$\begin{aligned} {\text {Hom}}(E,Q)\,\widetilde{\rightarrow }\,{\text {Ext}}^{1}(E,E(-D)) \end{aligned}$$

and a $\mathbf {k}$-linear inclusion

$$\begin{aligned} {\text {Ext}}^{1}(E,Q) \hookrightarrow {\text {Ext}}^{2}(E,E(-D)). \end{aligned}$$

If the strict inequality $m>3$ holds,  the $\mathbf {k}$-linear inclusion is in fact an isomorphism.

Proof

Twisting the exact sequence (1.4) by $\mathscr {O}(-D)$ and applying the ${\text {Hom}}(E,-)$ functor we obtain a long cohomology sequence

$$\begin{aligned}&\cdots \rightarrow {\text {Hom}}(E,\mathscr {O}_{{\mathbb {P}}^{m}}(-D)^{\oplus r}) \rightarrow {\text {Hom}}(E,Q) \rightarrow {\text {Ext}}^{1}(E,E(-D)) \\&\quad \rightarrow {\text {Ext}}^{1}(E,\mathscr {O}_{{\mathbb {P}}^{m}}(-D)^{\oplus r}) \rightarrow {\text {Ext}}^{1}(E,Q) \rightarrow {\text {Ext}}^{2}(E,E(-D)) \rightarrow {\text {Ext}}^{2}(E,\mathscr {O}_{{\mathbb {P}}^{m}}(-D)^{\oplus r}) \rightarrow \cdots \end{aligned}$$

and by Serre duality we have

$$\begin{aligned} {\text {Hom}}(E,\mathscr {O}_{{\mathbb {P}}^{m}}(-D)^{\oplus r})^\vee&\cong {\mathrm {H}}^{m}({\mathbb {P}}^{m},E(-m))^{\oplus r} \\ {\text {Ext}}^{i}(E,\mathscr {O}_{{\mathbb {P}}^{m}}(-D)^{\oplus r})^\vee&\cong {\mathrm {H}}^{m-i}({\mathbb {P}}^{m},E(-m))^{\oplus r} \end{aligned}$$

for $i=1,2$, so that the result follows from the vanishings of Lemma 2.4. $\square$

We have thus essentially obtained the proof of the following result.

Proposition 2.6

If $m\ge 3,$ the natural transformation $\eta _0:{\mathsf {Q}}_{x_0} \rightarrow {\mathsf {Fr}}_{y_0}$ of local moduli functors induces an isomorphism on tangent spaces and an injection on obstruction spaces. Hence,  $\eta _0$ is a natural equivalence.

Proof

The first statement follows from Lemma 2.5. The conclusion follows from Proposition 2.2. $\square$

We can now finish the proof of our main result.

Theorem 2.7

Fix integers $m\ge 2,$ $r\ge 1$ and $n\ge 0$. The morphism of schemes

$$\begin{aligned} \eta :\mathrm{Quot}_{{\mathbb {A}}^m}(\mathscr {O}^{\oplus r},n) \rightarrow {\mathrm {Fr}}_{r,n}({\mathbb {P}}^m) \end{aligned}$$

constructed in Proposition 2.3 is an isomorphism if and only if $m\ge 3$ or $(m,r) = (2,1)$.

Proof

The case $(m,r) = (2,1)$ is proved in [18, Thm. 2.1]. However, a direct argument is as follows: for fixed n, both schemes are smooth and irreducible of dimension 2n, so since $\eta :\text {Hilb}^n({\mathbb {A}}^2) \rightarrow {\mathrm {Fr}}_{1,n}({\mathbb {P}}^2)$ is bijective (Proposition 2.3), it has to be an isomorphism by Zariski’s main theorem.

Assume $m\ge 3$ for the rest of the proof. The morphism $\eta$ is locally of finite type, since the Quot scheme is of finite type. Next, we check that $\eta$ is formally étale, using the infinitesimal criterion. Consider a square zero extension $S \hookrightarrow \overline{S}$ of fat points (i.e. spectra of objects A, B of $\text {Art}_{\mathbf {k}}$), denote by ${\mathfrak {m}}$ the closed point of S and form a commutative diagram

where the dotted arrow u is the unique extension of h we have to find in order to establish formal étaleness of $\eta$ at $x_0 = h({\mathfrak {m}}) \mapsto y_0 = \overline{h}({\mathfrak {m}})$. We shall use the notation ${\text {Hom}}_p(T,Y)$, for T a fat point and p a point on a scheme Y, to indicate the set of morphisms $T\rightarrow Y$ sending the closed point to $p\in Y$. Using pro-representability of $\mathsf {Q}_{x_0}$ and ${\mathsf {Fr}}_{y_0}$, the condition that $\eta _0$ is a natural equivalence (proved in Proposition 2.6) translates into a commutative diagram

where the vertical maps are the isomorphisms $\eta _{0,\overline{S}}$ and $\eta _{0,{S}}$ respectively. Since $\overline{h} \in {\text {Hom}}_{y_0}(\overline{S},{\mathrm {Fr}}_{r,n}({\mathbb {P}}^m))$ lifts to a map

$$\begin{aligned} u \,\in \, {\text {Hom}}_{x_0}(\overline{S},\mathrm{Quot}_{{\mathbb {A}}^m}(\mathscr {O}^{\oplus r},n)) \end{aligned}$$

and both $u \circ i$ and h map to $\eta \circ h \in {\text {Hom}}_{y_0}(S,{\mathrm {Fr}}_{r,n}({\mathbb {P}}^m))$, they must be equal, since the vertical map on the right is also a bijection. Thus u is the unique lift we wanted to find.

We conclude that $\eta$ is étale. Since it is bijective by Proposition 2.3, it is an isomorphism. $\square$

Remark 2.8

If $m=2$, we still have ${\text {Hom}}(E,\mathscr {O}_{{\mathbb {P}}^m}(-D)) \cong {\mathrm {H}}^2({\mathbb {P}}^2,E(-2))^\vee = 0$, inducing a (proper) linear inclusion

$$\begin{aligned} {\text {Hom}}(E,Q) \hookrightarrow {\text {Ext}}^1(E,E(-D)), \end{aligned}$$

but ${\text {Ext}}^1(E,\mathscr {O}_{{\mathbb {P}}^2}(-D))\cong {\mathrm {H}}^1({\mathbb {P}}^2,E(-2))^\vee \cong \mathbf {k}^n$ does not vanish.

Remark 2.9

We thank A. Henni for suggesting that it might also be possible to give a proof of Theorem A combining the formalism of perfect extended monads [14, 15] with the result of Abe–Yoshinaga (Theorem 1.5). The 3-dimensional case is also studied along these lines in [5, Sec. 2.1.2].

Corollary 2.10

The scheme ${\mathrm {Fr}}_{r,n}({\mathbb {P}}^3)$ is a global critical locus,  i.e. it can be written as the scheme-theoretic zero locus of an exact 1-form ${\mathrm {d}}f,$ where f is a function on a smooth variety $U_{r,n,3}$.

Proof

This follows by combining Theorem 2.7 with [2, Thm. 2.6], which works over an arbitrary algebraically closed field of characteristic 0. The pair $(U_{r,n,3},f)$ will be given in Remark 3.1. $\square$

Remark 2.11

Another Quot scheme on ${\mathbb {A}}^3$ that has been recently proven to be a global critical locus is $\mathrm{Quot}_{{\mathbb {A}}^3}({\mathscr {I}}_L,n)$, where ${\mathscr {I}}_L \subset {\mathbb {C}}[x,y,z]$ is the ideal sheaf of a line $L \subset {\mathbb {A}}^3$ [9]. This was the starting point for the motivic refinement of the local DT/PT (or, ideal sheaves/stable pairs) correspondence around a smooth curve in a 3-fold [22, 23].

Set $\mathbf {k}= {\mathbb {C}}$. By Oprea’s construction [20, Thm. 1 and Sec. 4.4], there exists a symmetric perfect obstruction theory

$$\begin{aligned} {\mathbb {E}}= \mathbf{R}\pi _*{\mathbf {R}{\mathscr {H}\text {om}}}({\mathscr {E}}(-D),{\mathscr {E}}\otimes \omega _{\pi })[2] \rightarrow {\mathbb {L}}_{{\mathrm {Fr}}_{r,n}({\mathbb {P}}^3)} \end{aligned}$$

on ${\mathrm {Fr}}_{r,n}({\mathbb {P}}^3)$, where $\pi :{\mathbb {P}}^3 \times _{{\mathbb {C}}} {\mathrm {Fr}}_{r,n}({\mathbb {P}}^3)\rightarrow {\mathrm {Fr}}_{r,n}({\mathbb {P}}^3)$ is the projection, $({\mathscr {E}},\Phi )$ is the universal framed sheaf, and ${\mathbb {L}}$ denotes the truncated cotangent complex. On the other hand, the critical locus structure on the Quot scheme [2, Thm. 2.6]

$$\begin{aligned} {\mathrm {Q}} = \mathrm{Quot}_{{\mathbb {A}}^3}(\mathscr {O}^{\oplus r},n) = \{{\mathrm {d}}f = 0\} \subset U = U_{r,n,3} \end{aligned}$$

induces a canonical ‘critical’ symmetric perfect obstruction theory

$$\begin{aligned} {\mathbb {E}}_{{\text {crit}}} = \bigl [ T_{U}\big |_{{\mathrm {Q}}}\xrightarrow {{\mathsf {Hess}}(f)}\Omega _{U}\big |_{{\mathrm {Q}}}\bigr ] \rightarrow {\mathbb {L}}_{{\mathrm {Q}}}. \end{aligned}$$

See [3] for background on symmetric obstruction theories. See also [21, 25] for the construction of virtual fundamental classes on several Quot schemes for varieties of dimension at most 3.

We propose the following conjecture, essentially a higher rank version of [13, Conj. 9.9].

Conjecture 2.12

The isomorphism $\eta$ of Theorem 2.7 induces an isomorphism of perfect obstruction theories

$$\begin{aligned} {\mathbb {E}}_{{\text {crit}}} \,\cong \,\eta ^*{\mathbb {E}}\end{aligned}$$

over the truncated cotangent complex of $\mathrm{Quot}_{{\mathbb {A}}^3}(\mathscr {O}^{\oplus r},n)$.

4 Relation to quiver gauge theories

In this section we set $\mathbf {k}= {\mathbb {C}}$, essentially to be coherent with the literature on the subject. We start by recalling the explicit description of the Quot scheme as a closed subscheme of a nonsingular variety, the so-called non-commutative Quot scheme, which can be seen as the moduli space of stable r-framed representations on a quiver (Fig. 1); the relations cutting out $\mathrm{Quot}_{{\mathbb {A}}^m}({\mathscr {O}}^{\oplus r},n)$ are precisely given by annihilating the commutators between all the matrices arising from the m loops in the quiver. This story is particularly rich in the case $m=3$, where such relations agree with a single vanishing relation ‘${\mathrm {d}}f = 0$’ (Remark 3.1). We emphasise this since it is the starting point of higher rank Donaldson–Thomas theory of points in all its flavours: enumerative [2, 25], motivic [6, 24], K-theoretic [13].

We conclude this final section by stressing the dichotomy between the case $m=2$ and the case $m\ge 3$. More precisely, in Sect. 3.2 we exhibit the equations cutting out $\mathrm{Quot}_{{\mathbb {A}}^2}({\mathscr {O}}^{\oplus r},n)$ inside the moduli space ${\mathrm {Fr}}_{r,n}({\mathbb {P}}^2)$ of framed sheaves on ${\mathbb {P}}^2$. In the case of higher rank $r>1$, the describes $\mathrm{Quot}_{{\mathbb {A}}^2}({\mathscr {O}}^{\oplus r},n)$ as a closed singular subvariety of ${\mathrm {Fr}}_{r,n}({\mathbb {P}}^2)$ of codimension $n(r-1)$.

4.1 Embedding in the non-commutative Quot scheme

The Quot scheme

$$\begin{aligned} \mathrm{Quot}_{{\mathbb {A}}^m}(\mathscr {O}^{\oplus r},n) \end{aligned}$$

can be embedded in a smooth quasiprojective variety $U_{r,n,m}$, called the non-commutative Quot scheme in [2, 13], as follows. Consider the m-loop quiver, i.e. the quiver $L_m$ with one vertex ‘0’ and m loops. Now consider the quiver $\widetilde{L}_m$ obtained by adding one additional vertex ‘$\infty$’ along with r edges $\infty \rightarrow 0$ (see Fig. 1). This construction is called r-framing—for $m=3$ it has some relevance in motivic Donaldson–Thomas theory [6, 7] and K-theoretic Donaldson–Thomas theory [13]. It is also performed with care in [15] in the $r=1$ case and in [14] for arbitrary r.

Fig. 1

The r-framed m-loop quiver $\widetilde{L}_m$

The space of representations of $\widetilde{L}_m$ of dimension vector (n, 1) is the affine space

$$\begin{aligned} \text {Rep}_{(n,1)}(\widetilde{L}_m) = {\text {End}}({\mathbb {C}}^n)^{\oplus m}\oplus {\text {Hom}}({\mathbb {C}},{\mathbb {C}}^n)^{\oplus r} \end{aligned}$$

of dimension $mn^2+rn$. Now consider the open subscheme

$$\begin{aligned} W_{r,n,m} \subset \text {Rep}_{(n,1)}(\widetilde{L}_m) \end{aligned}$$

consisting of those tuples $(A_1,\ldots ,A_m,v_1,\ldots ,v_r)$ for which the vectors generate the underlying representation $(A_1,\ldots ,A_m) \in \text {Rep}_n(L_m)$ of the m-loop quiver. Explicitly, this means that

$$\begin{aligned} \dim _{{\mathbb {C}}} \text {Span}\{A_1^{\alpha _1}\cdots A_m^{\alpha _m}\cdot v_i|\alpha _i\ge 0,1\le \ell \le r\} = n. \end{aligned}$$

Of course, $W_{r,n,m}$ could be defined without reference to quivers, but it is interesting to notice that there exists a quiver stability condition $\theta$ on $L_m$ such that the open subscheme of $\text {Rep}_{(n,1)}(\widetilde{L}_m)$ consisting of $\theta$-stable representations is precisely $W_{r,n,m}$. The gauge group $\text {GL}_n$ acts freely on the smooth quasi-affine scheme $W_{r,n,m}$, by conjugation on the matrices and via the natural action on the vectors. Therefore the quotient

$$\begin{aligned} U_{r,n,m} = W_{r,n,m}/\text {GL}_n \end{aligned}$$

is a smooth quasiprojective variety, of dimension $(m-1)n^2+rn$. The Quot scheme is realised as the closed subscheme

$$\begin{aligned} \mathrm{Quot}_{{\mathbb {A}}^m}(\mathscr {O}^{\oplus r},n) \subset U_{r,n,m} \end{aligned}$$

(3.1)

cut out as the locus where the m matrices commute, i.e. by the vanishing relations

$$\begin{aligned} {[}A_i,A_j] = 0,\quad 1\le i<j\le m. \end{aligned}$$

Remark 3.1

If $m=3$, then the inclusion (3.1) is cut out scheme-theoretically by the single relation

$$\begin{aligned} {\mathrm {d}}f = 0, \end{aligned}$$

where $f \in \Gamma (U_{r,n,3},\mathscr {O})$ is the function $(A_1,A_2,A_3,v_1,\ldots ,v_r)\mapsto \text {Tr}A_1[A_2,A_3]$, see [2, Thm. 2.6].

Remark 3.2

The scheme $\mathrm{Quot}_{{\mathbb {A}}^m}(\mathscr {O}^{\oplus r},1)$ is smooth of dimension $m-1+r$, because it is equal to $U_{r,1,m}$. If $m=1$, all Quot schemes $\mathrm{Quot}_{{\mathbb {A}}^1}(\mathscr {O}^{\oplus r},n)$ are smooth. If $r=1$, then the Quot scheme is just the Hilbert scheme of points $\text {Hilb}^n{\mathbb {A}}^m$, which is nonsingular (of dimension mn) if and only if $m\le 2$ or $n\le 3$. Finally, if $m\ge 2$ and $r\ge 2$, the Quot scheme $\mathrm{Quot}_{{\mathbb {A}}^m}(\mathscr {O}^{\oplus r},n)$ is in general singular, as Example 3.3 shows.

4.2 The 2-dimensional case

The following example shows that the Quot scheme of a surface, such as ${\mathbb {A}}^2$, is often singular.

Example 3.3

Let S be a smooth surface, $p \in S$ a point, and fix $n = r > 1$. Consider a quotient

$$\begin{aligned} \xi = \bigl [\mathscr {O}_S^{\oplus r} \twoheadrightarrow \mathscr {O}_p^{\oplus r}\bigr ]\,\in \,\mathrm{Quot}_S(\mathscr {O}_S^{\oplus r},r). \end{aligned}$$

Then the tangent space to $\mathrm{Quot}_S(\mathscr {O}_S^{\oplus r},r)$ at $\xi$ is given by

$$\begin{aligned} {\text {Hom}}({\mathscr {I}}_p^{\oplus r},\mathscr {O}_p^{\oplus r}) = {\text {Hom}}({\mathscr {I}}_p,\mathscr {O}_p)^{\oplus r^2} \,\cong \, {\mathbb {C}}^{2r^2}, \end{aligned}$$

using that ${\text {Hom}}({\mathscr {I}}_p,\mathscr {O}_p)$ is 2-dimensional, being the tangent space to the smooth scheme $\text {Hilb}^1S = S$ at p. On the other hand, the Quot scheme $\mathrm{Quot}_{{\mathbb {A}}^2}(\mathscr {O}^{\oplus r},n)$ is irreducible of dimension $(r+1)n$, as was proven by Ellingsrud and Lehn [11]. Since $2r^2>(r+1)r$, the point $\xi$ is a singular point.

In the case of ${\mathbb {P}}^2$, we already mentioned that Theorem A does not hold (unless $r=1$). In this case, we do have a closed immersion

$$\begin{aligned} \mathrm{Quot}_{{\mathbb {A}}^2}(\mathscr {O}^{\oplus r},n) \hookrightarrow {\mathrm {Fr}}_{r,n}({\mathbb {P}}^2) \end{aligned}$$

(3.2)

of codimension $n(r-1)$, which is an isomorphism if and only if $r=1$. The moduli space of framed sheaves is smooth and irreducible of dimension 2nr, and can be realised as

$$\begin{aligned} \left\{ (B_1,B_2,i,j)\,\Bigg | \begin{array}{c} [B_1,B_2]+ij=0, \text { and there is no subspace} \\ \ S\subsetneq {\mathbb {C}}^n\text { such that }B_\alpha (S)\subset S\text { and }{\mathrm {im}}\,i \subset S \end{array} \right\} \Bigg {/} \text {GL}_n, \end{aligned}$$

where $B_i \in {\text {End}}({\mathbb {C}}^n)$, $i \in {\text {Hom}}({\mathbb {C}}^r,{\mathbb {C}}^n)$ and $j \in {\text {Hom}}({\mathbb {C}}^n,{\mathbb {C}}^r)$. See [18, Thm. 2.1] and the references therein. The inclusion (3.2) is obtained as the locus $j = 0$. In particular, $\mathrm{Quot}_{{\mathbb {A}}^2}(\mathscr {O}^{\oplus r},n)$ is a (singular) scheme, cut out as the zero locus of a section of a tautological bundle of rank nr on the smooth quiver variety ${\mathrm {Fr}}_{r,n}({\mathbb {P}}^2)$.