Goodness-of-fit test for $\alpha$-stable distribution based on the quantile conditional variance statistics

Abstract

The class of $\alpha$-stable distributions is ubiquitous in many areas including signal processing, finance, biology, physics, and condition monitoring. In particular, it allows efficient noise modeling and incorporates distributional properties such as asymmetry and heavy-tails. Despite the popularity of this modeling choice, most statistical goodness-of-fit tests designed for $\alpha$-stable distributions are based on a generic distance measurement methods. To be efficient, those methods require large sample sizes and often do not efficiently discriminate distributions when the corresponding $\alpha$-stable parameters are close to each other. In this paper, we propose a novel goodness-of-fit method based on quantile (trimmed) conditional variances that is designed to overcome these deficiencies and outperforms many benchmark testing procedures. The effectiveness of the proposed approach is illustrated using extensive simulation study with focus set on the symmetric case. For completeness, an empirical example linked to plasma physics is provided.

1 Introduction

The $\alpha$-stable distributions were first introduced in the 1920s in Lévy (1924); see also Khinchine and Lévy (1936). They are a natural extension of the Gaussian distribution which allow more sophisticated noise modelling. Indeed, due to the Generalized Central Limit Theorem, one could show that $\alpha$-stable distributions attract distributions of sums of random variables with diverging variance, in the same sense that the Gaussian law attracts distributions with finite variance; see Jakubowski and Kobus (1989).

The $\alpha$-stable distribution were first applied to financial time series modeling in Mandelbrot (1960). Then, in Chambers et al. (1976) it was showed that $\alpha$-stable distribution is a very suitable model for noise on telephone lines. In the 1990s, $\alpha$-stable distribution became of interest to wider audience, mainly due to Shao and Nikias (1993), which defined the initial signal processing framework, and due to the book Samorodnitsky and Taqqu (1994) which provided a unified mathematical treatment. In recent years, the $\alpha$-stable distributions have found many interesting applications, e.g. in physics, biology, medicine, climate dynamics, financial markets, telecommunications, and condition monitoring. We refer the reader to Majka and Góra (2015); Kosko and Mitaim (2004); Barthelemy et al. (2008); Sokolov et al. (1997); Lomholt et al. (2005); Durrett et al. (2011); Lan and Toda (2013); Peng et al. (1993); Rachev and Mittnik (2000); Bidarkota et al. (2009); Middleton (1999); Li et al. (2019); Yu et al. (2013); Żak et al. (2017, 2016); Ditlevsen (1999); Wyłomańska et al. (2015) and references therein. Also, we refer the reader to the classical book related to the $\alpha$-stable distributed signals – Nikias and Shao (1995); see also Janicki and Weron (1994) and Wegman et al. (1989).

While $\alpha$-stable distributions are characterized by four parameters, the most important one, arguably, is the stability index $\alpha \in (0,2]$ which is responsible for the heavy-tailed behavior. In a nutshell, the smaller the $\alpha$ the higher the probability that the corresponding random variable takes extreme values. For $\alpha <2$ the $\alpha$-stable distributions belong the the wide class of the heavy-tailed distributions and in this case the corresponding random variable has infinite variance. On the other hand, the $\alpha$-stable distribution can be considered as the extension of the Gaussian one, indeed for $\alpha =2$ it reduces to normal distribution.

In the literature, one can find many statistical methods linked to $\alpha$-stable distributions. This includes estimation methods, Bayesian MCMC frameworks, and goodness-of-fit tests. See Tuo (2018); Wolpert and Schmidler (2012); Jabłońska et al. (2017); Nolan (2001); Koblents et al. (2016); McCulloch (1986); Koutrouvelis (1980); Kratz and Resnick (1996); Bee and Trapin (2018); de Haan and Resnic (1998); Lombardi (2007); Buckle (1996); Godsill and Kuruoglu (1999); Peters et al. (2012); Tsionas (2000); Chakravarti et al. (1967); Srinivasan (1971); Watson (1961); Anderson (1962); Anderson and Darling (1954); Matsui and Takemura (2008); Beaulieu et al. (2014) for exemplary contributions.

However, under the assumption that the random sample comes from the $\alpha$-stable distribution, the fitting algorithms require very large sample size to be effective and do not efficiently discriminate $\alpha$-stable distributions when the parameters are close to each other; see Burnecki et al. (2012, 2015). In particular, most goodness-of-fit procedures for $\alpha$-stable distribution are based on the generic distance measurement statistics, when the whole empirical and theoretical cumulative distribution functions (or characteristic functions) are compared with each other. Consequently, the computational time needed for comprehensive data assessment is rather high, at least compared to assessments based on simple statistics (like moments for the finite-variance distributions). To sum up, there is a need for further development of fast and efficient $\alpha$-stable distribution testing methods that are also effective for small number of observations.

In this paper, we propose a new goodness-of-fit method based on the quantile conditional variance (QCV) class of statistics that is designed to overcome the aforementioned problems; the set conditional variances are obtained by applying the standard variance function to a double quantile-trimmed (sample) data; see Sect. 3 for details. Although the theoretical variance for $\alpha$-stable distribution with $\alpha <2$ is infinite, the QCV always exist and can be used to fully characterize the $\alpha$-stable distribution. Our approach is the base of a novel testing procedure which seems to be superior in comparison to benchmark approaches based on the distance measurement between theoretical and empirical distributions. Moreover, the test statistics we propose are very easy to implement as they are based on simple characteristics. As we demonstrated in this paper, the new testing procedure is very effective, also for small samples, and the proposed approach can be effectively used to discriminate the light- and heavy-tailed distributions, even if they are close to each other, e.g. when $\alpha$ is close to 2. While in this paper we focus on tail-impact assessment tests for symmetric $\alpha$-stable distributions, our approach could be generalised to tackle the generic $\alpha$-stable distribution fit assessment; potential generalisations are discussed in Sects. 6 and  7.

A similar approach based on the QCV statistics was recently proposed in Jelito and Pitera (2020) to assess tail heaviness in reference to the Gaussian distribution. It has been shown that exemplary normality test based on QCV statistic and the 20/60/20 Rule outperform many benchmark frameworks including Jarque-Bera, Anderson-Darling, and Shapiro-Wilk tests; see Jaworski and Pitera (2016) where the 20/60/20 Rule in the context of the Gaussian distribution is studied. Also, we refer to Hebda-Sobkowicz et al. (2020b, 2020a), where a similar approach was used in signal analysis for fault disgnostics. Moreover, it has been recently shown in Jaworski and Pitera (2020) that QCV could be used to characterise the underlying distribution up to an additive constant – this lays out a theoretical basis for efficient testing procedures based on QCV statistics. While the QCV statistic is a natural (local) extension of the standard variance, so far it has been not considered in the literature apart from the mentioned papers. This might be surprising, as the conditional second moments seem to be a very natural tool e.g. for engineering and financial applications. In particular, this refers to flexibility coming from using conditional second moments instead of higher-order unconditional moments, see e.g. Cioczek-Georges and Taqqu (1995). Our paper builds upon those remarks and exploits interconnection between Jaworski and Pitera (2020) and Jaworski and Pitera (2016) in reference to $\alpha$-stable distributions. While we focus on goodness-of-fit testing, our approach is in fact quite general and could be applied in other contexts, e.g. for parameter fitting.

The rest of the paper is organized as follows: in Sect. 2 we define $\alpha$-stable distributions and indicate their main properties which are useful in the further analysis. In Sect. 3, we introduce the conditional variance characterisation of $\alpha$-stable distribution. Next, in Sect. 4 we analyze the sample quantile conditional variance for $\alpha$-stable distribution and the properties of the QCV estimatior. Next, in Sect. 5, we propose an exemplary statistical test for symmetric $\alpha$-stable distribution and check it efficiency on simulated datasets. This is the core part of the paper as our focus is set on the symmetric case. In particular, we compare the effectiveness of the test with known algorithms used for $\alpha$-stable distribution testing. Moreover, we demonstrate the efficiency of the new algorithm for the case when the stability index is close to 2. In Sect. 6, we comment on a more generic statistical testing for $\alpha$-stable distribution. In particular, we show a possible approach to non-symmetric goodness-of-fit testing. Then, in Sect. 7, we introduce a novel generic $\alpha$-stable distribution goodness-of-fit visual test based on the QCV statistics. Finally, in Sect. 8, we provide empirical analysis which show how the results presented in this paper could be applied. Datasets analyzed in this paper were studied already in Burnecki et al. (2015), where the problem of discriminating between the light- and heavy-tailed distributions was discussed; see also Burnecki et al. (2012). Our results provide further (statistically significant) quantification of claims made in the past and point out to additional features embedded into empirical datasets that were not discussed before. The last section concludes the paper.

2 The $\alpha$-stable distribution

The $\alpha$-stable random variable X is typically characterized by four real parameters: the stability index $\alpha \in (0,2]$, the scale parameter $c>0$, the skewness parameter $\beta \in [-1,1]$ and the location parameter $\mu \in \mathbb {R}$. One of the most common definition of the $\alpha$-stable distribution is through its characteristic function; see e.g. Samorodnitsky and Taqqu (1994); Nolan (2020).

Definition 1

We say that X follows the $\alpha$-stable distribution if its characteristic function is given by

$$\begin{aligned} \phi _X(t)={\mathbb {E}}e^{itX}=\left\{ \begin{array}{ll} \exp \left\{ -c^{\alpha }|t|^{\alpha }\left( 1-i\beta {{\,\mathrm{sgn}\,}}(t)\tan \left( \frac{\pi \alpha }{2}\right) \right) +i\mu t\right\} &{} \alpha \ne 1,\\ \exp \left\{ -c|t|\left( 1+i\beta \,\frac{2}{\pi } {{\,\mathrm{sgn}\,}}(t)\ln \left( |t|\right) \right) +i\mu t\right\} &{} \alpha = 1, \end{array}\right. \end{aligned}$$

(1)

where $\alpha \in (0,2]$, $\beta \in [-1,1]$, $c>0$, and $\mu \in {\mathbb {R}}$. For brevity, we write $X\sim S(\alpha ,c,\beta ,\mu )$. Also, in the case $\beta =0$, we say that X follows the symmetric (around median $\mu$) $\alpha$-stable distribution and write $X\sim S\alpha S(\alpha ,c,\mu )$.

The $\alpha$-stable distributions are considered as the generalisation of the Gaussian distribution. In fact, for $\alpha =2$ the $\alpha$-stable distribution is the Gaussian distribution with mean equal to $\mu$ and variance equal to $2c^2$; $\beta$ parameter is unimportant here. If $\alpha <2$, then the second moment (and thus the variance) of $\alpha$-stable distributed random variable X does not exist. Also, if $\alpha <1$, then the expected value of X is infinite. Let us now briefly discuss each parameter’s role.

First, the stability index parameter $\alpha \in [0,2]$ is responsible for the so-called heavy-tailed property of $\alpha$-stable distribution. This property is strongly related to the power-law behavior, which means that for $\alpha <2$, the distribution tail of $X\sim S(\alpha ,c,\beta ,\mu )$ is a power function

$$\begin{aligned} \left\{ \begin{array}{ll} \lim _{x\to\infty } x^{\alpha }P\{X>x\}=D_{\alpha }\frac{1+\beta }{2}c^\alpha ,\\ \lim _{x\to\infty } x^{\alpha }P\{X<-x\}=D_{\alpha }\frac{1-\beta }{2}c^\alpha , \end{array}\right. \end{aligned}$$

(2)

where $D_{\alpha }=\left( \int _0^{\infty }x^{-\alpha }\sin (x)dx\right) ^{-1}=\frac{1}{\pi } \Gamma (\alpha )\sin (\frac{\pi \alpha }{2})$ and $\Gamma (\cdot )$ is the Gamma function, see Samorodnitsky and Taqqu (1994).

Second, the skewness parameter $\beta \in [-1,1]$ gives the information about the symmetry of the distribution. Note that it cannot be directly linked to the usual skewness statistic as the the 3rd central moment of $\alpha$-stable distribution does not exist when $\alpha <2$.

Finally, the scale and location parameters $c>0$ and $\mu \in {\mathbb {R}}$ refer to the standard distributional properties related to affine transformations. Following Samorodnitsky and Taqqu (1994), we know that if $X\sim S(\alpha ,c,\beta ,\mu )$ then for any $b,a \in {\mathbb {R}}$, $a>0$, we get $aX+b\sim S(\alpha , ac,\beta , {\tilde{\mu }})$, where

$$\begin{aligned} {\tilde{\mu }} = {\left\{ \begin{array}{ll} a\mu +b &{}~\text{ if }~\alpha \ne 1;\\ a\mu -\frac{2}{\pi } a\ln |a|c\beta +b &{}~\text{ if }~\alpha = 1. \end{array}\right. } \end{aligned}$$

While $\alpha$-stable random variables are absolutely continuous for any set of parameters, their probability density function (PDF) in general has no closed (analytic) form. However, there are some instances, where it could be given explicitly. For example, this refers to the Gaussian distribution family $S\alpha S(2,c,\mu )$ with the PDF given by

$$\begin{aligned} f_X(x)=\frac{1}{2\pi c}e^{-\frac{(x-\mu )^2}{4c^2}},~~x\in {\mathbb {R}}, \end{aligned}$$

(3)

the Cauchy distribution family $S\alpha S(1,c,\mu )$ with the PDF defined as

$$\begin{aligned} f_X(x)=\frac{c}{\pi ((x-\mu )^2+c^2)},~~x\in {\mathbb {R}} \end{aligned}$$

(4)

and the Lévy distribution family $S(1/2,c,1,\mu )$ with the PDF given by

$$\begin{aligned} f_X(x)=\mathbb {1}_{(\mu ,\infty )}(x)\left( \frac{c}{2\pi }\right) ^{1/2}\frac{1}{(x-\mu )^{3/2}}e^{-\frac{c}{2(x-\mu )}},\,x\in {\mathbb {R}}. \end{aligned}$$

(5)

Also, the PDF of the $\alpha$-stable random variable X can be represented in a series or integral form. For instance, following Shao and Nikias (1993) and assuming that $\mu =0$ and $c=1$, we can represent $X\sim S \alpha S(\alpha ,1,0)$ PDF as

$$\begin{aligned} f_X(x)={\left\{ \begin{array}{ll}\displaystyle \frac{1}{\pi x}\sum _{k=1}^{\infty }\frac{(-1)^{k-1}}{k!}\Gamma \left( \alpha k+1\right) |x|^{-\alpha k}\sin \left( \frac{k\alpha \pi }{2}\right) , ~\text{ if }~0<\alpha <1\\ \displaystyle \frac{1}{\pi \alpha }\sum _{k=0}^{\infty }\frac{(-1)^k}{(2k)!}\Gamma \left( \frac{2k+1}{\alpha }\right) x^{2k}, ~\text{ if }~ 1 \le \alpha \le 2.\end{array}\right. } \end{aligned}$$

(6)

The series given in (6) is absolutely convergent for any $x\in {\mathbb {R}}$; see Bergstrom (1952); Feller (1966). Although, the series expansions of PDF for symmetric $\alpha$-stable random variables are known, the asymptotic of series expansions are good only in the tails. The origin of the PDF deviate from the theoretical PDF for intermediate values, see Tsihrintzis and Nikias (1993). For other representations, we refer the reader for instance to Nolan (2020, 1997); Cizek et al. (2005).

3 Conditional variance characterisation of the $\alpha$-stable distributions

For now, let us assume that X is a generic absolutely continuous random variable. For any $A\in \Sigma$, such that $\mathbb {P}[A]\ne 0$, we define the conditional variance of Xon A by

$$\begin{aligned} {{\,\mathrm{Var}\,}}[X| A]:=\mathbb {E}\left[ (X - \mathbb {E}[X| A])^2 \,|\,A\right] , \end{aligned}$$

(7)

where $\mathbb {E}[\cdot |A]$ is the standard conditional (set) expectation operator; note that (7) might be non-finite. For brevity, for any $0\le a<b \le 1$, we also define the quantile trimmed subdomain of X by $A_X(a,b):= \{X\in (F^{-1}_X(a),F^{-1}_X(b))\} \in \Sigma$ and related quantile conditional variance (QCV) of X given by

$$\begin{aligned} \sigma ^2_X(a,b):= {{\,\mathrm{Var}\,}}[X| A_X(a,b)]. \end{aligned}$$

(8)

For completeness, note that: (a) $\mathbb {P}[A_X(a,b)]=b-a> 0$ so the definition is well posted; (b) for $0<a<b<1$ the value of (8) is finite; (c) for any $c>0$ and $\mu \in \mathbb {R}$ we get $\sigma ^2_{c X+\mu }(\cdot ,\cdot )=c^2\sigma ^2_{X}(\cdot ,\cdot )$; (d) ${{\,\mathrm{Var}\,}}[X]=\sigma ^2_{X}(0,1)$.

Recently, it has been shown in Jaworski and Pitera (2020) that the family of QCVs could act as law classifiers; see Theorem 2.¹

Theorem 2

Let X, Y be (absolutely continuous) random variables such that $\sigma ^2_X(a,b)=\sigma ^2_Y(a,b)$, for $0\le a<b \le 1$. Then, there exists $\mu \in {\mathbb {R}}$ such that $F_X(t)=F_{Y+\mu }(t)$, $t\in {\mathbb {R}}$, i.e. the laws of X and Y coincide almost surely up to an additive-constant.

Note that in Theorem 2, using standard limit arguments, we get that consideration of limit values $a=0$ and $b=1$ (for which QCV might be non-finite) is in fact not required to get full classification. Because of that, from now on, we assume that $0<a<b<1$. In particular, this implies that all QCVs in scope are finite.

Based on Theorem 2 we can characterise the $\alpha$-stable distribution by providing information about QCVs. While the general analytic formula for the QCV of $\alpha$-stable distribution is unknown, it could be efficiently computed using standard methods. In particular, for $S\alpha S(\alpha ,c,\mu )$ class, we can use the series expansion given in (6) to get the formula of QCV; see Proposition 3.

Proposition 3

Let $X\sim S\alpha S(\alpha ,c,\mu )$ and let $0<a<b<1$. Then, the following holds

$$\begin{aligned} \sigma ^2_X(a,b)= {\left\{ \begin{array}{ll}\displaystyle \frac{c^2}{\pi \alpha }\sum _{k=0}^{\infty }\frac{(-1)^k}{(2k)!}\Gamma \left( \tfrac{2k+1}{\alpha }\right) A_{2k+3}-\left( \frac{c}{\pi \alpha }\sum _{k=0}^{\infty }\frac{(-1)^k}{(2k)!}\Gamma \left( \tfrac{2k+1}{\alpha }\right) A_{2k+2}\right) ^2, &{} \text {if } \alpha \ge 1,\\ \displaystyle \frac{c^2}{\pi }\sum _{k=1}^{\infty }\frac{(-1)^{k-1}}{k!}\Gamma \left( \alpha k+1\right) \sin \left( \tfrac{k\alpha \pi }{2}\right) B_{2-\alpha k}-\left( \frac{c}{\pi }\sum _{k=1}^{\infty }\frac{(-1)^{k-1}}{k!}\Gamma \left( \alpha k+1\right) \sin \left( \tfrac{k\alpha \pi }{2}\right) B_{1-\alpha k}\right) ^2, &{} \text {if }\alpha <1, \end{array}\right. } \end{aligned}$$

(9)

where $A_i:=[F_X^{-1}(b)^{i}- F_X^{-1}(a)^{i}]/i(b-a)$, and $B_i:=[\text {sign}(F_X^{-1}(b))F_X^{-1}(b)^{i}-\text {sign}(F_X^{-1}(a))F_X^{-1}(a)^{i}]/i(b-a)$, for $i\in \mathbb {R}\setminus \{0\}$.

Proof

Let $0<a<b<1$. From (7), we get $\sigma ^2_X(a,b)=\mathbb {E}[X^2 \,|\,A_X(a,b)]- \mathbb {E}^2\left[ X \,|\,A_X(a,b)\right]$. Without loss of generality we can assume that $\mu =0$ and $c=1$. Recalling that $A_X(a,b)= \{X\in (F^{-1}_X(a),F^{-1}_X(b))\}$, which implies $\mathbb {P}[A_X(a,b)]=b-a$, we get

$$\begin{aligned} \sigma ^2_X(a,b)= & {} \frac{1}{b-a}\mathbb {E}\left[ \mathbb {1}_{A_X(a,b)}X^2\right] - \frac{1}{(b-a)^2}\mathbb {E}^2\left[ \mathbb {1}_{A_X(a,b)}X\right] \nonumber \\= & {} \int _{F_X^{-1}(a)}^{F_X^{-1}(b)}\frac{x^2f_X(x)}{b-a}dx-\left( \int _{F_X^{-1}(a)}^{F_X^{-1}(b)}\frac{xf_X(x)}{b-a}dx\right) ^2. \end{aligned}$$

(10)

Next, by plugging (6) directly into (10) and doing standard algebraic calculations, we get (9). $\square$

Note that representation (9) is useful when one wants to quickly calculate the value of QCV for symmetric $\alpha$-stable distributions. Also, for some special cases, representation (6), and consequently (9), reduces to a more elegant non-series form. In particular, for $\alpha =2$, i.e. when $X\sim S\alpha S(2,c,\mu )$ has Gaussian distribution, we use (3) to get closed form formula for the conditional variance given by

$$\begin{aligned} \sigma ^2_X(a,b)= 2c^2\left( \frac{\Phi ^{-1}(a)\phi (\Phi ^{-1}(a))-\Phi ^{-1}(b)\phi (\Phi ^{-1}(b))}{b-a} -\frac{\left( \phi (\Phi ^{-1}(a))-\phi (\Phi ^{-1}(b))\right) ^2}{(b-a)^2}+1\right) , \end{aligned}$$

where $\Phi (\cdot )$ and $\phi (\cdot )$ denote the standard normal cumulative distribution function (CDF) and PDF; see Section 13.10.1 in Johnson et al. (1994). Similarly, assuming $\alpha =1$, i.e. when $X\sim S\alpha S(1,c,\mu )$ has Cauchy distribution, we use (4) to get

$$\begin{aligned}&\sigma _X^2(a,b)=\frac{c^2}{b-a}\left( \frac{F_X^{-1}(b)-F_X^{-1}(a)}{D_X(a,b)}-1\right) \nonumber \\&\quad -\frac{c^2}{4D_X^2(a,b)(b-a)^2}\ln ^2\left( \frac{1+F^{-1}_X(b)^2}{1+F^{-1}_X(a)^2}\right) , \end{aligned}$$

(11)

where $D_X(a,b):=tan^{-1}\left( F_X^{-1}(b)\right) -tan^{-1}\left( F_X^{-1}(a)\right)$; see Nadarajah and Kotz (2006) for details.

While in the non-symmetric case the formula for QCV is not available, it is relatively easy to approximate it using simulated data. Also, using (5), we can get concise formula for the QCV for (non-symmetric) Lévy distributions, i.e. for $X\sim S(1/2,c,1,\mu )$ we obtain

$$\begin{aligned} \sigma _X^{2}(a,b)=\frac{c^2}{3(b-a)}\left( F_X^{-1}(b)G_1(F^{-1}_X(b))-F_X^{-1}(a)G_1(F^{-1}_X(a))-H_X(a,b)\right) -\frac{c^2}{(b-a)^2}H_X^2(a,b), \end{aligned}$$

(12)

where $H_X(a,b):=[G_1(F^{-1}_X(b))-G_1(F^{-1}_X(a))] + [G_2(F^{-1}_X(b))-G_2(F^{-1}_X(a))]$, $G_1(z):=\sqrt{\tfrac{2z}{\pi }}e^{-\frac{1}{2z}}$, $G_2(z):=erf((2z)^{-\frac{1}{2}})$, and erf is the standard error function. The above formula is a consequence of applying the Lévy distribution PDF (5) to the Eq. (10).

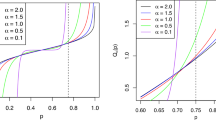
To conclude this section, we illustrate the dynamics of the QCV for exemplary parameter shifts for $\alpha$-stable distribution; see Fig. 1. Monotonic behaviour visible on the graphs indicate that distribution parameters might be represented via QCV. Nevertheless, the detailed analysis of this fact is out of scope of the paper.

Fig. 1

Illustration of QCV for $S(\alpha ,1,\beta ,0)$ distribution as a function of $\alpha$ (left panel), $\beta$ (middle panel), and quantile interval (a, b) (right panel). In the left panel, we present QCV values for five $\beta$ parameter values and $(a,b)=(0.2,0.8)$ showing how QCV is changing as $\alpha$ increases. In the middle panel, we demonstrate QCV values for five $\alpha$ parameter values and $(a,b)=(0.2,0.8)$ showing how QCV is changing with respect to $\beta$ parameter. In the right panel, we assume that $b=1-a$ and $\beta =0$, and demonstrate QCV values for $a\in [0.1,0.5]$. The calculations are performed based on $100\,000$ Monte Carlo simulations. To increase the transparency, we restrict $\alpha$ parameter values to (1, 2]

4 The sample quantile conditional variance estimator and its properties for the $\alpha$-stable distributions

In this section we introduce the sample QCV estimator and comment on it basic properties. This will be a core object used for goodness-of-fit testing. While in this section we focus on a generic choice of quantile thresholds $0<a<b<1$ for a single QCV, in practical applications one choose specific linear combinations (or ratios) of QCVs with different predefined thresholds in order to allow efficient statistical testing of certain distributional assumptions such as heavy-tails or asymmetry. We refer to Sects. 5 and  6 for details.

Given independent and identically distributed (i.i.d.) sample $(X_1,\ldots , X_n)$ and quantile values $0<a<b<1$, the sample estimator of $\sigma ^2_X(a,b)$ is given by

$$\begin{aligned} {\hat{\sigma }}_X^2(a,b):=\frac{1}{[nb]-[na]}\sum _{i=[na]+1}^{[nb]} \Big (X_{(i)}-{\hat{\mu }}_X(a,b)\Big )^2, \end{aligned}$$

(13)

where ${\hat{\mu }}_X(a,b):=\frac{1}{[nb]-[na]}\sum _{i=[na]+1}^{[nb]}X_{(i)}$ is the conditional sample mean, $X_{(k)}$ is the kth order statistic of the sample, and $[x]:=\max \{k\in {\mathbb {Z}}:k\le x\}$ denotes the integral part of $x\in \mathbb {R}$. Note that while (13) might look complicated, it could be computed by applying the following straightforward logic: first, sort the sample; second, take a subset of observations induced by empirical quantiles linked to a and b²; third, compute standard sample variance on the subset of observations. Using standard arguments one can check that for any $0<a<b<0$ the QCV estimator $\hat{\sigma }_X^2(a,b)$ is consistent and follows the usual CLT dynamics; these facts are summarised in Proposition 4.

Proposition 4

Let $X \sim S (\alpha ,c,\beta ,\mu )$. Then, for any $0<a<b<1$, we get

$$\begin{aligned} \hat{\sigma }_X^2(a,b) \xrightarrow {\,\,\mathbb {P}\,\,} \sigma _X^2(a,b),\qquad ~\text{ when }~ n\to\infty, \end{aligned}$$

i.e. the QCV sample estimator is consistent, and

$$\begin{aligned} \sqrt{n}\left( \hat{\sigma }_X^2(a,b)-\sigma ^2_X(a.b)\right) \xrightarrow {\,\,d\,\,}{\mathcal {N}}(0,c\tau ),\qquad ~\text{ when }~ n\to \infty , \end{aligned}$$

where $\tau >0$ is a fixed constant depending on the stability index $\alpha$, symmetry parameter $\beta$ and quantile interval (a, b).

Proof

The proof is based on the standard trimmed-mean arguments introduced e.g. in Stigler (1973). For completeness, let us show an outline of the second part of the proof; see Jelito and Pitera (2020) for details. Let $0<a<b<1$ and let $(X_i)$ be a sample from the same distribution as X. First, noting that X is absolutely continuous, using (Jelito and Pitera 2020, Lemma 1) and (Jelito and Pitera 2020, Lemma 2) we know that ${\hat{\mu }}_{X}(a,b)\xrightarrow {\,{\mathbb {P}}\,}\mu _{X}(a,b)$ and $\sqrt{n}\left[ {\hat{\mu }}_{X}(a,b)- \mu _{X}(a,b)\right] \xrightarrow {\,d\,}{\mathcal {N}}(0,\eta )$, $n\to \infty$, where $\mu _{X}(a,b)$ is the theoretical conditional mean of X and $\eta$ is some constant. Also, using (Jelito and Pitera 2020, Lemma 3), we get $\sqrt{n}\left( \hat{\sigma }_X^2(a,b)-{\hat{s}}_X^2(a,b)\right) \xrightarrow {\,{\mathbb {P}}\,}0$, as $n\to\infty$, where

$$\begin{aligned} {\hat{s}}_X^2(a,b):=\frac{1}{[nb]-[na]}\sum _{i=[na]+1}^{[nb]} \Big (X_{(i)}-\mu _X(a,b)\Big )^2. \end{aligned}$$

Consequently, it is enough to show that $\sqrt{n}\left( {\hat{s}}_X^2(a,b)-\sigma ^2_X(a.b)\right) \xrightarrow {\,\,d\,\,}{\mathcal {N}}(0,d)$, as $n\to\infty$, for some constant $d\in \mathbb {R}$. For brevity, we introduce additional notation

$$\begin{aligned} Z_n :=\sqrt{n}\,{\hat{s}}_X^2(a,b),\quad A_n :=\sum _{i=1}^n \mathbb {1}_{\{X_i\le F^{-1}_X(a) \}},\quad B_n :=\sum _{i=1}^n \mathbb {1}_{\{X_i\le F^{-1}_X(b) \}},\quad m_n:=[nb]-[na], \end{aligned}$$

and define the directed sum

$$\begin{aligned} \mathop {S}_{{i=k}}^l a_i:= {\left\{ \begin{array}{ll} \sum _{i=k+1}^l a_i, &{}\text {if }k<l,\\ 0, &{}\text {if k}=l\\ -\sum _{i=l+1}^k a_i, &{}\text {if }k>l,\\ \end{array}\right. } \end{aligned}$$

for any sequence of numbers $(a_i)$. The first step of the proof is to split $Z_n$ into two parts: one representing the deterministic trimmed mean component and one representing the residual component from quantile estimated thresholds. Namely, we have

$$\begin{aligned} Z_n&= \frac{\sqrt{n}}{m_n} \Bigg (\sum _{i=A_n+1}^{B_n} S_{(i)} + \mathop {S}\limits _{{i=[na]}}^{A_n} S_{(i)} + \mathop {S}\limits _{{i=B_n}}^{[nb]}S_{(i)}\Bigg ), \end{aligned}$$

(14)

where $S_{(i)}:=\left( X_{(i)}-\mu _X(a,b) \right) ^2$. Introducing $K(\cdot ):=\left( F^{-1}_X(\cdot )-\mu _X(a,b)\right) ^2$, we can rewrite formula (14) as

$$\begin{aligned} Z_n&= \frac{\sqrt{n}}{m_n} \Bigg (\Bigg (\sum _{i=A_n+1}^{B_n} S_{(i)} +(A_n-[na])K(a) +([nb]-B_n)K(b)\Bigg )\nonumber \\&\quad + \mathop {S}\limits _{{i=[na]}}^{A_n} \left( S_{(i)}-K(a)\right) + \mathop {S}\limits _{{i=B_n}}^{[nb]}\left( S_{(i)}-K(b)\right) \Bigg ). \end{aligned}$$

(15)

In the second step of the proof, we show that

$$\begin{aligned} \frac{\sqrt{n}}{m_n}\mathop {S}\limits _{{i=[na]}}^{A_n} \left( S_{(i)}-K(a)\right) \xrightarrow {{\mathbb {P}}} 0\quad \text {and}\quad \frac{\sqrt{n}}{m_n}\mathop {S}\limits _{{i=B_n}}^{[nb]} \left( S_{(i)}-K(b)\right) \xrightarrow {{\mathbb {P}}} 0. \end{aligned}$$

(16)

For brevity, we only show the proof for of the first convergence; the proof for the second convergence is analogous. First, note that

$$\begin{aligned} 0\le \left| \frac{\sqrt{n}}{m_n}\mathop {S}\limits _{{i=[na]}}^{A_n} \left( S_{(i)}-K(a)\right) \right| \le \frac{A_n-[na]}{m_n/\sqrt{n}}\left| \max \{S_{([na])}-K(a),S_{([A_n])}-K(a)\}\right| . \end{aligned}$$

Second, due to consistency of quantile estimators $X_{([na])}$ and $X_{([A_n])}$, we get $S_{([na])}-K(a)\xrightarrow {{\mathbb {P}}}0$ and $S_{(A_n)}-K(a)\xrightarrow {{\mathbb {P}}}0$, so it is enough to show that $\frac{A_n-[na]}{m_n/\sqrt{n}}$ converges to normal distribution. Noting that $m_n/n \to b-a$ and $(na-[na])/\sqrt{n}\to 0$, as $n\to \infty$, and applying Central Limit Theorem combined with Slutsky’s Theorem (see Ferguson (1996)) to $A_n\sim B\left( n,a\right)$, we get

$$\begin{aligned}&\frac{A_n-[na]}{m_n / \sqrt{n}} =\frac{\sqrt{n}\left( \frac{1}{n}A_n-a\right) }{m_n/ n}\\&\quad +\frac{(na-[na])/\sqrt{n}}{m_n / n} \xrightarrow {\,\,\,\,d\,\,\,\,} {\mathcal {N}}\left( 0,\sqrt{\frac{a(1-a)}{b-a}}\right) . \end{aligned}$$

This concludes the proof of (16). The third and final step of the proof is to apply Central Limit Theorem to $Z_n$. Noting that $(na-[na])/\sqrt{n}\to 0$ and $(nb-[nb])/\sqrt{n}\to 0$, we can rewrite (15) as

$$\begin{aligned} Z_n = \frac{\sqrt{n}}{m_n} \Bigg (\sum _{i=A_n+1}^{B_n} S_{(i)} +(A_n-na)K(a) +(nb-B_n)K(b)\Bigg ) +r_n, \end{aligned}$$

where $r_n \xrightarrow {{\mathbb {P}}}0$. Thus, recalling definitions of $S_{(i)}$, $A_n$ and $B_n$, we get

$$\begin{aligned} Z_n= & {} \frac{\sqrt{n}}{m_n} \sum _{i=1}^{n} \Bigg (\mathbb {1}_{\left\{ F_X^{-1}(a)\le X_i \le F_X^{-1}(b)\right\} }\left( X_{i}-\mu _X(a,b) \right) ^2 \\&\quad +(\mathbb {1}_{\{X_i\le F^{-1}_X(a) \}}-a)K(a) +(b-\mathbb {1}_{\{X_i\le F^{-1}_X(b) \}})K(b)\Bigg ) +r_n. \end{aligned}$$

Applying Central Limit Theorem combined with Slutsky’s Theorem to the sum and noting that for $1\le i\le n$ we get

$$\begin{aligned}&\frac{1}{b-a}\mathbb {E}\left[ \mathbb {1}_{\left\{ F_X^{-1}(a)\le X_i \le F_X^{-1}(b)\right\} }\left( X_{i}-\mu _X(a,b) \right) ^2\right] \\&\quad =\sigma ^2_X(a,b),\quad \mathbb {E}\left[ \mathbb {1}_{\{X_i\le F^{-1}_X(a) \}}-a\right] =0,\quad \text {and}\quad \mathbb {E}\left[ b-\mathbb {1}_{\{X_i\le F^{-1}_X(b)\}}\right] =0, \end{aligned}$$

we conclude the proof. $\square$

Note that the constant $\tau >0$ in Proposition 4 might be easily approximated using Monte Carlo simulations. Moreover, in some specific cases one might provide an explicit formula for $\tau$; see Appendix A in Jelito and Pitera (2020) where closed-form formula for $\tau$ in the case of the Gaussian distribution is provided. Also, it should be noted that using Proposition 4 and (multivariate) Central Limit Theorem we immediately get that any linear combination of QCV sample estimators is also asymptotically normal, i.e. we get

$$\begin{aligned} \sqrt{n}\left( \sum _{i=1}^{k}d_i\hat{\sigma }_X^2(a_i,b_i)-\sum _{i=1}^{k}d_i\sigma ^2_X(a_i,b_i)\right) \xrightarrow {\,\,d\,\,}{\mathcal {N}}(0,c\tau )\qquad n\to \infty , \end{aligned}$$

(17)

where $0<a_i<b_i<0$ and $d_i\in \mathbb {R}$ for ($i=1,2\ldots ,k$), and $\tau >0$ is some fixed constant. Dividing (17) by another (non-degenerate) linear combination of quantile conditional variances we get a statistic that is a pivotal quantity with respect to both location parameter $\mu \in \mathbb {R}$ and scale parameter $c>0$. This could be easily shown using e.g. Slutsky’s Theorem; see Ferguson (1996). For an outline of the proof of those facts, we refer to the proof of Theorem 6.1 in Jelito and Pitera (2020).

5 Statistical test for symmetric $\alpha$-stable distribution based on the quantile conditional variances statistics

Based on (17), we know that one can use the linear combination of sample QCVs for efficient goodness-of-fit parameter testing. Arguably, the stability index parameter $\alpha \in (0,2]$ is the most important $\alpha$-stable distribution shape parameter as it controls tail-heaviness. In fact, most $\alpha$-stable distribution goodness-of-fit test focus on this parameter in the symmetric case; location and scale oriented testing is usually performed using more standard methods. We refer to Matsui and Takemura (2008) and Wilcox (2017) for details.

In this section we present a test statistic family that might be used to test stability index $\alpha$ parameter specification for $S\alpha S(\alpha ,c,\mu )$ distributions. We refer to Sect. 6 for a discussion about skewness parameter inclusion in the proposed goodness-of-fit method and to Sect. 7 for a more generic QCV overall distribution fit framework that takes into account stability index, skewness, and scale parameters.

Recalling that the stability index $\alpha$ could be linked to tail behavior, we decided to follow the approach similar to the one introduced in Jelito and Pitera (2020). More explicitly, we decided to compare tail QCVs with central region QCV to assess how heavy are the tails.

The generic family of test statistics we consider that could be used for goodness-of-fit testing for any distribution is given by

$$\begin{aligned} \text {N}:= \sqrt{n}\, \frac{ d_1{\hat{\sigma }}^2_x(a_1,a_2) +d_2 {\hat{\sigma }}^2_x(a_2,a_3) + d_3{\hat{\sigma }}^2_x(a_3,a_4)}{{\hat{\sigma }}^2_x(a_1,a_4)}, \end{aligned}$$

(18)

where $x=(x_1,\ldots ,x_n)$ is a sample from the same distribution as the random variable X, $d_1,d_2,d_3\in \mathbb {R}$ are fixed weight parameters, $0<a_1<a_2<a_3<a_4<1$ correspond to quantile split parameters, and ${\hat{\sigma }}^2_x(a,b)$ denote QCV empirical estimator for sample x on quantile interval (a, b). Note that ${\hat{\sigma }}_x(a_1,a_4)$ is used for normalisation purposes: it makes $\text {N}$ invariant to affine transformations of X. In other words, the choice of location parameter $\mu$ and scale parameter c do not impact values of $\text {N}$ making it a pivotal quantity. Next, we find specific choices of parameters that could be used for generic $\alpha$-stable goodness-of-fit testing.

5.1 Specific choice of parameters of test statistic for symmetric $\alpha$-stable distribution

Taking into account that X is symmetric, we decided to set $a_4:=1-a_1$, $a_3:=1-a_2$, and $d_1:=d_3$, which reduced the number of input specification parameters to four, i.e. $a_1$, $a_2$, $d_1$, and $d_2$. For given $a_1$ and $a_2$, we fix values of $d_1$ and $d_2$ in such a way, that the resulting test statistic $\text {N}$ is normalised when $\alpha =2$. To be more precise, we assume that $d_1>0$ and find values of $d_1$ and $d_2$ in such a way that $\text {N}$ is (asymptotically) close to standard normal (for $\alpha =2)$; please recall that theoretical QCV values could be obtained from Proposition 3. Consequently, we can focus on the choice of the quantile parameters $(a_1,a_2)$.

For transparency, we decided to take three $(\alpha _1,\alpha _2)$ quantile splits. Namely, we take values $(5\%,25\%)$, $(0.5\%,25\%)$ and $(0.5\%,4\%)$; they correspond to quantile ratio data splits

$$\begin{aligned} 5/20/50/20/5,\quad 0.5/24.5/50/24.5/0.5, \quad \text {and}\quad 0.5/3.5/92/3.5/0.5. \end{aligned}$$

The first parameter set, $(5\%,25\%)$, is a generic choice which should be good for general testing for all sample sizes. We compare 50% central region QCV with the trimmed tail QCVs; the top and bottom 5% trimming should ensure finiteness of tail QCVs while not inducing severe (reduced conditional sample size) volatility. The second choice, $(0.5\%,25\%)$, might be seen as a modification of the first one for larger samples. We reduced top and bottom trimming from 5% to 0.5% while maintaining the central 50% area. This should increase sensitivity of tail QCVs allowing more accurate $\alpha$ testing when the underlying sample size is large. The third statistic, $(0.5\%,4\%)$, is designed to detect minor $\alpha$ changes for large sample sizes. It is focused on extreme tail QCVs and should be good for very small $\alpha$ change tests; note this is aligned with results observed in the right plot in Fig. 6. To sum up, we introduce three different versions of test statistic (18) that are given by

$$\begin{aligned} \text {N}_1&:=\sqrt{n}\cdot \frac{1.00\cdot {\hat{\sigma }}^2_x(5\%,25\%)-1.01\cdot {\hat{\sigma }}^2_x(25\%,75\%)+ 1.00\cdot {\hat{\sigma }}^2_x(75\%,95\%)}{{\hat{\sigma }}^2_x(5\%,95\%)};\end{aligned}$$

(19)

$$\begin{aligned} \text {N}_2&:=\sqrt{n}\cdot \frac{0.60\cdot {\hat{\sigma }}^2_x(0.5\%,25\%)-1.61\cdot {\hat{\sigma }}^2_x(25\%,75\%)+ 0.60\cdot {\hat{\sigma }}^2_x(75\%,99.5\%)}{{\hat{\sigma }}^2_x(0.5\%,99.5\%)};\end{aligned}$$

(20)

$$\begin{aligned} \text {N}_3&:=\sqrt{n}\cdot \frac{1.15\cdot {\hat{\sigma }}^2_x(0.5\%,4\%)-0.17\cdot {\hat{\sigma }}^2_x(4\%,96\%)+ 1.15\cdot {\hat{\sigma }}^2_x(96\%,99.5\%)}{{\hat{\sigma }}^2_x(0.5\%,99.5\%)}. \end{aligned}$$

(21)

For completeness, in Fig. 2 we present the plots of the limit values of $\text {N}_i$, $i=1,2,3$ depending on $\alpha \in (1,2]$ without the factor $\sqrt{n}$. Note that in the limit all test statistic are decreasing functions of $\alpha$, so that their asymptotic power is equal to one (within the class of symmetric $\alpha$-stable distributions).

Test statistics $N_1$, $N_2$, and $N_3$ establish a generic statistical framework that could be used for efficient goodness-of-fit testing for (symmetric) $\alpha$-stable distributions for all possible choices of parameters and sample sizes. Essentially, the specific choice of an appropriate statistic depends on the underlying goal and sample size. If one is interested in generic $\alpha$-stable goodness-of-fit test for moderate sample size, then $N_1$ is the best choice. If the sample size is larger and we want to test $\alpha$ parameter values which are relatively close to 2, e.g. when $1.5<\alpha <1.9$ then one should use $N_2$. Finally, if we are interested in efficient discrimination of parameters for values of $\alpha$ very close to 2, e.g. when $1.9<\alpha$ then we recommend using $N_3$. See Sects. 5.2.2 and  5.2.3 when a comprehensive comparison study with focus set on test power is made. Nevertheless, it should be noted that our choice of three conditioning sets and related specifications are just exemplary choices – QCV based tests allow very flexible statistic construction which could be tailored to particular testing needs. Still, given a specific sample at hand, one should avoid specific tuning of parameters $a_i$ and $d_i$ as it would effectively reduce the statistical power of the test, see Miller (2012) and references therein.

Fig. 2

Illustration of the values of $\text {N}$ statistic for $S\alpha S(\alpha ,1,0)$ distribution for three exemplary parameter specifications, see (19)-(21), with respect to the $\alpha$ parameter. For transparency, we restrict parameter set to $\alpha \in (1,2]$; similar behaviour is observed on the full parameter range

5.2 Power simulation study

In this section we check the effectiveness of the proposed testing procedure by Monte Carlo simulations. More precisely, we calculate the power of the introduced goodness-of-fit tests based on $N_1, N_2$ and $N_3$ test statistics defined in (19), (20) and (21), respectively. We compare the powers of the tests based on the QCV statistics with benchmark tests for $\alpha$-stable distribution that are based on the empirical and theoretical distribution distance.

5.2.1 Comparison to other tests

In order to demonstrate how effective is the test based on the QCV statistics, we consider the power of the tests based on $N_1$, $N_2$ and $N_3$ statistics defined in (19)-(21). In this subsection, for simplicity, we consider only the two-sided (TS) tests; in the further analysis we show results for one-sided tests as well. We perform the analysis under $H_0$ hypothesis stating that the sample comes from the symmetric $\alpha$-stable distribution $S\alpha S(\alpha _0,1,0)$, where $\alpha _0:=1.5$; note that scale and location parameters are not important here as test statistics $N_1$, $N_2$ and $N_3$ are invariant to affine transformations. The values of $N_1$, $N_2$, and $N_3$ statistics under the $H_0$ hypothesis are calculated based on the $100\,000$ strong Monte Carlo simulation for various sample size $n\in \{20,50,100,500,1000,2000\}$. We check the powers of the tests for $H_1$ hypotheses stating that random sample comes from distribution $S\alpha S(\alpha _1,1,0)$, where $\alpha _1\in \{1.1, 1.2,\ldots ,2.0\}$. It should be mentioned that in the real application the $\alpha$-stable distribution with $\alpha \le 1$ is rarely applied, thus we decided present the results for $\alpha > 1$. For each case, the power is calculated using the $10\,000$ simulations for the sample corresponding to the $H_1$ hypothesis.

For comparison, powers of $N_1$, $N_2$, and $N_3$ tests are confronted with powers of the benchmark tests for $\alpha$-stable distribution. We decided to consider the standard goodness-of-fit tests that are based on measuring the distance between the empirical and theoretical distributions. Namely, we consider Kolmogorov-Smirnov (KS) cumulative probability test, the Kuiper test, the Watson test, the Cramer-von Mises (CvM) test, and the Anderson-Darling (AD) test, see Chakravarti et al. (1967); Srinivasan (1971); Watson (1961); Anderson (1962); Anderson and Darling (1954). These statistical tests could be considered as benchmark choices that are commonly used for the $\alpha$-stable distribution testing and are considered to be very efficient in the real data analysis; see Cizek et al. (2005) for details. For consistency, all benchmark test powers are calculated using similar framework with the same number of strong Monte Carlo simulations for $H_0$ and $H_1$ hypotheses, for $n=20,50,100,500,1000,2000$. In particular, please note that this gives us control over Type I errors that are encoded into the underlying significance levels.

In Fig. 3, we present test powers for the significance level $5\%$. Results for significance level $1\%$ are similar and deferred to the Appendix; see Fig. 13. Surprisingly, as one can see, the tests based on the QCV statistics outperform all other considered tests, even for small sample sizes ($n=20$ and $n=50$).

Fig. 3

Power of the tests based on the QCV statistics ($N_1,N_2,N_3$) with comparison to other benchmark goodness-of-fit tests for different sample lengths. For the comparison we took into consideration the following tests: Kolmogorov-Smirnov two-samples test (KS), Kuiper test (Kuiper), Watson test (Watson), Cramer-von Mises test (CvM) and Anderson-Darling test (AD). The $H_0$ hypothesis is $S\alpha S(1.5,1,0)$. Powers are calculated on the basis of $10\,000$ Monte Carlo simulations for samples corresponding to $H_1$ hypothesis, i.e. for $S\alpha S(\alpha ,1,0)$. The significance level is equal to $5\%$. For all sample sizes, the QCV based tests outperform benchmark frameworks; note that in the top left plot ($n=20$) the values for $N_3$ are not available due to low quantile specification for this test statistic. For transparency, we added the legend only to the top left plot. See Figure 13 for results for significance level $1\%$

It should be highlighted that the $N_1$-based test seems to be the most effective for $\alpha _1<1.5$, i.e. when the tested $\alpha$ corresponding to $H_1$ hypothesis is smaller than the $\alpha$ corresponding to the $H_0$ hypothesis, while the $N_2$ test is the best one in the case $\alpha _1>1.5$, i.e. when $\alpha$ from $H_1$ hypothesis is higher than $\alpha$ for $H_0$ hypothesis. This might be potentially traced back to the fact that the higher the $\alpha$ the more stable (slimmer) the tails. In consequence, the standard error of the QCV estimator of ${\hat{\sigma }}^2_X(0.5\%,25\%)$ in (20) is decreasing. This improves the performance of $N_2$ in reference to $N_1$.

The $N_3$ test is ineffective for small sample size ($n=20$) because of the extreme quantile specification. Due to the fact that $\lfloor 20\cdot 0.04\rfloor <1$ we have only one observation in the tail conditioning sets which is not sufficient to estimate tail QCV. In general, $N_3$ test is more effective when $\alpha _1>1.5$.

For large sample sizes, all considered tests seem to be effective. However, the tests based on the QCV statistics are more restrictive. In Table 1, we demonstrate the details of the results presented in Fig. 3 for exemplary sample size $n=500$. One can see the difference between the powers of the tests proposed in this paper ($N_1$ test and $N_2$ test) are clearly higher that the powers of other considered tests. For completeness, test powers for other sample sizes are collected in tables 4, 5, 6,7, 8 in Appendix B.

Table 1 Comparison of the powers of the tests for $S\alpha S(1.5,1,0)$ distribution ($H_0$ hypothesis) against $S\alpha S(\alpha _1,1,0)$ distribution for ($H_1$ hypothesis)

To provide further insight in reference to Type I and Type II errors as well as sample size impact analysis we pick one representative $H_1$ alternative hypothesis for $\alpha _1=1.7$ and study corresponding p-value distributions. Also, we study test powers for more granular sample size specification. The results for other alternative hypotheses are essentially the same and are available from the authors upon request.

In Fig. 4 we present comparison of p-value distributions of the tests for $S\alpha S(1.5,1,0)$ distribution ($H_0$ hypothesis) against $S\alpha S(1.7,1,0)$ distribution ($H_1$ hypothesis) for various sample sizes n. In particular, one can observe stochastic dominance of $N_2$ test p-values with respect to all benchmark tests. Overall, the results prove that within $\alpha$-stable framework our test should give best control over both Type I and Type II errors; please recall that all p-values are based on sample-size tailored Monte Carlo simulation which links them to Type I errors.

Fig. 4

Comparison of p-value cumulative distributions of the tests for $S\alpha S(1.5,1,0)$ distribution ($H_0$ hypothesis) against $S\alpha S(1.7,1,0)$ distribution ($H_1$ hypothesis) at $t\in [0,0.15]$ for various sample sizes n. The following tests are taken under consideration: the two-sided $N_1$, $N_2$ and $N_3$ tests proposed in this paper, Kolmogorov-Smirnov (KS) two-samples test, Kuiper test, Watson test, Cramer-von Mises (CvM) test and Anderson-Darling (AD) test. For all sample sizes, $N_2$ test p-values stochastically dominate all benchmark test p-values; note that in the top left plot ($n=20$) the p-values for $N_3$ are not available due to low quantile specification for this test statistic. For transparency, we added the legend only to the top left plot

Next, in Fig. 5 we present test power as a function of sample size $n\in [10,2000]$ for $\alpha _0=1.5$ and $\alpha _1=1.7$. For completeness, we include the results for significance level $5\%$ as well as $1\%$. From the results one can see that test power comparison presented in Fig. 3 for representative set of sample sizes ($n=20,50,100,500,1000,2000$) consistently propagates to other sample sizes and the payoff between test power and sample size is optimal for QCV based tests. In particular, $N_2$ test statistic outperforms all other benchmark tests.

Fig. 5

Comparison of test powers for $S\alpha S(1.5,1,0)$ distribution ($H_0$ hypothesis) against $S\alpha S(1.7,1,0)$ distribution ($H_1$ hypothesis) for various sample sizes n. The following tests are taken under consideration: the two-sided $N_1$, $N_2$ and $N_3$ tests proposed in this paper, Kolmogorov-Smirnov (KS) two-samples test, Kuiper test, Watson test, Cramer-von Mises (CvM) test and Anderson-Darling (AD) test. Results for confidence levels 1 and 5% are presented. For all sample sizes, the QCV based tests outperform benchmark frameworks; note that for small sample sizes ($n<50$) the values for $N_3$ are not available due to low quantile specification for this test statistic. For transparency, we added the legend only to left plot

To sum up, our analysis shows that QCV-based test statistics outperform benchmark frameworks. The supreme performance of the introduced statistics $N_1$, $N_2$, and $N_3$ in reference to other benchmark framework could be traced back to two main reasons. First, most benchmark methods are based on the generic whole distribution fit rather than local fit in the non-central part of the distribution – introduction of QCV based statistics allowed more efficient local densitty discrimination. Second, our test statistic are tailored to measure fat-tail behaviour which is very efficient when assessing the value of $\alpha$. In fact, the value of $N_1$, $N_2$, or $N_3$ could be used as a measure of tail fatness; see Jelito and Pitera (2020), where tail-fatness analysis in reference to similar test statistic in the Gaussian context is performed.

For completeness, in Appendix Fig. 14, we present a simplified R source code that could be used to compute $N_1$ statistic and estimate (two-sided) test power for true $\alpha _0=1.5$ and alternative $\alpha _1=1.7$ for sample size $n=50$ at $5\%$ significance level. One can easily modify the R code to get results for other QCV statistics and parameters sets.

5.2.2 Generic test power check

In Sect. 5.2.1, we have shown that $N_1$ statistic given in (19) has a decent test power and is outperforming all competing benchmark frameworks for multiple sample sizes and one exemplary choice of (true) $\alpha =1.5$. In this section, we fix sample size to $n=500$ and perform a more comprehensive power study focusing on all three $N_1$, $N_2$, and $N_3$ statistics, given in (19)–(21). Using Monte Carlo method, for each $\alpha \in (0,2]$ on the 0.025 span-grid, we simulated $m=10\,000$ samples; each simulation is a random sample from $S\alpha S(\alpha ,1,0)$ distribution of size n. Next, we calculate m values of $N_1$, $N_2$, and $N_3$, for each $\alpha \in (0,2]$, and use this to get Monte Carlo densities of all test statistics. Using the obtained densities, we calculate two-sided test powers. Note that due to a simplistic nature of conditional variance estimators, this simulation is very easy to implement and fast to compute.³ In this part, we decided to consider the whole range of the $\alpha$ parameter in order to see the effectiveness of the proposoed testing approach. Using the results, for a chosen $5\%$ significance level, we were able to approximate test power of $N_1$, $N_2$, and $N_3$ for all null and alternative $\alpha$ shape (simple) hypothesis. The results (for two-sided tests) are presented in Fig. 6.

Fig. 6

$N_1$, $N_2$, and $N_3$ test power level plot (two-sided); $n=500$; $\alpha \in (0,2]$. Apart from $\alpha$ close to 2, statistic $N_1$ seems like the best choice. This is due to the fact that $0.005\%$ quantile trimming introduced in $N_2$ and $N_3$ is to extreme. Nevertheless, for $\alpha =2$ the tails became more stable, which results in better performance of $N_2$ and $N_3$. Note that relatively small sample size impacts performance of $N_3$ due to non-robust estimation of conditional variance on small 3.5% probability set

From Fig. 6 we see that apart from $\alpha$ close to 2, the power of test statistic $N_1$ seems to be the best among all considered statistics. On average, for sample size $n=500$, if the difference between the true $\alpha _0$ and alternative $\alpha _1$ is higher than 0.2 then $N_1$ test power is very close to 1 (for 5% significance level). Good performance of $N_1$ could be traced back to heaviness of the tails. The smaller the $\alpha$, the harder it is to estimate the extreme $0.5\%$ quantile which is needed for $N_2$ and $N_3$. This impacts the standard error of the conditional variance estimator, reducing it’s test power. Also, note that estimation of small $3.5\%$ probability set in $N_3$ makes this statistic test power smaller than $N_2$. On the other hand, for $\alpha$ close to 2, the situation is entirely different. First, note that $N_2$ outperforms $N_1$ for $\alpha \ge 1.5$; see also Fig. 3. While $N_2$ seems to be an adequate overall choice when the true $\alpha$ is in the range [1.5, 2], the closer to 2 we are, the better is the performance of $N_3$. In fact, for $\alpha$ very close to 2 it looks like $N_3$ is outperforming $N_2$. We decided to investigate this in details in Sect. 5.2.3.

Also, note that from Figs. 6 and  2 one can deduce that test statistics $N_1$, $N_2$, and $N_3$ could be used for more generic testing. Namely, since the true values of test statistic are monotone wrt. $\alpha$, given null hypothesis $H_0$ of the form $\alpha =\alpha _0$, we can consider an alternative hypothesis $H_1$ of the form $\alpha <\alpha _0$ rather that $\alpha =\alpha _1$.

5.2.3 Generic test power check for symmetric $\alpha$-stable distribution with $\alpha$alpha close to 2

In this section we decided to repeat the exercise from Sect. 5.2.2 assuming that $\alpha \in [1.8,2.0]$ and $n=2000$. In other words, we want to check the performance of our testing framework when one wants to investigate near-Gaussian tails for relatively large sample. In fact, a similar case will be considered in the real data analysis presented Sect. 8. To get better accuracy, we increased Monte Carlo strong sample size to $m=50\,000$ and grid density to 0.01. To sum up, for each $\alpha \in \{1.80,1.81,\ldots ,1.99,2.00\}$, we simulated strong Monte Carlo sample of size $m=50\,000$, where each simulation is a random sample from $S\alpha S(\alpha ,1,0)$ distribution of size n. Next, as in Sect. 5.2.2, using the obtained test statistic densities we calculate two-sided test powers for $N_1$, $N_2$, and $N_3$. The results of the simulations for significance level $5\%$ are presented in Fig. 7.

Fig. 7

$N_1$, $N_2$, and $N_3$ tests power level plots (two-sided); $n=2000$; $\alpha \in [1.8,2]$. Overall, the results for $N_2$ and $N_3$ tests are comparable, but the closer to $\alpha =2$ we get, the better the performance of $N_3$ tests. Note that the outcomes for $N_1$ test are not satisfactory, i.e. while $N_1$ is best to test the overall $\alpha$-stable fit, it might not discriminate near-Gaussian distributions as well as $N_2$ or $N_3$

First, we note that in the considered region of $\alpha$ parameter, the performance of $N_1$ test is not satisfactory. On the other hand, the performance of $N_2$ and $N_3$ tests is comparable – the higher the $\alpha$ the better is the performance of $N_3$ test in comparison to $N_2$ test. This is consistent with the results presented in Sect. 5.2.2. Note that increased sample size $(n=2000)$ resulted in narrowed test power bounds. Now, if the difference between the true $\alpha _0$ and alternative $\alpha _1$ is higher than approximately 0.1 then $N_3$ test power is very close to 1 (for 5% significance level); for $n=500$ this was equal to 0.2. To illustrate this, let us present a table with one-sided and two-sided test powers for $N_2$ and $N_3$ tests for (true) parameter $\alpha =1.90$. For completeness, apart from significance level 5%, we also present test powers for significance level 1%; see Table 2.

Table 2 The table presents Monte Carlo test power for $N_2$ and $N_3$ for true $\alpha =1.90$; columns refer to different alternative hypothesis $\alpha _1$ values

6 Statistical tests for generic $\alpha$-stable distribution based on quantile conditional variance estimators

While in this paper our focus is set on goodness-of-fit testing of the symmetric $\alpha$-stable distribution, one could easily expand the framework presented in Sect. 5 to allow more generic tests. For completeness, in this section we provide a short comment on possible extensions of our testing framework that includes analysis of the skewness parameter $\beta \in [-1,1]$. Please recall that scale $c>0$ and location $\mu \in \mathbb {R}$ goodness-of-fit adequacy testing is typically performed using more standard methods and most $\alpha$-stable goodness-of-fit tests are invariant to affine transformations, see e.g. Matsui and Takemura (2008).

First, from Fig. 1 we see that QCV could be used to efficiently measure $\alpha$-stable distribution skewness. Indeed, the central exhibit of Fig. 1 shows the dynamics of (theoretical) QCV strongly depends on the underlying choice of skewness parameter $\beta$ so one should be able to develop symmetry-oriented statistical test.

Second, we note that test statistics $N_1$, $N_2$, and $N_3$ introduced in Sect. 5.1 are tailored to symmetrically measure tail-heaviness impact that is encoded in parameter $\alpha$ and one would expect them to be generally invariant to the choice of the skewness parameter $\beta$. This could be traced back to specific constraints imposed on quantile split parameters and weights parameters in (18). Namely, we assumed that $a_4=1-a_1$, $a_3=1-a_2$, $d_1=d_3$, and $d_1d_2<0$ which resulted in test statistic that (symmetrically) measures the impact of tail-set QCVs on central-set QCV. This observation is illustrated in the left exhibit of Fig. 8, where two-sided tests power level plot for $N_1$ test statistic for exemplary set of null hypothesis parameters $\alpha _0=1.5$ and $\beta _0=0$ is confronted with various alternative hypotheses for $\alpha _1\in [1.0,2.0]$ and $\beta _1\in [-1,1]$. As expected, the power of the test is almost invariant to the choice of the skewness parameter.

Fig. 8

$N_1$, $N^a_1$, and $N^b_1$ tests power level plots (two-sided) for $\alpha _0=1.5$ and $\beta _0=0$; $n=500$; $\alpha _1\in [1,2]$; $\beta _1\in [-1,1]$. Overall, we note that test statistic $N_1$ is almost invariant to the choice of $\beta$, while test statistics $N_1^a$ and $N_1^b$ could be used for skewness identification

For brevity, we now focus on test statistic $N_1$ and show how it can be modified to allow better skewness impact measurement. We follow the setting similar to the one introduced in Sect. 5.2.1. Namely, we fix sample size $n=500$, confidence level $5\%$, and assess test power of modified statistics in a same manner that was done in Fig. 6 but taking into account the impact of $\beta$. Two possible natural modifications of $N_1$ are given by

$$\begin{aligned}&\text {N}^a_1 :=\sqrt{n}\cdot \frac{ {\hat{\sigma }}^2_x(5\%,25\%)- {\hat{\sigma }}^2_x(75\%,95\%)}{{\hat{\sigma }}^2_x(5\%,95\%)}\\&\quad \text {and}\quad \text {N}^b_1 :=\sqrt{n}\cdot \frac{2.00\cdot {\hat{\sigma }}^2_x(5\%,25\%)-1.01\cdot {\hat{\sigma }}^2_x(25\%,75\%)}{{\hat{\sigma }}^2_x(5\%,95\%)}. \end{aligned}$$

In both cases, we simply change the input weights $d_1,d_2,d_3\in \mathbb {R}$; see (18). In the first case, weights change results in a statistic $N_1^a$ that measures the QCV difference between left and right tail. Theoretically, the more symmetric the distribution, the closer to zero the values of $N_1^a$. In the second case, we modified $N_1$ in such a way that only the relation between left tail and central set QCVs is taken into account. Statistic $N_1^b$ should be able to detect changes in both $\alpha$ and $\beta$ among some fixed QCV induced level-set. The test power results are presented in Fig. 8.

From the plot one could deduce that the distribution of $N_1^a$ and $N_1^b$ does depend on parameter $\beta$ and those statistic could be used for skewness indentification. In particular, note that $N_1^a$ seems to correctly capture the actual skewness effect that is partly encoded in $\beta$. Note that the bigger the value of $\alpha$, the smaller the impact of $\beta$ on the actual distribution skewness which results in widening power level sets. In particular, for $\alpha =2$, the distribution reduces to (symmetric) Gaussian and the choice of $\beta$ does not matter.

Of course, one could easily improve the obtained results by considering different test statistics that are focused on symmetry measurement. For instance, one could remove the central QCV in (18) by setting $a_2=a_3=0.5$ and $d_2=0$, or consider maximum of $N_1^b$ and it analogue that takes into account right tail. Nevertheless, we want to emphasize that the main focus on this article is on the symmetric case and tail-heaviness assessment framework. The detailed derivation of efficient $\beta$-sensitive statistic is out of scope of this article. That saying, we refer to Sect. 7 where the overall distribution fit using QCV framework is studied. In particular, it is shown how possible $\beta$ parameter misspecification could impact the structure of sample QCVs; see e.g. Fig. 9 for details.

7 General $\alpha$-stable distribution goodness-of-fit visual test using quantile conditional variance estimators

In this section we introduce a generic (visual) fit test based on quantile conditional variance that uses the results of Theorem 2. It should be noted that the procedure introduced in this section could also be embedded into more formal statistical language, e.g. by introducing a multiple (composite) testing framework. This section complements the results from Sects. 5 and 6.

Let us assume we have an i.i.d. sample from the same distribution as X, say $x=(x_1,\ldots ,x_n)$, $n\in \mathbb {N}$, and we want to check whether this sample comes from a specific $S(\alpha ,c,\beta ,\mu )$ distribution. Furthermore, let us assume that we are not interested in the location parameter fit; note there are standard methods to assess this based e.g. on trimmed mean analysis, see Wilcox (2017); Ferguson (1978, 2001). Due to Theorem 2 combined with Proposition 4 we know that $X\sim S(\alpha ,c,\beta ,{\tilde{\mu }})$, for some ${\tilde{\mu }}\in \mathbb {R}$, if and only if for any $0<a<b<1$ we get

$$\begin{aligned} \hat{\sigma }_X^2(a,b) \xrightarrow {\,\,\mathbb {P}\,\,} {\sigma _Z^2}(a,b),\qquad n\to \infty , \end{aligned}$$

(22)

where $Z\sim S(\alpha ,c,\beta ,0)$. Thus, to assess the adequacy of the distribution fit, we can check Property (22) for representative set of quantile intervals $(a_i,b_i)$, where $i\in \{1,2,\ldots ,I\}$ and $I\in \mathbb {N}$.

The rational choice is to use non-overlapping quantile intervals with (a.s) interconnected union, i.e set $b_{i}=a_{i+1}$, for $i\in \{1,2,\ldots ,I-1\}$. For simplicity, we might also assume that all intervals are of equal length, i.e. there exist $\epsilon >0$ such that $b_i-a_i =\epsilon$, for $i\in \{1,2,\ldots ,I\}$. Also, we can normalise (22) by considering a set of convergence conditions $[\hat{\sigma }_X^2(a_i,b_i) \,/\, \sigma _Z^2(a_i,b_i)-1]\rightarrow 0$, $n\to\infty$. To control error of the fit, given a set of pre-defined parameters $(\alpha ,c,\beta )$ and $n\in \mathbb {N}$, one could consider a series of statistics

$$\begin{aligned} {{\hat{R}}}_i=\sqrt{n}\, \left[ \frac{\hat{\sigma }_X^2(a_i,b_i)}{\sigma _Z^2(a_i,b_i)}-1\right] , \quad i=1,2\ldots ,I, \end{aligned}$$

(23)

where $Z\sim S(\alpha ,c,\beta ,0)$; note that the (null-hypothesis) confidence intervals, for any fixed $n\in \mathbb {N}$, could be easily computed numerically using e.g. Monte Carlo simulations. If we are not interested in the scale $c>0$ parameter fit, we can further normalise ${{\hat{R}}}_i$ by multiplying inner variance ratio e.g. by ${\sigma }_Z^2(a_1,b_I) \,/\, {\hat{\sigma }}_X^2(a_1,b_I)$; we will refer to such statistic as normalised ${{\hat{R}}}_i$. Of course, the choice of the number of intervals $I\in \mathbb {N}$ and exterior points $0<a_1$ and $b_I<1$ should depend on the sample size so that the resulting QCV estimators are relatively dense and robust.

To illustrate how the sanity check based on test statistics (23) might look like, let us present a simple example.

Example 5

Let us consider a 4.5% quantile grid with 0.005% cut-offs, i.e. we set $I=22$ with quantile intervals

$$\begin{aligned} a_{i}:= 0.005 +0.045\cdot (i-1)\quad \text {and}\quad b_{i}:= 0.005 +0.045\cdot i, \quad \text {for } i=1,2,\ldots I; \end{aligned}$$

note that $b_{I}=1-a_{1}=0.995$. Assume that we have an i.i.d. sample $x=(x_1,\ldots ,x_{2000})$ from the same distribution as the random variable X, where

$$\begin{aligned} X\sim S(1.85,1,0,0). \end{aligned}$$

For $n=2000$, each conditional variance ${\hat{\sigma }}^2_X(a_i,b_i)$ is estimated using $\lfloor 0.045n\rfloor = 90$ observations from x; 10 smallest and 10 biggest values of x are excluded due to trimming. Let us check whether the sample x comes from three other $\alpha$-stable distributions given via random variables

$$\begin{aligned} X_1\sim S(2,1,0,0),\qquad X_2\sim S(1.85,1,0.7,0),\qquad X_3\sim S(1.85,0.9,0,0). \end{aligned}$$

To do so, we construct test statistics ${{\hat{R}}}^1_i$, ${{\hat{R}}}^2_i$, and ${{\hat{R}}}^3_i$, for $i=1,2,\ldots ,22$, which correspond to the distributions of $X_1, X_2$, and $X_3$, respectively. In the first case, the distribution has fatter tails, which should make ${{\hat{R}}}^1_i$ positive for tail conditional variances. In the second case, the non-symmetric nature of the distribution should result in non-symmetric behaviour of ${{\hat{R}}}^2_i$. In the latter case, the statistics ${{\hat{R}}}^3_i$ should be positive (and not centred around 0) due to smaller scale parameter value.

To verify this, we simulate $10\,000$ strong Monte Carlo samples from the distributions corresponding to $X_1$, $X_2$ and $X_3$, where each simulation is of size $n=2000$. Next, we use simulated values to get MC densities of ${{\hat{R}}}^1_i$, ${{\hat{R}}}^2_i$, and ${{\hat{R}}}^3_i$, for $i=1,2,\ldots ,22$, under the correct model specification. Finally, we compare value of ${{\hat{R}}}_i$, coming from X sample, with 1% and 5% confidence bounds obtained using the Monte Carlo analysis. The results of the exercise are illustrated in Fig. 9.

Fig. 9

The plot illustrates how one can use sample conditional variance ratios ${{\hat{R}}}_i$ given in (23) to check the overall parameter fit for $\alpha$-stable distribution. In each plot, ${\hat{R}}_i$ for exemplary sample from $X\sim S(1.85,1,0,0)$ of size $n=2000$ is confronted with the ratios corresponding to other $\alpha -$stable distributions. In the left plot, we tested the fit for $\alpha =2$, which resulted in tail conditional variance misalignment. In the middle plot, we introduced skewness by setting $\beta =0.7$, which made the outcome non-symmetric. In the right plot, we set $c=0.9$ which results in up-lifted values of ${{\hat{R}}}_i$. The dashed lines correspond to extreme (point-wise) quantiles of ${{\hat{R}}}_i$, $i=1,2,\ldots ,22$, under the correct model specification; they were obtained using 10 000 Monte Carlo run

8 Statistics of plasma turbulence in fusion device

In this section we illustrate how to use statistical framework based on QCV statistics for goodness-of-fit testing of real data. We take datasets examined in Burnecki et al. (2015), see also Burnecki et al. (2012). Specifically, we investigate the data obtained in experiments on the controlled thermonuclear fusion device “Kharkov Institute of Physics and Technology”, Kharkov, Ukraine. Stellarators and similar devices, like e.g., tokamaks and compact toroids are used to study the properties of magnetically confined thermonuclear plasmas. They serve as smaller prototypes of the International Thermonuclear Experimental Reactor (ITER), the most expensive scientific endeavor in history aimed to demonstrate the scientific and technological feasibility of fusion energy for peaceful use.⁴

It is a well-known fact that the magnetically confined plasma produced in such devices is always in a highly non-equilibrium state. This phenomenon called plasma turbulence is characterized by an anomalously high levels of fluctuations of the electric field and particle density and plays a decisive role in the generation of anomalous particle and heat fluxes from plasma confinement region, see Krasheninnikov et al. (2020). This circumstance constitute one of the main obstacles on the way of the magnetic confinement implementation, and this is the reason why the statistical properties of plasma turbulence are intensively investigated. In particular, during such studies a remarkable phenomenon called L-H transition have been observed in many fusion devices. Namely, a sudden transition from the low confinement mode (L mode) to a high confinement mode (H mode) is accompanied by suppression of turbulence and a rapid drop of turbulent transport at the edge of thermonuclear device, see Connor and Wilson (2000) and Wagner (2007). The implementation of the H-mode regime, which is chosen as the operating mode for the future ITER device requires detailed investigation of the physics of such transition. We here focus on statistical properties of turbulent plasma fluctuations before and after L-H transition phenomenon in stellarator-torsatron URAGAN-3M.

We examine four datasets which are denoted as Dataset 1, Dataset 2, Dataset 3, and Dataset 4. They are obtained by the use of high resolution measurements of the electric potential (floating potential) fluctuations with the help of movable Langmuir probe arrays. The detailed description of the experimental set-up and measurement procedure can be found in Beletskii et al. (2009). In a nutshell, Dataset 1 and Dataset 2 describe the floating potential fluctuations (in volts) in turbulent plasma, registered by Langmuir probe for torus radial position r = 9.5 cm. While Dataset 1 is related to the fluctuations before the transition point, Dataset 2 describe the fluctuation after the transition. Dataset 3 and Dataset 4 describe the potential fluctuations for torus radial position r = 9.6 cm. As before, Datasets 3 is related to prior-transition fluctuations while Dataset 4 is linked to posterior-transition fluctuations. The considered datasets contain 2000 normalized observations each and are presented in Fig. 10.

Fig. 10

Plasma data for torus radial position $r=9.5$ cm (Dataset 1 and Dataset 2) and $r=9.6$ cm (Dataset 3 and Dataset 4). The Dataset 1 and Dataset 3 describe the fluctuations before the L-H transition point. The Dataset 2 and Dataset 4 represent the fluctuation of the plasma after the L-H transition point

Before we present our analysis, let us comment on the results from Burnecki et al. (2015). The authors introduced a visual test that pointed out to differences between prior transition point and posterior transition point data. Namely, while the (two-sample) Kolmogorov-Smirnov test did not reject the hypothesis stating that the distributions of Datasets 1 and Dataset 2, or Dataset 3 and Dataset 4, respectively, is the same, the introduced visual framework indicated slight regime change between the considered datasets. The authors demonstrated that the distribution corresponding to Dataset 1 is the $\alpha$-stable with $\alpha <2$, Dataset 2 and Dataset 3 can be modeled by the Gaussian distribution, while Dataset 4 belongs to the domain of attraction of the Gaussian law however it is non-Gaussian.

The results obtained with QCV framework in general confirm the analysis from Burnecki et al. (2015). However, the results obtain here are more rigorous and are statistically significant since they are not based just on the visual inspection of the considered statistic. Since the sample size is relatively big ($n=2000$) and we are interested in $\alpha$ values close to 2 we took into consideration only test statistics $\text {N}_2$ and $\text {N}_3$, i.e. we excluded $\text {N}_1$ from the analysis; see Sect. 5.2 for discussion. Moreover, rather than performing a single statistical test oriented at verification of the non-normality hypothesis (e.g. by setting $H_1$ to $\alpha <1.98$), we decided to present testing results for a wide range of parameters for both statistics. This is done to provide a more complete picture and for better illustration.

First, we calculated the values of $\text {N}_2$ and $\text {N}_3$ for all empirical datasets and confronted it with various theoretical $\text {N}_2$ and $\text {N}_3$ quantiles obtained for $\alpha$-stable distributions. The 1% and 5% quantiles were constructed based on $50\,000$ Monte Carlo strong simulation for samples (of length 2000) coming from $S\alpha S(\alpha ,1,0)$, where $\alpha \in [1.8,2.0]$ values are restricted to the 0.01 dense grid. The results are illustrated in Fig. 11.

Fig. 11

The plots present tail quantiles for $\text {N}_2$ (left) and $\text {N}_3$ (right) test statistics for $\alpha \in [1.8,2]$ and sample size $n=2000$. For each $\alpha$, using Monte Carlo simulations we approximated test statistics median, 1% tail quantiles, and 5% tail quantiles; note that those could be linked to one-sided test significance levels. Horizontal lines indicate values of $\text {N}_2$ (left) and $\text {N}_3$ (right) for empirical datasets. Normality ($\alpha =2$) for Dataset 1 is rejected by both statistics, but only $N_2$ rejects normality for Dataset 4. For both datasets, the intersection of 1% upper quantiles and vertical lines indicate how heavy (in terms of $\alpha$) might be the tail of the sample distribution

From left panel of Fig. 11 we see that $N_2$ statistic rejects Gaussian distribution hypothesis for Dataset 1 at 1% significance level. Also, since $N_2$ test statistics for Dataset 2, Dataset 3, and Dataset 4 fall into the constructed confidence intervals for $\alpha =2$, one cannot reject normality for those samples. On the other hand, for $N_3$, the hypothesis of the Gaussian distribution for Dataset 1 and Dataset 4 is rejected on $1\%$ significance level (see the right panel of Fig. 11). For Dataset 1, the values of $N_2$ and $N_3$ statistics fall into the constructed confidence intervals for $\alpha \in [1.85,1.93]$ which suggests that $S\alpha S(\alpha ,1,0)$ distribution on this parameter range might be a suitable modelling choice. For Dataset 4, taking into account $N_3$ statistic values, we conclude that the desired $\alpha$ stability index range is in [1.85, 1.97].

For completeness, we also present p-values for goodness-of fit tests based on $N_2$ and $N_3$ statistics for $H_0$ hypotheses of $S\alpha S(\alpha ,1,0)$ distribution for selected $\alpha$ parameters and for all datasets; see Table 3. The p-values presented in Table 3 are calculated based on the $50\, 000$ Monte Carlo simulations. More precisely, for each $\alpha$ we simulate 50 000 times a sample of length 2000 from $S\alpha S(\alpha ,1,0)$ distribution in order to calculate 50 000 sample test statistics $N_2$ and $N_3$. Next, using obtained results, we construct a Monte Carlo distribution of $N_2$ and $N_3$ and confront it with $N_2$ and $N_3$ statistics for the given dataset, say $N_2^X$ and $N_3^X$. Finally, denoting by ${\hat{q}}_i^X$ the value of the Monte Carlo CDF for the test statistic $N_i$ ($i=2,3$) at point $N_i^X$, the corresponding p-value is calculated as the minimum of ${\hat{q}}_i^X$ and $1-{\hat{q}}_i^X$. This correspond to the minimum of left-sided and right-sided statistical test p-values for $N_2$ and $N_3$ test statistics.

Table 3 The tables present p-values for all considered datasets and $H_0$ hypothesis of $S\alpha S(\alpha ,1,0)$ distribution with $\alpha \in [1.80,2.00]$; p-values are based on $50\,000$ Monte Carlo simulation.

As in Fig. 11, the results from Table 3 clearly indicate that based on the $N_2$ and $N_3$ statistics, the hypothesis of Gaussian distribution for Dataset 1 and Dataset 4 should be rejected. Moreover, the corresponding (acceptable) $S\alpha S(\alpha ,1,0)$ distribution for Dataset 1 and Dataset 4 should have the stability index in the range $\alpha \in [1.84,1.93]$ and $\alpha \in [1.88,1.96]$, respectively; this is consistent with results deduced from Fig. 11. For Datasets 2, we observe highest p-values for $\alpha =2$ (in case of $N_2$) and $\alpha =1.98$ (in case of $N_3$) which may suggest the Gaussian (or very close to Gaussian) distribution. For Dataset 3, the highest p-values are observed for $\alpha =1.98$ for both considered statistics. This may also suggests the $\alpha$-stable distribution with stability index very close to Gaussian.

To sum up, our analysis shows that the hypothesis of the Gaussian distribution for Dataset 2 and Dataset 3 cannot be rejected while Dataset 1 and Dataset 4 can be modeled by the distribution from the domain of attraction of the $\alpha$-stable law with $\alpha$ parameter close to 2. Also, note that the analysis of the results based only on one of the statistics (i.e. $N_2$) does not give the whole picture of the distribution related to the data. The results presented in Table 3 confirm that $N_3$ is the best choice when performing analysis of the near-Gaussian data for relatively big sample sizes; this is consistent with remarks made in Sect. 5.1 when each statistic purpose was outlined.

Next, for better illustration and to have more clear picture about the sample distribution properties, we decided to follow the approach introduced in Sect. 7. This should check the overall symmetric $\alpha$-stable distribution parameter fit for the analyzed datasets. Taking into account the p-values presented in Table 3, we decided to perform a (visual) check of the following $\alpha$ parameter fits: (1) $\alpha =1.93$ for Dataset 1; (2) $\alpha =2.0$ for Dataset 2; (3) $\alpha =2.0$ for Dataset 3; (4) $\alpha =1.96$ for Dataset 4. We followed the approach introduced in Example 5 using the normalised version of ${{\hat{R}}}_i$ statistics; see Sect. 7 for details. The equivalents of plots presented in Fig. 9 for empirical datasets and the chosen specifications are presented in Fig. 12.

Fig. 12

The plots illustrates the overall fit for all empirical datasets given a specific choice of $S\alpha S(\alpha ,1,0)$ distribution; the reference $\alpha$ levels are presented in the titles of the plots. The dashed lines correspond to extreme (point-wise) quantiles of ${{\hat{R}}}_i$, $i=1,2,\ldots ,22$, under the correct model specification; they were obtained using a 10 000 Monte Carlo run. One could see that the hypothesis of Gaussian distribution can not be rejected for Dataset 2 and Dataset 3 at the significance level $1\%$ as well as $5\%$. The results for Dataset 1 and Dataset 4 indicate the the $H_0$ hypothesis of tested distribution should be rejected. The realised values of $R_i$ statistics exceed the constructed confidence bound for low (in case of Dataset 1) and high conditional variance subsets (in case of Dataset 4)

The results point out to further sample properties. We see that (tail) Gaussian distribution hypothesis for Dataset 2 and Dataset 3 cannot be rejected. In fact, in both cases, the values of the normalized ${{\hat{R}}}_i$ statistics fall into the constructed confidence intervals for $S\alpha S(2,1,0)$ distribution for almost any conditional variance subset. Next, for Dataset 1, we observe that the extreme left tail QCV is breaching the quantile threshold which might suggest that the true left tail is higher than the left tail of $S\alpha S(1.93,1,0)$. On the other hand, for Dataset 4, we observe breach in the right tail QCV combined with a slight increasing trend in QCVs. This phenomena may suggest the non-symmetric behavior of the analyzed vector of observations and to the conclusion that the $H_0$ hypothesis should be rejected.

Let us finish this section with the comment on practical consequences of such statistical analysis of plasma fluctuations. At first, we note that non-Gaussian heavy-tailed distributions for low frequency plasma turbulence have also been observed in a number of toroidal plasma confinement systems such as T-10 tokamak, L-2M, TJ II, and LHD stellarators as well as in astrophysical plasmas, see Korolev and Skvortsova (2006), Dendy and Chapman (2006), and Watkins et al. (2009). The fluctuations with $\alpha$-stable behavior have been reported in experiments on stellarators URAGAN-3M, Heliotron J, and on the tokamak ADITYA, see Gonchar et al. (2003), Mizuuchi et al. (2005), and Jha et al. (2003), respectively. This phenomenon is called “Lévy turbulence”, and here we confirm its existence in the stellarator URAGAN-3M. Moreover, we conclude that not only the turbulence level, but the very statistics of the turbulence changes at the L-H transition. Such observation brings the necessity to build adequate theoretical models of the plasma turbulence before and after the L-H transition. We hope that the change of statistics observed in the data taken from URAGAN-3M will inspire plasma experimental groups to check if the change of statistics is also observed in other fusion devices where L-H transition has been detected.

9 Conclusions

In this paper, we introduced a novel generic goodness-of-fit testing approach based on the quantile conditional variance (QCV) statistics which builds upon recent results obtained in Jaworski and Pitera (2020) and Jelito and Pitera (2020). We studied probabilistic properties of sample QCV statistics for $\alpha$-stable distributed random variables and shown that the QCV analysis could be used to efficiently characterise $\alpha$-stable distribution. Our Monte-Carlo based analysis indicates that the proposed goodness-of-fit test statistics outperforms many benchmark goodness-of-fit tests that are typically used in reference to $\alpha$-stable distributions. Although our focus was on the symmetric case, the simulation study indicates that the proposed test statistics might be in fact almost invariant to skewness specification encoded in $\beta$ parameter, see Fig. 8. In other words, same methodology can be applied to test $\alpha$ parameter fit also for the asymmetric $\alpha$-stable distributions.

We want to emphasize, that our paper is the first one that applies quantile conditional variance statistical approach to $\alpha$-stable distributed samples. The presented results indicate that the proposed methodology can be considered as the universal one when $\alpha$-stable distribution testing is considered. In fact, we believe that the approach based on quantile conditional moments might be used to effectively solve the challenge stated in Nolan (2020), where it was said that: “In general, it appears to be challenging to find an omnibus test for stability”.

Finally, we have demonstrated how to utilize our framework in the analysis of real-data from plasma physics and showed that our approach efficiently discriminate between light- and heavy-tailed distributions. This proves that the presented methodology can be also useful in practical problems which require using efficient methods for specific data analysis.

Appendices

Appendix A Tests power comparison for significance level 1%

See Fig. 13.

Fig. 13

Power of the tests based on the QCV statistics ($N_1,N_2,N_3$) with comparison to other benchmark goodness-of-fit tests for different sample lengths and for he significance level equal to $1\%$. Results are consistent with those obtained for significance level 5%; see Fig. 3 caption for more details. For transparency, we added the legend only to the top left plot

Appendix B Numerical comparison of the tests’ powers for significance level 5%

In Tables 4, 5, 6,7, 8 we present the powers of the tests considered in Sect. 5.2.1. In each case the the $H_0$ hypothesis is that the random sample comes from $S\alpha S(1.5,1,0)$ distribution. The $H_1$ hypothesis is that vector of observations constitutes the random sample from $S\alpha S(\alpha _1,1,0)$ distribution for $\alpha _1\in \{1.1,1.2,\cdots ,2.0\}$. The number of Monte Carlo simulations used to calculate the values of the test statistics under $H_0$ hypothesis is $100\,000$ while the number of Monte Carlo simulations used to calculate the powers of the tests is $10\,000$. The significance level is assumed to be $5\%$. In each case we highlight the best result.

Table 4 Comparison of the powers of the tests for $S\alpha S(1.5,1,0)$ distribution ($H_0$ hypothesis) against $S\alpha S(\alpha _1,1,0)$ distribution for ($H_1$ hypothesis)

Table 5 Comparison of the powers of the tests for $S\alpha S(1.5,1,0)$ distribution ($H_0$ hypothesis) against $S\alpha S(\alpha _1,1,0)$ distribution for ($H_1$ hypothesis)

Table 6 Comparison of the powers of the tests for $S\alpha S(1.5,1,0)$ distribution ($H_0$ hypothesis) against $S\alpha S(\alpha _1,1,0)$ distribution for ($H_1$ hypothesis)

Table 7 Comparison of the powers of the tests for $S\alpha S(1.5,1,0)$ distribution ($H_0$ hypothesis) against $S\alpha S(\alpha _1,1,0)$ distribution for ($H_1$ hypothesis)

Table 8 Comparison of the powers of the tests for $S\alpha S(1.5,1,0)$ distribution ($H_0$ hypothesis) against $S\alpha S(\alpha _1,1,0)$ distribution for ($H_1$ hypothesis)

Appendix C Source code

See Fig. 14.

Fig. 14

A simplified R source code, that can be used to compute $N_1$. For completeness, we also show how to compute exemplary (two-sided) test power for true $\alpha _0=1.5$ and alternative $\alpha _1=1.7$ for sample of size $n=50$ at 5% significance level. The calculations take 6 seconds on 13” MacBook Air (2017) with 8 GB RAM and 1.8 GHz Dual-Core Intel i5 processor