1 Introduction

Electrical, mechanical and energy micro-scaled systems, which incorporate microchannels subject to convective heat and mass transfer, attracted much attention of scientists and engineers in recent decades.

Microchannels filled with porous media are often integrated in engineering devices and technologies. For instance, heat removal techniques using porous media are based on solid matrix material structures made of a material characterized by high thermal conductivity, which intensifies heat transfer to the coolant (Smakulski and Pietrowicz 2016). Used are porous irregular structures of sintered particles and ordered package of spherical pebbles. Microchannel heat sinks being in fact small-scale heat exchangers with channels a fraction of a millimeter wide are employed for cooling of electronic components. These two techniques are in that the heat transfer enhancement is attained by increasing the contact heat transfer area, as well as due to fluid flow intensification inside the channels (Smakulski and Pietrowicz 2016).

Micrometer dimensions of the studied geometries are accompanied by different proximity rates and overall energy of fluid molecules. In rarified gases, average spacing between gas molecules usually exceeds one molecule diameter. In liquids, this average spacing is less than a molecule diameter, which causes different approaches to modeling of substance transport in gases and liquids (Calvert and Baker 1998).

Hung et al. (2013) studied numerically effects of enlarging the channel outlet on the heat transfer in a porous microchannel heat sink with the throughflow of water used as a coolant. It was demonstrated that the overall pressure losses and heat transfer increased significantly in microchannels with porous inserts in comparison with microchannels without them. With the help of parametrical studies, it was also revealed that overall pressure losses can be substantially reduced, and heat transfer intensity simultaneously maintained at the same or even higher level via replacing the constant aspect ratio porous channels with diverging porous channels. Taamneh and Omari (2013)examined numerically heat transfer at slip flow of power-law fluid using the modified Darcy–Brinkman–Forchheimer model for porous media. The authors studied effects of the Knudsen and Darcy numbers, power-law index and inertia parameter to suggest optimal regimes of functioning of porous microchannels. Dehghan et al. (2015) modeled analytically forced convection in heat exchangers made of parallel plates subject to effects of thermal conductivity of porous medium filling the channel using the Brinkman–Forchheimer–extended Darcy model. It was demonstrated that a linear increase in the thermal conductivity of the porous medium causes a semi-linear increase in heat transfer. Dehghan et al. (2016) extended their study to cover wide range of different parameters to suggest better designs of micro-heat exchangers to provide heat transfer enhancement at the expense of possible minimal pressure drop. Avramenko et al. (2018,2019) modeled mixed convection in vertical flat and circular porous microchannels using the first- and second-order boundary conditions. The authors studied effects of the Knudsen and Rayleigh numbers, as well as porosity on heat transfer intensity and pressure losses in porous microchannels. It was revealed that the shape of the channel cross-section and the type of the boundary conditions affect significantly the heat transfer and fluid flow pattern. Avramenko et al. (2020) obtained an analytical solution for film boiling in porous media using Darcy–Brinkman and Darcy–Brinkman–Forchheimer approximations.

Under certain physical conditions, instability phenomena in porous channels can occur. The occurrence of flow instability can play either positive or negative role depending on the particular technological process and geometry, which inevitably calls for the investigation of this phenomenon.

There are two ways to study the influence of various factors on the flow stability: experimental and theoretical (analytical and numerical). Both are actively used in practice.

Experimental studies enable obtaining reliable research results with an accuracy determined only by measuring equipment. For instance, Lee et al. (2019) used the experimental methodology to identify and suppress the dominant charge transition instability on form of oscillations during boiling of flow of the coolant R134a in a radiator with microchannels. However, the experimental possibilities are often very limited technologically. And the cost of such research, most often, is very significant. Therefore, researchers make extensive use of analytical and numerical methods.

Dodgson and Rees (2013) studied the onset of convective instability in a horizontal porous layer heated from below and subject to imposed throughflow. They considered effect of finite Prandtl-Darcy number in the relation for the critical Darcy–Rayleigh number. Barletta et al. (2013,2016; Barletta 2016) studied convective and absolute instability in horizontal porous channels with different physical boundary conditions, such as permeable and conducting side boundaries and variable-viscosity dissipation. Barletta and Celli (1224) investigated the onset of two-dimensional convective instability in steady-state mixed convection in a vertical porous layer including the effects of dynamic boundary conditions. Celli et.al. (2016) focused on a study of nonlinear stability of Darcy’s flow in a horizontal porous channel with impermeable walls heated from above. Deepika and Narayana (2015) performed linear stability analysis to study convective instability in a horizontal porous layer with through flow including the effects of viscous dissipation and concentration based internal heat source on the critical thermal Rayleigh number. Kumari and Murthy (2018) investigated convective instability in throughflow of power-law fluid for double-diffusive convection with Soret effect in a vertical porous layer. Naveen et al. (2018) also focused on a study of stability in a vertical anisotropic porous layer in frames of natural convection under thermal nonequilibrium conditions. Avramenko et al. (2007) performed numerical simulations of stability in slip flow in a channel filled with a hyperporous medium saturated by a rarefied gas.

As can be seen from the above works, the problem of studying the instability of fluid flow in channels is very urgent and requires involvement of complex mathematical methods.

The recent study of Avramenko and Shevchuk (2020) shed light on the peculiarities of convective instability in vertical circular microchannels in slip flow of a pure fluid. However, convective instability in vertical porous circular microchannels with account for slippage effects and conjugate heat transfer have not been studied yet. Nevertheless, knowing the mechanism of this instability and the ability to quantify it is important in modeling of the flow regimes in micro-electromechanical and microenergy systems, such as heat sinks and heat pipes. In view of this, the main objective of the present study is an analytical study of convective instability in fluid flow in a vertical cylindrical porous microchannel heated from below. We will solve a conjugate problem (which considers heat conduction in the solid walls of the channel) over the wide range of the Darcy, Prandtl and Knudsen numbers, as well as the ratio of the thermal conductivities of the fluid and the solid wall. Certain inevitable simplifications are outweighed by the advantages of the closed-form solution and its subsequent analysis. The novelty of the present study includes this analytical solution, its parametric study together with the subsequent analysis and interpretation. To the knowledge of the authors, such analytical solution, its analysis and interpretation have never appeared in the published literature yet.

2 Problem Statement and Governing Equations

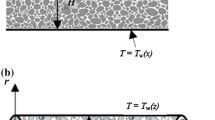
We consider here a vertical located porous microchannel of circular cross-section with a semi-infinite length, radius R and permeability K surrounded by a continuous medium (Fig. 1).

Fig. 1
figure 1

Sketch of the porous microchannel surrounded by a continuous solid medium

Full size image

The equations that describe fluid flow and heat transfer in this channel have the form

$$\nabla \cdot \tilde{v} = 0$$
(1)
$$\left( {\tilde{v} \cdot \nabla } \right)\tilde{v} = - \frac{1}{{\rho _{0} }}\nabla \tilde{p} + \nu \Delta \tilde{v} - \frac{\nu }{K}\tilde{v} + g\beta \tilde{T}k$$
(2)
$$\left( {{\mathbf{\tilde{v}}} \cdot \nabla } \right)\tilde{T} = \alpha \Delta \tilde{T}$$
(3)
$$\Delta \tilde{T} = 0$$
(4)

where \({\mathbf{\tilde{v}}}\) is the velocity vector, \(\tilde{p}\) is the absolute pressure, \(\rho _{0}\) is the density, \(\nu\) is the kinematic viscosity, K is the permeability, α is the thermal diffusivity, β is the coefficient of thermal expansion, g is the gravitational acceleration, \(\tilde{T}\) is the local temperature, \({\mathbf{k}}\) is the unit vector directed streamwise. The buoyancy force per unit volume (the last term in Eq. (3)) is modeled with the help of the Boussinesq approximation.

The third term in the right-hand side of Eq. (3) considers the effects of porosity. For K → ∞, this term vanishes and Eqs. (2)–(5) become valid only for geometries without porous inserts (Avramenko and Shevchuk 2020; Gershuni and Zhukhovitskii 1976).

A real prototype of such a system can be a porous thermal micropipe with a diameter of the order of a few millimeters with micron pores (Nemec 2017). The range of porosity is from 30 to 75%, and the permeability is of the order of 10–14… 10–13 m2. A real fluid can be either gas or liquid. According to Gad-el-Hak (1999), the slip length for liquids is defined as a function of shear rate. The range of the Knudsen numbers involved in the study 10–3 < Kn < 10–1 is determined by the range of the slip mode, when the equation of a continuous medium with slip effects on the channel wall can be used for modeling (Gad-el-Hak 1999).

Fluid flow in the considered microchannel is subject to so-called slip boundary conditions, which mathematically describe velocity and temperature jumps at the contact surface between the porous and continuous media (see Eqs. (25)). Like in the previous studies (Dehghan et al. 2015, 2016; Avramenko et al. 2018, 2019; Avramenko and Shevchuk 2020), velocity and temperature jumps are governed by the value of the Knudsen number.

The heat is supplied to the channel from below. This causes linear temperature distribution in the vertical direction with a constant gradient B, which corresponds to undisturbed state of the system (Avramenko and Shevchuk 2020; Gershuni and Zhukhovitskii 1976)

$$\tilde{v}_{0} = 0,\,\tilde{T}_{0} = - B\tilde{z} + {\text{const}}$$
(5)

where \({\mathbf{\tilde{v}}}_{0}\) and \(\tilde{T}_{0}\) are the undisturbed velocity and temperature profiles in fluid in rest. This requires for the temperature of the contact surface between the porous and continuous media to vary also linearly in the vertical direction.

In the current study, the Brinkman’s law was extended to the Darcy’s law for porous media in order to satisfy the boundary conditions on the walls of the porous channel. This is a common practice in porous channel flow studies. The same is true for porous microchannels. Here, the no-slip conditions on the wall are replaced by the slip conditions expressed in terms of the velocity and temperature jumps quantified using the Knudsen and Prandtl numbers. We have successfully applied these conditions in the calculations of forced and mixed convection (Avramenko et al. 2018, 2019; Avramenko and Shevchuk 2020).

In the present study, we restrict ourselves to stationary disturbances. Of course, this narrows the range of studied types of instability. However, this approach enables obtaining instability criteria in analytical form as a function of dimensionless parameters, which is very convenient in practice.

Let us assume the velocity and temperature distributions to be a sum of undisturbed components \({\mathbf{\tilde{v}}}_{0}\) and \(\tilde{T}_{0}\) and perturbation components \({\mathbf{\tilde{v}}}_{A}\) and \(\tilde{T}_{A}\), respectively,

$$\tilde{v}\left( {\tilde{z},\tilde{r},\phi } \right) = \tilde{v}_{0} \left( {\tilde{z},\tilde{r}} \right) + \tilde{v}_{A} \left( {\tilde{r},\phi } \right) = \tilde{v}_{A} \left( {\tilde{r},\phi } \right)$$
(6)
$$\left. \begin{gathered} \tilde{T}\left( {\tilde{z},\tilde{r},\phi } \right) = \tilde{T}_{0} \left( {\tilde{z}} \right) + \tilde{T}_{A} \left( {\tilde{r},\phi } \right),\;\tilde{r} < R \hfill \\ \tilde{T}\left( {\tilde{z},\tilde{r},\phi } \right) = \tilde{T}_{0} \left( {\tilde{z}} \right) + \tilde{T}_{w} \left( {\tilde{r},\phi } \right),\;\tilde{r} > R \hfill \\ \end{gathered} \right\}$$
(7)

where \(\tilde{z},\tilde{r},\phi\) are cylindrical coordinates (see Fig. 1).

In doing so, we assume the perturbation components \({\mathbf{\tilde{v}}}_{A}\) and \(\tilde{T}_{A}\) to be independent of z.

In this case, this assumption is justified, since in an infinite channel the base velocity is zero and the temperature gradient along the entire length is constant. Consequently, all points along the channel height are equivalent from the point of view of disturbances.

As the next step, we assume that the perturbations develop only along the channel axis (Avramenko and Shevchuk 2020; Gershuni and Zhukhovitskii 1976)

$$\tilde{v}_{A} \left( {\tilde{r},\phi } \right) = \tilde{u}_{A} \left( {\tilde{r},\phi } \right),\,\tilde{\upsilon }_{A} = 0,\,\tilde{w}_{A} = 0$$
(8)

where \(\tilde{u}_{A} ,\,\,\tilde{\upsilon }_{A} ,\,\tilde{w}_{A}\) are dimensional perturbation velocity components in the cylindrical coordinate system \(\tilde{z},\tilde{r},\phi\), respectively (see Fig. 1).

Substitution of model assumptions (5), (6)–(8) into Eqs. (1)–(4) written in cylindrical coordinates and performing non-dimensionalization of the resulting equations for the perturbation components yields

$$\frac{{\partial ^{2} u_{A} }}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial u_{A} }}{{\partial r}} + \frac{1}{{r^{2} }}\frac{{\partial u_{A} }}{{\partial \phi }} - \frac{{u_{A} }}{{Da}} + RaT_{A} = \frac{{{\text{d}}p}}{{{\text{d}}z}} = C$$
(9)
$$\frac{{\partial ^{2} T_{A} }}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial T_{A} }}{{\partial r}} + \frac{1}{{r^{2} }}\frac{{\partial T_{A} }}{{\partial \phi }} = - u_{A}$$
(10)
$$\frac{{\partial ^{2} T_{w} }}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial T_{w} }}{{\partial r}} + \frac{1}{{r^{2} }}\frac{{\partial T_{w} }}{{\partial \phi }} = 0$$
(11)

where C is the constant of separation of variables, which determines the constant longitudinal pressure gradient (introduced in line of the approach of (Gershuni and Zhukhovitskii 1976)).

$$p = \frac{{\tilde{p}R^{2} }}{{\alpha \nu \rho _{0} }},u_{A} = \frac{{\tilde{u}R}}{\alpha },\,T_{A} = \frac{{\tilde{T}_{A} }}{{BR}},\,T_{w} = \frac{{\tilde{T}_{w} }}{{BR}},\,z = \frac{{\tilde{z}}}{R},\,r = \frac{{\tilde{r}}}{R}$$
(12)

R is the radius of the channel.

The definition of the Rayleigh number is

$${\text{Ra}} = \frac{{g\beta {\text{BR}}^{4} }}{{\alpha \nu }}$$
(13)

,

whereas the Darcy number is defined as

$${\text{Da}} = \frac{K}{{R^{2} }}$$
(14)

For the further transformations, we will use so-called excess temperatures

$$T_{N} = T_{A} - \frac{C}{{{\text{Ra}}}},\,T_{M} = T_{w} - \frac{C}{{{\text{Ra}}}}$$
(15)

which help recast Eqs. (9)–(11) to the following form

$$\frac{{\partial ^{2} u_{A} }}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial u_{A} }}{{\partial r}} + \frac{1}{{r^{2} }}\frac{{\partial u_{A} }}{{\partial \phi }} - \frac{{u_{A} }}{{{\text{Da}}}} + {\text{Ra}}T_{N} = 0$$
(16)
$$\frac{{\partial ^{2} T_{N} }}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial T_{N} }}{{\partial r}} + \frac{1}{{r^{2} }}\frac{{\partial T_{N} }}{{\partial \phi }} = - u_{A}$$
(17)
$$\frac{{\partial ^{2} T_{M} }}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial T_{M} }}{{\partial r}} + \frac{1}{{r^{2} }}\frac{{\partial T_{M} }}{{\partial \phi }} = 0$$
(18)

The fourth term in Eq. (16) including the Darcy number takes stands for the effects of porosity. For Da → ∞, this term vanishes and Eqs. (16)–(18) transform to the system valid only for microchannels without porous inserts (i.e., for pure fluids) (Avramenko and Shevchuk 2020; Gershuni and Zhukhovitskii 1976).

As in the case of pure fluids, the variables in Eqs. (16)–(18) can be separated, once the perturbation velocity uA and temperatures TN and TM are varying as harmonic functions

$$u_{A} = U\left( r \right)\cos \left( {n\phi } \right)$$
(19)
$$T_{N} = \Theta \left( r \right)\cos \left( {n\phi } \right)$$
(20)
$$T_{M} = \theta \left( r \right)\cos \left( {n\phi } \right)$$
(21)

where U is the dimensionless amplitude of the perturbation velocity uA, whereas \(\Theta\) and \(\theta\) are dimensionless perturbation amplitudes for the excess temperatures of the fluid TN and the wall TM, respectively.

Substitution of Eqs. (19)–(21) into Eqs. (16)–(18) leads to a system of ordinary differential equations

$$DU - \frac{U}{{{\text{Da}}}} + {\text{Ra}}\Theta = 0$$
(22)
$$D\Theta + U = 0$$
(23)
$$D\theta = 0$$
(24)

where

$$D = \frac{{{\text{d}}^{2} }}{{\partial r^{2} }} + \frac{1}{r}\frac{{\text{d}}}{{{\text{d}}r}} - \frac{{n^{2} }}{{r^{2} }}$$
(25)

The term containing the Darcy number in Eq. (22) accounts for porosity, which is the novelty against previous studies. Setting Da → ∞ yields the system of equations valid for pure fluids (Avramenko and Shevchuk 2020; Gershuni and Zhukhovitskii 1976).

The boundary conditions for the dimensionless perturbation amplitudes U, \(\Theta\) and \(\theta\) are

$$\frac{{dU}}{{dr}} = 0,\Theta = {\text{const at}}\;r = 0$$
(26)
$$U = - {\text{Kn}}\frac{{{\text{d}}U}}{{{\text{d}}r}},\Theta = \theta - \frac{{{\text{Kn}}}}{{\Pr }}\frac{{{\text{d}}\Theta }}{{{\text{d}}r}},\;\lambda \frac{{{\text{d}}\Theta }}{{{\text{d}}r}} = \frac{{{\text{d}}\theta }}{{{\text{d}}r}}\;{\text{at}}\;r = 1$$
(27)
$$\theta \to {\text{const}}{\text{. at }}r \to \infty$$
(28)

Here

$${\text{Kn}} = \frac{L}{R}$$
(29)

is the Knudsen number, L is the free path of a molecule,

$$\Pr = \frac{\nu }{\alpha }$$
(30)

is the Prandtl number,

$$\lambda = \frac{k}{{k_{w} }}$$
(31)

is the ratio of thermal conductivities of the fluid k and the solid medium (i.e., wall) kw, respectively.

3 Instability Analysis

Using Eqs. (22), (23) one can eliminate the temperature and obtain an equation for the velocity. However, this equation does not have an analytical solution, and therefore, we investigate system  (22) ,(23) for eigenvalues using the Galerkin method.

An exact analytical study Gershuni and Zhukhovitskii (1976) focused on convective instability for a pure fluid without slipping on the channel walls. This study showed that the most dangerous are diametrically antisymmetric disturbances (n = 1), which correspond to the smallest (critical) values of the Rayleigh number. In this work, the same critical values were obtained using the Galerkin method. The approach of Gershuni and Zhukhovitskii (1976) was successfully extended to the case of instability in a pure fluid in a vertical circular microchannel in our recent work Avramenko and Shevchuk (2020). Comparisons of the exact and approximate solutions showed that already in the second approximation the Galerkin method leads to results that practically do not differ from the exact solutions. Therefore, we will apply the Galerkin method for our case.

In the present study, we also performed computations for different modes in the range of n = 0, 1, 2, 3, 4. These computations indicated that the most dangerous are diametrically antisymmetric disturbances (n = 1) with the smallest critical values of the Rayleigh number. Therefore, all further computations were performed for the mode with n = 1.

Following Gershuni and Zhukhovitskii (1976), let us set the velocity profile in the following form

$$U = \left( {1 - r^{2} + 2{\text{Kn}}} \right)\sum\limits_{{k = 1}}^{\infty } {C_{k} r^{{2k - 1}} }$$
(32)

This expression is modified in comparison with the work Gershuni and Zhukhovitskii (1976) by adding a term with the Knudsen number to satisfy the boundary condition (27). We restrict ourselves to the second approximation (32), which gives an almost exact coincidence with the exact solution for a pure fluid without slipping. Then,

$$U = \left( {1 - r^{2} + 2{\text{Kn}}} \right)\left( {C_{1} r + C_{2} r^{3} } \right)$$
(33)

Let us substitute this function into Eq. (23) and solve it together with Eq. (24) to satisfy the boundary conditions (26–28). As a result, we have

$$\begin{gathered} \Theta = C_{1} \frac{r}{2}\left( {\left( {\frac{1}{3} + \frac{{{\text{3Kn}}}}{2} - \frac{{1 + 6{\text{Kn}}}}{{{\text{6}}\left( {{\text{1}} + {\text{Kn/Pr}} + \lambda } \right)}}} \right) - \frac{{r^{2} }}{2}\left( {\frac{1}{2} + {\text{Kn}}} \right) + \frac{{r^{4} }}{{12}}} \right) + \hfill \\ C_{2} \frac{r}{{48}}\left( {\left( {3 + {\text{20Kn}} - \frac{{2 + 16{\text{Kn}}}}{{\left( {{\text{1}} + {\text{Kn/Pr}} + \lambda } \right)}}} \right) - 4r^{4} \left( {\frac{1}{{24}} + {\text{Kn}}} \right) + r^{6} } \right) \hfill \\ \end{gathered}$$
(34)
$$\theta = \frac{{\lambda \left( {2C_{1} \left( {{\text{1}} + 6{\text{Kn}}} \right) + C_{2} \left( {{\text{1}} + 8{\text{Kn}}} \right)} \right)}}{{24\left( {{\text{1}} + {\text{Kn/Pr}} + \lambda } \right)r}}$$
(35)

Substitution of Eqs. (33) and (34) into Eq. (22) yields the residual

$$\begin{gathered} {\text{Res}} = \frac{{C_{1} r}}{{48}}\left( { - \frac{{48r^{2} \left( {1 + 2{\text{Kn}} + {\text{8Da}} - r^{2} } \right)}}{{{\text{Da}}}} + 2{\text{Ra}}\left( {4 - 3r^{2} + r^{4} + 6{\text{Kn}}\left( {3 - r^{2} } \right) - \frac{{2 + 12{\text{Kn}}}}{{{\text{1}} + {\text{Kn/Pr}} + \lambda }}} \right)} \right) + \hfill \\ \frac{{C_{2} r}}{{48}}\left( {384\left( {1 + 2{\text{Kn}} - 3r^{2} } \right) - \frac{{48r^{2} \left( {1 + 2{\text{Kn}} - r^{2} } \right)}}{{{\text{Da}}}} + {\text{Ra}}\left( {3 - 2r^{4} + r^{6} + 4{\text{Kn}}\left( {5 - r^{4} } \right) - \frac{{2 + 16{\text{Kn}}}}{{{\text{1}} + {\text{Kn/Pr}} + \lambda }}} \right)} \right) \hfill \\ \end{gathered}$$
(36)

Based on the Galerkin method, we compose the following equations.

$$\int\limits_{{\text{0}}}^{{\text{1}}} {{\text{Res }}r^{2} \left( {1 - r^{2} } \right){\text{d}}r} = 0,\int\limits_{{\text{0}}}^{{\text{1}}} {{\text{Res }}r^{4} \left( {1 - r^{2} } \right){\text{d}}r} = 0$$
(37)

When compiling these relationships, it was considered that the integration is performed over the area element rdr. As a result, the weight r appears in Eqs. (37).

Equation (37) generate a system of linear homogeneous algebraic equations for C1 and C2. The condition for the existence of a nontrivial solution to this system is that the determinant composed of the coefficients Aij at C1 and C2 vanishes, i.e.

$$\det \left\| {A_{{ij}} } \right\| = 0,\;i = 1,2\;j = 1,2$$
(38)

where i is the column number and j is the row number. In Eq. (38),

$$A_{{11}} = \frac{1}{{2880}}\left( {\left( {2\left( {14 + 75{\text{Kn}}} \right) - \frac{{20\left( {1 + 6{\text{Kn}}} \right)}}{{{\text{1}} + {\text{Kn/Pr}} + \lambda }}} \right){\text{Ra}} - \frac{{120\left( {1 + 4{\text{Kn}} + {\text{16Da}}} \right)}}{{{\text{Da}}}}} \right)$$
(39)
$$A_{{12}} = \frac{1}{{2880}}\left( {\left( {\left( {13 + 94{\text{Kn}}} \right) - \frac{{10\left( {1 + 8{\text{Kn}}} \right)}}{{{\text{1}} + {\text{Kn/Pr}} + \lambda }}} \right){\text{Ra}} - \frac{{48\left( {1 + 5{\text{Kn}} + {\text{20Da}}\left( {1 - 4{\text{Kn}}} \right)} \right)}}{{{\text{Da}}}}} \right)$$
(40)
$$A_{{21}} = \frac{1}{{40320}}\left( {\left( {14\left( {13 + 72{\text{Kn}}} \right) - \frac{{140\left( {1 + 6{\text{Kn}}} \right)}}{{{\text{1}} + {\text{Kn/Pr}} + \lambda }}} \right){\text{Ra}} - \frac{{672\left( {1 + 5{\text{Kn}} + {\text{20Da}}} \right)}}{{{\text{Da}}}}} \right)$$
(41)
$$A_{{22}} = \frac{1}{{40320}}\left( {\left( {\left( {87 + 644{\text{Kn}}} \right) - \frac{{70\left( {1 + 8{\text{Kn}}} \right)}}{{{\text{1}} + {\text{Kn/Pr}} + \lambda }}} \right){\text{Ra}} - \frac{{336\left( {1 + 6{\text{Kn}} + {\text{16Da}}\left( {2 - 5{\text{Kn}}} \right)} \right)}}{{{\text{Da}}}}} \right)$$
(42)

In the first approximation, when only one test function is considered, the solution of the system is reduced to the condition

$$A_{{11}} = \frac{1}{{2880}}\left( {\left( {2\left( {14 + 75{\text{Kn}}} \right) - \frac{{20\left( {1 + 6{\text{Kn}}} \right)}}{{{\text{1}} + {\text{Kn/Pr}} + \lambda }}} \right){\text{Ra}} - \frac{{120\left( {1 + 4{\text{Kn}} + {\text{16Da}}} \right)}}{{{\text{Da}}}}} \right) = 0$$
(43)

From this, we obtain the critical value of the Rayleigh number in the first approximation

$$Ra_{{{\text{cr}}}}^{{(1)}} = \frac{{60\left( {1 + 4{\text{Kn}} + 16{\text{Da}}} \right)\left( {1 + {\text{Kn}}/\Pr + \lambda } \right)}}{{{\text{Da}}\left( {15{\text{Kn}}\left( {1 + 5{\text{Kn}}/\Pr + 5\lambda } \right) + 2\left( {2 + 7{\text{Kn}}/\Pr + 7\lambda } \right)} \right)}}$$
(44)

In the absence of slippage, Eq. (42) is reduced to

$$\left( {{\text{Ra}}_{{{\text{cr}}}}^{{{\text{(1)}}}} } \right)_{{{\text{Kn}} \to {\text{0}}}} = \frac{{{\text{1}} + \lambda }}{{{\text{2}} + 7\lambda }}\left( {480 + \frac{{30}}{{{\text{Da}}}}} \right)$$
(45)

At (Da → ∞), Eq. (43) is transformed into a relation for pure fluid (Gershuni and Zhukhovitskii 1976).

For a pure fluid, it follows from Eq. (44)

$$\left( {{\text{Ra}}_{{{\text{cr}}}}^{{{\text{(1)}}}} } \right)_{{{\text{Da}} \to \infty }} = \frac{{960\left( {{\text{1}} + {\text{Kn/Pr}} + \lambda } \right)}}{{{\text{15Kn}}\left( {{\text{1}} + 5{\text{Kn/Pr}} + 5\lambda } \right) + 2\left( {{\text{2}} + 7{\text{Kn/Pr}} + 7\lambda } \right)}}$$
(46)

In the second approximation, Eq. (38) turns into a quadratic equation, the smaller root of which is

$${\text{Ra}}_{{{\text{cr}}}}^{{{\text{(2)}}}} = \frac{{6\left( {S - D\sqrt G } \right)}}{{{\text{Da}}\left( {\left( {{\text{5}}\left( {{\text{1}} + 7\left( {{\text{Kn/Pr}} + \lambda } \right)} \right) + 15{\text{Kn}}\left( {{\text{3}} + 29\left( {{\text{Kn/Pr}} + \lambda } \right)} \right) + 8{\text{4Kn}}^{{\text{2}}} \left( {{\text{1}} + 11\left( {{\text{Kn/Pr}} + \lambda } \right)} \right)} \right.} \right)}}$$
(47)

where

$$\begin{gathered} S = \left( {{\text{9}} + {\text{99}}\left( {{\text{Kn/Pr}} + \lambda } \right) + {\text{4Kn}}\left( {{\text{71}} + 281\left( {{\text{Kn/Pr}} + \lambda } \right) + 140{\text{Kn}}\left( {{\text{1}} + 4{\text{Kn/Pr}} + 4\lambda } \right)} \right)} \right. + \hfill \\ \left. {48{\text{Da}}\left( {{\text{3}}3 + {\text{1}}03\left( {{\text{Kn/Pr}} + \lambda } \right) + {\text{70Kn}}\left( {{\text{1}} + 7\left( {{\text{Kn/Pr}} + \lambda } \right) - 2{\text{Kn}}\left( {{\text{1}} + {\text{Kn/Pr}} + \lambda } \right)} \right)} \right)} \right) \hfill \\ \end{gathered}$$
(48)
$$\begin{gathered} G = S^{2} - 112\left( {1 + 960{\text{Da}}^{{\text{2}}} + 10{\text{Kn}}\left( {{\text{1}} + 2{\text{Kn}}} \right) + 80{\text{Da}}\left( {{\text{1}} + 3{\text{Kn}}} \right)} \right)\left( {{\text{1}} + {\text{Kn/Pr}} + \lambda } \right) \hfill \\ \left( {5\left( {{\text{1}} + {\text{7}}\left( {{\text{Kn/Pr}} + \lambda } \right)} \right) + 15{\text{Kn}}\left( {{\text{3}} + {\text{2}}9{\text{1}}\left( {{\text{Kn/Pr}} + \lambda } \right)} \right) + 84{\text{Kn}}^{{\text{2}}} \left( {{\text{1}} + {\text{11}}\left( {{\text{Kn/Pr}} + \lambda } \right)} \right)} \right) \hfill \\ \end{gathered}$$
(49)

For a pure fluid without slipping, Eq. (45) transforms into

$$\left( {{\text{Ra}}_{{{\text{cr}}}}^{{{\text{(2)}}}} } \right)_{{{\text{Da}} \to \infty ,{\text{Kn}} \to {\text{0}}}} = \frac{{96\left( {3\left( {{\text{33}} + \lambda } \right) - \sqrt {3(2567 + 147947\lambda + 26927\lambda ^{2} } } \right)}}{{\left( {{\text{5}} + 7\lambda } \right)}}$$
(50)

which fully corresponds to the results of the study Gershuni and Zhukhovitskii (1976).

To summarize, in the approach used in the present work, the effect of the porous medium permeability (Darcy number) is considered not through the test functions (32) and (33), but directly through Eq. (22) itself. This can be seen from the solutions (44) and (47) for the critical Rayleigh number. In comparison, we tried to consider the permeability (Darcy number) through the trial functions. However, this led to a solution in the form of very cumbersome expressions, which contained cylindrical (Bessel) and hypergeometric functions. Comparisons of these cumbersome equations with the results by Eqs. (44), (47) demonstrated a difference of only a few percent. This is understandable, because the Galerkin method is conservative with respect to the choice of trial functions. The main point is to satisfy the boundary conditions, which is provided by the involvement of the Knudsen number in the trial function (33).

As to the eigenfunctions of the Galerkin’s method, their role plays the trial functions used to analyze the linearized system of differential equations. In other words, in our case the eigenfunctions are Eqs.(33), (34),(35). The exact eigenfunctions for the case Da → ∞ are Eqs. (51), (52)

4 Verification of the Galerkin Approach

To validate the obtained equation for the critical Rayleigh number in the Galerkin approximation, let us compare these results with the exact model for a pure fluid. For a pure fluid (Da → ∞), the system of Eqs. (22)–(23) with boundary conditions (26)–(28) has an exact solution

$$U = \left( {1 + \gamma {\text{Kn}}\frac{{I^{\prime}_{n} \left( \gamma \right)}}{{I_{n} \left( \gamma \right)}}} \right)\frac{{J_{n} \left( {\gamma r} \right)}}{{J_{n} \left( \gamma \right)}} - \left( {1 + \gamma {\text{Kn}}\frac{{J^{\prime}_{n} \left( \gamma \right)}}{{J_{n} \left( \gamma \right)}}} \right)\frac{{I_{n} \left( {\gamma r} \right)}}{{I_{n} \left( \gamma \right)}}$$
(51)
$$\Theta = \frac{1}{{\gamma ^{2} }}\left( {\left( {1 + \gamma {\text{Kn}}\frac{{I^{\prime}_{n} \left( \gamma \right)}}{{I_{n} \left( \gamma \right)}}} \right)\frac{{J_{n} \left( {\gamma r} \right)}}{{J_{n} \left( \gamma \right)}} + \left( {1 + \gamma {\text{Kn}}\frac{{J^{\prime}_{n} \left( \gamma \right)}}{{J_{n} \left( \gamma \right)}}} \right)\frac{{I_{n} \left( {\gamma r} \right)}}{{I_{n} \left( \gamma \right)}}} \right)$$
(52)
$$\theta = \left( {\frac{2}{{\gamma ^{2} }} + {\text{Kn}}\frac{{1 + \Pr }}{{\gamma \Pr }}\left( {\frac{{J^{\prime}_{n} \left( \gamma \right)}}{{J_{n} \left( \gamma \right)}} + \frac{{I^{\prime}_{n} \left( \gamma \right)}}{{I_{n} \left( \gamma \right)}}} \right) + \frac{{2{\text{Kn}}^{2} }}{{\Pr }}\frac{{J^{\prime}_{n} \left( \gamma \right)}}{{J_{n} \left( \gamma \right)}}\frac{{I^{\prime}_{n} \left( \gamma \right)}}{{I_{n} \left( \gamma \right)}}} \right)\frac{1}{{r^{n} }}$$
(53)

This solution enables obtaining the transcendent equation for the critical Rayleigh number

$$\frac{{2n}}{{\gamma \lambda }} + \frac{{J^{\prime}_{n} \left( \gamma \right)}}{{J_{n} \left( \gamma \right)}} + \frac{{I^{\prime}_{n} \left( \gamma \right)}}{{I_{n} \left( \gamma \right)}} + Kn\left( {\frac{{n\left( {1 + \Pr } \right)}}{{\lambda \Pr }}\left( {\frac{{J^{\prime}_{n} \left( \gamma \right)}}{{J_{n} \left( \gamma \right)}} + \frac{{I^{\prime}_{n} \left( \gamma \right)}}{{I_{n} \left( \gamma \right)}}} \right) + \frac{{I^{\prime}_{n} \left( \gamma \right)}}{{I_{n} \left( \gamma \right)}}\frac{{J^{\prime}_{n} \left( \gamma \right)}}{{J_{n} \left( \gamma \right)}}} \right) + \frac{{{\text{Kn}}^{2} }}{{\Pr }}\frac{{2n\gamma }}{\lambda }\frac{{J^{\prime}_{n} \left( \gamma \right)}}{{J_{n} \left( \gamma \right)}}\frac{{I^{\prime}_{n} \left( \gamma \right)}}{{I_{n} \left( \gamma \right)}} = 0$$
(54)

Here Jn is the Bessel function of the first kind and In is the modified Bessel function of the first kind.

Comparisons of the calculation results for the two models are shown in Table 1.

Table 1 Comparison of the calculation results for critical Rayleigh number
Full size table

Comparisons of the exact and approximate solutions show that the second Galerkin approximation at all tested points agrees with the exact solution with a relative error of no more than 10%, and at many points, this error does not exceed 1%. Therefore, the second Galerkin approximation can be considered quite acceptable for studying instability in a porous channel. In any case, this approximation will correctly reflect the tendency of the influence of various factors on the instability criteria.

For adiabatic conditions λ → ∞, and in the absence of slippage, Eq. (45) takes the form

$${\text{Ra}}_{{{\text{cr}}}}^{{}} = \frac{{6\left( {99 + 4944{\text{Da}} - \sqrt {\left( {5881 + 665312{\text{Da}} + 20679936{\text{Da}}^{2} } \right)} } \right)}}{{35}}$$
(55)

In the case of Da → 0, this equation gives the limiting value \({\text{Ra}}_{{{\text{cr}}}}\) = 3.82. An exact solution of this problem (Wooding 1959) resulted in the value \({\text{Ra}}_{{{\text{cr}}}}\) = 3.39, that is, the relative error is about 11%. Since Eq. (43) was obtained considering the effects of slippage, porosity and thermal interaction, we can assume that the relative error is acceptable.

In the present study, perturbations in the form (8) were used for several reasons. First, this work is a continuation of the study (Gershuni and Zhukhovitskii 1976) for a pure fluid in an ordinary channel (not a microchannel), where the same form of perturbations was used. Therefore, this solution should converge to the results (Gershuni and Zhukhovitskii 1976), if \({\text{Da}} \to \infty {\text{, Kn}} \to {\text{0}}\), which is confirmed by Eq. (50). This speaks in favor of the correctness of the present solution. Second, in accordance with the Squire’s theorem, reducing the dimension of perturbations enables finding criteria for instability with enough margin. This theorem for a porous microchannel was proved in Avramenko et al. (2007). Third, comparison of Eq. (55) with the results of the work (Wooding 1959), where two-dimensional perturbations were used, demonstrates its good agreement. This also confirms the correctness of the present solution.

5 Results and Discussion

Equation (47) enables calculating the critical value of the Rayleigh number in the form

$${\text{Ra}}_{{{\text{cr}}}} = {\text{Ra}}_{{{\text{cr}}}} \left( {\lambda ,{\text{Kn,}}\Pr ,{\text{Da}}} \right)$$
(56)

It means that the conditions for the onset of convective instability can be determined depending on the ratio of thermal conductivities of the fluid and the solid wall, the magnitude of the velocity and temperature jumps on the wall (the flow slip), the properties of the fluid and the porosity. Also, based on Eq. (49), one can investigate the stability for limiting cases. In the absence of slippage (Kn = 0), Eq. (47) gives the critical Rayleigh numbers in the case of flow in a porous channel of arbitrary dimensions. The condition Da → ∞ enables calculating the conditions for the onset of convective instability for a pure fluid in a microchannel. With the simultaneous fulfillment of the conditions Kn = 0 and Da → ∞, Eq. (47) is transformed into a dependence for a pure fluid without slipping. For the condition λ → ∞, Eq. (47) gives the values of Racr for adiabatic conditions.

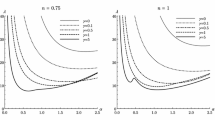
Figure 2 depicts the dependence of the critical Rayleigh number on the ratio of thermal conductivities of the fluid and the solid wall under the conditions Pr = const and the same Knudsen and Darcy number. As can be seen, a decrease in the thermal conductivity of the solid phase (an increase in the value of the parameter λ) causes destabilization of the flow and favors the onset of convective instability (decreased in the critical Rayleigh numbers). This is explained by the fact that a decrease in the thermal conductivity of the channel walls decreases the heat removal from the fluid, and therefore, a greater amount of heat is spent for the onset of instability. Thus, for the same Knudsen and Darcy numbers, the critical Rayleigh numbers decrease monotonically with increasing value of the parameter λ.

Fig.2
figure 2

Dependences of the critical Rayleigh number Racr on λ for Pr = 1: 1—Kn = 0, Da = 1000; 2—Kn = 0, Da = 0.5; 3—Kn = 0, Da = 0.01; 4—Kn = 0.2, Da = 1000; 5—Kn = 0.2, Da = 0.5; 6—Kn = 0.2, Da = 0.01

Full size image

It is also seen that a decrease in the Darcy number leads to stabilization of the system. This is obvious, since a decrease in the Darcy number means a decrease in permeability and, consequently, a deterioration in the conditions for the throughflow of the fluid due to an increase in hydraulic resistance according to the Darcy’s law. In this situation, the influence of the Darcy number on the critical Rayleigh number is significantly nonlinear (Fig. 3).

Fig.3
figure 3

Dependences of the critical Rayleigh number Racr on the Darcy number for Pr = 1, λ = 1: 1—Kn = 0; 2—Kn = 0.1; 3—Kn = 0.2

Full size image

Under the condition Da > 0.1, the effect of the porosity of the medium on Racr practically disappears, and the conditions for the onset of convection are decisively influenced by slippage effects (i.e., by the Kn number). Slippage effect, i.e., an increase in the velocity and temperature jumps on the wall (an increase in the Knudsen number), leads to a weakening of the stability of the system and the critical Rayleigh number will correspondingly decrease. This trend is observed in the entire range of the investigated values of the ratio of thermal conductivities of the fluid and the solid wall (0 … ∞) and the Prandtl numbers (0.01… 100). In this case, the decrease in the stability threshold is due to the weakening of the hydrodynamic and thermal interaction of the fluid with the channel walls due to slippage effects, when velocity and temperature jumps arise on the channel walls. This reduces the surface friction and thus favors higher velocities in the fluid. It should be pointed out that such effect of the slippage on the onset of convective instability is fundamentally different from other types of hydrodynamic instability. In the case of the Orr–Somerfeld instability (Avramenko et al. 2007; Lauga and Cossu 2005; Avramenko and Kuznetsov 2009) (the onset of pulsations in laminar flow) and the Taylor–Dean centrifugal instability (the onset of longitudinal macrovortices), the instability thresholds increase with the increasing Knudsen numbers. In these cases, the weakening of the interaction of the flow with the wall (a decrease in the surface friction) worsens the conditions for the onset of disturbances in a fluid, which already flows. Consequently, the threshold for the onset of these types of instability increases.

The influence of slippage on the critical Rayleigh number Racr is also nonlinear (Fig. 4). Moreover, the degree of nonlinearity depends on the Prandtl number. With an increase in the Prandtl number, the influence of the slippage on the onset of convection decreases. This is because of the degeneracy of the temperature jump on the channel wall at high values of the Prandtl number.

Fig.4
figure 4

Dependences of the critical Rayleigh number Racr on the Knudsen number Kn for Da = 0.01, λ = 1: 1—Pr = 0.01; 2—Pr = 1; 3—Pr = 100

Full size image

Figure 5 demonstrates the influence of the Prandtl number on Racr at different values of the ratio of the thermal conductivities of the fluid and the wall. It can be seen that an increase in the Prandtl number causes an increase in the stability. This is due to two reasons.

Fig.5
figure 5

Dependences of the critical Rayleigh number Racr different values of the ratio λ of the thermal conductivities of the fluid and the wall: Da = 0.01, Kn = 0.1: 1—λ = 0.01; 2—λ = 1; 3—λ = 10

Full size image

Firstly, an increase in the Prandtl number can be caused by an increase in the viscosity of the fluid, which naturally stabilizes the system. However, as it follows from Eq. (54), in the absence of slippage (Kn = 0), the Prandtl number is not the determining parameter of the stability criterion. In this case, the effect of viscosity follows from the definition of the Rayleigh number, according to which the increased viscosity causes an increase in the value of the temperature difference (gradient) required for the onset of convection.

Secondly, an increase in the Prandtl number leads to a decrease in the temperature jump on the wall, which, accordingly, enhances the heat removal. Consequently, more heat is used to create instability. In addition, Fig. 4 shows that the influence of the Prandtl number on the onset of instability depends on the ratio λ of the thermal conductivities of the fluid and the wall. With an increase in the value of λ, the Prandtl number effect weakens, since at λ → ∞ the heat transfer intensity, which is determined by the Prandtl number, decreases. Conversely, at high values of the Prandtl number (Pr > 10), its influence practically disappears. And the critical value of the Rayleigh number Racr is decisively influenced by the thermal conductivity of the system, since in this case the temperature jump degenerates.

6 Conclusions

A mathematical model of convective instability in a vertical cylindrical porous microchannel was developed, which represents the novelty of the present study. The stability analysis was performed based on the Galerkin method. As a result, the dependence of the critical Rayleigh number (criterion for the onset of instability) on the Darcy, Knudsen and Prandtl numbers, as well as the ratio of the thermal conductivities of the fluid and the wall, was obtained. It was shown that a decrease in the Darcy number causes the stabilization of the system, since this means a decrease in permeability of the porous medium and, therefore, a deterioration in the conditions for the throughflow of the fluid due to an increase in hydraulic resistance, according to the Darcy’s law. This effect is essentially nonlinear. Under the condition Da > 0.1, the porosity effect on Racr practically disappears, and the conditions for the onset of convection are decisively influenced by slippage effects (Kn). An increase in the velocity and temperature jumps on the wall causes a weakening of the system stability and a decrease in the critical Rayleigh number Racr. This trend is observed in the entire range of the investigated values of the ratio of the thermal conductivities of the fluid and the wall (0…∞) and the values of the Prandtl numbers (0.01…100).

The effect of slippage on Racr is also nonlinear. The degree of nonlinearity depends on the Prandtl number. With an increase in the Prandtl number, the influence of slippage on the onset of convection decreases. This is because of the degeneracy of the temperature jump on the channel wall at high values of the Prandtl number. A decrease in the thermal conductivity of the solid wall leads to the destabilization of the system, since in this case a greater amount of heat is spent on the onset of instability. The degree of influence of the Prandtl number on the onset of instability depends on the ratio of the thermal conductivities of the fluid and the wall. With an increase in the value of λ, the influence of the Prandtl number decreases, since at λ → ∞ the intensity of heat transfer decreases, the value of which is determined by the Prandtl number. The same effect is observed at high Prandtl numbers (Pr > 10).