1 Introduction

One of the most important properties of chaotic systems is the appearance of irregular behavior in their dynamics; indeed, the state variables of such systems are highly sensitive to the starting point. In other words, a small change in the initial conditions may cause a wide variation, or even divergence, in the system dynamics. Consequently, it is very important from both practical and theoretical viewpoints to analyze such complicated systems. The footsteps of chaos are found in various branches of sciences and technologies including economy, biology, physics, secure communications, and so on, and many scientists have devoted growing attention to the analysis, synchronization, and control of complex chaotic systems. In [1] a nonlinear control approach was examined to synchronize two identical hyperchaotic systems. In [2] the state-dependent Riccati equations were employed to control and synchronize chaotic attractors. In [3] a combination of state-feedback control and Lyapunov function was utilized for the synchronization and control of a fractional hyperchaotic model. In [4] the hyperchaotic Lorenz system and the chaotic Chen model were controlled by applying an adaptive terminal sliding mode control. In [5] the concept of nonidentical synchronization for three systems with different dimensions was studied by taking into account the theory of Lyapunov stability. In [6] a nonfeedback loop was designed for tumor cells to control the chaotic behaviors. In [7] a class of fractional chaotic systems with input nonlinearities was considered, and a projective synchronization was achieved by a fuzzy adaptive controller.

Over the past few decades, fractional-order systems have been considered for the modeling of realistic phenomena due to their possession of memory effects [8–12]. This feature makes the fractional-order models more practical to describe real-world processes compared to the classic integer-order models with ordinary time derivatives [13–18]. Besides, it was demonstrated that the fractional models are capable of describing chaotic systems properly, so these models have appeared in different fields dealing with chaos like mechanics, biology, and finance [19–21]. Hence, it is justifiable to focus more on the new fractional-order chaotic models; additionally, the irregular behaviors of such models should be compensated by developing effective control and synchronization strategies. Therefore, it is worth to study the problem of modeling and synchronization related to the new fractional chaotic systems; however, the implementation and synchronization with regard to these models acquire an extension of the numerical methods available in the literature [22–27]. These argumentations motivate us to study a novel fractional chaotic system with quadratic and cubic nonlinearities involving the Caputo differential operator. We utilize the fractional Routh–Hurwitz criteria to investigate the stability of the steady states. Then we design an efficient nonstandard finite difference (NSFD) scheme to implement the chaotic model and study its complex behaviors. Simulation results in time-domain and phase-plane indicate that the new system exhibits both chaotic and nonchaotic behaviors, so we find via the numerical simulations the lowest order in which the system remains chaotic. Next, we design an active controller to attain a nonidentical synchronization between the presented model and the fractional Volta equations. Theoretical analysis and simulation results verify the effectiveness of the proposed active control strategy.

The main structure of this paper is summarized as follows. Section 2 recalls a brief discussion about the fractional calculus and the NSFD scheme. In Sect. 3, we introduce a new chaotic system and discuss its stability and equilibrium points. In Sect. 4, we apply the NSFD scheme to implement the new model. Then we study a nonidentical synchronization between the novel fractional-order system and the fractional-order Volta equations. Finally, we finish the paper in the last section by some concluding remarks.

2 Preliminaries and notations

In this section, we briefly discuss the basic definitions in the fractional calculus and the NSFD discretization.

2.1 Fractional calculus

We first we define the Caputo fractional derivative and then recall the corresponding its Grünwald–Letnikov (GL) approximation for fractional differential equations (FDEs). To do so, let \(\alpha \in (0,1)\), and let x be a real-valued integrable function. Then the αth-order Caputo fractional derivative of x is defined by [28]

$$ {}^{\mathrm{C}} \!\mathscr{D}^{\alpha }x(t)= \frac{1}{\Gamma (1-\alpha )} \int _{0}^{t} \dot{x}(\tau ) (t-\tau )^{-\alpha } \,d\tau . $$
(1)

Next, we can discretize the FDE

$$ \textstyle\begin{cases} {}^{\mathrm{C}} \!\mathscr{D}^{\alpha }x(t)=g(x(t),t),\quad t \in [0,t_{f}], \\ x(0)=x_{0}, \end{cases} $$
(2)

where \(t_{f}\) is the final time, by

$$ \sum_{j=0}^{n+1} c_{j}^{\alpha }x_{n+1-j}=g(x_{n+1},t_{n+1}),\quad n=0,1,2, \ldots . $$
(3)

In this expression, \(x_{n}\) is the approximation of \(x(t_{n})\), \(t_{n} = nh\), \(c_{j}^{\alpha }\) is the GL coefficient computed from

$$ c_{0}^{\alpha }=h^{-\alpha },\qquad c_{j}^{\alpha }= \biggl(1-\frac{1+\alpha }{j} \biggr)c_{j-1}^{\alpha }, \quad j=1, 2, 3, \ldots , $$
(4)

and h is the time step-size.

2.2 Nonstandard finite difference scheme

In this part, we discuss the notion of NSFD scheme in both integer and fractional frameworks. To this end, we first take into account an ordinary differential equation (ODE) of the form

$$ \textstyle\begin{cases} \frac{dx(t)}{dt}=g(x(t),t,\lambda ),\quad t \in [0,t_{f}], \\ x(0) = x_{0}, \end{cases} $$
(5)

where \(t_{f}\) is the final time, and λ is a parameter. Considering the discretization \(t_{n}=nh\), we can construct the NSFD scheme by the next two steps:

  1. (i)

    Let \(x_{n}\) be the approximation of \(x(t_{n})\). Then we use the discrete approximation

    $$ \frac{dx(t)}{dt}\approx \frac{x_{n+1}-x_{n}}{\phi (h,\lambda )} $$
    (6)

    for the integer-order differentiation in (5).

  2. (ii)

    We utilize the expression \(G(x_{n+1},x_{n},\ldots ,t,\lambda )\) for the nonlinear term in Eq. (5), a nonlocal discrete representation depending on the previous approximations.

Therefore we get the NSFD scheme for the ODE (5) by

$$ \frac{x_{n+1}-x_{n}}{\phi (h,\lambda )}=G(x_{n+1},x_{n}, \ldots ,t, \lambda ). $$
(7)

Note that by setting \(\phi (h,\lambda )= h\) in Eq. (6) we can obtain the classical discretization for the first-order derivatives; hence the discrete representation (6) is a generalization of its classical counterpart. In addition, the following consistency condition must be satisfied by the denominator function \(\phi (h,\lambda )\):

$$ \phi (h,\lambda ) = h + \mathcal{O} \bigl({h^{2}} \bigr), $$
(8)

which ensures the convergence of the discrete approximation (6) to the associated continuous derivative as h tends to zero. We give some examples satisfying condition (8) [29, 30]:

$$ 1-e^{-h},\qquad \frac{1-e^{-\lambda h}}{\lambda },\qquad \sin h,\qquad h. $$
(9)

Mickens [31] presents a general technique to determine \(\phi (h,\lambda )\) for the system of ODEs. For instance, with regard to the ODE

$$ \frac{dx(t)}{dt} = \lambda x(t) + (\mathit{NL}), $$
(10)

in which NL represents nonlinear polynomial terms, Mickens [31] proposed the NSFD scheme

$$ \frac{{{x_{n + 1}} - {x_{n}}}}{\phi (h,\lambda )} = \lambda {x_{n}} + {(\mathit{NL})_{n}}, $$
(11)

where \(\phi (h,\lambda )=\frac{e^{\lambda h}-1}{\lambda }\) for \(\lambda \neq 0\) and \(\phi (h, \lambda )=h\) for \(\lambda =0\). Additionally, the NSFD scheme requires the discrete-time computational grids on which the dependent functions should be modeled. In this case, some examples include the expressions [29, 30]

$$ \begin{aligned} &xy \approx 2x_{n+1}y_{n}-x_{n+1}y_{n+1}, \qquad xy\approx x_{n}y_{n+1}, \\ &x^{3} \approx \biggl(\frac{x_{n+1}+x_{n-1}}{2}\biggr)x_{n}^{2}, \qquad x^{2} \approx 2x_{n} \frac{x_{n+1}+x_{n}}{2}. \end{aligned} $$
(12)

Now we extend the above-mentioned approach for the FDE

$$ \textstyle\begin{cases} {}^{\mathrm{C}} \!\mathscr{D}^{\alpha }x(t)=g(x(t),t,\lambda ),\quad t \in [0,t_{f}], \\ x(0)=x_{0}. \end{cases} $$
(13)

For this purpose, we employ the discretized GL approximation formula from relation (3). Therefore we can provide a modification of NSFD scheme in the fractional sense as follows:

$$\begin{aligned} x_{n+1}= \frac{- {\sum_{j=1}^{n+1}} c_{j}^{\alpha }x_{n+1-j}+g(x_{n+1},t_{n+1})}{c_{0}^{\alpha }},\quad n=0, 1, 2, \ldots , \end{aligned}$$
(14)

where

$$ c_{0}^{\alpha }= \bigl(\phi (h,\lambda ) \bigr)^{-\alpha }, \qquad c_{j}^{\alpha }= \biggl(1- \frac{1+\alpha }{j} \biggr)c_{j-1}^{\alpha },\quad j=1, 2, 3, \ldots . $$
(15)

3 The new chaotic system

In this section, we introduce a new chaotic system in both frameworks of classical and fractional calculus. Then we discuss its stability analysis in the integer- and fractional-order cases.

3.1 Integer-order case

Recently, the study [32] reported a new chaotic system with eight polynomial terms, and its butterfly-shaped chaotic attractors were investigated by means of a detailed theoretical discussion and some numerical simulations. The aforesaid system with abundant and complex chaotic dynamics is described by the following nonlinear integer-order differential equations with three quadratic nonlinearities and a cubic term:

$$ \begin{aligned} &\frac{dx(t)}{dt}=a \bigl(y(t)-x(t)\bigr)+by(t)z(t), \\ &\frac{dy(t)}{dt}=-10y^{3}(t)-y(t)+4x(t)z(t), \\ &\frac{dz(t)}{dt}=cz(t)-x(t)y(t), \end{aligned} $$
(16)

where a, b, and c are positive constants, x, y, and z are the state variables, and \(x(0)=x_{0}\), \(y(0)=y_{0}\), and \(z(0)=z_{0}\) are initial conditions.

3.1.1 Stability analysis

When \(a = 3\), \(b = 14\), and \(c = 3.9\), the new system (16) has five steady states

$$ \begin{aligned} &E_{1}=(0,0,0), \qquad E_{2}=(2.5905, 0.7670, 0.5095), \\ &E_{3}=(-2.5905, -0.7670, 0.5095),\qquad E_{4}=( 3.4089, -1.0449, -0.9134), \\ &E_{5}=( -3.4089, 1.0449, -0.9134). \end{aligned} $$
(17)

At the equilibrium point \(E_{1}=(0, 0, 0)\), the Jacobian matrix of system (16) is given by

J( E 1 )= [ − 3 3 0 0 − 1 0 0 0 3.9 ] ,

which has the eigenvalues

$$ \lambda _{1}=-3,\qquad \lambda _{2}=-1,\qquad \lambda _{3}=3.9. $$
(18)

Here \(\lambda _{3}\) is a positive real number, and \(\lambda _{1}\), \(\lambda _{2}\) are two negative real ones. Therefore the equilibrium point \(E_{1}=(0, 0, 0)\) is an unstable saddle point. In a similar way, at the equilibrium point \(E_{2}=(2.5905, 0.7670, 0.5095)\), the Jacobian matrix of system (16) is

J( E 2 )= [ − 3 10.1330 10.7380 2.0380 18.6487 10.3620 − 0.7670 − 2.5905 3.9 ] ,
(19)

whose eigenvalues are

$$ \lambda _{1}=-19.1228, \qquad \lambda _{2}=0.6871+3.4276i,\qquad \lambda _{3}=0.6871-3.4276i. $$
(20)

Here \(\lambda _{1}\) is a negative real number, and \((\lambda _{2},\lambda _{3})\) is a pair of complex conjugate eigenvalues with positive real parts. Therefore the equilibrium point \(E_{2}=(2.5905, 0.7670, 0.5095)\) is a saddle-focus point, and so it is unstable. Using a similar calculation, we can easily show that the other equilibria \(E_{3}\), \(E_{4}\), and \(E_{5}\) are also saddle points. Hence all five steady states of the novel chaotic system (16) are unstable.

3.2 Fractional-order case

In this part, we introduce the fractional form of Eq. (16) by the following system of FDEs:

$$ \begin{aligned} & {}^{\mathrm{C}} \!\mathscr{D}^{\alpha _{1}}x(t)=a\bigl(y(t)-x(t)\bigr)+by(t)z(t), \\ & {}^{\mathrm{C}} \!\mathscr{D}^{\alpha _{2}}y(t)=-10y^{3}(t)-y(t)+4x(t)z(t), \\ & {}^{\mathrm{C}} \!\mathscr{D}^{\alpha _{3}}z(t)=cz(t)-x(t)y(t), \end{aligned} $$
(21)

where \(\alpha _{1}, \alpha _{2},\alpha _{3} \in (0,1)\) are incommensurate fractional orders, and \(x(0)=x_{0}\), \(y(0)=y_{0}\), and \(z(0)=z_{0}\) are initial conditions.

3.2.1 Stability analysis

To discuss the stability of system (21), we first recall the stability theorems and the Routh–Hurwitz stability conditions for FDEs.

Theorem 3.1

[33] Let the incommensurate fractional-order system be

$$ \textstyle\begin{cases} {}^{\mathrm{C}} \!\mathscr{D}^{\alpha }x(t)=g(x(t)),\quad t \in [0,t_{f}], \\ x(0)=x_{0}, \end{cases} $$
(22)

where \(\alpha =(\alpha _{1},\ldots ,\alpha _{n})\), \(\alpha _{i}\in (0,1)\) for \(i=1,2,\ldots ,n\), and \(x\in \mathbb{R}^{n}\). Then the equilibrium point E of system (22) is locally asymptotically stable if all eigenvalues λ of the Jacobian matrix \(J(E)\) satisfy

$$ \bigl\vert \arg (\lambda ) \bigr\vert >\alpha _{M} \frac{ \pi }{2},\quad \alpha _{M}=\max_{i}( \alpha _{1},\ldots ,\alpha _{n}), i=1,\ldots ,n. $$
(23)

Concerning a commensurate fractional-order case, when \(\alpha _{1}=\alpha _{2}=\cdots =\alpha _{n}= \alpha _{M}\), the locally asymptotic stability of the equilibrium point E is achieved if all eigenvalues of the Jacobian matrix \(J(E)\) satisfy \(\vert \arg (\lambda )\vert >\alpha _{M} \frac{\pi }{2}\) [33].

With regard to the fractional-order system (21), the local stability conditions are analyzed by using the following results of Routh–Hurwitz stability conditions for FDEs [34].

Theorem 3.2

Let \(D(P)\) be the discriminant of the polynomial

$$ P(\lambda )= \lambda ^{3} +a_{1} \lambda ^{2}+a_{2} \lambda +a_{3}=0 $$
(24)

computed by

$$ D(P)=18a_{1} a_{2} a_{3} +(a_{1} a_{2})^{2} -4a_{3}a_{1}^{3}-4a_{2}^{3}-27a_{3}^{2}. $$
(25)
  1. (i)

    If \(D(P) > 0\), then the steady state E is locally asymptotically stable if and only if \(a_{1}, a_{3} > 0\) and \(a_{1}a_{2} - a_{3} > 0\).

  2. (ii)

    If \(D(P) < 0\), \(a_{1} , a_{2} \geq 0\), and \(a_{3} > 0\), then the steady state E is locally asymptotically stable for \(\alpha _{M} < \frac{2}{3}\). Nevertheless, if \(D(P) < 0\), \(a_{1},a_{2} < 0\), and \(\alpha _{M} > \frac{2}{3}\), then the condition \(\vert \arg (\lambda )\vert <\alpha _{M} \frac{ \pi }{2}\) is satisfied by all roots of the polynomial (24).

  3. (iii)

    If \(D(P) < 0\), \(a_{1} , a_{2} > 0\), and \(a_{1}a_{2} -a_{3} = 0\), then for all \(\alpha _{M} \in (0,1)\), the steady state E is locally asymptotically stable.

  4. (iv)

    The condition \(a_{3}>0\) is necessary for the locally asymptotic stability of the steady state E.

Now according to the aforementioned discussions, we investigate the locally asymptotic stability of the incommensurate fractional-order system (21). To this end, we first compute the Jacobian matrix J of the system (21) at the steady state \(E = (x_{e}, y_{e}, z_{e})\):

J(E)= [ − a a + b z e b y e 4 z e − 30 y e 2 − 1 4 x e − y e − x e c ] .
(26)

Substituting the coordinates of \(E_{1}\) into the Jacobian matrix (26) for \(a = 3\), \(b = 14\), and \(c = 3.9\), we get the characteristic polynomial

$$ \lambda ^{3}+0.1\lambda ^{2}-12.6 \lambda -11.7=0. $$
(27)

Since \(a_{3}=-11.7 < 0\), based on part (iv) of Routh–Hurwitz stability conditions (Theorem 3.2), the equilibrium point \(E_{1}\) is unstable for any \(\alpha _{M} \in (0,1)\). Considering the same values of parameters as above and substituting the coordinates of \(E_{2}\) or \(E_{3}\) into the Jacobian matrix (26), we get the characteristic polynomial

$$ \lambda ^{3}+ 17.7487\lambda ^{2} -14.0561\lambda +233.6935=0. $$
(28)

The eigenvalues of Eq. (28) are \(\lambda _{1}=-19.1228\) and \(\lambda _{2,3}=0.6871 \pm 3.4276i\). Here \(\lambda _{1}<0\), and the arguments of \(\lambda _{2,3}\) are 1.3730 and −1.3730, respectively. Hence, under the assumption

$$ \bigl\vert \arg (\lambda _{i}) \bigr\vert =1.3730 >\alpha _{M} \frac{\pi }{2}, \quad i=2,3, $$
(29)

taking into account that \(a_{3}=233.6935>0\) and \(D(P)=-7677060<0\), based on part (ii) of the Routh–Hurwitz stability conditions and Theorem 3.1, we can conclude that if \(\alpha _{M}<0.87\), then system (21) is stable at the steady states \(E_{2}\) and \(E_{3}\), although the real parts of the eigenvalues are positive. Considering \(a = 3\), \(b = 14\), and \(c = 3.9\) and substituting the coordinates of \(E_{4}\) or \(E_{5}\) into the Jacobian matrix (26), we can get the characteristic polynomial

$$ \lambda ^{3}+ 32.8545\lambda ^{2} -16.0712\lambda +721.5830=0, $$
(30)

whose eigenvalues are \(\lambda _{1}=-33.9537\) and \(\lambda _{2,3}=0.54962 \pm 4.5771i\). Here \(\lambda _{1}<0\) and the arguments of \(\lambda _{2,3}\) are 1.4513 and −1.4513, respectively. Hence, under the assumption

$$ \bigl\vert \arg (\lambda _{i}) \bigr\vert =1.4513 > \alpha _{M} \frac{\pi }{2},\quad i=2,3, $$
(31)

and considering \(a_{3}=721.5830>0\) and \(D(P)=-122981225<0\), based on part (ii) of Routh–Hurwitz stability conditions and Theorem 3.1, we can conclude that if \(\alpha _{M}<0.92\), then system (21) is stable at the steady states \(E_{4}\) and \(E_{5}\) although the real parts of the eigenvalues are positive.

4 Numerical simulations

In this section, we apply the NSFD scheme developed in Sect. 2.2 to illustrate the results of the previous section. Recall that Mickens suggested to write a general multistep numerical scheme approximating the solution of Eq. (5) in the form of Eq. (7), where \(\phi (h,\lambda )\) satisfies \(h+\mathcal{O}(h^{2})\), and \(G(x_{n+1},x_{n},\ldots ,t,\lambda )\) is a nonlocal discretization of the function \(g(x(t),t,\lambda )\) at some nodes of a grid. The terminology of nonlocal approximation comes from the fact that the approximation of a given function \(g(x(t),t, \lambda )\) at point \(t_{n}\) depends not only on \(x_{n}\) but also on more points of the grid. The examples of how the rules are used to develop the discretization were presented in Sect. 2.2 (see also [29–31] for more detail). Following the above approach, we can provide the following discretization for the integer-order system (16):

$$ \begin{aligned} &\frac{x_{n+1}-x_{n}}{\phi _{1}(h)}=a(y_{n}-x_{n+1})+by_{n}z_{n}, \\ &\frac{y_{n+1}-y_{n}}{\phi _{2}(h)}=-10y_{n+1}y^{2}_{n}-y_{n+1}+4x_{n+1}z_{n}, \\ &\frac{z_{n+1}-z_{n}}{\phi _{3}(h)}=cz_{n}-x_{n+1}y_{n+1}, \end{aligned} $$
(32)

where \(\phi _{1}(h)=\frac{e^{ah}-1}{a}\), \(\phi _{2}(h)=e^{h}-1\), and \(\phi _{3}(h)=\frac{e^{ch}-1}{c}\).

Then comparing model (16) and the difference equations (32), we observe that:

  1. (i)

    In the first equation of (16) the terms −x and yz are replaced by \(-x_{n+1}\) and \(y_{n}z_{n}\), respectively.

  2. (ii)

    In the second equation of (16) the terms \(-10y^{3}-y\) and xz are replaced by \(-10y_{n+1}y^{2}_{n}-y_{n+1}\) and \(x_{n+1}z_{n}\), respectively.

  3. (iii)

    In the third equation of (16) the terms z and \(-xy\) are replaced by \(z_{n}\) and \(-x_{n+1}y_{n+1}\), respectively.

Manipulating the discretization (32), we get the NSFD scheme for the integer-order model (16):

$$\begin{aligned} &x_{n+1}= \frac{\phi _{1}(h)(ay_{n}+by_{n} z_{n})+x_{n}}{1+a\phi _{1}(h)}, \\ &y_{n+1}= \frac{\phi _{2}(h)(4x_{n+1}z_{n})+y_{n}}{\phi _{2}(h)(10y^{2}_{n}+1)+1}, \\ &z_{n+1}=\phi _{3}(h) (cz_{n} -x_{n+1}y_{n+1})+z_{n}. \end{aligned}$$
(33)

Concerning the fractional-order model (21) and using the GL approximation from Sect. 2.1, we get

$$ \begin{aligned} & \sum_{j=0}^{n+1}c_{j}^{\alpha _{1}}x_{n+1-j}=a(y_{n}-x_{n+1})+by_{n}z_{n}, \\ & \sum_{j=0}^{n+1}c_{j}^{\alpha _{2}}y_{n+1-j}=-10y_{n+1}y^{2}_{n}-y_{n+1}+4x_{n+1}z_{n}, \\ & \sum_{j=0}^{n+1}c_{j}^{\alpha _{3}}z_{n+1-j}=cz_{n}-x_{n+1}y_{n+1}. \end{aligned} $$
(34)

Therefore we derive the following NSFD scheme for the FDEs (21):

$$ \begin{aligned} &x_{n+1}= \frac{- {\sum_{j=1}^{n+1}}c_{j}^{\alpha _{1}}x_{n+1-j}+ay_{n}+by_{n} z_{n}}{c_{0}^{\alpha _{1}}+a}, \\ &y_{n+1}= \frac{- {\sum_{j=1}^{n+1}}c_{j}^{\alpha _{2}}y_{n+1-j}+4x_{n+1}z_{n}}{c_{0}^{\alpha _{2}}+1+10y^{2}_{n}}, \\ &z_{n+1}= \frac{- {\sum_{j=1}^{n+1}}c_{j}^{\alpha _{3}}z_{n+1-j}+cz_{n} -x_{n+1}y_{n+1}}{c_{0}^{\alpha _{3}}}, \end{aligned} $$
(35)

where [35, 36]

$$ c_{0}^{\alpha _{1}}= \biggl(\frac{e^{ah}-1}{a} \biggr)^{-\alpha _{1}},\qquad c_{0}^{\alpha _{2}}= \bigl(e^{h}-1 \bigr)^{-\alpha _{2}}, \qquad c_{0}^{\alpha _{3}}= \biggl(\frac{e^{ch}-1}{c} \biggr)^{-\alpha _{3}}, $$
(36)

and \(c_{j}^{\alpha _{i}}\) are computed by the recursive formula (15).

4.1 Simulation results

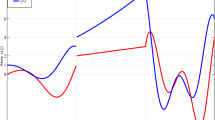
In this section, we present some numerical results displaying complex behaviors of the novel fractional dynamical system (21). We also verify the efficiency of the proposed NSFD scheme. The approximate solutions in the fractional sense are displayed in Figs. 1–6 for \(\alpha _{1}=\alpha _{2}=\alpha _{3}=0.85,0.9,0.95\), whereas the integer-order solutions are given in Figs. 7–8. Simulation results in both cases include the time-domain responses of the state variables and the two- and three-dimensional phase portraits. Additionally, we take into account \(a = 3\), \(b = 14\), \(c = 3.9\), and \((x_{0}, y_{0}, z_{0})=(0.2, 0.4, 0.2)\) for integer and fractional simulations. The plots in Figs. 1–6 show that system (21) exhibits a nonchaotic behavior for \(\alpha =0.85,0.9\), whereas for \(\alpha =0.95\), it portrays chaotic attractors as well as the integer-order model (16). The obtained results are also compatible with theoretical analysis, which explains that the lowest fractional order for system (21) to remain chaotic is \(\alpha =0.92\) when \(\alpha _{1}=\alpha _{2}=\alpha _{3}=\alpha \). Moreover, the above-mentioned figures confirm the effectiveness of the proposed NSFD scheme to exhibit both chaotic and nonchaotic behaviors of the novel fractional dynamical system (21).

Figure 1
figure 1

State variables of the fractional-order model (21) in the time-domain (\(\alpha _{i}=0.85\), \(i=1,2,3\))

Full size image
Figure 2
figure 2

State variables of the fractional-order model (21) in the phase-plane (\(\alpha _{i}=0.85\), \(i=1,2,3\))

Full size image
Figure 3
figure 3

State variables of the fractional-order model (21) in the time-domain (\(\alpha _{i}=0.9\), \(i=1,2,3\))

Full size image
Figure 4
figure 4

State variables of the fractional-order model (21) in the phase-plane (\(\alpha _{i}=0.9\), \(i=1,2,3\))

Full size image
Figure 5
figure 5

State variables of the fractional-order model (21) in the time-domain (\(\alpha _{i}=0.95\), \(i=1,2,3\))

Full size image
Figure 6
figure 6

State variables of the fractional-order model (21) in the phase-plane (\(\alpha _{i}=0.95\), \(i=1,2,3\))

Full size image
Figure 7
figure 7

State variables of the integer-order model (16) in the time-domain

Full size image
Figure 8
figure 8

State variables of the integer-order model (16) in the phase-plane

Full size image

5 Nonidentical synchronization

In this section, we study the nonidentical synchronization between the novel fractional-order system (21) and the fractional-order Volta equations [37] using the active controller developed in [38]. Let the novel fractional model in this paper represent the drive (master) system

$$ \begin{aligned} & {}^{\mathrm{C}} \!\mathscr{D}^{\alpha _{1}}x_{1}(t)=a\bigl(y_{1}(t)-x_{1}(t) \bigr)+by_{1}(t)z_{1}(t), \\ & {}^{\mathrm{C}} \!\mathscr{D}^{\alpha _{2}}y_{1}(t)=-10y_{1}^{3}(t)-y_{1}(t)+4x_{1}(t)z_{1}(t), \\ & {}^{\mathrm{C}} \!\mathscr{D}^{\alpha _{3}}z_{1}(t)=cz_{1}(t)-x_{1}(t)y_{1}(t), \end{aligned} $$
(37)

and let the response (slave) system be the fractional-order Volta equations

$$ \begin{aligned} & {}^{\mathrm{C}} \!\mathscr{D}^{\alpha _{1}}x_{2}(t)=-x_{2}(t)-a_{1}y_{2}(t)-z_{2}(t)y_{2}(t)+u_{1}(t), \\ & {}^{\mathrm{C}} \!\mathscr{D}^{\alpha _{2}}y_{2}(t)=-y_{2}(t)-b_{1}x_{2}(t)-x_{2}(t)z_{2}(t)+u_{2}(t), \\ & {}^{\mathrm{C}} \!\mathscr{D}^{\alpha _{3}}z_{2}(t)=c_{1}z_{2}(t)+x_{2}(t)y_{2}(t)+1+u_{3}(t), \end{aligned} $$
(38)

where \(a_{1}\), \(b_{1}\), \(c_{1}\) are known constant coefficients. Also, the unknown terms \(u_{1}\), \(u_{2}\), and \(u_{3}\) are active control functions to be determined. To this aim, we first define

$$ \textstyle\begin{cases} e_{1}(t)=x_{2}(t)-x_{1}(t), \\ e_{2}(t)=y_{2}(t)-y_{1}(t), \\ e_{3}(t)=z_{2}(t)-z_{1}(t), \end{cases} $$
(39)

as the error functions. Then relations (39) together with (37)–(38) yield the error system

$$ \begin{aligned} & {}^{\mathrm{C}} \!\mathscr{D}^{\alpha _{1}}e_{1}(t)=-e_{1}(t)-a_{1}e_{2}(t)+(a-1)x_{1}(t)-(a_{1}+a)y_{1}(t) \\ &\hphantom{{}^{\mathrm{C}} \!\mathscr{D}^{\alpha _{1}}e_{1}(t)={}}{}-z_{2}(t)y_{2}(t)-by_{1}(t)z_{1}(t)+u_{1}(t), \\ & {}^{\mathrm{C}} \!\mathscr{D}^{\alpha _{2}}e_{2}(t)=-b_{1}e_{1}(t)-e_{2}(t)-b_{1}x_{1}(t)-x_{2}(t)z_{2}(t)+10y_{1}^{3}(t)-4x_{1}(t)z_{1}(t)+u_{2}(t), \\ & {}^{\mathrm{C}} \!\mathscr{D}^{\alpha _{3}}e_{3}(t)=c_{1}e_{3}(t)+(c_{1}-c)z_{1}(t)+x_{2}(t)y_{2}(t)+1+x_{1}(t)y_{1}(t)+u_{3}(t). \end{aligned} $$
(40)

Now we define the active control functions \(u_{i}\) as

$$ \begin{aligned} &u_{1}(t)=-(a-1)x_{1}(t)+(a_{1}+a)y_{1}(t)+z_{2}(t)y_{2}(t)+by_{1}(t)z_{1}(t)+V_{1}(t), \\ &u_{2}(t)=b_{1}x_{1}(t)+x_{2}(t)z_{2}(t)-10y_{1}(t)^{3}+4x_{1}(t)z_{1}(t)+V_{2}(t), \\ &u_{3}(t)=-(c_{1}-c)z_{1}(t)-x_{2}(t)y_{2}(t)-1-x_{1}(t)y_{1}(t)+V_{3}(t), \end{aligned} $$
(41)

where \(V_{i}(t)\) is the new control variable. Substituting (41) into (40) gives

$$ \begin{aligned} & {}^{\mathrm{C}} \!\mathscr{D}^{\alpha _{1}}e_{1}(t)=-e_{1}(t)-a_{1}e_{2}(t)+V_{1}(t), \\ & {}^{\mathrm{C}} \!\mathscr{D}^{\alpha _{2}}e_{2}(t)=-b_{1}e_{1}(t)-e_{2}(t)+V_{2}(t), \\ & {}^{\mathrm{C}} \!\mathscr{D}^{\alpha _{3}}e_{3}(t)=c_{1}e_{3}(t)+V_{3}(t). \end{aligned} $$
(42)

The error dynamics in (42) constitute a linear system of FDEs with the control vector

[ V 1 ( t ) V 2 ( t ) V 3 ( t ) ] = [ a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ] ⏟ A [ e 1 ( t ) e 2 ( t ) e 3 ( t ) ] ,
(43)

where A is a real matrix chosen so that all eigenvalues \(\lambda _{i}\) of system (42) satisfy the stability condition in Theorem 3.1, that is, \(|\arg (\lambda _{i})|> \alpha _{M} \frac{ \pi }{2}\), \(i=1, 2, 3\). If we simply choose

A= [ 0 a 1 0 b 1 0 0 0 0 − 1 − c 1 ] ,
(44)

then the stability condition in Theorem 3.1 is satisfied, and so we achieve the required synchronization.

According to the analysis in [37], the Volta system (38) exhibits chaotic behaviors for \(\alpha =\alpha _{1}=\alpha _{2}=\alpha _{3} > 0.97\) and \((a_{1}, b_{1}, c_{1}) = (19,11,0.73)\). Therefore here we select the fractional orders as \(\alpha = 0.975,0.985,0.995\) in which both systems (37) and (38) show chaotic attractors. Figures 9–12 demonstrate the synchronization results, including the state variables and error dynamics, for the fractional orders \(\alpha = 0.975,0.985,0.995\) as well as in the integer-order case. In these simulations the initial values of the drive and response systems are taken as \((x_{1}(0),y_{1}(0),z_{1}(0))=(0.2, 0.4, 0.2)\) and \((x_{2}(0),y_{2}(0),z_{2}(0))=(8, 2, 1)\), respectively; thus the initial error is the vector \((e_{1}(0),e_{2}(0),e_{3}(0))=(7.8, 1.6, 0.8)\). In addition, we select the values of parameters \((a,b,c)=(3,14,3.9)\) and \((a_{1}, b_{1}, c_{1}) = (19,11,0.73)\) for the master and slave systems, respectively. From Figs. 9–12 it appears that the two nonidentical systems are successfully synchronized after a small time duration, a fact which verifies the effectiveness of the utilized active control synchronization strategy.

Figure 9
figure 9

Synchronization results between two nonidentical fractional-order systems (37) and (38) for \(\alpha _{1}=\alpha _{2}=\alpha _{3} = 0.975\)

Full size image
Figure 10
figure 10

Synchronization results between two nonidentical fractional-order systems (37) and (38) for \(\alpha _{1}=\alpha _{2}=\alpha _{3} = 0.985\)

Full size image
Figure 11
figure 11

Synchronization results between two nonidentical fractional-order systems (37) and (38) for \(\alpha _{1}=\alpha _{2}=\alpha _{3} = 0.995\)

Full size image
Figure 12
figure 12

Synchronization results between two nonidentical fractional-order systems (37) and (38) for \(\alpha _{1}=\alpha _{2}=\alpha _{3} = 1\) (integer-order case)

Full size image

6 Concluding remarks

In this research, we studied a new chaotic system including quadratic and cubic nonlinearities as well as the Caputo fractional derivative. The fractional Routh–Hurwitz criteria were employed to investigate the stability of the equilibrium points. Then we designed an efficient NSFD scheme to implement the chaotic model and discuss its complex behaviors. We portrayed the simulation results in Figs. 1–8, which indicate that the new system exhibits both chaotic and nonchaotic behaviors. Afterward, we designed an active controller to attain a nonidentical synchronization between the presented model and the fractional Volta equations. In this regard, the simulation results are displayed in Figs. 9–12, which confirm that the proposed active control scheme is efficient for the purpose of synchronization. As a future research plan, we can focus on the use of optimal control techniques (such as those discussed in [39–41]) for the stabilization and synchronization of chaotic dynamical attractors.