1 Introduction

When designing structures, consideration of the stress–strain state of the structural members within the linear theory of elasticity is often insufficient in practice. This is due to the fact that most structural materials obey Hooke's linear law only at small deformations, and in many cases, the studied objects are operated at deformations exceeding the linear region. At low loads, many materials differ in a nonlinear dependence of stresses on deformations; in addition, such materials exhibit different properties in tension and compression and are known as multimodulus materials [1]. Multimodulus properties are exhibited by natural materials like rock [2] and biological materials [3, 4] used in biomedicine. On the other hand, concrete [5], rubber [6], wood, metal alloys [7] and other structural materials are often employed in manufacturing and construction. In particular, graphene, the hardest material with minimal resistivity and considered as a magic material in the twenty-first century, has a higher modulus of compression than tensile modulus [8, 9]. Some popular composite materials, such as graphite epoxy resin with graphite as a filler, have different moduli. Surprisingly, graphite material is known to have a compression modulus four times greater than its tensile modulus [10].

When developing composite structures that include multimodulus materials, one should create mathematical models that would correspond to an adequate stress–strain state of the investigated objects. In this case, as in the case of the presence of inhomogeneities or damage in the structure, it is necessary to solve a physically nonlinear problem of the theory of elasticity. It is known that calculation of structures outside the limits of linear elasticity is a much more difficult task both due to the arising complex mathematical calculations and due to the inapplicability of some principles of the classical linear theory of elasticity (in particular, the impossibility of using the principle of independence of the action of forces, or the absence of the potential of internal forces). On the other hand, the nonlinear behavior of materials enables one to obtain additional reserves of strength and avoid overspending of material during design, which is important when developing new modern design solutions.

The problem of studying the behavior of materials with different modulus attracted the attention of researchers in the second half of the last century when the first models for multimodulus materials were proposed, including the archetypical models of Bert [11] and Ambartsumyan [12].

Bert's model is based on the criterion of positive–negative signs of deformations in longitudinal fibers and is widely used in multilayer composites [13,14,15,16]. Ambartsumian's bimodulus model is formulated for isotropic materials and evaluates different moduli in tension and compression based on positive–negative signs of fundamental stresses, which is especially important for the analysis and design of structures. Jones [17] proposed a modified model for isotropic and orthotropic bimodulus materials, a weighted correspondence matrix (WCM) model. In [18], an extensive overview of models for multimodulus materials is given.

The task of studying structures made of materials with different modulus is very difficult, and naturally, in order to obtain reliable results, models that reduce the spatial problem to two-dimensional or one-dimensional problems are used. These are the Euler–Bernoulli hypotheses for Kirchhoff–Love shells. Numerous other hypotheses that have been developed later require taking into account the transverse shears, bringing the calculation scheme of problems closer to its three-dimensional analogue. These hypotheses are reviewed in [19]. It is worth noting that in 1964, two Ukrainian scientists, Sheremetev and Pelekh [20], proposed a so-called third-order theory, which has been also successfully applied for the strain–stress analysis of plates and shells. The model was redeveloped by Levinson [21] and Reddy [22] 17 years later. Therefore, the state-of-the-art is such that in Eastern Europe (Russia, Ukraine, etc.), the approximation of beam deflection by third-order polynomials is associated with the names of Pelekh and Sheremetev, whereas in Western countries, this theory is referred to as the Reddy-Levinson theory. Motivated by the briefly described and documented historical reasons, the authors of the present study [23] suggested using the name ‘Sheremetev-Pelekh-Reddy-Levinson (SPRL) theory’ for this mathematical model.

Among the known algorithms for calculating physically nonlinear systems, there is no universal one, i.e., the efficiency of a particular method depends mainly on the type and parameters of nonlinearity. For instance, the method of elastic solutions by Ilyushin and Lensky [24] should be mentioned. In the work of Vorovich [25], it was proved that the method of elastic solutions converges to the result at a linear rate. Birger [26] proposed a modification of the method of elastic solutions, i.e., the method of variable parameters of elasticity, to solve physically nonlinear problems in the theory of plasticity and creep. In [27], based on the small parameter method, the distribution of stress intensity of vibrating plates was investigated taking into account geometric and physical nonlinearity. The regularities of the stress intensity distribution in the plate were analyzed. It was noted that in the case of nonlinear vibrations, not only the magnitude of the stress intensity, but also the nature of its distribution depended on the amplitude of the vibrations. In [28], on the basis of the theory of small elastic–plastic deformations, equations of the relationship between stress increments and strain increments under plane loading in the elastoplastic stage were obtained. The found constitutive relations were implemented in the algorithm for the formation of the stiffness matrix of the finite element of the shell under plane loading. Specific examples showed the effectiveness of the developed algorithms for calculating a shell with a plane load outside the elastic limits.

Analytical models make it possible to impose rather strong restrictions on the study of the stress–strain state; therefore, the study of the spatial plastic stress–strain state of beams and plates is one of the most important and complex issues in the mechanics of a deformable solid. Solving a spatial problem using analytical methods leads to significant mathematical difficulties. Keeping this in mind, various numerical methods have recently begun to be widely used (finite element method, finite difference method, the higher-order Bubnov–Galerkin method, etc.)

Chen et al. [29] employed the Timoshenko beam theory to study the dynamic stability of a bimodulus beam subjected to a periodic axial load. The instability zone was detected using Bolotin’s method. The parametric analysis included the effects of in-plane load, slenderness and modulus ratios on the instability zones.

In addition to mathematical models, one can find numerous works on experimental studies of the physical nonlinearity exhibited by beams. The work [30] is devoted to the transverse bending test of free-supported reinforced concrete beams. The work [31], in which the load-bearing capacity in tension is considered, deals with compression and transverse bending of different-modulus wooden beams as well as beams with steel plates, rectangular and including a two-tee section taking into account plastic deformations. The presence of experimentally obtained data emphasizes the importance of the issue under consideration and allows one to assess the adequacy of the constructed mathematical models.

In [32], finite element models of the traditional theory of the Timoshenko beam and the modified theory of the Timoshenko beam for static analysis of deformations were considered.

The large deflections of a thin beam under end moment were investigated by Baykara et al. [33]. In particular, the effect of a nonlinear bimodulus beam material with regard to the horizontal and vertical deflections was analyzed based on numerical simulations.

Shatnavi and Al-Sadder [34] found an exact solution for large deflection of nonprismatic cantilever beams made from the bimodulus material under tip concentrated moment. The presented numerical examples included effects of bimodulus properties, material parameter and the applied tip moment. The obtained analytical solution was validated by a comparative study with ADINA.

In [35], nonlinear deformations of a compressed-bent beam from a nonlinear elastic multimodulus material are considered using the Bernoulli–Euler kinematic hypothesis. The dependence of the bearing capacity of the beam on its elastic properties is investigated. In the works of Pavilaynen [36, 37], Pavilaynen and Naumova [38], the results of bending of multimodulus beams under the action of concentrated or distributed loads were presented. The standard Bernoulli–Euler hypotheses for beams and Ilyushin's theory of plasticity were used.

He et al. [39] obtained an analytical solution for a multimodulus beam under uniform loads. In the work of Wu et al. [40], an approximate solution for a multimodulus beam subjected to linearly distributed loads was proposed using the Kantorovich variational method. Yang et al. [41] obtained bimodulus elastic solutions for a cantilever beam. However, these solutions have certain limitations in terms of accuracy, since they are obtained based on a strong reduction procedure limited to one-degree-of-freedom approximation.

Lü et al. [42] obtained the elasticity solutions for bending and thermal deformations of functionally graded beams with various end conditions by employing the state space-based differential quadrature method. The considered beams were macroscopically isotropic with Young’s modulus varying exponentially along the thickness and longitudinal directions. The approach was validated by comparing the numerical results with the exact solutions for a specially functionally graded beam and with FEM results.

Gadjiev et al. [43] considered the problem of free lateral vibrations of a beam that is inhomogeneous in length and made of a multimodulus material on a viscoelastic inhomogeneous base. Numerical analysis was carried out using the Bubnov–Galerkin variable separation method.

Zhao and Ye [44] proposed a function for determining stresses in multimodulus beams based on the sensitivity at the boundaries. Furthermore, Yao and Ye [45] obtained formulas for calculating the neutral axis, normal stress, shear stress and displacement based on the bending of a beam in a state of plane stress. The results of the analytical solution were compared with the results obtained according to the classical theory based on the solution by the FEM, provided that the tensile modulus was equal to the compression modulus.

Gao and Yao [46] studied a response of a bimodulus Winkler foundation beam subjected to nonlinear temperature distribution along the beam height. A so-called line criterion was proposed to certify the number and position of neutral axis. The obtained analytical results were compared with FEM results (ABAQUS solution).

Gao et al. [47] carried out the temperature stress analysis for a bimodulus beam placed on a Winkler foundation. The analytical formulas of the normal stress, bending moment and displacement of the foundation beam were derived. The temperature stress was estimated using FEM, whereas the difference between the bimodulus and the classical modulus results was compared and discussed.

Awrejcewicz et al. [48] presented a new mathematical model for elastoplastic beams, rigidly clamped at the ends, under the action of transverse pressure. The model took into account traveling elastic bending waves, stationary and nonstationary plastic hinges, elastic–plastic tension and shear deformation.

1D and 2D analytical solutions for functionally graded and bimodulus beams were derived by Li et al. [49]. The physical parameters of bimodulus beams were compared with the classical problems. It was detected and discussed that the bimodulus functionally graded effect, the maximum tensile and compressive bending stresses may not take place at the beam bottom and top.

In a monograph by Rao [50], a three-dimensional plasticity problem was studied to determine concentrated loads acting on an elastic half-space. The paper [51] presented a nonlinear analysis of the deformation of a prestressed beam system used in the span of a road bridge or high-rise buildings employing a nonlinear material model.

Investigations carried out by Shi et al. [52] were aimed at studying the dynamic response of a restrained beam to shock loads from a rigid mass. Analytical formulas were derived for predicting the quasi-static force and deformation relationships of an elastoplastic beam during loading and unloading.

Kincannon et al. [53] formulated a differential equation governing the small-deflection elastic behavior of thin plates of cross-ply bimodulus materials. They presented an exact (approximate) closed-form solution for a fully clamped cross-ply plate made of orthotropic (isotropic) material under uniform normal pressure.

Patel et al. [54] studied free flexural vibrations of bimodulus laminated angle-ply composite plates, taking the account of the transverse shear and transverse normal deformations. The governing equations were yielded by the Lagrange equations of motion, and they were solved via FEM. Plate geometry, lay-up, ply-angle and material properties were investigated during the carried out parametric study.

He et al. [55] proposed a simplified model based on the Kirchhoff hypothesis to obtain solutions to the bimodulus thin plates in bending. In addition, the Ambartsumyan’s bimodulus model was adopted using FEM and the results were compared with the authors’ model showing good agreement between both results.

The study of problems of the theory of small elastic–plastic deformations for plates and shells using the FEM was carried out by Korlec and Stupkiewicz [56], and Wriggers and Hudobivnik [57].

In [58], a mathematical model of coupled boundary value problems of thermoelasticity was constructed for multilayer shallow Sheremetev–Pelekh–Reddy–Levinson shells with initial irregularities. A theorem on the uniqueness of the indicated boundary value problem was proved. It was also proved that an approximate solution of the second boundary value problem, which determines the condition of thermomechanical evolution for rectangular shallow homogeneous and isotropic shells, can be estimated through the Bubnov–Galerkin method.

In [55], thin plates made of materials that exhibit different mechanical behavior under tension and compression were studied. Ambartsumian's bimodal model for isotropic materials was used, and the main stresses at a point were investigated, which is especially important in the analysis and design of reinforced concrete structures. A simplified mechanical model based on the classical Kirchhoff hypothesis was proposed. In these and many other works, the computational models were based on the Kirchhoff system of hypotheses under the appropriate assumptions, which makes it possible to reduce a three-dimensional problem to a two-dimensional one, while strains and stresses vary linearly with respect to thickness.

In [48], a mathematical model of flexible physically nonlinear micro-shells was created taking into account the connectedness of the temperature and strain fields. Geometric nonlinearity was introduced according to Kármán's theory, and the shells were flat. The Kirchhoff–Love hypothesis was used. Physical nonlinearity was introduced according to the deformation theory of plasticity. The connectedness of the fields was taken into account using the Biot variational principle. Examples of calculation of nonlinear oscillations and dynamic loss of stability of flexible flat square micro-shells in terms of the connectivity of the temperature and strain fields and physical nonlinearity were reported.

In [59], a mathematical model of the contact interaction of two plates (Kirchhoff's kinematic model) was constructed, taking into account different modulus of materials, physical and structural nonlinearities. To study the stress–strain state of this complex mechanical system, the method of variational iterations was applied, which makes it possible to reduce the partial differential equations (PDEs) to ordinary differential equations (ODEs). The method of variable parameters of elasticity was employed [26]).

Sun et al. [60] reviewed the research aimed at mechanical problems dealing with a material of different modulus in tension and compression. They underlined the importance of the criterion of positive–negative signs of principal stress proposed by Ambartsumyan and its impact on the bimodulus materials. They also pointed out the importance of FEM-based iterative strategy and analytical methods adopted to study simplified models.

Ye et al. [61] developed an analytical experimental theory to determine the elastic tensile Et and compressive Ec moduli of materials simultaneously. The proposed approach was validated through a simple indirect tension test (the Brazilian disk test).

Cai et al. [62] proposed the material-replacement method to improve the computational efficiency for topology optimization of bimodulus structures. A few numerical studies demonstrated the effectiveness of the method.

Ling et al. [63] carried out the FEM analysis by judging positive and negative signs of the stress tensor to determine the tension/compression elastic modulus of the structure.

Cai et al. [64] solved the lay-out optimization problems of multiple bimodulus materials in a continuum where each bimodulus material was replaced by two distinct isotropic materials. Three numerical examples were given which demonstrated the validity and applicability of the approach.

The above review of the scientific literature on the study of structures of multimodulus materials enables us to conclude that research in this direction is at the initial stage of its development. There is no general theory for studying the stress–strain state of beams, plates and shells made of multimodulus materials. The available publications are devoted to analyzing the stress–strain state of beams and plates that obey the kinematic models of the first approximation, i.e., the Kirchhoff kinematic model. Numerical results are obtained by approximate methods, mostly as systems with one degree of freedom. The present work aims to fill the gap indicated above. A mathematical model was built based on the deformation theory of plasticity in a three-dimensional formulation for beams and plates. To obtain a numerical solution, the FEM was used for two types of elements—tetrahedrons and prisms. The problem is considered as a system with an infinite number of degrees of freedom. The proposed technique enables us to consider a wide class of problems in the theory of beams and plates made from various materials with arbitrary boundary conditions and loads in a static setting.

The paper is organized in the following way. General theoretical background aimed at mathematical modeling of a 3D body of the theory of elasticity, taking into account physical nonlinearity and multimodulus materials, is given in Sect. 2. The method of variable parameters of elasticity is described in Sect. 3. Computational analysis of beams and plates based on FEM are carried out in Sect. 4. The last Sect. 5 concludes our investigations.

2 Mathematical model of a 3D (spatial) problem including physical nonlinearity and multimodulus materials

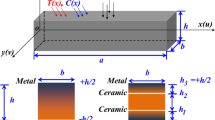
Consider a 3D body shown in Fiḡ. 1. Under the action of surface forces, the main stresses arise at each point of the body as \(\sigma_{x} ,\sigma_{y} ,\sigma_{z},\) and \(\tau_{xy} = \tau_{yx} ,\tau_{yz} = \tau_{zy} ,\tau_{xz} = \tau_{zx}\) are the shear stresses shown in the figure for an elementary parallelepiped cut around a point of the body.

Fig. 1
figure 1

Spatial body and stress distribution on the faces of an elementary parallelepiped

Full size image

Let us solve the problem in displacements with respect to (и, v, w). For this purpose, we write down the Cauchy equilibrium equations [65]:

$$ \begin{gathered} \frac{{\partial \sigma_{x} }}{\partial x} + \frac{{\partial \tau_{xy} }}{\partial y} + \,\frac{{\partial \tau_{xz} }}{\partial z} + q_{{\text{X}}} = 0, \hfill \\ \frac{{\partial \tau_{xy} }}{\partial x} + \frac{{\partial \sigma_{y} }}{\partial y} + \,\frac{{\partial \tau_{yz} }}{\partial z} + q_{{\text{Y}}} = 0, \hfill \\ \frac{{\partial \tau_{xz} }}{\partial x} + \frac{{\partial \tau_{yz} }}{\partial y} + \,\frac{{\partial \sigma_{z} }}{\partial z} + q_{{\text{Z}}} = 0, \hfill \\ \end{gathered} $$
(1)

where \(q_{{\text{X}}} ,q_{{\text{Y}}} ,q_{{\text{Z}}}\) are the surface loads acting in directions of the axes x, y, z.

The relationship between deformations and displacements is written in the form [65]

$$ \varepsilon_{{\text{x}}} = \frac{\partial u}{{\partial x}},\quad \gamma_{{{\text{xy}}}} = \frac{\partial v}{{\partial x}} + \frac{\partial u}{{\partial y}},\quad \,\,\varepsilon_{{\text{y}}} = \frac{\partial v}{{\partial y}},\quad \gamma_{{{\text{yz}}}} = \frac{\partial v}{{\partial z}} + \frac{\partial w}{{\partial y}},\,\,\quad \varepsilon_{{\text{z}}} = \frac{\partial w}{{\partial z}},\quad \gamma_{{{\text{zx}}}} = \frac{\partial w}{{\partial x}} + \frac{\partial u}{{\partial z}}, $$
(2)

where \(\varepsilon_{{\text{x}}} ,\varepsilon_{{\text{y}}} ,\varepsilon_{{\text{z}}}\) are major strains, whereas \(\gamma_{{{\text{xy}}}} ,\gamma_{{{\text{yz}}}} ,\gamma_{{{\text{zx}}}}\) present relationship between strains and stresses, i.e., we have

$$ \begin{gathered} \sigma_{x} = \lambda \theta + 2\mu \varepsilon_{x} ,\sigma_{xy} = \mu \gamma_{xy} , \hfill \\ \sigma_{y} = \lambda \theta + 2\mu \varepsilon_{y} ,\sigma_{yz} = \mu \gamma_{yz} , \hfill \\ \sigma_{z} = \lambda \theta + 2\mu \varepsilon_{z} ,\sigma_{zx} = \mu \gamma_{zx} , \hfill \\ \end{gathered} $$
(3)

where \(\theta = \frac{\partial u}{{\partial x}} + \frac{\partial v}{{\partial y}} + \frac{\partial w}{{\partial z}}\) and \(\lambda = \frac{E\,\vartheta }{{(1 + \nu )(1 - 2\nu )}}\), \(\mu = \frac{E}{2(1 + \nu )}\) are elastic Lamé constants. According to the method of variable parameters of elasticity of Birger [26], Poisson's ratio \(\nu (\varepsilon_{{\text{i}}} ,x,y),\) and Young's modulus \(E(\varepsilon_{{\text{i}}} ,x,y,z)\) depend on coordinates \(x,y,z\) and the intensity of strains \(\varepsilon_{i}\). Thereby, \(\lambda \,\) and \(\mu\) also depend on the coordinates and intensity of strains.

After appropriate transformations, the equilibrium Eqs. (1) are rewritten and they have the following form:

$$ \left\{ \begin{gathered} (\lambda + \mu )\,\theta_{x} + \mu \,\Delta u + \frac{\partial \lambda }{{\partial x}}\theta + 2\frac{\partial \mu }{{\partial x}}\frac{\partial u}{{\partial x}} + \frac{\partial \mu }{{\partial y}}(\frac{\partial v}{{\partial x}} + \frac{\partial u}{{\partial y}}) + \frac{\partial \mu }{{\partial z}}(\frac{\partial w}{{\partial x}} + \frac{\partial u}{{\partial z}}) + q_{X} = 0,\, \hfill \\ (\lambda + \mu )\theta_{y} + \mu \,\Delta v + \frac{\partial \lambda }{{\partial y}}\theta + \frac{\partial \mu }{{\partial x}}(\frac{\partial v}{{\partial x}} + \frac{\partial u}{{\partial y}}) + 2\frac{\partial \mu }{{\partial y}}\frac{\partial v}{{\partial y}} + \,\frac{\partial \mu }{{\partial z}}(\frac{\partial v}{{\partial z}} + \frac{\partial w}{{\partial y}}) + q_{Y} = 0, \hfill \\ (\lambda + \mu )\theta_{z} + \mu \,\Delta w + \,\frac{\partial \lambda }{{\partial z}}\theta + \frac{\partial \mu }{{\partial x}}(\frac{\partial w}{{\partial x}} + \frac{\partial u}{{\partial z}}) + \frac{\partial \mu }{{\partial y}}(\frac{\partial v}{{\partial z}} + \frac{\partial w}{{\partial y}}) + 2\frac{\partial \mu }{{\partial z}}\frac{\partial w}{{\partial z}} + q_{Z} = 0, \hfill \\ \end{gathered} \right. $$
(4)

where \(\Delta\) is the Laplace operator and \(\theta_{x}\),\(\theta_{y} ,\)\(\theta_{z}\) stand for partial derivatives \(\theta\) with respect to the coordinates \(x,y,z\), respectively. The displacements (и, v, w) must satisfy the boundary conditions on the surface, which, taking into account the generalized Hooke's law and the Cauchy conditions, take the following form [65]:

$$ \left\{ \begin{gathered} X_{v} = \lambda \theta l + G(\frac{\partial u}{{\partial x}}l + \frac{\partial u}{{\partial y}}m + \frac{\partial u}{{\partial z}}n) + G(\frac{\partial u}{{\partial x}}l + \frac{\partial v}{{\partial x}}m + \frac{\partial w}{{\partial x}}n), \hfill \\ Y_{v} = \lambda \theta m + G(\frac{\partial v}{{\partial x}}l + \frac{\partial v}{{\partial y}}m + \frac{\partial v}{{\partial z}}n) + G(\frac{\partial u}{{\partial y}}l + \frac{\partial v}{{\partial y}}m + \frac{\partial w}{{\partial y}}n), \hfill \\ Z_{v} = \lambda \theta n + G(\frac{\partial w}{{\partial x}}l + \frac{\partial w}{{\partial y}}m + \frac{\partial w}{{\partial z}}n) + G(\frac{\partial u}{{\partial z}}l + \frac{\partial v}{{\partial z}}m + \frac{\partial w}{{\partial z}}n), \hfill \\ \end{gathered} \right. $$
(5)

where \(l,m,n\) are the outer normal direction cosines; \(X_{v} ,Y_{v} ,Z_{v}\) are the distributed surface load components.

3 Method of variable parameters of elasticity

When deriving the sought equations, we assume that E (elastic modulus), \(\nu\) (Poisson's ratio) are a priori given. In order to concretize them, we will use Hencky's theory of small elastic–plastic deformations [66]. It is known that if unloading does not occur at any point of the body, then this theory coincides with the theory of an elastic physically nonlinear body. In the case of unloading, that is, a decrease in \(\varepsilon_{i}\) when passing from one loading step to another, we will mark these points on the graph. Assuming that materials have nonlinear elastic properties, we subject the unloading to the same laws as the loading process (see Fig. 2).

Fig. 2
figure 2

Dependence of \({\sigma }_{i}({\mathcal{E}}_{i})\) with marked linear (II) and nonlinear (I) parts

Full size image

The ratio of the theory of small elastic–plastic deformations is based on the assumption that at each point of the body, the loading path is straight. This limitation is quite strict. When constructing this theory, it was believed that it would give acceptable results for loading paths close to straight lines.

In the works of Budyansky [67] and Rabotnov [68], under the assumption of the singularity of surface loading, it was proved that Hencky's deformation theory does not contradict the postulates of plasticity [69] (it is physically consistent) when the trajectory of motion deviates from straight lines.

In [70], it was shown that in the case of an ideal elastoplastic diagram \({\sigma }_{i}\) and \({\varepsilon }_{i}\). without hardening, when using the von Mises plasticity criterion, Budyansky's criterion for the applicability of the deformation theory is satisfied. Thanks to these works, the theoretically based application of the deformation theory has expanded significantly, in spite of that the most complete verification can only be obtained by comparing the calculation results with experimental data.

It should be pointed out that small elastic–plastic deformations require that E and \(\nu\) depend not only on coordinates but also on the stress–strain state at a point.

In what follows, we employ Birger [26] method of variable parameters of the theory of elasticity, and therefore we briefly describe its main features.

Dependencies connecting deformations and stresses at \({\sigma }_{i}>{\sigma }_{T}\) are nonlinear. If, within elastic deformations (\({\sigma }_{i}<{\sigma }_{T}\)), an increase in stresses by a factor k causes the same increase in deformations, then when plastic deformations appear, proportionality is violated. The nonlinearity of physical equations of the theory of plasticity creates great difficulties in solving practical problems.

The method of variable parameters of elasticity reduces the solution of problems of the deformation theory of plasticity to the solution of a sequence of ordinary problems of elasticity, which significantly facilitates the calculations.

Intensities of strain at each point of the beam, which depend on the current stress–strain state, are estimated by the following formula:

$${\varepsilon }_{i}=\sqrt{2}/3\cdot \sqrt{{({\varepsilon }_{x}-{\varepsilon }_{y})}^{2}+{({\varepsilon }_{y}-{\varepsilon }_{z})}^{2}+{({\varepsilon }_{z}-{\varepsilon }_{x})}^{2}+3/2({\gamma }_{xy}^{2}+{\gamma }_{yz}^{2}+{\gamma }_{zx}^{2})}.$$
(6)

Although, in general, the dependence of the stress intensity on the strain intensity is determined experimentally, there are some analytical expressions, which are helpful in dealing with the problem.

Consider the Hencky's plasticity equation [66] of the form

$$ \begin{gathered} \varepsilon_{x} - \varepsilon = \psi \frac{1 + \nu }{E}\left( {\sigma_{x} - \sigma } \right),\quad \varepsilon_{y} - \varepsilon = \psi \frac{1 + \nu }{E}\left( {\sigma_{y} - \sigma } \right),\quad \varepsilon_{z} - \varepsilon = \psi \frac{1 + \nu }{E}\left( {\sigma_{z} - \sigma } \right), \hfill \\ \frac{1}{2}\gamma_{xy} = \psi \frac{1 + \nu }{E}\tau_{xy} ,\quad \frac{1}{2}\gamma_{yz} = \psi \frac{1 + \nu }{E}\tau_{yz} ,\quad \frac{1}{2}\gamma_{zx} = \psi \frac{1 + \nu }{E}\tau_{zx} , \hfill \\ \end{gathered} $$
(7)

where \(\psi = \frac{3E}{{2\left( {1 + \nu } \right)}}\frac{{\varepsilon_{i} }}{{\sigma_{i} }}\). Observe that \(\varepsilon_{x} - \varepsilon = \psi \frac{1 + \nu }{E}\left( {\sigma_{x} - \sigma } \right)\) subject to dependence \(\varepsilon = \psi \frac{1 - 2\nu }{E}\sigma\) takes the following form

$$ \varepsilon_{x} = \psi \frac{1 + \nu }{E}\left( {\sigma_{x} - \sigma } \right) + \varepsilon = \psi \frac{1 + \nu }{E}\left( {\sigma_{x} - \sigma } \right) + \psi \frac{1 - 2\nu }{E}\sigma . $$
(8)

Continuing the transformations, we represent the plasticity equations in its counterpart form.

$$ \varepsilon_{x} = \frac{1}{{E^{*} }}\left[ {\sigma_{x} - E^{*} \left( {\sigma_{y} + \sigma_{z} } \right)} \right],...,\;\gamma_{xy} = \frac{{2(1 + \nu^{*} )}}{{E^{*} }}\tau_{xy} ,...\left( {\overline{x,y,z} } \right). $$
(9)

Here, the variable parameters of elasticity \({E}^{*}\) and \(\nu^{*}\) are governed by the following formulas

$$ E^{*} = E\frac{3}{2(1 + \nu )\psi + (1 - 2\nu )},\quad \quad \nu^{*} = \frac{(1 + \nu )\psi - (1 - 2\nu )}{{2(1 + \nu )\psi + (1 - 2\nu )}},\quad $$
(10)

where: E–elastic modulus, \(\nu\)–Poisson's ratio (in the elastic region), ψ–plasticity parameter.

Parameters \({E}^{*}\) and \(\nu^{*}\) are called variable parameters of elasticity, since they depend on the stress state at a point (plasticity parameter ψ). It should be emphasized that in the elastic zone (II), ψ = 1 and \({E}^{*}=E,\) \(\nu^{*} = \nu \) (see Fig. 2).

For an incompressible body (Poisson's ratio \(\nu\) = 0.5), we have

$$ \begin{gathered} E^{*} = \frac{E}{\psi } = \frac{{\sigma_{i} }}{{\varepsilon_{i} }} = \frac{{\sigma_{0} }}{{\varepsilon_{i} }} = E_{C} ,\quad \quad \nu^{*} = 0.5\quad {\text{if}}\quad \sigma_{i} > 0, \hfill \\ E^{*} = \frac{E}{\psi } = \frac{{\sigma_{i} }}{{\varepsilon_{i} }} = \frac{{\sigma_{0} }}{{\varepsilon_{i} }} = E_{D} ,\quad \quad \nu^{*} = 0.5\quad {\text{if}}\quad \sigma_{i} \le 0, \hfill \\ \end{gathered} $$
(11)

where \({E}_{c}= {\sigma }_{0}/{\mathcal{E}}_{0}\) is the secant modulus. Taking the tensile strain curve as the generalized strain curve, we obtain the following expression for the plasticity parameter:

$$ \psi = \frac{3E}{{2(1 + \nu )}}\frac{{\varepsilon_{i} }}{{\sigma_{i} }} = \frac{3E}{{2(1 + \nu )}}\left( {\frac{E}{{E_{C} }} - \frac{1 - 2\nu }{3}} \right). $$
(12)

Now the relations (10) and (12) yield the basic formulas of the method of variable parameters of elasticity which are as follows:

$$ \begin{gathered} E^{*} = \frac{E}{\psi } = \frac{{\sigma_{i} }}{{\varepsilon_{i} }} = \frac{{\sigma_{0} }}{{\varepsilon_{i} }} = E_{C} ,\quad \quad \quad {\text{if}}\quad \sigma_{i} > 0, \hfill \\ E^{*} = \frac{E}{\psi } = \frac{{\sigma_{i} }}{{\varepsilon_{i} }} = \frac{{\sigma_{0} }}{{\varepsilon_{i} }} = E_{D} ,\quad \quad \quad {\text{if}}\quad \sigma_{i} \le 0, \hfill \\ \end{gathered} $$
(13)
$$ \begin{gathered} \nu^{*} = \frac{1}{2} - \frac{1 - 2\nu }{2}\frac{{E_{C} }}{E},\quad \quad {\text{if}}\quad \sigma_{i} > 0, \hfill \\ \nu^{*} = \frac{1}{2} - \frac{1 - 2\nu }{2}\frac{{E_{D} }}{E},\quad \quad {\text{if}}\quad \sigma_{i} \le 0. \hfill \\ \end{gathered} $$
(14)

Therefore, the equations of the deformation theory of plasticity can be represented as the equations of the theory of elasticity if the elastic modulus in them is replaced by a secant modulus. The convergence of the method of variable parameters of elasticity (its geometric interpretation) for tension is presented in Fig. 3, and the case for compression can be treated in a similar way. The correction of the Poisson's ratio according to formula (14) is less significant.

Fig. 3
figure 3

Convergence of the method of variable parameters of elasticity

Full size image

The developed algorithm of the method of variable parameters of elasticity can be briefly summarized as follows:

  1. 1.

    Initial data are entered: the value of external loads, single curve fit parameters \(\sigma_{i} = f(\varepsilon_{i} )\), as well as Poisson's ratio \(\nu\) and elastic modulus E.

  2. 2.

    At the initial stage, we take: \({E}^{*}=E,\) \(\nu^{*} = \nu\), \({E}_{c}=E\).

  3. 3.

    The elastic problem of calculating stress–strain state under load with the parameters \({E}^{*},\) \(\nu^{*}\) and the stresses and strains \((\sigma_{x} ,...\tau_{xy} ,...\varepsilon_{x} ,...\gamma_{xy} )\) are determined.

  4. 4.

    Stress intensities are estimated via \(\sigma_{i}\) and strains via \(\varepsilon_{i}\), which correspond to the solution of the elastic problem.

  5. 5.

    The following approximation of the values of the stress and strain intensities is found according to the rule \(\varepsilon_{i} = \varepsilon_{i(0)} ,\sigma_{i} = \left\{ \begin{gathered} E\varepsilon_{i(0)} \hfill \\ E_{c(1)} \varepsilon_{i(0)} \hfill \\ \end{gathered} \right..\)

  6. 6.

    If the condition for the end of iterations is satisfied, \(\left| {\frac{{\sigma_{i} - \sigma_{i(1)} }}{{\sigma_{i} }}} \right| < \delta\), where \(\delta\) stands for the given accuracy, then we go to step 7. If not, then the secant modulus is calculated as \(E_{c} = \sigma_{i} /\varepsilon_{i} ,\) and variable parameters of elasticity according to formulas (4) and calculations are repeated starting from step 3.

  7. 7.

    The values obtained by calculating the latest values of the intensity of deformations and stresses are taken as accepted stresses and strains.

Comment. This method of variable parameters of Birger elasticity is employed for a 3D problem of the theory of elasticity.

4 Computational analysis of beams and plates

Consider a 3D beam shown in Fig. 4\(\left\{ {x \in \left[ {0,l} \right],y \in \left[ {0,b} \right],z \in \left[ { - h/2,h/2} \right]} \right\} \in\) R3. Its walls are marked as: \(S_{1}{=}\left\{ {x = 0,y \in \left[ {0,b} \right],z \in \left[ { - h/2,h/2} \right]} \right\};S_{2}{=}\left\{ {x \in \left[ {0,l} \right],y \in \left[ {0,b} \right],z = h/2} \right\}; S_{3}{=}\left\{ {x = l, y \in \left[ {0,b} \right], z \in \left[ { - h/2,h/2} \right]} \right\};S_{4} = \left\{ {x\left[ {0,l} \right],y = b,z \in \left[ { - h/2,h/2} \right]} \right\};S_{5} = \{ x \in \left[ {0,l\left] {,y \in } \right[0,b} \right], z = - h/2]\} ; S_{6} = \left\{ {x \in \left[ {0,l} \right],y = 0,z \in \left[ { - h/2,h/2} \right]} \right\}\) \(.\)

Fig. 4
figure 4

Beam geometry with marked external faces Si

Full size image

It should be mentioned that in this paper we consider small elastic–plastic deformations of beams and plates. Let us analyze a beam under the action of a transverse static load acting on the face \(S_2={x\in[0,l],y\in[0,b],z=h/2}\). The faces \(S_{1} = \left\{ {x = 0,y \in \left[ {0,b} \right],z \in \left[ { - h/2,h/2} \right]} \right\}; S_{3} = \left\{ {x = l, y \in \left[ {0,b} \right], z \in \left[ { - h/2,h/2} \right]} \right\}\) are associated with the corresponding boundary conditions, whereas the faces \(S_{4} = \left\{ {x \in \left[ {0,l} \right],y = b,z \in \left[ { - h/2,h/2} \right]} \right\};S_{5} = \{ x \in \left[ {0,l\left] {,y \in } \right[0,b} \right], z = - h/2]\} ; S_{6} = \left\{ {x \in \left[ {0,l} \right],y = 0,z \in \left[ { - h/2,h/2} \right]} \right\}\) are free from loads. We assume that the material of the beam is elastic but inhomogeneous. In addition, it is different-modulus, that is, it has different characteristics under tension and compression. Its properties depend on the coordinates in which the beam is located and the intensity of strains. The classical results of deformation theory of plasticity are used in our further considerations.

In all considered case studies, the material has a shear modulus \(G_{0} = 25 \cdot 10^{9} \left[ {{\text{Pa}}} \right]\), Young's modulus \(E_{0} = 66.6 \cdot 10^{9} \left[ {{\text{Pa}}} \right]\) and volumetric modulus \(K = 1.94G_{0}\). Poisson's ratio is \(\nu = 0.35\). The material of the beam is a multimodulus material. As an example, we consider the diagram for pure aluminum [71]. For a multimodulus material, the dependence \(\sigma_{i} \left( {\varepsilon_{i} } \right)\) can be written as

$$ \begin{array}{*{20}c} {\sigma_{i} = k_{1} \sigma_{s} \left[ {1 - \exp ( - \frac{{\varepsilon_{i} }}{{\varepsilon_{s} }})} \right],\;{\text{if }}\;\sigma_{i} > 0}, \\ {\sigma_{i} = k_{2} \sigma_{s} \left[ {1 - \exp ( - \frac{{\varepsilon_{i} }}{{\varepsilon_{s} }})} \right],\;{\text{if}}\;\sigma_{i} \le 0,} \\ \end{array} $$
(15)

where \({\sigma }_{i}\le 0\) holds for compressive stress, \({\sigma }_{i}>0\) follows tensile stresses, and \(e_{s}\),\(\sigma_{s}\) are the limit values of the intensity of strains and stresses, respectively.

According to the method of variable parameters of elasticity and the theory of small elastic–plastic deformations, the shear modulus \(G\), Young's modulus \(E\) and Poisson's ratio \(\nu\) can be estimated by the following formulas:

$$ G = 1/3\,\left( {\sigma_{i} \left( {\varepsilon_{i} } \right)/\varepsilon_{i} } \right), $$
(16)
$$ E = 9KG/(3K + G), $$
(17)
$$ v = 1/2\,\,\left( {\left( {3K - 2G} \right)/\left( {3K + G} \right)} \right), $$
(18)

where \(K = K_{0} = {\text{const}}\) stands for the fixed volume modulus of linear elasticity theory.

The dependence of the stress intensity on the strain intensity is taken in the form of a diagram for pure aluminum (15), whereas \({\sigma }_{s}\) and \({\varepsilon }_{s}\) take the following values: \({\sigma }_{s}=1023 \left[\mathrm{bar}\right]=1.023\times {10}^{8}\left[\mathrm{Pa}\right]\) \({\varepsilon }_{s}=0.98\times {10}^{-3}\). Next, various ratios of the coefficients are considered \({(k}_{1}\) and \({k}_{2}).\) Three dependencies of the stress intensity on the strain intensity are studied, which are presented in Fig. 11 for beams and plates of various configurations under three types of boundary conditions:

Type I. The conditions \(\left\{ {u = v = w = 0\,\,} \right\} \in \,\,S_{1} ,\,\,\left\{ {u = v = w = 0\,\,} \right\} \in \,\,S_{3}\) are set on the beam faces S1 and S3.

Type II. The conditions \(\left\{ {u = v = w = 0\,\,} \right\} \in \,\,S_{1}\) are set on the beam face S1, whereas on the face S3, we take \(\left\{ {v = w = 0\,\,} \right\} \in \,\,S_{3}\).

Type III. On the beam faces S1 and S3: \(\left\{ {v = w = 0\,\,} \right\} \in \,\,S_{1} ,\,\,\left\{ {v = w = 0\,\,} \right\} \in \,\,S_{3}\).

In formula (15), the following dependence is employed \({k}_{2}=0.33{k}_{1}\), and the well-known von Mises test is carried out.

4.1 Beam length \(l/h = 40\) with evenly distributed load

Consider the stress–strain state of a beam in a 3D setting (Fig. 4), for \(l/h = 40\) (h = b). The load is evenly distributed over the entire length of the beam (Fig. 5). The calculations were carried out using FEM with the help of two types of finite elements, i.e., tetrahedron and prism. The system of linear algebraic equations was solved by the LU (lower–upper) expansion method.

Fig. 5
figure 5

The beam subjected to uniformly distributed surface load acting on S2

Full size image

The convergence of the FEM solution for this problem was validated for the boundary conditions: ∀ (u,v,w) ∊ S1 ∪ S3: и = 0,v = 0, w = 0). Table 1 reports the values of the maximum displacements of the beam \(w\)(20,0.5,0.5). The results were obtained for different numbers of finite elements (N) along the beam length l. The number of FEs, indicated in brackets Ns, corresponds to the beam cross section. The type of finite elements is defined in column 2. The third column contains the values of the maximum displacements of the beam \(w\)(20,0.5,0.5) with evenly distributed load q = 8. In the 4th column, the relative errors Δ in estimating the displacement values \(w\)(20,0.5,0.5) are given.

Table 1 Values of the maximum displacements of the beam \(w\) for different shapes and numbers of finite elements under load q = 8
Full size table

A further increase in the number of partitions in l, h, b did not lead to a significant change in the displacements. Therefore, the number of elements in the case of length was chosen as the limiting (validated) values of N = 70 and Ns = 9. For the same case study, the calculation of the stress–strain state of beams for prismatic finite elements was carried out. A comparison of the results, given in Table 1, showed that the best results were obtained for tetrahedron finite elements, and hence in further study preference was given to this type of finite elements.

The convergence of the method of variable parameters of elasticity depends significantly on the volume of plastic zones. Table 2 shows how the number of iterations of the method of variable elastic parameters depends on the intensity of the transverse load for single-modulus and multimodulus of elasticity materials.

Table 2 Values of the displacements of the beam \(w\)(20,0.5,0.5) for different loads q and number of iterations \(n_{it}\)
Full size table

As can be seen from Table 2, the number of required iterations of the method of variable parameters of elasticity increases with increasing load. The same observation holds for the zones of plastic deformations, both for a single-module material and for a multimodulus material. So, for example, for load q = 1, two iterations are enough, while for load q = 6, four iterations are required for a single-module material and five for a multimodulus material.

Table 3 shows the distribution of elastic–plastic deformations for various types and values of the load for the diagram of the dependence of the stress–strain intensity. Column 1 describes the boundary conditions (BC). The notation I, II, III is used to designate the corresponding types of boundary conditions. Column 2 shows the magnitude of the surface load q. Column 3 shows the 3D distribution of elastoplastic deformations. Hereinafter, the areas of plastic deformations during material compression are indicated in blue, the zones of plastic deformations during stretching of the material are indicated in red, and the green color indicates the areas in an elastic state, i.e., \(e_{i}\) < \(e_{s}\). Column 4 reports beam cross sections showing plastic deformation zones along the beam thickness for x = 0.5, x = 10, x = 20 and x = 39.5 (Fig. 6).

Table 3 Elastoplastic deformations of the 3D beam
Full size table
Fig. 6
figure 6

The location of the 3D beam cross sections

Full size image

The study of the zones of elastic–plastic deformation enables us to conclude that the location of the zones of plastic deformation depends significantly on the boundary conditions.

In the case of type I boundary conditions, an increase in the load from 4 to 6 leads to an increase in plastic zones at ends of the beam and the appearance of plastic deformation zones in beam center. The absence of plastic zones for type III boundary conditions at the beam ends shows the effect of hinge fastening. The location of plastic zones for mixed boundary condition (type II) for loads 3 and 2 shows a stronger effect of type I boundary condition by means of the presence of plastic zones. The asymmetry of the plastic zones relative to the middle surface is caused by the multimodulus material.

The dependencies of the maximum displacements on the load intensity for various boundary conditions and a distributed load are presented in Fig. 7. Dependencies for a single-modulus material, for the same types of boundary conditions, are indicated by dashed lines in the corresponding color. Figure 6 also shows the distribution of elastic–plastic deformations for some loads. The difference in maximum deflections under load q = 2, is 2.75 times for boundary conditions of types I and II, whereas for boundary conditions of types I and III, this value is 9.2 times.

Fig. 7
figure 7

Dependence of maximum w deflections versus the load intensity q for single-modulus and bi-modulus materials and for the boundary conditions of types I, II, III

Full size image

It should be noted that, regardless of the types of boundary conditions, the diagram considered for a multimodulus material shows an increase in both maximum deflections and plastic deformation zones relative to a diagram that does not take into account the properties of the different modulus. On the contrary, the different modulus has a significant impact on the distribution of plastic deformations.

Next, we consider the influence of the angle of inclination of the stress intensity diagram on the intensity of compression deformations. Figure 8 shows the considered dependencies of the stress intensity on the strain intensity with the tangent angle in compression marked by \({\varphi }_{1},{\varphi }_{2},{\varphi }_{3}\). Under tension, the dependence of the stress intensity on the intensity of strains remains unchanged for all considered problems; under compression, the considered dependencies have different angles of inclination of the tangent, i.e., we have \({\varphi }_{1}\,\mathrm{for}\,{k}_{2}=0.33{k}_{1},{\varphi }_{2}\,\mathrm{for}\,{k}_{2}=0.5{k}_{1},{\varphi }_{3}\,\mathrm{for}\,{k}_{2}=0.75{k}_{1}\) (see formula (15).

Fig. 8
figure 8

Dependencies of stress intensity on the strain intensity \({\sigma }_{i}\left({\varepsilon }_{i}\right)\) for multimodulus beam material

Full size image

Table 4 presents the distribution of elastic–plastic deformations for various types and values of the load. Column 1 indicates the type of boundary conditions (I, II, III). Column 2 lists the load values (the case of a distributed load is considered). Columns 3–5 show the type of elastic–plastic deformations in the volume of the beam for \({\varphi }_{1},{\varphi }_{2},{\varphi }_{3}\).

Table 4 Elastoplastic deformations for a beam in a 3D formulation for different q and \({\varphi }\)
Full size table

It should be noted that the parameter \(\varphi \) defined in Fig. 8 significantly affects the distribution of plastic deformations when for the value \({\varphi }_{1}\) zones of plastic deformation are most pronounced. Figure 8 shows the dependence of the maximum deflections on the load intensity under type I boundary conditions for three dependencies of the stress intensity on strains for three parameters \({\varphi }_{1},{\varphi }_{2},{\varphi }_{3}\) (Fig. 8). It also reports the zones of plastic deformation at q = 4. With the same load value, in spite of that the zones of plastic deformations remain practically identical, the value of the maximum deflections increases with a decrease in the angle of inclination during compression under type I boundary conditions.

Figure 9 shows the dependence of the maximum deflections on the load intensity for boundary conditions II (Fig. 10a). It also presents the zones of plastic deformation at q = 4 when the zones of plastic deformations at q = 1.5 are exhibited for the boundary conditions of type III (Fig. 10b).

Fig. 9
figure 9

Dependence of maximum deflections on the load intensity (BC type I)

Full size image
Fig. 10
figure 10

Dependence of maximum deflections on the load intensity (BC type II (a) and type III (b))

Full size image

It should be noted that under the same loads and boundary conditions of type II, the angle of inclination of the stress–strain diagram affects the distribution of plastic deformations during compression, whereas under the action of boundary conditions of type III, the effect manifests itself in a change in plastic zones under tension, while the limit of reaching plastic zones under compression is not achieved within the limits of the theory of small elastic–plastic deformations.

4.2 Beam length \(l/h = 80\) with evenly distributed load

Consider a beam \(l/h = 80\) subjected to a distributed load acting over the entire face S2. Table 5 shows the values of the maximum displacements of the beam \(w(20,0.5,0.5)\) depending on the number and shape of finite elements for the given problem under boundary conditions I and load q = 0.9. A comparison of the results with those shown in Table 1 shows that a twofold increase in \(l/h\) leads to a twofold increase in the number of finite elements to achieve the reliability of the results.

Table 5 Values of the maximum displacements of the beam \(w\) (20,0.5,0.5) for different shapes and number of finite elements under load q = 0.9
Full size table

The dependencies of the maximum deflections on the load intensity under the distributed load for the boundary conditions I, II, III are shown in Fig. 11. The difference in the value of the maximum deflection at q = 0.1 for boundary conditions of types I and II achieves 2.5 times, for boundary conditions of types I and III 3.2 times.

Fig. 11
figure 11

Dependencies w(q) of maximum deflections on the intensity of load for the boundary conditions of types I, II, III

Full size image

The beams \(l/h = 80\) were also examined with regard to three values of the coefficient \({\varphi }_{1},{\varphi }_{2},{\varphi }_{3}\). In this case, for displacements \(w \le 0.35h\), there are no zones of plastic deformation in the bulk of the beam. Dependencies w(q) of maximum deflections on the intensity of load obtained for boundary conditions of types I, II, III with respect to \({\varphi }_{1},{\varphi }_{2},{\varphi }_{3}\) are reported in Fig. 12.

Fig. 12
figure 12

Dependencies of maximum deflections on the load intensity for the boundary conditions of types I, II, III and for different \({\varphi }_{i}\), i = 1,2,3

Full size image

The analysis of the results obtained enables us to conclude that the slope of the dependence of the stress intensity has the greatest influence on the maximum deflections of the beam in the case of type III boundary conditions. On the other hand, for type I boundary conditions, this influence is minimal. In all the cases considered, the boundary conditions are not reached within the limit of reaching the elastic–plastic deformations.

4.3 Beam of length \(l/h = 40\) subjected to concentrated load

We consider a beam under a concentrated load (Fig. 13) acting along a part of its face S2. The load acts in the section from a quarter of the beam length to half of the beam length, and the rest of the faces are free from loads.

Fig. 13
figure 13

Beam subjected to concentrated surface load \(S_{7} = \left\{ {x \in \left[ {10,20} \right],\,\,y \in \left[ {0,b} \right]} \right\}\)

Full size image

Table 6 shows the distribution of elastic–plastic deformations for various values of the load q for the diagram of dependencies of stress intensity on the intensity of strains under \({\varphi }_{3}\). For the case of a concentrated load, the beam was investigated under type I boundary conditions. Column 1 shows the surface load intensity q. Column 2 presents the 3D distribution of elastoplastic deformations. Column 3 reports sections exhibiting plastic deformation zones along the beam thickness for x = 0.5, x = 10, x = 20 and x = 39.5 (Fig. 5).

Table 6 Elastoplastic deformations for a beam in a 3D setting
Full size table

With increasing load, a plastic deformation zone appears in the center of the beam, shifted to its hinge edge. Plastic zones for the case of local loads q = 15 and q = 10 are located in the zone of the load action, and an increase in the load leads to their growth. Furthermore, because of the multimodulus material, asymmetry is observed with respect to the median line.

The dependence of the maximum displacements on the intensity of the load w(q) for multimodulus beam materials (single-modulus and bi-modulus) is shown in Fig. 14, and the zones for loads q = 10 and q = 15 are indicated. The dependence for single-modulus material is indicated by a dotted line.

Fig. 14
figure 14

Dependence of maximum beam deflections on the load intensity for type I boundary condition and for single/bi-modulus material

Full size image

Under the action of a concentrated load, as in the case of a distributed load, the multimodulus material in the considered problem yields to an increase in the maximum deflections of the beam.

4.4 Plate

The previous sections dealt with the problems of the spatial theory of beams. However, with an increase in b in relation to \(l/ b\), the beam broadens and becomes a plate. In this section, we study the stress–strain state of 3D plates for type I boundary conditions {∀ (u,v,w) ∊ S1 ∪ S3: (и = 0,v = 0,w = 0)}. The beams and plates were analyzed at different ratios of thickness and width \(l/b=40,\text{\hspace{0.17em}\hspace{0.17em}}2,\text{\hspace{0.17em}\hspace{0.17em}}1\), for \(l/h = 40\). Elastoplastic problems were studied for 3D plates under the action of a distributed load over the face S2 for \(l/h = 40\). Table 7 shows the values of the maximum displacements \(w\)(20,0.5,0.5) depending on the number of finite elements and their type (BC I), and for distributed load q = 8. The number of elements with a relative error 0% by length l, as for the beam (Table 1) is 70. However, the number of elements in the cross section is 17.5 times greater.

Table 7 Values of maximum displacements w for various shapes and numbers of FE of the plate
Full size table

The dependence of maximum deflections on intensity of load for different values \(l/b\) is shown in Fig. 15, and zones of plastic deformation are reported for q = 4 and q = 6. The maximum difference in deflections at \(l/b = 40\), for q = 6, on \(l/b = 2\) is less than 1%, whereas for \(l/b = 1\) the difference is 3.5%.

Fig. 15
figure 15

Dependence of maximum deflections on the load intensity for different plate \(l/b\) ratios

Full size image

Plastic zones, depending on type I boundary conditions, are located and behave in a similar way. As the load increases, the maximum deflections change insignificantly.

The elastoplastic deformations of the plate are presented in Table 8. The first column shows the relationship \(l/b\), and the second (third) column presents the zones of plastic deformation for the load q = 4 (q = 6). Studies of the location of plastic zones depending on different values \(l/b = \left\{ {1,2,40} \right\}\) showed that under the boundary conditions of pinching the ends of the beam \(S_{1} ,\,\,S_{3}\), the zones are located in the same manner. Thus, a change in the parameter \(l/b\) does not significantly affect the location of elastic–plastic zones.

Table 8 Elastoplastic deformations of plates in 3D formulation
Full size table

The next considered problem was solved for three dependencies of stress intensity on strains with tangent angles \({\varphi }_{1},{\varphi }_{2},{\varphi }_{3}\) with respect to compression. The first column of Table 9 shows the relationship \(l/b\); the second presents the angle of the tangent dependencies of the intensity of stress on strains; in the third and fourth column, the zones of plastic deformations are reported (the load values are selected so that the maximum displacement w = 0.3). Observe that a change in the parameter \(l/b\) does not affect the position of elastic–plastic zones significantly for all considered dependencies.

Table 9 Elastoplastic deformations of plates in 3D formulation for different \(l/b\) and \({\varphi }_{i},\) i = 1,2,3
Full size table
Table 10 Elastoplastic deformations of plates in 3D formulation
Full size table

Dependencies of the maximum displacements w on the load intensity q for various dependencies of the stress intensity on strains and ratios \(l/b\) are shown in Fig. 16.

Fig. 16
figure 16

Dependence of w(q) maximum for different boundary conditions I, II, III and different l/b and \({\varphi }_{i}\)

Full size image

The angle of inclination of the dependence of the stress intensity on strains with the angle of the tangent (in compression) \({\varphi }_{1},{\varphi }_{2},{\varphi }_{3}\) affects the distribution of plastic deformations and manifests the occurrence of asymmetry relative to the middle surface, while the ratio \(l/b\) does not qualitatively change the picture of the distribution of plastic deformation zones.

Consider the problem for a plate, which differs from the previous one in t̄he boundary conditions: ∀ (u,v,w) ∊ S1 ∪ S3 ∪ S4 ∪ S6 (и = 0, v = 0, w = 0). The first column of Table 10 shows the relationship \(l/b\); the second and third columns show the zones of plastic deformations for different values of the loads. Provided that the entire lateral surface is pinched, the location of elastic and plastic zones depends on the value \(l/b\), unlike in the previous case. It should be noted that the area of plastic zones is larger for the parameter \(l/b = 1\), than for \(l/b = 2\) at the same load.

Table 11 Elastoplastic deformations of plates in 3D formulation for different \(l/b\), q and \(\varphi \)
Full size table

The dependence of maximum deflections on the intensity of load for different values \(l/b\) is shown in Fig. 17. The zones of plastic deformation are reported for \(l/b = 2\) and for q = 20, 40 as well as for \(l/b\) = 1 and for q = 10. The difference in deflections for \(l/b = 1\) and \(l/b = 2\) at the same load q = 10, achieves 9.45 times.

Fig. 17
figure 17

Dependence of maximum plate deflections vs. the load intensity for various values of \(l/b\) ratios

Full size image

Consider the plates characterized by different ratios of thickness and width \(l/b = 40,\,\,2,\,\,1\), for type I boundary conditions {∀ (u,v,w) ∊ S1∪S3: (и = 0,v = 0, w = 0)}. The first column of Table 11 shows the relationship \(l/b\), the second–the angle of the tangent dependencies of the stress intensity on strains, and the third and fourth columns show the zones of plastic deformations (the loads were chosen so that the maximum displacement w for each of the cases was equal to 0.2).

In this case, the ratio \(l/b\) affects the distribution of zones of plastic deformation. For \(l/b\) = 1, with the same w, displacements the greatest manifestation of zones of plastic deformation in compression occurs for a diagram for the angle \({\varphi }_{1},\) and the smallest for a the curve obtained for the angle \({\varphi }_{3}.\) For \(l/b\) = 2, this dependence is less pronounced.

Dependencies of w(q) maximum for various \({\varphi }\) and ratios \(l/b\) are presented in Fig. 18.

Fig. 18
figure 18

Dependence of w(q) maximum for boundary conditions I, II, III and for different \(l/b\) and \(\varphi .\)

Full size image

Under these boundary conditions, the angle of inclination of the dependence of the stress intensity on deformations with the angle of the tangent (in compression) \({\varphi }_{1},{\varphi }_{2},{\varphi }_{3}\), and the ratio \(l/b\) affects the displacement of the plate w.

Comment The main hypothesis when solving problems in a 3D setting was that problems were considered at small strains, for which displacements w should be less than \(0.35h\).

The results obtained show the effect of the multimodulus material on the stress–strain state, the distribution of plastic deformations, as well as on the displacement of beams and plates.

5 Concluding remarks

In this work, for the first time, mathematical models of beams and plates made from multimodulus materials have been constructed on the basis of the spatial theory of elasticity, taking into account the physical nonlinearity of the material. Based on the literature overview, we believe that the carried out investigations are pioneering since other works related to the problem are unknown to us. Algorithms and programs for studying the stress–strain state of beams and plates in a 3D setting have been developed. Physical nonlinearity has been taken into account based on the Hencky deformation theory of plasticity. For a numerical study, the FEM has been used in combination with Birger’s method of variable parameters of elasticity. The reliability of the results obtained has been ensured by investigating the convergence of the finite element method with regard to two types of FE, i.e., tetrahedron and prism.

The von Mises criterion has been adopted as the plasticity criterion. The study of zones of elastic–plastic deformation has been carried out depending on the parameter of the different modulus \(\varphi \), the type of load and the ratio of the length of the beam to its width \(l/b\). With small deflections, for \(l/b\) = 80, the beam is elastic unlike for \(l/b\) = 40. Plastic zones depend on the values \(l/b = \left\{ {1,2,40} \right\}\) and the type of boundary conditions. The zones of elastic–plastic deformations in the cross section depend significantly on the deformation diagram of materials and the parameter \(\varphi ,\) which is demonstrated in Fig. 8.