Structural Behaviour and Fire Design of Duplex and Ferritic Stainless Steel CHS Stub Columns

Abstract

This paper investigates the structural behaviour and design of duplex and ferritic stainless steel stub columns with a circular hollow cross-section (CHS) at elevated temperature. A numerical model is developed to supplement the limited test results on stainless steel CHS stub columns in the literature. Following validation, the numerical approach is employed to gain an understanding of the critical behavioural characteristics which have not previously been studied. In addition, the paper considers and extends the continuous strength method (CSM) to include duplex and ferritic stainless steel for CHS stub columns in fire. The CSM employs a base curve linking the cross-section resistance to its deformation capacity and implements an elastic, linear hardening material model. The cross-sectional resistances obtained from the proposed CSM are compared with those from the numerical analysis, as well as with the standardised procedures in the European, American and Australia/New Zealand design standards. It is demonstrated that CSM can lead to more accurate and less scattered strength predictions than current design codes.

1 Introduction

The use of stainless steel in structural applications is increasing due, in part, to the material’s aesthetics, ease of maintenance, corrosion resistance, low life cycle costs and fire resistance, as well as the availability of improved design guidance. With increased emphasis being given to the performance of structures at elevated temperatures (Bailey, 2004; Mohammed & Cashell, 2021), and a growing trend towards the use of bare steelwork (Wong et al., 1998), there have been a number of recent studies into the structural response of unprotected stainless steel elements exposed to fire (Baddoo & Gardner, 2000; Gardner & Baddoo, 2006; Liu et al., 2019; Mohammed & Afshan, 2019). Fire-resistant design methods tend to adopt either a prescriptive or performance-based approach and focus on the design of isolated elements rather than the complete structural assemblage (Wang, 2000). In any case, an accurate and efficient determination of the performance of the structure during a fire is of paramount importance. Inaccurate evaluation of the response could lead to an increase in member size and the required level of fire protection, both of which are economically and environmentally inefficient.

One of the key incentives for using stainless steel is the possibility of improved fire performance, relative to carbon steel, reducing the requirements for expensive fire protection. The cost of fire protection varies from project to project but for a typical multi-storey building, for example, the fire protection costs can be 20–30% of the total cost of the steel frame (Ala-Outinen & Oksanen, 1997; Wang, 2000). A reduction or even removal of the need for fire protection on some or all of the structural members has substantial economic incentives. These include lower construction costs, shorter construction time, more effective use of interior space and a better working environment (Baddoo, 2013). Stainless steel is inherently a more expensive material compared with carbon steel in terms of initial costs and therefore any savings and efficiencies that can be found, are important. Costs associated with stainless steel in comparison with carbon steel can be found in the SCI Design Manual for Structural Stainless Steel (2017) and Gardner (2008). In addition, as fire protection limits the re-usability of metallic sections, it also reduces the possibility for environmental savings. As well as the economic and environmental inducements, stainless steel is often selected for its aesthetic appeal and therefore covering the surface with fire protecting materials is not preferable. Though some fire protection methods do not impair aesthetics, these are generally very expensive (Parker et al., 2005).

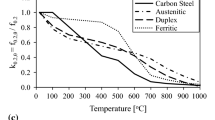
There are five families of stainless steel including the austenitic, ferritic, duplex, martensitic and precipitation hardening grades. The austenitic and duplex grades are most common in load-bearing structures, although ferritic stainless steels are also used in appropriate applications. Compared with carbon steel, the thermal and mechanical properties of stainless steel are quite different owing to variation in chemical composition between the materials. At elevated temperature, stainless steel exhibits enhanced retention of stiffness and strength compared to carbon steel, but displays a lower thermal conductivity and higher thermal expansion (Gardner, 2007). Though recent years have seen significant developments in the production of useful design guidance for structural stainless steel both at ambient and elevated temperature, much of this work has focussed on the austenitic grades. Figure 1a presents the stiffness reduction factors (k_E,θ) for the austenitic, duplex and ferritic grades as given in the SCI stainless steel design guide (SCI Design Manual for Structural Stainless Steel, 2017) as well as those for structural carbon steel in Eurocode 3 Part 1–2 (EN 1993-1-2, 2005). The stiffness reduction factor k_E,θ at a given temperature θ is defined as the elastic modulus at θ (E_θ) normalised by the corresponding value at room temperature E. Figure 1b presents the equivalent values for the strength reduction factor k_0.2,θ, defined as the elevated temperature 0.2% proof stress f_0.2,θ normalised by the corresponding value at room temperature f_0.2. Figure 1c shows the strength reduction factor k_2.0,θ which is very relevant in the design of stainless steel structures and is defined as the elevated temperature strength at 2% total strain normalised by the room temperature 0.2% proof stress. Figure 1c shows that at low temperatures, the k_2,θ reduction factors for all grades of stainless steel are substantially greater than unity, owing to the significant strain hardening properties of stainless steel.

Fig. 1

Retention factors for different grades of stainless steel and carbon steel at elevated temperature θ, including a stiffness, k_E,θ b 0.2% proof strength, k_0.2,θ and c strength at 2% total strain, k_2.0,θ (SCI Design Manual for Structural Stainless Steel, 2017)

The current paper focuses on the structural behaviour and fire design of circular hollow section stub columns made primarily from duplex and ferritic stainless steel, which have not previously been studied. The duplex stainless steel grades have a two-phase microstructure consisting of grains of ferritic and austenitic stainless steel. They offer excellent strength and stiffness but can be relatively expensive. A newer set of grades known as lean duplex stainless steel provide a more economical solution and still offer excellent structural and durability performance. The ferritic grades, on the other hand, have a lower material cost compared with the austenitic and duplex grades owing to their reduced nickel and chromium content (Baddoo, 2013). Furthermore, the ferritic grades tend to have a higher proof strength than austenitic grades and are less prone to stress corrosion cracking. Although traditionally there has been less research into the fire performance of duplex and ferritic stainless steels, compared with the austenitic grades, their respective qualities have drawn more attention in recent years and reduction factors are included in the latest edition of the SCI stainless steel design guide (2017), as presented in Fig. 1.

The structural behaviour and design of stainless steel structures exposed to fire conditions presents a challenge for both researchers and practising engineers owing to the complex behaviour and economic implications (Gardner, 2007). At elevated temperatures, like all metallic structural elements, stainless steel members experience the development of thermal strains and also significant deterioration of the material mechanical characteristics which are, in most circumstances, non-uniform through the cross-section and along the member length. These factors, combined with the fundamental uncertainty associated with fire loading, have motivated widespread research into the topic. The resistance of metallic structures under fire conditions can be considered on four different levels (He et al., 2019); (1) the material characteristics at elevated temperatures; (2) the cross-sectional behaviour which considers the local stability effects; (3) the member behaviour which considers the global stability effects; and (4) the global behaviour which considers the impact based on large deformations.

Experimental research into the behaviour of stainless steel structures under fire has generally been restricted to the structural response of isolated members (Level’s 2 and 3), due to the high costs and complexities associated with testing full-scale structural assemblies under fire. Nevertheless, isothermal fire tests at cross-sectional (He et al., 2019) and member (Gardner & Baddoo, 2006); level have been performed to investigate the effect of high temperature on the structural response of members failing by local and global buckling without the added complexity of the impact of heating rates; however, these tests have been limited to members made from austenitic stainless steel (Grade 1.4301). To date, the knowledge pertaining to the behaviour of structural elements and systems made from duplex and ferritic stainless steel is more limited although these grades are gaining increasing levels of attention from researchers and engineers. They have not been tested at a cross-sectional level at elevated temperature and there is a growing need to fundamentally examine their behaviour to understand how it affects structural fire design. This gap in knowledge is the motivation for the work presented in the current paper, which is focussed on stub columns made from stainless steel circular hollow sections (CHS).

This paper presents with an overview of the existing design guidance and a general state of the art on the behaviour and design of duplex and ferritic stainless steel structures at elevated temperature. Thereafter, a finite element model is developed to generate structural performance data for axially loaded stub column members in fire. The development of the numerical model is described, together with its validation against available test data. The model is then employed to conduct a parametric study, and the results are compared with the design values determined using the European (EN, 1993-1-4, 2015), American (SEI/ASCE 8-02, 2002) and Australian/New Zealand (AS/NZS 4673, 2001) design standards as well as the continuous strength method (CSM).

2 Design of stainless steel stub columns at elevated temperature

In general, the international design codes adopt similar fire design approaches for stainless steel structures and carbon steel members, despite the significant differences in material properties. Therefore, in the current work, and as described hereafter, some of the specific design rules for stainless steel members at ambient temperature and elevated temperature (i.e. in EN 1993-1-4 (2015), EN 1993-1-2 (2005), SEI/ASCE 8-02 (2002) and AS/NZS 4673 (2001) are employed together with the most current elevated temperature material properties for stainless steel to investigate the fire design of stainless steel stub columns. This approach is then scrutinised later in the paper.

2.1 Design standards

2.1.1 Eurocode 3

The analysis and design of stainless steel structures at ambient temperature is given in EN 1993-1-4 (2015), referring to EN 1993-1-2 (2005) for specific fire design guidance. Generally, the guidance given in EN 1993-1-2 for stainless steel fire design adopts a similar approach as the carbon steel rules, although different reduction factors are provided for the mechanical properties of stainless steel at different levels of elevated temperature. The behaviour of stainless steel material is fundamentally different to that of carbon steel, with substantial strain hardening and high levels of ductility, and this is very influential to the overall structural behaviour.

In the specific guidance for structural stainless steel (EN, 1993-1-4, 2015), the classification of a CHS at ambient temperature is determined by comparing the cross-section D/tε² ratio against prescribed slenderness limits, where D is the diameter of the section, t is the thickness of the cross-section, and ε is the material factor determined as ε = [(235/f_0.2)(E/210000)]^0.5. The Class 3 slenderness limit distinguishes slender (Class 4) sections, where local buckling occurs before the material 0.2% proof stress is obtained, from their non-slender (Class 1, 2 and 3) counterparts. EN 1993-1-4 prescribes the use of Eqs. 1 and 2 for the determination of compressive capacities of non-slender and slender stainless steel CHS stub columns at ambient temperature (N_u,EC3), respectively, in which A and A_eff,EC3 are the actual and effective cross-sectional areas of the CHS, respectively. A_eff,EC3 may be calculated using Eq. 3 (Buchanan et al., 2018).

$${\text{N}}_{{{\text{u}},{\text{EC}}3}} = {\text{Af}}_{{0.2}} \;\;\;{\text{for Class 1}},{\text{2 and 3}}\;{\text{cross - sections}}$$

(1)

$${\text{N}}_{{{\text{u}},{\text{EC}}3}} = {\text{A}}_{{{\text{eff}},{\text{EC}}3}} {\text{f}}_{{0.2}} \;\;\;{\text{for Class }}4\;{\text{cross - sections}}$$

(2)

$${\text{A}}_{{{\text{eff}},{\text{EC}}3}} = {\text{A}}\left( {\frac{{90}}{{{\text{D}}/{\text{t}}}}\frac{{235}}{{{\text{f}}_{{0.2}} }}\frac{{\text{E}}}{{210000}}} \right)^{{0.5}}$$

(3)

In fire design (EN 1993-1-2, 2005), the section classification for stainless steel members (or indeed carbon steel members) is determined using the same limits as for room temperature design but adopts a reduced material factor ε = 0.85[235/f_0.2]^0.5, where ${\mathrm{f}}_{0.2}$ is the 0.2% yield strength at room temperature. It is noteworthy that the SCI Design Manual for Structural Stainless Steel (2017) does include a specific method for classifying stainless steel cross-sections using a temperature-dependent value for ε_θ, determined as ε_θ = ε[k_E,θ/k_y,θ]^0.5. The structural response of steel and stainless steel structures at elevated temperature is characterised by significant deformations, which are more acceptable in extreme conditions such as a fire than in normal service. Accordingly, the resistance of stainless steel structural members in fire is typically based on the stress at 2% total strain (f_2,θ = k_2,θf_0.2, where k_2,θ is the reduction factor for the strength at 2% total strain at temperature θ) for Class 1, 2 and 3 cross-sections, and the 0.2% proof strength f_0.2,θ for slender sections.

2.1.2 SEI/ASCE-8

The current American specification SEI/ASCE-8 for stainless steel members at ambient temperature (2002) adopts an elastic buckling stress method for the design of hollow section compression members. The compression resistance of a column N_u,ASCE is determined as the product of the member flexural buckling stress f_n and the effective area of the cross-section at the flexural buckling stress A_eff,ASCE, given by Eq. 4:

$${\rm N}_{\rm u,ASCE}= {\text{f}}_{{\text{n}}} {\text{A}}_{{{\text{eff}},{\text{ASCE}}}}$$

(4)

In this expression, f_n and A_eff,ASCE are determined following Eqs. 5 and 6, respectively:

$${\text{f}}_{{\text{n}}} = \frac{{\pi ^{2} {\text{E}}_{{\text{t}}} }}{{\left( {{\text{kL}}/{\text{r}}} \right)^{2} }} \le ~{\text{f}}_{{0.2}}$$

(5)

$${\text{A}}_{{{\text{eff}},{\text{ASCE}}}} = {\text{A}}\left[ {1 - \left( {1 - \left( {\frac{{{\text{E}}_{{\text{t}}} }}{{\text{E}}}} \right)} \right)\left( {1 - {\text{k}}_{{\text{c}}} } \right)} \right]$$

(6)

in which E_t is the tangent modulus in compression corresponding to buckling stress which can be determined using the Ramberg–Osgood expression provided in Appendix B of the standard, L is the length of the member, r is the radius of gyration, k is the effective length factor of the column and equal to 0.5 for fixed-ended boundary conditions, and k_c is the reduction factor, as calculated using Eq. 7. In this expression, C is the ratio of the material proportional limit to the 0.2% proof stress as adopted in SEI/ASCE-8 (2002) and $\lambda _{{\text{c}}}$. is equal to 3.084C.

$${\text{k}}_{{\text{c}}} = \frac{{\left( {1 - {\text{C}}} \right)\left( {{\text{E}}/{\text{f}}_{{0.2}} } \right)}}{{\left( {8.93 - \lambda _{{\text{c}}} } \right)\left( {{\text{D}}/{\text{t}}} \right)}} + \frac{{5.882{\text{C}}}}{{8.93 - \lambda _{{\text{c}}} }}{\text{~}} \le 1$$

(7)

2.1.3 AS/NZS 4673

The current Australian/New Zealand standard AS/NZS 4673 (2001) adopts the same elastic buckling stress method for the determination of stainless steel hollow section column strengths as the American specification SEI/ASCE-8 (2002), except for the use of an alternative k_c for calculating the effective area, as given in Eq. 8:

$${\text{k}}_{{\text{c}}} = \frac{{\left( {1 - {\text{C}}} \right)\left( {{\text{E}}/{\text{f}}_{{0.2}} } \right)}}{{\left( {3.226 - \lambda _{{\text{c}}} } \right)\left( {{\text{D}}/{\text{t}}} \right)}} + \frac{{0.178{\text{C}}}}{{3.226 - \lambda _{{\text{c}}} }}{\text{~}} \le 1$$

(8)

2.2 The continuous strength method

In general, current room temperature design standards do not fully exploit the significant and beneficial strain hardening properties of stainless steel and limit the design strength to the yield (0.2% proof) strength. This approach typically yields safe but rather conservative designs for stainless steel members, owing to the excellent ductility and strain hardening capacity of stainless steel. The continuous strength method (CSM) is a novel deformation-based design method which was developed initially to exploit this additional strength after the yield point in ductile materials, and to provide a more efficient and reliable design method than existing procedures (Afshan & Gardner, 2013 and Buchanan et al., 2016). The CSM provides accurate predictions for the compressive resistance of stainless steel CHS stub columns at ambient temperature (Buchanan et al., 2016). The current paper focuses on the applicability of this method for the design of duplex and ferritic stainless steel CHS stub columns at elevated temperature.

The first step in this method is to calculate the cross-section deformation capacity using the CSM base curve, as defined by Eq. 9 for a CHS (Buchanan et al., 2016):

$$\frac{{\varepsilon _{{{\text{csm}}}} }}{{\varepsilon _{{\text{y}}} }} = \left\{ {\begin{array}{*{20}l} {\frac{{4.44~ \times 10^{{ - 3}} }}{{\bar{\lambda }_{{\text{c}}} }} \le \min ~\left( {15,~\frac{{{\text{c}}_{1} \varepsilon _{{\text{u}}} }}{{\varepsilon _{{\text{y}}} }}} \right)} & {for~\bar{\lambda }_{{\text{c}}} \le 0.3} \\ {\left( {1 - \frac{{0.224}}{{\bar{\lambda }_{{\text{c}}}^{{0.342}} }}} \right)\frac{1}{{\bar{\lambda }_{{\text{c}}}^{{0.342}} }}~} & {for~\bar{\lambda }_{{\text{c}}} \ge 0.3~} \\ \end{array} } \right.$$

(9)

In this expression, ε_csm is the limiting strain for CHS in compression, ε_y is the material yield strain, $\varepsilon _{{\text{u}}}$ is the ultimate strain determined as $\varepsilon _{{\text{u}}} = {\text{c}}_{3} \left( {1 - {\text{f}}_{{{\text{0}}{\text{.2}}}} /{\text{f}}_{{\text{u}}} } \right)$ and $\bar{\lambda }_{{\text{c}}}$ is the slenderness of the cross-section. $\bar{\lambda }_{{\text{c}}}$ is determined as $\bar{\lambda }_{{\text{c}}} = \sqrt {{\text{f}}_{{0.2}} /\sigma _{{{\text{cr}}}} }$, where $\sigma _{{{\text{cr}}}}$ is the elastic critical buckling stress and may be determined using Eq. 10, and ν is the Poisson's ratio:

$$\sigma _{{cr}} = \frac{{\text{E}}}{{\sqrt {3\left( {1 - {\text{v}}^{2} } \right)} }}\frac{{2{\text{t}}}}{{\text{D}}}$$

(10)

Once ε_csm is determined, a bi-linear material model as depicted in Fig. 2 is employed, which has a strain hardening slope E_sh, given as:

$${\text{E}}_{{{\text{sh}}}} = \frac{{{\text{f}}_{{\text{u}}} - {\text{f}}_{{0.2}} }}{{{\text{c}}_{2} \varepsilon _{{\text{u}}} - \varepsilon _{{\text{y}}} }}$$

(11)

Fig. 2

Elastic, linear strain hardening CSM material model

It is noteworthy that $\bar{\lambda }_{{\text{c}}}$ = 0.3 defines the boundary between slender and non-slender CHS’s, at which point ε_csm/ε_y is equal to unity. With reference to Fig. 2, c1, c2, and c3 are material parameters which have been calibrated based on a range of tensile test data (Buchanan et al., 2016) and are given in Table 1 for austenitic, duplex and ferritic stainless steels, respectively. These are constants employed in the CSM for defining the cut-off point for the strain (c₁), determining E_sh (c₂) and in the prediction of the ultimate strain (c₃). Equation 12 calculates the CSM design stress σ_csm, based on which the CSM design cross-section resistance in compression N_csm can be determined, as given in Eq. 13:

$$\sigma _{{{\text{csm}}}} = \left\{ {\begin{array}{*{20}c} {E\varepsilon _{{{\text{csm}}}} ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~for~\varepsilon _{{{\text{csm}}}} < ~\varepsilon _{{\text{y}}} } \\ {{\text{f}}_{{0.2}} + ~{\text{E}}_{{{\text{sh}}}} \left( {\varepsilon _{{{\text{csm}}}} - \varepsilon _{{\text{y}}} } \right)~~~~~~~~for~\varepsilon _{{{\text{csm}}}} \ge ~\varepsilon _{{\text{y}}} } \\ \end{array} } \right.$$

(12)

$${\text{N}}_{{{\text{csm}}}} = \sigma _{{{\text{csm}}}} {\text{A}}$$

(13)

Table 1 CSM material model coefficients (Buchanan, 2018)

3 Numerical modelling

A finite element model was developed in ABAQUS (2016) to analyse the behaviour of stainless steel CHS under fire conditions and is described herein. ABAQUS was selected as it is commercially available and is capable of depicting the material and geometric nonlinearities as well as the elevated temperature behaviour accurately (Mohammed & Afshan, 2019; and He et al., 2019). Due to the absence of test data on stainless steel CHS columns in fire conditions, experimental results from He et al. (2019) are employed to generate and validate the numerical approach. This test programme included 16 experiments on CHS austenitic stainless steel stub columns in Grade EN 1.4301, at room temperature. Fourteen of the tests were conducted in the post-fire condition and therefore heated to a target temperature θ, allowed to cool, and then tested at ambient temperature. The details are presented in Table 2, including the measured section diameter (D), thickness (t) and member length (L), as well as the failure load measured during the test (N_u,test). All of the tests failed by local buckling with an elephant foot pattern, irrespective of whether they were tested in the virgin (i.e. unheated) conditions or the post-fire condition. In later sections of this paper, the same FE model is employed to study the elevated temperature behaviour under isothermal loading, by adopting the material properties of the stainless steel measured at elevated temperatures. This strategy has been adopted by other researchers (Huang & Young, 2019).

Table 2 Details of CHS stainless steel columns at elevated temperature (He et al., 2019)

Accordingly, in the finite element (FE) model, the stainless steel columns are modelled isothermally, whereby stress–strain data corresponding to a target temperature θ is assigned to the stainless steel material. Nine target temperatures are adopted ranging from 30 °C to 1000 °C, and the representative temperatures are provided by He et al. (2019). Firstly, a linear elastic buckling analysis is conducted using the *BUCKLE step procedure in ABAQUS to determine the buckling mode shapes, using the material properties at the desired temperature (ambient or elevated temperature). This is followed by a nonlinear stress analysis using the modified *RIKS method in ABAQUS, incorporating the initial geometric imperfections from the buckling analysis, to determine the response under load. Both the material and geometric nonlinearities are accounted for in the numerical analysis, as well as the elevated temperature stress–strain response. The ABAQUS/Standard analysis method is used in this study.

The circular hollow sections are modelled using four-noded doubly-curved shell elements with reduced integration known as S4R elements in the ABAQUS (2016) library; these have been regularly used for the simulation of thin-walled hollow cross-sections (e.g. Mohammed & Afshan, 2019). Based on a mesh sensitivity assessment, an element size ranging between the cross-section thickness (t) and 0.5t are assigned to the sections. For stub columns models with fixed end boundary conditions, all translational degrees of freedom except axial displacement at the loaded end are restrained (i.e. ux ≠ 0, uy = 0 and uz = 0) while all rotational degrees of freedom at both ends are restrained (i.e. uRx = 0, uRy = 0 and uRz = 0). The load is applied concentrically to the circular hollow sections through a reference point at the top of the element.

The stress–strain response of grade 1.4301 stainless steel was examined through tensile testing in the experimental programme (He et al., 2019), and the data is incorporated into the numerical model for validation of the numerical approach. The tensile coupons were cut from the CHS specimens and then heated together with the corresponding stub column specimens to each pre-specified temperature level, to ensure that both the coupons and stub columns follow the same heating and cooling process. The two-stage elevated temperature Ramberg–Osgood material model reported in the SCI Design Manual for Structural Stainless Steel (2017) is used to represent the stress–strain behaviour of the stainless steel material as given in Eqs. 14 and 15. The Poisson’s ratio is set as 0.3 in accordance with Eurocode 3 Part 1–4 [14].

$$\varepsilon = {\text{~}}\left( {\frac{\sigma }{{\text{E}}}} \right) + {\text{~}}0.002\left( {\frac{\sigma }{{{\text{f}}_{{0.2}} }}} \right)^{{\text{n}}} \sigma ~ \le {\text{f}}_{{0.{\text{2}}}}$$

(14)

$$\varepsilon = {\text{~}}0.002 + \frac{{{\text{f}}_{{0.2}} }}{{\text{E}}} + \frac{{\sigma - {\text{f}}_{{0.2}} }}{{{\text{E}}_{{\text{y}}} }} + \varepsilon _{{\text{u}}} \left( {\frac{{\sigma - {\text{f}}_{{0.2}} }}{{{\text{f}}_{{\text{u}}} - {\text{f}}_{{0.2}} }}} \right)^{{\text{m}}} {\text{for}}\;\;\sigma > ~{\text{f}}_{{0.{\text{2}}}}$$

(15)

In these expressions, σ and ε are the engineering stress and strain, respectively, f_u and $\varepsilon _{{\text{u}}}$ are ultimate stress and strain, E_y is the tangent modulus at f_0.2 calculated using Eq. 16, and n and m are the strain hardening exponents adopted in the Ramberg–Osgood model.

$${\text{E}}_{{\text{y}}} = \frac{{\text{E}}}{{1 + 0.002{\text{nE}}/{\text{f}}_{{0.2}} }}$$

(16)

ABAQUS requires the translation of the measured engineering stress–strain curve into true stress-log plastic strain response. The true stress ($\sigma _{{{\text{true}}}}$) and log-plastic strain response ($\varepsilon _{{{\text{ln}}}}^{{{\text{pl}}}}$) are obtained using Eqs. 17 and 18, respectively, where $\sigma _{{{\text{nom}}}}$ is the engineering stress and $\varepsilon _{{{\text{nom}}}}$ is the engineering strain:

$$\sigma _{{{\text{true}}}} {\text{~ = ~}}\sigma _{{{\text{nom}}}} \left( {{\text{1 + }}\varepsilon _{{{\text{nom}}}} } \right)$$

(17)

$$\varepsilon _{{{\text{ln}}}}^{{{\text{pl}}}} {\text{~ = ~ln}}\left( {{\text{1 + }}\varepsilon _{{{\text{nom}}}} } \right) - \frac{{\sigma _{{{\text{true}}}} }}{{\text{E}}}$$

(18)

Residual stresses are not incorporated in the numerical models as they have been shown to have minimal influence in these types of arrangements (Cruise & Gardner, 2008). On the other hand, local geometric imperfections can significantly influence the structural behaviour of stainless steel thin-walled members, especially the ultimate post range, and therefore are included in the numerical model. The initial local geometric imperfection distribution pattern for each CHS stub column is taken as the corresponding lowest elastic critical local buckling mode shape under axial compression. Three initial local imperfection amplitudes, defined as t/10, t/100 and t/200, respectively, are used to scale the imperfection patterns and determine the most suitable imperfection values.

Table 2 presents the simulated load capacity (N_u,FE) for each of the tests conducted by He et al. (2019), for the three different initial imperfection values, presented as a ratio of N_u,FE to N_u,test, for ease of comparison. The precision of the numerical model in replicating the overall behaviour is assessed by comparing the full load-deformation behaviour as well as the failure modes obtained from the tests with those derived from the numerical simulations. As such, Fig. 3 compares the axial load versus end shortening responses derived from both the tests and the numerical model for (a) the D89-T800 and (b) the D89-T1000 CHS stub columns. These tests are selected for demonstration purposes and are representative of the comparisons for all of the simulations. The numerical model is observed to provide an accurate depiction of the load-deformation history of the stainless steel CHS columns. The failure loads obtained from the FE models with various initial imperfection values are compared with the corresponding experimental results in Table 2. It is evident that the FE models with all three of the considered imperfection amplitudes (ranging from t/10 to t/200) generally yield comparable failure loads to N_u,test, whilst the best predictions in terms of the load-end shortening response were captured for an the imperfection value of t/100. The failure modes from the numerical studies are also in good agreement with those from experiments, as shown in Fig. 4. There are some relatively small discrepancies between the experimental and numerical values as well as in the overall behaviour and these are most likely due to differences in the geometric and imperfection values used in the model compared with the physical specimens, and also the use of idealised boundary conditions in the model. In addition, with post-fire testing, there are many factors and variables which can occur during the test and these are not easy to measure or simulate accurately. Nevertheless, the key conclusion is that the FE model can capture the overall behaviour and provide a realistic estimation of the ultimate strength of hollow section. Based on these observations, it is concluded that the FE model offers a good simulation for stainless steel CHS stub columns under a homogenous temperature condition.

Fig. 3

Comparison of the experimental and numerical load–deflection responses for a CHS D89-T800 and b CHS D89-T1000 (He et al., 2019)

Fig. 4

Comparison of the test and FE failure modes for a CHS D89-T800 and b CHS D89-T1000 stub columns (He et al., 2019)

4 Behaviour of stainless steel stub columns at elevated temperature

4.1 General

The FE model is employed in this section to examine the cross-sectional response of CHS stainless steel stub columns at varying degrees of elevated temperature. For this study, the columns are modelled isothermally, in which the stress–strain data corresponding to a given temperature θ is assigned to the model, and the compressive load is then applied until failure is reached, similar to the validated approach previously described. As stated before, the focus of this paper is the behaviour of duplex and ferritic stainless steel CHS stub columns at elevated temperature, as these have not previously been studied. Austenitic stainless steels are also included in the analyses, for comparison.

The room temperature material properties recommended by Afshan et al. (2019) for austenitic, duplex and ferritic stainless steel are implemented in the model, and the key material properties are presented in Table 3. For each stainless steel grade considered, the cross-sections are classified as fully effective (Class 1) to slender (Class 4), in accordance with the EN 1993-1-4 (2015) limits at both ambient and elevated temperatures, and the columns are modelled with five different temperatures ranging between 20 °C and 800 °C. In total, sixty CHS stub columns were modelled, meaning for each grade five columns were classified for Class 1, 2, 3 and 4 with respect to their target temperature i.e. 20°, 200 °C, 400 °C, 600 °C and 800 °C.

Table 3 Room temperature material properties adopted in the parametric models

At elevated temperature, the reduction factors for austenitic, duplex and ferritic grades are taken from the SCI Design Manual for Structural Stainless Steel (2017), which are the most up-to-date set of reduction factors for stainless steel materials. They are applied to the nominal properties provided in Table 3 using the values presented in Tables 4, 5 and 6 for austenitic, duplex and ferritic stainless steel grades, respectively. The two-stage Ramberg–Osgood material model is employed to develop the full-range stress–strain relationships for the modelled temperatures, as given in Eqs. 14 and 15. The values for n_θ are taken as the room temperature values for n (in accordance with Afshan et al., 2019) and the values for m_θ are determined using Eq. 19 adopted from the SCI Design Manual for Structural Stainless Steel (2017):

$${\text{m}}_{\theta } = 1 + 2.8\left( {\frac{{{\text{f}}_{{0.2,\theta }} }}{{{\text{f}}_{{{\text{u}},\theta }} }}} \right)$$

(19)

Table 4 Summary of the austenitic stainless steel material properties

Table 5 Summary of the duplex stainless steel material properties

Table 6 Summary of the ferritic stainless steel material properties

Similar to the validation models, the initial geometric imperfections are introduced as eigenmodes that are scaled to a suitable magnitude. The local imperfections for CHS stub columns is set to t/100, where t is the thickness of the cross-section. The end support conditions of the columns are modelled as fixed at both ends, allowing longitudinal displacement along the column length.

4.2 Results and analysis

The accuracy of the design methods described earlier in Sect. 2 of this paper are assessed against a large number of FE data obtained from the parametric study. A total of 60 CHS columns are assessed with different cross-sectional geometries to achieve an even distribution of cross-section classifications between Class 1 and Class 4. The sections are classified at elevated temperature in accordance with the procedure outlined in the SCI Design Manual for Structural Stainless Steel (2017) as this is the most up-to-date and specific for stainless steel at elevated temperature.

Figure 5 presents a comparison of the FE compression resistances for austenitic (A), duplex (D) and ferritic (F) stainless steel CHS stub columns at elevated temperature (N_u,FE,θ), normalised by the respective design loads including the (a) Eurocode 3 Part 1–4 capacity, N_u,EC3-1-4,θ (b) Eurocode 3 Part 1–2 resistance, N_u,EC3-1-2,θ (c) ASCE value, N_u,ASCE,θ, (d) Australia and New Zealand standardised resistance, N_u,AUS/NZ,θ and (e) CSM prediction, N_u,CSM,θ. The data is presented against the D/tε_θ² ratios at five different temperatures 20–800 °C. In Fig. 5a, c–e, the cross-sectional yield strength is taken as k_0.2,θf_0.2 whereas in Fig. 5b, the cross-sectional yield strength is taken as k_2.0,θf_0.2. In all cases, the temperature-dependent material factor is determined as ε_θ = ε(k_E,θ/ k_2.0,θ)^0.5. All of the calculations are based on the measured geometric and elevated temperature material properties, and all partial factors are set to unity.

Fig. 5

Assessment of the accuracy of different design methods for stub columns made from austenitic (A), duplex (D) and ferritic (F) stainless steel circular hollow sections including a EN 1993-1-4 (2015), b EN 1993-1-2 (2005) c ASCE (2002), d AS/NZS 4673 (2001) and e the CSM (Buchanan, 2018)

The results indicate that the room temperature design rules given in EN 1993-1-4 (2015) can be safely applied to stainless steel CHS stub columns at all levels of elevated temperature examined in this study. However, the results are unduly conservative and also demonstrate significant scatter. Also, it is shown in Fig. 5a and presented in Table 7 that the mean ratio of FE resistance to the design loads are 1.432, 1.432, 1.074 for CHS stub columns made from austenitic, duplex and ferritic stainless steel, respectively, with corresponding coefficient of variation values (COV) of 0.111, 0.118, 0.065, respectively. This indicates that the members made from austenitic and duplex stainless steel achieve a greater strength overall compared with the design values, due largely to the development of strain hardening in these grades which is not fully accounted for in the codes. On the other hand, the corresponding ratio for the ferritic stainless steel members is lower as these grades behave more similarly to carbon steel with little strain hardening after yielding. This conservatism is mainly due to the fact that the design method ignores any strain hardening in the stainless steel and also employs f_0.2 (or f_0.2,θ at elevated temperature) as the design strength.

Table 7 Comparison of test and FE resistances predictions

On the other hand, with reference to Fig. 5b and the data in Table 7, the fire design method in EN 1993-1-2 (2005) provides equivalent mean N_u,FE,θ/N_u,EC3-1-2,θ ratios of 1.143, 1.185, 1.033 for CHS stub columns made from austenitic, duplex and ferritic stainless steel, respectively, as well as COV values of 0.143, 0.097, 0.067, respectively. This indicates that this method generally provides a safe design for austenitic, duplex and ferritic stainless steel columns in fire with less scatter than for EN 1993-1-4 (2015). This is mainly due to the utilisation of the 2% total strain strength at elevated temperature θ.

With reference to Fig. 5c and the data in Table 7, the American specification (ASCE) provides equivalent mean N_u,FE,θ/N_u,ASCE,θ ratios of 1.427, 1.411, 1.066 for CHS stub columns made from austenitic, duplex and ferritic stainless steel, respectively, as well as COV values of 0.118, 0.132, 0.068, respectively. This indicates that the ASCE design provision (SEI/ASCE-8, 2002) for austenitic, duplex and ferritic stainless steels are generally safe for the design of these members, but again leads to rather conservative and scattered compressive capacities. This is again mainly owing to the use of the 0.2% proof strength as the design strength without taking material strain hardening into account.

The suitability of the Australian/New Zealand AS/NZS 4673 code (2001) for the design of CHS austenitic, duplex and ferritic stainless steel stub columns at elevated temperature is presented in Fig. 5d, together with the data in Table 7. The mean N_u,θ/N_u,AS/NZS,θ ratio in this case is 1.418, 1.409, 1.065 for CHS stub columns made from austenitic, duplex and ferritic stainless steel, respectively, with corresponding COV values of 0.119, 0.133, 0.068. Therefore, this code also provides safe yet conservative predictions of the capacity of stainless steel CHS stub columns, both an ambient and elevated temperatures. The three existing codes are shown to provide conservative yet quite scattered predictions, with the Australian/New Zealand standard giving the most accurate mean resistance results, as demonstrated in Table 7. The main cause for these inaccuracies and scatter is the fact that the codified methods do not account for the additional and significant strength enhancements which occur owing to strain hardening of the stainless steel material at stresses greater than f_0.2. Nevertheless, in general, the existing design methods for CHS stainless steel cross-section are considered to be safe; however, there is scope for improvement and less over-conservatism, which would result in greater material efficiency and more realistic results.

In this context, the CSM compression resistances for CHS stub columns made from austenitic, duplex and ferritic stainless steel at elevated temperatures are also assessed herein. The CSM expressions are applied using the elevated temperature material properties given earlier in this paper to determine N_u,CSM,θ. Figure 5e presents the load capacities reached in the FE model normalised by N_u,CSM,θ (i.e. N_u,FE,θ/N_u,CSM,θ) plotted against the cross-section D/tε² ratios. The results indicate a high level of accuracy and consistency from the CSM compression resistance predictions. The mean N_u,FE,θ/N_u,CSM,θ ratio, as shown in Table 7, is equal to 1.208, 1.204 and 1.043 for CHS stub columns made from austenitic, duplex and ferritic stainless steel, respectively with corresponding COV values of 0.047, 0.065 and 0.035, respectively. This demonstrates that the CSM design method is capable of providing more precise and less scattered capacity predictions for the fire design of these members, compared with the standardised methods in the design codes. This is because the CSM includes a rational consideration of material strain hardening in the design, and generally provides a closer simulation of the real behaviour compared with the standards.

5 Conclusions

This paper presents an investigation of the structural behaviour and fire performance of stub columns made from austenitic, duplex and ferritic stainless steel circular hollow sections. A numerical model is developed using the ABAQUS software and is then validated against available test data, to facilitate this study. The FE-generated CHS stub column data are used to assess the design methods provided in EN 1993-1-4 (2015), EN 1993-1-2 (2005), SEI/ASCE (2002) and AS/NZS 4673 (2001) and it is shown that there is a high level of conservatism and also scatter in the predicted compression resistance values in the codes. The continuous strength method (CSM) is also assessed as a more rational alternative design approach, which allows for exploitation of the material strain hardening properties in calculating the cross-sectional resistance. The results and analysis presented herein indicates that the CSM yields accurate, consistent and reliable compression resistance predictions for austenitic, duplex and ferritic stainless steel CHS stub columns at elevated temperature.