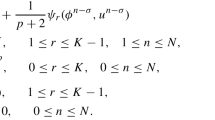1 Introduction

The space-fractional reaction–diffusion equations, in which the integer-order differential operator is replaced by a corresponding fractional one, have gained great popularity due to the wide application in physics [1], finance [2], and biology [3–6]. These new fractional-order models provide a more adequate description of many processes than those of the integer-order for many processes with anomalous diffusion. This is because factional-order operators possess the nonlocal nature property such that the models can describe the phenomena showing the effect of memory and hereditary properties [7].

In this paper, we consider the following two-dimensional space-fractional reaction–diffusion equation

$$ \textstyle\begin{cases} \frac{\partial u}{\partial t}= K_{x} \frac{\partial ^{\alpha _{x}}u}{\partial \vert x \vert ^{\alpha _{x}}}+ K_{y} \frac{\partial ^{\alpha _{y}}u}{\partial \vert y \vert ^{\alpha _{y}}}+F(u), \qquad (x,y) \in \Omega ,\quad t\in (0,T], \\ u(x,y,t)=0,\qquad (x,y)\in \partial \Omega ,\quad t\in (0,T], \\ u(x,y,0)=u_{0}(x,y), \qquad (x,y)\in \overline{\Omega }, \end{cases} $$
(1)

where \(1<\alpha _{x},\alpha _{y}\leq 2\) are the space fractional orders, \(K_{x},K_{y}>0\) are the diffusion constants. The Riesz fractional derivatives \(\frac{\partial ^{\alpha _{x}}u}{\partial |x|^{\alpha _{x}}}\) and \(\frac{\partial ^{\alpha _{y}}u}{\partial |y|^{\alpha _{y}}}\) are defined as follows:

$$\begin{aligned} &\frac{\partial ^{\alpha _{x}}u}{\partial \vert x \vert ^{\alpha _{x}}}= \textstyle\begin{cases} \frac{-1}{2\cos \frac{\pi \alpha _{x}}{2}}({}_{a}{D}_{x}^{ \alpha _{x}}u +{}_{x}{D}_{b}^{\alpha _{x}}u), & 1< \alpha _{x}< 2, \\ \frac{\partial ^{2}u}{\partial x^{2}},& \alpha _{x}=2, \end{cases}\displaystyle \end{aligned}$$
(2)
$$\begin{aligned} &\frac{\partial ^{\alpha _{y}}u}{\partial \vert y \vert ^{\alpha _{y}}}=\textstyle\begin{cases} \frac{-1}{2\cos \frac{\pi \alpha _{y}}{2}}({}_{c}{D}_{y}^{ \alpha _{y}}u +{}_{y}{D}_{d}^{\alpha _{y}}u),& 1< \alpha _{y}< 2, \\ \frac{\partial ^{2}u}{\partial y^{2}},& \alpha _{y}=2, \end{cases}\displaystyle \end{aligned}$$
(3)

where \({}_{a}{D}_{x}^{\alpha _{x}}\) and \({}_{x}{D}_{b}^{\alpha _{x}}\) are left and right Riemann–Liouville fractional derivatives defined as

$$\begin{aligned} &{}_{a}{D}_{x}^{\alpha }u=\frac{1}{\Gamma (2-\alpha )} \frac{\partial ^{2}}{\partial x^{2}} \int _{a}^{x} \frac{u(\xi ,y)}{(\xi -x)^{(\alpha -1)}}\,d\xi ,\\ &{}_{x}{D}_{b}^{ \alpha }u=\frac{1}{\Gamma (2-\alpha )} \frac{\partial ^{2}}{\partial x^{2}} \int _{x}^{b} \frac{u(\xi ,y)}{(x-\xi )^{(\alpha -1)}}\,d\xi. \end{aligned} $$
(4)

Here \(\Gamma (\cdot )\) denotes the standard Gamma function.

Owing to the applications of fractional differential equations in many fields, it is important to seek effective method for these fractional models. The fractional differential equations are solved and analyzed by various analytical methods, such as monotone iterative method [8], Green function method [9], Laplace transform method [10], homotopy perturbation transform method [11], and other methods [12–16]. However, the analytic solutions of special fractional differential equations are in the form of trigonometric series, and it is very difficult to calculate them. For this reason, the study for the numerical methods has become an important research topic that offers great potential.

In recent years, various classical numerical methods have been extended to solve the fractional reaction–diffusion equations, such as the finite difference method (FDM) [17–20], finite element method (FEM) [21–24], and spectral method [25–27]. The finite difference methods are accepted as one of the most popular numerical methods for fractional reaction–diffusion equations because they allow easy implementation. Meerschaert and Tadjeran proposed the first-order shifted Grünwald formula in [18]. Based on the former work, Tian et al. developed weighted shifted Grünwald–Letnikov (WSGD) formulas [20]. Ortigueira firstly proposed the so-called fractional central difference scheme in [19]. Then Çelik and Duman analyzed this approximation and applied it to fractional diffusion equations [17].

The space discretization of fractional reaction–diffusion equation leads to a nonlinear ordinary differential equations (ODEs). Accurate and efficient simulations of such systems have lead many researcher to the design of various time discretization methods. The most notable method among them is the alternating direction implicit (ADI) technique. However, the discretization matrix obtained is full. It means that the Thomas algorithm for tridiagonal matrix is no longer applicable. It also should be noted that the ADI methods are limited to second-order accuracy in time. In this paper, an efficient compact implicit integration factor (cIIF) method [28, 29] is developed. By introducing the compact representation for the matrix approximating the differential operator, the cIIF methods apply matrix exponential operations sequentially in every spatial direction. As a result, exponential matrices which are calculated and stored have small sizes, compared to those in the 1D problem. For two or three dimensions, the cIIF method is more efficient in both storage and CPU cost.

The main contributions of this work are as follows:

  • We provide an efficient approach to compute solutions of the two-dimensional fractional reaction–diffusion equations even with millions of difference points.

  • We prove that the second-order cIIF scheme is stable in the discrete \(L^{2}\)-norm.

  • We prove the second-order convergence of the proposed scheme, and the numerical tests verify the theoretical analysis.

The rest of the paper is organized as follows: In Sect. 2 we present some notations and discretize the two-dimensional fractional reaction–diffusion equations into nonlinear ODEs in matrix formulation. In Sect. 3, we present the cIIF time discretization scheme. In Sect. 4 we compute various fractional reaction–diffusion equations to demonstrate the convergence rates and the efficiency of the proposed scheme. Finally, we summarize our conclusion in Sect. 5.

2 Numerical method

2.1 Compact finite difference method

The computation domain Ω is discretized into grids described by the set \((x_{j},y_{k})=(a+jh_{x},c+kh_{y})\) where \(h_{x}=(b-a)/N_{x}, h_{y}=(d-c)/N_{y}\) and \(0\leq j\leq N_{x}, 0\leq k\leq N_{y}\). We first introduce the second-order WSGD method derived in [20] to approximate the Riemann–Liouville space fractional derivatives. The essential idea of this approximation is using the weighted average to eliminate the low-order leading terms in asymptotic expansions for the truncation errors. The WSGD formulas for the left and right Riemann–Liouville fractional derivatives in the x-direction are defined as

$$ \begin{aligned} &{}_{a}{D}_{x}^{\alpha }u(x_{j},y_{k})= \frac{1}{h_{x}^{\alpha }} \sum_{l=0}^{j+1}\omega _{l}^{(\alpha )}u(x_{j-l+1},y_{k})+o \bigl(h_{x}^{2}\bigr), \\ &{}_{x}{D}_{b}^{\alpha }u(x_{j},y_{k})= \frac{1}{h_{x}^{\alpha }} \sum_{l=0}^{N-j+1}\omega _{l}^{(\alpha )}u(x_{j+l-1},y_{k})+o \bigl(h_{x}^{2}\bigr), \end{aligned} $$
(5)

for \(j=1,\dots ,N_{x}-1, k=1,\dots ,N_{y}-1\). The coefficients \(\omega _{k}^{(\alpha )}\) of the second order in (5) are given as

$$ \omega _{0}^{(\alpha )}=\frac{\alpha }{2}g_{0}^{(\alpha )},\qquad \omega _{l}^{( \alpha )}=\frac{\alpha }{2}g_{l}^{(\alpha )}+ \frac{2-\alpha }{2}g_{l-1}^{( \alpha )},\quad l=1,2,\dots , $$
(6)

with

$$ g_{0}^{(\alpha )}=1,\qquad g_{l}^{(\alpha )}= \biggl(1-\frac{1+\alpha }{l} \biggr)g_{l-1}^{(\alpha )},\quad l=1,2,\dots. $$
(7)

We refer the reader to the paper [20] for the detailed proof of the truncation error expression.

Based on the discretization of Riemann–Liouville fractional derivatives, the Riesz fractional derivatives in the x-direction can be discretized as

$$ \frac{\partial ^{\alpha }u(x_{j},y_{k})}{\partial \vert x \vert ^{\alpha }} = \frac{-1}{2\cos \frac{\pi \alpha }{2}} \bigl({}_{a}{D}_{x}^{ \alpha }u(x_{j},y_{k})+{}_{x}{D}_{b}^{\alpha }u(x_{j},y_{k}) \bigr) =\delta _{x}^{\alpha }u(x_{j},y_{k})+o \bigl(h_{x}^{2}\bigr), $$
(8)

where \(\delta _{x}^{\alpha }u(x_{j},y_{k})= \frac{-1}{2\cos \frac{\pi \alpha }{2}}\frac{1}{h_{x}^{\alpha }} ( \sum_{l=0}^{j+1}\omega _{l}^{(\alpha )}u(x_{j-l+1},y_{k}) + \sum_{l=0}^{N-j+1}\omega _{l}^{(\alpha )}u(x_{j+l-1},y_{k}) )\). Similarly, Riesz fractional derivatives in the y-direction can be discretized as follows:

$$ \frac{\partial ^{\alpha }u(x_{j},y_{k})}{\partial \vert y \vert ^{\alpha }}= \delta _{y}^{\alpha }u(x_{j},y_{k})+o \bigl(h_{y}^{2}\bigr), $$
(9)

where \(\delta _{y}^{\alpha }u(x_{j},y_{k})= \frac{-1}{2\cos \frac{\pi \alpha }{2}}\frac{1}{h_{y}^{\alpha }} ( \sum_{l=0}^{k+1}\omega _{l}^{(\alpha )}u(x_{j},y_{k-l+1}) + \sum_{l=0}^{N-k+1}\omega _{l}^{(\alpha )}u(x_{j+l-1},y_{k}) )\).

Defining the grid function \(U_{j,k}(t)=u(x_{j},y_{k},t)\), the semidiscrete compact difference scheme for problem (1) can be written as

$$ \frac{\partial U_{j,k}(t) }{\partial t} =K_{x}\delta _{x}^{\alpha }U_{j,k}(t) +K_{y}\delta _{y}^{\alpha }U_{j,k}(t) +F \bigl(U_{j,k}(t)\bigr)+R_{j,k}(t), $$

where \(R_{j,k}(t)=O(h^{2})\), \(h=\min \{h_{x},h_{y}\}\), denotes the truncation error in space. Omitting the truncation term \(R_{j,k}(t)\) and replacing the grid function \(U_{j,k}(t)\) with its numerical approximation \(u_{j,k}(t)\), we obtain the following difference scheme:

$$ \frac{\partial u_{j,k}(t)}{\partial t} =K_{x}\delta _{x}^{\alpha }u_{j,k}(t) +K_{y}\delta _{y}^{\alpha }u_{j,k}(t) +F \bigl(u_{j,k}(t)\bigr). $$
(10)

To apply the time discretization method for the ODEs (10), we now rewrite them in a matrix form. Define the numerical solution in the following matrix forms:

$$ \mathbf{U}= \begin{pmatrix} u_{1,1} & u_{1,2} & \ldots & u_{1,N_{y}-1} \\ u_{2,1} & u_{2,2} & \ldots & u_{2,N_{y}-1} \\ \vdots & \vdots & \ddots & \vdots \\ u_{N_{x}-1,1} & u_{N_{x}-1,2} & \ldots & u_{N_{x}-1,N_{y}-1} \end{pmatrix}. $$
(11)

For a solution matrix \(\mathbf{U}\in \mathbb{R}^{N_{x}-1\times N_{y}-1}\), the discrete \(L^{2}\)-norm of U is defined as

$$ \Vert \mathbf{U} \Vert ^{2}=h_{x}h_{y}\sum _{j=1}^{N_{x}-1}\sum_{k=1}^{N_{y}-1} \vert u_{j,k} \vert ^{2}. $$

Then we have

$$ \Vert \mathbf{U} \Vert ^{2}=h_{x}h_{y} \Vert \mathbf{U} \Vert _{F}^{2} ,$$
(12)

where \(\|\mathbf{U}\|_{F}\) is Frobenius norm. The 2-norm for matrix U is defined as \(\|\mathbf{U}\|_{2}=\sigma _{\max }(\mathbf{U})\) where \(\sigma _{\max }(\mathbf{U})\) represents the largest singular value of matrix U. In the case of a normal matrix U, \(\|\mathbf{U}\|_{2}=\lambda _{\max }(\mathbf{U})\), with \(\lambda _{\max }(\mathbf{U})\) being the absolute value of the largest eigenvalue of U.

Then introducing the \(M\times M\) difference matrix \(\mathbf{D}_{M}^{\alpha }\) as follows:

$$ \mathbf{D}_{M}^{\alpha }= \begin{pmatrix} 2\omega _{1}^{(\alpha )} &\omega _{0}^{(\alpha )}+\omega _{2}^{( \alpha )} & \ldots & \omega _{N-1}^{(\alpha )} & \omega _{N}^{(\alpha )} \\ \omega _{0}^{(\alpha )}+\omega _{2}^{(\alpha )} &2\omega _{1}^{( \alpha )} & \omega _{0}^{(\alpha )}+\omega _{2}^{(\alpha )} & \ldots & \omega _{N-1}^{(\alpha )} \\ \vdots & \omega _{0}^{(\alpha )}+\omega _{2}^{(\alpha )} & 2\omega _{1}^{( \alpha )} & \ddots &\vdots \\ \omega _{N-1}^{(\alpha )} & \cdots & \ddots & \ddots & \omega _{0}^{( \alpha )}+\omega _{2}^{(\alpha )} \\ \omega _{N}^{(\alpha )} & \omega _{N-1}^{(\alpha )}& \ldots & \omega _{0}^{( \alpha )}+\omega _{2}^{(\alpha )} & 2\omega _{1}^{(\alpha )} \end{pmatrix}, $$
(13)

the difference scheme (8) and (9) can be written in the following matrix form:

$$ \begin{aligned} &\biggl(\frac{\partial ^{\alpha }U_{j,k}}{\partial \vert x \vert ^{\alpha }} \biggr)_{N_{x}-1,N_{y}-1} =\mathbf{D}_{N_{x}-1}^{\alpha }\mathbf{U}+o \bigl(h_{x}^{2}\bigr), \\ &\biggl(\frac{\partial ^{\alpha }U_{j,k}}{\partial \vert y \vert ^{\alpha }} \biggr)_{N_{x}-1,N_{y}-1} =\mathbf{U} \mathbf{D}_{N_{y}-1}^{\alpha }+o\bigl(h_{y}^{2} \bigr). \end{aligned} $$
(14)

Let \(K_{x}\mathbf{D}_{N_{x}-1}^{\alpha }=\mathbf{A}\) and \(K_{y}\mathbf{D}_{N_{y}-1}^{\alpha }=\mathbf{B}\). Then the ODEs (10) can be written in the following matrix form:

$$ \frac{d \mathbf{U}}{dt}=\mathbf{A}\mathbf{U}+ \mathbf{U}\mathbf{B}+ \mathbf{F}(\mathbf{U}), $$
(15)

where \(\mathbf{F}(\mathbf{U})\) is an \((N_{x}-1)\times (N_{y}-1)\) matrix with each element defined as \(F(u_{j,k})\).

2.2 Compact implicit integration factor method

Now we will apply the cIIF method to solve (15). Assume the final time is \(t=T\) and let time step \(\triangle t=T/N\), \(t_{n}=n\triangle t, 0\leq n< N\). The numerical approximation matrix for \(u_{j,k}(t)\) at time \(t_{n}\) is defined as \(\mathbf{U}_{n}\). To construct the cIIF methods for (15), we multiply it by the integration factor \(e^{-\mathbf{A}t}\) from the left, and by \(e^{-\mathbf{B}t}\) from the right, and then integrate over one time step from \(t_{n}\) to \(t_{n+1}\) to obtain

$$ \begin{aligned} \mathbf{U}_{n+1}={}&e^{\mathbf{A}\triangle t} \mathbf{U}_{n}e^{ \mathbf{B}\triangle t} \\ &{} +e^{\mathbf{A}\triangle t} \biggl( \int _{0}^{\triangle t}e^{- \mathbf{A}\tau }\mathbf{F}\bigl( \mathbf{U}(t_{n}+\tau )\bigr) e^{\mathbf{B}\tau }\,d \tau \biggr) e^{\mathbf{B}\triangle t}. \end{aligned} $$
(16)

Then we approximate the integrand in (16) by using the (\(r-1\))th order Lagrange interpolation polynomial with interpolation points at \(t_{n+1},t_{n},\ldots ,t_{n-r+2}\), namely

$$ \begin{aligned} \mathbf{U}_{n+1}={}&e^{\mathbf{A}\triangle t} \mathbf{U}_{n}e^{ \mathbf{B}\triangle t} \\ &{} +\triangle t \Biggl(\alpha _{1}\mathbf{F}(\mathbf{U}_{n+1})+ \sum_{j=0}^{r-2}\alpha _{-j} e^{(j+1)\mathbf{A}\triangle t } \mathbf{F}(\mathbf{U}_{n-j}) e^{(j+1)\mathbf{B}\triangle t} \Biggr), \end{aligned} $$
(17)

where

$$ \alpha _{-j}=\frac{1}{\Delta t} \int _{0}^{\Delta t}\prod_{ \substack{k=-1\\k\neq i}}^{r-2} \frac{\tau +k\Delta t}{(k-j)\Delta t}\,d \tau ,\quad -1\leq j\leq r-2. $$

The local truncation error is \(O(\Delta t^{r})\). In this paper we use the following second-order compact implicit integration factor (cIIF2) scheme:

$$ \mathbf{U}_{n+1}=e^{\mathbf{A}\triangle t} \biggl( \mathbf{U}_{n}+ \frac{\triangle t}{2} \mathbf{F}(\mathbf{U}_{n}) \biggr)e^{\mathbf{B} \triangle t} +\frac{\triangle t}{2} \mathbf{F}(\mathbf{U}_{n+1}). $$
(18)

The local truncation error for (18) can be written in matrix form as \(\mathbf{E}=(E_{jk})_{N_{x}-1\times N_{y}-1}\) with each element being \(E_{jk}=O(\Delta t^{3}+\Delta th^{2})\).

3 Stability and convergence

We will study the linear stability of the numerical scheme for equation (18) with reaction term \(\mathcal{F}(u)\) satisfying the Lipschitz continuity condition. To obtain the linear stability analysis, we need the following lemmas.

Lemma 3.1

(See [30])

When \(1<\alpha \le 2\), the WSGD operator matrix \(\mathbf{D}_{M}^{\alpha }\) in (13) is a symmetric and negative definite matrix.

Lemma 3.2

Let A and B be arbitrary \(N\times N\) square matrices. We have the following inequalities:

$$ \Vert \mathbf{AB} \Vert _{F}\leq \Vert \mathbf{A} \Vert _{2} \Vert \mathbf{B} \Vert _{F}, \qquad \Vert \mathbf{AB} \Vert _{F}\leq \Vert \mathbf{A} \Vert _{F} \Vert \mathbf{B} \Vert _{2}. $$

Proof

Write the matrix B as \(\mathbf{B}=(\mathbf{b}_{1},\mathbf{b}_{2},\ldots ,\mathbf{b}_{N})\), where the \(\mathbf{b}_{i},i=1,2,\ldots ,N\), are the columns of B. Then we have

$$ \Vert \mathbf{AB} \Vert _{F}^{2} =\sum _{i=1}^{N} \Vert \mathbf{A}\mathbf{b}_{i} \Vert _{2}^{2} \leq \Vert \mathbf{A} \Vert _{2}^{2}\sum_{i=1}^{N} \Vert \mathbf{b}_{i} \Vert _{2}^{2} = \Vert \mathbf{A} \Vert _{2}^{2} \Vert \mathbf{B} \Vert _{F}^{2}. $$

Taking square roots completes the proof. □

Theorem 3.3

Assume that function \(f(u)\) in (1) is globally Lipschitz continuous, i.e., there exists a real constant L such that \(|f(u)-f(v)|\leq L|u-v|\). The fourth-order cFDM coupled with cIIF2 scheme (18) is unconditionally stable in the discrete \(L^{2}\)-norm.

Proof

Assume that \(\mathbf{U}^{1}_{n+1}\) and \(\mathbf{U}^{2}_{n+1}\) are two different solutions of (18) with different initial data sets. Let \(\boldsymbol{\Phi }_{n+1}=\mathbf{U}^{1}_{n+1}-\mathbf{U}^{2}_{n+1}\), then it satisfies

$$ \boldsymbol{\Phi }_{n+1} =e^{\mathbf{A}\triangle t} \bigl(\boldsymbol{ \Phi }_{n}+ \mathbf{F}\bigl(\mathbf{U}^{1}_{n} \bigr)-\mathbf{F}\bigl(\mathbf{U}^{2}_{n}\bigr) \bigr) e^{ \mathbf{B}\triangle t} +\mathbf{F}\bigl(\mathbf{U}^{1}_{n+1}\bigr)- \mathbf{F}\bigl( \mathbf{U}^{2}_{n+1}\bigr). $$
(19)

By Lemma 3.2 and Lipschitz continuity, taking Frobenius norm for (19) results in

$$ \Vert \boldsymbol{\Phi }_{n+1} \Vert _{F} \leq \bigl\Vert e^{\mathbf{A}\triangle t} \bigr\Vert _{2}\biggl(1+ \frac{L\Delta t}{2}\biggr) \Vert \boldsymbol{\Phi }_{n} \Vert _{F} \bigl\Vert e^{\mathbf{B} \triangle t} \bigr\Vert _{2} + \frac{L\Delta t}{2} \Vert \boldsymbol{\Phi }_{n+1} \Vert _{F}. $$
(20)

Since the matrices A and B are negative definite, the eigenvalues of matrix \(e^{\mathbf{A}\triangle t}\) are smaller than 1 such that \(\|e^{\mathbf{A}\triangle t}\|_{2}\leq 1\) and \(\|e^{\mathbf{B}\triangle t}\|_{2}\leq 1\). We get the following result from (20):

$$ \Vert \boldsymbol{\Phi }_{n+1} \Vert _{F}\leq \biggl( \frac{1+\frac{L\triangle t}{2}}{1-\frac{L\triangle t}{2}} \biggr) \Vert \boldsymbol{\Phi }_{n} \Vert _{F}. $$
(21)

With time iterations, we have

$$ \Vert \boldsymbol{\Phi }_{n} \Vert _{F}\leq \biggl( \frac{1+\frac{L\triangle t}{2}}{1-\frac{L\triangle t}{2}} \biggr)^{n} \Vert \boldsymbol{\Phi }_{0} \Vert _{F}. $$
(22)

From the above result (22), it can be concluded that

$$ \Vert \boldsymbol{\Phi }_{n} \Vert _{F}\leq \biggl( \frac{1+\frac{L\triangle t}{2}}{1-\frac{L\triangle t}{2}} \biggr)^{n} \Vert \boldsymbol{\Phi }_{0} \Vert _{F} = \biggl(\frac{1+\frac{L\triangle t}{2}}{1-\frac{L\triangle t}{2}} \biggr)^{\frac{T}{\Delta t}} \Vert \boldsymbol{\Phi }_{0} \Vert _{F}. $$
(23)

Then (23) yields the following result:

$$ \Vert \boldsymbol{\Phi }_{n} \Vert _{F}\leq 2e^{LT} \Vert \boldsymbol{\Phi }_{0} \Vert _{F}. $$
(24)

Now we complete the proof by (12). □

Theorem 3.4

Assume that function \(f(u)\) in (1) is globally Lipschitz continuous. The fourth-order cFDM coupled with cIIF2 scheme (18) converges to the solution of fractional problem (1) with order of \(O(\Delta t^{2}+h^{4})\) in the discrete \(L^{2}\)-norm.

Proof

We denote by \(\boldsymbol{\widetilde{U}}\) and U the exact value and the approximation of solution matrix of (1), respectively. Substituting \(\boldsymbol{\widetilde{U}}\) into (18), we have

$$ \boldsymbol{\widetilde{U}}_{n+1}=e^{\mathbf{A}\triangle t} \biggl( \boldsymbol{\widetilde{U}}_{n}+\frac{\triangle t}{2} \mathbf{F}( \mathbf{ \widetilde{U}}_{n}) \biggr)e^{\mathbf{B}\triangle t} + \frac{\triangle t}{2} \mathbf{F}(\boldsymbol{\widetilde{U}}_{n+1})+ \mathbf{E}, $$
(25)

where \(\mathbf{E}=(E_{jk})_{N_{x}-1\times N_{y}-1}\) and \(E_{jk}=O(\Delta t^{3}+\Delta th^{4})\). Denote \(\boldsymbol{\Psi }=\boldsymbol{\widetilde{U}}-\mathbf{U}\). Subtracting (25) from (18) yields the following error equation:

$$ \boldsymbol{\Psi }_{n+1}=e^{\mathbf{A}\triangle t} \biggl(\boldsymbol{ \Psi }_{n}+ \frac{\triangle t}{2} \bigl(\mathbf{F}(\mathbf{ \widetilde{U}}_{n})- \mathbf{F}(\mathbf{U}_{n})\bigr) \biggr)e^{\mathbf{B}\triangle t} + \frac{\triangle t}{2} \bigl(\mathbf{F}(\mathbf{ \widetilde{U}}_{n+1})- \mathbf{F}(\mathbf{U}_{n+1}) \bigr)+ \mathbf{E}. $$
(26)

It is obvious that \(\boldsymbol{\Psi }_{0}=0\) for the initial condition. Taking Frobenius norm for (26) and applying Theorem 3.3, we obtain

$$ \begin{aligned} \Vert \boldsymbol{\Psi }_{n+1} \Vert _{F} \leq{}& \bigl\Vert e^{\mathbf{A}\triangle t} \bigr\Vert _{2}\biggl(1+ \frac{L\Delta t}{2}\biggr) \Vert \boldsymbol{\Psi }_{n} \Vert _{F} \bigl\Vert e^{\mathbf{B} \triangle t} \bigr\Vert _{2}\\ &{} + \frac{L\Delta t}{2} \Vert \boldsymbol{\Psi }_{n+1} \Vert _{F}+C \Delta t(N_{x}-1) (N_{y}-1) \bigl(\Delta t^{2}+h^{4}\bigr), \end{aligned} $$
(27)

by Lipschitz continuity. Here C denotes a positive constant independent of discretization parameters, which may take different values at different occurrences. As in the proof of Theorem 3.3, we have

$$ \Vert \boldsymbol{\Psi }_{n+1} \Vert _{F}\leq \biggl( \frac{1+\frac{L\triangle t}{2}}{1-\frac{L\triangle t}{2}} \biggr) \Vert \boldsymbol{\Psi }_{n} \Vert _{F}+\frac{C\Delta t}{1-\frac{L\triangle t}{2}}(N_{x}-1) (N_{y}-1) \bigl( \Delta t^{2}+h^{4}\bigr). $$
(28)

As time evolves, we have

$$\begin{aligned} \Vert \boldsymbol{\Psi }_{n} \Vert _{F}&\leq \biggl( \frac{1+\frac{L\triangle t}{2}}{1-\frac{L\triangle t}{2}} \biggr)^{n} \Vert \boldsymbol{\Psi }_{0} \Vert _{F}+\sum_{k=1}^{n} \biggl( \frac{1+\frac{L\triangle t}{2}}{1-\frac{L\triangle t}{2}} \biggr)^{k}C \Delta t(N_{x}-1) (N_{y}-1) \bigl(\Delta t^{2}+h^{4}\bigr) \\ &\leq \biggl( \frac{1+\frac{L\triangle t}{2}}{1-\frac{L\triangle t}{2}} \biggr)^{n}Cn \Delta t(N_{x}-1) (N_{y}-1) \bigl(\Delta t^{2}+h^{4} \bigr) \\ &\leq CT(N_{x}-1) (N_{y}-1) \bigl(\Delta t^{2}+h^{4}\bigr). \end{aligned}$$

Multiplying by \(h_{x}h_{y}\) on both sides of the above inequality, we get \(\|\boldsymbol{\Psi }_{n}\|\leq CT(b-a)(d-c)(\Delta t^{2}+h^{4})\). This completes the proof. □

4 Numerical experiments

In this section, we will demonstrate the performance of the proposed scheme on some test problems. Firstly, in order to verify our theoretical analysis, we test our scheme for a nonlinear reaction–diffusion equation with exact solution. Then we apply the scheme to the two-dimensional space Riesz fractional Fitzhugh–Nagumo model which represents one of the simplest models for studying excitable media. In all the numerical experiments, we used a uniform spatial step size along each direction, i.e., \(h_{x}=h_{y}=h\). All the computations were performed in Matlab based on a ThinkPad desktop with i3-3110 CPU and 4 GB memory.

Example 1

We consider the following nonlinear reaction–diffusion equation on a square \(\Omega =[0,1]^{2}\):

$$ \textstyle\begin{cases} \frac{\partial u}{\partial t}= K \frac{\partial ^{\alpha _{x}}u}{\partial \vert x \vert ^{\alpha _{x}}}+ K \frac{\partial ^{\alpha _{y}}u}{\partial \vert y \vert ^{\alpha _{y}}}+F(u)+f(x,y,t), \qquad (x,y)\in \Omega ,\quad t\in (0,T], \\ u(x,y,t)=0, \qquad (x,y)\in \partial \Omega , \quad t\in (0,T], \\ u(x,y,0)=x^{2}(1-x)^{2}y^{2}(1-y)^{2}, \qquad (x,y)\in \overline{\Omega }, \end{cases} $$
(29)

with \(F(u)=-u^{2}\). The exact solution of this equation is \(u=e^{-t}x^{2}(1-x)^{2}y^{2}(1-y)^{2}\). The final computation time is \(T=1\). The function \(f(x,y,t)\) is determined by the exact solution. For details of \(f(x,y,t)\), please refer to [31].

We use the second-order WSGD method coupled with cIIF scheme to demonstrate the accuracy of space and time discretization. The orders of convergence in space and time are computed as \(q=\log _{2} (e(h)/e(h/2) )\) and \(p=\log _{2} (e(\tau )/e(\tau /2) )\), respectively. Table 1 displays the \(L^{2}\) errors of the WSGD scheme with different values of \(\alpha _{x}\) and \(\alpha _{y}\). The order of convergence is computed using a very small time step \(\Delta t=1\mathrm{E}-3\). In Table 2, the temporal errors and convergence order of the cIIF2 scheme are given for different time steps and \(\alpha _{x}\) and \(\alpha _{y}\), with \(h=1/256\). From Tables 1 and 2, we conclude that the convergence rate in space and time is of second order. The numerical results are well in line with the theoretical analysis.

Table 1 Error, order of accuracy with different values of \(\alpha _{x}\) and \(\alpha _{y}\) for Example 1
Full size table
Table 2 The temporal errors and convergence order for CIIF2 scheme in Example 1
Full size table

Example 2

Consider the following space fractional Fitzhugh–Nagumo model on a square \(\Omega =[0,2.5]^{2}\):

$$ \textstyle\begin{cases} \frac{\partial u}{\partial t}= K_{x} \frac{\partial ^{\alpha _{x}}u}{\partial \vert x \vert ^{\alpha _{x}}}+ K_{y} \frac{\partial ^{\alpha _{y}}u}{\partial \vert y \vert ^{\alpha _{y}}}+u(1-u)(u-\mu)-w,\quad (x,y)\in \Omega , t\in (0,T], \\ \frac{\partial w}{\partial t}=\varepsilon (\beta u-\gamma w-\delta ), \quad (x,y)\in \Omega , t\in (0,T], \end{cases} $$
(30)

with \(\mu =0.1,\varepsilon =0.01,\beta =0.5,\gamma =1\), and \(\delta =0\). The Fitzhugh–Nagumo model is used to describe the propagation of the transmembrane potential in the nerve axon. The initial conditions in this example are taken as

$$ \begin{aligned} &u(x,y,0)=\textstyle\begin{cases} 1, &(x,y)\in (0,1.25]\times (0,1.25], \\ 0, &\text{elsewhere,} \end{cases}\displaystyle \\ &w(x,y,0)=\textstyle\begin{cases} 0, &(x,y)\in (0,2.5)\times (0,1.25), \\ 0.1, &(x,y)\in (0,2.5)\times [1.25,2.5), \end{cases}\displaystyle \end{aligned} $$
(31)

with homogeneous Dirichlet boundary condition.

The Fitzhugh–Nagumo model can generate the stable patterns in the form of spiral waves. Initially, we set the state in the lower-left quarter of the domain as \(u=1\) and in the upper-half part as \(w=0.1\). Then the trivial state \((u,w)=(0,0)\) was perturbed and further curved and rotated clockwise, generating the spiral pattern.

In our simulation, the computation domain is discretised using \(N_{x}=N_{y}=256\) points in each spatial coordinate. The time step is chosen as \(\Delta t=0.2\) and the final time is set to be \(T=1000\). We first consider the integer-order Fitzhugh–Nagumo model (i.e., \(\alpha _{x}=\alpha _{y}=2\)). The spiral wave solutions for two diffusion coefficients \(K_{x}=K_{y}=1\mathrm{E}-4\) and \(K_{x}=K_{y}=1\mathrm{E}-5\) are shown in Fig. 1. We find that the number of wavefronts increases with decreasing the diffusion coefficient. Keeping the coefficients \(K_{x}=K_{y}=1\mathrm{E}-4\) and reducing the fractional powers \(\alpha _{x}\) and \(\alpha _{y}\), we then get the stable rotating solution for \(\alpha _{x}=\alpha _{y}=1.8 \) (Fig. 2(a)) and \(\alpha _{x}=\alpha _{y}=1.5\) (Fig. 2(b)). As expected, the width of the excitation wavefront (red areas) reduces with decreasing \(\alpha _{x}\) and \(\alpha _{y}\), so does the number of the wavefronts. However, it is noted that the role of reducing the fractional power is not equivalent to the influence of a decreased diffusion coefficient in the integral order case. This can be clearly observed by comparing Figs. 1 and 2.

Figure 1
figure 1

Solutions of Example 2 with \(\alpha _{x}=\alpha _{y}=2\) for varying diffusion coefficient: (a) \(K_{x}=K_{y}=1\mathrm{E}-4\) and (b) \(K_{x}=K_{y}=1\mathrm{E}-5\)

Full size image
Figure 2
figure 2

Solutions of Example 2 with \(K_{x}=K_{y}=1\mathrm{E}-4\) for varying fractional power: (a) \(\alpha _{x}=\alpha _{y}=1.8\) and (b) \(\alpha _{x}=\alpha _{y}=1.5\)

Full size image

We take the different diffusion coefficients in the x- and y-directions as \(K_{x}=1\mathrm{E}-4, K_{y}=2.5\mathrm{E}-5\). Figure 3(a) displays the wave propagation at \(T=1000\). The smaller diffusion coefficient in the y-direction leads to an elliptical pattern. Next we consider the anisotropic fractional power \(\alpha _{x}=2, \alpha _{y}=1.7\) with \(K_{x}=K_{y}=1\mathrm{E}-4\). A similar pattern is displayed in Fig. 3(b), showing that the superdiffusion effect in the y-direction causes a similar elliptic spiral wave.

Figure 3
figure 3

Solutions of Example 2 for varying diffusion coefficient and fractional power: (a) \(\alpha _{x}=\alpha _{y}=2\) and \(K_{x}=1\mathrm{E}-4, K_{y}=2.5\mathrm{E}-5\), (b) \(\alpha _{x}=2, \alpha _{y}=1.7\) and \(K_{x}=K_{y}=1\mathrm{E}-4\)

Full size image

5 Concluding remarks

In this paper, the weighted shifted Grünwald difference method is developed to solve the two-dimensional Riesz space fractional nonlinear reaction–diffusion equation, in which the temporal component is discretized by the compact implicit integration factor method. The advantage of the method is that computing exponentials of large matrices is reduced to the computation of exponentials of matrices of significantly smaller sizes. The stability and convergence are strictly proven, which shows that the compact implicit integration factor method is stable in \(L^{2}\)-norm and convergent with second-order accuracy. The WSGD method coupled with cIIF method is applied to solve the fractional Fitzhugh–Nagumo model. Numerical experiments are provided to verify the theoretical analysis. The numerical results confirm that the proposed method is a powerful and reliable method for the fractional reaction–diffusion equations. Given its efficiency and good stability conditions, the cIIF method can be extended to the fourth-order fractional parabolic equations (e.g., Cahn–Hilliard equations), which will also be further explored in the future work.