Rayleigh–Bénard Instability of an Ellis Fluid Saturating a Porous Medium

Abstract

The Ellis model describes the apparent viscosity of a shear–thinning fluid with no singularity in the limit of a vanishingly small shear stress. In particular, this model matches the Newtonian behaviour when the shear stresses are very small. The emergence of the Rayleigh–Bénard instability is studied when a horizontal pressure gradient, yielding a basic throughflow, is prescribed in a horizontal porous layer. The threshold conditions for the linear instability of this system are obtained both analytically and numerically. In the case of a negligible flow rate, the onset of the instability occurs for the same parametric conditions reported in the literature for a Newtonian fluid saturating a porous medium. On the other hand, when high flow rates are considered, a negligibly small temperature difference imposed across the horizontal boundaries is sufficient to trigger the convective instability.

1 Introduction

The investigation of the threshold conditions for the onset of buoyancy–driven convection of non–Newtonian fluids is a research topic that displayed a significant development in the last decades (Shenoy 1994; Nield and Bejan 2017). The analysis of thermal instability in porous media saturated by viscous non–Newtonian fluids is of great importance for its applications in several engineering, biomedical and geophysical areas. Examples are the extraction of crude oils either onshore or offshore, blood perfusion in biological tissues, as well as the design of food industry processes. Among non–Newtonian fluids, the shear–thinning also well–known as pseudoplastic fluids are extremely common. Pseudoplastic fluids are important for different research areas. For instance, polymer solutions display shear–thinning behaviour. The same happens for some biological fluids like blood and a significant number of liquid foods (Shenoy 1994).

The viscosity of pseudoplastic fluids is often described by employing the Ostwald–De Weale (power–law) model. The drawback of this model is in its singular behaviour for negligibly small shear stresses. In fact, for this particular case, the power–law model predicts that pseudoplastic fluids display an infinite apparent viscosity (Bird 1965). The Ellis model is employed to overcome this issue. This rheological model yields the Newtonian viscosity when the shear stresses applied to the shear–thinning fluid are extremely small (Bird et al. 1987). The Ellis model is a three–parameter rheological model where the law establishing the relationship between stress and strain depends on the power–law index n, on the reference apparent viscosity $\eta _0$ and reference shear stress $\tau _0$. The latter parameter is the shear stress value corresponding to a halved apparent viscosity $\eta =\eta _0/2$.

A version of the Rayleigh–Bénard problem for a Newtonian fluid saturating a porous medium has been widely studied over the last fifty years starting from the pioneering papers by Horton and Rogers (1945), and by Lapwood (1948). Prats (1966) extended such studies by including a horizontal throughflow across the porous medium. In recent years, the analysis of the Rayleigh–Bénard instability in a porous medium has been further developed to the case where a power–law fluid saturates the solid matrix (Barletta and Nield 2011; Alves and Barletta 2013).

The analysis presented in this paper is aimed to study the threshold conditions for the onset of buoyancy–driven convection in shear–thinning fluids saturating a porous medium. Since the stresses involved at onset of thermal instability may be negligibly small, the Ellis model will be employed. More precisely, the Rayleigh–Bénard instability will be analysed when an Ellis fluid saturates a horizontal porous layer. Isothermal impermeable boundaries kept at different temperatures are envisaged providing a heating–from–below condition. In perspective, the results of this study are important as they can be suitable for an experimental validation by using, for instance, a Hele–Shaw cell system (Celli et al. 2017). In fact, the most unstable rolls for shear–thinning fluids were predicted to be transverse (Barletta and Nield 2011; Celli and Barletta 2018), by employing a power–law model.

2 Mathematical Modelling

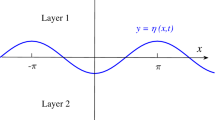
The height of the horizontal porous layer is H, and the boundaries of the layer are impermeable and isothermal such that a heating–from–below configuration is present. The lower boundary is held at temperature $T_0 + \varDelta T$ (with $\varDelta T>0$), while the upper boundary is held at temperature $T_0$, as displayed in Fig. 1. A basic throughflow is imposed by prescribing a horizontal pressure gradient. Since a non–Newtonian extension of Darcy’s law is employed, a flat basic velocity profile (plug flow) is obtained.

Fig. 1

Sketch of the porous layer heated from below with horizontal throughflow

2.1 The Ellis Model

The rheological Ellis model defines the apparent viscosity $\eta$ of the non–Newtonian shear–thinning fluid as reported in Savins (1969), namely

$$\begin{aligned} \eta =\dfrac{\eta _0}{1+\left( \dfrac{\tau }{\tau _0}\right) ^{\frac{1-n}{n}} }, \end{aligned}$$

(1)

where n is a positive parameter such that $0<n<1$, $\tau _0$ represents the value of $\tau$ at which the apparent viscosity drops by half its reference value $\eta _0$, $\tau$ is the scalar quantity

$$\begin{aligned} \tau =\sqrt{\dfrac{{\varvec{\tau }}: {\varvec{\tau }}}{2}}. \end{aligned}$$

(2)

Here ${\varvec{\tau }}$ is the shear stress tensor and ${\varvec{\tau }}: {\varvec{\tau }}=\tau _{ij} \tau _{ij}$, where the Einstein notation for the sum over repeated indices is implied. The behaviour of the viscosity ratio $\eta /\eta _0$ versus the shear stress ratio $\tau /\tau _0$ for different values of n is reported in Fig. 2 together with the behaviour of $\eta /\eta _0$ versus n for different values of $\tau /\tau _0$. The apparent viscosity obtained by employing the Ellis model for the limiting cases $\tau _0 \rightarrow 0$, $\tau _0 \rightarrow \infty$, $n\rightarrow 0$, $n \rightarrow 1$ is presented in Table 1.

On the other hand, when the fluid undergoes intense shear stresses, $\tau \gg \tau _0$, Eq. (1) simplifies to

$$\begin{aligned} \eta =\eta _0\left( \dfrac{\tau }{\tau _0}\right) ^{\frac{n-1}{n}} . \end{aligned}$$

(3)

Table 1 Apparent viscosity for some limiting cases

2.1.1 Ellis Model and Power–Law Model

The power–law fluid model prescribes that the apparent viscosity of the fluid be the following function of the shear stress:

$$\begin{aligned} \eta =\chi ^{\frac{1}{n}} \, \tau ^{\frac{n-1}{n}}, \end{aligned}$$

(4)

where $\chi$ is the consistency factor and n is the power–law index. The limiting case described in Eq. (3) thus coincides with the power–law model Eq. (4) if one defines $\chi =\eta _0^n \, \tau _0^{1-n}$.

Fig. 2

Values of $\eta /\eta _0$ versus $\tau /\tau _0$ for different values of n, left–hand frame. Values of $\eta /\eta _0$ versus n for different values of $\tau /\tau _0$, right–hand frame

2.2 Modified Darcy’s Law for an Ellis Fluid

The momentum balance equation for a Newtonian fluid saturating a porous medium is Darcy’s law, namely

$$\begin{aligned} \mathbf {u} =\dfrac{K}{\eta } \,\mathbf {f}_d, \end{aligned}$$

(5)

where $\mathbf {u}$ is the filtration velocity vector of components (u, v), K is the permeability of the porous medium, and $\mathbf {f}_d$ is the drag force defined as follows:

$$\begin{aligned} \mathbf {f}_d=- {\varvec{\nabla }}p - \rho _0 \, \mathbf {g} \, \beta \, ( T-T_0). \end{aligned}$$

(6)

In Eq. (6), the Oberbeck–Boussinesq approximation is invoked, p is the pressure head, $\rho _0$ is the fluid density evaluated at the reference temperature $T_0$, $\mathbf {g}$ is the gravity acceleration vector, and $\beta$ is the thermal expansion coefficient of the fluid. A modified Darcy’s law that describes a porous medium saturated by an Ellis fluid has been proposed by Sadowski and Bird (1965), as well as by Sadowski (1965), namely

$$\begin{aligned} \mathbf {u} =\dfrac{K}{\eta _0} \left( 1 + A\, |\mathbf {f}_d|^{\frac{1-n}{n} } \right) \mathbf {f}_d, \end{aligned}$$

(7)

where A is a fluid property $[(\mathrm{Pa/m})^{1-1/n}]$. Sadowski and Bird (1965) propose, for a porous bed with average pore diameter $D_p$, the relationship

$$\begin{aligned} A=\frac{4\, n}{3 \, n +1}\,\left( \frac{D_p }{\tau _0}\right) ^{\frac{1-n}{n}}. \end{aligned}$$

(8)

In the limiting case of $A |\mathbf {f}_d|^{1/n-1} \ll 1$, that is when negligible drag forces are acting on the fluid, Eq. (7) matches Darcy’s law (5). It is worth noting that at the onset of natural convection the intensity of the drag forces may be negligibly small.

2.3 Governing Equations

The governing equations describing the problem here presented are

$$\begin{aligned}&{{\overline{{\varvec{\nabla }}}}} \varvec{\cdot }\overline{\mathbf {u}} = 0,\nonumber \\&\frac{\eta _0}{K}\; \overline{\mathbf {u}} = \left( 1 + A\, |\overline{\mathbf {f}}_d|^{\frac{1-n}{n}} \right) \overline{\mathbf {f}}_d ,\nonumber \\&{\overline{\mathbf {f}}_d=- {{\overline{{\varvec{\nabla }}}}} {\overline{p}} - \rho _0 \, \mathbf {g} \, \beta \, ( {\overline{T}}-T_0),}\nonumber \\&\sigma \, \frac{\partial \overline{T}}{\partial \overline{t}} + \overline{\mathbf {u}} \varvec{\cdot }{{\overline{{\varvec{\nabla }}}}} {\overline{T}} = \alpha \, {{\overline{\nabla }}}^2 {\overline{T}},\nonumber \\&{\overline{y}}=0 : \qquad {\overline{v}} = 0, \quad {\overline{T}} = T_0 + \varDelta T, \nonumber \\&{\overline{y}}=H : \qquad {\overline{v}} = 0, \quad {\overline{T}} = T_0 , \end{aligned}$$

(9)

where the bars over the quantities identify dimensional fields, coordinates and time, $\sigma$ is the ratio between the average volumetric heat capacity of the porous medium and the volumetric heat capacity of the fluid, and $\alpha$ is the average thermal diffusivity of the saturated porous medium. The following scaling allows us to express Eq. (9) in a dimensionless formulation:

$$\begin{aligned}&\mathbf {x}=\frac{\overline{\mathbf {x}}}{H}, \quad \mathbf {u}=\dfrac{H}{\alpha }\overline{\mathbf {u}}, \quad p = \dfrac{K}{\eta _0 \, \alpha }{\overline{p}} ,\quad t = \dfrac{\alpha }{\sigma H^2} {\overline{t}}, \quad T=\dfrac{{\overline{T}}- T_0}{\varDelta T }, \end{aligned}$$

(10)

where $\mathbf {x}$ is the Cartesian position vector of components (x, y, z). By substituting Eq. (10) into Eqs. (9) one may write

$$\begin{aligned}&{\varvec{\nabla }}\varvec{\cdot }\mathbf {u} = 0, \end{aligned}$$

(11a)

$$\begin{aligned}&\mathbf {u}= \left( 1+\mathrm {El}\, |\mathbf {f}_d|^{\frac{1-n}{n}} \right) \mathbf {f}_d , \end{aligned}$$

(11b)

$$\begin{aligned}&\frac{\partial {T}}{\partial {t}} + \mathbf {u} \varvec{\cdot }{\varvec{\nabla }}T = \nabla ^2 T, \end{aligned}$$

(11c)

$$\begin{aligned}&y=0 : \qquad v = 0, \quad T = 1, \end{aligned}$$

(11d)

$$\begin{aligned}&y=1 : \qquad v = 0, \quad T = 0 , \end{aligned}$$

(11e)

where

$$\begin{aligned} \mathbf {f}_d= - {\varvec{\nabla }}p +\mathrm {R}\, T\, \mathbf {e}_y. \end{aligned}$$

(12)

The parameter $\mathrm {El}$ is the Darcy–Ellis number and the parameter $\mathrm {R}$ is the Darcy–Rayleigh number. They are defined as follows:

$$\begin{aligned} \mathrm {El}=A\left( \dfrac{\alpha \, \eta _0}{H \, K}\right) ^{\frac{1-n}{n}}, \qquad \mathrm {R}=\dfrac{\rho \, g \, \beta \, H \, K \, \varDelta T}{\alpha \, \eta _0}. \end{aligned}$$

(13)

2.4 Basic State

The stationary solution of Eqs. (11) employed for the stability analysis is composed by a fully developed basic flow along the horizontal direction and a purely vertical constant temperature gradient. The horizontal flow is assumed to be generated by a prescribed pressure gradient, which is independent of the x and z coordinates, such that

$$\begin{aligned}&u_b =-\frac{\partial {p_b}}{\partial {x}}\left( 1+\mathrm {El}\, \left| \frac{\partial {p_b}}{\partial {x}}\right| ^{\frac{1-n}{n}} \right) , \quad v_b=0, \nonumber \\&w_b=0, \quad \frac{\partial {p_b}}{\partial {y}}=\mathrm {R}\, T_b, \quad \frac{\partial {p_b}}{\partial {z}}=0,\quad T_b = 1 - y , \end{aligned}$$

(14)

where the subscript b denotes the basic state fields. It is not restrictive to assume that $\partial {p_b}/\partial {x}\leqslant 0$ so that $u_b \geqslant 0$. By taking the average value of the velocity profile, one obtains the definition of the Péclet number, namely

$$\begin{aligned}&\mathrm {Pe}=\int _0^1 u_b \, \mathrm {d}y \qquad \longrightarrow \qquad \mathrm {Pe}=\left| \frac{\partial {p_b}}{\partial {x}}\right| \left( 1+\mathrm {El}\, \left| \frac{\partial {p_b}}{\partial {x}}\right| ^{\frac{1-n}{n}} \right) . \end{aligned}$$

(15)

For $\mathrm {El}\rightarrow 0$ with $|\partial {p_b}/\partial {x}|\ne 0$ one may simplify Eqs. (11) and (14) to obtain the basic state employed by Prats (1966). For $\mathrm {El}\rightarrow 0$ with $|\partial {p_b}/\partial {x}|=0$ Eqs. (11) and (14) yields the basic state employed by Horton and Rogers (1945) and Lapwood (1948).

2.5 Linear Stability Analysis

By employing Eq. (11a) and by applying the divergence operator to Eq. (11b), we can express Eqs. (11) according to a pressure–temperature formulation,

$$\begin{aligned}&{\varvec{\nabla }}\varvec{\cdot }\left[ \left( 1+\mathrm {El}\, |\mathbf {f}_d|^{\frac{1-n}{n}} \right) \mathbf {f}_d \right] =0 , \end{aligned}$$

(16a)

$$\begin{aligned}&\frac{\partial {T}}{\partial {t}} +\left[ \left( 1+\mathrm {El}\, |\mathbf {f}_d|^{\frac{1-n}{n}} \right) \mathbf {f}_d \right] \varvec{\cdot }{\varvec{\nabla }}T = \nabla ^2 T, \end{aligned}$$

(16b)

$$\begin{aligned}&{\mathbf {f}_d= - {\varvec{\nabla }}p +\mathrm {R}\, T\, \mathbf {e}_y,} \end{aligned}$$

(16c)

$$\begin{aligned}&y=0 : \qquad \frac{\partial {p}}{\partial {y}} = R, \quad T = 1, \end{aligned}$$

(16d)

$$\begin{aligned}&y=1 : \qquad \frac{\partial {p}}{\partial {y}} = 0, \quad T = 0 , \end{aligned}$$

(16e)

where the impermeability conditions in Eqs. (11d) and (11e) result into pressure conditions, Eqs. (16d) and (16e). The system (16) is perturbed by defining the pressure and temperature fields as composed by a basic state plus small–amplitude disturbances expressed in terms of normal modes, namely

$$\begin{aligned}&p (x,y,z,t)= p_b(y) + \varepsilon \, f(y)\, e^{\lambda \, t } e^{i \left( k_x \, x +k_z \, z - \omega \, t \right) }, \nonumber \\&T (x,y,z,t)= T_b(y) + \varepsilon \, h(y) \, e^{\lambda \, t } e^{i \left( k_x \, x +k_z \, z - \omega \, t \right) } . \end{aligned}$$

(17)

Here, f and h are, in general, complex functions, $\lambda$ is the growth rate, $\mathbf {k}=(k_x,0,k_z)$ is the wave vector, $\omega$ is the angular frequency. By assuming that the disturbance amplitude is small, $\varepsilon \ll 1$, we perform a linear stability analysis where we consider only terms $O(\varepsilon )$. The aim of the forthcoming investigation is finding the threshold for the onset of thermal convection. This threshold is obtained when the neutrally stable modes are considered. These modes are characterised by null growth rate. Thus, from now on, $\lambda$ is set equal to zero. By substituting Eq. (17) into Eqs. (16), and by employing

$$\begin{aligned}&{\tilde{f}}=(1+{\tilde{\mathrm {El}}})\, f, \; \; \; \; {{\tilde{\mathrm {R}}}}=(1+{\tilde{\mathrm {El}}})\, \mathrm {R}, \; \; \;\; {{\tilde{\omega }}}=\omega -k \, \mathrm {Pe}, \nonumber \\&{\tilde{\mathrm {El}}}=\mathrm {El}\left| \frac{\partial {p_b}}{\partial {x}}\right| ^{\frac{1-n}{n}}, \quad k_x=k\, \cos \phi , \quad k_z=k\, \sin \phi , \nonumber \\&{\tilde{n}}=\dfrac{ {\tilde{\mathrm {El}}}+n\, ({\tilde{\mathrm {El}}}+2) +{\tilde{\mathrm {El}}}\, (1-n) \cos (2 \phi )}{2 \, n \, ({\tilde{\mathrm {El}}}+1) }, \end{aligned}$$

(18)

one obtains

$$\begin{aligned}&{\tilde{f}}''-{\tilde{n}} \, k^2\, {\tilde{f}}-{{\tilde{\mathrm {R}}}} \, h'=0, \end{aligned}$$

(19a)

$$\begin{aligned}&h''- \left( k^2- {\tilde{\mathrm {R}}}-i \, {{\tilde{\omega }}} \right) h-{\tilde{f}}'=0,\end{aligned}$$

(19b)

$$\begin{aligned}&y=0,1 : \qquad {\tilde{f}}'= 0, \quad h = 0, \end{aligned}$$

(19c)

where $\phi$ is the inclination angle between the wave vector and the x–axis. For $\phi =0$ the wave vector is parallel to the x–axis so that the rolls axes are perpendicular to the basic flow (transverse rolls). For $\phi =\pi /2$ the wave vector is parallel to the z–axis. In this case, the rolls axes are parallel to the basic flow (longitudinal rolls). In Appendix A, we prove analytically that ${{\tilde{\omega }}}=0$ and, hence, we conclude that the eigenvalue problem (19) features real eigenfunctions and eigenvalues. It is worth noting that the Péclet number is not present, at least explicitly, in Eqs. (19). The definition of the rescaled angular frequency is a classical practice (Barletta et al. 2009a, b) for this kind of problems proposed by Prats (1966). This procedure is equivalent to performing the stability analysis in the comoving reference frame.

On account of Eqs. (15) and (18), one may obtain $\mathrm {Pe}$ as a function of $\mathrm {El}$, ${{\tilde{\mathrm {El}}}}$ and n, namely

$$\begin{aligned} \mathrm {Pe}=\left( 1+{{\tilde{\mathrm {El}}}} \right) \left( \dfrac{{{\tilde{\mathrm {El}}}}}{\mathrm {El}} \right) ^{\frac{n}{1-n}} . \end{aligned}$$

(20)

Fig. 3

Neutral stability curves $\mathrm {R}(k)$ for $n=0.2$ and different values of ${\tilde{\mathrm {El}}}$

3 Results

The eigenvalue problem (19) is solved both numerically and analytically. The numerical procedure, reported in Appendix B, is employed for comparison with the results obtained analytically. We assume that ${\tilde{f}}$ and h are trigonometric functions satisfying the boundary conditions in Eq. (19c), namely

$$\begin{aligned} {\tilde{f}}=\cos (\ell \, \pi \, y), \qquad h=B_{\ell } \, \sin (\ell \, \pi \, y), \end{aligned}$$

(21)

where $\ell$ is a positive integer and $B_{\ell }$ is the constant. By employing Eqs. (18)–(21), one obtains the dispersion relation

$$\begin{aligned} \mathrm {R}=\dfrac{k^2+\pi ^2 \, \ell ^2}{({\tilde{\mathrm {El}}}+1)}+\dfrac{2\, \pi ^2 \,\ell ^2\, n \left( k^2+\pi ^2 \,\ell ^2\right) }{k^2 [{\tilde{\mathrm {El}}}\, (1-n) \cos (2 \phi )+{\tilde{\mathrm {El}}} \,(n+1)+2 \, n]}. \end{aligned}$$

(22)

The most relevant parametric configuration for the stability analysis is the one characterised by the lowest values of $\mathrm {R}$. It is worth noting that, in order to minimise the value of $\mathrm {R}$, the integer and positive parameter $\ell$ must be minimum, i.e. $\ell =1$. Moreover, by recalling that $0\leqslant \phi \leqslant \pi /2$, the minimum values of $\mathrm {R}$ are obtained for transverse rolls, $\phi =0$, since this angle minimises the contribution of the second term in the right–hand side of Eq. (22). Thus, at the onset of instability, Eq. (22) can be simplified to

$$\begin{aligned} \mathrm {R}=\dfrac{\left( k^2+\pi ^2\right) \left[ k^2 ({\tilde{\mathrm {El}}} +n)+n\, \pi ^2 \, ({\tilde{\mathrm {El}}} +1) \right] }{k^2 \,({\tilde{\mathrm {El}}} +1) ({\tilde{\mathrm {El}}} +n)}. \end{aligned}$$

(23)

Equation (23) allows one to draw the neutral stability curves presented in Fig. 3. This figure is obtained for the sample $n=0.2$ and different values of ${\tilde{\mathrm {El}}}$.

The absolute minimum of each neutral stability curve defines the parametric threshold for the onset of convective instability. The term “critical values” is employed to denote these threshold values of the governing parameters R and k. In order to obtain the critical values, we calculate through Eq. (23) the derivative of $\mathrm {R}$ with respect to k. Hence, the critical values are given by

$$\begin{aligned} \mathrm {R}_c=\frac{\pi ^2 }{1+{\tilde{\mathrm {El}}}}\Bigg \{\left[ \frac{n \,(1+{\tilde{\mathrm {El}}})}{n+{\tilde{\mathrm {El}}}}\right] ^{1/2}+1\Bigg \}^2, \qquad k_c=\pi \left[ \dfrac{n\, (1+{\tilde{\mathrm {El}}})}{n+{\tilde{\mathrm {El}}}}\right] ^{1/4}. \end{aligned}$$

(24)

The values of $\mathrm {R}_c$ and $k_c$ given by Eq. (24) are reported versus n in Fig. 4, for different values of ${\tilde{\mathrm {El}}}$. These critical values are shown to be monotonic decreasing functions of the parameter ${\tilde{\mathrm {El}}}$, while they are monotonic increasing functions of n. The four limiting cases ${\tilde{\mathrm {El}}} \rightarrow 0$, ${\tilde{\mathrm {El}}} \rightarrow \infty$ and $n\rightarrow 1$ deserve some particular attention.

Fig. 4

Critical values of $\mathrm {R}$ and k versus n for different values of ${\tilde{\mathrm {El}}}$

Fig. 5

Lines $p(x,y,z,0)=\textit{constant}$ (left frame) and lines $\theta (x,y,z,0)=\textit{constant}$ (right frame). The figure is obtained for $n=0.2$ and ${{\tilde{\mathrm {El}}}}=10$

3.1 Limiting Cases

On account of Eq. (18), the limit ${\tilde{\mathrm {El}}} \rightarrow 0$ can be obtained either for $\mathrm {El}\rightarrow 0$ with a finite nonzero $|\partial p_b/\partial x|$, or by letting $|\partial p_b/\partial x| \rightarrow 0$ with a finite nonzero $\mathrm {El}$. The limit $\mathrm {El}\rightarrow 0$ can be approximated by assuming a fluid with extremely small thermal diffusivity and/or apparent reference viscosity. The limiting case $|\partial p_b/\partial x| \rightarrow 0$ describes the classical Darcy–Bénard system. For a given value of n such that $0< n < 1$, in the limiting case ${\tilde{\mathrm {El}}} \rightarrow 0$, Eq. (24) simplifies to

$$\begin{aligned} \mathrm {R}_c=4 \, \pi ^2 , \qquad k_c= \pi . \end{aligned}$$

(25)

The critical values given by Eq. (25) coincide, as anticipated in Sect. 2.4,with those obtained by Prats (1966), by Horton and Rogers (1945), as well as by Lapwood (1948).

By employing Eq. (18), the limit ${\tilde{\mathrm {El}}} \rightarrow \infty$ yields either $\mathrm {El}\rightarrow \infty$ with a nonzero $|\partial p_b/\partial x|$, or $|\partial p_b/\partial x |\rightarrow \infty$ with a nonzero $\mathrm {El}$. The limit $\mathrm {El}\rightarrow \infty$ can be approximately obtained with an extremely viscous fluid having a large thermal diffusivity. The limiting case $|\partial p_b/\partial x| \rightarrow \infty$ describes a condition of infinite flow rate. For $0< n < 1$, in the limiting case ${\tilde{\mathrm {El}}} \rightarrow \infty$, Eq. (24) yields

$$\begin{aligned} \mathrm {R}_c=0, \qquad k_c=\pi \, n^{1/4}. \end{aligned}$$

(26)

These results coincide with those reported in Barletta and Nield (2011) for the limiting case $|\partial p_b/\partial x |\rightarrow \infty$.

For the limiting case $n \rightarrow 1$, Eq. (24) simplifies to

$$\begin{aligned} \mathrm {R}_c=2\, \pi ^2 , \qquad k_c= \pi . \end{aligned}$$

(27)

In fact, the definition of R, given by Eq. (13), involves the reference apparent viscosity $\eta _0$, while the viscosity of a Newtonian fluid in the limit $n\rightarrow 1$ is $\eta _0/2$ (see Eq. (1)). As a consequence, instead of obtaining the classical results $R_c=4 \pi ^2$, Eq. (24) yields $R_c=2\, \pi ^2$. We also point out that, from Eqs. (8), (13) and (18), ${\tilde{\mathrm {El}}}\rightarrow 1$ when $n\rightarrow 1$.

Fig. 6

Plots of $R_c/\pi ^2$ and $k_c/\pi$ versus the dimensional basic pressure drop $\varDelta p/L ~ [\mathrm{Pa/m}]$. We consider a porous layer with thickness $H=10^{-1}~\mathrm{m}$, permeability $K=10^{-9}{\mathrm{m}}^2$ and average pore diameter $D_p=10^{-5}~\mathrm{m}$ saturated by a polyacrylamide solution at room temperature (data taken from Park 1972 and Hirata et al. 1993)

Figure 6 displays plots of $R_c/\pi ^2$ and $k_c/\pi$ versus the dimensional pressure drop [Pa m] of the basic flow for a sample case involving a porous layer $10^{-1}~\mathrm{m}$ thick having permeability $10^{-9} ~{\mathrm{m}}^2$ and an average pore diameter of $10^{-5}~\mathrm{m}$. We devise a situation where the porous layer is saturated by a polyacrylamide solution at room temperature. The values of the thermophysical properties of the polyacrylamide solution are taken from Park (1972) and Hirata et al. (1993). This figure illustrates very clearly the asymptotic cases where the pressure drop tends to zero (Newtonian behaviour, Eq. (25)) or the pressure drop tends to infinity (power–law behaviour, Eq. (26)).

3.2 Shape of the Disturbances

Figure 5 displays the shape of the disturbances defined in Eq. (17). This figure is obtained by employing the critical wavenumber calculated for $n=0.2$ and ${{\tilde{\mathrm {El}}}}=10$ by means of Eq. (24), namely $k_c=\pi (11/51)^{1/4}$. The lines defined by $p(x,y,z,0)=\textit{constant}$ and the lines defined by $\theta (x,y,z,0)=\textit{constant}$ are plotted for a single period $2 \pi / k$. Since the shape of the disturbances does not depend on the values of n and ${{\tilde{\mathrm {El}}}}$, as one may infer from Eqs. (17) and (21), only one case has been reported. Figure 5 refers to transverse rolls, $\phi =0$, and thus it is plotted on the plane (x, y).

4 Conclusions

The onset of convective instability inside a horizontal porous layer saturated by a non-Newtonian fluid has been investigated. The fluid is shear–thinning and its apparent viscosity is defined by the Ellis model. The layer is heated from below and a basic horizontal pressure gradient is assumed. A linear stability analysis has been performed by means of the normal mode method. The governing parameters are the Darcy–Rayleigh number, $\mathrm {R}$, the modified Darcy–Ellis number, ${{\tilde{\mathrm {El}}}}$, and the Ellis power–law index, n. The modified Darcy–Ellis number is a function of the Péclet number associated with the basic flow rate, of the Ellis number and of the Ellis power–law index. The main conclusions drawn from the stability analysis are the following:

• The critical values of the governing parameters can be expressed analytically as functions of n and ${{\tilde{\mathrm {El}}}}$.

• The most unstable rolls are transverse, having their axes perpendicular to the direction of the basic throughflow.

• The angular frequency of the transverse rolls is equal to the product between the wavenumber and the Péclet number. Such rolls are non–travelling in the reference frame comoving with the basic throughflow.

• For ${{\tilde{\mathrm {El}}}}\rightarrow 0$, the critical value of the Darcy–Rayleigh number tends to $4 \pi ^2$ while the wavenumber approaches $\pi$. This limiting case identifies those configurations where the basic pressure gradient is absent and/or the fluid is Newtonian. The critical values of the governing parameters match those found in the literature for either the Prats problem or the Horton–Rogers–Lapwood problem.

• For ${{\tilde{\mathrm {El}}}}\rightarrow \infty$, the critical value of the Darcy–Rayleigh number tends to zero and the wavenumber tends to $\pi \, n^{1/4}$. This limiting case identifies those configurations where the basic pressure gradient is extremely intense and/or the fluid is strongly shear–thinning. In other words, for this parametric configurations, a fluid characterised by an extremely low apparent viscosity is considered and thus a negligibly small temperature gap between the horizontal boundaries is sufficient to trigger the onset of convection.

• The parameters ${\tilde{\mathrm {El}}}$ and n play different roles: as ${\tilde{\mathrm {El}}}$ increases we have a destabilising effect on the basic state, while as n increases we have a stabilising effect.

We finally point out that our study has been based on the Ellis model for the fluid rheology in order to encompass the singular behaviour of the simpler power–law model. In particular, as pointed out in Barletta and Nield (2011), the use of the power–law model leads to the prediction of an either zero or infinite critical value of the Darcy–Rayleigh number when the flow rate in the basic state is zero. On the other hand, when the basic flow rate tends to zero, the use of the Ellis model leads to a non–singular behaviour where the same critical value of the Darcy–Rayleigh number as predicted for the case of a Newtonian fluid, namely $4\,\pi ^2$, is attained.

Appendices

Appendix A. Proof that ${{\tilde{\omega }}}=0$

One can multiply Eq. (19a) by ${\tilde{f}}^*$, that is the complex conjugate of the eigenfunction ${\tilde{f}}$, and integrate by parts over the domain $y \in (0,1)$ to obtain

$$\begin{aligned} \int _0^1 |{\tilde{f}}'|^2 \, \mathrm {d}y+k^2\, {\tilde{n}} \, \int _0^1|{\tilde{f}}|^2 \, \mathrm {d}y+{{\tilde{\mathrm {R}}}}\int _0^1 h' {\tilde{f}}^* \, \mathrm {d}y=0. \end{aligned}$$

(28)

From Eq. (28), one may conclude that the last integral on the left hand side is real. By taking the complex conjugate of this integral and, on integrating it by parts, one concludes that

$$\begin{aligned} \int _0^1 {\tilde{f}}' h^* \, \mathrm {d}y \end{aligned}$$

(29)

is real. This result will be invoked later on. One can now multiply Eq. (19b) by $h^*$, that is the complex conjugate of the eigenfunction h, and integrate by parts over the domain $y \in (0,1)$ to obtain

$$\begin{aligned} \int _0^1 |h'|^2 \, \mathrm {d}y+\left( k^2-{\tilde{\mathrm {R}}}-i \, {{\tilde{\omega }}} \right) \int _0^1 |h|^2 \, \mathrm {d}y+ \int _0^1 {\tilde{f}}' h^* \, \mathrm {d}y=0. \end{aligned}$$

(30)

By employing Eq. (29), one may infer that the imaginary part of Eq. (30) is

$$\begin{aligned} {{\tilde{\omega }}} \int _0^1 |h|^2 \, \mathrm {d}y=0. \end{aligned}$$

(31)

Equation (31) implies either ${{\tilde{\omega }}}=0$ or $h={\tilde{f}}=0$. Since the trivial solution $h={\tilde{f}}=0$ is not acceptable, one may conclude that ${{\tilde{\omega }}}=0$.

Appendix B. Numerical Method

The numerical method employed to solve the stability eigenvalue problem is the shooting method. The first step consists in defining (and solving) the initial value problem obtained from Eqs. (19) simplified as a consequence of the results reported in Appendix A, namely

$$\begin{aligned}&{\tilde{f}}''-{\tilde{n}} \, k^2\, {\tilde{f}}-{{\tilde{\mathrm {R}}}} h'=0,\nonumber \\&h''- \left( k^2- {\tilde{\mathrm {R}}} \right) h-{\tilde{f}}'=0,\nonumber \\&{\tilde{f}}(0)=1, \quad {\tilde{f}}'(0)= 0, \quad h(0) = 0,\quad h'(0)=\xi . \end{aligned}$$

(32)

Here, the condition ${\tilde{f}}(0)=1$ can be imposed because the governing equations in Eq. (32) are homogeneous, while $\xi$ is an unknown real parameter. The problem (32) is solved numerically by means of the Runge–Kutta method. The obtained eigenfunctions ${\tilde{f}}$ and h depend on four governing parameters, $(k,{\tilde{n}}, {{\tilde{\mathrm {R}}}},\xi )$.

The second step of the shooting method is based on the target conditions

$$\begin{aligned} {\tilde{f}}'(1)= 0, \quad h(1) = 0 . \end{aligned}$$

(33)

Such conditions serve to obtain numerically, by employing a root–finding algorithm, two out of the four governing parameters $(k,{\tilde{n}},{{\tilde{\mathrm {R}}}},\xi )$. Thus, for every given ${\tilde{n}}$, one obtains the neutral stability curve ${{\tilde{\mathrm {R}}}}(k)$.

The critical values are obtained by solving the initial value problem given by Eq. (32) and the derivative with respect to k of Eq. (32). The conditions employed in the root–finding algorithm are the two conditions given by Eq. (33) together with their derivatives with respect to k.

A comparison between the results obtained analytically and those obtained numerically is reported in Table 2. The critical values of the wavenumber k and the critical values of $\mathrm {R}$, both evaluated for $n=0.2$, $\phi =0$ and different values of ${\tilde{\mathrm {El}}}$, are provided in this table. The subscript a refers to the data obtained analytically, while the subscript n is relative to the numerical data. The results obtained by employing these two different approaches coincide within 12 significant figures.

Table 2 Critical values of $\mathrm {R}$ and k for $n=0.2$, $\phi =0$, and different values of ${\tilde{\mathrm {El}}}$. The subscript a identifies those solutions obtained analytically while subscript n identifies those solutions obtained numerically